Hyperfine structure-tunneling coupling in trans-1,2-cyclohexanediamine revealed by rotational spectroscopy†
L. H.
Coudert
 *a,
Fan
Xie‡
b and
Melanie
Schnell
*a,
Fan
Xie‡
b and
Melanie
Schnell
 b
b
aUniversité Paris-Saclay, CNRS, Institut des Sciences Moléculaires d'Orsay, 91405 Orsay, France. E-mail: laurent.coudert@cnrs.fr
bDeutsches Elektronen-Synchrotron DESY, 22607 Hamburg, Germany. E-mail: fan.xie@desy.de
First published on 15th April 2025
Abstract
The microwave spectrum of the non-rigid trans-cyclohexanediamine (C6H10(NH2)2) is investigated. It displays a large amplitude interconversion motion during which both amino groups are rotated through 117° leading to tunneling splittings on the order of 21 MHz and line splittings on the order of 42 MHz for b- and c-type transitions. The tunneling is mediated by the quadrupole coupling hyperfine structure arising from both nitrogen atoms which leads to splittings on the same order of magnitude. The frequencies of the rotation-tunneling-hyperfine transitions are analyzed using a new theoretical model in which the large amplitude motion and the quadrupole coupling are treated simultaneously. Hyperfine matrix elements between (within) tunneling sublevels depend on the difference (sum) of the quadrupole coupling of the two nitrogen atoms. Using the theoretical formalism, 249 experimental frequencies are reproduced with an RMS value of 10 kHz, close to the experimental uncertainty. The spectroscopic parameters determined include usual rotational and distortion parameters; tunneling parameters describing the magnitude of the tunneling and its rotational dependence; and various components of the effective quadrupole coupling tensors.
1 Introduction
Molecules displaying both a large amplitude motion and a hyperfine coupling have been the subject of many high-resolution spectroscopic investigations. These species are best exemplified by the non-rigid ammonia molecule where hyperfine splittings were first observed in 19461 and modeled with a kilohertz accuracy less than 10 years later.2 Non-rigid molecules where the atoms giving rise to the hyperfine coupling are exchanged by a large amplitude motion are not so numerous and are slightly more difficult to model. In the non-rigid hydrazine molecule (N2H4), the large amplitude motions3,4 exchange the two equivalent nitrogen atoms responsible for the quadrupole coupling which leads to a hyperfine structure strongly dependent on the symmetry species of the tunneling sublevels.5 In triply deuterated acetaldehyde (CD3COH), the large amplitude torsional motion6 exchanges the three equivalent deuterium atoms giving rise to the quadrupole coupling, and this leads to a hyperfine structure depending on the A and E torsional symmetry of the rotation–torsion energy levels.7 In non-rigid dinitrogen pentoxide (N2O5), displaying internal rotations of its two nitro groups giving rise to large torsional splittings, an averaging of the quadrupole coupling of the two equivalent nitrogen atoms takes place, but the dependence of the corresponding coupling constants on the rotational and torsional quantum numbers8,9 is not yet understood.Trans-1,2-cyclohexanediamine (C6H10(NH2)2), depicted in Fig. 1, is a non-rigid species displaying an internal hydrogen bond between its two amino groups and a prominent quadrupole coupling hyperfine structure arising from its two equivalent nitrogen atoms. The large amplitude interconversion motion displayed by this molecule is a concerted torsion of these two amino groups during which the donor group becomes the acceptor group and vice versa. Like in hydrazine, triply deuterated acetaldehyde, and dinitrogen pentoxide,5,7,8 the large amplitude motion exchanges the atoms giving rise to the hyperfine coupling. However, trans-1,2-cyclohexanediamine (CDA) is of greater theoretical interest because the tunneling splitting and the hyperfine coupling are of similar magnitude. The former is on the order of 20 MHz while the latter gives rise to splittings ranging from 0 to 5 MHz. For this reason, unlike in the aforementioned molecules,5,7,8 hyperfine coupling effects need to be evaluated within as well as between tunneling sublevels.
The microwave spectrum of CDA is experimentally and theoretically investigated in this paper. Its centimeter wave rotational-tunneling spectrum is recorded using a chirped-pulse Fourier transform microwave (CP-FTMW) spectrometer.10 The rotational-tunneling spectrum of the lowest lying conformer is analyzed with a new theoretical approach where the hyperfine coupling and the tunneling motion are treated simultaneously. It is found that non-diagonal hyperfine coupling matrix elements between different tunneling states are key to reproduce the experimental frequencies within experimental uncertainties.
2 Experimental method
The COMPACT (compact-passage-acquired coherence-technique) spectrometer10 was used to measure the rotational spectrum of CDA in the 2–8 and 8–12 GHz frequency ranges. The instrument's principle and settings have been previously published,10 and a brief overview is provided here. Racemic samples of CDA with a purity of 98% purchased from Sigma-Aldrich were used without additional purification. The samples were heated to 40 °C to increase their vapor pressure and were then mixed with neon carrier gas at a backing pressure of 3 bars. The gas mixture was expanded supersonically into the spectrometer's vacuum chamber at 6 Hz via a pulse valve. Fast frame memory transfer was applied during averaging to obtain 8 measurements per gas pulse, leading to an effective repetition rate of 48 Hz. The nominal duration of each molecular pulse was about 500 μs. The free induction decay (FID) in the time domain was collected for 40 μs for each measurement after excitation, and about 4 million FID acquisitions were averaged. The time-domain signal was processed with a Kaiser window function (σ = 9.5) and zero padding, and finally employing the fast Fourier transformation (FFT) algorithm to obtain the spectrum in the frequency domain. The final spectral resolution achieved was 25 kHz at an experimental uncertainty for the line frequency of 10 kHz. The assignment of the spectrum is described in Section 5.3 Potential energy surface and configurations
The atom numbering chosen for CDA is defined in Fig. 1 which also shows the two angles describing the large amplitude motion, the dihedral angles τ1 = ∠H5N1C7C8 and τ2 = ∠H6N2C8C7. The conformers of CDA were searched for along these angles, scanning the relaxed potential energy surface (PES) calculated at the B3LYP-D3(BJ)/def2-TZVP level of theory with the ORCA computational package.11–13 This surface is plotted in Fig. 2 and displays at least eight stationary points (ST). The lowest lying ones include five minima and three saddle points. Their coordinates τ1 and τ2, their energy, and their rotational constants are listed in Table 1. Due to the symmetry of the PES about the τ1 = τ2 diagonal, several ST are energetically equivalent and characterized by the same rotational constants. The energetically equivalent minima, numbered 1 and 2, correspond to the lowest lying conformer which will be named M1; the energetically equivalent minima numbered 4 and 5 correspond to the higher lying M2 conformer, 67 cm−1 above the previous one.| ST | 1 | 2 | 3 | 4 | 5 | S1 | S2 | S3 |
|---|---|---|---|---|---|---|---|---|
| τ 1 | 310.1 | 193.0 | 283.9 | 190.3 | 74.0 | 298.1 | 245.4 | 156.0 |
| τ 2 | 193.0 | 310.1 | 283.9 | 74.0 | 190.3 | 245.4 | 298.1 | 156.0 |
| E | 0 | 253 | 67 | 439 | 1234 | |||
| A | 2743 | 2739 | 2713 | 2735 | 2759 | |||
| B | 1922 | 1940 | 1923 | 1930 | 1913 | |||
| C | 1226 | 1223 | 1223 | 1222 | 1222 | |||
Table 1 emphasizes that the most feasible large amplitude motion is the interconversion motion connecting minima 1 and 2. This large amplitude motion is indeed characterized by a low barrier of only 439 cm−1. The corresponding tunneling path goes through saddle point S1, minimum 3, and saddle point S2, and is plotted in Fig. S1 of the ESI.† Another interconversion motion, connecting minima 4 and 5, goes through saddle point S3 and is characterized by a higher barrier of 1234 cm−1.
4 Theoretical modeling
Tunneling effects are modeled with an internal axis method14,15 (IAM) which accounts for the rotational dependence of the tunneling splitting due to the Coriolis coupling between the large amplitude motion and the overall rotation. This IAM approach is well suited in the high barrier limit and allows us to derive an effective rotation-tunneling fitting Hamiltonian. Since this IAM approach has already been applied by Christen et al.16,17 to the fitting of the microwave spectrum of glycol, a molecule analogous to CDA also displaying a large amplitude interconversion motion, most of the results of these authors are used in the present investigation. The modeling of the hyperfine structure, which has not been carried out by Christen et al., is also presented below.4.1 Coordinate system and tunneling path
The equation relating the space-fixed Cartesian coordinates to a set of molecule-fixed reference coordinates is| Ri = R + S−1(χ, θ, ϕ)·[ai(τ1, τ2) + di], i = 1 to 22, | (1) |
The three important configurations for the large amplitude interconversion motion are shown in Fig. 3. Configurations 1 and 2 correspond respectively to the minima 1 and 2 described in Section 3; the intermediate configuration, corresponding to minimum 3, displays a 2-fold axis of symmetry parallel to the molecule-fixed y axis. The equilibrium values of τ1 and τ2 describing Configuration 1 will be denoted τeq1 and τeq2 and are given in Table 1. The symmetry group to be used for the present tunneling problem is the permutation inversion symmetry group G2 isomorphic to the C2 point group.16 The character table of this group along with the effects of the symmetry operation on the large amplitude coordinates τ1 and τ2, and on the Eulerian angles can be found in Table III of Christen et al.16 where the permutation operation (01)(23)(45)(67)(89) should be changed into (12)(34)(56)(78) and the coordinates ζ1, ζ2 into τ1, τ2 for this work.
 | ||
| Fig. 3 The two nonsuperimposable equilibrium configurations of CDA, numbered 1 and 2, which are connected by the large amplitude interconversion motion. The intermediate configuration for this tunneling motion is also drawn. The color coding of the amino groups' hydrogen atoms is the same as for Fig. 1(b). H3, H4, H5, and H6 are drawn in green, blue, yellow and red, respectively. The molecule-fixed xyz axis system is shown at the bottom center of the figure. | ||
In agreement with the IAM treatment,14,15 the Eulerian-type angles χ2, θ2, ϕ2 describing the rotational dependence of the tunneling splitting are determined solving eqn (33) of Hougen.14 The tunneling path retrieved in Section 3 and drawn in Fig. S1 of the ESI,† is used. It is parameterized with the coordinate η such that −1 ≤ η ≤ + 1, η = −1 at Configuration 1, η = 0 at the Intermediate Configuration, and η = +1 at Configuration 2. The parameterization of all internal coordinates in terms of η is given in Section S1 of the ESI.† Numerically solving eqn (33) of Hougen14 yields χ2 = 269.094°, θ2 = 0.577°, and ϕ2 = 89.094°. The 180° difference between χ2 and ϕ2 was theoretically substantiated in Christen et al.16 and arises because of the nature of the tunneling problem and because of the way the molecule-fixed xyz axis system is attached to the molecule.
4.2 Rotation-tunneling Hamiltonian
A fitting rotation-tunneling Hamiltonian HRT is derived using the IAM approach described in Section 4.C of Christen et al.16 Like these authors, we use the framework wavefunctions of Configurations 1 and 2, ΨJKα1 and ΨJKα2, which are defined in their eqn (6). These wavefunctions are identified by a configuration number and depend on the rotational quantum numbers JKα describing the Wang-type rotational functions introduced in eqn (5) of Christen et al.16 Their rotational symmetry species ΓR is A and B when α(−1)J+K is +1 and −1, respectively. The framework wavefunctions are used to evaluate non-tunneling and tunneling matrix elements of the Hamiltonian. The non-tunneling matrix elements, HJK′α′1;JK′′α′′1 and HJK′α′2;JK′′α′′2, are the matrix elements of the rotational Hamiltonian HR. Since the IIr representation is used in the present investigation instead of the Ir as in Christen et al.,16 the rotational Hamiltonian should be rewritten as: | (2) |
The Hamiltonian can be block-diagonalized using the symmetry-adapted ΨvJKα rovibrational wavefunctions defined in eqn (11) of Christen et al.16 which are characterized by the rotational quantum numbers JKα and the quantum number v which is 0 or 1. Their symmetry species is ΓS = ΓR ⊗ Γv, where Γv = A and B when v = 0 and 1, respectively. Hamiltonian matrix elements between two such wavefunctions,  , are given in eqn (12) and (13) of Christen et al.16 for Δv = v′ − v′′ = 0 and ±1, respectively. In the limit of a slow rotational dependence of the tunneling splitting, when θ2 ≈ 0 and ϕ2 ≈ π/2, the Δv = ±1 matrix elements of the Hamiltonian vanish, v becomes the actual tunneling quantum number as emphasized by eqn (16) of Christen et al.,16 and the tunneling splitting is 2|h2|.
, are given in eqn (12) and (13) of Christen et al.16 for Δv = v′ − v′′ = 0 and ±1, respectively. In the limit of a slow rotational dependence of the tunneling splitting, when θ2 ≈ 0 and ϕ2 ≈ π/2, the Δv = ±1 matrix elements of the Hamiltonian vanish, v becomes the actual tunneling quantum number as emphasized by eqn (16) of Christen et al.,16 and the tunneling splitting is 2|h2|.
Rotation-tunneling energies are calculated considering a Hamiltonian matrix setup with symmetry-adapted basis set wavefunctions characterized by either ΓS = A or B. The resulting energy levels are assigned with the usual rotational quantum numbers JKaKc and the tunneling quantum number v; their eigenfunction can be obtained from eqn (15) of Christen et al.16 rewritten below for completeness:
 | (3) |
In accordance with symmetry considerations, the selection rules for a-type lines are Δv = 0, and for b- and c-type lines, Δv = ±1. This means that a-type lines consist of two nearly overlapped tunneling components while b- and c-type lines consist of two tunneling components separated by twice the tunneling splitting.
4.3 Hyperfine coupling Hamiltonian
The equivalent operator used for ΔJ = 0 matrix elements of the quadrupole coupling hyperfine Hamiltonian is written:20,21 | (4) |
| Cy(π)·χ1(τ2, τ1)·Cy(π) = χ2(τ1, τ2), | (5) |
| HQ = H+QO+R + H−QO−R, | (6) |
 | (7) |
The operators H±Q and O±R belong to the G2 symmetry species A and B for the upper and lower sign, respectively. The |(I1I2)IJF〉 hyperfine wavefunctions are used and correspond to the coupling scheme:
I1 + I2 = I ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and and![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I + J = F, I + J = F, | (8) |
| |I, JKαv, FMF〉, | (9) |
 | (10) |
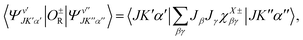 | (11) |
 | (12) |
| χ± = 〈Φ1|χ1 ± χ2|Φ1〉 ≈ χ1(τeq1, τeq2) ± χ2(τeq1, τeq2), | (13) |
 | (14) |
The matrix elements of the symmetry adapted hyperfine operators H±Q in eqn (10) should be computed using eqn (2)–(8) of Robinson and Cornwell.22 The ΔI = I′ − I′′ = 0, ±2 matrix elements of H+Q should be obtained from their eqn (6) and (8) where X+ should be set to 1; the ΔI = ±1 matrix elements of H−Q should be obtained from their eqn (7) where the product X−R should also be set to 1. In both cases, the result should be divided by (J + 1)(2J + 3)/2 because the Casimir's function used in the present paper is not defined in the same way as in Robinson and Cornwell.22
The dominant contribution in eqn (10) arises from the tensor χS± displaying diagonal K′ = K′′ and α′ = α′′ rotational matrix elements. Therefore, in eqn (11), the largest |Δv| = 0 and 1 hyperfine matrix elements involve χS+ and χS−, respectively. This means that matrix elements within (between) tunneling sublevels depend mainly on the sum (difference) of the quadrupole coupling of the two nitrogen atoms.
4.4 Rotation-tunneling-hyperfine energy levels
Hyperfine energies are calculated for given values of the total angular momentum F, of the rotational angular momentum J, and of the rotation-tunneling-hyperfine symmetry species ΓRH. The matrix of HRT + HQ is set up using as basis functions the rotation-tunneling-hyperfine wavefunctions |I, JKaKc, v, FMF〉 which with the help of eqn (3) are expressed in terms of the symmetry-adapted rovibrational-hyperfine wavefunctions of eqn (9) as: | (15) |
The 2(2J + 1) rotational-tunneling levels arising for a given J-value are associated with hyperfine functions characterized by I = 0, 1, and 2 so that the basis set functions in this equation belong to the selected ΓRH symmetry species. With these basis set functions, the matrix of HRT is diagonal, with diagonal matrix elements equal to the rotation-tunneling energy, and the matrix of the hyperfine Hamiltonian HQ should be obtained from eqn (10). Diagonalization of the HRT + HQ matrix yields hyperfine energies that can be assigned with F and with I, although the latter is no longer a good quantum number, and with the rotation-tunneling quantum numbers JKaKc and v.
The results of the present approach are illustrated in the case of the hyperfine structure of the two tunneling components of the 101 ← 000 transition. Hyperfine levels are calculated using the rotational constants in Table 1, the values of θ2 and ϕ2 reported in Section 4.1, and the effective quadrupole coupling constants in Table 2. For the upper level, the hyperfine Hamiltonian matrices involve the six rotation-tunneling levels JKaKc,v with JKaKc = 101, 111, and 110; and v = 0 and 1. For the lower level, only two rotation-tunneling levels are involved with JKaKc = 000 and v = 0 and 1. The relative line intensities of hyperfine components were computed with the results of Cook and De Lucia.23 Several values of the tunneling parameter h2 ranging from 0 to −3 MHz were considered and the corresponding stick spectra are shown in Fig. 4. This figure emphasizes that the present approach leads to a fast variation of the hyperfine structure with the tunneling parameter h2. When h2 = 0, the molecule displays no tunneling and the hyperfine structure is that of a rigid molecule with two inequivalent nitrogen atoms. The hyperfine structure displays transitions with ΔI even and odd. For h2 = −3 MHz, the hyperfine structure is that of a molecule with two equivalent nitrogen atoms dominated by hyperfine components with ΔI even. The calculated frequencies of the two tunneling components are 3148.0008 and 3147.9992 MHz for v = 0 and 1, respectively, leading to a very small line splitting of only 1.6 kHz which cannot be seen with the scale of Fig. 4.
| N 1 | N 2 | N 1 | N 2 | ||
|---|---|---|---|---|---|
| χ xx | −4.555 | 2.210 | χ xy | −1.183 | 0.967 |
| χ yy | 2.334 | −1.876 | χ xz | 1.157 | 0.498 |
| χ zz | 2.221 | −0.334 | χ yz | 0.680 | −3.742 |
5 Line frequency analysis
The experimental spectrum was assigned starting from the rotational constants in Table 1. Ignoring the hyperfine structure, transitions were assigned in terms of rotational and tunneling quantum numbers. A preliminary line frequency analysis was carried out where the rotational-tunneling parameters were varied except for θ2 and ϕ2 which were constrained to the values computed in Section 4.1. The lines were then assigned in terms of hyperfine quantum numbers predicting their hyperfine pattern with the approach described in Section 4.4 and setting the effective quadrupole coupling constants to the values in Table 2. When enough hyperfine lines were assigned, another line frequency analysis was carried out where the hyperfine parameters were varied in addition to the rotational-tunneling parameters. This enabled us to identify additional hyperfine lines. A total of 249 hyperfine components were thus assigned up to J = 3 and Ka = 2.In the final analysis, line frequencies were least-squares fitted to the rotation-tunneling and hyperfine parameters introduced in Section 4, computing the rotation-tunneling-hyperfine energies with the approach described in Section 4.4. Lines were given a weight equal to the inverse of their experimental uncertainty squared. Instead of the diagonal components of the tensors χ±, defined in eqn (14), the following hyperfine parameters were used:
| χ± = (χ±xx − χ±yy)/2 and χ±z = 3/2χ±zz. | (16) |
All three diagonal components can be obtained from these equations remembering that the relation χ±xx + χ±yy + χ±zz = 0 holds.
The unitless standard deviation of the analysis was 1 and the root mean square deviation of the observed minus calculated residuals was 10 kHz. Table S1 of the ESI,† reports assignments, observed frequencies, and residuals. Inspection of this table shows that the largest residual is 33.5 kHz for the F = 1, I = 2 ← 1, 0 hyperfine component of the 212, 0 ← 101, 1 rotational-tunneling transition at 6386.7041 MHz.
Table 3 reports the fitted spectroscopic parameters. The rotation-tunneling parameter ϕ2 was constrained to the value computed in Section 4.1 and the hyperfine parameters χ+xz, χ+xy, χ+yz, χ−xz, χ−xy, and χ−yz, to those reported in Table 2. Table 3 shows that there is a very good agreement between fitted and calculated values for the rotational constants as the discrepancies are at most 9 MHz. A very satisfactory agreement also arises for the hyperfine parameters χ+ and χ+z for which the differences are less than 0.33 MHz. For the hyperfine parameters χ− and χ−z, the agreement is less satisfactory and this may be due to the fact that they are involved in non-diagonal matrix elements, as emphasized by eqn (10). For b- and c-type transitions, Fig. 5 of the paper and Fig. S2 and S3 of the ESI,† show comparisons between the observed spectrum and a spectrum computed from the results of the line frequency analysis. A fairly good agreement between observed and calculated spectra can be seen.
| Parametera | Analysisb | Calculatedc |
|---|---|---|
| a Parameters are defined in Sections 4.2, 4.3 and 5. 249 hyperfine transitions were reproduced with a root mean square deviation of 10 kHz. b In MHz except for θ2 and ϕ2 which are in degrees. c Calculated value when available. d Constrained value (see text). | ||
| h 2 | −10.573(1) | |
| θ 2 | 1.311(27) | 0.577 |
| ϕ 2 | 89.094d | |
| A | 2734.155(1) | 2743 |
| B | 1918.930(3) | 1922 |
| C | 1224.707(1) | 1226 |
| D K × 103 | 8.898(3300) | |
| D KJ × 103 | −10.532(3800) | |
| D J × 103 | 1.889(650) | |
| d 2 × 103 | 0.876(320) | |
| χ + | −1.409(4) | −1.401 |
| χ + z | 2.492(8) | 2.830 |
| χ + xz | 0.828d | |
| χ + xy | −0.108d | |
| χ + yz | −1.531d | |
| χ − | 4.722(57) | 5.488 |
| χ − z | −2.366(200) | −3.832 |
| χ − xz | −0.329d | |
| χ − xy | 1.075d | |
| χ − yz | −2.211d | |
 | ||
| Fig. 5 Comparisons between the observed spectrum and a calculated stick spectrum for the 110, 1 ← 000, 0 and 110, 0 ← 000, 1 transitions. Both spectra are plotted as a function of the frequency in MHz. The lists of predicted hyperfine transitions are given in Table S2 of the ESI.† | ||
6 Discussion
Cyclohexane is a benchmark molecule for the ring inversion (or ring puckering) large amplitude motion24 which allows the molecule to interconvert among its low lying D3d chair conformations and its higher lying C2v boat conformations overcoming a barrier with a height25 of about 8600 cm−1. The effects of this large amplitude motion can be observed using NMR spectroscopy,26 but they cannot be studied using microwave spectroscopy as cyclohexane has no dipole moment. Several mono- and bisubstituted species of cyclohexane do display a dipole moment and their microwave spectrum have been investigated.27,28 However, in these species, the large amplitude inversion motion does not take place as the two chair configurations are no longer energetically equivalent. This result also applies for the molecule investigated in this paper. It does, however, display two energetically equivalent configurations due to another large amplitude motion which is a concerted rotation of both amino groups.In this paper, the microwave spectrum of CDA has been recorded in the 2 to 12 GHz frequency range and analyzed using a new theoretical approach developed to account for both its large amplitude interconversion motion and its quadrupole coupling hyperfine structure. CDA is unusual from the spectroscopic point of view in that the effects of the large amplitude motion and those of the hyperfine quadrupole coupling are of the same order of magnitude. This leads to new effects, not observed in spectroscopic investigations of similar species,5,7,8 which in the new theoretical approach are described by matrix elements, given in eqn (10), of the quadrupole coupling Hamiltonian between rotational-tunneling levels split by the large amplitude motion.
The results of the line frequency analysis of the new microwave data are satisfactory as evidenced by an unitless standard deviation of 1. Fig. 5 of the paper and Fig. S2 and S3 of the ESI,† emphasize that there remain a few discrepancies between observed and calculated hyperfine patterns. These may be due to the neglect of the magnetic spin-rotation and spin–spin hyperfine couplings.29,30 Also, in a heavy molecule like CDA, low energy small amplitude vibrational modes may also prevent treating the ground vibrational state as an isolated state. The ab initio calculations carried out in this work yield a vibrational frequency of only 129 cm−1 for the lowest energy vibrational mode which, like in the parent species cyclohexane,31 is a skeletal mode involving mainly the carbon atoms.
An interesting outcome of the present investigation is shown in Fig. 6 where observed and calculated hyperfine patterns are shown for the 110, v ← 000, v, with v = 0 and 1, nearly overlapped rotation-tunneling transitions. Although both transitions are forbidden, the weak strength of their hyperfine components comes from the mixing between rotation-tunneling levels due to the hyperfine coupling Hamiltonian. In order to be compatible with the symmetry of the molecule, these hyperfine components are characterized by ΔI odd.
 | ||
| Fig. 6 Comparisons between the observed spectrum and a calculated stick spectrum, plotted as a function of the frequency in MHz, for the hyperfine structure of the transitions 110, v ← 000, v, with v = 0 and 1. These transitions being forbidden, their hyperfine components gain strength through mixings due to the hyperfine coupling Hamiltonian. The lists of predicted hyperfine transitions are given in Table S2 of the ESI.† | ||
The matrix elements of the hyperfine Hamiltonian between rotational-tunneling levels split by the tunneling motion are described, in agreement with eqn (10), by the tensors χS− and χA− of eqn (14) which give rise to the hyperfine parameters χ−, χ−z, χ−xz, χ−xy, and χ−yz. Setting these five parameters to zero amounts to neglecting matrix elements of the hyperfine Hamiltonian between rotational-tunneling levels split by the tunneling motion. This is the large tunneling splitting limit which leads to a much less satisfactory RMS value of 34 kHz and does not allow us to predict the forbidden transitions shown in Fig. 6. In this limit, the fitting Hamiltonian can be shown to be equivalent to an SPFIT fitting32 with one set of rotational and distortion constants for each tunneling sublevels along with a tunneling splitting, a Coriolis coupling term in Fab, and quadrupole coupling constants equal to the average of those of the two nitrogen atoms.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support by the Deutsche Forschungsgemeinschaft in the context of the priority program SPP1807. F. X. acknowledges the support of the Alexander von Humboldt postdoctoral fellowship and of the 100 Talents Project of Chinese Academy of Sciences.Notes and references
- W. E. Good, Phys. Rev., 1946, 70, 213–218 CrossRef CAS.
- J. P. Gordon, Phys. Rev., 1955, 99, 1253–1263 CrossRef CAS.
- J. T. Hougen, J. Mol. Spectrosc., 1981, 89, 296–327 CrossRef CAS.
- S. Tsunekawa, T. Kojima and J. T. Hougen, J. Mol. Spectrosc., 1982, 95, 133–152 CrossRef CAS.
- L. H. Coudert, J. T. Hougen and R. D. Suenram, J. Mol. Spectrosc., 1989, 135, 314–333 CrossRef CAS.
- C. C. Lin and J. B. Swalen, Rev. Mod. Phys., 1959, 31, 841–892 CrossRef CAS.
- L. H. Coudert and J. C. López, J. Mol. Spectrosc., 2006, 239, 135–145 CrossRef CAS.
- J.-U. Grabow, A. M. Andrews, G. T. Fraser, K. K. Irikura, R. D. Suenram, F. J. Lovas, W. J. Lafferty and J. L. Domenech, J. Chem. Phys., 1996, 105, 7249–7262 CrossRef CAS.
- J. L. Domenech, G. T. Fraser, A. R. Hight Walker, W. J. Lafferty and R. D. Suenram, J. Mol. Spectrosc., 1997, 184, 172–176 CrossRef CAS.
- D. Schmitz, V. A. Shubert, T. Betz and M. Schnell, J. Mol. Spectrosc., 2012, 280, 77–84 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- J. T. Hougen, J. Mol. Spectrosc., 1985, 114, 395–426 CrossRef CAS.
- L. H. Coudert and J. T. Hougen, J. Mol. Spectrosc., 1988, 130, 86–119 CrossRef CAS.
- D. Christen, L. H. Coudert, R. D. Suenram and F. J. Lovas, J. Mol. Spectrosc., 1995, 172, 57–77 CrossRef CAS.
- D. Christen, L. H. Coudert, J. A. Larsson and D. Cremer, J. Mol. Spectrosc., 2001, 205, 185–196 CrossRef CAS PubMed.
- D. Papoušek and M. R. Aliev, Molecular vibrational-rotational spectra, Elsevier Scientific, The Netherlands, 1982 Search PubMed.
- J. K. G. Watson, Vibrational Spectra and Structure, Elsevier, Amsterdam, 1977, vol. 6, pp. 1–89 Search PubMed.
- C. H. Townes and A. L. Schawlow, Microwave Spectroscopy, McGraw-Hill, New York, 1955 Search PubMed.
- M. R. Aliev and J. T. Hougen, J. Mol. Spectrosc., 1984, 106, 110–123 CrossRef CAS.
- G. W. Robinson and C. D. Cornwell, J. Chem. Phys., 1953, 21, 1436–1442 CrossRef CAS.
- R. L. Cook and F. C. De Lucia, Am. J. Phys., 1971, 39, 1433–1454 CrossRef CAS.
- L. Chan, G. R. Hutchison and G. M. Morris, J. Chem. Inf. Model., 2021, 61, 743–755 CrossRef CAS PubMed.
- H. J. Chun, E. J. Ocola and J. Laane, J. Phys. Chem. A, 2016, 120, 7677–7680 CrossRef CAS PubMed.
- E. E. Burnell, C. A. de Lange and R. Y. Dong, Liq. Cryst., 2020, 47, 1965–1974 CrossRef CAS.
- D. Damiani, F. Scappini, W. Caminati and G. Corbelli, J. Mol. Spectrosc., 1983, 100, 36–53 CrossRef CAS.
- A. D. Richardson, K. Hedberg, K. Utzat, R. K. Bohn, J.-X. Duan and W. R. Dolbier, J. Phys. Chem. A, 2006, 110, 2053–2059 CrossRef CAS PubMed.
- P. Thaddeus, L. C. Krisher and J. H. N. Loubser, J. Chem. Phys., 1964, 40, 257–273 CrossRef CAS.
- R. M. Garvey, F. C. De Lucia and J. W. Cederberg, Mol. Phys., 1976, 31, 265–287 CrossRef CAS.
- H. Takahashi, T. Shimanouchi, K. Fukushima and T. Miyazawa, J. Mol. Spectrosc., 1964, 13, 43–56 CrossRef CAS.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00586h |
| ‡ Present address: Hefei National Research Center for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei, Anhui, 230026, China. Email: xiefan@ustc.edu.cn |
| This journal is © the Owner Societies 2025 |



