Electron deficient oxygen species in highly OER active iridium anodes characterized by X-ray absorption and emission spectroscopy

Abstract

Water splitting is a promising technology for storing energy, yet it is challenged by the lack of stable anode materials that can overcome the sluggishness of the oxygen evolution reaction (OER). Iridium oxides are among the most active and stable OER catalysts, however how these materials achieve their performance remains under discussion. The activity of iridium based materials has been attributed to both high metal oxidation states and the appearance of O 2p holes. Herein we employ a combination of techniques—X-ray absorption at the Ir L_II,III-edge, X-ray absorption and emission at the O K-edge, along with ab initio methods—to identify and characterize ligand holes present in highly OER-active X-ray amorphous oxides. We find, in agreement with the original proposition based on X-ray absorption measurement at the O K-edge, that O 2p holes are present in these materials and can be associated with the increased activity during OER.

---

Introduction

Electrocatalytic generation of high-purity hydrogen via water splitting represents an attractive means of storing excess energy from intermittent sources.¹ While electrolyzer systems based on proton-exchange-membranes (PEMs) can operate under varying power inputs (i.e., wind and solar sources), their acidic working environment requires the use of corrosion-resistant catalysts with high activity.^2,3 However, only iridium oxide-based materials are known to combine stability in the harsh acidic environment with activity in the oxygen evolution reaction (OER)² making them indispensable for PEM electrolyzers.

Understanding the uniqueness of iridium oxide-based materials and finding ways to further increase their electrocatalytic Ir-mass based activity remains a challenge. The electronic structure and mechanistic aspects of iridium oxide catalysts have been extensively investigated through, for instance, operando X-ray absorption spectroscopy (XAS) at the Ir L_III-edge.^4–8 These studies have provided insights into the oxidation states of Ir under reaction conditions and the dynamic changes occurring during the OER. XAS studies at the oxygen K-edge have helped highlight the importance of metal–ligand covalency as essential for understanding catalytic properties.^8–11

Recent studies have shown that amorphous and nanostructured iridium oxides (IrO_x) exhibit significantly higher OER activity compared to their rutile-type counterparts^2,12,13 and that alloying strategies can increase water splitting activity.^3,12–14 Interestingly, alloys containing a non-noble metal, such as IrO_x/SrIrO₃¹³ and Ni-Ir mixed oxides,³ have shown significant OER enhancement after intentional leaching of the non-noble metal.

Oxygen-rich stoichiometries, or so-called hole-doped oxides,¹⁵ have been studied for their roles in the OER mechanism on iridium electrodes.^{3,5,6,9,15–17} O K-edge XAS studies on highly-OER-active amorphous-IrO_x have revealed a low excitation energy resonance (529 eV), attributed to electron-deficient oxygen species, originally denoted as an O^I− species,^5,9 although such species are characterized by strong covalency, which could make Ir^IV+δ–O^(I+δ)− a more correct description, see ref. 11 and 18. This will be discussed later, however we retain the O^I− nomenclature to be consistent with previous work and highlight the redox active nature of this oxygen. The O^I− species are also present in Ni-leached NiIr oxides³ but nearly absent from rutile-type IrO₂.^5,9 It has been argued that O^I− could be responsible for the high activity of oxygen-rich amorphous-IrO_x^5,6,15 (x > 2) and Ni-leached IrNi oxides.¹⁵ A key argument for the involvement of O^I− species in the OER is their electrophilic nature,¹⁷ which facilitates O–O bond formation during the reaction.^6,17In situ XAS reveals that oxygen species exhibiting the same spectral resonance appear on sputtered iridium films before the OER onset and their concentration scales with catalytic activity.⁶ Together, these observations suggest that a (partially) ligand-centered oxidation from O^II− to O^I− takes place on iridium-based electrodes before the OER onset,⁶ as opposed to the oxidation of Ir^IV to Ir^V proposed by other authors,^4,14,19–21 making O^I−, and the local atomic environments that can stabilize it,²² potentially critical for the OER on iridium.^6,7,15,22,23

This proposed ligand-centered oxidation closely parallels insights gained from oxygen evolution in Photosystem II (PSII), where an oxyl radical has long been hypothesized as a key intermediate of the catalytic cycle, with experimental studies of oxygen-evolving complex offering structural and spectroscopic evidence supporting the formation of an oxyl radical in the Mn₄CaO₅ cluster embedded within PSII.^24–26 Additionally, computational studies reinforce the theoretical feasibility of an oxyl intermediate in biological water oxidation.^27,28 The similarities between PSII and iridium-based electrocatalysts suggest that O^II− → O^I− oxidation may be a general feature of efficient OER catalysts.

Herein, we test the hypothesis that electron-deficient oxygen species are present in highly OER-active amorphous-IrO_x and absent from rutile-type IrO₂, by examining both the occupied and unoccupied states using synchrotron-based spectroscopy and ab initio calculations. We found that average oxidation state of iridium in amorphous-IrO_x is only slightly higher than the formal IV+ in rutile-type IrO₂ (but less than V+). O K-edge X-ray emission (XE) and XA spectra show that the amorphous-IrO_x has a significant reduction in occupied O 2p states near the Fermi energy (E_F) as compared to the rutile-type oxide. Our findings confirm the potential role of high-valent iridium in the OER with oxidation states greater than IV+, observed in oxygen-rich stoichiometries relative to IrO_x (x > 2) and complement the extensive literature on iridium oxide electrocatalysis.^5,8,11,16

Materials and methods

Commercial rutile-type IrO₂ and amorphous-IrO_x were employed in all experiments. Sample preparation and characterization followed the approach outlined in ref. 5 and 9 to ensure accurate direct comparison. Specifically, a hydrated, X-ray amorphous powder, IrO_x, was obtained from AlfaAesar and the rutile-type IrO₂ used in this work was purchased from Sigma Aldrich (99.9% purity) and was calcined at 1073 K in 1 bar O₂ before use. For the Ir L_II,III-edge measurements iridium metal and a formally Ir^III+ oxyhydroxide were also employed to allow an accurate conversion of the relative number the d holes in the amorphous compound into an absolute number. The IrOOH standard, a high-performance OER catalyst,²⁹ was synthesized following ref. 30.

XAS measurements at the Ir L_II,III-edges were performed at the BL17C1 beamline in Hsinchu (Taiwan).³¹ Photons were supplied from a 25 poles wiggler (W20) with 20 cm period length and a 2 mm × 6 mm spot size. All spectra were measured in transmission mode using an ionization chamber detector. XES was measured at the TPS 45A Beamline in Hsinchu (Taiwan).³²

DFT calculations were performed with the Quantum ESPRESSO package³³ using norm-conserving pseudopotentials with a kinetic energy cutoff of 160 Ry. We used the Perdew and Wang's local density approximation (LDA)³⁴ in this work, as it has been demonstrated, both the generalized gradient approximation^5,9,35 and local density approximation¹⁷ can faithfully capture the nonmagnetic ground state of rutile-type IrO₂.^36,37

Rutile-type IrO₂ was modelled with the 24-atom cell as in ref. 5 and 9 (see Fig. 1). The Brillouin zone was sampled with a (10 × 10 × 10) Monkhorst–Pack k-point grid. Methfessel–Paxton smearing³⁸ was used with a width of 0.005 Ry. We tested the effect of onsite repulsion between two electrons in the same orbital on Ir using a simplified LDA+U functional at a fixed geometry. A Hubbard-like interaction term parameterized by the F⁰, F², and F⁴ Slater integrals was used to explicitly account for the onsite dd Coulomb interaction.^39–44 As expected for a 5d transition metal oxide, results comparable with experiment can only be obtained for small values of U_eff. Thus, in this work we report XA and XE spectra with U_eff = 0 eV. Similar to previous work,³⁵ we found the non-magnetic solution to be the lowest energy in the 8-formula unit-cell of rutile-type IrO₂.

Fig. 1 The IrO₂ (left) and Ir₇O₁₆ (right) super-cells used to model rutile-type IrO₂. Iridium atoms are shown by way of grey spheres and oxygen red. Note the Ir vacancy in the centre of the Ir₇O₁₆ cell.

Further oxidation, or the addition of electron holes–hole-doping—of the rutile-type IrO₂ was accomplished by removing one iridium atom from the 24-atom cell and allowing full relaxation. Ground state calculations were performed with 200 Kohn–Sham states, which were used to compute the projected density of states (PDOS). A one-electron Fermi's golden rule expression was used to compute the Ir L_III-edge both in the absence and presence of a static core-hole within the framework of projector augmented wave method.^45–47 Two projectors were included for the l = 1 and l = 2 channels. The spectra were broadened to account for the finite lifetime of the final-state using a Lorentzian with a constant width of 5.0 eV, which is approximately the natural width of the Ir L_III-edge.⁴⁸ The assumption of constant lifetime broadening is expected to be a reasonable approximation for the L_III-edge white lines, for which we wish to compare to experiment, though it will lead to discrepancies at higher excitation energies. The edges were aligned to experiment.

To compute the XA and non-resonant XE spectra at the O K-edge, DFT wavefunctions were used with the NIST core-level Bethe–Salpeter equation solver (NBSE)^49,50 through the OCEAN package.^51,52 This approach captures the screened core-hole potential, which allows accurate ab initio calculations of the XA and XE spectra at the O K-edge. Screening calculations were converged with 700 bands. Absolute alignment of the spectra was accomplished with ΔSCF calculations using rutile-type IrO₂ as a reference. Spectral broadening was used with an excitation/emission energy dependent line width, Γ(E), where Γ increases linearly with the energy, that is, for XAS Γ(E) = 0.2 eV + 0.1 (E − E_F) eV. The initial broadening of 0.2 eV is the approximate natural linewidth of oxygen⁵³ and the slope of 0.1 was chosen following ref. 5 and 9 while Gaussian broadening was ignored.

Results

Ir L_III,II-Edges

The first aspect of the electronic structure of rutile-type IrO₂ and amorphous-IrO_x to consider is the average number of 5d holes in the materials, 〈n_d〉. The number of 5d electrons is defined as 10 − 〈n_d〉, where 10 is the total number of possible 5d electrons. Then, the formal oxidation state of the iridium centers can be defined as 〈n_s〉 + 〈n_d〉 − 3, where 〈n_s〉 is the number of 6s holes, which will be 2 for iridium oxides. While core level XPS has been used to gain some insight into the oxidation state of iridium in its oxides and oxyhydroxides, their tendency to display reverse core level shifts makes such an analysis challenging.^5,9,30 Thus, we turned to XAS at the Ir L_III- and L_II-edges, where the absorption coefficient reflects the probability for electronic transition from the 2p_3/2 and 2p_1/2 core levels to unoccupied states, respectively, and can be used to quantify 〈n_d〉.

At the L_III,II-edge the electric dipole selection rule governing XAS allows transitions from the core Ir 2p to empty 5d and 6s states, giving rise to the sharp white-line, step-edge, and additional fine structure seen in Fig. 2. (Note the X-ray attenuation coefficient has been normalized to 1 at the L_III-edge (top)—and ½ at the L_II-edge (bottom) to reflect the number of initial core electrons available.) While the step-edge is due to excitation into the continuum, the white-lines centered at ca. 11.22 keV in the L_III- and 12.827 keV in the L_II-edge measurements are due to 2p → 5d transitions; other features near the absorption edge are from 2p → 6s transitions.⁵⁴

Fig. 2 Measured L_III-edges (top) and L_II-edges (bottom) of three compounds with known oxidation states, Ir metal (gray), IrOOH (red), and rutile-type-IrO₂ (black) along with that of amorphous-IrO_x (blue). The dashed red lines show the normalized X-ray attenuation coefficients. The inset in L_II-edges shows the white line maxima.

For comparison purposes, we will consider the compounds with known formal oxidation states: iridium metal, IrOOH, and rutile-type IrO₂, which contain formally Ir⁰, Ir^III, and Ir^IV, respectively. Inspection of Fig. 2 reveals that the intensity of the L_III- and L_II-edge white-lines, I_LIII and I_LII, increase through this series. This increase reflects an L-edge sum rule: the number of d holes, 〈n_d〉, is proportional to the integral intensity of the L_III- and L_II-edge white-lines^55–59 that is: 〈n_d〉 ∝(I_LIII + I_LII). The use of the sum of the integrals reflects the fact that the white-line intensities need not follow the 2 : 1 statistical branching ratio.^60,61 Instead, the dipole selection rule requires the change in total angular momentum, ΔJ, to be 0 or ±1, which allows transition of the 2p_1/2 electrons to only 5d_3/2; the 2p_3/2 electrons probe both the empty 5d_3/2 and 5d_5/2. When spin–orbit coupling is small the J = 5/2 and J = 3/2 multiplets are degenerate and the I_LIII : I_LII branching ratio will reflect the number of initial core electrons available for the transitions, that is, 2 : 1. Spin–orbit effects will alter the distribution of 5d_5/2 : 5d_3/2 character at the Fermi level; and, as the d_3/2 lie lower in energy, I_LIII : I_LII will tend to exceed 2 : 1. This non-statistical branching is particularly apparent in 5d compounds,^54,59–62 though the 〈n_d〉 sum rule continues to hold in iridium based materials.⁵⁸ Application of the sum rule, however, requires the continuum jump and contributions from the 2p → 6s transitions to be removed.

To quantitatively analyze the L_III- and L_II-edge white-lines, the continuum jump was modeled as an arctangent centered at the inflection point of the white-line, following the approach used in ref. 59, see Fig. 3. The integral white-line intensity was then defined as the intensity above this edge-jump up to the point where the X-ray attenuation coefficient first intersects the arctangent, the shaded region of the figure. As shown below, this approach also effectively removes contributions from 2p → 6s transitions.

Fig. 3 The arctangent (black) used to model the continuum jump as described in the text shown using the rutile-type IrO₂ L_III-edge (top) and L_II-edge (bottom). The shaded region represents the contribution from the white-line. The inset in L_II-edge shows the white line maximum.

The results of these integrations are shown in Fig. 4 and Table 1, where I_LIII and I_LII have Ir with known formal oxidation state, the expected linear relationship between I_LIII + I_LII and 〈n_d〉 is found—black filled circles in Fig. 4. Performing the same analysis with only I_LIII yields a similar relationship, albeit with a steeper slope—blue filled circles. The discrepancy between the two approaches lies in the aforementioned change in branching ratio with increased spin–orbit expectation value. This can be seen in Table 1, which summarizes the numerical values of normalized I_LIII + I_LII along with the I_LIII/I_LII branching ratio and spin–orbit expectation value computed from it, 〈L·S〉.^60,63,64

Fig. 4 Relationship between formal number of d holes, 〈n_d〉, and integral white-line intensity for the three standard compounds, Ir⁰ metal, Ir^IIIOOH, Ir^IVO₂, are shown by the filled circles (right). Note that IrOOH may contain a mix of Ir^IIIIr^IV (ref. 65). The number of d holes for the amorphous-IrO_x (empty circles) is computed using a linear fit to the standards. The black points show the sum I_LIII + I_LII. The blue points show I_LIII alone.

Table 1 White-line intensities, branching ratios, and spin–orbit expectation values derived from the measured L_II,III-edges

System	I LIII + ILII	I LIII/ILII	〈L·S〉[ħ^2]
Ir	1.00	3.1	−0.8
IrOOH	1.30	3.9	−1.6
Rutile-type IrO2	1.62	4.3	−2.2
Amorphous-IrOx	1.64	4.8	−2.4

---

Our values for the I_LIII/I_LII branching ratios of the standards agree with previous experiments. For metallic iridium the branching ratio of 3.1 lies between the previously reported 2.4 and 3.6,⁵⁹ whereas we find both the Ir^III in IrOOH and Ir^IV in rutile-type IrO₂ have I_LIII/I_LII ∼ 4. The branching ratio for rutile-type IrO₂ is 4.3 which falls within the range of previously reported values ∼2.75–3.5⁵⁴ but is lower than the 6.9 reported in ref. 59. It is unclear why the results in ref. 59 differ from ours and those in ref. 54. It is also worth noting that previous measurements of IrCl₃ also show the Ir^III halide has a branching ratio approximately equal to that of rutile-type IrO₂, suggesting the combination of charge transfer and crystal field effects thought to lead to the increase in branching ratio upon oxidation of iridium⁵⁴ are similar for the Ir^III and Ir^IV compounds. Of all the materials, at 4.8, the amorphous-IrO_x has the most extreme branching ratio and 〈L·S〉. Thus, for the reference compounds the ratio of unoccupied 5d_5/2 : 5d_3/2 character tends to increase with formal oxidation state.

With the relationship between 〈n_d〉 and I_LIII + I_LII defined using a linear fit to the standard materials it is also possible to estimate the average formal oxidation state of iridium in the amorphous-IrO_x sample. Note that IrOOH may contain a mix of Ir^IIIIr^IV see ref. 65, which would alter the quantitative assignment of the average oxidation state, but we prefer to use the oxyhydroxide as reference over a halide to compare only oxide/oxyhydroxide materials. When both I_LIII and I_LII are used to define 〈n_d〉 a value of 5.1 electron holes is found for iridium in amorphous-IrO_x, corresponding to an average formal iridium oxidation state of +4.1, see the empty black circle in Fig. 4. And though the I_LIII/I_LII branching ratio of the IrO_x compound is higher than that of IrO₂, performing the analysis with only I_LIII yields an average iridium formal oxidation state of +4.2, see the empty blue circle in Fig. 4. It appears, however, that ignoring the L_II-edge has a minor impact on the average number of d holes found through an L-edge analysis; including or excluding I_LII leads to the conclusion the iridium in amorphous-IrO_x has an average oxidation state marginally higher than the formally IV+ found in rutile-type IrO₂ but significantly less than V+. The amorphous powder contains an estimated 2.4 wt% metallic iridium, thought to lie in the cores of the particles.⁹ Since the iridium L-edge XAS/XES is bulk sensitive, this metallic iridium will tend to reduce the white-line intensity found for the amorphous-IrO_x, simple analysis of I_LIII + I_LII shows this small amount of metal will alter 〈n_d〉 by less than 0.1 electron hole. It should also be noted that the average iridium oxidation state found in this work, Ir(4.1), through integration of the Ir L_III,II-edges is in reasonable agreement with the iridium oxidation state of 3.9 found in ref. 16 through analysis of the L_III edge position. Both values are, however, larger than the iridium oxidation state of 3.6 found for the oxidized part of IrO_x in ref. 5 through temperature programmed reduction. It is unclear why the chemical measurement results in a lower measured oxidation state than analysis of the Ir L-edges.

Since spin–orbit effects play a minor role on the average number of 5d holes determined by analysis of the Ir L-edges, it is interesting to further consider these effects on the electronic structure. This was done by computing the PDOSs with and without the inclusions of spin–orbit coupling on the valence. Comparison of the 5d PDOSs computed with and without spin–orbit coupling shows near quantitative agreement (see the black lines in Fig. 5). Both results agree with previous results based on the Perdew–Burke–Ernzerhof (PBE) functional,^3,35,66 and its revision for solids (PBEsol).^67,68 Thus, spin–orbit coupling can safely be ignored when considering properties linked to the low-energy region of the PDOS. One such property is the bonding nature of the 5d electrons.

Fig. 5 PDOS of rutile-type IrO₂ computed with (top) and without (bottom) spin–orbit coupling. In the scalar relativistic results, the 5d states are decomposed into σ – like (d_σ), π – like (d_π), and non-bonding (d_nb) states. The geometry around a single IrO₆ octahedron is also shown (top).

Investigation of the low-energy region of the PDOS allows the nature of the Ir 5d states to be assigned. To do so we can consider the geometry around the single IrO₆ octahedron shown in Fig. 5. In this representation the d_z² and d_xy are σ-like (anti-)bonding states; the d_xz and d_yz are π-like (anti-)bonding states; the d_x²−y² are primarily non-bonding. With this in mind, the narrow band at −8 eV relative to the Fermi energy can be assigned to 5d σ-like bonding states, whereas π-like bonding states are centered at ∼5 eV below E_F. At ∼2 eV a narrow non-bonding 5d band can be seen, which contains some π* – like anti-bonding character, though a majority of the π* – like character is centered at E_F. These π* – like antibonding states are then expected be the first to respond to small changes in the oxidation state of iridium.

As it was determined that spin–orbit effects are minor, the computed PDOS and the average number of 5d holes found by an analysis of the measured Ir L-edge, we can expect the calculation of the Ir L_III-edge within an independent electron approximation⁴⁷ will yield reliable results when neglecting the spin–orbit coupling on the valence states. Doing so offers the advantage of a direct connection between the Ir-PDOSs and L_III-edge. The uncertainty in this regard is the treatment of the core-hole. While the modifications to the PDOS due to the core-hole are governed by the final-state rule⁶⁹—core-hole effects are expected in XAS due to the core-hole in the final state—a priori it is difficult to correctly recover the screened core–valence interaction within a single particle approximation.^47,70,71 Thus, we have taken the pragmatic approach of computing the spectra with and without a full 2p core hole on the absorbing iridium. In both cases the Ir L_III-edge of rutile-type IrO₂ was computed using the 24-atom rutile-type cell described in the Methods Section. The tendency for hole localization on iridium upon oxidation was then investigated by introducing a neutral iridium vacancy into the super-cell shown in Fig. 1. Introduction of the vacancy leads to the formal appearance of four electron holes, resulting in the Ir₇O₁₆ model identical to that previously used to recover the O K-edge of amorphous-IrO_x.^5,9 Here, however, we will focus on the Ir L_III-edge's response to the additional holes.

Comparing the computed Ir L_III-edge of rutile-type IrO₂ (solid black line in Fig. 6) with the Ir₇O₁₆ (solid blue line in Fig. 6) reveals oxidation of the rutile-type IrO₂ leads to changes consistent with the measurement of amorphous-IrO_x. Inspection of the figure reveals the iridium in the oxidized model has an increased white-line intensity compared to rutile-type IrO₂, regardless of the assumed strength of the core-hole. Furthermore, both sets of results show the 6s contribution to the white-line (dashed lines in Fig. 6) is negligible, demonstrating the earlier assertion that the white-line is almost exclusively due to dipole allowed 2p → 5d transitions. The single particle results then demonstrate the Ir₇O₁₆ model recovers the electronic structure of the iridium centers in the highly-OER-active amorphous-IrO_x material, indicating the iridium centers of IrO₂ display only a slight loss of 5d π* – like character upon oxidation.

Fig. 6 Computed Ir L_III-edge without (top) and with (bottom) a 2p core-hole on the absorbing atom. The solid black curve shows the result for rutile-type IrO₂, and the blue curve shows the electron deficient iridium in the oxidized model compound Ir₇O₁₆, see methods. The two dashed line show the 6s contribution to each spectrum. See Fig. 1 for structural models.

In summary, analysis of the Ir L_II,III-edges reveals the iridium in amorphous-IrO_x has a marginally higher average oxidation state in the bulk than iridium in rutile-type IrO₂—4.1 compared to 4—which can also be seen by analysis of the L_III-edge alone. Calculations of the Ir L_III-edge show an oxidized rutile-type model, Ir₇O₁₆, can recover the observed changes. However, as we will see in the next section, the electron deficiency of the iridium in this model structure cannot completely account for the changes in formal oxidation state with respect IrO₂. Instead, as it will be shown below, oxidation if the dioxide leads to a significant increase in oxygen hole character.

XES and XAS at the O K-edge

To test for hole character on oxygen in amorphous-IrO_x we turned to XES and XAS at the O K-edge. At small momentum transfer the O K-edge XE spectra is subject to the same selection rule as O K-edge XAS, that is, transitions between s and p states. As with XAS, because the O 1s core hole is nearly static and structureless,^17,72 XES measures O 2p states. In the case of emission, only occupied states are probed, making it the natural complement to the unoccupied O 2p measured with XAS. The modifications to the PDOS due to the core-hole are governed by the final-state rule.⁶⁹ Such effects are then negligible during emission because the final-state has no core-hole, whereas the core-hole has been shown to be well-screened in XA spectra of iridium oxides.^3,5 Thus, we can view both the XE and XA spectra as accurate measures of the occupied and unoccupied O 2p states, respectively.

The O K-edge XE and XA spectra of rutile-type IrO₂ and the Ir₇O₁₆ model were computed using the same super-cells as for the Ir L_III-edge. Now, however, our focus is on hole localization on oxygen upon hole-doping. The resultant O K-edge XE and XA spectra of rutile-type IrO₂ are shown in Fig. 7 (black lines), along with those of the Ir₇O₁₆ model (blue lines).

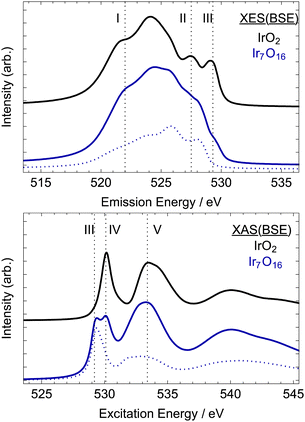Fig. 7 Computed XE (top) and XA (bottom) O K-edge spectra of rutile-type IrO₂ (black) and the oxidized model considered in ref. 5, Ir₇O₁₆ (blue). The dotted blue line in the Ir₇O₁₆ model shows the contribution from the electron-deficient oxygen referred to as O^I−. See Fig. 1 for structural models.

The computed O K-edge XE spectrum of rutile-type IrO₂ shows the typical features expected for the filled O 2p states of the conducting oxide. The center of the O 2p band can be seen to be at ∼525 eV, which is ∼5 eV below E_F. The oxygen contribution to the Ir-O σ-like bonding states appear as a broad shoulder ∼3 eV below this band center, labeled I in Fig. 7 (one can also compare it to Fig. 5). There are also two features at lower excitation energies labeled II and III. The oxygen contribution at II can be attributed to oxygen weakly hybridized with the narrow band of iridium non-bonding states seen in Fig. 5, while that at III is associated with the partially filled π* – like Ir–O anti-bonding states. Computed O K-edge XA spectrum also shows the expected features for unoccupied O 2p states. The oxygen contribution to the nominally π* anti-bonding states in the computed XA spectrum can be seen to give a sharp resonance at ∼530 eV, labeled IV. The O 2p contribution to the σ* anti-bonding states gives a resonance at ∼534 eV, labeled V. These features have previously been described in detail, and we refer the reader to those works for a more detailed discussion.^3,5

Oxidation of rutile-type IrO₂ can be seen to lead to slight changes of the computed O K-edge XE spectrum at low excitation energies and significant changes near the Fermi energy. Inspection of the O K-edge XE spectrum computed for the Ir₇O₁₆ model, blue line in Fig. 7, reveals oxidation leads to a slight reduction in the intensity of the O 2p contribution to the σ bonding states at I and a small shift in the center of O 2p band towards higher excitation energies. Moreover, oxidation results in a significant reduction in the number of the oxygen states at III.

The reason for the loss of intensity at III in Fig. 7 for Ir₇O₁₆ relative to rutile-type IrO₂ can be seen by examining the O^I− contribution alone (dotted blue line). Doing so we see there are no O^I− states at III and the O 2p states that were present at II for an O^II− species have shifted to 0.5 eV higher excitation energy. The residual intensity at I in the calculation of the Ir₇O₁₆ model is then mainly due to the remaining O^II−. The disappearance of the states at I upon hole-doping can be further clarified by turning to the unoccupied states probed by XAS.

In the absorption spectra, further oxidation of rutile-type IrO₂ leads to the appearance of a new resonance in the O K-edge.⁶ This new resonance, labeled III in Fig. 7 (right), is at the same excitation energy as that lost from the occupied part of the XE spectrum upon oxidation of O^II− to O^I−. In other words, the higher energy occupied O 2p states appearing in the O K-edge XES for the O^II− species are emptied when O^II− is oxidized to O^I− and then appear as unoccupied states in O K-edge XAS. Thus, together, the computed XE and XA spectra predict that the oxidation of IrO₂ tends to create O 2p holes, and if IrO_x contains such holes it should be apparent in both the O K-edge XE and XA spectra.

The experimental results confirm these theoretical predictions. Fig. 8 shows the measured O K-edge XE and XA spectra of rutile-type IrO₂ (black lines) and the X-ray amorphous-IrO_x sample (blue lines). We also note that simulations on Ir₇O₁₆ predict a higher fraction of O^I− than is observed in experiment; to match the measured pre-peak intensities through linear combinations of the computed O^II− and O^I− contributions, we would need to assume ca. 33% O^I− is present in the IrO_x sample. See Fig. S1 (ESI†) for higher resolution XA spectra.

Fig. 8 Measured XE and XA O K-edge spectra of rutile-type IrO₂ (top) and X-ray amorphous-IrO_x (bottom), see also Fig. S1 (ESI†) for higher resolution XA spectra. See Fig. 1 for structural models.

For rutile-type IrO₂ the O K-edge XE spectrum confirms the low energy branch of the O 2p band is at ∼525 eV with the oxygen σ-bonding states giving a broad shoulder at ∼522 eV. The experimental resolution is also sufficient to confirm the presence of the high energy oxygen states labeled II and III. In particular, the rutile-type oxide has a strong oxygen contribution at 529 eV, labeled III, which agrees with computational findings. The measured absorption spectrum of rutile-type IrO₂ is also consistent with the calculations and previous results. It shows the π* – and σ* – antibonding states at 530 and 533 eV, respectively,^3,5 but no resonance at 529 eV.

Evaluation of the measured O K-edge XE spectrum of the X-ray amorphous-IrO_x sample confirms the loss of O 2p states at 529 eV compared to the rutile-type oxide (labeled III) in Fig. 8(top). Instead, the 529 eV resonance appears in the O K-edge XA spectrum of IrO_x (labeled III), see also Fig. S1 (ESI†) for higher resolution XA spectra of the same materials. The XA resonance at ∼529 eV was previously assigned to a formally O^I− species in the amorphous powder, while the 530 eV resonance was attributed to remaining O^II−, see ref. 5 though as we have seen, there is a high degree of covalency in Ir^IV–O^I−, making it Ir^IV+δ–O^(I+δ)−. The measured XE spectrum confirms this assertion by demonstrating that the amorphous powder shows the loss in occupied O 2p states relative to rutile-type IrO₂ expected if ground state oxygen holes are present in amorphous-IrO_x. Thus, when considering both the O K- and Ir L_II,III-edges it appears that holes introduced upon oxidation of an IV+ iridium oxide reside, in a zero-order approximation, on oxygen.

Conclusions

The proposed ability of iridium-based materials to form a formally O^I− species^5,9 that is thought to be linked to their high OER activity^3,6,7,15,17 has been tested using a variety of experimental and computational methods. Analysis of the Ir L_II,III-edges of a highly-OER-active X-ray amorphous-IrO_x powder shows the iridium centers are, on average, slightly more oxidized than in rutile-type IrO₂. The latter was confirmed by XAS calculations on a Ir₇O₁₆ model, where this trend was recovered, though hole-character is also found in the O 2p band leading to the appearance of an O^I− species, or more correctly Ir^IV+δ–O^(I+δ)−. A comparison of the measured and computed O K-edge XAS/XES confirms the appearance of the O^I− species in the amorphous-IrO_x powder and their absence from rutile-type IrO₂. In this case occupied oxygen states seen in XES of the rutile-type oxide are found to become unoccupied upon further oxidation of the rutile-type oxide and appear in the XAS of the amorphous IrO_x. DFT and BSE simulations support the assignment of the O^I− in the amorphous oxide.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

TEJ and LAV acknowledge support from the Laboratory Directed Research and Development program of Los Alamos National Laboratory under project number 20240061 DR. We acknowledge Los Alamos National Laboratory's Institutional Computing Program from computational resources. LJF acknowledges the support by the Alexander von Humboldt Foundation.

Notes and references

1. J. P. Barton and D. G. Infield, Energy storage and its use with intermittent renewable energy, IEEE Trans. Energy Convers., 2004, 19, 441–448.
2. T. Reier, M. Oezaslan and P. Strasser, Electrocatalytic oxygen evolution reaction (OER) on Ru, Ir, and Pt catalysts: A comparative study of nanoparticles and bulk materials, ACS Catal., 2012, 2, 1765–1772.
3. T. Reier, Z. Pawolek, S. Cherevko, M. Bruns, T. Jones, D. Teschner, S. Selve, A. Bergmann, H. N. Nong, R. Schlögl, K. J. J. Mayrhofer and P. Strasser, Molecular insight in structure and activity of highly efficient, low-Ir Ir–Ni oxide catalysts for electrochemical water splitting (OER), J. Am. Chem. Soc., 2015, 137, 13031–13040.
4. H. G. Sanchez Casalongue, M. L. Ng, S. Kaya, D. Friebel, H. Ogasawara and A. Nilsson, In situ observation of surface species on iridium oxide nanoparticles during the oxygen evolution reaction, Angew. Chem., Int. Ed., 2014, 53, 7169–7172.
5. V. Pfeifer, T. E. Jones, J. J. Velasco Vélez, C. Massué, M. T. Greiner, R. Arrigo, D. Teschner, F. Girgsdies, M. Scherzer, J. Allan, M. Hashagen, G. Weinberg, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, The electronic structure of iridium oxide electrodes active in water splitting, Phys. Chem. Chem. Phys., 2016, 18, 2292–2296.
6. V. Pfeifer, T. E. Jones, J. J. Velasco Vélez, R. Arrigo, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, In situ observation of reactive oxygen species forming on oxygen-evolving iridium surfaces, Chem. Sci., 2017, 8, 2143–2149.
7. V. A. Saveleva, L. Wang, D. Teschner, T. Jones, A. S. Gago, K. A. Friedrich, S. Zafeiratos, R. Schlögl and E. R. Savinova, Operando evidence for a universal oxygen evolution mechanism on thermal and electrochemical iridium oxides, J. Phys. Chem. Lett., 2018, 9, 3154–3160.
8. T. E. Jones, D. Teschner and S. Piccinin, Toward realistic models of the electrocatalytic oxygen evolution reaction, Chem. Rev., 2024, 124, 9136–9223.
9. V. Pfeifer, T. E. Jones, J. J. Velasco Vélez, C. Massué, R. Arrigo, D. Teschner, F. Girgsdies, M. Scherzer, M. T. Greiner, J. Allan, M. Hashagen, G. Weinberg, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, The electronic structure of iridium and its oxides, Surf. Interface Anal., 2015, 48, 261–273.
10. F. Frati, M. O. J. Y. Hunault and F. M. F. de Groot, Oxygen K-edge X-ray absorption spectra, Chem. Rev., 2020, 120, 4056–4110.
11. J.-J. Velasco-Vélez, E. A. Carbonio, C.-H. Chuang, C.-J. Hsu, J.-F. Lee, R. Arrigo, M. Hävecker, R. Wang, M. Plodinec, F. R. Wang, A. Centeno, A. Zurutuza, L. J. Falling, R. V. Mom, S. Hofmann, R. Schlögl, A. Knop-Gericke and T. E. Jones, Surface electron-hole rich species active in the electrocatalytic water oxidation, J. Am. Chem. Soc., 2021, 143, 12524–12534.
12. H. N. Nong, L. Gan, E. Willinger, D. Teschner and P. Strasser, IrOx core-shell nanocatalysts for cost- and energy-efficient electrochemical water splitting, Chem. Sci., 2014, 5, 2955–2963.
13. L. C. Seitz, C. F. Dickens, K. Nishio, Y. Hikita, J. Montoya, A. Doyle, C. Kirk, A. Vojvodic, H. Y. Hwang, J. K. Nørskov and T. F. Jaramillo, A highly active and stable IrO_x/SrIrO₃ catalyst for the oxygen evolution reaction, Science, 2016, 353, 1011–1014.
14. S. Geiger, O. Kasian, M. Ledendecker, E. Pizzutilo, A. M. Mingers, W. T. Fu, O. Diaz-Morales, Z. Li, T. Oellers, L. Fruchter, A. Ludwig, K. J. J. Mayrhofer, M. T. M. Koper and S. Cherevko, The stability number as a metric for electrocatalyst stability benchmarking, Nat. Catal., 2018, 1, 508–515.
15. P. Strasser, Free electrons to molecular bonds and back: closing the energetic oxygen reduction (ORR)–oxygen evolution (OER) cycle using core–shell nanoelectrocatalysts, Acc. Chem. Res., 2016, 49, 2658–2668.
16. N. Diklić, A. H. Clark, J. Herranz, D. Aegerter, J. S. Diercks, A. Beard, V. A. Saveleva, P. Chauhan, M. Nachtegaal, T. Huthwelker, D. Lebedev, P. Kayser, J. A. Alonso, C. Copéret and T. J. Schmidt, Surface Ir⁵⁺ formation as a universal prerequisite for O₂ evolution on Ir oxides, ACS Catal., 2023, 13, 11069–11079.
17. V. Pfeifer, T. E. Jones, S. Wrabetz, C. Massué, J. J. Velasco Vélez, R. Arrigo, M. Scherzer, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, Reactive oxygen species in iridium-based OER catalysts, Chem. Sci., 2016, 7, 6791–6795.
18. E. A. Carbonio, F. Sulzmann, D. Teschner, J. J. Velasco-Vélez, M. Hävecker, A. K. Gericke, R. Schlögl and T. Jones, Thermal synthesis of electron-deficient oxygen species on crystalline IrO₂, Catal. Sci. Technol., 2024, 14, 572–580.
19. R. Kötz, H. Neff and S. Stucki, Anodic iridium oxide films: XPS studies of oxidation state changes and O₂ evolution, J. Electrochem. Soc., 1984, 131, 72–77.
20. M. Hüppauff and B. Lengeler, Valency and structure of iridium in anodic iridium oxide films, J. Electrochem. Soc., 1993, 140, 598–602.
21. M. A. Petit and V. Plichon, Anodic electrodeposition of iridium oxide films, J. Electroanal. Chem., 1998, 444, 247–252.
22. M. Elmaalouf, M. Odziomek, S. Duran, M. Gayrard, M. Bahri, C. Tard, A. Zitolo, B. Lassalle-Kaiser, J. Y. Piquemal, O. Ersen, C. Boissière, C. Sanchez, M. Giraud, M. Faustini and J. Peron, The origin of the high electrochemical activity of pseudo-amorphous iridium oxides, Nat. Commun., 2021, 12, 3793.
23. A. Grimaud, A. Demortière, M. Saubanère, W. Dachraoui, M. Duchamp, M.-L. Doublet and J.-M. Tarascon, Activation of surface oxygen sites on an iridium-based model catalyst for the oxygen evolution reaction, Nat. Energy, 2016, 2, 16189.
24. J. Messinger, J. H. Robblee, U. Bergmann, C. Fernandez, P. Glatzel, H. Visser, R. M. Cinco, K. L. McFarlane, E. Bellacchio, S. A. Pizarro, S. P. Cramer, K. Sauer, M. P. Klein and V. K. Yachandra, Absence of Mn-centered oxidation in the S₂ → S₃ transition: implications for the mechanism of photosynthetic water oxidation, J. Am. Chem. Soc., 2001, 123, 7804–7820.
25. J. Yano and V. Yachandra, Mn₄Ca cluster in photosynthesis: where and how water is oxidized to dioxygen, Chem. Rev., 2014, 114, 4175–4205.
26. J. Kern, R. Chatterjee, I. D. Young, F. D. Fuller, L. Lassalle, M. Ibrahim, S. Gul, T. Fransson, A. S. Brewster, R. Alonso-Mori, R. Hussein, M. Zhang, L. Douthit, C. de Lichtenberg, M. H. Cheah, D. Shevela, J. Wersig, I. Seuffert, D. Sokaras, E. Pastor, C. Weninger, T. Kroll, R. G. Sierra, P. Aller, A. Butryn, A. M. Orville, M. Liang, A. Batyuk, J. E. Koglin, S. Carbajo, S. Boutet, N. W. Moriarty, J. M. Holton, H. Dobbek, P. D. Adams, U. Bergmann, N. K. Sauter, A. Zouni, J. Messinger, J. Yano and V. K. Yachandra, Structures of the intermediates of Kok's photosynthetic water oxidation clock, Nature, 2018, 563, 421–425.
27. P. E. M. Siegbahn, Theoretical studies of O–O bond formation in photosystem II, Inorg. Chem., 2008, 47, 1779–1786.
28. P. E. M. Siegbahn and R. H. Crabtree, Manganese oxyl radical intermediates and O–O bond formation in photosynthetic oxygen evolution and a proposed role for the calcium cofactor in photosystem II, J. Am. Chem. Soc., 1999, 121, 117–127.
29. D. Weber, L. M. Schoop, D. Wurmbrand, S. Laha, F. Podjaski, V. Duppel, K. Müller, U. Starke and B. V. Lotsch, IrOOH nanosheets as acid stable electrocatalysts for the oxygen evolution reaction, J. Mater. Chem. A, 2018, 6, 21558–21566.
30. D. Weber, L. M. Schoop, D. Wurmbrand, J. Nuss, E. M. Seibel, F. F. Tafti, H. Ji, R. J. Cava, R. E. Dinnebier and B. V. Lotsch, Trivalent iridium oxides: layered triangular lattice iridate K_0.75Na_0.25IrO2 and oxyhydroxide IrOOH, Chem. Mater., 2017, 29, 8338–8345.
31. K.-L. Tsang, C.-H. Lee, Y.-C. Jean, T.-E. Dann, J.-R. Chen, K. L. D’Amico and T. Oversluizen, Wiggler x-ray beamlines at Synchrotron Radiation Research Center, Rev. Sci. Instrum., 1995, 66, 1812–1814.
32. C.-L. Dong, J.-W. Chiou, H.-M. Tsai, H.-W. Fu, H.-J. Lin, C. T. Chen and W.-F. Pong, Photon-in/photon-out soft x-ray spectroscopy at the TPS 45A beamline, Synchrotron Radiat. News, 2017, 30, 24–29.
33. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502.
34. J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
35. Y. Ping, G. Galli and W. A. Goddard III, Electronic structure of IrO₂: the role of the metal d orbitals, J. Phys. Chem. C, 2015, 119(21), 11570–11577.
36. W. D. Ryden and A. W. Lawson, Magnetic susceptibility of IrO₂ and RuO₂, J. Chem. Phys., 1970, 52, 6058–6061.
37. D. Von Dreifus, A. J. A. de Oliveira, A. V. do Rosario and E. C. Pereira, Magnetic and structural characterization of IrO₂ and Co:IrO₂ samples synthesized via Pechini method, J. Supercond. Nov. Magn., 2012, 26, 2319–2321.
38. M. Methfessel and A. T. Paxton, High-precision sampling for Brillouin-zone integration in metals, Phys. Rev. B, 1989, 40, 3616–3621.
39. M. Cococcioni and S. de Gironcoli, Linear response approach to the calculation of the effective interaction parameters LDA + U method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
40. V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
41. V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyżyk and G. A. Sawatzky, Density-functional theory and NiO photoemission spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929–16934.
42. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA + U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
43. B. Himmetoglu, R. M. Wentzcovitch and M. Cococcioni, First-principles study of electronic and structural properties of CuO, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115108.
44. M. Cococcioni, in Correlated Electrons: From Models to Materials Modeling and Simulation, ed. E. Pavarini, E. Koch, F. Anders and M. Jarrell, Forschungszentrum Jülich, 2012, vol. 2, pp. 1–40.
45. M. Taillefumier, D. Cabaret, A.-M. Flank and F. Mauri, X-ray absorption near-edge structure calculations with the pseudopotentials: Application to the K edge in diamond and α-quartz, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 195107.
46. C. Gougoussis, M. Calandra, A. P. Seitsonen and F. Mauri, First-principles calculations of x-ray absorption in a scheme based on ultrasoft pseudopotentials: From alpha-quartz to high Tc compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 075102.
47. O. Bunău and M. Calandra, Projector augmented wave calculation of x-ray absorption spectra at the L_2,3 edges, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205105.
48. M. O. Krause and J. H. Oliver, Natural widths of atomic K and L levels, Kα X-ray lines and several KLL Auger lines, J. Phys. Chem. Ref. Data, 1979, 8, 329–338.
49. E. L. Shirley, Ti 1s pre-edge features in rutile: a Bethe-Salpeter calculation, J. Electron Spectrosc. Relat. Phenom., 2004, 136, 77–83.
50. J. A. Soininen and E. L. Shirley, Scheme to calculate core hole–electron interactions in solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 165112.
51. J. Vinson, J. J. Rehr, J. J. Kas and E. L. Shirley, Bethe-Salpeter equation calculations of core excitation spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115106.
52. J. Vinson and J. J. Rehr, Ab initio Bethe-Salpeter calculations of the x-ray absorption spectra of transition metals at the L-shell edges, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195135.
53. A. Menzel, S. Benzaid, M. O. Krause, C. D. Caldwell, U. Hergenhahn and M. Bissen, Natural widths in open-shell atoms: The K absorption spectrum of atomic oxygen, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54, R991–R994.
54. Y. Cho, J. Park, J. Yu and J. G. Park, X-ray absorption spectroscopy studies of spin-orbit coupling in 5d transition metal oxides, J. Phys.: Condens. Matter, 2012, 24, 055503.
55. A. F. Starace, Potential-barrier effects in photoabsorption. I. General theory, Phys. Rev. B, 1972, 5, 1773–1784.
56. J. A. Horsley, Relationship between the area of L2,3 x-ray absorption edge resonances and the d orbital occupancy in compounds of platinum and iridium, J. Chem. Phys., 1982, 76, 1451–1458.
57. J. Stöhr, X-ray magnetic circular dichroism spectroscopy of transition metal thin films, J. Electron Spectrosc. Relat. Phenom., 1995, 75, 253–272.
58. T. K. Sham, L-edge x-ray-absorption systematics of the noble metals Rh, Pd, and Ag and the main-group metals In and Sn: A study of the unoccupied density of states in 4d elements, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 1888–1902.
59. J. P. Clancy, N. Chen, C. Y. Kim, W. F. Chen, K. W. Plumb, B. C. Jeon, T. W. Noh and Y. J. Kim, Spin-orbit coupling in iridium-based 5d compounds probed by X-ray absorption spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195131.
60. B. T. Thole and G. van der Laan, Branching ratio in x-ray absorption spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3158–3171.
61. M. Brown, R. E. Peierls and E. A. Stern, White lines in x-ray absorption, Phys. Rev. B, 1977, 15, 738–744.
62. Y. Jeon, B. Qi, F. Lu and M. Croft, Transition-metal (Au, Pt, Ir, Re) bonding to Al, Si, Ge: X-ray-absorption studies, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 1538–1545.
63. G. van der Laan and B. T. Thole, Local probe for spin-orbit interaction, Phys. Rev. Lett., 1988, 60, 1977–1980.
64. B. T. Thole and G. van der Laan, Linear relation between x-ray absorption branching ratio and valence-band spin-orbit expectation value, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 1943–1947.
65. L. Falling, der Technischen Universität Berlin, 2021.
66. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
67. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Erratum: Restoring the density-gradient expansion for exchange in solids and surfaces [Phys. Rev. Lett. 100, 136406 (2008)], Phys. Rev. Lett., 2009, 102, 039902.
68. J. M. Kahk, C. G. Poll, F. E. Oropeza, J. M. Ablett, D. Céolin, J.-P. Rueff, S. Agrestini, Y. Utsumi, K. D. Tsuei, Y. F. Liao, F. Borgatti, G. Panaccione, A. Regoutz, R. G. Egdell, B. J. Morgan, D. O. Scanlon and D. J. Payne, Understanding the electronic structure of IrO₂ using hard-X-ray photoelectron spectroscopy and density-functional theory, Phys. Rev. Lett., 2014, 112, 117601.
69. G. D. Mahan, Final-state potential in X-ray spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 1421–1431.
70. T. E. Jones, T. C. R. Rocha, A. Knop-Gericke, C. Stampfl, R. Schlögl and S. Piccinin, Thermodynamic and spectroscopic properties of oxygen on silver under an oxygen atmosphere, Phys. Chem. Chem. Phys., 2015, 17, 9288–9312.
71. V. Mauchamp, M. Jaouen and P. Schattschneider, Core-hole effect in the one-particle approximation revisited from density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235106.
72. J. J. Rehr, J. A. Soininen and E. L. Shirley, Final-state rule vs. the Bethe-Salpeter equation for deep-core X-ray absorption spectra, Phys. Scr., 2005, 207, 207–211.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03415e

---