 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Decomposition of organometallic precursor tricarbonyl(trimethylenemethane)ruthenium Ru(C4H6)(CO)3+/0 in the gas phase investigated by thermal desorption spectrometry†
Ken
Miyajima
 *a,
Toshiaki
Nagata
*a,
Toshiaki
Nagata
 b,
Fumitaka
Mafuné
b,
Fumitaka
Mafuné
 b,
Tomohiro
Tsugawa
c and
Ryosuke
Harada
c
b,
Tomohiro
Tsugawa
c and
Ryosuke
Harada
c
aKOMEX, School of Arts and Sciences, The University of Tokyo, Komaba, Meguro, Tokyo 153-8902, Japan. E-mail: miyajima@cluster.c.u-tokyo.ac.jp
bDepartment of Basic Science, School of Arts and Sciences, The University of Tokyo, Komaba, Meguro, Tokyo 153-8902, Japan
cChemical Materials Development Department, Global Marketing/R&D Supervisory Department, TANAKA PRECIOUS METAL TECHNOLOGIES Co., Ltd., 22, Wadai, Tsukuba, Ibaraki 300-4247, Japan
First published on 8th April 2025
Abstract
Thermal decomposition of an organometallic precursor Ru(C4H6)(CO)3+/0 was observed using gas-phase thermal desorption spectrometry. It was found that the CO ligands were readily released, forming Ru(C4H6)+ at 600 K. Then, Ru(C4H4)+ and Ru(C2H2)+ were produced as a result of sequential H2 and C2H2 release above 800 K. The activation energies of the ligand losses were estimated from the temperature dependences, and were consistent with the available internal energies obtained by DFT calculations. Based on experimental and computational results, Ru(C4H4)+ was identified as a ruthenium complex with unsubstituted cyclobutadiene, [η4-(C4H4)Ru]+. For the thermal decomposition of neutral Ru(C4H6)(CO)3, the appearance of photoionized Ru(C4H6)(CO) is evidence of CO loss from Ru(C4H6)(CO)2 at 740 K. The decomposition further proceeds above 800 K, forming Ru(C4H6).
1. Introduction
Ruthenium is attracting attention owing to its promising properties such as good thermal, chemical, and mechanical stability, significantly low bulk resistivity (∼7.1 μΩ cm),1 and catalytic activity. Ruthenium thin films have been well studied in the field of future semiconductor processing, and some reported applications include gate materials as replacements for W, capacitor electrodes for dynamic random access memory (DRAM),2,3 local interconnects (M0), and narrow metal lines (M1, M2) as diffusion barriers in logic devices.4,5 Conventionally, ruthenium thin films are deposited using physical vapor deposition methods such as sputtering, evaporation, and chemical vapor deposition (CVD). Ruthenium carbonyl compounds are widely used as organometallic precursors for catalysts and CVD processes.6–10Atomic layer deposition (ALD) is an emerging process that can be used to deposit thin films with extremely uniform and conformal quality.11–16 A film with a thickness of a few nanometers can be precisely deposited by controlling the number of ALD cycles. In the ALD process, the self-limiting nature of the deposition technique ideally requires moderate thermal stability in the vapor phase and reactivity with the reactant gas on the substrate at a relatively low processing temperature. Gao et al. deposited Ru thin films using η4-2,3-dimethylbutadiene ruthenium tricarbonyl [Ru(DMBD)(CO)3] with H2O as the reaction gas at a deposition rate of 0.1 nm per cycle at a steady-state deposition temperature of 160–210 °C.13 They proposed that the ligand dimethylbutadiene is desorbed when the molecule is adsorbed on the surface, while CO forms CO2 and H2 in the water–gas shift (WGS) reaction catalyzed by the Ru metal center. Schneider et al. investigated the growth mechanism of Ru thin films using in situ quartz-crystal microbalance and quadrupole mass spectrometry for the same Ru(DMBD)(CO)3.16 They found no evidence of WGS reaction. They proposed that the dominant Ru deposition mechanism is via the thermal desorption of labile CO ligands, regenerating active sites for further Ru precursor adsorption. Although the detailed reaction mechanism is not yet clear, the difference in the ease of desorption between the two ligands can be used to select the deposition temperature and control the properties of the Ru thin film. Information on the bond dissociation and activation energies of individual precursors in the intrinsic thermal decomposition mechanism is useful for determining the deposition process conditions.
In our previous study, the thermal decomposition of triruthenium dodecacarbonyl Ru3(CO)12 in the gas phase was investigated using photoionization mass spectrometry and thermal desorption spectrometry (TDS).17 It was found that CO ligand molecules were sequentially released in the temperature range 400–900 K, forming Ru3. Among the intermediate cluster compositions, Ru3(CO)7 was the most thermally durable cluster, whereas Ru3(CO)3, Ru3(CO)5, and Ru3(CO)10 were less durable and decomposed within a narrow temperature range.
Kotsugi et al. reported the ALD of a Ru metal–organic precursor, tricarbonyl(trimethylenemethane)ruthenium, Ru(tmm)(CO)3 (tmm = trimethylenemethane, C4H6), with O2 as a reactant.18 They found that the simple and small molecular structure of the precursor weakened the intermolecular forces in the liquid phase, resulting in high vapor pressure at room temperature. Additionally, the relatively small ligands of the precursor facilitate efficient ALD, and typical self-limiting growth is observed along with significantly high growth per cycle (GPC) (∼1.7 Å) at a moderate temperature (493 K). The Ru precursor permits enhanced nucleation and GPC at relatively low deposition temperatures to construct high-quality Ru films with significantly low resistivity using simple, plasma-free techniques and is suitable for the fabrication of emerging Ru films to replace Cu-based interconnects. Unlike homoleptic precursors such as Ru3(CO)12, the deposition can be more precisely controlled by temperature and coreactant conditions when using two different ligands.
Ru(C4H6)(CO)3, [[η4-((CH2)3C)]Ru(CO)3], is one of the 18 electron systems:19 The Ru atom donates two electrons to tmm,20 forming Ru2+ and C4H62−, and it comprises six d-electrons from Ru2+, six π-electrons from C4H62−, and six electrons from three CO ligands. Therefore, they are stable organometallic compounds that can be handled in the air. Additionally, this compound has a heteroleptic coordination environment, in contrast to the simple Ru carbonyl cluster Ru3(CO)12, which exhibits homoleptic coordination of the CO ligands. As a mentioned above, typical self-limiting growth and an ALD temperature window of 493–513 K are observed in the deposition system using Ru(C4H6)(CO)3 with O2, but the ALD system using Ru3(CO)12 as a precursor has not been reported so far, probably for the less thermal stability. Therefore, information on the thermal properties of the precursor is attractive for understanding the differences in the effects of coordinated ligands between organometallic and metal carbonyl compounds such as Ru3(CO)12.
To elucidate the intrinsic thermal decomposition mechanism, it is important to investigate the precursor compound in the gas phase, which is free from complicated interactions with substrate materials and other chemical species.21 In this study, the thermal decomposition of Ru(C4H6)(CO)3, [[η4-((CH2)3C)]Ru(CO)3], was investigated.22,23 The products of thermal decomposition were identified using temperature-variable mass spectrometry by observing the native cationic species formed by laser plasma or photoionized species using an F2 laser. The activation energies of the thermal decomposition process were calculated and discussed.
2. Methodologies
Thermal decomposition of Ru(C4H6)(CO)3+/0 in the gas phase was investigated using TDS and mass spectrometry. The details of the experimental setup have been previously reported.17,24 Therefore, the cluster generation and mass spectrometry sections of the experimental setup are outlined here. A liquid of Ru(C4H6)(CO)3 (TANAKA PRECIOUS METAL TECHNOLOGIES Co., Ltd.) was loaded into a short 1/4-inch Teflon tube connected via a 1/4-inch stainless steel T-joint to the helium carrier gas line upstream of the general valve, as shown in Fig. S1 (ESI†). Sufficient vapor pressure was obtained without increasing the temperature of the vapor source.18 Ru(C4H6)(CO)3 vapor was mixed with 0.17% O2 (>99.9%) seeded He gas or pure He gas (>99.99995%; 0.62 MPa) and introduced into the vacuum chamber via a pulsed valve. It is common to mix oxidizing or non-oxidizing reaction gases, such as oxygen, water, and hydrazine, as coreactants in industrial applications such as ALD. In this study, helium gas mixed with oxygen was used as a gas to transport precursor vapor, but no changes due to oxidation of the precursor or pyrolysis products were observed. However, it was observed that molecular oxygen attachments were formed and that they desorbed O2 upon heating.When we carried out mass spectrometry without photoionization by an F2 laser, Ru(C4H6)(CO)3 was ionized by laser plasma, which was formed by irradiating a Ru metal rod (99.95%, 5 mm dia.) with a focused pulse laser (second harmonic of a Nd:YAG laser; 532 nm, 10 Hz, ∼6 mJ per pulse) downstream of the pulsed nozzle. The carrier gas pulse passed through an extension tube (copper tube, 10 mm outer diameter, 4 mm inner diameter, 116 mm length) in which the temperature was controlled in the range of 300–1022 K. The residence time of the species in the carrier gas pulse in the tube was estimated to be approximately 100 μs, and the number density of the helium atoms exceeded 1018 cm−3. Hence, the molecules underwent more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 collisions with helium, ensuring that thermal equilibrium was achieved in the tube.
000 collisions with helium, ensuring that thermal equilibrium was achieved in the tube.
For mass analysis, the reaction products in the carrier gas were expanded into vacuum at the end of the extension tube. After passing through a skimmer, the ions gained kinetic energy of 3.5 keV in the acceleration region. To measure the neutral species, they were photoionized by an F2 laser (MPB PSX-100, ∼0.4 mJ cm−2). The ions traveled in a 1 m field-free region and were reflected by a dual-stage reflectron. Subsequently, they were detected using a Hamamatsu double-microchannel plate detector. The averaged time-of-flight (TOF) spectra (averaged over 200 sweeps) were sent to a computer for analysis. The mass resolution was sufficiently high (m/Δm ≈ 600 at m/z = 240) to distinguish isotopic peaks in the mass spectra. The attribution of the mass spectra observed at 303 and 1022 K by the peak distribution of the isotope distribution for each species is shown in Fig. S2 of ESI.† Thermal desorption spectra were recorded under the same conditions while heating the extension tube at a linear heating rate of 8.7 K min−1.
The stable geometries of Ru(C4H6)(CO)k+/0 (k = 1–3), Ru(C4H6)+/0, and Ru(C4H4)+/0 were obtained by quantum chemical calculations using Gaussian 16.25 ωB97X-D and Def2-TZVPP basis sets were used for the calculations. Here, the inner 28 electrons of Ru atoms are treated as a frozen core by an effective core potential that accounts for relativistic effects. Natural bond orbital (NBO) analyses were also performed to calculate atomic charges and spin densities.26,27 The optimized isomers were examined using vibrational frequency calculations to ensure that the optimized structures reflected the true potential minimum. All calculated energies described below include the zero-point vibrational energy correction. The internal available energy was calculated using thermal analysis based on the calculated vibrational frequencies. Binding energy was calculated as the difference like E(Ru(C4H6)(CO)k−1+) + E(CO) − E(Ru(C4H6)(CO)k+). The formation energy in this study refers to the sum of the electronic and zero-point vibrational energies.
3. Results and discussion
3.1. Thermal decomposition of Ru(C4H6)(CO)3+ at different temperatures
To observe the thermal decomposition of Ru(C4H6)(CO)3+, the ion was heated in He carrier gas inside the extension tube in the presence of O2. The mass spectra obtained at different temperatures are shown in Fig. 1(a). At 303 K, mass peaks corresponding to Ru(C4H6)(CO)3+ are predominantly observed. The appearance of these peaks proves that the intact Ru(C4H6)(CO)3 molecule, introduced into the vacuum, was ionized by the laser plasma without any significant fragmentation. At higher temperatures, mass peaks of Ru(C4H6)+ were observed at 700 K, and those of Ru(C4H4)+ and Ru(C2H2)+ were observed at 1000 and 1022 K. It is evident that the thermal decomposition of the tmm ligand occurred at higher temperatures.To closely examine the variation in the product species with temperature, an intensity map and TDS plot were obtained, as shown in Fig. 1(b) and Fig. 2. Evidently, Ru(C4H6)(CO)3+ remained intact within the temperature range of 300–500 K. Decomposition by CO loss proceeded sequentially in the temperature range of T = 500–700 K.
 | (1) |
 | (2) |
 | (3) |
To verify the effect of oxygen addition, a parallel experiment was conducted using helium carrier gas without oxygen. We begin with the differences observed in the mass spectra of the positive ions without heating. As shown in Fig. S3 of the ESI,† mass peaks of dimer, [Ru3(C4H6)(CO)3]2+, and peaks resulting from gradual CO desorption were observed on the heavy side of the mass spectrum, although weak. The amount of compositions resulting from CO desorption was higher in the absence of oxygen than in the presence of oxygen. The intensities of these minor peaks were sufficiently weak compared with those of the Ru3(C4H6)(CO)3+ monomer, and their decomposition contributions were not included in the analysis.
The TDS plot for the case without oxygen in the He carrier gas is shown in Fig. 3. The TDS curves showed a more complex shape over a wider temperature range than those in the presence of oxygen and did not clearly separate each step of the desorption reaction. The curves shown in Fig. 3 without oxygen showed large fluctuations, whereas those in Fig. 2 with oxygen exhibited small fluctuations.
Comparing the cases with and without oxygen, a commonality is found in the upper temperature limits: Ru(C4H6)(CO)2,3+ disappeared at 650 K, whereas Ru(C4H6)(CO)+ disappeared at 700 K in both cases. The ratios of Ru(C4H6)+, Ru(C4H4)+, and Ru(C2H2)+ at 950–1022 K were almost identical. Although the upper limits of the observed temperatures were the same, in the absence of oxygen, clusters with CO already coexisted even at room temperature as shown in Fig. S3 (ESI†), and the percentage of such clusters gradually increased up to 700 K. The changes observed at 500–700 K in the presence of oxygen started at room temperature and slowly progressed over a wide temperature range of 300–700 K in the absence of oxygen. Possible explanations for the differences observed with and without oxygen are as follows. (1) Oxygen quenched the excited helium atoms produced by the laser plasma, reducing the decomposition of the precursor and increasing the amount of ionized intact Ru-containing species because of soft ionization. (2) In the presence of oxygen, the excess energy gained by collisions with plasma-derived excited species in the ionization process was initially removed by the release of oxygen molecules, which were more weakly attached than CO and C4H6, and consequently the desorption of CO was suppressed in the low temperature range.
It is estimated that the distribution of precursor-related compositions observed in the absence of oxygen, including water-attached and protonated ions, is sensitive to laser plasma conditions and possibly affects the distribution of the reaction products of Ru(tmm)(CO)3 molecules. This may explain why the fluctuations in the data in Fig. 3 were larger than those with oxygen shown in Fig. 2.
Above 700 K, all the three CO ligands were completely removed, and the Ru(C4H6)+ was exclusively produced. With a further increase in temperature, Ru(C4H6)+ decreased, and Ru(C4H4)+ and Ru(C2H2)+ increased gradually above 800 K. The concomitant intensity changes suggest that Ru(C4H4)+ was generated by the dehydrogenation of Ru(C4H6)+. The reaction proceeded further, releasing acetylene from Ru(C4H4)+ to form Ru(C2H2)+.
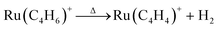 | (4) |
 | (5) |
In the presence of oxygen, Ru(C4H4)+ and Ru(C2H2)+ were not formed until 800 K. In the absence of oxygen, Ru(C4H4)+ gradually increases from 400 K, which is also on the lower side. These results suggest that in the presence of oxygen, the oxygen molecules inhibit CO desorption, and the tmm ligand changes by some mechanism.
3.2. Geometrical structures
Fig. 4 shows the geometrical structures of Ru(C4H6)(CO)0–3+ and Ru(C4H4)(CO)0–3(H2)+ calculated using DFT calculations. The atomic coordinates of the DFT-calculated structures and the natural charges and spins of the atoms obtained by NBO analysis are shown in Table S1 (ESI†). The most stable structures of both the cations and neutrals of Ru(C4H6)(CO)0–3+/0 are shown in Fig. S4 of the ESI.† There was little difference in the appearance of the most stable structures of positive ions and neutrals. The shape of the neutral Ru(C4H6)(CO)3 is similar to that of a piano stool, like Fe(C4H4)(CO)3, except that the ligand is square or umbrella-shaped, as shown in Fig. 5. | ||
| Fig. 5 Geometrical structures of Fe(C4H4)(CO)328 and Ru(C4H6)(CO)3,23,29 and a photograph of a vintage piano stool owned by the author. | ||
The stable spin state was found to be a doublet for all the ions. Thus, the delegated ions, Ru(C4H6)(CO)0–2+, retained the original geometries of the piano stool. The obtained geometrical structures of (CH2)3CRu(CO)1–3 resemble the optimized structure of the analogs of iron, umbrella-shaped trimethylenemethane complexes, (CH2)3CFe(CO)1–3.30 For Ru(C4H6)(CO)3+, the tmm ligand leans slightly, and one of the outer C atoms binds farther than the other two C atoms. According to the NBO analysis, this C atom carries a high spin density (+0.60e), suggesting that the p-electron was removed upon ionization. Namely, tmm is regarded as singly charged, tmm1−, in Ru(C4H6)(CO)3+, although tmm is doubly charged in neutral Ru(C4H6)(CO)3. In contrast, Ru(C4H6)+ shows nearly C3v symmetry, in which all three peripheral C atoms bind equidistantly to the Ru atom. Indeed, NBO analysis shows that all the peripheral C atoms carry similar low spin densities (ca. −0.08e), suggesting that tmm is doubly charged in Ru(C4H6)+. Instead, the Ru atom has a high spin density (+1.19e), which can be explained by the fact that the Ru atom is ionized to Ru3+ with five d-electrons.
3.3. Activation energy of the CO loss
Since each TDS curve in Fig. 2 represents the ion intensity as a function of temperature, the activation energy of ligand release, Ea, can be estimated using the Arrhenius equation.24Table 1 and Fig. S5 (ESI†) summarize the activation energies of each step. Activation energies were estimated from repeated measurements. The first two steps showed good reproducibility, whereas the third step exhibited a larger variation, likely due to the narrower temperature range over which this process occurred. The activation energy of reaction (1) is higher than those of reactions (2) and (3), which can be interpreted as destabilization with a decrease in the CO ligands.We also obtained the available internal energies of the ions at the ligand loss temperatures, which correspond to the total vibrational energies above the zero-point energies (Table 1) in the DFT calculations. Note that the vibrational degree of freedom decreased with the loss of the ligand, and the available energy also decreased, even at the same temperature.
The available energies of the ions at the ligand loss temperatures are almost the same as the activation energies, which indicates that the ions overcome the activation barrier with their internal energies, consistent with the basic idea of the RRK theory.31,32 The concept of available energy represents the total vibrational energy accessible at a given temperature, calculated as the sum of vibrational mode populations above the zero-point energy. While the activation energy represents the energetic barrier for CO dissociation, the available energy defines the portion of internal energy that can contribute to overcoming this barrier.
The agreement between these two values suggests that CO dissociation proceeds through an energy redistribution mechanism, where internal vibrational energy plays a key role in surpassing the activation barrier. This trend suggests that the activation energy is effectively governed by the internal energy available within the cluster, rather than solely by the intrinsic CO binding strength. As the number of ligands decreases, the reduction in vibrational degrees of freedom limits the available energy for overcoming the barrier, leading to the observed stepwise decrease in activation energy.
However, a puzzling issue remains: The activation energy for the CO loss should be almost the same as the binding energy of CO, as the release of CO does not require significant structural changes. This apparent discrepancy may be explained by considering that the experimental activation energies are lower than the computed binding energies because, at high temperatures, CO dissociation is facilitated not only by the energy difference between the initial and final states of CO release, but also by the redistribution of internal vibrational energy within the molecule.
Nevertheless, the activation energies of CO desorption from Ru(C4H6)(CO)k+ for the experimental TDS process were estimated to be 0.95 eV (k = 3), 0.63 eV (k = 2), and 0.66 eV (k = 1), which are consistent with the typical binding energy of CO to the transition metal atoms, such as Fe(CO)x+ and Cr(CO)x+.33,34 The experimentally observed activation energies were much lower than the binding energies. This difference cannot be explained by the simple release of CO. We simulated the possibility that the precursor ion takes a different form Ru(C4H4)(CO)3(H2)+, 5, with cyclobutadiene and H2 ligands. The formation energy from the most stable structure for the isomer is less stable than 1, +1.11 eV. The Ru–CO binding energies in 5, 6, and 7 were 0.91, 1.44, and 1.38 eV, respectively. Thus, the energy of the first CO loss decreased slightly, but the energies required for the subsequent steps were almost the same as those for 1–4. To clarify the details of the observed pyrolysis process, it is necessary to discuss the energy differences and reaction rates between several coexisting intermediates.35 If the back-and-forth between isomers is sufficiently fast to be regarded as equilibrium, the energy weighted by the equilibrium ratio is the effective energy.36
| Reaction | Activation energy (exptl.) | Available energy | Binding energy |
|---|---|---|---|
| k = 3 → 2 | 0.95 ± 0.01 | 0.90 | 1.50 |
| k = 2 → 1 | 0.63 ± 0.01 | 0.67 | 1.32 |
| k = 1 → 0 | 0.66 ± 0.06 | 0.52 | 1.53 |
3.4. Structures for Ru(C4H4)+
Wasendrup et al. investigated reactivity of M+ (M = Ru and Rh) with butadiene and acetylene (ethyne), finding that dehydrogenation of butadiene by M+ generates MC4H4+:37 The key intermediate reacted with ethyne to yield benzene C6H6 and bare M+. Structural investigations of MC4H4+ by collision-induced dissociation and ion–molecule reactions suggested that metallacyclopentadiene, or a structure with a C–C–C–C–Ru five-membered ring, for RuC4H4+ and a rhodium–cyclobutadiene complex were the most probable structures. In the present study, we observed an ion with the same stoichiometry generated via the dehydrogenation of Ru(C4H6)+. Although the structure of RuC4H4+ generated by thermal decomposition does not need to be the same as that of the key intermediate for the catalytic formation of benzene, the formation of a species with the same stoichiometry is interesting. Now, a question arises regarding the geometrical structure of RuC4H4+.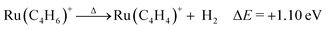 | (6) |
Fig. 6 shows the stable structures of RuC4H4+ obtained by DFT calculations. The most stable structure is ruthenium–cyclobutadiene complex, 9. The geometrical structure and spin density show that all four C atoms are equivalent, suggesting that C4H4 is a dianion. Hence, this complex was considered to be composed of Ru3+ and C4H42−. The significant stability of this complex is considered to originate from the aromaticity of C4H42−, which satisfies the Hückel rule.19 For neutral RuC4H4, the ruthenium–cyclobutadiene complex was not the most stable among the possible isomers because the charge state of the Ru atom was +2, which may not be the stable charge state for Ru (Fig. 7). Based on the formation energy, the dehydrogenation reaction is calculated to be endothermic by 1.10 eV.
 | ||
| Fig. 6 Stable structures of RuC4H4+, 9–12, determined by DFT calculations. The formation energies from the most stable structure, 9, are also shown. | ||
 | ||
| Fig. 7 Stable structures of neutral RuC4H4 obtained by DFT calculations. The formation energy with respect to the most stable structure is also shown. | ||
The second most stable structure is metallacyclopentadiene (cis-1,3-butadiene-1,4-diyl coordinated Ru), 10, the third one is 1-butene-3-yne coordinated Ru complex, 11, and the fourth one is bis-(ethyne) complex, 12. However, their formation energies are quite high compared to 9. Furthermore, the activation energy of dehydrogenation is higher, considering that dehydrogenation requires significant structural changes. In contrast, the experimentally observed activation energy of dehydrogenation was 1.12 eV. This value was comparable to the available internal energy of RuC4H6+ at 900 K (0.76 eV). Hence, the formation of complexes 10–12 is not plausible. We concluded that complex 9 was the only accessible complex.
3.5. Thermal decomposition of neutral Ru(C4H6)(CO)3
The thermal decomposition mechanism of neutral compounds has attracted considerable attention for application as precursors for CVD/ALD.9,38 The TDS plot of neutral Ru(C4H6)(CO)3, shown in Fig. 8, was interpreted based on the results of the cationic compound and DFT calculations. Note that no oxygen was added and only He was used as the carrier gas in this neutral species measurement. Unfortunately, Ru(C4H6)(CO)3 and Ru(C4H6)(CO)2 were not observed in this study. In the present experiment, the species produced by thermal decomposition at different temperatures were irradiated with an F2 excimer laser at 157 nm (7.87 eV); hence, only the species with ionization energies lower than 7.87 eV were photoionized and mass analyzed. The ionization energy of a Ru atom is known (7.36 eV); hence, the Ru atom can be ionized. For other species that were possibly produced by thermal decomposition, the vertical ionization energies were obtained by DFT calculations (see Table 2).| Species | Ionization energy |
|---|---|
| Ru(C4H6)(CO)3 | 9.11 |
| Ru(C4H6)(CO)2 | 8.55 |
| Ru(C4H6)(CO) | 7.68 |
| Ru(C4H6) | 6.87 |
| Ru(C4H4) | 6.15 |
| Ru(C2H2) | 7.06 |
| RuC | 7.42 |
The ionization energies of the intact Ru(C4H6)(CO)3 and Ru(C4H6)(CO)2 were so high that these species could not be photoionized. As we confirmed that Ru(C4H6)(CO)3 was introduced inside vacuum in an intact form, the missing signal at 300–500 K suggests Ru(C4H6)(CO)3 and/or Ru(C4H6)(CO)2. Appearance of Ru(C4H6)(CO)+ is the clear evidence of the CO loss occurring at 740 K as
 | (7) |
The decomposition proceeded further above 800 K, forming Ru(C4H6).
 | (8) |
The dehydrogenation of Ru(C4H6) was observed to form Ru(C4H4); however, its abundance was lower than that of cationic ions. This is consistent with the fact that neutral RuC4H4 is not very stable, as the charge state of the Ru atom is +2, which may not be the stable charge state for Ru. In the neutral case, RuC was abundantly formed at higher temperatures. Although the formation mechanism is unknown, it is highly likely that RuC was generated by the thermal decomposition of the ligand.
Ru(C4H6) and Ru(C4H4) were observed even at 300 K, suggesting that Ru(C4H6) and Ru(C4H4) may co-exist in the original sample. However, we consider that the amounts of Ru(C4H6) and Ru(C4H4) were sufficiently low because the intensities of Ru(C4H6)+ and Ru(C4H4)+ were lower than the noise level in the cationic mode. The ion intensities in the neutral mode are highlighted because of their low ionization energy and high ion detection efficiency at lower temperatures.
Conclusions
Thermal decomposition of cationic Ru(C4H6)(CO)3+ and neutral Ru(C4H6)(CO)3 was observed using gas-phase thermal desorption spectrometry. It was found that CO ligands were readily released, forming Ru(C4H6)+ at 600 K. Subsequently, Ru(C4H4)+ and Ru(C2H2)+ were produced as a result of H2 and C2H2 release above 800 K. Based on the experimental and computational results, Ru(C4H4)+ was identified as a ruthenium complex with unsubstituted cyclobutadiene, which is composed of Ru3+ and C4H42−. The high stability of this complex originates from the aromaticity of C4H42−, which satisfies the Hückel rule. The activation energy of ligand loss was estimated from the temperature dependence and was found to be consistent with the available energy at 600 K obtained from DFT calculations. This agreement explains the experimentally observed trend that the activation energy decreases as the number of CO ligands decreases. For the thermal decomposition of neutral Ru(C4H6)(CO)3, the appearance of photoionized Ru(C4H6)(CO)+ is a clear evidence of CO loss occurring at 740 K from Ru(C4H6)(CO)2. The decomposition further proceeds above 800 K, forming Ru(C4H6).Author contributions
Ken Miyajima: conceptualization, methodology, software, formal analysis, investigation, resources, data curation, writing – original draft, visualization. Toshiaki Nagata: investigation, methodology, visualization, writing – review & editing, Fumitaka Mafuné: conceptualization, writing – original draft, resources, writing – review & editing, supervision, project administration, funding acquisition. Tomohiro Tsugawa: writing – review & editing, visualization, resources, supervision. Ryosuke Harada: supervision, project administration.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by TANAKA PRECIOUS METAL TECHNOLOGIES Co., Ltd. This work was supported by KAKENHI Grant Number JP21K14583 from the Japan Society for the Promotion of Science (JSPS).References
- M. H. Hayes, C. L. Dezelah and J. F. Conley Jr., ECS Trans., 2018, 85, 743 CrossRef CAS
.
- J. H. Han, S. W. Lee, G. J. Choi, S. Y. Lee, C. S. Hwang, C. Dussarrat and J. Gatineau, Chem. Mater., 2009, 21, 207–209 CrossRef CAS
.
- H. J. Jung, J. H. Han, E. A. Jung, B. K. Park, J. H. Hwang, S. U. Son, C. G. Kim, T. M. Chung and K. S. An, Chem. Mater., 2014, 26, 7083–7090 CrossRef CAS
.
- H. Kim, T. Koseki, T. Ohba, T. Ohta, Y. Kojima, H. Sato and Y. Shimogaki, J. Electrochem. Soc., 2005, 152, G594 CrossRef CAS
.
- D. Josell, D. Wheeler, C. Witt and T. P. Moffat, Electrochem. Solid-State Lett., 2003, 6, C143 CrossRef CAS
.
- P. Kumar, R. K. Gupta and D. S. Pandey, Chem. Soc. Rev., 2014, 43, 707 RSC
.
- D. E. Trent, B. Paris and H. H. Krause, Inorg. Chem., 1964, 3, 1057 CrossRef CAS
.
- A. F. Bykov, N. B. Morozova, I. K. Igumenov and S. V. Sysoev, J. Therm. Anal., 1996, 46, 1551–1565 CrossRef CAS
.
- R. Gaur, L. Mishra, M. A. Siddiqi and B. Atakan, RSC Adv., 2014, 4, 33785–33805 RSC
.
- T. Aoyama and K. Eguchi, Jpn. J. Appl. Phys., 1999, 38, L1134–L1136 CrossRef CAS
.
- D. Z. Austin, M. A. Jenkins, D. Allman, S. Hose, D. Price, C. L. Dezelah and J. F. Conley Jr., Chem. Mater., 2017, 29, 1107–1115 CrossRef CAS
.
- D. Z. Austin, M. A. Jenkins, D. Allman, S. Hose, D. Price, C. L. Dezelah and J. F. Conley Jr., Chem. Mater., 2018, 30, 8983–8984 CrossRef CAS
.
- Z. Gao, D. Le, A. Khaniya, C. L. Dezelah, J. Woodruff, R. K. Kanjolia, W. E. Kaden, T. S. Rahman and P. Banerjee, Chem. Mater., 2019, 31, 1304–1317 CrossRef CAS
.
- S. Cwik, K. N. Woods, M. J. Saly, T. J. Knisley and C. H. Winter, J. Vac. Sci. Technol., A, 2020, 38, 012402 CrossRef CAS
.
- M. Hayes, M. A. Jenkins, J. Woodruff, D. F. Moser, C. L. Dezelah and J. F. Conley Jr., J. Vac. Sci. Technol., A, 2021, 39, 052402 CrossRef CAS
.
- J. R. Schneider, C. de Paula, J. Lewis, J. Woodruff, J. A. Raiford and S. F. Bent, Small, 2022, 18, 2105513 CrossRef CAS
.
- K. Miyajima and F. Mafuné, Chem. Phys. Lett., 2022, 786, 139191 CrossRef CAS
.
- Y. Kotsugi, S.-M. Han, Y.-H. Kim, T. Cheon, D. K. Nandi, R. Ramesh, N.-K. Yu, K. Son, T. Tsugawa, S. Ohtake, R. Harada, Y.-B. Park, B. Shong and S.-H. Kim, Chem. Mater., 2021, 33, 5639–5651 CrossRef CAS
.
- E. Hückel, Z. Phys., 1931, 70, 204–286 CrossRef
.
- P. Dowd, Acc. Chem. Res., 1971, 5, 242–248 CrossRef
.
- L. M. Fillman and S. C. Tang, Thermochim. Acta, 1984, 75, 71–84 CrossRef CAS
.
- M. D. Jones, R. D. W. Kemmitt and A. W. G. Platt, J. Chem. Soc., Dalton Trans., 1986, 1411–1418 RSC
.
- G. E. Herberich and T. P. Spaniol, J. Chem. Soc., Dalton Trans., 1993, 2471–2476 RSC
.
- K. Miyajima and F. Mafuné, J. Phys. Chem. A, 2015, 119, 8055–8061 CrossRef CAS
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
-
E. Glendening, A. Reed, J. Carpenter and F. Weinhold, NBO Version 3.1 Search PubMed
.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1998, 83, 735 CrossRef
.
- G. F. Emerson, K. Ehrlich, W. P. Giering and P. C. Lauterbur, J. Am. Chem. Soc., 1966, 88, 3172–3173 CrossRef CAS
.
- W. Strohmeier and G. Schönauer, Z. Naturforsch. B, 1962, 17, 848–854 CrossRef
.
- Q. Fan, H. Feng, W. Sun, Y. Xie, R. B. King and H. F. Schaefer III, Organometallics, 2012, 31, 3610–3619 CrossRef CAS
.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 2658–2661 CrossRef CAS
.
- R. A. Marcus, J. Chem. Phys., 1970, 52, 1018 CrossRef
.
- R. H. Schultz, K. C. Crellin and P. B. Armentrout, J. Am. Chem. Soc., 1991, 113, 8590–8601 CrossRef CAS
.
- F. A. Khan, D. E. Clemmer, R. H. Schultz and P. B. Armentrout, J. Phys. Chem., 1993, 97, 7978–7987 CrossRef CAS
.
- S. M. Lang, K. Miyajima, T. M. Bernhardt, F. Mafuné, R. N. Barnett and U. Landman, Phys. Chem. Chem. Phys., 2018, 20, 7781–7790 RSC
.
- T. Nagata, K. Miyajima and F. Mafuné, J. Phys. Chem. A, 2015, 119, 10255–10263 CrossRef CAS PubMed
.
- R. Wesendrup and H. Schwarz, Organometallics, 1997, 16, 461–466 CrossRef CAS
.
- A. Schneider, N. Popovska, I. Jipa, B. Atakan, M. A. Siddiqi, R. Siddiqui and U. Zenneck, Chem. Vap. Deposition, 2007, 13, 389–395 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Schematic of the cluster source, mass spectra, structural changes and differences in the formation energies of CO and H2 desorption processes, estimated activation energies for the thermal decomposition reactions, and atomic coordinates of DFT-calculated structures. See DOI: https://doi.org/10.1039/d5cp00200a |
| This journal is © the Owner Societies 2025 |





