Open Access Article
Open Access ArticleExtremely persistent dense active fluids
Grzegorz
Szamel
* and
Elijah
Flenner

Department of Chemistry, Colorado State University, Fort Collins, CO, USA. E-mail: grzegorz.szamel@colostate.edu
First published on 18th June 2024
Abstract
We study the dynamics of dense three-dimensional systems of active particles for large persistence times τp at constant average self-propulsion force f. These systems are fluid counterparts of previously investigated extremely persistent systems, which in the large persistence time limit relax only on the time scale of τp. We find that many dynamic properties of the systems we study, such as the mean-squared velocity, the self-intermediate scattering function, and the shear-stress correlation function, become τp-independent in the large persistence time limit. In addition, the large τp limits of many dynamic properties, such as the mean-square velocity and the relaxation times of the scattering function, and the shear-stress correlation function, depend on f as power laws with non-trivial exponents. We conjecture that these systems constitute a new class of extremely persistent active systems.
1 Introduction
Self-propelled or active particles, which use energy from their environment to perform persistent motion, behave in surprising and interesting ways.1–3 Recently, novel intermittent dynamics was identified in extremely persistent dense homogeneous two-dimensional systems.4–7 These systems were shown to relax on the time-scale of the persistence time τp by going through sequences of mechanical equilibria in which self-propulsion forces balance interparticle forces. In contrast, at low and moderate densities and long persistence times active matter undergo motility-induced phase separation (MIPS), and separate into regions with dramatically different densities.Here we examine the fluid counterparts of systems considered in ref. 4–7; extremely persistent homogeneous three-dimensional active fluids in which the interparticle interactions never manage to balance the self-propulsion forces, which influence particles’ motion in a nontrivial way. Although our fluid systems are less dense that those considered in ref. 4–7, they are dense enough such that we do not observe MIPS.
The parameter space of active systems is much larger than that of passive ones. At a minimum, one has to specify the average strength of active forces and their persistence time in addition to the set of parameters characterizing the corresponding passive system. If one considers athermal active systems, this results in a three-dimensional control parameter space. Thus, when comparing results of diverse studies, one needs to specify the path in the parameter space that one is following.
Early studies of dense homogeneous active systems focused on the glassy dynamics and the active glass transition.8–17 Many of these studies considered a limited range of persistence times and often examined the behavior at constant active temperature Ta that characterizes the long-time motion of an isolated active particle. For many models of self-propulsion, with increasing τp at constant Ta, the strength of active forces decreases and dense active systems typically become glassy, see Fig. 2(c) of ref. 6 for a recent example. Thus, to investigate the effects of extremely persistent active forces it is common to fix the force strength while increasing the persistence time.4,5,7
Recently, it has been shown that interesting behavior emerges for large persistence times in dense active particle systems.4–7,18 First, it was found that some extremely persistent dense active systems relax only on the time scale of τp.4–7 In these systems, the mean squared displacement (MSD) and the two-point overlap function exhibit well-defined large τp limits when plotted versus time rescaled by the persistence time.5 Distributions of velocity components were found to exhibit fat exponential tails.6 An intermediate-time plateau in the MSD was absent. Instead, a region of super-diffusive MSD scaling with time as tβ with β ≈ 1.6 for times less than τp was identified.6
Second, a recent study of two-dimensional active systems that remain fluid in the large persistence time limit showed that mesoscale advective flows, forming streams and vortices, emerge for large persistence times.18 These flow patterns resemble turbulent flows, and thus this phenomenon was identified as a type of “active turbulence”.
Here we study dense homogeneous three-dimensional active systems that do not undergo dynamic arrest in the large persistence time limit. In contrast to findings of ref. 4–7, for large persistence times τp many dynamic properties of our systems become τp-independent and their relaxation functions exhibit well-defined limits when plotted versus time not scaled by the persistence time. Also, the large persistence time limits of many properties depend on the strength of active forces f as power laws. We emphasize that both the active systems studied in ref. 4–7 and the fluid-like active systems studied here exhibit universal behavior, but on very different time scales.
It could be surmised that, in the infinite τp limit, our systems lie in the un-jammed phase of the active yielding phase diagram studied (in two dimensions) by Liao and Xu.19 However, these authors studied systems of particles interacting via a harmonic repulsion, in which interparticle forces are bounded, and thus strong enough self-propulsion forces are always able to induce motion. In contrast, in our systems interparticle forces are un-bounded, and thus their jamming phase diagram may be different from that obtained by Liao and Xu.
2 Simulations
We study a three-dimensional 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 binary mixture of spherically symmetric active particles interacting via the Weeks–Chandler–Andersen20 potential,
50 binary mixture of spherically symmetric active particles interacting via the Weeks–Chandler–Andersen20 potential, | (1) |
We use the athermal active Ornstein–Uhlenbeck particle model without thermal noise.21–23 The equation of motion for the position rn of particle n is
| ξ0ṙn = Fn + fn, | (2) |
 and fn is the active force. ξ0 = 1 is the friction coefficient of an isolated particle and ξ0σBB2/ε sets the unit of time.
and fn is the active force. ξ0 = 1 is the friction coefficient of an isolated particle and ξ0σBB2/ε sets the unit of time.
In turn, the self-propulsion forces evolve according to the Ornstein–Ulenbeck process. The equation of motion for the self-propulsion force acting on particle n reads
| τpḟn = −fn + ζn, | (3) |
 . The time step for the simulations ranged from 0.01 to 0.0001 with a smaller time step needed for larger f and longer τp. We simulated at least 10 τp for each of 4 productions runs, which required up to 109 time steps.
. The time step for the simulations ranged from 0.01 to 0.0001 with a smaller time step needed for larger f and longer τp. We simulated at least 10 τp for each of 4 productions runs, which required up to 109 time steps.
To check for finite size effects we studied systems of 1k, 8k, and 64k particles at large persistence times. We did not find any system size dependence of the system's dynamics or properties. The results shown in this work are for 1K particles unless otherwise noted in the figure caption.
3 Single-particle dynamics
We start by examining the persistence time dependence of the mean square velocity, , which is shown in Fig. 1. With increasing persistence time v2 decreases and then saturates. For the range of f that we studied, the cancellation of the interparticle and active forces is never complete and the system does not become arrested on the time scale of the persistence time.5,7
, which is shown in Fig. 1. With increasing persistence time v2 decreases and then saturates. For the range of f that we studied, the cancellation of the interparticle and active forces is never complete and the system does not become arrested on the time scale of the persistence time.5,7
Next, we examine the persistence time dependence of the MSD
 | (4) |
 | ||
| Fig. 2 The mean squared displacement (MSD) 〈δr2(t)〉 for f = 5.48 and several τp. For shorter τp MSDs display a glassy plateau followed by diffusive motion. With increasing τp an extended superdiffusive region appears that is analyzed in Fig. 4(a). | ||
 | ||
| Fig. 3 The long time diffusion coefficient D for fixed active force strength f as a function of persistence time. D grows with increasing τp and is proportional to τp in the large τp limit. | ||
At long times, the MSD exhibits diffusive behavior. The self-diffusion coefficient,  , is shown in Fig. 3. For a given f it monotonically increases with increasing τp. At large τp we find that D ∼ τp, indicated by the dashed lines.
, is shown in Fig. 3. For a given f it monotonically increases with increasing τp. At large τp we find that D ∼ τp, indicated by the dashed lines.
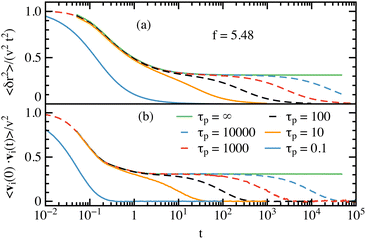
We find a surprising time-dependence of the MSD between the initial ballistic and the long-time diffusive regimes. In Fig. 4(a) we show the MSD divided by v2t2 to show this time-dependence more clearly. The MSD exhibits a superdiffusive behavior that does not follow a single power law. Instead, a second, intermediate time ballistic regime appears, with velocity v1. In the τp → ∞ limit the systems stays in the second ballistic regime.
The time-dependence of the MSD shown in Fig. 4(a) is reflected in the time-dependence of the velocity auto-correlation function,  , shown in Fig. 4(b). We observe a two-step decay, which becomes increasingly more pronounced with increasing τp. This agrees with the observation in ref. 18, except that, since we keep strength of active forces f constant, we find the plateau level to be τp independent. We note that the plateau levels are the same in both panels of Fig. 4. The plateau level decreases with increasing self-propulsion force f.
, shown in Fig. 4(b). We observe a two-step decay, which becomes increasingly more pronounced with increasing τp. This agrees with the observation in ref. 18, except that, since we keep strength of active forces f constant, we find the plateau level to be τp independent. We note that the plateau levels are the same in both panels of Fig. 4. The plateau level decreases with increasing self-propulsion force f.
Results shown in Fig. 4 suggest that, in the large τp limit, the diffusion can be thought of as a random walk consisting of steps of length v1τp taken every τp. This reasoning rationalizes the observed scaling D ∼ τp. We note that while the physical picture of a random walk of steps of length v1τp taken every τp is identical to the behavior expected at low densities, our systems exhibit highly non-trivial dependence of v1 on the average self-propulsion force f, which we will discuss at the end of this section. This dependence suggests that the observed effective behavior is strongly influenced by interparticle interactions.
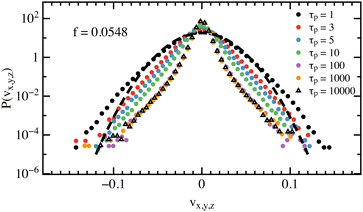
In Fig. 5 we show velocity distributions. As found by Keta et al.,6 the distributions are strongly non-Gaussian. Their broad tails become more prominent with increasing τp and then saturate.
The evolution of the MSD with the persistence time is reflected in the τp dependence of the self-intermediate scattering function
 | (5) |
We chose k = 5.3, which is approximately equal the first peak of the total static structure factor. In Fig. 6 we show Fs(k;t) for f = 0.0548. With increasing τp the intermediate time glassy plateau disappears and the decay changes from stretched exponential, to exponential, then to compressed exponential. Shown in the inset to Fig. 6 is the parameter Γ obtained from fits to Fs(k;t) = ae−(t/τs)Γ where we restrict a ≤ 1. Γ increases with increasing τp and reaches a plateau above τp ≈ 94.
We find that the large persistence time limits of several properties discussed above depend on the strength of the active forces as power laws. In Fig. 7 we show the large τp limits of v2 (squares), D/τp (circles) and τs (triangles). We find that the former two quantities follow a power law with f with statistically the same exponent, 2.6 ± 0.1 for v2 and 2.5 ± 0.1 for D/τp. We note that v2 is bound from above by f2, which corresponds to the limit in which interactions become irrelevant compared to active forces. Thus, we do not expect the power law for v2 to extend up to arbitrary large f. The power law of the relaxation time, τs ∼ f−1.3 can be related to that of v2; in the large τp limit Fs decays on the time scale on which a particle moves over its diameter, which scales as v.
We also analyzed the dependence of v1 on the strength of the active forces. To this end, we extracted v12 for each f by finding the plateau in 〈δr2(t)〉/t2 for large τp. We find that v12 grows with f as a power law with an exponent of 2.5 ± 0.2, which is statistically the same as the exponent for v2.
We emphasize that, although in the large τp limit the motion of individual particles is close to ballistic, it is still influenced by the interparticle interactions in a highly non-trivial way. If there were no interparticle interactions, scaling exponents discussed above would have values 2 and −1.
4 Collective dynamics
The quantities discussed in Section 3 describe the single particle motion in our many-particle systems. To examine collective properties we investigated the persistence time dependence of the stress fluctuations and the rheological response. First, we examined the shear-stress correlation function Σαβ(t) = V−1〈σαβ(t)σαβ(0)〉, where | (6) |
In Fig. 8 we report the normalized shear stress correlation function, Σxy(t)/Σxy(0), for f = 0.0548 and a large range of τp. For small τp there is a rapid decay to an emerging plateau followed by a slow decay to zero. With increasing persistence time, the decay of Σxy(t) becomes less stretched; it is exponential for a long enough τp. In the inset we show the dependence of the initial value, Σxy(0), on τp. We see that the initial value first grows with τp and then plateaus.
To probe the rheological response of our active systems we simulated shear flow by adding to the equations of motion (2) a bulk non-conservative force F![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n = ξ0
n = ξ0![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ynex with Lees–Edwards boundary conditions.25 In Fig. 9 we show the average shear stress, 〈σxy〉/
ynex with Lees–Edwards boundary conditions.25 In Fig. 9 we show the average shear stress, 〈σxy〉/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , for f = 0.548 and a large range of τp. In Fig. 10 we show the τp dependence of the zero-shear-rate viscosity obtained from the small
, for f = 0.548 and a large range of τp. In Fig. 10 we show the τp dependence of the zero-shear-rate viscosity obtained from the small ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) plateaus of 〈σxy〉/
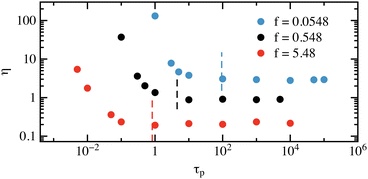
plateaus of 〈σxy〉/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . We find that η initially decreases and reaches a τp-independent plateau.
. We find that η initially decreases and reaches a τp-independent plateau.
 | ||
Fig. 9 Average shear stress 〈σxy〉 divided by the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) at constant f = 0.548 for a range of persistence times. The zero-shear-rate viscosity η can be obtained from the small shear rate plateau. at constant f = 0.548 for a range of persistence times. The zero-shear-rate viscosity η can be obtained from the small shear rate plateau. | ||
We find that large τp limits of collective properties also scale with f as power laws. In Fig. 11 we show the dependence of the large τp limits of the relaxation time of the normalized stress tensor autocorrelation function and of the viscosity on the strength of the self-propulsion.
5 Static structure
When analyzing the dynamics in passive systems, one usually tries to make connections between the average distribution of the particles and their dynamics. To check how the average arrangement of the particles in our active systems changes with increasing τp we evaluated the total steady-state structure factor | (7) |
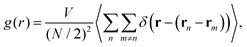 | (8) |
In Fig. 12 we show that the peak height of S(k) initially decreases with increasing τp, which nicely correlates with relaxation getting faster and viscosity decreasing. The peak height then saturates at a large persistence time. The large τp limit of the structure factors still looks liquid-like, and thus it does not signal the interesting dynamics we uncovered. To describe the dynamics of extremely persistent dense active fluids one cannot rely upon static structure factors only.
We note that the absence of any small wavevector peak implies that our systems are homogeneous. We confirmed this observation by evaluating local density histograms at several simulated state points. Incidentally, the homogeneity allows us to rationalize the absence of shear thickening that was observed at large self-propulsions in ref. 26, which was attributed to clustering and was dubbed motility-induced shear thickening.
In Fig. 13 and 14 we show the pair correlation function between the large particles. In contrast to the behavior exhibited by the structure factor, g(r) is not very sensitive to the changes in the persistence time. However, the height of the first peak of g(r) decreases rapidly with increasing self-propulsion force f while the position of the first peak shifts to the smaller r, suggesting that the system becomes effectively less crowded with increasing f. This rationalizes decreasing large persistence time limits of the relaxation times and of the viscosity and increasing large persistence time limit of the diffusion coefficient.
 | ||
Fig. 13 The pair correlation function between the large particles for f = 0.548 and f = 5.48 and two representative persistence times τp = 1 and τp = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. For small f the first peak in g(r) is sharply peaked; it is shown in Fig. 14. There is little dependence of g(r) on the persistence time. 000. For small f the first peak in g(r) is sharply peaked; it is shown in Fig. 14. There is little dependence of g(r) on the persistence time. | ||
6 Conclusions
We conjecture that the systems we presented here form a new class of extremely persistent active matter systems. Earlier investigations5,7 revealed systems that relax on the time scale of the self-propulsion and exhibit intermittent dynamics. The systems with intermittent dynamics slow down with increasing τp at fixed f, but they exhibit universal dynamics when investigated as a function of time rescaled by τp. In contrast, the systems we presented exhibit universal dynamics for large τp but as a function of un-scaled time. We expect that for higher volume fractions there is a transition between the regime in which the relaxation becomes independent of the persistence time of the self-propulsion, which is the regime we analyzed, and the regime in which the system flows only on the time scale of the self-propulsion, which is the regime investigated earlier.5,7 At a fixed strength of the active forces the transition is driven by the density. Since interparticle interactions in our systems are not bounded, it is not obvious whether, at constant density, the transition can be induced by changing the force strength, like in two-dimensional systems with harmonic interactions, which were investigated by Liao and Xu.19For the systems studied here, the single-particle motion exhibits two ballistic regions separated by a superdiffusive regime. Classic signatures of two-step relaxation seen in glassy systems are absent both in the MSD and Fs(k;t). Therefore, our systems are not close to a glass transition. Many properties that quantify the large persistence time limit of the relaxation depend on the strength of the active forces as a power law.
In contrast to Keta et al.,18 we did not observe essential features of “active turbulence”. In particular, mean-squared displacement difference of initially close by particles monitored by Keta et al. was only slightly smaller than the MSD. This may not be surprising since our systems have somewhat lower density and larger active forces.
Finally, we note that approximate theories developed to describe the relaxation in active fluids27–32 we tested against computer simulations for rather limited range of self-propulsion force f and persistence time τp. The discovery of a new paradigm of extremely persistent active fluids with non-trivial power laws calls for additional theoretical work. The single-particle motion in the systems that we investigated can perhaps be described as a persistent random walk with renormalized density and self-propulsion-dependent velocity. However, it is unlikely that such a simple picture could also account for the collective dynamic properties.
Data availability
Data for this article is available on Dryad at https://doi.org/10.5061/dryad.xsj3tx9q4.Conflicts of interest
There are no conflicts to declare.Appendices
Motility induced phase separation (MIPS) is often reported and extensively studied in active systems. In two-dimensional systems it has been shown that MIPS will occur with increasing τp and fixed f over a range of densities.24 We note that, in three-dimensional systems states with MPIS, coexistence is metastable with respect to active crystallization in a large region of the parameter space.33 Here we claim that our system is not undergoing MIPS at any of the state points studied.To determine if the system undergoes MIPS one can examine structural signatures and density distributions. One structural signature is an upturn of the structure factor S(k) at small wavevectors k. However, an upturn can occur if there are large density fluctuations but no MIPS. The density distribution is another method to examine MIPS, where two peaks indicate that the system has separated into high density and low density regions. We use these two methods.
To calculated the density distribution we divide the system into boxes of length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2.6082 and determine the density inside each box. For each configuration used in the calculation we determine the density distribution of the small boxes and then average these distributions. To examine smaller wavevectors and to get a more accurate density distribution we present results for our 64k systems.
= 2.6082 and determine the density inside each box. For each configuration used in the calculation we determine the density distribution of the small boxes and then average these distributions. To examine smaller wavevectors and to get a more accurate density distribution we present results for our 64k systems.
As shown in Fig. 12 we don’t see any evidence of an upturn in the low wavevector values of S(k) for f = 0.548. The only f we do observe an upturn at small wavevectors is f = 54.8, Fig. 15(a). We note that the small k upturn does not increase with increasing τp, and thus we don’t expect any changes with increasing τp. The density distribution for these state points do not show a two peak structure and remains statistically unchanged when increasing τp, Fig. 15(b). We conclude that there are large density fluctuations, but the system is not yet undergoing MIPS. For larger f we expect that this system will exhibit MIPS.
 | ||
| Fig. 15 (a) The structure factor S(k) for f = 54.8 for our 64k system. There is a distinct upturn at small wavevectors which is not see for our other f. (b) The density distribution for the same f, N, and τp as shown in (a), and for two state points for which structure factors were shown in Fig. 12. We do not observe the two peak structure expected for systems undergoing motility induced phase separation. | ||
Acknowledgements
We thank L. Berthier and P. Sollich for discussions and comments on the manuscript. Part of this work was done when GS was on sabbatical at Georg-August Universität Göttingen. He thanks his colleagues there for their hospitality. We gratefully acknowledge the support of NSF Grant No. CHE 2154241.Notes and references
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. Aditi Simha, “Hydrodynamics of soft active matter”, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- J. Elgeti, R. G. Winkler and G. Gompper, “Physics of microswimmers-single particle motion and collective behavior: a review”, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, “Active particles in complex and crowded environments”, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- R. Mandal, P. J. Bhuyan, P. Chaudhuri, C. Dasgupta and M. Rao, “Extreme active matter at high densities”, Nat. Commun., 2020, 11, 2581 CrossRef CAS PubMed.
- R. Mandal and P. Sollich, “How to study a persistent active glassy system”, J. Phys.: Condens. Matter, 2021, 33, 184001 CrossRef CAS.
- Y.-E. Keta, R. L. Jack and L. Berthier, “Disordered Collective Motion in Dense Assemblies of Persistent Particles”, Phys. Rev. Lett., 2022, 129, 048002 CrossRef CAS.
- Y.-E. Keta, R. Mandal, P. Sollich, R. L. Jack and L. Berthier, “Intermittent relaxation and avalanches in extremely persistent active matter”, Soft Matter, 2023, 19, 3871–3883 RSC.
- L. Berthier and J. Kurchan, “Non-equilibrium glass transitions in driven and active matter”, Nat. Phys., 2013, 9, 310–314 Search PubMed.
- L. Berthier, “Nonequilibrium Glassy Dynamics of Self-Propelled Hard Disks”, Phys. Rev. Lett., 2014, 112, 220602 CrossRef PubMed.
- R. Ni, M. A. Cohen Stuart and M. Dijkstra, “Pushing the glass transition towards random close packing using self-propelled hard spheres”, Nat. Commun., 2013, 4, 2704 CrossRef PubMed.
- G. Szamel, E. Flenner and L. Berthier, “Glassy dynamics of athermal self-propelled particles: Computer simulations and a nonequilibrium microscopic theory”, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 062304 CrossRef.
- R. Mandal, P. J. Bhuyan, M. Rao and C. Dasgupta, “Active fluidization in dense glassy systems”, Soft Matter, 2016, 12, 6268–6276 RSC.
- L. Berthier, E. Flenner and G. Szamel, “Perspective: Glassy dynamics in dense systems of active particles”, J. Chem. Phys., 2019, 150, 200901 CrossRef PubMed.
- N. Klongvessa, F. Ginot, C. Ybert, C. Cottin-Bizonne and M. Leocmach, “Active Glass: Ergodicity Breaking Dramatically Affects Response to Self-Propulsion”, Phys. Rev. Lett., 2019, 123, 248004 CrossRef CAS PubMed.
- L. Janssen, “Active glasses”, J. Phys.: Condens. Matter, 2019, 31, 503002 CrossRef CAS PubMed.
- E. Flenner, G. Szamel and L. Berthier, “The nonequilibrium glassy dynamics of self-propelled particles”, Soft Matter, 2016, 12, 7136–7149 RSC.
- L. Berthier, E. Flenner and G. Szamel, “How active forces influence nonequilibrium glass transitions”, New J. Phys., 2017, 19, 125006 CrossRef.
- Y.-E. Keta, J. U. Klamser, R. L. Jack and L. Berthier, “Emerging mesoscale flows and chaotic advection in dense active matter”, Phys. Rev. Lett., 2024, 132, 218301 CrossRef CAS.
- Q. Liao and N. Xu, “Criticality of the zero-temperature jamming transition probed by self-propelled particles”, Soft Matter, 2018, 14, 853–860 RSC.
- J. D. Weeks, D. Chandler and H. C. Andersen, “Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids”, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- G. Szamel, “Self-propelled particle in an external potential: Existence of an effective temperature”, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012111 CrossRef PubMed.
- U. M. B. Marconi, N. Gnan, M. Paoluzzi, C. Maggi and R. Di Leonardo, “Velocity distribution in active particles systems”, Sci. Rep., 2016, 6, 23297 CrossRef CAS PubMed.
- E. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. van Wijland, “How Far from Equilibrium Is Active Matter?”, Phys. Rev. Lett., 2016, 117, 038103 CrossRef PubMed.
- M. Paoluzzi, D. Levis and I. Pagonabarraga, “From motility-induced phase-separation to glassiness in dense active matter”, Commun. Phys., 2022, 5, 111 CrossRef.
- A. W. Lees and S. F. Edwards, “The computer study of transport processes under extreme conditions”, J. Phys. C: Solid State Phys., 1972, 5, 1921–1929 CrossRef.
- A. Gülce Bayram, L. Biancofiore, F. J. Schwarzendahl, H. Löwen and L. Biancofiore, “Motility-induced shear thickening in dense colloidal suspensions”, Soft Matter, 2023, 19, 4571–4578 RSC.
- G. Szamel, “Theory for the dynamics of dense systems of athermal self-propelled particles”, Phys. Rev. E, 2016, 93, 012603 CrossRef PubMed.
- A. Liluashvili, J. Ónody and T. Voigtmann, “Mode-coupling theory for active Brownian particles”, Phys. Rev. E, 2017, 96, 062608 CrossRef PubMed.
- M. Feng and Z. Hou, “Mode coupling theory for nonequilibrium glassy dynamics of thermal self-propelled particles”, Soft Matter, 2017, 13, 4464–4481 RSC.
- J. Reichert, L. F. Granz and T. Voigtmann, “Transport coefficients in dense active Brownian particle systems: mode-coupling theory and simulation results”, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 27 CrossRef CAS PubMed.
- M. Feng and Z. Hou, “Mode-coupling theory for the dynamics of dense underdamped active Brownian particle system”, J. Chem. Phys., 2023, 158, 024102 CrossRef CAS PubMed.
- V. E. Debets and L. M. C. Janssen, “Mode-coupling theory for mixtures of athermal self-propelled particles”, J. Chem. Phys., 2023, 159, 014502 CrossRef CAS PubMed.
- A. K. Omar, K. Klymko, T. GrandPre and P. L. Geissler, “Phase Diagram of Active Brownian Spheres: Crystallization and the Metastability of Motility-Induced Phase Separation”, Phys. Rev. Lett., 2021, 126, 188002 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |