Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structured bubbling in vibrated gas-fluidized beds of binary granular particles: experiments and simulations†
Jagan Mohan
Sanghishetty
a,
Naimah M.
Russ
c,
Christopher
Spitler
a,
Qiang
Guo
 a,
D. R.
Nagaraj
b,
Raymond S.
Farinato
a,
D. R.
Nagaraj
b,
Raymond S.
Farinato
 b and
Christopher M.
Boyce
b and
Christopher M.
Boyce
 *a
*a
aDepartment of Chemical Engineering, Columbia University, New York, NY 10027, USA. E-mail: cmb2302@columbia.edu
bDepartment of Earth and Environmental Engineering, Columbia University, New York, NY 10027, USA
cDepartment of Chemical Engineering, Tuskegee University, Tuskegee, AL 36088, USA
First published on 21st June 2024
Abstract
Mixing and segregation of granular particles on the basis of size and density from vertical vibration or upward gas flow is critical to a wide range of industrial, agricultural and natural processes. Recently, combined vibration and gas flow under certain conditions has been shown to create periodically repeating structured bubbling patterns within a fluidized bed of spherical, monodisperse particles. Here, we demonstrate with experiments and simulations that structured bubbling can form in binary mixtures of particles with different size and density, but with similar minimum fluidization velocities. Structured bubbling leads to particles mixing regardless of initial particle configuration, while exciting particles with only gas flow produces smaller unstructured bubbles which act to segregate particles. Discrete particle simulations match the experimental results qualitatively and, in some regards quantitatively, while continuum particle simulations do not predict mixing in the case of structured bubbling, highlighting areas for future model improvement.
1. Introduction
Granular particles can be “fluidized” or excited into a fluid-like state by subjecting them to external forces which overcome gravitational force, typically either via vertical vibration1,2 or vertical gas flow.3,4 Gas flow fluidizes particles when the drag force overcomes gravity, given by the superficial gas velocity U being greater than Umf, the minimum fluidization velocity.3 Vertical vibration can bring grains into a fluid-like state when the peak vibrational acceleration is greater than gravitational acceleration, expressed non-dimensionally by the vibration strength: , where f and A are the vibration frequency and amplitude, respectively, and g is the gravitational acceleration.5,6 Combined gas flow and vibration in a vibrated gas-fluidized bed is often used to fluidize cohesive particles, and recent studies have demonstrated that combined gas flow and vibration can induce scalable, structured flow patterns in grains,7 such as structured bubbling,8 convective cells9 and surface waves.10
, where f and A are the vibration frequency and amplitude, respectively, and g is the gravitational acceleration.5,6 Combined gas flow and vibration in a vibrated gas-fluidized bed is often used to fluidize cohesive particles, and recent studies have demonstrated that combined gas flow and vibration can induce scalable, structured flow patterns in grains,7 such as structured bubbling,8 convective cells9 and surface waves.10
Mixing of particles of different size, density and shape is critical to a number of industrial and agricultural processes.11–18 Fluidization of grains via vibration or gas flow can cause different types of grains to mix if vigorous convection is induced in the particles. However, vigorous fluidization of particles tends to be chaotic in nature,19,20 making the dynamics difficult to scale and optimize, often causing granular flow processes operate inefficiently.21 Less vigorous fluidization via Γ ∼ 1 or U/Umf ∼ 1 often causes particles to segregate vertically on the basis of size or density.22–25
Gas voids or bubbles often rise through gas fluidized beds, inducing mixing mainly based on particles rising in the wake of bubbles.26 The dynamics of these bubbles are typically mathematically chaotic;19 however, oscillating gas flow19,20 or combined constant gas flow and vibration8 can structure bubbles to form and rise in a triangular array pattern. Structured bubbling has been demonstrated to form the same bubble patterns when scaled vertically27 and horizontally8 as well as create predictable particle convection patterns,28 thus addressing issues with scale-up and optimization of fluidized bed processes.19 So far, structured bubbling has only been demonstrated in monodisperse particles.
Here, we demonstrate that structured bubbling can form in binary mixtures of particles of different size and density subject to combined constant gas flow and vibration. Structured bubbling causes the particles to mix, despite their differences in size and density. When subject to gas flow alone at the same velocity, the particles segregate with the denser particles falling to the bottom. Discrete particle and continuum particle simulations reproduce the structured bubbling in binary granular particles; however, while discrete particle simulations predict the particles mixing, continuum particle simulations predict the particles segregating.
2. Methods
2.1 Experiments
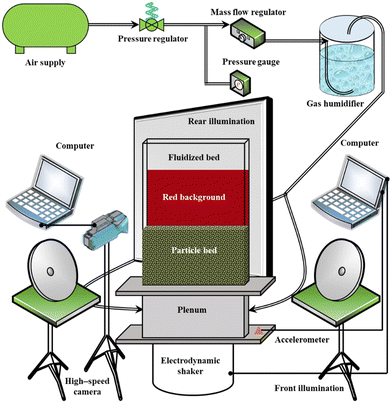
Transparent polymethyl methacrylate (PMMA) sheets were used to construct a pseudo-2D fluidized bed with 200 mm (width) × 8 mm (horizontal thickness) × 500 mm (height) dimensions. A 3 mm thick sintered bronze porous plate with an average pore size of 15 µm (HENGKO Tech.) was used to support the particle bed and distribute gas flow uniformly across the base of the fluidized bed. The fluidized bed was mounted onto the top plate of an electrodynamic shaker (Labworks; ET-140), powered by its amplifier (Labworks Inc., FS-140) to induce vertical vibration. The instantaneous vibrational peak-to-peak displacement and frequency are measured and controlled using an accelerometer (PCB, J352C33), attached to the base of the bed. The shaker was operated and controlled using VibeLab software on a desktop computer. A schematic of the experimental setup is shown in Fig. 1.Fluidizing air was fully humidified using a water bubbler to avoid static charge buildup. Antistatic liquid was sprayed on the internal surfaces of the bed as well as on the particles before they were poured into the bed. The top of the fluidized bed was open to air at atmospheric pressure. All the particles that are used in the experiments are spherical in shape with property specifications as given in Table 1. The “light particles” had a density of ρ = 4100 kg m−3 and a diameter of dp = 400–600 µm, while the “heavy particles” had ρ = 6100 kg m−3 and dp = 400–500 µm. Both particle types had a minimum fluidization velocity Umf = 0.37 m s−1. The bed was filled with particles to a total height of 50 mm. The minimum fluidization velocity for each of the components was determined experimentally, separately, by reducing the superficial gas velocity steadily with time with no vertical vibration applied, from a vigorously bubbling state until no bubbles and no particle motion were observed. In these de-fluidization experiments, the pressure drop across the bed was monitored using a LabVIEW program. The value of Umf was determined as the highest superficial velocity at which the pressure drop across the bed was below the value needed to support the weight of the bed per unit cross-sectional area. For bubbling fluidization experiments, the gas flow rate was kept at a constant value, corresponding to U/Umf = 1.4. A mass flow controller (Alicat; MCP-250 slpm), was used to control the gas flow rate. These gas flow and vibration conditions were chosen because they have been shown previously in monodisperse particles8 to create the highest level of structured bubbling, and the level of structuring decreases significantly with minor changes in gas flow and vibration conditions. We only use these gas flow conditions with and without vibration so as to compare highly structured bubbling with unstructured bubbling directly. We leave it to future studies to compare across a range of vibration and gas flow conditions to study the effects of partial bubble structuring on binary particle mixtures.
| Method | Component | Size range (µm) | Material density (kg m−3) | Material | U mf (m s−1) | Color |
|---|---|---|---|---|---|---|
| Experiment | Light | 400–600 | 4100 | Ceramic | 0.368 | White |
| Experiment | Heavy | 400–500 | 6100 | Ceramic | 0.372 | Black |
| CFD-DEM | Light | 500 | 4000 | Ceramic | 0.332 | White |
| CFD-DEM | Heavy | 415 | 6000 | Ceramic | 0.332 | Black |
| MFM | Light | 500 | 4000 | Ceramic | 0.284 | White |
| MFM | Heavy | 415 | 6000 | Ceramic | 0.293 | Black |
Optical imaging and high-speed videos of the front view of the bed were captured using an advanced color camera (AOS Technologies AG, PROMON U750) at a framerate of 50 frames per second, corresponding to ten times the vibration frequency of the shaker. The experiments were carried out over the course of 180 s. A red colored non-reflecting background was used in optical imaging to aid the particle tracking to provide color contrast with particles. The white-colored light particles and black-colored heavy particles contrasted with the red background. Five different initial conditions or particle arrangements are used in the experiments to study the mixing and segregation characteristics as shown in Fig. 2. In binary configurations, equal bulk volumes of both types of particles were added. The bottom 12 mm of particles of the bed cannot be observed as they are blocked by the horizontal opaque acrylic plate that joins fluidized bed to the gas distributor. Thus, the bottom layer of particles appears to be shorter than the top layer in experiments, although the two layers in fact are equal in height.
The gas flow rate for all the experiments was kept at 1.4Umf along with vibration conditions of f = 5 Hz and A = 4.5 mm, corresponding to a vibration strength of Γ = 0.45. These gas flow and vibration conditions were chosen because prior experimental results indicated that they produced the most structured or patterned bubbling for a range of monodisperse particles.8 Gas flow and vibration were induced simultaneously to start the experiment. Front-lighting was used to quantify the mixing characteristics of the system. After recording the front-lighting case for 180 s, the system was switched to backlighting while keeping the gas flow and vibration in progress. A back-lighting video was recorded to image bubble dynamics after a statistical-steady-state had been reached.
2.2 CFD-DEM simulations
Computational fluid dynamics-discrete element method (CFD-DEM)29 simulations were used to model the coupled gas-granular flow. This method models the interstitial gas as a continuum using CFD and tracks the particles using DEM.30 In CFD-DEM, the CFD cells are larger than the particles, and gas flow is solved for using volume-averaged Navier–Stokes equations31 accounting for the gas volume fraction of each cell. Particle motion is tracked using Newtonian kinematics with contact forces accounted for based on springs and dashpots for the overlap between “soft” spheres. Particle and gas flow are coupled based on buoyancy and a drag law32 based on the particle Reynolds number and local particle volume fraction. CFDEMCoupling open-source software was used for these simulations; this software couples the CFD of OpenFOAM with the DEM of LIGGGHTS. The full CFD-DEM model equations are provided in the ESI.†g = 9.81 + (2πf)2A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft) sin(2πft) | (1) |
2.3 MFM simulations
Multi-fluid model (MFM) Simulations were carried out using MFiX,34 an open-source software package created by the National Energy Technology Lab for modelling multiphase gas-granular flows. The solid particles are approximated to be a continuous medium, interpenetrating with fluidizing gas and other solids species within a Eulerian grid. This simulation method is advantageous over methods, such as CFD-DEM, that resolve individual particles, as it is much less computationally intensive and capable of simulating larger systems. Behavior of the fluidized solids are modelled according to the kinetic theory of granular flows (KGTF)35 combined with frictional solids stress models from soil mechanics for high particle volume fractions.36 Conservation of momentum for each solid species is solved for and coupled to the gas momentum equation via a drag law, in this case the Gidaspow drag model.37 The overall particle rheology was simulated using the Guo–Boyce model.8 Further, a momentum exchange model between the two solids phases was used.38 The full MFM model equations are provided in the ESI.†2.4 Post-processing
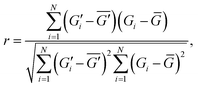 | (2) |
 are the intensity at pixel i in one frame and a frame two vibration periods later, respectively. Overbars indicate averages over space and time after statistical steady state has been reached. For experiments, the G values are taken based on the grayscale value of signal intensity in backlit images with pixels gathered together into square groups 4.0 mm in side length to match the size of CFD cells in simulations. In CFD-DEM, the G values are taken based on the void fraction in the CFD cells.
are the intensity at pixel i in one frame and a frame two vibration periods later, respectively. Overbars indicate averages over space and time after statistical steady state has been reached. For experiments, the G values are taken based on the grayscale value of signal intensity in backlit images with pixels gathered together into square groups 4.0 mm in side length to match the size of CFD cells in simulations. In CFD-DEM, the G values are taken based on the void fraction in the CFD cells.
s(k) = x1(k)ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x1(k) + x2(k)ln x1(k) + x2(k)ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x2(k) x2(k) | (3) |
 | (4) |
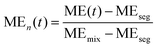 | (5) |
3. Results and discussion
3.1 Flow dynamics
Experiments, CFD-DEM simulations and MFM simulations demonstrate flow dynamics in binary mixtures of particles with (i) different initial particle configurations and (ii) gas flow alone vs. combined gas flow and vibration to investigate the effects of these parameters on bubble dynamics and particle mixing. | ||
| Fig. 5 Time series of front-lit images of experimental cases with combined gas flow and vibration for different initial configurations (a)–(c). | ||
Experiments with only gas flow through particles show that gas bubbles smaller than those seen in the vibration cases rise in a disordered manner through the particles, regardless of the initial particle condition (Fig. 6). At steady-state in binary mixture cases, particles are somewhat mixed, yet heavy particles tend to gather at the bottom of the bed and light particles tend to gather at the top of the bed throughout the bubble dynamics (Fig. 7). From the start of the experiments, if heavy particles are on bottom, the heavy particles stay on bottom, but if heavy particles are on top, heavy particles migrate to the bottom over the course of the experiment (Fig. 8). Heavy particles migrate to the bottom faster if heavy particles are on top in the initial configuration as compared to an initially mixed configuration (Fig. 8).
 | ||
| Fig. 10 Time series of images of CFD-DEM simulations with combined gas flow and vibration for different initial particle configurations (a)–(c). | ||
When no vibration is used in CFD-DEM simulations (Fig. 11), bubbles are smaller than those under vibration conditions, regardless of initial particle configuration, matching experimental results qualitatively. Further, in binary particle mixtures heavy particles migrate to the bottom once statistical steady state is achieved throughout the bubble rise process, regardless of initial particle configuration (Fig. 11), matching experimental results qualitatively. Over time, particles segregate in binary mixtures (Fig. 12), and particles segregate faster if light particles are on top than if particles are initially mixed, matching experimental results qualitatively. Particle segregation is more complete in CFD-DEM simulations than that observed in experiments.
 | ||
| Fig. 14 Time series of images of MFM simulations with combined gas flow and vibration for different initial particle configurations (a)–(c). | ||
3.2 Structured bubbling quantification
Pearson's correlation coefficient is used to quantify the amount of structuring in the bubbles for the experimental and CFD-DEM cases with and without vibration once statistical steady-state is achieved (Fig. 17). Experiments, CFD-DEM and MFM simulations all show that cases with vibration have significantly higher bubble structuring than cases without vibration, and there is no significant difference in correlation coefficient in vibration cases with varying initial conditions. CFD-DEM simulations match experimental results quantitatively accurately with vibration, but CFD-DEM simulations without vibration have higher correlation coefficients than experiments, possibly due to the fact that a sintered bronze porous plate was used as distributor in experiments, while a uniform gas flow was induced from the bottom in simulations. MFM simulations predict correlation coefficients significantly higher than those in all experimental cases, essentially 1.0 in vibrated cases, as well as smaller standard deviations in correlation coefficients, indicating MFM simulations fail to capture the disordered dynamics of fluidization.3.3 Mixing quantification
The amount of mixing over time in experiments as well as CFD-DEM and MFM simulations with and without vibration and with different initial configurations is quantified using the mixing entropy (Fig. 18). Experimental and CFD-DEM cases show that particles are well-mixed when vibration is used (as shown by a steady-state value above 0.5), but well-segregated when no vibration is used (as shown by a value below 0.5). Rates of particle mixing in CFD-DEM simulations match experiments fairly well for the vibration cases, yet at steady state, CFD-DEM simulations predict more segregation in cases without vibration than observed experimentally. In contrast, MFM simulations predict the same low levels of mixing whether or not vibration is used, missing the key experimental insight that vibration promotes mixing. The amount of segregation predicted by MFM for the no vibration case matches experiments more closely than that of CFD-DEM, but the MFM simulations are still qualitatively inaccurate in that MFM predicts the same level of segregation with and without vibration.Fig. 20 is equivalent to Fig. 19, but Fig. 20 shows the CFD-DEM case without vibration. Particle convection patterns are much slower around bubbles (as seen from much smaller green arrows), and thus there are no solid-like regions surrounding bubbles, as demonstrated by lower particle packing fractions and particle pressures. As such, with fluid-like regions everywhere in the system at all times, bubbles can form at any time and any place at the distributor and bubbles form randomly. Since bubbles are forming at all times, there is not as much gas to channel to bubbles when they form, and bubbles are smaller than in the case with vibration and more bubbles are formed (Fig. 20). Thus, the formation of solid-like regions in the case with vibration and the lack of solid-like regions in the case without vibration explains the difference in bubble dynamics between these two cases.
MFM simulations with vibration (Fig. 21) show that particle convection patterns around bubbles lead to solid-like regions preventing bubble formation both directly below bubbles and to the side of bubbles at φ = 0 in the vibration cycle (i). Particle convection patterns then lead to a fluid-like region forming below and in-between bubbles at φ = π/6 (ii), explaining the formation of a new bubble in this region and a triangular bubble pattern. However, due to the formation of a broad pocket of gas low in the bed, the switching between solid-like and fluid-like behavior only forms roughly halfway through the bed vertically, and thus structured bubbling only forms in the upper half of the bed. Thus, the difference in the vertical location of switching solid-like and fluid-like regions in CFD-DEM simulations and MFM simulations with vibrations explains the difference in the structured bubbling patterns formed.
MFM simulations without vibration (Fig. 22) show that particle convection patterns lead to some areas of high packing fraction and particle pressure below bubbles, but there is no pattern of when and where these regions form, and thus no structured bubbling pattern forms. These results from MFM are somewhat different from those in CFD-DEM (Fig. 20) in which no solid-like regions form, but due to a lack of temporal and spatial formation of solid-like regions, both simulation techniques predict random bubble dynamics, matching experiments.
We further investigate why structured bubbling leads to greater mixing than unstructured bubbling (as seen in both experiments and CFD-DEM simulations) by investigating CFD-DEM simulations in-depth. Fig. 23 shows CFD-DEM simulations (a) without vibration and (b) with vibration over time through the course of two vibration cycles in the binary particle mixture after statistical steady state is reached. Simulations results show that there are somewhat fast upward and downward velocities surrounding small bubbles in the unstructured bubbling case without vibration (a), but overall the vertical particle velocities are close to zero. As such, in unstructured bubbling, there is not enough vertical motion of particles for inertia to overcome the buoyancy which keeps heavy particles at the bottom, and insignificant vertical mixing is observed over time. When vibration is used (b), large structured bubbles form and while bubbles rise through the center of the bed at the start of the vibration cycles, particles fall quickly through and to the sides of the bubbles. As bubbles break through the top of the bed at the middle of the vibration cycle, particles rise rapidly through the majority of the bed. As such, these dynamics of particles surrounding bubbles over the course of the vibration cycle create rapid up and down motion enabling inertia in the particles to overcome buoyant forces and allow heavy and light particles to mix vertically. Particle tracers (Fig. 23(b, ii)) show that most of the mixing occurs in the middle two vertical layers, while the top and bottom layers do not mix as much, which tracks with the fastest particle speeds seen in the vertical center of the bed. These tracer results explain why particle mixing is not complete in experiments and CFD-DEM simulations, but rather the top fourth of the bed is largely composed of light particles and the bottom fourth is largely composed of heavy particles.
CFD-DEM captured the bubbling and mixing dynamics quantitatively in the structured bubbling case with vibration and qualitatively in the unstructured bubbling case without vibration. The increased accuracy of CFD-DEM as compared to MFM can be attributed to the direct capturing of particle–particle and particle–wall contacts in CFD-DEM, thus avoiding the need to model solids rheology and solids-wall boundary conditions needed in MFM. The quantitative inaccuracies in CFD-DEM for predicting bubbling and resulting mixing dynamics in the unstructured bubbling case are most likely attributable to the drag law, since any drag law does not fully capture the no-slip boundary condition between particles and gas. Further, the drag law is key to predicting the particular size and rise velocity of bubbles in simulations,42 since drag is the force that forms bubbles and causes them to rise in fluidized beds. These discrepancies may also form due to the fact that particles were modeled without a size distribution in the CFD-DEM simulations, and size distribution has been shown to be critical to bubble dynamics experimentally in fluidized beds.43
4. Conclusions and future work
Experimentally, we demonstrated that periodic, structured bubbling can form in binary mixtures of spherical granular particles with similar Umf values when subject to combined gas flow and vibration at specific conditions. The large bubbles formed by structured bubbling act to mix particles despite large differences in particle density, and mixing occurs regardless of the initial configuration of particles. When only gas flow is used, the bubbles formed are smaller and unstructured in nature, which leads to particles segregating, with light particles rising to the top. This ability to induce mixing with the use of vibration or segregation without the use of vibration provides the potential to use one mode when particle mixing is desired and another when segregation is desired for an engineering process, and thus these insights can be applied to industrial processes in future work. This study only investigated one particular set of gas flow and vibration conditions as well as one particular binary mixture of particles. Future studies could include a range of gas flow and vibration conditions as well as particles of different sizes, densities and shapes, including ternary and polydisperse mixtures, investigating their effects on bubble structuring and particle mixing.Using computational modeling, CFD-DEM simulations provide predictions of structured bubbling and particle mixing which match experiments qualitatively and in some cases quantitatively. Detailed analysis of these simulations demonstrate that the structured bubbling forms due to particles below bubbles entering a solid-like state, causing a new row of bubbles to form at points horizontally in between the prior row of bubbles. Further, simulation analysis shows that the larger bubbles formed by structured bubbling cause a stronger inertial upwelling of particles in the wakes of bubbles, allowing these particles to overcome gravitational forces pulling them down to induce mixing. MFM simulations require the bed height to be increased in order to reproduce structured bubbling dynamics and do not predict mixing induced by structured bubbling. These results demonstrate the accuracy in predictions gained by extra computational cost using CFD-DEM as compared to MFM and indicate the importance of improving aspects of MFM simulations, such as solids phase rheology and solids-wall boundary conditions, in future work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the National Science Foundation Grant #2144763 and Office of Naval Research (ONR) grant N00014-22-1-2142.References
- H. K. Pak and P. R. Behringer, Nature, 1994, 371, 231–233 CrossRef.
- P. B. Umbanhowar, F. Melo and H. L. Swinney, Nature, 1996, 382, 793–796 CrossRef CAS.
- J. F. Davidson and D. Harrison, Fluidised Particles, Cambridge University Press, Cambridge, 1963 Search PubMed.
- L. de Martín, C. Ottevanger, J. R. van Ommen and M.-O. Coppens, Phys. Rev. Fluids, 2018, 3, 034303 CrossRef.
- C. Bizon, M. D. Shattuck, J. R. de Bruyn, J. B. Swift, W. D. McCormick and H. L. Swinney, J. Stat. Phys., 1998, 93, 449–465 CrossRef.
- C. Bizon, M. D. Shattuck, J. B. Swift, W. D. McCormick and H. L. Swinney, Phys. Rev. Lett., 1998, 80, 57–60 CrossRef CAS.
- Q. Guo, C. Spitler, J. M. Sanghishetty and C. M. Boyce, Curr. Opin. Chem. Eng., 2023, 42, 100977 CrossRef.
- Q. Guo, Y. Zhang, A. Padash, K. Xi, T. M. Kovar and C. M. Boyce, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2108647118 CrossRef CAS PubMed.
- Q. Guo, Y. Zhang, T. M. Kovar, K. Xi and C. M. Boyce, Soft Matter, 2022, 18, 3323–3327 RSC.
- Q. Guo, W. Da, R. Wu, Y. Zhang, J. Wei and C. M. Boyce, Phys. Rev. E, 2023, 107, 034603 CrossRef CAS.
- T. M. Gernon, M. A. Gilbertson, R. S. J. Sparks and M. Field, J. Volcanol. Geotherm. Res., 2008, 174, 49–56 CrossRef CAS.
- D. Kadau, J. S. Andrade and H. J. Herrmann, Granular Matter, 2011, 13, 219–223 CrossRef.
- J. Adanez, A. Abad, F. Garcia-Labiano, P. Gayan and L. F. de Diego, Prog. Energy Combust. Sci., 2012, 38, 215–282 CrossRef CAS.
- I.-S. Han and C.-B. Chung, Chem. Eng. Sci., 2001, 56, 1951–1971 CrossRef CAS.
- A. Kiashemshaki, N. Mostoufi and R. Sotudeh-Gharebagh, Chem. Eng. Sci., 2006, 61, 3997–4006 CrossRef CAS.
- A. S. Mujumdar and K. Erdesz, Drying Technol., 1988, 6, 255–274 CrossRef.
- B. Rambali, L. Baert and D. L. Massart, Int. J. Pharm., 2001, 220, 149–160 CrossRef CAS PubMed.
- J. M. Ottino and D. V. Khakhar, Annu. Rev. Fluid Mech., 2000, 32, 55–91 CrossRef.
- M. O. Coppens and J. R. van Ommen, Chem. Eng. J., 2003, 96, 117–124 CrossRef CAS.
- C. S. Daw, C. E. A. Finney, M. Vasudevan, N. A. van Goor, K. Nguyen, D. D. Bruns, E. J. Kostelich, C. Grebogi, E. Ott and J. A. Yorke, Phys. Rev. Lett., 1995, 75, 2308–2311 CrossRef CAS PubMed.
- E. W. Merrow, Self-Organization and Chaos in a Fluidized Bed, 1984.
- B. Formisani, G. D. Cristofaro and R. Girimonte, Chem. Eng. Sci., 2001, 56, 109–119 CrossRef CAS.
- N. Burtally, P. J. King and M. R. Swift, Science, 2002, 295, 1877–1879 CrossRef CAS PubMed.
- S. R. Dahl and C. M. Hrenya, Chem. Eng. Sci., 2005, 60, 6658–6673 CrossRef CAS.
- A. Rosato, K. J. Strandburg, F. Prinz and R. H. Swendsen, Phys. Rev. Lett., 1987, 58, 1038–1040 CrossRef PubMed.
- C. C. Lakshmanan and O. E. Potter, Chem. Eng. Sci., 1990, 45, 519–528 CrossRef CAS.
- Q. Guo and C. M. Boyce, AIChE J., 2022, 68, e17709 CrossRef CAS.
- L. A. Vandewalle, V. Francia, K. M. Van Geem, G. B. Marin and M.-O. Coppens, Chem. Eng. J., 2022, 430, 133063 CrossRef CAS.
- Y. Tsuji, T. Kawaguchi and T. Tanaka, Powder Technol., 1993, 77, 79–87 CrossRef CAS.
- P. A. Cundall and O. D. L. Strack, Géotechnique, 1979, 29, 47–65 CrossRef.
- T. B. Anderson and R. Jackson, Ind. Eng. Chem. Fundam., 1967, 6, 527–539 CrossRef CAS.
- D. Gidaspow, Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions, Academic Press, 1994 Search PubMed.
- C. M. Boyce, D. J. Holland, S. A. Scott and J. S. Dennis, Ind. Eng. Chem. Res., 2015, 54, 10684–10697 CrossRef CAS.
- J. M. Musser and J. E. Carney, Theoretical Review of the MFIX Fluid and Two-Fluid Models, NETL, 2020 Search PubMed.
- C. K. K. Lun, S. B. Savage, D. J. Jeffrey and N. Chepurniy, J. Fluid Mech., 1984, 140, 223–256 CrossRef.
- R. Jackson, Theory of Dispersed Multiphase Flow, Elsevier, 1983, pp. 291–337 Search PubMed.
- J. Ding and D. Gidaspow, AIChE J., 1990, 36, 523–538 CrossRef CAS.
- D. Gera, M. Syamlal and T. J. O’Brien, Int. J. Multiphase Flow, 2004, 30, 419–428 CrossRef CAS.
- P. C. Johnson and R. Jackson, J. Fluid Mech., 1987, 176, 67–93 CrossRef CAS.
- K. Pearson and O. M. F. E. Henrici, Philos. Trans. R. Soc. London, Ser. A, 1896, 187, 253–318 Search PubMed.
- M. M. H. D. Arntz, W. K. den Otter, W. J. Briels, P. J. T. Bussmann, H. H. Beeftink and R. M. Boom, AIChE J., 2008, 54, 3133–3146 CrossRef CAS.
- D. Liu and B. van Wachem, Powder Technol., 2019, 343, 145–158 CrossRef CAS.
- J. W. Chew and R. A. Cocco, Chem. Eng. J., 2021, 420, 129880 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00072b |
| This journal is © The Royal Society of Chemistry 2024 |