Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Swimmers at interfaces enhance interfacial transport†
Jiayi
Deng
a,
Mehdi
Molaei
b,
Nicholas G.
Chisholm
 c,
Scarlett E.
Clarke
c and
Kathleen J.
Stebe
c,
Scarlett E.
Clarke
c and
Kathleen J.
Stebe
 *a
*a
aDepartment of Chemical and Biomolecular Engineering, University of Pennsylvania, Philadelphia, PA 19104, USA. E-mail: kstebe@seas.upenn.edu
bPritzker School of Molecular Engineering, University of Chicago, Chicago, IL, USA
cMathematical Sciences, Worcester Polytechnic Institute, Worcester, MA, USA
First published on 21st June 2024
Abstract
The behavior of fluid interfaces far from equilibrium plays central roles in nature and in industry. Active swimmers trapped at interfaces can alter transport at fluid boundaries with far reaching implications. Swimmers can become trapped at interfaces in diverse configurations and swim persistently in these surface adhered states. The self-propelled motion of bacteria makes them ideal model swimmers to understand such effects. We have recently characterized the swimming of interfacially trapped Pseudomonas aeruginosa PA01 moving in pusher mode. The swimmers adsorb at the interface with pinned contact lines, which fix the angle of the cell body at the interface and constrain their motion. Thus, swimmers become trapped at interfaces in diverse configurations and swim persistently in these surface adhered states. We observe that most interfacially trapped bacteria swim along circular paths. Fluid interfaces also typically form incompressible two-dimensional layers. These effects influence the flow generated by the swimmers. In our previous work, we have visualized the interfacial flow around a pusher bacterium and described the flow field using two dipolar hydrodynamic modes; one stresslet mode whose symmetries differ from those in bulk, and another bulk mode unique to incompressible fluid interfaces. Based on this understanding, swimmer-induced tracer displacements and swimmer–swimmer pair interactions are explored using analysis and experiment. The settings in which multiple interfacial swimmers with circular motion can significantly enhance interfacial transport of tracers or promote mixing of other swimmers on the interface are identified through simulations and compared to experiment. This study shows the importance of biomixing by swimmers at fluid interfaces and identifies important factors in the design of biomimetic active colloids to enhance interfacial transport.
1 Introduction
Bacteria have long been studied as prototypical active colloids whose self-propulsion and interaction generate exciting collective behaviors. Swimming bacteria share a common and simple machinery, with rotating motors in their cell envelope that are coupled to the flagella, enabling bacterial self-propulsion.1 Hydrodynamic interactions and the chaotic nature of bacterial swimming give rise to intriguing non-equilibrium phenomena in active suspensions, including enhanced diffusion,2–8 long-range correlations in velocity and orientation fields9–15 and active phase separation.16–19 These findings have inspired biomimetic active colloid systems designed to recapitulate bacteria's swimming and collective behavior.20–24In addition to their interesting collective behavior, swimmers are also studied to understand their impact on mixing. The concept of biomixing by hydrodynamic interactions with a moving body25 has received intense renewed interest. Recent studies have suggested that mixing by mass displacement generated by swimming organisms can rival the energy input of winds and tides in oceanic settings.26 For small swimmers moving with negligible inertia, the “drift volume” or volume of fluid entrained by such swimmers is comparable to the volume of the swimmers themselves. The drift volume is generated by the net displacement of fluid elements along the swimmer's path. Each fluid element in the domain undergoes a Lagrangian displacement by hydrodynamic interactions with passing swimmers. Given the symmetry of the force dipoles, fluid elements far from the swimmer path are displaced along closed loops as swimmers move along infinite straight paths.7 Interactions with multiple swimmers randomize these displacements, generating diffusive mixing.4,6,8,27–29 Effective diffusion coefficients30,31 and probability distributions32,33 of displacements for fluid elements interacting with multiple swimmers have been predicted in inviscid and highly viscous fluids based on analysis of the Lagrangian displacement of the fluid elements far from the swimmers. Furthermore, fluid elements close to passing swimmers can be entrained by the swimmer and move over significant distances that diverge for head-on collisions.34 The measurement of displacements of fluid elements generated by micro-scale swimmers is tremendously challenging owing to the importance of the Brownian motion of the swimmers and tracer particles.
Boundaries alter swimmer and tracer interactions. Interactions between swimmers and passive tracers in liquid suspension and near solid surfaces reveal enhanced diffusion and non-Gaussian statistics in experiments that differ from thermally driven Brownian motion.2,4,9,35,36 While the role of solid boundaries in altering swimmer–colloid and swimmer–swimmer interactions is well appreciated, the role of fluid interfaces in altering such interactions has not been addressed.
We have previously studied swimming behaviors of Pseudomonas aeruginosa PA01 at aqueous–hexadecane interfaces. These monotrichous bacteria move in pusher or puller modes by reversing the sense of rotation of their single flagellum. The cell bodies of P. aeruginosa may be approximated as a spherocylinder with a characteristic length of approximately 1 μm. The flagellum is approximately 10 μm in length. The bacteria can swim adjacent to the interface, or they can adsorb with cell bodies spanning the interface and swim in an adhered state, a phenomenon unique to fluid interfaces. In this surface-adhered state, the bacteria cell bodies become trapped at fluid interfaces with pinned contact lines, constraining their swimming behavior (Fig. 1a). Furthermore, surfactant adsorption to the fluid interfaces gives rise to complex surface stresses. For example, surfactants can generate Marangoni stresses that render the interface incompressible and alter swimmer motion.
 | ||
| Fig. 1 Dipolar flow generated by a pusher bacterium on a fluid interface. (a) Schematic of an interfacially trapped bacterium interacting with a tracer particle. (b) Measured flow field generated by an ensemble of pusher bacteria located at the origin moving in the y direction (right panel). Theoretical fit of the flow field generated by a pusher on the interface (left panel). Streamlines indicate the local direction of the flow, and the color scheme indicates its magnitude. The flow field is reprinted from ref. 37. The dipolar flow consists of (c) S and (d) B modes. The strength, positions, and orientations for both modes are fitted simultaneously to the observed field. Specifically, this entails fitting the strength S, and orientation ϕS of the S mode, the strength B and orientation ϕB of the B mode and the common position δy of both modes using the non-linear least squares fitting method in python (scipy.optimize.curvefit). (e) Schematic of a tracer particle entrained by a bacterium swimming along a circular path. | ||
Interface-associated bacteria have complex trajectories that differ from those in bulk or near solid surfaces.38,39 Interfacially trapped motile bacteria swim preponderantly in curly or circular paths with curvatures ranging from 0.1–1.0 μm−1. This circular swimming generates a ‘self-caging’ plateau in their mean square displacements (MSD). Weak displacements of their centers of rotation owing to active diffusion processes decorrelate their positions at long lag times40 allowing them to move diffusively at the interface. The bacteria's active diffusivities are attributed to diverse athermal stochastic or noisy processes including fluctuations in flagellar rotation, switching between pusher and puller modes and interactions with other swimmers.37,41
We have measured the ensemble-averaged interfacial flow field generated by a PA01 bacterium moving in a pusher mode using correlated displacement velocimetry37,42 (Fig. 1a). The bacteria and passive tracer colloids were trapped at interfaces of hexadecane and aqueous suspensions of bacteria in TRIS-based motility medium buffer; details are given in ref. 37. This flow field features unexpected asymmetries that do not arise for their bulk-fluid counterparts (see Fig. 1b). Analysis reveals that the interfacial velocity field can be decomposed into two dipolar hydrodynamic modes associated with interface incompressibility, an interfacial stresslet (S mode) corresponding to a parallel force dipole on the interface (Fig. 1c), and a second mode (B mode) generated from an off-interface forcing by the flagellum immersed in the bulk fluid beneath the interfacial plane that is balanced by Marangoni stresses (Fig. 1d). The relative importance of these modes is determined by the cell bodies’ trapped configurations.37
In this study, we exploit these findings to analyze the impact of interfacially trapped bacteria as model swimmers on interfacial transport (see the schematics in Fig. 1e). The measurement of the flow fields and their decomposition into leading order hydrodynamic modes allows analytical prediction of tracer advection via hydrodynamic interactions with swimmers, and of pair interactions between swimmers. To appreciate the importance of the circular trajectories on bacteria–tracer interactions, we consider swimmers that follow either straight or circular trajectories and calculate the corresponding trajectories of tracer particles. We find that circular swimmers at interfaces generate tracer displacements in which tracers also move in closed loops unless the swimmers and tracer particles are in close proximity. Essentially, we determine using analysis and theory the Lagrangian displacements generated by hydrodynamic interactions of tracer particles and bacteria moving at fluid interfaces. Throughout, while we refer to tracer paths, these correspond to the Lagrangian paths of fluid elements moving via hydrodynamic interactions with a swimmer and our discussion of hydrodynamic diffusion of colloidal tracers corresponds to the effective diffusion of a fluid element.
We also study the manner in which neighboring swimmers interact, and find circular swimmers in close proximity can reorient and generate net displacements of their neighbors. Interactions between a tracer particle and multiple swimmers are then studied to understand the impact of hydrodynamic interactions on tracer diffusion processes. For scant swimmers and low active noise, tracers have self-caged displacements owing to their loopy displacement trajectories. We find that higher swimmer concentration and active noise allow swimmers to break the caging effect, and therefore to further enhance interfacial mixing. To further understand the role of swimmers in generating active noise in the interface, we study hydrodynamic pairwise interactions among multiple swimmers. We find multiple pairwise interactions randomize the directions of bacteria and contribute to the active noise in their trajectories. We compare theoretical and numerical prediction to experiments for PA01 swimming at fluid interfaces.
2 Pair interactions between a tracer and a swimmer
We employ correlated displacement velocimetry (CDV) to construct flow fields generated by source colloids moving in interfaces using tracer particles in the interface. This method is effective even when the tracers and source particles are Brownian and in relatively crowded conditions that would preclude the use of standard particle displacement velocimetry methods.37,42 CDV relies on measuring the correlated displacement of the source colloid and tracer particles of a small lag time τ. In the method, a coordinate system (x, y) is constructed, with the source colloid at the origin and y axis corresponding to the source colloid's direction of motion. The correlated displacement vectors of tracer particles located at different positions are mapped to this coordinate system. This process is repeated for every source particle on the interface and the displacement fields are superposed. Displacement vectors are then binned to allow signal to be differentiated from noise. Thus, Brownian noise is filtered, and the correlated displacement of tracers reveals the hydrodynamic interactions. The flow field generated by the bacterium moving in pusher mode, reported in Fig. 1b, was reported in ref. 37. It represents the displacement field of colloids at the interface generated by an ensembled averaged bacterium swimming in pusher mode.Chisholm and Stebe43 theoretically describe the flow fields that can be generated by an interfacially trapped, motile bacterium. This description reveals that, sufficiently far from the bacterium, the flow in the interface is generally dominated by a superposition of two dipolar flow modes, named the “S” and “B” modes.43 These modes result from a multipole expansion of the velocity field due to a self-propelled object adsorbed to the interface. The S mode (called the “S|| mode” in Chisholm and Stebe43) is an incompressible interfacial stresslet determined by the balance of flagellar thrust and the counteracting drag on the bacterium's body projected on the interfacial plane. The B mode, on the other hand, is associated with Marangoni stresses generated by the protrusion of the bacterium's body and flagellum into the surrounding bulk fluid phases.
Superposition of the S and B modes leads to the fore-aft asymmetric flow shown in Fig. 1b. Mathematically, each of these modes can be characterized by a magnitude and a direction; they also share a common origin or pole where the fluid velocity is singular. The magnitude, origin, and direction of the S and B modes were fitted to the observed flow field. The magnitudes, or strengths, for the S and B modes are S = 0.36 ± 0.05 pN μm and B = 0.82 ± 0.02 pN μm, respectively. The direction of the stresslet is offset from the swimming direction by an angle ϕS = −8.0 ± 2.3° for the S mode and ϕB = 192.7 ± 4.0° for the B mode. The “pole” of the multipole expansion giving the S and B modes is located slightly behind the body's center at (0, δy) with δy = −1.33 ± 0.14 μm. The resulting flow field reflects the forces distributed around the swimmer, which are related to the configuration of the trapped bacteria. Furthermore, the form of this flow reveals that the bacteria swim on an incompressible fluid interface with negligible surface viscosity.
We use the measured flow field to study the “drift trajectories” or paths traced by tracer colloids when they interact hydrodynamically over prolonged times with a pusher bacterium that is moving over either straight or circular paths. These displacements are found by appropriate segmentation and summing of the flow field reported in Fig. 1b. Like the flow field, these paths cannot be directly measured using standard particle velocimetry owing to the Brownian motion of bacteria and tracers and the relatively crowded state of the interface that can not preclude interactions of a single tracer with multiple swimmers over the time scales of interest. Theory allows the tracer paths to be predicted for interfacial dipolar modes, and also provides guidance on how the measured flow fields can be used to reconstruct an experimental tracer Lagrangian path. The Lagrangian displacement or “drift”7,30,31 of a tracer particle in a bacterial flow field (see the schematics in Fig. 1e) as a function of time with initial tracer position xp,0 is given by
 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ(t′), cos
ϕ(t′), cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ(t′)〉 is a unit vector giving the bacterium's swimming direction, and ϕ is the angle between the bacterium's swimming direction and the y axis. The fluid velocity u(x′, q) is calculated by superposition of the velocity contributions from the S and B modes, uS(x′, qS) and uB(x′, qB), given by
ϕ(t′)〉 is a unit vector giving the bacterium's swimming direction, and ϕ is the angle between the bacterium's swimming direction and the y axis. The fluid velocity u(x′, q) is calculated by superposition of the velocity contributions from the S and B modes, uS(x′, qS) and uB(x′, qB), given by | (2) |
 | (3) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is the average viscosity of the bulk fluids. The unit vectors
is the average viscosity of the bulk fluids. The unit vectors| qS = 〈−sin(ϕ + ϕS), cos(ϕ + ϕS)〉 |
| qB = 〈−sin(ϕ + ϕB), cos(ϕ + ϕB)〉 |
In the limit of large tracer–swimmer separation distance, tracer displacements are small compared to this distance, r ≫ Δxp, allowing the approximation x′ ≈ xp,0 −xs. This assumption allows analytical integration of eqn (1) to find the tracer displacement by the velocity contributions from the S and B modes, ΔxSp and ΔxBp, respectively. The tracer displacements can be calculated by,
| Δxp = ΔxSp(x′, qS) + ΔxBp(x′, qB). | (4) |
We perform this integration to find ΔxSp and ΔxBp for the dipolar strengths, positions and orientations fitted to Fig. 1b. Similarly, we generate an experimental tracer trajectory from integration over the displacement vectors Δxp extracted from the experimental data. Experimental displacement Δxp(t) during a time interval of Δt is approximated as u(x′(t),q(t))Δt by properly shifting and rotating the velocity vectors from the measured flow field. The time increment Δt is chosen based on the spacing of velocity vectors.
2.1 Tracer displacements by a bacterium swimming in a straight line
We first consider the case of a bacterium swimming along a straight line with q = êy at constant speed v = 10 μm s−1. A tracer initially located at xp,0 = 〈xp,0〉 is displaced by the swimmer moving along a straight line from xs = 〈0,−L/2〉 to 〈0,L/2〉. Tracers are advected by the streamlines in the flow generated by the swimmer.To construct the ‘experimental’ tracer path, displacements of a tracer at short lag time Δt, approximated as Δxp(t) = u(x′(t), êy)Δt, are obtained by extracting velocity vectors at position x′ from the measured flow field aligned along the y axis. These displacement vectors are summed for the swimmer moving along a straight path with xs(t) = 〈xp,0,ys(t)〉 over the range ys = −L/2 to L/2, where L = 120 μm. This length corresponds to the size of the domain over which the flow field was measured. The time increment used in this calculation is Δt = L/Nbv, where Nb is the number of the integrated displacement vectors equal to the number of grid points along the straight paths, Nb = 50 (for details see S1, ESI†).
Analytical prediction of the tracer displacement relies on evaluating the integrals in eqn (1) respectively for ΔxS and ΔxB and adding the results to represent the tracer path. The y location of the swimmer changes over time as ys(t) = yi + vt. The initial position of the swimmer with respect to the tracer yi is defined by the y-positions of S and B modes with respect to the center of the cell body, thus yi = −L/2 + δy. Assuming S and B modes are aligned with the y axis (ϕS = 0 and ϕB = π), a closed form of Δxp(t) can be obtained, with the contribution from the S mode given by,
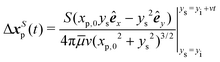 | (5) |
 | (6) |
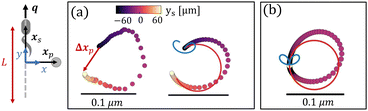
As suggested by the form of the flow (Fig. 1b), when the swimmer approaches and passes the tracer, the tracer is pushed away by the outflow in front of the swimmer and subsequently is pulled toward the swimmer by the inflow at the rear. This yields a loopy tracer path as shown in Fig. 2a. The contributions from each mode are also calculated from numerical integration of both modes, with the multiple lobes in the S mode generating a two-lobed “lima-bean” shaped path for the tracer (blue curve), while the B mode generates a symmetric loop with a net displacement in the direction opposite the bacterial swimming direction (red curve). These displacements superpose to yield an asymmetric tracer path with a tilted loop, with an opening Δxp due to the finite swimmer path. As expected, for this straight swimmer, the tracer path closes as the bacterial trajectory elongates, generating zero net displacement for an infinite swimmer trajectory (Fig. 2b). The closed loop is also observed for swimmers in bulk fluids with infinite trajectory.7 Theoretically, the shape and size of the tracer's path depends on the swimmer's speed, the relative strength of dipolar modes, the path length, and the initial position of the tracer.
2.2 Tracer displacements by a bacterium swimming in a circular path
A related approach allows prediction of tracer displacements near a pusher swimming in circles, xs = Rs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Ωt)êx + Rs
cos(Ωt)êx + Rs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Ωt)êy, where Rs is the radius of the swimmer's circular trajectory and Ω is its rotational velocity. For tracers far from the bacterium, and for swimmers that rotate at nearly fixed positions with highly curved trajectories (r ≫ Rs), the position vector characterizing tracer–swimmer separation, x′ can be assumed to be independent of time (x′ = xp,0), while the swimmer's orientation changes periodically as q = −sin(ϕ)êx + cos(ϕ)êy, where ϕ is the rotation angle of the swimmer, ϕ(t) = Ωt.
sin(Ωt)êy, where Rs is the radius of the swimmer's circular trajectory and Ω is its rotational velocity. For tracers far from the bacterium, and for swimmers that rotate at nearly fixed positions with highly curved trajectories (r ≫ Rs), the position vector characterizing tracer–swimmer separation, x′ can be assumed to be independent of time (x′ = xp,0), while the swimmer's orientation changes periodically as q = −sin(ϕ)êx + cos(ϕ)êy, where ϕ is the rotation angle of the swimmer, ϕ(t) = Ωt.
The experimental tracer path can be graphed by integrating over displacement vectors Δxp(t) = u(x′,ϕ(t))Δt from the measured flow field at a fixed position x′ with the flow field rotating CCW by Δϕ at each time interval from ϕ = 0 to ϕ = 2π. To achieve this, the measured flow field is reconstructed on a polar grid of equivalent radial spacing and equivalent angle intervals of Δϕ = π/15 (for details see S1, ESI†). Equivalent to integrating over velocity vectors at fixed x′ from a rotating field, we extract the velocity vectors in a circular path from a flow field oriented in the y direction. The velocity vectors at x′ = 〈xp,0,ϕ(t)〉 in polar coordinate are rotated CCW by ϕ(t) and integrated from ϕ = 0 to 2π. The spacing between the velocity vectors along the circular path determines the time interval over which displacement is measured as Δt = Δϕ/Ω, where Ω is approximated as 2 s−1.
Similarly, tracer displacements can be constructed analytically. The relative distance between the tracer and the two dipolar modes is assumed to remain fixed, x′ = 〈xp,0,0〉, while the bacterium's rotational angle changes as ϕ = ϕi + Ωt, where ϕi is the initial orientation of the bacterium with respect to the y axis; ϕi is corrected to ϕSi = ϕS for the S mode and ϕBi = ϕB for the B mode to account for the differing alignment of the S and B modes. Integration of uS over circular paths of the swimmer in the limit of r ≫ Rs yields,
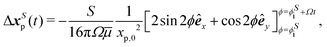 | (7) |
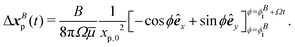 | (8) |
As the swimmer completes a circle, the tracer moves in a closed loop, as can be predicted from analysis in eqn (7) and (8). The S mode leads to two ellipse-shaped tracer displacement loops for each period (Fig. 3a, blue curve), while the B mode generates a single circular loop (Fig. 3a, red curve). Because of this period doubling, the S mode generates smaller tracer displacements than the B mode does for interaction times that do not correspond to multiples of the bacteria's period of rotation. Superposition of the displacements generated by these two modes results in a closed loop with a rounded triangular shape (Fig. 3a, right); the size of this loop scales as Ω−1r−2. The predicted tracer path agrees with that extracted from the measured flow field (Fig. 3a, left). The tilted tip of the triangle results from the differing orientations of the S and B modes (ϕB and ϕS).
We also consider the tracer placed at the center of the circular path of bacteria with xp,0 ≪ Rs, thus the distance between the swimmer and the tracer remains unchanged (r = Rs) over the time, while the direction of their relative separation x′ remains perpendicular to the swimmer orientation q. Thus, the tracer follows a circular path with a constant speed determined by its initial separation from the swimmer ( = 〈−Rs, 0〉) and the swimmer's initial orientation (qi = êy). The velocity vector at
= 〈−Rs, 0〉) and the swimmer's initial orientation (qi = êy). The velocity vector at  is extracted from the measured flow field, rotated continuously in a CCW sense by an interval of Δϕ = π/12 and integrated from ϕ = 0 to 2π. The nearly-circular resulting tracer path extracted from the experimental flow field is shown in Fig. 3b (left). Analytical integration of the velocity uS yields a circular path of tracer given by,
is extracted from the measured flow field, rotated continuously in a CCW sense by an interval of Δϕ = π/12 and integrated from ϕ = 0 to 2π. The nearly-circular resulting tracer path extracted from the experimental flow field is shown in Fig. 3b (left). Analytical integration of the velocity uS yields a circular path of tracer given by,
 | (9) |
 | (10) |
While microswimmers moving over long, straight trajectories or fully closed circles lead to negligible tracer displacements, even small displacements generated by hydrodynamic interactions are not irrelevant. We have considered hydrodynamic pair interactions between the swimmer and tracer. In understanding the effect of many such “scattering” trajectories, even those with minute displacements contribute significantly to the total diffusivity and they are very important to tracer transport.
2.3 Tracer displaced by a bacterium in close proximity
While no net hydrodynamic displacement of tracers is induced by a swimmer moving in complete circles when the swimmer and tracer are well-separated, a finite displacement is predicted for tracers and swimmers in closer proximity. In this limit, changes in the separation distance between the swimmer and the tracer, x′, cannot be neglected when calculating the fluid velocity at the tracer's location. In this regime, the determination of the displacement of a tracer by a swimmer requires numerical integration. We perform this integration for a bacterium swimming in CCW circles with its orientation q normal to its position vector xs. The induced velocity u(x′(t),q(t)) is integrated to find the position of the tracer and to calculate x′(t). Thus, we numerically solve eqn (1) using an Euler integration method with a step size of Δt = 10−4 s to calculate the changes in their separation distance, x′(t) = xp(t) − xs(t), due to the finite displacements of tracers. With the step size of Δt = 10−4 s, the error of the numerical integration of the tracer displacement at each rotational circle is negligible compared to tracer displacement. The details of the numerical integration and error are discussed in S2, ESI.†We find that the changes in x′(t) break the symmetry of the system and generate a directed tracer displacement after full rotation of the swimmer. A tracer originally positioned just outside of the swimmer's circle moves along a loop-shaped path depicted in Fig. 3c with an important feature; this loop has a finite opening. We find similar results for a tracer positioned inside of the swimmer's circle (Fig. 3d). Furthermore, continuous swimming over many circles yields a looped tracer trajectory which orbits around the swimmer over long times, as shown in the insets to Fig. 3c and d, where each point represents the position of the tracer at the beginning of each period of the swimmer's circular motion. However, no attraction or repulsion is detected over a period of swimmer motion due to the divergence free nature of the incompressible interface. This looped motion generates significant net displacements at long lag times, providing a mechanism for directed tracer motion and enhanced tracer dispersion.
3 Pair interactions between swimmers
We now consider cases of two bacteria whose circular paths are perturbed via advection and reorientation by each other's flow fields. The position vector of a bacterium swimming in the laboratory frame with initial position xs,0 is given by | (11) |
 denotes the fluid velocity generated by a neighboring swimmer with orientation q′(t) and position
denotes the fluid velocity generated by a neighboring swimmer with orientation q′(t) and position  . The contributions to torque associated with the bacterium's interfacially-trapped state and flagellar rotation drive a change in orientation
. The contributions to torque associated with the bacterium's interfacially-trapped state and flagellar rotation drive a change in orientation  in polar coordinates. In addition, the vorticity ω′ and strain rate E′ at position xs −
in polar coordinates. In addition, the vorticity ω′ and strain rate E′ at position xs −  generated by the neighbor changes the swimmer's orientation. Assuming an ellipsoidally shaped bacterium, this re-orientation is given by,
generated by the neighbor changes the swimmer's orientation. Assuming an ellipsoidally shaped bacterium, this re-orientation is given by, | (12) |
 | (13) |
 , and it is only comparable to the rate of intrinsic rotations (1 − 10 s−1) for swimmers separated by less than ten microns. We study two swimmers at such separation distances. In this regime, the reorientating effect of a neighboring swimmer ∼vΔt2dqext/dt is more pronounced than its advection effect ∼u′Δt during an interaction time Δt > 0.1 s via hydrodynamic interaction.
, and it is only comparable to the rate of intrinsic rotations (1 − 10 s−1) for swimmers separated by less than ten microns. We study two swimmers at such separation distances. In this regime, the reorientating effect of a neighboring swimmer ∼vΔt2dqext/dt is more pronounced than its advection effect ∼u′Δt during an interaction time Δt > 0.1 s via hydrodynamic interaction.
3.1 Reorientation of swimmers with initially straight swimming paths
When two bacteria approach, each is reoriented with a rotational velocity determined by the vorticity and strain rate generated by its neighbor, described in eqn (12). The net effect of this rotation on swimmers' long-term trajectories depends on the swimmers' initial relative positions and orientations and the shapes of their swimming paths. We focus here on swimmers moving along initially straight paths. Parallel swimmers positioned initially adjacent to each other and moving at the same speed are repelled from each other (Fig. 4a). In this case, the interaction is persistent, and the net effects on the swimmers' long-term paths are pronounced. On the other hand, anti-parallel swimmers deviate only weakly from their straight paths. As they approach, they rotate away from each other. Their sense of rotation reverses as they pass each other. They rotate back to co-alignment as they move away from each other, eventually resuming their straight paths (Fig. 4b). In this case, the interaction is transient, and the net effects on swimming paths are weak. To understand swimmers on perpendicular paths, Fig. 4c, we must first discuss the reorientation of swimmers more generally. | ||
| Fig. 4 Reorientation of the neighboring swimmer due to the S and B modes of a source swimmer. (a) Trajectories of pairs of initially parallel swimmers initially oriented along the y axis. (b) Trajectories of pairs of initially anti-parallel swimmers initially swimming in ±y directions. (c) Trajectories of pairs of initially perpendicular swimmers. (d) Reorientation of a neighboring swimmer moving parallel or anti-parallel to a source swimmer. The source swimmer moves in the +y direction at the origin. Upper panel: Rotational velocity field ΩS. Lower panel: Rotational velocity field ΩB. Red zones: neighbor rotates in the CW sense. Blue zones: neighbor rotates in the CCW sense. The heat map indicates the magnitude of the angular velocity with brighter color calculated using the values for S and B modes that correspond to the flow field in Fig. 1. The angular velocity decays as r3. The scale bar is 5 μm. (e) Reorientation of a neighboring swimmer moving along the +x direction, perpendicular to a source swimmer that moves in the +y direction at the origin. Panels and colors similar to those in (d). | ||
To illustrate the predicted range of behaviors in greater detail, we discuss the reorientation for swimmers moving initially on straight paths as a function of the initial position. We define a source swimmer that moves along the y axis and reorients its neighbor. The neighbor can be rotated counterclockwise (CCW) or clockwise (CW) depending on its position and orientation with respect to the source. This sense of rotation changes with the polar angle φ of the neighbor in the x–y plane in Fig. 4. We summarize the rotational velocity fields ΩS and ΩB for the S and B modes, respectively. For each mode, we depict zones in which a neighbor would undergo CW rotation in red and CCW rotation in green. Rotation generated by the S mode is determined by the vorticity field and the strain rate of the source swimmer, whereas, the B mode, being irrotational, reorients its neighbors only via its local strain rate. To make these arguments more concrete, we relate this discussion to our experiments. We adopt the values for S and B that correspond to the experimental flow field, and consider distances greater than 1 μm from the origin; this cut off corresponds to the cell body size. The domain shown in Fig. 3 corresponds to a region of 20 μm per side.
 | (14) |
 | (15) |
 | (16) |
 | (17) |
In summary, when swimmers at interfaces interact, the net effect of their velocity fields depends on the balance of the S and B modes, which is determined by their trapped configuration at the interface, and the instantaneous separation and orientations of the swimmers.
3.2 Pair interactions between swimmers with circular paths
Predicted trajectories can deviate significantly from the swimmer's trajectories in isolation, suggesting that swimmer hydrodynamic interactions can be an important source of active noise. For swimmers moving periodically along circular paths, such changes in orientation and position can result in a small net displacement in each period. Given that swimmers can interact over many periods, these effects can result in significant displacements over prolonged interaction times (Fig. 5). The swimmers can attract or repel each other depending on their initial orientations and positions. This prediction is particularly important, since interfacially trapped pushers typically swim along circular paths.4 Tracers interacting with multiple swimmers
Tracer displacements are known to be significantly enhanced by interactions with multiple swimmers.3,6,7,9,46 While such micro-mixing is well studied for swimmers moving through bulk fluids, the effects of key features of interfacial swimmers remain unprobed, including the role of surface incompressibility in altering the surface flow field from that in the bulk, and the properties of the swimmer paths. We perform analysis to find the tracer's surface diffusivity due to hydrodynamic interactions for swimmers moving in straight paths that randomize via run and tumble events at incompressible fluid interfaces. (This result does not address swimmers moving in circular paths. The analytical approximation of the surface diffusivity in that case is an interesting topic for future work.)The importance of the properties of swimmer paths, including their curvilinear shapes and the eventual decorrelation of their swimming direction by active perturbations40 is also studied. Active perturbations generate diffusive displacements at long lag times and can be described as an active diffusivity Dact.40 This diffusivity randomly perturbs the tracer–swimmer separation distance and the swimmers’ orientation, and therefore alters tracer advection. While thermal diffusion of the tracer and bacterium can also generate randomizing effects, here we focus on the role of Dact, bacterial density, and hydrodynamic interactions.
4.1 Analytical approximation of hydrodynamic tracer diffusivity
We may approximate analytically the hydrodynamic tracer diffusivity for swimmers traversing straight-line paths interrupted by random reorientation events associated with bacteria that undergo “run-and-tumble” trajectories. The path segments are assumed to have fixed length L, and all reorientation directions are assumed to be equally likely. We assume that there is no appreciable pause in swimming between runs (i.e., reorientations are instantaneous). For a dilute interfacial suspension of run-and-tumble swimmers, the mean squared displacement due to swimmer–tracer interactions is given by,31,34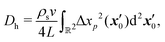 | (18) |
 | (19) |
 .
.
Using eqn (4), (5), and (6) together with eqn (18), we find that the hydrodynamic tracer diffusivity may be evaluated as
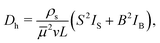 | (20) |
 | (21) |
 | (22) |
| p(ξ, η) = ξ4(3η4 − 3η2 + 1) + ξ2(η6 − 5η4 + 3η2 − 1) + η2, | (23) |
 measured from the midpoint of the swimmer run. This relationship is given by
measured from the midpoint of the swimmer run. This relationship is given by | (24) |
 | (25) |
 axis from
axis from 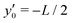 to
to  over the time interval of t = L/v.
over the time interval of t = L/v.
Both integrands in eqn (21) and (22) contain non-integrable singularities at (ξ, η) = (1, ±1). These singularities arise from large displacements of tracers initially positioned near the endpoints of the swimmer runs. Following Pushkin and Yeomans,34 we regularize the integrals by setting the lower integration limit in ξ to ξ = 1 + a/L, where a/L ≪ 1. Here a can be roughly interpreted as a minimum swimmer–tracer separation distance due to the excluded volume of the swimmer. Setting a = 2 μm and L = 20 μm, corresponding to a swimmer run time of 2 s before reorientation occurs. In this case, numerical integration of (21) and (22) yield IS ≈ 3.671 × 10−3 and IB ≈ 0.1394. Interestingly, the value of IB is over an order of magnitude larger than that of IS, which suggests that the B mode contributes a relatively large amount to the tracer diffusivity compared to the S mode. This result is perhaps unsurprising recalling the trajectories shown in Fig. 2; the B mode displacements are generally larger than those due to the S mode.
Having obtained IS and IB, we evaluate Dh using the parameters ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) = 2.17 cP and v = 10 μm s−1. A plot of Dhversus ρs is shown in Fig. 6f.
= 2.17 cP and v = 10 μm s−1. A plot of Dhversus ρs is shown in Fig. 6f.
4.2 Simulation of tracer displacements
Here, we simulate displacements of tracer beads moving via pair hydrodynamic interactions with swimmers that follow circular trajectories. In each simulation, a single tracer is placed in the center of an unbounded plane. To this plane, Ns swimming bacteria with S and B modes with dipolar strength of measured values are introduced simultaneously at random locations within a square domain of side length b = 100 μm centered around the tracer's initial location (Fig. 6a). We neglect collision and near-field effects between the tracer and the swimmers and set the minimum distance between bacteria and tracer to be Rmin = 2 μm in order to avoid divergence problems in the simulation results. The tracer particle displacement generated by Ns swimmers at each time interval of Δt = 0.02 s is advanced in an explicit Euler scheme. Each swimmer moves with a velocity vk selected from random numbers which follow a Poisson distribution with a mean value of 10 μm s−1 and with a fixed angular speed Ω = 2 s−1. The radius of curvature for each bacteria Rc = vk/Ω has a mean value of 5 μm. The center of its rotation diffuses with active diffusivity Dact. The active noise ε(t) added to the displacements of swimmers has a decorrelation timescale τ = 0.2 s and active diffusivity Dact to preserve the ballistic characteristic of the swimmers' motions at short lag times and diffusive behavior at long lag times. The interface is dilute, with number density ρs = Ns/b2 < 0.013 μm−2, so interactions between swimmers and multi-body interactions are neglected. This simulation continues for a time period of T of 2000 s. For each combination of Ns and Dact, we repeat this simulation 100 times to provide representative statistics to calculate key quantities. For a bacterium swimming in a cycle of radius Rc with its direction decorrelated in a time scale of τc, the maximum active diffusivity was estimated as Dact,m = Rc2/τc ≈ 6 μm2 s−1 to maintain the circular signature of the bacterial path.40 The Euler scheme used to integrate tracer paths generates an error of roughly 10% in the resulting diffusivities. The details of the numerical integration error are discussed in S4, ESI.†4.3 Enhanced diffusion of tracers
We compare the simulation and experiment to assess the importance of hydrodynamic interactions on the displacement of tracer colloids. In Fig. 3c and d, we show that a tracer interacting with a bacterium swimming on a circular path moves in a looped trajectory. The importance of such tracer–swimmer interactions on micro-mixing can be assessed by measuring the MSD of a single tracer interacting with a swimmer moving on a circular path perturbed by active noise. To quantify the effect of this interaction, we study the magnitude of the MSD and its local logarithmic slope | (26) |
To quantify the effects of active diffusion and swimmer density, we simulate trajectories of a single tracer advected by Ns from 2 to 128 swimmers with Dact = 0.2 to 6.4 μm2 s−1 introduced at random locations in the domain with minimum distance from the tracer of 2 μm. The diffusion coefficient of the tracers due to hydrodynamic interaction with bacteria, Dh, is obtained at long lag times where the MSD increases linearly. Two different tracer diffusion processes are observed. For low Ns or weak Dact, as suggested by the pairwise interaction between a single swimmer and tracer, the tracer MSD (for example, Fig. 6b) evolves from an initial super-diffusive regime through a sub-diffusive plateau indicating the caging effect of moving along looped trajectories, towards a diffusive regime. The decorrelation time scale at which the tracer becomes uncaged, τc, decreases with increasing Ns or Dact. Above some threshold values for these quantities, τc becomes comparable to τs, and the form of the tracer MSD changes abruptly as the caging effect disappears. At such high Ns or large Dact, the MSD evolves from superdiffusive at short lag time with α < 2 towards diffusive with no apparent caging at intermediate lag time (Fig. 6c). The Ns and Dact that yield caged behavior are summarized in Fig. 6d as square symbols and the cases for which tracers do not become caged are depicted by circles. The predicted effective hydrodynamic diffusivity Dh at given Ns and Dact, indicated by the symbol colors, increases sharply as the system transitions to uncaged states and increases thereafter with ρs. These simulation results show that increases in swimmer number Ns and active diffusivity Dact randomize tracer direction, weaken tracer caging, and enhance tracer diffusion. The Dh simulated for ρs > 0.006 μm−2 is of the same order of magnitude as the Brownian diffusivity of micron sized colloids, indicating that hydrodynamic interactions can significantly impact tracer displacements. This effect can be amplified by increasing swimmer velocity, dipolar strength, and density.
In experiments, tracer diffusivities are enhanced on P. aeruginosa-laden interfaces. Caution must be taken in attributing these enhancements solely to bacteria swimming in pusher mode, as the bacteria undergo frequent switching events as they switch between pusher and puller modes, and swim in puller modes with flow fields that differ significantly from those generated by pushers. We measure the MSD of passive tracers interacting with bacteria in the interface. The diffusivity of the passive tracers, Dp is extracted at long lag time. The motion of passive tracers at supernatant-hexadecane interfaces (with no bacteria at the interface) is governed by thermal fluctuations in the system. Without bacteria, the tracers move with diffusivity Dt = 0.13 μm2 s−1. This purely thermal MSD is depicted as a dashed black line in Fig. 6e and its inset for reference. The dependence of tracer MSD on the bacteria's surface density ρs are shown in Fig. 6e. These data are re-plotted in the figure inset against a linear abscissa to show their differences. The MSD at high surface density undergoes a transition from short lag time super-diffusive behavior to diffusive behavior at longer lag times, similar to the simulation results presented in Fig. 6b. The enhanced diffusivity due to hydrodynamic interactions (Dh = Dp − Dt) measured from experiments increases with bacterial surface density in the dilute limit in a manner similar to simulations (Fig. 6f) so that Dh is similar in magnitude to Dt, like in the prediction. However, the predicted caging effect or looping structure in tracer trajectories due to hydrodynamic interactions with bacteria is masked by strong Brownian noise at hexadecane–water interfaces.
We have illustrated that the interaction of a tracer with multiple swimmers generates enhanced diffusion at the interface in this simulation. However, analytical evaluation of the hydrodynamic tracer diffusivity as described in ref. 31 and 34 using our far-field hydrodynamic model leads to a divergent result. The divergent result suggests that a far-field model is not sufficient for resolving the tracer diffusivity. The problem is likely to be resolved by accounting for the finite swimmer size, which would inherently exclude divergent flow singularities from the region of integration. This is an interesting point for future work.
5 Interactions among multiple swimmers generate active noise
To demonstrate the importance of hydrodynamic interactions and of active diffusion on the displacement of ensembles of swimmers at interfaces, we compare simulation and experiment. Hydrodynamic interactions among swimmers at high surface densities are a significant source of noise over lag times compared to the time to swim in circular trajectories. We simulate the pairwise interaction of multiple pushers moving on circular paths with radii selected randomly from 1.5 μm to 2.5 μm and with random initial orientations (Fig. 7a). The effect of reorientation from all neighboring swimmers is superposed to update their swimming directions and superposed displacements are used to update the swimmers' displacements. The resulting MSD of the center of rotation of the “center bacterium”, shown in Fig. 7b, is reported to illustrate the effect of hydrodynamic interactions as a function of surface density of neighboring swimmers. The predicted MSD is ballistic at short lag time, caged thereafter and diffusive at a long lag time. Hydrodynamic interactions are highly sensitive to the separation distance between nearest neighbors. The timescale for the center of rotation to become diffusive decreases from ∼20 s to ∼1 s and the diffusivity increases from 0.0005 μm2 s−1 to 0.02 μm2 s−1 as the center-to-center distance between neighboring swimmers decreases from 8 μm (brown trajectories in Fig. 7a) to 7 μm (grey trajectories in Fig. 7a) and 6 μm (blue and pink trajectories in Fig. 7a). As the bacteria become more densely packed, rare events in which two swimmers become proximate can generate torques and forces with large magnitudes that destabilize the swimmer paths as shown for the pink trajectories in Fig. 7a and the corresponding MSD of the center of rotation becomes purely diffusive as shown in pink in Fig. 7b. This diffusion of the center of rotation will lead to diffusion in bacterial path at long lag times. These simulations must be treated with care, as they ignore higher order hydrodynamic modes and other phenomena like flagellar entanglements that can occur for bacteria in the very near field. Notably, similar to active-passive interactions described in Fig. 6, fluctuations in bacterial speed, angular speed, and the active noise in swimmer paths from other sources can further randomize the paths of their neighboring swimmers resulting in a higher chance of near-field interactions. The randomizing effect of hydrodynamic interactions can also lead to higher chances of bacterial collision and near-contact interactions. Therefore, prior to the regime at high bacterial density where hydrodynamic interaction between swimmers generates coherence, at intermediate density these interactions promote chaos in the system. While direct comparison of experiment and prediction must be treated with care, active noise is indeed observed for bacteria trapped at fluid interfaces. In experiments, we have measured the MSDs of bacteria at interfaces with increasing surface density ρs and extracted the diffusion coefficients at large lag times, as reported in Fig. 7c. For all surface densities, the MSDs oscillate at moderate lag times reflecting their circular motion and become diffusive at long lag times. The orientation of bacteria at high surface density decorrelates more rapidly and the MSDs show higher diffusivities. These effects can be attributed in part to the predicted hydrodynamic interactions in pusher mode, although our bacteria also switch between pusher and puller modes.6 Conclusions
We analyze the impact of interfacially-trapped bacteria on interfacial transport based on their induced flow fields. We calculate tracer displacements due to hydrodynamic interaction with swimmers and compare the predicted tracer paths to those constructed from experiments. We find that while hydrodynamic interaction with well-separated swimmers drives tracers in closed loops, net tracer displacement can occur for swimmers and tracers in closer proximity. These displacements rely on broken symmetry in swimmer–tracer separation, and lead to loopy tracer paths around the swimmer at long lag times. We also find that swimmers can attract or repel each other due to hydrodynamic interactions; such interactions among multiple swimmers are likely to induce active diffusion that has been observed for bacteria at interfaces. To further assess the effect of interfacial pushers on colloidal transport, we predict the interactions of a tracer particle with multiple swimmers with various active diffusivities. We find a “caging” effect in tracer mean square displacements due to the looplike structure of tracer paths; this caging is eliminated by a swimmer's active diffusivity and by multiple swimmer–tracer interactions. The combined effects of active diffusion and multiple swimmer–tracer interactions generate a hydrodynamic diffusivity that can be comparable to thermal diffusivity.In nature and in biotechnology, these results have implications in understanding the initial stages of biofilm formation at fluid interfaces, including cluster formation and nutrient supply near the bacteria-populated interface. Furthermore, these results can inform the design of biomimetic active colloids as active surface agents to promote interfacial mass transport to improve the efficiency of interfacial reaction and separation processes. One could envision design strategies for active colloids that impose particular trapping orientations and positions of propulsion sites to promote mixing that could significantly impact chemical engineering processes like reactive separations near fluid interfaces.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research was made possible by a grant from the National Science Foundation (NSF grant no. CBET-1943394 and DMR-1607878). SEC acknowledges support from Worcester Polytechnic Institute's Early Research Experience in E-Term program, which was sponsored in part by the Women's Impact Network. The authors acknowledge Sarah D. Olson for useful discussions regarding the calculations of tracer diffusivity.Notes and references
- H. Terashima, S. Kojima and M. Homma, International Review of Cell and Molecular Biology, Elsevier, 2008, vol. 270, pp. 39–85 Search PubMed.
- X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017–3020 CrossRef CAS.
- K. Kanazawa, T. G. Sano, A. Cairoli and A. Baule, Nature, 2020, 579, 364–367 CrossRef CAS PubMed.
- G. Miño, T. E. Mallouk, T. Darnige, M. Hoyos, J. Dauchet, J. Dunstan, R. Soto, Y. Wang, A. Rousselet and E. Clement, Phys. Rev. Lett., 2011, 106, 048102 CrossRef.
- P. T. Underhill, J. P. Hernandez-Ortiz and M. D. Graham, Phys. Rev. Lett., 2008, 100, 248101 CrossRef PubMed.
- T. V. Kasyap, D. L. Koch and M. Wu, Phys. Fluids, 2014, 26, 081901 CrossRef.
- D. O. Pushkin, H. Shum and J. M. Yeomans, J. Fluid Mech., 2013, 726, 5–25 CrossRef.
- G. L. Miño, J. Dunstan, A. Rousselet, E. Clément and R. Soto, J. Fluid Mech., 2013, 729, 423–444 CrossRef.
- H. Kurtuldu, J. S. Guasto, K. A. Johnson and J. P. Gollub, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10391–10395 CrossRef CAS.
- S. Nambiar, P. Garg and G. Subramanian, J. Fluid Mech., 2021, 907, A26 CrossRef CAS.
- C. J. Miles, A. A. Evans, M. J. Shelley and S. E. Spagnolie, Phys. Rev. Lett., 2019, 122, 098002 CrossRef CAS.
- A. J. Mathijssen, F. Guzmán-Lastra, A. Kaiser and H. Löwen, Phys. Rev. Lett., 2018, 121, 248101 CrossRef CAS.
- S. Belan and M. Kardar, J. Chem. Phys., 2019, 150, 064907 CrossRef.
- V. Škultéty, C. Nardini, J. Stenhammar, D. Marenduzzo and A. Morozov, Phys. Rev. X, 2020, 10, 031059 Search PubMed.
- D. Krishnamurthy and G. Subramanian, J. Fluid Mech., 2015, 781, 422–466 CrossRef CAS.
- S. Thutupalli, D. Geyer, R. Singh, R. Adhikari and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5403–5408 CrossRef CAS.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- J. Zhang, R. Alert, J. Yan, N. S. Wingreen and S. Granick, Nat. Phys., 2021, 17, 961–967 Search PubMed.
- R. Alert, J. Casademunt and J.-F. Joanny, Annu. Rev. Condens. Matter Phys., 2022, 13, 143–170 Search PubMed.
- G. Kokot, S. Das, R. G. Winkler, G. Gompper, I. S. Aranson and A. Snezhko, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12870–12875 CrossRef CAS PubMed.
- M. Spellings, M. Engel, D. Klotsa, S. Sabrina, A. M. Drews, N. H. P. Nguyen, K. J. M. Bishop and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E4642–E4650 CrossRef CAS.
- A. Sokolov, M. M. Apodaca, B. A. Grzybowski and I. S. Aranson, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 969–974 CrossRef CAS.
- A. Shklarsh, G. Ariel, E. Schneidman and E. Ben-Jacob, PLoS Comput. Biol., 2011, 7, e1002177 CrossRef CAS PubMed.
- R. Di Leonardo, L. Angelani, D. DellArciprete, G. Ruocco, V. Iebba, S. Schippa, M. P. Conte, F. Mecarini, F. De Angelis and E. Di Fabrizio, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9541–9545 CrossRef CAS.
- C. Darwin, Math. Proc. Cambridge Philos. Soc., 1953, 49, 342–354 CrossRef.
- K. Katija and J. O. Dabiri, Nature, 2009, 460, 624–626 CrossRef CAS PubMed.
- A. Morozov and D. Marenduzzo, Soft Matter, 2014, 10, 2748 RSC.
- H. Nordanger, A. Morozov and J. Stenhammar, J. Fluid Mech., 2023, 974, A25 CrossRef.
- A. J. T. M. Mathijssen, D. O. Pushkin and J. M. Yeomans, J. Fluid Mech., 2015, 773, 498–519 CrossRef CAS.
- J.-L. Thiffeault and S. Childress, Phys. Lett. A, 2010, 374, 3487–3490 CrossRef CAS.
- Z. Lin, J.-L. Thiffeault and S. Childress, J. Fluid Mech., 2011, 669, 167–177 CrossRef.
- J.-L. Thiffeault, Phys. Rev. E, 2015, 92, 023023 CrossRef.
- A. Baule, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2308226120 CrossRef PubMed.
- D. O. Pushkin and J. M. Yeomans, Phys. Rev. Lett., 2013, 111, 188101 CrossRef PubMed.
- K. C. Leptos, J. S. Guasto, J. P. Gollub, A. I. Pesci and R. E. Goldstein, Phys. Rev. Lett., 2009, 103, 198103 CrossRef PubMed.
- L. Angelani, C. Maggi, M. L. Bernardini, A. Rizzo and R. Di Leonardo, Phys. Rev. Lett., 2011, 107, 138302 CrossRef CAS PubMed.
- J. Deng, M. Molaei, N. G. Chisholm and K. J. Stebe, J. Fluid Mech., 2023, 976, A18 CrossRef CAS.
- D. Lopez and E. Lauga, Phys. Fluids, 2014, 26, 071902 CrossRef.
- E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400–412 CrossRef CAS PubMed.
- J. Deng, M. Molaei, N. G. Chisholm and K. J. Stebe, Langmuir, 2020, 36, 6888–6902 CrossRef CAS.
- R. Großmann, F. Peruani and M. Bär, New J. Phys., 2016, 18, 043009 CrossRef.
- M. Molaei, N. G. Chisholm, J. Deng, J. C. Crocker and K. J. Stebe, Phys. Rev. Lett., 2021, 126, 228003 CrossRef CAS PubMed.
- N. G. Chisholm and K. J. Stebe, J. Fluid Mech., 2021, 914, A29 CrossRef CAS.
- T. J. Pedley and J. O. Kessler, Annu. Rev. Fluid Mech., 1992, 24, 313–358 CrossRef.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940–10945 CrossRef CAS.
- E. W. Burkholder and J. F. Brady, Phys. Rev. E, 2017, 95, 052605 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00140k |
| This journal is © The Royal Society of Chemistry 2024 |