Open Access Article
Open Access ArticleDynamics of a self-interacting sheet in shear flow†
William T.
Funkenbusch
 ,
Kevin S.
Silmore
,
Kevin S.
Silmore
 and
Patrick S.
Doyle
and
Patrick S.
Doyle
 *
*
Massachusetts Institute of Technology Department of Chemical Engineering, 25 Ames St, Cambridge MA, 02139, USA. E-mail: pdoyle@mit.edu
First published on 21st May 2024
Abstract
Solution processing of 2D materials such as graphene is important for applications thereof, yet a complete fundamental understanding of how 2D materials behave dynamically in solution is lacking. Here, we extend previous work by Silmore et al., Soft Matter, 2021, 17(18), 4707–4718 by adding short-ranged Lennard–Jones interactions to 2D sheets in shear flow. We find that the addition of these interactions allows for a rich landscape of conformations which depend on the balance between shear strength, bending rigidity, and interaction strength as well as the initial configuration of the sheet. We explore this conformational space and classify sheets as flat, tumbling, 1D folded, or 2D folded based on their conformational properties. We use kinetic and energetic arguments to explain why sheets adopt certain conformations within the folded regime. Finally, we calculate the stresslet and find that, even in the absence of thermal fluctuations and multiple sheet interactions, shear-thinning followed by shear-thickening behavior can appear.
1 Introduction
Solution processing and liquid exfoliation are important aspects of the production and application of 2D materials such as graphene, graphene oxide, transition metal dichalcogenides, and, more recently, 2D polymers,1–19 but fundamental understanding of many properties of suspended 2D sheets is lacking. For example, much work has been devoted to the transition from a flat to a crumpled state with increasing temperature,20–28 but there is still debate as to whether self-avoiding sheets crumple or are flat at all temperatures.29–42 The introduction of attractive interactions, which appear in real systems in the form of, for example, dispersion forces, has been explored as a potential way to induce conformational changes in sheets,36,43,44 and a series of folding transitions have also been theorized and observed in thermal simulations.45One can also apply a flow field to sheets, resulting in dynamics which are even less well understood than the equilibrium behavior. Xu and Green studied the rotation of semi-flexible sheets under shear and extensional flows and found shear-thinning rheological behavior.46,47 Yu and Graham found coil-stretch-like and compact-stretched transitions for stiff sheets in extensional flows.48,49 They found that flexible sheets in extensional flows additionally exhibit wrinkling which significantly modifies the aforementioned transitions. Salussolia and Botto characterized the separation of multi-sheet systems (although in 2D) with long- and short-range hydrodynamics in shear and found that separating sheets can reassemble under certain conditions.50 Recently, Perrin and Botto also showed (again in 2D) that, despite multi-layer sheets having a higher bending rigidity than single-layer sheets,51 a lateral hydrodynamic force at moderate sheet separations can cause the sheets to bend for shear rates much lower than expected.52
Previous work by Silmore et al.53,54 showed that Jeffery's equations for the rotation of rigid ellipsoids in shear55 matched well with the behavior of semi-flexible sheets in shear under certain conditions.53 Introducing thermal energy resulted in shear-thinning followed by shear-thickening rheological behavior54 which has been observed in dilute graphene suspensions56 as well as dilute graphene oxide suspensions.57 These experiments showed the same stronger shear-thinning at higher temperatures. Because these simulations involved only single sheets, they show that conformational changes may contribute to this non-monotonic rheological behavior in addition to sheet-sheet interactions (e.g. the buildup and breakdown of agglomerates or the formation of lamellar layers).
In many real systems, however, such as graphene, bending rigidity is several orders of magnitude greater than thermal energy58,59 (graphene oxide being an exception, with bending rigidity about the same as thermal energy at room temperature60). This raises the question as to whether non-monotonic rheological behavior can be generated in the athermal limit. As discussed earlier, self-interactions are a potential method of producing conformational changes in sheets, which can affect their rheological properties.
In this work, we study athermal, semi-flexible sheets with long-range hydrodynamics using the model developed in previous work53 but with the addition of attractive self-interactions. We show that single sheets with attractive self-interactions can exhibit diverse and interesting conformational and rotational behaviors. The parameters in the system allow us to define two dimensionless groups which map out the conformational space, showing several distinct regions of different conformational behaviors. These behaviors, together with rotation, give rise to non-monotonic rheological behavior. We use kinetic and energetic arguments to explain our results.
2 Models and methods
2.1 Simulation method
Similar to the model employed in previous work,53,54 we construct hexagonal sheets with circumradius L = 39a with beads of radius a such that each interior bead has 6 tangent neighbors, totalling N = 1141 beads. We also apply many of the same forces to beads within the sheets. We use harmonic forces between neighboring beads with in-plane stiffness k and dihedral forces between neighboring triangles of beads with bending rigidity (out-of-plane stiffness) κ. This discrete bending rigidity can be mapped to a continuum bending rigidity, , with
, with  for this specific triangulation.61 We set the in-plane stiffness of the sheets to be much larger than their out-of-plane stiffness, as in true in many real system. This can be quantified using the Föppl–von Kármán number, FvK ∼ kL2/κ, which was between 103 and 107 for the simulations in this paper. Thus, the sheets are inextensible relative to bending. We also apply hard-sphere interactions between non-neighboring beads with a pair-potential which places overlapping beads tangent to each other under Rotne–Prager–Yamakawa dynamics, which give long-range hydrodynamics (see below).
for this specific triangulation.61 We set the in-plane stiffness of the sheets to be much larger than their out-of-plane stiffness, as in true in many real system. This can be quantified using the Föppl–von Kármán number, FvK ∼ kL2/κ, which was between 103 and 107 for the simulations in this paper. Thus, the sheets are inextensible relative to bending. We also apply hard-sphere interactions between non-neighboring beads with a pair-potential which places overlapping beads tangent to each other under Rotne–Prager–Yamakawa dynamics, which give long-range hydrodynamics (see below).
Finally, we apply a short-ranged interaction in the form of a truncated Lennard–Jones potential between non-neighboring beads:
 | (1) |
 .
.
Beads can interact via this potential along the sheet surface, which may change the in-plane behavior of the sheets. However, we find empirically that, even for the largest interaction strengths used, the harmonic bonds between neighboring beads in a flat sheet extend by less than 0.1% of their equilibrium distance. Therefore, we expect that self-interactions do not significantly affect the in-plane interactions of the sheet.
We integrate this system forward in time using an Euler–Maruyama integrator with the following equations of motion for Brownian dynamics with hydrodynamics:
 | (2) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) δm1δn2 is the velocity gradient tensor for simple shear with shear rate
δm1δn2 is the velocity gradient tensor for simple shear with shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and Ui is the sum of the applied potentials on bead i. To achieve long-range hydrodynamics, we use the Rotne–Prager–Yamakawa tensor62 for
and Ui is the sum of the applied potentials on bead i. To achieve long-range hydrodynamics, we use the Rotne–Prager–Yamakawa tensor62 for ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ij, which is given analytically by
ij, which is given analytically by | (3) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) is the unit vector pointing from particle i to particle j.
is the unit vector pointing from particle i to particle j.
The Rotne–Prager–Yamakawa tensor models long-range, pairwise hydrodynamic interactions between beads, with each bead acting as a regularized Stokeslet.53 Thus, finite discretizations of these beads as sheets have some degree of permeability. However, Yu and Graham recently showed that, for similarly discretized sheets, the permeation velocity (i.e. the fluid velocity normal to the sheet surface) in extensional flows tends to be small (on the order of 1% relative to the sheet size and strain rate).49 We expect shear flows to carry similar permeation velocities. Second, for small enough sheets, lubrication forces are relatively small compared to the forces from self-interaction. We discuss this assumption and the sheet size limit in Appendix A. Conceptually, because the applied self-interaction includes a repulsive component and equilibrium distance, small enough sheets do not approach closely enough for lubrication forces to be significant.
Initially flat sheets aligned with the flow-vorticity plane were rotated by an angle θ = 5° about the vorticity axis and then by a varying angle ϕ about the flow axis. We sample from ϕ = 0° to ϕ = 90° with samples at every 5°. In averages over ϕ, we give relative weights to each ϕ proportional to sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, corresponding to initially randomly oriented sheets. We use a time step of
ϕ, corresponding to initially randomly oriented sheets. We use a time step of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δt = 2 × 10−4 for all simulations. Simulations were run for 2000 strain cycles (
Δt = 2 × 10−4 for all simulations. Simulations were run for 2000 strain cycles (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t = 2000) and results were calculated using the last 200 strain cycles using data from every 100
t = 2000) and results were calculated using the last 200 strain cycles using data from every 100![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t, as analysis of the autocorrelation of sheet properties such as the radius of gyration at small interaction strengths (i.e. for tumbling sheets, as described later, as they have the slowest decaying autocorrelations) showed that approximately every 100
t, as analysis of the autocorrelation of sheet properties such as the radius of gyration at small interaction strengths (i.e. for tumbling sheets, as described later, as they have the slowest decaying autocorrelations) showed that approximately every 100![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t are independent. Simulations were run using HOOMD-blue on NVIDIA GeForce GTX 1080 Ti's63 with a custom package from Silmore et al.53 which was adapted from Fiore et al.64 All images of sheets were rendered using Ovito.65
t are independent. Simulations were run using HOOMD-blue on NVIDIA GeForce GTX 1080 Ti's63 with a custom package from Silmore et al.53 which was adapted from Fiore et al.64 All images of sheets were rendered using Ovito.65
2.2 Dimensionless groups
The addition of self-interaction adds two new parameters to the system: the interaction strength, ε, and interaction range, σ. To give a roughly continuous energy landscape for two sheets sliding parallel to each other, we require σ ≫ a. As mentioned earlier, for all sheets in this work, we choose . While ε is the energy scale for the interaction between two beads, the energy scale for the interaction of a bead with a plane of beads separated by the equilibrium distance of σ is
. While ε is the energy scale for the interaction between two beads, the energy scale for the interaction of a bead with a plane of beads separated by the equilibrium distance of σ is | (4) |
 is the interaction energy density of the sheet. For two parallel sheets of characteristic size L aligned with the shear-vorticity plane and separated by a distance σ, shear acts as a force trying to separate the two sheets by sliding them along each other, while their interaction resists this sliding. Taking the ratio of these two forces gives a dimensionless group characterizing the ability of attractive interaction to resist shear:
is the interaction energy density of the sheet. For two parallel sheets of characteristic size L aligned with the shear-vorticity plane and separated by a distance σ, shear acts as a force trying to separate the two sheets by sliding them along each other, while their interaction resists this sliding. Taking the ratio of these two forces gives a dimensionless group characterizing the ability of attractive interaction to resist shear: | (5) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate. This dimensionless group characterizes the ability of nearby sections of the sheet to slide along each other. A more detailed derivation of this dimensionless quantity can be found in Appendix B.
is the shear rate. This dimensionless group characterizes the ability of nearby sections of the sheet to slide along each other. A more detailed derivation of this dimensionless quantity can be found in Appendix B.
We note the existence of the bead radius, a, in this dimensionless number. In previous work,53,54a was the smallest resolvable length scale and did not play a role in the dynamics. Here, because interactions happen between individual beads, a is relevant. The quantity (L/a) is proportional to the number of interactions along the edge of the sheet. In a physical system, a now corresponds to the interacting elements of a sheet, for example, individual carbon atoms in a graphene sheet interacting via van der Waals forces. Typical solution-processed sheets have sizes ranging from nanometers to micrometers66 and may interact at a wide range of distances.67 Further control over the shear rate in experiments means that this dimensionless number can span several orders of magnitudes, and we thus expect this dimensionless number to reveal interesting transitions in real systems.
While the ratio of bending rigidity to shear, denoted S in previous work53,54 with
 | (6) |
 | (7) |
Interaction tries to move sections of the sheet together by folding, while bending rigidity resists this folding. Thus, when K ≫ 1, attraction interactions cannot overcome bending rigidity, and we expect the sheet to behave as in previous work.53,54 This dimensionless group is also convenient because it is a function of material properties, while χ can be tuned experimentally by adjusting shear rate.
Plots varying K and χ−1 thus have a convenient physical interpretation: moving along the first axis adjusts the material property of bending rigidity to interaction strength, while moving along the second axis changes the experimental property of shear force relative to interaction strength. The value of S can be determined from the values of χ, K, σ and a with S = 6χK(a/L)(σ/L).
3 Conformational properties
3.1 Identifying sheet conformations
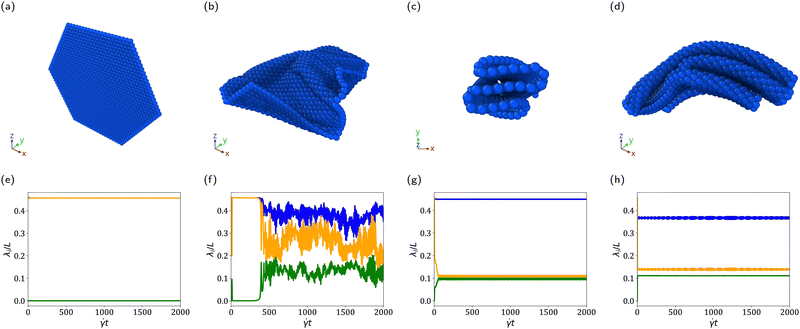
The conformational properties of sheets are highly sensitive to experimental conditions (χ), material properties (K), and initial conditions (e.g. the initial orientation of the sheets relative to the flow axis, ϕ). We identify four different conformations that sheets can exhibit: flat, tumbling, 1D folding, and 2D folding. An example of each is shown in Fig. 1. Videos of simulations for each conformation along with their corresponding average signed local mean curvature (see Section 3.3) are included in the ESI.† We examine how the values of χ, K, and ϕ lead to each of these conformations in future sections. In this section, we show how each conformation can be characterized.We identify these conformations by looking at the square root of the eigenvalues of the gyration tensor, λi (i = 1, 2, 3 with λ1 > λ2 > λ3), which correspond to the three characteristic lengths of the conformation. We take averages of each λi over the last 250![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t of the simulation every 0.25
t of the simulation every 0.25![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t, denoted
t, denoted ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) i.
i.
Flat sheets have almost no bends and therefore ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) 1 and
1 and ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) 2 are near their maximum value of 0.456L at all times. We categorize sheets as flat if
2 are near their maximum value of 0.456L at all times. We categorize sheets as flat if ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) 2 > 0.4L. They are the only sheet conformation we observe which are not necessarily continuously rotating about the vorticity axis.
2 > 0.4L. They are the only sheet conformation we observe which are not necessarily continuously rotating about the vorticity axis.
Tumbling sheets are characterized by impermanent folds which cause their λi to fluctuate significantly throughout the simulation. We categorize sheets as tumbling if, regardless of ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) i, the smallest standard deviation in λi (over the last 200
i, the smallest standard deviation in λi (over the last 200![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t) is greater than 7 × 10−3L or the largest standard deviation in λi is greater than 3 × 10−2L.
t) is greater than 7 × 10−3L or the largest standard deviation in λi is greater than 3 × 10−2L.
1D folded sheets are characterized by a series of parallel folds, resulting in a λ1 close to the maximum value, but a much smaller λ2. We categorize sheets as 1D folded when ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) 1 > 0.4L and
1 > 0.4L and ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) 2 < 0.4L.
2 < 0.4L.
2D folded sheets are characterized by the appearance of non-parallel folds, causing λ1 to deviate significantly from its maximum value. We categorize sheets as 2D folded when ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) 1 < 0.4L. 1D folded and 2D folded sheets are referred to together as folded sheets. Folded sheets are distinct from tumbling sheets, which also have folds, because their folds are persistent over time.
1 < 0.4L. 1D folded and 2D folded sheets are referred to together as folded sheets. Folded sheets are distinct from tumbling sheets, which also have folds, because their folds are persistent over time.
The boundaries between different sheet conformations were chosen by looking at histograms of ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) i and the standard deviation in λi, included in the ESI.† There is a clear gap in the histogram of
i and the standard deviation in λi, included in the ESI.† There is a clear gap in the histogram of ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) 2 at 0.4L, making
2 at 0.4L, making ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) 2 > 0.4L a natural choice for characterizing a sheet as flat. The transition between 1D and 2D folded sheets appears continuous in that sheets can have both parallel and non-parallel folds. The cutoff between these conformations was therefore chosen by eye by finding a value of
2 > 0.4L a natural choice for characterizing a sheet as flat. The transition between 1D and 2D folded sheets appears continuous in that sheets can have both parallel and non-parallel folds. The cutoff between these conformations was therefore chosen by eye by finding a value of ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) 1 which seems to correspond to the beginning of the appearance of non-parallel folds. For tumbling sheets, the cutoffs were chosen again by eye such that each distribution of standard deviations for tumbling sheets appears normal-like.
1 which seems to correspond to the beginning of the appearance of non-parallel folds. For tumbling sheets, the cutoffs were chosen again by eye such that each distribution of standard deviations for tumbling sheets appears normal-like.
3.2 Phase map of sheet conformations
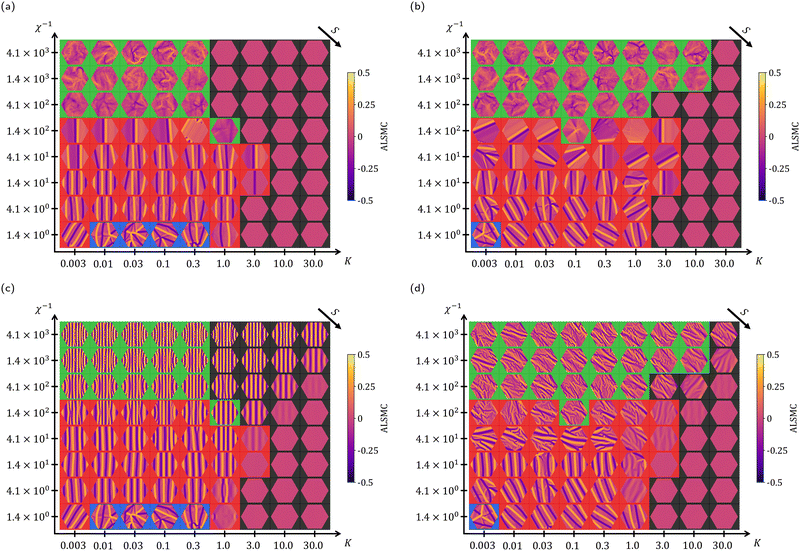
We performed a parameter sweep across χ, K, and ϕ and categorized each conformational state as flat, tumbling, 1D folded, or 2D folded. We plot using χ−1 instead of χ as increasing χ−1 corresponds to increasing shear rate, as one might see in a rheological experiment. As this is a large, 3D phase space, we present 2 slices at ϕ = 0° and ϕ = 45°, shown in Fig. 2. First looking at the phase plot for ϕ = 0°, we see clear divisions between each conformation. For large K (>1), attractive interactions cannot overcome bending rigidity, and sheets tend to be flat. At large χ−1 (>100) and low K (≲1), shear is able to break local attractive interactions, and the sheets tumble. At low χ−1 (≲100) and low K (≲1), shear is unable to break local attractive interactions, so folds are permanent and the sheets are 1D or 2D folded. Lower values of χ−1 at low K (<1) correspond to less well-aligned folds and thus more 2D folded sheets.At ϕ = 45°, the features of the plot remain the same with one notable exception. The tumbling region expands to occupy the high χ−1 (>100), high K (>1) regime, similar to Fig. 6 in previous work,53 where the continuously tumbling regime was larger for larger ϕ. The specific sheets which tumble for K ≳ 1 are unpredictable, but on average tumbling behavior is more common at larger ϕ and χ−1. This makes sense, as larger ϕ mean larger initial deformations from the flat conformation and larger χ−1 at constant K mean stronger initial buckling due to a reduced value of S, the dimensionless ratio of bending rigidity to shear strength. However, the tumbling behaviors in the sheets in this work are notably different than in previous work53 due to the presence of self-interaction. For example, in Fig. 3, the sheet forms several, slowly sliding folds which continuously flip in sequence. We term this “teacup” behavior. This behavior was observed for many initial orientations near the tumbling/folded boundary (1.4 × 102 ≤ χ−1 ≤ 1.4 × 103). Teacup behavior is usually transient in the sense that sheets alternate between it and more typical tumbling behavior over long time scales (several hundred ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t). It is classified as tumbling due to the existence of non-persistent folds and is difficult to distinguish from typical tumbling behavior using the values of
t). It is classified as tumbling due to the existence of non-persistent folds and is difficult to distinguish from typical tumbling behavior using the values of ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) i and the standard deviations of λi. A video of a simulation with this behavior is included in the ESI.†
i and the standard deviations of λi. A video of a simulation with this behavior is included in the ESI.†
Within a given region (flat, tumbling, and folded), sheet behavior can be predicted reliably. Near the boundaries between regions, sheet behavior may be highly sensitive to initial orientation.
3.3 Bending modes of 1D folded sheets
As in previous work,53 we calculate the signed local mean curvature of the sheets and calculate the average over 101 equally spaced snapshots during the last 200![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t, giving an average signed local mean curvature (ASLMC). We plot these for the ϕ = 0° and ϕ = 45° conditions in Fig. 4. These plots correspond well to the characterizations given in the previous section. Flat sheets have no local mean curvature, and thus have an ASLMC of about 0 at all points. Tumbling sheets have significant but non-persistent folds, and their ASLMC's thus appear noisy. Folded sheets have persistent folds, and thus are characterized by sharp bands of high magnitude ASLMC. 1D folded sheets have folds which are aligned along a single axis, while 2D folded sheets have non-parallel folds which can branch off into more folds. Some sheets, especially for ϕ = 45° have characteristics of both 1D and 2D folded sheets.
t, giving an average signed local mean curvature (ASLMC). We plot these for the ϕ = 0° and ϕ = 45° conditions in Fig. 4. These plots correspond well to the characterizations given in the previous section. Flat sheets have no local mean curvature, and thus have an ASLMC of about 0 at all points. Tumbling sheets have significant but non-persistent folds, and their ASLMC's thus appear noisy. Folded sheets have persistent folds, and thus are characterized by sharp bands of high magnitude ASLMC. 1D folded sheets have folds which are aligned along a single axis, while 2D folded sheets have non-parallel folds which can branch off into more folds. Some sheets, especially for ϕ = 45° have characteristics of both 1D and 2D folded sheets.
1D folded sheets at the boundary with tumbling sheets (e.g. χ−1 = 1.4 × 102) typically have two close parallel folds and moderate curvature throughout the rest of the sheet. These 1D folded sheets take on a “rolled-up” conformation, as seen in Fig. 5. A video of a simulation of a rolled-up sheet is included in the ESI.† Interaction is strong enough to cause an initial folding of the sheet, but shear is strong enough to anneal all but the last two folds. This results in rolled-up sheets being an even more energetically favorable state due to the high degree of contact for self-interactions and gentle folding throughout. 1D folded sheets have a number of folds ranging from 2-folds in rolled up sheets, to 6, evenly spaced folds. There appears to be no clear pattern to the exact number of folds that will appear, although roughly the number appears to increase with decreasing χ−1 unless the sheet 2D folds.
 | ||
| Fig. 5 Example of a 1D folded sheet that adopts a rolled-up conformation. x is the flow direction and y is the shear direction. | ||
We can estimate the expected number of folds using a simple energetic argument balancing the bending and interaction energies of a 1D folded sheet, which is detailed in Appendix C. Doing so, we obtain the following estimate for the optimal number of folds,  , in a rectangular 1D folded sheet:
, in a rectangular 1D folded sheet:
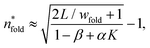 | (8) |
For small χ−1 (≲41), shear is not strong enough to break up all the folds, and the sheet can obtain an energetically stable folded configuration. In the small K limit for sheets with L = 39a, eqn (8) approaches about 4.46, which is close to 4, the most common number of folds observed. For sheets with L = 79a, eqn (8) approaches about 6.62. A series of simulations run with L = 79a and ϕ = 0° in the 1D folded regime showed 6 folds at higher χ−1 (shear rates) and 8 folds at lower χ−1.
For slightly higher χ−1 (≈141), shear is strong enough to break up all but 2 folds and the sheet adopts a more energetically favorable rolled-up conformation, which is not modelled by eqn (8). At even higher χ−1 (≳410), shear is strong enough to continuously break new folds which form as the sheet tumbles.
Because α ≈ 0.05, the number of folds predicted by eqn (8) does not decrease significantly until K ≈ 20. The sheets flattening at about K = 3.0, a full order of magnitude lower, is therefore likely a kinetic phenomenon, which we explore in the next section.
3.4 Creation of persistent folds in 1D folded sheets
To explain why sheets in shear adopt configurations with parallel folds as opposed to other configurations (e.g. the “double folded” configuration observed by Abraham and Kardar45), we return to previous work,53 which calculated the buckling modes of sheets in shear as a function of the ratio of bending rigidity to shear, S = κ/πη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) L3, at ϕ = 0° and at the maximal in-plane stress for a flipping sheet, θ = 45°. This analysis did not consider attractive interactions, which could change the buckling behavior, however we believe it to still be useful. Lines of constant S correspond to lines of slope 1 in plots of K versus χ−1. In our simulations, S × 105 ranges from 9.4 × 10−4 to 2.8 × 104, which covers more than 10 of the first buckling transitions. Notably, the calculated buckling modes from previous work53 have alternating signs in curvature, just like what is observed in the 1D folded sheets in this work.
L3, at ϕ = 0° and at the maximal in-plane stress for a flipping sheet, θ = 45°. This analysis did not consider attractive interactions, which could change the buckling behavior, however we believe it to still be useful. Lines of constant S correspond to lines of slope 1 in plots of K versus χ−1. In our simulations, S × 105 ranges from 9.4 × 10−4 to 2.8 × 104, which covers more than 10 of the first buckling transitions. Notably, the calculated buckling modes from previous work53 have alternating signs in curvature, just like what is observed in the 1D folded sheets in this work.
Fig. 4 shows the local mean curvature for sheets averaged over the last 200![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t and during their initial flip (determined as when the average normal vector of the triangles in the sheet is closest to θ = 45°). As χ−1 decreases for low K, the number of folds at the initial buckle decreases as expected because the effective bending rigidity increases relative to shear strength (given by S). In the 1D folded regime, sheets have folds which which are sharper in the initial buckle than the buckles that appear in the absence of interactions, showing that interaction is strong enough to affect the initial buckling. In this regime, the number of folds often decreases from the initial buckle to the final conformation, showing annealing to a more energetically stable configuration. As K increases, the magnitude of the curvature in the initial flip decreases, again due to an increasing S, until the sheet eventually appears flat. While the analysis done in previous work53 was only done for sheets with ϕ = 0°, the same trends are seen in sheets with any value of ϕ, as seen in Fig. 4d.
t and during their initial flip (determined as when the average normal vector of the triangles in the sheet is closest to θ = 45°). As χ−1 decreases for low K, the number of folds at the initial buckle decreases as expected because the effective bending rigidity increases relative to shear strength (given by S). In the 1D folded regime, sheets have folds which which are sharper in the initial buckle than the buckles that appear in the absence of interactions, showing that interaction is strong enough to affect the initial buckling. In this regime, the number of folds often decreases from the initial buckle to the final conformation, showing annealing to a more energetically stable configuration. As K increases, the magnitude of the curvature in the initial flip decreases, again due to an increasing S, until the sheet eventually appears flat. While the analysis done in previous work53 was only done for sheets with ϕ = 0°, the same trends are seen in sheets with any value of ϕ, as seen in Fig. 4d.
We propose that persistent folds in 1D folded sheets are formed during the initial buckling of the sheet during the first flip followed by annealing caused by shear towards an energetically stable state. If shear is too strong (χ−1 ≳ 410), the folds formed during buckling are not persistent, and the sheet tumbles or flattens. At an intermediate value of shear (χ−1 ≈ 141), folds form during buckling but most are broken up by shear, resulting in an energetically favorable rolled-up sheet. At lower values of shear (χ−1 ≲ 41), shear anneals the sheets towards their energetically preferred number of folds as predicted by eqn (8). If shear is too weak, it can only anneal partially (thus why some 1D folded sheets have more than 4 folds). Annealing can only decrease the number of folds. So, if the number of bends in the initial buckle is less than the energetically ideal number of folds, it is kinetically trapped with that number of folds. Because the buckling modes of sheets in shear have parallel folds, the resulting conformations have parallel folds.
At low K, interactions are stronger than buckling, so buckling will propagate into folds. For K ≳ 1, interactions are not strong enough to overcome bending, so the extent of buckling is determined by the competition between bending rigidity and shear (i.e. the value of S). This explains how sheets can transition from flat to 1D folded and back to flat with increasing shear at K = 3.0. At low shear, the sheets do not buckle strongly, and interactions are insufficient to fold the sheet. As shear increases, S decreases, and the sheets buckle more strongly. Only if the buckling is strong enough can it initiate folding through interactions. Once shear becomes too strong, however, interaction is not strong enough to create persistent folds, so the sheet is flat. The critical value of S × 105 above which sheets will not buckle if K ∼ 3 is about 943 (which is indeed the lowest value of S in these simulations above the first buckling transition determined in previous work53). The critical value of χ × 105 below which shear is too strong for sheets to fold is approximately 710.
S = 6χK(a/L)(σ/L), so depending on the size of a given sheet, the 1D folded region between two flat regions may be inaccessible. Specifically, given a critical S* and χ*, we require S < S*, χ > χ*, and K ∼ 1. As L increases, S decreases relative to χ, and we expect the 1D folded region to increase in width. Similarly, the region decreases in width with increasing σ. Therefore, this region increases in size as the size of the sheet increases relative to interaction range. Because χ* ≈ S*, K ∼ 1, and (L/a) ≫ 1, this region should exist if σ is not much larger than L (if (σ/L) ≲ (1/K)(S*/6χ*)(L/a)), that is, if sheets are not much smaller than the range of their interactions. In such a system, χ is no longer the relevant dimensionless parameter as each bead would interact with every other bead in the sheet and therefore ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) σ2 is no longer the relevant energy scale.
σ2 is no longer the relevant energy scale.
If both χ−1 and K are small, small deviations from the alignment of the folds caused by finite-size, edge, and/or initial orientation effects will cause the spontaneous formation of more folds, and the sheet can 2D fold. This is supported by the 2D folded sheets in Fig. 4c, which are already in their 2D folded configuration at the first flip.
It is important to consider how sheet behavior would change with sheet shape. The equation for the optimal number of folds was derived for a rectangular sheet but the overall arguments are valid as long as the number of beads vertically along the folds does not change quickly across the width of the sheet (relative to the width of folded regions). This, along with the equation matching with the hexagonal sheet simulations in this work, suggest that eqn (8) is applicable for a broad range of sheet shapes with slowly changing widths.
Changing the sheet shape will affect the bending modes of the sheet and therefore the critical values of S corresponding to different buckling modes. This might affect the shape of the right edge of the folded/flat boundary due to the earlier discussion of the importance of S. Additionally, videos of 1D folded sheets (provided in the ESI†) show that the process of a 1D folded sheet losing folds involve these folds “sliding” along the width of the sheet until it hits the edge of the sheet, where the fold disappears. This process may be affected by the shape of the sheet. Simulations with different sheet shapes (e.g. rectangular or circular) would be valuable in illuminating the effects of sheet shape on the formation and breaking of 1D folds.
4 Rheological properties
4.1 Sheet viscosity calculations
The stress of a dilute suspension of force-free rigid particles is | (9) |
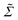 is the stresslet (the first moment of the stress on a particle).68 As in previous work,54 we calculate an approximate upper bound on the stresslet using the minimum-bounding ellipsoid of the sheet, its Jeffrey orbits,55 and the stress for an ellipsoidal particle as found in Kim and Karilla.69 The resulting average off-diagonal (flow-gradient) contribution to the stress over the last 200
is the stresslet (the first moment of the stress on a particle).68 As in previous work,54 we calculate an approximate upper bound on the stresslet using the minimum-bounding ellipsoid of the sheet, its Jeffrey orbits,55 and the stress for an ellipsoidal particle as found in Kim and Karilla.69 The resulting average off-diagonal (flow-gradient) contribution to the stress over the last 200![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t, which is expected to grow linearly with the viscosity of a dilute suspension of these sheets, is shown in Fig. 6.
t, which is expected to grow linearly with the viscosity of a dilute suspension of these sheets, is shown in Fig. 6.
The sheet viscosity shows 2 different behaviors based on K. For K ≳ 10.0, sheets have a small sheet viscosity at low χ−1 (i.e. low shear rates). Flat sheets which rotated about the vorticity axis contributed a higher stress than flat sheets in the flow-vorticity plane, with 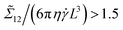 . These sheets were ones initially oriented with their normal close to the vorticity axis (ϕ = 85° or 90°). Finally, once shear is strong enough to induce tumbling, shear-thickening behavior begins.
. These sheets were ones initially oriented with their normal close to the vorticity axis (ϕ = 85° or 90°). Finally, once shear is strong enough to induce tumbling, shear-thickening behavior begins.
For K ≲ 1.0, there is steady shear-thinning followed by shear-thickening behavior which appears near the same critical χ−1 as for the high K behavior. We discuss the origin of these behaviors in the next section.
4.2 Explanation of non-monotonic rheological properties
The nature of this shear-thinning into shear-thickening behavior is different than that with thermal energy but no interactions, which resulted from the “u-turn” radius of a flipping sheet.54 In our current work, sheets in the shear-thinning regime are 1D or 2D folded.We calculate three summary statistics, the radius of gyration, Rg/L, the relative shape anisotropy, ζ2, and the orientation of the largest axis of the minimum bounding ellipsoid of the sheet dotted with the vorticity axis, |v1·ẑ|, which we term the “alignment” of the sheet. The relative shape anisotropy varies from 0 to 1, with 0 occurring only if all beads are on the same line, and 1 occurring only if the beads have spherical symmetry. The alignment also varies from 0 to 1, with 0 occurring if the largest axis of the sheet is in the shear-flow plane, and 1 occurring if the largest axis of the sheet is along the vorticity axis. Scatter plots of the sheet viscosity versus each of these quantities are included in the ESI,† however we note several notable features of these plots in the following discussion.
In Fig. 7, we plot these three summary statistics as a function of χ−1 and K to explain the observed rheological behavior.
 | ||
Fig. 7 (a) Radius of gyration, (b) relative shape anisotropy, and (c) alignment averaged over the last 200![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t and all ϕ. Error bars are 95% confidence intervals. Dotted lines drawn to guide the eye. t and all ϕ. Error bars are 95% confidence intervals. Dotted lines drawn to guide the eye. | ||
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) L3) and one with a lower sheet viscosity (∼0.2 × 6πη
L3) and one with a lower sheet viscosity (∼0.2 × 6πη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) L3).
L3).
This can be explained by looking at the average alignment of the sheets, which increases with shear rate. For prolate spheroids (ellipsoids with one large axis and two small axes) such as the minimum bounding ellipsoid of 1D folded sheets, large average alignment (“log-rolling”) behavior is favored, which is why large average alignments result in lower sheet viscosities. Conceptually, this is because the distance the sheet “sticks out” into the shear axis is lower. These two types of motions (high and low average alignment) were observed in the past as the long-time behavior for ellipsoidal particles in shear.70
Indeed, for 1D folded sheets, most sheets have an average alignment close to either 1 or 0, indicating that they reach one of these terminal behaviors. The mechanism for these sheets deviating from their Jeffrey orbits to reach this high or low average alignment state is possibly the deformability of the sheets, which has been shown to influence the orbits sheets take in this manner.71,72 1D folded sheets with high average alignments have lower stresses than 1D folded sheets with low average alignments, explaining the two clusters observed in a scatter plot of sheet viscosity versus the Rg/L. The behavior of individual sheets is erratic, necessitating an average over initial condition. Thus, shear-thinning is due to a statistical average over many initial conditions. At higher shear rates, sheets on average adopt more log-rolling behavior, causing shear-thinning. This makes sense, as stronger shears cause greater perturbations in sheets, and thus allow for them to be more likely to be able to access the more favorable, lower stress, rotational behavior. Note that the decrease in average alignment at χ−1 ∼ 1.4 × 102 is due to the rare appearance of tumbling sheets at this value of χ−1.
Sheets exhibiting teacup behavior have similar sheet viscosities to folded sheets. This behavior is seen as a low sheet viscosity cluster of low average alignment tumbling sheets at a range of Rg/L. This behavior decreases in frequency at higher shear rates as it is a self-interaction-dependent behavior, which could contribute to the shear-thickening behavior. However, because this behavior is relatively rare, we expect that its effect is small. A detailed study of teacup behavior, its frequency as a function of χ−1 and K, and its effects on the sheet viscosity would be enlightening.
Another interesting aspect of tumbling sheets is their tumbling time, which is roughly the time for a sheet to make half a revolution about the vorticity axis. Scaling arguments for the tumbling time of 2D polymers have been proposed and confirmed with simulations for flipping sheets in previous work.53 These scaling arguments are indeed only valid for relatively inflexible sheets. Because tumbling sheets are constantly deforming, it is difficult to both develop scaling arguments for the tumbling time as well as calculate it in simulations. This is further complicated by the existence of self-interactions in these sheets, which can change their effective macroscopic bending rigidities and affect their conformational behaviors. However, we believe that a detailed study on tumbling times for these sheets would be valuable and merits further investigation. Flipping times for folded sheets could likely be predicted using the average rotational velocity of its corresponding Jeffrey orbit. However, because the sheets are deformable, they are likely to adopt different trajectories according to an effective orbit constant and aspect ratio.73 A study of the flipping dynamics of folded sheets was not conducted in this work, but would also be valuable in the future.
The value of K ∼ 3.0 appears to be right at the boundary between low K and high K behaviors and exhibits a mix of both behaviors, resulting in complex trends in Rg/L, ζ2, and average alignment.
In Fig. 6, we scale the sheet viscosity to L3. However, given two additional length scales, a and σ, this is not necessarily the proper scale. Furthermore, the proper scale for the sheet viscosity might be different for flat vs. tumbling vs. folded sheets. We have not confirmed any such scalings in this work, but we believe it warrants investigation and discuss predicted scalings in Appendix D.
Note that thermal energy would cause deviations from the discussed conformational behaviors which would decrease with increasing shear rate, likely resulting in the shear-thinning behavior seen in previous work.54
5 Conclusions
In this work, we examined the role of short-ranged attractive interactions for semi-flexible, athermal sheets in shear flow. We found a rich set of conformations which depend on two dimensionless groups: the material properties of the sheet (K) and experimental conditions (χ). We characterized these sheets as flat, tumbling, 1D folded, or 2D folded based on the eigenvalues of the gyration tensor. We found roughly that sheets folded when K ≲![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1) and χ−1 ≲
(1) and χ−1 ≲ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (102), tumbled when K ≲
(102), tumbled when K ≲ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1) and χ−1 >
(1) and χ−1 > ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (102), and were flat otherwise, although the exact behavior depended highly on initial condition near the boundaries.
(102), and were flat otherwise, although the exact behavior depended highly on initial condition near the boundaries.
We used the average signed local mean curvature of the sheets to show the nature of each type of sheet. Specifically, we identified parallel folds in 1D folded sheets and non-parallel folds in 2D folded sheets. We used a simple energetic argument to estimate the number of folds in a 1D folded sheet and showed that our equation matched well with the number of folds for these sheets in the low K limit. We also showed the relevance of the bending rigidity to shear (S) in inducing folding when K ∼ 3. From this, we proposed a mechanism of an initial buckling followed by shear-induced annealing towards the most energetically favorable number of folds. The strength of shear determines the degree of annealing which is possible. We also discussed the expected effect of changing L on the rheological properties of the sheet based on the predicted number of folds in a 1D folded sheet.
Finally, we calculated an approximate upper-bound on the stresslet, which is expected to grow linearly with the viscosity of a dilute suspensions of these sheets. We found shear-thinning followed by shear-thickening behavior with increasing shear rate, with different behavior depending on whether K is greater than or less than 1. This shear-thinning is present in the absence of sheet-sheet interactions and thermal fluctuations. Instead, it is a result of the average conformational and rotational behaviors of folded sheets. The changes in the conformation of a sheet with changing initial conditions follow trends, but are chaotic in the sense that small changes in the initial conformation can cause unpredicted changes in the final conformation near the boundaries between different conformations, similar to previous work.53 We have yet to study the effect of changes in θ, the initial orientation of the sheet about the vorticity axis.
We note here that thermal fluctuations cause out-of-plane stiffening for sheets,20,22,58,74 which can change their bending rigidity quite significantly. Translating this work from the athermal limit to real systems, therefore, requires careful consideration of the effective bending rigidity of the system.
This type of shear-thinning into shear-thickening behavior is often attributed to the buildup and breakdown of agglomerates or other multi-sheet structures. However, we show that even in the dilute limit, this behavior can still emerge.
Author contributions
William T. Funkenbusch – methodology, investigation, visualization & writing. Kevin S. Silmore – methodology & writing. Patrick S. Doyle – supervision & writing.Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A: neglecting lubrication forces
As parallel sections of sheet approach each other, a lubrication force is generated. Consider two parallel sections of sheet of area, A, approaching due to shear and initially separated by a distance, 2σ. The strongest lubrication forces will be generated when the characteristic length of these sheet sections is L. The lubrication force goes as the lubrication pressure, plub, times the area of the sheet sections:| Flub ∼ plubA. | (10) |
The scaling for plub can be obtained from the lubrication equation:
 | (11) |
The x direction goes laterally along the sheets and the z direction goes perpendicularly from the sheets. Therefore, dx ∼ L and dz ∼ σ. u is the lateral velocity. The maximum relative velocity of the two sheet sections due to shear is σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . The lateral velocity, to satisfy the continuity equation, thus goes as u ∼ L
. The lateral velocity, to satisfy the continuity equation, thus goes as u ∼ L![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Together,
. Together,
 | (12) |
The energetic benefit of bringing a bead from non-interacting to interacting with a neighboring sheet section goes as ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) σ2. The distance it must travel to go from non-interacting to interacting goes as σ. In bringing two parallel sheet sections together, the number of beads which become interacting with the neighboring sheet section goes as A/a2. Therefore, the force of interaction goes as
σ2. The distance it must travel to go from non-interacting to interacting goes as σ. In bringing two parallel sheet sections together, the number of beads which become interacting with the neighboring sheet section goes as A/a2. Therefore, the force of interaction goes as
 | (13) |
Taking the ratio between the lubrication and interaction forces gives their relative strength:
 | (14) |
Our simulations, which neglect lubrication forces, are valid when this ratio is much less than unity. For example, graphene has inter-atom separation, a ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1 Å), and athermal Lennard Jones interaction strength,
(1 Å), and athermal Lennard Jones interaction strength, ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ∼
∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (0.1 eV Å) with interaction range σ ∼
(0.1 eV Å) with interaction range σ ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1 nm).67 We use the above approximation for the lubrication force even though the continuum approximation breaks down at these length scales. This means that even at high shear rates,
(1 nm).67 We use the above approximation for the lubrication force even though the continuum approximation breaks down at these length scales. This means that even at high shear rates, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼
∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (103 s−1), lubrication forces are small for graphene sheets in water as long as the sheet size, L ≪ 10 μm. This is reasonable for the
(103 s−1), lubrication forces are small for graphene sheets in water as long as the sheet size, L ≪ 10 μm. This is reasonable for the ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (μm) flakes produced by exfoliation techniques75–77 and becomes better for smaller shear rates or larger interaction ranges. Furthermore, the repulsive nature of the Lennard–Jones interaction at small distances restricts sheet segments from getting too close, similarly to lubrication forces. For purely attractive potentials, lubrication forces could fill a similar role in restricting the distance between neighboring sheet segments. Thus, we believe our decision to neglect lubrication forces is valid for real systems.
(μm) flakes produced by exfoliation techniques75–77 and becomes better for smaller shear rates or larger interaction ranges. Furthermore, the repulsive nature of the Lennard–Jones interaction at small distances restricts sheet segments from getting too close, similarly to lubrication forces. For purely attractive potentials, lubrication forces could fill a similar role in restricting the distance between neighboring sheet segments. Thus, we believe our decision to neglect lubrication forces is valid for real systems.
Appendix B: derivation of χ
Consider 2 parallel sheets of characteristic size L interacting via a short-ranged potential of range σ and separated by their equilibrium distance, σ. If the sheets are sheared such that the flow-vorticity plane cuts between them, the shear force trying to separate the sheets can be approximated asFshear = 6πηaσ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Nbeads, Nbeads, | (15) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the relative velocity induced on the sheets due to shear (6πηaσ
is the relative velocity induced on the sheets due to shear (6πηaσ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the Stokes' drag on a sphere) and Nbeads ∼ (L/a)2 is the number of beads in each sheet.
is the Stokes' drag on a sphere) and Nbeads ∼ (L/a)2 is the number of beads in each sheet.
We now consider the force required to slide the sheets and break the short-ranged interactions between them. Assuming the sheet is large (L ≫ a) and the separation is large (σ ≫ a), the energy of the beads in the bulk of the sheet does not change as the sheets slide relative to each other – only beads which are at the leading and trailing edges of the slide matter. The number of beads which separate as a result of a slide of distance σ can be approximated as
 | (16) |
The change in energy for each of these beads is approximately
ΔEbead ∼ ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) σ2 σ2 | (17) |
Thus, the force required to separate the beads is approximately
 | (18) |
Taking the ratio of these two forces gives the dimensionless parameter we desire to an order 1 geometry-, orientation-, and packing-specific constant:
 | (19) |
Appendix C: derivation and confirmation of  scaling
scaling
We wish to obtain an approximation for the optimal number of folds in a 1D folded sheet. We make the following simplifying assumptions. First, the folds are parallel and equally spaced across the length of the sheet, with regions of flat sheet between them. Second, only neighboring parallel sections of sheet will interact with each other (i.e. the interaction is short-ranged). Third, the sheet is rectangular with characteristic length 2L and characteristic width 2W. Fourth, that there is no stretching or compression of the sheet (i.e. FvK ≫ 1). We define nfold to be the number of folds in the sheet, wfold to be the width of a fold, and wflat to be the width of a flat region. With these assumptions, we obtain the following balance for the length of the sheet:| 2L = nfoldwfold + (nfold + 1)wflat. | (20) |
The energy of bending roughly goes as the number of triangles which are within folds times the bending rigidity,
 | (21) |
The energy of interaction goes as
 | (22) |
| E = α′Ebending − Einteraction | (23) |
 . The term α′ is a fold geometry-specific parameter added as a measure of the relative strength of bending rigidity to interaction strength. Doing so, we obtain
. The term α′ is a fold geometry-specific parameter added as a measure of the relative strength of bending rigidity to interaction strength. Doing so, we obtain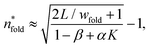 | (24) |
We confirm this scaling by generating rectangular sheets (such that each interior bead of these sheets has 6 neighbors) and finding their optimal number of folds. All neighboring beads in these sheets, even the ones in folds, are a constant distance, 2a, apart, and neighboring parallel regions of sheet are a constant distance, σ, apart. We choose wfold = 6a and  for consistency with our simulations. A folded region consists of 1 row of beads within a flat region, 1 row at the “crease” of the fold, and 1 row within the neighboring flat region. We find the optimal number of folds for a given K and L/wfold with constant W/wfold = 50.0. We then fit these data to eqn (24) using least-squares regression, and find α = 0.0618 ± 0.0010 and β = 0.528 ± 0.003 (± one standard deviation). The fit can be seen in Fig. 8. This equation appears to fit the data quite well, with R2 = 0.989. The data also collapse fairly well onto a master curve, with the largest deviation coming from the smallest sheet, where edge effects are the most relevant. This suggests that
for consistency with our simulations. A folded region consists of 1 row of beads within a flat region, 1 row at the “crease” of the fold, and 1 row within the neighboring flat region. We find the optimal number of folds for a given K and L/wfold with constant W/wfold = 50.0. We then fit these data to eqn (24) using least-squares regression, and find α = 0.0618 ± 0.0010 and β = 0.528 ± 0.003 (± one standard deviation). The fit can be seen in Fig. 8. This equation appears to fit the data quite well, with R2 = 0.989. The data also collapse fairly well onto a master curve, with the largest deviation coming from the smallest sheet, where edge effects are the most relevant. This suggests that  , as predicted.
, as predicted.
 | ||
Fig. 8 (a) Optimal number of folds for varying K and L/wfold. Points are data points and solid lines are eqn (24). Optimal values of α and β were found to be α = 0.0618 ± 0.0010 and β = 0.528 ± 0.003 (± one standard deviation) using least-squares regression with R2 = 0.989. (b) Master curve using eqn (24) to collapse all plots of  . . | ||
Appendix D: discussion of L dependence of rheological properties
Because wfold ∼ a, where a is the equivalent of a molecular or atomistic length scale in a 2D sheet, the number of folds is expected to increase for larger sheets, with , as derived in Appendix C. For a 1D folded sheet, its largest characteristic size scales as L because this dimension is parallel to the folds. Another characteristic size is the width of each folds times the number of folds: σnfold ∼ σ(L/a)1/2. The last characteristic size is the width of each flat region: wflat ∼ L/nfold ∼ a(L/a)1/2. The sheet viscosity will grow roughly as the cross-sectional area of the sheet in the shear-vorticity plane times the length of the sheet along the shear axis. If the sheet is log-rolling, for example, its cross-sectional area in the shear-vorticity plane goes as L3/2 and its length along the shear axis goes as L1/2. The sheet viscosity would therefore go as L2. Orientations of sheets with their largest dimension rotating about the vorticity plane have sheet viscosities which go as L5/2. Rolled-up sheets occupy a roughly circular area perpendicular to their largest axis which goes as Lσ, so its other characteristic sizes go as
, as derived in Appendix C. For a 1D folded sheet, its largest characteristic size scales as L because this dimension is parallel to the folds. Another characteristic size is the width of each folds times the number of folds: σnfold ∼ σ(L/a)1/2. The last characteristic size is the width of each flat region: wflat ∼ L/nfold ∼ a(L/a)1/2. The sheet viscosity will grow roughly as the cross-sectional area of the sheet in the shear-vorticity plane times the length of the sheet along the shear axis. If the sheet is log-rolling, for example, its cross-sectional area in the shear-vorticity plane goes as L3/2 and its length along the shear axis goes as L1/2. The sheet viscosity would therefore go as L2. Orientations of sheets with their largest dimension rotating about the vorticity plane have sheet viscosities which go as L5/2. Rolled-up sheets occupy a roughly circular area perpendicular to their largest axis which goes as Lσ, so its other characteristic sizes go as 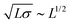 , so its sheet viscosity will have the same scaling as sheets with many folds. Assuming each characteristic size of a tumbling sheet scales with L, the stress scales as L3, which is stronger than in the 1D folded regime.
, so its sheet viscosity will have the same scaling as sheets with many folds. Assuming each characteristic size of a tumbling sheet scales with L, the stress scales as L3, which is stronger than in the 1D folded regime.
If we were to treat a as simply the smallest resolvable length scale in the system, we would expect wfold to grow proportionally to L. In this case,  is not a function of L, and the three characteristic sizes of the sheet grow as, from largest to smallest, L, L, and σ. In the limit of L ≫ σ, the sheet will preferentially align itself with the flow-vorticity plane, and behave effectively as a flat sheet with a small width. The sheet viscosity, assuming the largest axis is aligned with the vorticity axis, would thus grow as Lσ2, which is weaker than when a is the atomistic or molecular length scale in the system. This highlights the importance of treating a as an explicit length scale in these systems.
is not a function of L, and the three characteristic sizes of the sheet grow as, from largest to smallest, L, L, and σ. In the limit of L ≫ σ, the sheet will preferentially align itself with the flow-vorticity plane, and behave effectively as a flat sheet with a small width. The sheet viscosity, assuming the largest axis is aligned with the vorticity axis, would thus grow as Lσ2, which is weaker than when a is the atomistic or molecular length scale in the system. This highlights the importance of treating a as an explicit length scale in these systems.
As L increases, χ−1 increases, and sheets are pushed toward the tumbling regime. Sheet suspensions are often poly-disperse78 and the total contribution to the viscosity in a dilute suspension is the sum of the individual sheet viscosities. So, the total contribution to the viscosity is a weighted sum of the sheet viscosity from each particle size's sheet viscosity, each of which is non-monotonic with shear rate.
Appendix E: movies
Movies of sheet trajectories can be found in the ESI† and include trajectories for flat, tumbling, 1D folded, and 2D folded sheets. They also include trajectories for a sheet with a low average alignment (1D folded), a sheet exhibiting teacup behavior (tumbling), and a rolled-up sheet (1D folded). All trajectories are accompanied by movies of the corresponding signed local mean curvatures of the sheets. Sheet trajectories were rendered in Ovito.65Acknowledgements
Patrick S. Doyle acknowledges partial support from a Robert T. Haslam (1911) chair and NSF Grant CBET-1936696.Notes and references
- Y. Xu, H. Cao, Y. Xue, B. Li and W. Cai, Nanomaterials, 2018, 8, 942 CrossRef PubMed.
- J. Stafford, A. Patapas, N. Uzo, O. K. Matar and C. Petit, AIChE J., 2018, 64, 3246–3276 CrossRef CAS.
- A. Amiri, M. Naraghi, G. Ahmadi, M. Soleymaniha and M. Shanbedi, FlatChem, 2018, 8, 40–71 CrossRef CAS.
- A. Ambrosi and M. Pumera, Chem. Soc. Rev., 2018, 47, 7213–7224 RSC.
- J. N. Coleman, M. Lotya, A. O’Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De and R. J. Smith, et al. , Science, 2011, 331, 568–571 CrossRef CAS PubMed.
- V. Nicolosi, M. Chhowalla, M. G. Kanatzidis, M. S. Strano and J. N. Coleman, Science, 2013, 340, 1226419 CrossRef.
- E. Varrla, C. Backes, K. R. Paton, A. Harvey, Z. Gholamvand, J. McCauley and J. N. Coleman, Chem. Mater., 2015, 27, 1129–1139 CrossRef CAS.
- R. Jha and P. K. Guha, J. Mater. Sci., 2017, 52, 7256–7268 CrossRef CAS.
- T. Gibaud, C. N. Kaplan, P. Sharma, M. J. Zakhary, A. Ward, R. Oldenbourg, R. B. Meyer, R. D. Kamien, T. R. Powers and Z. Dogic, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3376–E3384 CrossRef CAS PubMed.
- F. Ding, J. Liu, S. Zeng, Y. Xia, K. M. Wells, M.-P. Nieh and L. Sun, Sci. Adv., 2017, 3, e1701212 CrossRef PubMed.
- G. Shao, Y. Lu, F. Wu, C. Yang, F. Zeng and Q. Wu, J. Mater. Sci., 2012, 47, 4400–4409 CrossRef CAS.
- F. Tardani, W. Neri, C. Zakri, H. Kellay, A. Colin and P. Poulin, Langmuir, 2018, 34, 2996–3002 CrossRef CAS PubMed.
- P. Davidson, C. Penisson, D. Constantin and J.-C. P. Gabriel, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6662–6667 CrossRef CAS PubMed.
- A. Laskar, O. E. Shklyaev and A. C. Balazs, Sci. Adv., 2018, 4, eaav1745 CrossRef CAS PubMed.
- C. Kamal, S. Gravelle and L. Botto, Nat. Commun., 2020, 11, 2425 CrossRef CAS PubMed.
- A. R. Klotz, B. W. Soh and P. S. Doyle, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 121–127 CrossRef CAS PubMed.
- P. Liu, A. T. Liu, D. Kozawa, J. Dong, J. F. Yang, V. B. Koman, M. Saccone, S. Wang, Y. Son and M. H. Wong, et al. , Nat. Mater., 2018, 17, 1005–1012 CrossRef CAS PubMed.
- B. Tang, Z. Xiong, X. Yun and X. Wang, Nanoscale, 2018, 10, 4113–4122 RSC.
- B. Tang, E. Gao, Z. Xiong, B. Dang, Z. Xu and X. Wang, Chem. Mater., 2018, 30, 5951–5960 CrossRef CAS.
- D. Nelson, T. Piran and S. Weinberg, Statistical mechanics of membranes and surfaces, World Scientific, 2004 Search PubMed.
- Y. Kantor and D. R. Nelson, Phys. Rev. Lett., 1987, 58, 2774 CrossRef CAS PubMed.
- D. Nelson and L. Peliti, J. Phys., 1987, 48, 1085–1092 CrossRef CAS.
- B. Duplantier, Phys. Rev. Lett., 1987, 58, 2733 CrossRef PubMed.
- M. Paczuski, M. Kardar and D. R. Nelson, Phys. Rev. Lett., 1988, 60, 2638 CrossRef PubMed.
- E. Frey and D. R. Nelson, J. Phys. I, 1991, 1, 1715–1757 CrossRef CAS.
- M. J. Bowick and A. Travesset, Phys. Rep., 2001, 344, 255–308 CrossRef CAS.
- A. Košmrlj and D. R. Nelson, Phys. Rev. B, 2016, 93, 125431 CrossRef.
- M. J. Bowick, A. Košmrlj, D. R. Nelson and R. Sknepnek, Phys. Rev. B, 2017, 95, 104109 CrossRef.
- Y. Kantor, M. Kardar and D. R. Nelson, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 35, 3056 CrossRef CAS PubMed.
- M. Kardar and D. R. Nelson, Phys. Rev. Lett., 1987, 58, 1289 CrossRef PubMed.
- M. Plischke and D. Boal, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 4943 CrossRef PubMed.
- F. F. Abraham, W. Rudge and M. Plischke, Phys. Rev. Lett., 1989, 62, 1757 CrossRef CAS PubMed.
- J.-S. Ho and A. Baumgärtner, Phys. Rev. Lett., 1989, 63, 1324 CrossRef PubMed.
- F. F. Abraham and D. R. Nelson, Science, 1990, 249, 393–397 CrossRef CAS PubMed.
- F. F. Abraham and D. R. Nelson, J. Phys., 1990, 51, 2653–2672 CrossRef CAS.
- G. S. Grest and I. B. Petsche, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, R1737 CrossRef CAS PubMed.
- M. J. Bowick, A. Cacciuto, G. Thorleifsson and A. Travesset, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5, 149–160 CrossRef CAS.
- R. Chianelli, E. Prestridge, T. Pecoraro and J. DeNeufville, Science, 1979, 203, 1105–1107 CrossRef CAS PubMed.
- T. Hwa, E. Kokufuta and T. Tanaka, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, R2235 CrossRef CAS PubMed.
- X. Wen, C. W. Garland, T. Hwa, M. Kardar, E. Kokufuta, Y. Li, M. Orkisz and T. Tanaka, Nature, 1992, 355, 426–428 CrossRef CAS.
- M. Spector, E. Naranjo, S. Chiruvolu and J. Zasadzinski, Phys. Rev. Lett., 1994, 73, 2867 CrossRef CAS PubMed.
- S. B. Babu and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 1–7 CrossRef CAS PubMed.
- D. Liu and M. Plischke, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 7139 CrossRef CAS PubMed.
- P. Li, S. Wang, F. Meng, Y. Wang, F. Guo, S. Rajendran, C. Gao, Z. Xu and Z. Xu, Macromolecules, 2020, 53, 10421–10430 CrossRef CAS.
- F. F. Abraham and M. Kardar, Science, 1991, 252, 419–422 CrossRef CAS PubMed.
- Y. Xu and M. J. Green, J. Chem. Phys., 2014, 141, 024905 CrossRef PubMed.
- Y. Xu and M. J. Green, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 1247–1253 CrossRef CAS.
- Y. Yu and M. D. Graham, Soft Matter, 2021, 17, 543–553 RSC.
- Y. Yu and M. D. Graham, Phys. Rev. Fluids, 2022, 7, 023601 CrossRef.
- G. Salussolia, C. Kamal, J. Stafford, N. Pugno and L. Botto, Phys. Fluids, 2022, 34, 053311 CrossRef CAS.
- N. Lindahl, D. Midtvedt, J. Svensson, O. A. Nerushev, N. Lindvall, A. Isacsson and E. E. Campbell, Nano Lett., 2012, 12, 3526–3531 CrossRef CAS PubMed.
- H. Perrin, H. Li and L. Botto, Phys. Rev. Fluids, 2023, 8, 124103 CrossRef.
- K. S. Silmore, M. S. Strano and J. W. Swan, Soft Matter, 2021, 17, 4707–4718 RSC.
- K. S. Silmore, M. S. Strano and J. W. Swan, Soft Matter, 2022, 18, 768–782 RSC.
- G. B. Jeffery, Proc. R. Soc. London, Ser. A, 1922, 102, 161–179 Search PubMed.
- X. Zhang, Y. Tang, X. Wang, J. Zhang, D. Guo and X. Zhang, J. Polym. Environ., 2018, 26, 3502–3510 CrossRef CAS.
- Y. H. Shim, H. Ahn, S. Lee, S. O. Kim and S. Y. Kim, ACS Nano, 2021, 15, 13453–13462 CrossRef CAS PubMed.
- P. Liu and Y. Zhang, Appl. Phys. Lett., 2009, 94, 231912 CrossRef.
- J.-W. Jiang, Z. Qi, H. S. Park and T. Rabczuk, Nanotechnology, 2013, 24, 435705 CrossRef PubMed.
- P. Poulin, R. Jalili, W. Neri, F. Nallet, T. Divoux, A. Colin, S. H. Aboutalebi, G. Wallace and C. Zakri, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11088–11093 CrossRef CAS PubMed.
- G. Gompper and D. Kroll, J. Phys. I, 1996, 6, 1305–1320 CrossRef.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4837 CrossRef CAS.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363 CrossRef CAS.
- A. M. Fiore, F. Balboa Usabiaga, A. Donev and J. W. Swan, J. Chem. Phys., 2017, 146, 124116 CrossRef PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- L. Liu, Z. Shen, M. Yi, X. Zhang and S. Ma, RSC Adv., 2014, 4, 36464–36470 RSC.
- G. Klimchitskaya and V. Mostepanenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075439 CrossRef.
- G. Batchelor, J. Fluid Mech., 1970, 41, 545–570 CrossRef.
- S. Kim and S. J. Karrila, Microhydrodynamics: principles and selected applications, Courier Corporation, 2013 Search PubMed.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1923, 103, 58–61 Search PubMed.
- T. Omori, Y. Imai, T. Yamaguchi and T. Ishikawa, Phys. Rev. Lett., 2012, 108, 138102 CrossRef PubMed.
- H. Zhao and E. S. Shaqfeh, J. Fluid Mech., 2013, 725, 709–731 CrossRef.
- X. Zhang, W. A. Lam and M. D. Graham, Phys. Rev. Fluids, 2019, 4, 043103 CrossRef PubMed.
- A. Fasolino, J. Los and M. I. Katsnelson, Nat. Mater., 2007, 6, 858–861 CrossRef CAS PubMed.
- K. R. Paton, E. Varrla, C. Backes, R. J. Smith, U. Khan, A. O’Neill, C. Boland, M. Lotya, O. M. Istrate and P. King, et al. , Nat. Mater., 2014, 13, 624–630 CrossRef CAS PubMed.
- U. Khan, A. O’Neill, H. Porwal, P. May, K. Nawaz and J. N. Coleman, Carbon, 2012, 50, 470–475 CrossRef CAS.
- J.-Y. Moon, M. Kim, S.-I. Kim, S. Xu, J.-H. Choi, D. Whang, K. Watanabe, T. Taniguchi, D. S. Park and J. Seo, et al. , Sci. Adv., 2020, 6, eabc6601 CrossRef CAS PubMed.
- J. Amaro-Gahete, A. Bentez, R. Otero, D. Esquivel, C. Jiménez-Sanchidrián, J. Morales, Á. Caballero and F. J. Romero-Salguero, Nanomaterials, 2019, 9, 152 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Includes videos of notable sheet behaviors and histograms of gyration tensor eigenvalues. See DOI: https://doi.org/10.1039/d4sm00197d |
| This journal is © The Royal Society of Chemistry 2024 |