 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of the nucleus for cell mechanics: an elastic phase field approach†
Robert
Chojowski
 ab,
Ulrich S.
Schwarz
ab,
Ulrich S.
Schwarz
 ab and
Falko
Ziebert
ab and
Falko
Ziebert
 *ab
*ab
aInstitute for Theoretical Physics, Heidelberg University, Philosophenweg 19, 69120 Heidelberg, Germany. E-mail: f.ziebert@thphys.uni-heidelberg.de
bBioQuant, Heidelberg University, Im Neuenheimer Feld 267, 69120 Heidelberg, Germany
First published on 17th May 2024
Abstract
The nucleus of eukaryotic cells typically makes up around 30% of the cell volume and has significantly different mechanics, which can make it effectively up to ten times stiffer than the surrounding cytoplasm. Therefore it is an important element for cell mechanics, but a quantitative understanding of its mechanical role during whole cell dynamics is largely missing. Here we demonstrate that elastic phase fields can be used to describe dynamical cell processes in adhesive or confining environments in which the nucleus acts as a stiff inclusion in an elastic cytoplasm. We first introduce and verify our computational method and then study several prevalent cell-mechanical measurement methods. For cells on adhesive patterns, we find that nuclear stress is shielded by the adhesive pattern. For cell compression between two parallel plates, we obtain force-compression curves that allow us to extract an effective modulus for the cell–nucleus composite. For micropipette aspiration, the effect of the nucleus on the effective modulus is found to be much weaker, highlighting the complicated interplay between extracellular geometry and cell mechanics that is captured by our approach. We also show that our phase field approach can be used to investigate the effects of Kelvin–Voigt-type viscoelasticity and cortical tension.
1 Introduction
Many essential biological processes depend on the mechanical properties of animal cells and their ability to dynamically react to mechanical cues from their environment. Classical examples include the spreading behaviour of cells on substrates of variable stiffness,1,2 cell migration in the direction of larger stiffness3,4 and cell differentiation in response to environmental stiffness.5,6 A typical cell response to variable environmental stiffness is to adapt the own stiffness to match the one of the environment.7,8 However, there are also situations in which it is favorable for cells to work with a different stiffness then the surrounding. One prominent example are migratory immune and cancer cells in confined spaces, which tend to increase their softness in order to more easily squeeze through the pores in their environment.9–11The main determinant of cell mechanics is the cytoskeleton, a crosslinked and highly dynamical polymer network, giving the cell stability and the ability to quickly change its mechanics.12–14 In particular, the cytoskeleton allows cells to generate forces, mainly pushing forces through polymerization and pulling forces through motor activity, both of which convert chemical energy into mechanical work and thus make the cell an active system.13,15 Although the plasma membrane typically does not contribute much to cell mechanics directly, it is important in the sense that it determines cell volume and surface area; in addition, it provides guidance for the organization of the cell cortex generated by the cytoskeleton as a thin polymeric network wrapping the whole cell.16,17
In recent years, it has become clear that a third important mechanical component of animal cells is the nucleus.18 The nucleus harbours the genetic information of the cell and is separated from the cytoplasm by its nuclear envelope. Due to its overarching role for gene expression, it has long been overlooked that the nucleus also plays an important role in mechanics. Having a cell-type dependent diameter of several micrometers and occupying a large fraction of the overall cell volume (typically up to 30%), the nucleus is the largest and most prominent of all cellular organelles.19 The mechanics of the nucleus is determined by the interplay between the two nuclear membranes, the embedded nuclear pore complexes, the nuclear lamina, the nuclear cytoskeleton (which includes actin filaments and myosin motors) and the different chromatin domains. The combined effect of these factors leads to an effective nuclear stiffness that can be up to 10-fold stiffer than the rest of the cell,20 which together with its size already suggests its importance in whole-cell mechanics. A very recent computational study showed that even a spatially varying nuclear stiffness can be described on the whole cell level by one effective modulus for the nucleus.21
During recent years, it has been shown in many experimental studies that the nucleus indeed has very specific mechanical roles in animal cells. In matrix-driven cell differentiation, the nuclear stiffness correlates with tissue and matrix compliance, leading to stiffer cell nuclei on stiffer substrates and pointing at its ability of perceiving mechanical cues and adapting to them.22 Recently, it has been demonstrated that nuclear deformations instruct migratory behaviour of cells in confined spaces, indicating that the nucleus serves as a ruler and mechanosensor.23,24 Moreover, nuclear size and stiffness limit the minimal size of constrictions through which a migratory cell can squeeze through.10 In turn, it has been observed that nuclear softening during passage of narrow constrictions is often associated with nuclear envelope rupture and DNA damage, which in our context are not only failure processes, but also signaling events.10,25,26 Stresses and strains on the nucleus can also lead to structural changes in chromatin packing and a subsequent softening of the nucleus.27 It also has been shown that metastatic cancer cells use the nucleus as a “battering ram” to invade soft tissue.28 In cell migration, the nucleus is positioned by the microtubule-organizing center either at the front or the back, depending also on the properties of the environment; when positioned at the front, it can be used as a ram during cell migration. Last but not least, it is known that forces originating from the interplay between cytoskeleton and the cellular surrounding can be directly transmitted to the nuclear envelope leading to nuclear deformations, triggering transcriptional activities and cellular reactions to these stimuli. This direct mechanotransduction pathway includes the LINC protein complexes establishing a direct physical connection between nucleus and cytoskeleton.29,30
Despite this growing body of evidence of its importance for cell mechanics and mechanotransduction, the nucleus is often neglected when modelling whole-cell mechanics, often due to lack of an appropriate theoretical framework. We here propose an extension of our previously developed elastic phase field approach for cell mechanics31 that also includes the nucleus. In the spirit of multi-phase field approaches,32–34 the nucleus is introduced as an additional field, as was done in previous phase field studies of cells,35,36 but this time, we associate to the nucleus elastic material characteristics and make them different from the ones of the rest of the cell. This enables us to study the effect of the nucleus on the cell's mechanical behaviour in a variety of different and biologically highly relevant situations, including various boundary conditions between an adherent cell and the substrate as well as compression and micropipette suction experiments of spherical cells. We also show that our approach is sufficiently general to allow for the investigation of viscoelasticity and cortical tension, which paves the way towards more detailed models of nuclear mechanics in the future.
This work is structured as follows. First, we present the modelling approach for an elastic cell with a nucleus in Section 2. We then demonstrate its applicability for homogeneously and locally adhered cells in Section 3, already pointing out an important role of the nucleus. For the simple geometry of an isotropically contracting, homogeneously adhering, disk-like cell with a nucleus, we can use analytical solutions to validate the numerical solution. We then proceed with discussing numerical studies of more complex experimental setups, namely patterned adhesion and dynamic failure of an adhesion point including viscoelastic relaxation of Kelvin–Voigt type. In Section 4 we finally turn to cells in confinement and discuss as examples the compression of cells between two parallel plates as well as micropipette aspiration. In this section we also study viscoelastic effects of Kelvin–Voigt type. We conclude with a discussion and outlook on possible applications and further extensions of the proposed method.
2 Elastic phase field model for a cell with nucleus
To explicitly account for the cell's nucleus in a model of an elastic cell in both stationary and dynamic situations, we extend the previously introduced elastic phase field approach.31 The phase field method, originally developed in the context of solidification processes37 is nowadays widely used, especially in the communities of fracture mechanics38,39 and poly-crystalline structures.40 Due to its ease in describing deformable or moving boundary problems, applications spread out to soft matter physics, e.g. vesicles in flow41 or growing actin gels.42 In the context of cellular biophysics, it proved efficient to model single cell migration43–47 and cell collectives,32–34,48 as well as more recently cell31 and tissue49 mechanics. Phase field models for a cell containing an explicit nucleus have been already proposed. However, ref. 35 neglected mechanics by solely considering the dynamics of two internal chemicals, while ref. 36 assumed Stokesian hydrodynamics. To our knowledge, no phase field model has been proposed yet that would account for elastic continuum mechanics and allow to model several cellular compartments – here the cytoplasm and the nucleus – having different material properties.The study of moving boundary problems is a computationally expensive task because at each point in time the location of the boundary has to be determined anew in order to impose the respective boundary conditions. The phase field approach circumvents this problem by introducing an evolution equation for an auxiliary order parameter field ϕ(x, t) (the phase field) describing the object of interest. It differentiates between two bulk “phases”, in our context the inside of the object (ϕ = 1) and its outside (ϕ = 0), defined by the minima of a double-well potential. Interfaces between these phases are then given by smooth tanh-like transitions from one bulk value to the other. The location of the interface can be identified with the location of the maximum of the phase field gradient |∇ϕ|, or simpler, with the position of the isosurface with ϕ = 1/2. If the evolution equation for the phase field is coupled adequately to the other model equations that describe the physical quantities of interest in the two phases (e.g. deformation, flow or diffusing chemicals), the domain deforms and/or moves in response to the processes described by these model equations.
In our approach, the cell and its nucleus are represented by two phase fields, ρ(x, t) and ψ(x, t), respectively, cf.Fig. 1A. Each field has its own evolution equation which follows an overdamped relaxational dynamics
 | (1) |
 . In general, the two interface widths could be chosen to be different. The second term is the derivative of a double-well potential of the form g(ϕ) = ϕ2(1 − ϕ)2. Its minima are associated with the interior of the cell/the nucleus (ϕ = 1) and the space outside the cell/the nucleus (ϕ = 0), respectively, cf. again Fig. 1A. It should be noted that the exact form of the double-well potential is arbitrary; we opted for the simplest one. Inherent to the phase field approach is a wall energy (surface tension) that tends to pull together curved interfaces.50–52 Employing the third term in eqn (1), proportional to the interface curvature κϕ = −∇·(∇ϕ/|∇ϕ|), allows to remedy this effect.51 Finally, we couple the phase field dynamics to the continuum mechanics via the last term in eqn (1). It describes a movement of the phase field in case the mechanical force balance, ∇·Σ + Ftot = 0 with Σ being the stress tensor and Ftot all the forces acting on the domain, is not fulfilled.
. In general, the two interface widths could be chosen to be different. The second term is the derivative of a double-well potential of the form g(ϕ) = ϕ2(1 − ϕ)2. Its minima are associated with the interior of the cell/the nucleus (ϕ = 1) and the space outside the cell/the nucleus (ϕ = 0), respectively, cf. again Fig. 1A. It should be noted that the exact form of the double-well potential is arbitrary; we opted for the simplest one. Inherent to the phase field approach is a wall energy (surface tension) that tends to pull together curved interfaces.50–52 Employing the third term in eqn (1), proportional to the interface curvature κϕ = −∇·(∇ϕ/|∇ϕ|), allows to remedy this effect.51 Finally, we couple the phase field dynamics to the continuum mechanics via the last term in eqn (1). It describes a movement of the phase field in case the mechanical force balance, ∇·Σ + Ftot = 0 with Σ being the stress tensor and Ftot all the forces acting on the domain, is not fulfilled.
The evolution of the displacement field u can be written, using the common assumption of overdamped dynamics for cells and tissues, as
| ξ∂tu = ∇·Σ + Ftot. | (2) |
The stress tensor Σ has to be defined on the entire computational domain. In case of several compartments with different material properties, the phase field stress tensor has to interpolate the stress tensors σ (and lastly material parameters) of the individual considered phases, with smooth transitions at the respective interfaces. For this purpose, we use weighting functions of the form h(ϕ) = ϕ2(3 − 2ϕ) for the cell and the nucleus, respectively.42,53 The total phase field stress tensor Σ is then defined as
| Σ(ρ, ψ) = [h(ρ) − h(ψ)]σC + h(ψ)σN | (3) |
Finally, we have to specify the constitutive relation for the cytoplasm and the nucleus, respectively. We assume linear elasticity54 with the stress tensors defined as σα = 2μαε + λα![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tr(ε)1, where α = {C, N} for cytoplasm (C) and nucleus (N). Here, μα and λα are the Lamé coefficients of each compartment. The strain tensor ε is defined in index notation as εij = (1/2)(∂ui/∂xj + ∂uj/∂xi) and 1 is the identity matrix.
tr(ε)1, where α = {C, N} for cytoplasm (C) and nucleus (N). Here, μα and λα are the Lamé coefficients of each compartment. The strain tensor ε is defined in index notation as εij = (1/2)(∂ui/∂xj + ∂uj/∂xi) and 1 is the identity matrix.
In three-dimensions, the Lamé coefficients are given by λ3D = νE/[(1 + ν)(1 − 2ν)] and μ3D = E/[2(1 + ν)] with Young's modulus E and Poisson's ratio ν. Depending on the geometry of the considered problem, different two-dimensional approximations can be used: strongly spread cells, having a height d (assumed to be along the z-axis) considerably smaller than the lateral extensions, can be approximated as thin elastic sheets in plane stress formulation. In this case the stress components σzz = σxz = σyz = 0 vanish and the problem becomes effectively two-dimensional with thickness-averaged λ2D = νEd/(1 − ν2) and μ2D = Ed/[2(1 + ν)].55 For a cell having the shape of a long cylinder (again in z-direction), the plane strain formulation can be applied, where εzz = εxz = εyz = 0.55 Here, the Lamé coefficients are identical to the three-dimensional ones. We will specifically mention the used approximation for each experiment discussed in the following.
3 Modeling spread cells
We now demonstrate the applicability of the proposed method by investigating a cell of height d spread onto a compliant substrate in 2D plane stress formulation. This situation is biologically highly important, since cells are able to sense the mechanical properties of their environment via internal force generation and transmission of these forces to the outside.8 The received information can then be used by the cell to adapt its mechanical properties and morphology, and possibly even to induce division, differentiation or motility (processes which are beyond the scope of this work). To model a spread cell, we have to include active cell contractility and cell–substrate adhesion as central features into the proposed method.Active stresses Σact can be straightforwardly introduced into the phase field stress tensor, eqn (3), as an additive contribution. In principle, the active stress can be time- and space-dependent. Contractile stresses within a cell arise due to the activity of myosin II motor proteins, which slide cytoskeletal actin filaments relatively to each other.56 While some part of the contracting cytoskeleton spans over the nucleus, other parts can also bind directly to it via LINC complexes, exerting contractile stress on the nuclear boundary.29,30 Using the common approximation of an isotropic contractile stress σact = σ0d1, with σ0 > 0 and 1 the identity matrix, we write the active stress tensor as
| Σact = [h(ρ) − fh(ψ)]σ0d1. | (4) |
The second feature needed to model spread cells is cell–substrate adhesion, anchoring the cell and allowing for force transmission from the cytoskeleton to the substrate via integrin-mediated adhesion sites. A simple approximation for a fully elastic substrate is an elastic foundation, where adhesion sites are modeled as a spring stiffness density Y(x) resisting cell deformations.58–60 The associated restoring force entering the elastic eqn (2) is then given by
| F(x) = −Y(x)h(ρ)u | (5) |
3.1 Adhering cell with radial symmetry
We first study a circular cell which is spread and actively contracting on an elastic foundation, as shown in Fig. 2A. This geometry was originally used to explain the experimentally observed concentration of traction forces at the cell periphery from a mechanical perspective and is analytically solvable for homogeneously adhered cells.15,59,60 Recently, an analytical solution for the case where adhesion is restricted to a ring at the cell's periphery has been also given.61 To benchmark our numerical framework, we generalized the homogeneous adhesion model by additionally considering a disk-like nucleus in the cell's center; the analytical solution is given in Appendix B. To specify the different possible geometries, we introduce the cell's radius RC, the nucleus' radius RN and the radius of the adhesive ring RY, meaning that the cell adheres for RY ≤ r ≤ RC.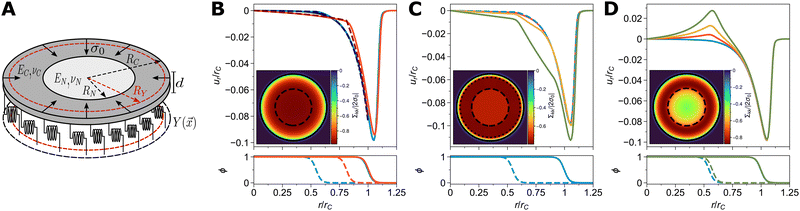 | ||
| Fig. 2 (A) Sketch of the model for a cell (thickness d, radius RC) with a concentric nucleus (radius RN). The cell is contracting isotropically with active stress σ0 while being adhered to a substrate via a spring stiffness density Y(x) on a ring RY ≤ r ≤ RC. The cytoplasm (EC, νC) and the nucleus (EN, νN) can have different material properties. (B) The homogeneous adhesion case with RY = 0. Shown in the upper panel are the phase field (solid) and analytical (dashed) solutions for the radial displacement field ur, normalized by the cell radius in mechanical equilibrium, rC. Shown are the cases: EN/EC = 10, RN/RC = 0.5 (blue); EN/EC = 10, RN/RC = 0.75 (red); and the phase field solution for EN/EC = 1 and RN/RC = 0.5 (black, mostly covered by the blue curve). The inset shows the trace of the stress tensor, normalized by the active stress σ0, for EN/EC = 10, RN/RC = 0.5; the contour lines correspond to ρ = 0.5 (cell, solid) and ψ = 0.5 (nucleus, dashed). The lower panel shows the radial profile of ρ (cell, solid) and ψ (nucleus, dashed) in mechanical equilibrium with colors corresponding to the upper panel. (C) Adhesion on an outer ring only. In the upper panel phase field solutions for ur/rC are shown for EN/EC = 10, RN/RC = 0.5 and varying RY/RC = 0.5, 0.6, 0.7, 0.8 (blue to green). The inset shows the normalized stress for the case RY/RC = 0.8 (dotted line marks inner ring boundary) and the lower panel the phase field profiles for the case RY/RC = 0.5 (blue). (D) Until now, the case f = 0 was considered (cf.eqn (4)) i.e. the whole cell was contracting. When gradually restricting contraction to the cytoplasm by varying f = 0, 0.2, 0.5, 1 (blue to green), cf. the discussion in the main text, extensile forces are exerted on the nucleus of radius RN/RC = 0.5. The lower panel shows the phase field profiles for f = 0 (blue) and f = 1 (green). The inset shows the normalized stress for the case EN/EC = 10 and f = 1, for better comparison with the insets of B and C. All simulations were performed on N = 512 × 512 grid points on a domain of 50 μm × 50 μm. If not specified above, the other mechanical parameters are RC = 12.5 μm, d = 1 μm, EC = σ0 = 1 kPa, νC = νN = 0.5 and Y0 = 0.8 nN μm−3. Further parameters are as in Table 1. | ||
We begin with the simplest case of a cell fully and homogeneously adhered to the substrate, i.e. Y(x) = Y0 and RY → 0, and assume the contracting cytoskeleton spans over the nucleus, f = 0. Fig. 2B upper panel shows the phase field (solid curves) and analytical solutions (dashed) for the radial displacement field ur for different nuclear stiffnesses and radii. Both are in very good agreement, confirming our approach. Deviations result from the diffuse description of the nucleus–cytoplasm boundary in the phase field framework and can be reduced by decreasing its interface width. The kink at the nucleus–cytoplasm interface, occurring in both the analytical and numerical solution, is due to the different rigidities of the two considered cell compartments. Consistent with previous results, the highest deformations are at the cell periphery.59 This is associated with high traction stresses at the periphery and lowered total internal stresses, as visualized in the inset of Fig. 2B by plotting the trace of the stress tensor, normalized by the active stress level σ0.
How important is the nucleus for the mechanics? For a nucleus of half the cell's radius, RN/RC = 0.5, the nucleus stiffness EN has only a negligible effect on the cell's deformation. Increasing the nuclear radius, a realistically stiff (EN/EC = 10) nucleus (red curves) leads to considerably different slopes in the displacement field. However, the overall position of the cell periphery remains approximately the same, cf. the solid curves in the lower panel of Fig. 2B, displaying the radial phase field profiles.
It is important to note that the displacement field in the nucleus always remains small. This demonstrates that strong cell adhesion protects the nucleus against large deformations and stresses. The determining factors are the distance between the nucleus and the cell boundary, RC – RN, and the characteristic distance over which stress can propagate through the cytoplasm, which for an adhering cell is given by the localization length  .59 Peripheral cell adhesion is sufficient for protecting the nucleus, corresponding to the experimental observation of strong adhesions forming mostly at the cell periphery, while the basal side under the nucleus is mostly adhesion free.62
.59 Peripheral cell adhesion is sufficient for protecting the nucleus, corresponding to the experimental observation of strong adhesions forming mostly at the cell periphery, while the basal side under the nucleus is mostly adhesion free.62
This shielding can have a major impact on the nuclear mechanosensing ability of stimuli originating at the cell edge. In a second study we therefore restrict the adhesion to a ring at the cell periphery of inner radius RY, to see whether the nuclear deformation increases, indicating a higher perception of mechanical stimuli. In most cell types, the nucleus occupies not more than a third of the cellular volume. Therefore, we fix the nucleus radius to RN/RC = 0.5, for which we found above that the nuclear stiffness has only a negligible effect on cell mechanics, and the stiffness to EN/EC = 10. We then examine the radial deformation upon varying the inner radius RY of the adhesion ring as shown in the upper panel of Fig. 2C. Note that the deformation field is linear in the non-adhered cell parts, i.e. both in the nucleus and the inner part of the cytoplasm. As visible from the displacement field, a larger RY, and therefore a decreased adhesion area, increases the deformation the nucleus experiences. This demonstrates that adhesion restricted to the cell periphery leads to an increased stress propagation to the nucleus, as also visible in the inset of Fig. 2C. Nevertheless large deformations are prevented as shown by the only slightly increased deformation peak compared to the fully adhered case in Fig. 2B upper panel. This agrees with recent experiments on optogenetic activation of whole cells that showed that disc and ring geometries give little differences in regard to whole-cell contractility.63
Lastly, we study the situation of a fully adhered disk, but now with a varying parameter f as described above. Increasing f from 0 to 1, leads to an extensile stress on the nuclear boundary. Fig. 2D upper panel demonstrates the radial displacement field for RN/RC = 0.5 and EN/EC = 2 for different f = 0, 0.2, 0.5, 1, the peaks close to the nucleus–cytoplasm interface clearly showing a radial stretching of the nucleus, which is also visible in the lower panel of Fig. 2D showing the phase field profiles for the cases f = 0 (blue) and f = 1 (green). Similar observations can be made for other nuclear rigidities. For increasing parameter f, the nucleus experiences higher extensile stresses, also visualized in the inset of Fig. 2D in contrast to the previous discussed cases.
In summary, the above results verify our elastic phase field approach and indicate that the transmission of mechanical cues to the nucleus strongly depends on the actual adhesion geometry and the force transmission from the cytoskeleton to the nucleus.
3.2 Contractile cells on adhesion patterns
Micro-patterned adhesive substrates are a standard setup for studying cellular behaviour in structured environments.64–67 Adherent cells are always under contraction, as nicely demonstrated by the ubiquitous invaginated arcs that form when cells adhere with point-like adhesions.15,68 Here, we investigate the impact of the nucleus on the overall cell morphology in such geometries. As a first example, we study a rectangular pattern with four circular adhesive patches of radius radh located at its corners. We start with a 2D rectangular cell, described in plane stress, and allow it to form focal adhesions at the corners and contracting isotropically under a contractile stress σ0. The nucleus initially has a circular shape of radius RN with physiological nucleus-to-cell volume ratio VN/VC ≈ 0.17. We consider the case that the cytoskeleton contracts the whole cell, i.e. f = 0. For the adhesion strength Y(x) we use a smoothly varying field, transitioning in a tanh-like manner from the maximal value Y0 in the focal adhesion towards zero outside of it. Primarily, this ensures numerical stability compared to pinning the cell completely to the focal adhesion (via the boundary condition u = 0, cf. also ref. 31). It also would allow to study different adhesive strengths in different focal adhesions.Representative results are shown in Fig. 3. The panels of Fig. 3A study a centered nucleus and demonstrate the effect of an increased nuclear–cytoplasmic stiffness ratio EN/EC. Clearly, the nucleus is deformed by the invaginated arcs for low nuclear stiffness. A higher nuclear stiffness rather changes the shape of the cell, demonstrating again that localized adhesion and an increased nuclear stiffness protect the nucleus against large deformations/stresses. Yet one also sees how stress bridges start to emerge between nucleus and adhesions, which look like precursors of stress fibers. Similar perturbations are observable for example for cells spreading on nanonets.69
 | ||
| Fig. 3 A cell adhering in a rectangular shape due to adhesive spots in the corners. Adhesive spots (dotted) have a radius radh = 1.15 μm with high Y0 = 16 nN μm−3, to prevent slipping from the adhesion sites. The cell contracts under an isotropic contractile stress σ0/EC = 0.4. Shown is the normalized trace of the stress tensor for the cases EN/EC = 1, 2, 10 (top to bottom) with an initially circular nucleus (A) centered in the cell and (B) shifted in x-direction by 1.5RN. The contour lines correspond to ρ = 0.5 (solid, cell) and ψ = 0.5 (dashed, nucleus). (C) and (D) show the trace of the stress tensor along the symmetry line y = 0 for the corresponding simulations shown in (A) and (D). All simulations were performed on N = 1024 × 512 grid points on a domain of 50 μm × 25 μm. Initial cell dimensions are 30 μm × 15 μm with RN = 5 μm, d = 1 μm, EC = 1 kPa and νC = νN = 0.5. Rest as in Table 1. | ||
Similar to the previous study in circular geometry, the distance between the nucleus and the cell edge is a determining factor for the magnitude of the morphology perturbation. If the nucleus position is shifted away from the cell's center, cf.Fig. 3B, a stress accumulation at the cytoplasm–nucleus boundary can be observed, while the stress is lowered on the opposite side of the nucleus. In Fig. 3C and D the trace of the stress along the symmetry line y = 0 is depicted, clearly showing the stress decrease for higher EN/EC and its asymmetry when shifting the nucleus. Interestingly, as visible in Fig. 3B, the stress “builds a bridge” between the closeby focal adhesions and the nucleus,70 quite possibly impacting the mechanosensing of the nucleus. Furthermore, one can hypothesize that the asymmetric stress distribution for shifted nuclei allows the cell to differentiate between left and right, which may be important to polarize for cell migration.
3.3 Failure of a focal adhesion
Having demonstrated that the proposed modeling framework is able to describe static spread elastic cells with nucleus in complex geometries, we now give an example of a simple dynamic response. Similar to the last example, we consider a cell on a micro-patterned adhesive environment favoring a hexagonal cell shape. The cell first contracts isotropically under a stress σ0 until it reaches mechanical equilibrium. The resulting shape, including stress focusing at the adhesion spots and invaginated arcs in between, is shown in the left panel of Fig. 4A. Afterwards, one of the adhesion spots (here, the most right one) is suddenly removed, mimicking the rupture/dissolution of a focal adhesion, and the cell deforms into a new mechanical equilibrium given by this geometry, see the right panel of Fig. 4A. One can clearly see that the cell relaxes an substantial amount of stress in the area of the missing adhesion point. The stress inside the nucleus is also reduced, in the shown example by 14.5%, and again shows an asymmetry. Note that the cell does not fully round up in the region close to the detached adhesion point, which is a consequence of the reference state of the elastic model. | ||
| Fig. 4 (A) A cell with nucleus was allowed to spread in a hexagonal adhesion pattern and to contract isotropically with σ0/EC = 0.4 until it reached mechanical equilibrium (left panel). Subsequently the most right adhesion spot was removed and the cell evolved towards a new mechanical equilibrium (right panel). The colormap shows the normalized trace of the stress tensor. The cell shape (isocline ρ = 0.5, solid black) and nucleus shape (ψ = 0.5, dashed black) are also shown. (B) Shown is the average displacement 〈δ|u|〉, with respect to the initial reference displacement in (A), as a function of time t for different friction coefficients ξ. For all tested ξ, the behavior is the one of a Kelvin–Voigt model. The simulations were performed on N = 512 × 512 grid points on a domain of 50 μm × 50 μm. Initial cell edge length is 17.5 μm and RN = 6.65 μm with cell height d = 1 μm resulting in VN/VC ≈ 0.17. Further, EN/EC = 10 with EC = 1 kPa, νC = νN = 0.5, radh = 1.25 μm and Y0 = 16 nN μm−3. Rest as in Table 1. | ||
To quantify the dynamics of this relaxation, we investigated the cell-averaged displacement  , where the cell's volume is given by
, where the cell's volume is given by  . Fig. 4B shows 〈δ|u|〉 = 〈|u|〉 − 〈|uref|〉, i.e. the deviation from the reference displacement at the time point of the removal of the focal adhesion, as a function of time and for different friction coefficients ξ (cf.eqn (2)) and EN/EC = 10. As can be seen, the displacement 〈δ|u|〉 always levels at the same plateau value, reflecting that mechanical equilibrium is reached, with ξ determining the relaxation time.
. Fig. 4B shows 〈δ|u|〉 = 〈|u|〉 − 〈|uref|〉, i.e. the deviation from the reference displacement at the time point of the removal of the focal adhesion, as a function of time and for different friction coefficients ξ (cf.eqn (2)) and EN/EC = 10. As can be seen, the displacement 〈δ|u|〉 always levels at the same plateau value, reflecting that mechanical equilibrium is reached, with ξ determining the relaxation time.
It should be noted that in ref. 31 the elasto-dynamic formulation of eqn (2) was introduced out of necessity to couple the phase field dynamics with elasticity in a reversible fashion. Hence, if one wants to describe a system with “pure” elastic behavior, one should not probe the system on time scales τ faster then the one set by ξ. On the flip side, if one does so, the average displacement follows the relaxation behaviour of a viscoelastic material with long-term elastic behavior. This is reflected by the dashed curves in Fig. 4B where we applied a Kelvin–Voigt model, predicting 〈δ|u(t)|〉 = umax[1 − exp(−t/τR)], to interpret the data, which fits perfectly. Here umax is the maximum average displacement and τR the characteristic relaxation timescale. The Kelvin–Voigt model is a widely used and experimentally validated model for cellular mechanics, describing that mechanical relaxation does not occur instantaneously (as in linear elasticity), but is retarded by internal friction, stemming from viscous flow and cytoskeletal reorganization. For a Kelvin–Voigt material the relaxation timescale is given by τR = η/E, where E is the Young's modulus and η the material's viscosity. We verified that the correspondence to a Kelvin–Voigt model holds for all tested nucleus stiffnesses and the above comparison hence allows to associate ξ with an effective viscosity η. Note that, however, since the cell is a composite material of cytoplasm and nucleus, both E and η entering τR are cell-averaged quantities. We will revisit viscoelastic effects in Section 4.2.
4 Cells in confinement and modulus measurements
We now turn to the problem of cells in confinement, again focusing on the effects of the nucleus. On the one hand, in their physiological environment, cells are often subject to (dynamic) straining induced by their surrounding. Examples include cyclic stretching in lung and vascular tissue or the migration of immune cells and metastatic cancer cells through narrow openings in tissues or fibrous networks. On the other hand, several experimental methods have been developed to probe cellular mechanical responses, including compression of cells between two plates23,24,71–75 and cell aspiration by micropipettes.76–81 Here, we show how the latter two can be modeled using our framework to extract effective elastic moduli.In both experimental setups, the interaction of the examined cell with the confining obstacles – the plates of the compression apparatus or the tube walls of the micropipette – is crucial. In the phase field method, such “obstacles” can be described by implementing another, static phase field φ(x), also having tanh-like transitions from φ = 1 within the obstacle to φ = 0 outside, and which is assumed here to be perfectly rigid. The local presence of the obstacle is then manifesting itself by interactions of the cell's phase field with φ. Motivated by a phenomenological excluded volume potential of the form  presented earlier,32,33,46 we add the following excluded volume force to the force Ftot entering eqn (1) and (2):
presented earlier,32,33,46 we add the following excluded volume force to the force Ftot entering eqn (1) and (2):
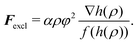 | (6) |
 with a small ε ≪ 1 implements saturation of the force in case the phase field gradient becomes too steep.33
with a small ε ≪ 1 implements saturation of the force in case the phase field gradient becomes too steep.33
4.1 Compressing cells between two parallel plates
Compressing cells between two parallel plates is nowadays a standard experimental technique to mechanically probe global cell mechanics.20,72–75,82,83 For instance, in combination with computational predictions, it has been demonstrated that for mitotic cells the cell cortex dominates cell mechanics.75 Beyond that, also cellular responses to increased confinement have been addressed, evidencing that it can induce the mesenchymal-amoeboid transition84 and trigger cell migration.23,24 In the latter studies it was suggested that the extent of nuclear compression determines the onset of this response. Also a recent computational study has shown that a stiff nucleus increases the effective stiffness of cells as probed in such experiments.21We model compression experiments by implementing the upper and lower plates via the field φ(x). Both plates are initially not in contact with the cell, such that Fexcl = 0. They are moved towards each other successively by the grid spacing Δx each time the cell has relaxed into mechanical equilibrium. Having reached the desired compression level/plate distance, this procedure can be reversed to release the cell from the confinement. Note that we study the quasi-static, purely elastic process first, to be able to compare with analytical solutions. Cell compression that is continuous in time, where the response will then be of Kelvin–Voigt-type, cf. Section 3.3, will be investigated in Section 4.2.
So far, in Section 3 we used an effectively 2D plane stress approach, which was justified for a thin, spread cell. In the compression experiment, the simplest effective 2D problem would be the plane strain approach, corresponding to a long cylinder with circular cross-section. To see how sensitive the compression experiment is to the geometry, we compared this simple case (unrealistic for a cell) to the axially symmetric case of a 3D sphere compressed between the plates. Note that the latter needs solving all equations defined above in cylindrical coordinates.
Fig. 5A shows the distribution of stresses, visualised via tr(Σ), within the cross-section of a cell in plane strain (top, cylinder geometry; note that this implies that the nucleus is also a cylinder) and of a spherical cell in axial symmetry (bottom). The nuclear stiffnesses are EN/EC = 2 (left) and 10 (right), respectively. In the snapshots, the plates have a distance of 90% of the initial cell diameter 2RC. Both cases show an increased stress concentration for increasing nuclear stiffness in the regions between the nucleus and the plates, with a band-like stress accumulation connecting the cell edge in contact with the plates and the nucleus. The plane strain case shows an overall higher stress, since it does not allow a considerable stress relaxation within the nucleus, leading to slightly higher cytoplasmic deformations and therefore a higher eccentricity of the cross-sectional shape as compared to the axially symmetric situation. Nevertheless, overall the behavior is rather similar.
 | ||
| Fig. 5 (A) Compression of a cylindrical cell with plane strain (top) versus compression of a spherical cell with axial symmetry (bottom). Shown are the cases EN/EC = 2 and EN/EC = 10. (B) Numerically obtained force–compression curves. The symbols are numerical solutions with plane strain (triangles) and axial symmetry (circles), respectively, cf. panel A. The solid curves are fits to the respective analytical solutions (available in the absence of the nucleus). (C) For the case of axial symmetry, we extracted an effective elastic modulus from fits as shown in panel B. In the physiological range of nucleus sizes and stiffness, the effective modulus measured in compression is up to three times larger than the one of the pure cytoplasmic stiffness. Colors in B: EN/EC = 2 in axial symmetry (blue), EN/EC = 10 in axial symmetry (yellow); EN/EC = 2 in plane strain (red), EN/EC = 10 in plane strain (green). Colors in C: nucleus size of VN/VC = 0.125 (blue); nucleus size VN/VC = 0.3 (red). (D) Compression experiment similar to (A) but for an axially symmetric, pancake-shaped cell. Simulations for (A)–(C) were performed on N = 512 × 512 grid points and for (D) on N = 512 × 256 grid points. Mechanically relevant parameters for all shown simulations (if not mentioned otherwise) are RN = 6.25 μm in (A) and (D), EC = 1 kPa, νC = νN = 0.48, and α = 6 kPa. Rest as in Table 1. | ||
To further quantify the compression experiments, we obtained the force–compression curves for the results shown in Fig. 5A. This was done by calculating the total force  in mechanical equilibrium for the respective total compression δ of the cell, normalized by the cell diameter 2RC, as shown in Fig. 5B. As can be noticed, a consistently higher force is required to deform a plane strain cylinder (triangles) by the same δ as compared to a sphere in axial symmetry (circles), consistent with Fig. 5A. Note that for the resulting line contact problem in plane strain, the fundamental measure for this case is the in-plane force per length F/L.85 In order to compare the force–compression curves in both geometries, we determined the length of the cylinder L = 4/3RC in plane strain, such that the cylinder volume is equal to the sphere volume in axial symmetry, and multiplied the average force per length by L.
in mechanical equilibrium for the respective total compression δ of the cell, normalized by the cell diameter 2RC, as shown in Fig. 5B. As can be noticed, a consistently higher force is required to deform a plane strain cylinder (triangles) by the same δ as compared to a sphere in axial symmetry (circles), consistent with Fig. 5A. Note that for the resulting line contact problem in plane strain, the fundamental measure for this case is the in-plane force per length F/L.85 In order to compare the force–compression curves in both geometries, we determined the length of the cylinder L = 4/3RC in plane strain, such that the cylinder volume is equal to the sphere volume in axial symmetry, and multiplied the average force per length by L.
Importantly, for both contact problems studied here, plane strain and axial symmetry, there exists an analytical solution for the force–compression relation in the absence of the nucleus.85 The force–compression relation of an elastic sphere compressed by two rigid plates is the Hertz problem with F ∝ δ3/2 for an arbitrary pressure distribution.85,86 In plane strain, the relation is more complicated and can be given as 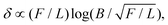 where B is a constant containing information about the cell size and its effective stiffness.85Fig. 5B shows, apart from the numerically obtained data (symbols), also fits to these relations (solid curves), resulting in a very good agreement for both geometries. Importantly, the Hertzian theory F ∝ δ3/2 is still valid, even in the presence of a rather large and stiff nucleus.
where B is a constant containing information about the cell size and its effective stiffness.85Fig. 5B shows, apart from the numerically obtained data (symbols), also fits to these relations (solid curves), resulting in a very good agreement for both geometries. Importantly, the Hertzian theory F ∝ δ3/2 is still valid, even in the presence of a rather large and stiff nucleus.
As the two-plate setup is extensively used to measure cellular stiffnesses, we tried to infer the effective Young's modulus Eeff (i.e. cell plus nucleus as measured in the respective apparatus) of our model cell in the physically relevant axial symmetric situation. We used the full Hertzian law 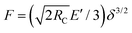 for a parabolic pressure distribution with F the total force per plate and
for a parabolic pressure distribution with F the total force per plate and  . Here Eeff and νeff are the effective elastic parameters of the cell–nucleus composite for rigid plates.86 We assumed here that νeff = νC = νN. Fig. 5C then shows that Eeff increases non-linearly with increasing nucleus stiffness EN. For physiological nucleus sizes VN/VC = 0.125–0.3, the effective modulus Eeff experiences an up to three-fold increase for EN/EC = 10. Note, that for EN/EC = 1 the comparison with Hertzian theory yields an effective modulus slightly Eeff < 1, resulting from the unknown pressure distribution in the phase field simulation.
. Here Eeff and νeff are the effective elastic parameters of the cell–nucleus composite for rigid plates.86 We assumed here that νeff = νC = νN. Fig. 5C then shows that Eeff increases non-linearly with increasing nucleus stiffness EN. For physiological nucleus sizes VN/VC = 0.125–0.3, the effective modulus Eeff experiences an up to three-fold increase for EN/EC = 10. Note, that for EN/EC = 1 the comparison with Hertzian theory yields an effective modulus slightly Eeff < 1, resulting from the unknown pressure distribution in the phase field simulation.
The acto-myosin system tends to reinforce under tensile stresses, but to disassemble under compressive stresses.13 As long as the cell is not spreading on an adhesive substrate and therefore generating tensile stresses, but only is subjected to compression from the outside, we do not expect an upregulation of the contractile cytoskeleton. Consequently, since we consider plates that are not strongly adhesive, we did not include any active stress above. If we nevertheless include active stress in our simulations, we find similar stress patterns, but the fit to Hertz-theory did not work well anymore (results not shown).
Our simulations can also be used to study the effect of different cell shapes. Fig. 5D shows the compression of an initially pancake-like shaped cell in axial symmetry, similarly as studied in ref. 75, for different nucleus stiffnesses EN/EC = 1, 2, 10. It can be directly compared to the initially spherical cell in Fig. 5A, bottom. Again, for increasing nucleus stiffness a redistribution of stresses within the cell is visible. For EN/EC = 1, the regions of highest stress are located close to the cell boundary at the transition points from vanishing to finite curvature, as predicted before.75 However, for increasing nucleus stiffness the upper and lower poles of the nucleus, nearest to the plates, become the zones of highest stress. Again a band-like stress from the cell boundary in contact with the plates to the nucleus boundary is visible. The main impact of cell morphology (sphere vs. pancake) on nuclear straining thereby comes from the distance between the nucleus and the cell boundary: forces are better propagated to the nucleus for flatter cell shapes.
Finally, we studied the effect of cortical tension on the force–compression curves of spherical cells. Cortical tension is due to myosin II motor activity in the actin cortex located directly underneath the plasma membrane. Since the cortex is thin compared to the cell dimension, effectively this effect can be described as a surface tension λS. Hence in the phase field sense,51,87 we add the force
 | (7) |
In the simulation, the cell is first allowed to mechanically relax under the applied cortical tension, then the compression is started. Hence we now normalized the compression height δ by the cell diameter 2rC in mechanical equilibrium, with applied surface tension but before compression. We chose a lower cell stiffness than before, EC = 0.5 kPa, to make the effect more apparent, and a realistic cortical surface tension range of up to λS = 2 nN μm−1.88,89Fig. 6 shows the obtained force–compression curves for nuclear stiffnesses EN/EC = 2 and 10. One can see that increasing λS results in an increase of the required force for compression, especially for larger compression. However, the stiffer the nucleus, the smaller is the effect relative to the case without surface tension.
 | ||
| Fig. 6 Force–compression curves for a spherical cell subject to a cortical surface tension of varying strength λS = 0, 1, 2 nN μm−1 for different nuclear stiffnesses EN/EC = 2 and 10. The symbols are the numerical results and the solid lines fits according to the Hertz law. Note that the deformation of the cell due to the cortical tension, prior to compression, changes its diameter (from 2RC to 2rC), which is used to normalize δ. The compression is quasi-stationary; parameters are EC = 0.5 kPa and ξ = 0.04 nN s μm−3 for better numerical stability. Other parameters as in Fig. 5 and Table 1. | ||
To quantify, we again performed a comparison to Hertz theory (solid lines in Fig. 6), yielding good fits for all tested cases. For the extracted effective cell stiffnesses Eeff we found an increase of ∼63% for EN/EC = 2 (from Eeff = 0.53 kPa for λS = 0 nN μm−1 to Eeff = 0.82 kPa for λS = 2 nN μm−1) and of ∼25% for EN/EC = 10 (from Eeff = 0.91 kPa for λS = 0 nN μm−1 to Eeff = 1.22 kPa for λS = 2 nN μm−1). Hence cortical surface tension effectively stiffens cells, as is to be expected since compression increases the surface area. The effect decreases with increasing nuclear rigidity, and also with increasing cytoplasmic stiffness.
4.2 Compressing cells: viscoelastic effects
The mechanics of cells is much more complicated than the simple assumption of elasticity used until now. We already demonstrated in Fig. 4 that our approach represents viscoelastic effects of Kelvin–Voigt-type and we now demonstrate this again in the context of cell compression. We consider again the case of a spherical cell with nucleus. Now the plates are moved towards each other in a continuous fashion with a velocity v.Fig. 7A shows resulting force–compression curves for nuclear stiffnesses EN/EC = 2 (left) and EN/EC = 10 (right) and for different plate velocities v. The blue curve marks the quasi-static case discussed in Fig. 5. One clearly sees that increasing the plate velocity increases the force required to reach the same relative compression δ. We also note that if the plate motion is stopped in between, the force relaxes and reaches the corresponding lower bound given by the quasi-stationary case (blue curve), as observed in experiments.75
 | ||
| Fig. 7 (A) Numerically obtained force–compression curves for a spherical cell between two plates in axial symmetry. The plates are moved with a velocity of v = 0, 0.5, 1.25, 1.875, 2.5 μm s−1 (blue to grey); v = 0 corresponds to the quasi-stationary case studied in Fig. 5. Left panel: EN/EC = 2; right panel EN/EC = 10. (B) Force-velocity curve extracted from (A) at a given δ, here the last time point where δ/(2RC) ≤ 0.05. The force required for the same compression increases with plate velocity, as time becomes increasingly insufficient to relax stress. (C) Shown is the strain energy (left) and the dissipated energy (right), as a function of time for different nuclear stiffnesses EN/EC = 1, 2, 10. At t = 0 the plates were suddenly removed and the cell allowed to relax back to its spherical, undeformed state. The numerically obtained solutions (circles) are fit (solid lines) allowing to extract relaxation times and effective viscosity. (D) Table giving Eeff obtained from Fig. 5C, the average τR from the fits in (C) and the resulting ηeff = Eeff·τR. Parameters as in Fig. 5 with VN/VC = 0.125, i.e. RN = 6.25 μm. Other parameters as in Table 1. | ||
In accordance to the previous results, comparing the cases EN/EC = 2 and EN/EC = 10 of Fig. 7A shows that increasing the nuclear stiffness increases the force. On the other hand, the stiffer the nucleus, the smaller the effect of the compression velocity becomes. To further quantify these observations, Fig. 7B shows the force-velocity relation, obtained by calculating the total force experienced by the cell at a certain δ (here at the last time point where δ/(2RC) ≤ 0.05), for the plate velocities v shown in Fig. 7A. An almost linear increase of the force with plate velocity v is visible, with only a marginal difference between EN/EC = 1 and EN/EC = 2, suggesting that soft nuclei have only a small effect. The increase of the force with plate velocity v is due to insufficient time of viscoelastic stress relaxation to mechanical equilibrium for finite plate velocity. Such a higher (not completely relaxed) stress should consequently lead to the higher effective stiffness for the cell–nucleus composite at a given velocity. However, we refrained from fitting the force–compression curves to the Hertz law, as it is only valid in the stationary case.
As a second test to show that the phase field model describes viscoelastic effects of Kelvin–Voigt-type correctly, we analyzed a relaxation experiment. A spherical cell was compressed in a quasi-stationary manner as described in the last section. After reaching a compression δ of 10% of the initial cell diameter (2RC), the plates were removed instantly and the cell allowed to relax back to its initial, undeformed configuration. Fig. 7C shows the time evolution of the strain energy 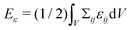 (left) and of the dissipated energy Ed = E0 − Eε (right) from the time point of plate removal (t = 0) of elastic energy E0 = Eε(t = 0), for different nuclear stiffnesses EN/EC. The circles are the numerically obtained results, showing that the strain energy decays exponentially and that the dissipated energy levels to a plateau for large times, both indicating the mechanical equilibrium of the undeformed state.
(left) and of the dissipated energy Ed = E0 − Eε (right) from the time point of plate removal (t = 0) of elastic energy E0 = Eε(t = 0), for different nuclear stiffnesses EN/EC. The circles are the numerically obtained results, showing that the strain energy decays exponentially and that the dissipated energy levels to a plateau for large times, both indicating the mechanical equilibrium of the undeformed state.
As discussed already in Section 3.3, in the viscoelastic regime our phase field model is of Kelvin–Voigt type. We hence can fit the corresponding strain energy function, Eε(t) = E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2t/τR), and dissipated energy function ED = E0[1 − exp(−2t/τR)], to the numerical data, cf. the solid curves in Fig. 7C, allowing to extract the relaxation timescale τR (here we average over the results from strain energy and dissipated energy) for the different nuclear stiffnesses considered. Together with the effective cell–nucleus rigidities, obtained previously in Fig. 5C for VN/VC = 0.125, we are able to infer the effective viscosities ηeff = Eeff·τR. The obtained values are given in the table Fig. 7D. As expected, the relaxation times decrease with nuclear stiffness but the effective viscosity ηeff remains approximately constant, as it is determined by ξ in eqn (2). This shows that ξ sets the effective viscosity of the composite model under compression, similar as had been shown in Section 3.3 for the adhesion geometry. We note that we used a small ξ here, to get a relaxation on a time scale of seconds, since the numerical time step in the compression geometry is very small (10−4 s). This value corresponds more to intracellular relaxation time scales, while those for a whole cell are of the order of tens of seconds or minutes.90 We stress that there is no problem to increase ξ, and consequently the effective viscosity and τR, as exemplified in Fig. 4B for the adhesion geometry.
exp(−2t/τR), and dissipated energy function ED = E0[1 − exp(−2t/τR)], to the numerical data, cf. the solid curves in Fig. 7C, allowing to extract the relaxation timescale τR (here we average over the results from strain energy and dissipated energy) for the different nuclear stiffnesses considered. Together with the effective cell–nucleus rigidities, obtained previously in Fig. 5C for VN/VC = 0.125, we are able to infer the effective viscosities ηeff = Eeff·τR. The obtained values are given in the table Fig. 7D. As expected, the relaxation times decrease with nuclear stiffness but the effective viscosity ηeff remains approximately constant, as it is determined by ξ in eqn (2). This shows that ξ sets the effective viscosity of the composite model under compression, similar as had been shown in Section 3.3 for the adhesion geometry. We note that we used a small ξ here, to get a relaxation on a time scale of seconds, since the numerical time step in the compression geometry is very small (10−4 s). This value corresponds more to intracellular relaxation time scales, while those for a whole cell are of the order of tens of seconds or minutes.90 We stress that there is no problem to increase ξ, and consequently the effective viscosity and τR, as exemplified in Fig. 4B for the adhesion geometry.
4.3 Micropipette aspiration
An alternative to cell compression experiments for measuring cellular rheological responses are micropipette experiments.76,79–81,91 In this setup, cells are sucked into a pipette tube by applying a pressure difference ΔP between the tube's interior and the exterior space. In this setup, forces are more locally applied compared to global straining in compression experiments. Micropipette aspiration has already been studied numerically and together with experiments showed that cells can have elastic and viscous signatures.92 Therefore, this experiment has been used to measure both the elastic modulus E and viscosity η of cells.76We are again interested in the influence of the nucleus on the measurement of the effective cell stiffness, in the context of this more local force application. Considering a spherical cell with axial symmetry, the stationary pipette wall can be modeled as in the previous example by using a field φ(x), placing it closely to the cell membrane. Before sucking the cell into the pipette, we first let the cell relax into mechanical equilibrium due to the interaction with the pipette walls, cf.eqn (6). To prevent any rigid body motion of the cell, we let it adhere to a sphere (field ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) (x)) on the side opposite to the pipette, as also done experimentally77,78 using an adhesion force
(x)) on the side opposite to the pipette, as also done experimentally77,78 using an adhesion force
Fadh = Y(∇![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) )(∇h(ρ))u. )(∇h(ρ))u. | (8) |
Applying now a pressure, P1, in the micropipette tube that is smaller than the pressure P0 in the cell's interior (the outside pressure is assumed to be P0 as well) leads to a boundary force acting at the cell membrane within the pipette like
 | (9) |
Fig. 8A shows results for the aspiration of spherical nucleated cells (RC = 15 μm, RN = 7.5 μm) for nucleus stiffnesses EN/EC = 1, 2 and 10 into a micropipette of radius Rp = 2/3RN = 5 μm using a pressure difference of ΔP/EC = 0.5. As expected, the highest positive stresses occur at the cell membrane within the pipette, while negative stresses arise at the edges of the micropipette, where it effectively pushes against the cell. Furthermore, in the case of stiff nuclei (EN/EC = 10), stress accumulation occurs again in the vicinity of the nucleus boundary nearest to the pipette. This again suggests the possible perception of mechanical stimuli by the nucleus, even for very locally applied forces. While stiffer nuclei only deform marginally and are shifted within the cell towards the pipette position, soft nuclei (EN/EC = 1, 2) show some egg-like asymmetry in their morphology due to deformation. The black curves in the panels of Fig. 8A show the cell and nucleus boundaries (0.5-phase field isocurves) for three different time points, to exemplify the dynamic nature of the problem.
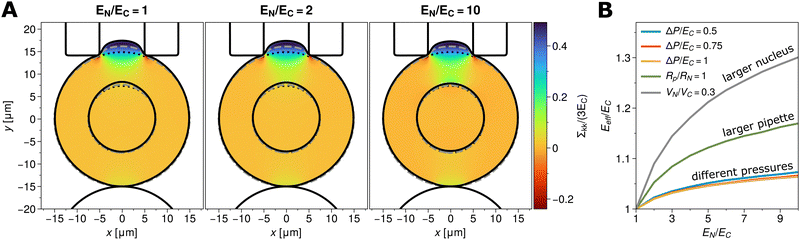 | ||
| Fig. 8 (A) Micropipette aspiration of a spherical cell (RC = 15 μm) with nucleus (RN = 7.5 μm) into a pipette of Rp/RN = 2/3 with ΔP/EC = 0.5 in axial symmetry. Shown are the cases EN/EC = 1, EN/EC = 2 and EN/EC = 10. Cell and nucleus boundary are depicted for three different time points: before pressure application (dotted black), during pressure application (dashed gray) and in mechanical equilibrium (solid black). The solid line outside the cell marks the edges of the pipette walls (top) and the spherical bead the cell adheres to (bottom). The color map shows the trace of the stress tensor normalized by the cytoplasmic stiffness EC. (B) Effective moduli extracted from experiments as shown in A at ΔP/EC = 0.5 (blue), for higher pressures ΔP/EC = 0.75 (red) and ΔP/EC = 1 (yellow), and at ΔP/EC = 0.5 but for a larger nucleus VN/VC = 0.3 (gray) or for a larger pipette Rp/RN = 1 (green). All cases show an increase in effective modulus with nucleus stiffness, but much smaller as compared to the compression experiment in Fig. 5C. Note, due to the unknown shape factor for the micropipette, we shifted the curves slightly such that for EN/EC = 1 the expected modulus is recovered. Simulations were performed on N = 512 × 512 grid points. If not mentioned otherwise, the parameters used are RC = 15 μm, RN/RC = 0.5, EC = 1 kPa, νC = νN = 0.48, α = 6 kPa and Y = 5 nN μm−2 (unit for adhesion strength is now different due to phase field-type definition, eqn (8)). Other parameters as in Table 1. | ||
Also in the micropipette geometry, one can extract an effective modulus for the cell–nucleus composite. Within the elastic regime of aspiration, the stiffness can be approximated by the relation E = (3ζ/2π)ΔP(Rp/Lp), where Rp is the inner micropipette radius and ζ is a shape factor for the micropipette geometry.93 No closed form exists for calculating the shape factor ζ.
To calculate the effective cell stiffness Eeff from the numerics, we determine the aspiration length Lp and, knowing the applied pressure difference and the micropipette radius, we estimated the effective modulus over a range of nucleus stiffnesses, nucleus sizes, pressure differences and micropipette radii, cf.Fig. 8B. All tested cases yield Eeff ≈ 1 for EN/EC = 1 with a deviation of less than 5% for ΔP/EC = 0.5. Since the shape factor is unknown, we hence shifted all results such that for EC = EN we get the correct modulus. There also is a slight dependence on the applied pressure. However, with increasing pressure (from blue to yellow curves in Fig. 8B), the extracted effective moduli Eeff approach each other, indicating that the method is best suited for sufficiently large applied pressures.
All studied cases show an increase in effective stiffness for stiffer nuclei. However, this increase is approximately 30% for the largest and stiffest nuclei. Hence the localized force application due to the micropipette geometry leads to much lower measured Eeff compared to the global cell compression geometry, cf.Fig. 5. This clearly demonstrates – and quantifies – that experimentally measured effective cell stiffnesses do not only depend on the inner structure of the cell, but also on the experimental setup.
5 Discussion and conclusions
Cell mechanics and mechanotransduction are strongly influenced by the largest cellular organelle, the nucleus. Despite increasing evidence of its mechanical importance, models explicitly accounting for nuclear mechanics are still rare. We here developed a two-phase field approach for modelling cell mechanics with an additional internal compartment associated with nuclear elastic properties and investigated the mechanical response of cells in a selection of biologically relevant geometries and experimental setups. We also verified our approach in several cases for which analytical solutions are available to the elastic equations and investigated the effects of cortical tension and viscoelasticity.In the first part described in Section 3, we considered the case of spread cells in unstructured and structured environments using a 2D plane stress formulation. For homogeneous adhesion, the effect of a physiologically sized nucleus on the mechanical response of the cell is small as the adhesion to the substrate effectively shields the nucleus from deformations and stresses. Even peripheral adhesion on a ring pattern is still sufficient to protect the nucleus. However, in more structured environments with highly localized adhesion sites, a much higher transmission of stresses to the nucleus was observed. These observations demonstrate theroretically that the actual adhesion geometry can be sensed by cells at the nucleus, similar to recent conclusions with a purely elastic model (no phase field).61
When modeling micro-patterned environments, stiffer nuclei also change the cellular morphology, by perturbing the formation of the invaginated arcs. Additionally, the nuclear position largely effects the stress distribution within the cell, which may be an important input for the cell with regard to the determination of its polarity, e.g. when having to distinguish between front and back. For stiff nuclei, “stress bridges” resembling stress fibers form from close-by focal adhesions to the nuclear boundary, suggesting an effect on the perception of mechanical cues. Again a similar effect can be seen in purely elastic models (no phase fields).70
The here-proposed phase field method allows to model not only stationary but also dynamic situations. As a simple example we considered the failure of a focal adhesion for a cell on a hexagonal micro-patterned substrate. The coupling of phase field dynamics and elasticity made it necessary to use an elastodynamic formulation for the evolution of the displacement field.31 We here showed, that the relaxation into mechanical equilibrium is of Kelvin–Voigt type. In turn, if a purely elastic behaviour of the system is desired, it should not be probed on timescales shorter than the respective relaxation time. It should also be noted that the elastic description memorizes the initial condition (i.e. the reference state of the elastic displacement) of the cell before the application of forces or stresses. Hence in situations such as the study of adhesion failure in Fig. 4A, the cell does not relax to a (deformed) pentagonal shape with an invaginated arc at the cell edge where the disappeared focal adhesion was located. In the future, the memory effect can be removed by an extra dynamics for the reference state.
In the second part, described in Section 4, we modeled compression experiments of cells between two parallel plates and the aspiration of cells into micropipettes in an axial symmetric geometry. Again, stiffer nuclei showed stress accumulation near their boundary pointing towards a significant role of nuclear mechanics in determining the properties of the cellular environment. Importantly, our model allowed the extraction of effective elastic moduli of the cell–nucleus composite for both experimental methods, yielding consistently lower effective moduli for local pressure application in micropipette experiments compared to more global cell compression. This shows theoretically that the determination of effective cell moduli is not only dependent on cell geometry but also the experimental setup used. A similar conclusion has been reached when experimentally comparing different methods to probe whole cell mechanics.94 For the micropipette aspiration experiments the extraction of elastic moduli is best suited for sufficiently large pressures. Low pressure application leads to a slight underestimation in the range of 5% of the effective cell stiffness, which is partially influenced by the unknown shape factor for the pipette, cf. the discussion of Fig. 8B. We also investigated the effect of cortical tension in the compression geometry. It results in an increase of the required force needed for compression. The stiffer the nucleus, the smaller is the effect relative to the case without cortical tension.
The quasi-stationary compression of cells is described well by Hertz theory and therefore allows the identification of an effective modulus, similar to a very recent computational study with elasticity (no phase field).21 We next demonstrated that our phase field approach is also applicable in the viscoelastic regime, e.g. for dynamic compression with different plate velocities and relaxation studies. The force required for the same compression increases with plate velocity, as time becomes increasingly insufficient to relax the stress induced by the plate motion. From numerical relaxation experiments we could extract the relaxation time scale, which can be adjusted in the model varying the parameter ξ in eqn (1) and (2), and the effective viscosity, confirming that our approach is fully consistent with the Kelvin–Voigt viscoelastic solid. At the current stage, our model does not describe viscoelasticity of Maxwell type, that is a viscoelastic fluid without memory. The best way to achieve this in our context might be to introduce an own dynamics for the reference state.
In the future, the here-developed method should prove useful for investigating the effect of a nucleus and/or other cellular organelles, potentially described with different material laws, in a large variety of situations. Additional new insights on mechanotransduction could be gained by examining the effect of the nuclear position within the cell in fully three-dimensional (3D) situations. In this respect, the phase field method can be extended relatively easily to 3D, making it possible to consider more complex environments like fibrous network geometries or non-symmetric constrictions.95–97 The presented method could also be used to describe the role of cell nucleus mechanics in tissues, using the multi-phase field approach.32–34 Note that recently, a new jamming transition due to the presence of nuclei was predicted for tissues by an active foam model.98 It would be interesting to study the same effect in our dynamic continuum framework.
Another important context of cell and nuclear mechanics is cell migration through constrictions, where the minimal constriction size is predominantly determined by the nuclear size and stiffness.10 We envision to supplement the current approach by self-organized internal driving forces inducing cellular motility, that could be implemented by an actin “polarization” field44 and should naturally enter the elastodynamic eqn (2). In the context of mechanotransduction, the coupling of the proposed method to a system of reaction–diffusion equations should allow to model nuclear translocation of proteins like YAP/TAZ in response to nuclear straining (and opening of nuclear pore complexes99–101). This could elucidate further – and more directly – the role of nuclear mechanics on spatio-temporal import dynamics and mechanically induced signalling events.
In summary, the elastic phase field approach for modelling the mechanics of nucleated cells is very versatile and easy to generalize for future applications. The results presented should be useful to quantify experiments and last but not least point to many interesting implications with regard to the role of the nucleus on whole cell mechanics, mechanosensing and related subjects.
Author contributions
R. C., U. S. S. and F. Z. developed the model together. R. C. performed the calculations, developed the numerical code and analyzed the data. U. S. S. and F. Z. designed and supervised the research. All authors wrote the paper.Conflicts of interest
There are no conflicts to declare.Appendices
A Other parameters of the model
Table 1 contains the default values for additional parameters used, if not specified otherwise in the figure captions.| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| a For ϕ ∈ {ρ, ψ}, i.e. cell and nucleus. Sets the interface width to 0.5 μm. b Note, in plane strain and axial symmetry the unit is nN s μm−4. | |||
| Time step | Δt | 0.001 | s |
| Diffusion coeff. phase field (PF)a | D ϕ | 1.25 | μm2 s−1 |
| Friction coefficientb | ξ | 0.004 | nN s μm−3 |
| Local suppression coeff.b | γ(x) | 0.014–0.04 | nN s μm−3 |
| Regularization parameter | ε | 0.0025 | μm2 |
| Diffusion coeff. adhesion PF | D Y | 0.25 | μm2 s−1 |
| Diffusion coeff. obstacle PF | D φ | 0.625 | μm2 s−1 |
In Section 4 Δt = 10−4 s.
B Analytical solution for an adherent contractile disk-like cell with nucleus
We consider a concentric cell and its nucleus with possibly different Young's moduli EN and EC and Poisson's ratio νN and νC as depicted in Fig. 2A. Further we assume a homogeneous and isotropic contractile stress σ0(x, t) = σ0 and spring stiffness density Y(x, t) = Y. Both nucleus and cytoplasm are assumed to be linearly elastic. In each of these two cell compartments the equation of mechanical equilibrium| ∇·σ − Yu = 0 | (10) |
 | (11) |
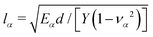 being the localization lengths59 for cytoplasm (α = C) and nucleus (α = N), respectively. Note, that Y could also vary between cytoplasm and nucleus. Eqn (11) is a modified Bessel equation with general solution
being the localization lengths59 for cytoplasm (α = C) and nucleus (α = N), respectively. Note, that Y could also vary between cytoplasm and nucleus. Eqn (11) is a modified Bessel equation with general solution | (12) |
| uNr(0) = 0 and σrr(RN) = −σNd, | (13) |
| σrr(RC) = −σ0d and uNr(RN) − uCr(RN) = 0. | (14) |
 | (15) |
 | (16) |
Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy EXC 2181/1 – 390900948 (the Heidelberg STRUCTURES Excellence Cluster). USS is a member of the Interdisciplinary Center for Scientific Computing (IWR).References
- R. Pelham Jr and Y. Wang, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 13661–13665 CrossRef CAS PubMed.
- N. Nisenholz, K. Rajendran, Q. Dang, H. Chen, R. Kemkemer, R. Krishnan and A. Zemel, Soft Matter, 2014, 10, 7234–7246 RSC.
- C.-M. Lo, H.-B. Wang, M. Dembo and Y.-L. Wang, Biophys. J., 2000, 79, 144–152 CrossRef CAS PubMed.
- R. Sunyer, V. Conte, J. Escribano, A. Elosegui-Artola, A. Labernadie, L. Valon, D. Navajas, J. M. García-Aznar, J. J. Muñoz, P. Roca-Cusachs and X. Trepat, Science, 2016, 353, 1157–1161 CrossRef CAS.
- R. McBeath, D. M. Pirone, C. M. Nelson, K. Bhadriraju and C. S. Chen, Dev. Cell, 2004, 6, 483–495 CrossRef CAS.
- A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689 CrossRef CAS.
- J. Solon, I. Levental, K. Sengupta, P. C. Georges and P. A. Janmey, Biophys. J., 2007, 93, 4453–4461 CrossRef CAS PubMed.
- U. Schwarz, Soft Matter, 2007, 3, 263–266 RSC.
- J. Guck, S. Schinkinger, B. Lincoln, F. Wottawah, S. Ebert, M. Romeyke, D. Lenz, H. M. Erickson, R. Ananthakrishnan, D. Mitchell, J. Käs, S. Ulvick and C. Bilby, Biophys. J., 2005, 88, 3689–3698 CrossRef CAS.
- H.-R. Thiam, P. Vargas, N. Carpi, C. L. Crespo, M. Raab, E. Terriac, M. C. King, J. Jacobelli, A. S. Alberts, T. Stradal, A.-M. Lennon-Dumenil and M. Piel, Nat. Commun., 2016, 7, 10997 CrossRef CAS PubMed.
- T. Fuhs, F. Wetzel, A. W. Fritsch, X. Li, R. Stange, S. Pawlizak, T. R. Kießling, E. Morawetz, S. Grosser, F. Sauer, J. Lippoldt, F. Renner, S. Friebe, M. Zink, K. Bendrat, J. Braun, M. H. Oktay, J. Condeelis, S. Briest, B. Wolf, L.-C. Horn, M. Höckel, B. Aktas, M. C. Marchetti, M. L. Manning, A. Niendorf, D. Bi and J. A. Käs, Nat. Phys., 2022, 1–10 Search PubMed.
- J. Stricker, T. Falzone and M. L. Gardel, J. Biomech., 2010, 43, 9–14 CrossRef PubMed.
- M. Murrell, P. W. Oakes, M. Lenz and M. L. Gardel, Nat. Rev. Mol. Cell Biol., 2015, 16, 486–498 CrossRef CAS PubMed.
- A. F. Pegoraro, P. Janmey and D. A. Weitz, Cold Spring Harb. Perspect. Biol., 2017, 9, 1–12 Search PubMed.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327–1381 CrossRef CAS.
- G. Salbreux, G. Charras and E. Paluch, Trends Cell Biol., 2012, 22, 536–545 CrossRef CAS PubMed.
- T. M. Svitkina, Trends Cell Biol., 2020, 30, 556–565 CrossRef CAS PubMed.
- Y. Kalukula, A. D. Stephens, J. Lammerding and S. Gabriele, Nat. Rev. Mol. Cell Biol., 2022, 23, 583–602 CrossRef CAS PubMed.
- J. Lammerding, Mechanics of the Nucleus, John Wiley & Sons, Ltd, 2011, pp. 783–807 Search PubMed.
- N. Caille, O. Thoumine, Y. Tardy and J.-J. Meister, J. Biomech., 2002, 35, 177–187 CrossRef PubMed.
- S. Wohlrab, S. Mueller and S. Gekle, Biomech. Model. Mechanobiol., 2024, 1–10 Search PubMed.
- J. Swift, I. L. Ivanovska, A. Buxboim, T. Harada, P. C. D. P. Dingal, J. Pinter, J. D. Pajerowski, K. R. Spinler, J.-W. Shin, M. Tewari, F. Rehfeldt, D. W. Speicher and D. E. Discher, Science, 2013, 341, 1240104 CrossRef PubMed.
- A. J. Lomakin, C. J. Cattin, D. Cuvelier, Z. Alraies, M. Molina, G. P. F. Nader, N. Srivastava, P. J. Sáez, J. M. Garcia-Arcos, I. Y. Zhitnyak, A. Bhargava, M. K. Driscoll, E. S. Welf, R. Fiolka, R. J. Petrie, N. S. D. Silva, J. M. González-Granado, N. Manel, A. M. Lennon-Duménil, D. J. Müller and M. Piel, Science, 2020, 370, eaba2894 CrossRef CAS PubMed.
- V. Venturini, F. Pezzano, F. C. Castro, H.-M. Häkkinen, S. Jiménez-Delgado, M. Colomer-Rosell, M. Marro, Q. Tolosa-Ramon, S. Paz-López, M. A. Valverde, J. Weghuber, P. Loza-Alvarez, M. Krieg, S. Wieser and V. Ruprecht, Science, 2020, 370, eaba2644 CrossRef CAS PubMed.
- C. M. Denais, R. M. Gilbert, P. Isermann, A. L. McGregor, M. te Lindert, B. Weigelin, P. M. Davidson, P. Friedl, K. Wolf and J. Lammerding, Science, 2016, 352, 353–358 CrossRef CAS PubMed.
- M. Raab, M. Gentili, H. de Belly, H.-R. Thiam, P. Vargas, A. J. Jimenez, F. Lautenschlaeger, R. Voituriez, A.-M. Lennon-Duménil, N. Manel and M. Piel, Science, 2016, 352, 359–362 CrossRef CAS PubMed.
- M. M. Nava, Y. A. Miroshnikova, L. C. Biggs, D. B. Whitefield, F. Metge, J. Boucas, H. Vihinen, E. Jokitalo, X. Li, J. M. García Arcos, B. Hoffmann, R. Merkel, C. M. Niessen, K. N. Dahl and S. A. Wickström, Cell, 2020, 181, 800–817.e22 CrossRef CAS PubMed.
- R. Kristal-Muscal, L. Dvir and D. Weihs, New J. Phys., 2013, 15, 035022 CrossRef CAS.
- M. Crisp, Q. Liu, K. Roux, J. Rattner, C. Shanahan, B. Burke, P. D. Stahl and D. Hodzic, J. Cell Biol., 2005, 172, 41–53 CrossRef PubMed.
- M. L. Lombardi, D. E. Jaalouk, C. M. Shanahan, B. Burke, K. J. Roux and J. Lammerding, J. Biol. Chem., 2011, 286, 26743–26753 CrossRef CAS PubMed.
- R. Chojowski, U. S. Schwarz and F. Ziebert, Eur. Phys. J. E, 2020, 43, 63 CrossRef CAS PubMed.
- M. Nonomura, PLoS One, 2012, 7, 1–9 CrossRef PubMed.
- J. Löber, F. Ziebert and I. S. Aranson, Sci. Rep., 2015, 5, 9172 CrossRef PubMed.
- D. Wenzel and A. Voigt, Phys. Rev. E, 2021, 104, 054410 CrossRef CAS PubMed.
- B. A. Camley, Y. Zhang, Y. Zhao, B. Li, E. Ben-Jacob, H. Levine and W.-J. Rappel, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14770–14775 CrossRef.
- A. Moure and H. Gomez, Biomech. Model. Mechanobiol., 2020, 19, 1491–1508 CrossRef PubMed.
- A. Karma and W.-J. Rappel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 57, 4323 CrossRef CAS.
- I. S. Aranson, V. A. Kalatsky and V. M. Vinokur, Phys. Rev. Lett., 2000, 85, 118–121 Search PubMed.
- A. Karma, D. A. Kessler and H. Levine, Phys. Rev. Lett., 2001, 87, 045501 Search PubMed.
- J. A. Warren, R. Kobayashi, A. E. Lobkovsky and W. C. Carter, Acta Mater., 2003, 51, 6035–6058 CrossRef CAS.
- T. Biben and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 031908 CrossRef CAS.
- K. John, P. Peyla, K. Kassner, J. Prost and C. Misbah, Phys. Rev. Lett., 2008, 100, 068101 CrossRef PubMed.
- D. Shao, W.-J. Rappel and H. Levine, Phys. Rev. Lett., 2010, 105, 108104 CrossRef PubMed.
- F. Ziebert, S. Swaminathan and I. S. Aranson, J. R. Soc., Interface, 2012, 9, 1084 CrossRef PubMed.
- J. Löber, F. Ziebert and I. S. Aranson, Soft Matter, 2014, 10, 1365 RSC.
- F. Ziebert and I. S. Aranson, npj Comput. Mater., 2016, 2, 16019 CrossRef.
- A. Moure and H. Gomez, Biomech. Model. Mechanobiol., 2018, 17, 1243–1268 CrossRef PubMed.
- S. Najem and M. Grant, Phys. Rev. E, 2016, 93, 052405 Search PubMed.
- G. Zhang and J. M. Yeomans, Phys. Rev. Lett., 2023, 130, 038202 Search PubMed.
- J. W. Cahn and S. M. Allen, J. Phys., Colloq., 1977, 38, C7-51–C7-54 CrossRef.
- R. Folch, J. Casademunt, A. Hernández-Machado and L. Ramírez-Piscina, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1999, 60, 1724–1733 CrossRef CAS PubMed.
- D. Jamet and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041903 CrossRef CAS PubMed.
- K. Kassner, C. Misbah, J. Müller, J. Kappey and P. Kohlert, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 036117 Search PubMed.
- L. D. Landau and E. M. Lifschitz, Theory of elasticity, Pergamon Press, Oxford, 2nd edn, 1963 Search PubMed.
- P. Howell, G. Kozyreff and J. Ockendon, Applied solid mechanics, Cambridge Univ. Press, Cambridge, 2009 Search PubMed.
- J. Howard, Mechanics of Motor Proteins and the Cytoskeleton, Sinauer, Sunderland, 2001 Search PubMed.
- S. B. Khatau, C. M. Hale, P. J. Stewart-Hutchinson, M. S. Patel, C. L. Stewart, P. C. Searson, D. Hodzic and D. Wirtz, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19017 CrossRef CAS PubMed.
- C. M. Edwards and S. J. Chapman, Bull. Math. Biol., 2007, 69, 1927–1942 CrossRef PubMed.
- C. M. Edwards and U. S. Schwarz, Phys. Rev. Lett., 2011, 107, 128101 CrossRef PubMed.
- S. Banerjee and M. C. Marchetti, Phys. Rev. Lett., 2012, 109, 108101 Search PubMed.
- J. Solowiej-Wedderburn and C. M. Dunlop, Biophys. J., 2022, 121, 1777–1786 Search PubMed.
- E. Zamir and B. Geiger, J. Cell Sci., 2001, 114, 3583–3590 CrossRef CAS PubMed.
- T. Andersen, D. Wörthmüller, D. Probst, I. Wang, P. Moreau, V. Fitzpatrick, T. Boudou, U. S. Schwarz and M. Balland, Biophys. J., 2023, 122, 684–696 CrossRef CAS PubMed.
- C. S. Chen, M. Mrksich, S. Huang, G. M. Whitesides and D. E. Ingber, Science, 1997, 276, 1425–1428 CrossRef CAS PubMed.
- M. Théry, A. Pépin, E. Dressaire, Y. Chen and M. Bornens, Cell Motil. Cytoskelet., 2006, 63, 341–355 Search PubMed.
- D. Lehnert, B. Wehrle-Haller, C. David, U. Weiland, C. Ballestrem, B. A. Imhof and M. Bastmeyer, J. Cell Sci., 2004, 117, 41–52 Search PubMed.
- R. Link, K. Weißenbruch, M. Tanaka, M. Bastmeyer and U. S. Schwarz, Adv. Funct. Mater., 2023, 2302145 Search PubMed.
- I. B. Bischofs, F. Klein, D. Lehnert, M. Bastmeyer and U. S. Schwarz, Biophys. J., 2008, 95, 3488–3496 CrossRef CAS PubMed.
- A. Jana, A. Tran, A. Gill, A. Kiepas, R. K. Kapania, K. Konstantopoulos and A. S. Nain, Adv. Sci., 2022, 9, 2203011 CrossRef PubMed.
- W. Ronan, V. S. Deshpande, R. M. McMeeking and J. P. McGarry, Biomech. Model. Mechanobiol., 2014, 13, 417–435 CrossRef PubMed.
- M. Yoneda, J. Exp. Biol., 1964, 41, 893–906 CrossRef CAS.
- O. Thoumine and A. Ott, J. Cell Sci., 1997, 110, 2109–2116 CrossRef CAS.
- G. Ofek, D. C. Wiltz and K. A. Athanasiou, Biophys. J., 2009, 97, 1873–1882 Search PubMed.
- D. Mitrossilis, J. Fouchard, A. Guiroy, N. Desprat, N. Rodriguez, B. Fabry and A. Asnacios, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18243–18248 Search PubMed.
- E. Fischer-Friedrich, Y. Toyoda, C. J. Cattin, D. J. Müller, A. A. Hyman and F. Jülicher, Biophys. J., 2016, 111, 589–600 Search PubMed.
- E. Evans and A. Yeung, Biophys. J., 1989, 56, 151–160 CrossRef CAS.
- S. E. Chesla, P. Selvaraj and C. Zhu, Biophys. J., 1998, 75, 1553–1572 CrossRef CAS.
- E. Evans, A. Leung, V. Heinrich and C. Zhu, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 11281–11286 CrossRef CAS.
- M. Herant, V. Heinrich and M. Dembo, J. Cell Sci., 2005, 118, 1789–1797 CrossRef CAS PubMed.
- J.-Y. Tinevez, U. Schulze, G. Salbreux, J. Roensch, J.-F. Joanny and E. Paluch, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18581–18586 Search PubMed.
- T. Luo, K. Mohan, P. A. Iglesias and D. N. Robinson, Nat. Mater., 2013, 12, 1064–1071 Search PubMed.
- N. Desprat, A. Guiroy and A. Asnacios, Rev. Sci. Instrum., 2006, 77, 055111 Search PubMed.
- M. Mokbel, K. Hosseini, S. Aland and E. Fischer-Friedrich, Biophys. J., 2020, 118, 1968–1976 CrossRef CAS PubMed.
- Y.-J. Liu, M. Le Berre, F. Lautenschlaeger, P. Maiuri, A. Callan-Jones, M. Heuzé, T. Takaki, R. Voituriez and M. Piel, Cell, 2015, 160, 659–672 CrossRef CAS PubMed.
- K. L. Johnson, Contact Mechanics, Cambridge Univ. Press, Cambridge, 1985 Search PubMed.
- H. Hertz, J. für die Reine und Angew. Math., 1882, 92, 156–171 CrossRef.
- B. Winkler, I. S. Aranson and F. Ziebert, Phys. D, 2016, 318, 26 CrossRef.
- J. Peukes and T. Betz, Biophys. J., 2014, 107, 1810 CrossRef CAS PubMed.
- P. Chugh, A. G. Clark, M. B. Smith, D. A. D. Cassani, K. Dierkes, A. Ragab, P. P. Roux, G. Charras, G. Salbreux and E. K. Paluch, Nat. Cell Biol., 2017, 19, 689 CrossRef CAS PubMed.
- B. Fabry, G. Maksym, J. Butler, M. Glogauer, D. Navajas and J. Fredberg, Phys. Rev. Lett., 2001, 87, 148102 CrossRef CAS PubMed.
- R. M. Hochmuth, J. Biomech., 2000, 33, 15–22 CrossRef CAS PubMed.
- J. L. Drury and M. Dembo, Biophys. J., 1999, 76, 110–128 CrossRef CAS PubMed.
- D. P. Theret, M. J. Levesque, M. Sato, R. M. Nerem and L. T. Wheeler, J. Biomech. Eng., 1988, 110, 190–199 CrossRef CAS PubMed.
- P.-H. Wu, D. R.-B. Aroush, A. Asnacios, W.-C. Chen, M. E. Dokukin, B. L. Doss, P. Durand-Smet, A. Ekpenyong, J. Guck and N. V. Guz, et al. , Nat. Methods, 2018, 15, 491–498 CrossRef CAS PubMed.
- A. Moure and H. Gomez, Comput. Methods Appl. Mech., 2017, 320, 162–197 CrossRef.
- B. Winkler, I. S. Aranson and F. Ziebert, Commun. Phys., 2019, 2, 82 CrossRef.
- A. R. Gonthier, E. L. Botvinick, A. Grosberg and A. Mohraz, ACS Biomater. Sci. Eng., 2023, 9(10), 5666–5678 CrossRef CAS PubMed.
- S. Kim, R. Amini and O. Campàs, bioRxiv, 2022, preprint DOI:10.1101/2022.07.31.502244.
- A. Elosegui-Artola, I. Andreu, A. E. M. Beedle, A. Lezamiz, M. Uroz, A. J. Kosmalska, R. Oria, J. Z. Kechagia, P. Rico-Lastres, A.-L. Le Roux, C. M. Shanahan, X. Trepat, D. Navajas, S. Garcia-Manyes and P. Roca-Cusachs, Cell, 2017, 171, 1397–1410.e14 CrossRef CAS PubMed.
- I. Andreu, I. Granero-Moya, N. R. Chahare, K. Clein, M. Molina-Jordán, A. E. M. Beedle, A. Elosegui-Artola, J. F. Abenza, L. Rossetti, X. Trepat, B. Raveh and P. Roca-Cusachs, Nat. Cell Biol., 2022, 24, 896–905 CrossRef CAS PubMed.
- C. E. Zimmerli, M. Allegretti, V. Rantos, S. K. Goetz, A. Obarska-Kosinska, I. Zagoriy, A. Halavatyi, G. Hummer, J. Mahamid, J. Kosinski and M. Beck, Science, 2021, 374, eabd9776 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00345d |
| This journal is © The Royal Society of Chemistry 2024 |

