Role of interaction range on the microstructure and dynamics of attractive colloidal systems

Abstract

Colloidal gelation phase diagram has been traditionally characterized using three key factors: particle volume fraction, strength of attraction, and range of attraction. While there's a rich body of literature on the role of attraction strength and particle volume fraction, majority of studies have been limited to short range interactions. Using Brownian dynamics simulations, we explored the effect that the range of attractions has on the microstructure and dynamics of both weakly and strongly attractive colloidal systems. Although gelation occurs significantly faster at high attraction strength, by an order of magnitude compared to low strength, we did not observe any clear trend in gelation-rate with respect to a change in the range of interaction. However, as the attraction range increases in both systems, the final structure undergoes a transition from a single connected network to a fluid of dense clusters. This results in a new gelation phase boundary for long range attractive colloids.

---

1 Introduction

Colloidal gels are ubiquitous in nature and in various industries ranging from pharmaceuticals to food,^1,2 with a potential to be used as designer materials with tunable properties. However, realizing this potential requires a deep understanding of the structure formation and dynamics as the primary particle-level characteristics change. Colloidal gels generally consist of an intricate network of particles within a solvent, imparting soft solid-like properties to the gel. Formation of this network can be driven by various mechanisms, including arrested spinodal decomposition and the jamming of preformed fractal clusters.^3–5 Colloidal gels may be permanent or transient, depending on the nature of the interaction between aggregated particles.⁶ In dilute systems with strong particle attractions, colloidal gels form with long-lasting bonds and fractal structures. In contrast, weaker attractions lead to gels with less fractal, bicontinuous structures where bonds can easily break and reform. This bond reversibility enables gels to transition between solid and liquid-like states based on external conditions.

In a broader context, gelation onset can be characterized using three key factors: the particle volume fraction, strength of attraction, and range of attraction. These factors collectively establish a three-dimensional state diagram, within which a gelation boundary separates liquid-like from solid-like characteristics. In general, each of these state variables can be independently controlled. Volume fraction of particles is simply a measure of the solid content. The strength and range of interaction between colloidal particles can often be adjusted, or tailored, by various means such as adding electrolyte or non-adsorbing polymers to the suspension or modifying the particle surface coating. For instance, in depletion gels where addition of non-adsorbing polymers to the system induces effective attraction between the particles, concentration of the added polymer directly changes the strength of attraction. However, the range of attraction is controlled by the hydrodynamic radius of the added polymer. Seminal work of Lu et al.⁷ introduced a gelation phase diagram based on these state variables.

Current understanding of colloid gelation focuses on short-range attractive forces,^8–12 despite the potential importance of long-range interactions in various nanoscience applications. Experiments with short-range attractions suggest gelation is initiated by spinodal decomposition, forming a network of particles.⁸ Brownian dynamics (BD) simulations provide further insight into the evolving structure, particle dynamics, and rheological properties of aging colloidal gels.¹⁰ While some studies incorporate long-range repulsion with short-range attraction,^13–16 a systematic understanding of long-range attractions in gelation remains elusive.

This knowledge gap stems from several challenges in systematically studying long-range interactions. First, experimentally, in most colloid–polymer mixtures, the size of colloid is intentionally chosen in the range of 1 μm to slow down the dynamics and thus enable tracking of particle-level structure. Second, the dynamics of particles and polymers become intricately linked when their sizes are comparable, and simple fluid behavior is no longer applicable.^17,18 Finally, while at short-range limit, the details of interaction potential can be overlooked, for long-range interactions, the interaction density can also become important. Some studies have explored the influence of attraction range on phase behavior in colloid–polymer mixtures.^7,19–21 The critical point of fluid–fluid transition varies with the range of attraction in colloidal dispersion.²² Experimental studies have reported the observation of a fluid of colloid clusters, with the cluster morphology strongly dependent on the attraction range.⁷ Teece and her colleagues²¹ found three distinct regimes in gel evolution with long-range attraction, including collapse under gravity in the final stages of phase separation. Nonetheless, the detailed effects of long-range attraction on the dynamics and final microstructure of colloidal assemblies remains unknown.

In this paper, we numerically investigate the effect of the attraction range on the microstructure and dynamics in both weakly and strongly attractive colloidal systems. Specifically, we examine the impact of adjusting the attraction range from ξ = 0.1–1.5a (where a is the particle radius) at two different attraction strengths, u₀ = 6k_BT and 12k_BT, representing weak and strong interactions respectively. In practice, gelation may be induced by different means, such as addition of salt which results in screening of the stabilizing charges on the surface of particles, or addition of non-adsorbing polymers to the system resulting in depletion interactions. In general, the larger attraction ranges in this study are not achievable through salt-based gelation only, and as such one may argue that the lower limit and the upper limits of the range studied here require different types of interaction potentials; nonetheless, here and in order to isolate the role of attraction range from any other additional effects such as the details of interaction potential we keep the form of effective interaction potential unchanged. Although gelation occurs significantly faster at high strength, by an order of magnitude compared to low strength, we observe no clear trend in gelation kinetics concerning the range of interaction. As the attraction range increases in both systems, we instead see a transition in the nature of final structures formed by the attractive colloids, from a fractal configuration to a fluid of dense clusters. In very dilute system with very-long range attraction, we observe only a fluid of clusters, regardless of the attraction strength.

2 Methods

In this study, a system of monodisperse colloid particles with radii a = 1 is simulated in a cubic box with periodic boundary conditions using the Brownian dynamics method. Hydrodynamic interactions between particles are neglected. The simulation is conducted at varying particle volume fractions of ϕ = 0.05–0.15 with 100 000 colloidal particles. The simulation is performed using a, k_BT, and τ = 6πηa³/k_BT as characteristic units for length, energy, and time, respectively. Here, k_B is the Boltzmann constant, T is temperature, τ is the diffusive time scale of a single colloidal particle, and η is the dynamic fluid viscosity. The attraction between colloid particles is modeled using a pairwise additive Morse potential U_Morse = u₀(exp^−2κh_ij − 2exp^−κh_ij), where h_ij is the surface-to-surface distance between particles, u₀ and κa control the strength and range of attraction, respectively. The equation of motion is then described by the equation:where δt is the integration time-step, F^C_i and F^B_i are the total attractive and Brownian force on the particle i, respectively. F^Core_i is the semi-hard potential interaction used to prevent any non-physical overlap of colloid particles during simulation.

The study is carried out at two different attraction strengths, u₀ = 6k_BT and 12k_BT, representing weak and strong interactions. The attraction range ξ = 3/κa is varied from 0.1a to 1.5a (equivalent to 2 ≤ κa ≤ 30), spanning from short-range to long-range attractions.

The simulations consist of two steps. In the first stage, an equilibrium configuration is generated by randomly placing the colloids within the simulation box, followed by running the simulation for 1 × 10⁵ iterations with no attractive interactions between the colloids, to eliminate any non-physical overlap of the colloidal particles. In the second stage, gel formation occurs under attractive interactions. During this phase, we ensure that a quasi-steady structure is reached without significant alterations to the microstructure. This requires running simulations for times equal to 500τ. All simulations are performed using HOOMD-blue,²³ an open-source molecular dynamics simulation toolkit.

3 Results and discussion

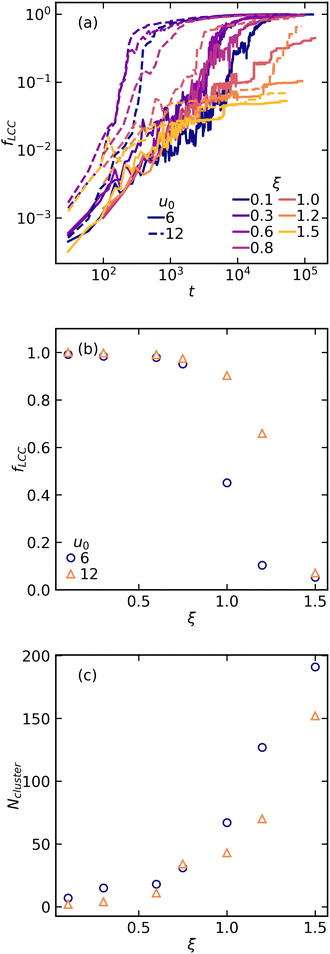
Snapshots of the final structures for different ranges of attractions of weakly and strongly interacting colloids are presented in Fig. 1. The top panel corresponds to the weak attraction of u₀ = 6k_BT, and the bottom panel corresponds to the strong attraction of u₀ = 12k_BT. Particles are color coded based on the number of bonded neighbours from blue (low) to yellow (high) coordination numbers. Generally, stronger interactions result in relatively more inter-connected structures with lower particle–particle bonds. However, there is much more visible effect as the range of attraction increases. Both [weak and strong] systems exhibit coarsening of the colloidal domains as the range of attraction increases, eventually leading to formation of disconnected and large particulate clusters at the longest ranges studied here (Fig. 1(c) and (f)). Having access to all particle positions during the self-assembly and at the final stage, in the following we characterize the system at the particle-level [microscale], cluster-level [mesoscale], and at the global-level [macroscale] to understand the role of attraction range on the structure at different scales.

Fig. 1 Gel structure for attraction strengths (a)–(c) U₀ = 6k_BT and (d)–(f) 12k_BT for range (a) and (d) ξ = 0.1, (b) and (e) 0.6 and (c) and (f) 1.5. Cluster-level structures are shown in the inset. Particles are color-coded using blue-yellow scheme based on their coordination number.

We define the particles bonded when the separation distance between colloids fall in between the first maximum and the first minimum of the pair correlation function. In depletion gels such as ones studied here, one commonly observes formation of a single inter-connected network of particles that span the entire sample. This can be easily quantified by calculating the fraction of number of particles in the largest connected component f_LCC at each time. However, it's important to highlight that we define the final phase behavior based on whether there's a single rigid structure spanning all directions and contacting all faces of the simulation box, not solely on the largest connected components. Evolution of f_LCC also clearly shows a percolation transition at which virtually the entire system becomes a single interconnected network Fig. 2(a). For a strongly attractive system, u₀ = 12k_BT, the percolation transition occurs nearly one order of magnitude faster than the weakly attractive systems, u₀ = 6k_BT. However, for both strengths considered, there's no clear trend in the percolation time as we increase the attraction range. In small attraction ranges, this transition seems unaffected by the range, probably due to diffusion control. On the other hand, for larger attraction ranges, the transition takes much longer time compared to gelation at smaller ranges, often by one to two orders of magnitude. We also analyze f_LCC and number of clusters as function of attraction range once the system reaches a quasi steady-state. At relatively short-range attractions (ξ ≤ 0.6), we observe a plateau representing a single particulate network (Fig. 2(b)). However, with further increases in attraction range, this fraction rapidly diminishes. At the longest range studied (ξ = 1.5), the largest connected component comprises only 10% of the total particles. It's noteworthy that while f_LCC exhibits a rapid decay with ξ, the total number of clusters (N_cluster) shows a slow continuous increase. f_LCC focuses on identifying the single largest connected component whereas N_cluster measures the total number of aggregated clusters including the single particles. Additionally, we observe that weakly attractive colloids are generally more sensitive to the range of attraction, as this drop in the largest connected component occurs more appreciably for the weakly interacting system.

Fig. 2 (a) Evolution of the fraction of number of particles in the largest connected component (LCC) as a function of time, for different attraction ranges from 0.1 to 1.5, for weakly (u₀ = 6k_BT) and strongly (u₀ = 12k_BT) attractive colloids at ϕ = 0.1. (b) Fraction of colloids within the largest connected component at the quasi steady-state structure. (c) Number of clusters within the entire system at the quasi steady-state structure.

While LCC provides a quantitative measure for the global structure and its final size (relative to the entire system), it does not offer any insight into particle-level structure. Hence, we investigated the effect of the attraction range on the local structure through coordination number (number of bonded neighbours to each colloid), 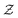, and its distribution. Since interaction ranges are at the core of what is being interrogated, one should pay additional attention to how bonded particles are defined. Coordination number, , can be defined in two main different ways: one using a fixed cutoff distance of r_c = 0.1 to provide a systematic way of comparing different gels, and another based on the distance corresponding to the first minimum of the pair-correlation function which is a true measure of a physical bond between interacting colloids. In Fig. 3(a) and (b), we show the evolution of the average coordination number .

Fig. 3 (a) and (b) Evolution of the ensemble-averaged coordination number over time, and (c) and (d) distribution of coordination number at final configuration at the volume fraction of ϕ = 0.1 for weakly (u₀ = 6k_BT) and strongly (u₀ = 12k_BT) attractive colloids. In (a) and (c) the coordination number is defined based on the true attraction range of colloids (separation between the first minimum and maximum of the pair correlation function, g(r)), and in (b) and (d) coordination number is defined for a fixed cut-off distance of r_c = 0.1. The inset in (b) shows the evolution of over time on semi-log scale.

When employing a variable cutoff distance, the average coordination number increases as the attraction range increases for both high and low strength systems, as shown in Fig. 3(a). For short-ranged attractions, the ensemble-averaged coordination number of a strongly attractive system is systematically smaller than that of a weakly attractive system. This is because weaker attractions allow for more exploration of the entire energy landscape by the particles and thus lowering their energy by forming additional bonds resulting in coarser structures.²⁴ Nonetheless, at the largest range of attraction this visible difference vanishes as both interactions result in coarse clusters rather than a percolated network. On the other hand, when using a fixed cutoff distance, we observe intriguing behavior. For weak attractions (u₀ = 6k_BT), the coordination number decreases as the attraction range increases, while for strong ones (u₀ = 12k_BT), 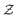increases as the attraction range increases (Fig. 3(b)). For weakly attractive systems, increasing the range of attraction allows for the particles to more freely explore their local environment and favor higher number of neighbours with larger distances. As a result, on average half a particle's neighbours fall outside the immediate range of r_c = 0.1. However, for strongly interacting systems systems, the attractive force dominates and particles are generally contained within closer separation distances, and thus a similar trend to the overall number of bonds in Fig. 3(a) is observed.

These local arrangements are more evident when distribution of coordination number is considered rather than its ensemble-averaged value. Coordination number distributions at the final configurations are shown in Fig. 3(c) and (d) for the same bond definitions as in Fig. 3(a) and (b) respectively. When employing a variable cutoff, a uni-modal distribution for small attraction ranges (ξ < 0.6) and a bimodal distribution for longer ranges (ξ ≥ 0.6) are observed (Fig. 3(c)). While the distribution generally broadens and shifts towards higher coordination numbers [regardless of the interaction strength] as the range increases, for the longest range of attraction a population of particle with emerges. Considering the fact that we simulate an ideally monodispersed system of particles, emergence of within the coordination number distribution suggests that within the bulk of large particle clusters, colloids potentially form ordered structures in which the coordination number can be significantly larger than the gel state. However, these ordered arrays differ from a crystalline domain, evident from the distributions using the fixed cutoff (Fig. 3(d)). Disappearance of the clear peaks at at short separation distances suggest that while some extent of order is formed, the particles remain mobile to explore the lowest energy states and are not strictly conformed to crystalline domains. Interestingly, in high strength systems (u₀ = 12k_BT), the population with the highest coordination number increases as the attraction range increases, but for low strength systems this population decreases as the range increases.

With a quantitative measure of the structure at the [microscale] particle-level 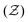and at the [macroscale] system size (LCC), we then examined the cluster-level [mesoscale] structure by analyzing the static structure factor S(q) as a function of wave number q at low angles, defined as:²⁵

where ρ is the particle number density and g(r) is pair-correlation function. g(r) for different attraction ranges in both systems are shown in the Fig. 7. A noticeable peak appears in the range of 0.1 < q < 0.4 for all strengths and ranges, indicating an abundance of large aggregates and network structures with a length scale falling within 16a < l < 60a (Fig. 4(a)). Notably, the peak intensity increases with a greater attraction range, which is associated with both the degree of correlation between clusters and the number of particles in these clusters.²⁶ The q-value at which the peak is observed is an indicator of the size of clusters, however, the peak intensity itself is a measure of the relative population of such clusters within the overall structure. As such, the heightened intensities of the structure factor at small q values suggests the presence of somewhat more dominant clusters in low-strength systems than those observed with higher strength. Additionally, for small attraction ranges and high strengths we observe a slow decay of the structure factor at low values of q. This indicates a higher level of structural homogeneity associated specifically with short-ranged strong interactions. To quantify this power-law decay, we compute the fractal dimension D_f using the box-counting technique. The fractal dimension is larger at small attraction strengths compared to high attraction strengths, suggesting a more ramified structure at high strength (Fig. 4(b)). Furthermore, we observe that the fractal dimension increases with increasing attraction range, indicating more compact clusters at larger attraction ranges (Fig. 4).

Fig. 4 (a) Structure factor S(q) as function of q for final structures at the volume fraction of ϕ = 0.1 for weakly (u₀ = 6k_BT) and strongly (u₀ = 12k_BT) attractive colloids, (b) fractal dimension D_f as function of attraction range ξ for both systems.

In addition to quantifying the colloidal domains at the cluster-level, we also characterize them based on the distribution of interstitial void sizes within the final structure using a method introduced by Gubbins and colleagues.²⁷ This method involves selecting an arbitrary point in the void space and then determining the largest possible radius of a sphere that can encapsulate that point without overlapping with any other particle. Overall, for both attraction systems, we find that the pore size distribution becomes broader, and the average pore size increases as the attraction range increases (Fig. 5). At short ranges, strong interactions result in smaller pore sizes compared to weaker interactions; nonetheless, as the range increases and the system [micro]phase separates into large particle clusters, the pore size distribution becomes insensitive to the strength of attraction between colloids. Furthermore, we notice a tiny initial peak at small pore sizes relative to individual particles, which represents pores contained within clusters (intra-pores within the cluster). With increase in the attraction range, clusters become denser, resulting in a higher number of these very small pores within the cluster and consequently causing the initial dip in the distribution.

Fig. 5 (a) Distribution of pore sizes, (b) maximum pore size, and (c) average pore size as function of attraction range in final structures, obtained at the volume fraction of ϕ = 0.1, for weakly (u₀ = 6k_BT) and strongly (u₀ = 12k_BT) attractive colloids, all measured in particle size units. The inset in (b) highlights the largest spherical pore that fits within the void space.

Having characterized the resulting structures at different length-scales, we finally re-construct the gelation phase diagram based on the system's state variables, with a special attention to larger ranges of attraction (Fig. 6). Lu's pioneering work depicted gelation phase boundary as a monotonic function of the attraction range, in which at the very short range gels are formed at the higher attraction strengths and volume fractions, quickly decaying with increasing the fraction of solid and/or the strength of attraction. However, our results here clearly indicate a non-monotonic trend, at longer ranges of attraction [not studied by Lu et al.]. While increasing the strength of attraction at the very short range, for a fixed volume fraction of solids results in a gel to form, for very dilute systems (ϕ = 0.05) with long-range attraction (ξ ≥ 0.6), only a fluid of clusters is observed regardless of the attraction strength.

Fig. 6 (a) u₀ − ξ − ϕ state diagram for colloidal gelation. Symbols represent two different phases observed in the system: gel (circle) and micro-phase separated fluids of clusters (triangle). Blue surface is drawn to guide the eye. Gels are above the surface and phase separation is below the surface. Phase boundaries for volume fractions ϕ = (b) 0.05 and (c) 0.1. Data points for very small attraction ranges (ξ < 0.05) have been obtained from Lu et al.⁷

4 Conclusions

In this study, the effect of interaction range on the microstructure and phase behavior in both weak and strong attractive colloidal systems was systematically studied. Gelation, generally defined as the formation of a percolated network of colloids spanning the entire system, was found to occur significantly faster for strongly attractive systems to weak ones; nonetheless, the range of interaction did not result in any observable changes to the percolation transition. Regardless of the strength of interaction between colloids, longer ranges result in coarsening of the structure which can be directly characterized through structure factor and pore size distributions in the system. At these intermediate length-scales, longer ranges of attraction systematically resulted in coarser structures with pore sizes twice larger than ones found at short-range attractions. Additionally, for the very long ranges of interactions, the overall structure as well as kinetics of self-assembly become insensitive to the strength of attraction, as the final morphology consists of isolated large particulate clusters. Within these large clusters, colloids can explore the energy landscape by finding more neighbours and hence lowering their overall energies. This results in emergence of particle populations with , indicative of order formation within the bulk of larger clusters. Finally, we constructed a gelation phase diagram based on system's state variables, similar to that of Lu et al.,⁷ with a particular focus on the longer ranges of attraction. Our revisited gelation phase diagram clearly indicates a non-monotonic role played by the range of attraction. At both extreme ends of the attraction range axis (very short or very long) gelation is only possible at higher volume fractions and/or attraction strengths. The difference however is that long range attractions promote formation of larger scale clusters, and very short range attractions generally result in isolated so-called monomeric colloidal systems.

Our results suggest that even if a known size of polymer is introduced in colloid–polymer mixtures, polymer depletents with broader size polydispersity can directly result in enhanced structural heterogeneities. The role of attraction range and the ability to directly control them also present an opportunity for new mesostructural design pathways for targeted hierarchical properties. In our study, we modeled colloid interactions using pairwise additive Morse potential, while ignoring hydrodynamic interactions, and more importantly the non-central bending potentials induced through three-body interactions.^12,28 It is well-understood that specific non-central interactions can lead to lower gelation percolation thresholds, and different mechanics of the overall structure,²⁹ and such interactions can be directly modeled using anisotropic effective interactions^9,12,30 resulting in a more realistic view of the gel structure depending on the nature of particle-level interactions. Nonetheless, the general observations of transitioning to fluids of clusters at longer ranges of attraction here are expected to hold for such non-central interactions. In our future work, we aim to explore how these anisotropic interactions and hydrodynamic effects may influence our findings.

Conflicts of interest

There are no conflicts to declare.

Appendix

Pair correlation distribution

Fig. 7 depicts how the pair-correlation distribution g(r) is affected by attraction range for both attraction strength systems. Each curve has been shifted vertically for better visualization. In both systems, we notice a similar pattern: g(r) exhibits a sharp peak at a short distance (r ∼ 2a), indicating a high likelihood of finding particles close to each other at this distance. As the attraction range increases, the intensity of this peak decreases. The first minimum of g(r), which occurs between r ∼ 2a–3a, shifts slightly towards larger distances as the attraction range increases. This minimum is significant as it reflects the effective range of attraction between particles. Notably, for very small attraction range ξ = 0.1, we observe considerable noise in the data, suggesting a lack of structural order. As we move to larger distances, g(r) approaches 1, indicating a more random distribution of particles like a simple fluid.

Fig. 7 Pair correlation distributions for different attraction ranges ξ at two different attraction strengths u₀ (a) 6 and (b) 12. Curves have been shifted vertically for better visualization.

Acknowledgements

This work was supported by the National Science Foundation (CBET-2118962 and CBET-2104869). Computational resources were generously provided by the Massachusetts Green High-Performance Computing Center in Holyoke, MA.

Notes and references

1. E. Dickinson, An introduction to food colloids, Oxford University Press, 1992.
2. E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101.
3. S. Manley, H. Wyss, K. Miyazaki, J. Conrad, V. Trappe, L. Kaufman, D. Reichman and D. Weitz, Phys. Rev. Lett., 2005, 95, 238302.
4. M. A. Miller, R. Blaak, C. N. Lumb and J.-P. Hansen, J. Chem. Phys., 2009, 130, 114507.
5. H. Tsurusawa, S. Arai and H. Tanaka, Sci. Adv., 2020, 6, eabb8107.
6. E. Dickinson, Adv. Colloid Interface Sci., 2013, 199, 114–127.
7. P. J. Lu, J. C. Conrad, H. M. Wyss, A. B. Schofield and D. A. Weitz, Phys. Rev. Lett., 2006, 96, 028306.
8. P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503.
9. J. Colombo and E. Del Gado, Soft Matter, 2014, 10, 4003–4015.
10. R. N. Zia, B. J. Landrum and W. B. Russel, J. Rheol., 2014, 58, 1121–1157.
11. S. Jamali, R. C. Armstrong and G. H. McKinley, Mater. Today Adv., 2020, 5, 100026.
12. M. Bantawa, B. Keshavarz, M. Geri, M. Bouzid, T. Divoux, G. H. McKinley and E. Del Gado, Nat. Phys., 2023, 19, 1178–1184.
13. F. Sciortino, P. Tartaglia and E. Zaccarelli, J. Phys. Chem. B, 2005, 109, 21942–21953.
14. A. I. Campbell, V. J. Anderson, J. S. van Duijneveldt and P. Bartlett, Phys. Rev. Lett., 2005, 94, 208301.
15. M. B. Sweatman, R. Fartaria and L. Lue, J. Chem. Phys., 2014, 140, 124508.
16. Z. Varga and J. Swan, Soft Matter, 2016, 12, 7670–7681.
17. A. Zhang and E. S. Shaqfeh, J. Rheol., 2023, 67, 499–516.
18. A. Zhang and E. S. Shaqfeh, J. Rheol., 2023, 67, 517–540.
19. G. Foffi, G. D. McCullagh, A. Lawlor, E. Zaccarelli, K. A. Dawson, F. Sciortino, P. Tartaglia, D. Pini and G. Stell, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031407.
20. M. Dijkstra, R. van Roij, R. Roth and A. Fortini, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041404.
21. L. J. Teece, M. A. Faers and P. Bartlett, Soft Matter, 2011, 7, 1341–1351.
22. D. Fu, Y. Li and J. Wu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011403.
23. J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363.
24. S. Jamali, G. H. McKinley and R. C. Armstrong, Phys. Rev. Lett., 2017, 118, 048003.
25. A. Filipponi, J. Phys.: Condens. Matter, 1994, 6, 8415.
26. C. Muzny, B. Butler and H. Hanley, MRS Online Proc. Libr., 1995, 407, 87.
27. L. D. Gelb and K. Gubbins, Langmuir, 1999, 15, 305–308.
28. F. Bonacci, X. Chateau, E. M. Furst, J. Fusier, J. Goyon and A. Lematre, Nat. Mater., 2020, 19, 775–780.
29. F. J. Müller, L. Isa and J. Vermant, Nat. Commun., 2023, 14, 5309.
30. S. Saw, N. L. Ellegaard, W. Kob and S. Sastry, Phys. Rev. Lett., 2009, 103, 248305.

---