 Open Access Article
Open Access ArticleNonwoven-fabric-based microfluidic devices for solution viscosity measurements†
Mayumi Otoba
Uno
 *a,
Mariko
Omori
a and
Kenji
Sakamoto
b
*a,
Mariko
Omori
a and
Kenji
Sakamoto
b
aOsaka Research Institute of Science and Technology, 2-7-1 Ayumino, Izumi, Osaka, Japan. E-mail: uno@orist.jp
bDepartment of Intelligent and Control Systems, Kyushu Institute of Technology, 680-4 Kawazu, Iizuka, Fukuoka 820-8502, Japan
First published on 16th August 2024
Abstract
Microfluidic chips designed to measure viscosity with extremely small amounts of liquids are expected to examine biological fluids, such as for the prediction of disease states and stress assessment, and for the evaluation of the physical properties of novel synthetic materials. However, these devices typically require sample volumes of several tens of μL or more, which has limitations when collecting biological samples from individuals nearly non-invasively. In this study, we fabricated a flow channel on a nonwoven fabric substrate with tailored hydrophilic and hydrophobic properties to enable viscosity measurements with the small-volume flow of aqueous solutions, such as 3 μL of saline. By measuring the electrical conductivity of the liquid using comb-shaped printed electrodes in contact with the flow path, we quantified the time and distance of liquid flow driven by capillary action to estimate solution viscosity. Using a mixture of glycerol and saline solution with varying viscosities, while maintaining a constant ion concentration, we demonstrated the capability to assess the relative viscosity of solutions. This was achieved by evaluating the correlation coefficient between the flow time and distance, and the net electrical conductivity, which is influenced by the viscosity and ion concentration of the solutions. This study lays the groundwork for developing a low-cost technique to measure the viscosity of solutions with a few μL, offering potential for routine health monitoring and disease prevention.
1 Introduction
In big data utilization, there exists a strong need for a facile low-cost sensing technology that can be monitored on a daily basis, in addition to expensive and high-precision measurement technology. In this respect, microfluidic paper-based analytical devices (μPADs)1–11 show great potential to be used as diagnostic devices because of their numerous advantages, such as low cost, disposability, easy availability, minute liquid volume, and not requiring external micropumps due to natural capillary action. These advantages can be leveraged in fields such as distributed health care, preventive medicine and early detection of diseases, inspection of food safety and spoilage, and monitoring plant growth in agriculture.Martinez et al. reported μPADs to create simple and cost-effective diagnostic chips.1,2 These devices were fabricated by patterning hydrophobic barriers on paper to form microfluidic channels, facilitating tests for substances such as glucose and protein in synthetic urine. Various devices have been developed using the μPADs technology, such as electrochemical devices,3 immunoassays,4 pH indicators,5 gas sensors,6 electrophoretic separation,7 fluid mixing devices,8 and tests for food chemistry.9 Recent advancements have integrated μPADs with smartphone technology10 for more accessible diagnostics and have incorporated artificial intelligence into point-of-care testing (PoCT) devices.11 Fabrication techniques for μPADs include resin photolithography,1 wax printing,12 inkjet printing,13 and origami-based methods,14 which involve paper folding and layering to create three-dimensional structures.2 These methods have been extensively reviewed in the literature.15
Previously reported μPADs have been vigorously studied for chemical and biosensors; moreover, test devices for physical properties, such as electrical conductivity and viscosity, have also been reported. The viscosity and electrical conductivity of liquids provide information on the ionic concentration and content of the liquid and can therefore be applied to the testing of biological fluids and used in medical diagnostics and food chemistry. For example, PoCT devices for blood cholesterol and triglyceride assays,16 methods for measuring blood viscosity,17 the relationship between saliva viscosity and stress levels18 and the correlation between saliva conductivity and dehydration and chronic kidney disease19 have been investigated. Additionally, it has been demonstrated that the risk levels of heat stroke can be determined by monitoring the ionic concentration of sweat.20
Conventional viscosity evaluation methods include the Ostwald viscometer, rotational methods and electro magnetically spinning method (EMS)21 viscometers. In principle, these measurements require a liquid volume of 0.3–10 ml or more. In contrast, viscosity measurements using μPADs have been reported,22–27 where the fluid is made to flow through a channel by capillary action, and in much smaller quantities of a few 10–100 μL. They are based on the Lucas–Washburn equation, which considers the time taken for a fluid to travel a certain distance by capillary action to be proportional to its viscosity. Rayaprolu et al. reported μPADs for fluid viscosity measurements by recording the time taken by the liquid to travel between two points, at 12–20 μL liquid volume.22 The relationship between protein folding and viscosity has also been discussed. Jang et al. proposed a fast flow μPAD23 to measure fluid viscosity using air gaps made from two papers held together by double-sided adhesives; however, the required volume of liquid was 100 μL. Gautam et al. used sample volumes of 30–70 μL and have demonstrated viscometry of blood plasma using μPADs technology.24
However, all of these μPADs still face limitations: one is that the measurements of the time and position of the start and end points of fluid flow have been performed by camera or visual inspection, which requires manual measurements or a separate imaging device, and are not completed by signal outputs from μPADs alone. It is difficult to measure transparent fluids such as saliva and sap, from optical measurements, and the measurements have been reported using a dye mixture in the sample liquid. Puneeth et al. demonstrated a system with two electrodes at the start and end points to measure capillary action, which automatically detects the time when the liquid reaches the end point applying a DC voltage, with a liquid volume of 50–100 μL.25 However, their process also requires synchronisation of the timing of the power supply and the start of the liquid flow and their manual input, and does not allow viscosity calculation from electrical measurements alone. Another challenge for viscosity measurement is the need for good and stable wetting of the test samples and the paper substrate, which currently requires several pre-wetting treatments of the paper before conducting the test.25,26 It has been reported that wetting treatments for eight times26 or several times25 are required before actual tests to obtain stable results. When measuring biological fluids such as saliva and blood, or liquids in plants, an innovative, easy-to-use testing device that can measure as little as a drop of blood obtained by pricking a finger with a needle, i.e., 10 μL or less, is urgently needed. A device that does not require camera imaging or manual operation is expected to be a revolutionary testing device that is easy to disseminate to the general public.
In this study, we introduce μPADs utilizing nonwoven sheets (μPADs-NW) that can perform electrical measurements and evaluate solution viscosity using extremely low fluid volumes, approximately 3 μL or less. Generally, the term ‘paper’ refers to materials composed of short cellulose fibres; however, in this context, it involves nonwoven sheets fabricated from polymeric long fibres. The viscosity was measured based on the same principle as in the reported method, relationship between time and distance as the liquid travels by capillary action, and a device designed to perform the same measurement under four different conditions. Viscosity was estimated independently from the measured conductivity values, based on the empirical rule that the product of the viscosity and conductivity of a liquid is constant. We propose that these two methods, obtained from the same measurements, can be used to estimate the viscosity of liquids for which the viscosity and ionic concentration are unknown. Although these methods need to be calibrated with a liquid of known viscosity, there is no need for a human to set up external equipment, such as a camera, which is completed only by electrical measurements, to measure the starting and ending points. When measuring the electric conductivity of a liquid, the problem with applying a DC voltage is that the current value changes over time because the concentration of the ions that compose the conductivity changes with time. Therefore, in this study, an AC voltage was applied to measure conductivity.
Conventional μPADs encounter challenges in creating flow channels within hydrophilic materials such as filter paper that has been wetted several times for stable results. In our approach, a section of the inherently hydrophobic nonwoven sheet is modified to become hydrophilic, serving as the flow channel. This hydrophilic region is generated by exposing the designated channel area to vacuum ultraviolet (VUV) light through a photomask only on the flow channel.28 Subsequently, microfluidic channels capable of conducting aqueous solutions (e.g., saline) are fabricated. By integrating comb-shaped printed silver electrodes adjacent to these channels, we measured the electrical conductivity across the electrodes and monitored the conductivity of the solutions as they were flowing, thereby measuring their permeation rate four times using four channels through capillary action. From the relationship between the time and distance the solution penetrates, we determined that the viscosity of glycerol (glycerine)-mixed saline solutions can be estimated within a range of 0.8–6.0 mPa s. Given that the hydrophilicity induced by VUV light exposure is temporary, we also assessed the durability of this modification.
This study offers a promising technique for assessing the viscosity of liquids in minute volumes. We expect that this technology will be beneficial for health monitoring and agricultural applications that involve the measurement of small samples of liquids as it offers a less burdensome and cost-effective alternative for users.
2 Materials and methods
2.1 Selection of nonwoven fabrics suitable for liquid flow
To identify suitable nonwoven fabrics for the construction of microfluidic devices that facilitate the flow of aqueous solutions, we conducted experiments to evaluate the controllability of hydrophobicity and hydrophilicity in various materials, including the characteristics of nonwoven sheets.In a preliminary experiment, we irradiated different polymer films with VUV light using a partially transparent photomask and measured the water contact angles before and after irradiation. The polymers tested included Lumirror® #50-T60 (polyester, PET) from Toray Industries, Inc., Japan; RAYFAN® 1401 (nylon) from Toray Industries, Inc., Japan; Vecstar™ CTF-25 (polyarylate, PAR) from Kuraray Corp., Japan; and TORAYFAN® ZK207 (polypropylene, PP) from Toray Industries, Inc., Japan. Subsequently, we selected nonwoven sheets made from polymers that exhibited a shift to hydrophilicity post-VUV irradiation and measured their water contact angles in a similar manner. The nonwoven fabrics tested included ELTAS-PET™ E05070 (PET) from Asahi-Kasei Co., Ltd., Japan; ELTAS-Nylon™ (nylon) from Asahi-Kasei Co., Ltd., Japan; VECRUS™ (PAR) from Kuraray, Japan; and ELTAS-PP™ P03030 (PP) from Asahi-Kasei Co., Ltd., Japan.
The irradiation was performed using a 172 nm wavelength system (M.D.COM Inc., Japan) through a 1.2 mm-thick transparent quartz glass, which corresponds to the thickness of the mask pattern used in subsequent experiments. The quartz mask was positioned 7 mm from the lamp surface, with a lamp intensity of 70 mW cm−2 at the surface. The integral intensity was adjusted by varying the irradiation duration. Water contact angles were measured at three points on the polymer sheets and five points on the nonwoven sheets using a contact angle meter (LSE-ME3; Nick Co., Japan). The results including mean values and variations are presented.
A photomask coated with a chromium (Cr) film on quartz was utilized to pattern VUV light radiation. The Cr film was etched to create transparent areas. Dumbbell-shaped flow-channel areas were fabricated with varying channel widths to facilitate capillary action of the liquid. The patterned mask was placed in direct contact with the sample and subjected to repeated sweeps and irradiations with VUV light under previously described conditions. Thereafter, 3.0 μL of ultrapure water containing 0.26 wt% Brilliant blue FCF (FUJIFILM Wako Pure Chemical Corp., Japan) was deposited onto one end of the dumbbell, and the time required for the water to travel a specified distance was measured using a timer. This procedure was replicated three times with different samples to assess the consistency of penetration speed across various channel widths.
2.2 Fabrication of μPADs-NW
To measure the electrical conductivity of a solution, a device was designed (Fig. 1A) comprising two comb-shaped electrodes facing each other, connected by a hydrophilic channel. As the conductive liquid traversed one of the comb-shaped electrodes, the resistance between the electrodes decreased, enabling the measurement of the time required for the liquid to traverse a predetermined distance. Four channels bridging the comb electrodes were provided, starting with the first channel, Ch. 1, Ch. 2, Ch. 3, and Ch. 4. The channel width was 1 mm, and the length of each channel was 5 mm, 3 mm, 2.5 mm and 1 mm, respectively, in order from Ch. 1. The channel lengths were gradually shortened on the side where the flow proceeds because the resistance between the comb electrodes was gradually reduced and the resistance change should be as large as possible. The width of the comb teeth part of the comb electrodes was set to 300 μm. Before pattern designing, the width of the comb teeth section was screen printed at different widths of 300 μm, 250 μm, 200 μm, 150 μm, and 100 μm to check for wire breaks. | ||
| Fig. 1 Device design and fabrication processes. (A) Design drawing, (B) fabrication processes (upper) and device photos (lower) of μPAD-NWs, and (C) photograph of the measurement setup. | ||
The device fabrication process (Fig. 1B) was initiated with the screen printing of comb-shaped electrode patterns using silver paste (ELEPASTE AF4820, Taiyo-Ink Co., Ltd, Japan) on a PAR-based melt-blown nonwoven fabric (VECRUS™) via screen printing. Subsequently, a hydrophilic area was created by irradiating VUV light from the opposite side of the silver patterns using a Cr mask with a flow-path pattern, under the same conditions described previously. The VUV light was irradiated from the rear of the silver patterns to prevent obstruction by the silver.
2.3 Methods of viscosity measurement
Two methods were used to estimate viscosity: one measures the time and distance that the liquid travels through the channel via capillary action, and the other is inferred from the conductivity of the sample solution based on Walden's law when the ionic concentration of the solution is constant. Ultrapure water, physiological saline solution (0.9 wt% saline), and saline solutions mixed with glycerine (0–50 wt%, Sakamoto Chemical, Japan) were utilized as test samples.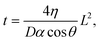 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). In this work, four channels for measuring the time and distance of liquid flow were installed to enable simultaneous measurement of the four conditions of time and distance in a single channel (Fig. 1A). When the sample liquid passes through one of the comb electrodes, the combined resistance Rp between the two comb electrodes decreases significantly due to the addition of a new resistive element in parallel. Rp was monitored against time, and the time at which this sudden drop in resistance occurred was read as the time the liquid passed through.
θ). In this work, four channels for measuring the time and distance of liquid flow were installed to enable simultaneous measurement of the four conditions of time and distance in a single channel (Fig. 1A). When the sample liquid passes through one of the comb electrodes, the combined resistance Rp between the two comb electrodes decreases significantly due to the addition of a new resistive element in parallel. Rp was monitored against time, and the time at which this sudden drop in resistance occurred was read as the time the liquid passed through.
Eqn (1) can be written as follows for the device design shown in Fig. 1A:
| ti − t1 = A(Li2 − L12), | (2) |
| ti = ALi2 − AL12, | (3) |
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α
α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is discussed. To verify the obtained values, the viscosity of the same samples was also measured using glass capillaries as flow channels under different pressures and derived from the relationship between the time and distance the liquid travelled.30
θ is discussed. To verify the obtained values, the viscosity of the same samples was also measured using glass capillaries as flow channels under different pressures and derived from the relationship between the time and distance the liquid travelled.30
| ση = k, | (5) |
The experimental setup included a nonwoven sheet covered with a silicone resin sheet, except for the flow channel. Both the upper and lower parts of the setup were completely enclosed with a PET sheet. Sample liquid was dropped manually using a micropipette. Once the sample liquid was introduced through the inlet port, the port was sealed with the PET sheet to prevent evaporation. The same measurements were made for three devices from different lots and the standard deviations are indicated by error bars. All experiments were conducted in a clean room, maintained at a temperature of 22 ± 1 °C and a relative humidity of 60 ± 10%.
2.4 SEM observation of nonwoven sheets and μPADs-NW
The surface and cross-sectional profiles of the fabricated μPADs-NW were observed using a low-vacuum scanning electron microscope (SEM) (TM3030PLUS; Hitachi, Japan) at an acceleration voltage of 15 kV.2.5 Determination of the shelf life of flow channel hydrophilicity
To examine the durability of hydrophilicity in the channel sections, the change in contact angle on PAR nonwoven fabrics irradiated with VUV light for 60 s was measured. This was conducted similarly to previous experiments, under three different storage temperature conditions: (1) in a clean room at 21 ± 1 °C (RT: room temperature), (2) in a refrigerator at 6 ± 2 °C, and (3) in a freezer ranging from −20 °C to −5 °C. The water contact angle was recorded at intervals of 1 h, 3 h, 6 h, 1 d, 3 d, 7 d and 10 d post-irradiation.3 Results and discussion
3.1 Fabrication of μPADs-NW and flow validation
For all tested polymer films, except PP, the surfaces transitioned from hydrophobic to hydrophilic after VUV light exposure, as illustrated by a photograph of a water droplet on a PAR film before and after 60 s of VUV light exposure (Fig. 2A). The PP film did not exhibit hydrophilicity post-irradiation, possibly because of its low VUV light absorption,32 attributed to its lack of oxygen content—materials rich in oxygen atoms typically have higher VUV light absorption. The results for water contact angles on films and nonwoven fabrics, both before and after VUV light irradiation, for several materials are listed in Table 1. All materials exhibited water repellence on the films, which was more pronounced on the nonwoven sheets made from the same materials, exhibiting a contact angle of 110° or higher.| Material | Film | Nonwoven sheet | ||
|---|---|---|---|---|
| As is (°) | As is (°) | After VUV irradiatione (°) | Manufacture, model number | |
| a Lumirror® #50-T60, Toray, Japan. b RAYFAN® 1401, Toray, Japan. c Vecstar™ CTF-25, Kuraray Corp., Japan. d TORAYFAN® ZK207, Toray, Japan. e VUV light irradiation time: 60 s. | ||||
| PET | 92.1 ± 0.5a | 130.0 ± 2.6 | <10 | Asahi Kasei Corp., ELTAS PET E05070 |
| Nylon | 87.2 ± 0.8b | 112.4 ± 2.2 | <10 | Asahi Kasei Corp., ELTAS Nylon N05070 |
| PAR | 98.9 ± 0.5c | 119.8 ± 4.3 | 20.0 ± 1.1 | Kuraray Co., Ltd., VECRUS™ |
| PP | 102.0 ± 2.1d | 132.7 ± 5.0 | 123.5 ± 4.1 | Asahi Kasei Corp., ELTAS PP P03030 |
The hydrophobicity of the nonwoven fabric was found to be greater than that of films made from the same hydrophobic material. Similar to the lotus leaf phenomenon,33 this effect is ascribed to the microscale voids and fibres that create complex structures on the surface of the fabric, thereby enhancing its hydrophobic properties. Following VUV light irradiation, nonwoven PET, nylon, and PAR exhibited significant hydrophilicity, with a contact angle of 30° or lower. Consequently, hydrophilic and hydrophobic regions can be patterned on the surface of a nonwoven fabric without any coatings, such as fluorine-based materials. The increase in hydrophilicity post-irradiation can be attributed to the breaking of chemical bonds on the surface, leading to the formation of –OH groups on the dangling bonds, as previously confirmed by experiments.34 The PAR nonwoven sheet which is not embossed and relatively uniform, was selected for use in microfluidic devices. The uniformity of hydrophilicity across the sheet was assessed by varying the VUV light irradiation time (as portrayed in Fig. 2D). Following 60 s of irradiation, the variation in hydrophilicity by location was minimised, achieving relatively uniform hydrophilicity as demonstrated in Fig. 2B and D.
To investigate whether the treated hydrophilic region could be used as a microfluidic channel, the flow rate of water was measured at various channel widths using a PAR nonwoven sheet, as depicted in Fig. 3. The narrower the channel width, the longer the flow time. Lot-to-lot variation was not significant in the range of the channel widths narrowing down to 1 mm, while the variation was rather large at a channel width of 0.5 mm, and with 0.2 mm, the liquid could not flow to a point 12.5 mm in length. This is probably because the walls of the channel are hydrophobic; consequently, the narrower the channel width, the greater the influence of the walls, inhibiting the flow of aqueous solutions with poor affinity to the hydrophobic walls. The water flowed for approximately 7.7 s and 21.7 s in average to the points located 7.5 mm and 12.5 mm away, respectively, with a channel width of 1 mm, which is in close agreement with the t ∝ L2 relationship described in eqn (1). Fig. 3C shows a time-lapse photograph of the dye water flowing through a device with electrodes fabricated with a hydrophilic channel width of 1 mm. When the channel width is 1 mm or more, the installation of several electrode patterns in this flow channel would enable the real-time measurement of the electrical conductivity of the liquid while it flows. A video of ultrapure water flowing through a 1 mm wide channel using a device with electrodes is available in ESI.†
To determine the conditions for AC measurements of saline-based solutions, a hydrophilic channel was created by irradiating VUV light only in the Ch. 1 with the width of 2 mm, and Rp was measured when filled with saline solution by varying the frequency and RMS value of the applied voltage (Fig. S1†). It can be observed that the Rp of the saline solution decreases gradually up to an AC voltage frequency of approximately 100 kHz, with a larger decrease at 200 kHz. Additionally, the Rp is constant up to an RMS voltage value of about 0.8 V, and decreases at higher voltages. In the following experiments, AC measurements were carried out with a fixed frequency of 1 kHz and an RMS voltage value of 0.5 V.
3.2 Capillary force measurements and viscosity evaluation of aqueous solutions with different viscosities
Using the fabricated μPADs-NW with comb-shaped silver electrodes and a hydrophilic pattern created through VUV light irradiation, as depicted in the bottom right photo of Fig. 1B, a 3 μL drop of physiological saline (0.9 wt% saline) was placed at the end of the flow channel. The resistance between the two electrodes was then measured in real time, as shown in Fig. 4A. The time when the liquid bridged Ch. 1 was set to zero and the elapsed time was plotted on the horizontal axis. As observed in Fig. 4A, the saline permeates the hydrophilic area via capillary action, causing the resistance to decrease each time it crosses the teeth of the comb-shaped electrodes. This allows the determination of the passage time. | ||
| Fig. 4 Results of electrical measurements and viscosity analysis. (A) Resistance change between comb electrodes during saline flow. The inset shows a magnified view before and after the liquid passes through Ch. 3. The red arrows indicate the time when the liquid has passed through one of the comb electrodes. (B) Plots of the elapsed time versus square of the distance for saline and for solutions with 20%, 40%, and 50% mixed glycerol. (C) Relationship between the slope of the graph shown in Fig. 4B and ηdP. (D) Relationship between Rp and ηdP for mixtures of saline and glycerol and sodium chloride solutions when only Ch. 1 is conducting. | ||
Once the liquid passed through the electrode, the resistance stabilized at a constant value, indicating that the liquid spread was not entirely uniform and that the contact resistance between the liquid and electrodes decreased as the contact area increased incrementally. Consequently, when Rp reached a specific value, it was considered indicative of the electrical conductivity of the channel.
The flow measurements were also performed using solutions of varying viscosities achieved by mixing 20, 40, and 50 wt% glycerol with saline. The relationship between t and L2 deduced from the conductivity measurements for all solutions is plotted in Fig. 4B, which indicates the proportionality of ti ∝ Li2. Plots where error bars are not seen contain statistical errors within the plot. This proportionality coefficient A was determined for each liquid by the least squares method. Table 2 summarises the viscosity ηdP measured with the previously reported method using glass capillaries,30 the literature values ηref,35–37 proportionality coefficient A obtained in this work and its coefficient of determination, and the viscosity ηcapil determined from ηref of saline as a calibration fluid. Viscosity values for mixtures of water and glycerol are given as reference for mixtures of saline and glycerol. ηdP was measured by varying the pressure inside the glass capillary and measuring the difference in the time taken for the liquid to travel by capillary action,30 which was consistent with the literature values.35–37ηcapil was estimated by multiplying the value of ηref of the saline solution by the ratio of the proportionality coefficient A for each glycerol mixture solution to that of the saline solution, based on eqn (4). Measurements were made using three devices from different lots and the standard deviation is shown as the error. The graph of A against the measured viscosity ηdP suggests that the coefficients A and viscosity ηdP are approximately proportional to each other (Fig. 4C). One of the reasons for the deviation is probably that a distribution occurs in the flow speed at which the liquid reaches the comb electrode, and the change in resistance is detected with the liquid that first reaches the electrode, which may lead to a smaller estimate of time t. In the case of high viscosity, this distribution may appear accentuated due to the longer arrival time. Although analysing the exact specifications of the flow path is difficult owing to the complex geometry of the capillaries, D can be approximated as a constant by assuming that the nonwoven fabric was uniform in all directions, and α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is regarded as a constant when the pressure is assumed to be constant.30 Thus, the proportionality factor A is a linear function of η, assuming the above assumptions hold, which enables the estimation of the magnitude of viscosity.
θ is regarded as a constant when the pressure is assumed to be constant.30 Thus, the proportionality factor A is a linear function of η, assuming the above assumptions hold, which enables the estimation of the magnitude of viscosity.
| Sample liquid | η ref (mPa s) | η dP (mPa s) | Measurement by capillary action | Measurement from conductivity | |||
|---|---|---|---|---|---|---|---|
| A (s mm2) | Coefficient of determination | η capil (mPa s) | R p of Ch. 1 (MΩ) | η Res (mPa s) | |||
| a Ref. 36. b Ref. 37. | |||||||
| 0.9 wt% saline | 0.891a | 0.882 ± 0.012 | 0.178 | 0.980 | — | 0.225 ± 0.0107 | — |
| +glycerol 20 wt% | (1.54)b | 1.58 ± 0.019 | 0.294 | 0.984 | 1.47 | 0.385 ± 0.0110 | 1.51 ± 0.0435 |
| +glycerol 40 wt% | (3.18)b | 3.42 ± 0.045 | 0.611 | 0.989 | 3.06 | 0.886 ± 0.00309 | 3.47 ± 0.0121 |
| +glycerol 50 wt% | (5.34)b | 6.04 ± 0.076 | 0.952 | 0.988 | 4.77 | 1.70 ± 0.0744 | 6.68 ± 0.292 |
Calculating the flow path volume in the proposed device is challenging due to the presence of randomly oriented fibres. However, we estimated this volume by incrementally adding water droplets to the hydrophilic region until the water covered the entire channel, determining the volume to be approximately 2.2 μL. Additionally, we estimated the volume of the hydrophilic area by calculating the mesh size and density of the fibres, the area of the pattern design, and the thickness of the fibres, reaching a volume of 2.0 μL, which closely aligns with the actual measurement. Accordingly, electrical conductivity measurements were performed using a minimal liquid volume on an inexpensive nonwoven fabric sheet.
The device was constructed from non-woven polymer long-fibre fabrics. To the best of the authors' knowledge, this is the first reported method for fabricating μPADs where the hydrophilic part is created via VUV irradiation using hydrophobic materials. Previously reported methods for fabricating μPADs have relied on hydrophilic materials as the substrate. Consequently, it is essential to establish a non-permeable area surrounding the channels to prevent water infiltration. This has typically required the application of photoresist, wax, or resin to form a barrier around the channel. In the devices proposed here, the inherent hydrophobic properties of nonwoven fabric are utilised, and only VUV light irradiation is required to create the channels. This process can be completed rapidly, for instance, within 60 s as demonstrated in this study, although preparation of a mask pattern is required.
Viscosity measurements were performed using a considerably smaller amount of liquid of 3 μL compared to previous microfluidic devices. By reading the change in resistance when the liquid passes through the comb electrode, the start and end points of capillary action can be determined automatically, thus eliminating the requirement for camera photography or manual switching. Thus, even transparent liquids can be measured using the present device.
3.3 Viscosity evaluation from the electrical resistance of the solution
From the same plot of conductivity measurements as in Fig. 4A, the Rp values at the same channel length for solutions with different concentrations of glycerol, with only Ch. 1 bridged, was determined from the value when Rp became constant (Table 2), and the Rp values were plotted against ηdP measured by the conventional method using a glass capillary (Fig. 4D). As observed in Fig. 4D, the measured Rp and ηdP yielded an almost linear relationship. The viscosity ηRes obtained by multiplying the value of the saline viscosity with the ratio of Rp to the saline value in each solution is shown in Table 2, which is in good agreement with the viscosity ηdP. Thus, if the η/Rp ratio at a certain temperature is calibrated, the value of η can be inferred from the Rp. For sodium chloride solutions without glycerol, the values of Ch. 1 resistance (Table S1 and Fig. S2†) versus ηdP are plotted simultaneously in Fig. 4D varying its concentration from 0.1–1.1 wt% (viscosity of pure water is employed in the plots for 0.1–0.6 wt%). Fig. 4D indicates that the Rp was properly increased when the ionic concentration was reduced without glycerol. The lower the ion concentration and the higher the resistance, the greater the variation, whereas stable measurements can be conducted at around 1 MΩ or less (Fig. S2†).In the diagnosis using biological fluids, both the viscosity (η) and the ion concentration of the solution are initially unknown. However, the two previously discussed viscosity estimation methods can be employed to estimate both parameters. Fig. 4B illustrates the relationship between time (t) and the square of the length (L2), which does not incorporate the term for ionic concentration. Consequently, the viscosity (η) can be independently determined, and the ionic concentration in the solution can be inferred from the obtained η value, the constant k in eqn (2), and the measured resistance (Rp). When a solution with a known ion concentration is used, the viscosity (η) can be estimated using both methods, allowing for cross-verification. The present findings suggest that even solutions with unknown properties demonstrate distinct capillary behaviours at varying viscosities, which can be approximately determined using the proposed microfluidic device. For measurements in actual biological fluids, the accuracy of these estimations requires further validation, and future research will involve experiments with solutions of varying ionic concentrations.
3.4 SEM observations of the flow channel
Stereo microscope images of screen-printed comb electrodes with varying the widths with 300 μm, 250 μm, 200 μm, 150 μm, and 100 μm are shown in Fig. 5A. The conduction measurements with a continuity tester on five samples showed that conduction was observed in all samples with a width of 150 microns and above. The width of the comb-teeth electrode was set to 300 μm (Fig. 5A right magnified image).SEM images that depict the top-view and cross-sectional structure of the flow device fabricated on a PAR sheet are presented in Fig. 5B and C, respectively. In the PAR-based device, the surface of the nonwoven fabric was lightly thermally bonded to prevent the separation of the multifibre, and printed silver electrodes were applied to this surface. The thickness of the flow channel was estimated to be approximately 53 μm, and the fibre diameter of the nonwoven fabric was approximately 2–3 μm, which closely aligns with the 2.6 μm specified by the manufacturer.
3.5 Self life of the hydrophilicity of flow paths
The study examined the durability of the hydrophilic state on a PAR surface, which was found to revert to its original hydrophobic state over time, as depicted in Fig. 6. Error bars in Fig. 6 show the variation of three measurements on the same nonwoven sheet. When stored in a clean room at 22 ± 1 °C (RT), the contact angle remained below 40° for up to 3 h following VUV light exposure, maintaining a consistent flow of the sample liquid. Under frozen conditions, this angle was sustained for up to 7 days. These findings indicate that the disrupted bonds on the PAR surface gradually reformed, influenced by thermal conditions. Addressing this limitation in storage life is crucial for the functionality of the device. Future studies will focus on detailed evaluations and methods to prolong hydrophilicity, such as the introduction of hydrophilic groups.4 Conclusions
A microfluidic device was successfully developed by creating a hydrophilic area on a naturally hydrophobic nonwoven fabric using VUV light irradiation and integrating a printed comb electrode pattern. The device facilitates the evaluation of electrical characteristics as an aqueous solution permeates through the hydrophilic channel. By adjusting the viscosity of the solutions through varying the saline and glycerol mix ratios, it was determined that the time (t) and the square of the permeation distance (L2) were proportional to coefficients derived from the solution viscosities. This proportionality suggests that the device can be effectively used to estimate the viscosity of liquids. Additionally, it was demonstrated that the electrical conductivity of aqueous solutions could be measured with small volumes, such as 2.2 μL, and that ionic concentration can be estimated by correlating viscosity measurements with capillary action results.This study developed microfluidic devices characterized by minimal volumes and low costs, potentially advancing affordable biochip technology for healthcare applications. Future work will focus on integrating sensing capabilities, including measurements of pH and antigen–antibody reactions.
Data availability
The data supporting this article have been included in tables in the main text and the ESI.†Author contributions
Conceptualization, M. O. U., methodology, M. O. U., M. O., K. S., formal analysis, M. O. U., data curation, M. O. U., M. O., K. S., validation, M. O. U., M. O., K. S., writing – original draft, M. O. U., writing – review and editing, M. O. U., M. O., K. S. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would thank Kuraray Corp. Ltd. for providing polyarylate nonwoven fabrics and films. The authors also thank Asahi Kasei Advance Corp. for providing PET, PP and Nylon nonwoven fabrics.Notes and references
- A. W. Martinez, S. T. Phillips, M. J. Butte and G. M. Whitesides, Angew. Chem., Int. Ed., 2007, 46, 1318 CrossRef CAS PubMed.
- A. W. Martinez, S. T. Phillips and G. M. Whitesides, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 19606 CrossRef CAS PubMed.
- W. Dungchai, O. Chailapakul and C. S. Henry, Anal. Chem., 2009, 81, 5821 CrossRef CAS PubMed; Z. Nie, C. A. Nijhuis, J. Gong, X. Chen, A. Kumachev, A. W. Martinez, M. Narovlyansky and G. M. Whitesides, Lab Chip, 2010, 10, 477 RSC; Z. Nie, F. Deiss, X. Liu, O. Akbulut and G. M. Whitesides, Lab Chip, 2010, 10, 3163 RSC.
- L. S. A. Busa, S. Mohammadi, M. Maeki, A. Ishida, H. Tani and M. Tokeshi, Analyst, 2016, 141, 6598 RSC; X. Tang, Q. Zhang, X. Ding, J. Jiang, W. Zhang and P. Li, Anal. Chim. Acta, 2019, 1078, 142 CrossRef CAS PubMed; C. Lu, S. Xu, S. Wang, T. Wang, W.-L. Wang, C. Yang and Y. Zhang, Anal. Chem., 2024, 96, 2387 CrossRef PubMed.
- N. L. Ruiz, V. F. Curto, M. M. Erenas, F. B. Lopez, D. Diamond, A. J. Palma and L. F. C. Vallvey, Anal. Chem., 2014, 86(19), 9554 CrossRef CAS PubMed; Y. Li, Y. Wang, S. Chen, Z. Wang and L. Feng, Anal. Chim. Acta, 2021, 1154, 338275 CrossRef PubMed.
- J. V. Vaghasiya, C. C. M. Martinez, K. K. Sonigara, P. Lazar and M. Pumera, Adv. Mater., 2023, 35, 2304694 CrossRef CAS PubMed.
- C. Xu, M. Zhong, L. Cai, Q. Zheng and X. Zhang, Electrophoresis, 2016, 37, 476 CrossRef CAS PubMed.
- A. R. Rezk, A. Qi, J. R. Friend, W. H. Li and L. Y. Yeo, Lab Chip, 2012, 12, 773 RSC.
- T. Li, G. Guo, H. Xing, S. Tang, H. Hu, L. Wang, X. Qian and D. Chen, Food Chem., 2023, 429, 136947 CrossRef CAS PubMed.
- T. S. Park, W. Li, K. E. McCracken and J.-Y. Yoon, Lab Chip, 2013, 13, 4832 RSC; G. Xiao, J. He, X. Chen, Y. Qiao, F. Wang, Q. Xia, L. Yu and Z. Lu, Cellulose, 2019, 26, 4553 CrossRef CAS; S. Rasheed, M. A. ul Haq, N. Ahmad, Sirajuddin and D. Hussain, Food Chem., 2023, 429, 136925 CrossRef PubMed.
- Y. Ding, J. Chen, Q. Wu, B. Fang, W. Ji, X. Li, C. Yu, X. Wang, X. Cheng, H.-D. Yu, Z. Hu, K. Uvdal, P. Li, L. Li and W. Huang, SmartMat, 2023, e1214 Search PubMed; Y. Liu, Y. Zhang, F. Long, J. Bai, Y. Huang and H. Gao, J. Food Eng., 2024, 363, 111772 CrossRef CAS.
- Y. Lu, W. Shi, L. Jiang, J. Qin and B. Lin, Electrophoresis, 2009, 30, 1497 CrossRef CAS PubMed.
- X. Li, J. Tian, G. Garnier and W. Shen, Colloids Surf., B, 2010, 76, 564 CrossRef CAS PubMed.
- L. Ge, S. Wang, X. Song, S. Ge and J. Yu, Lab Chip, 2012, 12, 3150 RSC.
- D. M. Cate, J. A. Adkins, J. Mettakoonpitak and C. S. Henry, Anal. Chem., 2015, 87, 19 CrossRef CAS PubMed; C.-T. Kung, C.-Y. Hou, Y.-N. Wang and L.-M. Fu, Sens. Actuators, B, 2019, 301, 126855 CrossRef; T. Ozer, C. McMahon and C. S. Henry, Annu. Rev. Anal. Chem., 2020, 13, 85 CrossRef PubMed.
- S. Rapi, C. Bazzini, C. Tozzetti, V. Sbolci and P. A. Modesti, Transl. Res., 2009, 153, 71 CrossRef PubMed; Y. Fu and J. Guo, IEEE Transactions on Biomedical Circuits and Systems, 2018, 12, 784 Search PubMed.
- G. D. O. Lowe, A. J. Lee, A. Rumley, J. F. Price and F. G. R. Fowkes, Br. J. Haematol., 1997, 96, 168 CrossRef CAS PubMed.
- R. T. Chatterton Jr., K. M. Vogelsong, Y. Luc, A. B. Ellman and G. A. U. Hudgens, Clin. Physiol., 1996, 16, 433 CrossRef CAS PubMed; U. M. Nater and N. Rohleder, Psychoneuroendocrinology, 2009, 34, 486 CrossRef PubMed; S. Chojnowska, I. P. Sarosiek, A. Kepka, M. Knas and N. Waszkiewicz, J. Clin. Med., 2021, 10, 517 CrossRef PubMed; J. M. Yoshizawa, C. A. Schafer, J. J. Schafer, J. J. Farrell, B. J. Paster and D. T. W. Wong, Clin. Microbiol. Rev., 2013, 26, 781 CrossRef PubMed; D. H. Hellhammer, S. Wust and B. M. Kudielka, Psychoneuroendocrinology, 2009, 34, 163 CrossRef PubMed.
- Y.-P. Lu, J.-W. Huang, I.-N. Lee, R.-C. Weng, M.-Y. Lin, J.-T. Yang and C.-T. Lin, Sci. Rep., 2019, 9, 14771 CrossRef CAS PubMed; Y. Thepchuay, R. B. R. Mesquita, D. Nacapricha and A. O. S. S. Rangel, Anal. Bioanal. Chem., 2020, 412, 3167 CrossRef PubMed.
- H. Momose, M. Takasaka, T. W. Asaka, M. Hayashi, D. Maejima, Y. Kawai and T. Ohhashi, Sci. Rep., 2023, 13, 416 CrossRef CAS PubMed; T. Glennon, C. O'Quigley, M. McCaul, G. Matzeu, S. Beirne, G. G. Wallace, F. Stroiescu, N. O'Mahoney, P. White and D. Diamond, Electroanalysis, 2016, 28, 1283 CrossRef.
- K. Sakai, T. Hirano and M. Hosoda, Appl. Phys. Express, 2010, 3, 016602 CrossRef; K. Sakai, T. Hirano and M. Hosoda, Appl. Phys. Express, 2012, 5, 036601 CrossRef.
- A. Rayaprolu, S. K. Srivastava, K. Anand, L. Bhati, A. Asthana and C. M. Rao, Anal. Chim. Acta, 2018, 1044, 86 CrossRef CAS PubMed.
- I. Jang, K. E. Berg and C. S. Henry, Sens. Actuators, B, 2020, 319, 128240 CrossRef CAS.
- N. Gautam, R. Ram, V. Bishnoi and A. Sarkar, Microfluid. Nanofluid., 2023, 27–41, 39 Search PubMed.
- S. B. Puneeth and G. Sanket, IEEE Trans. Electron Devices, 2019, 66, 3196 CAS.
- E. Elizalde, R. Urteaga and C. L. A. Berli, J. Mater. Chem., 2018, 6, 3143 Search PubMed.
- K. Sakamoto, Y. Hachiya, K. Kobayashi and K. Yoshitama, IEEJ Transactions on Sensors and Micromachines, 2023, 143, 269 CrossRef , (in Japanese).
- M. Nitani, K. Nakayama, K. Maeda, M. Omori and M. O. Uno, Org. Electron., 2019, 71, 164 CrossRef CAS.
- E. W. Washburn, Phys. Rev., 1921, 17, 273 CrossRef CAS; R. Lucas, Kolloid-Z., 1918, 23, 15 CrossRef.
- K. Sakamoto, N. Okazaki, K. Makino, Y. Osawa, N. Sanari, Y. Hachiya and K. Ohno, Jpn. J. Appl. Phys., 2022, 61, 066507 CrossRef CAS.
- P. Z. Walden, Organic solutions-and ionisation means. III. Chapter: Internal friction and its connection with conductivity, Z. Phys. Chem., 1906, 55, 207 CrossRef CAS.
- A. Holländer and J. E. K. Sapiehaan, J. Polym. Sci., Part A: Polym. Chem., 1995, 33, 2013 CrossRef.
- M. Yamamoto, N. Nishikawa, H. Mayama, Y. Nonomura, S. Yokojima, S. Nakamura and K. Uchida, Langmuir, 2015, 31, 7355 CrossRef CAS PubMed.
- K. Maeda, M. Nitani and M. Uno, Polym. J., 2020, 52, 405 CrossRef CAS.
- J. B. Segur and H. E. Oberstar, Ind. Eng. Chem., 1951, 43, 2117 CrossRef CAS.
- H. Ozbek, VISCOSITY OF AQUEOUS SODIUM CHLORIDE SOLUTIONS FROM 0 - 150oC, Lawrence Berkeley National Laboratory, 1977, Retrieved from https://escholarship.org/uc/item/3jp6n2bf37 Search PubMed.
- R. C. Ernst, C. H. Watkins and H. H. Ruwe, J. Phys. Chem., 1936, 40, 627 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sd00188e |
| This journal is © The Royal Society of Chemistry 2024 |




