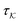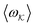Open Access Article
Open Access ArticleMori generalized master equations offer an efficient route to predict and interpret polaron transport†
Srijan
Bhattacharyya
,
Thomas
Sayer
and
Andrés
Montoya-Castillo
 *
*
Department of Chemistry, University of Colorado Boulder, Boulder, CO 80309, USA. E-mail: Andres.MontoyaCastillo@colorado.edu
First published on 23rd September 2024
Abstract
Predicting how a material's microscopic structure and dynamics determine its transport properties remains a fundamental challenge. To alleviate this task's often prohibitive computational expense, we propose a Mori-based generalized quantum master equation (GQME) to predict the frequency-resolved conductivity of small-polaron forming systems described by the dispersive Holstein model. Unlike previous GQME-based approaches to transport that scale with the system size and only give access to the DC conductivity, our method requires only one calculation and yields both the DC and AC mobilities. We further show how to easily augment our GQME with numerically accessible derivatives of the current to increase computational efficiency, collectively offering computational cost reductions of up to 90%, depending on the transport regime. Finally, we leverage our exact simulations to demonstrate the limited applicability of the celebrated and widely invoked Drude–Smith model in small-polaron forming systems. We instead introduce a cumulant-based analysis of experimentally accessible frequency data to infer the microscopic Hamiltonian parameters. This approach promises to provide valuable insights into material properties and facilitate guided design by linking macroscopic terahertz measurements to the microscopic details of small polaron-forming systems.
Introduction
Prediction of a material's intrinsic charge transport rate is a fundamental goal of theoretical chemistry and materials science, with a direct impact on energy and electronics research.1,2 While an atomistically faithful (twin) model of materials encodes all desired response coefficients, solving the requisite quantum statistical dynamics of such constructions is infeasible in all but the smallest, homogeneous systems. Instead, a minimal but physically motivated model that discards unimportant degrees of freedom, fluctuations, and couplings has become the standard tool for calculating quantities like the macroscopic transport coefficient. This is the source of the celebrated spin-boson,3,4 Holstein,5,6 Anderson,7 and Hubbard8,9 models, which have been critical in understanding processes ranging from charge transfer reactions in solution10,11 to conductivity in polymers12,13 and through nanojunctions,14–16 and even magnetism17,18 and superconductivity.19,20 After this ‘downfolding’ of atomistic complexity, one needs to solve for the dynamics of a sufficiently large model over appropriately long times to enable extraction of macroscopic observables free from finite-size artifacts. Yet, this is generally difficult or even computationally impossible with the available resources. What is more, to unlock general, microscopic insight from the dynamics of the model, one needs a physically transparent interpretation of its defining parameters and how these ultimately determine experimental observables.Even when one knows how to map an atomistic system to a physically transparent model, its large, potentially infinite-dimensional Hilbert space makes solving its quantum dynamics a significant challenge. For example, recent work using the Holstein model to understand transport properties in covalent organic frameworks resorted to employing a finite vibrational basis in order to afford their targeted system size.21 Alternatively, an exact, systematically adjustable, and often advantageous solution is to employ projection operator techniques22,23 to reduce the dimensionality and predict only the evolution of particular observables of interest,  . While performing a projection sacrifices access to arbitrary observables of the full system, one gains a low-dimensional framework to predict the dynamics of the observables of interest via the Mori–Nakajima–Zwanzig (MNZ) equation24–26
. While performing a projection sacrifices access to arbitrary observables of the full system, one gains a low-dimensional framework to predict the dynamics of the observables of interest via the Mori–Nakajima–Zwanzig (MNZ) equation24–26
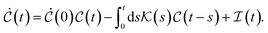 | (1) |
In this generalized quantum master equation (GQME), the evolution of the projected variables in 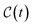 requires knowledge of the inhomogeneous term,
requires knowledge of the inhomogeneous term, 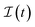 —which can be removed via the proper choice of a projection operator and is zero for us—and the memory kernel,
—which can be removed via the proper choice of a projection operator and is zero for us—and the memory kernel,  , where
, where  is the time after which
is the time after which  . By writing the projected dynamics in terms of this memory kernel, both the complex (non-Markovian) short-time behavior and the detailed balance of the long-time populations can be captured using only short-time data. A recent example of this principle is the computation of mean first passage times in the folding of large biomolecules, where only 25 ps of reference simulation data contain the information needed to model events over tens of μs, i.e., three orders of magnitude longer.27 This also shows that the GQME is a reformulation of the dynamics problem that shifts the target of dynamical computation to the memory kernel and, as such, is compatible with any dynamical method the user may wish to adopt,27–29 including approximate techniques such as surface-hopping30–32 and Ehrenfest dynamics.33,34 Yet, the cost savings of this dimensionality reduction procedure rely upon a separation of timescales between the variables of interest and those whose dynamics one does not explicitly track. Indeed, the memory kernel remains as long-lived as the slowest variables excluded from the projected space. It is thus crucial to put all the slowest degrees of freedom in the projected space, even if they are not required for the final calculation of, say, a transport coefficient.
. By writing the projected dynamics in terms of this memory kernel, both the complex (non-Markovian) short-time behavior and the detailed balance of the long-time populations can be captured using only short-time data. A recent example of this principle is the computation of mean first passage times in the folding of large biomolecules, where only 25 ps of reference simulation data contain the information needed to model events over tens of μs, i.e., three orders of magnitude longer.27 This also shows that the GQME is a reformulation of the dynamics problem that shifts the target of dynamical computation to the memory kernel and, as such, is compatible with any dynamical method the user may wish to adopt,27–29 including approximate techniques such as surface-hopping30–32 and Ehrenfest dynamics.33,34 Yet, the cost savings of this dimensionality reduction procedure rely upon a separation of timescales between the variables of interest and those whose dynamics one does not explicitly track. Indeed, the memory kernel remains as long-lived as the slowest variables excluded from the projected space. It is thus crucial to put all the slowest degrees of freedom in the projected space, even if they are not required for the final calculation of, say, a transport coefficient.
At the practical level, the choice of the projection operator has significant consequences on computational feasibility. This is because constructing  , a dynamical N × N matrix, typically requires at least N distinct simulations. For example, previous work pursued a nonequilibrium strategy of projecting onto the populations of localized electronic states to calculate polaronic transport coefficients along a model one-dimensional chain.35 This GQME formally scales with the number of sites, N.36 Here, we pursue a different strategy via the Kubo formula that relates a material's frequency-resolved conductivity to the equilibrium fluctuations of the current. This relation suggests adopting a Mori-type projection operator26 with the current operator as the only observable of interest. A remarkable consequence of this choice is that one needs only one equilibrium calculation to construct the GQME, making the method's scaling independent of system size. Our work shows that this strategy offers a compact and efficient route to encode the current response and frequency-resolved conductivity.
, a dynamical N × N matrix, typically requires at least N distinct simulations. For example, previous work pursued a nonequilibrium strategy of projecting onto the populations of localized electronic states to calculate polaronic transport coefficients along a model one-dimensional chain.35 This GQME formally scales with the number of sites, N.36 Here, we pursue a different strategy via the Kubo formula that relates a material's frequency-resolved conductivity to the equilibrium fluctuations of the current. This relation suggests adopting a Mori-type projection operator26 with the current operator as the only observable of interest. A remarkable consequence of this choice is that one needs only one equilibrium calculation to construct the GQME, making the method's scaling independent of system size. Our work shows that this strategy offers a compact and efficient route to encode the current response and frequency-resolved conductivity.
Why has it taken until now to bridge the Kubo formalism with Mori–Zwanzig theory for electrical conductivity predictions in polaron-forming materials? While path integral simulations on the ground electronic state have become mainstream,37–43 calculating equilibrium time correlation functions of quantum mechanical systems with nonadiabatic effects remains a fundamental challenge. The challenge can be broken down into two problems. The first centers on obtaining a sufficiently accurate representation of the correlated canonical density of the system, and the second lies in generating the subsequent dynamics. A variety of schemes have emerged to tackle these problems, including path integrals,44–47 semiclassics,48–51 and density matrix renormalization group.52–54 We exploit recent algorithmic advances55,56 that have enabled the calculation of these correlation functions using the hierarchical equations of motion (HEOM).57
The benefits of using the current as the sole projected quantity surpass merely practical considerations. Although non-equilibrium approaches, like population relaxation, are popular and can offer a view of the full relaxation to equilibrium,35,58 they are limited to the zero frequency component of the transport coefficient (i.e., the DC mobility). In contrast, the current autocorrelation function, CJJ, encodes the full dynamical conductivity,
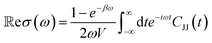 | (2) |
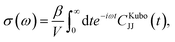 | (3) |
To investigate the advantages of the Mori approach, we employ HEOM to generate numerically exact dynamics of a physically transparent model of polaron formation and transport: the dispersive Holstein Hamiltonian. With our CJJ simulations, which determine σ(ω), we also test the applicability of the Drude–Smith model to small polaron-forming materials and find that it does not offer a satisfying fit. As an alternative, we introduce a frequency-space analysis that reveals a simple relationship between the cumulants of memory function and the parameters of the Hamiltonian that generated it, offering a route to map experimental results directly onto a microscopic Hamiltonian. While we focus on exact quantum dynamics as a means to illustrate our approach for predicting and elucidating polaron transport, our findings are broadly applicable and stand to benefit the calculation of general transport coefficients and systems, whether using quantum or classical dynamics, including ab initio molecular dynamics.
Theory and method
The Holstein Hamiltonian has been extensively used to predict transport in materials spanning organic crystals and polymers,13,66,67 covalent organic frameworks,68 and nanomaterials.69 It describes carriers (excitons, electrons, or holes) that move on a lattice of N sites and interact locally with their nuclear environment to form a small polaron consisting of the original electronic excitation and the material deformation it causes in its immediate environment. While the classic Holstein model assumes localized coupling to a single optical phonon mode,5,6,70 we focus on the dispersive Holstein model, which couples to a continuum of phonon modes of varying frequencies and more faithfully describes organic crystals and disordered polymers.71,72 To connect with previous studies focusing on transport in organic semiconductors,13,35,58,73 we adopt the dilute limit (one electron or hole) in a homogeneous lattice with degenerate lattice sites and only nearest-neighbor hopping, v = 50 cm−1, at a temperature of 300 K. We investigate the behavior that the model displays as one varies the strength of carrier-lattice coupling (encoded by the reorganization energy, η) and the characteristic speed at which the local lattice relaxes, encoded by frequency ωc. For additional details, see the ESI.†Our Mori-type projector focuses on the current operator, Ĵ, yielding a GQME for the current autocorrelation function (see the ESI†) in the Kubo formula, eqn (2),
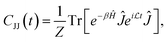 | (4) |
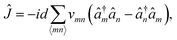 | (5) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) 0 ≡ e−βĤĴ, that one can then evolve and use to measure Ĵ at time t. See the ESI† for computational details. Despite requiring this equilibration step, we show that the protocol offers efficiency gains.
0 ≡ e−βĤĴ, that one can then evolve and use to measure Ĵ at time t. See the ESI† for computational details. Despite requiring this equilibration step, we show that the protocol offers efficiency gains.
Results
We illustrate the performance of the Mori-type GQME for a dispersive Holstein ring. To compare fairly across methods, we converge each protocol to the macroscopic size limit with the same parameters η/v = 6.26, ωc/v = 0.82, which we choose to align with previous work on organic semiconductors.58,73Fig. 1 shows the size dependence of the DC mobility given by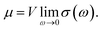 | (6) |
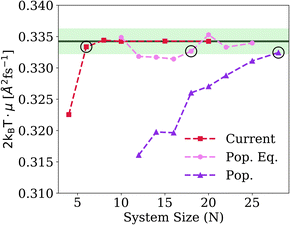 | ||
| Fig. 1 Convergence of μ with system size for the three methods considered and η/v = 6.26 and ωc/v = 0.82. We take the converged value to be given by the current-based Mori GQME for N = 20, and allow ±0.002 precision error (green shaded region). We mark the point where each method enters—and stays within—this region with circles. The population methods have no data for low N since finite size effects preclude a plateau in dMSD(t)/dt used to identify diffusive motion (see ref. 58 for a full discussion). | ||
For this parameter regime, the Mori GQME requires only N = 6 sites compared to N = 18 and N = 28 for the population-based methods shown below, consistent with our previous findings.58
Fig. 2–left displays the real and imaginary parts of the current autocorrelation function. Although, graphically, CJJ → 0 within 150 fs, Fig. 2–right shows that convergence of μ to three significant figures takes 269 fs, almost twice as long. Fig. 2–middle illustrates the memory kernel associated with these dynamics. The inset of Fig. 2–right shows μ obtained from the dynamics generated from  truncated at time τ, demonstrating that μ can be computed with only
truncated at time τ, demonstrating that μ can be computed with only  fs of data, slightly reducing the cost of the simulation: that is, one needs only 235/269 = 87% of the original simulation time.
fs of data, slightly reducing the cost of the simulation: that is, one needs only 235/269 = 87% of the original simulation time.
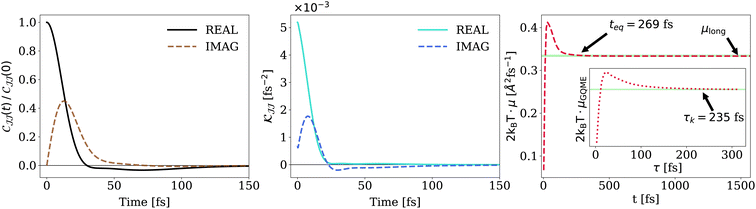 | ||
Fig. 2 Dispersive Holstein simulations for η/v = 6.26 and ωc/v = 0.82. Left: CJJ(t) converges to zero, as expected in dissipative systems. Middle: memory kernel for CJJ(t). Right: convergence of μ as a function of the integral limit in eqn (6). CJJ takes teq = 269 fs to reach ± 0.002 of the long-time value. The green shaded region is the same as in Fig. 1. Inset: convergence of the GQME estimate of μlong with respect to the cutoff time τ. We find  . . | ||
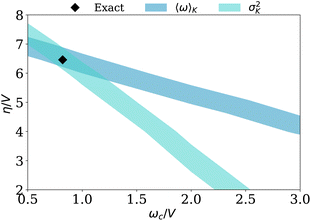
Since the computational saving is a property of the system parameters, we quantify the effort reductions over a grid of 20 different instances of the model parameters in Fig. 3–left. The dark portion of Fig. 3–left shows the region with 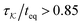 , where the brute force calculation and the Mori GQME incur comparable computational costs; the parameters we used in Fig. 2 lie in this region. The light blue region, where
, where the brute force calculation and the Mori GQME incur comparable computational costs; the parameters we used in Fig. 2 lie in this region. The light blue region, where  , offers modest computational savings. The light green region has
, offers modest computational savings. The light green region has  in many places, enabling significant savings with an order-of-magnitude reduction in the required effort. See the ESI† for the current correlation functions, memory kernels, and conductance of the dispersive Holstein model over the parameter space. Hence, the GQME truncation offers maximal efficiency gains when a material displays relatively low charge-lattice coupling (small η) and fast decorrelating environments (large ωc). Still, the Mori-type approach can yield additional routes to efficiency, to which we now turn.
in many places, enabling significant savings with an order-of-magnitude reduction in the required effort. See the ESI† for the current correlation functions, memory kernels, and conductance of the dispersive Holstein model over the parameter space. Hence, the GQME truncation offers maximal efficiency gains when a material displays relatively low charge-lattice coupling (small η) and fast decorrelating environments (large ωc). Still, the Mori-type approach can yield additional routes to efficiency, to which we now turn.
To investigate if one can obtain even greater efficiency gains, we adopt the strategy of including derivatives of the observable in the projector.26,75,76 While HEOM is unable to sample the current's time derivative explicitly owing to the presence of bath operators, our C(t) has sufficient temporal resolution to use its numerical time derivatives to augment the projector (see the ESI†). The results, displayed in Fig. 3–right, are surprising. It is indeed possible to decrease the lifetime of the memory kernel required to predict the transport coefficient via CJJ by simply augmenting the projector with derivatives of the motion, but only for particular combinations of the Hamiltonian parameters. Over large regions of the parameter space, such as where η is large, there is no advantage. However, when ωc ≈ η we obtain a ∼70% reduction in cost. To our knowledge, this parameter-dependent benefit has not previously been reported and represents a simple and parsimonious way to potentially further reduce the computational effort required to capture equilibrium time correlation functions.
We are now in a position to contextualize the results from the Mori approach in terms of the advantages offered by the nonequilibrium population-based GQME. Unlike the population-based GQME, which generally requires more simulations to construct its memory kernel, our Mori GQME requires only one, and converges significantly faster with system size, as Fig. 1 demonstrates. However, the population-based GQME may still offer a competitive advantage if its memory kernel lifetime,  , is sufficiently short. To test this, we consider two different population-based initializations: one corresponding to an instantaneous Franck–Condon excitation and the other to a Marcus-like description of equilibrium charge transfer. Note that the generation of the Marcus-like initial condition in HEOM requires a pre-production simulation (see the ESI†). Table 1 summarizes the results.
, is sufficiently short. To test this, we consider two different population-based initializations: one corresponding to an instantaneous Franck–Condon excitation and the other to a Marcus-like description of equilibrium charge transfer. Note that the generation of the Marcus-like initial condition in HEOM requires a pre-production simulation (see the ESI†). Table 1 summarizes the results.
The computational savings of the Mori GQME are vast: it is more than 20 times cheaper than the pre-equilibrated population-based method, and over two orders of magnitude for the non-equilibrated alternative. What is most impressive is that these are the savings one would obtain for the set of parameters investigated in Fig. 2, which lead to the smallest efficiency gains. For this parameter regime, the computational saving arises mainly due to the single entry in the projector, and not from the reduction in cost due to the memory kernel method. Hence, especially in systems with static disorder that require N simulations for the parameterization of the population-based GQME, the Mori GQME stands to yield significant efficiency gains, particularly for systems with small reorganization energies dominated by charge coupling to high-frequency, optical phonon modes.
Drude–Smith equation and backmapping
Beyond efficiency gains, our approach also yields accurate current autocorrelation functions, which we now employ to analyze the applicability of the frequently invoked phenomenological Drude and Drude–Smith theories. Fig. 2 shows that the real part of CJJ becomes negative. This behavior does not arise in the charge transport of normal metals, where the dynamics is well-described by a decaying exponential77 with kDrude = 1/τ before the onset of interband transitions. Describing this negative region, or ‘cage effect’, necessitates a functional form more complex than a simple exponential. The Smith reformulation of this process assigns these additional terms to Poisson distributed collisions (characterized by constant τ) of the charge carriers with their lattice ions.60 The coefficients cn of these terms represent what fraction of the initial velocity is retained after the nth collision. The Fourier transform of this current autocorrelation function, i.e., the conductivity in eqn (2), then takes the form60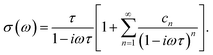 | (7) |
The standard approximation truncates the sum at the first term, with −1 ≤ c ≤ 0, which has been shown to describe experimental data well over the limited frequency range that is normally accessible.61–64 How well does it capture our exact response over the full dynamical range?
To perform this analysis, we consider how to connect the Drude–Smith analysis to our quantum mechanically exact response. The quantum mechanical CJJ is complex and gives the transport coefficient via the linear response relation, eqn (2), but the Drude and Drude–Smith expressions consider only classical and real current autocorrelation functions. Thus, to compare to eqn (7), we replace the classical function with the Kubo-transformed correlation function, CKuboJJ, which displays the same symmetries as classical correlation functions (i.e., it is real and symmetric about t)42,59 and is used to derive the harmonic correction factor to approximate quantum correlation functions by using their classical counterparts.78,79
We can now assess the applicability of a Drude–Smith decomposition of our CKuboJJ(t). Performing the inverse transform to eqn (7) truncated at n = 1 yields80
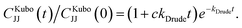 | (8) |
Focusing first on η/v = 2 and ωc/v = 1, Fig. 4 shows that the form of eqn (8) cannot capture the qualitative shape of CKuboJJ(t), missing the curvature near t = 0. This functional form can correctly capture the long-time decay for some parameter regimes but not for this example, remaining above zero for too long. Finally, although the depth of the negative well is reasonable, the position of its minimum is incorrect. This qualitative description of the mismatch applies across the parameter space, even as the negative region becomes less pronounced.
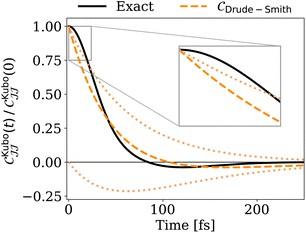
This is not unexpected since the Drude–Smith form implies the memory kernel decays as a single exponential (see the ESI†). Fig. 5(a) and (b) show that the normalized real part  is a complicated function of frequency. Here, the simplest curve shown (η/v = 2 and ωc/v = 3) has an approximately Gaussian shape—not Lorentzian, as expected for a single exponential—and as η increases the distribution becomes broader and more structured. The complexity of these curves shows that prescribing a simple, few-parameter form for the memory kernel is overly optimistic. What is more, even if one obtained a better fit to the Drude–Smith model in eqn (7) by considering n > 1, it would be difficult to interpret the coefficients of higher-order collisions in terms of a microscopic picture of polaron formation and transport.
is a complicated function of frequency. Here, the simplest curve shown (η/v = 2 and ωc/v = 3) has an approximately Gaussian shape—not Lorentzian, as expected for a single exponential—and as η increases the distribution becomes broader and more structured. The complexity of these curves shows that prescribing a simple, few-parameter form for the memory kernel is overly optimistic. What is more, even if one obtained a better fit to the Drude–Smith model in eqn (7) by considering n > 1, it would be difficult to interpret the coefficients of higher-order collisions in terms of a microscopic picture of polaron formation and transport.
To go beyond the limitations of the Drude–Smith model, we show that one can infer the parameters of the microscopic Hamiltonian responsible for the measured signal using only the frequency-resolved, complex conductivity, σ(ω) (see ESI Sec. VI†). Working with the Kubo memory kernel, which has equivalent information via , we seek a statistical characterization of
, we seek a statistical characterization of  from the measured data. We get this from its moments, noting that all frequency moments of the response function (which is directly related to the memory kernel) must exist.81 The nth moment takes the usual form,
from the measured data. We get this from its moments, noting that all frequency moments of the response function (which is directly related to the memory kernel) must exist.81 The nth moment takes the usual form,
 | (9) |
Since we explore a 2D parameter space, we use the mean 〈ω〉K and variance σK2 = 〈ω2〉K − 〈ω〉K2 to characterize our set of [η/v, ωc/v]. The contour plots in Fig. 5(c) and (d) show that the first two cumulants have a straightforward, monotonic relationship with the Hamiltonian parameters. Crucially, the dependences of panels (c) and (d) are quantitatively different, which means that together they triangulate the [η/v, ωc/v] which give rise to a particular combination [〈ω〉K,σK2]. We illustrate this protocol using the data in Fig. 2, which are not included in the 16-point grid in Fig. 5(c) and (d). Fig. 6 successfully extracts the correct location in parameter space using only the first two moments of  computed from the measured
computed from the measured  . To characterize a higher dimensional space (for example, as a function of temperature), one would use a simple generalization of this procedure considering higher moments. Therefore, this strategy provides a route to obtain corresponding dispersive Holstein parameters from experimental data, provided sufficient observational range and precision to sample the moments,82–84 with recent experiments reaching ∼75 THz.85,86
. To characterize a higher dimensional space (for example, as a function of temperature), one would use a simple generalization of this procedure considering higher moments. Therefore, this strategy provides a route to obtain corresponding dispersive Holstein parameters from experimental data, provided sufficient observational range and precision to sample the moments,82–84 with recent experiments reaching ∼75 THz.85,86
 | ||
| Fig. 6 Demonstration of back-mapping from the memory kernel cumulants to the dispersive Holstein parameters. Blue contour line: predicted using 〈ωK〉 = 0.096 fs−1 from Fig. 5(c). Green contour line: predicted using σK2 = 0.0057 fs−2 from Fig. 5(d). The intersection of these two contours suggests the location in Hamiltonian parameter space, and the black diamond indicates the exact parameters. | ||
Conclusion
In this paper, we employed a Mori-type GQME approach to determine transport coefficients in polaron-forming systems by using current as the primary member of the projection operator. Our approach can offer significant computational advantages of up to 90% for regimes dominated by weak charge-lattice couplings and fast-decorrelating lattices (i.e., those dominated by coupling to high-frequency optical phonons). In addition, in contrast to previous GQME-based approaches that project onto the nonequilibrium site population dynamics and scale with the size of the system, our approach requires only one calculation to build the GQME, rendering the construction of the memory kernel independent of system size. In addition to using numerically exact methods to obtain the memory kernels, one can also use the Mori-type GQME as a starting point for approximate treatments, including perturbation theory. Furthermore, we introduced a simple protocol to incorporate derivatives of current into the projection operator, leading to additional computational savings that vary across parameter space.While we showcased the advantages of this methodology through quantum dynamics simulations of electronic transport in a 1-dimensional periodic Holstein chain, the Mori approach for capturing transport phenomena can be applied to diverse systems and is agnostic to the level of sophistication employed to describe the many–body interactions (physically transparent models, ab initio, semiempirical, and empirical) and dynamics (path integrals, semiclassics, and classical dynamics) of the system. What is more, this Mori approach can offer significant computational savings and be easily adapted to a wide range of transport calculations.87,88
Beyond computational benefits, our approach yields valuable insights into the experimental measurements of materials. For example, we demonstrated the inadequacy of fitting the Drude–Smith equation to our theoretically unambiguous dynamics of polaron-forming systems, and introduced a cumulant-based method to map experimentally accessible memory kernels (via conductance measurements) to parameters of the dispersive Holstein Hamiltonian. This link enables the interpretation of AC measurements of polaron-forming materials in terms of their underlying Hamiltonian, thereby facilitating material design modifications. While we presented a proof-of-principle example of this backmapping procedure using our theoretical dataset, a comprehensive investigation of backmapping with experimental data from real materials remains a focus for future research.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
S. B. performed the simulations and did the derivations. S. B. and T. S. performed the analysis and wrote the initial draft of the paper. A. M. C. conceptualized and supervised the research and edited the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A.M.C. acknowledges the start-up funds from the University of Colorado Boulder for partial support of this research. Acknowledgment is made to the donors of the American Chemical Society Petroleum Research Fund for partial support of this research (No. PRF 66836-DNI6). S. B. acknowledges the John Bailar Memorial Endowment for partial support of the research. We thank Prof. Qiang Shi for sharing his HEOM code with us; Dr Matt Beard for helping us navigate the state-of-the-art terahertz measurements; and Andrew Monaghan for his help in using the Alpine high-performance computing resources at the University of Colorado Boulder. Alpine is jointly funded by the University of Colorado Boulder, the University of Colorado Anschutz, Colorado State University, and the National Science Foundation (award 2201538).References
- S. Fratini, M. Nikolka, A. Salleo, G. Schweicher and H. Sirringhaus, Charge transport in high-mobility conjugated polymers and molecular semiconductors, Nat. Mater., 2020, 19, 491–502 CrossRef CAS PubMed.
- T. Nematiaram, D. Padula, A. Landi and A. Troisi, On the largest possible mobility of molecular semiconductors and how to achieve it, Adv. Funct. Mater., 2020, 30, 2001906 CrossRef CAS.
- A. J. Leggett, S. Chakravarty, A. T. Dorsey, M. P. Fisher, A. Garg and W. Zwerger, Dynamics of the dissipative two-state system, Rev. Mod. Phys., 1987, 59, 1 CrossRef CAS.
- U. Weiss, Quantum Dissipative Systems, World Scientific, 2012 Search PubMed.
- T. Holstein, Studies of polaron motion: Part i. the molecular-crystal model, Ann. Phys., 1959, 8, 325–342 CAS.
- T. Holstein, Studies of polaron motion: Part ii. the “small” polaron, Ann. Phys., 1959, 8, 343–389 CAS.
- P. W. Anderson, Localized magnetic states in metals, Phys. Rev., 1961, 124, 41 CrossRef CAS.
- J. Hubbard, Electron correlations in narrow energy bands, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1963, 276, 238–257 Search PubMed.
- J. Hubbard, Electron correlations in narrow energy bands. ii. the degenerate band case, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1964, 277, 237–259 Search PubMed.
- J. Bader, R. Kuharski and D. Chandler, Role of nuclear tunneling in aqueous ferrous–ferric electron transfer, J. Chem. Phys., 1990, 93, 230–236 CrossRef CAS.
- X. Song and R. Marcus, Quantum correction for electron transfer rates. comparison of polarizable versus nonpolarizable descriptions of solvent, J. Chem. Phys., 1993, 99, 7768–7773 CrossRef CAS.
- R. Ghosh and F. C. Spano, Excitons and polarons in organic materials, Acc. Chem. Res., 2020, 53, 2201–2211 CrossRef CAS PubMed.
- J. H. Fetherolf, D. Golež and T. C. Berkelbach, A unification of the holstein polaron and dynamic disorder pictures of charge transport in organic crystals, Phys. Rev. X, 2020, 10, 021062 CAS.
- D. Segal and B. K. Agarwalla, Vibrational heat transport in molecular junctions, Annu. Rev. Phys. Chem., 2016, 67, 185–209 CrossRef CAS.
- M. Thoss and F. Evers, Perspective: Theory of quantum transport in molecular junctions, J. Chem. Phys., 2018, 148, 030901 CrossRef PubMed.
- F. Evers, R. Korytár, S. Tewari and J. M. Van Ruitenbeek, Advances and challenges in single-molecule electron transport, Rev. Mod. Phys., 2020, 92, 035001 CrossRef CAS.
- J. Ishizuka and Y. Yanase, Periodic anderson model for magnetism and superconductivity in ute 2, Phys. Rev. B, 2021, 103, 094504 CrossRef CAS.
- A. Mielke and H. Tasaki, Ferromagnetism in the hubbard model: Examples from models with degenerate single-electron ground states, Commun. Math. Phys., 1993, 158, 341–371 CrossRef.
- H.-C. Jiang and S. A. Kivelson, Stripe order enhanced superconductivity in the hubbard model, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2109406119 CrossRef CAS PubMed.
- B. Nosarzewski, E. Huang, P. M. Dee, I. Esterlis, B. Moritz, S. Kivelson, S. Johnston and T. Devereaux, Superconductivity, charge density waves, and bipolarons in the holstein model, Phys. Rev. B, 2021, 103, 235156 CrossRef CAS.
- R. Ghosh and F. Paesani, Unraveling the effect of defects, domain size, and chemical doping on photophysics and charge transport in covalent organic frameworks, Chem. Sci., 2021, 12, 8373–8384 RSC.
- H. Grabert, Projection Operator Techniques in Nonequilibrium Statistical Mechanics, Springer, vol. 95, 2006 Search PubMed.
- E. Fick, G. Sauermann, and W. D. Brewer, The Quantum Statistics of Dynamic Processes, Springer, vol. 86, 1990 Search PubMed.
- S. Nakajima, On quantum theory of transport phenomena: Steady diffusion, Prog. Theor. Phys., 1958, 20, 948–959 CrossRef.
- R. Zwanzig, Ensemble method in the theory of irreversibility, J. Chem. Phys., 1960, 33, 1338–1341 CrossRef CAS.
- H. Mori, Transport, collective motion, and brownian motion, Prog. Theor. Phys., 1965, 33, 423–455 CrossRef.
- A. J. Dominic III, T. Sayer, S. Cao, T. E. Markland, X. Huang and A. Montoya-Castillo, Building insightful, memory-enriched models to capture long-time biochemical processes from short-time simulations, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2221048120 CrossRef.
- W. C. Pfalzgraff, A. Kelly and T. E. Markland, Nonadiabatic dynamics in atomistic environments: Harnessing quantum-classical theory with generalized quantum master equations, J. Phys. Chem. Lett., 2015, 6, 4743–4748 CrossRef CAS.
- A. Montoya-Castillo and D. R. Reichman, Approximate but accurate quantum dynamics from the mori formalism: I. nonequilibrium dynamics, J. Chem. Phys., 2016, 144, 184104 CrossRef PubMed.
- S. Giannini, A. Carof and J. Blumberger, Crossover from hopping to band-like charge transport in an organic semiconductor model: Atomistic nonadiabatic molecular dynamics simulation, J. Phys. Chem. Lett., 2018, 9, 3116–3123 CrossRef CAS.
- A. Carof, S. Giannini and J. Blumberger, How to calculate charge mobility in molecular materials from surface hopping non-adiabatic molecular dynamics–beyond the hopping/band paradigm, Phys. Chem. Chem. Phys., 2019, 21, 26368–26386 RSC.
- S. Roosta, F. Ghalami, M. Elstner and W. Xie, Efficient surface hopping approach for modeling charge transport in organic semiconductors, J. Chem. Theory Comput., 2022, 18, 1264–1274 CrossRef CAS PubMed.
- A. Heck, J. J. Kranz, T. Kubar and M. Elstner, Multi-scale approach to non-adiabatic charge transport in high-mobility organic semiconductors, J. Chem. Theory Comput., 2015, 11, 5068–5082 CrossRef CAS PubMed.
- Z. Xu, Y. Zhou, L. Groß, A. De Sio, C. Y. Yam, C. Lienau, T. Frauenheim and G. Chen, Coherent real-space charge transport across a donor acceptor interface mediated by vibronic couplings, Nano Lett., 2019, 19, 8630–8637 CrossRef CAS PubMed.
- Y. Yan, M. Xu, Y. Liu and Q. Shi, Theoretical study of charge carrier transport in organic molecular crystals using the nakajima-zwanzig-mori generalized master equation, J. Chem. Phys., 2019, 150, 234101 CrossRef.
- Ref. 35 assumed a homogeneous system, which necessitates only a single simulation by symmetry. This is not generally the case.
- T. E. Markland and M. Ceriotti, Nuclear quantum effects enter the mainstream, Nat. Rev. Chem, 2018, 2, 0109 CrossRef CAS.
- D. Chandler and P. G. Wolynes, Exploiting the isomorphism between quantum theory and classical statistical mechanics of polyatomic fluids, J. Chem. Phys., 1981, 74, 4078–4095 CrossRef CAS.
- J. Cao and G. A. Voth, A new perspective on quantum time correlation functions, J. Chem. Phys., 1993, 99, 10070–10073 CrossRef CAS.
- M. Parrinello and A. Rahman, Study of an f center in molten kcl, J. Chem. Phys., 1984, 80, 860–867 CrossRef CAS.
- S. Jang and G. A. Voth, A derivation of centroid molecular dynamics and other approximate time evolution methods for path integral centroid variables, J. Chem. Phys., 1999, 111, 2371–2384 CrossRef CAS.
- I. R. Craig and D. E. Manolopoulos, Quantum statistics and classical mechanics: Real time correlation functions from ring polymer molecular dynamics, J. Chem. Phys., 2004, 121, 3368–3373 CrossRef CAS.
- J. Cao and G. A. Voth, The formulation of quantum statistical mechanics based on the feynman path centroid density. ii. dynamical properties, J. Chem. Phys., 1994, 100, 5106–5117 CrossRef CAS.
- J. Shao and N. Makri, Iterative path integral formulation of equilibrium correlation functions for quantum dissipative systems, J. Chem. Phys., 2002, 116, 507–514 CrossRef CAS.
- Y. Tanimura, Reduced hierarchical equations of motion in real and imaginary time: Correlated initial states and thermodynamic quantities, J. Chem. Phys., 2014, 141, 044114 CrossRef PubMed.
- L. Song and Q. Shi, Calculation of correlated initial state in the hierarchical equations of motion method using an imaginary time path integral approach, J. Chem. Phys., 2015, 143, 194106 CrossRef.
- A. Montoya-Castillo and D. R. Reichman, Path integral approach to the wigner representation of canonical density operators for discrete systems coupled to harmonic baths, J. Chem. Phys., 2017, 146, 024107 CrossRef.
- J. Liu and W. H. Miller, Using the thermal gaussian approximation for the boltzmann operator in semiclassical initial value time correlation functions, J. Chem. Phys., 2006, 125, 224104 CrossRef PubMed.
- Q. Shi and E. Geva, Semiclassical theory of vibrational energy relaxation in the condensed phase, J. Phys. Chem. A, 2003, 107, 9059–9069 CrossRef CAS.
- J. A. Poulsen, G. Nyman and P. J. Rossky, Practical evaluation of condensed phase quantum correlation functions: A feynman–kleinert variational linearized path integral method, J. Chem. Phys., 2003, 119, 12179–12193 CrossRef CAS.
- A. Montoya-Castillo and D. R. Reichman, Approximate but accurate quantum dynamics from the mori formalism. ii. equilibrium time correlation functions, J. Chem. Phys., 2017, 146, 084110 CrossRef.
- T. Barthel, Precise evaluation of thermal response functions by optimized density matrix renormalization group schemes, New J. Phys., 2013, 15, 073010 CrossRef.
- C. Karrasch, D. Kennes and F. Heidrich-Meisner, Spin and thermal conductivity of quantum spin chains and ladders, Phys. Rev. B, 2015, 91, 115130 CrossRef.
- C. Karrasch, J. Bardarson and J. Moore, Reducing the numerical effort of finite-temperature density matrix renormalization group calculations, New J. Phys., 2013, 15, 083031 CrossRef.
- Q. Shi, L. Chen, G. Nan, R.-X. Xu and Y. Yan, Efficient hierarchical liouville space propagator to quantum dissipative dynamics, J. Chem. Phys., 2009, 130, 084105 CrossRef.
- K. Song, S. Bai and Q. Shi, A time domain two-particle approximation to calculate the absorption and circular dichroism line shapes of molecular aggregates, J. Chem. Phys., 2015, 143, 064109 CrossRef PubMed.
- Y. Tanimura and R. Kubo, Time evolution of a quantum system in contact with a nearly gaussian-markoffian noise bath, J. Phys. Soc. Jpn., 1989, 58, 101–114 CrossRef.
- S. Bhattacharyya, T. Sayer and A. Montoya-Castillo, Anomalous transport of small polarons arises from transient lattice relaxation or immovable boundaries, J. Phys. Chem. Lett., 2024, 15, 1382–1389 CrossRef CAS PubMed.
- R. Kubo, M. Toda, and N. Hashitsume, “Statistical mechanics of linear response,” Statistical Physics II: Nonequilibrium Statistical Mechanics, 1991, pp, 146–202 Search PubMed.
- N. Smith, Classical generalization of the drude formula for the optical conductivity, Phys. Rev. B, 2001, 64, 155106 CrossRef.
- G. R. Yettapu, D. Talukdar, S. Sarkar, A. Swarnkar, A. Nag, P. Ghosh and P. Mandal, Terahertz conductivity within colloidal cspbbr3 perovskite nanocrystals: remarkably high carrier mobilities and large diffusion lengths, Nano Lett., 2016, 16, 4838–4848 CrossRef CAS.
- B. Pattengale, J. Neu, S. Ostresh, G. Hu, J. A. Spies, R. Okabe, G. W. Brudvig and C. A. Schmuttenmaer, metal–organic framework photoconductivity via time-resolved terahertz spectroscopy, J. Am. Chem. Soc., 2019, 141, 9793–9797 CrossRef CAS PubMed.
- K. S. Kumar, G. L. Prajapati, R. Dagar, M. Vagadia, D. S. Rana and M. Tonouchi, Terahertz electrodynamics in transition metal oxides, Adv. Opt. Mater., 2020, 8, 1900958 CrossRef CAS.
- T. J. Magnanelli, S. Engmann, J. K. Wahlstrand, J. C. Stephenson, L. J. Richter and E. J. Heilweil, Polarization dependence of charge conduction in conjugated polymer films investigated with time-resolved terahertz spectroscopy, J. Phys. Chem. C, 2020, 124, 6993–7006 CrossRef CAS.
- E. Li, J. Wei, T. Zhang, H. Wan, Y. Cheng, J. Xie, H. Li, K. Zhang, J. Xu and J. Hu, et al., Charge carriers localization effect revealed through terahertz spectroscopy of mxene: Ti3c2tx, Small, 2023, 2306200 Search PubMed.
- D. L. Cheung and A. Troisi, Modelling charge transport in organic semiconductors: from quantum dynamics to soft matter, Phys. Chem. Chem. Phys., 2008, 10, 5941–5952 RSC.
- F. Ortmann, F. Bechstedt and K. Hannewald, Charge transport in organic crystals: interplay of band transport, hopping and electron–phonon scattering, New J. Phys., 2010, 12, 023011 CrossRef.
- R. Ghosh and F. Paesani, Topology-mediated enhanced polaron coherence in covalent organic frameworks, J. Phys. Chem. Lett., 2021, 12, 9442–9448 CrossRef CAS.
- H. Mousavi and H. Rezania, Electron–phonon interaction in carbon nanotubes, Mod. Phys. Lett. B, 2010, 24, 2947–2954 CrossRef CAS.
- G. D. Mahan, Many-Particle Physics, Springer Science & Business Media, 2000 Search PubMed.
- T. Nematiaram and A. Troisi, Modeling charge transport in high-mobility molecular semiconductors: Balancing electronic structure and quantum dynamics methods with the help of experiments, J. Chem. Phys., 2020, 152, 190902 CrossRef CAS PubMed.
- Y. Yan, L. Song and Q. Shi, Understanding the free energy barrier and multiple timescale dynamics of charge separation in organic photovoltaic cells, J. Chem. Phys., 2018, 148, 084109 CrossRef PubMed.
- L. Song and Q. Shi, A new approach to calculate charge carrier transport mobility in organic molecular crystals from imaginary time path integral simulations, J. Chem. Phys., 2015, 142, 174103 CrossRef PubMed.
- The easiest to construct and fastest initial condition to equilibrate corresponds to a zeroth order approximation to e−βĤ/Z, i.e., e−βĤelec/Zelec × e−βĤB/ZB.
- D. R. Reichman and P. Charbonneau, Mode-coupling theory, J. Stat. Mech.: Theory Exp., 2005, 2005, P05013 Search PubMed.
- L. M. Janssen, Mode-coupling theory of the glass transition: A primer, Front. Phys., 2018, 6, 97 CrossRef.
- P. B. Allen, Electron transport, Contemp. Concepts Condens. Matter Sci., 2006, 2, 165–218 Search PubMed.
- S. Egorov, K. Everitt and J. Skinner, Quantum dynamics and vibrational relaxation, J. Phys. Chem. A, 1999, 103, 9494–9499 CrossRef CAS.
- J. S. Bader and B. Berne, Quantum and classical relaxation rates from classical simulations, J. Chem. Phys., 1994, 100, 8359–8366 CrossRef CAS.
- W.-C. Chen and R. A. Marcus, The drude-smith equation and related equations for the frequency-dependent electrical conductivity of materials: Insight from a memory function formalism, ChemPhysChem, 2021, 22, 1667–1674 CrossRef CAS.
- D. Forster, Hydrodynamic Fluctuations, Broken Symmetry, and Correlation Functions, CRC Press, 2018 Search PubMed.
- R. Ulbricht, E. Hendry, J. Shan, T. F. Heinz and M. Bonn, Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy, Rev. Mod. Phys., 2011, 83, 543 CrossRef CAS.
- J. Lloyd-Hughes and T.-I. Jeon, A review of the terahertz conductivity of bulk and nano-materials, J. Infrared, Millimeter, Terahertz Waves, 2012, 33, 871–925 CrossRef CAS.
- P. Kužel and H. Němec, Terahertz spectroscopy of nanomaterials: a close look at charge-carrier transport, Adv. Opt. Mater., 2020, 8, 1900623 CrossRef.
- D. Cooke, F. C. Krebs and P. U. Jepsen, Direct observation of sub-100 fs mobile charge generation in a polymer-fullerene film, Phys. Rev. Lett., 2012, 108, 056603 CrossRef CAS PubMed.
- A. Leitenstorfer, A. S. Moskalenko, T. Kampfrath, J. Kono, E. Castro-Camus, K. Peng, N. Qureshi, D. Turchinovich, K. Tanaka and A. G. Markelz, et al., The 2023 terahertz science and technology roadmap, J. Phys. D: Appl. Phys., 2023, 56, 223001 CrossRef.
- N. Y. Lin, M. Bierbaum and I. Cohen, Determining quiescent colloidal suspension viscosities using the green-kubo relation and image-based stress measurements, Phys. Rev. Lett., 2017, 119, 138001 CrossRef PubMed.
- S. Baroni, R. Bertossa, L. Ercole, F. Grasselli, and A. Marcolongo, “Heat transport in insulators from ab initio green-kubo theory,” Handbook of Materials Modeling: Applications: Current and Emerging Materials, 2020, pp. 809–844 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc03144j |
| This journal is © The Royal Society of Chemistry 2024 |


![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif)