Cobalt-free layered perovskites RBaCuFeO_5+δ (R = 4f lanthanide) as electrocatalysts for the oxygen evolution reaction

Abstract

Co-based perovskite oxides are intensively studied as promising catalysts for electrochemical water splitting in an alkaline environment. However, the increasing Co demand by the battery industry is pushing the search for Co-free alternatives. Here we report a systematic study of the Co-free layered perovskite family RBaCuFeO_5+δ (R = 4f lanthanide), where we uncover the existence of clear correlations between electrochemical properties and several physicochemical descriptors. Using a combination of advanced neutron and X-ray synchrotron techniques with ab initio DFT calculations we demonstrate and rationalize the positive impact of a large R ionic radius in their oxygen evolution reaction (OER) activity. We also reveal that, in these materials, Fe³⁺ is the transition metal cation the most prone to donate electrons. We also show that similar R³⁺/Ba²⁺ ionic radii favor the incorporation and mobility of oxygen in the layered perovskite structure and increase the number of available O diffusion paths, which have an additional, positive impact on both, the electric conductivity and the OER process. An unexpected result is the observation of a clear surface reconstruction exclusively in oxygen-rich samples (δ > 0), a fact that could be related to their superior OER activity. The encouraging intrinsic OER values obtained for the most active electrocatalyst (LaBaCuFeO_5.49), together with the possibility of industrially producing this material in nanocrystalline form should inspire the design of other Co-free oxide catalysts with optimal properties for electrochemical water splitting.

---

Broader context

Co oxides with perovskite-related structure are particularly promising, cost-effective OER catalysts. However, the increasing Co demand by the battery industry is pushing the search for Co-free alternatives. Here we investigate the potential of the Co-free layered perovskite family RBaCuFeO_5+δ (R = 4f lanthanide), where we identify the critical structural and electronic variables leading to high OER catalytical performance. The employed methodology, based in the use of advanced neutron and X-ray synchrotron techniques combined with ab initio DFT calculations allowed to reveal LaBaCuFeO_5+δ as new, promising Co-free electroctalyst. Moreover, we could show that this material can be industrially produced in nanocrystalline form. We believe that the reported results and methodology may contribute to the implementation of new technologies aimed to generate energy with lower carbon emissions, and can also inspire the scientific community in their search of other Co-free materials with good OER electrocatalytical properties.

1. Introduction

The targeted decarbonisation of human activities by 2050 requires the rapid development of green technologies able to generate energy using renewable sources and convert (or store) it to zero-carbon emission carriers. Among them, the use of hydrogen produced by the water-splitting process is considered among the most promising to meet the decarbonisation goal. However, the anodic reaction in water electrolysers, the oxygen evolution reaction (OER), is a complex process involving a transfer of four electrons that is affected by a slow dynamic (high kinetic overpotential) that controls de facto the water splitting efficiency. Perovskite-type oxides with general formula ABO₃ (henceforth perovskite oxides) are particularly promising for electrocatalysis in alkaline media due to their structural flexibility, which allows accommodating a large variety of cations in the A and B sites and the creation of both, anionic and cationic defects.^1–7 This provides a plethora of possibilities for tailoring their physicochemical properties, which can be effectively tuned to boost the activity of the OER process.^4–6

In most perovskite oxide catalysts the A-positions are occupied by 4f lanthanides and/or alkaline earth cations, whereas the B positions host cations of abundant transition metals (TM) such as Mn, Fe, Co or Ni.^2,5,8 Among them, Co is particularly well suited for reactions involving electron exchange (such as the OER) due to the close values of their intra-atomic exchange energy J_H and crystal electric field (CEF) splitting 10D_q, which results in small energy differences between their spin-state and oxidation states.^9–12 The presence of cobalt on the B-sites has indeed emerged as beneficial for the OER process, with Co-based perovskites such as the three-dimensional (3D) cubic oxide Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ or the layered double perovskite PrBaCo₂O_5+δ showing OER activities as good as or even higher than established catalysts.¹³

Despite its outstanding properties for electrochemical water splitting, Co-based perovskites have a few drawbacks, e.g., cobalt toxicity. Also critical is the high Co price linked to the increasing demand by the battery industry, which is driving the search for alternative, Co-free perovskite oxide catalysts. In the recent literature, some Mn, Ni and/or Fe-based 3D perovskites have been found to display good figures of merit.^1,2,14 However, to our best knowledge, Co-free oxides with the layered perovskite structure have not been investigated to date. Interestingly, this structural framework seems to be at the origin of the excellent electrochemical performance and stability reported for layered Co perovskites, seemingly superior to those of their 3D Co-based counterparts.¹⁵ It is thus tempting to investigate whether this trend is also verified in isostructural, Co-free materials.

In this work, we address this question by investigating the layered perovskite family RBaCuFeO_5+δ (R = 4f lanthanide). These Co-free materials have recently attracted a lot of attention due to their promise as spin-driven multiferroics for low-power magnetoelectric applications,^16–20 and some of them have also been investigated as potential cathodes for intermediate-temperature solid oxide fuel cells.^21–23 However, they have never been considered before as OER electrocatalysts as far as we know. Interestingly, their layered perovskite structure²⁴ is similar to that of PrBaCo₂O_5+δ, one of the most OER-active perovskite-related oxides reported to date. Moreover, the possibility of incorporating the complete 4f lanthanide series in one of the two A-sites provides an attractive, novel possibility for crystal structure and physical property tuning that has no equivalent in 3D perovskites.

Here, we use this knob to tune the electrocatalytical performance in the RBaCuFeO_5+δ family. Our measurements reveal a complex modification of the OER activity upon 4f cation replacement, which shows no direct correlation with the lanthanide ionic radius (R_ionic) or the electric conductivity σ. We rationalize these results in terms of the changes in the crystal and electronic structures that we investigate here in detail using a combination of ab initio calculations and advanced neutron and X-ray synchrotron techniques. The results of this combined analysis uncover an intriguing dependence of the OER activity on the parity of the 4f electron count for the compounds with δ = 0. Moreover, they reveal a positive impact of the oxygen excess (δ > 0) in the conductivity, which leads to the partial oxidation of Fe³⁺ into Fe⁴⁺ while keeping the Cu²⁺ valence nearly constant. This results in a sharp rise of the Fe–O hybridization and in the creation of new hole-states in the gap, whose combined effect is at the origin of the abrupt increase of σ upon oxygen uptake. Contrarily to the results reported for some 3D Fe-based perovskites,²⁵ growing values of Fe⁴⁺ (and σ) alone do not grant a simultaneous increase of the OER activity, which requires also sufficient weakly bound oxygen and a distribution of oxygen vacancies that ensures enough two-dimensional oxygen diffusion channels in the catalysts‘bulk. This observation suggests an active participation of the perovskite lattice oxygen in the OER process, the lattice oxygen evolution reaction (LOER), theoretically postulated^26,27 and experimentally supported^28–30 by some previous studies. To conclude, we show that the material with the best figures of merit of this study (LaBaCuFeO_5.49) can reach intrinsic OER activities approaching those of Co-based oxide perovskites and can be industrially produced in nanocrystalline form.

2. Results

2.1. OER activity of RBaCuFeO_5+δ layered perovskites

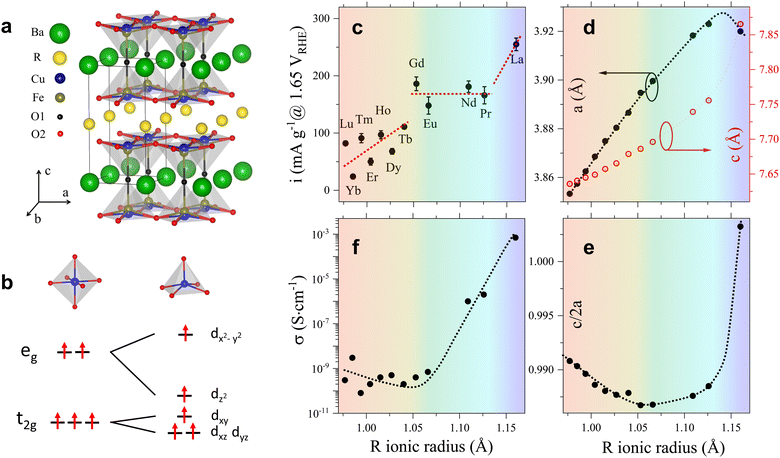
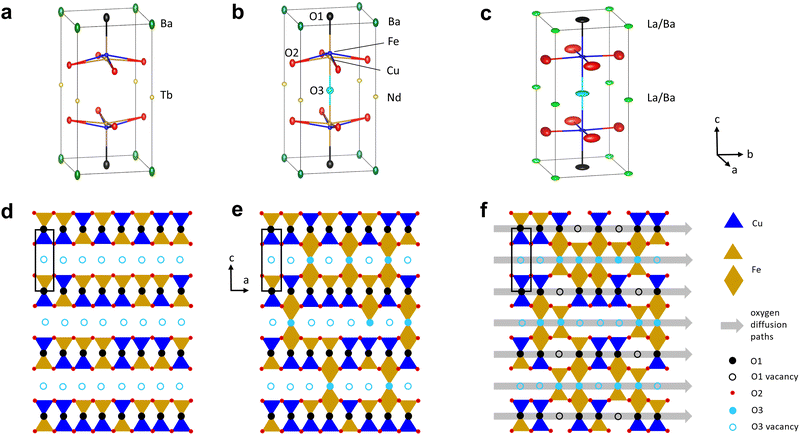
The crystal structure of the RBaCuFeO_5+δ layered perovskites with δ = 0, shown in Fig. 1a, is characterized by a tetragonal unit cell a_c × a_c × c (c ≈ 2a_c) where a_c denotes the pseudocubic perovskite unit-cell parameter.²⁴ The doubling of the c-parameter is due to the ordering of the A-cations R³⁺ and Ba²⁺ in layers perpendicular to this crystal axis, which is triggered by the large difference in ionic radius between the lanthanides and barium. The B positions are occupied by Cu²⁺ and Fe³⁺, which contrarily to the A-cations, display some preparation-dependent degree of disorder.^31,32 This chemical disorder is represented in Fig. 1a by the splitting of the B site inside the pyramids, where Cu and Fe have slightly different z-coordinates. An important difference with 3D perovskites is that the B-cations are in square-pyramidal coordination due to the existence of 1/6 of ordered oxygen vacancies localized in the lanthanide layers. This leads to the stabilization of the d_xz, d_yz and d_z² orbitals with respect to the energies of the t_2g and e_g levels of octahedral parentage, as shown schematically in Fig. 1b. The stabilization is particularly pronounced in the case of d_z², which as we show later, may reach energies close to that of the t_2g orbitals. It is worth mentioning that the lanthanide layers can incorporate additional oxygen (1 > δ > 0), which for intermediate compositions, leads to the coexistence of B-cations in square-pyramidal and octahedral coordination.^33–35

Fig. 1 (a) Crystal structure of the RBaCuFeO_5+δ compounds with δ = 0. The figure highlights the R/Ba order in the A-sites, the Cu/Fe disorder in the B-sites, and the absence of oxygen in the R-layers. (b) Splitting of the transition metal 3d orbitals under the action of octahedral and square-pyramidal crystal fields. (c)–(f) Modification of the OER activity, lattice parameters (a and c), c/2a ratio and electric conductivity σ upon R-cation replacement. The error bars in (c) and (f) are the standard deviations obtained after repeating the measurements at least three times. In (d) they are the values provided by the Rietveld software FullProf Suite, and in (e) they have been calculated from the (d) values using error propagation formulas. The color background highlights the regions with different dependence of the OER activity with R_ionic. Dotted lines are guides for the eye.

Since the focus of this investigation was on identifying the critical variables leading to the best OER catalytic performance, we compared first the changes in the OER activity upon R cation replacement with those observed in several structural variables, namely, lattice parameters, interatomic distances and angles, oxygen content, oxygen vacancy distribution and degree of cation intermixing. A necessary condition to obtain precise values of these quantities is the use of well-crystallized materials. We thus synthesized twelve RBaCuFeO_5+δ ceramic samples with R = La, Pr, Nd, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb and Lu using the solid-state reaction technique, which yields powders with large particle sizes and narrow Bragg reflections in the powder diffraction patterns (ESI†). Another crucial point is the use of analytical techniques able to determine precisely the atomic coordinates of the different O sites, their occupations and their anisotropic mean-square displacements (MSD). We thus employed powder neutron diffraction (PND), more sensitive than X-ray diffraction to light elements such as oxygen. The obtained structural data were used as starting point for density functional theory (DFT) calculations, employed here to interpret the X-ray absorption spectroscopy (XAS) measurements, and to investigate the evolution of different electronic variables (band gap, energy position of the empty states associated to the different 3d orbitals, centre of gravity of the O valence band, TM–O covalency, and electron filling of the Cu and Fe 3d orbitals), proposed in the recent literature as OER descriptors.³ The changes in the OER activity upon replacement of the 4f R-cation were then contrasted with those observed in the different structural and electronic parameters in order to uncover their degree of correlation with the OER electrochemical performance.

The OER activity of all samples was measured in a three-electrode cell configuration as described in the ESI.† The measured currents in the OER region were initially stabilized with a series of cyclic voltammetry measurements between 1 and 1.7 V_RHE, during which the activity of most of the RBaCuFeO_5+δ electrocatalysts increased over cycling (Fig. S1a, ESI†). The largest activity increment was obtained in the initial 14 cycles with an average increase of ∼70% of the current recorded in the 2nd cycle. The Tafel slopes, the mass-specific current density at 1.65 V_RHE and the overpotentials at 10 mA g⁻¹ of the RBaCuFeO_5+δ samples are listed in Table S1 (ESI†), while the Tafel plots are shown in Fig. S2 (ESI†).

The OER electrochemical activities of the twelve RBaCuFeO_5+δ samples, expressed as gravimetric current densities at 1.65 V_RHE, are shown in Fig. 1c as a function of the R ionic radius. Due to the large particle size of our samples, their surface areas were too small to be accurately determined by Brunauer–Emmett–Teller (BET)³⁶ measurements. This prevented the evaluation of surface area normalized current densities. However, from the comparable size and shape of the particles, as estimated from scanning electron microscopy (SEM) and from X-ray powder diffraction using the Scherrer formula, and the akin double layer capacitances (Fig. S1b, ESI†), similar behaviors of the gravimetric and surface-normalized activities along the 4f series can be reasonably expected (Materials and methods, Fig. S3 and Table S2, ESI†). As shown in Fig. 1c, the OER electrocatalytic activity is the highest for R = La, the lanthanide with the largest atomic radius. Although smaller R ionic radii result in general on a lower electrocatalytic performance, the OER activity is not a linear function of R_ionic, with deviations from linearity well beyond the error bars. Instead, three different regimes are clearly observed. In the first one, the activity alternates with the occupation of the 4f orbitals, with higher values for cations with even 4f occupations (Lu³⁺, Tm³⁺, Ho³⁺, Tb³⁺) and lower for those with odd occupations (Yb³⁺, Er³⁺, Dy³⁺). In the second (Gd³⁺, Eu³⁺, Nd³⁺, Pr³⁺), the activity is approximately constant. In the third (La³⁺), a substantial activity jump with respect to the previous region is observed. These results are at odds with the behaviour expected from the monotonic increase of the R ionic radius along the 4f series, and suggest that additional variables may be controlling the OER activity. As we show in the next sections, several structural and electronic descriptors show anomalies at the same R_ionic values that define the three OER activity regions.

2.2. Modification of the crystal structure upon insertion of increasingly larger lanthanides

Lattice parameters. To get insight into the mechanism behind the evolution of the electrochemical response we investigated the modifications of the layered perovskite framework induced by the insertion of the different lanthanides. High-resolution structural data have been reported previously by some of us for the smallest 4f cations (Lu to Dy) using PND,¹⁸ and we complete them here for R = Tb, Gd, Eu, Nd, Pr and La. For the compounds with R = Eu and Gd, where the high neutron absorption cross-section of these cations prevents the use of PND, we used powder X-ray diffraction (PXRD) instead (Fig. S4, S5 and Tables S2, S3, ESI†).

Fig. 1d and Table S2 (ESI†) show the modification of the lattice parameters a and c with the R-cation ionic radius. As expected, both increase with R_ionic, However, their evolution along the 4f series differs from the linear increase expected from Vegard's law and observed in other structurally-related perovskites.³⁷ This deviation is better appreciated in Fig. 1e, showing the changes in the tetragonal distortion c/2a of the pseudocubic unit cell with R_ionic, where c/2a = 1 corresponds to a RBaCuFeO_5+δ layered perovskite containing two perfectly cubic perovskite units. For the smaller lanthanides (Lu to Gd) c/2a takes values smaller than one and decreases with R_ionic, indicating a tensile distortion that becomes more pronounced for growing R ionic radii. For R = Gd, exactly in the middle of the 4f series, this tendency is reversed, and c/2a increases with R_ionic until R = Pr. For LaBaCuFeO_5+δ, the last member of the series, c/2a undergoes a huge increase, rising up to a value slightly larger than 1. The tetragonal distortion of this material is thus slightly compressive, and much smaller than in the rest of the family. Interestingly, the variation of c/2a defines three distinct regions that nicely coincide with those inferred from that of the OER activity. We also note that the c/2a minimum is very close to that observed in the electric conductivity σ (Fig. 1f) that, as the OER activity, does not change in a monotonic way with the R ionic radius.

Interatomic distances, angles, oxygen content, oxygen vacancy distribution and A-cation intermixing. To rationalize these observations we examined the evolution of several interatomic distances and angles along the series, and compared them with the behaviour of the electrochemical response. Fig. 2a shows the changes in the separation between the bipyramid slabs d₁ (directly related to the lanthanide size) and the slab thickness d₂. As expected, d₁ increases linearly with R_ionic. d₂, in contrast decreases, albeit to a slightly slower rate. Interestingly, both trends are sharply interrupted for R = La, where the large difference between d₁ and d₂ observed in the remaining RBaCuFeO_5+δ compounds (d₂ = ∼1.7d₁) disappears and both distances become nearly identical (Fig. 2b). This suggests the existence of an important structural reorganization in LaBaCuFeO_5+δ that, as shown in Fig. 1f and c, results in a substantial increase in both, the conductivity (note the log scale) and the OER activity.

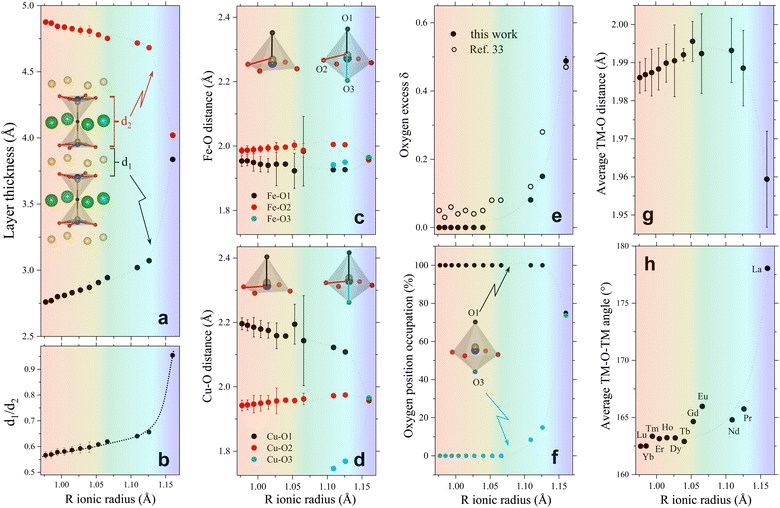Fig. 2 Evolution of different crystallographic descriptors with the R-cation ionic radius in RBaCuFeO_5+δ layered perovskites. (a) Thickness of the R-containing layers (d₁) and the bipyramid layers (d₂). (b) d₁/d₂ ratio. (c) Fe–O interatomic distances. (d) Cu–O interatomic distances. (e) Oxygen excess δ. (f) Occupation (in %) of the two apical position O1 and O3. (g) Average TM–O distance. (h) Average TM–O–TM superexchange angle. The atomic positions and occupations employed to calculate these descriptors are from our previous work (Lu to Dy),¹⁸ and from this study (Tb to La, Table S3, ESI†). They were all determined from high-resolution PND data with the exception of R = Gd and Eu (ESI†). Dotted lines are guides for the eye. The color background highlights the regions with different dependence of the OER activity with R_ionic.

To verify this point, we had a closer look at the changes within the bipyramid slabs, which host the B-cations Fe and Cu. Fig. 2c and d show the evolution of the in-plane and out-of-plane distances in the FeO₅ and CuO₅ pyramids. We note that the Fe coordination polyhedron is extremely regular, as expected from its symmetric Fe³⁺ high-spin electronic configuration (t³_2g e²_g), with one electron per 3d orbital. In contrast, the CuO₅ pyramids are strongly distorted, with four short in-plane distances and a very long apical distance, in line with the Cu²⁺ Jahn–Teller active configuration (t⁶_2g e³_g). As shown in Fig. 2c and d, the distortion of the Fe and Cu coordination polyhedra changes very little with the lanthanide size for the compounds with R = Lu to Eu. In contrast, a major modification is observed for those with R = Nd, Pr and La, where the Rietveld fits of the PND data indicate the presence of additional oxygen (O3) in the R-layers (Fig. 2e and f). The correct stoichiometry for these compounds is thus RBaCuFeO_5+δ, with δ = 0.081(1), 0.150(5) and 0.49(1) for Nd, Pr and La, respectively. This contrasts with the compounds with the smallest lanthanides (Lu to Tb), where δ = 0 within the PND detection limit. For R = Gd and Eu the impossibility to perform PND measurements prevents the determination of the oxygen content and its distribution in the structure. However, a quadratic extrapolation suggests that the oxygen uptake could already start for R = Gd. Interestingly, it is precisely for R = Gd where a discontinuity in the evolution of the tetragonal distortion c/2a (Fig. 1e), the OER activity (Fig. 1c) and the electric conductivity (Fig. 1f) is observed.

Besides revealing the incorporation of additional oxygen in the R-layers for the larger lanthanides, the changes observed in the Fe–O and Cu–O interatomic distances confirm the anomalous behaviour of LaBaCuFeO_5.49. At odds with the rest of the series, the basal and apical distances of this compound are nearly identical for the Cu and Fe coordination polyhedra (Fig. 2c and d). Moreover, PND reveals not only a large O excess (δ = 0.49) but also the existence of a significant number of vacancies in the apical oxygen position O1, fully occupied in the remaining members of the family (Fig. 2f). For R = La, the distribution of the extra O and the O-vacancies in the structure is thus completely different from that observed in the other compounds. The reason behind is the intermixing of the La³⁺ and Ba²⁺ cations, which results in a dramatic structural homogenization of the two pseudocubic units in the layered perovskite structure (Table S3, ESI†). Ba (green) and the R cations (yellow) are indeed perfectly ordered for R = Lu to Pr (Fig. 1a). However, this is not anymore the case for R = La, where about 55% of the Ba²⁺ sites are occupied by La³⁺ cations (and vice versa) due to the similarity between their ionic radii. This breaks the perfect alternation of the A-site cations along the crystallographic c-direction observed for the other lanthanides, allowing the creation of O vacancies also in the Ba layers thanks to the simultaneous presence of La³⁺, which prefers lower O-coordination than Ba²⁺. The resulting decrease of layered character leads to a pseudo-cubic unit cell with c/2a ratio very close to 1 (Fig. 1e). We note that a small tetragonal distortion (c/2a = 1.0032) is nevertheless preserved due to the combined impact of the slightly asymmetric La³⁺/Ba²⁺ distribution in the two A-sites, and a small difference in the percentage of oxygen vacancies at the O1 and O3 apical sites (≈25(1)% and ≈26.1(1)%, respectively, Fig. 2f). As we will see in the next sections, this residual distortion has an important impact on the oxygen displacement pattern in the structure.

Link between crystal structure and electric conductivity. Since the electric conductivity σ is linked to the bandwidth, which depends on the degree of Cu/Fe 3d–O 2p overlap W, we can use our structural data to estimate this quantity and to check whether it scales with σ. We employ here the expression W = cos[(180 − θ)/2]/d_TM–O^3.5 reported in ref. 38 and 39 which reflects the positive impact of short average TM–O distances d_TM–O and large average TM–O–TM superexchange angles θ in the degree of TM–O overlap. The W values obtained using the experimental values of d_TM–O (Fig. 2g) and θ (Fig. 2h) are shown as red markers in Fig. 3a, together with those of σ (black) and δ (blue). We observe strong similarities between the behaviour of W and σ along the series, namely, low values and a smooth decrease with R_ionic for the compounds with δ = 0, a minimum around R = Gd, and an abrupt increase as soon as additional oxygen (O3) is incorporated in the R layers. This last observation suggests that the partial occupation of the O3 position breaks the physical isolation of the CuO₅–FeO₅ bipyramidal slabs along the c axis thanks to the creation of new TM–O bonds, which open a new electronic conduction channel in the structure and increase the degree of TM–O overlap (Fig. 3a). Surprisingly, this conductivity increase has little effect on the OER activities of the compounds with R = Gd, Eu, Nd and Pr, which remain nearly constant (Fig. 3b). In contrast, a clear, discontinuous increase is observed for R = La coinciding with the appearance of La/Ba intermixing and the creation of oxygen vacancies in the O1 apical positions.

Fig. 3 (a) Evolution of the electric conductivity σ, the hybridization parameter W = cos[(180 − θ)/2]/d_TM–O^3.5 and the oxygen excess δ with the R ionic radius. The plot highlights the correlation between σ, δ and W, and the lack of correlation between the evolution of these three variables and that of the OER activity, shown in (b).

Anisotropic mean-squared displacements, O mobility and link to OER activity. A key to understand these unexpected observations is given by the dramatic change in the shape of the anisotropic thermal ellipsoids in LaBaCuFeO_5.49, particularly those of the oxygen sites. As shown in Fig. S6 (ESI†) and Fig. 4a and b, PND reveals anisotropic thermal ellipsoids relatively small and slightly elongated along the c direction for R = Lu to Pr. In contrast, a huge change in size and shape is observed for R = La, where the largest ellipsoid axes correspond now to atomic displacements in the ab plane (Fig. 4c). The observation of larger in-plane atomic displacement parameters may arise from the quasi-random static ionic displacements associated to the Ba/La intermixing, the increase on the O3 occupation, and the appearance of vacancies in the O1 position. However, they can also be due to the onset of the oxygen diffusion in the ab planes.⁴⁰ Based on the crystallographic data alone it is not possible to distinguish between these two possibilities. However, the simultaneous observation of a large increase in both, the electric conductivity and the OER activity suggests that the second possibility is not unlikely. It is well established that the mobility of diffusing ions in ionic conductors largely depends on the connectivity between the available hopping sites. The existence of oxygen vacancies in the two apical positions is thus expected to favor in-plane O1 and O3 hopping (Fig. 4d–f), and is consistent with the disk-shape of their thermal ellipsoids. For the O2 position, our PND data could not reveal the presence of oxygen vacancies. Hence, their large mean-squared displacements in the ab plane are most probably a static response to the O and R/Ba chemical disorder.

Fig. 4 (a)–(c) Thermal ellipsoids (60% probability) at RT for TbBaCuFeO_5.00 (R/Ba order, δ = 0), NdBaCuFeO_5.08 (R/Ba order, δ > 0) and LaBaCuFeO_5.49 (R/Ba intermixing, δ > 0, apical O sites O1 and O3 partially occupied). (d)–(f) Schematic representation of the O vacancy distribution and the O diffusion paths suggested by the combined structural (PND) and spectroscopic (XAS) analysis, which represent the three different situations shown in (a)–(c). The Ba²⁺ and R³⁺ cations are not shown for clarity.

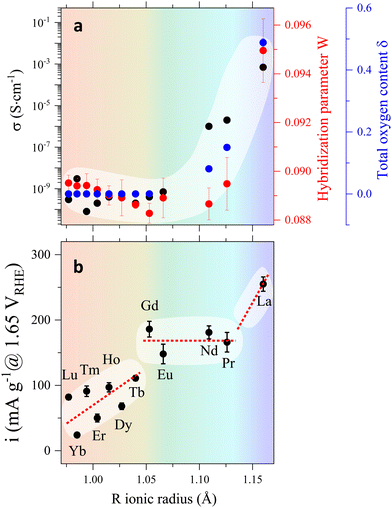
To summarize, our results indicate that the behaviour of the electric conductivity in RBaCuFeO_5+δ layered perovskites is closely linked to the modification of the crystal structure upon R cation replacement, and in particular, to its impact on the Cu/Fe 3d – O 2p overlap W. This parameter, which depends on the average values of the TM–O distances and TM–O–TM angles, was calculated exactly from the PND structural data, and its evolution with R_ionic was found to scale with that of σ. However, neither W nor σ scale with the OER activity, which also depends on the details of the A-cation and O vacancy distribution in the layered structure. Hence, improving conductivity though the incorporation of additional O does not grant an increase in the OER activity in RBaCuFeO_5+δ layered perovskites, which also requires a distribution of oxygen vacancies in the structure that provides sufficient weakly bonded oxygen and enough oxygen diffusion pathways. This last scenario, realized in LaBaCuFeO_5.49, suggests the involvement of the lattice oxygen in the OER process for this material, where the reaction mechanism could be the theoretically postulated LOER.^26–30

2.3. Stability of the Cu and Fe oxidation states

The impact of the initial B-cation electronic configuration in the OER activity has been intensively debated in the literature, particularly for Co-based perovskites, and there is increasing evidence suggesting that it plays an essential role in the catalyst electrochemical behaviour and OER performance.^1,2 In RBaCuFeO_5+δ perovskites the best figures of merit are found for the O-rich samples, but the B-position is occupied by two different cations. A pertinent question is thus which one among them (Cu²⁺ or Fe³⁺) will be the most prone to provide electrons that compensate the incorporation of additional oxygen in the structure, and what will be the resulting 3d orbital occupation(s). A technique that can provide insight on the changes in the Cu and Fe electronic configuration is X-ray absorption spectroscopy (XAS), which can selectively probe the empty states of the different atomic species (ESI†).

4f lanthanide M-edges. In oxide perovskites, R cations are usually assumed to be inert, formally trivalent spacers with electronic configurations 4fⁿ, with n taking values between 0 (La) and 14 (Lu). However, some lanthanides (among them Ce, Pr and Tb) may display both, +3 and +4 oxidation states depending on the synthesis conditions. Since the stabilization of tetravalent R cations may have an impact in the valence assignation of Fe and Cu, we investigated the R oxidation state in the full series by examining the M edges of the R cations, which probe the unoccupied density of R 4f states. The main contribution to these edges comes from the excitation of electrons from the spin–orbit-split levels 3d_5/2 and 3d_3/2 into empty states of 4f symmetry, which appear as two intense, well-separated line groups denoted as M₅ and M₄, respectively. The M_5,4 lines are characterized by a fine structure that is governed by the Coulomb and exchange interaction between the 3d⁹ core hole and the 4f electrons. Since these interactions depend on the number of electrons in the 4f shell, the details of the fine structure are characteristic of each 4f electronic configuration. Transitions from 3d levels into empty 6p states are also dipole-allowed, but their intensity is much weaker than that of the M_5,4 lines, in particular for the lanthanides with a large number of 4f holes.

The M edges measured for our twelve RBaCuFeO_5+δ samples using the total electron yield (TEY) mode are shown Fig. S7 (ESI†). For R = Lu, the absence of the M_5,4 lines brings to light the weak 3d → 6p signal, indicating a full 4f¹⁴ occupation consistent with the presence of Lu³⁺. The M_5,4 lines are well visible in the remaining spectra, and we have compared their fine structures with those reported in ref. 41 for well characterized oxides with trivalent R cations, as well as with the calculations of Thole et al.⁴² A detailed comparison was not possible for R = Pr due to the superposition between the Pr M_5,4 and the Cu L_3,2 edges. However, for remaining R-cations, the comparison shows that all our M_5,4 spectra correspond to 4f lanthanides in a triply ionized ground state. Given that they were recorded in TEY mode, which probes mainly the surface of the catalyst's particles (2–5 nm), we can conclude that the nominal bulk valence of R cations in our RBaCuFeO_5+δ layered perovskites (+3) is preserved in the particle's surface, where they remain trivalent for all the compounds investigated.

Fe and Cu K-edges. The high penetration of the energies associated to the Fe and Cu K-edges (∼7 and ∼9 keV respectively) make them ideal probes to investigate the oxidation state of these elements in the particle's bulk. Fig. S8a (ESI†) shows the Fe K-edge X-ray absorption near-edge spectra region measured for the compounds with R = Lu, Yb, Tm, Er, Ho, Dy, Tb and La. This edge cannot be accessed for the remaining compounds (R = Gd to Pr) due to the overlap with the L-edges of the R cations. However, this reduced set includes representatives of the δ = 0 (Lu to Tb) and δ > 0 (La) stoichiometries. The main contribution to the 3d TM K-edges comes from the excitation of TM 1s core electrons into empty states of 4p symmetry. The information about the TM 3d filling is thus only indirect. However, for absorbers with the same ligands and the similar coordination polyhedra, the energy position of the main absorption threshold, which we define here as the maximum of the edge's first derivative (Fig. S8b, ESI†), has been shown to correlate positively with the cation oxidation state.⁴³ For the compounds with R = Lu to Tb, the edge position (Fig. S8c (ESI†) and blue markers in Fig. 5b) displays little changes with the R ionic radius, the only appreciable modification being a smooth displacement of the edge position towards lower energies (ΔE ∼ −0.22 eV). Given the perfect oxygen stoichiometry of these compounds, this is probably linked to the small increase of the average Fe–O distance with R_ionic, which according to Natoli's rule⁴⁴ should result in a small energy displacement proportional to the inverse of the squared average bond length. This smooth evolution is abruptly reversed for LaBaCuFeO_5.49, the compound with the highest OER activity, whose Fe K-edge undergoes a huge displacement towards higher energies (ΔE ≈ +0.73 eV) when moving from R = Tb to La. This observation strongly suggests that the extra oxygen incorporated by this material results in a substantial increase of the Fe oxidation state, possibly because of a preferential bonding to this transition metal.

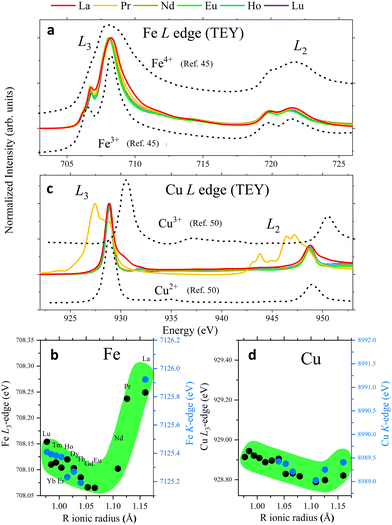Fig. 5 L and K-edge features of representative RBaCuFeO_5+δ layered perovskites (see also Fig. S8 and S9, ESI†). (a) Fe L-edges. (b) Left axis: maximum of the Fe K-edges's 1st derivative; right axis: Fe L₃-edges's maximum. (c) Cu L-edges. The different shape for R = Pr is due to the superposition with the Pr M_5,4 edges (see also Fig. S7, ESI†). (d) Left axis: maximum of the Cu K-edges's 1st derivative; right axis: Cu L₃-edges's maximum. All L-edges were measured using the TEY mode.

If the extra oxygen binds preferentially to the Fe sites, most of the (nominally divalent) Cu sites will preserve the square-pyramidal coordination, and the Cu oxidation state will remain nearly unchanged (Fig. 4f). To check whether this is the case we examined the evolution of the Cu K-edges. Due to overlap with the L-edges of the R-cations, the only accessible Cu K-edges are those of the compounds with R = Tb, Gd, Eu, Nd, Pr and La (Fig. S8d, ESI†). Luckily, this reduced set also includes representatives of the δ = 0 (Tb) and δ > 0 stoichiometries (Gd to La). As shown in Fig. 5d (blue markers) and Fig. S8f (ESI†), the edge position decreases smoothly with R_ionic for R = Tb, Gd, Eu and Nd, where δ is either 0 or very small. Since the average Cu–O distance also increases with R_ionic, this is most probably another manifestation of the Natoli's rule. For R = Pr and La, with δ values substantially larger, this tendency is broken, and the edge positions move to slightly higher energies. The displacement is however much smaller than in the case of the Fe K-edges. To illustrate this point we can compare the positions of the Tb and La samples in the Fe and Cu K-edges. The Fe K-edge of the La sample is +0.73 eV higher than the one with Tb. In contrast, the Cu K-edge positions of both samples are nearly identical. This suggests that the electrons needed to compensate the incorporation of oxygen in the structure are primarily provided by Fe³⁺, which partially oxidizes to Fe⁴⁺. The Cu²⁺ valence appears to be more robust against oxidation, but for R = Pr and La our data suggest that Cu²⁺ oxidizes partially to Cu³⁺, albeit in a much smaller amounts. It is worth mentioning that these conclusions apply to the sample bulk. However, we will show in the next section that the analysis of the Fe and Cu L-edges measured using the TEY mode supports a similar behaviour also in the particle's surface.

Fe and Cu L-edges. The main contribution to the Fe and Cu L-edges comes from the excitation of electrons from the spin–orbit-split levels 2p_3/2 and 2p_1/2 into empty states of 3d symmetry. This results in two strong absorption lines, (L₃ and L₂ edges, respectively) whose shape and fine structure encode information about the absorber's electronic configuration. The Fe L-edges of the twelve RBaCuFeO_5+δ layered perovskites measured using the TEY mode are displayed in Fig. 5a and Fig. S9a (ESI†). For the samples with δ = 0 (R = Lu to Eu) the spectra are very similar to the Fe L-edge of LaFeO₃ reported in ref. 25 and 45 where Fe is nominally trivalent. However, their shape starts to change as soon as O is incorporated in the structure. The changes are particularly pronounced for the L₃ edges, where the sharp feature at ∼707 eV smears out, additional intensity appears at energies between 709–711 eV, and the L₃ maximum moves towards higher energies. Since the L-edges of SrFeO₃^25,45 and BaFeO₃,⁴⁶ where Fe is nominally tetravalent, share these characteristics, the evolution of the L-edges in the O-rich samples (R = Nd, Pr and La) strongly suggests a progressive oxidation of Fe³⁺ to Fe⁴⁺ upon O uptake (see also Fig. S9a, ESI†). The strong broadening of the SrFeO₃ L-edge, more pronounced than that of LaBaCuFeO_5.49 (the material with the highest O content of this study) suggests nevertheless that the Fe³⁺ → Fe⁴⁺ oxidation is incomplete for all the samples investigated.

The different behaviour of the O-poor (δ = 0) and O-rich samples is illustrated in Fig. 5b, where the black symbols show the evolution of the L₃ maximum with R_ionic. For R = Lu to Eu we observe a small displacement towards lower energies, possibly related with the small changes in the square-pyramidal crystal field splitting with R_ionic (Fig. 2c).⁴⁷ In contrast, the L₃ maximum undergoes a sharp displacement towards higher energies for R = Nd, Pr and La, where oxygen is progressively incorporated to the structure. Given that the spectra were measured using the TEY detection mode, these changes are expected to reflect the Fe oxidation in the particle's surface. Interestingly, a comparison between the evolution of the L₃ maximum and the position of the Fe K-edge along the series (black and blue markers in Fig. 5b, respectively) reveals a nice scaling between the two sets of data, and suggests that Fe oxidizes upon O incorporation both, in the bulk and in the surface.

We compare now this behaviour with that of the Cu L-edges. As shown in Fig. 5c and Fig. S9b (ESI†), the spectra of the materials with R = Lu to Nd are very similar to that reported for CuO^48,49 or some Cu(II) complexes⁵⁰ where Cu is nominally divalent. For R = Pr some changes start to become evident, but they are partially hidden by the overlap with the Pr M_5,4 lines (Fig. S7, ESI†). This tendency is confirmed for R = La, where new features (see also Fig. S9b, ESI†) are clearly observed at energies very close to those of the L₃ and L₂ lines of NaCuO₂,^48,49 where Cu is nominally trivalent.

As in the case of the Fe L-edges, the Cu L₃ maximum moves slightly towards lower energies by increasing the R ionic radii (black markers in Fig. 5d), an observation that we also ascribe to changes in the crystal field splitting of the CuO₅ pyramids (Fig. 2d). This tendency changes for R = Pr and La, where the energy position of the L₃ maximum moves slightly towards higher energies. However, the displacement is much less pronounced than in the case of the Fe L₃ edge. This behaviour is again very similar to that of the Cu K-edges (blue markers in Fig. 5d), whose position scales nicely with that of the Cu L₃ maximum. This suggests that Cu is more robust against oxidation not only in the catalyst bulk, but also in the surface.

To summarize, the analysis of the rare-earth M-edges, Cu/Fe K-edges and Cu/Fe L-edges converges towards a scenario where the electrons needed to compensate the oxygen uptake are primarily provided by Fe³⁺, which partially oxidizes to Fe⁴⁺ both, in the bulk and in the particles surface. Interestingly, the Fe⁴⁺ electronic configuration (t³_2g e¹_g) features the e¹_g filling proposed by Suntivich et al. as optimal for the OER activity in perovskite oxides.¹

2.4. Electronic structure close to the Fermi level: bulk versus surface

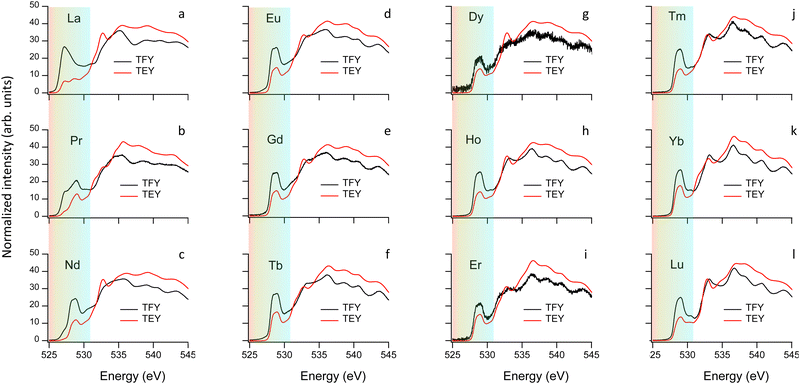
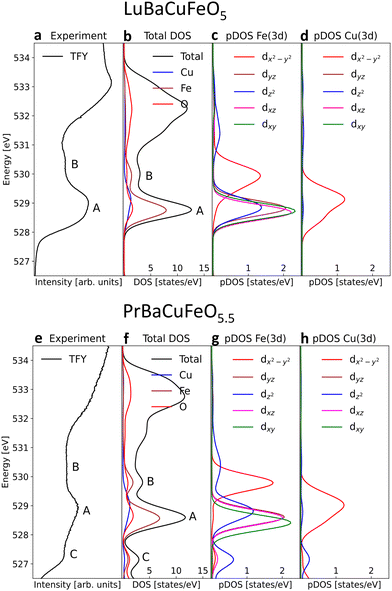
After addressing the impact of the O incorporation on the Fe and Cu 3d electron filling and its link to the OER activity, we focus on the modifications of the electronic structure near the Fermi level E_F. The occupied and unoccupied density of states (DOS) near E_F determine not only the gap, directly linked to the conductivity, but also the adsorption interaction and the electron exchange rate between the OER reaction intermediates and the catalysts surface. To access these states we employ here XAS at the O K-edge that we combine DFT+U ab initio calculations.

O K-edges. According to the electric dipole selection rules, the main contribution to O K-edges comes from the excitation of O 1s electrons into empty O states of 2p symmetry. However, it is also possible to obtain information about the density of empty 3d states of the TM cations thanks to their hybridization with the O 2p states. In perovskite oxides these states usually appear in the lowest energy part of the spectra, and reflect the O 2p weight in states of predominantly 3d character.⁵¹

Fig. 6 shows the normalized O K-edges of our RBaCuFeO_5+δ layered perovskites measured using the total fluorescence yield (TFY) and TEY detection modes (ESI†). Since TFY can be considered a bulk probe whereas TEY is more sensitive to the particle's surface, the use of both detection modes allows for a depth-profile analysis of the RBaCuFeO_5+δ particles. By comparing the two sets of data, we note that the pre-edge intensities of all samples (shaded region) are systematically higher in the TFY spectra. Moreover, the pre-edge shapes measured using the two detection techniques are very similar in the samples with δ = 0, but notoriously different in the O-rich samples. Since the pre-edge structures of TM oxides reflect the CEF splitting of the 3d orbitals,⁵¹ the similar TFY and TEY pre-edge shapes of the compounds with R = Lu to Eu (δ = 0) suggest a common TM environment in the bulk and the surface. The lower intensity of the TEY pre-edges suggests nevertheless a reduced O 2p–TM 3d surface hybridization, possibly due to slightly longer TM–O distances and/or smaller TM–O–TM angles in the TMO₅ pyramids compared with the bulk. For the samples with R = Nd, Pr and La (δ > 0), the different shapes of the TFY and TEY pre-edges suggests in contrast that existence of an important surface reconstruction happening exclusively in these O-rich materials.

Fig. 6 O K-edges of RBaCuFeO_5+δ layered perovskites measured using the TFY and TEY modes. The color-shaded areas indicate the energy range associated to empty 3d TM states hybridized with the O 2p states.

DFT calculations: O-poor RBaCuFeO_5+δ samples (δ = 0). To rationalize these observations we used fully-relaxed ab initio DFT calculations, whose details are described in the Materials and Methods section (ESI,† Fig. S10–S13). The calculations were performed for the bulk materials, but as we show later, they are also a good starting point to understand the catalyst’ surface. As shown in ref. 51 DFT-calculated density of empty states are in general quite close to the experimentally measured O K-edges. This is illustrated in Fig. 7a and b, where we compare the low-energy part of the LuBaCuFeO₅ O K-edges measured using the TFY mode with the bulk DFT calculation. The calculated DOS confirms that the structures below ≈531 eV correspond to O states hybridized with empty Fe and Cu 3d states. Moreover, the main contribution to the TM empty DOS comes from the Fe 3d orbitals (Fig. 7b). This is consistent with nominal Fe (+3) and Cu (+2) oxidation states, with five and one 3d holes respectively. Moreover, their energies reflect their CEF splitting in square-pyramidal coordination, which is significantly different from the familiar t_2g–e_g splitting observed in octahedral coordination. The main difference is the strong stabilization of the d_z² orbital (Fig. 1b), which has now energies close to that of the d_xy, d_yz and d_xz orbitals. In LuBaCuFeO₅, this gives rise to an intense, broad absorption maximum labelled “A” and centered around ≈529 eV that corresponds to transitions into four of the five half-occupied Fe³⁺ 3d orbitals (d_z², d_xy, d_yz and d_xz), plus the only half-occupied Cu²⁺ 3d orbital d_x²–y² (Fig. 7c and d). The transition into empty Fe 3d_x²–y² states labelled “B” appears about 1.5 eV higher (≈ 530.5 eV), and has a considerably lower intensity consistent with the smaller number of accessible empty states.

Fig. 7 Comparison between the O K-edges measured in TFY mode and the DOS from DFT calculations together with the Fe, Cu and O partial-DOS and the contributions of the different empty Fe and Cu 3d orbitals. (a)–(d) LuBaCuFeO₅. (e)–(h) PrBaCuFeO_5.5.

For the remaining RBaCuFeO₅ materials with δ = 0 (R = Lu to Eu) the agreement between the measured pre-edges (Fig. 6) and the calculated DOS (Fig. S12, ESI†) is also remarkably good. Moreover, the calculations are able to reproduce the energies and relative intensities of the “A” and “B” features in both, the TFY and the TEY spectra, as well as their practical invariance with R_ionic. This supports our initial guess concerning the absence of significant differences between bulk and surface 3d crystal field splittings for these materials, suggestive of a surface Cu/Fe environment quite similar to that of the particle's bulk.

DFT calculations: O-rich RBaCuFeO_5+δ samples (δ > 0). For the materials with oxygen excess, a new feature labeled “C” and centered around ≈527 eV starts to become evident for R = Nd in both, the TFY and the TEY spectra. It grows continuously with δ in both sets of data, albeit at a much faster rate in the bulk-related TFY spectra. Its intensity is particularly large for the TFY pre-edge of the La sample, where it dominates the low energy part of the unoccupied DOS. Since this feature is clearly linked to the incorporation of extra O in the structure we performed two additional sets of (bulk) DFT calculations for the oxygen-rich samples using two additional O stoichiometries (RBaCuFeO_5.5 and RBaCuFeO₆), the last one representing the end case of the O incorporation (Fig. S10, S13 and S14, ESI†).

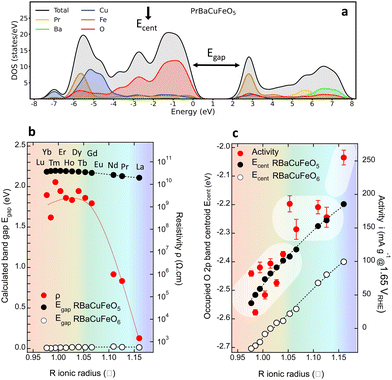
The agreement between theory and experiment is illustrated in Fig. 7e and f, showing a comparison between the observed TFY pre-edge of the Pr sample and the DOS calculated for PrBaCuFeO_5.5. Besides reproducing the energies and approximate relative intensities of the different pre-edges features, the calculation allows also to identify the “C” feature. As shown in Fig. S14 (ESI†), the appearance of these states upon O incorporation results in a drastic reduction of the gap, which disappears already for δ = 0.5. Moreover, the DFT-calculated DOS also reveals the appearance of additional O 2p hole states at energies very close to those of the Fe 3d_x²–y² orbitals (B-feature). This increases substantially the Fe 3d–O 2p intermixing, in excellent agreement with the sharp rise of the hybridization parameter W for the materials with δ > 0 (Fig. 3a). Another interesting observation is that the overlap between the 3d_x²–y² empty states and new O 2p holes is much larger for Fe than for Cu. This, together with the additional contribution to the O 2p–Fe 3d_z² hybridization from the “C” feature is consistent with the preferential oxidation of Fe³⁺ into Fe⁴⁺ upon oxygen incorporation, in agreement with the conclusions inferred from the analysis of the K and L TM edges.

For the O-rich materials, we note that the agreement between the measured TFY pre-edge intensities and the calculated DOS is less good than in the case of the O-poor compounds, in particular for R = La. This could arise from the difference between the actual O content and the δ values employed in the calculations, but also from the difficulty of implementing in DFT complex O vacancy distributions and R/Ba intermixing patterns while keeping reasonable computing times. A comparison between the experimental PFY O K-edges and the calculated DOS indicates nevertheless that the supercells used in this study (Fig. S10, ESI†) are a good compromise that allows to capture the main features of the PFY pre-edges of the O-rich samples. This concerns the energies of the “A”, “B” and “C” features, their approximate relative intensities, as well as the progressive metallization of RBaCuFeO_5+δ layered perovskites upon O incorporation into the lattice.

We address now the possible origins of the strong differences between the TFY and TEY pre-edges observed in the O-rich samples. The most salient among them is the growth rate of the “C” feature with δ, much faster in the bulk TFY than in the surface-related TEY spectra. Since this feature is related to the O 2p–Fe 3d_z² hybridization, we can tentatively assign the lower intensity in the TEY pre-edges to an oxygen depletion in the surface. However, it could also arise from a structural rearrangement in the particle's surface involving a decrease of the O 2p–Fe 3d_z² overlap. An example of the last possibility was recently provided by our recent study on the isostructural layered cobaltite PrBaCo₂O_5.43, where the existence of a surface reconstruction with less efficient Co 3d–O 2p overlap was suspected from the differences between the TFY and TEY O K-edge spectra and further confirmed by high-resolution scanning transmission electron microscopy (STEM) measurements.³⁰ This last technique revealed important displacements of the Co sites with respect to the bulk positions in a thin surface layer (∼2 unit cells) compatible with a reduced Co 3d–O 2p hybridization. Given the absence of high-resolution STEM measurements for our O-rich samples we cannot unambiguously claim a similar origin for the TFY-TEY differences based in our O K-edge data alone. However, given the common layered perovskite structure, similar O content, and strong similarities between the bulk and surface O K spectra of PrBaCo₂O_5.43 and LaBaCuFeO_5.49, it seems reasonable to assume that such possibility is not unlikely.

Besides Co displacements, STEM measurements also revealed the existence of Ba depletion in the PrBaCo2O_5.43 particles surface. Ba segregation has already been reported in the literature for long, high-temperature annealing processes on Ba containing perovskites with δ > 0,⁵² and given the synthesis procedure employed in this study, it could also happen in our samples. In order to check this possibility we measured the Ba M_5,4 absorption edges, whose main contribution comes from the excitation of electrons from the transition of electrons from the spin–orbit-split levels 3d_5/2 and 3d_3/2 into empty states of 4f symmetry. The Ba M_5,4 spectra recorded using the surface-sensitive TEY mode, are shown in Fig. S15a (ESI†) and look very similar to those reported in compounds containing Ba²⁺.⁵³ Moreover, in contrast with the behaviour observed in the L_3,2 Fe edges (Fig. 5), the M_5,4 lines change very little with the R ionic radii, without appreciable discontinuities in the M₅ and M₄ maxima at the setup of the oxygen uptake (Fig. S15b, ESI†). This observation suggests that the surface reconstruction of the O-rich samples does not involve significant changes in the Ba coordination, which would remain similar to that of the samples with δ = 0.

DFT calculations: band gap and O 2p valence band centroid. The calculated DOS provides also an estimation of the band gap E_gap, shown schematically in Fig. 8a. For the samples with δ = 0 (R = Lu to Eu) E_gap takes values close to 2.2 eV, typical of semiconductors and compatible with the measured resistivity ρ = 1/σ values (Fig. 8b). Moreover, its smooth decrease for increasingly larger R ionic radii is consistent with the practical invariance of ρ and the hybridization parameter W (Fig. 3a) in these materials. For the O-rich samples (R = Nd, Pr, La) the resistivity decreases very fast upon O incorporation, reaching values more than six orders of magnitude lower typical of metals in the case of R = La. This trend is nicely reproduced by DFT calculations, where the appearance of new hole states for growing δ values leads to the progressive reduction of the gap (Fig. S14, ESI†), fully closed in the RBaCuFeO₆ materials (white markers in Fig. 8b).

Fig. 8 (a) Calculated DOS for PrBaCuFeO₅ showing the location of the valence band O 2p centroid E_cent and the band gap E_gap. (b) Left axis: calculated E_gap for the RBaCuFeO₅ and RBaCuFeO₆ bulk materials. Right axis: experimental resistivity. (c) Comparison between the changes in the experimental OER activity upon R-cation replacement with those in the calculated valence band O 2p E_cent for RBaCuFeO₅ and RBaCuFeO₆.

A further parameter delivered by DFT calculations is the valence O 2p band centroid E_cent relative to the Fermi level (black vertical arrow in Fig. 8a), reported to positively correlate with the OER activity in Co-based layered perovskites RBaCo₂O_5+δ with δ > 0 under the assumption that the catalyst’ surface is fully oxidized (δ = 1).¹⁵ The evolution of this variable for the RBaCuFeO_5+δ ferrocuprates with δ = 0 and δ = 1, shown in Fig. 8c and Fig. S12, S13 (ESI†) indicates that, in both cases, E_cent approaches monotonically E_F for increasing R_ionic values. However, it also reveals that E_cent moves away from E_F by increasing the oxygen content δ. The use of the valence O 2p band centroid as OER descriptor relies thus on whether the catalyst surface can be considered fully oxidized in all the materials under comparison.

In our RBaCuFeO_5+δ samples, where the bulk O content changes between 5 (Lu to Eu) and 5.49 (La), the degree of surface oxidation can be assessed from the intensity of the “C” feature in the TEY spectra, which indicates the presence of O excess in the surface. This feature, absent in the samples with δ = 0, is clearly present in TEY spectra of the materials with R = Nd, Pr and La. Moreover, its intensity increases with δ and is systematically lower than in the TFY spectra, which reflect the bulk O excess (always lower than 0.5). These observations are difficult to conciliate with a common, fully oxidized surface (δ = 1). The proposed positive correlation between OER activity and E_Op is thus not expected to apply to our samples, at least in their pristine form. The confirmation of this guess is illustrated in Fig. 8c, where the correlation between OER activity (red markers) and E_cent is positive only for the samples with the same O content (R = Lu to Eu, δ = 0). For R = Nd, Pr and La the OER activity increases continuously but E_cent decreases due to their increasingly large O content. The OER–E_cent correlation is thus negative. Operando or post-operando O K-edge measurements will be necessary to assess whether the surface oxygen content is modified after the OER process with respect to the pristine materials.

2.5. Role of 4f electrons

Traditionally, the role of the A cations in the OER process has been considered marginal, and the few studies suggesting their involvement for some perovskite oxides have only been reported recently.⁵⁴ In the particular case of RBaCuFeO_5+δ layered perovskites, an active participation of the R cations, with localized 4f electrons contributing very little to the DOS close of the Fermi level (Fig. S12, ESI†) seems unlikely. The alternating behaviour of the activity with the parity of the 4f electron count observed in the compounds with δ = 0 (Fig. 1c) is thus unexpected, and suggests a possible impact of the ground state of the R³⁺ cations (a singlet and a Kramers doublet for even and odd 4f electrons counts, respectively). Additional support in this sense is provided by the loss of the 4f electron count alternation at the setup of the extra oxygen uptake (R = Gd), where the increased structural disorder and inhomogeneity are expected to modify the symmetry of the R³⁺ cation ground state. Finding what is the exact role of the 4f electrons in the OER activity of the O-poor materials is nevertheless beyond the scope of this study and will require additional experimental and theoretical work.

2.6. Intrinsic OER activity: comparison between LaBaCuFeO_5+δ and PrBaCo₂O_5+δ

The use of well-crystallized samples prepared by solid-state synthesis was necessary to obtain PND data with sharp Bragg reflections suitable for a detailed structural analysis. However, it was clearly detrimental for the electrochemical performance due to their large particle sizes. To evaluate the impact of this variable we prepared a nanometer-sized LaBaCuFeO_5+δ sample using flame-spray synthesis, an easily scalable synthetic method proved to be very efficient in the large production of perovskites nanopowders.^13,55 The conditions used for the synthesis guaranteed a good compromise between particle size (Fig. S3 and Table S3, ESI†) and sample purity, with only minor amounts of precursors still present in the final sample (Fig. S16a, ESI†). As shown in Fig. 9 and Table S1–2 (ESI†), reducing the average LaBaCuFeO_5+δ particle size from the micro to the nano-range increases the OER gravimetric activity at 1.65 V_RHE by a factor of ∼5. This increase occurs in spite of an eight orders of magnitude decrease in conductivity due to the increased grain-boundaries resistance (Table S1, ESI†), and the presence of secondary phases in the catalyst powder, which result in the underestimation of the nano-electrocatalyst activity.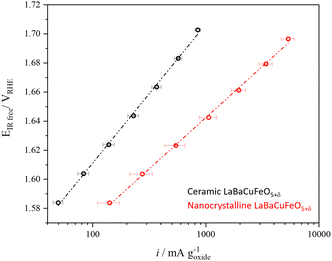

Fig. 9 Comparison between the gravimetric activity of the ceramic and nanocrystalline LaBaCuFeO_5+δ samples.

Next, we compared the intrinsic (i.e., surface-normalized activity) of our nano-sample with that of nano-sized PrBaCo₂O_5+δ synthesized using the same technique and measured at the same pH (=13).¹³ Normalization to the BET-measured surface area (5.8 m² g⁻¹) gives an OER activity of 0.0047 mA cm⁻² at 1.60 V_RHE for the LaBaCuFeO_5+δ nanopowder, a value ≈25 times smaller than the activity reported for PrBaCo₂O_5+δ nanoparticles at the same V_RHE (0.12 mA cm⁻²).¹³ The activity of the ferrocuprate is also lower than the value reported for La_0.6Sr_0.4CoO₃ thin films at the same pH and V_RHE (≈0.1 mA cm⁻²),⁵⁶ although in this case a comparison is less straightforward due to the different purity and geometry of both materials. Given the absence of cobalt and the exploratory nature of our study, the results obtained for the LaBaCuFeO_5+δ nanopowder are nevertheless encouraging, and call for additional investigations aimed at improving this promising result.

3. Discussion and conclusions

In this study, we have investigated the potential of the layered perovskite family RBaCuFeO_5+δ as Co-free OER catalysts, with cheap, abundant transition metals in the B-positions. Our OER activity measurements reveal a complex behaviour along the 4f series, with no direct correlation with the R ionic radius, the electric conductivity or the valence O 2p band centroid. To rationalize these results we investigated in detail the changes in the crystal and electronic structures using a combination of ab initio calculations and advanced neutron and X-ray synchrotron techniques. The behaviour of the OER activity along the 4f series was then contrasted with that of different structural and electronic parameters proposed as OER descriptors in the recent literature.

Our combined analysis reveals a positive impact of the oxygen excess (δ > 0) in the conductivity, which leads to the preferential oxidation of Fe³⁺ into Fe⁴⁺ while keeping the Cu²⁺ valence nearly unchanged. The creation of Fe⁴⁺ sites upon oxygen incorporation results in a sharp rise of the Fe–O hybridization and in the creation of new hole-states in the gap. The combined effect of these two mechanisms is at the origin of the abrupt increase of the electric conductivity, which remains nearly constant in the O-poor samples (δ = 0). Interestingly, growing σ values do not grant a simultaneous increase of the OER activity, which requires also sufficient weakly bound oxygen and a distribution of oxygen vacancies that ensures enough oxygen diffusion channels in the catalysts bulk.

In RBaCuFeO_5+δ layered perovskites, the R/Ba alternation restricts the oxygen vacancies to the R-planes due to the stronger affinity of Ba²⁺ for high oxygen coordination compared to that of the R³⁺ cations. The incorporation of weakly bonded oxygen to these planes opens a new electronic conduction channel along the c-axis, and was also expected to enable O diffusion in the R-layers. The shape of the thermal ellipsoids suggest however that this extra oxygen remains static as long as the R/Ba order along the c-axis is preserved. Interestingly, a certain degree of Ba/R intermixing (observed here only for R = La) has a huge impact in the shape of the O thermal ellipsoids, which is now compatible with the existence of O 2D diffusion both, in the La and in the Ba planes. The presence of some low-coordinated La cations in the Ba layers allows indeed the creation of O vacancies also in these layers. Moreover, it homogenizes the interatomic distances and angles (Fig. 2), resulting in a smoother potential landscape that lowers the energy barrier for O jumps and facilitates the setup of O diffusion.

It is worth mentioning that our structural data alone do not prove the presence of O diffusion in LaBaCuFeO_5.45, However, they strongly support it based on similar observations in other ionic conductors.^40,57,58 Incidentally, LaBaCuFeO_5.45 shows also the best electrochemical performance of this study. It is thus tempting to make the link between O diffusion in the catalyst's bulk and OER activity, a link that, at least for this material, suggests the participation of the lattice oxygen in the OER process (LOER).^3,30,59

A further interesting result of this investigation is the observation of an important reconstruction of the catalysts surface exclusively in the O-rich samples. For the O-poor materials (δ = 0), the close similarity between the O K-edges measured using the TFY and TEY modes indicates only minor differences between the catalyst's bulk and surface. In contrast, the pronounced differences observed in the O rich samples indicate the existence of major structural changes involving either O depletion, and/or a huge decrease of TM–O hybridization. Intriguingly, our data do not provide any clear evidence for modification of the Ba environment in particle's surface by increasing the O content. A possible reason could be a preference for surface terminations containing the R-cations. The RBaCuFeO_5+δ oxides are indeed layered materials with a preference for surface terminations perpendicular to the c axis. Since the strongest bonds correspond to the Cu–O/Fe–O layers, the planes containing the R-cations are prominent candidates due the reduced number of R–O bonds compared with the Ba–O planes. Interestingly, such a scenario could bring the 4f orbitals close to OER intermediates, giving some hints to understand the intriguing alternation of the OER activity with the 4f electron count. Experiments on RBaCuFeO_5+δ thin films with different surface terminations could help to establish whether this is the case in the RBaCuFeO_5+δ family.

Since the best OER performance of this study corresponds to LaBaCuFeO_5.45, which has lost some of its layered character due to the partial La/Ba intermixing, a pertinent question is whether a cubic material with the same composition (including O content) but perfectly random A-site disorder would be a more performant electrocatalyst. Our results suggest that some layered character, even if it is reduced by the R/Ba intermixing, helps to create a stack of physically separated R–O and Ba–O planes with a smooth potential landscape for O ionic diffusion, seemly advantageous for a high OER activity. This situation is not found in cubic materials, where O diffusion paths can be more intricate. The better suitability of the layered perovskite framework for the OER process has also been proposed in some recent studies, and attributed to the optimal position of the calculated O 2p valence band centroid E_cent with respect to the Fermi level, close to E_F but more distant than in the case or 3D perovskites. In the case of the RBaCuFeO_5+δ family, the highest OER activity corresponds to R = La, the materials where E_cent is the most distant from E_F, and the only one that is pseudocubic. The proposed trend is thus not verified in our samples. A possible reason for the disagreement is that the O 2p band centroid calculations in ref. 15 were performed assuming a fully oxidized (δ = 1) catalyst surface in the materials under comparison, a condition that is not verified in our samples, at least in their pristine form. Operando or post-operando O K-edge measurements will be necessary to assess whether the surface oxygen content is modified after the OER process with respect to the pristine materials.

As a concluding remark, we would like to point out that the results presented in this study allowed to identify several strategies that could help to design a Co-free layered perovskite with improved OER performance. One of the most critical variables appears to be the choice of the A and A′ cations, whose ionic radii should be close enough to allow intermixing but different enough to preserve some degree of layered character. La³⁺/Ba²⁺ and perhaps Pr³⁺/Ba²⁺ look as the most promising candidates, but other R³⁺-cations can be also suitable using synthetic techniques favoring an intimate mixing of the material's precursors. Concerning B-cations, our XAS data point towards a large number of empty 3d orbitals, in particular those enabling Sigma-bonding and thus a higher degree of TM 3d–O 2p hybridization. Configurations with a large number of e_g holes such as t³_2g e¹_g (Fe⁴⁺, Mn³⁺) or t⁶_2g e¹_g (Ni³⁺, Co²⁺) appear thus as ideally suited. If we exclude Co²⁺, as well as Ni³⁺ that may require the use of high O pressure,⁶⁰ possible candidate materials could be the solid solutions LaBaCu_1−xMn_xFeO_5+δ (δ < 0.5) and LaBaCu_1−xFe_xO_5+δ (δ > 0.5) where the stability of the Cu²⁺ oxidation state is expected to favour large amounts of Fe and Mn with electronic configurations close to e¹_g. An additional strategy could be to determine, for each candidate material, the optimal oxygen content. In this case, it will be important to avoid “magical” O contents such as O_5.5, prone to O vacancy order and electronic localization.⁶¹ LaBaCuFeO_5.49, the material with the best figures of merit of our study, is close to this composition, but contrarily to the A-site ordered cobaltite PrBaCo₂O_5.48,³⁰ O-vacancy order was not observed, most probably because of the huge structural inhomogeneity caused by the La/Ba disorder. The growth of layered perovskites in thin film form, which allows obtaining extremely pure materials with large active surfaces, could also be a possible approach.⁶² Interestingly, previous studies on the layered Co perovskite PrBaCo₂O_5+δ grown as epitaxial thin films indicate that, as reported in this study, structural disorder – and in particular A-site intermixing – is beneficial for the OER activity.⁶³ A further approach could be to exploit the multiferroic nature of some such materials,⁶⁴ which has been shown to be beneficial for the catalytic activity in some recent studies.^65–67

To summarize, we have experimentally investigated the potential of RBaCuFeO_5+δ perovskites as Co-free OER catalysts. Our detailed structural characterization constitutes one of the few attempts to rationalize electrochemical properties in terms of TM–O interatomic distances, TM–O–TM angles, O content and chemical disorder and mean-square displacements, which were determined in this study with great precision. By combining these data with the results of X-ray spectroscopies and DFT calculations we could identify the critical structural and electronic variables leading to high OER catalytic performance, which can be exploited for the design of other Co-free layered perovskites. Moreover, our study revealed LaBaCuFeO_5+δ as a new promising OER catalyst candidate that can be industrially produced in nanocrystalline form. Altogether, our results provide additional support to the layered perovskite structure as a promising structural framework to search for OER catalysts, and could accelerate the discovery of Co-free materials with optimal properties for electrochemical water splitting and H₂ production.

Author contributions

Elena Marelli (lead author): formal analysis, investigation, methodology, visualization, writing – original draft. Jike Lyu (equal contribution): formal analysis, investigation, methodology, visualization, writing – original draft. Mickaël Morin (supporting author): investigation, methodology, writing – reviewing & editing. Maxime Leménager (supporting author): investigation, methodology, writing – reviewing & editing. Tian Shang (supporting author): investigation, methodology, writing – reviewing & editing. Sena Yüzbasi (supporting author): investigation, methodology, writing – reviewing & editing. Dino Aegerter (supporting author): investigation, methodology, writing – reviewing & editing. Jinzhen Huang (supporting author): investigation, methodology, writing – reviewing & editing. Nieli D. Daffé (supporting author): investigation, methodology, writing – reviewing & editing. Adam H. Clark (supporting author): investigation, methodology, software, writing – reviewing & editing. Denis Sheptyakov (supporting author): investigation, methodology, writing – reviewing & editing. Thomas Graule (supporting author): validation, writing – reviewing & editing. Maarten Nachtegaal (supporting author): writing – reviewing & editing. Ekaterina Pomjakushina (supporting author): validation, writing – reviewing & editing. Thomas J. Schmidt (supporting author): writing – reviewing & editing. Mattias Krack (corresponding author): formal analysis, investigation, methodology, software, visualization, writing – reviewing & editing. Emiliana Fabbri (corresponding author): conceptualization, funding acquisition, project administration, methodology, supervision, validation, writing – reviewing & editing. Marisa Medarde (corresponding author): conceptualization, funding acquisition, project administration, methodology, investigation, formal analysis, supervision, writing – original draft.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is based on experiments performed at the Swiss spallation neutron source SINQ (HRPT diffractometer), and the Swiss Light Source (SuperXAS and Xtreme beamlines) at the Paul Scherrer Institute, Villigen, Switzerland. It was supported by the Swiss National Science Foundation (Grants No. 200021-141334/1, 200021-141334/2 and 206021-139082), and by the PSI internal funding instrument CROSS. We acknowledge access to Piz Daint at the Swiss National Supercomputing Centre, Switzerland under PSI's share with the project ID psi01.

References

1. J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Nat. Chem., 2011, 3, 546–550.
2. J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385.
3. C. E. Beall, E. Fabbri and T. J. Schmidt, ACS Catal., 2021, 11, 3094–3114.
4. X. Cheng, E. Fabbri, Y. Yamashita, I. E. Castelli, B. Kim, M. Uchida, R. Haumont, I. Puente-Orench and T. J. Schmidt, ACS Catal., 2018, 8, 9567–9578.
5. W. T. Hong, M. Risch, K. A. Stoerzinger, A. Grimaud, J. Suntivich and Y. Shao-Horn, Energy Environ. Sci., 2015, 8, 1404–1427.
6. J. Hwang, R. R. Rao, L. Giordano, Y. Katayama, Y. Yu and Y. Shao-Horn, Science, 2017, 358, 751–756.
7. E. Fabbri, A. Habereder, K. Waltar, R. Kötz and T. J. Schmidt, Catal. Sci. Technol., 2014, 4, 3800–3821.
8. M. A. Alkhalifah, B. Howchen, J. Staddon, V. Celorrio, D. Tiwari and D. J. Fermin, J. Am. Chem. Soc., 2022, 144, 4439–4447.
9. M. Medarde, C. Dallera, M. Grioni, J. Voigt, A. Podlesnyak, E. Pomjakushina, K. Conder, T. Neisius, O. Tjernberg and S. N. Barilo, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 054424.
10. C. Frontera, J. L. García-Muñoz, A. E. Carrillo, C. Ritter, D. Martíny Marero and A. Caneiro, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 184428.
11. A. J. Baron-Gonzalez, C. Frontera, J. L. Garcia-Munoz, J. Blasco and C. Ritter, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 054427.
12. J. Herrero-Martin, J. L. Garcia-Munoz, S. Valencia, C. Frontera, J. Blasco, A. J. Baron-Gonzalez, G. Subias, R. Abrudan, F. Radu, E. Dudzik and R. Feyerherm, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115131.
13. B.-J. Kim, X. Cheng, D. F. Abbott, E. Fabbri, F. Bozza, T. Graule, I. E. Castelli, L. Wiles, N. Danilovic, K. E. Ayers, N. Marzari and T. J. Schmidt, Adv. Funct. Mater., 2018, 28, 1804355.
14. L. Wang, K. A. Stoerzinger, L. Chang, J. Zhao, Y. Li, C. S. Tang, X. Yin, M. E. Bowden, Z. Yang, H. Guo, L. You, R. Guo, J. Wang, K. Ibrahim, J. Chen, A. Rusydi, J. Wang, S. A. Chambers and Y. Du, Adv. Funct. Mater., 2018, 28, 1803712.
15. A. Grimaud, K. J. May, C. E. Carlton, Y.-L. Lee, M. Risch, W. T. Hong, J. Zhou and Y. Shao-Horn, Nat. Commun., 2013, 4, 2439.
16. B. Kundys, A. Maignan and C. Simon, Appl. Phys. Lett., 2009, 94, 072506.
17. A. Scaramucci, H. Shinaoka, M. V. Mostovoy, R. Lin, C. Mudry and M. Muller, Phys. Rev. Res., 2020, 2, 013273.
18. T. Shang, E. Canévet, M. Morin, D. Sheptyakov, M. T. Fernández-Díaz, E. Pomjakushina and M. Medarde, Sci. Adv., 2018, 4, eaau6386.
19. X. D. Zhang, A. Romaguera, O. Fabelo, F. Fauth, J. Herrero-Martin and J. L. Garcia-Munoz, Acta Mater., 2021, 206, 116608.
20. J. Lyu, M. Morin, T. Shang, M. T. Fernandez-Diaz and M. Medarde, Phys. Rev. Res., 2022, 4, 023008.
21. Q. J. Zhou, T. M. He, Q. He and Y. Ji, Electrochem. Commun., 2009, 11, 80–83.
22. X. Z. Zhang, J. E. Zhou and Y. Q. Wang, Ionics, 2013, 19, 941–945.
23. A. I. Klyndyuk, E. A. Chizhova, D. S. Kharytonau and D. A. Medvedev, Materials, 2022, 15, 141.
24. M. Morin, A. Scaramucci, M. Bartkowiak, E. Pomjakushina, G. Deng, D. Sheptyakov, L. Keller, J. Rodriguez-Carvajal, N. A. Spaldin, M. Kenzelmann, K. Conder and M. Medarde, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 064408.
25. Z. C. Shen, Y. B. Zhuang, W. W. Li, X. C. Huang, F. E. Oropeza, E. J. M. Hensen, J. P. Hofmann, M. Y. Cui, A. Tadich, D. C. Qi, J. Cheng, J. Li and K. H. L. Zhang, J. Mater. Chem. A, 2020, 8, 4407–4415.
26. T. Binninger, R. Mohamed, K. Waltar, E. Fabbri, P. Levecque, R. Kötz and T. J. Schmidt, Sci. Rep., 2015, 5, 12167.
27. J. Wang, Y. Gao, H. Kong, J. Kim, S. Choi, F. Ciucci, Y. Hao, S. H. Yang, Z. P. Shao and J. Lim, Chem. Soc. Rev., 2020, 49, 9154–9196.
28. E. Fabbri, M. Nachtegaal, T. Binninger, X. Cheng, B.-J. Kim, J. Durst, F. Bozza, T. Graule, R. Schäublin, L. Wiles, M. Pertoso, N. Danilovic, K. E. Ayers and T. J. Schmidt, Nat. Mater., 2017, 16, 925–931.
29. H. M. A. Amin, P. Königshoven, M. Hegemann and H. Baltruschat, Anal. Chem., 2019, 91, 12653–12660.
30. E. Marelli, J. Gazquez, E. Poghosyan, E. Muller, D. J. Gawryluk, E. Pomjakushina, D. Sheptyakov, C. Piamonteze, D. Aegerter, T. J. Schmidt, M. Medarde and E. Fabbri, Angew. Chem., Int. Ed., 2021, 60, 14609–14619.
31. M. Morin, E. Canevet, A. Raynaud, M. Bartkowiak, D. Sheptyakov, V. Ban, M. Kenzelmann, E. Pomjakushina, K. Conder and M. Medarde, Nat. Commun., 2016, 7, 13758.
32. A. Romaguera, X. D. Zhang, O. Fabelo, F. Fauth, J. Blasco and J. L. Garcia-Munoz, Phys. Rev. Res., 2022, 4, 043188.
33. A. I. Klyndyuk and E. A. Chizhova, Inorg. Mater., 2006, 42, 550–561.
34. A. A. Taskin, A. N. Lavrov and Y. Ando, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 134414.
35. S. Streule, A. Podlesnyak, J. Mesot, M. Medarde, K. Conder, E. Pomjakushina, E. Mitberg and V. Kozhevnikov, J. Phys.: Condens. Matter., 2005, 17, 3317–3324.
36. S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319.
37. M. Guillaume, P. Allenspach, W. Henggeler, J. Mesot, B. Roessli, U. Staub, P. Fischer, A. Furrer and V. Trounov, J. Phys.: Condens. Matter., 1994, 6, 7963–7976.
38. W. A. Harrison, Electronic Structure and the Properties of Solids: The Physics of the Chemical Bond, Dover Publications, 2012.
39. M. Medarde, J. Mesot, P. Lacorre, S. Rosenkranz, P. Fischer and K. Gobrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 9248–9258.
40. M. Medarde, M. Mena, J. L. Gavilano, E. Pomjakushina, J. Sugiyama, K. Kamazawa, V. Y. Pomjakushin, D. Sheptyakov, B. Batlogg, H. R. Ott, M. Mansson and F. Juranyi, Phys. Rev. Lett., 2013, 110, 266401.
41. E. Suljoti, M. Nagasono, A. Pietzsch, K. Hickmann, D. M. Trots, M. Haase, W. Wurth and A. Fohlisch, J. Chem. Phys., 2008, 128, 134706.
42. B. T. Thole, G. Vanderlaan, J. C. Fuggle, G. A. Sawatzky, R. C. Karnatak and J. M. Esteva, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 5107–5118.
43. M. Medarde, C. Dallera, M. Grioni, B. Delley, F. Vernay, J. Mesot, M. Sikora, J. A. Alonso and M. J. Martinez-Lope, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245105.
44. G. A. Bianconi and C. R. Natoli, Bond length determination using XANES. EXAFS and Near Edge Structure, Springer, Berlin, 1983.
45. M. Abbate, F. M. F. Degroot, J. C. Fuggle, A. Fujimori, O. Strebel, F. Lopez, M. Domke, G. Kaindl, G. A. Sawatzky, M. Takano, Y. Takeda, H. Eisaki and S. Uchida, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4511–4519.
46. T. Tsuyama, T. Matsuda, S. Chakraverty, J. Okamoto, E. Ikenaga, A. Tanaka, T. Mizokawa, H. Y. Hwang, Y. Tokura and H. Wadati, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 115101.
47. F. M. F. Degroot, J. C. Fuggle, B. T. Thole and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 5459–5468.
48. M. J. Huang, G. Deng, Y. Y. Chin, Z. Hu, J. G. Cheng, F. C. Chou, K. Conder, J. S. Zhou, T. W. Pi, J. B. Goodenough, H. J. Lin and C. T. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 014520.
49. Y. Y. Chin, H. J. Lin, Z. W. Hu, Y. Shimakawa and C. T. Chen, Physica B, 2019, 568, 92–95.
50. M. F. Qayyum, R. Sarangi, K. Fujisawa, T. D. P. Stack, K. D. Karlin, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2013, 135, 17417–17431.
51. F. Frati, M. O. J. Y. Hunault and F. M. F. de Groot, Chem. Rev., 2020, 120, 4056–4110.
52. B. Wei, M. Schroeder and M. Martin, ACS Appl. Mater. Interfaces, 2018, 10, 8621–8629.
53. J. Y. P. Ko, Y. M. Yiu, H. B. Liang and T. K. Sham, J. Chem. Phys., 2010, 132, 234701.
54. C. Lawley, M. Nachtegaal, J. Stahn, V. Roddatis, M. Döbeli, T. J. Schmidt, D. Pergolesi and T. Lippert, Nat. Commun., 2020, 11, 1728.
55. D. Aegerter, M. Borlaf, E. Fabbri, A. H. Clark, M. Nachtegaal, T. Graule and T. J. Schmidt, Catalysts, 2020, 10, 984.
56. L. Heymann, M. L. Weber, M. Wohlgemuth, M. Risch, R. Dittmann, C. Baeumer and F. Gunkel, ACS Appl. Mater. Interfaces, 2022, 14, 14129–14136.
57. D. T. Qui, J. J. Capponi, J. C. Joubert and R. D. Shannon, J. Solid State Chem., 1981, 39, 219–229.
58. S. Balijapelly, S. Sundaramoorthy, D. J. Mondal, S. Konar, N. Gerasimchuk, A. Chernatynskiy and A. Choudhury, Inorg. Chem., 2023, 62, 3888–3895.
59. E. Fabbri and T. J. Schmidt, ACS Catal., 2018, 8, 9765–9774.
60. Y. M. Klein, M. Kozlowski, A. Linden, P. Lacorre, M. Medarde and D. J. Gawryluk, Cryst. Growth Des., 2021, 21, 4230–4241.
61. A. A. Taskin and Y. Ando, Phys. Rev. Lett., 2005, 95, 176603.
62. M. L. Weber, C. Baeumer, D. N. Mueller, L. Jin, C. L. Jia, D. S. Bick, R. Waser, R. Dittmann, I. Valov and F. Gunkel, Chem. Mater., 2019, 31, 2337–2346.
63. F. Gunkel, L. Jin, D. N. Mueller, C. Hausner, D. S. Bick, C. L. Jia, T. Schneller, I. Valov, R. Waser and R. Dittmann, ACS Catal., 2017, 7, 7029–7037.
64. A. Scaramucci, H. Shinaoka, M. V. Mostovoy, M. Muller, C. Mudry, M. Troyer and N. A. Spaldin, Phys. Rev. X, 2018, 8, 011005.
65. Y. Li, J. Li, W. G. Yang and X. D. Wang, Nanoscale Horiz., 2020, 5, 1174–1187.
66. N. A. Spaldin, I. Efe, M. D. Rossell and C. Gattinoni, J. Chem. Phys., 2021, 154, 154702.
67. D. Kim, I. Efe, H. Torlakcik, A. Terzopoulou, A. Veciana, E. Siringil, F. Mushtaq, C. Franco, D. von Arx, S. Sevim, J. Puigmarti-Luis, B. Nelson, N. A. Spaldin, C. Gattinoni, X. Z. Chen and S. Pane, Adv. Mater., 2022, 34, 2110612.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ey00142c

‡ These authors contributed equally to this work.

---