Open Access Article
Open Access ArticleProbing the structure–property relationships of supported copper oxide nanoclusters for methane activation†
Xijun
Wang
 ,
Kaihang
Shi
,
Anyang
Peng
and
Randall Q.
Snurr
,
Kaihang
Shi
,
Anyang
Peng
and
Randall Q.
Snurr
 *
*
Department of Chemical and Biological Engineering, Northwestern University, Evanston, IL 60208, USA. E-mail: snurr@northwestern.edu
First published on 16th November 2023
Abstract
Supported metal oxide nanoclusters (MeO-NCs) have gained significant attention for their remarkable versatility in various energy and sustainability applications. Despite rapid advancements in atomic-scale synthesis and characterization techniques, the rational design of MeO-NCs with desired catalytic properties remains challenging. This challenge arises from the elusive and difficult-to-quantify structure-catalytic property relationships, particularly in the case of amorphous nanoclusters. Exploiting first-principles calculations at the density functional theory (DFT) level, we conducted a systematic investigation into the growth, geometries, and catalytic performance of a series of tetra-copper oxide nanoclusters (Cu4O-NCs) for methane activation. Focusing on the most representative geometries, we applied machine learning to extract two physically insightful descriptors involving the spin density, the p-band center of the oxygen site, and the d-band center of adjacent Cu sites. These descriptors enable us to predict free energy barriers associated with both the homolytic and heterolytic mechanisms of methane activation. This descriptor-driven approach enables rapid and intuitive prediction of the preferred reaction mechanism. Our findings lay a solid foundation for future advancements in catalysts based on amorphous nanoclusters and provide valuable insights into the mechanistic landscape of methane activation.
Broader contextActivation of the C–H bonds in methane and selective conversion of methane and other components of natural gas to useful products represents a “holy grail” in the field of catalysis, with both fundamental scientific importance and potential economic impact for utilizing stranded natural gas. Recently, there has been significant interest in copper oxide nanoclusters for this reaction (in zeolites and MOFs) but little investigation of tailoring their composition for optimal catalytic performance. Here, we report a comprehensive computational study to navigate the complex structure–property relationships of small metal oxide nanoclusters with varying compositions and provide guidance for designing and optimizing nanoclusters for methane conversion. Nanoclusters constitute an interesting, not widely studied intermediate size between single-atom catalysts and larger nanoparticles. Modeling such nanoclusters is challenging because they are usually amorphous. We present a systematic approach to modeling amorphous nanoclusters, with a focus on their growth, geometries, and catalytic performance, using DFT calculations combined with recent developments for exploring rough potential energy surfaces. In addition, we have leveraged machine learning to identify two physically-based descriptors for accurate prediction of free energy barriers associated with both homolytic and heterolytic methane activation mechanisms. |
1. Introduction
Metal oxide nanoclusters (MeO-NCs) have attracted increasing attention in the catalysis community due to their remarkable catalytic properties in various energy and sustainability applications.1–6 Compared to conventional bulk materials or nanoparticles in the size range of 1 to 100 nm, these nanoclusters typically consist of a few to tens of metal and oxygen atoms with sizes smaller than 2 nm,7 offering higher surface-to-volume ratios and enhanced metal utilization. Additionally, MeO-NCs exhibit molecule-like discrete energy states, enabling orbital hybridization and bonding formation,8,9 which are highly desirable for catalytic applications. Consequently, the precise control of size, composition, and local coordination environments in well-defined MeO-NCs holds great potential for achieving distinctive catalytic performance, as evidenced by some recent studies tackling challenging reactions.10–12One such reaction of significant interest is methane conversion, driven by the abundant supply of natural gas and the demand for value-added products such as methanol.13–15 However, activating the inert C–H σ-bond in methane poses a prohibitive energy barrier (435 kJ mol−1). In recent years, copper oxide nanoclusters (CuO-NCs) have emerged as promising candidate catalysts for methane activation, exhibiting encouraging results in several studies.16–24 For instance, Lercher et al. developed a series of mono- and di-nuclear copper nanoclusters dispersed on porous materials for selective conversion of methane to methanol at 150–200 °C.17,21–24 Román-Leshkov et al. synthesized copper-exchanged zeolites for continuous and selective partial oxidation of methane to methanol, demonstrating that the [Cu–O–Cu]2+ motif is an active center in the cages of zeolites.18 Moreover, several theoretical studies have been conducted to investigate the catalytic mechanisms of Cu–oxo moieties for selective methane-to-methanol conversion.25–27 These pioneering studies highlight the promise of CuO-NCs in efficient methane activation and conversion.
However, despite these efforts, achieving a rational tailoring of the composition and geometry of CuO-NCs to maximize their catalytic activity remains challenging, primarily due to a lack of comprehensive understanding of the structure–property relationships. While state-of-the-art experimental characterization techniques like X-ray absorption near-edge structure (XANES) and extended X-ray absorption fine structure (EXAFS) can probe the local coordination and electronic structures of specific atoms,28,29 determining the 3D structure of complex MeO-NCs, especially under experimental conditions, remains a daunting task. The amorphous nature of most MeO-NCs, coupled with dynamic structural changes during reactions, further complicates the situation. Worse still, the most active species may account for only a tiny proportion, adding another uncertainty to identifying the active centers. With these limitations, accurately determining the geometric structure of MeO-NCs through experimental characterization has been achieved only for a few systems to date.18,22
To mitigate these challenges, first-principles DFT calculations provide a complementary approach for quantifying structure–property relationships at the atomic scale. For instance, our previous theoretical studies,30,31 along with others,17,22,25,26 have validated the feasibility of growing di-copper oxide NCs using atomic layer deposition (ALD) for direct methane-to-methanol conversion under accessible conditions (e.g., 473 K). These studies have highlighted the essential role of the Cu(μ-O)Cu moiety in methane activation. Furthermore, DFT can elucidate the inherent correlation between electronic structure and catalytic activity.32–34 For instance, it is widely recognized that oxygen atoms with higher spin density generally have enhanced activity,17,25–27,30,31,35–37 but the precise quantitative correlation remains unclear. Unraveling such a connection, or even deriving generalizable electronic descriptors for catalytic activity, would greatly advance rapid screening and rational design of catalysts.
Opportunities are always accompanied by challenges. Probing the structure–property relationships for more complex CuO-NC systems beyond di-copper nanoclusters has been rarely reported, primarily due to the increased complexity. Firstly, as the number of Cu atoms in a CuO-NC increases, the possibilities for compositions, atomic arrangements, and coordination environments grow exponentially, making it impractical to exhaustively explore all options for larger nanoclusters. Secondly, nanoclusters with more transition metal atoms typically present varied electronic structures, encompassing an increased range of possibilities in magnetic coupling and spin states. These uncertainties lead to increased computational expense, especially when intertwined with the different potential geometric configurations of these amorphous nanoclusters under practical conditions.
To tackle these challenges, we conducted a DFT-based study focused on systematically exploring the coordination environments, geometric structures, and catalytic behaviors of ALD-grown tetra-copper oxide nanoclusters (Cu4O-NCs) for methane activation. Our study commenced with comprehensive thermodynamic analyses to identify the most stable hydrated structure of the Cu4O-NCs under experimental conditions. Subsequently, we employed the stochastic surface walking (SSW) method38,39 to scan the potential energy surface (PES) and propose plausible isomers of the hydrated Cu4O-NCs. From this exploration, we selected three representative isomers with multiple open oxygen sites to investigate their catalytic performance in methane activation, ultimately resulting in predictive descriptors. Encouragingly, these descriptors exhibited remarkable accuracy in predicting the free energy barriers associated with both the homolytic and heterolytic mechanisms of methane activation. Our study introduces a comprehensive yet manageable simulation approach for investigating the geometries and catalytic properties of amorphous nanoclusters. The findings from this study provide novel insights and theoretical guidance for the future design and optimization of MeO-NC catalysts.
2. Computational details
2.1. DFT calculations
First-principles calculations for the cluster models were carried out at the DFT level using Gaussian 16.40 The geometry optimizations, vibrational frequency calculations, and transition state searches were performed using the M06-L functional41 with ultrafine integration grids. The def2-SVP basis set42 was utilized for C, H, and O, while the def2-TZVP basis set,43 along with its associated effective core potential, was used for Cu and Al. This combination of functional and basis sets has proven to have a high performance-to-cost ratio, providing reliable descriptions of geometric and electronic structures in previous computational studies of relevant MeO-NCs systems.17,30,31 The calculations also included the D3 dispersion correction with zero damping to account for dispersion interactions.44 To enhance computational tractability, a simplification was made by replacing part of the substrate with a hydrogen atom, as depicted in Fig. S1 (ESI†). This simplification preserves charge balance and has been shown to have negligible impact on important properties compared to their supported counterparts in previous studies.30,31For each representative structure, a range of possible spin multiplicities was explored during geometric optimization to determine the ground spin state, which is illustrated in Table S1 (ESI†). Within the ground spin state, the expectation values of the squared total spin, 〈Ŝ2〉, consistently approximated the S(S + 1) value, exhibiting deviations less than 5%, where S represents ½ of the total number of unpaired electrons. This indicates that spin contamination is negligible for these nanoclusters. Furthermore, our exploration into the broken symmetry states of two representative systems revealed a general preference for ferromagnetically coupled Cu sites over their ferrimagnetic and antiferromagnetic counterparts (Fig. S2 and Table S2, ESI†). This aligns with earlier studies on the magnetic couplings of copper oxide nanoclusters and nanoparticles.30,45,46,47 We thus adopted the ferromagnetic couplings as the initial spin states for our subsequent nanocluster calculations.
The nature of all stationary points on the potential energy surface, including minima and transition states, was determined through harmonic vibrational analyses, which were also used to calculate thermal corrections. The thermal and entropic contributions to Gibbs free energies were estimated using vibrational frequency calculations under the harmonic oscillator approximation. Frequencies below 50 cm−1 were replaced with a value of 50 cm−1 to avoid the break-down of the harmonic oscillator model at very low vibrational frequencies.48,49 Translational and rotational contributions to free energies were disregarded for the cluster and bound species to mimic the behaviours of solid-state species. The Gibbs formation free energy (ΔGform) of the Cu4OxHy clusters, as a function of temperature (T) and the partial pressures of O2 (pO2) and H2O (pH2O), is defined as:
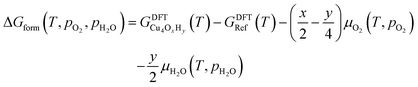 | (1) |
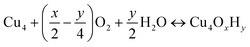 , where μgas = GDFTgas + kBT
, where μgas = GDFTgas + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(pgas/p0) represents the DFT-computed free energy of gas-phase species, p0 is the standard pressure, and GDFTRef(T) denotes the DFT-computed free energy of the nanocluster chosen as the energy reference.
ln(pgas/p0) represents the DFT-computed free energy of gas-phase species, p0 is the standard pressure, and GDFTRef(T) denotes the DFT-computed free energy of the nanocluster chosen as the energy reference.
2.2. SSW method
To explore the potential energy surface (PES) and identify local or global minima, we employed the stochastic surface walking (SSW) method38,39 implemented by the large-scale atomistic simulation with neural network potential (LASP) code.50 SSW is a bias-potential based method, which smoothly manipulates the structural configurations on the PES, allowing for transitions from one minimum to another by surmounting energy barriers along the trajectories. The Metropolis Monte Carlo method was utilized to automatically accept or reject each move during the simulations.The LASP code has an interface with the Vienna ab initio Simulation package (VASP).51 The latter was applied to calculate the energies along the SSW trajectories. The calculations employed the projector augmented wave (PAW) potentials52 and the Perdew–Burke–Ernzerhof (PBE) functional53 with D3 correction.44 The cluster models were placed in a box of 30 × 30 × 30 Å3 to avoid artificial disturbance caused by the periodic boundary conditions. The kinetic energy cutoff for the plane-wave expansion of the electronic wave function was set to 400 eV, and the convergence criteria of force and energy were set as 0.01 eV Å−1 and 10−5 eV, respectively. Only the gamma k-point was used for sampling the first Brillouin zone. Accurately determining the ground spin state for a given nanocluster has historically been a challenging task.54,55 To make the DFT calculations tractable, spin polarization was considered in the self-consistent field calculations with the initial magnetic moments set to the default value of 1.0μB for each atom. The structures obtained from the local or global minima along the SSW trajectories were used as initial guess structures for further reoptimizations using Gaussian 16, following the settings described in Section 2.1.
2.3. SISSO method
To establish the mathematical relationship between free energy barriers and electronic features, we employed the sure independence screening and sparsifying operator (SISSO) algorithm.56 SISSO is designed to identify the most important features or variables in a dataset and explores the mathematical dependence of target properties on a set of input features within the framework of compressed-sensing based dimensionality reduction. In the realm of material science and catalysis, SISSO aims to streamline the complexity of the feature space while retaining essential chemical information. This not only enhances the interpretability and transferability of machine learning models but also ensures that robust prediction capabilities are maintained.For the supervised learning tasks involved in this study, SISSO works in several steps. First, the SISSO algorithm creates a feature space combining each feature by a given mathematical operator set, namely Ĥ(m) ≡ {I, +, −, ×, ÷, log, exp, exp−, −1, 2, 3, 6, √, |![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |, sin, cos}, where only physically meaningful combinations, such as those between features with the same unit, are retained (indicated by the (m) notation). By employing these operators, a wide range of non-linear expressions, resulting from combinations of the given features and mathematical operators, are generated, forming an extensive candidate space for further analysis. Next, the sure-independence screening (SIS), a powerful feature selection technique, is applied to rank the descriptors by evaluating their correlation with the target property, effectively screening them by assessing their independence with the target variable. Through this process, a subset of descriptors that exhibit strong correlations with the target variable is selected. Subsequently, a Sparsifying Operator (SO) is applied to further promote sparsity in the descriptor space. The SO encourages most of the descriptor coefficients to be zero or close to zero, effectively reducing the dimensionality of the problem.
|, sin, cos}, where only physically meaningful combinations, such as those between features with the same unit, are retained (indicated by the (m) notation). By employing these operators, a wide range of non-linear expressions, resulting from combinations of the given features and mathematical operators, are generated, forming an extensive candidate space for further analysis. Next, the sure-independence screening (SIS), a powerful feature selection technique, is applied to rank the descriptors by evaluating their correlation with the target property, effectively screening them by assessing their independence with the target variable. Through this process, a subset of descriptors that exhibit strong correlations with the target variable is selected. Subsequently, a Sparsifying Operator (SO) is applied to further promote sparsity in the descriptor space. The SO encourages most of the descriptor coefficients to be zero or close to zero, effectively reducing the dimensionality of the problem.
In contrast to black-box machine learning methods like artificial neural networks, SISSO stands out by its ability to uncover mathematical mappings that can convey physical insights. This capability is important for developing meaningful descriptors in various physical and chemical applications. Unlike other symbolic regression approaches, such as genetic algorithms and random search, SISSO offers reduced bias since it conducts an exhaustive search of the solution space, evaluating all expressions within a certain complexity. Additionally, the resulting SISSO descriptors tend to have low complexity, enhancing their resilience to data noise. Particularly when the desired formula involves only a few coefficients, SISSO may require a smaller training dataset, which is a significant advantage considering the challenges of acquiring large amounts of data using DFT.57
3. Results and discussion
3.1. Formation of Cu4O-NCs via ALD
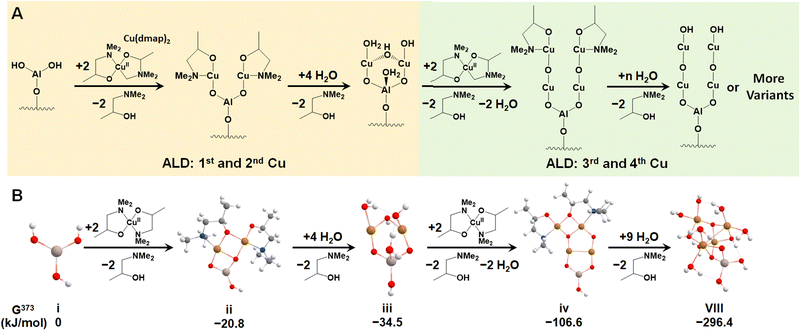
We first investigated the feasibility of growing Cu4O-NCs through ALD following an experimental procedure outlined by Avila et al.58 The first step involves an ALD cycle using an Al3+ precursor, such as Al3+(CH)3, to generate the –Al(OH)2 site on metalated tetra-acid free-base porphyrins, like the aluminum(III) hydroxo tetrakis(4-carboxyphenyl) porphyrin (AlIII(OH)-TCPP), depicted in Fig. S1 (ESI†). During this step, the Al3+ precursor is deposited on the porphyrin substrate via reacting with a surface –OH group, followed by the reaction of the two remaining CH3 ligands on the Al3+ precursor with two H2O molecules. This initial step has been well-established in our previous report.30 Thus, we focus solely on the second step, which centers around the deposition of four Cu atoms on the –Al(OH)2 site. This is achieved by alternately adding Cu precursors to place the Cu atoms and removing the remaining ligands with water vapor, as illustrated in Fig. 1A. For triggering the ALD process, we selected a widely used Cu-based precursor, copper dimethyl amino-2-propoxide (Cu(dmap)2),59 which is capable of adding two Cu atoms and liberating two by-product Hdmap molecules for each half cycle of the ALD process. The addition of the first and second Cu atoms is depicted in the left panel of Fig. 1A, while the addition of the third and fourth Cu atoms is shown in the right panel. This representation illustrates a possible scheme for the ALD process. To simulate the experimental conditions of ALD, we assumed a low feed pressure of 1 Torr for both Cu(dmap)2 and H2O, along with a commonly used temperature of 373 K. As all the reaction products are continuously purged and replaced with fresh reactants during the ALD process, the partial pressure of Hdmap was set to an extremely low value of 10−7 torr to mimic its highly dilute concentration. Under these settings, the proposed pathways for growing the four Cu atoms were found to be exothermic, with a significantly negative (favorable) total reaction energy of −296 kJ mol−1, as shown in Fig. 1B.We note that the di-copper cluster (iii, Cu2AlO7H7, in Fig. 1B) could have multiple configurations, as suggested by our previous study.30 In this study, we adopted the configuration with the lowest energy (−34.5 kJ mol−1, taking configuration i, AlO3H3, as the energy reference). There are other species, such as the one coordinately saturated with hydroxyl and aqua groups (iii′, Cu2AlO11H15, in Fig. S3, ESI†), which could also be a potential option, as its energy (−30.3 kJ mol−1 relative to i) is only slightly higher than that of iii, and the difference falls within the error range of DFT. A coordination environment similar to iii′ has been reported for Cu complexes in pre-activated Cu-ZSM560 and Cu-NU-1000.21 We also note that in the experimental hydration environment, the end product in Fig. 1 can exist in various configurations, binding with different numbers of H2O molecules, and potentially presenting multiple isomers. We have thus introduced an approach to systematically sample representative configurations, incrementally increasing the number of bound H2O molecules and accounting for potential isomers (detailed in Section 3.2). Based on the phase diagram under experimental ALD conditions (Fig. S4, ESI†), the most stable configuration, referred to as configuration VIII, is illustrated in Fig. 1B.
3.2. Sampling possible configurations of Cu4O-NCs for methane activation
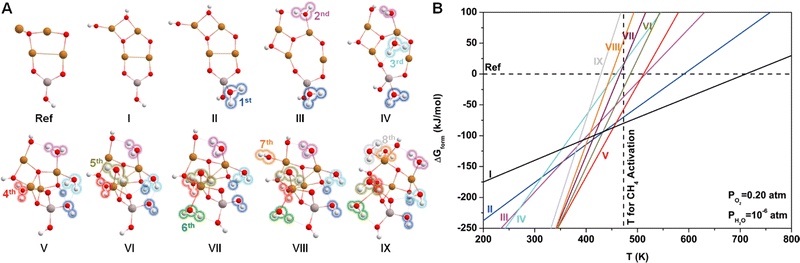
Since water vapor is used as a reactant in the ALD process, the resultant Cu4O-NCs should be surrounded by H2O molecules. To explore the relative stability of different hydration configurations of the Cu4O-NCs under typical methane activation conditions (PO2 = 0.2 atm, PH2O = 10−6 atm, and T = 473 K),30 we chose a straightforward guess structure, configuration I (Cu4AlO7H3), as the starting point, which can simply be derived from configuration iv in Fig. 1B by removing two Hdmap groups and adding two H2O molecules. Then, we sampled different variants of configuration I, as illustrated in Fig. S5 (ESI†), including the removal of 2 OH groups (Cu4AlO5H, chosen as the energy reference), the removal of one H2O molecule (Cu4AlO6H, I.i), and eight isomers generated by adjusting the positions of the two OH groups in configuration I (I.ii–I.x). Additionally, as methane activation is usually accomplished by flowing O2 to replenish the oxygen sites on the catalysts, we also explored possible configurations after oxidative dehydrogenation (I.xi–I.xiii), oxidation (I.xiv–I.xviii), and combinations of oxidative dehydrogenations and oxidations (I.xix–I.xxi) as shown in Fig. S6 (ESI†). However, the computed ΔGform values of all these studied variants are at least 20 kJ mol−1 higher than that of configuration I under the experimental condition of methane activation. These results suggest that configuration I might be a thermodynamically stable configuration for the methane activation process.Next, we introduced more H2O molecules into configuration I to mimic higher degrees of hydration. As illustrated in Fig. S7 (ESI†), we attempted to add one H2O molecule on multiple sites of configuration I, including the on-top site of each Cu atom, the bridge site between two Cu atoms, and the hollow site in the center of three Cu atoms. These operations eventually resulted in seven configurations after structural relaxations. Among these seven isomers, the one with a H2O binding on the Al site, denoted by II.i (Cu2AlO8H5), was found to be the most stable. Continuing this operation and always starting from the most stable configurations, we added the second to the eighth H2O molecules, giving rise to configurations III.iv (Fig. S8, ESI†), IV.i (Fig. S9, ESI†), V.v (Fig. S10, ESI†), VI.ii (Fig. S11, ESI†), VII.iv (Fig. S12, ESI†), VIII.ii (Fig. S13, ESI†), IX.ii (Fig. S14, ESI†), each representing the most stable configuration for the compositions of Cu4AlO9H7, Cu4AlO10H9, Cu4AlO11H11, Cu4AlO12H13, Cu4AlO13H15, Cu4AlO14H17, and Cu4AlO15H19, respectively. These structures are summarized in Fig. 2A, where their labels were simplified as II–IX for convenience.
Fig. 2B shows the phase diagram of configurations I–IX, revealing a clear trend, where the ΔGform values of the configurations with lower hydration degrees are relatively less sensitive to temperature, while the ones with higher hydration degrees display the opposite behavior, with their ΔGform values increasing dramatically as the temperature rises. This trend indicates that at higher temperatures, water molecules tend to desorb from the Cu4O-NCs, exposing more oxygen sites that can facilitate methane activation. Specifically, configuration I was found to be more energetically favourable than the other configurations around the temperature of methane activation (473 K), while configuration V may dominate the temperature range slightly below the reaction temperature (350–450 K). Considering the potential computational errors in DFT, both configurations I and V were chosen for subsequent calculations. It is important to note that while the structural sampling approach used here can hardly be exhaustive and may potentially miss configurations with even lower ΔGform, it nevertheless provides the same trend as revealed in the previous study on di-copper oxide NCs,30 where all the possible configurations were exhaustively studied.
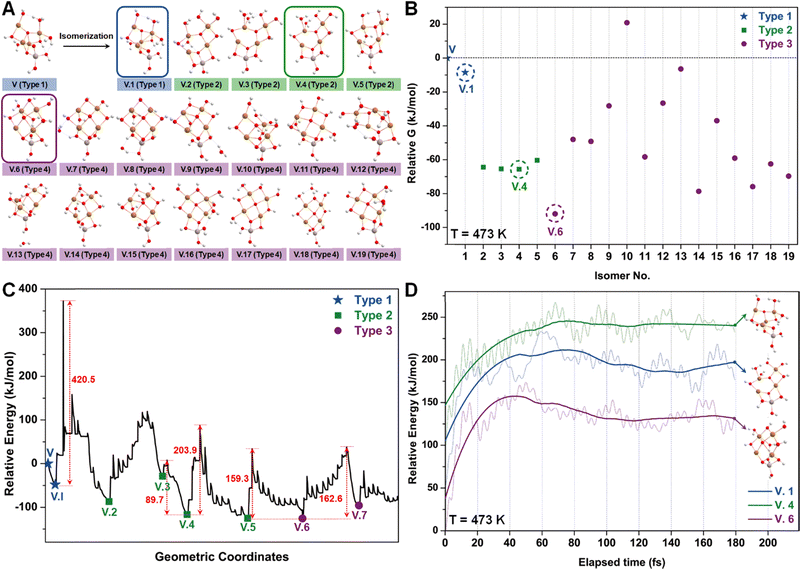
After identifying configurations I (Cu4AlO7H3) and V (Cu4AlO11H11) as potentially stable under experimental conditions, we conducted further investigations to explore possible isomers and 3D arrangements of atoms that could lead to configurations closer to real-world structures. To accomplish this, we employed the SSW method, which is an unbiased PES scanning method based on bias-potential-driven dynamics (refer to Section 2.2 for more details), to suggest possible local or global minimum structures on the PES. Using this approach, we identified 64 isomers of configuration I, denoted as I.1 to I.64 in Fig. 3. These isomers exhibit nine types of geometric structures, distinguished by the number of key metal–oxo moieties (O–2Cu, O–3Cu, O–4Cu, Al–O–Cu, Al–O–2Cu) present in these clusters, as described in Table 1. These isomers, we believe, are representative and sufficiently diverse in capturing potential structural variations. Searching for additional minima would likely be an endless and unnecessary task, as these isomers already provide significant insights into the possible 3D arrangements of atoms within the Cu4O-NCs.
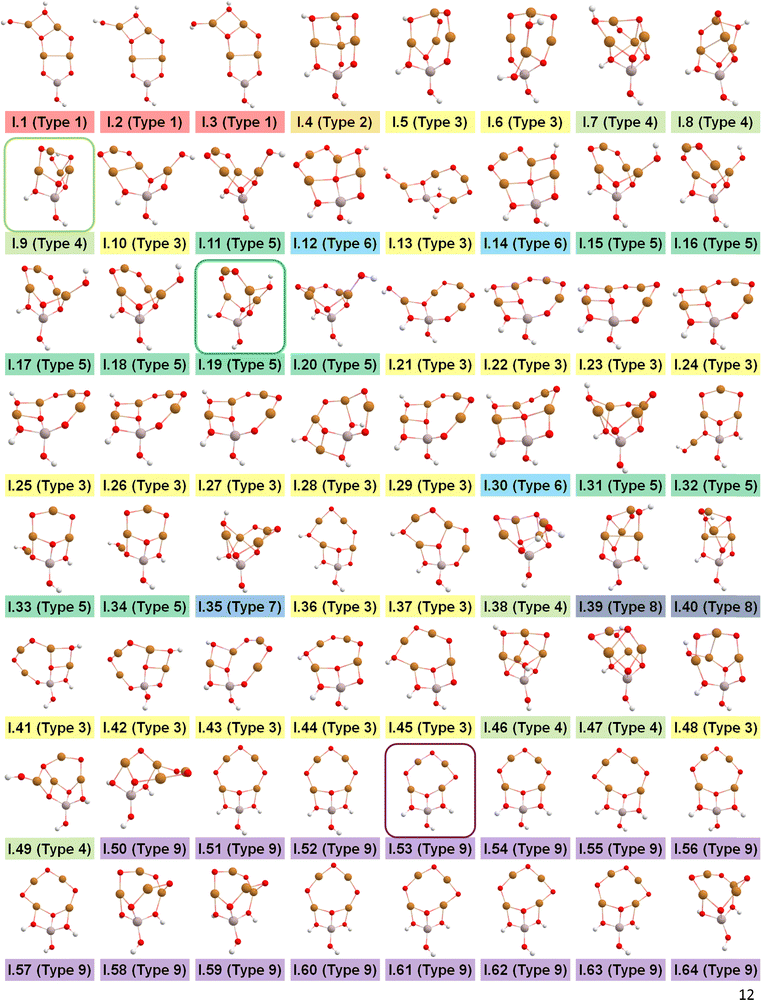 | ||
| Fig. 3 Optimized geometric structures of the isomers of configuration I (Cu4O7H3) suggested by the SSW method. White, red, golden, and light peach spheres represent H, O, Cu, and Al atoms, respectively. These isomers are classified into 9 types based on the number of key metal–oxo moieties in Table 1, indicated by distinct color-coded labels. | ||
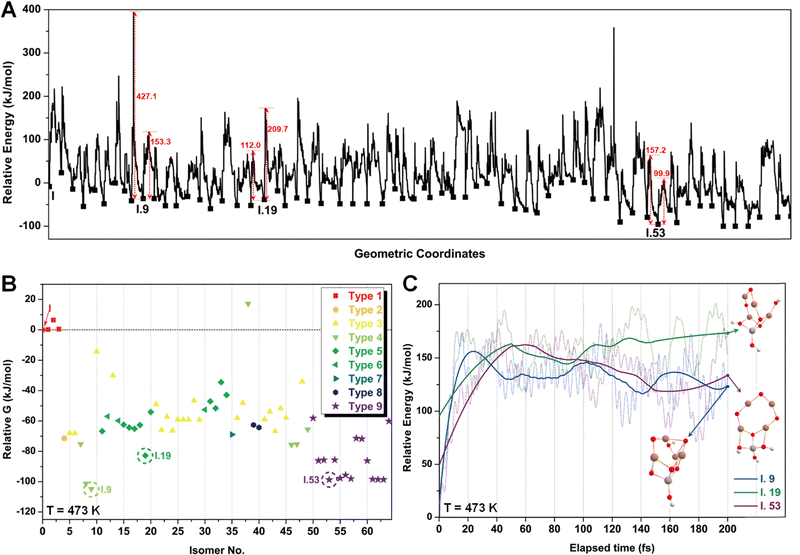
The energy profile along the SSW pathway connecting the 64 obtained minima is depicted in Fig. 4A. The plot reveals many prohibitively high barriers between minima, indicating that the isomerization between certain configurations is energetically unfavorable. For instance, the energy barriers for the isomerization of I.9 to I.8 and I.10 are 427.1 and 153.3 kJ mol−1, respectively, suggesting that configuration I.9 might be a stable geometry from both thermodynamic and kinetic perspectives. However, it is worth mentioning that the energy barriers given by SSW do not solely determine the stability of a structure because: (1) they are DFT total energies rather than Gibbs free energies under experimental conditions; (2) the randomly sampled trajectory does not guarantee the inclusion of all feasible isomerization pathways. We also note that the direction of structural sampling using SSW is random. Consequently, the order of the resulting structures along the SSW trajectory does not reflect their relative stabilities.
Following the SSW searching, the resultant local or global minimum structures were reoptimized at the same level of theory used for all the other calculations in this study (M06L-D3/def2-SVP/def2-TZVP), with free energy corrections being calculated. The relative free energies of these isomers are presented in Fig. 4B. It can be observed that the configurations in types 4 (light green), 5 (dark green), and 9 (purple) generally exhibit lower free energies compared to those in other types. We, therefore, selected I.9, I.19, and I.53 for subsequent methane activation, as they represent the most stable configurations for the three lower-energy isomer types (types 4, 5, and 9). To further validate their stabilities, we conducted ab initio molecular dynamics (AIMD) calculations61 with a step size of 0.1 fs at 473 K. The results, presented in Fig. 4C, demonstrate that the mean energies of these isomers remained nearly unchanged over a timescale of approximately 200 fs. Table S3 (ESI†) summarizes the changes in key bond lengths (Å) surrounding the active oxygen sites throughout the AIMD simulations. The data indicates no notable structural distortions, site aggregation, or proton transfers, underscoring the stability of these structures.
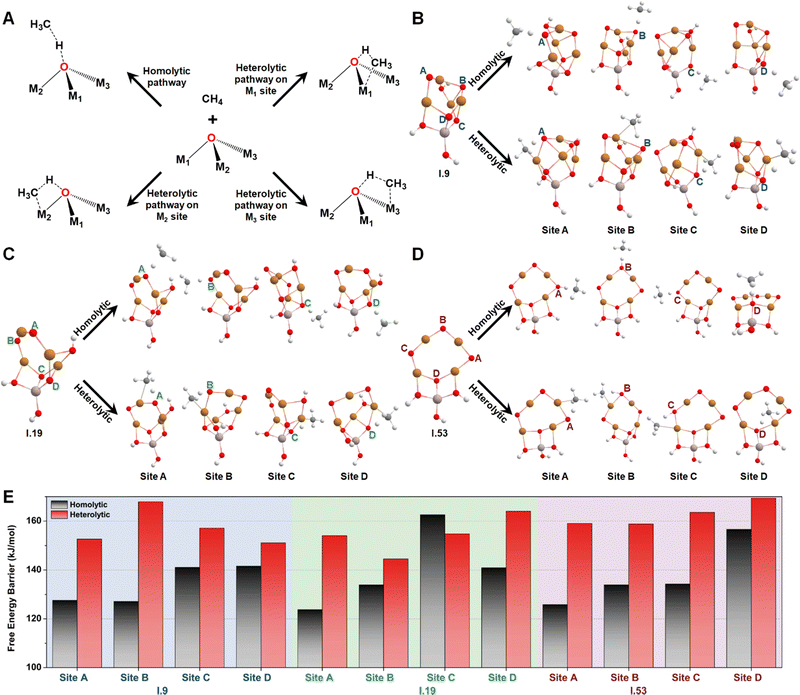
Then, we studied the catalytic activities of all the exposed oxygen sites on configurations I.9, I.19, and I.53. Fig. 5A provides an illustration of two well-known mechanisms for methane activation: the homolytic and heterolytic mechanisms.62–64 The homolytic mechanism, also known as the hydrogen atom transfer (HAT) mechanism, involves the homolytic dissociation of one of the four C–H bonds in a methane molecule. This process releases a hydrogen atom that transfers to an active oxygen site and a free-standing CH3 radical that retains one unpaired electron. The heterolytic mechanism considered in this study involves a proton-coupled electron transfer (PCET) process, where a C–H bond cleaves heterolytically. This process transfers a proton, instead of a hydrogen atom, to the active oxygen site, while the negatively charged methyl species relocates to an adjacent metal site, which acts as a Lewis acid center. Different systems have shown varying competitiveness between these two mechanisms. For instance, the homolytic mechanism was found to be more favorable for certain metal oxide nanoclusters containing specific metal–oxo moieties, such as Cu(μ-O)Cu30 and Mg(μ-O)Mg.62 In contrast, the heterolytic mechanism is more competitive in other moieties such as Co–Ob–M (M = Ni, Co, Fe, Mn, Ti)63 and all the M1(μ-O)M2 clusters (M1 and M2 = Mn, Fe, Co, Ni, Cu, and Zn) except for Cu(μ-O)Cu.31 These findings suggest that both the homolytic and heterolytic mechanisms should be considered in computing methane activation energies on MeO-NC systems.
Considering both the homolytic and heterolytic mechanisms for methane activation, we performed transition state (TS) searches for all the exposed oxygen sites on configurations I.9, I.19, I.53 (Fig. 5B–D). This included one O–2Cu (site A), one O–3Cu (site B), and two Al–O–2Cu (sites C and D) on I.9; two O–2Cu (sites A and B) and two Al–O–2Cu (sites C and D) on I.19; three O–2Cu (sites A, B, and C) and one Al–O–2Cu (site C) on I.53. The resultant free energy barriers along the homolytic (ΔG‡homo) and heterolytic pathways (ΔG‡heter) are summarized in Fig. 5E. For oxygen sites that connect with multiple metals, we chose the most energetically favorable TS of the heterolytic pathways. Comparing these histograms, we observe that these clusters generally exhibit a preference for the homolytic mechanism over the heterolytic one, with the only exception being site C on I.19, which may be attributed to minor structural distortions in the TS structures. Another interesting finding is that bi-coordinated oxygen atoms are generally more active than tri-coordinated ones, probably because the latter are too stable to be active. The only exception is site B on I.19, which transitions from being tri-coordinated to bi-coordinated in the TS along the homolytic pathway (breaking one Cu–O bond). The ΔG‡homo values for all the bi-coordinated oxygen sites are around 125 kJ mol−1, which is close to the value we previously observed for the di-copper cluster (111 kJ mol−1).30 These findings provide a rationalization for the high activity of the Cu(μ-O)Cu moiety reported by previous studies.17–24
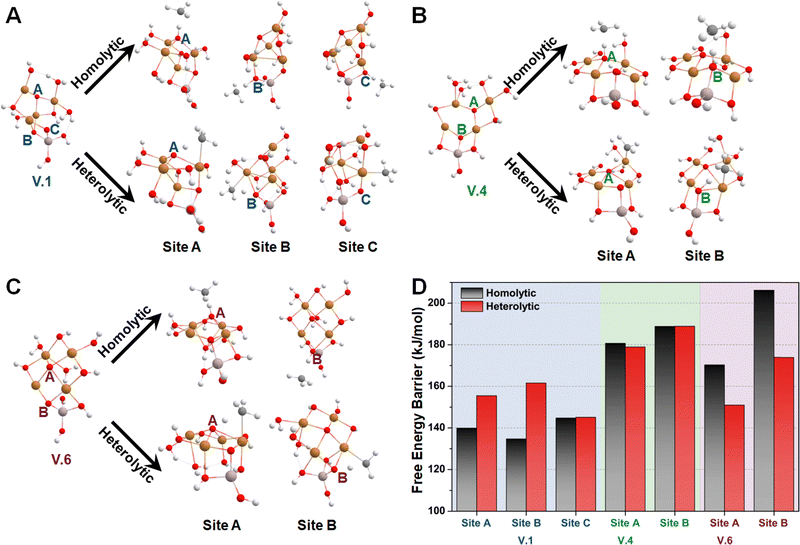
Similar to the studies of configuration I, we employed the SSW method again to examine various isomers of configuration V (Fig. 6A), which can be roughly categorized into three types based on the number of tri-coordinated oxygen atoms. Among these isomers, we highlight the configurations V.1, V.4, and V.6 as they exhibit the lowest energies within each type (Fig. 6B). Furthermore, converting these isomers to their adjacent local minimum structures was found to be energetically unfavorable along the SSW trajectory, as evidenced by Fig. 6C. Their stabilities were further confirmed using AIMD calculations, which indicated minimal changes in mean energies (Fig. 6D) and geometries (Table S3, ESI†) under experimental conditions.
Subsequently, we investigated the methane activation steps for configurations V.1, V.4, and V.6 along both the homolytic and heterolytic pathways, as depicted in Fig. 7A–C. Due to their higher hydration levels, these configurations have fewer exposed oxygen sites compared to the isomers of configuration I. We focused on studying methane activation on the following oxygen sites: O–3Cu (site A), Al–O–2Cu (site B), and Al–O–Cu (site C) on V.1; O–3Cu (site A) and Al–O–2Cu (site B) on V.4; O–4Cu (site A) and Al–O–2Cu (site B) on V.6. The corresponding free energy barriers are summarized in Fig. 7D. We observe that the barriers along the homolytic pathways are consistently lower than or comparable to those along the heterolytic pathways for bi- and tr-coordinated oxygen atoms. However, this trend reverses for the tetra-coordinated oxygens, as the barriers along the homolytic pathways become significantly higher (>170 kJ mol−1). This phenomenon can be understood since activity and stability pose a trade-off in many systems. Furthermore, when considering the results in Fig. 5, we found that all the Al-involved oxygen sites, such as Al–O–Cu (ΔG‡homo = ∼140 kJ mol−1), exhibit lower activity compared to their Cu–oxo counterparts (e.g., O–2Cu with a ΔG‡homo of ∼125 kJ mol−1). This suggests that methane activation is more likely to occur on the Cu oxide nanoclusters themselves rather than at their junction with the substrates, emphasizing the importance of Cu–oxo moieties in the catalytic process.
3.3. Extracting electronic descriptors for free energy barriers of methane activation
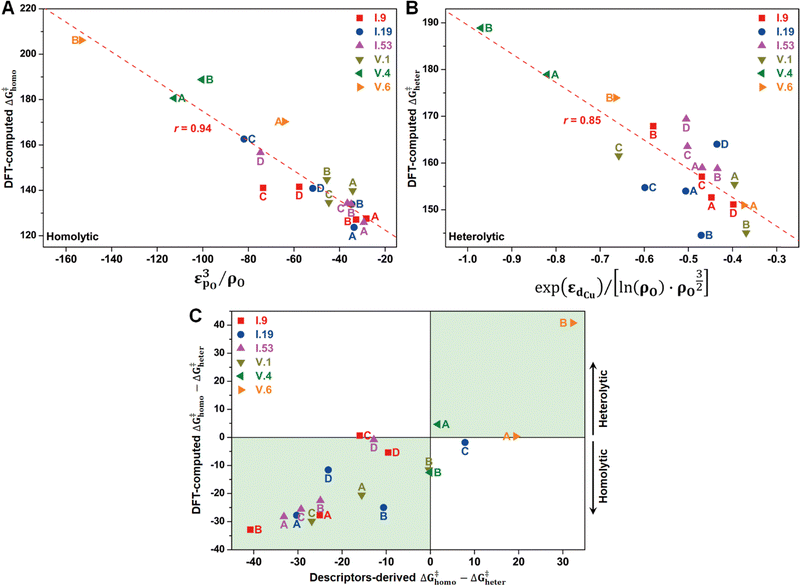
In principle, the catalytic activity of an oxygen site is expected to have a strong correlation with its spin density (ρO), especially in the context of the homolytic mechanism. This correlation arises from the spin-polarized interactions between the unpaired electron on the abstracted hydrogen atom and the one on the active oxygen site. Such spin-polarized interactions have been suggested to play a beneficial role in activating the inert C–H bonds.17,25–27,30,31 In our present study, we also observed an inverse proportionality, although not strictly linear, between ρO and ΔG‡homo (Fig. S15A, ESI†). However, we observed that a single parameter associated with the oxygen site, such as ρO, is not sufficient to predict the value of ΔG‡homo, let alone ΔG‡heter, which is not likely to be determined solely by the properties of the oxygen site (Fig. S15B, ESI†). Therefore, we aimed to incorporate additional electronic features in our analysis to improve the description of the free energy barriers, guided by our chemical intuition. These features include the spin density of Cu (ρCu), partial charges of O (qO) and Cu atoms (qCu), and electronic state features, such as the p-band center of oxygen (εpO) and the d-band center of Cu (εdCu). We note that all these features were derived from the Cu4O-NCs prior to methane binding and activation. Our goal was to predict the target free energy barriers, namely ΔG‡homo and ΔG‡heter. Unveiling the correlations between these electronic features and the target properties can both enrich our understanding of the structure–property relationships and substantially reduce the computational resources needed to evaluate the reactivity of copper oxide-based nanoclusters in future investigations.To achieve this goal, we employed the SISSO method, a statistical tool designed to identify such correlations (refer to Section 2.3 for more details). For the homolytic mechanism, we identified a simple yet physically meaningful descriptor that combines the chemical information of the oxygen p-band center and spin density (εpO3/ρO). This descriptor exhibited considerable accuracy in predicting the ΔG‡homo values for the studied systems, with a high Pearson correlation coefficient (r) of 0.94 (Fig. 8A). The excellent performance of this descriptor can be explained by two factors. First, a more positive filling of the oxygen p-band center leads to a reduced filling of anti-bonding states,65,66 thereby enhancing the binding of the hydrogen atom. Second, as mentioned earlier, a higher spin density corresponds to increased catalytic activity. Importantly, this descriptor demonstrated potential for generalizability. It was derived solely from the datasets of configuration V, yet it can successfully predict the ΔG‡homo values for the oxygen sites on configuration I. This finding suggests that this descriptor has the potential to be adapted to a broader range of systems.
Furthermore, we discovered an electronic descriptor for ΔG‡heter that integrates the information of the d-band center of Cu and spin density of oxygen: 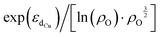 , as shown in Fig. 8B. This descriptor captures the essence of the d-band center theory,67,68 where more positive values of εd correspond to a reduced occupation of anti-bonding orbitals, resulting in stronger bonding between Cu and CH3, which favors methane activation. However, the correlation (r = 0.85) is not as good as that for ΔG‡homo, possibly due to two reasons. Firstly, this descriptor may reduce the dimension of the feature space excessively, leading to the loss of essential information, such as the partial charge or spin density of Cu. Secondly, the electronic features we considered may not fully account for the structural distortions caused by CH3 binding in the TS structures, which can have a nonnegligible impact on ΔG‡heter.
, as shown in Fig. 8B. This descriptor captures the essence of the d-band center theory,67,68 where more positive values of εd correspond to a reduced occupation of anti-bonding orbitals, resulting in stronger bonding between Cu and CH3, which favors methane activation. However, the correlation (r = 0.85) is not as good as that for ΔG‡homo, possibly due to two reasons. Firstly, this descriptor may reduce the dimension of the feature space excessively, leading to the loss of essential information, such as the partial charge or spin density of Cu. Secondly, the electronic features we considered may not fully account for the structural distortions caused by CH3 binding in the TS structures, which can have a nonnegligible impact on ΔG‡heter.
Despite the presence of some prediction errors, we found that these descriptors were sufficiently accurate in predicting the preferred mechanism of methane activation for most species, as demonstrated in Fig. 8C. We utilized the sign of (ΔG‡homo − ΔG‡heter) to represent the preference for the mechanisms, with a negative sign indicating a preference for the homolytic mechanism and a positive sign indicating a preference for the heterolytic mechanism. We observed that nearly all the studied species fall within the green areas, where the DFT-computed and descriptors-derived (ΔG‡homo − ΔG‡heter) values have the same sign. This verifies the feasibility of the descriptor-based approach in rapidly predicting reaction mechanisms.
4. Conclusion
In summary, we have leveraged DFT calculations to investigate the fundamental relationships between the geometric and electronic structures and the catalytic activity for a series of Cu4O-NCs in the context of methane activation. Specifically, we focused on the amorphous nature of nanoclusters grown using ALD and extensively studied various coordination and isomerization possibilities under experimental conditions, resulting in the identification of representative configurations. These configurations enable us to delve into the relationships between their electronic structures and the catalytic properties for methane activation. Intriguingly, we extracted two electronic descriptors that effectively captured the key chemical information from electronic features for predicting the free energy barriers along the homolytic and heterolytic reaction pathways. Using these descriptors, we achieved rapid prediction of the preferred catalytic mechanisms with considerable accuracy. The findings in this study provide valuable insights that can contribute to the development of MeO-NCs for methane activation and extend their application beyond C1 chemistry. Computational studies focusing on amorphous nanoclusters are relatively scarce. Therefore, this study can serve as a prototype and provide methodological guidance for integrating multiple computational modeling approaches to gain insights into the catalytic behaviors of amorphous nanomaterials.Author contributions
Conceptualization and supervision: R. Q. S. Investigation, resources, and visualization: X. W., K. S., A. P., and R. Q. S. Writing – original draft: X. W. Writing – review and editing: R. Q. S.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Zhipan Liu and Cheng Shang at Fudan University for their valuable methodological support. This work was supported by the Institute for Catalysis in Energy Processes (ICEP) via the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DOE DE-FG02-03ER15457. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC02-05CH11231 using NERSC award BES-ERCAP0023154. This research was also supported in part through the computational resources and staff contributions provided for the Quest high-performance computing facility at Northwestern University which is jointly supported by the Office of the Provost, the Office for Research, and Northwestern University Information Technology.References
- F. Jiao and H. Frei, Energy Environ. Sci., 2010, 3, 1018–1027 RSC.
- H. Park, D. J. Shin and J. Yu, J. Chem. Educ., 2021, 98, 703–709 CrossRef CAS.
- J. Yu, W. Chen, F. He, W. Song and C. Cao, J. Am. Chem. Soc., 2023, 145, 1803–1810 CrossRef CAS PubMed.
- I. Lee, M.-S. Lee, L. Tao, T. Ikuno, R. Khare, A. Jentys and T. Huthwelker, et al. , JACS Au, 2021, 1, 1412–1421 CrossRef CAS PubMed.
- T. ul Haq and Y. Haik, ACS Sustainable Chem. Eng., 2022, 10, 6622–6632 CrossRef.
- Y. Hu, C. Song, C. Li and J. Wang, J. Mater. Chem. A, 2022, 10, 8172–8177 RSC.
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- Y. Xiao, Q.-L. Mo, G. Wu, K. Wang, X.-Z. Ge, S.-R. Xu, J.-L. Li, Y. Wu and F.-X. Xiao, J. Mater. Chem. A, 2023, 11, 2402–2411 RSC.
- Z. Tang, D. A. Robinson, N. Bokossa, B. Xu, S. Wang and G. Wang, J. Am. Chem. Soc., 2011, 133, 16037–16044 CrossRef CAS PubMed.
- X. Li, N. Guo, Z. Chen, X. Zhou, X. Zhao, Y. Du and L. Ma, et al. , Adv. Funct. Mater., 2022, 32, 2200933 CrossRef CAS.
- Z. Liu, Y. Zhang, J. Bai, H. Yang, L. Yang, L. Bai, D. Wei, W. Wang, Y. Liang and H. Chen, Fuel, 2023, 334, 126753 CrossRef CAS.
- X. Zheng, M. Qin, S. Ma, Y. Chen, H. Ning, R. Yang, S. Mao and Y. Wang, Adv. Sci., 2022, 9, 2104636 CrossRef CAS PubMed.
- C. World Energy Council, World Energy Resources 2013 Survey: Summary, World Energy Council, London, UK, 2013, p. 29 Search PubMed.
- P. Chawdhury, K. V. S. S. Bhargavi and C. Subrahmanyam, Sustainable Energy Fuels, 2021, 5, 3351–3362 RSC.
- P. Khirsariya and R. K. Mewada, Proc. Eng., 2013, 51, 409–415 CrossRef CAS.
- J. N. Hall, M. Li and P. Bollini, Catal. Sci. Technol., 2022, 12, 418–435 RSC.
- J. Zheng, J. Ye, M. A. Ortuño, J. L. Fulton, O. Y. Gutiérrez, D. M. Camaioni and R. K. Motkuri, et al. , J. Am. Chem. Soc., 2019, 141, 9292–9304 CrossRef CAS PubMed.
- K. T. Dinh, M. M. Sullivan, K. Narsimhan, P. Serna, R. J. Meyer, M. Dincă and Y. Román-Leshkov, J. Am. Chem. Soc., 2019, 141, 11641–11650 CrossRef CAS PubMed.
- L. Tao, I. Lee and M. Sanchez-Sanchez, Catal. Sci. Technol., 2020, 10, 7124–7141 RSC.
- X. Yu, L. Zhong and S. Li, Phys. Chem. Chem. Phys., 2021, 23, 4963–4974 RSC.
- T. Ikuno, J. Zheng, A. Vjunov, M. Sanchez-Sanchez, M. A. Ortuño, D. R. Pahls and J. L. Fulton, et al. , J. Am. Chem. Soc., 2017, 139, 10294–10301 CrossRef CAS PubMed.
- I. Lee, M.-S. Lee, L. Tao, T. Ikuno, R. Khare, A. Jentys and T. Huthwelker, et al. , JACS Au, 2021, 1, 1412–1421 CrossRef CAS PubMed.
- J. Zheng, I. Lee, E. Khramenkova, M. Wang, B. Peng, O. Y. Gutiérrez and J. L. Fulton, et al. , Chem. – Eur. J., 2020, 26, 7563–7567 CrossRef CAS PubMed.
- T. Ikuno, S. Grundner, A. Jentys, G. Li, E. Pidko, J. Fulton, M. Sanchez-Sanchez and J. A. Lercher, J. Phys. Chem. C, 2019, 123, 8759–8769 CrossRef CAS.
- M. H. Mahyuddin, T. Tanaka, Y. Shiota, A. Staykov and K. Yoshizawa, ACS Catal., 2018, 8, 1500–1509 CrossRef CAS.
- X. Yu, L. Zhong and S. Li, Phys. Chem. Chem. Phys., 2021, 23, 4963–4974 RSC.
- M. H. Mahyuddin, A. Staykov, Y. Shiota and K. Yoshizawa, ACS Catal., 2016, 6, 8321–8331 CrossRef CAS.
- H. Oyanagi, Z. H. Sun, Y. Jiang, M. Uehara, H. Nakamura, K. Yamashita and Y. Orimoto, et al. , J. Appl. Phys., 2012, 111, 084315 CrossRef.
- S. Padovani, I. Borgia, B. Brunetti, A. Sgamellotti, A. Giulivi, F. d’Acapito, P. Mazzoldi, C. Sada and G. Battaglin, Appl. Phys. A: Mater. Sci. Process., 2004, 79, 229–233 CrossRef CAS.
- H. A. Doan, Z. Li, O. K. Farha, J. T. Hupp and R. Q. Snurr, Catal. Today, 2018, 312, 2–9 CrossRef CAS.
- H. A. Doan, X. Wang and R. Q. Snurr, J. Phys. Chem. Lett., 2023, 14, 5018–5024 CrossRef CAS PubMed.
- X. Wang, S. Jiang, W. Hu, S. Ye, T. Wang, F. Wu and L. Yang, et al. , J. Am. Chem. Soc., 2022, 144, 16069–16076 CrossRef CAS PubMed.
- X. Wang, S. Ye, W. Hu, E. Sharman, R. Liu, Y. Liu, Y. Luo and J. Jiang, J. Am. Chem. Soc., 2020, 142, 7737–7743 CrossRef CAS PubMed.
- M. Barona, C. A. Gaggioli, L. Gagliardi and R. Q. Snurr, J. Phys. Chem. A, 2020, 124, 1580–1592 CrossRef CAS PubMed.
- A. S. Rosen, J. M. Notestein and R. Q. Snurr, ACS Catal., 2019, 9, 3576–3587 CrossRef CAS.
- H. Schwarz, S. Shaik and J. Li, J. Am. Chem. Soc., 2017, 139, 17201–17212 CrossRef CAS PubMed.
- T. Tian, X. Sun, T. Weiske, Y. Cai, C. Geng, J. Li and H. Schwarz, ChemPhysChem, 2019, 20, 1812–1821 CrossRef CAS PubMed.
- C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 1838–1845 CrossRef CAS PubMed.
- C. Shang, X.-J. Zhang and Z.-P. Liu, Phys. Chem. Chem. Phys., 2014, 16, 17845–17856 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 19 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 15 CrossRef PubMed.
- E. Batsaikhan, C. H. Lee, H. Hsu, C. M. Wu, J. C. Peng, M. H. Ma, S. Deleg and W. H. Li, ACS Omega, 2020, 5(8), 3849–3856 CrossRef CAS PubMed.
- S. Dolai, R. Dey, S. N. Sarangi, S. Hussain, R. Bhar and A. K. Pal, J. Magn. Magn. Mater., 2020, 495, 165903 CrossRef CAS.
- S. Rehman, A. Mumtaz and S. K. Hasanain, J. Nanopart. Res., 2011, 13, 2497–2507 CrossRef CAS.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS PubMed.
- M. Z. Ertem, L. Gagliardi and C. J. Cramer, Chem. Sci., 2012, 3, 1293–1299 RSC.
- S.-D. Huang, C. Shang, P.-L. Kang, X.-J. Zhang and Z.-P. Liu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1415 CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. Qian, M. Zhu, Z. Wu and R. Jin, Acc. Chem. Res., 2012, 45(9), 1470–1479 CrossRef CAS PubMed.
- A. Fernando, K. L. D. M. Weerawardene, N. V. Karimova and C. M. Aikens, Chem. Rev., 2015, 115(12), 6112–6216 CrossRef CAS PubMed.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2018, 2, 083802 CrossRef CAS.
- J. Lee, J. Shin, T.-W. Ko, S. Lee, H. Chang and Y. Hyon, Mater. Res. Express, 2021, 8, 026302 CrossRef CAS.
- J. R. Avila, J. D. Emery, M. J. Pellin, A. B. F. Martinson, O. K. Farha and J. T. Hupp, ACS Appl. Mater. Interfaces, 2016, 8, 19853–19859 CrossRef CAS PubMed.
- B. H. Lee, J. K. Hwang, J. W. Nam, S. U. Lee, J. T. Kim, S.-M. Koo, A. Baunemann, R. A. Fischer and M. M. Sung, Angew. Chem., 2009, 121, 4606–4609 CrossRef.
- M. H. Groothaert, P. J. Smeets, B. F. Sels, P. A. Jacobs and R. A. Schoonheydt, J. Am. Chem. Soc., 2005, 127, 1394–1395 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- H. Schwarz, S. Shaik and J. Li, J. Am. Chem. Soc., 2017, 139, 17201–17212 CrossRef CAS PubMed.
- C. A. Gaggioli, J. Sauer and L. Gagliardi, J. Am. Chem. Soc., 2019, 141, 14603–14611 CrossRef CAS PubMed.
- C. Geng, J. Li, T. Weiske, M. Schlangen, S. Shaik and H. Schwarz, J. Am. Chem. Soc., 2017, 139, 1684–1689 CrossRef CAS PubMed.
- Y.-L. Lee, J. Kleis, J. Rossmeisl, Y. Shao-Horn and D. Morgan, Energy Environ. Sci., 2011, 4, 3966–3970 RSC.
- X. Wang, E. Krzystowczyk, J. Dou and F. Li, Chem. Mater., 2021, 33, 2446–2456 CrossRef CAS.
- B. Hammer and J. K. Norskov, Nature, 1995, 376, 238–240 CrossRef CAS.
- B. J. K. N. Hammer and J. K. Nørskov, Surf. Sci., 1995, 343, 211–220 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ey00234a |
| This journal is © The Royal Society of Chemistry 2024 |