Open Access Article
Open Access ArticleCerium(III) and 5-methylisophthalate-based MOFs with slow relaxation of magnetization and photoluminescence emission†
Oier
Pajuelo-Corral
 a,
MCarmen
Contreras
b,
Sara
Rojas
a,
MCarmen
Contreras
b,
Sara
Rojas
 b,
Duane
Choquesillo-Lazarte
b,
Duane
Choquesillo-Lazarte
 c,
José M.
Seco
a,
Antonio
Rodríguez-Diéguez
c,
José M.
Seco
a,
Antonio
Rodríguez-Diéguez
 b,
Alfonso
Salinas-Castillo
b,
Alfonso
Salinas-Castillo
 d,
Javier
Cepeda
d,
Javier
Cepeda
 *a,
Andoni
Zabala-Lekuona
*a,
Andoni
Zabala-Lekuona
 *a and
Iñigo J.
Vitorica-Yrezabal
*a and
Iñigo J.
Vitorica-Yrezabal
 *b
*b
aDepartamento de Química Aplicada, Facultad de Química, Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU), 20018, Donostia, Spain. E-mail: andoni.zabala@ehu.eus; javier.cepeda@ehu.es
bDepartamento de Química Inorgánica, Facultad de Ciencias, Universidad de Granada, 18071, Granada, Spain. E-mail: vitorica@ugr.es
cLaboratorio de Estudios Cristalograficos, IACT, CSIC-Universidad de Granada, Av. De las palmeras 4, Armilla, Granada E-18100, Spain
dDepartamento de Química Analítica, Facultad de Humanidades, Universidad de Granada, 18071, Granada, Spain
First published on 14th June 2024
Abstract
Two novel Ce(III) metal organic frameworks (MOFs) with formulas [Ce(5Meip)(H-5Meip)]nGR-MOF-17 and [CeCl(5Meip)(DMF)]nGR-MOF-18 (5Meip = 5-methylisophthalate, DMF = N,N-dimethylformamide) have been synthesized, forming 3-dimensional frameworks. Magnetic measurements show that both compounds present field-induced slow magnetic relaxation under a small applied dc field. For GR-MOF-17, the temperature dependence of relaxation times is best described by a Raman mechanism, whereas for GR-MOF-18, relaxation occurs through a combination of Raman and local-mode pathways. Moreover, when avoiding short Ce⋯Ce interactions by magnetic dilution in GR-MOF-17@La and GR-MOF-18@La, only the local-mode mechanism is responsible for magnetic relaxation. Photophysical studies show the occurrence of ligand-centred luminescence in both compounds and phosphorescence emission at low temperature for GR-MOF-17.
Introduction
In the last few decades, there has been a significant research effort on the design of metal–organic frameworks (MOFs) not only for the fascinating structures and topologies they present, but also due to their interesting properties relevant to applications such as gas adsorption, magnetism, luminescence, and catalysis, among others.1 At present, there is a lack of a rational synthetic strategy to control the resulting structures and properties,2 due to the involvement of a wide range of factors driving the MOF self-assembly process such as metallic salt, organic ligands, solvents, stoichiometry, temperature, etc.3Above all, the selection of metal ions and organic ligands is the overriding factor in the design and control of possible structures and their applications.4 Lanthanide ions are known to yield flexible and larger coordination geometries owing to their shielded 4f electrons that are hardly affected by the crystal field. Moreover, the presence of these paramagnetic centres may afford fascinating magnetic properties, which can be tuned according to the metallic coordination environment.5 MOFs containing magnetic nodes can generate organized and well-insulated magnetic nanostructures. The controlled spatial organization of the magnetic centres with slow magnetic relaxation properties may result in applications in quantum computing since each magnetic centre may be used as a quantum bit. In the last few years, there has been a substantial increase of publications reporting the use of some lanthanide ions to give single-molecule magnets (SMMs) due to their large magnetic moment and significant single-ion anisotropy derived from the spin–orbit coupling effect.6 SMMs are discrete molecules consisting of mono- or polynuclear entities that exhibit slow relaxation of magnetization and magnetic hysteresis at low temperatures, as well as quantum phenomena such as quantum tunnelling of magnetization (QTM).7 This characteristic behaviour arises from the presence of an energy barrier (Ueff) that prevents the spin relaxation once magnetized. Initially, the first materials consisted of transition metal-based clusters seeking the largest possible spin values considering the dependence of the spin on the barrier (U = S2·|D| or U = (S2 − 1/4)·|D| for integer and non-integer spin values, respectively). However, Ishikawa and coworkers demonstrated that a single paramagnetic ion was able to display slow relaxation of magnetization with large energy barriers. In fact, a Tb(III)- and phthalocyanine-based double-decker complex showed an energy barrier of 330.9 K.8 During the last few years, Dy(III)-based systems have monopolized the field of SMMs over other ions with a large magnetic moment such as Tb(III),9 since the former possesses large magnetic anisotropy and, being a Kramers ion, QTM is less probable to occur.10,11
Cerium represents a potential candidate for the synthesis of stable MOFs at a relatively low cost that could potentially present interesting properties. It presents an average abundance in the Earth's crust of over 60 ppm, comparable to other metals such as zinc, copper or tin, being more abundant than the rest of the lanthanide elements.12 Despite the wide variety of lanthanide-based MOFs that have been designed in these years, slow magnetic relaxation for Ce(III)-based SMMs has been mainly reported for mononuclear or mixed Nd–Ce(III) complexes, whereas Ce(III)-based MOFs remain somewhat unexplored.13,14
Luminescent MOFs present tuneable emission properties which can be rationally designed not only from the MOF components, but also from their interactions with guest molecules, analytes, composites, etc.15,16 As a consequence, many examples of luminescent MOFs showing potential applications as chemical sensors to detect and quantify ions, temperature, pressure, pH and biomolecules have been reported.17,18 The luminescence properties of MOFs are traditionally based on emissions from the metal ions and/or organic ligands and/or a charge transfer between them. Low molar extinction coefficients of lanthanide ions are caused by their forbidden electronic transitions between valence f orbitals, which translates into poor excitation and subsequent low quantum yields Charge transfer between ligands and lanthanides through the well-known antenna effect, gerenally improves the metals excitation process, enhacing the final quatum yields.19 Nonetheless, the contribution of the 5d orbitals of Ce(III) in electronic transitions makes it sensitive to the coordination environment, in such a way that Ce-centred emission is more probable than in other lanthanides.20 Ce(III)-based compounds display unusually broad absorption and emission bands compared to the rest of the lanthanide ions21 and their emission, typically occurring in the UV and/or blue spectral region, can be shifted to much longer wavelengths depending on the coordination environment.22 Moreover, Ce(III)-based MOFs tend to exhibit weaker luminescence emissions than other Ln(III) ions, i.e. Eu, Tb and Dy, for which the former have been scarcely the object of study in photoluminescence and sensing applications.23 Instead, porous stable Ce(III)-MOFs were employed in some practical applications in gas sorption and separation of CO2 and N2,24 as well as in heterogeneous catalysis in different reactions (oxidation, acetylation, asymmetric cyanosilylation), involving the contribution of Ce as an open-metal site.25 The use of Ce-based MOFs in sensor applications represents an emerging field, where two aspects are investigated: (i) the use of the redox properties of Ce(III/IV) and (ii) the use of functionalized linker molecules. A recent example was reported by Dong et al. where a Ce(III)-H3BTC (H3BTC = 1,3,5-benzene tricarboxylalic acid)-based MOF functionalised with Au nanoparticles (NPs) and DNA presents the electrochemical detection of telomerase activity.26
Besides the potential sensing applications that could offer luminescent MOFs, the combination of both magnetic and emissive properties is not unintended as they could complement each other in terms of applications. For instance, slow magnetic relaxation is extremely temperature-dependent and, therefore, a rigorous control of it is mandatory. Considering that the emission is often temperature-dependent, luminescence thermometry is a practical application for the temperature control.27 Moreover, the emission bands of lanthanides are strictly correlated with the electronic structure and, consequently, they could provide valuable information of the energy diagram.28 This information is fundamental in order to understand the relaxation dynamics of the studied systems.
On the other hand, the chemical nature of the organic ligand is no less important since, for example, aromatic spacers offer higher rigidity than aliphatic ones due to their geometrical characteristics that can restrict the topological variety, a very relevant fact when only a single ligand is used.29 Specifically, the isophthalate ligand (1,3-benzenedicarboxylate) is a widely used linker for which changing the substituent at the aromatic 5-position has been shown to be a successful strategy to increase the structural variety of the material formed.30 For example, our group has synthesized a wide variety of MOFs, introducing different functional groups such as cyanide and tetrazole in that position, obtaining systems with different topologies.31 Taking these considerations into account, in this work we have chosen the linker 5-methylisopthalate (5Meip) as a ligand with the aim of studying the effect that the methyl group can contribute to the construction of three-dimensional structures.32,33 Furthermore, the compounds formed should present good luminescence properties given the ability of the 5Meip carboxylate ligand to efficiently transfer energy to the lanthanide centres, generating intense emissions in both the visible and NIR regions, as we have already demonstrated in other previous studies.33
With all the above, and to the best of our knowledge, we report the first examples of multifunctional Ce(III)-MOFs with slow relaxation of magnetization and phosphorescence properties. The two novel Ce(III)-MOFs consist of Ce(III) metal ions linked by the 5Meip ligand, named GR-MOF17 and GR-MOF18. These materials consist of multifunctional three-dimensional coordination polymers that present interesting magnetic and luminescence properties.
Results and discussion
Synthesis and crystal structure
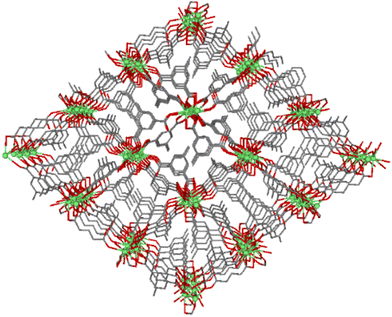
Compound GR-MOF-17 crystallizes as yellow crystals from an aqueous solution heated to 413 K for 72 hours in a Teflon-lined container enclosed in a stainless-steel vessel. As shown in the formula of the compound, the asymmetric unit contains two crystallographically independent 5Meip ligands, showing distinct deprotonation degrees and coordination modes. The crystal structure of GR-MOF-17 comprises Ce(III) metallic centres coordinated to two chelating and four monodentate carboxylate groups as well as to one carboxylic acid group belonging to seven adjacent 5Meip ligands forming a CeO9 coordination sphere, which fits best to a muffin polyhedron according to SHAPE calculations (ESI, Table S1†).34,35 It is worth highlighting that the protonated monodentate carboxylic acid group forms an intramolecular O–H⋯O hydrogen bond with an adjacent carboxylate group, as shown in Fig. S1.† The Ce–O bond distances (as shown in ESI, Table S4†) range from 2.415(2) to 2.700(2) Å depending on the coordination mode of the carboxylate group. The symmetry-related Ce1 atoms are sequentially triply bridged by a μ-syn,syn carboxylate group and two μ-O bridges pertaining to carboxylate groups adopting an asymmetric chelating terminal coordination mode. These bridges are further extended along infinite chains running along the crystallographic a axis, rendering Ce⋯Ce distances of ca. 4.23 Å. On its part, these Ce-carboxylate rods are further interlinked by the 5-methylisophthalate linkers forming a structurally non-porous 3D coordination polymer (Fig. 1).Compound GR-MOF-18 crystallizes as yellow crystals from an N,N-dimethylformamide (DMF) solution heated to 413 K for 72 hours in a Teflon-lined container enclosed in a stainless-steel vessel. The crystal structure of GR-MOF-18 presents two main differences in the crystallographically independent Ce centres with respect to the aforementioned MOF: (i) the coordination of a DMF molecule and (ii) a Cl− ion. Therefore, the asymmetric unit only contains a fully deprotonated 5Meip ligand to counterbalance the positive charge of Ce(III). The Ce centre presents a CeCl2O7 coordination with Ce–Cl bonds ranging from 2.8940(4) to 2.9164(9) Å and the coordination of two chelating and two monodentate carboxylate groups, in addition to the DMF oxygen atom. Continuous shape measures reveal that, as in GR-MOF-17, the Ce(III) coordination sphere fits best to a muffin polyhedron (Table S1†). The Ce atoms are also linked one another into infinite metal–organic rods running along the a axis, in which the chloride ions replace the syn,syn carboxylate group in the triple bridge, in such a way the Ce⋯Ce distance is slightly shortened to ca. 4.07 Å (as shown in ESI, Table S4†). Within these chains, it is worth highlighting that the coordinated DMF molecules are disordered into two equivalent positions and arranged in a coplanar disposition to the carboxylate groups, which results in a significant C–H⋯π interaction between the DMF and the aromatic plane of the 5Meip ligand (see Fig. S2 and Table S3 in the ESI†). The 1D inorganic polymer is further expanded by the coordination of 5Meip ligands in the (110) and (−1−10) directions, forming an open 3D coordination MOF. As shown in Fig. 2, the potential pores resulting from the release of coordinated DMF molecules have a diamond shaped structure with edge-sharing chloride atoms.
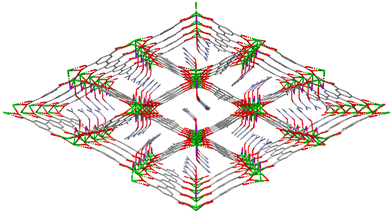 | ||
| Fig. 2 Perspective view of GR-MOF-18 along the c axis. Colour code is the same as in Fig. 1 with chlorides are represented in purple. | ||
Static magnetic properties
The temperature dependence of the magnetic susceptibility was measured on polycrystalline samples for GR-MOF-17 and GR-MOF-18 in the 2–300 K temperature range under an applied magnetic field of 1 kOe (Fig. 3). At room temperature, the χMT values of 0.649 and 0.704 cm3 mol−1 K for GR-MOF-17 and GR-MOF-18, respectively, are close to the expected value of 0.8 cm3 mol−1 K for one isolated Ce(III) ion at the ground state (2F5/2). On cooling down, both complexes display a similar behaviour with a gradual decrease of the χMT product reaching minimum values of 0.319 and 0.329 cm3 mol−1 K at 2 K. This behaviour could be ascribed as a progressive depopulation of the mJ states, but weak intermolecular antiferromagnetic interactions could not be completely discarded considering the direct carboxylate and/or chloride bridges between Ce(III) ions present in both structures. This hypothesis is also supported by the sudden drop of the χMT values observed at low temperature for GR-MOF-17 and by the discrepancy found at low temperature between the experimental χMT(T) curves and those computationally calculated for models based on a monomeric moiety of the structure (ESI, Fig. S27 and S28†), where the exchange interactions are not considered (see Computational details and also the next section for further details). | ||
| Fig. 3 Variable-temperature dc magnetic susceptibility data for GR-MOF-17 and GR-MOF-18 collected under a 1 kOe applied dc field. | ||
Additionally, the field dependence of the magnetization was measured for both compounds in the 2–7 K temperature range (Fig. S3 and S4†). At 2 K and at the highest applied magnetic field of 7 T, magnetization values of 0.790 and 0.894NμB were obtained for GR-MOF-17 and GR-MOF-18, respectively. The lack of a clear saturation at the highest applied magnetic field could be indicative of magnetic anisotropy.
Computational magnetic results
In trivalent Ce(III), the 4f1 electron is expected to give rise to a 2F5/2 ground state due to the spin–orbit coupling. In the presence of an appropriate ligand field, the ground state could split in three Kramers doublets (KDs, i.e. mJ = ±5/2, ±3/2 and ±1/2), and depending on their separation and order in a given environment, it could result in slow relaxation of magnetization. Therefore, RASSI calculations on top of CASSCF calculations were performed for both compounds using the monomeric complexes obtained from X-ray coordinates as representative models (see the Computational details section). Both metal centres are characterized by a predominant axial anisotropy in view of the large gz component of the ground Kramers doublet (Table 1), although these values are still below of what is expected for a perfectly axial Ce(III) ion (gz = 4.19). Therefore, a partially mixed ground state majorly composed of the mJ = ±5/2 is anticipated for both compounds.| Compound | g x | g y | g z |
|---|---|---|---|
| 1 | 0.459 | 0.879 | 3.752 |
| 2 | 0.438 | 0.518 | 3.723 |
The decomposition analysis of the lowest lying KDs confirms this hypothesis showing a dominant mJ = ±5/2 (above 89%) ground state in both compounds, although the axial character is not fully preserved for the excited states being admixtures of ±3/2 and ±1/2 (see ESI, Tables S5 and S6†). A further analysis on the basis of the orientation of the gz component in the coordination environment has been performed to understand the relative axiality of the compounds. Given the oblate f electron density of the Ce(III) ion for an mJ = ±5/2 ground state, a perpendicular orientation of the gz component respect to the electron density is expected in order to reduce the metal–ligand electrostatic repulsion. To that end: (i) gz must be aligned with the shortest Ce–O bond distances and (ii) the longest coordination bond distances are all placed in a plane so that the f electron density conforms a disc. None of the studied compounds meets both requirements, although the coordination environment of GR-MOF-18 better adapts to them (Fig. 4). The shortest Ce–O distances (with O5 < O3 < O1, in that relative order, ESI, Table S4†) are displaced along the (011) crystallographic plane, in such a way that the O5 atom is placed in an opposite position of the coordination sphere with respect to edge-sharing (adjacent) O1 and O3 positions. The gz vector is able to align close to the three key atoms. However, the two longest coordination distances resulting from Ce–Cl bonds do not remain in the same plane but the Cl1 atom is placed out from the mean plane formed by the rest of the atoms (O1, O2, O3, O4 and Cl1(i)). In contrast, the shortest Ce–O bond distances in GR-MOF-17 (with O3 < O8 < O4, in that relative order) are arranged in three consecutive edge-sharing vertexes, in such a way that neither the gz vector can be aligned to all the closest oxygen nor the remaining atoms (those showing the longest bond distances) can arrange into a plane.
The calculation of the lowest lying KD energies and transition probabilities are shown in Fig. 4. As observed, transition probabilities between the ground state KDs are quite large for both compounds in agreement with the admixture found for the mJ states in each of the doublets, in such a way that fast relaxation through quantum tunnelling of the magnetization (QTM) may be present in both cases. Moreover, the large energy separation between the first excited and ground states (at ca. 400 and 300 cm−1, respectively, for GR-MOF-17 and GR-MOF-18), especially for GR-MOF-17, establishes an exceedingly large energy barrier, in addition to the low matrix elements of the transition, which may prevent the slow relaxation operating through the Orbach mechanism.
Dynamic magnetic properties
As mentioned in the introduction, lanthanides are ideal candidates for the synthesis of SMMs. In contrast to transition metals, the outer 5s2 and 5p6 electrons protect the valence 4f electrons of rare earth ions and, therefore, the orbital angular momentum is not quenched by the ligand field providing large magnetic anisotropy, which is the present case as previously suggested by the computational calculations performed.With the aim of discovering the potential SMM behaviour in compounds GR-MOF-17 and GR-MOF-18, dynamic magnetic susceptibility studies were performed by applying an alternating current of 3.5 Oe. In the absence of an external magnetic field (Hdc = 0 Oe), none of the samples presented signals in the out-of-phase magnetic susceptibility (Fig. S7 and S8†), which could be expected by the quite probable QTM observed in the preceding section and/or the existence of short Ce⋯Ce intermolecular interactions. On applying an external field of 1 kOe, both compounds displayed frequency- and temperature-dependent signals in χ′′M (very weak for GR-MOF-17 and sizeable for GR-MOF-18, see ESI, Fig. S7 and S8†). As observed, field-induced slow relaxation of magnetization emerges under these conditions. Thus, the field dependence of relaxation times was studied at a fixed temperature (4 and 3.2 K for GR-MOF-17 and GR-MOF-18) in the 250–2500 Oe range for both systems (ESI, Fig. S9 and S14†). This dependence could be often described by the contribution of different relaxation processes included in eqn (1):
 | (1) |
The three terms refer to direct, QTM and field-dependent Raman mechanisms (this last term is field-dependent according to the Brons–van Vleck equation), respectively. As shown in ESI, Fig. S9,† the field-dependent maxima shift towards lower frequencies at high fields, which is evidence of the receding relaxation times. This is well reproduced in Fig. S10,† where the inverse of the relaxation times shows a gradual decrease upon application of larger magnetic fields. As illustrated by the group of Gómez-Coca in a recent work,14 the τ−1(H) curves display a “U” shape when the three terms involved in eqn (1) are operative. Indeed, the low-field τ−1 decay is related to the quenching of QTM, the flat intermediate regime corresponds to the Raman term and, lastly, the rapid increase at high fields is best described by the faster relaxation times due to the direct term (in good agreement with the H4 dependence). In the case of GR-MOF-17, however, the decay at low fields is not that pronounced and the direct process does not seem to occur. In fact, the data were fitted to a single Raman process (third term in eqn (1)) and the following set of parameters were obtained: dTn = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 s−1, e = 10.61 T−2 and f = 26.08 T−2. Note that no reasonable fit was obtained when including the QTM term. All the fitting parameters of this section are summarized in Table 2.
489 s−1, e = 10.61 T−2 and f = 26.08 T−2. Note that no reasonable fit was obtained when including the QTM term. All the fitting parameters of this section are summarized in Table 2.
| τ −1 (H) | τ −1 (T) | ||||||
|---|---|---|---|---|---|---|---|
| Raman | Raman | Local-mode | |||||
| dT n (s−1) | e (T−2) | f (T−2) | D(H) (s−1 K−n) | n | C (s−1) | ω (K) | |
| GR-MOF-17 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 489 |
10.61 | 26.08 | 44.00 | 3.6 | — | — |
| GR-MOF-18 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 942 942 |
64.81 | 145.50 | 83.85 | 4.3 | 6.84 × 108 | 41.5 |
| GR-MOF-17@La | — | — | — | — | — | 5.91 × 107 | 57.6 |
| GR-MOF-18@La | — | — | — | — | — | 1.16 × 107 | 24.8 |
Once studied the field dependence, temperature- and frequency-dependent measurements were carried out with an external magnetic field of 2.5 kOe. As a result, maxima in the χ′′M(υ) curves were found in the 2.0–7.0 K temperature range (Fig. 5), and the relaxation times for each temperature were obtained. As for the field dependence, the temperature dependence of the relaxation times is typically described by the combination of several mechanisms summarized in eqn (2):
 | (2) |
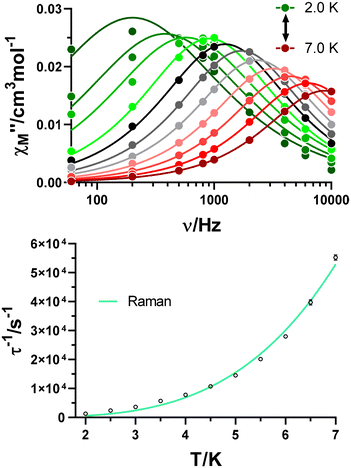 | ||
| Fig. 5 Variable-temperature frequency dependence of the χ′′M signal under a 2.5 kOe applied field for GR-MOF-17 (top). Dependence of the inverse of the relaxation time on the temperature (bottom). | ||
Only the fourth and fifth terms are new in this equation, which correspond to the local-mode and Orbach mechanisms. In the case of GR-MOF-17, only the Raman term was used for fitting the data. Moreover, the D(H) Raman term 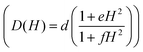 was fixed to 44.00 s−1 K−n taking advantage of the field dependent measurements and, therefore, being n the only free variable. A reasonable fit was obtained with n = 3.6.
was fixed to 44.00 s−1 K−n taking advantage of the field dependent measurements and, therefore, being n the only free variable. A reasonable fit was obtained with n = 3.6.
The same approach was accomplished for GR-MOF-18. Similarly, field-dependent relaxation times acquired at a fixed temperature of 3.2 K were fitted to a Raman mechanism (eqn (1)), with no need for including the QTM or direct process terms (Fig. S15,†dTn = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 942 s−1, e = 64.81 T−2 and f = 145.50 T−2). Subsequently, frequency- and temperature-dependent measurements were carried out by applying an external magnetic field of 1 kOe (Fig. 6, top). χ′′M(υ) curves were analysed in the 2.0–4.0 K temperature range by obtaining relaxation times for each temperature. As for GR-MOF-17, we initially attempted fitting the inverse of the dependence of relaxation times with temperature using a single Raman mechanism by fixing D(H) to 83.85 s−1 K−n (Fig. 6, bottom: turquoise line). However, a single relaxation pathway it is not able to describe the temperature dependence of relaxation times in the whole regime. Therefore, we initially considered including, besides the Raman process, an Orbach mechanism to the fit. Nonetheless, this process would involve an excited state at around 300 cm−1 (see Table S6† in the Theoretical calculations section), which is not consistent with our data. Thus, the local-mode mechanism, involving a two-phonon process where the molecule relaxes from a vibrational excited state of the electronic ground state, was chosen.36,37 The inverse of the relaxation times were consequently fitted using the third and fourth terms in eqn (2) (Fig. 6, bottom: orange line): n = 4.3, C = 6.84 × 108 s−1 and ω = 41.5 K.
942 s−1, e = 64.81 T−2 and f = 145.50 T−2). Subsequently, frequency- and temperature-dependent measurements were carried out by applying an external magnetic field of 1 kOe (Fig. 6, top). χ′′M(υ) curves were analysed in the 2.0–4.0 K temperature range by obtaining relaxation times for each temperature. As for GR-MOF-17, we initially attempted fitting the inverse of the dependence of relaxation times with temperature using a single Raman mechanism by fixing D(H) to 83.85 s−1 K−n (Fig. 6, bottom: turquoise line). However, a single relaxation pathway it is not able to describe the temperature dependence of relaxation times in the whole regime. Therefore, we initially considered including, besides the Raman process, an Orbach mechanism to the fit. Nonetheless, this process would involve an excited state at around 300 cm−1 (see Table S6† in the Theoretical calculations section), which is not consistent with our data. Thus, the local-mode mechanism, involving a two-phonon process where the molecule relaxes from a vibrational excited state of the electronic ground state, was chosen.36,37 The inverse of the relaxation times were consequently fitted using the third and fourth terms in eqn (2) (Fig. 6, bottom: orange line): n = 4.3, C = 6.84 × 108 s−1 and ω = 41.5 K.
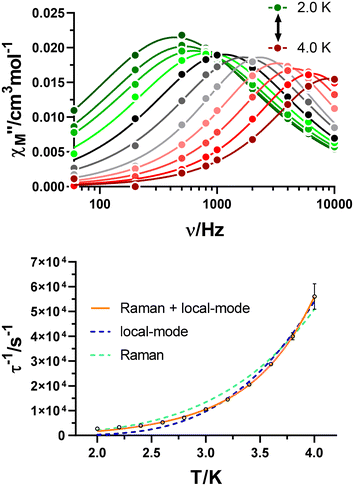 | ||
| Fig. 6 Variable-temperature frequency dependence of the χ′′M signal under a 1 kOe applied field for GR-MOF-18 (top). Dependence of the inverse of the relaxation time on the temperature (bottom). | ||
As previously described, the crystal structures of GR-MOF-17 and GR-MOF-18 compounds involve Ce(III) ions that are bridged by carboxylate groups, giving rise to short Ce⋯Ce distances (4.2301(7) and 4.0735(2) Å, respectively). Often, this results in weak dipolar interactions that facilitate the undesired QTM.38,39 Thus, magnetic dilution was also attempted for both systems. For this purpose, diamagnetic La(III) was selected considering the similar ionic radius between the Ce(III) and La(III) atoms. As a result, isostructural and magnetically diluted counterparts GR-MOF-17@La and GR-MOF-18@La were obtained. These materials were synthesized by carrying out the same procedure as for the synthesis of pure GR-MOF-17 and GR-MOF-18 using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 Ce
10 Ce![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) La ratio. The relaxation dynamics of the new materials were studied under an applied magnetic field of 2.5 kOe (Fig. S19–S26†) in order to maximize the effect of the field according to the field-dependent behaviour observed for the relaxation time (Fig. S10 and S15†).
La ratio. The relaxation dynamics of the new materials were studied under an applied magnetic field of 2.5 kOe (Fig. S19–S26†) in order to maximize the effect of the field according to the field-dependent behaviour observed for the relaxation time (Fig. S10 and S15†).
As it could be expected from the elimination of the weak Ce⋯Ce dipolar interactions, improved magnetic properties were obtained for both diluted materials. On the one hand, for GR-MOF-17@La, maxima were found up to 8.2 K in the χ′′M(υ) curves (Fig. S21†), which at the same time led to slower relaxation times at all temperatures as can be seen in Fig. 7, top. Moreover, the mechanism that best describes the temperature dependence of relaxation times is the local-mode pathway and not Raman as concluded for GR-MOF-17 (C = 5.91 × 107 s−1 and ω = 57.6 K). On the other hand, two main differences could be observed in GR-MOF-18@La. First, the maxima in the χ′′M(υ) plot expand in the whole frequency range (Fig. S25†), which means slower relaxation times as shown in the bottom of Fig. 7. Second, the temperature dependence of relaxation times is best described by only considering a local-mode mechanism, with no need of including the Raman relaxation pathway. The best fit was obtained with C = 1.16 × 107 s−1 and ω = 24.8 K.
 | ||
| Fig. 7 Dependence of the inverse of the relaxation time on the temperature for GR-MOF-17/GR-MOF-17@La (top) and GR-MOF-18/GR-MOF-18@La (bottom). | ||
The comparison of the results suggests that: (i) the importance of quantum tunnelling relaxation in the MOFs in the absence of an external magnetic field (Hdc = 0 Oe), as none of the samples presented signals in the out-of-phase magnetic susceptibility. The fields required for observing slow relaxation of magnetization in GR-MOF-17 and GR-MOF-18 are one order of magnitude larger than the molecular cerium SMMs reported by Gómez-Coca et al., as they present larger Ce⋯Ce distances in addition to the absence of carboxylate/chloride-mediated superexchange bridges, both effects minimizing the QTM process.14 (ii) The temperature dependence of the inverse of relaxation times shows a Raman spin relaxation process in GR-MOF-17, a mixture between the Raman and local-modes is found in GR-MOF-18 and the local-mode is only found for GR-MOF-17@La and GR-MOF-18@La. We may assume that larger Ce⋯Ce distances in diamagnetically diluted counterparts are responsible for the absence of Raman spin relaxation. (iii) The faster temperature-dependent spin relaxation is caused by short Ce⋯Ce distances providing dipolar interactions in both pure compounds, which highlights the relevance of isolating magnetic centres.
At this point, it is important to note that the fitting parameters that were found for GR-MOF-17, GR-MOF-18 and diluted counterparts are in the range of those found by Gómez-Coca et al. for discrete molecular systems. Ce(III) has been poorly studied yet and, as a consequence, the mechanisms that govern the relaxation dynamics are not very well known for this ion. Indeed, as summarized by Gómez-Coca et al., the Orbach mechanism has been widely used to evaluate the performance of these SMMs, but as pointed out in recent works40,41 and in the present one, this is not the most appropriate as it often implies experimentally calculated Ueff values that are one order of magnitude smaller than the theoretically calculated ones. Thus, further Ce(III)-based studies are required to properly understand the behaviour of this ion.
Photoluminescence properties
The photoluminescence properties of GR-MOF-17 and GR-MOF-18 were studied for polycrystalline samples in the solid state given the good emissive properties shown by the 5Meip ligand with other lanthanide(III)-based CPs.33 As aforementioned in the introduction, the Ce(III)-centred emission has not been largely studied as compared to other lanthanide(III) ions because 5d orbitals are close in energy to the 4f shell due to ligand and crystal fields, in such a way that Ce(III) can show 5d–4f-transitions which lie in the visible range.42 Given that both ground and first excited states derived from the f1 configuration are spin doublets (2F5/2 and 2F7/2), the Ce(III)-centred emission usually consists of two bands split by spin–orbit coupling, which are sensitive to the coordination environment due to their partial d orbital character. Under UV laser excitation (λex = 325 nm), a wavelength close to the absorption maxima observed in the diffuse reflectance spectra (Fig. S35†), both compounds present a wide emission band containing several overlapped maxima (Fig. 8). Table 3 gathers the most relevant photophysical data of the compounds and free ligand samples.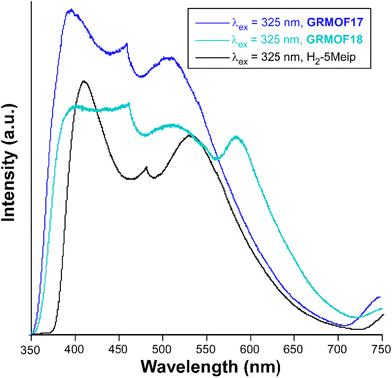 | ||
| Fig. 8 Room temperature emission spectra under λex = 325 nm excitation in the visible range of GR-MOFs compared with the free ligand. | ||
| Compound |
λ
abs,max![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a,b a,b |
λ
em,max![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a,c a,c |
τ
av![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
QY (%) |
|---|---|---|---|---|
| a These data are given in nm; w: weak band and sh: shoulder. b These data are taken from diffuse reflectance spectra. c These data are taken from PL emission spectra. d Values recorded at RT given in ns unless specified. | ||||
| H2-5Meip | 253/300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420(sh) 420(sh) |
408/479/530 | 5.0/—/5.6 | 0.8 (5) |
| GR-MOF-17 | 245/295 | 397/462/510 | 0.2 ns/—/25.9 μs | 1.0 (3) |
| 320(sh) | ||||
| GR-MOF-18 | 250/300 | 398/460/514/584 | 3.5/4.3/—/23.5 | 2.3 (4) |
| 325(sh) | ||||
GR-MOF-17 shows an emission spectrum consisting of three main contributions: (i) a wide maximum peaking at λem = 397 nm that dominates the spectrum, (ii) a much narrower maximum showing a very sharp profile at λem = 462 nm, and (iii) a third wide maximum of similar intensity at λem = 510 nm. In this compound, all the emission maxima can be attributed to the free H2-5Meip ligand-centred processes (π–π* transitions) owing to the great similarity shown by the present spectrum with that of the ligand, in which not only the number, but also the shape of the bands are reproduced (see Fig. 8). In fact, the emission of GR-MOF-17 is only distinguished from that of the ligand by its small blue shift (see Table 3) and the higher relative intensity of the second band, effects that may be related to the coordination of the ligand to Ce(III) ions in the crystal structure.43 The most relevant excitation and emission processes discussed herein are summarized in Scheme 1.
In agreement with the LC character of the emission, the excitation spectrum only presents a weak and wide band centred at λex = 310 nm, which resembles that found for H2-5Meip (see ESI, Fig. S36 and 37†) and that is also in agreement with the main absorption band present in the diffuse reflectance spectra of the compounds (Fig. S35†). Taking into account the highest- and lowest-energy absorption and emission bands, the Stokes shift may be estimated to be of ca. 6000 cm−1. To better characterize the nature of the emission bands, decay curves were measured. A very short emission lifetime was observed for the dominant maximum at λem = 397 nm, in which the decay tail could be hardly distinguished from the pulse of the lamp. Therefore, a fluorescence lifetime of ca. 0.2 ns was estimated by deconvolution (ESI, Fig. S38a†), which is surprisingly shorter than that found for the free ligand by deconvolution of the two main bands (τav of 5 ns, λem = 408 and 530 nm, ESI, Fig. S39†). In line with this fact, the solid sample presents a quite low emission quantum yield based on UV excitation (maximum QY = 1.0(3)% under λex = 325 nm). Nonetheless, the emission at the third maximum of GR-MOF-17 (λem = 510 nm) shows a much long-lived (three orders of magnitude) component with an average lifetime of ca. 26 μs from a tail fitting with a multiexponential expression [(It = A0 + A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(t/τ1) + A2
exp(t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(t/τ2)] (ESI, Fig. S38b†), thus falling in the typical range of phosphorescence.44 A Gd(III)-based CP, with formula [Ln2(μ4-5Meip)3(DMF)]n and thus considered as a representative compound in which the 5Meip ligand presents a comparable structure, showed a phosphorescence emission with a τav of 494 μs at 13 K,33 from which it was concluded that such phosphorescence comes from the emission of an excited triplet state (centred on the ligand) lying at about 22
exp(t/τ2)] (ESI, Fig. S38b†), thus falling in the typical range of phosphorescence.44 A Gd(III)-based CP, with formula [Ln2(μ4-5Meip)3(DMF)]n and thus considered as a representative compound in which the 5Meip ligand presents a comparable structure, showed a phosphorescence emission with a τav of 494 μs at 13 K,33 from which it was concluded that such phosphorescence comes from the emission of an excited triplet state (centred on the ligand) lying at about 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 over the ground state. Taking into account that the phosphorescence signal is usually quenched at room temperature by the vibrational modes of the molecules, the measurements were repeated at 15 K in order to slow down the molecular vibrations in the GR-MOF-17 framework. Two main changes were observed in the spectra at that low temperature: (i) the excitation band at λex = 310 nm increases the intensity and is clearly distinguished from the background and, more importantly, (ii) the first emission maximum (at λem = 397 nm) decreases its relative intensity, having the three maxima with similar intensities. The phosphorescence signal is substantially enhanced by one order of magnitude up to 273 μs, meaning that triplet excitons are better shielded in the frozen structure of the compound and/or that the intersystem crossing (the mechanism by which triplet states are populated from excited singlet states)44 rate is increased at that low temperature. To better characterize the phosphorescence signal, the delayed emission was also recorded from time-resolved emission spectral (TRES) experiment by collecting the decay curves in the 350–700 nm range. Focusing on the delayed emission spectrum in which all fluorescence has already disappeared, it can be confirmed that the phosphorescence emission describes a band centred at 525 nm (Fig. S40†), confirming the accessibility of low-lying triplet states.
000 cm−1 over the ground state. Taking into account that the phosphorescence signal is usually quenched at room temperature by the vibrational modes of the molecules, the measurements were repeated at 15 K in order to slow down the molecular vibrations in the GR-MOF-17 framework. Two main changes were observed in the spectra at that low temperature: (i) the excitation band at λex = 310 nm increases the intensity and is clearly distinguished from the background and, more importantly, (ii) the first emission maximum (at λem = 397 nm) decreases its relative intensity, having the three maxima with similar intensities. The phosphorescence signal is substantially enhanced by one order of magnitude up to 273 μs, meaning that triplet excitons are better shielded in the frozen structure of the compound and/or that the intersystem crossing (the mechanism by which triplet states are populated from excited singlet states)44 rate is increased at that low temperature. To better characterize the phosphorescence signal, the delayed emission was also recorded from time-resolved emission spectral (TRES) experiment by collecting the decay curves in the 350–700 nm range. Focusing on the delayed emission spectrum in which all fluorescence has already disappeared, it can be confirmed that the phosphorescence emission describes a band centred at 525 nm (Fig. S40†), confirming the accessibility of low-lying triplet states.
The room temperature emission spectrum of GR-MOF-18 presents a similar pattern to that shown by GR-MOF-17, in which the first three bands peak at the same wavelengths (in turn blue-shifted with respect to the free ligand), although it also exhibits a fourth wide band peaking at λem = 584 nm. The excitation spectra recorded at the four emission maxima show similar patterns featuring the presence of a weak and broad band (concordant with the absorption profile found in the diffuse reflectance spectrum, Fig. S35†) and the absence of narrow bands, which at first sight is characteristic of a ligand-centred process. Moreover, the excitation band maximum is shifted towards higher wavelengths according to the increasing λem monitored in the compound (Fig. S44†). Consequently, the Stokes shift (of ca. 5580 cm−1) is smaller than for GR-MOF-17. In order to confirm this latter assumption, decay curves were measured at the four emission band maxima of GR-MOF-18, finding very short lifetimes of few nanoseconds (of the same order of magnitude of those observed by the free ligand, Fig. S45†), except for the fourth band (at λem = 584 nm), in which a longer lifetime of ca. 23.5 ns is recorded. With all these results, it can be argued that the last least energetic emission band present in GR-MOF-18 and absent in GR-MOF-17 does not correspond to a 4f ← 5d intraionic transition, which is known to appear in the 300–460 nm range,45 but it may be related to an exciplex (excitation complex) derived from the interaction between the coordinated DMF and 5Meip molecules (see Fig. S2 and Table S3† for further details). The occurrence of additional emission bands derived from such interactions between DMF and carboxylate ligands has been previously observed.46,47 Finally, it is worth noting that the absolute QY of GR-MOF-18 (maximum QY = 2.3(4)% under λex = 380 nm) practically doubles that of GR-MOF-17, which could be related to the presence of the protonated carboxylate group, i.e. the O–H group, known to act as an efficient quencher of the luminescence in lanthanide(III)-based CPs and MOFs.48
Conclusions
Two 3D frameworks based on Ce(III) and the 5-methylisophthalate ligand, especially a condensed network of [Ce(5Meip)(H-5Meip)]n formula (GR-MOF-17) or an open framework of [CeCl(5Meip)(DMF)]n formula (GR-MOF-18), were obtained by carrying out their solvothermal reaction in distinct stoichiometries and solvents. As expected for Ce(III)-based compounds, slow relaxation of magnetization only occurs in the presence of an external magnetic field. Under optimal conditions, the temperature-dependent spin relaxation is dominated by the Raman process for GR-MOF-17, a combination between Raman and local-modes for GR-MOF-18, and the local-mode only for diamagnetically diluted GR-MOF-17@La and GR-MOF-18@La. The inclusion of the less common local-mode term in the fitting procedure of relaxation times was supported by theoretical calculations. Indeed, the Orbach mechanism was discarded due to the large energy difference found between the two lowest lying Kramers doublets. When avoiding Ce⋯Ce interactions by diamagnetic dilution with La(III), both GR-MOF-17@La and GR-MOF-18@La displayed slower relaxation times in the studied temperature range. Moreover, Raman relaxation seemed to be quenched and, instead, the local-mode relaxation pathway is the only active mechanism. With regard to their photoluminescence properties, both compounds present similar emission profiles, although GR-MOF-18 characterizes for the occurrence of an additional featureless emission band attributed to an exciplex derived from the C–H⋯π interactions taking place between DMF and 5Meip ligands, all of which results in a more intense emission (which doubles the QY of GR-MOF-17). The characteristic phosphorescence of isophthalate derivatives is present in GR-MOF-17, with an average lifetime of ca. 25 at room temperature, meaning that low-lying triplet states are accessible. A detailed analysis of the photoluminescence properties confirms the absence of intraionic d–f or f–f transitions.In this study, we have presented the first examples of multifunctional Ce(III)-based MOFs presenting slow magnetization relaxation and phosphorescence properties. Nevertheless, more examples of Ce(III)-MOFs with SMMs and phosphorescence behaviour are required to fully understand the spin relaxation and triplet state population processes in this new family of compounds.
Experimental section
Chemicals
All chemicals were of reagent grade and used as commercially obtained with any further purification.Synthesis of GR-MOF-17
2 mL of an aqueous solution containing CeCl3 (0.1 mmol, 0.0246 g) was added dropwise to another aqueous solution (5 mL) containing 5-methylisophthalic acid (0.2 mmol, 0.0360 g) which was previously basified with Et3N (42 μL). The resulting mixture was transferred to a Teflon-lined container enclosed in a stainless-steel vessel and heated for 72 hours at 140 °C. Small crystals of GR-MOF-17 were observed when opening the vessel, which were filtered off and washed with water and ethanol. Yield (based on metal): 45%. Anal. Calc for C18H13CeO8 (%): C, 43.46; H, 2.63; N, 0.00. Found: C, 43.50; H, 2.66; N, 0.03.Synthesis of GR-MOF-18
5-Methylisophthalic acid (0.1 mmol, 0.0180 g) and CeCl3 (0.1 mmol, 0.0246 g) were dissolved in 10 mL of DMF, heated for 72 hours at a temperature of 140 °C in a Teflon-lined stainless-steel autoclave and then slowly cooled down to room temperature. Single crystals corresponding to GR-MOF-18 were obtained, which were filtered off and washed with water and ethanol. Yield (based on metal): 60%. Anal. Calc for C12H13CeClNO5 (%): C, 33.77; H, 3.07; N, 3.28. Found: C, 33.71; H, 3.09; N, 3.25.Chemical characterization
Elemental analyses (C, H, N) were performed on a Leco CHNS-932 microanalyzer. Magnetic susceptibility measurements (with an applied dc field) were carried out on the polycrystalline samples of the compounds with a Quantum Design SQUID MPMS-7T susceptometer at an applied magnetic field of 1000 G. The susceptibility data were corrected for the diamagnetism estimated from Pascal's tables,49 the temperature-independent paramagnetism, and the magnetization of the sample holder. Alternating current measurements were performed on a physical property measurement System-Quantum Design model 6000 magnetometer under a 3.5 G ac field and frequencies ranging from 60 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz.
000 Hz.
X-ray diffraction data collection and structure determination
Suitable single crystals of compounds GR-MOF-17 and GR-MOF-18 were mounted on a Bruker VENTURE diffractometer equipped with a PHOTON 3 detector, graphite monochromated Mo-Kα radiation (λ = 0.71073 Å) and an Oxford cryosystem. 100 K single crystal X-ray diffraction data were collected and processed using APEX III software. Adsorption correction was applied using SADABS software by empirical methods measuring symmetry equivalent reflections at different azimuthal angles. All structures were solved using the SHELXT program and refined using least squares refinement methods on all F2 values as implemented within SHELXL.50,51 Both SHELXT and SHELXL were operated through the Olex2 (v1.5) interface.52 All atoms were refined anisotropically and atomic displacement parameters were refined with suitable restraints or constraints applied to keep them physically reasonable. Hydrogen atoms were placed in calculated positions and refined with idealised geometries and fixed occupancies and isotropic displacement parameters were assigned. Crystallographic refinement details can be found in Table S2 in the ESI.†X-ray powder diffraction (XRPD) (section S6, Fig. S46–S49 in the ESI†) patterns were measured on grounded single crystals or polycrystalline samples. A Philips X'PERT powder diffractometer, equipped with Cu-Kα radiation (λ = 1.5418 Å), was used to measure the diffractograms over the 5 < 2θ < 50° range with a step size of 0.026° and an acquisition time of 2.5 s per step at 25 °C. Indexation of the diffraction profiles was made using the FULLPROF program (pattern matching analysis)53 on the bases of the space group and cell parameters obtained from the single crystal X-ray diffraction data.
Photoluminescence measurements
Fluorescence excitation and emission spectra and lifetime measurements in the solid state were recorded on an Edinburgh Instruments FLS920 spectrometer at variable temperatures using a closed cycle helium cryostat enclosed in the spectrometer. For steady-state measurements, a Müller-Elektronik-Optik SVX1450 Xe lamp or an IK3552R-G He–Cd continuous laser (325 nm) were used as excitation sources, whereas a microsecond pulsed μF900 lamp was used for recording the decay curves. The emission spectra in the NIR region and the decay curves were acquired on a Hamamatsu NIR-PMT PicoQuant FluoTime 200 detector. For the variable temperature measurements in the solid state, the samples were first placed under high vacuum (of ca. 10−9 mbar) to avoid the presence of oxygen or water in the sample holder. The quantum yield was measured in the solid state by means of a Horiba Quanta-f integrating sphere using an Oriel Instruments MS257 lamp as the excitation source and an iHR550 spectrometer from Horiba to analyse the emission. Five measurements were accomplished to properly estimate the mean and standard deviation values for each compound.Computational details
The Gaussian 16 package54 was employed for the partial optimization of the models of the two compounds used in the simulation of the magnetic properties. These models consisted of monomeric excerpts taken from the X-ray coordinates of the compounds. Optimizations were performed at the DFT level of theory using the UB3LYP functional55 and the “Stuttgart/Dresden” basis sets and effective core potentials were used to describe the lanthanide(III) ions,56 and the 6-311G++(d,p) basis set was used for the rest of the non-metal atoms.57 On the other hand, ab initio calculations to calculate the magnetic properties of these compounds were conducted with the ORCA software suite (version 5.0.2)58,59 using the B3LYP functional.60,61 The second-order Douglas–Kroll–Hess (DKH)62,63 scalar relativistic Hamiltonian was used to treat the scalar relativistic effects, in combination with the recontracted def2-TZVP basis sets for all atoms except for the lanthanide atoms, for which SARC2-DKH-QZVP was employed. RIJCOSX approximation with appropriate auxiliary basis sets (SARC/J)64 were employed to speed up all calculations. Calculations with the state-average complete active space self-consistent field (SA-CASSCF) method were performed by incorporating the seven f-orbitals and one electron and 14 doublet states. After convergence of CASSCF energies, spin–orbit coupling (SOC) effects were included in a subsequent quasi-degenerate perturbation theory (QDPT) step. Spin Hamiltonian parameters were also calculated from these converged results by means of SINGLE_ANISO code as implemented in ORCA.65,66Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
O. Pajuelo-Corral: design of experiments, optimization of the synthesis, and analysis of magnetic properties. M. C. Contreras: synthesis of original materials and physico-chemical characterization. S. Rojas: methodology, investigation, and supervision. D. Choquesillo-Lazarte: advanced integration of the X-ray diffraction data and structural refinement. J. M. Seco: method, analysis, and supervision. A. Rodríguez-Diéguez: design of experiments, funding acquisition, and writing of the original manuscript. A. Salinas-Castillo: measurement of photoluminescence properties, analysis and review. J. Cepeda: measurement and analysis of photoluminescence properties, computational calculations, writing, review, and funding acquisition. A. Zabala-Lekuona: analysis of the magnetic properties, writing, review and editing. I. Vitorica-Yrezabal: project management, analysis of X-ray data, writing, review and editing. All the authors have discussed the results and agreed to publish the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Gobierno Vasco/Eusko Jaurlaritza (IT1755-22, IT1500-22), Red Guipuzcoana de Ciencia, Tecnología e Innovación (FA385/2023, DG23/16) and Junta de Andalucía (FQM-394, P21_00386 and ProyExcel_00386). The authors acknowledge the technical and human support provided by SGIker of UPV/EHU and European funding (ERDF and ESF). S. R. thanks Ministerio de Ciencia e Innovación for a Ramón y Cajal contract (the publication is part of the grant RYC2021-032522-I funded by MCIN/AEI/10.13039/501100011033 and the European Union “Next Generation-EU”/PRTR”).References
- Q. Zhang, S. Yan, X. Yan and Y. Lv, Sci. Total Environ., 2023, 902, 165944 CrossRef CAS PubMed.
- V. Guillerm, D. Kim, J. F. Eubank, R. Luebke, X. Liu, K. Adil, M. S. Lah and M. Eddaoudi, Chem. Soc. Rev., 2014, 43, 6141–6172 RSC.
- N. Stock and S. Biswas, Chem. Rev., 2012, 112, 933–969 CrossRef CAS PubMed.
- K. Suresh, A. P. Kalenak, A. Sotuyo and A. J. Matzger, Chem. – Eur. J., 2022, 28, e202200334 CrossRef CAS PubMed.
- G. Mínguez Espallargas and E. Coronado, Chem. Soc. Rev., 2018, 47, 533–557 RSC.
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143 CrossRef CAS.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 0652, 1–9 Search PubMed.
- C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E. S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202 CrossRef CAS PubMed.
- V. Sridharan and J. C. Menéndez, Chem. Rev., 2010, 110, 3805–3849 CrossRef CAS PubMed.
- F. Pointillart, O. Cador, B. Le Guennic and L. Ouahab, Coord. Chem. Rev., 2017, 346, 150–175 CrossRef CAS.
- F. A. Mautner, F. Bierbaumer, R. C. Fischer, À. Tubau, S. Speed, E. Ruiz, S. S. Massoud, R. Vicente and S. Gómez-Coca, Inorg. Chem., 2022, 61, 11124–11136 CrossRef CAS PubMed.
- W. Yang, G. Chang, H. Wang, T. L. Hu, Z. Yao, K. Alfooty, S. Xiang and B. Chen, Eur. J. Inorg. Chem., 2016, 2016, 4470–4475 CrossRef CAS.
- M. Gutiérrez, Y. Zhang and J. C. Tan, Chem. Rev., 2022, 122, 10438–10483 CrossRef PubMed.
- Y. Zhao, H. Zeng, X. W. Zhu, W. Lu and D. Li, Chem. Soc. Rev., 2021, 50, 4484–4513 RSC.
- Z. Li, F. Jiang, M. Yu, S. Li, L. Chen and M. Hong, Nat. Commun., 2022, 13, 2142 CrossRef CAS PubMed.
- M. Yuan, Q. Tang, Y. Lu, Z. Zhang, X. H. Li, S. M. Liu, X. W. Sun and S. X. Liu, J. Chem. Educ., 2019, 96, 1256–1261 CrossRef CAS.
- A. Farahmand Kateshali, S. Gholizadeh Dogaheh, J. Soleimannejad and A. J. Blake, Coord. Chem. Rev., 2020, 419, 213392 CrossRef CAS.
- Y. Garcia, B. L. Su, R. J. Roberts, J. C. Ahern, H. H. Patterson and D. B. Leznoff, Eur. J. Inorg. Chem., 2016, 2016, 2082–2087 CrossRef.
- K. V. Vasudevan, N. A. Smith, B. L. Scott, E. A. McKigney, M. W. Blair, J. C. Gordon and R. E. Muenchausen, Inorg. Chem., 2011, 50, 4627–4631 CrossRef CAS PubMed.
- F. Saraci, V. Quezada-Novoa, P. R. Donnarumma and A. J. Howarth, Chem. Soc. Rev., 2020, 49, 7949–7977 RSC.
- Y. P. He, Y. X. Tan and J. Zhang, Inorg. Chem., 2013, 52, 12758–12762 CrossRef CAS PubMed.
- J. Jacobsen, A. Ienco, R. D'Amato, F. Costantino and N. Stock, Dalton Trans., 2020, 49, 16551–16586 RSC.
- P. Dong, L. Zhu, J. Huang, J. Ren and J. Lei, Biosens. Bioelectron., 2019, 138, 111313 CrossRef CAS PubMed.
- M. Fondo, J. Corredoira-Vázquez, A. M. García-Deibe, J. Sanmartín-Matalobos, M. Amoza, A. M. P. Botas, R. A. S. Ferreira, L. D. Carlos and E. Colacio, Inorg. Chem. Front., 2020, 7, 3019–3029 RSC.
- A. Zabala-Lekuona, X. Lopez De Pariza, I. F. Díaz-Ortega, J. Cepeda, H. Nojiri, N. P. Gritsan, A. A. Dmitriev, A. López-Ortega, A. Rodríguez-Diéguez, J. M. Seco and E. Colacio, Dalton Trans., 2024, 53, 7971–7984 RSC.
- W. Lu, Z. Wei, Z. Y. Gu, T. F. Liu, J. Park, J. Park, J. Tian, M. Zhang, Q. Zhang, T. Gentle, M. Bosch and H. C. Zhou, Chem. Soc. Rev., 2014, 43, 5561–5593 RSC.
- J. M. Seco, I. Oyarzabal, S. Pérez-Yáñez, J. Cepeda and A. Rodríguez-Diéguez, Inorg. Chem., 2016, 55, 11230–11248 CrossRef CAS PubMed.
- A. J. Calahorro, A. Salinas-Castillo, J. M. Seco, J. Zuñiga, E. Colacio and A. Rodríguez-Diéguez, CrystEngComm, 2013, 15, 7636–7639 RSC.
- L. J. McCormick, S. A. Morris, A. M. Z. Slawin, S. J. Teat and R. E. Morris, CrystEngComm, 2016, 18, 1123–1132 RSC.
- O. Pajuelo-Corral, L. Razquin-Bobillo, S. Rojas, J. A. García, D. Choquesillo-Lazarte, A. Salinas-Castillo, R. Hernández, A. Rodríguez-Diéguez and J. Cepeda, Nanomaterials, 2022, 12, 3977 CrossRef CAS PubMed.
- M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE v2.1, Barcelona, 2013 Search PubMed.
- A. Ruiz-Martínez, D. Casanova and S. Alvarez, Chem. – Eur. J., 2008, 14, 1291–1303 CrossRef PubMed.
- D. Aravena and E. Ruiz, Dalton Trans., 2020, 49, 9916–9928 RSC.
- C. E. Jackson, I. P. Moseley, R. Martinez, S. Sung and J. M. Zadrozny, Chem. Soc. Rev., 2021, 50, 6684–6699 RSC.
- S. Titos-Padilla, J. Ruiz, J. M. Herrera, E. K. Brechin, W. Wersndorfer, F. Lloret and E. Colacio, Inorg. Chem., 2013, 52, 9620–9626 CrossRef CAS PubMed.
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS.
- F. A. Mautner, F. Bierbaumer, R. C. Fischer, À. Tubau, S. Speed, E. Ruiz, S. S. Massoud, R. Vicente and S. Gómez-Coca, Inorg. Chem., 2022, 61, 11124–11136 CrossRef CAS PubMed.
- A. López, C. Cruz, V. Paredes-Garcí, N. Veiga, F. Lloret, J. Torres and R. Chiozzone, New J. Chem., 2023, 47, 21781 RSC.
- J. Heine and K. Müller-Buschbaum, Chem. Soc. Rev., 2013, 42, 9232–9242 RSC.
- J.-C. G. Bünzli, Coord. Chem. Rev., 2015, 293–294, 19–47 CrossRef.
- Phosphor Handbook, ed. S. Shionoya, W. M. Yen and H. Yamamoto, CRC Press, Boca Ranton, 2007 Search PubMed.
- J. Heine and K. Müller-Buschbaum, Chem. Soc. Rev., 2013, 42, 9232–9242 RSC.
- O. Pajuelo-Corral, A. Rodríguez-Diéguez, G. Beobide, S. Pérez-Yáñez, J. A. García, E. San Sebastian, J. M. Seco and J. Cepeda, J. Mater. Chem. C, 2019, 7, 6997–7012 RSC.
- M. D. Allendorf, C. A. Bauer, R. K. Bhakta and R. J. T. Houk, Chem. Soc. Rev., 2009, 38, 1330–1352 RSC.
- G. E. Dobretsov, T. I. Syrejschikova and N. V. Smolina, Biophysics, 2014, 59, 183–188 CrossRef CAS.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- J. Rodríguez-Carvajal, FULLPROF 2000, version 2.5d, Laboratoire Léon Brillouin (CEA-CNRS), Centre d’Études deSaclay, Gif sur Yvette Cedex, France, 2003 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- M. Dolg, H. Stoll and H. Preuss, Theoret. Chim. Acta, 1993, 85, 441–450 CrossRef CAS.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS.
- M. Reiher, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 139–149 CAS.
- J. D. Rolfes, F. Neese and D. A. Pantazis, J. Comput. Chem., 2020, 41, 1842–1849 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Chem. – Eur. J., 2017, 23, 3708–3718 CrossRef CAS PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Data collections and crystal structure refinement. CCDC 2322750 and 2322751 for GR-MOF17 and GR-MOF18. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00401a |
| This journal is © The Royal Society of Chemistry 2024 |