Co-orchestration of multiple instruments to uncover structure–property relationships in combinatorial libraries

Abstract

The rapid growth of automated and autonomous instrumentation brings forth opportunities for the co-orchestration of multimodal tools that are equipped with multiple sequential detection methods or several characterization techniques to explore identical samples. This is exemplified by combinatorial libraries that can be explored in multiple locations via multiple tools simultaneously or downstream characterization in automated synthesis systems. In co-orchestration approaches, information gained in one modality should accelerate the discovery of other modalities. Correspondingly, an orchestrating agent should select the measurement modality based on the anticipated knowledge gain and measurement cost. Herein, we propose and implement a co-orchestration approach for conducting measurements with complex observables, such as spectra or images. The method relies on combining dimensionality reduction by variational autoencoders with representation learning for control over the latent space structure and integration into an iterative workflow via multi-task Gaussian Processes (GPs). This approach further allows for the native incorporation of the system's physics via a probabilistic model as a mean function of the GPs. We illustrate this method for different modes of piezoresponse force microscopy and micro-Raman spectroscopy on a combinatorial Sm-BiFeO₃ library. However, the proposed framework is general and can be extended to multiple measurement modalities and arbitrary dimensionality of the measured signals.

---

Introduction

Novel automatized approaches in combinatorial synthesis have revolutionized material design by enhancing cost-effectiveness and significantly accelerating the synthesis rate of new materials.^1–5 Among the oldest examples of high-throughput synthesis are combinatorial libraries. Recent examples include pipetting robotics, printing, and many other modalities.⁴ However, while this synthesis approach has been well established for decades, there has long been a bottleneck associated with the characterization aspects. Over the last several years, automated scanning probe microscopy (SPM), X-ray spectroscopy, Raman microscopy, etc. have opened the way for the readout of structural and functional information from combinatorial libraries and high-throughput synthesis that can feed into physical models and material optimization.

Often, of interest are multiple aspects of the structure and functionalities across combinatorial libraries. The investigation of such couplings entails a comprehensive study of multiple electric, mechanical, chemical, and structural properties of materials. This demands the utilization of a diverse array of local investigative methods, such as SPM, electron microscopy, and Raman microscopy. Each method serves as a critical tool for revealing distinct aspects of these couplings, allowing for a thorough understanding of different dimensions and properties. However, the extensive range of the required characterization methods often makes the exploration process time-consuming, creating a significant gap between the rates of synthesis and exploration.

In recent years, the extensive adoption of machine learning (ML) workflows has facilitated a reduction in the substantial gap between the synthesis and characterization rates, accelerating the exploration and optimization of targeted material functionalities.³ The deployed ML agents can provide support in various aspects, from mundane data treatment, including image segmentation and features detection,^6,7 to big data analysis,⁸ as well as automating decision-making processes and governing the experiment itself.^9,10 The concept of automated experimentation (AE) in microscopy involves the automatic, i.e., beyond human choice, operation of the microscope, typically establishing the sequence of imaging or spectroscopy measurement locations. This approach enables operators to redirect their focus from the tedious task of equipment tuning and microscope control at each exploration step toward more advanced result analysis and higher-level decision-making, such as establishing experimental objectives.

AE exploration frequently relies on Bayesian Optimization (BO), which has proven its efficiency in many studies, serving as a robust solution for both material design^1,11–13 and automated material characterization.^14–18 The Gaussian Process (GP) is the most used probabilistic surrogate model for approximating the true objective function in BO.^19,20 It is important to note, however, that employing entirely data-driven approaches has limited effectiveness in material discovery due to the complex nature of materials' properties.²¹ Physics-informed and structured GPs allow overcoming this issue by providing a diverse array of opportunities to integrate physical insights.²² Depending on our awareness of a system, additional knowledge can be incorporated through physical-derived prior mean functions,^16,21 and kernel functions,²³ alongside the implementation of optimization constraints and regularization techniques.²⁴ The widely used multi-fidelity BO methods combine information from different sources, that provide various levels of precision or require different computational resources, to efficiently integrate and exploit these datasets to balance the accuracy with the computational expenses to achieve optimal results.^25,26 In microscopy, BO has been successfully employed for governing explorations using multiple methods, including SPM,^17,27–29 scanning transmission electron microscopy electron energy-loss spectroscopy (STEM-EELS),³⁰ 4D STEM,³¹ and neutron and X-ray scattering.^32–34

The rapid growth of automated labs has brought forth the challenge of the co-orchestrated operation of multiple tools. One example of this is the exploration of a given materials system with multimodal tools, where, due to technical limitations, data in different modalities can be acquired sequentially. Another example is the use of combinatorial libraries that can be explored in multiple locations using various tools simultaneously. The third involves similar synthesis systems at different geographic locations with dissimilar downstream analytics. Numerous scalable frameworks have been introduced to integrate various devices and their configurations – sometimes distributed worldwide – into autonomous or semi-autonomous automated experimental cycles.^5,10,35,36 By entrusting the orchestrating role in such systems to AI, these frameworks can dynamically adjust experimental trajectories in response to real-time data, human interventions, and predefined constraints. Despite the diversity in architectures among these frameworks, their common feature lies in their ability to leverage data from various agents, thereby facilitating the accelerated exploration and optimization of material systems.

The alterations in compositions in combinatorial libraries prompt variations in the structures and multiple functional properties of materials, necessitating the utilization of numerous methods (multimodal discovery) to study their correlations and intrinsic nature. While implementing BO with high-dimensional input spaces is challenging due to the exponential growth of the search space (the curse of dimensionality), the complexity of constructing accurate surrogate models, and the difficulty of optimizing the acquisition function, the low-dimensional compositional space of a combinatorial library is an ideal candidate for employing BO for automated discovery.^37,38 However, different measurements provide specific insights into the system, often resulting in high-dimensional datasets, like spectra or images. In this case, the straightforward implementation of BO requires constructing multi-output surrogate models, leading to the same scalability problems as for high-dimensional input spaces.^39,40 To address this challenge, one effective solution is to leverage the encoding capabilities of techniques like variational autoencoders (VAEs) to transform the high-dimensional raw data into a lower-dimensional representation.⁴¹ The combination of a VAE with the GP-based BO has been proven to be efficient for such tasks as molecule design optimization,^42,43 and the optimization of robot controllers.⁴⁴ Typically, BO optimization processes data in the reduced latent space, while the selected objects are mapped back to the real space by the decoder.

In combinatorial libraries, the objective of active experimentation (AE) is to uncover the correlation between the local composition and target functionality or between different functionalities in as few steps as possible. Despite the diverse nature of the measured signals, it is anticipated that the property-changing profiles along the compositional change axis in a combinatorial library will exhibit similarity. The essence of multimodal orchestration lies in leveraging knowledge about a compositional correlation uncovered for one property to expedite the exploration of another property measured by a different method, thereby accelerating the overall characterization process. Accelerated autonomous property optimization in combinatorial libraries by embedding additional compositional information through pre-acquired phase mapping was recently demonstrated by A. G. Kusne et al.⁵

Here, we take the next step by introducing the multimodal co-orchestration framework. The proposed framework optimizes the exploration trajectory within the compositional spaces of combinatorial libraries by leveraging the compositional dependencies of VAE latent variables as objective functions for BO surrogate models. This approach allows the AI agent to handle the initial data interpretation, enabling the training of GPs on the compositional dependencies of complex features without the need for their direct interpretation. While this workflow was developed for combinatorial libraries, it could also be used for similar synthesis systems.

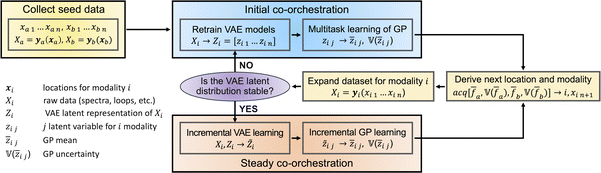
Co-orchestration workflow

A delineation of the automated experiment with co-orchestration is provided for two modalities, designated as methods a and b. To simplify, we also confine our analysis to a case of the 1D compositional space of the combinatorial library. However, these principles can be extended and adapted for exploration across a larger compositional space dimensionality and number of modalities as well. The workflow for co-orchestration can be described as a three-stage process involving a (1) seeding stage, (2) initial co-orchestration, and (3) steady co-orchestration (Fig. 1).

Fig. 1 Working schematics of multimodal co-orchestration.

Seeding stage

At the preparation stage, the locations x_a1,…,x_an and x_b1,…,x_bm for the seed measurements should be chosen for both modalities. The number of predefined positions can be different for various modalities (m ≠ n). However, it seems logical to opt for seed positions at the opposite edge of the compositional space, effectively constraining the area of exploration. Thereafter seed measurements performed in the chosen locations result in the multidimensional seed datasets X_a = [y_a(x_a1),…,y_a(x_an)], X_b = [y_b(x_b1),…,y_b(x_bm)], – either for spectra or images.

Initial co-orchestration

The received high-dimensional seed datasets are mirrors in a low-dimensional latent representation by VAE encoding independently (X_a → Z_a and X_b → Z_b). The dimensionality of the VAE latent space is a hyperparameter that the operator needs to tune. Typically, we expect we need to use only one of the latent variables for subsequent GP learning. However, reflecting high-dimensional data into a 1D latent space makes the latent variable intricate, encompassing both the composition-dependent part and all the side and parasitic influences. From this perspective, opting for 2D latent representations increases the degrees of freedom for the VAE. This allows for the potential separation of the target compositional impact from any secondary influences across different latent variables. We select one latent variable from each modality to form a learning dataset for multi-task GP (MTGP). The objective of MTGP is to predict both the mean values (z̄_aj, z̄_bj) and uncertainties 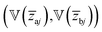associated with the selected latent variables (modalities) within the compositional latent space. The multimodal acquisition function is built based on the MTGP outcomes. This guides the selection of the next measurement modality i and location x_i by maximizing/minimizing the acquisition function 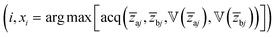. Finally, we augment the seed dataset of the selected modality with the newly acquired data and iterate this initial co-orchestration stage from the beginning.

During the initial co-orchestration stage, the amount of gathered knowledge about the system is limited. Therefore, introducing new data at each exploration step can markedly alter the VAE distributions and the profiles of the latent variables throughout the latent space. This mirrors the evolution of our knowledge about the system (i.e., our understanding of the relationships between the composition and functionality) with acquiring new data. The significant alterations in the VAE distributions require retraining the VAE and MTGP at each step from scratch.

Steady co-orchestration

As information about the system accumulates, injecting new data does not drastically alter the VAE distribution. The stability of the VAE distribution and consequent steady latent variable profiles across the compositional space allow for the application of incremental training. This means that with each new data addition, the VAE and MTGP models can be updated without having to restart the training from scratch because the acquired data only augments the existing knowledge of the system rather than revolutionizes it. This incremental learning is associated with the final steady co-orchestration experiment stage.

It is important to note that the transition toward a steady co-orchestration happens independently for different modalities at different times. The number of exploration steps needed for this transition indicates the complexities of the composition-dependent functionalities measured by the specific modality (i.e., method).

Experimental

We employed the Sm-doped BiFeO₃ (Sm-BFO) combinatorial library as a model system to demonstrate the capabilities of the multimodal co-orchestration. The exploring library was prepared by a pulsed laser deposition (PLD) technique on a (001) SrTiO₃ (STO) substrate. The combinatorial PLD system was equipped with an automated shadow mask and a multitarget system. For fabricating composition spread libraries, gradient wedge layers of end compositions of the library were deposited alternatively in opposing directions by moving the shadow mask back and forth at the epitaxial deposition condition. The thickness of the wedge layer was controlled by the number of shots of the laser pulses, while their thick ends were thinner than the pseudocubic perovskite unit cell (0.4 nm). The fabrication of the unit-cell's height wedge layers is critical for obtaining the atomic-scale mixing of the deposited constituent compositions. The wedge layer depositions were repeated until the film thickness reached the desired value.⁴⁵

For our experiment, we utilized two predefined datasets showcasing local electromechanical hysteresis loops and local Raman spectra both measured for identical compositions within the Sm-BFO combinatorial library. Both datasets consisted of 94 spectra (hysteresis loops), collected at equidistant intervals along the axis of a compositional gradient. The local composition at the measured locations changed from 20% Sm-BFO at location 0 to pure BFO at location 93.

In the SPM experiment, a motorized stage in the NanoSurf DriveAFM microscope (Switzerland) was used to automatically position the sample under the SPM probe, enabling the selection of various compositions. We developed a Python-based workflow to automatically capture hysteresis loops across the combinatorial library. To avoid sample or probe damage during long-distance movements driven by the motorized stage, the SPM probe was withdrawn (∼200 μm above the surface) before each motorized stage movement. After reaching the next location, the probe re-approached to resume the hysteresis measurements. The electromechanical hysteresis loops measurements were done in the band-excitation piezoresponse switching spectroscopy mode (BEPS)⁴⁶ using the AEcroscopy platform that was detailed in our previous work.⁴⁷ The loops appear as a response to the modulated triangle waveform applied by the scanning probe microscope's tip. This approach enables the study of the local ferroelectric switching dynamic.^48,49 The measurements were performed within a rectangular grid of locations for obtaining better statistics. Following this, the data were averaged along the constant composition axis, resulting in a dataset comprising 94 averaged loops measured along the Sm concentration gradient axis.

The Raman experiments were performed utilizing a 633 nm wavelength laser, which was focused using a 20× lens. This configuration offered a spatial resolution of approximately 5.54 μm. The sampling estimated optical depth was ∼134 nm (n_BFO = 2.6). We normalized the raw Raman spectra by area to exclude the influence of the focus position (Fig. S1b†). The spectra primarily captured the response from the bulk STO, while the contribution from the Sm-BFO epitaxial film constituted only a minor portion of the overall signal. We extracted a BFO proxy signal by taking the difference between the local Raman spectra and the mean spectrum across the entire dataset (Fig. S1c†). This enabled us to eliminate the influence of the STO bulk substrate from the collected response. It is important to note that the resulting footprint spectra should not be directly interpreted as BFO Raman spectra. However, the observed changes in them, occurring with the compositional alterations, were associated with the structural variation within the Sm-BFO compositional library. The spectra were also collected at locations within the square grid and averaged along the constant composition axis. The resulting dataset comprised spectra collected for similar Sm concentrations as those used for the BEPS hysteresis loop measurements.

The multi-task GPs were implemented by the GPax Python package.⁵⁰ The linear model of coregionalization (LMC) with two latent processes was used to capture the correlations across tasks. We utilized radial basis functions (RBFs) as kernels for the latent processes. A brief theoretical description of the LMC-based MTGP is provided in the ESI Section.†

The experiments were driven by pure exploration, employing a maximum uncertainty acquisition function. Each automated experiment began with 3 seed measurements at randomly selected compositions (locations), followed by 30 exploration steps.

Result and discussion

Co-orchestration experiments

The co-orchestration workflow capabilities were assessed through a multimodal exploration of the Sm-doped BiFeO₃ combinatorial library. This system possesses transition with an increase in Sm content from the ferroelectric state of pure rhombohedral BiFeO₃ to a non-ferroelectric state of orthorhombic 20% Sm-doped BiFeO₃.⁵¹ The complex nanoscale structural ordering observed for some intermediate states may be a cause of the enhanced electromechanical responses, making the compositional dependencies more convoluted.^52,53 Previously, we explored the properties of this combinatorial library by high-resolution STEM.^54,55 Moreover, Sm-BFO has been employed to showcase the capabilities of the hypothesis-learning Bayesian optimization workflow.¹⁶

The AEs were conducted in the simulation mode using pre-acquired BEPS and Raman datasets (see the Experimental section). Three distinct modalities were utilized: out-of-field polarization (represented by amp·cos(phase) of BEPS hysteresis loops),⁴⁸ Raman spectra, and the frequency of electromechanical resonance observed during BEPS hysteresis loop measurements under applied voltage. Despite the simultaneous measurement of the polarization and frequency signals in real SPM experiments, their interdependence is indirect.⁵⁶ This allows us to consider them as separate modalities for the AE simulation.

Linear VAE. VAE representations play a key role in the co-orchestration of AE. The shape and orientation of the latent distribution dictate how the explored data features are aligned to the specific latent variables. In our experiments, at each exploration step, we analyzed the current latent distributions of points available at that specific iteration, along with the whole latent distributions derived by encoding the entire dataset using the VAE trained solely on the currently available data. It should be noted, that in real experiments, the whole latent distributions are unavailable during the exploration. Here however it provides the ground truth behavior of the system.

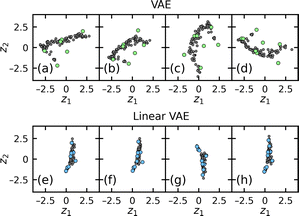
After a few initial exploration steps, we obtained that the substantial expansion of the VAE training datasets by the newly acquired data did not result in significant alterations in the configuration of both the whole and current latent distributions (Fig. 2a–d). The variations between distributions at different exploration steps were constrained by their position, degrees of compression/extension in some directions, and random orientation within the latent space. An observed stability in the general shape of the latent distributions indicates the potential ability to move from the initial co-orchestration to a steady co-orchestration stage. However, a random orientation of the latent distributions at each subsequent step results in a redistribution of the encoded features among latent variables. This alters the latent variables' dependencies on the composition used to train the MTGP.

Fig. 2 Raman spectrum latent distributions encoded by (a–d) vanilla VAE and (e–h) LVAE models for the subsequent step in co-orchestration AE. The models were trained from scratch with available data (marked by green and blue points) at each exploration step.

The stabilization of the orientation of the latent distribution within the latent space was achieved by introducing the linear VAE (LVAE), a modified version of vanilla VAE. LVAE incorporates custom loss in addition to the standard reconstruction and KL divergence losses. This custom loss is computed as the absolute difference between the first latent variable (z₁) and its corresponding position along the compositional axis, normalized within the range of [0,1] (x′):

custom loss = |z₁ − x′|, x′ ∈ [0,1] (1)

By introducing the custom loss, we encouraged the accumulation of linear dependencies in the z₁ latent variable, specifically aiming to normalize z₁ within the range of [0,1]. This approach stabilizes the orientation of the latent distribution within the latent space (Fig. 2e–h), enabling a transition toward a steady co-orchestration. It is important to note that LVAE does not eliminate distribution random reflections and variations in its expansion degree. As a result, the profiles of the compositional dependencies for different modalities may also reflect and be “stretched” relative to the horizontal axis, preserving their overall shape. Some variability in the orientation is also conserved and can be regulated through adjustment of the custom loss normalization range.

The ground truth latent distributions and corresponding compositional dependencies of the latent variables were computed for all modalities by training the LVAE with the entire datasets (Fig. 3). To evaluate the proficiency of the trained LVAE models in encoding and reconstructing the raw data, we decoded spectra from different locations within the compositional profile and compared them with the original raw data. The predicted spectra effectively mirrored the dependencies present in the raw data, reducing instrumental noise (Fig. S2†).

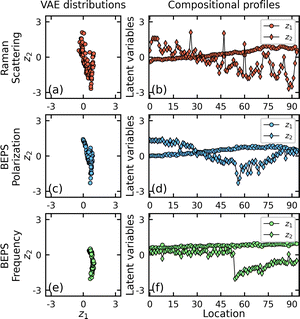Fig. 3 LVAE ground truth: (a, c, and e) latent distributions and (b, d, and f) compositional dependencies of the latent variables for Raman, BEPS polarization, and BEPS frequency modalities.

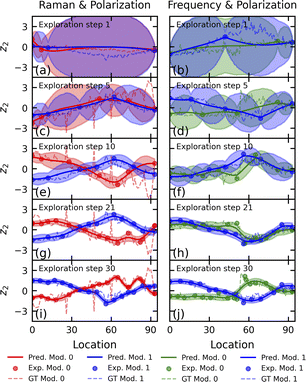
The LVAE fosters the accumulation of features with a proportional relationship between the latent representation and the local composition within the z₁ latent variable. Simultaneously, it isolates features with complex compositional dependencies within the z₂ latent variable. We utilized the latent variable z₂ to construct the multimodal space for learning the multi-task GP. Therefore, the primary objective of the co-orchestration AE algorithm was to reconstruct the compositional dependencies (profiles) of the z₂ latent variable for each modality, leveraging the correlation between them to expedite the process (Fig. 3b, d and f). We observed a predominantly linear downward trend with a few noticeable outlying points in the dependence of z₂ on the local composition (location) for the Raman measurements (Fig. 3b). The z₂ values exhibited a growing variability as the composition shifted toward pure BFO. More intriguing dependencies were observed in the latent dependencies of the BEPS modalities. The z₂ for the BEPS polarization dependence exhibited an extremum at the midpoint of the exploring compositional range (Fig. 3d). The downward trend preceding the extremum transitioned into a gradual raise in the second part of the profile, accompanied by a noticeable increase in noise levels. This extremum position also aligned with a sharp drop in the BEPS frequency latent variable profile (Fig. 3f), where z₂ maintained a constant value before this descent. The significant alterations in the middle of the library were associated with the phase transition of the system to the ferroelectric state.

Multimodal co-orchestration. In our simulations, we implemented two distinct autonomous experiments. In the first experiment, we concurrently explored Raman spectra (Modality 0) and hysteresis loops for BEPS out-of-field polarization (Modality 1) (Fig. 4a, c, e, g and i). In the second experiment, we co-orchestrated the exploration of the out-of-field polarization (Modality 0) along with the BEPS frequency (Modality 1) (Fig. 4b, d, f, h and j). The multimodal exploration trajectories were guided by the maximum uncertainty acquisition function. In both cases, a total of 30 exploration steps were proceeded. The entire experiments were conducted employing the initial co-orchestration approach. We utilized the LMC model to capture correlations among modalities. In the LMC, each modality is expressed through the linear combination of shared GP latent processes. For simplicity of analysis, the correlation between the modalities was captured by the MTGP with just two latent processes. It is important to note that the number of latent processes is a hyperparameter in multi-task learning, exerting a substantial influence on the model's performance in terms of its generalization and learning speed. While the LMC is a flexible approach, implementing alternative MTGP models, for instance, convolutional MTGP⁵⁷ or using spectral mixture kernels,⁵⁸ may result in performance improvements in cases where modeling complex cross-task covariance structures is crucial.

Fig. 4 MTGP reconstruction at the various exploration steps for the (a, c, e, g, and i) first and (b, d, f, h, and g) second exploration experiments. The GP predictions are represented by solid lines, circles depict the acquired points, and the ground truth (GT) compositional profiles are illustrated by dashed lines.

The LVAE, trained with the data available at each exploration step, was employed to encode the entire dataset, establishing the step-specific ground truth (GT) for the z₂ compositional dependence (represented by the dashed lines in Fig. 4). In both experiments, the ground truth z₂ profiles for both modalities maintained their shapes consistently throughout the entire exploration. However, random latent variable profile reflections relative to the horizontal line were observed. Toward the end of the experiment, we observed quite accurate GP predictions for both modalities in the first experiment and specifically for Modality 1 in the second experiment. The reconstruction of the latent variable profile for Modality 0 in the second experiment was hindered by the presence of a sharp drop. For effective reconstruction, it is essential to employ a structural GP and introduce a suitable mean function.

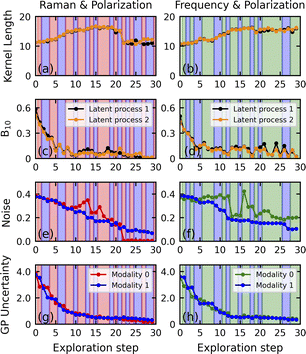
For a more consistent analysis, we monitored the evolution of the key characteristics of the multi-task BO throughout the entire exploration in both experiments (Fig. 5). The experiments exhibited similar behavioral patterns but with some noticeable differences from each other.

Fig. 5 MTGP parameters for AE: (a and b) kernel length, (c and d) coregularization coefficient between modalities, (e and f) prior noise, and (g and h) GP uncertainty for the (a, c, e, and g) first and (b, d, f, and h) second experiments. The background colour strips indicate the selected modality for the spectral measurements at each exploration step.

The overall downward trends in the kernel lengths, B₀₁ coefficients of the coregularization matrices (see the ESI†), prior noise, and GP uncertainties were consistent and preserved in both experiments. The gradual reduction of the GP uncertainties, asymptotically approaching zero as the experiments advanced, reflected the exploration process (Fig. 5g and h). Interestingly, the rate of decrease in GP uncertainties was equal for both modalities. The incremental reduction in B₁₀ provides evidence that multi-task coupling played a significant role at the beginning of the experiment, but its importance diminished progressively with the ongoing exploration (Fig. 5c and d). There were noticeable jumps in the B₁₀ coefficients during the final exploration steps, particularly evident in the second experiment, corresponding to the occasional appearance of compositional profile reflections relative to the horizontal line (Fig. S3†). The prior noise for Modality 0 (BEPS frequency) in the second experiment exhibited higher values and a more noticeable variability (Fig. 5f). This peculiarity aligns with the sharp drop of the z₂ value in the middle of the compositional profile. To reconstruct such dependencies, structural GP is commonly employed, whereas the implementation of vanilla GP (including the MTGP used here) demonstrates limited effectiveness.

We observed a gradual rising trend in the kernel lengths of the latent processes at the beginning of the AE with subsequent saturation in both experiments (Fig. 5a and b). However, during the final steps of exploration in the first experiment, there was a noticeable reduction in the kernel lengths (Fig. 5a), which was accompanied by a gradual decrease to zero for B₁₀ for both latent processes (Fig. 5c). We interpret this phenomenon as evidence of the existence of two subsequent exploration phases in the first experiment. During the main part of the exploration, the model endeavors to capture the general trends in the compositional profiles of the modalities and the correlations between them. This leads to the gradual adjustment and stabilization of both the coregularization coefficients and the kernel lengths of the latent processes, consequently facilitating a smooth decrease in the GP uncertainties and prior noises (Fig. 5e and g). Once general trends are discovered, the algorithm transitions to the second phase, where the noise characteristics of the profiles are explored, resulting in a reduction of the kernel lengths and a decrease to zero in the coupling coefficients. The transition to the second phase may be regarded as the trigger to conclude the exploration. We speculate that, in the second simulation, the process did not reach the point of transitioning to noise exploration.

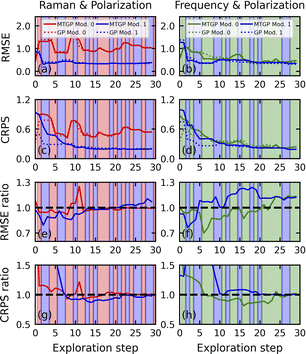
To evaluate the performance of the co-orchestration workflow in comparison to independent vanilla GP explorations, we trained vanilla GPs for both modalities at each iteration using identical kernel lengths and noise prior distributions as those employed in the MTGP (Fig. 6). The RMSE and CRPS metrics were calculated relative to the step-specific ground truth. As the evolution of the absolute values of the RMSE and CRPS throughout the experiment (Fig. 6a–d) was not highly informative due to the constant changes in ground truth compositional profiles, we analyzed the ratio of the error metrics estimated for the MTGP and the vanilla GP (Fig. 6e–h). In regions where the ratios RMSE_MTGP/RMSE_GP and CRPS_MTGP/CRPS_GP were less than one, the MTGP algorithm outperformed the vanilla GP.

Fig. 6 Comparison of the MTGP and vanilla GP for the (a, c, e, and g) first and second (b, d, f, and h) experiments. (a and b) RMSE and (c and d) CRPS errors estimated relative to the step-specific ground truth compositional profiles. The ratios (e and g) RMSE_MTGP/RMSE_GP and (g and h) CRPS_MTGP/CRPS_GP. The background color strips indicate the selected modality for the spectral measurements at each exploration step.

During the exploration, we identified several areas where the MTGP and the vanilla GP exhibited varying performance relative to each other. In the very first few steps in both experiments, the vanilla GP showcased a higher RMSE but much better CRPS, accompanied by fast changes in the B₁₀ coefficient (Fig. 5c and d). Such behavior may be explained by the lack of acquired information at the initial stage necessary to build an effective coupling model, leading to controversial results. We speculate that in this area, the performance of MTGP may be higher as well as lower than the vanilla GP depending on the specific shape of the compositional profiles. In the first experiment, at most of the steps after the initial region, MTGP performed better or equal to the vanilla GP by both metrics. However, at the terminal stage of exploration, the vanilla GP showed better RMSE results for Modality 1, while for Modality 0, both algorithms demonstrated equal RMSE values (Fig. 6e). In contrast, MTGP demonstrated an advantage in CRPS for Modality 1 and performed equally to the vanilla GP for Modality 0 (Fig. 6g). We attributed this behavior to the vanilla GP's quicker transition to noise exploration in the compositional dependencies of Modality 1 compared to MTGP, resulting in a better RMSE metric for the noisy ground truth. The second experiment produced notably controversial results, as both the RMSE and CRPS ratios consistently remained at or above one after the initial stage for Modality 1 (Fig. 6f and h). Interestingly, for Modality 0, where a sharp drop was presented in the compositional profiles, MTGP showed an advantage in both metrics till the last 6 steps, where the RMSE ratio became higher than one. Hence, for Experiment 1, we cannot conclusively state that the co-orchestration with MTGP outperformed the vanilla GP, at least in terms of reconstructing the step-specific compositional profiles at each iteration.

In the final stage of our investigation, we delved into the possibilities of identifying the point at which the shift from the initial co-orchestration to a steady co-orchestration state becomes feasible. The Kolmogorov–Smirnov (KS) criterion, which measures the maximum difference in cumulative distribution functions, was utilized to evaluate the divergence between the distributions of VAE latent variables and estimate their stability throughout the exploration. At each step, we encode the entire distributions using the VAE, trained on the available points. After that, we calculated the ground truth KS (GT KS) criteria between the encoded distribution and the ground truth latent distribution for the corresponding modality (Fig. 7, diamonds). Moreover, KS criteria were also computed at each step to compare a specific latent distribution (represented by only available points) with the distribution from the previous step (Fig. 7, circles). We calculated the criterion for each iteration exclusively for the modality to which a data point was added during that specific step. It should be noted that in the real AE, only the KS criterion could be defined, while GT KS was available only in our simulation.

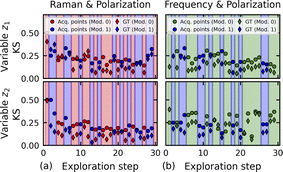Fig. 7 Kolmogorov–Smirnov criterion evolution defined for the z₁ and z₂ latent variables for both the (a) first and (b) second experiments.

The KS and GT KS criteria presumably indicated a downward trend, except for the final two steps in Experiment 1, in the latent distributions of the linearized z₁ variable (Fig. 7). However, the KS criteria for the z₂ latent distribution exhibited distinct behaviors in the first and second experiments. In Experiment 1, when the latent distributions were stable and exhibited minimal changes with ongoing simulation, we observed the stabilization of the KS and GT KS criteria around 0.2 (Fig. 7a). The steady and small values of the KS criterion throughout the exploration can be considered indicative triggers for transitioning toward a stable co-orchestration. Oppositely, in the second experiment, the instability of the latent distribution of Modality 1 (BEPS frequency) resulted in elevated values to be observed in both the KS and GT KS criteria (Fig. 7b). Developing approaches to enhance the stability of the latent distribution, particularly by mitigating random reflections, is an important future task.

Conclusions

In summary, we introduced a robust co-orchestration workflow designed to guide the exploration of the structure–property relationships in combinatorial libraries through the simultaneous application of multiple methods. The proposed approach is driven by multimodal Bayesian optimization, outlining the optimal exploration trajectory in the compositional space comprising the low-dimensional representations of the raw spectra acquired by different methods. The key advantage of this co-orchestration workflow lies in the real-time utilization of acquired knowledge about the compositional dependency of one property to accelerate the exploration of other properties measured by different methods. This expedites the overall characterization process.

We proposed the utilization of variational autoencoders to encode raw spectra into low-dimensional representations. To improve the orientational stability of the VAE latent distributions throughout the experiment, we introduced the linear VAE model. In the LVAE, a special custom loss was incorporated alongside the standard reconstruction and KL divergence losses during model training to stabilize the resulting representations. Ensuring the stability of the latent distribution throughout the experiment enables the acquisition of steady compositional dependencies of the latent variables. The stability of the compositional profiles of latent variables, in turn, allows a possible transition from the initial co-orchestration stage, where the VAE and MTGP are trained from scratch, toward a steady co-orchestration characterized by incremental learning.

The capabilities of multimodal co-orchestration were validated by autonomous experimentation simulations in the Sm-BFO combinatorial library. The workflow demonstrated its effectiveness at optimizing the exploration trajectory, especially when latent variables exhibit smooth compositional dependencies. Nevertheless, partial effectiveness was also demonstrated in multimodal co-orchestration with a piecewise compositional dependency. The KS criterion, computed for the latent distributions at the subsequent exploration steps, is proposed as an indicative signal to determine the possibility of transitioning from the initial to the steady co-orchestration stages.

The co-orchestration workflow is expected to significantly enhance the efficiency of combinatorial library exploration, thereby narrowing the gap between the current synthesis and characterization rates. Further potential improvements could encompass the development of advanced methods for stabilizing VAE representations, the incorporation of structured GPs, and the implementation of cost-aware policies for multimodal Bayesian optimization.

We believe that novel multi-task approaches mark the beginning of a new chapter in autonomous experimentation. The proposed co-orchestration workflow offers a flexible and reliable algorithm for the efficient exploration of combinatorial libraries and similar material systems.

Data availability

The code of the multimodal co-orchestrations available without restrictions at https://github.com/Slautin/2024_Co-orchestration. The GP code is implemented using GPax package https://github.com/ziatdinovmax/gpax.

Author contributions

Boris N. Slautin: conceptualization (equal); methodology (equal); software (equal); writing – original draft. Utkarsh Pratiush: methodology (equal); software (equal). Ilia N. Ivanov: investigation (equal), data curation (equal). Yongtao Liu: investigation (equal), data curation(equal), writing – review & editing (equal). Rohit Pant: resources (equal). Xiaohang Zhang: resources (equal). Ichiro Takeuchi: resources (lead). Maxim A. Ziatdinov: methodology (equal); software (equal); writing – review & editing (equal). Sergei V. Kalinin: conceptualization (lead); methodology (lead); supervision; writing – review & editing (lead).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work (workflow development, reward-driven concept) was supported (S. V. K.) by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences as part of the Energy Frontier Research Centers program: CSSAS-The Center for the Science of Synthesis Across Scales under award number DE-SC0019288. Confocal Raman and Band Excitation Piezoresponse Spectroscopy characterization were conducted at the Center for Nanophase Materials Sciences (CNMS), which is a US Department of Energy, Office of Science User Facility at Oak Ridge National Laboratory. The work at the University of Maryland was partially supported by ONR MURI N00014172661 and the NIST collaborative agreement 70NANB23H226.

References

1. Y. Li, L. Xia, Y. Fan, Q. Wang and M. Hu, ChemPhysMater, 2022, 1, 77.
2. E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown, K. G. Reyes, J. Schrier, S. Billinge, T. Buonassisi, I. Foster, C. P. Gomes, J. M. Gregoire, A. Mehta, J. Montoya, E. Olivetti, C. Park, E. Rotenberg, S. K. Saikin, S. Smullin, V. Stanev and B. Maruyama, Matter, 2021, 4, 2702.
3. M. Seifrid, R. Pollice, A. Aguilar-Granda, Z. M. Chan, K. Hotta, C. T. Ser, J. Vestfrid, T. C. Wu and A. Aspuru-Guzik, Acc. Chem. Res., 2022, 55, 2454.
4. J. M. Gregoire, L. Zhou and J. A. Haber, Nat. Synth., 2023, 2, 493.
5. A. G. Kusne, H. Yu, C. Wu, H. Zhang, J. Hattrick-Simpers, B. DeCost, S. Sarker, C. Oses, C. Toher, S. Curtarolo, A. V. Davydov, R. Agarwal, L. A. Bendersky, M. Li, A. Mehta and I. Takeuchi, Nat. Commun., 2020, 11, 5966.
6. M. Ziatdinov, O. Dyck, X. Li, B. G. Sumpter, S. Jesse, R. K. Vasudevan and S. V. Kalinin, Sci. Adv., 2019, 5, eaaw8989.
7. A. Maksov, O. Dyck, K. Wang, K. Xiao, D. B. Geohegan, B. G. Sumpter, R. K. Vasudevan, S. Jesse, S. V. Kalinin and M. Ziatdinov, npj Comput. Mater., 2019, 5, 12.
8. J. F. Rodrigues, L. Florea, M. C. F. de Oliveira, D. Diamond and O. N. Oliveira, Discovery Mater., 2021, 1, 12.
9. S. V. Kalinin, Y. Liu, A. Biswas, G. Duscher, U. Pratiush, K. Roccapriore, M. Ziatdinov and R. Vasudevan, Microsc. Today, 2023, 32, 35.
10. A. G. Kusne and A. McDannald, Matter, 2023, 6, 1880.
11. B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89.
12. Y. K. Wakabayashi, T. Otsuka, Y. Krockenberger, H. Sawada, Y. Taniyasu and H. Yamamoto, APL Mater., 2019, 7, 101114.
13. R. Shimizu, S. Kobayashi, Y. Watanabe, Y. Ando and T. Hitosugi, APL Mater., 2020, 8, 111110.
14. M. Ziatdinov, Y. Liu, K. Kelley, R. Vasudevan and S. V. Kalinin, ACS Nano, 2022, 16, 13492.
15. Y. Liu, A. N. Morozovska, E. A. Eliseev, K. P. Kelley, R. Vasudevan, M. Ziatdinov and S. V. Kalinin, Patterns, 2023, 4, 100704.
16. M. A. Ziatdinov, Y. Liu, A. N. Morozovska, E. A. Eliseev, X. Zhang, I. Takeuchi and S. V. Kalinin, Adv. Mater., 2022, 34, 2201345.
17. A. Biswas, Y. Liu, N. Creange, Y.-C. Liu, S. Jesse, J.-C. Yang, S. V. Kalinin, M. A. Ziatdinov and R. K. Vasudevan, npj Comput. Mater., 2024, 10, 29.
18. A. G. Kusne, A. McDannald, and B. DeCost, arXiv, 2023, preprint, arXiv:2311.06228,  DOI:10.48550/arXiv.2311.06228.
19. C. E. Rasmussen, in Advanced Lectures on Machine Learning, Lecture Notes in Computer Science, ed. O. Bousquet, U. von Luxburg and G. Rätsch, Springer, Berlin, 2004, vol. 176, p. 63.
20. X. Wang, Y. Jin, S. Schmitt and M. Olhofer, ACM Comput. Surv., 2023, 55, 287.
21. M. A. Ziatdinov, A. Ghosh and S. V. Kalinin, Mach. Learn.: Sci. Technol., 2022, 3, 015003.
22. E. J. Cross, T. J. Rogers, D. J. Pitchforth, S. J. Gibson, S. Zhang and M. R. Jones, Data-Centric Eng., 2024, 5, e8.
23. E. J. Cross and T. J. Rogers, IFAC-Pap., 2021, 54, 168.
24. L. P. Swiler, M. Gulian, A. L. Frankel, C. Safta and J. D. Jakeman, J. Mach. Learn. Model. Comput., 2020, 1, 119.
25. Z. Z. Foumani, M. Shishehbor, A. Yousefpour and R. Bostanabad, Comput. Methods Appl. Mech. Eng., 2023, 407, 115937.
26. C. Fare, P. Fenner, M. Benatan, A. Varsi and E. O. Pyzer-Knapp, npj Comput. Mater., 2022, 8, 257.
27. Y. Liu, K. P. Kelley, R. K. Vasudevan, W. Zhu, J. Hayden, J. Maria, H. Funakubo, M. A. Ziatdinov, S. Trolier-McKinstry and S. V. Kalinin, Small, 2022, 18, 2204130.
28. Y. Liu, K. P. Kelley, R. K. Vasudevan, H. Funakubo, M. A. Ziatdinov and S. V. Kalinin, Nat. Mach. Intell., 2022, 4, 341.
29. Y. Liu, J. Yang, R. K. Vasudevan, K. P. Kelley, M. Ziatdinov, S. V. Kalinin and M. Ahmadi, J. Phys. Chem. Lett., 2023, 14, 3352.
30. K. M. Roccapriore, S. V. Kalinin and M. Ziatdinov, Adv. Sci., 2022, 9, 2203422.
31. K. M. Roccapriore, O. Dyck, M. P. Oxley, M. Ziatdinov and S. V. Kalinin, ACS Nano, 2022, 16, 7605.
32. A. McDannald, M. Frontzek, A. T. Savici, M. Doucet, E. E. Rodriguez, K. Meuse, J. Opsahl-Ong, D. Samarov, I. Takeuchi, W. Ratcliff and A. G. Kusne, Appl. Phys. Rev., 2022, 9, 021408.
33. M. M. Noack, P. H. Zwart, D. M. Ushizima, M. Fukuto, K. G. Yager, K. C. Elbert, C. B. Murray, A. Stein, G. S. Doerk, E. H. R. Tsai, R. Li, G. Freychet, M. Zhernenkov, H. Y. N. Holman, S. Lee, L. Chen, E. Rotenberg, T. Weber, Y. Le Goc, M. Boehm, P. Steffens, P. Mutti and J. A. Sethian, Nat. Rev. Phys., 2021, 3, 685.
34. S. Maruyama, K. Ouchi, T. Koganezawa and Y. Matsumoto, ACS Comb. Sci., 2020, 22, 348.
35. A. Dorri, S. S. Kanhere and R. Jurdak, IEEE Access, 2018, 6, 28573.
36. C. P. Gomes, J. Bai, Y. Xue, J. Björck, B. Rappazzo, S. Ament, R. Bernstein, S. Kong, S. K. Suram, R. B. van Dover and J. M. Gregoire, MRS Commun., 2019, 9, 600.
37. M. Binois and N. Wycoff, ACM Transactions on Evolutionary Learning and Optimization, 2022, 2, 8.
38. E. Siivola, A. Paleyes, J. González and A. Vehtari, Appl. AI Lett., 2021, 2, e24.
39. M. A. Bhouri, M. Joly, R. Yu, S. Sarkar and P. Perdikaris, Comput. Methods Appl. Mech. Eng., 2023, 417, 16428.
40. W. J. Maddox, M. Balandat, A. G. Wilson and E. Bakshy, in 35th Conference on Neural Information Processing Systems (NeurIPS 2021), arxiv, 2021, preprint, arxiv:2106.12997,  DOI:10.48550/arXiv.2106.12997.
41. M. Valleti, Y. Liu and S. V. Kalinin, arXiv, 2023, preprint, arXiv:2303.18236,  DOI:10.48550/arXiv.2303.18236.
42. R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268.
43. R. R. Griffiths and J. M. Hernández-Lobato, Chem. Sci., 2020, 11, 577.
44. R. Antonova, A. Rai, T. Li and D. Kragic, in Proceedings of the Conference on Robot Learning, 2020, vol. 100, p. 456.
45. S. Fujino, M. Murakami, V. Anbusathaiah, S. H. Lim, V. Nagarajan, C. J. Fennie, M. Wuttig, L. Salamanca-Riba and I. Takeuchi, Appl. Phys. Lett., 2008, 92, 202904.
46. S. Jesse and S. V Kalinin, J. Phys. D: Appl. Phys., 2011, 44, 464006.
47. Y. Liu, K. Roccapriore, M. Checa, S. M. Valleti, J.-C. Yang, S. Jesse and R. K. Vasudevan, Small Methods, 2024, 230740.
48. S. Jesse, H. N. Lee and S. V. Kalinin, Rev. Sci. Instrum., 2006, 77, 073702.
49. S. Hong, J. Woo, H. Shin, J. U. Jeon, Y. E. Pak, E. L. Colla, N. Setter, E. Kim and K. No, J. Appl. Phys., 2001, 89, 1377.
50. M. Ziatdinov, https://gpax.readthedocs.io/en/latest, accessed: April, 2024.
51. D. Kan, L. Pálová, V. Anbusathaiah, C. J. Cheng, S. Fujino, V. Nagarajan, K. M. Rabe and I. Takeuchi, Adv. Funct. Mater., 2010, 20, 1108.
52. I. O. Troyanchuk, D. V. Karpinsky, M. V. Bushinsky, O. S. Mantytskaya, N. V. Tereshko and V. N. Shut, J. Am. Ceram. Soc., 2011, 94, 4502.
53. J. Walker, H. Simons, D. O. Alikin, A. P. Turygin, V. Y. Shur, A. L. Kholkin, H. Ursic, A. Bencan, B. Malic, V. Nagarajan and T. Rojac, Sci. Rep., 2016, 6, 19630.
54. C. T. Nelson, R. K. Vasudevan, X. Zhang, M. Ziatdinov, E. A. Eliseev, I. Takeuchi, A. N. Morozovska and S. V. Kalinin, Nat. Commun., 2020, 11, 6361.
55. M. Ziatdinov, C. T. Nelson, X. Zhang, R. K. Vasudevan, E. Eliseev, A. N. Morozovska, I. Takeuchi and S. V. Kalinin, npj Comput. Mater., 2020, 6, 127.
56. S. Jesse, B. Mirman and S. V. Kalinin, Appl. Phys. Lett., 2006, 89, 022906.
57. M. Alvarez and N. D. Lawrence, in Advances in Neural Information Processing Systems, 2008, vol. 21, p. 57.
58. G. Parra and F. Tobar, in Advances in Neural Information Processing Systems, 2017, p. 6684.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00109e

---