Deep-learning enabled photonic nanostructure discovery in arbitrarily large shape sets via linked latent space representation learning

Abstract

The vast array of shapes achievable through modern nanofabrication technologies presents a challenge in selecting the most optimal design for achieving a desired optical response. While data-driven techniques, such as deep learning, hold promise for inverse design, their applicability is often limited as they typically explore only smaller subsets of the extensive range of shapes feasible with nanofabrication. Additionally, these models are often regarded as ‘black boxes,’ lacking transparency in revealing the underlying relationship between the shape and optical response. Here, we introduce a methodology tailored to address the challenges posed by large, complex, and diverse sets of nanostructures. Specifically, we demonstrate our approach in the context of periodic silicon metasurfaces operating in the visible wavelength range, considering large and diverse shape set variations. Our paired variational autoencoder method facilitates the creation of rich, continuous, and parameter-aligned latent space representations of the shape–response relationship. We showcase the practical utility of our approach in two key areas: (1) enabling multiple-solution inverse design and (2) conducting sensitivity analyses on a shape's optical response to nanofabrication-induced distortions. This methodology represents a significant advancement in data-driven design techniques, further unlocking the application potential of nanophotonics.

---

1 Introduction

Fundamental studies of the last decade investigating the light–matter interaction in nanostructures have paved the way for a multitude of applications, ranging from freespace meta-optics¹ to nanostructured building blocks for integrated photonics.² Leveraging modern nanofabrication techniques, researchers now benefit from unprecedented lateral resolution, wide-area writing capabilities with high stitching accuracy, and support for precision-aligned layering. Furthermore, the field of nanophotonics currently encompasses a diverse range of materials, including plasmonic metals, high and low index dielectrics, index-tunable metal oxides and chalcogenide materials, and exotic 2D materials such as graphene. This diversity underscores the vast array of fabrication-accessible designs and underscores the critical need for ‘inverse design’ methods in nanophotonics. Inverse design techniques are aimed at discovering designs that closely match a targeted response with reasonable computational burden, while also exhibiting reduced sensitivity to fabrication imperfections.³ Formal inverse design methods essentially constitute searches⁴ within high-dimensional design parameter spaces. Traditionally, such searches have been classified as either localized (e.g., topology optimization⁵) or global (e.g., various evolutionary algorithms⁶ like genetic algorithms). However, the curse of dimensionality accompanies the increase in degrees of freedom, that is, the solution space expands exponentially with each additional dimension. Consequently, obtaining optimal designs from searches within such high-dimensional solution spaces poses a formidable challenge. It is well established that in high-dimensional spaces, localized searches often become trapped in local minima, while global searches necessitate substantial computational resources and exhibit slow convergence rates.

In the current landscape, the surge of activity in machine learning, deep learning, and other data-driven⁷ techniques aimed at overcoming the challenges posed by high dimensionality warrants attention.^8–15 These methodologies typically involve training deep neural networks (DNNs) through supervised learning processes. Given sufficient training data, DNNs can effectively map the empirical relationship between nanophotonic geometries and their optical behavior. Once a model is trained, design methodologies can primarily be categorized¹⁶ into two main streams: (1) surrogate optimization-based inverse design and (2) all-DNN-based inverse design. In surrogate optimization,¹⁷ a DNN capable of accurately predicting spectral behaviors from given geometries (forming a one-to-one manifold¹⁸) can serve as a surrogate for a full-wave electromagnetic solver. Conversely, in the all-DNN method, the DNN directly provides a solution without the need for an optimization procedure. Both approaches offer dramatic speed improvements compared to formal inverse design methods reliant on electromagnetic solver calls. However, it is imperative that expediting the search process does not compromise the attainment of an optimal design. As researchers transition from the initial exploration phase, where the feasibility of this approach was convincingly demonstrated, critical attention is now being directed towards addressing the shortcomings inherent in the data-driven approach.¹⁷

One glaring limitation of these approaches lies in the fact that nearly all models are trained on relatively small subsets of the extensive array of shapes accessible through fabrication. Most reports in the literature have relied on easily parameterized geometries like polygons. Typically, in such smaller subsets, the range of optical responses is limited, potentially leading to an overestimation of the technique's effectiveness. A rudimentary approach to expanding the shape set involves considering binary images where each pixel can be toggled on or off.¹⁹ However, most shapes within this set do not yield feasible designs due to the absence of coherent structure, rendering it impractical to train accurate models with reasonably sized datasets. Liu and colleagues²⁰ have proposed a generative network approach employing unsupervised learning to generate larger and meaningful shape sets. However, the reliance on a separate network to recognize feasible shapes limits the shape sets to single “blob”-like shapes. Subsequent studies by Liu et al.²¹ have notably extended the size of feasible subsets. Jiang et al.²² used GAN-based inverse design techniques for metagratings,²³ using topology-optimized geometries^24,25 to generate complex structures. Recent advancements, such as the Progressive Growing GAN (PGGAN) method integrated with self-attention layers by Wen et al.,²⁶ show promise in producing fabrication-feasible and robust shape sets; however these methods have complicated workflows and exhibit loss oscillations. The well-known challenges of adversarial training protocols²⁷ and the need for a handcrafted network to guide the generation towards reasonable shapes are a shortcoming of these techniques. Thus, the challenge of training a DNN on a sufficiently broad shape set while simultaneously ensuring sample efficiency^17,28 continues to be a significant hurdle to the widespread applicability of data-driven inverse design methods.

A second major challenge is that neural networks are essentially black boxes where the interpretability of neural network predictions remains a challenge.²⁹ A crucial step in the process is representation learning, which is when machine learning algorithms take significant patterns out of unprocessed data to produce simpler representations. Some researchers have turned to the use of autoencoders,³⁰ a form of representation learning, to extract valuable insights from trained models.^18,31 Kiarashinejad and colleagues³² used autoencoders to solve the difficulty of computational complexity by reducing the dimensionality while also improving knowledge of design parameter responsibilities. Zandehshahvar and colleagues³³ proposed a novel metric-learning technique combining triplet loss and mean-squared error, which can enhance machine learning methods for inverse design of nanophotonic devices and knowledge discovery. However, the work recognizes the need for additional research and optimization efforts for effectively addressing the issues related to metric learning in nanophotonics. Furthermore, the work does not specifically address the incorporation of structural features into the dataset, indicating a possible field of additional research. In the context of all-DNN-based inverse design, the issue of design “dead zones” resulting from the one-to-many nature of the response–structure mapping has been identified.³⁴ The potential of conditionally trained generative adversarial networks (cGANs) or conditional (adversarial) autoencoders to dynamically encode multiple potential solutions, along with the benefits of representation learning,^16,35 suggests that this approach warrants further refinement to facilitate inverse design within the all-DNN framework. In this contribution, we propose linked latent space representational learning to tackle the shortcomings mentioned above. The motivation for this approach stems from a simple observation – two structures, although geometrically different, may be considered similar if their optical responses share similarities.

Latent space representations provide a notion of similarity based on Euclidean distance between two shapes in the learned latent space. By simultaneously training a latent representation of shape and the optical response, and then linking them through cross-training, our approach is able to grasp similarity relationships not only in shape, but also in the optical response axis. The method does not place any restriction on the shape set used for training, allowing users to construct such a set based on their intuition and knowledge. Furthermore, using variational autoencoding, continuous latent representations are learned. We demonstrate that this approach leads to rapid inverse design with possible multiple candidate solutions ranked according to the sensitivity of each design to fabrication imperfections. While this concept has not yet been exploited in the context of inverse design, it is gaining foothold in other data-science domains. Jo et al.³⁶ introduced a groundbreaking technique that merges cross-modal association with multiple modal-specific autoencoders, enabling seamless integration of various modalities while preserving their encoded information within individual latent spaces. Their model's efficacy on a modest dataset underscores its suitability for semi-supervised learning applications (Yu and co-workers³⁷ in natural language processing, Stein and co-workers in conditioned image generation,³⁸ and Radhakrishnan and co-workers³⁹ in medical diagnostics using multiple modalities). Closer to our domain, two reports deserve special mention. (1) Lu and co-workers⁴⁰ introduced a novel application of paired Variational Autoencoders (VAE) for integrating 2D small-angle X-ray scattering (SAXS) patterns and scanning electron microscopy (SEM) images; and (2) Yaman⁴¹ and co-workers have reported a shared dual-VAE approach to correlate the gold nanoparticle cluster geometry with optical responses in hyperstructural darkfield microscopy.

The rest of the paper is organized as follows: after this introduction, in Section 2, we summarize the salient points of the methodology; in Section 3, we first examine the characteristics of the linked latent space representations. Finally, we showcase the utility of our method for rapid inverse design before concluding in Section 4.

2 Methodology

2.1 Shape and spectrum encoding, training dataset

To demonstrate the methodology, we consider the design of periodic metasurfaces with arbitrarily shaped subwavelength unit-cells, specifically, crystalline silicon (material properties⁴²) metasurface on a glass (SiO₂) substrate. The unit cell geometries are represented as a (64 × 64) binary distribution of pixels, where ‘1’ indicates the presence of silicon and ‘0’ indicates its absence (see Fig. 1A). We consider a shape library comprising 21 classes of shapes depicted in Fig. 1B (see ESI Fig. S1† for the complete details of the construction of the shape set). We illuminate the metasurface with linearly polarized (s and p) white light and record the transmittance and reflectance spectra over the wavelength range of 400 nm to 700 nm, with a spacing of 5 nm. Given that the lattice constant is subwavelength (340 nm), the metasurface does not exhibit any diffraction. The recorded spectra encoded in a 2D tensor constitute the response. The lattice size and substrate height of the unit cell are fixed to be 340 nm and 90 nm, respectively. The shapeset uses a wide diversity of shapes including single and multiple nanoantenna shapes (and the complimentary void shapes). The magnetic and electric multipoles of each resonator can interact via the near-field and coherently interact with other unit cells also. This provides a rich diversity in the optical response.

Fig. 1 Overview of the proposed methodology (linked latent space representation learning) and its use cases in photonics inverse design. (A) Schematic of the unit cell of a periodic metasurface considered in the study, encoded in a binary pixellated format. s and p-polarized white light is incident on the metasurface, and the transmittance and reflectance spectra for both polarizations in the form of a 2D tensor encode the response. (B) Shape library – exemplar shapes of the 21 classes considered in the study. (C) Schematic of the cross-linked autoencoder neural network architecture used in this study (with size details) highlighting the various data-flow pathways. (D) and (E) Use-case of the trained neural networks specifying the relevant data-flow pathways for each task. Targeted spectrum and resultant multiple solutions are seen in the inverse design use in (D). (E) Rapid sensitivity analysis of a design geometry involving the generation of a set of perturbed shapes for a base shape and the resulting spectrum variance.

2.2 Model architecture

Fig. 1C depicts the neural network architecture employed in this study, which centres around two variational autoencoders: a shape variational autoencoder and a spectrum variational autoencoder, tailored to handle the shape and spectrum tensors, respectively. Each autoencoder employs a bottleneck architecture, reducing the dimensionality of the shape and spectrum tensors to an 8-dimensional latent vector, thereby generating latent spaces, LS_geometry, and LS_spectrum. Once trained, the first half of the network serves as an ‘encoder,’ encoding the shape/spectrum into an 8-dimensional tensor, while the second half functions as a decoder, reconstructing the shape/spectrum from the encoded 8-dimensional tensor. It's noteworthy that the input formats for the shape and spectrum encoders, and the output formats of the shape and spectrum decoders, are distinct. Specifically, the shape is encoded as a (64, 64, 1) tensor, while the spectrum is encoded as a (60, 4, 1) tensor. These specifications dictate the sizes of the various convolutional and fully-connected layers in the corresponding encoders and decoders. The network architecture hyperparameter optimization is discussed in Fig. S2 of the ESI.†

Following the training phase, it is essential to highlight the numerous possibilities for data flow, as depicted in Fig. 1C. Data path 1–2 solely utilizes a top variational autoencoder for the reconstruction of the input geometry image, while data path 5–6 solely employs a bottom variational autoencoder for the reconstruction of the input spectra data. The key innovation of our work lies in the dataflow paths 4–2 and 3–6. Path 3–6 enables us to retrieve the spectrum of a given shape via its latent vector, while 4–2 enables the recovery of a shape via a spectrum latent vector. Although a given shape possesses a definite and unique spectral response, a given response may be attributable to one or more shapes. The neighboring points of a given latent vector in the spectral latent space may thus decode to one or more shapes dynamically. In the shape variational autoencoder, shapes are arranged in the geometry latent space to ensure that similar shapes are positioned close to each other. Similarly, similar-looking spectra are neighbors in the spectrum latent space. However, the inclusion of cross-linkages enables the network to associate two distinct shapes that may still yield similar optical responses. Without training the cross-linkages, we would only be able to group shapes based on their geometric similarity. However, by incorporating the cross-linkages, we are now able to introduce a similarity metric based on the similarity of their responses as well. This enhancement allows for a more comprehensive understanding of the relationship between shapes and their optical responses, thereby enriching our ability to analyze and manipulate nanophotonic structures effectively. Fig. 1D illustrates the use-case of the trained encoders and decoders in nanophotonics inverse design. First, given a targeted spectral response, we can rapidly recover potentially multiple solution shapes. Second, each shape can then be assessed for the sensitivity of its optical response to fabrication-induced imperfections. Specifically, by sampling in the latent space neighbourhood of a given shape, we can simulate shape distortions and subsequently determine the variance in the spectral response. From a given set of target shapes, we can identify a shape least susceptible to fabrication-induced imperfections. This approach enables us to optimize the design of nanophotonic structures with enhanced robustness to fabrication constraints.

2.3 Model training

We use the well-known variational autoencoder formalism^43–45 in our work which is known to create a smooth and continuous latent space representation.

Encoder: the input of shape/spectra data is processed by the encoder network and transformed into a probability distribution within the latent space. This means that the VAE encodes the data as a range of possible values rather than a single point, allowing it to capture a variety of possible representations of the input shape/spectra data. To ensure that the latent space matches the desired distribution, usually a standard normal distribution, variational inference is employed to approximate the posterior distribution of the latent space representation. For this purpose, random sampling is performed to generate latent space points, and the distribution parameters, i.e., μ (mean) and σ (standard deviation), are optimized using KL divergence loss. Due to the presence of this sampling node (stochastic) in the computational graph, backpropagation is not feasible. To allow smooth optimization during training, the reparameterization trick is utilized, which allows gradients to backpropagate through the sampling process:

z = μ(x) + σ(x) × ε (1)

where ε ∼ N(0, 1) is drawn from a standard normal distribution. This step ensures that the latent variables z keep the probabilistic nature of the encoder, setting the VAE apart from a standard autoencoder.

Decoder: the decoder network obtains samples from the latent distribution to reconstruct the original input shape/spectra data. During training, the model adjusts both the encoder and decoder to minimize reconstruction loss, which measures the difference between the original input and the reconstructed output. It also shapes the latent space to adhere to a specified distribution. This process balances two key components: reconstruction loss and the regularization term (often Kullback–Leibler divergence). Reconstruction loss ensures faithful input reproduction, while regularization molds the latent space to match the chosen distribution. By iteratively adjusting these parameters, the VAE learns to represent input data effectively, enabling accurate reconstructions and the generation of new samples by sampling from its learned latent distribution.

A Variational Autoencoder (VAE) not only converts the input data x into a latent space representation z and reconstructs it back to x̃, but it also adds a regularization technique to the encoder. A prior distribution p(z) of the latent space is included in this regularization process. The purpose of this regularization is to restrict the latent representations to a particular distribution. Using an encoder function z ∼ Enc(x) = q(z|x) (posterior distribution of the latent variable z given the input variable x), the VAE learns how to encode input data x into latent variables z during training. The decoder x̃ ∼ Dec(z) = p(x|z) (ref. 46) (p(x|z) represents the likelihood of the input data x given the latent variable z) takes a latent variable z to reconstruct the original input data. Typically, these functions are designated as Enc for encoding and Dec for decoding. The reconstruction loss and the regularization term obtained from the prior distribution form the loss function of the VAE, which is represented by the symbol L_VAE:

where represents an expectation over the learned distribution of latent variables given the input x. ln p(x|z) represents the likelihood of x given z is measured by the log-likelihood of the data given the latent variables, and negative sign indicates that minimizing the negative log-likelihood ensures the better reconstruction of the original input data. The Kullback–Leibler divergence (D_KL) includes weights denoted by β, which regulate the contribution of the divergence term in the overall loss function of the VAE. Eqn (2) is the general form of VAE. We use a coupling variational autoencoder framework in our study. With this method, we can develop a coupling VAE that is specifically designed to extract a linked latent space that works well with heterogeneous data. 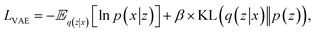So, the losses of shape and spectrum VAE's are given by:where L_VAE1 represents the loss of the shape variational autoencoder and L_VAE2 represents the loss of the spectrum variational autoencoder. The first term represents the reconstruction loss between the input and output data, while the second term represents the Kullback–Leibler (KL) divergence loss, weighted by β. This term is associated with the standard Gaussian distribution . μ_x and σ_x are the mean and variance of the Gaussian distribution. The two autoencoders are trained simultaneously to minimize the following custom loss:

L_{Total loss} = L_VAE1 + L_VAE2 + D₁‖X₁ − X̃₁(Z₂)‖ + D₂‖X₂ − X̃₂(Z₁)‖. (4)

In training the model, we have six loss terms. These include two reconstruction losses, the KL divergences for both shape and spectrum, and two cross-reconstruction losses. The third term of eqn (4) represents the cross-reconstruction loss from shape to spectrum. Specifically, X₁ is the input shape data, and X̃₁(Z₂) is the reconstructed shape data. In this reconstruction, we sample random points from the learned latent space (Z₂) of the spectrum and pass them through the shape decoder (see ESI Fig. S3†). The fourth term of eqn (4) represents the cross-reconstruction loss from spectrum to shape. Here, X₂ is the input spectrum data, and X̃₂(Z₁) is the reconstructed spectrum data. We sample random points from the learned latent space (Z₁) of the shape and pass them through the spectrum decoder. This cross-sampling technique ensures that each latent space can effectively reconstruct data from the other domain, enhancing the model's ability to handle heterogeneous data. C₁, C₂, D₁, D₂, β₁ and β₂ are the regularization coefficients of each loss term. We found C₁ = 1, C₂ = 1, D₁ = 1, D₂ = 1, β₁ = 1 × 10⁻⁶ and β₂ = 1 × 10⁻⁵ in our implementation as the well suited values for these weights are determined through experimentation. The detailed description of the training procedure is given in Fig. S4 of the ESI.†

3 Results and discussion

The study was conducted using the Keras deep learning framework with a Tensorflow backend, executed on a workstation featuring an Intel™ i9–7920X CPU and 128 GB RAM, (access to the source code, datasets, and stored models will be provided to the public upon acceptance of the research). The Stanford Stratified Structure Simulator (S⁴),⁴⁷ which uses the S-matrix algorithm and the Rigorous Coupled Wave Analysis (RCWA) technique to solve Maxwell's equations in layered periodic structures, was used to generate the ground truth. The number of basis function parameters in the S⁴ solver was set to 50 for generating ground-truth spectra. Additional details of training dataset generation for both shape and spectrum are given in the ESI Section S-1.†

3.1 Visualization of the learned latent space

We begin by visualizing the structure of the learned latent spaces, aiming to understand both their global and local structures, which is crucial for comprehending how shapes cluster together, with their distances indicating similarity. To achieve this, we employ Uniform Manifold Approximation and Projection (UMAP), a robust algorithm for nonlinear dimensionality reduction that preserves meaningful distances between data points, facilitating the visualization and clustering of high-dimensional datasets.⁴⁸ We opt for the Euclidean distance metric to construct the nearest neighbour graph due to its efficacy in capturing correlation features. By fine-tuning the parameters, including setting the number of neighbours to 10 and the minimum distance to 0, we enhance the performance of UMAP, facilitating better separation and clustering of the validation dataset.⁴⁹

Fig. 2 shows a scatter-plot visualization of the 2D projection of the 8-dimensional shape and spectral latent spaces colour-coded by the 21 classes (refer to this GitHub link which provides the latent representation for all 21 classes individually: https://github.com/22510064/UMAP-Representation-) of shapes considered in this study (see Fig. S5† for better visualization). A clustering of similar shapes and spectra, contrasted with the distinct separation of dissimilar ones within the embedding space⁵¹ is observed, underscoring the model's adeptness in capturing the intricate intra- and inter-relationships between shapes and spectra, effectively segregating them into distinct clusters. In the examination of the shape latent space, a cohesive clustering of various geometric entities is observed, including ellipses (blue), double ellipses (orange), Perlin noise (pink), 2-fold (cyan), plus shapes (magenta), triangles (salmon), half moons (gold), and their corresponding cavities. These entities coalesce into a unified cluster with overlapping boundaries, signifying shared geometric characteristics, see ESI Fig. S5A.† However, distinct clusters emerge for rings (green), L-shapes (light gray), and C-shapes (lime), revealing multiple clusters that intertwine with other shapes. Furthermore, upon closer inspection, two distinct subclusters are identified within the H-shape (dark olive green), delineated by the arrangement of transverse lines. Similarly, the polygon shape (black) displays two distinct subclusters, one for symmetrical polygons and another for asymmetrical polygons. This differentiation underscores the unique characteristics inherent within subsets of the H and polygon shapes, with each subcluster demonstrating clear separation, indicative of diverse structural configurations. Additionally, a small subcluster featuring multiple concentric rings is observed within the ring category, further accentuating its unique shape characteristic within the latent space, see ESI Fig. S5B.† We have added plots using t-distributed Stochastic Neighbor Embedding⁵² (t-SNE) in Fig. S5C.†t-SNE is known for effectively revealing local neighbourhoods, offering a potentially clearer picture of local clusters than UMAP.

Fig. 2 Visualization of the 8-dimensional shape and spectrum latent spaces projected into a 2-dimensional space. (A) Showcases the shape latent space and (B) corresponding spectrum latent space. Both visualizations utilize UMAP projection techniques.⁵⁰ (C) Display points in both shape and spectral latent space are colour-coded using 21 shape classes.

Transitioning to the spectral latent space, a well-defined clustering pattern is discerned, encompassing spectral profiles such as ellipses (blue), double ellipses (oranges), 2-fold shapes (cyan), plus shapes (magenta), half moons (gold), and their corresponding cavities, alongside rings (green), triangle cavities (violet) and H-shapes (dark olive green). Delineating discrete category boundaries proves more challenging for spectral profiles like Perlin noise (pink) and its cavities, L-shapes (light gray), C-shapes (lime), ring cavities (brown), and triangles (salmon). Furthermore, the polygon (black) exhibits two subclusters that manifest clear distinctions from other clusters, mirroring the clustering patterns observed in the shape latent space. This divergence underscores the inherent complexity in spectral signatures, where distinct shapes may yield similar spectra, as evidenced by instances where multiple shapes correspond to the same spectrum.

Next, we examine the continuity aspects of the learned latent space representations. Continuity in the learned latent spaces is crucial to ensure that latent vectors decode to meaningful shapes or spectra. This continuity allows for the generation of novel and meaningful shapes and spectra beyond the original training dataset while also facilitating smooth interpolation between designs. We test the continuity at a local scale as well as a global scale.^53–55

We utilised local interpolation within the latent space of shapes by focusing on a specific data point and its near neighbouring points. This procedure entails sampling data points from a distribution centred around the chosen point, typically utilising a normal distribution with a slight standard deviation, as illustrated in Fig. 3A for the 2-fold image. These sampled data points are then decoded using shape and linked spectrum decoders. Through this process, we can observe similar shapes and their corresponding reconstructed spectral responses for reflection in s and p-polarized light as depicted in Fig. 3B, validating the reconstructed spectra against the original spectra (generated using the S⁴ solver). This illustrates the efficacy of the training model in reconstructing spectra close to the original and highlights the smoothness and continuity of the latent space at the local level. By delving into the variability and diversity within this local region of the shape latent space, we can generate new shapes and corresponding spectra that maintain similarities to the original data points while introducing minor variations. This methodology facilitates the creation of diverse and novel samples, enriching the generative capabilities of the model and deepening our understanding of the underlying data distribution.^16,56

Fig. 3 Exploring local and global continuity in the shape latent space. (A) Demonstrating the procedure for testing local continuity – an input shape is encoded to Z in the shape latent space. Seven random local neighbors, generated using a normal distribution (mean = Z, standard deviation = 0.2), and are decoded using a shape and cross-linked spectrum decoder. (B) Displays the neighboring shapes of the base shape alongside their predicted and ground truth spectra. (C) Illustrating the procedure for testing global continuity – two input shapes are encoded to obtain their latent points Z₁ and Z₂. Linear interpolation, Z = αZ₁ + (1 − α)Z₂, is performed between these points, and the resulting point Z is passed through the shape and cross-linked decoder. (D) Depicts the six generated shapes through interpolation alongside their predicted and ground truth spectra.

For global interpolation, we select two distinct data points representing images with the half-moon cavity and L shapes, intentionally chosen to be distant in the latent space. Employing a linear interpolation algorithm,^57,58 we sample the latent variables between these two points and subsequently decode the resulting sampled points using both the shape and linked spectrum decoders, as illustrated in Fig. 3C. The reconstruction of the interpolation between latent vectors of two geometrical shapes and their corresponding spectra reveals a smooth transition from one shape to another. Given that the Variational Autoencoder latent space follows a Gaussian distribution, it is expected to yield smoother and more diverse transitions between two geometrical shapes. Fig. 3D showcases the reconstructed shapes and corresponding predicted spectra alongside the original spectra (generated using the S⁴ solver) between the latent vector of the actual half-moon cavity and the L shape. As depicted, with each step, the cavity gradually shifts towards the L shape with slight noise at step 4 due to a small gap in the latent space. This suggests that the model has learned to disentangle the underlying factors of variation rather than merely memorising the training dataset.^16,54 Similar continuity is also observed in the spectrum latent space at the local and the global levels (see ESI Fig. S6 and S7†). Due to the one-to-many mapping between the response and structure, neighborhood points in the spectral space can correspond to varying classes of shapes within the cross-link data path.

3.2 Multiple-solution inverse design

The inverse design^59,60 aims to find a geometry that yields an optical response close to the specified target. Specifically, we can independently specify the reflectance and transmittance spectra for each linear polarization. The inverse design here is purely DNN-based and does not require an external optimizer. Predicting geometry from a given spectral behavior inherently faces the challenges of non-uniqueness, as a single spectral behavior can correspond to multiple geometries. To address this, we provide a given target spectrum (60 × 4 × 1), and we generate its latent representation (8 × 1). By introducing random noise into this latent representation, we explore the adjacent neighborhood around this latent space. These perturbed latent points are then passed through a geometry decoder. Addition of this noise results in predicting multiple geometries that exhibit identical spectral behavior. This will yield one or many solution shapes, which are then verified using full-wave electromagnetic solvers. Specifically, here we showcase the design of polarization-independent and polarization-dependent, transmission, and reflection mode spectral filters.

Fig. 4A and B showcase the results of an inverse design process for polarization-independent spectral filters. The spectral responses of the output geometry are compared with the target spectra, both predicted (given by DNN) and actual (evaluated using S⁴). Two sets of results are presented: one where the input tensor is the same for both Fig. 4A(i) and (ii), resulting in different classes of geometries (cross and ring shapes). Another set (Fig. 4A(iii) and (iv)) demonstrates a similar study but with only reflection spectra as input, generating two distinct classes of shapes. Moving to Fig. 4B, it illustrates the inverse design of a polarization-independent dual-band reflection filter (dual-band notches in transmittance) with Gaussian target spectra. Finally, Fig. 4C showcases the results of an inverse design for polarization-dependent color filters. A single geometry set produces bandpass and band-stop filter characteristics for s- and p-polarization in transmission and reflection modes. On our workstation, a single inverse design step which yields ten viable shapes takes an average of approximately 3.2 seconds. Additionally, each of the discovered viable shapes is passed through the full electromagnetic solver, and only those shapes whose spectra closely match exact calculations are retained (this verification step takes an additional 2 minutes for 10 shapes).

Fig. 4 Evaluation of the performance of the cross-linked neural network in inverse design of metasurfaces. The DNN-predicted spectra and ground truth spectra (obtained using S⁴) of the inverse designed geometries are compared with given target spectra. (A) Inverse design of polarization independent transmission and reflection mode spectral filters. The DNN predicts two classes of geometries for identical target spectra – (i) plus shape class and (ii) circle shape class, showcasing the DNN model's ability to generate multiple suitable shape classes. (A) (iii) and (iv) Similar study as in (i) and (ii) with Gaussian target spectra. Here also the DNN model shows the ability to predict multiple suitable shape classes for given target spectra. (B) Inverse design of polarization independent dual band spectral filters. (C) Inverse design polarization-dependent transmission and reflection mode color spectrum filters. (B) and (C) The given shape classes are found to be unique for the given target spectra showcasing a one-to-one mapping.

3.3 Sensitivity analysis

The achievement of precise geometric shapes through inverse design encounters notable hurdles during the fabrication process, particularly when employing lithography techniques. Vercruysse et al.⁶¹ have delineated critical constraints and limitations pertinent to the creation of arbitrary geometrical shapes with heightened degrees of freedom. These constraints encompass minimum feature size restrictions, which dictate specific thresholds for feature sizes, and gap size constraints, where smaller gaps between shapes pose fabrication challenges. Furthermore, curvature constraints assume significance, as sharp or highly curved features may deviate from the intended geometry during fabrication.^62,63 For instance, the plus-shaped design obtained through inverse design may not align seamlessly with the fabrication process due to curvature constraints, as evidenced by Vashistha et al.⁶⁴ Consequently, relying solely on a singular design becomes impracticable, necessitating the generation of multiple shapes akin to those derived through inverse design, albeit with slight variations to preserve desired spectral characteristics. Utilizing trained networks, such sensitivity analysis can be rapidly conducted.

For this experiment, two classes of inverse designed geometries, the plus and circle shapes, are utilized as the base shapes. Fig. 1E outlines the encoding process of the base shape through the shape encoder into latent space. In this space, a random noise is introduced into the shape latent point, ranging from 0 to 1.8 in increments of 0.2. Subsequently, the corresponding shapes and spectra are reconstructed from these noisy latent points using the shape and spectrum decoders. The average time taken for the generation of these derived shapes is ∼42 s, whereas the verification of these spectra (that uses the S⁴ tool) takes ∼3.20 min. Illustrated in Fig. 5A and C are a diverse array of these derived shapes, accompanied by their predicted spectra, illustrating the outcomes of this iterative process. As noise is incrementally introduced with each iteration, the derived shape further diverges from the base shape. To assess the sensitivity of the derived shapes, we compute the mean of squared errors (MSE) between the target spectra for inverse design and the predicted spectra of the derived shapes. Specifically, we iterate the generation process 15 times for the derived shape with the highest noise value and a statistical analysis is shown in Fig. S8.† The MSE value for the plus shape is observed to be having a wider distribution as compared to the MSE of the circle shape, thus depicting a higher sensitivity of the plus shape class.

Fig. 5 Sensitivity analysis of inverse-designed geometries is performed, where eight different shapes are derived from the latent point of the base shape by introducing noise. (A) and (C) The derived geometries from two base shape classes (plus shape and circle shape) are illustrated alongside their respective predicted and ground truth spectra. Ground truth spectra of the base shapes are also included. (B) and (D) The spread of predicted spectral deviations among all derived geometries, along with the predicted spectra of the base shape.

Evidently, as illustrated in Fig. 5B and D, the ground truth and predicted spectra of the derived plus shapes display a greater deviation from the base shape compared to the derived circle shapes. Therefore, it can be inferred that the predicted optical response of the base circle shape is more resilient to fabrication tolerances and process variability, which inherently impact the final geometrical shape. The spectra of the final geometry closely align with the desired performance characteristics of the base shape's ground truth spectrum.

4 Conclusions

In summary, we present an improved methodology for deep-learning-based inverse design in nanophotonics, where arbitrarily large and diverse shapesets can be employed. The use of cross-modal training adapted in this work can ensure multiple-solution inverse designs and sensitivity ranking in a single rapid design process without coupling with an external optimization routine. Expanding the scope to metagratings where multiple reflection and transmission orders are present and to excitation beyond normal incidence is an obvious extension of this study. Multilayered^65,66 aligned metasurfaces as well as multi-material geometries⁶⁷ are another possible extension. Rapid prediction of near-field and far-field responses of nanostructures⁶⁸ and implementation of deep transfer learning⁶⁹ that leverages computational and experimental data open a number of avenues for further extension of this work.

The reported training of locally and globally continuous cross-linked latent representations can take advantage of manifold¹⁸ and metric learning³³ and also facilitate the search for novel responses. The versatility of this approach makes it easier to explore complex shape sets and enables innovative research in various kinds of research areas through combining multiple data modalities. Multimodal approaches⁷⁰ like UNITER⁷¹ and triplet network training⁷² along with scalable semi-supervised learning on graph-structured data⁷³ can find extreme relevance in our approach. Large language models (LLM) are proving adept at interpreting scientific papers. We envision that with the help of LLM and the proposed methodology, it may be possible to learn the structure–response relationships in very large shapes acquired from published literature.

Data availability

The data analysis scripts of this paper are available in the colab notebook. (1) Code displays the main results of the paper: https://colab.research.google.com/drive/1hHneyyomCr-pXrJDnWJImFLS1nJVm27b. (2) Code displays the main results as well as ESI† of the paper: https://colab.research.google.com/drive/18DVtn5QjINvF3_15awfLYHBMzx5KaDHn#scrollTo=bo9psJ2z4Ouh.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support received from the DST Nanomission extramural grant SR/NM/NS65/2016.

References

1. H.-D. Jeong, H. Kim and S.-Y. Lee, Curr. Opt. Photonics, 2024, 8, 16–29.
2. P. Cheben, R. Halir, J. H. Schmid, H. A. Atwater and D. R. Smith, Nature, 2018, 560, 565–572.
3. M. M. Elsawy, S. Lanteri, R. Duvigneau, J. A. Fan and P. Genevet, Laser Photonics Rev., 2020, 14, 1900445.
4. S. D. Campbell, D. Sell, R. P. Jenkins, E. B. Whiting, J. A. Fan and D. H. Werner, Opt. Mater. Express, 2019, 9, 1842–1863.
5. J. S. Jensen and O. Sigmund, Laser Photonics Rev., 2011, 5, 308–321.
6. F. Meng, X. Huang and B. Jia, J. Comput. Phys., 2015, 302, 393–404.
7. C. Yeung, B. Pham, R. Tsai, K. T. Fountaine and A. P. Raman, ACS Photonics, 2022, 10, 884–891.
8. A. Khaireh-Walieh, D. Langevin, P. Bennet, O. Teytaud, A. Moreau and P. R. Wiecha, Nanophotonics, 2023, 12, 4387–4414.
9. W. Cai, Y. Liu, J. Rho, H. Suchowski and P. Wiecha, Opt. Mater. Express, 2021, 11, 3431–3432.
10. Z. Liu, D. Zhu, L. Raju and W. Cai, Advanced Science, 2021, 8, 2002923.
11. R. S. Hegde, Nanoscale Adv., 2020, 2, 1007–1023.
12. W. Ma, Z. Liu, Z. A. Kudyshev, A. Boltasseva, W. Cai and Y. Liu, Nat. Photonics, 2021, 15, 77–90.
13. S. So, T. Badloe, J. Noh, J. Bravo-Abad and J. Rho, Nanophotonics, 2020, 9, 1041–1057.
14. J. Jiang, M. Chen and J. A. Fan, Nat. Rev. Mater., 2021, 6, 679–700.
15. L. Huang, L. Xu and A. E. Miroshnichenko, Advances and Applications in Deep Learning, 2020, vol. 65.
16. P. R. Wiecha, A. Arbouet, C. Girard and O. L. Muskens, Photonics Res., 2021, 9, B182–B200.
17. S. S. Panda and R. S. Hegde, Nanophotonics, 2022, 11, 345–358.
18. M. Zandehshahvar, Y. Kiarashinejad, M. Zhu, H. Maleki, T. Brown and A. Adibi, ACS Photonics, 2022, 9, 714–721.
19. I. Sajedian, J. Kim and J. Rho, Microsyst. Nanoeng., 2019, 5, 27.
20. Z. Liu, D. Zhu, S. P. Rodrigues, K.-T. Lee and W. Cai, Nano Lett., 2018, 18, 6570–6576.
21. Z. Liu, D. Zhu, K.-T. Lee, A. S. Kim, L. Raju and W. Cai, Adv. Mater., 2020, 32, 1904790.
22. J. Jiang and J. A. Fan, Nanophotonics, 2020, 9, 1059–1069.
23. M. Chen, J. Jiang and J. A. Fan, ACS Photonics, 2020, 7, 3141–3151.
24. C. Yeung, B. Pham, Z. Zhang, K. T. Fountaine and A. P. Raman, Opt. Express, 2024, 32, 9920–9930.
25. Z. A. Kudyshev, A. V. Kildishev, V. M. Shalaev and A. Boltasseva, Applied Physics Reviews, 2020, 7, 021407.
26. F. Wen, J. Jiang and J. A. Fan, ACS Photonics, 2020, 7, 2098–2104.
27. R. Razavi-Far, A. Ruiz-Garcia, V. Palade and J. Schmidhuber, Generative adversarial learning: architectures and applications, Springer, 2022.
28. R. Patel, N. R. Mohapatra and R. S. Hegde, Solid-State Electron., 2023, 199, 108505.
29. C. C. Nadell, B. Huang, J. M. Malof and W. J. Padilla, Opt. Express, 2019, 27, 27523–27535.
30. L. Zhu, Y. Li, Z. Yang, D. Zong and Y. Liu, Plasmonics, 2023, 1–12.
31. W. Ma, F. Cheng and Y. Liu, ACS Nano, 2018, 12, 6326–6334.
32. Y. Kiarashinejad, S. Abdollahramezani and A. Adibi, npj Comput. Mater., 2020, 6, 12.
33. M. Zandehshahvar, Y. Kiarashi, M. Zhu, D. Bao, M. H Javani, R. Pourabolghasem and A. Adibi, ACS Photonics, 2023, 10, 900–909.
34. Y. Kiarashinejad, M. Zandehshahvar, S. Abdollahramezani, O. Hemmatyar, R. Pourabolghasem and A. Adibi, Advanced Intelligent Systems, 2020, 2, 1900132.
35. W. Ma, F. Cheng, Y. Xu, Q. Wen and Y. Liu, Adv. Mater., 2019, 31, 1901111.
36. D. U. Jo, B. Lee, J. Choi, H. Yoo and J. Y. Choi, arXiv, 2019, preprint, arXiv:1905.12867, 12867.
37. W. Yu, L. Wu, Q. Zeng, S. Tao, Y. Deng and M. Jiang, arXiv, 2020, preprint, arXiv:2005.02557,  DOI:10.48550/arXiv.2005.02557.
38. H. S. Stein, D. Guevarra, P. F. Newhouse, E. Soedarmadji and J. M. Gregoire, Chem. Sci., 2019, 10, 47–55.
39. A. Radhakrishnan, S. F. Friedman, S. Khurshid, K. Ng, P. Batra, S. A. Lubitz, A. A. Philippakis and C. Uhler, Nat. Commun., 2023, 14, 2436.
40. S. Lu and A. Jayaraman, JACS Au, 2023, 3, 2510–2521.
41. M. Y. Yaman, S. V. Kalinin, K. N. Guye, D. S. Ginger and M. Ziatdinov, Small, 2023, 19, 2205893.
42. D. E. Aspnes and A. Studna, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 985.
43. W. Zhong and H. Meidani, Computer Methods in Applied Mechanics and Engineering, 2023, 403, 115664.
44. D. P. Kingma, M. Welling, et al., Foundations and Trends® in Machine Learning, 2019, vol. 12, pp. 307–392.
45. S. Odaibo, arXiv, 2019, preprint, arXiv:1907.08956, 08956.
46. M. Gong, X. Niu, T. Zhan and M. Zhang, International Journal of Remote Sensing, 2019, 40, 3647–3672.
47. V. Liu and S. Fan, Comput. Phys. Commun., 2012, 183, 2233–2244.
48. M. Thomas, F. H. Jensen, B. Averly, V. Demartsev, M. B. Manser, T. Sainburg, M. A. Roch and A. Strandburg-Peshkin, J. Anim. Ecol., 2022, 91, 1567–1581.
49. M. S. Nasr, A. Hajighasemi, P. Koomey, P. B. Malidarreh, M. Robben, J. R. Saurav, H. H. Shang, M. Huber and J. M. Luber, 2023 IEEE 20th International Symposium on Biomedical Imaging (ISBI), 2023, pp. 1–5.
50. L. McInnes, J. Healy and J. Melville, arXiv, 2018, preprint, arXiv:1802.03426,  DOI:10.48550/arXiv.1802.03426.
51. T. Sainburg, M. Thielk and T. Q. Gentner, BioRxiv, 2019, 870311.
52. L. Van der Maaten and G. Hinton, Journal of Machine Learning Research, 2008, 9, 2579–2605.
53. Z. Liu, L. Raju, D. Zhu and W. Cai, IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2020, 10, 126–135.
54. X. Hou, L. Shen and G. Qiu, Deep Feature Consistent Variational Autoencoder, 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), 2016, pp. 1133–1141.
55. P. Cristovao, H. Nakada, Y. Tanimura and H. Asoh, IEEE Access, 2020, 8, 149456–149467.
56. S. An and J.-J. Jeon, Pattern Recognition Letters, 2024, 177, 54–60.
57. D. Berthelot, C. Raffel, A. Roy and I. Goodfellow, arXiv, 2018, preprint, arXiv:1807.07543, p. 07543,  DOI:10.48550/arxiv.1807.07543.
58. P. Shamsolmoali, M. Zareapoor, H. Zhou, D. Tao and X. Li, IEEE Transactions on Image Processing, 2023, 4486–4500.
59. Y. Zhou, C. Mao, E. Gershnabel, M. Chen and J. A. Fan, Laser Photonics Rev., 2024, 2300988.
60. M. Chen, R. E. Christiansen, J. A. Fan, G. Işiklar, J. Jiang, S. G. Johnson, W. Ma, O. D. Miller, A. Oskooi and M. F. Schubert, et al. , J. Opt. Soc. Am. B, 2024, 41, A161–A176.
61. D. Vercruysse, N. V. Sapra, L. Su, R. Trivedi and J. Vučković, Sci. Rep., 2019, 9, 8999.
62. S. S. Panda, H. S. Vyas and R. S. Hegde, Opt. Mater. Express, 2020, 10, 3145–3159.
63. S. S. Panda, S. Choudhary, S. Joshi, S. K. Sharma and R. S. Hegde, Opt. Lett., 2022, 47, 2586–2589.
64. V. Vashistha, G. Vaidya, R. S. Hegde, A. E. Serebryannikov, N. Bonod and M. Krawczyk, ACS Photonics, 2017, 4, 1076–1082.
65. E. Arbabi, A. Arbabi, S. M. Kamali, Y. Horie and A. Faraon, Opt. Express, 2016, 24, 18468–18477.
66. Y. Zhou, I. I. Kravchenko, H. Wang, J. R. Nolen, G. Gu and J. Valentine, Nano Lett., 2018, 18, 7529–7537.
67. S. S. Panda, S. Kumar, D. Tripathi and R. S. Hegde, J. Nanophotonics, 2023, 17, 036006.
68. P. R. Wiecha and O. L. Muskens, Nano Lett., 2019, 20, 329–338.
69. D. Jha, K. Choudhary, F. Tavazza, W.-k. Liao, A. Choudhary, C. Campbell and A. Agrawal, Nat. Commun., 2019, 10, 5316.
70. J. Gao, P. Li, Z. Chen and J. Zhang, Neural Computation, 2020, 32, 829–864.
71. Y.-C. Chen, L. Li, L. Yu, A. El Kholy, F. Ahmed, Z. Gan, Y. Cheng and J. Liu, European conference on computer vision, 2020, pp. 104–120.
72. F. Huang, X. Zhang, J. Xu, Z. Zhao and Z. Li, IEEE Transactions on Cybernetics, 2019, 51, 1506–1518.
73. T. N. Kipf and M. Welling, arXiv, 2016, preprint, arXiv:1609.02907,  DOI:10.48550/arXiv.1609.02907.

---

Footnotes

† Electronic supplementary information (ESI) available: Shape set details and dataset generation, CNN model training and hyperparameter optimization, and additional experimental details including sensitivity analysis. See DOI: https://doi.org/10.1039/d4dd00107a

‡ The authors contributed equally and are considered as first authors.

---