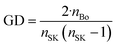Insights into pharmacokinetic properties for exposure chemicals: predictive modelling of human plasma fraction unbound (f_u) and hepatocyte intrinsic clearance (Cl_int) data using machine learning

Abstract

An external chemical substance (which may be a medicinal drug or an exposome), after ingestion, undergoes a series of dynamic movements and metabolic alterations known as pharmacokinetic events while exerting different physiological actions on the body (pharmacodynamics events). Plasma protein binding and hepatocyte intrinsic clearance are crucial pharmacokinetic events that influence the efficacy and safety of a chemical substance. Plasma protein binding determines the fraction of a chemical compound bound to plasma proteins, affecting the distribution and duration of action of the compound. The compounds with high protein binding may have a smaller free fraction available for pharmacological activity, potentially altering their therapeutic effects. On the other hand, hepatocyte intrinsic clearance represents the liver's capacity to eliminate a chemical compound through metabolism. It is a critical determinant of the elimination half-life of the chemical substance. Understanding hepatic clearance is essential for predicting chemical toxicity and designing safety guidelines. Recently, the huge expansion of computational resources has led to the development of various in silico models to generate predictive models as an alternative to animal experimentation. In this research work, we developed different types of machine learning (ML) based quantitative structure–activity relationship (QSAR) models for the prediction of the compound's plasma protein fraction unbound values and hepatocyte intrinsic clearance. Here, we have developed regression-based models with the protein fraction unbound (f_u) human data set (n = 1812) and a classification-based model with the hepatocyte intrinsic clearance (Cl_int) human data set (n = 1241) collected from the recently published ICE (Integrated Chemical Environment) database. We have further analyzed the influence of the plasma protein binding on the hepatocyte intrinsic clearance, by considering the compounds having both types of target variable values. For the fraction unbound data set, the support vector machine (SVM) model shows superior results compared to other models, but for the hepatocyte intrinsic clearance data set, random forest (RF) shows the best results. We have further made predictions of these important pharmacokinetic parameters through the similarity-based read-across (RA) method. A Python-based tool for predicting the endpoints has been developed and made available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home/pkpy-tool.

---

1. Introduction

Once a chemical substance (a medicinal drug or an exposome) is ingested, it undergoes a series of pharmacokinetic (PK) events inside the body depending on its chemical and physiological nature. The pharmacodynamic (PD) properties of the chemical determine the different range of actions it exerts through interaction with the macromolecular target.^1,2 The PD behavior of a chemical is mainly dependent on the affinity for the target molecule and the PK properties of that chemical.^3–5 The PK properties refer to the absorption, distribution, metabolism, and excretion, commonly abbreviated as ADME. The ADME behavior of a chemical depends on its chemical properties, formulation, and individual characteristics of the person who ingests it. The ADME parameters play a pivotal role in determining the chemical's concentration at the site of action and its effects on the body. Understanding these processes is crucial for predicting the effects and potential toxicity of a chemical, as well as designing safety regimens.⁶ Fig. S1† shows the basic workflow of the ADME process of a chemical inside the body. Several factors control the ADME behavior of an ingested chemical inside the body, with protein binding and clearance being the prime factors that determine the chemical's fate within the body.^7,8

The binding of a chemical substance with plasma proteins is a reversible process that significantly affects both the PK and PD properties of the substance.⁹ A substance generally binds with two types of plasma protein, namely serum albumin (for acidic compounds) and α-1-acid glycoprotein (for basic compounds).¹⁰ The extent of plasma protein binding varies with the nature and concentration of the chemical compound. A chemical entity's tissue distribution becomes limited, if its binding with plasma protein is poor. Binding with plasma protein helps to solubilize lipophilic compounds and influence their pharmacokinetics; but if it is too strong, the compound never reaches the minimum concentration required to show any action.¹¹ The fraction unbound (f_u) is an essential parameter that determines the concentration for minimum tolerable toxicity threshold, and macromolecular interaction and helps to develop the pharmacokinetic–pharmacodynamic relationship.¹² A high plasma protein binding leads to a higher fraction of compounds present in the blood compartment and a low volume of distribution, meaning less partition of that compound within the tissue.¹¹ However, only the free portion of a compound can exert pharmacological action; so the unbound fraction of that compound is essential for the correlation with its observed activity.¹² Although a compound may have a high degree of protein binding, only the free portion of the compound can undergo any elimination action, such as metabolism and excretion. This means that the elimination half-life of a compound can increase due to high protein binding.¹³ The process of protein binding generally serves as a storage mechanism for a chemical substance. As the free portion of a compound decreases, the drug bound to the protein dissociates to maintain equilibrium and prolong the compound's effects.¹⁴

Clearance is the process of removing a chemical substance irreversibly from a hypothetical volume of plasma or serum per unit of time. It is an important factor that determines the residence time of a chemical substance within the body.¹⁵ The efficiency of the organ in eliminating a chemical substance is represented by the clearance value, with higher values indicating better efficiency. A detailed description of the clearance method is provided in ESI SI-2.†

Therefore, it is crucial to accurately determine the fraction of unbound chemicals and their clearance properties to ensure safety and create effective safety guidelines. Various methods such as equilibrium dialysis, rapid equilibrium dialysis, and ultrafiltration are utilized to estimate the plasma protein binding.¹² All of these methods involve a huge amount of cost, time, and resources. In recent years, various computational methods have been employed to develop PK models that estimate the PK properties of chemical compounds. The main advantage of the computational method is that it does not involve any kind of animal experimentation and reduces the wastage of resources and time.

Currently, various data-driven approaches, such as Machine Learning (ML), Quantitative Structure–Activity Relationship (QSAR), and Read-Across (RA), are used to develop predictive models. ML is a branch of artificial intelligence that helps machines to learn and improve their performance based on previous data and helps to predict unknown data.¹⁶ There are different ML algorithms, which can be categorized as supervised, unsupervised, and reinforcement, based on their application to data-related problems. Supervised ML is used for labeled datasets, unsupervised ML for unlabeled datasets, and reinforcement for feedback-based learning. In reinforcement learning, the learning agent is rewarded for every right action and penalized for every wrong action.¹⁷ ML methods have a wide range of applications, but they also have several disadvantages, they require large amounts of high-quality data, have complex algorithms, and lack interpretation.¹⁸ To address the problem of interpretation, presently different explainable methods like SHAP have been adopted for interpreting ML algorithms.¹⁹ On the other hand, statistical methods like QSAR are used to develop relationships between molecular structures and the observed activity. In the QSAR model development, compounds with known activity are used, and predictions are made for unknown chemicals.²⁰ QSAR models provide a simple, interpretable model, but the model becomes non-reliable when the size of the dataset is small.²¹ In such situations, similarity-based methods like RA can be used for prediction, which can be used for both smaller and larger datasets.²² RA is not a statistical approach but uses similarity values to make predictions. The RA method can be classified into two groups: the analog approach (where only one similar compound is used for the prediction) and the category approach (where multiple similar compounds are used for the prediction).²³ The RA method is mainly used by regulatory agencies to make regulatory decisions and is also widely used for data gap-filling.²¹

Previously, a large number of attempts were made to develop in silico models to correlate molecular structure with plasma fraction unbound^24–28 and hepatocyte intrinsic clearance.^29–32 A quantitative structure–property relationship model was developed by the group of Yun et.al. by using experimentally derived fraction unbound data.²⁴ Esaki et.al. developed a computational method for the prediction of the amount fraction of unbound drugs present in the human brain. By using this model, they tried to estimate CNS toxicity, and for the model development, they used 253 compounds.²⁵ Ryu et.al. and coworkers evaluated the safety and efficacy of different drugs through the evaluation of the drug fraction unbound across 7 different tissues and 5 different species.²⁶ Zhivkova and Doytchinova developed a quantitative structure-plasma protein binding relationships (QSPPBR) model for the prediction of the amount of unbound fraction of a compound present in the plasma. In their study, they used 132 diverse acidic drugs and 178 molecular descriptors for model development.²⁷ Riedl et.al. developed a deep learning model for the prediction of plasma fraction unbound with the tokenized SMILE strings.²⁸ Paixão et.al. developed an artificial neural network for the prediction of hepatocyte intrinsic clearance with calculated molecular descriptors. For this research work, they used 71 drugs for modeling and 18 drugs for evaluation.²⁹ Sternbeck et.al. developed a predictive model with hepatic and microsome intrinsic clearance data for 52 drugs.³⁰ Lombardo et.al. developed a random forest-based machine-learning model with 1340 compounds from human clearance data.³¹ Nikolic and Agababa developed a QSAR model with 29 drugs of different structures, for the prediction of human hepatic microsomal intrinsic clearance.³²

In our research, we have devised various predictive models to determine the length of time different chemical substances remain in the body. These models use plasma fraction unbound and hepatocyte intrinsic clearance parameters to evaluate the body residence time. We have developed separate machine learning-based QSAR models for each type of endpoint data. Our study also examines the impact of plasma fraction unbound on compound clearance, taking into account common compounds found in both data sets. To achieve our objectives, we employed several machine learning models, including random forest, adaboost, gradient boost, xgboost, support vector machine, linear support vector machine, ridge regression, and partial least squares models. Additionally, we analyzed the data sets using a similarity-based read-across method. Ultimately, our goal has been to create predictive model hypotheses for estimating residence time of chemicals within the body which may be helpful for their toxicity assessments.

2. Methods and materials

2.1 Data collection

The current work deals with the development of machine learning (ML) based quantitative structure–activity relationship (QSAR) models for the pharmacokinetic properties f_u (plasma fraction unbound) and Cl_int (hepatocyte intrinsic clearance). Both types of data were collected from the recently published ICE (Integrated Chemical Environment) database (https://ice.ntp.niehs.nih.gov/DATASETDESCRIPTION) which is run by the National Toxicology Program U.S. Department of Human and Health Service. Here, we collected a total of 2165 f_u data points and 1489 Cl_int data points, and both types of data contain human and rat in vitro experimental data, as shown in Fig. S2.† In this work, we only used human experimental data, that is 1830 f_u data points and 1249 Cl_int data points, for the development of the predictive models. Among these data points, there are 1046 common data points, that is for these compounds both f_u and Cl_int data are present. The data points in the f_u data set (range: 0–1) have no unit and the Cl_int data points (range: 0–9879) have the unit of μl min⁻¹ 10⁻⁶ cells. In this work, we performed log transformation to the response values as customary in QSAR analysis. The information about the data points is given in the ESI SI-1† in .xlsx format while some details of the methods are provided in ESI SI-2.† The details of molecular structure information are given in ESI SI-3.† To the best of our knowledge, no prior QSAR nodleing work has been reported using these data sets.

2.2 Data curation

The structural information (SMILEs) for both types of data sets is retrieved from the PubChem database (https://pubchem.ncbi.nlm.nih.gov/). In both types of data sets, few compounds were present for which no structural information was available, so these types of compounds were removed from both data sets. The inorganic compounds and the compounds with large diverse structures like amino acid chains or oligonucleotides present in the data sets are also removed. There are also a few duplicate compounds present in both types of data sets; for these duplicate compounds, we have taken the average of the response values. Finally, a total of 1812 compounds of the f_u data set (human) and 1241 compounds of the Cl_int data set (human) were used for further analysis.

2.3 Structure drawing and descriptor calculation

The SMILES notations for the chemical compounds, which were retrieved from the PubChem database, were used for the generation of the molecular structures by using Marvin sketch software (https://chemaxon.com/marvin). All the generated molecular structures were saved in .mol file format and then all the molecules were converted to a single .sdf file by using Open Babel software (https://sourceforge.net/projects/openbabel/). During the generation of the molecular structure, the chemical compounds present in the salt form are manually converted to the neutral molecular moiety. This generated .sdf file was then used for the calculation of the molecular descriptor by using the alvaDesc software.³³

The descriptors can be classified into different groups like 0D to 7D based on the dimensionality of the descriptor, but generally, 2D and 3D descriptors are used for the QSAR model development. This research work is performed by using only 2D descriptors, to avoid the conformational complexity of the molecular structures. The 2D descriptors also have another advantage over 3D descriptors: the values of 2D descriptors are easy to interpret and reproducible.²⁰ In this work, we calculated a total of 2400 descriptors belonging to the 9 different classes namely: constitutional indices, ring descriptors, connectivity descriptors, ETA indices, functional group counts, atom-centred fragments, atom-type E-state indices, 2D atom pair, and molecular properties.

2.4 Data pre-treatment

The calculated descriptor matrix contains lots of missing values, a descriptor column with constant values, and several intercorrelated descriptors. These types of descriptors should be removed before further analysis; otherwise, this may cause errors in model development and interpretation. Here, we used a Java-based tool DataPreTreatmentGUI 1.2 (available from http://teqip.jdvu.ac.in/QSAR_Tools/) for the data pre-treatment by providing variance cut-off 0.1 and descriptor intercorrelation cut-off 0.9.

2.5 Detection and removal of activity cliff

The development of a good quality and robust QSAR model depends upon the selection of an appropriate data set. In the QSAR studies, there are two types of outliers present: structural outliers and activity outliers (including activity cliffs). The presence of outliers in the QSAR model can lead to development in the instability of the model and the presence of activity outliers can significantly affect the external predictive power of the model.³⁴

Here we found that a portion of the data set does not follow the basic assumption of the QSAR analysis which is that similar compounds have similar activity or properties.³⁵ This anomaly behavior is known as the “Cliff” in the descriptor space where drastic changes in the activity or properties occur with small changes in the descriptor values. In other words, if we add or remove a few such data points there will be a significant change in the quality of the QSAR model. The cliff is defined as the ratio of the difference in activity between two compounds to the distance of separation in descriptor space,³⁶ as shown in eqn (1):

A = activity cliff between two chemicals, Y_i = activity of the ith chemical compound, Y_j = activity of the jth chemical compound, d = distance between two chemical compounds in chemical space, in the QSAR modeling, an activity cliff is one of the major problems that should be considered before model development.

Here, we used a similarity-based method for the detection of the activity outliers present in the data set and removed these compounds before model development. We have calculated two similarity-based coefficients s_m¹ and s_m², for the detection of the activity outliers,³⁷ which are mathematically represented below in eqn (2) and (3):

Here, MaxPos and MaxNeg represent the similarity values for the closest positive and negative source compounds respectively. PosAvgSim and NegAvgSim indicate the average similarity values of the selected positive and negative close source compounds respectively, for each query compound. The main idea behind this is to classify the response data based on the mean value, the compounds present above the mean are denoted as positive and the compounds present below the mean are denoted as negative. Then, the structural similarity between each compound with other compounds is measured by using different similarity-measuring functions. Now, for a positive compound if the most similar compound is positive then MaxPos > MaxNeg and s_m¹ becomes positive. But if the most similar compound is negative then MaxPos < MaxNeg and s_m¹ becomes negative which indicates the outlier behavior of that compound; i.e., although two compounds have similar structures, they have different response value classes. Similarly, for negative compounds, MaxNeg should be greater than MaxPos i.e., s_m¹ should be negative, but it becomes positive when the most similar compound is positive which indicates an outlier behavior.

Also, for a positive compound, PosAvgSim should be greater than NegAvgSim i.e., s_m² should be positive otherwise the compound is considered an outlier. Similarly, for the negative compound, the s_m² value should be negative.

The compounds that are detected as outliers by both s_m¹ and s_m² coefficients are removed from the data set before model development and used as a true external set for validation. In this work, only from the f_u data set we removed the response outliers and a total of 362 compounds were removed before modeling (but kept aside for an external set for making predictions). Here, we used a Java-based in-house tool RASAR-Desc-Calc-v3.0.2 (available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home) for the calculation of s_m¹ and s_m² coefficients at a default hyper-parameter setting (CTC = 10) by using Euclidean distanced-based similarity method.

2.6 Data set division

The primary aim of the QSAR analysis is to develop a good predictive model that can be used for the prediction of activity or properties of newly developed compounds.³⁸ But before using a QSAR model for predictions, the prediction power of that model should be evaluated and validated. For the model validation, the original dataset is divided into a training set and a test set, where the training set is used for the development of the QSAR model, and the test set is used for the model validation.²⁰

Here, we have used Java-based tools datasetDivisionGUI1.2 and ModifiedKMedoid_4 (available from http://teqip.jdvu.ac.in/QSAR_Tools/) to divide the data set. Both the data sets were divided into 3 : 1 ratio, and after division training and test sets were subjected to the data pre-treatment using dataPreTreatmentTrainTest1.0 (available from http://teqip.jdvu.ac.in/QSAR_Tools/).

2.7 Feature selection

The selection of features is the most important integral part of the QSAR modeling, to find the most significant features for the models. The feature selection process helps to reduce the higher-dimensional feature space to the lower dimension by removing insignificant and noisy descriptors.³⁹ The major advantage of the feature selection is that a model with fewer features is easier to interpret, visualize, improve model performance, and reduce the chances of model overfitting or overtraining.⁴⁰ So, the main aim of the feature selection is to remove redundant, noisy, and irrelevant descriptors during QSAR model building, and in this way dimensionality of the feature matrix is reduced without loss of any significant information. The selection of the proper features by using the suitable algorithm is a challenging task for the modeler. Several feature selection techniques are employed in the QSAR modeling such as forward selection,^41,42 backward elimination,^43,44 stepwise selection,⁴⁵ simulated annealing,⁴⁶ genetic algorithms,^47–49 and many more.

Here, we used the genetic algorithm (GA) and best subset feature selection methods to identify the most significant features for modeling the f_u data set. The genetic algorithm was used for the reduction of the initial feature pool, and then the best subset method was used to find the best modellable feature combination. The hyperparameters used in the GA method are the number of iterations, the number of features, cross-over probability, mutation probability, the initial number of equations generated, and the number of equations selected in each generation. The process of feature selection through the GA method is discussed in detail in the ESI SI-2.† Here, we used the prediction error-based metric (mean absolute error) for the convergence of the GA method.

The GA method of feature selection was performed by using the tool GeneticAlgorithm_v4.1_Train (available from http://teqip.jdvu.ac.in/QSAR_Tools/) which uses an error-based fitness score for optimization. This tool was run multiple times using only the training set, and the best feature combinations were selected based on the model's internal quality which is developed with GA-selected features. These selected features were merged and subjected to the best subset feature method using BestSubsetSelectionModified_v2.1 (available from http://teqip.jdvu.ac.in/QSAR_Tools/). This tool develops a multiple linear regression (MLR) model for all the possible combinations of the feature and evaluates its quality metrics. Here, we select the best feature combinations based on the model's internal quality metrics.

The random forest feature importance was used to identify the relevant features of the Cl_int data set.⁵⁰ Random Forest is a tree-based machine-learning modelling technique that builds multiple decision trees during model training.⁵¹ In the random forest models, the relative importance of a feature can be calculated which is used for the selection of appropriate contributing features. The importance of a feature is calculated based on how much it contributes to the reduction of the impurity (gini impurity) across all the trees in the forest. The feature that leads to a decrease in the impurity significantly is considered to be a more important feature.^52,53 Here, we have used the Python-based Scikit-learn module for the calculation of the feature importance and used them for the development of the QSAR models.

2.8 QSAR model development

In this work, we have developed machine learning (ML) based quantitative structure–activity relationship (QSAR) models with the selected set of descriptors. Here, we standardized the both training and test sets, based on the training set mean and stander deviation of the corresponding columns, before the model development. In this research work, we developed regression-based models for the f_u data set and classification-based models for the Cl_int data set. Here, we have developed regression models like a random forest (RF),⁵¹ adaboost (ADB), gradient boost (GB),⁵⁴ extreme gradient boost or xgboost (XGB),⁵⁵ support vector machine (SVM), linear support vector machine (LSVM),⁵⁶ ridge regression (RR)⁵⁴ and partial least square (PLS)²⁰ model for the f_u data set. We built linear discriminant analysis (LDA),⁵⁷ logistic regression (LR),⁵⁸ random forests (RF), and support vector machines (SVM) models with the Cl_int dataset. The models that were developed with f_u data sets, were used to make predictions for the compounds that have been removed from the data set due to activity cliff behavior. The details about the developed model are provided in ESI SI-2.†

In this work, we have used Machine Learning Regression v2.1 and Machine Learning v1.0 (available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home/machine-learning-model-development-guis) tools for the development of the ML models. These tools use a Python-based Scikit-learn module for the development of the models. Here, we optimized the hyperparameters of the ML models using the GridSearchCV method by 5-fold cross-validation using the tool Tuning+CV v1.0 available from the above link.

2.9 Statistical quality and validation metrics

A developed model should be properly evaluated and validated because based on this evaluation further use of the model is determined. The statistical evaluation of a regression model is done by determining its quality, goodness-of-fit, robustness, and predictivity. The model's quality is evaluated based on the value of the determination coefficient (R²), mean absolute error of the training set (MAE_training), and root mean square error of calibration (RMSEC) which are calculated on the training set. There are two types of model validation metrics are present – internal validation metrics and external validation metrics. The internal validation metrics are checked to determine the model's goodness-of-fit and robustness by using only the training set whereas external validation metrics are used to check the model's predictivity by using a test set. Here, we calculated internal validation metrics like leave-one-out correlation coefficient (Q_LOO²), leave-one-out mean absolute error (MAE_LOO), and leave-one-out mean squared error (MSE_LOO). The model's predictivity is checked by external validation metrics like Q_F1², Q_F2², Q_F3², mean absolute error of test set (MAE_test), and root mean square error of prediction (RMSEP), using the test set.²⁰ Here, we calculated different classification-based metrics for the evaluation of the classification models of the Cl_int data set. The classification-based metrics like sensitivity, specificity, accuracy, precision, F1-score, Cohen's κ, and Matthew's correlation coefficient (MCC) are calculated for the evaluation of the models. All the above-mentioned metrics are shown in ESI SI-2 from the eqn S5–S22.†

2.10 SHAP analysis

SHAP (SHapley Additive exPlanations) analysis is a powerful tool for interpreting and understanding the predictions of machine learning models.^19,50 It is based on Shapley's values from cooperative game theory and provides a unified measure of feature importance. Developed by Lloyd Shapley, Shapley values allocate the contribution of each player in a cooperative game.⁵⁹ In the context of SHAP analysis, features are considered players, and the prediction outcome is the payoff. Shapley values distribute the contribution of each feature to the prediction fairly among all features. They consider all possible combinations of features and calculate the average contribution of each feature.⁶⁰ SHAP values provide insights into the impact of each feature on a particular prediction. Positive SHAP values indicate a feature's positive contribution to the prediction, while negative values signify a negative impact. Aggregating SHAP values across all instances allows the assessment of global feature importance. It helps in understanding which features consistently contribute more to model predictions.⁶¹

Here, we developed a SHAP summary plot and local force plot for the determination of the feature contribution globally and locally. In the summary plot, features are distributed along the vertical axis according to their feature importance, and along the horizontal axis, SHAP value distribution is represented. In this plot, each instance is represented by dots which are colored based on the feature value and help to determine the direction of the feature contribution. The local force plot indicates the feature contribution to the prediction for a particular data point and also helps to determine the direction of the contribution, whether positive or negative.

2.11 Modelling of the common compounds

As described above, the human data sets contain a large number of common compounds that have both plasma protein fraction unbound (f_u) and hepatocyte intrinsic clearance (Cl_int) data. Here, a total of 1046 compounds have both f_u and Cl_int data, 203 compounds have only Cl_int data and 784 compounds have only f_u data. In this present work, we developed a classification-based model with these 1046 compounds by considering f_u data as a descriptor and Cl_int data as a response. Here, we used a similar approach as we used for the Cl_int data set, for the development of the model. Four data points have been eliminated from these compounds since they were repeated or the structural information was not available. Finally, 1042 compounds were used for model development and predictions. Similarly, here we also used log-transformed response data for the modeling and converted that response to categorical data (0 and 1) based on the mean. Here, we also divided the data set with a 3 : 1 ratio in multiple combinations and selected the best division based on the model quality. The features for the model development were selected based on the random forest feature importance. Finally, different ML-based models like RF, SVM, LDA, and LR, were developed with the selected set of descriptors, at an optimized hyper-parameter setting. All the models are evaluated based on the classification-based metrics as described above, in the eqn S16 to S22.† Here, we also performed a SHAP analysis to determine the features' importance.

These models were used for the prediction of the compounds with 203 unique Cl_int data, and for this prediction, we have used model-derived f_u data (obtained from the regression-based f_u model). These models were also used for the prediction of the compounds having unique f_u data points.

2.12 Read-across

The Read-across (RA) is a similarity-based prediction method, where predictions are made based on the similarity between the target compound and the close source compound.²³ In this research work, we have used the final modeled training and test set for further analysis through the read-across method. The similarity between target and source compounds is calculated through three different similarity functions namely – Euclidean Distance (ED), Gaussian Kernel (GK), and Laplacian Kernel (LK). Here, the default hyper-parameter setting (σ = 1, γ = 1, CTC = 10) was used to make the prediction.

2.13 Software development

In this research work, a Python-based tool (PKPy v1.0) was developed for the prediction of protein fraction unbound (f_u) and hepatocyte intrinsic clearance parameters for untested chemicals. This tool gives predictions based on the structural features of an unknown chemical using the best model. This tool is free, easy to handle, and can be downloaded from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home/pkpy-tool. This tool takes query data set in .xlsx format and gives the output.

The complete working process of this research is graphically represented in Fig. 1.

Fig. 1 Complete flow diagram of the working process.

3. Results and discussion

Our research involves the development of quantitative structure–activity (QSAR) models utilizing machine learning for two distinct data sets. We have also taken into account the impact of the protein fraction unbound on hepatocyte intrinsic clearance by examining compounds with quantitative values of both types of response variables. These models are effective in predicting the response values for compounds that do not have the reported experimental values. Additionally, we evaluated the data sets using the similarity-based read-across method to ensure accuracy.

3.1 Modelling of the plasma protein fraction unbound (f_u)

In this research work, we developed eight different types of machine learning models with the fraction unbound data set. The most significant and statistically robust machine models in terms of training and test set quality and validation metrics are represented in Table 1. Here, all the models were developed with the 12 most significant descriptors, and for model development, we used standardized descriptors and response values. From these results, we can find out that the results of the support vector machine (SVM) model supersede other machine learning models in terms of both internal and external validation metrics. All the models are developed with optimized hyper-parameter settings, and the optimization was performed by a 5-fold cross-validation method with the GridSearchCV method. Here, we also reported different types of cross-validation statistics using training sets to determine whether the developed models are overfitted or not. Here, we performed 1000 times shuffle split cross-validation by considering mean R² and mean MAE as the objective functions. In the shuffle split cross-validation method, a cross-validator with a specified number of splits (here 1000) and a validation set (here 30%) is created. This cross-validator then iterates over each split to train the model and evaluate on validation set. The score of the cross-validation method is then used for the evaluation of the performance of the model. The results of these methods are also included in Table 1 and represented graphically in Fig. S3.† From this illustration, we can also find out that the SVM model shows superior results in terms of both cross-validated R² and MAE; it also shows the lowest standard error measure (SEM) value. Here, random forest (RF), gradient boost (GB), and extreme gradient boost (XGB) models also show comparable results. Here, we also performed the read-across analysis with the modeled training and test sets by using different similarity functions. The validation metrics for the read-across prediction have been shown in Table S1 in ESI SI-2.†

Table 1 Results of the machine learning model for fraction unbound data

Modeling method	Training set statistics						Cross-validation statistics		Test set statistics						Hyper-parameter setting
	R ^2	Q LOO ^2	MAEtraining	RMSEC	MAELOO	MSELOO	ShuffleSplit CV		Q F1 ^2	Q F2 ^2	Q F3 ^2	MAEtest	RMSEP	CCC
							R ^2 ± SEM	MAE ± SEM
RF	0.75	0.66	0.35	0.50	0.41	0.34	0.64 ± 0.001	0.42 ± 0.001	0.68	0.68	0.68	0.40	0.56	0.80	{‘n_estimators’: 300, ‘min_weight_fraction_leaf’: 0.0, ‘min_samples_split’: 4, ‘min_samples_leaf’: 5, ‘min_impurity_decrease’: 0.0, ‘max_leaf_nodes’: None, ‘max_depth’: 5, ‘criterion’: ‘squared_error’}
ADB	0.58	0.55	0.54	0.65	0.54	0.45	0.54 ± 0.002	0.56 ± 0.002	0.57	0.57	0.57	0.56	0.66	0.68	{‘n_estimators’: 200, ‘loss’: ‘linear’}
GB	0.74	0.68	0.36	0.51	0.40	0.32	0.67 ± 0.001	0.40 ± 0.001	0.70	0.70	0.70	0.39	0.55	0.81	{‘subsample’: 1.0, ‘n_estimators’: 80, ‘min_weight_fraction_leaf’: 0.0, ‘min_samples_split’: 3, ‘min_samples_leaf’: 4, ‘min_impurity_decrease’: 0.0, ‘max_depth’: 2, ‘loss’: ‘squared_error’, ‘learning_rate’: 0.1, ‘criterion’: ‘friedman_mse’}
XGB	0.77	0.67	0.35	0.48	0.42	0.33	0.65 ± 0.001	0.43 ± 0.001	0.68	0.68	0.68	0.40	0.56	0.80	{‘n_estimators’: 100, ‘max_depth’: 3, ‘learning_rate’: 0.1, ‘booster’: ‘gbtree’}
SVM	0.75	0.69	0.32	0.50	0.37	0.31	0.68 ± 0.001	0.38 ± 0.001	0.75	0.75	0.75	0.34	0.50	0.85	{‘gamma’: ‘auto’, ‘degree’: 3, ‘C’: 1.0}
LSVM	0.59	0.57	0.49	0.64	0.49	0.42	0.57 ± 0.001	0.49 ± 0.001	0.63	0.63	0.63	0.46	0.61	0.76	{‘C’: 10.0}
RR	0.61	0.60	0.49	0.63	0.50	0.40	0.59 ± 0.001	0.50 ± 0.001	0.64	0.64	0.64	0.47	0.60	0.76	{‘alpha’: 40.0}
PLS	0.61	0.60	0.49	0.63	0.49	0.40	0.59 ± 0.001	0.49 ± 0.001	0.65	0.65	0.65	0.46	0.59	0.77	Component 4

---

A scatter plot has been generated to visually represent the performance of the SVM model. The X and Y-axes of the plot display the observed and predicted fraction unbound values, respectively, as shown in Fig. 2. The calculated Pearson's correlation coefficient for the scatter plot is 0.869, revealing a robust positive correlation between the observed and predicted values. Here, we developed learning curves for the SVM model by using mean absolute error (MAE) and R² as the objective functions, which are shown in Fig. S4.† A learning curve is a good diagnostic tool to find out whether the model is going to benefit by adding more training data or not. It also helps to determine whether a model suffers from variance or bias problems. A learning curve is generated by training a model at varying training sizes and testing it on the validation set, finally training and validation set scores are used to determine the model performance.

Fig. 2 Observed vs. predicted log(1 + f_u) scatter plot for the SVM model.

From Fig. S4,† we can see that with increasing the training size the training and validation curves reach their plateau state, which that means with increasing the training data model performance is not going to change significantly. The small difference between the training and validation curve indicates the good quality of the model. Here, we also developed validation curves for the SVM model with respect to the parameter C and degree by considering R² and MAE as the objective functions, as shown in Fig. S5.† A validation curve is a good tool to measure the sensitivity of a model with changes in model hyper-parameters visually. From these plots, we can see that the gap between the training and validation curve increases (both R² and MAE) with C, which signifies that the model performs well for a small C value. On the other hand, the validation and training curves remain constant for the parameter degree which indicates that model performance is not going to be affected by the degree parameter. The residual values of the training and test sets were used to generate the violin plot, which helps to understand the data distribution of different categories, as shown in Fig. S6.† From this plot, we can see that the density or frequency of the data points is higher at values close to zero, which indirectly indicates good prediction quality.

Here, we also performed an analysis to understand the response outliers (activity cliffs) behavior of the data points present in the data set. Here, we calculated pair-wise similarity through the Laplacian kernel similarity function and also calculated the pair-wise difference between the response values. A scatter plot is generated by plotting pair-wise similarity along the X-axis and response value differences along the Y-axis (Fig. 3), and then the plot is equally divided into four quadrants. The compounds that are present in the upper right quadrant have high activity differences although they have higher structural similarity and can thus be considered as activity cliffs.

Fig. 3 Activity cliff plot by using Laplacian kernel similarity function (fraction unbound data).

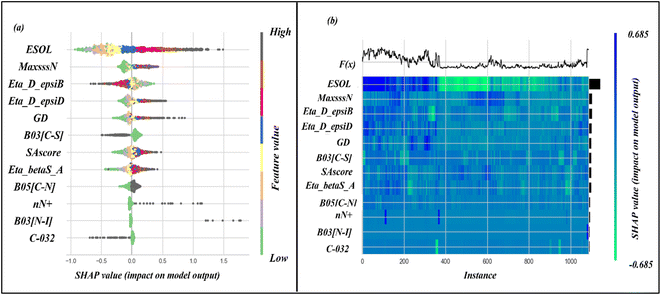
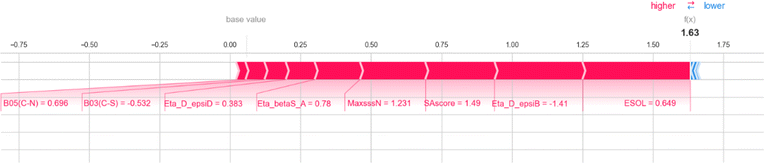
In our study, we conducted a SHAP analysis for the SVM model, which helped us to identify the most crucial descriptors for accurate predictions. We have presented the results in the form of a summary plot and a heat map plot in Fig. 4. The summary plot shows the features arranged on the vertical axis, according to their importance, with the most important features appearing at the top. The horizontal axis represents the SHAP value distribution for all the data points. The SHAP heat map plot shows the global importance of the features and also illustrates how the importance of each feature varies across all data points. Based on these plots, we can conclude that the descriptor ESOL is the most important for accurate predictions, while C-032 has the least importance.

Fig. 4 (a) SHAP summary plot (b) SHAP heat map plot in the SVM model.

3.1.1 Interpretation of the features. The support vector machine (SVM) model has been found to deliver superior outcomes in comparison to other models concerning both training and test set metrics. The importance of the twelve modeled descriptors is demonstrated in Fig. 4 through a SHAP summary and a heat map plot. The mechanistic interpretation of the modeled descriptor in the SVM model and their influence on the response value are discussed below:

ESOL is a molecular property descriptor that represents the estimated solubility parameter (LogS) for aqueous solubility. It is calculated using the consensus octanol–water partition coefficient (LOGPcons).⁶² This descriptor shows the highest importance for predictions made by the model. From Fig. 4, we can see that an increasing value of this feature is positively correlated with an increase in the SHAP value for the data points. This indicates that the feature contributes positively to the response value, meaning that an increasing value of this feature increases the amount of unbound fraction of a chemical substance. The positive contribution of this descriptor can be indicated by the compounds 1247 (ESOL = 3.38, log(1 + f_u) = 2.02), and 1227 (ESOL = 3.33, log(1 + f_u) = 1.94) where compounds have higher ESOL values. The opposite effect can be seen for the compounds where the ESOL values are small such as for compounds 1711 (ESOL = −2.93, log(1 + f_u) = −0.71), 598 (ESOL = −2.93, log(1 + f_u) = −0.83). The compounds with higher aqueous solubility (ESOL values) indicate that the compounds are more hydrophilic and are thus less prone to bind with the plasma proteins increasing the amount of free compounds in the plasma.⁶³

The second most important descriptor is MaxsssN, which is an atom-type E-state (or electrotopological) descriptor that represents the maximum electronic and topological state of the single bonded nitrogen atom in the molecule (>N−). This descriptor contributes positively to the response value which can be represented by the following example: compound 1518 (MaxsssN = 2.08, log(1 + f_u) = 1.11), 1796 (MaxsssN = 2.08, log(1 + f_u) = 0.87), and 1501 (MaxsssN = −0.72, log(1 + f_u) = -0.23). This descriptor increases polar functionality within a molecule and decreases the probability of binding with the plasma protein which in turn increases the free amount in plasma.⁶⁴

The Extended Topochemical Atom (ETA) descriptor Eta_D_epsiB can be utilized to quantify the level of unsaturation within a molecule. The ETA descriptors are derived through an H-suppressed molecular graph, where the vertex holds both the molecular core and its valence electronic environment. This measure of ETA amalgamates the core count and valence electron number to derive topochemical indices. Such a tool is beneficial for understanding the chemical properties of a molecule and its potential applications across various fields. The descriptor Eta_D_epsiB can be represented mathematically as, , where ε₁ indicates the summation of the epsilon value in a molecule relative to the number of all atoms in the molecule, and ε₄ indicate summed epsilon value relative to atoms including hydrogen of the saturated carbon skeleton.⁶⁵ This descriptor shows a negative correlation to the response variable, which can be depicted by the following examples: compound 1601 (Eta_D_epsiB = 5.05, log(1 + f_u) = −0.84), 1525 (Eta_D_epsiB = 4.26, log(1 + f_u) = −0.84), 191 (Eta_D_epsiB = −1.23, log(1 + f_u) = 1.69), and 913 (Eta_D_epsiB = −1.41, log(1 + f_u) = 2.04).

Two other ETA descriptors Eta_D_epsiD (representing the ETA measure of hydrogen bond donor) and Eta_betaS_A (representing the ETA sigma average of the VEM count) show a positive correlation for the response values. The mathematical calculation of the Eta_D_epsiD descriptor can be represented as follows: 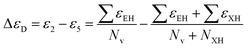, where, ε₂ indicates the sum of the epsilon count of the molecule except hydrogen atom relative to the number of non-hydrogen atoms (giving a measure of electronegative atom count) and ε₅ indicates the sum of the epsilon values of a molecule (for the hydrogen atom, only heteroatoms-connected hydrogen atoms are considered) relative to the number of non-hydrogen atoms and hydrogen atoms connected to the electronegative atom. The Eta_betaS_A descriptor can also be represented mathematically as shown below:

where the ∑β_s is the sum of β values for all sigma bonds and N_v is the number of non-hydrogen atoms. This descriptor gives information about electronegative atom count relative to the molecular size.⁶⁶ Based on the preceding discussion, we can conclude that these two descriptors have a positive impact on the polarity of the molecule. This leads to a decrease in the binding of the chemical compound with plasma protein and an increase in the fraction of free compound, which in turn explains the positive contribution of these descriptors.⁶⁷ The positive contribution can also be depicted by the following examples, where a higher value increases free fraction: 1363 (Eta_D_epsiD = 4.16, log(1 + f_u) = 2.04), 111 (Eta_D_epsiD = 4.11, log(1 + f_u) = 1.96) for Eta_D_epsiD; 1238 (Eta_betaS_A = 2.86, log(1 + f_u) = 1.14), 1223 (Eta_betaS_A = 2.83, log(1 + f_u) = 2.04) for Eta_betaS_A, and vice versa for the compounds 1819 (Eta_D_epsiD = −1.01, log(1 + f_u) = −0.79), 1826 (Eta_D_epsiD = −1.01, log(1 + f_u) = −0.62) for Eta_D_epsiD; 287 (Eta_betaS_A = −3.40, log(1 + f_u) = −0.57), 145 (Eta_betaS_A = −3.50, log(1 + f_u) = −0.52) for Eta_betaS_A.

GD (or graph density) is a constitutional index, and it is used to calculate from the hydrogen-suppressed molecular graph, which can be mathematically represented as follows:

Here, n_Bo is the number of non-hydrogen bonds and n_SK is the number of non-hydrogen atoms. This description refers to the size of the molecule's surface area, where surface area decreases with an increased GD value.⁶⁸ The surface area of a molecule impacts the number of potential binding sites available for interaction with plasma proteins. Molecules with a larger surface area generally have more potential binding sites, which may lead to more extensive binding to plasma proteins. As a result, they may have a higher proportion of the chemical compounds bound to plasma proteins and a lower concentration of free chemical compounds present in circulation. The binding affinity between a chemical molecule and plasma proteins can be influenced by the molecule's surface area. Binding affinity is the strength of the interaction between the molecule and the protein. Molecules with a larger surface area can make more extensive contact with the binding sites on plasma proteins, leading to a stronger binding interaction. When binding affinity is strong, a greater proportion of the molecule remains bound to plasma proteins, resulting in a lower concentration of free portions in plasma.⁶⁹ The positive contribution of this descriptor can be depicted by the compounds with GD value also consisting of high response value – 1385 (GD = 12.80, log(1 + f_u) = 1.92), 1342 (GD = 7.96, log(1 + f_u) = 1.90) and vice versa for the compounds with low GD value 1710 (GD = −1.47, log(1 + f_u) = −0.66), 1711 (GD = −1.47, log(1 + f_u) = −0.71).

The molecular property descriptor, SAscore indicates the synthetic accessibility or ease of synthesis of a molecule. The range of SAscore varies from 1 to 10, where 1 indicates easy to make and 10 indicates very difficult to make. The estimation of the SAscore depends upon fragment contribution and molecular complexity, where molecular complexity indicates the presence large ring, non-standard molecular structure, ring fusion, stereo-complexity, and molecular size.⁷⁰ This descriptor contributes positively to the response value, which may be due to the increase of molecular interaction with an increase in molecular size and structural complexity. The positive contribution can be represented by the following examples – compound 113 (SAscore = 6.38, log(1 + f_u) = 0.84), and 270 (SAscore = −1.86, log(1 + f_u) = −0.83).

Two 2D atom pair descriptors B05[C–N] (indicating the presence or absence of carbon and nitrogen atoms at the topological distance of 5), B03[N–I] (indicating the presence or absence of nitrogen and iodine atoms at the topological distance of 3), and one functional group count descriptor nN+ (representing the number of positively charged nitrogen atoms) contribute positively to the response values. The positive contribution of these descriptors indicates that the presence of these fragments leads to a decrease in the amount of compound binding with plasma protein and an increase in the free fraction of the molecule. These fragments generally increase the polarity of the molecule by introducing polar fragments within the structure which in turn decrease protein binding.⁶⁴ The positive contribution of these descriptors can be represented by the following example: 113 (B05[C–N] = 0.695, log(1 + f_u) = 0.84) and 1712 (B05[C–N] = −1.44, log(1 + f_u) = −0.78) for B05[C–N]; 1555 (B03[N–I] = 10.94, log(1 + f_u) = 2.04) and 1712 (B03[N–I] = −0.091, log(1 + f_u) = −0.78) for B03[N–I]; 1215 (nN+ = 9.47, log(1 + f_u) = 1.06) and 1712 (nN+ = −0.14, log(1 + f_u) = −0.78) for nN+.

The 2D atom pair descriptor B03[C–S] (representing the presence or absence of carbon and sulfur atoms at the topological distance of three) and an atom-centered fragment descriptor C-032 (represents the fragment X–CX–X; where X is any electronegative atom connected to the carbon atom through single bond) contribute negatively to the response value. The negative contribution of these descriptors can be represented by the following example: 1523 (B03[C–S] = 1.88, log(1 + f_u) = 0.053) and 228 (B03[C–S] = −0.53, log(1 + f_u) = 2.04) for B03[C–S]; 1799 (C-032 = 9.32, log(1 + f_u) = −0.78) and 848 (C-032 = 2.99, log(1 + f_u) = 1.36) for C-032.

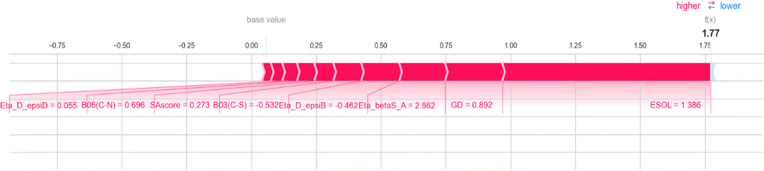
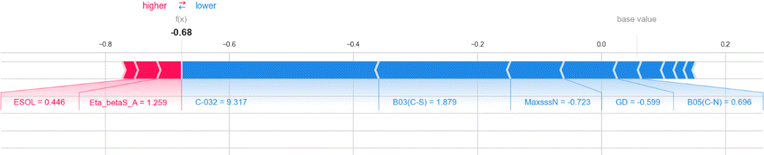
Here, we also represent the feature interpretation through the SHAP local force plot which is shown in Table 2. The local force plot indicates the importance of the feature for the prediction of a particular data point. The positive contribution is indicated by the red color (pushes the model score higher) and the negative contribution (pushes the model score lower) is represented by the blue color. The feature present closer to the separation boundary has the highest importance for the prediction and the impact of that feature is represented by the size of the bar.

Table 2 Interpretation of the feature importance through SHAP local force plot

Descriptor	Force plot	Molecular structure
ESOL
MaxsssN
Eta_D_epsiB
Eta_D_epsiD
Eta_betaS_A
GD
SAscore
B05[C–N]
B03[N–I]
nN+
B03[C–S]
C-032

---

3.1.2 External set predictions. The compounds that had been removed from the data set before the model development due to the response outlier behavior were used for the prediction through the developed models. The results of these predictions were represented through different classification metrics like accuracy, precision, sensitivity, specificity, etc. Here, the predicted and observed values were converted into a binary form based on their mean value, before calculating the classification metrics. Here, we represent these results through a scatter plot, as shown in Fig. 5, and also shown in Table S2.†

Fig. 5 Scatter plot for the results of the external set predicted values.

3.2 Modelling of the hepatocyte intrinsic clearance (Cl_int)

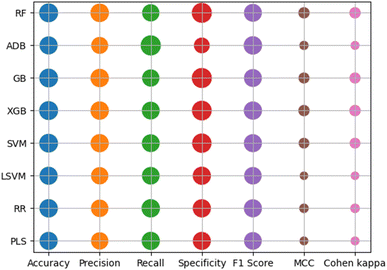
Classification-based machine-learning models were developed for the hepatocyte intrinsic clearance dataset. Here, all the models were developed with the 10 most significant descriptors, and the results for these models are shown in Table 3. Here, all the models were developed with standardized descriptor values. From, these results we can see that all the models show good results but the random forest model has a higher difference between the training set metrics and cross-validation metrics. From the test set quality metrics, we can conclude that the support vector machine (SVM) model shows superior results compared with the other developed machine learning model. Here, all the models were developed at an optimized hyper-parameter setting, where optimization was performed by the GridsearchCV method by considering the accuracy as an objective function. Here, we performed different cross-validation analyses, such as 20 times repetitive 5-fold cross-validation and 1000 times shuffle split cross-validation, to determine whether models are overfitted or not. The results of these cross-validation statistics also help to identify the best learning algorithm. The results of the cross-validation analysis are also included in Table 3 and represented graphically in Fig. S7.† From this figure, we can see that all the models have comparable results in terms of both accuracy and F1 score, and all the methods also have low standard error measure (SEM) values.

Table 3 Results of the machine learning models for Hepatocyte intrinsic clearance data

Modeling method	Data set	Accuracy	Precision	Specificity	Recall	F1-score	MCC	Cohen κ	ROC-AUC	Cross-validation statistics								Hyper-parameters setting
										Repeated 5 fold CV				Shuffle split CV
										Accuracy	Recall	Precision	F1 score	Accuracy	Recall	Precision	F1 score
RF	Training	0.998	0.998	0.998	0.998	0.998	0.996	0.996	1	0.69 ± 0.003	0.70 ± 0.005	0.68 ± 0.005	0.69 ± 0.003	0.68 ± 0.001	0.69 ± 0.001	0.68 ± 0.001	0.68 ± 0.001	{‘criterion’: ‘entropy’, ‘max_depth’: None, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘n_estimators’: 700}
	Test	0.702	0.695	0.701	0.704	0.699	0.405	0.405	0.780
SVM	Training	0.710	0.685	0.660	0.763	0.722	0.424	0.421	0.791	0.66 ± 0.003	0.71 ± 0.005	0.64 ± 0.005	0.67 ± 0.003	0.66 ± 0.001	0.71 ± 0.001	0.64 ± 0.001	0.67 ± 0.001	{‘C’: 1.0, ‘gamma’: ‘scale’, ‘kernel’: ‘rbf’}
	Test	0.709	0.689	0.675	0.743	0.715	0.419	0.418	0.769
LDA	Training	0.660	0.642	0.622	0.699	0.669	0.322	0.321	0.718	0.65 ± 0.003	0.69 ± 0.005	0.64 ± 0.005	0.66 ± 0.004	0.65 ± 0.001	0.69 ± 0.002	0.64 ± 0.001	0.66 ± 0.001	{‘solver’: ‘svd’}
	Test	0.663	0.640	0.605	0.724	0.679	0.331	0.328	0.731
LR	Training	0.675	0.658	0.643	0.708	0.682	0.351	0.350	0.724	0.66 ± 0.003	0.69 ± 0.005	0.64 ± 0.005	0.67 ± 0.003	0.66 ± 0.001	0.69 ± 0.001	0.64 ± 0.001	0.66 ± 0.001	{‘C’: 10.0, ‘penalty’: ‘l1’, ‘solver’: ‘liblinear’}
	Test	0.667	0.649	0.631	0.704	0.675	0.335	0.334	0.734

---

Here, we have also explored the final modeled training and test sets through different similarity-based read-across methods. The read-across predictions were made at the default hyper-parameter settings (σ = 1, γ = 1, CTC = 10) with a classification threshold value of 0.5. The results for the read-across prediction are represented in Table S3 in ESI SI-2† in terms of different classification metrics.

In this analysis, we created learning curves for the Support Vector Machine (SVM) model using accuracy and F1 score as our objective functions, as shown in Fig. S8.† The learning curve was generated by training the model with increasingly larger training sets and testing it on the validation set. From the generated plots, we can see that the learning curve for both the training and validation sets come closer together and reach a plateau as the size of the training set increases when accuracy is the objective function. This indicates that adding more training data will not lead to an improvement in the model performance. The small gap between the training and validation learning curve suggests that the model has low variance error. However, when we use the F1 score as the objective function, the learning curves for both the training and validation sets become similar, indicating the robustness of the model. Here, we also generated a validation curve for the SVM model at different values of the hyper-parameter C. According to the observations made in Fig. S9,† it can be inferred that the score of the training set is significantly higher than the validation set as the value of C increases. This implies that the optimal result is obtained at a lower value of C. Here, we have generated a ROC curve (Fig. 6) for the SVM model and calculated the corresponding ROC-AUC scores for the training and test sets, the scores obtained were 0.79 and 0.77, respectively. These scores are indicative of the model's strong predictive power, which is a desirable characteristic for any model. It is worth noting that the SVM model's performance was found to be consistent across both sets, which suggests that it is capable of generalizing well to new data. These findings serve to highlight the potential utility of the SVM model as a tool for classification tasks in related domains.

Fig. 6 Receiver operating characteristic (ROC) curve for the SVM model (hepatocyte intrinsic clearance data).

The SHAP analysis was performed in this research work to determine the feature importance for the prediction made by the model. Here, the feature importance is represented through the SHAP summary and heatmap plots, which are shown in Fig. 7. From these plots, we can see that the descriptors LOGPcons and N% have the highest importance to the response.

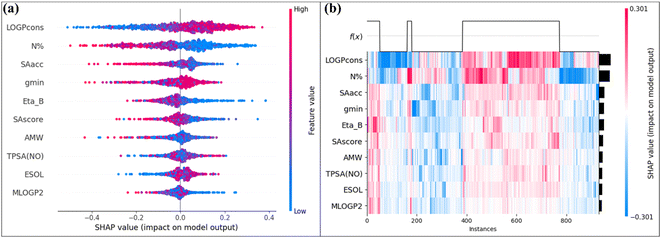Fig. 7 (a) SHAP summary plot (b) SHAP heatmap plot for the SVM model (hepatocyte intrinsic clearance data).

3.2.1 Interpretation of the features. Here, the importance of a feature for a learning algorithm is determined through the SHAP analysis as shown in Fig. 7. The impact of a particular feature on the prediction made by the model is illustrated below:

The molecular property descriptor LOGPcons indicates the octanol–water partition coefficient of a molecule, and it shows a positive effect on the hepatocyte intrinsic clearance. This descriptor provides information about the hydrophobicity of an organic molecule. The ability of a chemical to penetrate through a biological membrane is controlled by its hydrophobicity. An increase in hydrophobicity results in an increase in tissue perfusion of the chemical. Additionally, the metabolic clearance of the chemical by the liver also increases, indicating a positive role of this descriptor.⁷¹ The descriptor N% is a constitutional descriptor that represents the percentage of nitrogen atoms present in the molecule. In the presence of a higher percentage of nitrogen atoms, the polarity of a molecule is enhanced and lipophilicity is reduced. This reduction in lipophilicity leads to a reduction in the metabolic clearance of a molecule which signifies the negative effect of this descriptor.⁷² The descriptor SAacc is a molecular property descriptor that represents the surface area for the H-bond acceptor atom which is obtained from the P_VSA-like descriptors. The electronegative atoms containing loan pairs generally act as hydrogen bond acceptors and contribute to the polarity of a molecule. The negative effect of this descriptor indicates that with an increase in hydrogen bond acceptor atom surface area, the intrinsic clearance of a chemical is reduced. The atom type E-state descriptor gmin represents the minimum atom Electronic state value within the molecule and this descriptor generally represents the polarity of a molecule.⁷³ The ETA descriptor Eta_B represents the measure of the branching index for a particular molecule. The hydrophobicity of molecules decreases as the branching in the molecule is increased. The branched organic molecules are more compact and have a lower surface area compared with unbranched molecules. This decreased hydrophobicity leads to a decrease in the metabolic clearance of the molecule which signifies the negative effect of this descriptor for most of the data points. The descriptor SAscore is a molecular property descriptor that represents the ease of synthesis of a molecule (i.e., the complexity of the molecular structure). The SAscore estimation generally depends on the structure of the fragments present in the molecule. The value of the SAscore increases with an increase in the molecular complexity that is in the presence of a fused ring system, large ring, stereo-complexity, etc. The descriptor AMW belongs to the constitutional indices which indicate the average molecular weight of a molecule across all constituted atoms. This is one of the simplest descriptors that contain information regarding atomic composition. These two descriptors SAscore and AMW generally represent the molecular size, which is a limiting factor for drug metabolism. Both of these descriptors show a negative effect on the hepatocyte clearance. In general, smaller molecules tend to have higher intrinsic clearance rates compared to larger molecules. The reason for this is that larger molecules may have limited access to metabolizing enzymes within hepatocytes or may be metabolized at a slower rate due to their size. Additionally, the size of a molecule can affect its ability to be taken up by hepatocytes and to pass through cell membranes, which can further influence its metabolism and clearance rate.⁷⁴ The molecular property descriptor TPSA(NO) indicates the topological polar surface area which is calculated from the polar contribution of the nitrogen and oxygen atoms. This descriptor is calculated by summing the surface contribution provided by the electronegative atoms. This descriptor can be mathematically represented as follows: , where N_i is the frequency of the ith atom in the molecule and G_iis the surface contribution. The molecular property descriptor ESOL represents the estimated aqueous solubility (LogS) value for a particular molecule. This descriptor is generally derived from the consensus LOGP value of a molecule. The last descriptor MLOGP2 shows the least importance for the model prediction, which indicates the squared logarithmic octanol–water partition coefficient (LogP²) value derived by Moriguchi. This descriptor probably penalizes the LOGPcons term in the model.

3.3 Modeling of the hepatocyte intrinsic clearance (Cl_int) by considering plasma protein binding as a descriptor

Based on eqn S3,† it is apparent that the hepatocyte intrinsic clearance is affected by the binding of a chemical substance to plasma protein. When a chemical substance binds with plasma protein, it results in a reduction of the free substance present in the plasma. It is worth noting that only the unbound portion of a chemical substance can exhibit any pharmacodynamic action or undergo any elimination process such as metabolism or excretion. Consequently, protein binding of a chemical substance leads to a decrease in its clearance and an increase in its residence time within the body. This, in turn, could potentially increase its activity or it also can increase toxicity levels.

Here, the effect of plasma protein binding on the hepatocyte intrinsic clearance of a chemical substance was also explored through different types of classification-based predictive models. The models were developed with the compounds having both types of response parameters and used for the prediction of the compounds having single response values. Here, we developed four different machine learning models namely – random forest (RF), support vector machine (SVM), linear discriminant analysis (LDA), and logistic regression (LR), and all the models were developed with standardized descriptor values. The results of these models are represented in Table 4, in terms of training and test set metrics. Here, all the models were developed with the optimized hyper-parameter setting where optimization was performed by the GridsearchCV method with an accuracy objective function. The optimized hyper-parameter settings for all the developed models are also included in Table 4. From these results, we can conclude that the SVM model shows better results compared with other models, in terms of training, test, and cross-validation results. Here, we also performed a cross-validation analysis like 20 times repetitive and 1000 times shuffle split cross-validation with a 30 percent validation size. This cross-validation analysis helps to identify the quality of the model and also helps to compare the models. These cross-validation results are also included in Table 4, and a comparison of the models is visually represented in Fig. S10,† by considering accuracy and F1 score as the objective functions. From these plots, we can see that the SVM model shows better results compared with other models. In this research work, we also performed the read-across analysis with the final modeled training and test sets. Here, read-across predictions were also made at the default hyper-parameter setting with three similarity methods (ED, GK, LK). The prediction quality is represented in Table S4 of ESI SI-2† in the form of classification metrics. As mentioned above, the data sets contain a large number of compounds having both types of response variables, plasma fraction unbound and hepatocyte intrinsic clearance. On the other hand, there are a total of 987 compounds present that have only one type of response variable (either fraction unbound (784) or hepatocyte intrinsic clearance (203)). Here, we have used these compounds as an external set for prediction through different developed models. The prediction has been made for the compounds that have only plasma protein fraction unbound data, through the developed machine learning models and made available in ESI SI-1.† The compounds with only intrinsic clearance data were also used for the predictions. However, for these compounds, the fraction unbound data is derived from the SVM model for human plasma fraction unbound. These predicted values are also made available in the ESI SI-1 file.† These predicted values were then compared with the experimental value and represented in Table 4 through different classification-based quality metrics.

Table 4 The results of machine learning models for common compounds (for modeling Cl_int by taking f_u as a descriptor)

Modeling method	Data set	Accuracy	Precision	Specificity	Recall	F1-score	MCC	Cohen κ	ROC-AUC	Cross-validation statistics								Hyper-parameter setting
										Repeated 5 fold CV				Shuffle split CV
										Accuracy	Recall	Precision	F1 score	Accuracy	Recall	Precision	F1 score
a External set – compounds (203) having only experimental hepatocyte intrinsic clearance (Clint) data.
RF	Training	1	1	1	1	1	1	1	1	0.68 ± 0.004	0.67 ± 0.005	0.68 ± 0.005	0.68 ± 0.004	0.68 ± 0.001	0.67 ± 0.002	0.68 ± 0.001	0.67 ± 0.001	{‘criterion’: ‘gini’, ‘max_depth’: None, ‘min_samples_leaf’: 1, ‘min_samples_split’: 3, ‘n_estimators’: 250}
	Test	0.713	0.704	0.695	0.731	0.717	0.426	0.425	0.805
	External set^a	0.60	0.65	0.53	0.65	0.65	0.19	0.19	0.65
SVM	Training	0.736	0.714	0.689	0.784	0.746	0.475	0.472	0.820	0.68 ± 0.003	0.73 ± 0.005	0.66 ± 0.005	0.69 ± 0.004	0.67 ± 0.001	0.73 ± 0.001	0.66 ± 0.001	0.69 ± 0.001	{‘C’: 3.0, ‘gamma’: auto, ‘kernel’: ‘rbf’}
	Test	0.697	0.681	0.657	0.739	0.709	0.396	0.395	0.7923
	External set^a	0.66	0.69	0.55	0.75	0.72	0.30	0.30	0.66
LDA	Training	0.659	0.637	0.584	0.735	0.683	0.323	0.319	0.727	0.66 ± 0.004	0.73 ± 0.005	0.64 ± 0.005	0.68 ± 0.004	0.66 ± 0.001	0.73 ± 0.002	0.64 ± 0.001	0.68 ± 0.001	{‘solver’: ‘svd’}
	Test	0.720	0.694	0.657	0.785	0.737	0.445	0.441	0.772
	External set^a	0.69	0.75	0.69	0.70	0.72	0.38	0.38	0.71
LR	Training	0.658	0.633	0.571	0.746	0.685	0.322	0.317	0.714	0.65 ± 0.004	0.74 ± 0.005	0.63 ± 0.005	0.67 ± 0.004	0.65 ± 0.001	0.74 ± 0.002	0.63 ± 0.001	0.68 ± 0.001	{‘C’: 0.1, ‘penalty’: ‘l1’, ‘solver’: ‘saga’}
	Test	0.709	0.683	0.641	0.777	0.727	0.422	0.418	0.745
	External set^a	0.65	0.69	0.57	0.71	0.70	0.28	0.28	0.68

---

Here, we also generated learning curves for the SVM model with accuracy and F1 score as objective functions which are shown in Fig. S11.† From, these plots we can see that the training and validation curves become linear and closer to each other with an increase in the training size. This suggests that adding more training data is not going to improve the performance of the model. The small gap between the training and validation curves also indicates the quality of the developed model. The learning curves for the training and validation sets with the F1 scoring function look similar which also indicates the good quality of the model. Here, we also generated validation curves for the SVM model at the varying values of the parameter C, which is shown in Fig. S12.† From these plots, we can see that the difference between the scoring function for training and the validation curves increases with an increasing value of C, which suggests that the model becomes robust at the lower value of C. For the SVM model, we also generated a ROC curve and calculated the corresponding AUC-ROC score for both training and test sets, as shown in Fig. 8. The obtained AUC-ROC scores for the training and test sets are 0.82 and 0.79 which suggest that the models have good predictive power.

Fig. 8 Receiver operating characteristic (ROC) curves for the SVM model (for modeling Cl_int by taking f_u as a descriptor).

Here, we also performed the SHAP analysis to determine the importance of the features for the response parameter. The feature importance is represented in Fig. 9, in the form of a SHAP summary and a heatmap plot. From these plots, we can see that the plasma protein binding (log(1 + f_u)) has the highest importance for the clearance. The plot analysis signifies that protein binding exerts a significant limiting effect on clearance. This observation underscores the importance of protein binding in the context of metabolism and elimination. Specifically, the study highlights the negative correlation between protein binding and clearance rate. Here, other descriptors like LOGPcons, mindssC (atom type E-state indices that represent the minimum electronic state of double bond–single bond–single bond C atoms), ESOL, and gmin show positive contributions and the descriptors like Eta_B and SAacc show negative contributions.

Fig. 9 SHAP plots for the SVM model (for modeling Cl_int by taking f_u as a descriptor).

3.4 Comparison with the previous studies

Previously a large number of attempts^{25,27,29,75–80} were made to develop different predictive models for the analysis of the plasma protein binding and hepatocyte intrinsic clearance. Most of the models were developed with a large number of descriptors and fewer number of data points. Here, we perform a comparative analysis between our developed models and previously developed models. A proper comparison of the present study with the previous work is difficult due to the difference in training and test set composition, modeling algorithm, and method. However, here we represent the developed regression and classification models for plasma protein fraction unbound (f_u) and hepatocyte intrinsic clearance (Cl_int) human data (Table 5), reported by different groups. From Table 5, we can conclude that the developed classification and regression models perform better compared with the previously developed models. The main advantage of our model is that the models are simple, interpretable, and reproducible. The developed models also comply with the OECD norms which indicates their reliability for further use in the analysis of a new chemical compound.

Table 5 Comparison of the present study with previously reported models

PK parameter	Author	Model type	Modelling algorithm	Data set composition	n des	Metrics
Protein binding	Ingle et al.^75	Regression (fu)	Random forest (best model)	n training = 1045, ntest = 606	10	Training set: R^2 = 0.52, MAE = 0.146, RMSE = 0.214
						Test set: R^2 = 0.51, MAE = 0.131, RMSE = 0.218
	Watanabe et al.^76	Regression (fu)	Support vector machine (best model)	n training = 2192, ntest = 546	391	Test set: R^2 = 0.73, MAE = 0.100, RMSE = 0.145
	Esaki et al.^25	Regression (unbound fraction of drug in the brain [fu, brain])	Gradient boost (best model)	n train = 144, ntest = 36	53	Cross-validated: R^2 = 0.64, RMSE = 0.48
						Test set: R^2 = 0.63, RMSE = 0.48
	Sun et al.^77	Regression (modeling of protein binding parameter, fb)	Random forest (best model)	n train = 967, ntest = 870 (3 merged test set)	26	Cross-validation (10-fold CV): R^2 = 0.76, RMSE = 0.17, MAE = 0.13
						Test set (overall): R^2 = 0.59, RMSE = 0.18, MAE = 0.13
	Zhivkova et al.^27	Regression (fu)	Linear regression	— (the whole data set contains 132 acidic drugs)	16	Training set: R^2 = 0.771, q^2 = 0.737
	Present study	Regression	Support vector machine	n train = 1088, n test = 362	12	R ^2 = 0.75, Q LOO ^2 = 0.69, MAE = 0.32, Q F1 ^2 = 0.75, Q F2 ^2 = 0.75
Hepatocyte intrinsic clearance	Paixão et al.^29	Regression (Clint)	Artificial neural network	n train = 71, ntest = 18	21	Training correlation = 0.953, training RMSE = 0.236
						Test correlation = 804, test RMSE = 0.544
	Pirovano et al.^78	Regression (Clint)	Linear regression	n train = 79, ntest = 39	5	R adj ^2 = 0.67, QLOO^2 = 0.62, RMSELOO = 0.76, Rext^2 = 0.62, RMSEext = 0.80
	Ekins and Obach^79	Regression (Clint)	Multiple linear regression	n train = 18, ntest = 26	4	R ^2 = 0.88, RMSE = 0.28, Rext^2 = 0.79
	Li et al.^80	Regression (Clint)	Multiple linear regression	n train = 36, ntest = 13	13	R ^2 = 0.85, RMSE = 0.28, Rext^2 = 0.73
	Present study	Classification (Cl int )	Support vector machine	n train = 932, n test = 309	10	Training set: recall = 0.76, specificity = 0.66, accuracy = 0.71, precision = 0.68
						Test set: recall = 0.74, specificity = 0.68, accuracy = 0.71, precision = 0.69

---

The data we have used in our study was published recently (November 2022)⁸¹ and no QSAR modelling work on this data has been published yet (as far as our knowledge goes). Therefore, we have used the standard machine-learning (ML) algorithms to correlate the endpoints with the structural features and developed predictive models. In this present study, our main motive was not only to develop ML-based QSAR models but also to extract the important structural features from the present data set which are responsible for the variation in the endpoint values. The parameters fraction unbound (f_u) and hepatic intrinsic clearance (Cl_int) are complex and multifactorial endpoints. They are influenced by a number of factors including physiological, pharmacological, and biochemical elements. Attempting to model these endpoints solely based on structural features is challenging due to the intricate interplay of these various influences. Also, here we have used large data sets of diverse compounds for the modeling purpose. Considering the complexity of the endpoints and the large number of compounds used for modeling, the performance of the developed models is satisfactory. Further, we have also developed a Python-based tool that can predict the modeled endpoints (f_u and Cl_int) for new or unknown chemicals using the best (SVM) models. This tool is now available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home/pkpy-tool.

4. Conclusion

The length of time that a chemical substance stays in the body is determined by various pharmacokinetic parameters. The two main parameters that control this are plasma protein binding and hepatocyte clearance through metabolism. In this research study, we have analyzed these two parameters using different machine-learning models. For plasma protein binding, we took into account the fraction of the free portion (f_u) of a chemical present in the plasma, and for hepatocyte clearance, we analyzed the parameter hepatocyte intrinsic clearance (Cl_int). We developed 8 different regression-based models for the f_u endpoint and 4 different classification-based models for the Cl_int endpoint. After conducting statistical analyses, it was found that all of the models performed exceptionally well in terms of both internal and external validation metrics. These results indicate that the models are reliable and accurate in their predictions. The internal validation metrics suggest that the models are performing well on the data used to train them, while the external validation metrics show that the models can generalize to new data. These findings demonstrate the high quality of the models and their potential to be used in various applications. In the current research work, we conducted a comprehensive analysis to investigate the effect of protein binding on hepatocyte intrinsic clearance. To accomplish this, we employed different classification-based machine learning algorithms, which enabled us to examine the relationship between protein binding and clearance rates in greater detail.

Data and software availability

The structural information of the compounds for all three series of models are available in ESI SI-3.† The machine learning modeling tools used in this work are available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home/machine-learning-model-development-guis?authuser=0. The input files for machine learning model development are provided in ESI SI-1.† The developed prediction tool is available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home/pkpy-tool. The codes for the best models are available from https://github.com/004Souvik/Pharmacokinetic-properties.

Author contributions

SP: computation, validation, software tool development, initial draft; KR: conceptualization, supervision, and editing.

Conflicts of interest

The authors declare no conflict of interest.

References

1. L. B. Sheiner and J. L. Steimer, Pharmacokinetic/pharmacodynamic modeling in drug development, Annu. Rev. Pharmacol. Toxicol., 2000, 40, 67–95.
2. H. Derendorf, L. J. Lesko, P. Chaikin, W. A. Colburn, P. Lee, R. Miller, R. Powell, G. Rhodes, D. Stanski and J. Venitz, Pharmacokinetic/pharmacodynamic modeling in drug research and development, J. Clin. Pharmacol., 2000, 40, 1399–1418.
3. K. J. Himmelstein and R. J. Lutz, A review of the applications of physiologically based pharmacokinetic modeling, J. Pharmacokinet. Biopharm., 1979, 7, 127–145.
4. A. M. Ahmad, Recent advances in pharmacokinetic modeling, Biopharm. Drug Dispos., 2007, 28, 135–143.
5. F. Yamashita and M. Hashida, In silico approaches for predicting ADME properties of drugs, Drug Metab. Pharmacokinet., 2004, 19, 327–338.
6. L. Di and E. H. Kerns, Drug-like properties: concepts, structure design and methods from ADME to toxicity optimization, Academic Press, U.K, 2015.
7. J. Tibbitts, D. Canter, R. Graff, A. Smith and L. A. Khawli, Key factors influencing ADME properties of therapeutic proteins: A need for ADME characterization in drug discovery and development, MAbs, 2016, 8, 229–245.
8. N. A. Kratochwil, W. Huber, F. Müller, M. Kansy and P. R. Gerber, Predicting plasma protein binding of drugs: a new approach, Biochem. Pharmacol., 2002, 64, 1355–1374.
9. T. Bohnert and L. S. Gan, Plasma protein binding: from discovery to development, J. Pharm. Sci., 2013, 102, 2953–2994.
10. R. E. Olson and D. D. Christ, Plasma protein binding of drugs, Annu. Rep. Med. Chem., 1996, 31, 327–336.
11. S. Schmidt, D. Gonzalez and H. Derendorf, Significance of protein binding in pharmacokinetics and pharmacodynamics, J. Pharm. Sci., 2010, 99, 1107–1122.
12. D. Kalamaridis and N. Patel, Assessment of drug plasma protein binding in drug discovery, Optimization in Drug Discovery: In Vitro Methods, Humana Press, Totowa, NJ, 2014, pp. 21–37.
13. J. A. Roberts, F. Pea and J. Lipman, The clinical relevance of plasma protein binding changes, Clin. Pharmacokinet., 2013, 52, 1–8.
14. G. Lambrinidis, T. Vallianatou and A. Tsantili-Kakoulidou, In vitro, in silico and integrated strategies for the estimation of plasma protein binding. A review, Adv. Drug Delivery Rev., 2015, 86, 27–45.
15. D. A. Smith, K. Beaumont, T. S. Maurer and L. Di, Clearance in drug design: miniperspective, J. Med. Chem., 2018, 62, 2245–2255.
16. M. I. Jordan and T. M. Mitchell, Machine learning: Trends, perspectives, and prospects, Science, 2015, 349, 255–260.
17. I. H. Sarker, Machine learning: Algorithms, real-world applications and research directions, SN Comput. Sci., 2021, 2, 160.
18. T. Wuest, D. Weimer, C. Irgens and K. D. Thoben, Machine learning in manufacturing: advantages, challenges, and applications, Prod. Manuf. Res., 2016, 4, 23–45.
19. S. Pore, A. Banerjee and K. Roy, Machine Learning-Based q-RASPR Modeling of Power Conversion Efficiency of Organic Dyes in Dye-Sensitized Solar Cells, Sustainable Energy Fuels, 2023, 7, 3412–3431.
20. K. Roy, S. Kar and R. N. Das, Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment, Academic Press, NY, 2015.
21. E. N. Muratov, J. Bajorath, R. P. Sheridan, I. V. Tetko, D. Filimonov, V. Poroikov, T. I. Oprea, I. I. Baskin, A. Varnek, A. Roitberg and O. Isayev, QSAR without borders, Chem. Soc. Rev., 2020, 49, 3525–3564.
22. A. Banerjee, M. Chatterjee, P. De and K. Roy, Quantitative predictions from chemical read-across and their confidence measures, Chemom. Intell. Lab. Syst., 2022, 227, 104613.
23. M. Chatterjee, A. Banerjee, P. De, A. Gajewicz-Skretna and K. Roy, A novel quantitative read-across tool designed purposefully to fill the existing gaps in nanosafety data, Environ. Sci.: Nano, 2022, 9, 189–203.
24. Y. E. Yun, R. Tornero-Velez, S. T. Purucker, D. T. Chang and A. N. Edginton, Evaluation of quantitative structure property relationship algorithms for predicting plasma protein binding in humans, Comput. Toxicol., 2021, 17, 100142.
25. T. Esaki, R. Ohashi, R. Watanabe, Y. Natsume-Kitatani, H. Kawashima, C. Nagao and K. Mizuguchi, Computational model to predict the fraction of unbound drug in the brain, J. Chem. Inf. Model., 2019, 59, 3251–3261.
26. S. Ryu, D. Tess, G. Chang, C. Keefer, W. Burchett, G. S. Steeno, J. J. Novak, R. Patel, K. Atkinson, K. Riccardi and L. Di, Evaluation of fraction unbound across 7 tissues of 5 species, J. Pharm. Sci., 2020, 109, 1178–1190.
27. Z. Zhivkova and I. Doytchinova, Quantitative structure—plasma protein binding relationships of acidic drugs, J. Pharm. Sci., 2012, 101, 4627–4641.
28. M. Riedl, S. Mukherjee and M. Gauthier, Descriptor-Free Deep Learning QSAR Model for the Fraction Unbound in Human Plasma, Mol. Pharmaceutics, 2023, 20, 4984–4993.
29. P. Paixão, L. F. Gouveia and J. A. Morais, Prediction of the in vitro intrinsic clearance determined in suspensions of human hepatocytes by using artificial neural networks, Eur. J. Pharm. Sci., 2010, 39, 310–321.
30. A. K. Sohlenius-Sternbeck, L. Afzelius, P. Prusis, J. Neelissen, J. Hoogstraate, J. Johansson, E. Floby, A. Bengtsson, O. Gissberg, J. Sternbeck and C. Petersson, Evaluation of the human prediction of clearance from hepatocyte and microsome intrinsic clearance for 52 drug compounds, Xenobiotica, 2010, 40, 637–649.
31. F. Lombardo, J. Bentzien, G. Berellini and I. Muegge, Prediction of Human Clearance Using In Silico Models with Reduced Bias, Mol. Pharmaceutics, 2024, 21, 1192–1203.
32. K. Nikolic and D. Agababa, Prediction of hepatic microsomal intrinsic clearance and human clearance values for drugs, J. Mol. Graphics Modell., 2009, 28, 245–252.
33. A. Mauri, alvaDesc: A Tool to Calculate and Analyze Molecular Descriptors and Fingerprints, in Ecotoxicological QSARs. Methods in Pharmacology and Toxicology, ed. K. Roy, Humana, New York, NY, 2020.
34. D. S. Cao, Y. Z. Liang, Q. S. Xu, H. D. Li and X. Chen, A new strategy of outlier detection for QSAR/QSPR, J. Comput. Chem., 2010, 31, 592–602.
35. G. M. Maggiora, On outliers and activity cliffs why QSAR often disappoints, J. Chem. Inf. Model., 2006, 46, 1535.
36. A. Tropsha, Best practices for QSAR model development, validation, and exploitation, Mol. Inf., 2010, 29, 476–488.
37. A. Banerjee and K. Roy, Prediction-inspired intelligent training for the development of classification read-across structure–activity relationship (c-RASAR) models for organic skin sensitizers: assessment of classification error rate from novel similarity coefficients, Chem. Res. Toxicol., 2023, 36, 1518–1531.
38. P. Gramatica, Principles of QSAR models validation: internal and external, QSAR Comb. Sci., 2007, 26, 694–701.
39. P. M. Khan and K. Roy, Current approaches for choosing feature selection and learning algorithms in quantitative structure–activity relationships (QSAR), Expert Opin. Drug Discovery, 2018, 13, 1075–1089.
40. M. Goodarzi, B. Dejaegher and Y. V. Heyden, Feature selection methods in QSAR studies, J. AOAC Int., 2012, 95, 636–651.
41. F. G. Blanchet, P. Legendre and D. Borcard, Forward selection of explanatory variables, Ecology, 2008, 89, 2623–2632.
42. S. H. Unger, Consequences of the Hansch paradigm for the pharmaceutical industry, Med. Chem., 1980, 9, 47–119.
43. S. Derksen and H. J. Keselman, Backward, forward and stepwise automated subset selection algorithms: Frequency of obtaining authentic and noise variables, Br. J. Stat. Psychol., 1992, 45, 265–282.
44. M. Shahlaei, Descriptor selection methods in quantitative structure-activity relationship studies: a review study, Chem. Rev., 2013, 113, 8093–8103.
45. S. Yousefinejad and B. Hemmateenejad, Chemometrics tools in QSAR/QSPR studies: A historical perspective, Chemom. Intell. Lab. Syst., 2015, 149, 177–204.
46. P. Ghosh and M. C. Bagchi, QSAR modeling for quinoxaline derivatives using genetic algorithm and simulated annealing based feature selection, Curr. Med. Chem., 2009, 16, 4032–4048.
47. R. Leardi, Genetic algorithms in feature selection, in Genetic algorithms in molecular modeling, Academic Press, 1996.
48. I. S. Oh, J. S. Lee and B. R. Moon, Hybrid genetic algorithms for feature selection, IEEE Trans. Pattern Anal. Mach. Intell., 2004, 26, 1424–1437.
49. D. Rogers and A. J. Hopfinger, Application of genetic function approximation to quantitative structure-activity relationships and quantitative structure-property relationships, J. Chem. Inf. Comput. Sci., 1994, 34, 854–866.
50. J. Roy, S. Pore and K. Roy, Prediction of cytotoxicity of heavy metals adsorbed on nano-TiO2 with periodic table descriptors using machine learning approaches, Beilstein J. Nanotechnol., 2023, 14, 939–950.
51. V. Svetnik, A. Liaw, C. Tong, J. C. Culberson, R. P. Sheridan and B. P. Feuston, Random forest: a classification and regression tool for compound classification and QSAR modeling, J. Chem. Inf. Comput. Sci., 2003, 43, 1947–1958.
52. B. H. Menze, B. M. Kelm, R. Masuch, U. Himmelreich, P. Bachert, W. Petrich and F. A. Hamprecht, A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data, BMC Bioinf., 2009, 10, 1–16.
53. B. Gregorutti, B. Michel and P. Saint-Pierre, Correlation and variable importance in random forests, Stat. Comput., 2017, 27, 659–678.
54. A. Géron, Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow, O'Reilly Media, Inc., USA, 2022.
55. T. Chen and C. Guestrin, Xgboost: A scalable tree boosting system, in Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 2016, pp. 785–794.
56. S. Suthaharan and S. Suthaharan, Support vector machine. Machine learning models and algorithms for big data classification: thinking with examples for effective learning, Boston, MA, 2016, pp. 207–235.
57. P. Xanthopoulos, P. M. Pardalos, T. B. Trafalis, P. Xanthopoulos, P. M. Pardalos and T. B. Trafalis, Linear discriminant analysis, Robust data mining, New York, NY, 2013, pp. 27–33.
58. T. G. Nick and K. M. Campbell, Logistic regression, Topics in biostatistics, Humana Press, 2007, pp. 273–301.
59. L. Shapley, A Value for n-Person Games. Contributions to the Theory of Games II (1953) 307-317, Classics in Game Theory, ed. H. W. Kuhn, Princeton University Press, 1997, pp. 69–79.
60. S. M. Lundberg and S. I. Lee, A unified approach to interpreting model predictions, Adv. Neural Inf. Process. Syst., 2017, 30, 4765–4774.
61. R. Rodríguez-Pérez and J. Bajorath, Interpretation of machine learning models using shapley values: application to compound potency and multi-target activity predictions, J. Comput.-Aided Mol. Des., 2020, 34, 1013–1026.
62. J. S. Delaney, ESOL: estimating aqueous solubility directly from molecular structure, J. Chem. Inf. Comput. Sci., 2004, 44, 1000–1005.
63. M. J. Waring, Lipophilicity in drug discovery, Expert Opin. Drug Discovery, 2010, 5, 235–248.
64. R. G. Efremov, A. O. Chugunov, T. V. Pyrkov, J. P. Priestle, A. S. Arseniev and E. Jacoby, Molecular lipophilicity in protein modeling and drug design, Curr. Med. Chem., 2007, 14, 393–415.
65. K. Roy and R. N. Das, On some novel extended topochemical atom (ETA) parameters for effective encoding of chemical information and modeling of fundamental physicochemical properties, SAR QSAR Environ. Res., 2011, 22, 451–472.
66. K. Roy, Quantitative structure-activity relationships in drug design, predictive toxicology, and risk assessment, IGI Global, 2015.
67. P. Chène, Drugs targeting protein–protein interactions, ChemMedChem, 2006, 1, 400–411.
68. J. G. Krishna, P. K. Ojha, S. Kar, K. Roy and J. Leszczynski, Chemometric modeling of power conversion efficiency of organic dyes in dye sensitized solar cells for the future renewable energy, Nano Energy, 2020, 70, 104537.
69. J. Chen, N. Sawyer and L. Regan, Protein–protein interactions: General trends in the relationship between binding affinity and interfacial buried surface area, Protein Sci., 2013, 22, 510–515.
70. P. Ertl and A. Schuffenhauer, Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions, J. Cheminf., 2009, 1, 1–11.
71. M. Baker and T. Parton, Kinetic determinants of hepatic clearance: plasma protein binding and hepatic uptake, Xenobiotica, 2007, 37, 1110–1134.
72. S. Hurst, C. M. Loi, J. Brodfuehrer and A. El-Kattan, Impact of physiological, physicochemical and biopharmaceutical factors in absorption and metabolism mechanisms on the drug oral bioavailability of rats and humans, Expert Opin. Drug Metab. Toxicol., 2007, 3, 469–489.
73. L. B. Kier and L. H. Hall, Database organization and searching with E-state indices, SAR QSAR Environ. Res., 2001, 12, 55–74.
74. D. A. Smith, K. Beaumont, T. S. Maurer and L. Di, Clearance in drug design: miniperspective, J. Med. Chem., 2018, 62, 2245–2255.
75. B. L. Ingle, B. C. Veber, J. W. Nichols and R. Tornero-Velez, Informing the human plasma protein binding of environmental chemicals by machine learning in the pharmaceutical space: applicability domain and limits of predictability, J. Chem. Inf. Model., 2016, 56, 2243–2252.
76. R. Watanabe, T. Esaki, H. Kawashima, Y. Natsume-Kitatani, C. Nagao, R. Ohashi and K. Mizuguchi, Predicting fraction unbound in human plasma from chemical structure: improved accuracy in the low value ranges, Mol. Pharmaceutics, 2018, 15, 5302–5311.
77. L. Sun, H. Yang, J. Li, T. Wang, W. Li, G. Liu and Y. Tang, In silico prediction of compounds binding to human plasma proteins by QSAR models, ChemMedChem, 2018, 13, 572–581.
78. A. Pirovano, S. Brandmaier, M. A. Huijbregts, A. M. Ragas, K. Veltman and A. J. Hendriks, QSARs for estimating intrinsic hepatic clearance of organic chemicals in humans, Environ. Toxicol. Pharmacol., 2016, 42, 190–197.
79. S. Ekins and R. S. Obach, Three-dimensional quantitative structure activity relationship computational approaches for prediction of human in vitro intrinsic clearance, J. Pharmacol. Exp. Ther., 2000, 295, 463–473.
80. H. Li, J. Sun, X. Sui, J. Liu, Z. Yan, X. Liu, Y. Sun and Z. He, First-principle, structure-based prediction of hepatic metabolic clearance values in human, Eur. J. Med. Chem., 2009, 44, 1600–1606.
81. A. B. Daniel, N. Choksi, J. Abedini, S. Bell, P. Ceger, B. Cook, A. L. Karmaus, J. Rooney, K. T. To, D. Allen and N. Kleinstreuer, Data curation to support toxicity assessments using the Integrated Chemical Environment, Front. Toxicol., 2022, 4, 987848.

---

Footnote

† Electronic supplementary information (ESI) available: The raw data files used to develop the models are provided in SI-1. Some details of the methods and results are provided in SI-2. The structural information of the compounds are provided in SI-3. See DOI: https://doi.org/10.1039/d4dd00082j

---