Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Every atom counts: predicting sites of reaction based on chemistry within two bonds†
Ching Ching
Lam
 and
Jonathan M.
Goodman
and
Jonathan M.
Goodman
 *
*
Yusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK. E-mail: jmg11@cam.ac.uk
First published on 16th August 2024
Abstract
How much chemistry can be described by looking only at each atom, its neighbours and its next-nearest neighbours? We present a method for predicting reaction sites based only on a simple, two-bond model. Machine learning classification models were trained and evaluated using atom-level labels and descriptors, including bond strength and connectivity. Despite limitations in covering only local chemical environments, the models achieved over 80% accuracy even with challenging datasets that cover a diverse chemical space. Whilst this simplistic model is necessarily incomplete, it describes a large amount of interesting chemistry.
1 Introduction
The growth in the application of machine learning models in predicting chemical reactivity has brought numerous challenges in model construction to light.1–5 One such challenge is formulating representations of chemical reactions or reacting molecules for machine learning.6–8 The optimal representations should be interpretable by computers while covering the traits of the chemical system relevant to the target property to be predicted by the model.The most common approach involves treating each reaction or set of reacting molecules as a single entity, where the descriptors are derived or calculated at the molecular level.9,10 Multiple fingerprint features are commonly used in machine learning for their robustness and applicability in dealing with a wide range of chemistry problems.11 Besides fingerprints, computed and experimental physiochemical parameters that quantify electric and steric factors at the molecular level have also proven effective.12 For example, Aspuru-Guzik and Balcells et al.13 have used topological descriptors in training Bayesian-optimised artificial neural networks to predict the activation energy of reactions catalysed by Vaska's complex. In the work of Phipps and Sigman et al.,14 the multivariate linear regression based on a combination of physiochemical descriptors helps to identify high-yielding substrates for Minisci reactions. Text-based representations of molecules can also be utilised in machine learning to predict reactivity. The molecular transformer model from Lee et al.,15 where SMILES strings are tokenised for the training process, can suggest potential products of organic reactions. Our group has recently applied the T5Chem model from Zhang et al.16 in predicting reaction outcomes of C–H borylation.17
Using molecular-level representations necessitates the availability of extensive datasets, ideally comprising thousands of reactions. This not only introduces the challenge of data scarcity but also underscores the need to uphold quality during data gathering.18–20 The development of Chematica from Grzybowski et al. and Merck (under the name Synthia™) also show that AI-driven methods alone do not seem to work as well as hand-derived rules.21,22 Chematica is a synthesis planning software that adopts a hybrid approach, using machine learning algorithms and expert knowledge based on 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 manually derived reaction types. What are the limits of pure machine learning methods? We will investigate in this work.
000 manually derived reaction types. What are the limits of pure machine learning methods? We will investigate in this work.
Building from our previous work,23–25 this paper takes a different approach to predicting chemical reactivity. Atomistic approaches, or atomic fingerprint representations, have been explored in the construction of machine-learning potentials and for treating inorganic lattice structures.26–29 Within organic chemistry, Jensen et al. have utilized atomic-based descriptors for predicting the regioselectivity of electrophilic aromatic substitution reactions.30 This project is founded on the hypothesis that the reactivity of an atom can be predicted if we have adequate knowledge about the atom and its local environment within the molecule, specifically within a range two bonds to the atom. This is a simplistic approach, and we investigate it not because we think it will explain all of chemistry, but because we want to find out how far it can get. Here, machine learning models are trained on descriptors and labels designed for the individual atoms within a molecule. Such an approach allows the exploration of data-driven methods on a relatively small dataset. Even with a dataset containing only a hundred reactions, the number of descriptors is likely to be in the thousands as it is the product of the number of atoms and the number of reactions. Evaluations were conducted on various datasets with varying complexity and diversity in chemical space. This allowed us to discover the extent to which this simple model had the capacity to encompass a substantial portion of reactivity within the chemical space of three types of reaction datasets. The outcome of the investigation, models for predicting sites of reaction, is useful for providing insights into the molecule reactivity and hinting at the possible transformations.
2 Methodology
2.1 Data
| Type | Dataset | No. of reactions | No. of sets reactions with the same reactants (i.e. competitive pathways) | Average no. of atoms in the reactants | Average no. of non-H atoms in the reactants |
|---|---|---|---|---|---|
| A | First-year | 147 | 108 | 23 | 10 |
| B | [3 + 2] cycloaddition | 5953 | 2869 | 43 | 23 |
| B | Diels–Alder reaction | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 011 011 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 394 394 |
47 | 25 |
| C | RGD1 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 281 281 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 428 428 |
17 | 8 |
| C | Green | 321 | 252 | 13 | 7 |
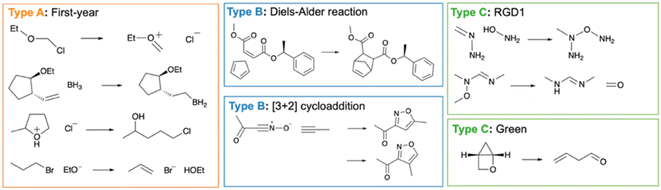
Type A reaction datasets were manually generated based on the contents of the first-year organic chemistry lecture course at the University of Cambridge.31 The first-year dataset was directly handpicked from the lecture handouts. The dataset comprises 147 reactions in total, including nucleophilic substitution, nucleophilic addition, elimination, enolisation and proton transfer (Fig. 2).
Type B reaction datasets comprise the computational dataset of [3 + 2] cycloaddition generated by Coley et al.32 and the Diels–Alder reaction dataset collected by Tang et al.33 We took the all [3 + 2] cycloaddition reactions and all training Diels–Alder reactions from the original datasets for data processing.
Type C reaction datasets include the Reaction Graph Depth 1 (RGD1) dataset from Savoie et al.34 and the elementary chemical reactions dataset from Green et al. (referred to as ‘the Green dataset’ below).35 These datasets were generated in an automated fashion with programmed methods. RGD1 dataset uses the graphically defined elementary reaction step method to explore the chemical space and enumerate the reactions.36,37 The Green dataset relies on the growing string method to explore the potential energy surface and find the reaction pathways.38–40 For this investigation, we filtered both datasets to ensure that the reactions are thermodynamically favourable (i.e. ΔHr < 0 kcal mol−1) with a low kinetic barrier (i.e. activation energy, EA <40 kcal mol−1) so that these reactions are feasible at room temperature. The selected RGD1 and Green reactions correspond to 6.5 and 6.4% of the original dataset respectively.
On each dataset, reactions with identical reactants (i.e. all components on the reactant side must be the same) were grouped together to account for competitive pathways. The SMILES strings of the reactants were converted to InChI to identify instances of the same reactant. Additionally, a few reactions contain molecules that cannot be processed by functions related to 3D structure generation in RDKit. These reactions were also filtered out from each dataset. See ESI Section 1.1† for the details. In the Diels–Alder dataset, reactions with hypervalent molecules and placeholder atoms were also removed.
We carried out atom-to-atom mapping, a procedure that matches atoms in the reactants to atoms in the products, on reactions in the first-year and Diels–Alder reaction datasets. The [3 + 2] addition dataset includes mapping information for the non-hydrogen atoms. Thus, atom-to-atom mapping was carried out on the hydrogen atoms only. All atoms in reactions of RGD1 and Green dataset have been mapped, where the reaction SMILES strings already contain the atom indexing. RXNMapper,41 a transformer neural network model explicitly designed for atom-to-atom mapping, was employed to map non-hydrogen atoms. Subsequently, the hydrogen atoms were mapped based on the mapping of the non-hydrogen atoms. As all reactions are elementary, we assumed that no more than one hydrogen atom has changed its connectivity. The atom mapping from RXNMapper is not always perfect but has achieved the highest accuracy in a recent benchmarking study.42 Schwaller et al. reported an 85% accuracy for RXNMapper,41 tested on the USPTO data. Therefore, all the mapped first-year reaction SMILES strings were checked. Three out of 147 reactions had mapping errors, which were subsequently corrected manually. For the Diels–Alder reaction datasets, we manually checked the mapping result in 100 reactions. Errors were found in eight out of 100 reactions. Thus, we assumed that errors are presented in 8% of the reactions in the Diels–Alder dataset.
The sequential steps described below were executed on each dataset individually. Within each set of reactions sharing the same reactants, the atoms were renumbered via GetSubstructMatch from RDkit to ensure consistent atom numbering while considering the atom-to-atom mapping result. GetSubstructMatch was unable to map match tautomer structures with difference connectivity. On rare occasions, reactions are grouped together as competitive pathways because reactants are tautomer of each other. This is an artefact of using InChI strings. Reactions in this situation were removed from the dataset.
2.2 Reactive site prediction model
In this project, the model is built on the assumption that a comprehensive understanding of an atom and its local chemical environment enables the prediction of its reactivity. Thus, the descriptors and labels are based on individual atoms. The descriptors for an atom were computed based on the reactant molecule only, while its label came from analysing reaction SMILES strings of competitive pathways involving the reactants. | ||
| Fig. 3 Illustrating the derivation of the ‘one-bond’, ‘two-bond’ and ‘two-bond +’ descriptor array for an oxygen atom in an example molecule. | ||
An ‘one-bond’ descriptor array contains features on
• Atom nature: this includes the group and period of the corresponding element and specifies whether the atom belongs to one of the key organic elements (i.e. H, C, N, O, B, F, Cl, Br, Si, P or S).
• Self-connectivity: this part of the descriptor array specifies the number of key organic element atoms among its neighbours and the total number of neighbouring atoms.
A ‘two-bond’ descriptor array includes:
• All features in the ‘one-bond’ descriptor array.
• Neighbours' connectivity: in accordance with the assumption that an atom has a maximum of 4 neighbours, this part of the descriptor array incorporates the self-connectivity descriptor arrays of the neighbouring atoms. Information of the neighbouring atoms was sorted according to their atomic number from high to low in the descriptor array.
A ‘two-bond +’ descriptor array includes:
• All features in the ‘two-bond’ descriptor array.
• Bond strength: Guided by the MolE8 analysis,23 we classify bonds into 86 classes which was calculated from a dataset of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules from ChEMBL-28 with the structure optimised by MMFF (ESI Section 2†).43 The bond strength descriptors explicitly provide information on the chemical environment of the atom beyond the two-bond range.
000 molecules from ChEMBL-28 with the structure optimised by MMFF (ESI Section 2†).43 The bond strength descriptors explicitly provide information on the chemical environment of the atom beyond the two-bond range.
• Rings: atoms that are in rings are marked, and the ring size is recorded if it is smaller than eight.
To derive the label, we compared the connectivity difference of each atom in the reactant and product for every reaction through comparing the adjacency matrices based on atom-to-atom mapping results. Here, changes in connectivity refer to changes in the neighbouring atoms only. Changes in bond order have not been accounted. In accounting for competitive reactions from the same reactants, an atom is considered reactive if it undergoes a connectivity change in one of the possible competitive reactions. The example in Fig. 4 shows three competitive reactions that share the same reactants. There are 22 atoms in the reactants. Thus, this set of reactions would yield 22 pairs of a descriptor array and a corresponding label on reactivity.
Atoms within the same chemical environment were assigned identical labels. In Fig. 4, both protons are likely to be extracted in the enolisation reaction, although only one of them will be involved in the actual reaction. Thus, for consistency, if one of the atoms within a chemical environment is found to be reactive, all other atoms within the same environment are regarded as reactive.
The chemical environment of atoms within a molecule was determined via in silico isotopic labelling. For example, let us consider two atoms from the same chemical environment in a molecule. Two copies of RDkit44 Chem.Mol objects are generated from the molecule, followed by isotopic labelling on each atom individually in each Chem.Mol objects. Subsequently, by converting the Chem.Mol objects to InChI45 representations, the two resulting InChI strings are expected to be identical. The above process was applied to all atoms, including H, within a molecule.
3 Results and discussion
Model training and evaluation were performed for each dataset with different descriptor compositions (i.e. the ‘one-bond’, ‘two-bond’ and ‘two-bond +’ descriptor array composition).Relatively small datasets were employed deliberately in model training to illustrate the effectiveness of the atomistic approach. We carried out the random sampling test to show the consistency in the result despite the small training dataset. The following procedures were conducted on each dataset individually and the results are presented in Table 2:
| Entry | Descriptors | % by atoms | % sets of reactants with | ||||
|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | No fault predictions | No more than one fault prediction | All reactive atoms predicted correctly | ||
| Type A | |||||||
| First-year reactions: train: 78, test: 30, i.e. 100% of the dataset | |||||||
| 1 | One-bond | 86.8 ± 1.4% | 54.1 ± 7.1% | 74.0 ± 4.5% | 9.7 ± 4.3% | 40.3 ± 5.3% | 31.7 ± 7.5% |
| 2 | Two-bond | 88.3 ± 1.3% | 58.3 ± 7.1% | 78.5 ± 4.5% | 16.3 ± 7.5% | 39.7 ± 9.0% | 37.3 ± 9.8% |
| 3 | Two-bond + | 89.1 ± 1.4% | 61.8 ± 6.1% | 79.8 ± 3.3% | 22.3 ± 8.2% | 45.0 ± 10.2% | 43.3 ± 8.7% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Type B | |||||||
| [3 + 2] cycloaddition: train: 100, test: 100, i.e. ∼7% of the dataset | |||||||
| 4 | One-bond | 94.5 ± 1.0% | 57.9 ± 9.0% | 77.9 ± 8.2% | 11.4 ± 6.8% | 25.4 ± 12.9% | 19.6 ± 10.6% |
| 5 | Two-bond | 98.7 ± 0.2% | 87.3 ± 2.6% | 99.2 ± 0.9% | 54.7 ± 8.2% | 86.2 ± 3.7% | 57.1 ± 9.0% |
| 6 | Two-bond + | 99.6 ± 0.3% | 96.5 ± 3.1% | 98.8 ± 1.4% | 82.8 ± 12.7% | 96.9 ± 4.0% | 86.2 ± 11.6% |
| Diels–Alder: train: 100, test: 100, i.e. ∼2% of the dataset | |||||||
| 7 | One-bond | 91.5 ± 0.7% | 27.3 ± 3.1% | 85.5 ± 4.4% | 1.4 ± 1.4% | 6.9 ± 2.4% | 2.3 ± 1.7% |
| 8 | Two-bond | 95.2 ± 0.8% | 66.3 ± 5.0% | 87.1 ± 1.7% | 30.7 ± 4.4% | 56.2 ± 4.3% | 42.0 ± 6.3% |
| 9 | Two-bond + | 96.0 ± 0.7% | 73.1 ± 4.3% | 89.0 ± 3.5% | 41.6 ± 5.6% | 62.9 ± 3.5% | 56.1 ± 4.7% |
| Combined: train: 100 [3 + 2] cycloaddition + 100 Diels–Alder, test: 100 [3 + 2] cycloaddition + 100 Diels–Alder | |||||||
| 10 | One-bond | 93.2 ± 0.5% | 39.8 ± 2.9% | 85.9 ± 1.9% | 10.8 ± 2.3% | 23.1 ± 3.0% | 12.7 ± 1.9% |
| 11 | Two-bond | 96.5 ± 0.5% | 73.7 ± 3.6% | 89.8 ± 1.2% | 33.3 ± 6.0% | 59.0 ± 5.5% | 42.5 ± 6.1% |
| 12 | Two-bond + | 97.3 ± 0.4% | 80.2 ± 3.8% | 91.7 ± 1.7% | 48.2 ± 7.3% | 71.0 ± 6.4% | 60.5 ± 8.0% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Type C | |||||||
| RGD1: train: 100, test: 100, i.e. ∼2% of the dataset | |||||||
| 13 | One-bond | 75.3 ± 2.0% | 44.6 ± 6.1% | 66.9 ± 5.7% | 2.8 ± 1.8% | 14.9 ± 3.7% | 14.5 ± 3.3% |
| 14 | Two-bond | 77.6 ± 1.3% | 52.0 ± 4.4% | 69.1 ± 3.2% | 4.6 ± 2.7% | 18.1 ± 2.3% | 18.6 ± 3.8% |
| 15 | Two-bond + | 78.0 ± 1.1% | 55.0 ± 4.7% | 66.4 ± 2.4% | 5.8 ± 1.8% | 19.5 ± 4.0% | 24.9 ± 5.4% |
| Green: train: 100, test: 100, i.e. ∼76% of the dataset | |||||||
| 16 | One-bond | 81.8 ± 1.5% | 73.4 ± 4.9% | 84.5 ± 1.9% | 16.4 ± 1.9% | 37.3 ± 3.3% | 31.7 ± 8.3% |
| 17 | Two-bond | 83.8 ± 1.1% | 77.5 ± 2.4% | 85.4 ± 1.7% | 25.6 ± 2.6% | 45.0 ± 2.0% | 42.7 ± 4.6% |
| 18 | Two-bond + | 84.1 ± 0.7% | 76.7 ± 1.9% | 86.8 ± 0.7% | 27.1 ± 2.8% | 46.1 ± 3.4% | 42.6 ± 3.2% |
| Combined: train: 100 RGD1 + 100 green, test: 100 RGD1 + 100 green | |||||||
| 19 | One-bond | 77.7 ± 1.1% | 56.0 ± 4.5% | 76.6 ± 2.4% | 9.7 ± 1.7% | 25.0 ± 1.8% | 20.3 ± 4.5% |
| 20 | Two-bond | 79.5 ± 1.1% | 64.5 ± 2.1% | 75.7 ± 1.9% | 13.4 ± 2.2% | 29.4 ± 2.8% | 29.9 ± 3.1% |
| 21 | Two-bond + | 80.0 ± 0.9% | 65.8 ± 2.1% | 76.2 ± 2.4% | 13.7 ± 1.5% | 30.5 ± 3.1% | 30.6 ± 1.7% |
| Combining all datasets: the global model | |||||||
| Train 78 first-year + 100 [3 + 2] cycloaddition + 100 Diels–Alder + 100 RGD1 + 100 green | |||||||
| Test: 30 first-year + 100 [3 + 2] cycloaddition + 100 Diels–Alder + 100 RGD1 + 100 green | |||||||
| 22 | One-bond | 86.9 ± 0.6% | 38.4 ± 3.7% | 68.2 ± 2.1% | 2.7 ± 1.5% | 9.6 ± 2.7% | 6.0 ± 2.1% |
| 23 | Two-bond | 90.6 ± 0.3% | 61.7 ± 2.4% | 76.6 ± 2.6% | 13.7 ± 2.1% | 31.5 ± 3.3% | 27.0 ± 4.1% |
| 24 | Two-bond + | 91.7 ± 0.4% | 67.3 ± 2.0% | 79.5 ± 2.1% | 20.2 ± 3.6% | 40.8 ± 3.9% | 38.0 ± 3.8% |
(1) Sets of reactions with the same reactants were randomly selected for training and testing, respectively. For the first-year dataset, 30 sets of reactions were randomly selected from the dataset for testing, leaving 78 sets of reactions for training (Table 2 entries 1–3). For all other datasets (i.e. [3 + 2] cycloaddition, Diels–Alder, RGD1 and Green; Table 2 entries 4–9 and 13–18), 100 sets of reactions were randomly selected for training and testing, respectively. Combinations of the datasets (Table 2 entries 10–12 and 19–24) were also considered to assess the generalisability of the model. Four reactions in RGD1 also appear in the Green dataset. These reactions were removed from the RGD1 dataset prior to selecting reactions of the combined dataset (see ESI Section 1.1† for details).
(2) Model training was performed and repeated using the ‘one-bond’, ‘two-bond’ and ‘two-bond +’ descriptor composition respectively. The metrics from the evaluation were recorded after the testing.
(3) The above steps were repeated ten times. The mean and standard deviation of the performance metrics were calculated.
The accuracy, precision and recall were on an atomistic basis. Precision is the number of true reactive predictions over the total number of reactive predictions. Recall is the number of true reactive predictions over the total number of reactive atoms in the dataset. At the molecular level, the percentage sets of reactants with no fault predictions, no more than one fault prediction and all reactive atoms predicted correctly were calculated. The standard deviations of the performance metrics are relatively small. This demonstrates the robustness of the model in covering the chemical space with only a fraction of the entire dataset.
3.1 Type A: the first-year dataset
The first-year dataset includes a variety of different reactions (Fig. 2). Hence, it is to our surprise that even a model trained with only the ‘one-bond’ descriptors can achieve an accuracy of 86.8% by atoms (Table 2 entry 1). The good performance can be explained by looking at the dataset composition. Many first-year reactions, such as SN2 reactions and nucleophilic addition reactions on carbonyl bonds, are quite simple and the sites of reaction only involve a few atoms. In these cases, the chemical environment within one bond to an atom is sufficient to determine the reactivity.The model performance improves when the neighbours' connectivity and bond strength descriptors are included in the model training. Fig. 5 showcases examples where noticeable improvements are observed when extending the range of chemical environments included in the descriptors for each atom. Example A4 shows possible enolisation reaction pathways from an 1,3-dicarbonyl compound. Alpha carbon atoms are correctly predicted as reactive when including the neighbours' connectivity and bond strength descriptors in model training. Example A5 describes a scenario where primary carbon atoms, which tend to be involved in SN2 or E2 reactions when connected to a good leaving group, are predicted incorrectly as reactive. These primary carbon atoms are predicted as unreactive in the model trained with the bond strength descriptors, which presumably reinforce the recognition that the carbon atoms are not connected to any good leaving group. The predictions on the reactivity can hint at the possible products from the reactants. In many cases, only the predictions from the ‘two-bond +’ model can account for all the competitive pathways in the dataset. These examples highlight the effectiveness of the bond strength and connectivity descriptors in describing the chemistry within a two-bond range and indicating the local chemical environment.
 | ||
| Fig. 5 Case studies on the results from model evaluation with the first-year dataset. The annotations on the fault predictions are in purple. | ||
The first-year reaction dataset covers a wide range of reactions. Thus, the model performance deficiencies could be due to the lack of corresponding examples in the training dataset for the types of reaction present in the test dataset. We split the first-year dataset and checked the compositions to ensure that all types of reactions present in the test dataset have appeared in the train dataset. Details of the split are presented in ESI Fig. S8.† With the selected dataset and using the ‘two-bond +’ descriptor array, there is no more than one fault prediction in 70.0% of the sets of reactants in the testing dataset (ESI Table S12† entry 3) as opposed to 45.0% from random sampling test (Table 2 entry 3).
Case studies also help to understand the limitations of the model. Firstly, it is within the expectations that the models cannot predict the reactivity of atoms which requires the consideration of the chemical environment beyond two bonds from the site of connectivity changes. While bond strength and the ring component descriptors recognise the different chemical environments, they do not explicitly describe the specific atom arrangements beyond the two-bond distance from the atom. Many of the false predictions of unreactive behaviour of the ‘two-bond +’ model come from the alpha proton of the carbonyl or leaving group in enolisation E2 reactions. The motif at the reaction site extends beyond two bonds for these reactions. An exception is example A1. The alpha protons in the aldehyde are accurately predicted as reactive even though the protons are three bonds away from the carbonyl group. Here, it is likely that the correct predictions are made based on the wrong reason. These protons are predicted to be reactive because they are at the alpha position relative to the chloride. Cases of mistaken reactive predictions, such as example A2, show that the model consistently predicted the alpha proton to the chloride group as reactive.
At times, the model may encounter challenges in extrapolating beyond the training data, even when there are reactions of the same type in the training dataset. This becomes especially apparent when dealing with unfamiliar chemical groups that involve changes in connectivity. Fig. 5 A6 illustrates such a scenario. ‘C–I’ has not been presented as a leaving group in the training dataset SN2 reactions, contributing to the fault unreactive prediction of the C atom in ‘C–I’ for example A6 in the testing dataset.
To assess the model trained on all first-year reactions (i.e. 2473 atomic descriptor arrays and labels from 108 sets of reactants), we conducted tests using past exam questions from the University of Cambridge. The outcome is presented in Fig. 6. There is no more than one mistaken prediction in each reaction. This demonstrates the performance of the model in a real-world context.
3.2 Type B: the [3 + 2] cycloaddition and the Diels–Alder dataset
The model performs well in predicting the atom reactivity in reactants of reactions where there are many similar examples in the training dataset. In type B datasets, only a single type of reaction is presented, and therefore, good performances were achieved. The accuracy by atom for type A datasets, the [3 + 2] cycloaddition and the Diels–Alder dataset, are close to 100% for the ‘two-bond +’ model (Table 2 entries 6 and 9). Example B1–B3 in Fig. 7 are cases of successful predictions from the model evaluation. These cases also demonstrate the improvements in performance when introducing the bond strength and neighbours' connectivity descriptor components (i.e. moving from ‘one-bond’ to ‘two-bond’ and ‘two-bond +’). Although the bond-forming carbon atoms are more than two bonds apart in the diene motif of substrates in Diels–Alder reactions, the bond strength descriptor components should be capable of distinguishing between the various carbon atoms within the diene motif. | ||
| Fig. 7 Case studies on the results from model evaluation with the type B datasets: the [3 + 2] cycloaddition32 and the Diels–Alder reaction33 dataset. | ||
Taking away the bond strength descriptors has not significantly defected the performance of the models trained on type B datasets. This is out of our expectations. One possible explanation is that the connectivity descriptors also implicitly indicate about the chemical environment beyond the range of two bonds. For example, the total number of neighbouring atoms of atoms at a two-bond distance may indirectly hint at the hybridisation of the atoms three bonds away. The self-connectivity descriptor components also include the number of neighbouring atoms for its neighbours. Thus, even for the ‘one-bond’ model, there are no fault predictions in 25% of the sets of reactants in the evaluation with the [3 + 2] cycloaddition dataset.
The quality of the dataset also matters. In data processing, we estimated that atom-to-atom mapping errors are presented in 8% of the reactions in the Diels–Alder reaction dataset. These errors lead to drop in performance of the models trained on Diels–Alder reactions. To verify this claim, we conducted tests on the 100 reactions for which we have manually checked for mapping errors. Take-one-out cross-validations were performed on the 100 Diels–Alder reactions before and after the corrections of atom-to-atom mapping errors. We saw an improvement, yet statistically insignificant, in the accuracy, precision and recall value by atoms (ESI Table S5†).
Another observation from the study on the Diels–Alder dataset is that the model may sometimes hint at potential competitive pathways leading to products not presented in the dataset (Fig. 7 B4). For instance, in the B4 Diels–Alder reaction, the model also highlights an alternative potential dienophile position in the substrate, which is a reasonable pathway.
3.3 Type C: the RGD1 and the green dataset
The RDG1 and the Green datasets are more challenging and complex compared to type A and type B datasets. The reactions often involve multiple steps mechanistically and are not the typical textbook reactions. We analysed the RDG-1 and the Green dataset based on reaction templates to quantify the types of reactions present in the dataset. A reaction template in SMILES string was generated for each reaction, highlighting the motif at the reaction site. The motif at the reaction site covers the atoms involved in changes in connectivity. If less than two atoms involved connectivity changes, the non-H neighbouring atoms of the reactive atoms were also accounted in the template. 100 random reactions were selected from each dataset for the test. 82 and 59 unique templates were generated from 100 RGD1 and 100 Green reactions respectively. However, even for the challenging RDG-1 and Green datasets, the trained models on just 100 sets of reactions with ‘two-bond +’ descriptors gave a surprisingly decent performance of 78.0% and 84.1% accuracy respectively (Table 2, Entry 15 and 18), which is much better than random guessing (i.e. the accuracy of random guessing is 50%). The cases presented in Fig. 8 are examples of the predictions from the model evaluation. Here, we hope to emphasise the representativeness of the above results despite the small dataset selected for training and evaluation for the RGD1 dataset. Repeating the test on the RGD1 dataset with different sets of randomly selected reactions gives consistent results (ESI Table S8†). This implies that models trained from 1% of the dataset can already cover quite a substantial amount of chemistry in the RGD1 dataset. | ||
| Fig. 8 Case studies on the results from model evaluation with the type C datasets: the RGD1 (ref. 34) and the Green35 dataset. In C4, the prediction accounts for the connectivity changes from the reactant to the proposed intermediate. | ||
It is also worth noting that the ‘one-bond’ models already exhibit decent performance. The enhancement in performance when incorporating ‘two-bond’ and ‘two-bond +’ descriptors is noticeable but less pronounced compared to the improvements seen in models trained with type A and B datasets. This observation can be explained by the fact that the chemical systems in RGD1 and Green reactions are relatively small. The average number of atoms in the reactants within type C datasets is below 17, in contrast to 23 in the first-year reaction dataset and exceeding 40 in the type B datasets (Table 1). The substructure covered by the ‘one-bond’ descriptors is often nearly half of the molecules in type C reactants. Thus, the models demonstrate satisfactory performance even without the additional ‘two-bond’ and ‘two-bond +’ descriptors.
Increasing the number of sets of reactions in the training dataset improves the performance of the ‘two-bond +’ RGD1 model significantly (Fig. 9 and ESI Table S6†). 100 sets of reactions are equivalent to 1% of the RGD1 dataset. The model trained with 300 sets of RGD1 reactions (i.e. 3% of the dataset) has an accuracy of 81.2%. The model trained with nearly all of the RGD1 dataset, i.e. equivalent to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 sets of reactions, has an accuracy of 84.3%.
300 sets of reactions, has an accuracy of 84.3%.
 | ||
| Fig. 9 Increasing the size of the training data leads to improved performance metrics for the ‘two-bond +’ model trained using the RGD1 (ref. 34) dataset. The percentage of data used in the training as part of the RGD1 dataset are labelled in the accuracy plot. The same dataset, consisting of 100 RGD1 reactions, was used for testing in the above evaluation of models. | ||
3.4 Model generalisability
We have also considered models trained from combinations of different datasets, specifically [3 + 2] cycloaddition + Diels–Alder, RGD1 + Green and all datasets together (Table 2 entries 10–12 and 19–24). In all three scenarios, we observed an improvement in the performance when moving from the model trained on the ‘one-bond’ to the ‘two-bond’ and ‘two-bond +’ descriptor composition. The accuracy values from the combined dataset models are very similar to the average accuracy of models trained from the individual datasets. For example, the average accuracy for the ‘two-bond +’ models trained from the individual datasets (Table 2 entries 3, 6, 9, 15 and 18) is 89.4%. The accuracy of the model trained from the combination of individual datasets (i.e. the global model, Table 2 entry 24) is 91.7%. The performance of this global model is comparable to that of the local models trained from the individual dataset in evaluation with reactions from the individual dataset (ESI Table S6†). The above demonstrates the robustness and generalisability of the global model.4 Conclusions
In this investigation, a framework for predicting the site of reactivity has been developed. Machine learning classification models were trained on labels and descriptors at the atomistic level. Descriptor array compositions that cover chemical environments within ‘one-bond’, ‘two-bond’ and ‘two-bond +’ to the atom have been considered.Thorough evaluations on models based on different descriptor compositions were conducted with various datasets. Improvements in the model performance were observed when the bond strength and neighbours' connectivity components were added to the descriptor array. Decent performance metrics were achieved for the Type A (i.e. first-year reaction) and the Type B (i.e. the [3 + 2] cycloaddition and Diels–Alder reaction) datasets, indicating that the chemical environment within two bonds of an atom can determine reactivity to a considerable extent. We demonstrate the applicability of the model framework with the more complex datasets that cover a diverse chemical space, namely the RGD1 and the Green dataset. Even for these challenging datasets, an accuracy of over 80% has been achieved with a small dataset.
There are models which can predict reactions with greater accuracy than this. Tailoring the descriptors to align with the nature of the data and the specific chemistry problem remains an ongoing challenge. Here, we have presented a very simple model. It works well enough to give helpful guidance about reactivity despite the small dataset and highlights the potential of data-driven methods in terms of transferability.
Data availability
Data and processing scripts for this paper are available in Goodman lab GitHub at: https://github.com/Goodman-lab/TwoBondChemAuthor contributions
Prof. J. M. Goodman conceptualised and supervised the project. C. C. Lam performed the research and wrote the paper with the guidance of Prof. J. M. Goodman.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Trinity College Cambridge and Krishnan-Ang Studentships Programme for the financial support of this project. This work was performed using resources provided by the Cambridge Service for Data Driven Discovery (CSD3), operated by the University of Cambridge Research Computing Service (http://www.csd3.cam.ac.uk/), provided by Dell EMC and Intel using Tier-2 funding from the Engineering and Physical Sciences Research Council (capital grant EP/P020259/1) and DiRAC funding from the Science and Technology Facilities Council (http://www.dirac.ac.uk).References
- K. Jorner, A. Tomberg, C. Bauer, C. Sköld and P.-O. Norrby, Nat. Rev. Chem, 2021, 5, 240–255 CrossRef CAS PubMed.
- M. Fitzner, G. Wuitschik, R. Koller, J.-M. Adam and T. Schindler, ACS Omega, 2023, 8, 3017–3025 CrossRef CAS PubMed.
- Z. Tu, T. Stuyver and C. W. Coley, Chem. Sci., 2023, 14, 226–244 RSC.
- F. Strieth-Kalthoff, F. Sandfort, M. Kühnemund, F. R. Schäfer, H. Kuchen and F. Glorius, Angew. Chem., Int. Ed., 2022, 61, e202204647 CrossRef CAS PubMed.
- M. P. Maloney, C. W. Coley, S. Genheden, N. Carson, P. Helquist, P.-O. Norrby and O. Wiest, Org. Lett., 2023, 25, 2945–2947 CrossRef CAS PubMed.
- D. S. Wigh, J. M. Goodman and A. A. Lapkin, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1603 Search PubMed.
- L. David, A. Thakkar, R. Mercado and O. Engkvist, J. Cheminf., 2020, 12, 56 CAS.
- G. Skoraczyński, P. Dittwald, B. Miasojedow, S. Szymkuć, E. P. Gajewska, B. A. Grzybowski, A. Gambin, G. Skoraczyñski, P. Dittwald, B. Miasojedow, S. Szymkuc, E. P. Gajewska, B. A. Grzybowski and A. Gambin, Sci. Rep., 2017, 7, 3582 CrossRef PubMed.
- S. Stocker, G. Csányi, K. Reuter and J. T. Margraf, Nat. Commun., 2020, 11, 1–11 CrossRef PubMed.
- S.-Q. Zhang, L.-C. Xu, S.-W. Li, J. C. A. Oliveira, X. Li, L. Ackermann and X. Hong, Chem. Eur J., 2023, 29, e202202834 CrossRef CAS PubMed.
- F. Sandfort, F. Strieth-Kalthoff, M. Kühnemund, C. Beecks and F. Glorius, Chem, 2020, 6, 1379–1390 CAS.
- W. L. Williams, L. Zeng, T. Gensch, M. S. Sigman, A. G. Doyle and E. V Anslyn, ACS Cent. Sci., 2021, 7, 1622–1637 CrossRef CAS PubMed.
- P. Friederich, G. dos Passos Gomes, R. De Bin, A. Aspuru-Guzik and D. Balcells, Chem. Sci., 2020, 11, 4584–4601 RSC.
- J. P. Reid, R. S. J. Proctor, M. S. Sigman and R. J. Phipps, J. Am. Chem. Soc., 2019, 141, 19178–19185 CrossRef CAS PubMed.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, ACS Cent. Sci., 2019, 5, 1572–1583 CrossRef CAS PubMed.
- J. Lu and Y. Zhang, J. Chem. Inf. Model., 2022, 62, 1376–1387 CrossRef CAS PubMed.
- R. Kotlyarov, K. Papachristos, G. P. F. Wood and J. M. Goodman, J. Chem. Inf. Model., 2024, 64, 4286–4297 CrossRef CAS PubMed.
- S. M. Kearnes, M. R. Maser, M. Wleklinski, A. Kast, A. G. Doyle, S. D. Dreher, J. M. Hawkins, K. F. Jensen and C. W. Coley, J. Am. Chem. Soc., 2021, 143, 18820–18826 CrossRef CAS PubMed.
- B. Dou, Z. Zhu, E. Merkurjev, L. Ke, L. Chen, J. Jiang, Y. Zhu, J. Liu, B. Zhang and G.-W. Wei, Chem. Rev., 2023, 123, 8736–8780 CrossRef CAS PubMed.
- E. Shim, A. Tewari, T. Cernak and P. M. Zimmerman, J. Chem. Inf. Model., 2023, 63, 3659–3668 CrossRef CAS PubMed.
- B. A. Grzybowski, S. Szymkuć, E. P. Gajewska, K. Molga, P. Dittwald, A. Wołos and T. Klucznik, Chem, 2018, 4, 390–398 CAS.
- B. A. Grzybowski, T. Badowski, K. Molga and S. Szymkuć, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, 13, e1630 Search PubMed.
- S. Lee, K. Ermanis and J. M. Goodman, Chem. Sci., 2022, 13, 7204–7214 RSC.
- C. C. Lam and J. M. Goodman, J. Chem. Inf. Model., 2023, 63, 4364–4375 CrossRef CAS PubMed.
- C. C. Lam and J. M. Goodman, Chem. Sci., 2023, 14, 12355–12365 RSC.
- R. Batra, H. D. Tran, C. Kim, J. Chapman, L. Chen, A. Chandrasekaran and R. Ramprasad, J. Phys. Chem. C, 2019, 123, 15859–15866 CrossRef CAS.
- L. Zhu, M. Amsler, T. Fuhrer, B. Schaefer, S. Faraji, S. Rostami, S. A. Ghasemi, A. Sadeghi, M. Grauzinyte, C. Wolverton and S. Goedecker, J. Chem. Phys., 2016, 144, 34203 CrossRef PubMed.
- G. Imbalzano, A. Anelli, D. Giofré, S. Klees, J. Behler and M. Ceriotti, J. Chem. Phys., 2018, 148, 241730 CrossRef PubMed.
- S. Boobier, Y. Liu, K. Sharma, D. R. J. Hose, A. J. Blacker, N. Kapur and B. N. Nguyen, J. Chem. Inf. Model., 2021, 61, 4890–4899 CrossRef CAS PubMed.
- N. Ree, A. H. Göller and J. H. Jensen, Digit. Discov., 2022, 1, 108–114 RSC.
- J. Clayden, N. Greeves and S. Warren, Organic Chemistry, Oxford University Press, 2nd edn, 2012 Search PubMed.
- T. Stuyver, K. Jorner and C. W. Coley, Sci. Data, 2023, 10, 66 CrossRef CAS PubMed.
- S. Li, X. Wang, Y. Wu, H. Duan and L. Tang, RSC Adv., 2022, 12, 33801–33807 RSC.
- Q. Zhao, S. M. Vaddadi, M. Woulfe, L. A. Ogunfowora, S. S. Garimella, O. Isayev and B. M. Savoie, Sci. Data, 2023, 10, 145 CrossRef CAS PubMed.
- C. A. Grambow, L. Pattanaik and W. H. Green, Sci. Data, 2020, 7, 137 CrossRef CAS PubMed.
- Q. Zhao and B. M. Savoie, Nat. Comput. Sci., 2021, 1, 479–490 CrossRef PubMed.
- Q. Zhao and B. M. Savoie, Angew. Chem., Int. Ed., 2022, 61, e202210693 CrossRef CAS PubMed.
- P. Zimmerman, J. Chem. Theory Comput., 2013, 9, 3043–3050 CrossRef CAS PubMed.
- P. M. Zimmerman, J. Comput. Chem., 2015, 36, 601–611 CrossRef CAS PubMed.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- P. Schwaller, B. Hoover, J.-L. L. Reymond, H. Strobelt and T. Laino, Sci. Adv., 2023, 7, eabe4166 CrossRef PubMed.
- A. Lin, N. Dyubankova, T. I. Madzhidov, R. I. Nugmanov, J. Verhoeven, T. R. Gimadiev, V. A. Afonina, Z. Ibragimova, A. Rakhimbekova, P. Sidorov, A. Gedich, R. Suleymanov, R. Mukhametgaleev, J. Wegner, H. Ceulemans and A. Varnek, Mol. Inf., 2022, 41, 2100138 CrossRef CAS PubMed.
- F. Berenger and K. Tsuda, J. Cheminf., 2021, 13, 88 CAS.
- RDKit Open-Source Cheminformatics, http://https//www.rdkit.org/, accessed December 18, 2020.
- J. M. Goodman, I. Pletnev, P. Thiessen, E. Bolton and S. R. Heller, J. Cheminf., 2021, 13, 40 CAS.
- F. Pedregosa, V. Gael, A. Gramfort, V. Michel, B. Tririon, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos and D. Cournapeau, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00092g |
| This journal is © The Royal Society of Chemistry 2024 |