Open Access Article
Open Access ArticleConnectivity stepwise derivation (CSD) method: a generic chemical structure information extraction method for the full step matrix†
Jialiang
Xiong
a,
Xiaojie
Feng
a,
Jingxuan
Xue
b,
Yueji
Wang
b,
Haoren
Niu
a,
Yu
Gu
b,
Qingzhu
Jia
b,
Qiang
Wang
a and
Fangyou
Yan
 *a
*a
aSchool of Chemical Engineering and Material Science, Tianjin University of Science and Technology, Tianjin 300457, P. R. China. E-mail: yanfangyou@tust.edu.cn
bSchool of Marine and Environmental Science, Tianjin University of Science and Technology, Tianjin 300457, P. R. China
First published on 8th August 2024
Abstract
Emerging advanced exploration modalities such as property prediction, molecular recognition, and molecular design boost the fields of chemistry, drugs, and materials. Foremost in performing these advanced exploration tasks is how to describe/encode the molecular structure to the computer, i.e., from what the human eye sees to what is machine-readable. In this effort, a chemical structure information extraction method termed connectivity step derivation (CSD) for generating the full step matrix (MSF) is exhaustively depicted. The CSD method consists of structure information extraction, atomic connectivity relationship extraction, adjacency matrix generation, and MSF generation. For testing the run speed of the MSF generation, over 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules have been collected covering organic molecules, polymers, and MOF structures. Test outcomes show that as the number of atoms in a molecule increases from 100 to 1000, the CSD method has an increasing advantage over the classical Floyd–Warshall algorithm, with the running speed rising from 28.34 to 289.95 times in the Python environment and from 2.86 to 25.49 times in the C++ environment. The proposed CSD method, that is, the elaboration of chemical structure information extraction, promises to bring new inspiration to data scientists in chemistry, drugs, and materials as well as facilitating the development of property modeling and molecular generation methods.
000 molecules have been collected covering organic molecules, polymers, and MOF structures. Test outcomes show that as the number of atoms in a molecule increases from 100 to 1000, the CSD method has an increasing advantage over the classical Floyd–Warshall algorithm, with the running speed rising from 28.34 to 289.95 times in the Python environment and from 2.86 to 25.49 times in the C++ environment. The proposed CSD method, that is, the elaboration of chemical structure information extraction, promises to bring new inspiration to data scientists in chemistry, drugs, and materials as well as facilitating the development of property modeling and molecular generation methods.
1. Introduction
In long-standing practice in the chemistry, drugs, and materials fields, the development quantitative structure–property relationship (QSPR)1 models has contributed to the reduction of time and resource consumption compared to experimental measurements of properties of interest and to the empirical design of target substances.2–4 With the advancement of machine learning (ML) and even deep learning5 techniques, QSPR shows tantalizing promise in the prediction of chemical, drug, and material properties (e.g., density,6 viscosity,6 dissociation constants,7 and conductivity8) as well as reaction kinetics,9 selectivity,10 yield,11etc.One of the universal paradigms for QSPR models12–14 is adopting algorithms such as artificial neural networks (ANN), support vector machines, or multiple linear regression (MLR) to capture the linear or non-linear relationships between chemical structure descriptors and their target properties.15–19 The descriptor is the numerical form of the chemical structure.1 The simplest is the 1D descriptor, which is based on molecular formulae to represent molecules, such as the number of atoms, atom type, and molar mass.1 Besides, there exist topological descriptors, norm descriptors, physicochemical descriptors, structural descriptors, quantum chemical descriptors, and so on. Among them, the topological and norm descriptors could be obtained by extracting the 2D structural information of molecules and converting it into numerical form.
For instance, with the descriptor from Dragon, Sadeghi et al.20 developed a quantitative structure–activity relationship model for the half-maximal inhibitory concentration (IC50) of PI3Kγ using MLR and ANN. Souyei et al.21 utilized descriptors computed with Dragon and established MLR analysis to establish a model for predicting the thermal energy of aliphatic aldehydes. The open-source cheminformatics toolkit RDKit offers descriptor calculation functions. Innumerable works have successfully developed QSPR models and designed novel molecules adopting the descriptor from RDKit, and so on. Recently, adopting the descriptor from RDKit, Yang et al.22 established the ML-QSPR model for gas permeability of polyimide (PI) membranes to He, H2, O2, N2, CO2, and CH4, and high-throughput screening of over 9 million hypothetical PIs to obtain the novel ultra-permeable candidates. The norm descriptor23 was proposed and refined during the long-term work of our group. Based on the norm descriptor, the QSPR models of organic properties with considerable accuracies were established, e.g., critical pressure, critical volume, and critical temperature,24 and further extended to specific systems' property predictions like ionic liquids,25 cyclodextrins,26 and PIs.27
An essential part of computing descriptors, including the norm descriptor, to describe key information about the molecular structure is to obtain the connectivity relationships between the atoms (or positional relationships of the atoms). The full step matrix (MSF), see eqn (1), is considered as one of the significant transformation forms for obtaining information about the connectivity relations between atoms in the 2D molecular structure.
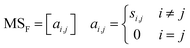 | (1) |
Through the MSF, one can describe how an atom in the molecule reaches all remaining atoms by the shortest step. It is worth mentioning that the MSF contains the adjacency matrix,28i.e., the case where one atom reaches another atom via one chemical bond. Some of the primary approaches to improve further the precision of QSPR models include incorporating information about the 3D spatial structure of atoms (e.g., coordinates, angles) into the descriptors29,30 and using the expertise of the predicted system to augment the descriptors. By extending the MSF from the 2D molecular structure to the 3D molecular structure,31–33 as well as superimposing the atomic property information with the atomic connectivity information contained in the MSF, it is possible to achieve the aforementioned approaches. The computer-generation process of the extended-connectivity fingerprints (ECFP)34 based on the Morgan algorithm and simplified molecular input line entry system (SMILES)35 also includes reading the connectivity relationships between atoms. More efforts have focused on providing clear explanations for modelling QSPR and designing novel molecules36–38 by descriptors. Descriptions of the process for converting from molecular structure graphs (i.e., what the human eye sees) to the adjacency matrix or even MSF (i.e., what is machine-readable) are rare. In this present effort, a generic chemical structure information extraction method for MSF is well-described for reference and flexible use by relevant researchers.
It is worth mentioning that the Floyd–Warshall39,40 algorithm in graph theory is a dynamic programming algorithm for solving the shortest paths between all pairs of nodes in a graph. The Floyd–Warshall algorithm is applied to calculate the shortest paths between all pairs of atoms in the molecular topology graph to generate the MSF, as used in the RDKit18,19 toolkit. A function that qualitatively describes the running time of the Floyd–Warshall algorithm, i.e. the time complexity, is O(n3) (n is any size of the input, where n is the number of atoms). Thus, as the number of atoms in the topology graph increases, the MSF generation time grows in a cubic manner. Adopting the Floyd–Warshall algorithm to generate MSF for organic small molecule systems consisting of mostly molecules with less than 100 atoms has an acceptable run-time. Nevertheless, when applying it to molecular systems with repeating structures (e.g., polymers, metal–organic frameworks), the running time is non-negligible. Meanwhile, the large dataset in the prediction task or the vast structural space in the molecular design task will further increase the run-time consumption.
In this effort, a chemical structure information extraction method termed connectivity step derivation (CSD) for generating MSF is depicted, along with reduced runtime compared to the classical Floyd–Warshall algorithm. The universal MOL file, GJF file of the computational chemistry package Gaussian,41 and HIN file of the HyperChem software42 are shown as examples for analyzing the whole process from the file structure to the MSF generation. Moreover, to test the speed of MSF generation by the CSD and Floyd–Warshall methods, a total of more than 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular structures containing the three systems of organic molecules, polymers, and MOF are collected from NIST,43 PubChem,44 PolyInfo,45 and ToBaCCo46 with 39
000 molecular structures containing the three systems of organic molecules, polymers, and MOF are collected from NIST,43 PubChem,44 PolyInfo,45 and ToBaCCo46 with 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 469, 9397, 2588, and 3189 molecular structures, respectively.
469, 9397, 2588, and 3189 molecular structures, respectively.
2. Methodology
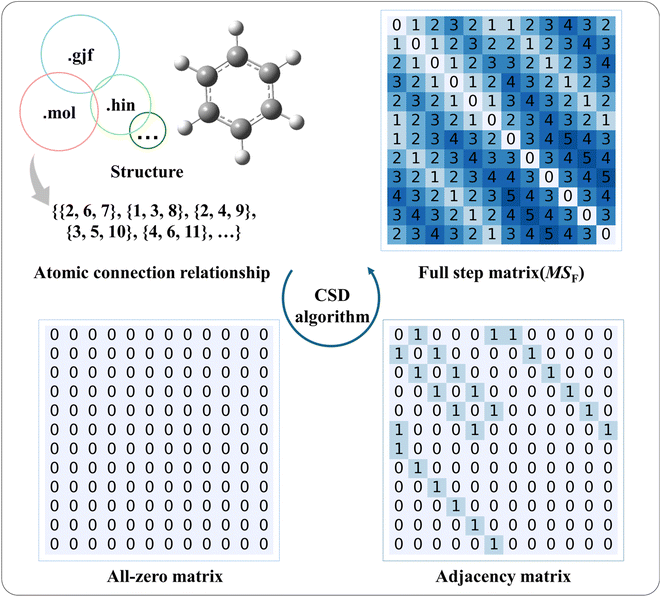
The CSD method consists of four main parts: structure information extraction, atomic connectivity relationship extraction, adjacency matrix generation, and MSF generation. The complete method is presented in Fig. 1.2.1 Structure information extraction
Opening the MOL, GJF, and HIN files with Notepad software, the file contents will be as shown in the left, middle, and right parts of Fig. 2, respectively. All three files contain atomic types, atomic coordinates, and bonding relationships between atoms. In the case of the MOL file (Fig. 2), the atomic types and their coordinates are in lines 5 to 16; for the GJF and HIN files (Fig. 2), they are in lines 6 to 17. The minor differences in atom information are related to the storage of information at the front of each file. For example, the “12 12” shown in line 4 of the MOL file (Fig. 2) is the number of atoms and the number of chemical bonds in the molecule, respectively.The descriptions of bonding relationships between atoms are different in the MOL, GJF, and HIN files. In the MOL file, the atomic relationships are extracted in groups of three characters. Like the one illustrated in Fig. 2, lines 17 to 28, the key block consists of key rows, where each row represents a key and follows the format of the first nine characters: aaabbbccc. When the number of atoms in the molecule is less than 1000, the ‘aaa’, ‘bbb’, and ‘ccc’ characters correspond to the meanings listed in Table 1. For GJF and HIN files, the atom connection information between atoms is separated by the empty strings with the symbol numbers of the two atoms and their chemical bond types. For example, line 19 in the GJF file and the end of line 6 in the HIN file indicate that atom 1 is connected to atoms 2, 6, and 7, corresponding to aromatic, aromatic, and single bonds, respectively. Note that the three files are not identical in their schematic representation of bond types. In the MOL file, the bond types are labeled as shown in the meaning of ‘ccc’ in Table 1; for the GJF file, the aromatic bond appears to be marked as ‘1.5’, the single bond is marked as ‘1.0’, and the double bond is marked as ‘2.0’; whereas for the HIN file, the single bond is labeled as ‘s’, the double bond is labeled as ‘d’, the triple bond is labeled ‘t’, and the aromatic bond is labeled ‘a’.
| Area | Definition | Content |
|---|---|---|
| aaa | First atom index | Starting from 1, less than 1000 |
| bbb | Second atom index | Starting from 1, less than 1000 |
| ccc | Bond type | (1) Single bond; (2) double bond; (3) triple bond; (4) aromatic bond; (5) single or double bond; (6) single or aromatic bond; (7) double or aromatic bond; (8) any bond |
2.2 Atomic connectivity relationship extraction
Encoding the atomic connectivity relationships in a molecular structure into a computer-readable form, such as the list, is an indispensable step in generating the adjacency matrix and the MSF. One way of encoding atomic connectivity relationships is shown in eqn (2).Lc = [LMi]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LMi = [mj] LMi = [mj] | (2) |
In the MOL file, the first three characters on line 4 represent n1, while characters 3–6 denote n2. The connection relationships of the atoms are saved from line n1 + 5 to line n1 + n2. Each line contains a group of three characters. The first two digits of each line are recorded by iterating through these lines to obtain the connection relationships of all atoms. For example, within line 17 of the MOL file data, “1 2…” (refer to Fig. 2), the number 2 is first stored in the LM1, followed by the storage of the number 1 in LM2.
In the GJF file, the file content blocks are separated by blank lines, and the 3rd to 4th blocks are related to atomic connectivity. When extracting connectivity information from each line, the contents are split by empty spaces. Specifically, if the first element mi is a number, the subsequent pairs of elements store the neighboring atoms' information with mi. For example, within line 19 of the MOL file data “1 2 1.5 6 1.5 7 1.0” (see Fig. 2), the numbers 2, 6, and 7 are first stored in the LM1, followed by the storage of the number 1 in LM2, LM6, and LM7.
In the HIN file, the atom connectivity is delineated with the character “atom” at the beginning, and each element is separated by empty strings. Thus, splitting by the empty strings yields a set of elements, where the second element holds the current atom index as mi, the 11th element stores the count of atoms adjacent to the atomic index mi, and the subsequent elements store information about the neighboring atoms. For instance, for line 6 (see Fig. 2) in the HIN file, the numbers 2, 6, and 7 are recorded into LM1 and the number 1 is stored in LM2, LM6, and LM7.
2.3 Adjacency matrix generation
The adjacency matrix (MSa) of a molecule can be generated by storing the atomic connectivity relationships in computer-readable form (see eqn (3)). | (3) |
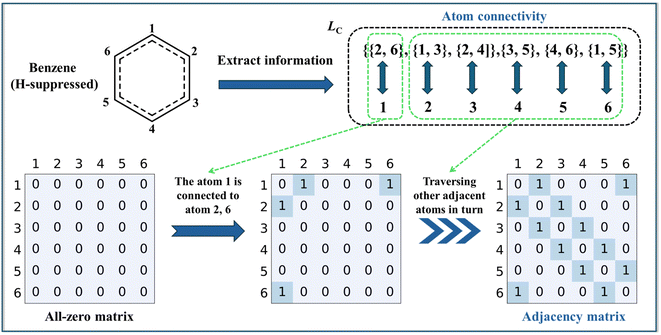
The adjacency matrix is a square matrix with dimensions equal to the number of atoms in the molecule, where the indexes of both rows and columns correspond to atomic symbols. As an example, the H-suppressed benzene molecule is illustrated in detail with the adjacency matrix generation process, which is displayed in Fig. 3. After the extraction of structural information completes, the computer-readable list Lc containing information about the atomic connectivity relationships is stored. For the Lc shown for the H-suppressed benzene molecule, it is indicated that atoms 2 and 6 are connected to atom 1, and similarly, atoms 1 and 3 are connected to atom 2…… After that, the atom connectivity stored by Lc is filled into an all-zero matrix with dimensions equal to the number of atoms in the molecule. Specifically, taking the numbers of the two bonded atoms as row and column numbers, respectively, number “1” in the MSa represents a direct bonding between two atoms. Based on the rule above, the atom connection relationship information of all atoms stored in Lc is filled into the all-zero matrix, i.e., the adjacency matrix. The generation of the adjacency matrix for benzene molecules containing hydrogen atoms is illustrated in Fig. S1.†
2.4 The full step matrix generation
On the basis of generating the adjacency matrix, the list of steps for MSF generation in the CSD method is given as follows and is illustrated in Fig. 4, where the step size (k) denotes the step passed from one atom to another.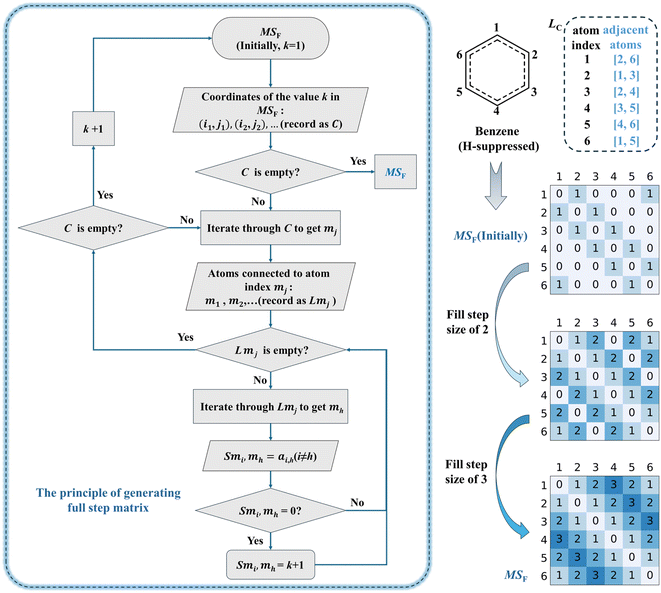 | ||
| Fig. 4 Flowchart of the steps to generate the MSF in the CSD method (left) and illustration of MSF generation from the H-suppressed benzene molecule (right). A schematic illustration of the generation of the MSF from the adjacency matrix of the H-added benzene molecule is shown in Fig. S2.† Fig. S3 and S4† show the MSF generated from H-suppressed poly(1,3-phenylene pyrrolidone) molecules and cubane molecules. Note: The MSF is converted from the relationship between two atoms in a molecule that are bonded together by a minimum number of chemical bonds. That is, if atoms are regarded as nodes and chemical bonds are regarded as edges, the MSF is converted from the shortest path between two nodes. Thus, the MSF of the benzene molecule is padded with 2 in row 1 and column 3 because a minimum of 2 aromatic bonds needs to be passed between atom 1 and atom 3. The process of generating MSF of the three-dimensional structure47 is demonstrated using cubane as an example. | ||
(1) Obtain the adjacency matrix (matrix initially containing only 0 and 1, and k is 1).
(2) Identify atom pairs with the step size of k in the MSF and store the coordinates of matrix in the C (i.e., (i1, j1), (i2, j2), …), representing directly connected atoms pairs.
(3) If the C is empty, indicating the current MSF has been fully generated, end the entire process, else continue to procedure (4).
(4) Iterate through the C to get the element mj.
(5) Find all atoms adjacent to atom index mj, and record them in the LMj (i.e., m1, m2, …).
(6) If the LMj is empty, indicating there is no atom adjacent to atom index mh currently, continue to procedure (10), else continue to procedure (7).
(7) Iterate through the LMj to get element mh.
(8) Record the ai,h(i ≠ h) from MSF as smi,mh.
(9) If the smi,mh is 0, indicating that the current position has never been filled before, fill the value of smi,mh with k + 1, then proceed to procedure (6). If the smi,mh is not 0, continue to procedure (6).
(10) If the C is empty, indicating the traversal of current atom pairs with the step size of k in MSF is complete, continue to procedure (11), else continue to procedure (4).
(11) k plus 1 and continue to procedure (1).
3. Results and discussion
3.1 Datasets
For testing the generating speed of the MSF, molecular structures containing three systems: organic molecules, polymers, and MOFs, are collected. More than 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 organic molecules are collected from the NIST database. Also, compounds with CIDs 1 to 10
000 organic molecules are collected from the NIST database. Also, compounds with CIDs 1 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 are retrieved from the PubChem database. Polymer structures mostly originated from the PolyInfo database with 2640 PIs. Over 30
000 are retrieved from the PubChem database. Polymer structures mostly originated from the PolyInfo database with 2640 PIs. Over 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOF structures (CIF files) have been generated employing ToBaCCo. The datasets from NIST, PubChem, and PolyInfo were validated using RDKit. However, since the CIF structures cannot be recognized by RDKit, the MOF data validation was conducted using the provided MOFX-DB database.48 The dataset ultimately used for testing consisted of 39
000 MOF structures (CIF files) have been generated employing ToBaCCo. The datasets from NIST, PubChem, and PolyInfo were validated using RDKit. However, since the CIF structures cannot be recognized by RDKit, the MOF data validation was conducted using the provided MOFX-DB database.48 The dataset ultimately used for testing consisted of 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 469 organic molecules originating from NIST, 9397 compounds from the PubChem database, 2588 unique polyimide ring repeating unit27 structures, and 3188 MOF structures.
469 organic molecules originating from NIST, 9397 compounds from the PubChem database, 2588 unique polyimide ring repeating unit27 structures, and 3188 MOF structures.
Fig. 5 illustrates the distribution of the number of atoms in the structures from the four sources. Among them, the substances in the NIST database consist of 3 to 93 atoms, with a concentration between 5 and 40 atoms. Collected from the PubChem database, compounds range from 3 to 186 atoms, with a central concentration between 20 and 100 atoms. The number of atoms in the polyimide repeat unit ranges from 10 to 127 and concentrates between 20 and 100 atoms. Of note, in the MOF structures, there exist MOF molecules with the number of atoms ranging from 30 to 900. Those MOF structures collected for testing have a major distribution of atoms between 100 and 800.
 | ||
| Fig. 5 The frequency distribution of the number of atoms in the structures from the four sources. (a) NIST, (b) PubChem, (c) Polymer, and (d) MOF. | ||
3.2 Runtimes of the CSD method
The time complexity of the Floyd–Warshall algorithm is O(n3), while the CSD algorithm is approximately O(n2), where n represents the atom numbers. Therefore, with the increase in the number of atoms, the calculating time of MSF generated by the Floyd–Warshall algorithm increases cubically, while the calculating time of the CSD algorithm is close to quadratic. This becomes especially evident when the number of atoms is large, where the gaps between the two algorithms become extremely apparent.To evaluate the generation speed of MSF across the collected datasets, the performance of self-implemented Floyd–Warshall algorithm and CSD algorithm programs in the Python environment is compared and the performance of RDKit and CSD algorithm programs for the same task in the C++ environment is evaluated. Additionally, given that RDKit is implemented in C++, the CSD algorithm is also implemented in C++ to ensure a fair comparison of performance across the collected datasets in the C++ environment. Furthermore, due to RDKit not being able to generate MSF from CIF files, a C++ program is implemented for the Floyd–Warshall algorithm as an alternative for testing purposes in the MOF dataset in the C++ environment. To illustrate the results, a fitting of the structure results is performed using the equation y = a × nb, and the fitting curves and coefficient can be seen in Fig. 6 and 7, and Tables 2 and 3.
| Datasets | CSD (Python) | Floyd–Warshall (Python) | f(n) | The number of atoms scope | ||
|---|---|---|---|---|---|---|
| a 1 | b 2 | a 2 | b 2 | |||
a Note: n is the number of atoms, and  . .
|
||||||
| NIST | 2.14 × 10−6 | 1.87 | 4.08 × 10−7 | 2.99 | 0.19n1.12 | n ∈ [3, 90] |
| PubChem | 1.36 × 10−6 | 1.99 | 4.51 × 10−7 | 2.97 | 0.33n0.98 | n ∈ [3, 186] |
| Polymer | 2.09 × 10−6 | 1.91 | 4.24 × 10−7 | 2.98 | 0.20n1.07 | n ∈ [10, 127] |
| MOF | 1.36 × 10−6 | 2.00 | 3.68 × 10−7 | 3.01 | 0.27n1.01 | n ∈ [30, 900] |
| Datasets | CSD (C++) | Floyd–Warshall (C++) | f(n) | Scope | ||
|---|---|---|---|---|---|---|
| a 1 | b 2 | a 2 | b 2 | |||
a Note: n is the number of atoms, and  . .
|
||||||
| NIST | 1.69 × 10−7 | 1.54 | 4.63 × 10−7 | 1.69 | 2.74n0.15 | n ∈ [3, 90] |
| PubChem | 1.11 × 10−7 | 1.69 | 1.62 × 10−8 | 2.44 | 0.15n0.75 | n ∈ [3, 186] |
| Polymer | 1.43 × 10−7 | 1.63 | 2.81 × 10−7 | 1.88 | 1.97n0.25 | n ∈ [10, 127] |
| MOF | 1.55 × 10−8 | 2.01 | 5.58 × 10−10 | 2.96 | 0.04n0.95 | n ∈ [30, 900] |
As depicted by NIST in Fig. 6(a) and Table 2, the Floyd–Warshall algorithm demonstrates a computation time 0.19n1.12 times that of the CSD algorithm for MSF calculation. This disparity becomes pronounced, reaching 29.45 times when the atom count comprises 90. In PubChem, as shown in Fig. 6(b) and Table 2, a similar phenomenon emerges, with the Floyd–Warshall algorithm requiring 0.33n0.98 times that of the CSD algorithm, notably evident as the atom count approaches 180, resulting in an increase of approximately 53.81 times in computation time. In Polymer, as shown in Fig. 6(c) and Table 2, the Floyd–Warshall algorithm's computation time is 0.2n1.07 times that of the CSD algorithm, particularly noticeable as the atom count encompasses 120, showing 34.04 times the computational time. Finally, in MOF, as shown in Fig. 6(d) and Table 2, the Floyd–Warshall algorithm takes 0.27n1.01 times that of the CSD algorithm to compute the MSF, which escalates to 260.68 times as the atom count climbs to 900. Additionally, as depicted in Fig. 6(e), within the NIST, PubChem, Polymer, and MOF datasets, the computational time of the Floyd–Warshall algorithm closely approximates a linear multiple relationship with that of the CSD algorithm.
Hence, in the Python environment, the Floyd–Warshall algorithm remains feasible for small molecule computations, while its efficiency significantly diminishes for large molecular structures, rendering it impractical. Conversely, the CSD algorithm consistently exhibits exceptional performance and stability, even with increasing atom count.
As illustrated by NIST in Fig. 7(a) and Table 3, RDKit (based on the Floyd–Warshall algorithm) exhibits a computation time 2.74n0.15 times that of the CSD algorithm (in the C++ environment, and the following is in the same environment) for calculating MSF. This difference becomes evident, reaching 5.39 times when the atom count is 90. In PubChem, as depicted in Fig. 7(b) and Table 3, a similar trend emerges, with RDKit requiring 0.15n0.75 times that of the CSD algorithm, notably evident as the atom count approaches 180, resulting in 7.18 times the computation time. In Polymer, as shown in Fig. 7(c) and Table 3, RDKit computation time is 1.97n0.25 times that of the CSD algorithm, particularly noticeable as the atom count reaches 120, showing 6.51 times the computational load. Finally, according to MOF, as shown in Fig. 7(d) and Table 3, RDKit takes 0.04n0.95 times that of the CSD algorithm to compute MSF, which escalates to 23.06 times as the atom count climbs to 900. Furthermore, in Fig. 7(e), across the PubChem and MOF datasets, the computation time of the Floyd–Warshall algorithm closely aligns with a linear multiple relationship observed with the CSD algorithm. As the quantity of molecules rises, the discernible gap in computation widens. In the NIST and Polymer datasets, the difference in computational time between the two algorithms is relatively small in terms of the multiple relationships.
Given that the MOF dataset involves a wide range of the number of atoms in the structure, we have counted the changes in the computation time of the CSD algorithm and the Floyd–Warshall algorithm in the C++ and Python environments for every increase of 100 atoms in the molecule from 100 to 800 atoms as listed in Table 4. Clearly, the order of calculation of the two algorithms in the two environments is CSD (C++) < Floyd–Warshall (C++) < CSD (Python) < Floyd–Warshall (Python) at the same level of number of atoms. Moreover, even if the calculation time of the CSD algorithm in the Python environment increases with the number of atoms in the molecule, it is acceptable compared to the calculation time of applying the Floyd–Warshall algorithm in the Python environment. When the number of atoms in the molecule increases to 600 atoms, the Floyd–Warshall algorithm calculates the MSF of one molecule in the Python environment in more than 1 min, which may consume valuable time of the researchers. Overall, the calculation time of the Floyd–Warshall algorithm in the C++ environment is considered manageable for small molecule datasets, but it is much longer for large molecule datasets. Nevertheless, the CSD algorithm consistently shows outstanding performance and stability, even as atom counts increase.
| Algorithm (environment) | Number of atoms | |||||||
|---|---|---|---|---|---|---|---|---|
| 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | |
| CSD (C++) | 0.0002 | 0.0007 | 0.0015 | 0.0026 | 0.0041 | 0.0059 | 0.0081 | 0.0106 |
| CSD (Python) | 0.0136 | 0.0544 | 0.1224 | 0.2176 | 0.3400 | 0.4896 | 0.6664 | 0.8704 |
| Floyd–Warshall (C++) | 0.0005 | 0.0036 | 0.0120 | 0.0281 | 0.0544 | 0.0933 | 0.1473 | 0.2187 |
| Floyd–Warshall (Python) | 0.3853 | 3.1042 | 10.5192 | 25.0062 | 48.9494 | 84.7390 | 134.7699 | 201.4414 |
4. Conclusions
In this contribution, a generic chemical structure information extraction method, the CSD method, is elaborately presented for the generation of MSF, subsequently allowing flexible calculation descriptors. Taking MOL, GJF, and HIN files as examples, the complete process of structural information extraction, atomic connectivity relationship generation, adjacency matrix generation, and MSF generation was described. It was tested on more than 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular structures encompassing organic molecules, polymers, and MOF systems, showing that the CSD method enhances the classic Floyd–Warshall algorithm for improved speed. In the Python environment, within the collected dataset, the computational speed of the CSD algorithm demonstrates an advantage over the Floyd–Warshall algorithm when the number of atoms exceeds 5. When the number of atoms reaches 900, the advantage increases significantly, reaching up to 260.68 times faster. Similar trends are observed in the C++ environment, where for datasets with more than 13 atoms, the CSD algorithm consistently outperforms the Floyd–Warshall algorithm. Particularly, when the number of atoms reaches 900, the advantage can be as high as 23.06 times faster. In datasets containing fewer than 13 atoms, only a few cases show slightly slower performance for the CSD algorithm.
000 molecular structures encompassing organic molecules, polymers, and MOF systems, showing that the CSD method enhances the classic Floyd–Warshall algorithm for improved speed. In the Python environment, within the collected dataset, the computational speed of the CSD algorithm demonstrates an advantage over the Floyd–Warshall algorithm when the number of atoms exceeds 5. When the number of atoms reaches 900, the advantage increases significantly, reaching up to 260.68 times faster. Similar trends are observed in the C++ environment, where for datasets with more than 13 atoms, the CSD algorithm consistently outperforms the Floyd–Warshall algorithm. Particularly, when the number of atoms reaches 900, the advantage can be as high as 23.06 times faster. In datasets containing fewer than 13 atoms, only a few cases show slightly slower performance for the CSD algorithm.
The proposed CSD method, that is, the elaboration of chemical structure information extraction, promises to bring new inspiration to data scientists in chemistry, drugs, and materials. Meanwhile, understanding the process of chemical structure information extraction may give rise to the birth of new critical molecular representation methods to facilitate the development of property modeling and molecular generation techniques.
Data availability
The conventional organic compound dataset is sourced from NIST (https://webbook.nist.gov/chemistry) and PubChem (https://pubchem.ncbi.nlm.nih.gov). The polymer dataset originates from collections made in 2022 and sourced from the PolyInfo database (https://polymer.nims.go.jp). The MOF dataset is generated by Tobacco46 and cross-checked with the provided MOFX-DB database (https://mof.tech.northwestern.edu/databases). The complete full step matrix (MSF) generation code is provided to GitHub (http://github.com/fangyouyan). The runtime environment is based on Linux with Python version 3.8.10, RDKit18 version 2023.9.5, using C++ standard 17, and GCC version 8.4.0. All these essential software packages are open-source.Author contributions
F. Y. Y. came up with the original idea; J. L. X., X. J. F. and F. Y. Y. contributed to method development; J. L. X. carried out the computations; J. L. X. and X. J. F. analyzed the data; J. L. X. wrote the manuscript; Q. W. and Q. Z. Q. jointly supervised the project; J. X. X., Y. J. W., H. R. N., and Y. G. reviewed and edited the manuscript and contributed to useful discussions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (22278319).Notes and references
- T. Le, V. C. Epa, F. R. Burden and D. A. Winkler, Chem. Rev., 2012, 112, 2889–2919 CrossRef CAS PubMed.
- W. P. Walters and R. Barzilay, Acc. Chem. Res., 2020, 54, 263–270 CrossRef.
- D. M. Anstine and O. Isayev, J. Am. Chem. Soc., 2023, 145, 8736–8750 CrossRef CAS.
- Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, Chem. Sci., 2018, 9, 513–530 RSC.
- A. C. Mater and M. L. Coote, J. Chem. Inf. Model., 2019, 59, 2545–2559 CrossRef CAS PubMed.
- P. Panwar, Q. Yang and A. Martini, J. Chem. Inf. Model., 2023, 64(7), 2760–2774 CrossRef PubMed.
- Q. Yang, Y. Li, J. D. Yang, Y. Liu, L. Zhang, S. Luo and J. P. Cheng, Angew. Chem., 2020, 132, 19444–19453 CrossRef.
- G. Qin, Y. Wei, L. Yu, J. Xu, J. Ojih, A. D. Rodriguez, H. Wang, Z. Qin and M. Hu, J. Mater. Chem. A, 2023, 11, 5801–5810 RSC.
- J. Burés and I. Larrosa, Nature, 2023, 613, 689–695 CrossRef PubMed.
- L. C. Gallegos, G. Luchini, P. C. St. John, S. Kim and R. S. Paton, Acc. Chem. Res., 2021, 54, 827–836 CrossRef CAS.
- J. P. Reid and M. S. Sigman, Nature, 2019, 571, 343–348 CrossRef CAS PubMed.
- C. Altintas, O. F. Altundal, S. Keskin and R. Yildirim, J. Chem. Inf. Model., 2021, 61, 2131–2146 CrossRef CAS PubMed.
- R. Gorantla, A. Kubincova, B. Suutari, B. P. Cossins and A. S. Mey, J. Chem. Inf. Model., 2024, 64, 1955–1965 CrossRef CAS PubMed.
- T.-Z. Long, D.-J. Jiang, S.-H. Shi, Y.-C. Deng, W.-X. Wang and D.-S. Cao, J. Chem. Inf. Model., 2024, 64(8), 3222–3236 CrossRef CAS PubMed.
- R. Todeschini and V. Consonni, Handbook of Molecular Descriptors, John Wiley & Sons, 2008 Search PubMed.
- A. Mauri, V. Consonni, M. Pavan and R. Todeschini, Match, 2006, 56, 237–248 CAS.
- G. Landrum, RDKit: A software suite for cheminformatics, computational chemistry, and predictive modeling, ed. G. Landrum, 2013, vol. 8, p. 5281 Search PubMed.
- RDKit: Open-Source Chemoinformatics, https://www.rdkit.org/ Search PubMed.
- C. W. Coley, W. H. Green and K. F. Jensen, J. Chem. Inf. Model., 2019, 59, 2529–2537 CrossRef CAS PubMed.
- F. Sadeghi, A. Afkhami, T. Madrakian and R. Ghavami, Sci. Rep., 2022, 12, 6090 CrossRef CAS PubMed.
- B. Souyei, S. Meneceur and A. Khechekhouche, Mater. Today: Proc., 2022, 51, 2157–2162 CAS.
- J. Yang, L. Tao, J. He, J. R. McCutcheon and Y. Li, Sci. Adv., 2022, 8, eabn9545 CrossRef CAS PubMed.
- F. Yan, S. Xia, Q. Wang and P. Ma, J. Chem. Eng. Data, 2012, 57, 805–810 CrossRef CAS.
- H. Niu, Y. Zhang, Q. Jia, Q. Wang and F. Yan, Chem. Eng. Sci., 2024, 119835 CrossRef CAS.
- X. Liu, Y. Gu, M. Yu, Q. Jia, Y.-N. Zhou, F. Yan and Q. Wang, ACS Sustain. Chem. Eng., 2023, 11, 13429–13440 CrossRef CAS.
- H. Niu, J. Wang, Q. Jia, Q. Wang, J. Zhao and F. Yan, Chem. Eng. Sci., 2024, 284, 119484 CrossRef CAS.
- M. Yu, Y. Shi, Q. Jia, Q. Wang, Z.-H. Luo, F. Yan and Y.-N. Zhou, J. Chem. Inf. Model., 2023, 63, 1177–1187 CrossRef CAS PubMed.
- G. Corso, H. Stark, S. Jegelka, T. Jaakkola and R. Barzilay, Nat. Rev. Methods Primers, 2024, 4, 17 CrossRef CAS.
- X. Fang, L. Liu, J. Lei, D. He, S. Zhang, J. Zhou, F. Wang, H. Wu and H. Wang, Nat. Mach. Intell., 2022, 4, 127–134 CrossRef.
- K. Atz, F. Grisoni and G. Schneider, Nat. Mach. Intell., 2021, 3, 1023–1032 CrossRef.
- S. D'Souza, K. Prema and S. Balaji, Drug Discovery Today, 2020, 25, 748–756 CrossRef PubMed.
- G. Zhou, Z. Gao, Q. Ding, H. Zheng, H. Xu, Z. Wei, L. Zhang and G. Ke, ChemRxiv, 2023, DOI:10.26434/chemrxiv-2022-jjm0j-v4.
- Y. Li, J. Pei and L. Lai, Chem. Sci., 2021, 12, 13664–13675 RSC.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- O. Mahmood, E. Mansimov, R. Bonneau and K. Cho, Nat. Commun., 2021, 12, 3156 CrossRef CAS PubMed.
- T. Sousa, J. Correia, V. Pereira and M. Rocha, J. Chem. Inf. Model., 2021, 61, 5343–5361 CrossRef CAS PubMed.
- S. R. Krishnan, N. Bung, S. R. Vangala, R. Srinivasan, G. Bulusu and A. Roy, J. Chem. Inf. Model., 2021, 62, 5100–5109 CrossRef PubMed.
- S. Hougardy, Inf. Process. Lett., 2010, 110, 279–281 CrossRef.
- R. W. Floyd, Commun. ACM, 1962, 5, 345 CrossRef.
- Gaussian, https://gaussian.com/ Search PubMed.
- HyperChem, http://www.hypercubeusa.com/ Search PubMed.
- National Institute of Standards and Technology (NIST), https://webbook.nist.gov/chemistry/, accessed 2022 Search PubMed.
- PubChem Database, https://pubchem.ncbi.nlm.nih.gov/ Search PubMed.
- Polymer Database (PoLyInfo), http://polymer.nims.go.jp/index_en.html Search PubMed.
- Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Cryst. Growth Des., 2017, 17, 5801–5810 CrossRef.
- L. D. Keer, K. I. Kilic, P. H. M. V. Steenberge, L. Daelemans, D. Kodura, H. Frisch, K. D. Clerck, M.-F. Reyniers, C. Barner-Kowollik, R. H. Dauskardt and D. R. D'hooge, Nat. Mater., 2021, 20, 1422–1430 CrossRef PubMed.
- MOFX-DB Database, https://mof.tech.northwestern.edu/databases Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00125g |
| This journal is © The Royal Society of Chemistry 2024 |