Open Access Article
Open Access ArticleAnisotropic atomic displacements, local orthorhombicity and anomalous local magnetic moment in Ba0.6K0.4Fe2As2 superconductor
L.
Tortora
a,
G.
Tomassucci
 a,
G. M.
Pugliese
a,
M. Y.
Hacisalihoglu
a,
G. M.
Pugliese
a,
M. Y.
Hacisalihoglu
 a,
L.
Simonelli
a,
L.
Simonelli
 b,
C.
Marini
b,
G.
Das
b,
C.
Marini
b,
G.
Das
 c,
S.
Ishida
c,
S.
Ishida
 d,
A.
Iyo
d,
A.
Iyo
 d,
H.
Eisaki
d,
H.
Eisaki
 d,
T.
Mizokawa
d,
T.
Mizokawa
 e and
N. L.
Saini
e and
N. L.
Saini
 *a
*a
aDipartimento di Fisica, Universitá di Roma “La Sapienza” – P. le Aldo Moro 2, 00185 Roma, Italy. E-mail: naurang.saini@roma1.infn.it
bCELLS - ALBA Synchrotron Radiation Facility, Carrer de la Llum 2-26, 08290, Cerdanyola del Valles, Barcelona, Spain
cElettra Sincrotrone Trieste, Strada Statale 14, Km 163.5, Basovizza, 34149 Trieste, Italy
dNational Institute of Advanced Industrial Science and Technology (AIST), Tsukuba, Ibaraki 305-8568, Japan
eDepartment of Applied Physics, Waseda University, Tokyo 169-8555, Japan
First published on 7th August 2024
Abstract
We have investigated the in-plane local structure of the Ba0.6K0.4Fe2As2 superconductor by polarized Fe K-edge extended X-ray absorption fine structure (EXAFS) measurements with temperature. The near neighbor bond distances and their stiffness, measured by polarized EXAFS in two orthogonal directions, are different suggesting in-plane anisotropy of the atomic displacements and local orthorhombicity in the title system. The X-ray absorption near edge structure (XANES) spectra reveal anisotropy of valence electronic structure that changes anomalously below ∼100 K. The local iron magnetic moment, measured by Fe Kβ X-ray emission spectroscopy (XES), increases below the anomalous temperature and shows a decrease in the vicinity of the superconducting transition temperature (Tc ∼ 36 K). The results provide a clear evidence of coupled local lattice, electronic and magnetic degrees of freedom to induce possible nematic fluctuations in an optimally hole doped iron-based superconductor.
1 Introduction
Iron-based superconductors have been the focus of debate and, in particular, for the still unknown nature of electron pairing in these materials. These systems are in fact characterized by a complex temperature-doping phase diagram, in which different structural and magnetic phases are often overlapped.1–5 Almost all members of this family present a tetragonal unit cell at room temperature, which undergoes a structural (tetragonal to orthorhombic) and magnetic (to striped antiferromagnetic (AFM)) phase transition at lower temperature. These transitions are suppressed by doping with the emergence of a superconducting dome characterized by a Tc, up to ∼55 K. In addition, these materials are characterized by a multiband electronic structure in which five Fe 3d bands are filled by six electrons resulting in a complex orbital structure to form the Fermi surface.6,7 The presence of Fermi surface nesting along the (0, π) or (π, 0) directions led many to speculate that some sort of spin-density-wave (SDW) related pairing might be driving the superconductivity in these compounds, although the idea remains heavily debated.8,9 The multi-orbital electronic state makes it hard to identify the leading order parameter for the phase transitions in iron-based compounds, as the magnetic, orbital and structural degrees of freedom of these systems are intertwined.5,10,11 Furthermore, exotic magnetic phases have been observed in some of these systems, such as a very rare hedgehog spin-vortex crystal phase in CaK(Fe1−xNix)4As4 and LaFeAs1−xOPx,12,13 while a nematic-superconducting state is commonly found in iron-based superconductors.11,14–19Usually, the insurgence of the nematic phase is accompanied by a symmetry breaking of the crystal unit cell, which loses the C4 rotational symmetry transition from the high temperature tetragonal phase to the low temperature orthorhombic configuration.11,14,15,18,19 In most compounds this structural phase transition occurs at a temperature TS in the vicinity of the magnetic transition temperature TN, possibly suggesting that the highly discussed nematic order may be a consequence of a change in the local structure.20,21 On the other hand, the magnetic order itself breaks the C4 rotational symmetry, making these compounds a viable choice for investigating such phenomena.
Among iron-based materials, BaFe2As2 has tetragonal structure at room temperature (Fig. 1) that undergoes structural phase transition at TS and magnetic phase transition at TN (with TS ∼ TN) and, when doped, exhibits superconductivity in the proximity of the argued nematic quantum critical point. However, there is no evidence of any lower-symmetry crystal environment around the optimum doping although in-plane anisotropy has been indicated in different degrees of freedoms.22–29 The in-plane anisotropy, assigned to nematic fluctuations, has been observed under uniaxial strain field also in doped iron-based compounds including in the hole doped BaFe2As2.30,31
 | ||
| Fig. 1 (a) Crystal unit cell of (Ba, K)Fe2As2 system plotted by Vesta;32 (b) temperature dependent magnetic susceptibility of Ba0.6K0.4Fe2As2 single crystal showing a sharp superconducting transition at Tc ∼ 36 K.; structural cartoons showing experimental geometries for the Fe K-edge, i.e. E‖a (c) and E‖b (d). | ||
On the other hand, local structure investigations by X-ray diffraction pair distribution function (PDF) on the isostructural Sr1−xNaxFe2As2 have revealed local orthorhombicity in the long range tetragonal phase,33,34 assigned to the nematic fluctuations that may last up to much higher temperature than the TS. The coherence length of the observed local orthorhombicity has been estimated to be in the range of 1–3 nm. Such a local orthorhombicity has been observed also in NaFe1−xNix As superconductor35 using X-ray and neutron diffraction PDF. Also, similar approach has been used to unearth nematic fluctuations in a Mott insulator La2O2Fe2OM2 (M = S, Se).36,37 In all these studies instantaneous local orthorhombic fluctuations slower than ∼10−13 s have been probed.
In this work, we have exploited temperature dependent X-ray absorption fine structure (XAFS) spectroscopy,38–40 a site selective local (∼1 nm) and fast (∼10−15 s) experimental probe of instantaneous atomic displacements, to determine the local orthorhombicity in an optimally hole doped iron-based superconductor. In particular, we show that the local structure of Ba0.6K0.4Fe2As2 is characterized by anisotropic atomic displacements and a local orthorhombicity. These displacements are probed by polarized extended X-ray absorption fine structure (EXAFS) analyses as a function of temperature on a single crystal sample. In the EXAFS process, photoelectron excited from a core-level of the selected atom travels in the structure as an electron wave, that gets scattered from the near-neighbor atoms and hence generates oscillations in the energy dependent X-ray absorption coefficient. If the X-ray beam is polarized, the photoelectron wave travels in the polarization direction, therefore, the information contained is directional with the length scale limited by the mean-free path (∼1 nm) of the excited photoelectron. In the present case, the polarization of the X-ray beam was confined within the Fe–Fe layer in the two orthogonal directions, i.e. E‖a and E‖b (see, e.g. the Fig. 1). Apart from differing bondlengths due to local orthorhombicity at a length scale of ∼1 nm, an anisotropic bond stiffness, determined by the temperature dependence of EXAFS Debye Waller factors38–40 has been observed. The X-ray absorption near edge structure (XANES) spectra are consistent with the anisotropic local geometry and valence electronic structure. The valence electronic states show an anomalous change ∼100 K. The results on the local structure and the valence electronic states are combined with the study of the local magnetic moment of iron, determined by Fe Kβ X-ray emission spectroscopy (XES)41 that reveals an anomalous increase below ∼100 K followed by a decrease around the Tc ∼ 36 K of the system. The results are discussed in the frame of nematic fluctuations in the optimally doped iron-based superconductors.
2 Experimental details
A single crystal of Ba0.6K0.4Fe2As2 sample showing a sharp superconducting transition below ∼36.1 K (Fig. 1b), was used for the XAFS and XES measurements. The sample, was characterized for its average structure and transport properties before the XAFS and XES measurements. Details on the synthesis and basic characterization of the sample can be found elsewhere.42 The Fe K-edge (7112 eV) measurements were performed in transmission mode at the XAFS beamline43 of Elettra synchrotron in Trieste (beam size ∼500 × 500 μm2). The bending magnet source at this beamline was monochromatized using a double crystal Si(111) monochromator with the measurement system containing three ionisation chambers: two for measuring the incident (I0) and transmitted (It) X-ray intensity, and one for the transmission of a reference sample. The single crystal sample was exfoliated to obtain required thickness for the transmission measurements. The sample was rotated by 90° within the azimuth for the measurements to keep the polarization parallel to the a (E‖a) and b (E‖b) axes within the plane (Fig. 1). The measurements were repeated in part at the CLAESS beamline44 of the 3 GeV ALBA synchrotron radiation facility in Cerdanyola del Valles (Barcelona) using similar transmission XAFS set-up (beam size ∼200 × 200 μm2).The Fe Kβ XES measurements were carried out using the CLEAR spectrometer45 at the CLAESS beamline, that is based on a diced Si(333) dynamically bent analyzer crystal and a position-sensitive Mythen detector. The data on the Fe Kβ lines were acquired by exciting the sample well above the Fe K-edge, with a total energy resolution of ∼0.9 eV. A minimum of four to five absorption/emission scans were acquired at each temperature. The sample temperature was carefully monitored and controlled with an accuracy of ± 1 K. A standard procedure based on spline fit was used for the EXAFS extraction38,39 while the XANES spectra were normalized with respect to a linear fit to the data in the extended region after subtraction of pre-edge background.38 Background signal was removed through the standard procedure performing a polynomial spline fit using the ATHENA software.46
3 Results and discussions
The Fe K-edge X-ray absorption fine structure measurements were carried out at different temperatures in the range of 20–300 K. Fig. 2 displays the Fourier transforms (FTs) of the EXAFS oscillations (multiplied by a factor k2) at several temperatures. The FTs are performed using a Gaussian window with the EXAFS k-range being 2.8–15 Å−1. The upper panel corresponds to the data in the E‖a polarization (Fig. 1c) while the lower panel represents the E‖b polarization (Fig. 1d). The main peak in the Fe K-edge FT magnitude (left panel), centered at ∼2.2 Å, contains contribution of the nearest neighbor As atoms and the next nearest neighbor Fe atoms in the respective polarization directions. The longer distances contributions in the structure can be seen beyond ∼3 Å in the FTs of the EXAFS oscillations. The modulus of the FTs reveals some apparent differences in the atomic distribution in the two polarizations. One can make three observations, i.e.: (i) the overall magnitude of the main peak is lower in the E‖b direction; (ii) the position of the main FT peak differs slightly in the two polarizations; and (iii) the temperature dependence is different in the two polarizations. On the other hand, the longer distances contributions show highly damped magnitude indicating disordered structure of Ba0.6K0.4Fe2As2.The differences in the local structure within the ab-plane can be quantified by EXAFS model fits. This has been done using the standard EXAFS equation with single scattering approximation.38,39 The average structure measured by diffraction3,42 has been the starting model for the Fe K-edge EXAFS containing the nearest neighbor As atoms and next nearest neighbor Fe atoms with two contributions mixed showing main peak as broad structure at ∼2.2 Å. The EXCURVE 9.275 code was used to calculate the backscattering amplitudes and the phase shift functions.47 The same code was used to perform the EXAFS model fits, in which S02 (amplitude reduction factor) and E0 (photoelectron energy zero) were fixed after a fit on the reference. The atomic positions Ri and related σi2 (describing the Debye–Waller factor) were the only free parameters in the model fits. Within the reported uncertainties the same results were obtained using the scattering amplitudes and phase shifts calculated by FEFF code48 and the model fits carried out by WINXAS package.49 The number of independent data points,  , was about 15 (interval in k space Δk = (15.0–2.8) Å−1 = 12.2 Å−1 and interval in R space ΔR = (3.1–1.2) Å = 1.9 Å) for the Fe K-edge EXAFS models fits in which the number of variables were 4. The model fits in the real space are shown in Fig. 2 (solid lines).
, was about 15 (interval in k space Δk = (15.0–2.8) Å−1 = 12.2 Å−1 and interval in R space ΔR = (3.1–1.2) Å = 1.9 Å) for the Fe K-edge EXAFS models fits in which the number of variables were 4. The model fits in the real space are shown in Fig. 2 (solid lines).
Fig. 3 shows the near neighbors distances determined by the polarized EXAFS measured in the two orthogonal directions with the polarizations E‖a and E‖b. The local Fe–As bonds (lower panel), measured by Fe K-edge EXAFS in the E‖a direction is slightly longer (∼0.02 Å) than the same distance measured in the E‖b geometry. The bondlengths measured in the two geometries have similar thermal expansion and the difference between the two hardly shows any temperature dependence. The differing Fe–As bondlengths can be understood by simple geometrical considerations displayed pictorially in Fig. 1(c and d) in which the Fe atoms have symmetrical form in the ab-plane while the As atoms are asymmetric. The asymmetrical form is related with differing occupation of px and py orbitals in the layered Ba0.6K0.4Fe2As2. Such an asymmetric shape will lead the Fe–As distance to be different in the two orthogonal polarizations if measured by the Fe K-edge. Indeed, linear dichroism in an isostructural EuFe1.8Co0.2As2 superconductor reveals uneven occupation of Fe dxz and dyz orbitals50 hybridized with As 4px,y orbitals.51
Similar to Fe–As, the Fe–Fe bondlengths are also different in the two orthogonal polarizations. The Fe–Fe distance, measured in the two polarizations can be different if there is a local C4 symmetry breaking. The local Fe–Fe bonds (middle panel), measured in the E‖a polarization is slightly longer (∼0.03 Å) than the one measured in the E‖b geometry. Such a local orthorhombicity is consistent with the one measured in undoped BaFe2As220,52 at low temperature. The local orthorhombicity has been estimated as (Ra − Rb)/(Ra + Rb) and shown plotted in Fig. 3 (upper), where Ra and Rb are the Fe–Fe bond lengths measured in the two polarization geometries. Remarkably the temperature dependence of the local orthorhombicity is similar to the one found in Sr1−xNaxFe2As2 by PDF.33,34 It should be noted that the local orthorhombicity measured in this work is slightly larger than the one measured by PDF, however, it is not surprising considering the fact that the EXAFS is more than hundred times faster that the PDF technique. Although small, the local orthorhombicity shows an increase at lower temperature. Nevertheless, the differing bondlengths in the two polarizations indicate local orthorhombicity and anisotropic atomic displacements within the ab plane. It should be mentioned that experimental approach used in this work is similar to the one already exploited for high Tc cuprates showing substantial differences in the bondlength distributions and the related atomic pair correlations.53,54 Similar approach has been exploited recently to measure linear dichroism signal in an isostructural iron-based EuFe1.8Co0.2As2 superconductor revealing uneven occupation of Fe dxz and dyz orbitals.50
The differing temperature dependence of the FT amplitudes in Fig. 2 indicates different characteristics of the Fe–As and Fe–Fe bondlengths that can be quantified by the temperature dependent mean square relative displacement (MSRD) parameter σi2. Indeed, bond stiffness is described by the Einstein frequency (ωE), i.e., κ = μωE2 with the μ being the reduced mass of the two bonded atoms. This information is accessible from the temperature dependence of σi2. In the harmonic approximation the σi2 can be described by the Einstein model,39,40,55i.e.,
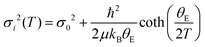 | (1) |
Fig. 4 shows the σi2 of Fe–As and Fe–Fe bondlengths measured by the Fe K-edge EXAFS in the two orthogonal directions. The temperature dependent behavior of the σi2 can be described by the Einstein model to determine the θE, i.e. the Einstein frequency (ωE). The Einstein temperatures determined for the Fe–As and Fe–Fe bondlengths are found to be ∼339 K and ∼237 K respectively in the E‖a polarization. The Einstein temperatures seem higher in the E‖b geometry, found to be ∼365 K and ∼266 K respectively for the two bondlengths suggesting anisotropic bond strength with the stiffer bonding along E‖b. The above results suggest anisotropic atomic fluctuations within the ab-plane of the optimally doped Ba0.6K0.4Fe2As2 superconductor. Therefore, the broken C4 symmetry due to local orthorhombicity fluctuations, is characterized by anisotropic atomic displacements within the ab-plane. These details on the fluctuating nematic phase in the optimally doped Ba0.6K0.4Fe2As2 superconductor are too subtle to be detected by long range experimental techniques without any external stimulant. Here, we are not ruling out mixing of nematic domains within the beam size with the observed anisotropy being due to inequivalent population of these domains. However, the fact that the anisotropy does not depend on the beam size, it should be intrinsic to the system.
The X-ray absorption near edge structure (XANES) is a very sensitive probe of the local geometry and the valence electronic states38,39 that can add further information on the observed anisotropy. Fig. 5 shows normalized Fe K-edge XANES spectra of Ba0.6K0.4Fe2As2 at 30 K (upper) and 300 K (lower) in the two orthogonal polarizations E‖a and E‖b. The XANES spectra are characterized by three main features A1, A2 and B, together with a clear pre-peak P. The features A1, A2 and B, well separated from the pre-peak P, are mainly due to the dipole allowed transitions from the Fe 1s to the unoccupied Fe 4p states in the continuum thus carrying useful information on the local geometry. The pre-peak feature P is due to quadrupole transition from the Fe 1s to the unoccupied Fe 3d states admixed with the p orbitals and directly probes the electronic structure of the unoccupied states and the Fe 3d–As 4p hybridization.51,56
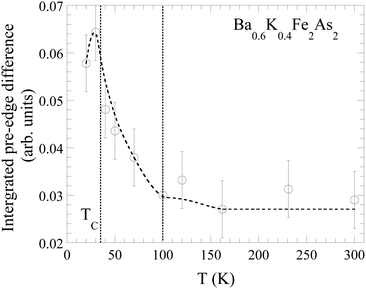
The XANES spectra in the two polarizations reveal some apparent differences. For instance, the energy of the spectral features is higher in the E‖b geometry as shown by the spectral difference (multiplied by 2) displayed in Fig. 5. The maximum difference is ∼6% with a clear change in the pre-peak P as well as in the continuum part at energy less than that of the feature B. Indeed, the spectral weight of the pre-peak P and continuum features seems higher due to higher Fe 3d–As 4p hybridization and lower energy for the E‖a direction. The lower energy of XANES features in the E‖a polarization is consistent with the longer near neighbor distances observed by the EXAFS analysis. We have plotted the integrated intensity difference of the pre-edge peak P as a function of temperature in Fig. 6. The pre-peaks differ in their spectral weight even at 300 K due to differing hybridization, however this spectral difference shows a clear increase below ∼100 K. Since the pre-peak P is mainly given by the Fe 1s to 3d transition, the increased difference suggests increased difference in 3d–4p hybridization in the two directions below ∼100 K. Although present at higher temperature, the increased electronic anisotropy below ∼100 K is a signature of the electronic nematic fluctuations in Ba0.6K0.4Fe2As2.57–59 It is also consistent with soft X-ray absorption study reporting uneven dxz and dyz population in EuFe1.8Co0.2As2.50
It is fair to partially summarize the EXAFS and XANES results obtained on Ba0.6K0.4Fe2As2. Both EXAFS and XANES reveal a clear anisotropy in the first order correlation function (near neighbor distances) and in the higher order correlation function (local geometry). Since the length scale is ∼1 nm and the time scale is ∼1 fs, the anisotropy is due to instantaneous orthorhombic fluctuations in the system. The question is up to what extent the observed anisotropy can be associated with the commonly discussed nematic phase in the iron-based superconductors. The primary difficulty is due to the fact that the average orthorhombic phase with static antiferromagnetism (AFM) and orbital order in BaFe2As2 is suppressed in the optimally hole doped Ba0.6K0.4Fe2As2 even at low temperature, whereas the observed anisotropy is present at least up to 300 K. However, considering the fact that the intrinsic time scale of EXAFS and XANES is smaller than ∼10−15 s, the observed instantaneous atomic correlation functions with anisotropy can be safely attributed to local orthorhombicity and nematic fluctuations at the length scale of ∼1 nm, that are observable also at much higher temperature and in an optimally doped Ba0.6K0.4Fe2As2 superconductor.
It should be recalled that the local orthorhombicity tends to increase at lower temperature (Fig. 3), however, without any apparent anomaly. Instead, the valence electronic structure anisotropy shows an abrupt increase below ∼100 K (Fig. 6) which is rather close to the TS or TN of BaFe2As2. The fact that electronic nematic phase is known to appear around ∼100 K, we do not rule out additional triggers to affect the fluctuating nematicity driven by the local orthorhombicity in Ba0.6K0.4Fe2As2. One of the possible triggers can be magnetoelastic coupling that is known to play an important role in the iron-based superconductors. The importance of magnetoelastic coupling has been shown by a variety of experiments in these materials.14,15 Indeed, it is common to find indicators of nematicity in the magnetic response function. Here, we have determined the local magnetic moment as a function of temperature in Ba0.6K0.4Fe2As2 to explore a possible correlation between the magnetic response and the fluctuating nematic phase. The local magnetic moment has been determined by Fe Kβ XES measurements performed on the same sample.
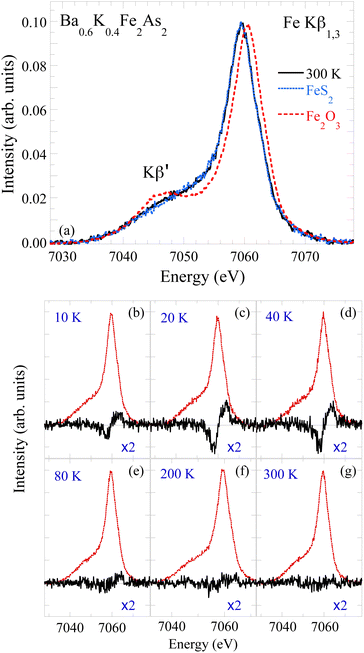
Fig. 7(a) shows the Fe Kβ1,3 XES (3p → 1s) of Ba0.6K0.4Fe2As2 at 300 K compared with the spectra of three references: Fe2O3 carrying magnetic moment of ∼4.6μB, the non-magnetic FeS2 and metallic iron carrying magnetic moment of ∼0.9μB. The spectra are shown normalized with respect to the total integrated area. The Fe Kβ XES probes the local magnetic moment due to (3p, 3d) exchange interactions,41 modifying the Kβ XES profile and splitting between the main Kβ1,3 emission line and the satellite Kβ′. The Kβ′ spectral weight as well as the Kβ1,3 energy increases with increasing 3d spin magnetic moment.41 Thus the energy position of the Kβ1,3 provides similar information on the magnetic moment as the Kβ′ satellite weight, reflecting the effective number of unpaired 3d electrons.41 The XES spectra reveal non-negligible change as a function of temperature due to differing local Fe magnetic moment.41,60–64 The local Fe magnetic moment μB can be quantitatively evaluated from the integrated area of the absolute XES intensity difference (IAD) with respect to a nonmagnetic reference sample (ref. 62–64). Fig. 7(b)–(g) show the XES on Ba0.6K0.4Fe2As2 at several temperatures together with the differences with respect to the one of FeS2. The difference spectra show a clear evolution by lowering the sample temperature from 300 K.
Fig. 8 shows the temperature dependence of the local magnetic moment estimated by the IAD procedure and comparison with the known magnetic moments of the three references. The magnetic moment at room temperature is ∼0.9μB, consistent with the magnetic moment reported earlier in the XES studies,63,64 albeit slightly different from the fluctuating moment reported by neutron scattering.5 By cooling down, the local moment shows an increase below ∼100 K, before showing a drop in the vicinity of the superconducting transition temperature. Considering the above, the increasing local magnetic moment below ∼100 K is likely to be associated with the nematic fluctuations in Ba0.6K0.4Fe2As2. On the other hand, decrease below the superconducting transition temperature is an indication of quenching of the local Fe magnetic moment, similar to the one found in other iron-based superconductors.65–67 The suppression of the magnetic moment is also suggestive of its role in the superconductivity of Ba0.6K0.4Fe2As2.
Looking at the electronic anisotropy (Fig. 6), it seems that the local magnetic moment correlates with the nematic fluctuations in Ba0.6K0.4Fe2As2. It is interesting to note that, while the local orthorhombicity hardly shows any anomalous change, the linear dichroism of the 1s to 3d electronic transition (in the XANES) and the local magnetic moment (in the XES), both showing a clear increase ∼100 K. Therefore, the system may host two kinds of nematicity, i.e., the former is due to orbital–lattice coupling while the latter is driven by the spin–lattice coupling. Nevertheless, the results suggest strong coupling of lattice, charge and magnetic degrees of freedom to drive nematic fluctuations in the iron-based superconductors.
4 Summary and conclusions
In summary, we have studied the anistropic local structure of an optimally doped Ba0.6K0.4Fe2As2 superconducting single crystal by polarized XAFS measurements performed with polarization of the X-ray beam parallel to the two in-plane directions (E‖a and E‖b). The local structure is found to be anisotropic with differing Fe–As and Fe–Fe bond lengths and their stiffness. Unlike the known average structure, the local structure shows clear traces of lower symmetry C2 phase in Ba0.6K0.4Fe2As2 even at 300 K suggesting local and instantaneaous orthorhombicity at the length scale of ∼1 nm. It is interesting to note that, using the experimental approach based on the polarized XAFS spectroscopy we are able to uncover the intrinsic anisotropy without using any external stimulant such as uniaxial pressure. The local orthorhombicity is consistent with the XANES results providing direct information on the local geometry and the valence electronic states. The electronic anisotropy due to differing orbital hybridization shows an anomalous change below ∼100 K where the commonly discussed nematic fluctuations occur. Furthermore, the local iron-magnetic moment measured by Fe Kβ XES shows an increase around the same temperature followed by a decrease in the proximity of the superconducting transition temperature. The results suggest that the observed nematic fluctuations are likely to be coupled with the magnetic fluctuations in the optimally doped iron-based superconductors. In conclusion, the combination of single crystal sample and polarization dependence of the X-ray absorption based spectroscopy is an efficient tool to probe instantaneous local orthorhombicity and related exotic phenomena in quantum materials.Author contributions
N. L. S., H. E. and T. M. Conceptualization. L. T., G. D., S. I., A. I., L. S., C. M., H. E. and N. L. S. Investigations. L. T., G. T., G. M. P., M. Y. H. and N. L. S. Data curation and formal analysis. L. T. and N. L. S Writing, review and editing. All authors discussed the results and commented on the manuscript.Data availability
The data that support the findings of this study are available from the corresponding author, [N. L. S.], upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the ALBA and Elettra staffs for the assistance during the measurements. We also thank G. Aquilanti for discussions and providing useful feedback on the manuscript. The work is partially supported by the Sapienza University of Rome and JSPS KAKENHI (No. JP19H05823).References
- A. Martinelli, F. Bernardini and S. Massidda, C. R. Phys., 2016, 17, 5–35 CrossRef CAS.
- Y. Gu, Z. Liu, T. Xie, W. Zhang, D. Gong, D. Hu, X. Ma, C. Li, L. Zhao, L. Lin, Z. Xu, G. Tan, G. Chen, Z. Y. Meng, Y.-F. Yang, H. Luo and S. Li, Phys. Rev. Lett., 2017, 119, 157001 CrossRef PubMed.
- X. Luo and X. Chen, Sci. China Mater., 2015, 58, 77 CrossRef CAS.
- J. Paglione and R. Greene, Nat. Phys., 2010, 6, 645–658 Search PubMed.
- P. Dai, Rev. Mod. Phys., 2015, 87, 855 CrossRef CAS.
- D. J. Singh, Phys. C, 2009, 469, 418–424 CrossRef CAS.
- K. Kuroki, S. Onari, R. Arita, H. Usui, Y. Tanaka, H. Kontani and H. Aoki, New J. Phys., 2009, 11, 025017 CrossRef.
- A. Patz, T. Li and S. Ran, et al. , Nat. Commun., 2014, 5, 3229 CrossRef PubMed.
- A. A. Kordyuk, Low Temp. Phys., 2012, 38, 888 CrossRef CAS.
- W. J. Meese, T. Vojta and R. M. Fernandes, Phys. Rev. B, 2022, 106, 115134 CrossRef CAS.
- R. M. Fernandes, A. V. Chubukov and J. Schmalian, Nat. Phys., 2014, 10, 97 Search PubMed.
- Q.-P. Ding, W. R. Meier, J. Cui, M. Xu, A. E. Böhmer, S. L. Bud'ko, P. C. Canfield and Y. Furukawa, Phys. Rev. Lett., 2018, 121, 137204 CrossRef CAS PubMed.
- R. Stadel, D. D. Khalyavin, P. Manuel, K. Yokoyama, S. Lapidus, M. H. Christensen, R. M. Fernandes, D. Phelan, D. Y. Chung, R. Osborn, S. Rosenkranz and O. Chmaissem, Commun. Phys., 2022, 5, 146 CrossRef CAS.
- A. E. Böhmer, J.-H. Chu, S. Lederer and M. Yi, Nat. Phys., 2022, 18, 1412 Search PubMed.
- J. Wang, Y. Wu, X. Zhou, Y. Li, B. Teng, P. Dong, J. He and Y. Li, Adv. Phys.: X, 2021, 6, 1878931, DOI:10.1080/23746149.2021.1878931.
- Y. Gallais and I. Paul, C. R. Phys., 2016, 17, 113–139 Search PubMed.
- J. Li, P. J. Pereira, J. Yuan, Y.-Y. Lv, M.-P. Jiang, D. Lu, Z.-Q. Lin, Y.-J. Liu, J.-F. Wang, L. Li, X. Ke, G. V. Tendeloo, M.-Y. Li, H.-L. Feng, T. Hatano, H.-B. Wang, P.-H. Wu, K. Yamaura, E. Takayama-Muromachi, J. Vanacken, L. F. Chibotaru and V. V. Moshchalkov, Nat. Commun., 2017, 8, 1880 Search PubMed.
- X. Lu, J. T. Park, R. Zhang, H. Luo, A. H. Nevidomskyy, Q. Si and P. Dai, Science, 2014, 345, 657 CrossRef CAS PubMed.
- A. E. Bohmer, F. Hardy, L. Wang, T. Wolf, P. Schweiss and C. Meingast, Nat. Commun., 2015, 6, 7911 CrossRef CAS PubMed.
- J. L. Niedziela, M. A. McGuire and T. Egami, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 174113 CrossRef.
- S. Li, M. Toyoda, Y. Kobayashi, M. Itoh, K. Ikeuchi, Y. Yoneda, A. Otani, D. Matsumura, S. Asano, J. Mizuki and M. Sato, Phys. C, 2018, 555, 45 CrossRef CAS.
- X. Chen, S. Maiti, R. M. Fernandes and P. J. Hirshfeld, Phys. Rev. B, 2020, 102, 184512 CrossRef CAS.
- S. Wu, Y. Song, Y. He, A. Frano, M. Yi, X. Chen, H. Uchiyama, A. Alatas, A. H. Said, L. Wang, T. Wolf, C. Meingast and R. J. Birgeneau, Phys. Rev. Lett., 2021, 126, 107001 CrossRef CAS PubMed.
- C. Wuttke, F. Caglieris, S. Sykora, F. Steckel, X. Hong, S. Ran, S. Khim, R. Kappenberger, S. L. Bud’ko, P. C. Canfield, S. Wurmehl, S. Aswartham, B. Buechner and C. Hess, npj Quantum Mater., 2022, 7, 82 CrossRef CAS.
- K. Ishida, M. Tsujii, S. Hosoi, Y. Mizukami, S. Ishida, A. Iyo, H. Eisaki, T. Wolf, K. Grube, H. v Lohneysenc, R. M. Fernandes and T. Shibauchi, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 6424–6429 CrossRef CAS PubMed.
- L. Liu, T. Mikami, S. Ishida, K. Koshiishi, K. Okazaki, T. Yoshida, H. Suzuki, M. Horio, L. C. C. Ambolode, II, J. Xu, H. Kumigashira, K. Ono, M. Nakajima, K. Kihou, C. H. Lee, A. Iyo, H. Eisaki, T. Kakeshita, S. Uchida and A. Fujimori, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 094503 CrossRef.
- M. Nakajima, S. Ishida, Y. Tomioka, K. Kihou, C. H. Lee, A. Iyo, T. Ito, T. Kakeshita, H. Eisaki and S. Uchida, Phys. Rev. Lett., 2012, 109, 217003 CrossRef CAS PubMed.
- J. Hecher, S. Ishida, D. Song, H. Ogino, A. Iyo, H. Eisaki, M. Nakajima, D. Kagerbauer and M. Eisterer, Phys. Rev. B, 2018, 97, 014511 CrossRef CAS.
- S.-F. Wu, W.-L. Zhang, V. K. Thorsmolle, G. F. Chen, G. T. Tan, P. C. Dai, Y. G. Shi, C. Q. Jin, T. Shibauchi, S. Kasahara, Y. Matsuda, A. S. Sefat, H. Ding, P. Richard and G. Blumberg, Phys. Rev. Res., 2020, 2, 033140 CrossRef CAS.
- I. R. Fisher, L. Degiorgi and Z. X. Shen, Rep. Prog. Phys., 2011, 74, 124506 CrossRef.
- L. Chen, T. T. Han, C. Cai, Z. G. Wang, Y. D. Wang, Z. M. Xin and Y. Zhang, Phys. Rev. B, 2021, 104, L060502 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS.
- B. A. Frandsen, K. M. Taddei, M. Yi, A. Frano, Z. Guguchia, R. Yu, Q. Si, D. E. Bugaris, R. Stadel, R. Osborn, S. Rosenkranz, O. Chmaissem and R. J. Birgeneau, Phys. Rev. Lett., 2017, 119, 187001 CrossRef PubMed.
- B. A. Frandsen, K. M. Taddei, D. E. Bugaris, R. Stadel, M. Yi, A. Acharya, R. Osborn, S. Rosenkranz, O. Chmaisse and R. J. Birgeneau, Phys. Rev. B, 2018, 98, 180505 CrossRef CAS.
- W. Wang, Y. Song, C. Cao, K.-F. Tseng, T. Keller, Y. Li, L. W. Harriger, W. Tian, S. Chi, R. Yu, A. H. Nevidomskyy and P. Dai, Nat. Commun., 2018, 9, 3128 CrossRef PubMed.
- B. Karki, A. Alfailakawi, B. A. Frandsen, M. S. Everett, J. C. Neuefeind, B. Xu, H. Wang, M. Fang and B. Freelon, Phys. Rev. B, 2021, 104, 064101 CrossRef CAS.
- B. Freelon, R. Sarkar, S. Kamusella, F. Brueckner, V. Grinenko, S. Acharya, M. Laad, L. Craco, Z. Yamani, R. Flacau, I. Swainson, B. Frandsen, R. Birgeneau, Y. Liu, B. Karki, A. Alfailakawi, J. C. Neuefeind, M. Everett, H. Wang, B. Xu, M. Fang and H.-H. Klauss, npj Quantum Mater., 2021, 6, 4 CrossRef CAS.
- D. C. Koningsberger and R. Prins, X-ray Absorption: Principles, Applications, Techniques of EXAFS, SEXAFS and XANES, Chemical Analysis: A Series of Monographs on Analytical Chemistry and Its Applications, Wiley, 1988 Search PubMed.
- G. Bunker, Introduction to XAFS, Cambridge University Press, 2010 Search PubMed.
- See, e.g. a review by J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621 CrossRef CAS.
- P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65 CrossRef CAS.
- K. Kihou, T. Saito, K. Fujita, S. Ishida, M. Nakajima, K. Horigane, H. Fukazawa, Y. Kohori, S. Uchida, J. Akimitsu, A. Iyo, C.-H. Lee and H. Eisaki, J. Phys. Soc. Jpn., 2016, 85, 034718 CrossRef.
- A. Di Cicco, G. Aquilanti, M. Minicucci, E. Principi, N. Novello, A. Cognigni and L. Olivi, J. Phys.: Conf. Ser., 2009, 190, 012043 CrossRef.
- L. Simonelli, C. Marini, W. Olszewski, M. Avila Perez, N. Ramanan, G. Guilera, V. Cuartero and K. Klementiev, Cogent Phys., 2016, 3, 1231987 Search PubMed.
- L. Simonelli, C. Marini, L. Ribo, R. Homs, J. Avila, D. Heinis, I. Preda and K. Klementiev, J. Synchrotron Radiat., 2023, 30, 235–241 CrossRef CAS PubMed.
- B. Ravel and M. Newville, Phys. Scr., 2006, 115, 1007–1010 Search PubMed.
- S. J. Gurman, J. Synchrotron Radiat., 1995, 2, 56 CrossRef CAS PubMed.
- A. L. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7565 CrossRef CAS.
- T. Ressler, J. Synchrotron Radiat., 1998, 5, 118 CrossRef CAS PubMed.
- D. Rybicki, M. Sikora, J. Stępień, L. Gondek, K. Goc, T. Strączek, M. Jurczyszyn, C. Kapusta, Z. Bukowski, M. Babij, M. Matusiak and M. Zajac, Phys. Rev. B, 2020, 102, 195126 CrossRef CAS.
- B. Joseph, A. Iadecola, L. Simonelli, Y. Mizuguchi, Y. Takano, T. Mizokawa and N. L. Saini, J. Phys.: Condens. Matter, 2010, 22, 485702 CrossRef CAS PubMed.
- S. Avci, O. Chmaissem, D. Y. Chung, S. Rosenkranz, E. A. Goremychkin, J.-P. Castellan, I. S. Todorov, J. A. Schlueter, H. Claus, A. Daoud-Aladine, D. D. Khalyavin, M. G. Kanatzidis and R. Osborn, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184507 CrossRef.
- N. L. Saini, A. Lanzara, A. Bianconi and H. Oyanagi, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 11768 CrossRef CAS.
- N. L. Saini, H. Oyanagi, M. Molle, K. B. Garg, C. Kim and A. Bianconi, J. Phys. Chem. Solids, 2004, 65, 1439 CrossRef CAS.
- E. Sevillano, H. Meuth and J. Rehr, Phys. Rev. B: Solid State, 1979, 20, 4908 CrossRef CAS.
- A. G. de Figueiredo, M. R. Cantarino, W. R. da Silva Neto, K. R. Pakuszewski, R. Grossi, D. S. Christovam, J. C. Souza, M. M. Piva, G. S. Freitas, P. G. Pagliuso, C. Adriano and F. A. Garcia, Phys. Rev. B, 2022, 105, 045130 CrossRef CAS.
- M. Hirano, Y. Yamada, T. Saito, R. Nagashima, T. Konishi, T. Toriyama, Y. Ohta, H. Fukazawa, Y. Kohori, Y. Furukawa, K. Kihou, C.-H. Lee, A. Iyo and H. Eisaki, J. Phys. Soc. Jpn., 2012, 81, 054704 CrossRef.
- S.-F. Wu, P. Richard, H. Ding, H.-H. Wen, G. Tan, M. Wang, C. Zhang, P. Dai and G. Blumberg, Phys. Rev. B, 2017, 95, 085125 CrossRef.
- P. Wiecki, M. Frachet, A.-A. Haghighirad, T. Wolf, C. Meingast, R. Heid and A. E. Bohmer, Nat. Commun., 2021, 12, 4824 CrossRef CAS PubMed.
- R. D. Cowan, The Theory of Atomic Structure and Spectra, University of California Press, Berkeley, ( 1981) Search PubMed.
- G. Vankó, T. Neisius, G. Molnár, F. Renz, S. Kárpáti, A. Shukla and F. M. F. de Groot, J. Phys. Chem. B, 2006, 110, 11647 CrossRef PubMed.
- S. Lafuerza, A. Carlantuono, M. Retegan and P. Glatzel, Inorg. Chem., 2020, 59, 12518 CrossRef CAS PubMed.
- H. Gretarsson, S. R. Saha, T. Drye, J. Paglione, J. Kim, D. Casa, T. Gog, W. Wu, S. R. Julian and Y.-J. Kim, Phys. Rev. Lett., 2013, 110, 047003 CrossRef CAS PubMed.
- H. Gretarsson, A. Lupascu, J. Kim, D. Casa, T. Gog, W. Wu, S. R. Julian, Z. J. Xu, J. S. Wen, G. D. Gu, R. H. Yuan, Z. G. Chen, N.-L. Wang, S. Khim, K. H. Kim, M. Ishikado, I. Jarrige, S. Shamoto, J.-H. Chu, I. R. Fisher and Y.-J. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 100509 CrossRef.
- L. Simonelli, T. Mizokawa, M. Moretti Sala, H. Takeya, Y. Mizuguchi, Y. Takano, G. Garbarino, G. Monaco and N. L. Saini, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214516 CrossRef.
- F. Stramaglia, G. M. Pugliese, L. Tortora, L. Simonelli, C. Marini, W. Olszewski, S. Ishida, A. Iyo, H. Eisaki, T. Mizokawa and N. L. Saini, J. Phys. Chem. C, 2021, 125, 10810 CrossRef CAS.
- G. Tomassucci, L. Tortora, G. M. Pugliese, F. Stramaglia, L. Simonelli, C. Marini, K. Terashima, T. Wakita, S. Ayukawa, T. Yokoya, K. Kudo, M. Nohara, T. Mizokawa and N. L. Saini, Phys. Chem. Chem. Phys., 2023, 25, 6684–6692 RSC.
| This journal is © the Owner Societies 2024 |