Open Access Article
Open Access ArticleQuantum and statistical state-to-state studies of cold Ar + H2+ collisions†
Maarten
Konings
 *a,
Tomás
González-Lezana
*a,
Tomás
González-Lezana
 b,
Simen
Camps
b,
Simen
Camps
 a and
Jérôme
Loreau
a and
Jérôme
Loreau
 *a
*a
aKU Leuven, Department of Chemistry, Celestijnenlaan 200F, B-3001 Leuven, Belgium. E-mail: maarten.konings@kuleuven.be; jerome.loreau@kuleuven.be
bInstituto de Física Fundamental, IFF-CSIC, Serrano 123, Madrid 28006, Spain
First published on 6th August 2024
Abstract
In this work we present new state-to-state integral scattering cross sections and initial-state selected rate coefficients for the 36Ar (1S) + H2+ (X2Σg+,v = 0,j) reactive system for collision energies up to 0.1 eV (with respect to the 36Ar (1S) + H2+ (X2Σg+,v = 0,j = 0) channel). To the best of our knowledge, these cross sections are the first fully state resolved ones that were obtained by performing time-independent quantum mechanical and quantum statistical calculations. For this purpose a new full-dimensional ground state 2A′ adiabatic electronic potential energy surface was calculated at the MRCI+Q/aug-cc-pVQZ level of theory, which was fitted by means of machine learning methods. We find that a statistical quantum method and a statistical adiabatic channel model reproduce quantum mechanical initial-state selected cross sections fairly well, thus suggesting that complex-forming mechanisms seem to be playing an important role in the reaction dynamics of the reaction that was studied.
1 Introduction
The exothermic reactions,| Ar (1S) + H2+ (X2Σg+) → ArH+ (X1Σ+) + H (2S) ΔE ≈ −1.30 eV, | (1) |
| Ar+ (2P) + H2 (X1Σg+) → ArH+ (X1Σ+) + H (2S) ΔE ≈ −1.56 eV, | (2) |
The electronic potential energy surfaces (PESs) for the reactions (1) and (2) are strongly coupled in the entrance arrangements. In fact, the PES for the first reaction is the only reactive one (directly correlating to the ArH+ (X1Σ+) product), and the Ar+ + H2 reactants only react to form ArH+ + H by an electronically non-adiabatic process.
A lot of our understanding of the reactions (1) and (2) comes from several studies1–4,10,11 that have primarily focussed on the nonadiabatic reaction dynamics involving the 40Ar isotope. Such theoretical approaches were usually based on DIMZO (diatomics in molecule with zero overlap) potential energy surfaces, as first introduced by Kuntz and Roach.12
In a more recent theoretical study from 2013,13 electronically adiabatic time-dependent quantum wave packet calculations were performed on an analytical fit of the ground state ab initio PES to obtain scattering cross sections for the reaction (1) with H2+ in its ground ro-vibrational state (vH2+ = 0,jH2+ = 0), and specifically for the atomic collider 40Ar; the maximum collision energy was constrained to 1.0 eV.
Similarly to the study by Hu et al.,13 the focus in the present work is on the reaction (1). However, our aim is twofold. (i) On the one hand we introduce the first quantum mechanical fully state resolved (i.e., state-to-state) integral scattering cross sections (ICSs) for collision energies up to 0.1 eV for the competing inelastic and reactive scattering events involving the collision partners 36Ar and H2+. Restriction to the aforementioned collision energies ensures that the collision happens electronically adiabatically since the lowest two excited states of the 36ArH2+ system are not accessible in this energy regime, thereby justifying the use of a single adiabatic PES.14 As shown in a recent work,14 above 0.1 eV non-adiabatic effects come into play, thereby strongly complicating the dynamics of reaction (1).
(ii) On the other hand we wish to investigate the statistical nature of reaction (1) and the applicability of statistical approaches, such as the statistical quantum method (SQM)15,16 and the statistical adiabatic channel model (SACM),17,18 that are commonly used in molecular collision theory. The reason being that the PES for reaction (1) (and also (2)) in ref. 14 shows the presence of an energy well separating reactants from products, thus justifying the use of these techniques, as seen in previous investigations where different dynamical features have been successfully reproduced by statistical means.17–19
To accomplish said objectives, a new full-dimensional ab initio ground state PES was computed and fitted by means of machine learning (ML) techniques.14 In particular Gaussian process (GP) regression was chosen for this purpose, which represents a kernel-based non-parametric fitting strategy that has been used for the purposes of fitting electronic potential energy surfaces (PESs) of molecular systems.14,20–26 Using this new PES, accurate time-independent quantum mechanical close-coupling (CC) calculations were carried out (related to objective (i)), as well as the aforementioned SQM and much less computationally expensive SACM calculations (objective (ii)).
This article is structured as follows: Section 2 contains a discussion about the use of Gaussian processes for fitting PESs, as well as a discussion about the details of the ab initio electronic structure calculations in relation to the 36ArH2+ system. In addition, the quantum mechanical and statistical approaches used for the computation of state-to-state integral cross sections are introduced. Section 3 is devoted to the analysis of the new ground state electronic PES, as well as the CC, SQM and SACM results that were obtained. In Section 4, we summarize our findings and provide an outlook regarding future studies involving the 36ArH2+ system.
2 Theoretical methods
2.1 Potential energy surface
 | ||
| Fig. 1 The system of internal coordinates which were used for the electronic structure calculations and GP regression fit relating to the ArH2+ system. | ||
The energies defining the ground state PES (transforming according to irreducible representation A′ in Cs symmetry), were calculated at the Davidson-corrected, internally contracted multireference configuration interaction (ic-MRCI+Q) level of theory, in conjunction with the aug-cc-pVQZ one-electron basis set for all the atoms. The multiconfigurational reference wavefunction for the configuration interaction calculations was obtained by means of the state-averaged complete active space self-consistent field (SA-CASSCF) approach, the molecular orbital space of which consisting of 5 inactive orbitals (4A′ + 1A′′) and 6 active orbitals (5A′ + 1A′′), and thus 9 active electrons. The molecular orbitals were obtained by minimizing the average of the electronic energy of the three lowest states (2A′ + 1A′′) with equal weights; this because of the involvement of the excited states in the diabatic fit for the small H2+ internuclear distances.
At this stage it is important to mention that these calculations are in principle very similar to those performed in our previous work on the PESs of the ArH2+ system in ref. 14. However, because of the nature of the quantum scattering calculations (as discussed in Section 2.2) we wanted to perform for reaction (1), it proved to be necessary to obtain a new PES for reasons discussed in more detail in Section 3.1. This new PES only describes the Ar + H2+ entrance asymptote, excluding the Ar+ + H2 asymptote, and is therefore free of spin–orbit effects.
All electronic structure calculations were carried out using the MOLPRO package 2020.2.27
In brief, there is a normal distribution of electronic energies, ρ(E) ∼ ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (μ,σ), at each point in the molecular configuration space of the system, which is conditioned by means of training geometries, {xi}, and associated energies, E = ({Ei}), such that the mean of this distribution at a geometry, x*,
(μ,σ), at each point in the molecular configuration space of the system, which is conditioned by means of training geometries, {xi}, and associated energies, E = ({Ei}), such that the mean of this distribution at a geometry, x*,
 | (3) |
k(xi,xj) = D(xi,xj,Σ)![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ν(xi,xj,l) + W(xi,xj,n), ν(xi,xj,l) + W(xi,xj,n), | (4) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ν(xi,xj,l) stands for the Matérn class of kernels, D(xi,xj,Σ) is the dot product kernel, and W(xi,xj,n) is the white noise kernel. The explicit mathematical forms of these individual kernels are given by,
ν(xi,xj,l) stands for the Matérn class of kernels, D(xi,xj,Σ) is the dot product kernel, and W(xi,xj,n) is the white noise kernel. The explicit mathematical forms of these individual kernels are given by, | (5) |
| D(xi,xj,Σ) = Σ2 + xi·xj | (6) |
| W(xi,xj,n) = nδxi,xj. | (7) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) ν is a modified Bessel function of the second kind, and its argument is given by
ν is a modified Bessel function of the second kind, and its argument is given by  , where d(x(k)i,x(k)j) represents the euclidean distance between the training points along the internal coordinate k. Γ(ν) is the gamma function and the value of the parameter ν was fixed at 3/2, such that the obtained ML representations are twice differentiable. As is apparent from eqn (5)–(7) there are 6 parameters (in this context often referred to as hyperparameters), namely, n, Σ, ν, and (l1,l2,l3). The values of these parameters (with the exception of ν) are determined in an optimisation procedure that involves the maximisation of the log marginal likelihood,
, where d(x(k)i,x(k)j) represents the euclidean distance between the training points along the internal coordinate k. Γ(ν) is the gamma function and the value of the parameter ν was fixed at 3/2, such that the obtained ML representations are twice differentiable. As is apparent from eqn (5)–(7) there are 6 parameters (in this context often referred to as hyperparameters), namely, n, Σ, ν, and (l1,l2,l3). The values of these parameters (with the exception of ν) are determined in an optimisation procedure that involves the maximisation of the log marginal likelihood, | (8) |
The ML model was trained in the Morse representation of the internuclear distances (see Fig. 1), exp(−rAB), thereby facilitating the accurate representation of both the short- and long-range potential.
2.2 Close-coupling method
Time-independent quantum mechanical close-coupling calculations for the 36Ar + H2+ collisional system on the aforementioned ground state adiabatic electronic PES (12A′) were performed using the ABC quantum reactive scattering program by Skouteris et al.31 Such calculations involve approximately solving the time-independent Schrödinger equation for the motion of the atomic nuclei on a single adiabatic electronic PES by means of a multi arrangement expansion of the nuclear wavefunctions in terms of Delves hyperspherical coordinates.32 In such an approach both reactive and non-reactive (elastic and inelastic) processes can be simulated in full state-to-state detail of the reactants and the products. Performing these ABC calculations requires the input of several parameters, the values of which are determined by means of convergence tests. Several convergence tests at total angular momentum, J = 0, were performed in order to find the optimal values of said parameters: Eint,max = 2.2 eV (maximum internal energy, Eint, in any channel), jmax = 33 (maximum value of the rotational quantum number, j, in any channel), ρmax = 50a0, 35a0 and 25a0 (maximum values of the hyperradius, ρ) and Nsec = 200 (number of log derivative propagation sectors). Before calculating cross sections, the S-matrix was transformed into a helicity adapted representation based on the prescription in ref. 31. We found that at the maximum collision energy considered (Emaxc = 0.1 eV) the state-to-state ICSs were converged at a total angular momentum quantum number, J = 51. At said value of J, convergence tests suggested that kmax = 4 (maximum value for the helicity quantum number, k) presented to optimal balance between accuracy and computation time.2.3 Statistical methods
For collisional systems that exhibit a (deep) potential energy well on their electronic PES, statistical theories of molecular scattering have been shown to provide reasonably accurate approximate results. Indeed, a collision proceeding through the formation and decay of an intermediate collision complex (i.e., complex-forming collisions, or sometimes, complex-mediated collisions), can behave statistically if the lifetime of the complex is long enough,33–35 which is typically the case for deep potential energy wells (with a large density of rovibrational states) and low collision energies (such that the number of open channels is small). Several statistical methods have been developed over the years; examples include, but are not limited to: phase space theory (PST)36 and its modified version, mean potential phase space theory (MPPST),37–39 the above mentioned SQM,15,16 its wave packet40 and quasi-classical trajectory versions,41–43 and variations of the statistical adiabatic channel model.17,18,44,45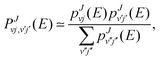 | (9) |
 and pJvj(E) are the capture probabilities, respectively, for the formation of the collision complex from the initial H2+(v,j) rovibrational state and for its fragmentation into the final 36ArH+(v′,j′) state, and the indices in the sum of the denominator, v′′j′′, run over all the energetically open rovibrational states both in reactants and products. As explained in ref. 16, those individual probabilities are calculated by means of a time-independent method which involves a log derivative propagation between a capture radius Rc and Rmax, the asymptotic distance, which in this case have been set to ∼3.7 Å and ∼44 Å, respectively. The final value of the capture radius is chosen after some tests in which no noticeable differences are found when this is varied. The reaction probability from eqn (9) is then employed for the calculation of ICSs:
and pJvj(E) are the capture probabilities, respectively, for the formation of the collision complex from the initial H2+(v,j) rovibrational state and for its fragmentation into the final 36ArH+(v′,j′) state, and the indices in the sum of the denominator, v′′j′′, run over all the energetically open rovibrational states both in reactants and products. As explained in ref. 16, those individual probabilities are calculated by means of a time-independent method which involves a log derivative propagation between a capture radius Rc and Rmax, the asymptotic distance, which in this case have been set to ∼3.7 Å and ∼44 Å, respectively. The final value of the capture radius is chosen after some tests in which no noticeable differences are found when this is varied. The reaction probability from eqn (9) is then employed for the calculation of ICSs: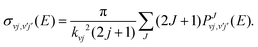 | (10) |
The SQM calculations have been performed within the CC framework with no further approximations regarding the helicity Ω coupling. However, given the large number of rovibrational states in the product channel only those (v′,j′) channels with energies beyond a certain cutoff value, Emin, have been included for a proper calculation of the corresponding 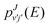 probabilities. For those other states with energies (including the corresponding centrifugal barrier contributions for each partial wave J) below such a Emin, a constant unity value,
probabilities. For those other states with energies (including the corresponding centrifugal barrier contributions for each partial wave J) below such a Emin, a constant unity value,  has been assumed. Test calculations have been performed in order to ensure the choice of Emin does not affect the state-to-state ICSs. Recent examples of applications of the SQM approach to reactive collisions involving protonated rare gas systems can be found in the literature.47,48
has been assumed. Test calculations have been performed in order to ensure the choice of Emin does not affect the state-to-state ICSs. Recent examples of applications of the SQM approach to reactive collisions involving protonated rare gas systems can be found in the literature.47,48
In the SACM approach, the state resolved integral cross sections are computed according to eqn (10). However, the state-to-state transition probabilities in eqn (9) are computed assuming the capture probabilities to be zero (for closed channels) or unity (for open channels). They are thus of the form,
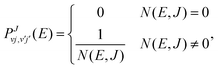 | (11) |
2.4 Rate coefficients
Based on the state-to-state ICSs, and assuming a Maxwell–Boltzmann distribution of collision energies, temperature-dependent rate coefficients, kif(T), are computed as follows, | (12) |
3 Results and discussion
3.1 Potential energy surface
To construct the ground state adiabatic electronic PES (12A′) of the ArH2+ system, we have performed single point calculations (utilising the electronic structure methods discussed in Section 2.1.1) at a total of 2004 symmetry unique training geometries. The ML fit is characterised by a root-mean-square-error (RMSE) of ∼ 5.97 × 10−4 eV, based on comparison with the test set data (the RMSE on the training data is ∼ 9.22 × 10−10 eV), which suggests that we have obtained a highly accurate representation of the PES appropriate for chemical dynamics simulations. The test data is comprised of 224 ab initio energies that were not part of the training set for machine learning, and the corresponding molecular structures were generated randomly within the ranges mentioned in Section 2.1.1. This potential is similar to the one reported in ref. 14, the major differences being: (i) the ML fit of this PES ignores the avoided crossing that exists in the entrance arrangement between the two lowest electronic states and pretends that the Ar+ + H2 channel doesn't exist by evolving diabatically for (
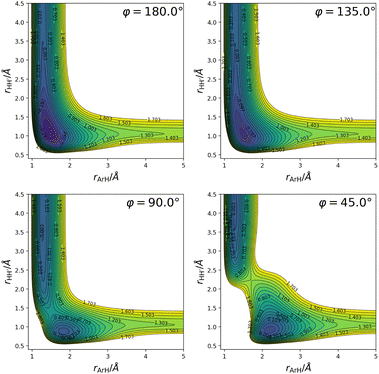
(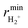 being the minimum in the PES along the H2+ internuclear distance for given rArH and φ), and consequently (ii) this PES does not include spin–orbit coupling effects since they are of importance only in the Ar+ + H2 channel. As already touched upon in the introduction (Section 1), this approach to the simulation of the reaction dynamics is valid as long as the total scattering energy is lower than the top of the barrier created by the aforementioned avoided crossing because (i) the excited states are not accessible energetically, and (ii) the zero-point vibrational energy of H2 does not allow for its formation under said energy constraint. Furthermore, such a modified fit is in fact a necessity since the CC calculations (as discussed in Section 2.2) require the construction of a multi-arrangement rovibrational basis, and the vibrational eigenstates in the entrance arrangement can only be computed properly in this way. So, with the exception of the crossing seam created by the interaction between the ground and lowest excited states, the general features of this ground state PES and the one recently published14 are the same; a more detailed account of the latter can be found in ref. 14. We only show here two-dimensional contour plots (Fig. 2) that provide some information regarding the topography of the PES for fixed bond angles, primarily because it is of interest when discussing the results from the quantum scattering calculations and the statistical calculations. From these plots in Fig. 2 the presence of a potential energy well (∼ −1.8 eV with respect to the Ar + H2+ asymptote for the H–H–Ar linear structure corresponding to the global minimum), as well as a barrier for small bond angles becomes apparent.
being the minimum in the PES along the H2+ internuclear distance for given rArH and φ), and consequently (ii) this PES does not include spin–orbit coupling effects since they are of importance only in the Ar+ + H2 channel. As already touched upon in the introduction (Section 1), this approach to the simulation of the reaction dynamics is valid as long as the total scattering energy is lower than the top of the barrier created by the aforementioned avoided crossing because (i) the excited states are not accessible energetically, and (ii) the zero-point vibrational energy of H2 does not allow for its formation under said energy constraint. Furthermore, such a modified fit is in fact a necessity since the CC calculations (as discussed in Section 2.2) require the construction of a multi-arrangement rovibrational basis, and the vibrational eigenstates in the entrance arrangement can only be computed properly in this way. So, with the exception of the crossing seam created by the interaction between the ground and lowest excited states, the general features of this ground state PES and the one recently published14 are the same; a more detailed account of the latter can be found in ref. 14. We only show here two-dimensional contour plots (Fig. 2) that provide some information regarding the topography of the PES for fixed bond angles, primarily because it is of interest when discussing the results from the quantum scattering calculations and the statistical calculations. From these plots in Fig. 2 the presence of a potential energy well (∼ −1.8 eV with respect to the Ar + H2+ asymptote for the H–H–Ar linear structure corresponding to the global minimum), as well as a barrier for small bond angles becomes apparent.
3.2 Scattering and statistical calculations
The present subsection is devoted to an analysis of the state-resolved integral scattering cross sections as a function of collision energy, obtained from quantum mechanical close-coupling calculations (described in Section 2.2) and statistical calculations (described in Section 2.3.1 and Section 2.3.2) all of which were performed on the new ground state adiabatic PES (described in Section 3.1). Quantum and statistical cross sections for inelastic collisions, | (13) |
| 36Ar + H2+ (vH2+,jH2+) → 36ArH+ (vArH+,jArH+) + H, | (14) |
 , and vArH+ = 0–4,jArH+ = 0–33.
, and vArH+ = 0–4,jArH+ = 0–33.
 | ||
Fig. 3 Close-coupling, SACM and SQM integral cross sections (in Å2) as a function of collision energy (in eV) for the inelastic excitations 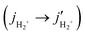 involving 36Ar and H2+. involving 36Ar and H2+. | ||
It is difficult to apply the same reasoning in the case of SQM. Given its intrinsically approximate nature, predictions obtained with this approach for the process shown in eqn (13) where rovibrational levels of the same species, H2+, are involved as reactants and products should be understood as result of a collision mediated by the formation and fragmentation of an intermediate complex. Whether this is exactly the same kind of processes described by means of the ABC approach may depend on the precise reaction under study. Therefore, in principle, differences with a purely statistical behaviour can be due to deviations from a purely complex-forming pathway.
(1) Within a given vibrational manifold vArH+, and for the collision energies considered, the ICSs generally increase with increasing rotational excitation of 36ArH+.
(2) Cross sections are larger for higher vibrational excitation of 36ArH+, suggesting that 36ArH+, when formed through reaction (1), is a vibrationally hot product. This has indeed been observed in previous studies on the matter.1,3 In order to more clearly show the effect of vibrational excitation of ArH+, the last panel in Fig. 4 shows the CC data for ArH+ (vArH+,jArH+ = 0).
Looking more closely at the comparison with the statistical predictions in the same figure (Fig. 4), we notice that the agreement between CC and SACM/SQM is quite good for vArH+ = 0. However, the agreement becomes progressively worse for higher vibrational excitation of 36ArH+. This observation seems to suggest that (vH2+ = 0,jH2+ = 0) → (vArH+ > 0,jArH+) transitions in the 36Ar + H2+ reactive system behave less statistically for increasing vArH+. Presumably, this is related to the large exothermicity of the reaction (∼ 1.32 eV),14 which would imply a large number of open rovibrational exit channels, and thus a lesser extent of randomisation of the available energy over the rovibrational states of the collision complex. Previous investigations where SQM predictions were compared with exact quantum mechanical results revealed that predictions at the state-to-state level were a much more stringent test for statistical techniques than those processes in which, for instance, only the initial state was selected (see, for example ref. 52 and 53.)
From the results already introduced, we can compute initial-state selected cross sections for the reaction in eqn (14) by summing over all accessible rovibrational states of 36ArH+ that are open for a given total scattering energy. In Fig. 5 we compare CC, SQM and SACM cross sections for reactive collisions starting in the rovibrational ground state of H2+. Overall, the results shown in Fig. 5, both quantum mechanical and statistical, agree well. Both statistical approaches (SQM and SACM) make very similar predictions, differing by at most a factor of ∼ 1.2, and they both underestimate the quantum cross section to within a factor of 2. We should also note that the stepwise behaviour of the SACM result smooths out with the inclusion of quantum tunnelling in the entrance channels (see Fig. 5, top panel); tunnelling was accounted for within the Wentzel–Kramers–Brillouin (WKB) approximation,54,55 implying that the capture probabilities,  , which are either 0 or 1 classically (as assumed by eqn (11)), are now replaced by a semiclassical transmission coefficient, the value of which can take any value between 0 and 1.
, which are either 0 or 1 classically (as assumed by eqn (11)), are now replaced by a semiclassical transmission coefficient, the value of which can take any value between 0 and 1.
As the initial-state selected cross sections for the reaction 36Ar + H2+ (vH2+ = 0,jH2+ = 0) agree very well, so do the initial-state selected rate coefficients (Fig. 5). The CC value varies from ∼ 6.13 × 10−10 cm3 s−1 at 1 K, to ∼ 2.68 × 10−9 cm3 s−1 at 150 K, which can be compared to the previous estimate ∼ 10−9 cm3 s−1 of ref. 5 used to estimate the abundance of ArH+ in astrophysical environments. In the same Fig. 5 also the close-coupling thermal rate coefficient is shown up to a temperature of 50 K, as well as the Langevin prediction (∼ 2.18 × 10−9 cm3 s−1) thereof.
4 Conclusions
In this study, we have computed the first fully state-resolved quantum mechanical integral scattering cross sections as a function of collision energy for collisions between 36Ar and H2+ (v = 0,j = 0–4) on a new full-dimensional adiabatic ground state potential energy surface (2A′). We have found that the initial-state selected rate coefficients for the reaction 36Ar + H2+ (v = 0,j = 0) → 36ArH+ + H, for temperatures up to 150 K, have a magnitude of ∼ 10−9 cm3 s−1, roughly similar to what was assumed before. Furthermore, we have investigated the statistical nature of the 36ArH2+ collisional system by means of comparison to statistical approaches, such as the statistical quantum method and the statistical adiabatic channel model. Based on the agreement we find between quantum mechanical and statistical initial-state selected cross sections for H2+ in its ground rovibrational state, one could conclude that the collision dynamics of the 36Ar + H2+ reaction has some statistical character, at least in the collision energy range that was studied, and without quantum-state resolution in the product channels. However, a more detailed investigation of said reaction, based on the state-to-state cross sections, suggests that statistical behaviour of the reaction dynamics decreases with vibrational excitation of the 36ArH+ product. We also find that SQM and SACM predictions are almost identical. A further comparison has shown that the statistical adiabatic channel model fails to accurately predict ICSs for inelastic collisions involving 36Ar and H2+, presumably because of its inability to account for barriers that hinder the formation of the product 36ArH+, as shown by the analysis of the topography of the ground state PES. The next step would be to extend the collision energy range considered in this work. However, as discussed, this would require an electronically non-adiabatic treatment, whereby one should account for the competition with 36Ar+ + H2 channels through charge exchange.Data availability
Some of the data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. L. acknowledges support from KU Leuven through grant no. C14/22/082. The resources and services used in the computations were provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation-Flanders (FWO) and the Flemish Government. T. G. L. thanks MCIN/AEI/10.13039/501100011033 PID2020-114654GB-I00 for its support.Notes and references
- F. Aguillon and M. Sizun, J. Chem. Phys., 1997, 106, 9551–9562 CrossRef CAS.
- S. Chapman and R. K. Preston, J. Chem. Phys., 1974, 60, 650–659 CrossRef CAS.
- S. Chapman, J. Chem. Phys., 1985, 82, 4033–4043 CrossRef CAS.
- M. Sizun, J.-B. Song and E. A. Gislason, J. Chem. Phys., 2002, 116, 2888–2895 CrossRef CAS.
- P. Schilke, D. A. Neufeld, H. S. P. Müller, C. Comito, E. A. Bergin, D. C. Lis, M. Gerin, J. H. Black, M. Wolfire, N. Indriolo, J. C. Pearson, K. M. Menten, B. Winkel, A. Sánchez-Monge, T. Möller, B. Godard and E. Falgarone, Astron. Astrophys., 2014, 566, A29 CrossRef.
- P. Dagdigian, Mon. Not. R. Astron. Soc., 2018, 477, 802–807 CrossRef CAS.
- M. J. Barlow, B. M. Swinyard, P. J. Owen, J. Cernicharo, H. L. Gomez, R. J. Ivison, O. Krause, T. L. Lim, M. Matsuura, S. Miller, G. Olofsson and E. T. Polehampton, Science, 2013, 342, 1343–1345 CrossRef CAS PubMed.
- H. S. P. Müller, S. Muller, P. Schilke, E. A. Bergin, J. H. Black, M. Gerin, D. C. Lis, D. A. Neufeld and S. Suri, Astron. Astrophys., 2015, 582, L4 CrossRef.
- R. M. García-Vázquez, M. Márquez-Mijares, J. Rubayo-Soneira and O. Denis-Alpizar, Astron. Astrophys., 2019, 631, A86 CrossRef.
- M. Baer and H. Nakamura, J. Chem. Phys., 1987, 87, 4651–4664 CrossRef CAS.
- J.-B. Song and E. A. Gislason, Chem. Phys., 2003, 293, 231–237 CrossRef CAS.
- P. J. Kuntz and A. C. Roach, J. Chem. Soc., Faraday Trans. 2, 1972, 68, 259–280 RSC.
- M. Hu, W. Xu, X. Liu, R. Tan and H. Li, J. Chem. Phys., 2013, 138, 174305 CrossRef PubMed.
- M. Konings, J. N. Harvey and J. Loreau, J. Phys. Chem. A, 2023, 127, 8083–8094 CrossRef CAS PubMed.
- E. J. Rackham, F. Huarte-Larranaga and D. E. Manolopoulos, Chem. Phys. Lett., 2001, 343, 356–364 CrossRef CAS.
- E. J. Rackham, T. Gonzalez-Lezana and D. E. Manolopoulos, J. Chem. Phys., 2003, 119, 12895–12907 CrossRef CAS.
- J. Loreau, F. Lique and A. Faure, Astrophys. J., 2018, 853, L5 CrossRef.
- M. Konings, B. Desrousseaux, F. Lique and J. Loreau, J. Chem. Phys., 2021, 155, 104302 CrossRef CAS PubMed.
- K. M. Hickson, P. Larrégaray, L. Bonnet and T. González-Lezana, Int. Rev. Phys. Chem., 2021, 40, 457–493 Search PubMed.
- A. Christianen, T. Karman, R. A. Vargas-Hernández, G. C. Groenenboom and R. V. Krems, J. Chem. Phys., 2019, 150, 064106 CrossRef PubMed.
- O. T. Unke, D. Koner, S. Patra, S. Käser and M. Meuwly, Mach. Learn.: Sci. Technol., 2020, 1, 013001 Search PubMed.
- H. Sugisawa, T. Ida and R. V. Krems, J. Chem. Phys., 2020, 153, 114101 CrossRef CAS PubMed.
- C. Qu, Q. Yu, B. L. Van Hoozen, J. M. Bowman and R. A. Vargas-Hernández, J. Chem. Theory Comput., 2018, 14, 3381–3396 CrossRef CAS PubMed.
- J. Dai and R. V. Krems, J. Chem. Theory Comput., 2020, 16, 1386–1395 CrossRef CAS PubMed.
- Q. Song, Q. Zhang and Q. Meng, J. Chem. Phys., 2020, 152, 134309 CrossRef CAS PubMed.
- A. Kamath, R. A. Vargas-Hernández, R. V. Krems, T. Carrington and S. Manzhos, J. Chem. Phys., 2018, 148, 241702 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, Cambridge, 2006 Search PubMed.
- R. V. Krems, Phys. Chem. Chem. Phys., 2019, 21, 13392–13410 RSC.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- D. Skouteris, J. Castillo and D. Manolopoulos, Comput. Phys. Commun., 2000, 133, 128–135 CrossRef CAS.
- G. A. Parker and R. T. Pack, J. Chem. Phys., 1993, 98, 6883–6896 CrossRef CAS.
- R. B. Bernstein, A. Dalgarno, H. S. W. Massey and I. C. Percival, Proc. R. Soc. London, Ser. A, 1963, 274, 427–442 CAS.
- J. C. Light, Discuss. Faraday Soc., 1967, 44, 14–29 RSC.
- W. H. Miller, J. Chem. Phys., 1970, 52, 543–551 CrossRef CAS.
- P. Pechukas, J. C. Light and C. Rankin, J. Chem. Phys., 1966, 44, 794–805 CrossRef CAS.
- P. Larrégaray, L. Bonnet and J.-C. Rayez, J. Phys. Chem. A, 2006, 110, 1552–1560 CrossRef PubMed.
- P. Larrégaray, L. Bonnet and J.-C. Rayez, J. Chem. Phys., 2007, 127, 084308 CrossRef PubMed.
- L. Bonnet, P. Larrégaray and J.-C. Rayez, Phys. Chem. Chem. Phys., 2007, 9, 3228–3240 RSC.
- S. Y. Lin and H. Guo, J. Chem. Phys., 2006, 124, 031101 CrossRef PubMed.
- F. J. Aoiz, V. Sáez Rábanos, T. González-Lezana and D. E. Manolopoulos, J. Chem. Phys., 2007, 126, 161101 CrossRef CAS PubMed.
- F. J. Aoiz, T. González-Lezana and V. Sáez Rábanos, J. Chem. Phys., 2008, 129, 094305 CrossRef CAS PubMed.
- P. G. Jambrina, F. J. Aoiz, C. J. Eyles, V. J. Herrero and V. Sáez Rábanos, J. Chem. Phys., 2009, 130, 184303 CrossRef CAS PubMed.
- M. Quack and J. Troe, Ber. Bunsenges. Phys. Chem., 1974, 78, 240–252 CrossRef CAS.
- M. Quack and J. Troe, Ber. Bunsenges. Phys. Chem., 1975, 79, 170–183 CrossRef CAS.
- T. González-Lezana, Int. Rev. Phys. Chem., 2007, 26, 29 Search PubMed.
- D. Koner, L. Barrios, T. González-Lezana and A. N. Panda, Molecules, 2021, 26(14), 4206 Search PubMed.
- M. J. Montes de Oca-Estévez, B. Darna, B. García-Ruiz, R. Prosmiti, T. González-Lezana and D. Koner, ChemPhysChem, 2023, 24, e202300450 CrossRef PubMed.
- J. Loreau, A. Faure and F. Lique, J. Chem. Phys., 2018, 148, 244308 CrossRef CAS PubMed.
- A. Faure, F. Lique and J. Loreau, Mon. Not. R. Astron. Soc., 2020, 493, 776–782 CrossRef CAS.
- B. Desrousseaux, M. Konings, J. Loreau and F. Lique, Phys. Chem. Chem. Phys., 2021, 23, 19202–19208 RSC.
- T. González-Lezana, O. Roncero, P. Honvault, J.-M. Launay, N. Bulut, F. Javier Aoiz and L. Bañares, J. Chem. Phys., 2006, 125, 094314 CrossRef PubMed.
- E. Carmona-Novillo, T. González-Lezana, O. Roncero, P. Honvault, J.-M. Launay, N. Bulut, F. Javier Aoiz, L. Bañares, A. Trottier and E. Wrede, J. Chem. Phys., 2008, 128, 014304 CrossRef PubMed.
- H. A. Kramers, Z. Phys., 1926, 39, 828–840 CrossRef.
- G. Wentzel, Z. Phys., 1926, 38, 518–529 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02179g |
| This journal is © the Owner Societies 2024 |