Vibrational synchronization and its reaction pathway influence from an entropic intermediate in a dirhodium catalyzed allylic C–H activation/Cope rearrangement reaction

Abstract

In reactions with consecutive transition states without an intermediate, and an energy surface bifurcation, atomic motion generally determines product selectivity. Understanding this dynamic-based selectivity can be straightforward if there is extremely fast descent from the first transition state to a product. However, in cases where a nonstatistical roaming/entropic intermediate occurs prior to product formation the motion that influences selectivity can be difficult to identify. Here we report quasiclassical direct dynamics trajectories for the dirhodium catalyzed reaction between styryldiazoacetate and 1,4-cyclohexadiene and prior experiments by Davies showed competitive allylic C–H insertion and Cope products. Trajectories confirmed the proposed energy surface bifurcation and revealed that dirhodium vinylcarbenoid when reacting with 1,4-cyclohexadiene can induce either a dynamically concerted pathway or a dynamically stepwise pathway with a nonstatistical entropic tight ion-pair intermediate. In the dynamically stepwise reaction pathway C–H insertion versus Cope selectivity is highly influenced by whether or not vibrational synchronization occurs in the nonstatistical entropic intermediate. This vibrational synchronization highlights the possible need for an entropic intermediate to have organized transition state-like motion to proceed to a product.

---

Introduction

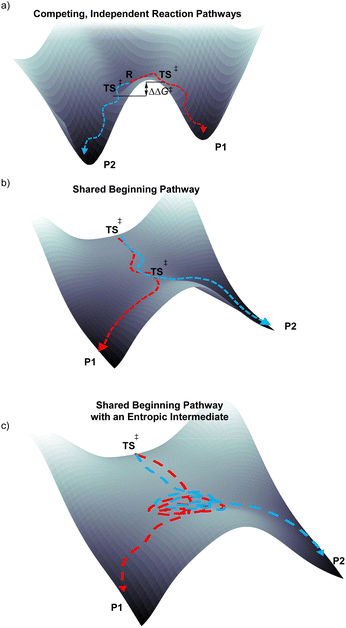
Control of product selectivity during a chemical reaction typically occurs through competing independent transition states from a fully established, long-lived intermediate (Fig. 1a). Within a statical model framework, such as transition state theory, the energy difference between the independent barrier heights or transition states (Curtin–Hammett type scenario) can be used to quantitatively evaluate and qualitatively understand the origin of product selectivity. An alternative product selectivity scenario occurs when there are two consecutive transition states without an intermediate.^1,2 In this scenario products share a pathway through the first transition state and then diverge when the potential energy surface bifurcates en route to the second transition, and this is depicted with the potential energy surface in Fig. 1b.

Fig. 1 (a) Illustration of a reaction where there are two independent reaction pathways leading from an intermediate (I) to products P1 and P2. In this scenario, the energy difference between the two transition states (TS) can be used to statistically model and understand the P1 versus P2 selectivity. (b) Illustration of a potential energy surface with two consecutive transition states, which is often referred to as a post-transition state bifurcation because the surface divides between the two transition states. (c) Illustration of a potential energy surface with two consecutive transition states and a roaming, entropic intermediate that occurs en route to forming either P1 or P2.

With a potential energy surface bifurcation selectivity is not controlled by an energy difference of pathways/statistics of crossing the kinetic bottlenecks, but rather controlled by atomic motion that occurs through and immediately after the first transition state,^3,4 and direct dynamics trajectories have emerged as a useful way to directly model this type of reaction selectivity.^5,6 Consecutive transition states without an intermediate have been proposed for several organic addition,^7–9 substitution,^10–13 pericyclic,^14,15 and rearrangement reactions.^16–22 Typically the proposed bifurcation determining selectivity in these reactions is based on calculation of an energy landscape or molecular dynamics simulations.

In reactions with an energy surface bifurcation where there is extremely fast descent (essentially concerted) from the first transition state to products it is possible, although nontrivial, to identify the specific vibrational motion responsible for product selectivity. For deazetization and electrocyclic ring opening reactions, with the aid of machine learning, we previously identified the vibrational motion that controls selectivity in these reactions.^23,24 However, it has recently become apparent that in some reactions with consecutive transition states and an energy landscape bifurcation the descent from the first transition state to products is delayed and there is formation of a nonstatistical roaming/entropic intermediate, which can mean that there is some but not complete intramolecular vibrational redistribution (IVR).^25–27 It is for this type of mechanistic scenario that we were interested in analyzing to determine if there are specific patterns of vibrational motion that dictate selectivity.

Therefore, our goal in this work was to perform direct dynamics simulations for a model of an experimentally relevant reaction that has an energy landscape bifurcation and an entropic type intermediate, and this would enable evaluation of vibrational motion that influences reaction selectivity. Our group is particularly interested in organometallic reactions and their dynamic-driven reaction mechanisms. Our goal for this work, and our interest in organometallic reactions, prompted us to use dynamics trajectories to examine the dirhodium catalyzed combined allylic C–H activation/Cope rearrangement reaction developed experimentally by Davies and coworkers (Scheme 1a).^28–31 This reaction was promising to examine because the experimental selectivity was previously proposed by Davies to result from a potential energy surface bifurcation and this was supported by static density functional theory (DFT) calculations, although no trajectories have been reported for this reaction. In addition, Tantillo^32,33 in very inspiring work previously demonstrated with dynamics trajectories that in a related reaction for the intramolecular dirhodium catalyzed C–H insertion reaction forming β-lactones there is a bifurcation that leads to competitive fragmentation with formation of a ketene and carbonyl compounds. Additionally, when our simulations were underway Tantillo further reported more simulations that showed β-lactone reaction trajectories roaming the energy surface before settling to a product, which is suggestive of an entropic intermediate.

Scheme 1 (a) Outline of the Rh-catalyzed combined allylic C–H activation/Cope rearrangement reaction between styryldiazoacetate 1 and 1,4-cyclohexadiene 2 reported by Davies.³⁴ (b) Depiction of the hydride transfer transition state TS1 and Cope rearrangement transition state TS2. (c) Comparison of s-cis and s-trans conformations of the reactive rhodium carbenoid and the proposed reaction products.

Scheme 1a shows the experimental product ratio for the combined allylic C–H activation/Cope rearrangement reaction between styryldiazoacetate 1 and 1,4-cyclohexadiene 2.³⁴ The E alkene Cope product 3 is formally the result of rhodium carbenoid C–H insertion followed by Cope rearrangement and was the overall major product of the reaction. The C–H insertion product 4 (the thermodynamically most stable product) and the Z alkene 5 were also observed in significant, but minor, amounts. Davies and coworkers also reported a DFT optimized C–H activation transition state TS1 that was described as a hydride transfer transition state and a Cope transition state (TS2).³⁴ Based on these static transition states and an intrinsic reaction coordinate (IRC) analysis, Davies and coworkers proposed that this reaction has a potential energy surface bifurcation. It was also proposed that the reacting s-cis rhodium carbenoid conformation leads to product 3 while the s-trans rhodium carbenoid conformation leads to a mixture of 4 and 5 (Scheme 1c).

As will be discussed, quasiclassical direct dynamics trajectories for the reaction between the rhodium vinylcarbenoid and 1,4-cyclohexadiene starting from s-cisTS1 generated the E alkene Cope product 3 as the dominant dynamic product and a very minor amount of the C–H insertion product. These trajectories were found to be dynamically concerted. In contrast, trajectories starting from the s-transTS1 resulted in significant quantities of both the C–H insertion product 4 and the Z alkene product 5. These trajectories were found to be dynamically stepwise with a leading hydride transfer stage to generate a tight ion-pair entropic intermediate followed by a later C–C bond forming stage. While this work was under review, Tantillo reported a similar discovery for the reaction with 1,3-cyclohexadiene.³⁵ Analysis of motion during these reaction trajectories revealed that C–H insertion is the dynamically direct pathway from the nonstatistical entropic intermediate, and for the Cope product to be formed there must be synchronization of the Cope vibrational mode along with several vibrational modes for carbon atom bending. Overall, this analysis illustrates the possibility of identifying key motion in an entropic intermediate that influences product selectivity.

Computational methods

All geometry optimizations and frequency calculations were carried out with Gaussian 16³⁶ using M06³⁷/def2-SVP³⁸ with the SuperFineGrid for numerical integration. M06 was selected because it provides the most general accuracy for treating second-row transition metals and organic compounds. The M06 functional gives results very similar to those of B3LYP-D3, which has been extensively used for dirhodium reactions.^33,35,39 Single point energies were also calculated using M06 with the larger def2-TZVP basis set. Stationary points were categorized as a potential energy minimum or first-order saddle point by analyzing the vibrational frequencies. Gibbs energies reported correspond to the quasi rigid-rotor harmonic oscillator approximation with Grimme's damping scheme to reduce the error from the entropy contribution of low-frequency modes.⁴⁰ Quasiclassical direct dynamics trajectories were performed with Milo⁴¹ which was interfaced with Gaussian 16 to compute energies and gradients at the M06/def2-SVP level. To demonstrate that the smaller def2-SVP (and only tractable) basis set would likely provide trajectories similar to the larger def2-TZVP basis set, we located s-transTS1 with M06/def2-TZVP. A comparison of the normal mode frequencies between def2-SVP and def2-TZVP structures showed very small differences. A 0.75 fs time step was used to propagate the equations of motion using the Verlet algorithm. Initial velocities were generated by local mode sampling incorporating the zero-point energy of each mode and thermal excitations for 298.15 K, which was the experimental temperature. The frequency of the imaginary mode was taken as 2 cm⁻¹ for the purpose of sampling. See the ESI† for additional details. The data that support the findings of this study are available in the ESI.† 3D molecular graphics were made using UCSF ChimeraX.⁴²

Results and discussion

We began by locating the C–H cleavage (hydride abstraction) transition states s-cisTS1 and s-transTS1 structures (Fig. 2). This was done for the reaction between 1,4-cyclohexadiene and a rhodium vinylcarbenoid intermediate derived from styryldiazoacetate 1 with model acetate ligands. We also optimized the Cope transition state, TS2. Fig. 2 provides 3D depictions of these transition-state structures and key distances. As expected, in the C–H cleavage transition state, there is elongation of the Rh–C distance, and the breaking C–H bond is significantly stretched. The forming C–H bond forms a nearly co-linear C–H–C arrangement with the breaking C–H bond, suggesting that there is only a small amount of bonding between the two carbon atoms. Also as expected, in a reaction with a possible energy surface bifurcation, the distances of the competing C–C interactions are relatively long. For example, in s-transTS1, the C–C distance for the Cope product is 3.22 Å and the C–C distance for the insertion product is 2.59 Å. Similarly, in s-cisTS1, the C–C distance for the Cope product is 3.12 Å, and the C–C distance that leads to the insertion product is 2.60 Å. From a structure perspective, it is important to note that if product prediction was based on the transition-state structure partial C–C distances, which can often be done in pericyclic reactions,^43–45 then each of these transition-state structures should only lead to an insertion product.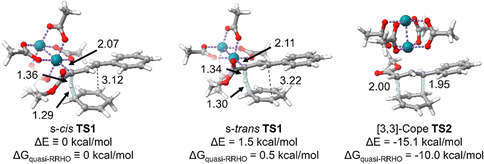

Fig. 2 M06/def2-SVP optimized transition-state structures for C–H cleavage (s-cisTS1 and s-transTS1) and Cope rearrangement (TS2). Distances in Å. Quasi-RRHO free energies are calculated at 298.15 K with 100 cm⁻¹ as the damping parameter.⁴⁰ Energies are reported at the M06/def2-TZVP//M06/def2-SVP level of theory.

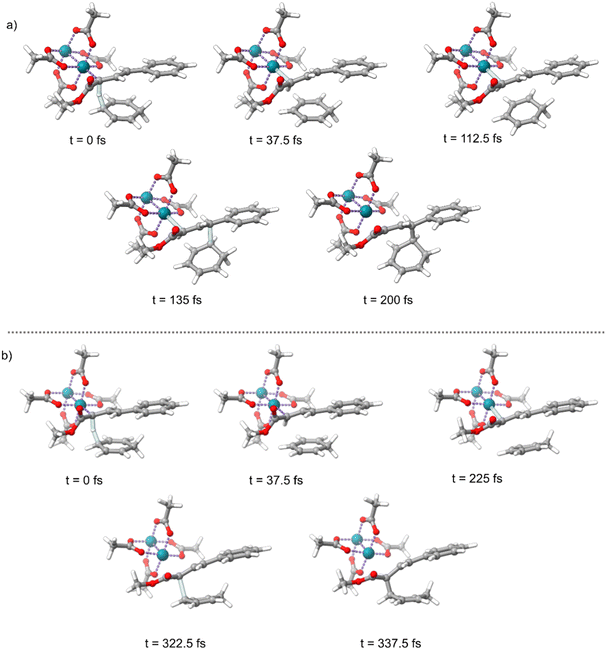
Intrinsic reaction coordinate (IRC)⁴⁶ calculations advance a reaction coordinate from a transition-state structure by steepest descent in mass-weighted coordinates with infinitesimal atomic velocity. The interpretation of reaction selectivity based on an IRC can be unclear in a reaction where dynamic vibrational motion (atomic velocity) determines selectivity. Because of this, we decided to use a dynamic reaction coordinate analysis to determine the direct energy surface connection after s-transTS1 and s-cisTS1. A dynamic reaction coordinate analysis involves a single direct dynamics trajectory starting with only kinetic energy derived from the reaction coordinate – the trajectory is started without kinetic energy in all other vibrational modes. Fig. 3 shows timing snapshots of the dynamic reaction coordinate calculations in the forward direction starting from both s-cisTS1 and s-transTS1. Despite the relative similarity of these transition-state structures and the shorter insertion C–C distance in both structures, the dynamic reaction coordinate showed that from s-cisTS1 there is a direct energy surface connection with the E alkene Cope product 3, and from s-transTS1 there is a direct energy surface connection with the C–H insertion product 4. These dynamic reaction coordinate trajectories correctly correspond to the dominant products found experimentally, but more importantly, they indicate that the direct result of TS1 can either be C–H insertion or Cope rearrangement. Tantillo has previously discussed the sensitivity of transition state conformations and the outcomes of dynamics trajectories.^32,33

Fig. 3 (a) Snapshots from a dynamic reaction coordinate analysis starting from s-cisTS1 and proceeding in the forward direction. (b) Snapshots from a dynamic reaction coordinate analysis starting from s-transTS1 and proceeding in the forward direction.

With the direct energy surface connections established, we then examined dynamic effects on the reaction pathway selectivity using full sampling of vibrational modes with quasiclassical direct dynamics trajectories. Random thermal sampling is used to determine the initial kinetic energy along all real modes, with each mode having at least its zero-point energy. Fig. 4 plots the two possible C–C forming bond distances for trajectories proceeding in the forward direction beginning at s-cisTS1 and s-transTS1. Purple colored lines represent trajectories where the C–C bond formed results in the C–H insertion product and red colored lines represent trajectories where the C–C bond formed results in the Cope product. These trajectories showed that for s-cisTS1, 38 of the 41 trajectories ended in the C–H Cope product 3, which is consistent with this being the dominant product. However, it does demonstrate that there is the possibility of a post-transition state bifurcation, but it would lead to the insertion product 4 and would be indistinguishable from the product 4 formed from s-transTS1. These trajectories showed that for s-transTS1, there was both formation of the Cope product 4 and the C–H insertion product 5, which is again consistent with experiments and demonstrates the dynamically controlled post-transition state bifurcation resulting in two products. While these trajectories underestimated the ratio of 4 to 5 compared to the experiment, the key qualitative conclusion is that significant amounts of both products are formed after s-transTS1 and this is different from the dynamic reaction coordinate that would suggest only the C–H insertion product would be formed.

Fig. 4 (a) Plot of 41 trajectories proceeding in the forward direction beginning at s-cisTS1. (b) Plot of 43 trajectories proceeding in the forward direction beginning at s-transTS1. The star represents the transition-state structure position. r(cope) and r(insertion) are the corresponding C–C distances that lead to each of these products. Purple colored lines represent trajectories that ended in a C–H insertion product and red colored lines represent trajectories that ended in a Cope product.

Fig. 5 provides plots of the time-resolved change in the breaking C–H bond distance and C–C distances. For trajectories starting from s-cisTS1 (Fig. 5a), the C–H bond was rapidly broken with complete breakage occurring within 50 femtoseconds (fs). The C–C bond corresponding to the Cope product is also rapidly formed, typically between 100 and 200 fs after the transition state. For the three trajectories that form the C–H insertion product, the C–C bond is formed between 200 and 300 fs after the transition state. This suggests that from s-cisTS1, the nearly exclusive formation of the C–H Cope product occurs because there is a very rapid, nearly dynamically concerted process that couples the C–H bond cleavage process with C–C bond formation.

Fig. 5 (a) Plot of key distances (in Å) versus time (in fs) for forward progress during trajectories starting from s-cisTS1. (b) Plot of key distances (in Å) versus time (in fs) for forward progress during trajectories starting from s-transTS1. r(cope) and r(insertion) are the C–C distances for the atoms involved in the formation of the corresponding product. r(C–H) is the breaking C–H bond length.

For s-transTS1 trajectories, similar to s-cisTS1 trajectories, the C–H bond was rapidly broken within 50 fs. Different, however, trajectories emanating from s-transTS1 showed a much longer period for forming a C–C bond. The insertion product C–C bond only begins to form at 200 fs and continues until 450 fs. The Cope C–C bond begins to form at 175 fs and continues beyond 400 fs. This points to a dynamically stepwise process with an entropic intermediate after s-transTS1 that lasts between ∼200 and 400 fs. Previously, an entropic intermediate has been defined as a subpicosecond Gibbs energy minimum that does not have a corresponding potential energy minimum and can be revealed by dynamics simulations.^25–27 Entropic intermediates have been proposed for several reactions with a flat caldera-like potential energy surface.^47–51 In this reaction, the entropic intermediate occurs after hydride transfer as a formal anion–carbocation tight ion pair. For this intermediate, while there is no enthalpy barrier for C–C bond formation, it exists for multiple molecular vibrations but is not long enough for complete IVR. Because there is an entropic intermediate, both C–H insertion and Cope products can be formed. Since this intermediate has incomplete IVR, the dynamic motion that occurs in and then out of the nonstatistical entropic intermediate will determine the pathway selectivity. Importantly, IVR in an intermediate effectively scrambles the vibrational information originally contained in the transition state, and so it was unclear if, with partial IVR in an entropic intermediate, we would be able to reveal the motion responsible for the formation of the C–H insertion product versus the formation of the Cope product.

With no potential energy minimum of the entropic intermediate, we examined the vibrational modes of s-transTS1 to identify motion that determines the dynamic selectivity of the entropic intermediate continuing to the products. Fig. 6 displays three transition state vibrational modes that provide motion with the potential formation of one of the two C–C bonds. The vibrational mode with v = 105 cm⁻¹ is the expected Cope type motion where there is synchronous stretching of one C–C distance and shortening of the other C–C distance. The vibrational mode with v = 287 cm⁻¹ also has stretching/compressing motion of these bonds. The vibrational mode with v = 987 cm⁻¹ has out-of-plane bending motion on both the carbenoid and diene carbons. In this mode these atoms synchronously bend away/towards one another.

Fig. 6 3D static images showing the key vibrational modes in s-transTS1 that contribute to Cope C–C bond motion.

If the formation of the insertion and Cope products utilizing transition state s-transTS1 was a dynamically concerted process, then directional excitation of these vibrational modes should induce control of the product formed, which we have previously demonstrated in other reactions.⁴⁰ We started several trajectories where one or all three modes were excited by about 5 kcal mol⁻¹ beyond the zero-point energy (all other vibrational modes remained in their original sampling) and in the direction to form the Cope product rather than the insertion product. However, in all cases, this strategy failed. The product ratio from these trajectories showed that the insertion product was still favored. This supports the idea that the reaction is dynamically stepwise with an entropic intermediate and the motion of the intermediate determines product selectivity.

Because the entropic intermediate likely requires organized motion to form a C–C bond, there is likely to be a pattern of dynamic motion responsible for shuttling the intermediate to either the C–H insertion product or the Cope product. This idea prompted us to analyze the synchronicity of the key motions that can induce either the formation of the C–C bond leading to the C–H insertion product or the formation of the C–C bond leading to the Cope product. The top of Fig. 7 highlights the three general motions analyzed. The first is the C–C distance for the Cope product (red), the second is the carbenoid out-of-plane bending angle (green), and the third is the diene out-of-plane bending angle (blue). Plots a–f in Fig. 7 show the magnitude of these three motions as a function of time. Inspection of the plots in Fig. 7a–c shows that all three motions are highly synchronized for at least 100 fs before the Cope product is formed. This is typical for almost all trajectories that start from s-transTS1 and result in the Cope product. Conversely, many trajectories that result in the C–H insertion product have sporadic synchronization. Fig. 7e and f shows several examples that form the insertion product. It is important to note that this vibrational synchronization is a generalization and not an absolute demarcation of pathways. For example, Fig. 7f shows a trajectory where the insertion product is formed despite highly synchronized motion. In this case, it is likely that the absolute magnitude of the motion is insufficient to overcome the predisposition to form the insertion product. Again, this synchronization analysis and the results from the dynamic IRC calculation indicate that from the entropic intermediate, there is generally direct formation of the C–H insertion product unless there is synchronized coupling of motions shown in Fig. 7 that provide shuttling of the intermediate into the Cope pathway. Importantly, this underscores the characterization and labeling of this reaction as having a dynamic or entropic intermediate. In other words, products in this reaction are not the result of random motion that might be expected in a general barrierless reaction step, but rather require motion akin to a normal intermediate traversing a transition state like structural bottleneck.

Fig. 7 Plots of key coordinates for the Cope and insertion reaction for two different MD simulations starting from s-transTS1. (a)–(c) Plot of key coordinates for a trajectory that resulted in the Cope product. (d)–(f) Plot of key coordinates for a trajectory resulting in the insertion product. Red regions highlight when the Cope C–C bond length is decreasing. Green areas highlight when the carbenoid carbon for the Cope product is bending away from the diene. Conversely, blue areas highlight when the Cope carbon on the diene is bending away from the carbenoid. Darker regions indicate all three of these occur simultaneously.

Conclusions

Quasiclassical direct dynamics trajectories for the combined allylic C–H activation/Cope rearrangement reaction between a rhodium vinylcarbenoid and 1,4-cyclohexadiene revealed that depending on the starting transition-state structure, there can either be a dynamically concerted or dynamically stepwise mechanism. In the dynamically concerted mechanism, the dominant Cope product was formed in <200 fs. In the dynamically stepwise mechanism, hydride transfer resulted in an ion-pair entropic intermediate with a lifetime between 200 and 400 fs. Analysis of motion in this nonstatistical entropic intermediate revealed that unsynchronized motion leads to the C–H insertion product while synchronization of the Cope vibrational mode along with several vibrational modes for carbon atom bending results in the formation of the Cope product.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Brigham Young University and the Fulton Supercomputing Lab for computational resources. This work was supported by the US National Science Foundation with award CHE-2244799.

References

1. S. R. Hare and D. J. Tantillo, Pure Appl. Chem., 2017, 89, 679–698.
2. D. H. Ess, S. E. Wheeler, R. G. Iafe, L. Xu, N. Çelebi-Ölçüm and K. N. Houk, Angew. Chem., Int. Ed., 2008, 47, 7592–7601.
3. J. Rehbein and B. K. Carpenter, Phys. Chem. Chem. Phys., 2011, 13, 20906–20922.
4. B. K. Carpenter, Annu. Rev. Phys. Chem., 2005, 56, 57–89.
5. H. Yamataka, in Advances in Physical Organic Chemistry, ed. J. P. Richard, Academic Press, 2010, vol. 44, pp. 173–222.
6. K. P. Upakarasamy Lourderaj and W. L. Hase, Int. Rev. Phys. Chem., 2008, 27, 361–403.
7. Y. Oyola and D. A. Singleton, J. Am. Chem. Soc., 2009, 131, 3130–3131.
8. J. O. Bailey and D. A. Singleton, J. Am. Chem. Soc., 2017, 139, 15710–15723.
9. Z. Chen, Y. Nieves-Quinones, J. R. Waas and D. A. Singleton, J. Am. Chem. Soc., 2014, 136, 13122–13125.
10. X. S. Bogle and D. A. Singleton, Org. Lett., 2012, 14, 2528–2531.
11. J. G. López, G. Vayner, U. Lourderaj, S. V. Addepalli, S. Kato, W. A. deJong, T. L. Windus and W. L. Hase, J. Am. Chem. Soc., 2007, 129, 9976–9985.
12. J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960–2969.
13. P. Manikandan, J. Zhang and W. L. Hase, J. Phys. Chem. A, 2012, 116, 3061–3080.
14. Z. Wang, J. S. Hirschi and D. A. Singleton, Angew. Chem., Int. Ed., 2009, 48, 9156–9159.
15. P. Yu, T. Q. Chen, Z. Yang, C. Q. He, A. Patel, Y.-H. Lam, C.-Y. Liu and K. N. Houk, J. Am. Chem. Soc., 2017, 139, 8251–8258.
16. B. Biswas, S. C. Collins and D. A. Singleton, J. Am. Chem. Soc., 2014, 136, 3740–3743.
17. B. Biswas and D. A. Singleton, J. Am. Chem. Soc., 2015, 137, 14244–14247.
18. S. R. Hare, A. Li and D. J. Tantillo, Chem. Sci., 2018, 9, 8937–8945.
19. R. P. Pemberton and D. J. Tantillo, Chem. Sci., 2014, 5, 3301–3308.
20. Y. J. Hong and D. J. Tantillo, Nat. Chem., 2014, 6, 104–111.
21. M. R. Siebert, J. Zhang, S. V. Addepalli, D. J. Tantillo and W. L. Hase, J. Am. Chem. Soc., 2011, 133, 8335–8343.
22. M. R. Siebert, P. Manikandan, R. Sun, D. J. Tantillo and W. L. Hase, J. Chem. Theory Comput., 2012, 8, 1212–1222.
23. J. Melville, C. Hargis, M. T. Davenport, R. S. Hamilton and D. H. Ess, J. Phys. Org. Chem., 2022, 35, e4405.
24. S. M. Maley, J. Melville, S. Yu, M. S. Teynor, R. Carlsen, C. Hargis, R. S. Hamilton, B. O. Grant and D. H. Ess, Phys. Chem. Chem. Phys., 2021, 23, 12309–12320.
25. C. Doubleday Jr, J. W. McIver Jr and M. Page, J. Phys. Chem., 1988, 92, 4367–4371.
26. Z. Yang, C. S. Jamieson, X.-S. Xue, M. Garcia-Borràs, T. Benton, X. Dong, F. Liu and K. N. Houk, Trends Chem., 2019, 1, 22–34.
27. O. M. Gonzalez-James, E. E. Kwan and D. A. Singleton, J. Am. Chem. Soc., 2012, 134, 1914–1917.
28. H. M. L. Davies, D. G. Stafford and T. Hansen, Org. Lett., 1999, 1, 233–236.
29. H. M. L. Davies and R. E. J. Beckwith, Chem. Rev., 2003, 103, 2861–2904.
30. H. M. L. Davies and Q. Jin, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5472–5475.
31. H. M. L. Davies and J. R. Manning, Nature, 2008, 451, 417–424.
32. S. R. Hare and D. J. Tantillo, Chem. Sci., 2017, 8, 1442–1449.
33. W. Guo, S. R. Hare, S.-S. Chen, C. M. Saunders and D. J. Tantillo, J. Am. Chem. Soc., 2022, 144, 17219–17231.
34. J. H. Hansen, T. M. Gregg, S. R. Ovalles, Y. Lian, J. Autschbach and H. M. L. Davies, J. Am. Chem. Soc., 2011, 133, 5076–5085.
35. W. Guo and D. J. Tantillo, J. Am. Chem. Soc., 2024, 146, 7039–7051.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016.
37. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
38. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
39. T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586.
40. S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964.
41. M. S. Teynor, N. Wohlgemuth, L. Carlson, J. Huang, S. L. Pugh, B. O. Grant, R. S. Hamilton, R. Carlsen and D. H. Ess, Milo version 1, 2021, https://github.com/DanielEss-lab/milo.
42. E. F. Pettersen, T. D. Goddard, C. C. Huang, E. C. Meng, G. S. Couch, T. I. Croll, J. H. Morris and T. E. Ferrin, Protein Sci., 2021, 30, 70–82.
43. Z. Yang, X. Dong, Y. Yu, P. Yu, Y. Li, C. Jamieson and K. N. Houk, J. Am. Chem. Soc., 2018, 140, 3061–3067.
44. S. Lee and J. M. Goodman, J. Am. Chem. Soc., 2020, 142, 9210–9219.
45. T. H. Peterson and B. K. Carpenter, J. Am. Chem. Soc., 1992, 114, 766–767.
46. K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
47. C. Doubleday Jr, R. N. Camp, H. F. King, J. W. McIver Jr, D. Mullally and M. Page, J. Am. Chem. Soc., 1984, 106, 447–448.
48. C. Doubleday, C. P. Suhrada and K. N. Houk, J. Am. Chem. Soc., 2006, 128, 90–94.
49. T. Bekele, C. F. Christian, M. A. Lipton and D. A. Singleton, J. Am. Chem. Soc., 2005, 127, 9216–9223.
50. C. Doubleday, G. Li and W. L. Hase, Phys. Chem. Chem. Phys., 2002, 4, 304–312.
51. C. Doubleday, M. Nendel, K. N. Houk, D. Thweatt and M. Page, J. Am. Chem. Soc., 1999, 121, 4720–4721.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00657g

---