Determining the quantum yield of photochemical reactions in crystals from simultaneous effects of photothermal and photochemical bending of needle-shaped crystals
Stanislav
Chizhik
 *,
Pavel
Gribov
*,
Pavel
Gribov
 ,
Viktor
Kovalskii
,
Viktor
Kovalskii
 and
Anatoly
Sidelnikov
and
Anatoly
Sidelnikov

Institute of Solid State Chemistry and Mechanochemistry SB RAS, Kutateladze 18, 630128 Novosibirsk, Russia. E-mail: stas@solid.nsc.ru
First published on 21st March 2024
Abstract
Photoinduced bending of needle crystals caused by photochemical transformation can be used as an extremely sensitive method for studying the kinetics of the transformation. However, the determination of the absolute value of the quantum yield of the reaction requires an accurate value of the intensity of light penetrating the crystal, in contrast to reactions in solutions where only the value of the total absorbed irradiation dose is sufficient. To address this problem, this study utilizes the effect of photothermal bending of a crystal due to its heating by light, occurring simultaneously with the bending due to transformation and proportional to the same value of light intensity. The ratio of the amplitudes of the two effects is independent of the light intensity, which allows the quantum yield to be determined without knowledge of the intensity value. In addition, the method allows the light intensity and thermal conductivity of the crystal to be estimated. The method is applied to measure wavelength dependence of the quantum yield of nitro-to-nitrito photoisomerization in [Co(NH3)5NO2]Cl(NO3) crystals. A monotonically decreasing value of the quantum yield φ from 0.19 to 0.04 in the range of λ from 403 to 523 nm was obtained. This result indicates the qualitative differences in the transformation mechanism in crystals and in solutions, where φ = 0.03 independent of λ in the same wavelength range.
1 Introduction
In the last decade, interest has grown in the study of dynamic crystal phenomena, which include various dynamic effects like bending, twisting, rapid displacements, and spontaneous destruction caused by phase or chemical transformations initiated by various stimuli such as heating or irradiation of crystals.1–8 All such phenomena are associated with the occurrence of inhomogeneous strains due to inhomogeneous development of transformations in crystals.9–12 Photomechanical effects, like bending of thin crystals caused by photoisomerization of the constituent molecules, are the most actively considered phenomena in this field as they can be used to create microactuators controlled by light.13–17But beyond that, these phenomena provide a pathway to new precision methods for studying photochemical reactions in crystals. In those cases where the transformation does not cause structural rearrangement of the crystal, its amorphization or plastic deformation, the transformation is unambiguously related to the resulting deformations, so that the solution of the inverse problem allows us to study the kinetics of transformation with sensitivity inaccessible to other methods.
This method historically originated from the study of photoinduced bending of needle-shaped crystals of [Co(NH3)5NO2]Cl(NO3), experiencing isomerization in the coordination of cobalt by the ambidentate ligand NO2− (from Co–NO2 to Co–ONO, nitro–nitrito isomerization).18,19 Further development of the method is able to provide detailed information on the absorption of light by the substance, the spatial distribution of the transformation in the crystal, and the value of the quantum yield, the most important characteristic of the photochemical reaction.20–23
However, there are still specific difficulties in determining the quantum yield in solids. In contrast to solutions, where it is sufficient to measure the total absorbed irradiation dose that caused the transformation, in the case of crystals it is necessary to know the light intensity. Without detailed information on the angular intensity distribution of the light source, this can lead to significant errors in the absolute value of the quantum yield determined in various experiments using averaged intensity in the light beam.20 Therefore, it is very desirable to develop an experimental approach that avoids the need to know the exact value of the light intensity to calculate the quantum yield.
In this study, it is proposed to use for this purpose the photothermal effect arising simultaneously with the transformation – the bending of a crystal due to inhomogeneous heating by the absorbed light.24 Since both photothermal and photochemical bending of a crystal are proportional to the same light intensity, their ratio does not depend on it and is determined by the ratio of strains caused by transformation and heating. In addition, the method can be used to determine the light intensity itself, as well as the thermal conductivity of the crystal.
Photochemical isomerization in [Co(NH3)5NO2]Cl(NO3) crystals was used to test the idea. Crystals and solutions of this complex experience the transformation from a thermally stable nitro isomer to a nitrito isomer under irradiation with visible or UV light at λ < 530 nm. The reverse isomerization occurs spontaneously: in a few days at room temperature, or in a few minutes with heating up to 80 °C.18–20,25–27 Isomerization in the crystals does not change the initial orthorhombic crystal structure, except for a linear change of lattice parameters with the degree of transformation,20 which makes it possible to follow the transformation kinetics by measuring the bending of a needle crystal irradiated from one side.
[Co(NH3)5NO2]X2 crystals with various anions (X = Cl, Br, and I) have been investigated earlier in a number of studies,26–32 but the only mention of the quantum yield measurement in the crystals can be found in a short report in ref. 33, where the quantum yield φ = 0.2 ± 0.05 is given without experimental details. Here, we demonstrate the use of the new method to obtain the wavelength dependence of quantum yield for visible light from 403 to 523 nm.
2 Experimental method
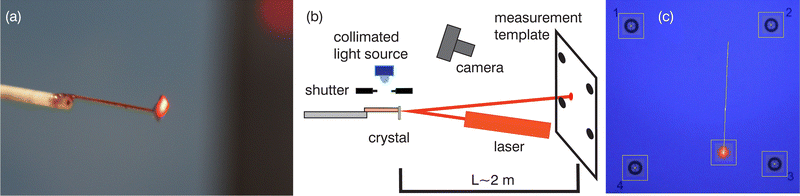
To study the dynamics of crystal bending, the displacement of the laser beam reflected from a micromirror (a small silicon plate) glued to the end of a cantilevered crystal was tracked (Fig. 1). Crystals with a length of 5–13 mm and a thickness of 180–280 μm were used.Collimated irradiation from 1 W LEDs (λ = 403 nm, 465 nm, 523 nm) and a 100 W xenon arc lamp with bandpass interference filters (405 nm, 425 nm, 436 nm, 461 nm, 491 nm) was used as the light source. A mechanical shutter was used to control the exposure periods.
The movement of the laser spot along the measuring template located at a distance of about 2 m from the crystal was recorded using a 50 fps video camera. The video files were analyzed using in-house developed software based on automatic tracking of the laser spot movement relative to the template marks located at the vertices of a 10 × 10 cm square (“Laser Spot Track” plugin for ImageJ34 is available at https://imagej.net/PhotoBend).
The spatial resolution of the laser spot movement achieved in the experiment was about 50 μm. For a crystal located at a 2 m distance this provides a resolution of 7 × 10−3 deg for the bending angle, or 60 nm deflection of the free end of a 1 cm long crystal. This corresponds to a transverse strain gradient resolution of 10−7 per 100 μm of crystal thickness, which can be caused, for example, by a temperature gradient of 10−3 K per 100 μm (for a thermal expansion coefficient of 10−4 K−1), or by 0.01% transformation in a 10 μm surface layer of such a crystal.
Fig. 2 demonstrates the dynamics of the reflected beam movement as a result of five exposure periods of different durations. Each time, at the onset of irradiation, the crystal experiences a rapid bending with the same amplitude in each cycle, taking a time of about 100 ms. This is followed by a slower curvature growth with the same rate in each cycle, related to the accumulation of the nitrito isomer in the surface layer. At the end of each exposure, a rapid limited unbending occurs, reversed in the direction and taking the same time as the rapid bending phase at the exposure start. Between exposures, the bending achieved due to isomerization does not change, since the rate of reverse isomerization at room temperature is negligible. The described rapid bending and unbending steps correspond to the photothermal effect. Deformations occurring during the establishment and disappearance of the transverse temperature gradient estimated here to be 0.035 K over the crystal thickness of 280 μm. The total transformation degree reached at the surface after five exposures is estimated to be 2.5%.
3 Model
3.1 Photothermal effect
One side of a needle crystal is heated by light due to nonradiative deactivation of photoexcited states appearing in the irradiated surface layer. A flux of quanta I0 [s−1 cm−2] carries an energy flux J0 = I0ħω onto the crystal. Absorbed in the surface layer ∼μ−1, this flux provides the bulk heat release w = J0μe−μx at depth x of the crystal with the absorption coefficient μ, according to the Bouguer–Beer–Lambert law. The temperature evolution is subject to the heat conduction equation with the volumetric heat release term | (1) |
The crystal temperature rise is limited by heat exchange with air at temperature T0, which can be described using empirical expressions for convective heat exchange of horizontal heated cylinders,35 and which defines the boundary condition of the problem
 | (2) |
An approximate solution of this problem can be obtained by splitting the heat source w into an average part wm = J0(1 − e−μh)/h and a residual w′ = w − wm. The latter corresponds to zero total heat release and, therefore, does not lead to the overall heating of the crystal, but only to a temperature inhomogeneity. The average component wm causes the overall heating of the crystal. Accordingly, the temperature change of the crystal can be represented as T(r,t) − T0 = Tm(t) + T′(r,t), where Tm(t) is the growth of the average temperature of the crystal, which does not cause its bending and is not important for the considered problem, T′(r,t) is the inhomogeneous component leading to the bending.
Due to the difference between κ and κg by more than an order of magnitude, the heat transfer to the gas is predominantly determined by the average crystal temperature Tm, whereas in the problem on T′ the heat transfer to the gas can be neglected. Further it will be shown that by the moment when the heat exchange with gas becomes essential, the condition T′ ≪ Tm is satisfied.
By integrating eqn (1) over the cross-section of the crystal, taking into account the boundary condition (2), and neglecting the inhomogeneity of temperature at the boundary, the following expression for Tm(t) can be obtained.
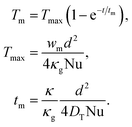 | (3) |
Since w′ depends only on x and the heat exchange with air can be neglected, the problem for T′ is formulated as the one-dimensional eqn (4)
 | (4) |
 | (5) |
| un = exp(−kn2DTt/h2), vn = cos(knx/h), | (6) |
 | (7) |
 | (8) |
 | (9) |
 .
.
As can be seen from (6), characteristic time of the slowest changing term in (5) can be determined using
 | (10) |
Next, the dynamics of the bending moment and curvature of the crystal can be determined from T′. The thermal strain moment is defined by the expression
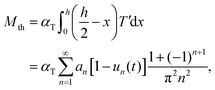 | (11) |
 .
.
A strain moment M causes a homogeneous crystal bending characterized by the curvature radius R defined by eqn (12)
 | (12) |
 | (13) |
It follows from (13) that the values of DT and κ can be obtained from the kinetics of the photothermal effect. Additionally, with the known αT and μ, the light intensity penetrating the crystal I0 = J0/ħω can be determined from the amplitude of the phototermal bending. In the case of strong absorption μh ≫ 1, the maximum photothermal bending does not depend on the thickness of the crystal, and is determined only by the intensity of the light and the properties of the substance R∞−1 → αTJ0/2κ.
A similar consideration of the crystal cooling after turning off the illumination shows that the curvature changes in the opposite way with respect to eqn (13): Rth−1 = R∞−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−DTt/π2h2).
exp(−DTt/π2h2).
3.2 Crystal bending by the photoisomerization
Simultaneously with heating, the absorbed light causes photoisomerization. Since the depletion of the initial isomer can be neglected for small degrees of isomerization, the reaction rate can be expressed using the equation | (14) |
 | (15) |
 | (16) |
3.3 Determination of quantum yield
With the irradiation onset, both processes begin simultaneously. The resulting curvature is determined by the sum of two effects R−1 = Rth−1 + Riso−1.The bending of a crystal of length l causes the mirror to be tilted by an angle l/R. The tilt results in the reflected ray move by a distance δ = 2lL/R along the wall located at a distance L.
The response of the crystal to irradiation predicted by the model occurs as follows: when the light is turned on, the curvature of the crystal increases by R∞−1 for a time ∼tc, according to (13). As a result, the laser beam is rapidly shifted to the distance δth
 | (17) |
 | (18) |
The ratio of the rate dδiso/dt to δth, measured in one experiment is independent of the light intensity
 | (19) |
Thus, the considered method allows to determine quite accurately the quantum yield of the photochemical reaction in crystals without knowing the value of the light intensity penetrating into the crystal. In addition, the analysis of the photothermal effect can be used as an independent method for determining the thermal conductivity coefficient of various substances, as well as the irradiation intensity.
4 Experimental results
The photothermal effect curves obtained at successive exposures of the 13 mm crystal are shown in Fig. 3, where all data are shifted to the origin for the ease of presentation. The results are jointly analyzed according to the given model, with common values of tc, δth, and dδiso/dt.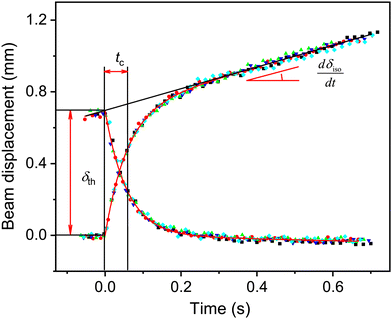 | ||
| Fig. 3 Photothermal effect at switching the irradiation on and off, corresponding to the data in Fig. 2 shifted to the common origin of coordinates. The dots of different colors correspond to five cycles of the irradiation on and off, the solid line is the fitted analytical model. | ||
The value of tc was 57 ± 4 ms for the 280 μm thick crystal, which corresponds to DT = 1.4 × 10−7 m2 s−1 and κ = 0.43 ± 0.04 J m−1 K−1 (the heat capacity was estimated by the Neumann–Kopp rule as 3 × 106 J m−3 K−1). From the value of δth = 0.7 mm the irradiation power penetrating the crystal in this experiment was evaluated to be J0 = 17 mW cm−2 according to eqn (13) and (17), which corresponds to the photon flux I0 = 3.9 × 1016 cm−2 s−1 for a 465 nm LED used in the experiment.
The resulting dependence φ(λ) obtained on different crystals is shown in Fig. 4. The dependence agrees with the data obtained earlier by another method, from the kinetics of photomechanical response of thin crystals, using the values of source intensities measured by the average radiation power in the light field.21 The method proposed here, however, gives more reliable information due to the independence of the absolute value of the obtained quantum yield from the intensity of the used source, while the use of the average intensity of the light beam can lead up to a 2-fold variation in the determined quantum yield.20
 | ||
| Fig. 4 Wavelength dependence of the quantum yield of isomerization obtained for four different crystals (geometrical dimension thickness × width × length are given in the figure). | ||
The value of φ = 0.2 ± 0.05 reported without specifying the wavelength in the only known measurement of the quantum yield of this reaction in [Co(NH3)5NO2]X2 crystals33 is in agreement with the present result at λ = 403 nm.
For isomerization of the complex in solutions, it was found that the quantum yield is constant ∼0.03 at λ > 400 nm, but increases with the excitation energy up to ∼0.2 at λ = 250 nm.36 The authors explain the obtained dependence by assuming that the reactive intermediates of the isomerization are ligand-to-metal charge-transfer (CT) excited states. At λ < 400 nm such excited states are formed directly upon light absorption and isomerize before reaching vibrational equilibrium, which leads to an increase in the quantum yield with the excitation energy. At λ > 400 nm nonreactive excited states are formed initially corresponding to the ligand field (LF) electronic transition which first reach the vibrational relaxed state, and then transform into the CT reactive states by the internal conversion process, thus providing a constant quantum yield in visible light.
The result obtained here shows a qualitative difference in the influence of the near environment on the studied reaction in solutions and in the crystal. The growth of φ with excitation energy at λ > 400 nm indicates that, in contrast to the reaction in solution, the isomerization is faster than the vibrational relaxation for LF excited states in crystals. This result also does not exclude that LF states can be directly reactive in crystal environments.
5 Conclusions
This study developed a technique for determining the quantum yield of photochemical reactions in crystals based on the joint analysis of two types of photomechanical effects simultaneously occurring during irradiation of needle crystals: rapid bending with a certain amplitude caused by heating of the crystal by light, and slower monotonic bending caused by photochemical transformation. Since the amplitudes of both effects are proportional to the same light intensity, their ratio is independent of it, which allows us to determine the quantum yield of a photochemical reactions occurring in crystals with zero information about the light intensity. In addition, the analysis of the photothermal effect allows us to determine the light intensity and thermal conductivity of crystals. The latter can be used as a method for measuring the thermal conductivity of various materials.In this study, the methodology is applied to determine the wavelength dependence of the quantum yield of nitro–nitrito isomerization in [Co(NH3)5NO2]Cl(NO3) crystals. For the wavelength range 403–523 nm, a monotonic decrease of the quantum yield from φ = 0.19 to φ = 0.04 was obtained, which is qualitatively different from the reaction in solutions, where φ = 0.03 regardless of λ within the same wavelengths. This result shows that new insights into this reaction can be obtained by methods based on the analysis of photomechanical effects.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by Russian Science Foundation, grant number 22-23-01130.Notes and references
- H. Finkelmann, E. Nishikawa, G. G. Pereira and M. Warner, Phys. Rev. Lett., 2001, 87, 015501 CrossRef CAS PubMed.
- N. K. Nath, M. K. Panda, S. C. Sahoo and P. Naumov, CrystEngComm, 2014, 16, 1850–1858 RSC.
- P. Commins, I. T. Desta, D. P. Karothu, M. K. Panda and P. Naumov, Chem. Commun., 2016, 52, 13941–13954 RSC.
- L. Zhu, F. Tong, R. O. Al-Kaysi and C. J. Bardeen, in Photomechanical Effects in Photochromic Crystals, ed. T. J. White, Wiley, 2017, pp. 233–274 Search PubMed.
- P. Naumov, S. Chizhik, M. K. Panda, N. K. Nath and E. Boldyreva, Chem. Rev., 2015, 115, 12440–12490 CrossRef CAS PubMed.
- P. Naumov, D. P. Karothu, E. Ahmed, L. Catalano, P. Commins, J. Mahmoud Halabi, M. B. Al-Handawi and L. Li, J. Am. Chem. Soc., 2020, 142, 13256–13272 CrossRef CAS PubMed.
- P. Commins, A. Natarajan, C.-K. Tsai, S. I. Khan, N. K. Nath, P. Naumov and M. A. Garcia-Garibay, Cryst. Growth Des., 2015, 15, 1983–1990 CrossRef CAS.
- Y. Nakagawa, M. Morimoto, N. Yasuda, K. Hyodo, S. Yokojima, S. Nakamura and K. Uchida, Chem. – Eur. J., 2019, 25, 7874–7880 CrossRef CAS PubMed.
- D. Kitagawa, R. Tanaka and S. Kobatake, Phys. Chem. Chem. Phys., 2015, 17, 27300–27305 RSC.
- A. Hirano, D. Kitagawa and S. Kobatake, CrystEngComm, 2019, 21, 2495–2501 RSC.
- D. Kitagawa and S. Kobatake, J. Phys. Chem. C, 2013, 117, 20887–20892 CrossRef CAS.
- T. Kim, L. Zhu, L. J. Mueller and C. J. Bardeen, J. Am. Chem. Soc., 2014, 136, 6617–6625 CrossRef CAS PubMed.
- F. Terao, M. Morimoto and M. Irie, Angew. Chem., Int. Ed., 2012, 51, 901–904 CrossRef CAS PubMed.
- D. Kitagawa and S. Kobatake, Chem. Commun., 2015, 51, 4421–4424 RSC.
- R. Chandrasekar, Small, 2021, 17, 2100277 CrossRef CAS PubMed.
- M. G. Kuzyk and N. J. Dawson, Adv. Opt. Photonics, 2020, 12, 847–1011 CrossRef.
- J. Mahmoud Halabi, E. Ahmed, S. Sofela and P. Naumov, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2020604118 CrossRef PubMed.
- E. V. Boldyreva, A. A. Sidelnikov, A. P. Chupakhin, N. Z. Lyakhov and V. V. Boldyrev, Dokl. Akad. Nauk SSSR, 1984, 277, 893–896 CAS.
- E. V. Boldyreva and A. A. Sidelnikov, Izv. Sib. Otd. Akad. Nauk SSSR, Ser. Khim. Nauk, 1987, 5, 139–144 Search PubMed.
- S. Chizhik, A. Sidelnikov, B. Zakharov, P. Naumov and E. Boldyreva, Chem. Sci., 2018, 9, 2319–2335 RSC.
- E. Ahmed, S. Chizhik, A. Sidelnikov, E. Boldyreva and P. Naumov, Inorg. Chem., 2022, 61, 3573–3585 CrossRef CAS PubMed.
- A. A. Sidelnikov, S. A. Chizhik, B. A. Zakharov, A. P. Chupakhin and E. V. Boldyreva, CrystEngComm, 2016, 18, 7276–7283 RSC.
- S. Chizhik, P. Gribov, V. Kovalskii and A. Sidelnikov, Appl. Sci., 2022, 12, 12007 CrossRef CAS.
- S. Hasebe, Y. Hagiwara, K. Takechi, T. Katayama, A. Furube, T. Asahi and H. Koshima, Chem. Mater., 2022, 34, 1315–1324 CrossRef CAS.
- B. Adell, Z. Anorg. Allg. Chem., 1952, 271, 49–64 CrossRef CAS.
- V. Balzani, R. Ballardini, N. Sabbatini and L. Moggi, Inorg. Chem., 1968, 7, 1398–1404 CrossRef CAS.
- M. Kubota and S. Ohba, Acta Crystallogr., Sect. B: Struct. Sci., 1992, 48, 627–632 CrossRef.
- I. Grenthe and E. Nordin, Inorg. Chem., 1979, 18, 1869–1874 CrossRef CAS.
- A. M. Heyns and D. de Waal, Spectrochim. Acta, Part A, 1989, 45, 905–909 CrossRef.
- N. Masciocchi, A. Kolyshev, V. Dulepov, E. Boldyreva and A. Sironi, Inorg. Chem., 1994, 33, 2579–2585 CrossRef CAS.
- W. W. Wendlandt and J. H. Woodlock, J. Inorg. Nucl. Chem., 1965, 27, 259–260 CrossRef CAS.
- B. Adell, Z. Anorg. Allg. Chem., 1955, 279, 219–224 CrossRef CAS.
- E. Rose and D. McClure, J. Photochem., 1981, 17, 171 CrossRef.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- W. Kays, M. Crawford and B. Weigand, Convective Heat and Mass Transfer, McGraw-Hill, 2005 Search PubMed.
- F. Scandola, C. Bartocci and M. A. Scandola, J. Phys. Chem., 1974, 78, 572–575 CrossRef CAS.
| This journal is © the Owner Societies 2024 |