Hierarchical structure growth across different length scales in the two-phase coexistence region of myristic acid Langmuir monolayers: correlation of static and dynamic heterogeneities
Received
30th January 2024
, Accepted 28th March 2024
First published on 29th March 2024
Abstract
We investigated the hierarchical structure growth of myristic acid monolayers at the air–water interface across different length scales in the two-phase coexistence region of the first order liquid expanded (LE)–liquid condensed (LC) phase transition. A combined study of surface pressure–area (π–A) isotherm measurements with Brewster angle microscopy (BAM) observations was done at different temperatures. At the nanometer scale, the analysis of the π–A isotherm by application of a thermodynamic cluster equation allowed us to obtain the π dependence of cluster size (cluster distribution) in the LE–LC coexistence region. The cluster distributions showed a peak at the midpoint pressure of the transition. At higher temperature the larger nanocluster size was obtained at the transition midpoint. At the micrometer scale, BAM showed that LC domains have characteristic textures depending on the temperature. At low temperature domain density was lower and the average size of circular domains was larger. A large number of circular domains revealed a virtual boojum texture from the initial to the late stage of the transition. At the final stage some circular domains coalesced to form larger circular stripe domains and others coalesced to each other without the formation of stripe domains, finally resulting in a uniform texture over the entire water surface. At high temperature the domain texture was predominantly uniform, and a small number of domains only included straight line defects from the intermediate to the late stage of the transition. All domains coalesced to each other without the development of any texture including the stripe, different from the case at low temperature. The phase boundary line tension is highly likely to play a key role for understanding the hierarchical growth and coarsening (coalescence) process in the LE–LC transition between the different length scales from the nanometer to the micrometer scale consistently together.
Introduction
Insoluble monomolecular films at the air–water interface (Langmuir monolayers) have been of great interest for their intriguing structural and dynamical properties.1–3 Langmuir monolayers provide an excellent platform for studying two-dimensional phase transition since they allow investigation of naturally forming two-dimensional systems that are relatively easy to prepare. Particularly, the existence of the so-called “hexatic” phases has attracted much attention as an example of unusual physics in two dimensions.4–6 From the viewpoints of rheophysics and microfluidics in two dimensions, they show highly nonlinear material properties and rich flow behavior.7–9 For biophysics community, monolayers have provided important model systems for the study of molecular interactions and dynamics in biomembranes.10 From an applied point of view, Langmuir–Blodgett films transferred onto solid supports from Langmuir monolayers are used for the fabrication of magnetic or optoelectronic nanodevices and chemical or biochemical sensors.11 The structure of the monolayer at different length scales from nano to micrometer scales can be investigated by means of various experimental techniques. The in-plane nanoscopic order was measured by grazing incidence X-ray diffraction (GIXD)12–14 from synchrotron sources. Polarized fluorescence microscopy (PFM)15,16 and Brewster angle microscopy (BAM)17,18 revealed the various phases dependent on the tilt angle (with respect to the monolayer normal) and tilt azimuth and the transitions between them at the mesoscale or larger. Since the tilt angle is normally uniform across the monolayer from the energetic perspective, PFM and BAM textures usually arise from a long range ordering of the molecular tilt azimuth. They include mosaic,19,20 stripe,21,22 star,16 and boojum.23–25 These textures can be understood in terms of a Landau – de Gennes theory of tilted hexatic phases that is modified to take into account the broken symmetry at the air–water interface.4 Infrared (IR) and UV-visible (UV) spectroscopic techniques provide information on the conformation of the adsorbed molecules and the chemical interactions between the constituent molecules of the monolayer.26 With the development over one century ago of methods for quantitative measurements of the surface pressure–area (π–A) isotherms in monolayers, it has been revealed that there are a variety of phases and that the singularities such as kinks and plateaus in the isotherm are signatures of the different phase transitions appearing in the monolayer.14,27 Of the isotherms that exhibit phase transitions, the isotherm behavior in the liquid expanded (LE)–liquid condensed (LC) transition has been much paid attention.28,29 It is usually found that the pressure does not remain constant but there is an upward slope of the π–A curve during the transition. Since in an exact thermodynamic treatment a first-order phase transition is defined as a transition for which there is a discontinuity in thermodynamic function, the non-horizontal behavior in this transition region observed by most researchers is different from that expected from a conventional first order transition. Mesoscopic PFM and BAM observations, however, gave a direct evidence of the two-phase coexistence (or a heterogeneous pattern composed of the isotropic LE and anisotropic LC phases) and the changes in the relative amounts of the phases followed the lever rule in the nonhorizontal slope.30 It is thus evident that this broad transition is first order. It should be here remembered that the sharpness of phase transition depends on the number of molecules forced to cooperate in transition. Regarding the appearance of non-horizontal plateau over a finite range of pressures in the coexistence region, the formation of two-dimensional molecular aggregates such as surface micelles31 or molecular nanoclusters32,33 was discussed. Experimental observations by transmission electron microscopy (TEM)34,35 and atomic force microscopy (AFM)36–38 revealed the existence of nanoclusters in the LE–LC coexistence region of monolayers transferred onto solid substrates. Experimentally, direct observations by optical microscopy of such nanoclusters on the water surface is, however, hampered by the fact that the length scale of the clusters is beyond the resolution of optical microscopy. Albrecht et al. attributed a finite slope of the isotherm to the limited cooperativity of the transition and estimated the size of the constant cooperative clusters.39 This approach was improved to obtain the π dependence of cooperative cluster size (cluster distribution) in the coexistence region.40 The LE–LC transition in monolayers, although a first order transition, is subject to strong in-plane density fluctuations. The computer simulation study of cooperative phenomena in lipid monolayers and bilayers showed a first-order transition with strong lateral density fluctuations and the density fluctuations in monolayers manifested themselves microscopically as the appearance of a dynamic heterogeneity or creation and annihilation of clusters and persistently fluctuating in size.41 The clusters are thus regarded as fluctuating objects of correlated lipids characterized by a correlation length (or an average linear cluster size) that depends on thermodynamic conditions. The density fluctuations in monolayer manifest themselves not only as the formation of dynamic clusters in the surrounding phase microscopically, but also as the appearance of a compressibility peak macroscopically. Any type of physical measurement is normally carried out on various length scales and the specific quantity measured on some length scale is often difficult to relate to physical properties that refer to measurements corresponding to other length scales. For monolayers that are strongly anisotropic systems, this problem is particularly severe since the monolayer displays distinct structures on the different length scales. In fact, cluster and domain distributions in two-phase coexistence region were investigated at each size scale with various experimental techniques and theoretical analysis. The size of clusters on the water surface estimated by isotherm analysis is found to be in the nanometer range,33,39,40 while the size of domains observed by PFM and BAM lies typically in the tens of μm (or even to mm).16,23–25,42 However, the hierarchical relation between cluster formation on the nanometer scale and domain growth on the micrometer scale is still not clear at present. It would be essential to deeply understand the growth behavior of monolayers in the LE–LC transition from the cluster formation at the nanometer scale to the domain growth and coarsening at the micrometer scale across the different length scales consistently together. The present study focused on the hierarchical growth and coarsening across the different length scales from nanoclusters to mesoscopic domains. We investigated the LE–LC transition of myristic acid (MYA) monolayers at the nanometer and micrometer scales simultaneously by combining the macroscopic isotherm measurements with the BAM observations at different temperatures. It was stressed that the interfacial line tension is crucial for understanding the hierarchical structure growth of monolayers from nanoscale to microscale.
Cluster size distribution n(π) in the LE–LC coexistence region
In short, we summarize the derivation of a thermodynamic cluster equation involving the isotherm data from which we can obtain cluster size distribution n(π) numerically.40 Over a finite pressure interval, thermodynamic equilibrium is established if the compression is made slowly enough. One can regard the reversible process of LE–LC transition as a process of transformation of LE and LC clusters to each other or as a two-state, “all-or-none” transition, 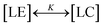 , with the two-state, isothermal equilibrium constant K = [LC]/[LE], where [LE] and [LC] are the densities of molecules in LE and LC phases, respectively. The fraction of molecules in the LC phase, or the order parameter, ξ = [LC]/([LE]+[LC]) can be defined thermodynamically with K (= ξ/(1 − ξ)). Molecules normally would not undergo the transition independently of each other but simultaneously in clusters of n molecules. The change of free energy per cluster at transition nΔG (ΔG: the difference of Gibbs free energy per molecule) can be related to K, ln
, with the two-state, isothermal equilibrium constant K = [LC]/[LE], where [LE] and [LC] are the densities of molecules in LE and LC phases, respectively. The fraction of molecules in the LC phase, or the order parameter, ξ = [LC]/([LE]+[LC]) can be defined thermodynamically with K (= ξ/(1 − ξ)). Molecules normally would not undergo the transition independently of each other but simultaneously in clusters of n molecules. The change of free energy per cluster at transition nΔG (ΔG: the difference of Gibbs free energy per molecule) can be related to K, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(π,T) = −nΔG(π,T)/kT. At a constant temperature, the pressure dependence of K(π) is K(π) = exp(−nΔA(π − πm)/kT), where πm is the surface pressure at the midpoint of the broad transition. One needs to relate the isothermal compressibility,27κT (= −(1/A)·(∂A/∂π)T) with the surface pressure dependent cluster distribution, n(π). When monolayer occupies a molecular area A located in the coexistence region, ξ is expressed by the application of the “lever rule”, ξ ≅ (A − ALE)/(ALC − ALE) = (1/ΔA)·(A − ALE), where ALE, ALC are the LE, LC phase boundary areas, respectively, and ΔA is the transition area width. Utilizing the chain rule, (∂ξ/∂A)T = (∂ξ/∂π)T·(∂π/∂A)T, we finally obtain the following equation to extract the distribution n(π):
K(π,T) = −nΔG(π,T)/kT. At a constant temperature, the pressure dependence of K(π) is K(π) = exp(−nΔA(π − πm)/kT), where πm is the surface pressure at the midpoint of the broad transition. One needs to relate the isothermal compressibility,27κT (= −(1/A)·(∂A/∂π)T) with the surface pressure dependent cluster distribution, n(π). When monolayer occupies a molecular area A located in the coexistence region, ξ is expressed by the application of the “lever rule”, ξ ≅ (A − ALE)/(ALC − ALE) = (1/ΔA)·(A − ALE), where ALE, ALC are the LE, LC phase boundary areas, respectively, and ΔA is the transition area width. Utilizing the chain rule, (∂ξ/∂A)T = (∂ξ/∂π)T·(∂π/∂A)T, we finally obtain the following equation to extract the distribution n(π):| | 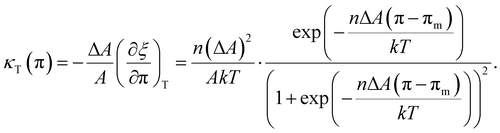 | (1) |
By solving the eqn (1) into which the measured data {(A,π,κT)} are incorporated, numerically, one can obtain the cluster size distribution n(π) in the LE–LC coexistence region.
Experimental
Myristic acid (MYA) was purchased from Sigma and claimed to be ≥99% pure. It was used without further purification. The monolayer was formed by preparing n-hexane (Merck, ACS) solution of MYA at a concentration between 0.5 and 0.8 mmol l−1 and by spreading about 25 μl of this solution onto the acidified pure water contained in a custom-built Teflon trough. The pH of the aqueous (Millipore Milli-Q at 18.1 MΩ cm) subphase was adjusted to pH 2 with dilute hydrochloric acid in order to avoid ionic dissociation of the MYA carboxylic head groups. After evaporation of the solvent for 20–30 min, the monolayer was compressed at a rate of 0.01 nm2·molecule−1·min−1. Langmuir isotherms were obtained by compressing monolayers uniaxially under the action of the barrier of the trough and the monolayer surface pressure (π) and the molecular area (A) were measured using a commercial film balance (R&K GmbH, Potsdam, Germany) equipped with Wilhelmy-type pressure measuring system and were automatically stored on disk. The surface pressure sensibility was 0.1 mN m−1. The isothermal compressibility κT was calculated from the numerical derivative of the isotherm using the digitally stored isotherm data. It was calculated over 60–120 interpolated points to avoid spurious finite difference noise. A Teflon-coated thermocouple immersed in the subphase was used to measure the subphase temperature and it was controlled within 0.1 °C by circulating water and two water cooled Peltier elements mounted directly on the back side of the copper plate. The copper bottom was coated with a 0.3 mm thin black Teflon foil. A home-built Brewster Angle Microscopy (BAM) visualized the Langmuir monolayer. A spatially filtered and collimated laser light from a diode module (30 mW, λ = 660 nm, He–Ne) mounted on the first arm was sent onto the air–water interface at the Brewster's angle (θB ≈ 53°). The incident beam was linearly polarized in the plane of incidence by a Glan-Thompson polarizer. The reflected beam from the monolayer was focused onto a 5× microscope objective mounted on the second arm. It was directed onto a CCD camera after passing a second Glan-Thomson prism (analyzer). Because the monolayer is not parallel to the focal plane of the microscope, only a region of about one-third of the field of view is in focus. Moreover, images obtained with this configuration are distorted, and the dimension parallel to the incidence plane is scaled by a factor of cos(θB) ≈ 0.6. Images presented in this paper were corrected for this geometrical distortion. The analyzer was oriented at ≈60° with respect to the plane of incidence throughout the experiments to optimize the contrast in the images. Spatial reflectivity modulations are correlated to coexistence of optically different monolayer phases with different packing density and lateral ordering. Phases with long-range orientational order result in modulations in the polarization state of the reflected light, which result in characteristic bright textures in BAM images. Akamatsu and Rondelez reported a detailed study of the LE–LC transition for MYA monolayers by isotherm measurements and fluorescence microscopy.43 Below a well-defined temperature T*(= 24.0 ± 0.5 °C), there were two successive phase transitions, namely LE–LC1 transition at low pressure followed by a very weak, first-order LC1–LC2 transition at high pressure. Above T* the LE phase did not go through the LC1 but directly transformed into the LC2 phase. Fluorescence microscopy observations in the coexistence region showed that below T* the shape of the growing LC1 domains were circular and highly deformable, while above T* the LC2 domains were highly ramified that evolved very slowly towards their equilibrium circular shape. ALE corresponds to the onset of the LE–LC1 transition below T* and of the LE–LC2 transition above T*. In the present study we focused our attention on the LE–LC1 transition below T* in which only equilibrium circular domains were observed and we hereafter refer LC1 phase as LC phase.
Results
π–A isotherms of MYA monolayers at different temperatures are shown in Fig. 1. The LE–LC transition plateau region is clearly seen to be nonhorizontal, being similar to previous data performed at similar conditions.43–45 The latent heat of the transition, ΔQ, can be determined from the Clausius–Clapeyron equation: ΔQ = ΔA·T·dπLE/dT, where πLE is the onset pressure of the LE–LC transition, ΔA(= ALE − ALC) the molecular area change during the transition. In the above equation the temperature T is expressed in kelvin. To determine the change in latent heat corresponding to the transition, one has to measure molecular areas ALE and ALC of the LE and the LC phases, respectively, and transition pressure πLE. Of these πLE and ALE can be determined rather accurately from the abrupt change in the isotherm slope. Since the termination of the transition on compression is normally not clearly observed in the π–A isotherm, the extrapolation method was used to estimate the ALC or the ΔA during the LE–LC transition.46 The ALC is obtained as the intercept between the extrapolated plateau and the large slope of the LC phase (dashed lines in Fig. 1). In the inset of Fig. 2, πLE is plotted as a function of T. Each point corresponds to an average of five to seven independent experiments. We can obtain the slope dπLE/dT = 1.15 mN m−1 from the linear fit to the data. By using this value, from the Clausius–Clapeyron equation we plot ΔQ as a function of T in Fig. 2. Extrapolation to T* ≈ 24 °C gives ΔQ ≈ 7.0 kJ mol−1, corresponding well to the value reported in the previous study.43Fig. 3 shows the isothermal lateral compressibilities κT(π) calculated from the isotherms shown in Fig. 1. They show pronounced peaks that shift toward higher pressure with increasing temperature. The transition midpoint pressure πm, defined as the position of the maximum in κT(π), can be evaluated easily from this figure (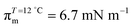 ;
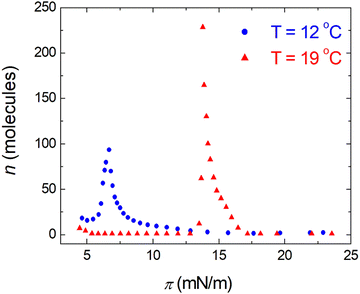
; 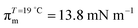 ). The shift to a higher surface pressure of the compressibility peak with increasing temperature corresponds to the change of transition pressure of the corresponding isotherm due to temperature variation. The higher the temperature, the higher the onset transition pressure. The increase in transition pressure with increasing temperature is explained by the increased thermal energy, which results in an increased entropic contribution to the chemical potential that can only be balanced by an increased enthalpic contribution. The average cluster size distribution, n(π), is obtained by using the measured isotherm data {(A,π,κT)} and the cluster eqn (1) (Fig. 4). We obtain
). The shift to a higher surface pressure of the compressibility peak with increasing temperature corresponds to the change of transition pressure of the corresponding isotherm due to temperature variation. The higher the temperature, the higher the onset transition pressure. The increase in transition pressure with increasing temperature is explained by the increased thermal energy, which results in an increased entropic contribution to the chemical potential that can only be balanced by an increased enthalpic contribution. The average cluster size distribution, n(π), is obtained by using the measured isotherm data {(A,π,κT)} and the cluster eqn (1) (Fig. 4). We obtain 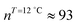 (
(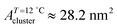 ) and
) and 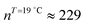 (
(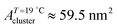 ) at the transition midpoint at 12 °C and 19 °C, respectively. Here the average cluster area, Acluster, is calculated using the relation, Acluster ≈ nmid·Amid, where nmid and Amid is the average cluster size and the molecular area at πm, respectively. From the data of Fig. 1 and 3 one can obtain amid = 0.303 nm2 and 0.260 nm2 at 12 and 19 °C, respectively. We introduce the asymmetry parameter α as a measure of the skew of a cluster distribution, α = (π2 − π1)/(π1 + π2), where π2(π1) is the half width at half maximum (HWHM) towards higher (lower) surface pressure values. The cluster distribution is larger at the higher pressure region
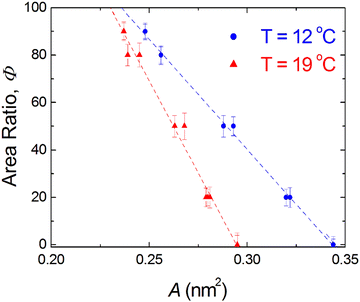
) at the transition midpoint at 12 °C and 19 °C, respectively. Here the average cluster area, Acluster, is calculated using the relation, Acluster ≈ nmid·Amid, where nmid and Amid is the average cluster size and the molecular area at πm, respectively. From the data of Fig. 1 and 3 one can obtain amid = 0.303 nm2 and 0.260 nm2 at 12 and 19 °C, respectively. We introduce the asymmetry parameter α as a measure of the skew of a cluster distribution, α = (π2 − π1)/(π1 + π2), where π2(π1) is the half width at half maximum (HWHM) towards higher (lower) surface pressure values. The cluster distribution is larger at the higher pressure region 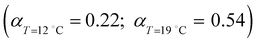 with increasing temperature. In Fig. 5 we show BAM images of coexistence between domains of LC phase and surrounding LE phase in MYA monolayers at 12 °C and 19 °C. During repetitive compression and expansion upon monolayer, nucleation events occurred randomly throughout the monolayer (not shown here), indicating homogeneous nucleation. At the initial stage of the LC domain growth (b, g), circular domains grow, indicating the presence of a finite line tension at the LE–LC boundary. The domains grow in size but not in number at the expense of the LE phase throughout the nonhorizontal coexistence plateau as long as the monolayer is steadily compressed at both temperatures. At 12 °C many domains contain virtual boojum textures from the initial to the late stage of the transition (Fig. 5(b)–(d)), while at 19 °C circular domains with line defects or uniform textures are only observed from the initial to the late stage (Fig. 5(g)–(i)). At the final stage of the transition at 12 °C (Fig. 5(e)), some domains coalesce to each other to form isolated stripe domains and others coalesce without going through the formation of any other textured domains, while at 19 °C all LC domains simply coalesce without the formation of striped or any other textured domains (Fig. 5(j)). Area ratio Φ [ = ALC/(ALE + ALC)] of the area of the LC phase to the total area of the image (digitized from the BAM) vs. A is plotted in Fig. 6. This plot is based on the assumption that the dark regions are homogeneously populated with LE phase. Each data point represents an average of five to seven images taken in different regions of the trough. The error bars correspond to the standard deviation of three independent measurements. This result indicates that although LC domains are heterogeneously distributed over the whole area of the monolayer the lever rule for the average amount of LC phase is valid. The domain growth behavior observed at the present experimental conditions clearly shows that thermodynamic equilibrium between both phases is established. The values of ALE from the isotherm measurements
with increasing temperature. In Fig. 5 we show BAM images of coexistence between domains of LC phase and surrounding LE phase in MYA monolayers at 12 °C and 19 °C. During repetitive compression and expansion upon monolayer, nucleation events occurred randomly throughout the monolayer (not shown here), indicating homogeneous nucleation. At the initial stage of the LC domain growth (b, g), circular domains grow, indicating the presence of a finite line tension at the LE–LC boundary. The domains grow in size but not in number at the expense of the LE phase throughout the nonhorizontal coexistence plateau as long as the monolayer is steadily compressed at both temperatures. At 12 °C many domains contain virtual boojum textures from the initial to the late stage of the transition (Fig. 5(b)–(d)), while at 19 °C circular domains with line defects or uniform textures are only observed from the initial to the late stage (Fig. 5(g)–(i)). At the final stage of the transition at 12 °C (Fig. 5(e)), some domains coalesce to each other to form isolated stripe domains and others coalesce without going through the formation of any other textured domains, while at 19 °C all LC domains simply coalesce without the formation of striped or any other textured domains (Fig. 5(j)). Area ratio Φ [ = ALC/(ALE + ALC)] of the area of the LC phase to the total area of the image (digitized from the BAM) vs. A is plotted in Fig. 6. This plot is based on the assumption that the dark regions are homogeneously populated with LE phase. Each data point represents an average of five to seven images taken in different regions of the trough. The error bars correspond to the standard deviation of three independent measurements. This result indicates that although LC domains are heterogeneously distributed over the whole area of the monolayer the lever rule for the average amount of LC phase is valid. The domain growth behavior observed at the present experimental conditions clearly shows that thermodynamic equilibrium between both phases is established. The values of ALE from the isotherm measurements 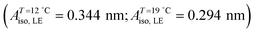 can be directly compared with the position of the LE–LC phase boundary
can be directly compared with the position of the LE–LC phase boundary 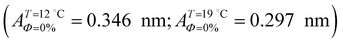 located by BAM using image analysis and the lever-rule technique. They correspond well to each other. The high-density boundary of the two-phase coexistence region, ALC, can also be estimated from the lever-rule analysis
located by BAM using image analysis and the lever-rule technique. They correspond well to each other. The high-density boundary of the two-phase coexistence region, ALC, can also be estimated from the lever-rule analysis 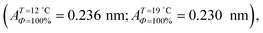 being in good agreement with the estimated values from the isotherm data
being in good agreement with the estimated values from the isotherm data 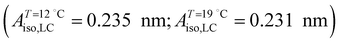 . Sometimes, already before the onset of the transition found in the isotherm, ALE, the LC phase starts to nucleate in the form of two-dimensional small particles at random positions. The occurrence of nuclei depends on the conditions of supersaturation, i.e., the local pressure excess generated. The above observation indicates that the surface pressure is not always uniform over the whole surface of the monolayer depending on the conditions of compression.
. Sometimes, already before the onset of the transition found in the isotherm, ALE, the LC phase starts to nucleate in the form of two-dimensional small particles at random positions. The occurrence of nuclei depends on the conditions of supersaturation, i.e., the local pressure excess generated. The above observation indicates that the surface pressure is not always uniform over the whole surface of the monolayer depending on the conditions of compression.
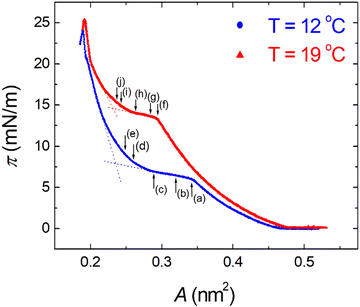 |
| | Fig. 1 Surface pressure π as a function of molecular area A for monolayers of myristic acid (MYA) at different temperatures. The dashed lines indicate how the extrapolation method was used to estimate the ALC during the LE–LC transition. Letters indicate positions of the corresponding BAM images in Fig. 5. | |
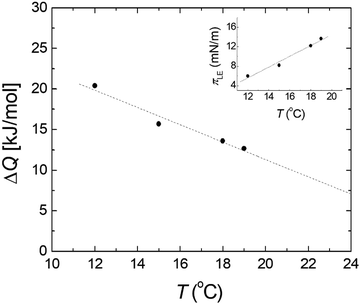 |
| | Fig. 2 Heat of transition ΔQ as a function of temperature T for MYA monolayers. Inset: Film pressure πLE, the onset of the LE–LC transition as a function of T. Dashed lines are the linear least-squares fits to the data. | |
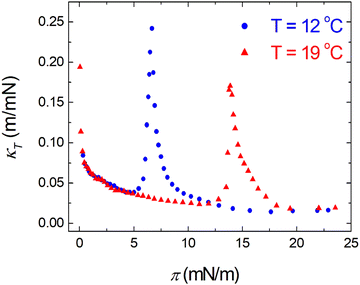 |
| | Fig. 3 Isothermal lateral compressibility κT – surface pressure π characteristics for MYA monolayers at different temperatures. | |
 |
| | Fig. 4 The average molecular cluster size distribution in the LE–LC coexistence region of MYA monolayers at different temperatures. They were obtained by solving the cluster eqn (1) substituted with the values of π–A and κT–π data shown in Fig. 1 and 3. | |
 |
| | Fig. 5 Mesoscopic LC Domain Growth in the LE–LC coexistence region of MYA monolayers at different temperatures. (a)–(e) 12 °C; (f)–(j) 19 °C. Molecular areas: (a) 0.344 nm2, (f) 0.295 nm2 (Nucleation stage, LC phase Area ratio Φ ≈ 0.0); (b) 0.321 nm2, (g) 0.280 nm2 (Initial stage, Φ ≈ 0.2); (c) 0.291 nm2, (h) 0.266 nm2 (Intermediate stage, Φ ≈ 0.5); (d) 0.256 nm2, (i) 0.242 nm2 (Late stage, Φ ≈ 0.8); (e) 0.248 nm2, (j) 0.237 nm2 (Final stage, Φ ≈ 0.9). The scale bar is 100 μm. | |
 |
| | Fig. 6 Area ratio Φ of the area of the LC phase to the total area of the image (digitized from the BAM) vs. A, the surface molecular area. Dashed lines indicate the linear least-squares fits to the data. The errors correspond to the standard deviation of the determined individual Φ values. | |
Discussion
Dynamic heterogeneity at the nanometer scale
In the usual first-order transition all elements of the system would go between the two states together at a single pressure or temperature. The LE–LC transition has characteristics largely different from the conventional first-order phase transition, since the former occurs through the formation of LC islands dispersed in a continuous phase of LE molecules. Since monolayers are quasi-two-dimensional systems, the existence of large density fluctuations is expected.47 The isothermal lateral compressibility, κT is related to the fluctuations in the molecular area density ρA (number of molecules per unit area) by the fluctuation–dissipation theorem:48| | 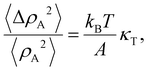 | (2) |
where ΔρA is the density deviation from its mean density value 〈ρA〉, ΔρA = ρA − 〈ρA〉, and 〈ΔρA2〉 = 〈ρA2〉 − 〈ρA〉2. The left-hand side of the eqn (2) is the relative mean square fluctuations in molecular area density. Hence, peaks in κT may be interpreted as indications of large molecular area density fluctuations. From the eqn (2) and the observed compressibility data it is seen that the monolayer is subject to large molecular area density fluctuations. Moreover, by utilizing the cluster eqn (1) involving the compressibility and the fluctuation–dissipation theorem (2), such local density fluctuations are manifested as a kind of cluster formation process. The average linear cluster size obtained from the present cluster equation is a measure of the correlation length that describes the range over which the cooperative molecular density fluctuations are operative. The occurrence of the clusters on the nanometer length scale clearly indicates that the molecular density fluctuations are cooperatively correlated in space with a correlation length corresponding to the average linear cluster size. Strong theoretical evidence for the presence and origin of the dynamically heterogeneous states, e.g., the dynamic heterogeneity in lipid bilayers was given by the theoretical calculations on specific molecular interaction models of lipid bilayers.49,50 It was demonstrated that although the average cluster size is an equilibrium property these clusters are dynamic and highly fluctuating entities induced by the cooperative density fluctuations of the bilayer and that they nucleate, grow, and disappear in time with finite lifetimes that depend on their size and the thermodynamic conditions. The appearance of dynamic heterogeneity is thus a natural consequence of the fact that the monolayer is a many-particle system sustaining strong lateral cooperative molecular area density fluctuations. It is extremely difficult experimentally to obtaining direct information on dynamic heterogeneity of the monolayer on the water surface, since this type of heterogeneity is manifested at nanoscopic length scales which are not easily accessible using current experimental techniques. The macroscopic manifestation of the persistence of dynamic nanoclusters or dynamic heterogeneity is however accessible from the corresponding thermodynamic response function by the combination of the thermodynamic cluster eqn (1) and the equilibrium fluctuation–dissipation theorem (2). The present thermodynamic scheme explicitly indicates the close relationship between microscopic dynamic heterogeneity characterized by average linear cluster size and macroscopic lateral compressibility determined from isotherm. Experimental advantage of the present thermodynamic procedure for obtaining a nanocluster size distribution in the LE–LC coexistence region is that the physical quantities (A,π,κT;ΔA,πm) involved in the thermodynamic cluster eqn (1) are all experimentally accessible from macroscopic measurements and that no adjustable parameters are required. As a conceptual advantage of the present approach, the dynamic character of clusters formed at the nanometer scale is clearly manifested by the existence of large molecular area density fluctuations revealed by the macroscopic compressibility involved in the eqn (1).
Ratio of interfacial line tensions at two different temperatures
A fluctuation-based approach seems to be more effective for the analysis of phase transitions in monolayer since from the Ginzburg criterion a wider temperature region for critical behavior is expected than in three dimensions.51 It was previously reported that the critical behavior from the thermodynamic as well as the structural data in lipid monolayers is consistent with the 2D Ising universality class.52 In this class the observables such as correlation length ξ and line tension λ follow general power laws and scaling relations, ξ ∝ |(T − Tc)/Tc|−ν and λ ∝ |(T − Tc)/Tc|μ.51 The critical exponent for line tension μ is related to that for correlation length ν through the number of dimensions in the system d, (μ = (d − 1)ν). For monolayer (d = 2), μ = ν, so we have λ ∝ ξ−1. Since the average linear cluster size accessible in this study is a measure of ξ, taking the above inverse relation between λ and ξ into consideration, we can expect the decrease in line tension with increasing temperature from the temperature dependence of n(π) at the nanoscopic level (Fig. 4). This is indeed consistent with previous fluorescence microscopy observations in which LC domain shapes became less progressively compact on compression with increasing temperature.53,54 The present BAM observations show the increase of number of mesoscopic LC domains with increasing temperature T. Previous fluorescence microscopy imaging studies revealed qualitatively similar results.53,55 Consider the case that the number of mesoscopic LC domains is determined by the nucleation process.55,56 Along the classical nucleation theory (CNT), the temperature dependence of the nucleation rate J for steady-state nucleation is given by J ∼ exp(−ΔE/kT).57 The activation energy ΔE to nucleate an LC domain at the expense of the LE fluid is given by ΔE = πλ2ALCπLE/ΔQΔπ, where Δπ is the degree of supersaturation.58,59 The increase of number of domains is expected with increasing temperature if ΔE is nearly constant although factors determining ΔE depend on temperature.55 Assuming that the activation energy ΔE and the supersaturation Δπ are almost kept constant for the experiment at two different temperatures, and by using the above expression for ΔE that involves a macroscopic latent heat ΔQ from the CNT the ratio of the line tensions at 12 °C and 19 °C, 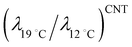 is given by
is given by 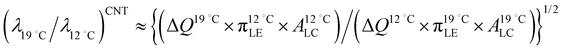 . Let us compare this estimated value with the corresponding value
. Let us compare this estimated value with the corresponding value 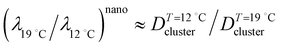 , obtained with the average linear cluster size Dcluster (= 2 × (Acluster/π)1/2) determined by nanocluster analysis. After the calculation we get
, obtained with the average linear cluster size Dcluster (= 2 × (Acluster/π)1/2) determined by nanocluster analysis. After the calculation we get 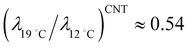 and
and 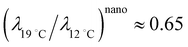 . We find that these two procedures are in fairly good agreement with each other.
. We find that these two procedures are in fairly good agreement with each other.
Effect of the line tension on LC domain nucleation, growth and coarsening
The dependency of line tension on cluster and thus domain size is essential. Domain size depends on the cluster nucleation rate and the ease of the cluster coalescence, both of which strongly depend on the line tension. According to the CNT, the interfacial line tension between the nucleating LC domains and the surrounding LE fluid regulates the rate of nucleation in supersaturated solution and therefore it dominates the nucleation density.59 In systems with lower line tensions the nucleation process is faster and the minimum size for a nucleus to be stable is lower. Therefore, the nucleation density should increase as the line tension decreases. In previous computer simulation studies60 the formation of a domain wall with low line tension in the gel–fluid transition was ascribed to the appearance of a large number of intermediate chain conformations states with defects along the cluster boundary microscopically. Therefore, the lowering of line tension of clusters would lead to a screening of the interaction between the clusters, and the coarsening (or the coalescence of clusters) would be hindered effectively. From the above arguments, small and more numerous micron-sized domains will occur at low line tension at high temperature, while high line tension at low temperature should result in a low nucleation density, causing the formation of fewer large micron-sized domains by facilitating cluster coalescence. Our BAM observations are consistent with the above picture of line tension-driven domain nucleation, growth and coarsening. We have attempted to explore the dependence of line tension on change in size and texture in the “circular” LC domain. As described in the Experimental section, T* (= 24.0 ± 0.5 °C) separates the LE–LC1 transition from the LE–LC2 transition in the T–A phase diagram. The structure of the LC domains strongly depends on the experimental conditions, especially the temperature relative to T*. Suresh et al. observed the unstable growth of LC domains in MYA Langmuir monolayers in the vicinity of T*.53 At a temperature of 20 °C, LC domains already showed an irregular, non-characteristic shape. For this reason, the isotherm and BAM measurements in the present study have been performed at two temperatures (e.g., 12 °C and 19 °C) where stable circular LC domains can be observed, of different distances from 20 °C. From the BAM measurements we have found that circular LC domains show simultaneous changes of size and texture from a large boojum texture at 12 °C (e.g., at high line tension) to a small uniform texture at 19 °C (e.g., at low line tension). At 19 °C we could not observe the coalescence of LC domains until at the final stage of the transition substantially. This result also strongly supports the idea that the decrease of the line tension effectively affects the slowing of growth and coarsening of domains.
Effect of the line tension on the formation of textures in LC domain
Interfacial line tension effect or the decrease of line tension between the coexisting phases works not only for growth and coarsening of nanoclusters and mesoscopic domains, but also for the appearance of different textures of domains at different temperatures. In the situation where elastic constants and line tension are of the same order of magnitude, we can expect to see domains that have a non-uniform molecular orientation and an anisotropic overall shape. The continuous variation of gray level (which corresponds to the continuous variation of molecular tilt azimuth) inside each LC domain is apparent from the initial to the late stage of the transition at T = 12 °C (Fig. 5). The particular distribution of molecular tilt azimuth is consistent with a texture called a virtual boojum with no line defects.23–25 In this texture, the defect core is placed outside the droplet to avoid the core energy higher compared to the splay energy, at the cost of a violation of normal boundary conditions to the LE–LC boundary imposed by the anisotropic part of line tension. Cusps are apparent in the boundaries closest to the defect core of virtual boojum domains. The appearance of such a cusp implies that the anisotropic part of the line tension of the LE/LC boundary is strong with respect to its isotropic part so that normal boundary conditions can be satisfied better, otherwise, droplets would remain round. As already described by Fischer et al.,4 without any connection to the boundary conditions, the uniform texture should be dominant. The significant decrease of line tension at high temperature would promote the decoupling of the orientational texture from the boundary conditions, resulting in the predominance of the uniform texture in the domains. In fact, at 19 °C, many LC domains observed in the experiments showed uniform texture and only a small number of domains included line defects inside.
Consistency with other experimental results
Finally, let us shortly compare the cluster sizes obtained from the present thermodynamic cluster analysis with those reported in the previous experimental studies on monolayers and bilayers. With regard to the limited cooperativity of molecules in monolayers at the air–water interface, it was suggested that the non-horizontal slope in the isotherm for DPPC monolayers results from the finiteness of the transition involving the cooperative clusters of about 60–190 molecules from the van’t Hoff analysis using the isotherm.39 Electron microscopy and diffraction study of phospholipid monolayers transferred from water surface to solid substrates showed the coexistence of LE and LC domains with correlation length of some 10 nm, corresponding to the average linear cluster size.34 AFM was applied for the main transition of supported DMPC bilayers as a quantitative structural calorimetry from a specific image analysis and provided a cooperative cluster size of 195 molecules.38 In calorimetric studies the size of a cooperative cluster of the lipid bilayer undergoing chain melting transition is estimated by the ratio of enthalpy derived from the van’t Hoff enthalpy to the corresponding calorimetric enthalpy. The gel–liquid crystalline transition in dilute aqueous suspensions of DMPC bilayers gave a cluster size of ≈200 molecules.61 Theoretically, Israelachvili31 developed a model for π–A curves involving the critical micelle area where the amphiphiles form surface micelles in monolayers. On the basis of the shapes of many measured π–A curves, it was concluded that nanoscale surface micelles of aggregation numbers in the tens to hundreds must exist. The values obtained from our thermodynamic scheme are thus generally consistent with the past experimental and theoretical studies. We note that the present thermodynamic procedure from π–A isotherm measurements is much simpler to be made compared to the other methods that have been done.
Conclusions
The LE–LC transition evolution in MYA monolayers has been investigated from the viewpoint of the formation, growth, and coarsening (coalescence) of nanoclusters and mesoscopic domains on the different length scales simultaneously. The LC domains with several tens to over one hundred micrometers in diameter were observed by BAM measurements, while the nanocluster distributions were determined from the application of a thermodynamic cluster equation utilizing the measured π–A data. In the nanometer range each cluster is well known to be a dynamic object that nucleates, grows, and disappears again and this phenomenon has been referred to as dynamic heterogeneity. The monolayer density fluctuations in the transition region are manifested in the formation of dynamic clusters of correlated molecules characterized by an average cluster size on the nanometer scale. In this study the formation of nanoclusters was revealed with the cluster equation involving the π–A data and the derived macroscopic response function, i.e., isothermal compressibility, which is a measure of the lateral density fluctuations, via the fluctuation–dissipation theorem. The ratio of interfacial line tensions at two different temperatures was discussed and determined from both the inverse relation of λ and correlation length ξ (≈ average linear cluster size) at the nanometer scale and the classical nucleation theory (CNT) with thermodynamic parameters derived from the macroscopic isotherm measurements. The line tension ratio obtained from the two approaches corresponded to each other reasonably well. We found that the size and the number of LC domains at the micrometer level are strongly correlated with cluster distribution at the nanometer level through the temperature-dependent line tension at the LE–LC boundary. It is highly suggested that dynamic heterogeneity (the formation of dynamic clusters) at the nanometer scale can effectively lead to static heterogeneity (the coexistence of LC domains and the surrounding LE phase) at the micrometer scale in the two-phase coexistence region. The close relationship between the two types of heterogeneities evidently indicates the existence of hierarchical structure in monolayer growth across the different length scales. Such a hierarchical approach could provide an effective method for deeply understanding the LE–LC transition in monolayers in which distinct structures are formed on the different length scales. The formation of nanoclusters will inevitably cause the creation of an interfacial environment which is defined by the borders between the clusters and the surrounding bulk liquid. The formation of interfacial regions with molecular chains with conformationally more disordered states would imply that of interface with a low line tension. The lowering of the line tension at the interface between LE and LC phases is extremely likely to promote the prolongation of the lifetime for individual clusters, resulting in the slowing down of the domain growth and coarsening. The line tension at the LE–LC phase boundary is therefore expected to play an essential role for understanding the hierarchical structure formation in monolayer growth from the nanometer range to the micrometer range consistently.
Author contributions
E. H. performed all the experimental works and thermodynamic analysis to the measurement data, and contributed to writing and editing the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was partially supported by JSPS KAKENHI grant number JP22K04853.
References
- H. M. McConnell, Annu. Rev. Phys. Chem., 1991, 42, 171–195 CrossRef CAS.
-
H. Möhwald, in Handbook of Biological Physics, ed. R. Lipowsky and E. Sackmann, Elsevier, Amsterdam, 1995, vol. 1, pp. 161–211 Search PubMed.
- C. M. Knobler, Annu. Rev. Phys. Chem., 1992, 43, 207–236 CrossRef CAS.
- Th. M. Fischer, R. Bruinsma and C. M. Knobler, Phys. Rev. E, 1994, 50, 413–428 CrossRef CAS PubMed.
- J. Ignés-Mullol and D. K. Schwartz, Langmuir, 2001, 17, 3017–3029 CrossRef.
- C. M. Knobler, Mol. Cryst. Liq. Cryst., 2001, 364, 133–140 CrossRef CAS.
-
Interfacial transport processes and rheology, ed. D. A. Edwards, H. Brenner and D. T. Wasan, Butterworth-Heinemann, 1991 Search PubMed.
- D. Langevin, Annu. Rev. Fluid Mech., 2014, 46, 47–65 CrossRef.
- C. Alonso and J. A. Zasadzinski, J. Phys. Chem. B, 2006, 110, 22185–22191 CrossRef CAS PubMed.
- C. Stefaniu, G. Brezesinski and H. Möhwald, Adv. Colloid Interface Sci., 2014, 208, 197–213 CrossRef CAS PubMed.
- O. N. Oliveira, Jr., L. Caseli and K. Ariga, Chem. Rev., 2022, 122, 6459–6513 CrossRef PubMed.
- P. Dutta, Colloids Surf., A, 2000, 171, 59–63 CrossRef CAS.
- J. Als-Nielsen, D. Jacquemain, K. Kjaer, F. Leveiller, M. Lahav and L. Leiserowitz, Phys. Rep., 1994, 246, 251–313 CrossRef CAS.
- V. M. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779–819 CrossRef CAS.
- V. T. Moy, D. J. Keller, H. E. Gaub and H. M. McConnell, J. Phys. Chem., 1986, 90, 3198–3202 CrossRef CAS.
- X. Qiu, J. Ruiz-Garcia, K. J. Stine, C. M. Knobler and J. V. Selinger, Phys. Rev. Lett., 1991, 67, 703–706 CrossRef CAS PubMed.
- S. Hénon and J. Meunier, Rev. Sci. Instrum., 1991, 62, 936–939 CrossRef.
- D. Honig and D. Mobius, J. Phys. Chem., 1991, 95, 4590–4592 CrossRef.
- S. Rivière, S. Hénon, J. Meunier, D. K. Schwartz, M.-W. Tsao and C. M. Knobler, J. Chem. Phys., 1994, 101, 10045–10051 CrossRef.
- D. K. Schwartz and C. M. Knobler, J. Phys. Chem., 1993, 97, 8849–8851 CrossRef CAS.
- J. Ruiz-Garcia, X. Qiu, M.-W. Tsao, G. Marshall, C. M. Knobler, G. A. Overbeck and D. Mobius, J. Phys. Chem., 1993, 97, 6955–6957 CrossRef CAS.
- D. K. Schwartz, J. Ruiz-Garcia, X. Qiu, J. V. Selinger and C. M. Knobler, Physica A, 1994, 204, 606–619 CrossRef CAS.
- G. A. Overbeck, D. Hönig and D. Möbius, Thin Solid Films, 1994, 242, 213–219 CrossRef CAS.
- D. K. Schwartz, M.-W. Tsao and C. M. Knobler, J. Chem. Phys., 1994, 101, 8258–8261 CrossRef CAS.
- S. Rivière and J. Meunier, Phys. Rev. Lett., 1995, 74, 2495–2498 CrossRef PubMed.
- P. Dynarowicz-Latka, A. Dhanabalan and O. N. Oliveira Jr, Adv. Colloid Interface Sci., 2001, 91, 221–293 CrossRef CAS PubMed.
-
G. L. Gaines, Insoluble monolayers at liquid–gas interfaces, Wiley, New York, 1966 Search PubMed.
- L. R. Arriaga, L. Lopez-Montero, J. Ignes-Mullol and F. Monroy, J. Phys. Chem. B, 2010, 114, 4509–4520 CrossRef CAS PubMed , and references therein.
- E. Hatta and K. Nihei, Phys. Rev. E, 2019, 100, 0228011 CrossRef PubMed.
- B. G. Moore, C. M. Knobler, S. Akamatsu and F. Rondelez, J. Phys. Chem., 1990, 94, 4588–4595 CrossRef CAS.
- J. Israelachvili, Langmuir, 1994, 10, 3774–3781 CrossRef CAS.
- E. Ruckenstein and B. Li, Langmuir, 1995, 11, 3510–3515 CrossRef CAS.
- E. Hatta and K. Nihei, Phys. Chem. Chem. Phys., 2021, 23, 22543–22550 RSC.
- A. Fischer and E. Sackmann, J. Phys., 1984, 45, 517–527 CrossRef CAS.
- F. Boury, A. Gulik, J. C. Dedieu and J. E. Proust, Langmuir, 1994, 10, 1654–1656 CrossRef CAS.
- L. F. Chi, M. Anders, H. Fuchs, P. R. Johnston and H. Ringsdorf, Science, 1993, 259, 213–216 CrossRef CAS PubMed.
- X.-M. Yang, D. Xiao, S.-J. Xiao, Z.-H. Lu and Y. Wei, Phys. Lett. A, 1994, 193, 195–198 CrossRef CAS.
- O. Enders, A. Ngezahayo, M. Wiechmann, F. Leisten and H.-A. Kolb, Biophys. J., 2004, 87, 2522–2531 CrossRef CAS PubMed.
- O. Albrecht, H. Gruler and E. Sackmann, J. Phys., 1978, 39, 301–313 CrossRef CAS.
- E. Hatta and T. Nishimura, J. Colloid Interface Sci., 2013, 391, 111–115 CrossRef CAS PubMed.
-
O. G. Mouritsen, Molecular Description of Biological Membrane Components by Computer Aided Conformational Analysis, CRC Press, Boca Raton, Florida, 1990, vol. I, pp. 3–83 Search PubMed.
- E. Hatta and Th. M. Fischer, Langmuir, 2002, 18, 6201–6206 CrossRef CAS.
- S. Akamatsu and F. Rondelez, J. Phys., 1991, 1, 1309–1322 CAS.
- M. C. Phillips and D. Chapman, Biophys. Biochim. Acta, 1968, 163, 301–313 CrossRef CAS PubMed.
- A. M. Bibo and I. R. Peterson, Adv. Mater., 1990, 2, 309–311 CrossRef CAS.
- P. Krüger, M. Schalke, Z. Wang, R. H. Notter, R. A. Dluhy and M. Lösche, Biophys. J., 1999, 77, 903–914 CrossRef PubMed.
-
L. D. Landau and E. M. Lifshitz, Statistical Physics, Pergamon, Oxford, 2nd edn, 1969 Search PubMed.
-
R. K. Pathria and P. D. Beale, Statistical Mechanics, Butterworth Heinemann, Oxford, 3rd edn, 2011 Search PubMed.
- Ole G. Mouritsen and K. Jørgensen, BioEssays, 1992, 14, 129–136 CrossRef CAS PubMed.
-
K. Jørgensen, J. H. Ipsen and O. G. Mouritsen, in Principles of Medical Biology, ed. E. E. Bittar and N. Bittar, Elsevier, Amsterdam, 1997, vol. 7, pp. 19–38 Search PubMed.
-
N. Goldenfeld, Lectures on Phase Transitions and the Renormalization Group, Addison-Wesley, New York, 1992 Search PubMed.
- L. K. Nielsen, T. Bjørnholm and O. G. Mouritsen, Langmuir, 2007, 23, 11684–11692 CrossRef CAS PubMed.
- K. A. Suresh, J. Nittmann and F. Rondelez, Progr. Colloid Polym. Sci., 1989, 79, 184–193 CAS.
- K. J. Stine and D. T. Stratmann, Langmuir, 1992, 8, 2509–2514 CrossRef CAS.
- C. A. Helm and H. Möhwald, J. Phys. Chem., 1988, 92, 1262–1266 CrossRef CAS.
- K. A. Suresh, J. Nittmann and F. Rondelez, Europhys. Lett., 1988, 6, 437–443 CrossRef CAS.
-
S. Toschev, in Crystal Growth, ed. P. Hartmann, North Holland, Amsterdam, 1973, pp.1–49 Search PubMed.
-
Y. Saito, Statistical Physics of Crystal Growth, World Scientific, Singapore and New Jersey, 1996 Search PubMed.
- C. D. Blanchette, W.-C. Lin, C. A. Orme, T. V. Ratto and M. L. Longo, Langmuir, 2007, 23, 5875–5877 CrossRef CAS PubMed.
- Ole G. Mouritsen, Biochim. Biophys. Acta, 1983, 731, 217–221 CrossRef CAS PubMed.
- H.-J. Hinz and J. M. Sturtevant, J. Biol. Chem., 1972, 247, 6071–6075 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
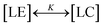 , with the two-state, isothermal equilibrium constant K = [LC]/[LE], where [LE] and [LC] are the densities of molecules in LE and LC phases, respectively. The fraction of molecules in the LC phase, or the order parameter, ξ = [LC]/([LE]+[LC]) can be defined thermodynamically with K (= ξ/(1 − ξ)). Molecules normally would not undergo the transition independently of each other but simultaneously in clusters of n molecules. The change of free energy per cluster at transition nΔG (ΔG: the difference of Gibbs free energy per molecule) can be related to K, ln
, with the two-state, isothermal equilibrium constant K = [LC]/[LE], where [LE] and [LC] are the densities of molecules in LE and LC phases, respectively. The fraction of molecules in the LC phase, or the order parameter, ξ = [LC]/([LE]+[LC]) can be defined thermodynamically with K (= ξ/(1 − ξ)). Molecules normally would not undergo the transition independently of each other but simultaneously in clusters of n molecules. The change of free energy per cluster at transition nΔG (ΔG: the difference of Gibbs free energy per molecule) can be related to K, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(π,T) = −nΔG(π,T)/kT. At a constant temperature, the pressure dependence of K(π) is K(π) = exp(−nΔA(π − πm)/kT), where πm is the surface pressure at the midpoint of the broad transition. One needs to relate the isothermal compressibility,27κT (= −(1/A)·(∂A/∂π)T) with the surface pressure dependent cluster distribution, n(π). When monolayer occupies a molecular area A located in the coexistence region, ξ is expressed by the application of the “lever rule”, ξ ≅ (A − ALE)/(ALC − ALE) = (1/ΔA)·(A − ALE), where ALE, ALC are the LE, LC phase boundary areas, respectively, and ΔA is the transition area width. Utilizing the chain rule, (∂ξ/∂A)T = (∂ξ/∂π)T·(∂π/∂A)T, we finally obtain the following equation to extract the distribution n(π):
K(π,T) = −nΔG(π,T)/kT. At a constant temperature, the pressure dependence of K(π) is K(π) = exp(−nΔA(π − πm)/kT), where πm is the surface pressure at the midpoint of the broad transition. One needs to relate the isothermal compressibility,27κT (= −(1/A)·(∂A/∂π)T) with the surface pressure dependent cluster distribution, n(π). When monolayer occupies a molecular area A located in the coexistence region, ξ is expressed by the application of the “lever rule”, ξ ≅ (A − ALE)/(ALC − ALE) = (1/ΔA)·(A − ALE), where ALE, ALC are the LE, LC phase boundary areas, respectively, and ΔA is the transition area width. Utilizing the chain rule, (∂ξ/∂A)T = (∂ξ/∂π)T·(∂π/∂A)T, we finally obtain the following equation to extract the distribution n(π):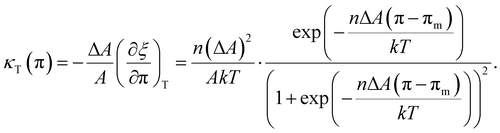
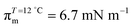 ;
; 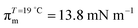 ). The shift to a higher surface pressure of the compressibility peak with increasing temperature corresponds to the change of transition pressure of the corresponding isotherm due to temperature variation. The higher the temperature, the higher the onset transition pressure. The increase in transition pressure with increasing temperature is explained by the increased thermal energy, which results in an increased entropic contribution to the chemical potential that can only be balanced by an increased enthalpic contribution. The average cluster size distribution, n(π), is obtained by using the measured isotherm data {(A,π,κT)} and the cluster eqn (1) (Fig. 4). We obtain
). The shift to a higher surface pressure of the compressibility peak with increasing temperature corresponds to the change of transition pressure of the corresponding isotherm due to temperature variation. The higher the temperature, the higher the onset transition pressure. The increase in transition pressure with increasing temperature is explained by the increased thermal energy, which results in an increased entropic contribution to the chemical potential that can only be balanced by an increased enthalpic contribution. The average cluster size distribution, n(π), is obtained by using the measured isotherm data {(A,π,κT)} and the cluster eqn (1) (Fig. 4). We obtain 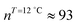 (
(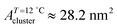 ) and
) and 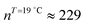 (
(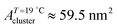 ) at the transition midpoint at 12 °C and 19 °C, respectively. Here the average cluster area, Acluster, is calculated using the relation, Acluster ≈ nmid·Amid, where nmid and Amid is the average cluster size and the molecular area at πm, respectively. From the data of Fig. 1 and 3 one can obtain amid = 0.303 nm2 and 0.260 nm2 at 12 and 19 °C, respectively. We introduce the asymmetry parameter α as a measure of the skew of a cluster distribution, α = (π2 − π1)/(π1 + π2), where π2(π1) is the half width at half maximum (HWHM) towards higher (lower) surface pressure values. The cluster distribution is larger at the higher pressure region
) at the transition midpoint at 12 °C and 19 °C, respectively. Here the average cluster area, Acluster, is calculated using the relation, Acluster ≈ nmid·Amid, where nmid and Amid is the average cluster size and the molecular area at πm, respectively. From the data of Fig. 1 and 3 one can obtain amid = 0.303 nm2 and 0.260 nm2 at 12 and 19 °C, respectively. We introduce the asymmetry parameter α as a measure of the skew of a cluster distribution, α = (π2 − π1)/(π1 + π2), where π2(π1) is the half width at half maximum (HWHM) towards higher (lower) surface pressure values. The cluster distribution is larger at the higher pressure region 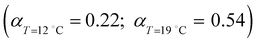 with increasing temperature. In Fig. 5 we show BAM images of coexistence between domains of LC phase and surrounding LE phase in MYA monolayers at 12 °C and 19 °C. During repetitive compression and expansion upon monolayer, nucleation events occurred randomly throughout the monolayer (not shown here), indicating homogeneous nucleation. At the initial stage of the LC domain growth (b, g), circular domains grow, indicating the presence of a finite line tension at the LE–LC boundary. The domains grow in size but not in number at the expense of the LE phase throughout the nonhorizontal coexistence plateau as long as the monolayer is steadily compressed at both temperatures. At 12 °C many domains contain virtual boojum textures from the initial to the late stage of the transition (Fig. 5(b)–(d)), while at 19 °C circular domains with line defects or uniform textures are only observed from the initial to the late stage (Fig. 5(g)–(i)). At the final stage of the transition at 12 °C (Fig. 5(e)), some domains coalesce to each other to form isolated stripe domains and others coalesce without going through the formation of any other textured domains, while at 19 °C all LC domains simply coalesce without the formation of striped or any other textured domains (Fig. 5(j)). Area ratio Φ [ = ALC/(ALE + ALC)] of the area of the LC phase to the total area of the image (digitized from the BAM) vs. A is plotted in Fig. 6. This plot is based on the assumption that the dark regions are homogeneously populated with LE phase. Each data point represents an average of five to seven images taken in different regions of the trough. The error bars correspond to the standard deviation of three independent measurements. This result indicates that although LC domains are heterogeneously distributed over the whole area of the monolayer the lever rule for the average amount of LC phase is valid. The domain growth behavior observed at the present experimental conditions clearly shows that thermodynamic equilibrium between both phases is established. The values of ALE from the isotherm measurements
with increasing temperature. In Fig. 5 we show BAM images of coexistence between domains of LC phase and surrounding LE phase in MYA monolayers at 12 °C and 19 °C. During repetitive compression and expansion upon monolayer, nucleation events occurred randomly throughout the monolayer (not shown here), indicating homogeneous nucleation. At the initial stage of the LC domain growth (b, g), circular domains grow, indicating the presence of a finite line tension at the LE–LC boundary. The domains grow in size but not in number at the expense of the LE phase throughout the nonhorizontal coexistence plateau as long as the monolayer is steadily compressed at both temperatures. At 12 °C many domains contain virtual boojum textures from the initial to the late stage of the transition (Fig. 5(b)–(d)), while at 19 °C circular domains with line defects or uniform textures are only observed from the initial to the late stage (Fig. 5(g)–(i)). At the final stage of the transition at 12 °C (Fig. 5(e)), some domains coalesce to each other to form isolated stripe domains and others coalesce without going through the formation of any other textured domains, while at 19 °C all LC domains simply coalesce without the formation of striped or any other textured domains (Fig. 5(j)). Area ratio Φ [ = ALC/(ALE + ALC)] of the area of the LC phase to the total area of the image (digitized from the BAM) vs. A is plotted in Fig. 6. This plot is based on the assumption that the dark regions are homogeneously populated with LE phase. Each data point represents an average of five to seven images taken in different regions of the trough. The error bars correspond to the standard deviation of three independent measurements. This result indicates that although LC domains are heterogeneously distributed over the whole area of the monolayer the lever rule for the average amount of LC phase is valid. The domain growth behavior observed at the present experimental conditions clearly shows that thermodynamic equilibrium between both phases is established. The values of ALE from the isotherm measurements 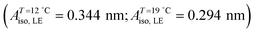 can be directly compared with the position of the LE–LC phase boundary
can be directly compared with the position of the LE–LC phase boundary 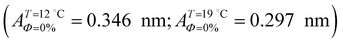 located by BAM using image analysis and the lever-rule technique. They correspond well to each other. The high-density boundary of the two-phase coexistence region, ALC, can also be estimated from the lever-rule analysis
located by BAM using image analysis and the lever-rule technique. They correspond well to each other. The high-density boundary of the two-phase coexistence region, ALC, can also be estimated from the lever-rule analysis 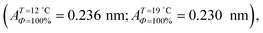 being in good agreement with the estimated values from the isotherm data
being in good agreement with the estimated values from the isotherm data 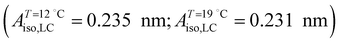 . Sometimes, already before the onset of the transition found in the isotherm, ALE, the LC phase starts to nucleate in the form of two-dimensional small particles at random positions. The occurrence of nuclei depends on the conditions of supersaturation, i.e., the local pressure excess generated. The above observation indicates that the surface pressure is not always uniform over the whole surface of the monolayer depending on the conditions of compression.
. Sometimes, already before the onset of the transition found in the isotherm, ALE, the LC phase starts to nucleate in the form of two-dimensional small particles at random positions. The occurrence of nuclei depends on the conditions of supersaturation, i.e., the local pressure excess generated. The above observation indicates that the surface pressure is not always uniform over the whole surface of the monolayer depending on the conditions of compression.



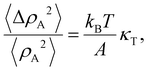
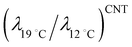 is given by
is given by 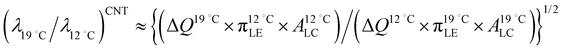 . Let us compare this estimated value with the corresponding value
. Let us compare this estimated value with the corresponding value 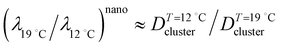 , obtained with the average linear cluster size Dcluster (= 2 × (Acluster/π)1/2) determined by nanocluster analysis. After the calculation we get
, obtained with the average linear cluster size Dcluster (= 2 × (Acluster/π)1/2) determined by nanocluster analysis. After the calculation we get 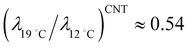 and
and 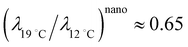 . We find that these two procedures are in fairly good agreement with each other.
. We find that these two procedures are in fairly good agreement with each other.



