Open Access Article
Open Access ArticleDynamics studies for the multi-well and multi-channel reaction of OH with C2H2 on a full-dimensional global potential energy surface†
Shuwen
Zhang
 a,
Qixin
Chen
a,
Lidong
Zhang
a,
Qixin
Chen
a,
Lidong
Zhang
 *b,
Jun
Li
*b,
Jun
Li
 *c,
Xixi
Hu
*c,
Xixi
Hu
 *de and
Daiqian
Xie
*de and
Daiqian
Xie
 ae
ae
aInstitute of Theoretical and Computational Chemistry, Key Laboratory of Mesoscopic Chemistry, School of Chemistry and Chemical Engineering, Nanjing University, Nanjing 210023, China
bNational Synchrotron Radiation Laboratory, University of Science and Technology of China, Hefei 230029, China; State Key Laboratory of Fire Science, University of Science and Technology of China, Hefei 230026, China. E-mail: zld@ustc.edu.cn
cSchool of Chemistry and Chemical Engineering & Chongqing Key Laboratory of Theoretical and Computational Chemistry, Chongqing University, Chongqing 401331, China. E-mail: jli15@cqu.edu.cn
dKuang Yaming Honors School, Nanjing University, Nanjing 210023, China. E-mail: xxhu@nju.edu.cn
eHefei National Laboratory, Hefei 230088, China
First published on 6th February 2024
Abstract
The C2H2 + OH reaction is an important acetylene oxidation pathway in the combustion process, as well as a typical multi-well and multi-channel reaction. Here, we report an accurate full-dimensional machine learning-based potential energy surface (PES) for the C2H2 + OH reaction at the UCCSD(T)-F12b/cc-pVTZ-F12 level, based on about 475![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ab initio points. Extensive quasi-classical trajectory (QCT) calculations were performed on the newly developed PES to obtain detailed dynamic data and analyze reaction mechanisms. Below 1000 K, the C2H2 + OH reaction produces H + OCCH2 and CO + CH3. With increasing temperature, the product channels H2O + C2H and H + HCCOH are accessible and the former dominates above 1900 K. It is found that the formation of H2O + C2H is dominated by a direct reaction process, while other channels belong to the indirect mechanism involving long-lived intermediates along the reaction pathways. At low temperatures, the C2H2 + OH reaction behaves like an unimolecular reaction due to the unique PES topographic features, of which the dynamic features are similar to the decomposition of energy-rich complexes formed by C2H2 + OH collision. The classification of trajectories that undergo different reaction pathways to generate each product and their product energy distributions were also reported in this work. This dynamic information may provide a deep understanding of the C2H2 + OH reaction.
000 ab initio points. Extensive quasi-classical trajectory (QCT) calculations were performed on the newly developed PES to obtain detailed dynamic data and analyze reaction mechanisms. Below 1000 K, the C2H2 + OH reaction produces H + OCCH2 and CO + CH3. With increasing temperature, the product channels H2O + C2H and H + HCCOH are accessible and the former dominates above 1900 K. It is found that the formation of H2O + C2H is dominated by a direct reaction process, while other channels belong to the indirect mechanism involving long-lived intermediates along the reaction pathways. At low temperatures, the C2H2 + OH reaction behaves like an unimolecular reaction due to the unique PES topographic features, of which the dynamic features are similar to the decomposition of energy-rich complexes formed by C2H2 + OH collision. The classification of trajectories that undergo different reaction pathways to generate each product and their product energy distributions were also reported in this work. This dynamic information may provide a deep understanding of the C2H2 + OH reaction.
I. Introduction
The dynamics investigation of the key elementary reactions in combustion processes can not only provide accurate dynamic data but also help in further exploration of the reaction mechanism, which is of great significance for the in-depth understanding of combustion processes. Acetylene is a major intermediate of most hydrocarbon flames and an important precursor of polycyclic aromatic hydrocarbons (PAHs) and soot.1–3 The reaction between C2H2 and OH is one of the main degradation pathways of acetylene and plays a key role in the combustion process. Therefore, it is necessary to study the dynamics of the C2H2 + OH reaction in detail.In the last sixty years, many works have focused on product analysis and rate coefficient determination of the C2H2 + OH reaction.4–34 Up to now, it is accepted that there are five major product channels:
Experimentally, the H2O + C2H (P1) channel was first proposed in the acetylene–oxygen reaction mechanism and was found to be an important high-temperature direct reaction channel in subsequent other studies.5,7 Gehring et al. and Kanofsky et al. reported the product channels of CO + CH3 (P5) and H + OCCH2 (P4), respectively, by using the crossed molecular beam technique in combination with mass spectrometry for this reaction.6,9 Because hydroxyacetylene (HCCOH) and ketene (OCCH2) have the same mass-to-charge ratio, the H + HCCOH (P2) channel was finally determined with the help of theoretical calculations.29 Currently, the P1, P2, P4, and P5 channels and the association reaction (M is a third body involved in energy transfer)
| C2H2 + OH + M → C2H2OH + M ΔrH298 = −36.4 kcal mol−1 |
In terms of reaction rates, the reactions between acetylene and hydroxyl radicals are dominated by electrophilic addition association reactions at low temperatures, and the reaction rates exhibit a strong pressure dependence.8,11–14,17,20,27 The pressure dependence arises mostly from the competition of collisional relaxation of nascent energy-rich complexes against prompt unimolecular reactions such as isomerization or decomposition.35 Smith et al. measured the rate coefficient for the C2H2 + OH reaction at 900, 1100, and 1300 K over a pressure range from 10 to 120 torr and found it to be pressure-dependent at 900 K and pressure-independent at 1100 and 1300 K, which is probably due to the contribution of the association reaction decreases at high temperatures.17 At high temperatures, the rate coefficient typically shows an Arrhenius-type temperature dependence.17,20,26,27
In theory, several theoretical groups have performed ab initio calculations of C2H2 + OH for several reaction pathways.28–31,36–42 Based on the BAC-MP4 (bond-additivity-corrected Möller–Plesset fourth-order perturbation theory) level of theory, Miller and Melius used statistical-theoretical methods to calculate rate coefficients.29 Senosiain et al. calculated the ab initio energies of reaction pathways in the RQCISD(T) (restricted quadratic configuration-interaction method with single, double, and perturbative triple excitations) method, then used the master equations (ME) to calculate the rate coefficients and product branching ratios.30 Nonetheless, the detailed microscopic dynamics of the C2H2 + OH reaction, including the energy transfer process, have not been studied yet.
In this work, aimed at a better understanding of the dynamical characterization of this important elementary reaction in combustion, extensive quasi-classical trajectory (QCT) calculations have been performed on a newly developed potential energy surface (PES). The accurate full-dimensional PES for the ground doublet state of the C2H2 + OH reaction is constructed using the permutation invariant polynomial-neural network (PIP-NN) method43,44 based on approximately 475![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ab initio energies calculated at the UCCSD(T)-F12b/cc-pVTZ-F12 level of theory, covering all possible product channels that can be reached below 3000 K. The dynamic information and the comprehensive reaction mechanisms would greatly expand our understanding of other multi-well and multi-channel reactions. The paper is organized as follows. Section II presents the details of the PES and QCT calculations. The PES characterization and the dynamical results are shown in Section III. Finally, conclusions are given in Section IV.
000 ab initio energies calculated at the UCCSD(T)-F12b/cc-pVTZ-F12 level of theory, covering all possible product channels that can be reached below 3000 K. The dynamic information and the comprehensive reaction mechanisms would greatly expand our understanding of other multi-well and multi-channel reactions. The paper is organized as follows. Section II presents the details of the PES and QCT calculations. The PES characterization and the dynamical results are shown in Section III. Finally, conclusions are given in Section IV.
II. Methods
A. Potential energy surface
The ab initio calculations employed the explicitly correlated unrestricted coupled cluster using the single, double, and perturbative triple excitations (UCCSD(T)-F12b) method45,46 here. The specially optimized correlation consistent basis sets (cc-pVnZ-F12 (n = D, T, and Q))47 were tested. We compared the ab initio energies of different basis sets at various stationary points, as shown in Table S1 (ESI†), where the single point calculations for all methods were performed on the optimized geometries obtained from the UCCSD(T)-F12b/cc-pVTZ-F12 method. The energies obtained from the cc-pVTZ-F12 basis set exhibit good consistency with those derived from the larger basis set (aug-cc-pV5Z),48 with energy differences less than 0.25 kcal mol−1 for all stationary points. For 6-core parallel computation, a single point calculation using this method takes about 8 minutes, which is 1/5 of the cost of the cc-pVQZ-F12 basis set. Hence, the cc-pVTZ-F12 basis set was chosen to calculate the potential energies for selected points.In coupled-cluster methods, the T1 diagnostic is seen as an indication of the importance of nondynamical electron correlations, with a large T1 value indicating the need for a multireference electron correlation treatment.49 For this system, the T1 value for most data points is small (below 0.05) in the entire configuration space. We also examined the shape of the PES in important regions along the minimal energy path (MEP), which is smooth and continuous, as shown in Fig. S1 (ESI†). Those very few points with T1 diagnostic values larger than 0.05 were discarded to get a more reliable ab initio data set. All the electronic structure calculations were performed using the MOLPRO 2015.1.0 program package.50
An appropriate sampling process is very helpful for constructing a high-dimensional global PES. We first selected an initial set of points by performing Born–Oppenheimer molecular dynamics (BOMD) simulations at the UB3LYP/6-31G level of theory51,52 using the Gaussian 16 package.53 Based on these energy points calculated at the UCCSD(T)-F12b/cc-pVTZ-F12 level, a primitive PES was fitted using the PIP-NN approach.43,44 Then, a large number of trajectories with different initial conditions were carried out on that PES to further explore the dynamic important configuration space and select more points to improve the PES according to both the distance and energetic criteria. The generalized Euclidean distance was used to describe the similarity degree of data points in configuration space, which is defined as 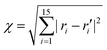 between a new point and a data point in the existing data set, in which ri or ri′ is the distance between every two atoms. Those points with χ ≤ 0.2 Å were not selected for the data set. After many iterations of adding points, finally, 477
between a new point and a data point in the existing data set, in which ri or ri′ is the distance between every two atoms. Those points with χ ≤ 0.2 Å were not selected for the data set. After many iterations of adding points, finally, 477![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821 points covering all the dynamical-relevant regions were selected to construct the final PES.
821 points covering all the dynamical-relevant regions were selected to construct the final PES.
The essence of the PIP-NN method is to use the symmetry functions of internuclear distances instead of the coordinates as the input vector in NN fitting.43,44 The PIP symmetric functions can be obtained by monomial symmetrization as the form 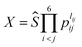 , from Morse-like variables of internuclear distances pij = exp(−rij/α) with rij as the internuclear distances and α = 2.0 bohr, where i and j denote atoms and the order is CCHHHO.54lij is the degree of pij, and Ŝ contains all symmetrization operators for the A2B3C molecule. In total, 134 symmetrized polynomials under the maximum degree 3 for the C2H3O system were used as the input layer of NN.
, from Morse-like variables of internuclear distances pij = exp(−rij/α) with rij as the internuclear distances and α = 2.0 bohr, where i and j denote atoms and the order is CCHHHO.54lij is the degree of pij, and Ŝ contains all symmetrization operators for the A2B3C molecule. In total, 134 symmetrized polynomials under the maximum degree 3 for the C2H3O system were used as the input layer of NN.
The standard forward-feed NN functional form can be written as
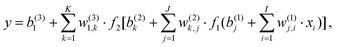 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 441 parameters. In each NN fitting, the database was randomly divided into the training (96%) and validation (4%) sets. The training data were fitted using the Levenberg–Marquardt algorithm,55 and the “early stopping” method56 was used to avoid overfitting. The root mean square error (RMSE) defined as
441 parameters. In each NN fitting, the database was randomly divided into the training (96%) and validation (4%) sets. The training data were fitted using the Levenberg–Marquardt algorithm,55 and the “early stopping” method56 was used to avoid overfitting. The root mean square error (RMSE) defined as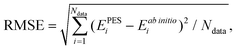 | (2) |
B. Quasi-classical trajectory calculations
The dynamic calculations were performed at several temperatures of 298, 500, 1000, 1500, 2000, 2500, and 3000 K, respectively, using the QCT method as implemented in the VENUS code.57,58 The maximum impact parameter bmax was set as 4.0 Å for all temperatures after testing. The impact parameter b for each trajectory was selected randomly from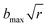 , where r is a uniform random number between 0 to 1. At each temperature above, a large number (400
, where r is a uniform random number between 0 to 1. At each temperature above, a large number (400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–4000
000–4000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) of trajectories were run on the PIP-NN PES, to make sure that the statistical error Δ = [(Ntotal − Nr)/(NtotalNr)]1/2 was reasonably small enough. The time step was selected to be 0.1 fs to guarantee convergence of total energy in the propagation. The trajectories were initiated at distances of 10.0 Å between reactants and stopped when the products reached a separation of 8.0 Å or reactants were separated by 13.5 Å. A few trajectories that failed to converge total energy within 0.01 kcal mol−1 or propagated for too long a time (>5.0 ns) were discarded. It should be noted that in QCT, the molecules involved in the reaction have approximately quantized energies in the initial ro-vibrational state, but not in the final state. To mitigate the zero-point energy (ZPE) leakage problem, we applied a “passive” method59 in this work, which is to remove the reactive trajectories where the sum of the vibrational energies is smaller than the total ZPE for all products. In the previous investigation for the O(3P) + CH4 reaction, QCT results corrected by this approach are closer to the corresponding quantum mechanical cross sections.60
000) of trajectories were run on the PIP-NN PES, to make sure that the statistical error Δ = [(Ntotal − Nr)/(NtotalNr)]1/2 was reasonably small enough. The time step was selected to be 0.1 fs to guarantee convergence of total energy in the propagation. The trajectories were initiated at distances of 10.0 Å between reactants and stopped when the products reached a separation of 8.0 Å or reactants were separated by 13.5 Å. A few trajectories that failed to converge total energy within 0.01 kcal mol−1 or propagated for too long a time (>5.0 ns) were discarded. It should be noted that in QCT, the molecules involved in the reaction have approximately quantized energies in the initial ro-vibrational state, but not in the final state. To mitigate the zero-point energy (ZPE) leakage problem, we applied a “passive” method59 in this work, which is to remove the reactive trajectories where the sum of the vibrational energies is smaller than the total ZPE for all products. In the previous investigation for the O(3P) + CH4 reaction, QCT results corrected by this approach are closer to the corresponding quantum mechanical cross sections.60
The thermal rate coefficients were calculated according to the following formula:
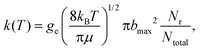 | (3) |
The scattering angle θ was given by 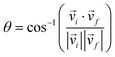 , where
, where ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i and
i and ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) f represent the initial and final relative velocities, respectively, and are denoted as
f represent the initial and final relative velocities, respectively, and are denoted as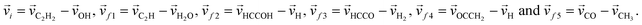 .
.
III. Results and discussion
A. Potential energy surface
In this work, we constructed a new PES for the C2H2 + OH reaction at the UCCSD(T)-F12b/cc-pVTZ-F12 level of theory. The new PES covered the reactant channel, five product channels, and the interaction regions with many deep potential wells and transition states, with a total RMSE of 0.38 kcal mol−1. The fitting errors of all the data points and their distribution are presented in Fig. 1(a) and (b). About 55.1% of all points are fitted well with a quite small absolute fitting error of 0–0.2 kcal mol−1, especially the points with potential energy lower than 100 kcal mol−1. The fitting performance is reasonably good for such a complex system involving six atoms and covering the quite large energy range of 0–160 kcal mol−1 with respect to the global minimum.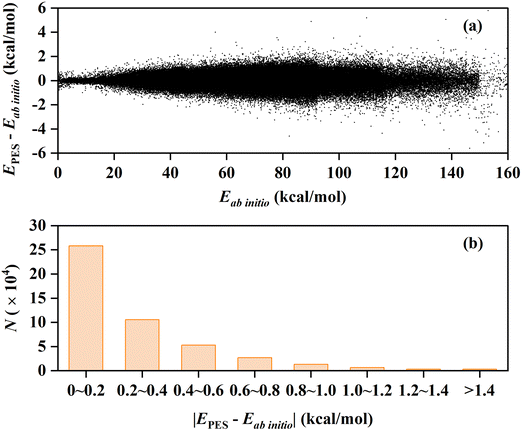 | ||
| Fig. 1 (a) Fitting errors of all the data points in the PIP-NN PES as a function of their corresponding ab initio energies. (b) Distribution of the absolute fitting errors for all the data points. | ||
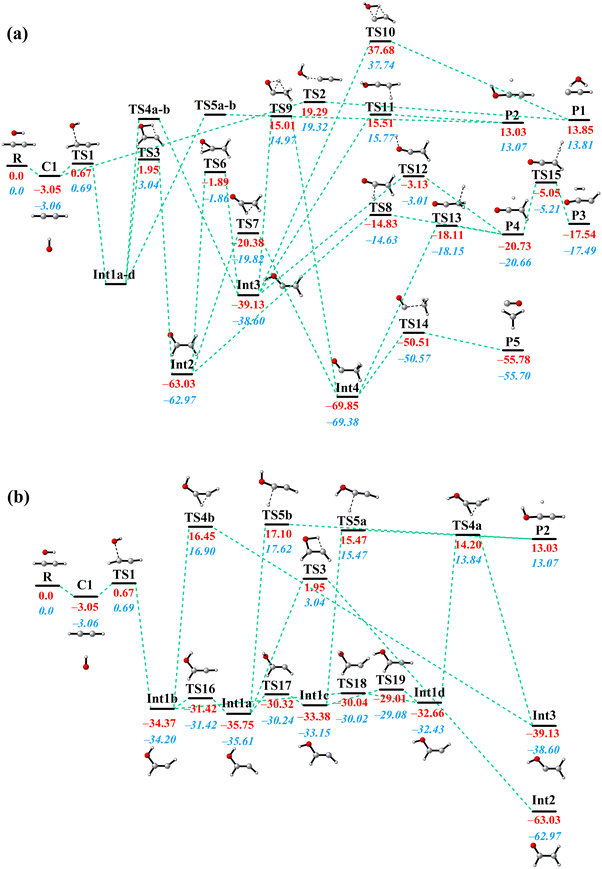
All stationary points along the MEP on the PIP-NN PES with their energies optimized by using the POLYRATE 17-C software62 are shown in Fig. 2. The C2H2 + OH reaction consists of seven intermediates, twenty-one transition states, and a van der Waals complex. The pre-reactive van der Waals complex is T-shaped, in which the hydrogen atom of the hydroxyl radical associates with the middle of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond. This configuration has been reported before, where the distance between the hydrogen atom of OH radical and the middle of the C
C triple bond. This configuration has been reported before, where the distance between the hydrogen atom of OH radical and the middle of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond is 2.371 Å at the UB3LYP/6-311++G(d,p) level,30 2.420 Å at the CBS-QB3 level,39,42 and 2.347 Å in this work with a slightly deeper depth than before. With the oxygen atom in the OH radical getting closer to one of the C atoms in acetylene, the complex strides TS1 and then forms the most important intermediate Int1 in this reaction. Int1 has four conformers (Int1a, Int1b, Int1c, and Int1d) which are connected by small isomerization barriers, as shown in Fig. 2(b). In the subsequent process, different kinds of H-migration barriers and dissociation barriers lead to different pathways. It is important to point out that the reactants also have the option of taking a direct pathway, in which they overcome a high energy barrier (TS2) to yield H2O and C2H (P1). The high barrier height (19.3 kcal mol−1) makes this direct hydrogen abstraction process possible only at high temperatures. As for the formation of H2 + HCCO (P3), there have been discrepancies in previous studies. Senosiain et al. reported a … → Int3 → TS → P3 pathway,30 while others reported … → P4 → TS → P3.31,36,38 On our PES, the latter mechanism from P4 to P3 was found and connected by TS15 while the former pathway was not found.
C triple bond is 2.371 Å at the UB3LYP/6-311++G(d,p) level,30 2.420 Å at the CBS-QB3 level,39,42 and 2.347 Å in this work with a slightly deeper depth than before. With the oxygen atom in the OH radical getting closer to one of the C atoms in acetylene, the complex strides TS1 and then forms the most important intermediate Int1 in this reaction. Int1 has four conformers (Int1a, Int1b, Int1c, and Int1d) which are connected by small isomerization barriers, as shown in Fig. 2(b). In the subsequent process, different kinds of H-migration barriers and dissociation barriers lead to different pathways. It is important to point out that the reactants also have the option of taking a direct pathway, in which they overcome a high energy barrier (TS2) to yield H2O and C2H (P1). The high barrier height (19.3 kcal mol−1) makes this direct hydrogen abstraction process possible only at high temperatures. As for the formation of H2 + HCCO (P3), there have been discrepancies in previous studies. Senosiain et al. reported a … → Int3 → TS → P3 pathway,30 while others reported … → P4 → TS → P3.31,36,38 On our PES, the latter mechanism from P4 to P3 was found and connected by TS15 while the former pathway was not found.
Fig. S1 (ESI†) shows a comparison of potential energies between ab initio calculations and fitted results from the PES for the MEPs. The energies obtained on the PES are in agreement with those from the ab initio calculations. The detailed geometrical parameters and harmonic frequencies for each stationary point are presented in Fig. S2 and Table S2 (ESI†), respectively. The small differences in some flexible coordinates such as dihedral angles may be due to the difficulty in fitting the PES. Fortunately, in those regions, the differences between the ab initio energies and the PES values are small and would have little effect on the QCT results.
B. Rate coefficients and branching ratios
Standard QCT calculations were carried out on the PIP-NN PES at temperatures ranging from 298 K to 3000 K, and the statistical errors are less than 9% at 298 K and 500 K, and less than 6% above 1000 K. More than 99.8% of trajectories conserved energy within the criterion of 0.01 kcal mol−1, which implied that the PES is smooth and free of discontinuity. Fig. 3 shows the rate coefficients of the QCT calculations for the C2H2 + OH reaction compared to experimental data4,10,11,17,20–22,26,27,33 and theoretical calculations30 in the literature. Above 1000 K, the QCT results agree well with most experimental measurements, and the rate coefficients exhibit a typical Arrhenius-type temperature dependence. At low temperatures (<1000 K), the QCT rate coefficients are lower than the previous low-pressure experimental results. The rate coefficients calculated by Miller and Melius29 were not shown in this work because the ab initio accuracy in their work is relatively low. Another previous theoretical work on this rate coefficient is the ME calculations of Senosiain et al., in which asymmetric Eckart barriers were employed to compute the effect of tunneling through the reaction barriers.30 Their ME data shown in Fig. 3 is the total rate coefficients in the zero-pressure limit, which agreed well with many experiments and our QCT results above 1000 K, and slightly lower than the experimental values but higher than ours at room temperature.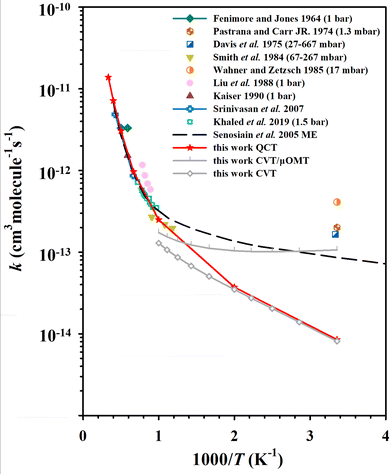 | ||
| Fig. 3 The rate coefficients for the C2H2 + OH reaction, compared with previous experimental4,10,11,17,20–22,26,27,33 and theoretical30 results. | ||
The key feature of the C2H2 + OH PES is that, at low temperatures, the MEPs for product formation have two roughly isoenergetic barriers (TS1 and TS3), with a deep potential well (Int1a-d) between the barriers ∼34 kcal mol−1 below the reactant energy. As a result, the complex will stay in this potential well for a long time, allowing the collisional relaxation of nascent energy-rich complexes to occur, which is similar to the dynamics of the HO + CO → H + CO2 reaction.63 At 298 K, 0.014% QCT trajectories propagate longer than 100 ps (as a footnote, unlike this, most of the direct reaction trajectories (R → TS2 → P1) have propagation times less than 1 ps), with values of 0.021% at 500 K and 0.015% at 1000 K. For comparison, the ratios of reactive trajectories to total trajectories at these temperatures are 0.0033% (298 K), 0.012% (500 K) and 0.063% (1000 K). From the difference between these, it can be seen that at 298 K, the fraction of long-time non-reactive trajectories in the total number of trajectories is significantly higher than the fraction of reactive trajectories. The significant fraction of long-time non-reactive trajectories suggests the reason why collisional relaxation processes have a large impact on the reaction rates under different pressure conditions. In experiments, the C2H2 + OH rate coefficients are generally determined by measuring the rate of the depletion of reactant, which is the sum of the bimolecular product formation rate and the association reaction rate. Our QCT calculations are simulations of the bimolecular reaction, and the collisional relaxation process with a third body cannot be taken into account. Thus, in the QCT results, the unconsidered association reaction rates may be one of the reasons for the discrepancy at low temperatures.
Another reason for the underestimation of the rate coefficient is that the QCT method does not consider quantum effects, such as tunneling which can allow the long-lived complexes to penetrate through barriers, thus leading to more products eventually. To estimate the influence of tunneling on the C2H2 + OH rate coefficients, we employed the micro-canonical optimized multidimensional tunneling (μOMT) approach.64 In the temperature regime 298∼1000 K, especially below 500 K, the reaction occurs mainly through the R(→C1) → TS1 → Int1a-d → TS3 → Int2 → TS8 → P4 and R(→C1) → TS1 → Int1a-d → TS3 → Int2 → TS7 → Int4 → TS14 → P5 pathways, forming H + OCCH2 (P4) and CO + CH3 (P5), respectively. In both pathways, TS3 is the highest potential barrier for both pathways and is therefore an important reaction bottleneck at low temperatures. For applying canonical variational transition-state theory (CVT)65 combined with the μOMT approach,64 we chose this highest TS as the dividing surface, and roughly estimated the overall reaction rate, omitting the recrossing among wells. The CVT/μOMT and CVT rate coefficients calculated using the POLYRATE 17-C software62 are also presented in Fig. 3. The difference between the two results suggests that the hydrogen migration process in TS3 may be affected by significant tunneling effects. Indeed, the tunneling correction given by CVT/μOMT is as large as over 10 below 300 K. One should note that both the previous ME work30 and current CVT/μOMT calculations can only treat quantum tunneling effects approximately. A better way to investigate the rate coefficients of the C2H2 + OH reaction by including the quantum tunneling is to employ the ring polymer molecular dynamics (RPMD) method.66–70
For each product channel, the product branching ratios and modified Arrhenius expressions are given in Table 1. To see more intuitively the variation of the product branching ratio with temperature, we compared the fitted curves of the rate coefficients for each product channel in Fig. 4. Below 1000 K, the C2H2 + OH reaction mainly produces H + OCCH2 (P4) and CO + CH3 (P5), where the production of ketene (OCCH2) is the predominant channel. At temperatures above 1000 K, the H2O + C2H (P1) and H + HCCOH (P2) channels open up and contribute significantly. Higher than 1900 K, the H2O + C2H (P1) becomes dominant. The production of H2 + HCCO (P3) can be negligible in all the aforementioned temperature regions.
| T (K) | 298 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 | |
|---|---|---|---|---|---|---|---|---|
| k total | 8.52 × 10−15 | 3.72 × 10−14 | 2.49 × 10−13 | 9.68 × 10−13 | 3.06 × 10−12 | 7.18 × 10−12 | 1.39 × 10−11 | |
| H2O + C2H (P1) | BR | 0 | 0 | 3.13% | 16.28% | 35.92% | 48.12% | 53.64% |
| k P1 | 4.085 × 10−12T0.4995 exp(−10197.5/T) | |||||||
| H + HCCOH (P2) | BR | 0 | 0 | 7.39% | 22.77% | 25.16% | 27.00% | 26.79% |
| k P2 | 4.085 × 10−12T0.2997 exp(−7559.8/T) | |||||||
| H2 + HCCO (P3) | BR | 0 | 0 | 0 | 0 | 0 | 0.02% | 0.12% |
| H + OCCH2 (P4) | BR | 65.69% | 66.54% | 62.50% | 47.13% | 30.95% | 20.75% | 16.03% |
| k P4 | 4.085 × 10−19T1.9635 exp(−629.5/T) | |||||||
| CO + CH3 (P5) | BR | 34.31% | 33.46% | 26.99% | 13.83% | 7.97% | 4.10% | 3.42% |
| k P5 | 4.085 × 10−18T1.4726 exp(−605.4/T) | |||||||
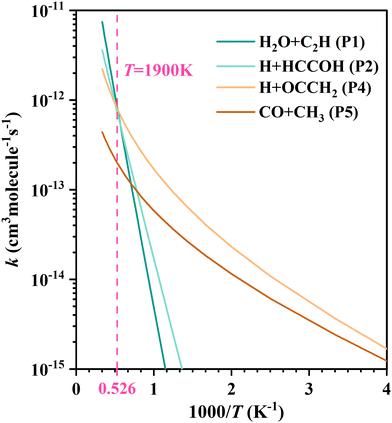 | ||
| Fig. 4 The fitted curves by the modified Arrhenius expression for each product channel in the C2H2 + OH reaction. | ||
C. Mechanism analysis and product energy distribution
To further understand the reaction mechanism, an analysis of the trajectories and product information was performed. The correlation between the scattering angle and the impact parameter is shown in Fig. 5. In the H2O + C2H (P1) channel, there is a correlation between the scattering angle and the impact parameter. The reaction exhibits a “rebound” mechanism when the impact parameter is small, and a “stripping” mechanism when the impact parameter is large, which is usually seen in direct reactions. It was found that H2O + C2H (P1) was produced dominantly by the direct hydrogen abstraction pathway (R → TS2 → P1) with a ratio of 96% at 2000 K, and 94% at 3000 K. These direct trajectories also present a distinct feature in propagation time (see Fig. 6), namely, the distribution of their propagation time is concentrated, mainly in the range of 0.3–1.2 ps.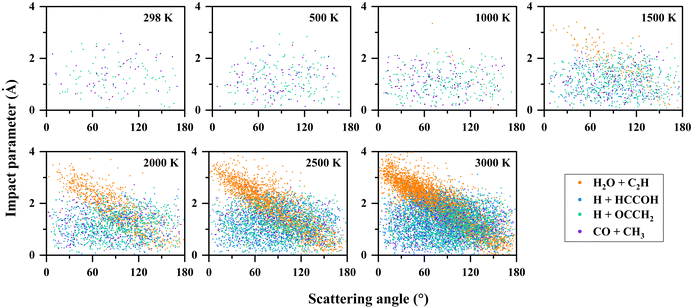 | ||
| Fig. 5 Correlation diagrams between the scattering angle and the impact parameter for the C2H2 + OH reaction at different temperatures. | ||
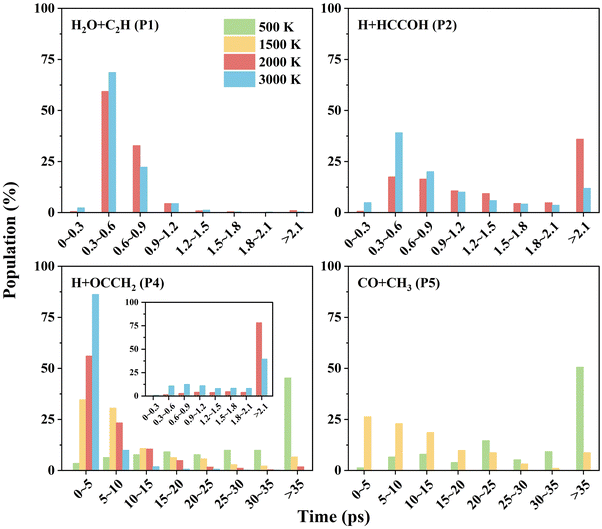
For the other channels, there is no clear correlation between the scattering angle and the impact parameter, and they all present a uniform distribution corresponding to a “long-lived complex” mechanism. The propagation time of such reaction trajectories is widely distributed, with very long propagation time at low temperatures (see Fig. 6). By determining whether certain intermediates are formed in the reaction, we can roughly classify the reaction pathways, where the intermediates are identified by the geometric parameters defined in Table S3 (ESI†). As for the H + HCCOH (P2) channel, the trajectories can be divided into two types of pathways: … → Int1a-d → TS5a-b → P2 and … → Int3 → TS11 → P2. The fractions of trajectories passing through the two pathways are 75% and 25% at 2000 K, and 67% and 33% at 3000 K. The former is slightly more significant on the whole. In the H + OCCH2 (P4) channel, the dominant pathway changes with increasing temperature. At 500 K, about 95% of the product is generated by the … → Int2 → TS8 → P4 pathway, and it becomes 61% as the temperature increases to 1500 K, with the rest passing through the … → Int3 → TS12 → P4 pathway. At 3000 K, the fractions for the … → Int2 → TS8 → P4 and … → Int3 → TS12 → P4 pathways are 39% and 57%. The … → Int4 → TS13 → P4 pathway is an insignificant one for the H + OCCH2 (P4) channel, with a contribution of less than 3% at different temperatures. In the CO + CH3 (P5) channel, the differences in pathways are mainly reflected in the Int4 formation, where the … → Int2 → TS7 → Int4 → TS14 → P5 pathway dominates with a fraction of more than 85% at temperatures below 2000 K.
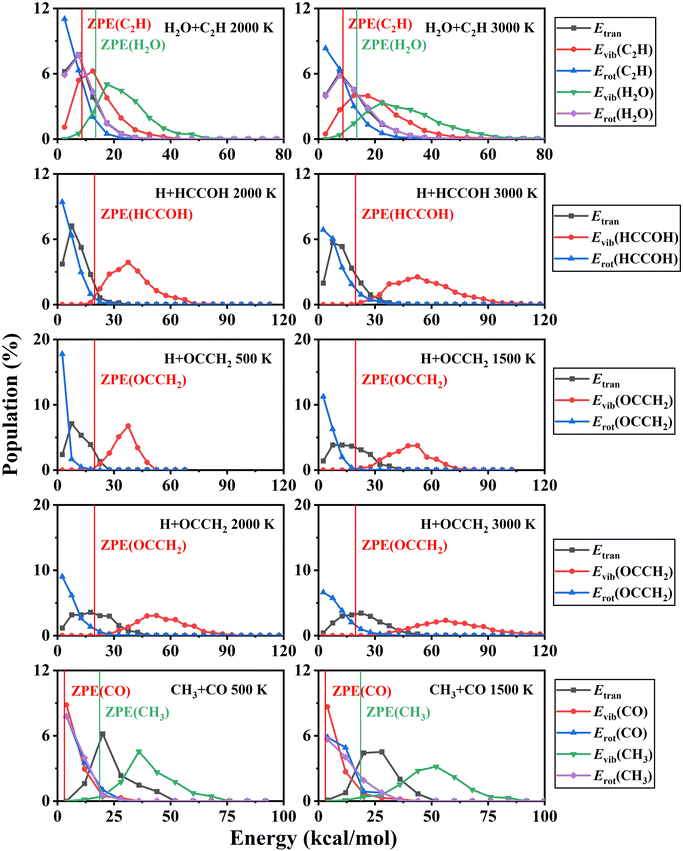
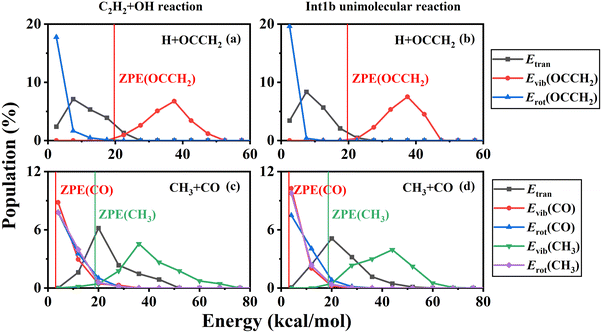
In addition, the product energy distributions have also been investigated in this work. We calculated the energy distributions of trajectories whose total vibrational energy of the products is larger than the sum of their ZPEs. The product energy distributions at each temperature are shown in Fig. 7. For the H + HCCOH (P2) and H + OCCH2 (P4) channels, the ratios of the relative translational, vibrational, and rotational energies of the products are less affected by temperature variations. A large fraction of the energy is deposited in the vibrational modes of the pentatomic products. In the CO + CH3 (P5) channel, product energy distributions are similar to that of the C2H2 + O(3P) → CO + CH2 reaction we had studied previously.71 The relative translational energy and the CH3 vibrational energy account for a relatively large fraction of the total available energy. The CO rotational state is highly excited, while the CO vibrational energy accounts for a small fraction, and the CO vibrational energy distribution is slightly characterized by a thermal equilibrium distribution. For the H2O + C2H (P1) channel, the available energy distributions for the relative translational, vibrational and rotational energies of the products are relatively close, and the energy flowing into the rovibrational modes of H2O is slightly larger than that of C2H.
At low temperatures, long-lived complexes generated by electrophilic addition decompose into products in a process similar to that of unimolecular reactions. Here, we simulated the unimolecular reaction of the energy-rich complex decomposition and compared it with the C2H2 + OH reaction. The initial molecule for the unimolecular reaction was set to Int1b and the total energy was fixed at the maximum probability of the total energy distribution at 500 K. The branching ratios for H + OCCH2 (P4) and CO + CH3 (P5) are 65.50% and 34.50% under these conditions, in general agreement with the product branching ratios for the C2H2 + OH reaction. The product energy distributions of the unimolecular reaction are shown in Fig. 8. In terms of comparison of the energy distributions, the overall results are approximately the same, except that the rotational energy of the products is slightly lower for the unimolecular reactions. Thus at low temperatures, especially below 500 K, the decomposition of the energy-rich complexes for the C2H2 + OH reaction could be approximated by unimolecular reactions.
IV. Conclusions
In this work, we developed the first full-dimensional chemically accurate PES for the C2H2 + OH reaction covering five reachable product channels below 3000 K using the PIP-NN method based on 477![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821 UCCSD(T)-F12b/cc-pVTZ-F12 data points. The new PES is accurate and smooth in important dynamical regions, which can be verified by the small fitting RMSE of 0.38 kcal mol−1 and a good representation of the minimum energy paths. Based on the PIP-NN PES, we used the QCT method to calculate the rate coefficients of the C2H2 + OH reaction over 298–3000 K and make a comparison with the previous experimental results. Above 1000 K, the QCT rate coefficient is in good agreement with the experimental values, but it is lower than the experimental values at low temperatures. The discrepancy might be mitigated by further considering quantum effects and the effect of the association reaction. At low temperatures, the C2H2 + OH reaction produces H + OCCH2 (P4) and CO + CH3 (P5). At about 1000 K, the H2O + C2H (P1) and H + HCCOH (P2) channels are open, and H2O + C2H (P1) mainly formed by a direct hydrogen abstraction pathway becomes the dominant product above 1900 K. While the probability of the H2 + HCCO (P3) channel is negligible in the C2H2 + OH reaction. Due to the similarity found in branching ratios and product energy distributions, the decomposition of the energy-rich complexes for the C2H2 + OH reaction could be approximated by unimolecular reactions at low temperatures. In addition, the modified Arrhenius expressions and the product energy distribution for the C2H2 + OH reaction were also reported in this work. We hope that these results will provide new insights into understanding this complex combustion reaction. This full-dimensional PES can be further used to investigate the mode specificity in the title reaction and the reaction dynamics for this system from other reactant channels.
821 UCCSD(T)-F12b/cc-pVTZ-F12 data points. The new PES is accurate and smooth in important dynamical regions, which can be verified by the small fitting RMSE of 0.38 kcal mol−1 and a good representation of the minimum energy paths. Based on the PIP-NN PES, we used the QCT method to calculate the rate coefficients of the C2H2 + OH reaction over 298–3000 K and make a comparison with the previous experimental results. Above 1000 K, the QCT rate coefficient is in good agreement with the experimental values, but it is lower than the experimental values at low temperatures. The discrepancy might be mitigated by further considering quantum effects and the effect of the association reaction. At low temperatures, the C2H2 + OH reaction produces H + OCCH2 (P4) and CO + CH3 (P5). At about 1000 K, the H2O + C2H (P1) and H + HCCOH (P2) channels are open, and H2O + C2H (P1) mainly formed by a direct hydrogen abstraction pathway becomes the dominant product above 1900 K. While the probability of the H2 + HCCO (P3) channel is negligible in the C2H2 + OH reaction. Due to the similarity found in branching ratios and product energy distributions, the decomposition of the energy-rich complexes for the C2H2 + OH reaction could be approximated by unimolecular reactions at low temperatures. In addition, the modified Arrhenius expressions and the product energy distribution for the C2H2 + OH reaction were also reported in this work. We hope that these results will provide new insights into understanding this complex combustion reaction. This full-dimensional PES can be further used to investigate the mode specificity in the title reaction and the reaction dynamics for this system from other reactant channels.
Data availability
The data and the PES code that support the findings of this study can be obtained by contacting the corresponding author X. Hu (xxhu@nju.edu.cn).Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (U1932147, 22122302 to X. H., and 21973009 to J. L.). This work was also supported by the Innovation Program for Quantum Science and Technology (2021ZD0303305). We are grateful to the High Performance Computing Center (HPCC) of Nanjing University for doing the QCT calculations on its blade cluster system. We sincerely thank Junxiang Zuo for useful discussions on the PES construction and Yongle Li for useful discussions on the rate coefficient calculations.References
- V. Chernov, M. J. Thomson, S. B. Dworkin, N. A. Slavinskaya and U. Riedel, Combust. Flame, 2014, 161, 592–601 CrossRef CAS.
- M. Mehl, W. J. Pitz, C. K. Westbrook and H. J. Curran, Proc. Combust. Inst., 2011, 33, 193–200 CrossRef CAS.
- A. Williams and D. B. Smith, Chem. Rev., 1970, 70, 267–293 CrossRef CAS.
- C. P. Fenimore and G. W. Jones, J. Chem. Phys., 1964, 41, 1887–1889 CrossRef CAS.
- G. P. Glass, G. B. Kistiakowsky, J. V. Michael and H. Niki, J. Chem. Phys., 1965, 42, 608–621 CrossRef CAS.
- M. Gehring, K. Hoyermann, H. Gg. Wagner and J. Wolfrum, Z. Naturforsch. A, 1970, 25, 675–676 CAS.
- J. E. Breen and G. P. Glass, Int. J. Chem. Kinet., 1971, 3, 145–153 CrossRef CAS.
- I. W. M. Smith and R. Zellner, J. Chem. Soc., Faraday Trans. 2, 1973, 69, 1617–1627 RSC.
- J. R. Kanofsky, D. Lucas, F. Pruss and D. Gutman, J. Phys. Chem., 1974, 78, 311–316 CrossRef CAS.
- V. A. Pastrana and R. W. Carr JR, Int. J. Chem. Kinet., 1974, 6, 587–595 CrossRef.
- D. D. Davis, S. Fischer, R. Schiff, R. T. Watson and W. Bollinger, J. Chem. Phys., 1975, 63, 1707–1712 CrossRef CAS.
- R. A. Perry, R. Atkinson and J. N. Pitts, J. Chem. Phys., 1977, 67, 5577–5584 CrossRef CAS.
- J. Vandooren and P. J. Van Tiggelen, Symp. (Int.) Combust., 1977, 16, 1133–1144 CrossRef.
- J. V. Michael, D. F. Nava, R. P. Borkowski, W. A. Payne and L. J. Stief, J. Chem. Phys., 1980, 73, 6108–6116 CrossRef CAS.
- R. A. Perry and D. Williamson, Chem. Phys. Lett., 1982, 93, 331–334 CrossRef CAS.
- R. Atkinson and S. M. Aschmann, Int. J. Chem. Kinet., 1984, 16, 259–268 CrossRef CAS.
- G. P. Smith, P. W. Fairchild and D. R. Crosley, J. Chem. Phys., 1984, 81, 2667–2677 CrossRef CAS.
- S. Hatakeyama, N. Washida and H. Akimoto, J. Phys. Chem., 1986, 90, 173–178 CrossRef CAS.
- S. M. Hwang, W. C. Gardiner, M. Frenklach and Y. Hidaka, Combust. Flame, 1987, 67, 65–75 CrossRef CAS.
- A. Liu, W. A. Mulac and C. D. Jonah, J. Phys. Chem., 1988, 92, 5942–5945 CrossRef CAS.
- E. W. Kaiser, J. Phys. Chem., 1990, 94, 4493–4499 CrossRef CAS.
- J. F. Bott and N. Cohen, Int. J. Chem. Kinet., 1991, 23, 1075–1094 CrossRef CAS.
- L.-H. Lai, Y.-C. Hsu and Y.-P. Lee, J. Chem. Phys., 1992, 97, 3092–3099 CrossRef CAS.
- I. T. Woods and B. S. Haynes, Symp. (Int.) Combust., 1994, 25, 909–917 CrossRef.
- K. W. McKee, M. A. Blitz, P. A. Cleary, D. R. Glowacki, M. J. Pilling, P. W. Seakins and L. Wang, J. Phys. Chem. A, 2007, 111, 4043–4055 CrossRef CAS PubMed.
- N. K. Srinivasan, M.-C. Su and J. V. Michael, Phys. Chem. Chem. Phys., 2007, 9, 4155–4163 RSC.
- F. Khaled, B. R. Giri and A. Farooq, Proc. Combust. Inst., 2019, 37, 213–219 CrossRef CAS.
- C. Sosa and H. B. Schlegel, J. Am. Chem. Soc., 1987, 109, 4193–4198 CrossRef CAS.
- J. A. Miller and C. F. Melius, Symp. (Int.) Combust., 1989, 22, 1031–1039 CrossRef.
- J. P. Senosiain, S. J. Klippenstein and J. A. Miller, J. Phys. Chem. A, 2005, 109, 6045–6055 CrossRef CAS PubMed.
- S. O. Adamson, Russ. J. Phys. Chem. B, 2016, 10, 143–152 CrossRef CAS.
- V. Schmidt, G. Y. Zhu, K. H. Becker and E. H. Fink, Ber. Bunsen-Ges. Phys. Chem., 1985, 89, 321–322 CrossRef CAS.
- A. Wahner and C. Zetzsch, Ber. Bunsen-Ges. Phys. Chem., 1985, 89, 323–325 CrossRef CAS.
- D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, Th. Just, J. A. Kerr, M. J. Pilling, D. Stocker, J. Troe, W. Tsang, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397 CrossRef CAS.
- L. Vereecken and J. S. Francisco, Chem. Soc. Rev., 2012, 41, 6259–6293 RSC.
- Y. H. Ding, X. Zhang, Z. S. Li, X. R. Huang and C. C. Sun, J. Phys. Chem. A, 2001, 105, 8206–8215 CrossRef CAS.
- J. B. Davey, M. E. Greenslade, M. D. Marshall, M. I. Lester and M. D. Wheeler, J. Chem. Phys., 2004, 121, 3009–3018 CrossRef CAS PubMed.
- S. A. Carl, H. M. T. Nguyen, R. M. I. Elsamra, M. T. Nguyen and J. Peeters, J. Chem. Phys., 2005, 122, 114307 CrossRef PubMed.
- M. J. Park, S. C. Jang and J. H. Choi, J. Chem. Phys., 2012, 137, 204311 CrossRef PubMed.
- S. C. Jang and J. H. Choi, Phys. Chem. Chem. Phys., 2014, 16, 23679–23685 RSC.
- H. M. T. Nguyen, H. T. Nguyen, T. N. Nguyen, H. V. Hoang and L. Vereecken, J. Phys. Chem. A, 2014, 118, 8861–8871 CrossRef CAS PubMed.
- S. H. Jung, S. C. Jang, J. W. Kim, J. W. Kim and J. H. Choi, J. Phys. Chem. A, 2015, 119, 11761–11771 CrossRef CAS PubMed.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 054112 CrossRef PubMed.
- J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 204103 CrossRef PubMed.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207 CrossRef.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schutz, WIREs Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26–34 CrossRef CAS PubMed.
- M. T. Hagan and M. B. Menhaj, IEEE Trans. Neural Netw., 1994, 5, 989–993 CrossRef CAS PubMed.
- L. M. Raff, R. Komanduri, M. Hagan and S. T. S. Bukkapatnam, Neural Networks in Chemical Reaction Dynamics, Oxford University Press, Oxford, 2012 Search PubMed.
- X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12, 1014–1024 CrossRef CAS.
- W. L. Hase, R. J. Duchovic, X. Hu, A. Komornicki, K. F. Lim, D. H. Lu, G. H. Peslherbe, K. N. Swamy, S. R. R. Vande Linde and A. Varandas, J. Quantum Chem. Program Exch. Bull., 1996, 16, 671 Search PubMed.
- Y. Guo, D. L. Thompson and T. D. Sewell, J. Chem. Phys., 1996, 104, 576–582 CrossRef CAS.
- G. Czako, R. Liu, M. H. Yang, J. M. Bowman and H. Guo, J. Phys. Chem. A, 2013, 117, 6409–6420 CrossRef CAS PubMed.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules, Springer, New York, 1979 Search PubMed.
- J. Zheng, J. L. Bao, R. Meana-Pañeda, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. Fernandez Ramos, B. A. Ellingson, V. S. Melissas, J. Villà, I. Rossi, E. L. Coitiño, J. Pu, T. V. Albu, A. Ratkiewicz, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, Polyrate-version 2017-C; University of Minnesota: Minneapolis, 2017.
- J. Li, C. J. Xie, J. Y. Ma, Y. M. Wang, R. Dawes, D. Q. Xie, J. M. Bowman and H. Guo, J. Phys. Chem. A, 2012, 116, 5057–5067 CrossRef CAS PubMed.
- Y. P. Liu, D. H. Lu, A. Gonzalezlafont, D. G. Truhlar and B. C. Garrett, J. Am. Chem. Soc., 1993, 115, 7806–7817 CrossRef CAS.
- D. G. Truhlar and B. C. Garrett, Annu. Rev. Phys. Chem., 1984, 35, 159–189 CrossRef CAS.
- I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2004, 121, 3368–3373 CrossRef CAS PubMed.
- I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2005, 123, 034102 CrossRef PubMed.
- I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2005, 122, 084106 CrossRef PubMed.
- R. Collepardo-Guevara, Y. V. Suleimanov and D. E. Manolopoulos, J. Chem. Phys., 2009, 130, 174713 CrossRef PubMed.
- Y. V. Suleimanov, R. Collepardo-Guevara and D. E. Manolopoulos, J. Chem. Phys., 2011, 134, 044131 CrossRef PubMed.
- S. Zhang, Q. Chen, J. Zuo, X. Hu and D. Xie, Molecules, 2022, 27, 754 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05811e |
| This journal is © the Owner Societies 2024 |