Impact of isoelectronic substitution on the excited state processes in polycyclic aromatic hydrocarbons: a joint experimental and theoretical study of 4a,8a-azaboranaphthalene†
Floriane
Sturm
a,
Michael
Bühler
 a,
Christoph
Stapper
a,
Johannes S.
Schneider
b,
Holger
Helten
a,
Christoph
Stapper
a,
Johannes S.
Schneider
b,
Holger
Helten
 b,
Ingo
Fischer
b,
Ingo
Fischer
 *a and
Merle I. S.
Röhr
*a and
Merle I. S.
Röhr
 *a
*a
aInstitute of Physical and Theoretical Chemistry, University of Würzburg, Am Hubland, 97074 Würzburg, Germany. E-mail: ingo.fischer@uni-wuerzburg.de; merle.roehr@uni-wuerzburg.de
bInstitute of Inorganic Chemistry and Institute for Sustainable Chemistry & Catalysis with Boron (ICB), University of Würzburg, Am Hubland, 97074 Würzburg, Germany. E-mail: holger.helten@uni-wuerzburg.de
First published on 14th February 2024
Abstract
Substituting CC with the isoelectronic BN units is a promising approach to modify the optoelectronic properties of polycyclic aromatic hydrocarbons. While computational studies have already addressed trends in the electronic structure of the various isosteres, experimental data are still scarce. Here, the excited state spectroscopy and dynamics of 4a,8a-azaboranaphthalene were studied by picosecond time-resolved photoionization in a supersonic jet and analyzed with the aid of XMS-CASPT2 and time-dependent DFT calculations. A resonance-enhanced multiphoton ionization spectrum (REMPI) reveals the S1 origin at ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 33
= 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830 ± 12 cm−1. Several vibrational bands were resolved and assigned by comparison with the computations. A [1+1] photoelectron spectrum via the S1 origin yielded an adiabatic ionization energy of 8.27 eV. Selected vibrational bands were subsequently investigated by pump–probe photoionization. While the origin as well as several low-lying vibronic states exhibit lifetimes in the ns-range, a monoexponential decay is observed at higher excitation energies, ranging from 400 ps at +1710 cm−1 to 13 ps at +3360 cm−1. The deactivation is attributed to an internal conversion of the optically excited S1 state via a barrier that gives access to a conical intersection (CI) to the S0 state. The doping significantly changes the energetic ordering of CIs and lowers the corresponding energy barrier for the associated deactivation pathway, as revealed by nudged elastic band (NEB) calculations.
830 ± 12 cm−1. Several vibrational bands were resolved and assigned by comparison with the computations. A [1+1] photoelectron spectrum via the S1 origin yielded an adiabatic ionization energy of 8.27 eV. Selected vibrational bands were subsequently investigated by pump–probe photoionization. While the origin as well as several low-lying vibronic states exhibit lifetimes in the ns-range, a monoexponential decay is observed at higher excitation energies, ranging from 400 ps at +1710 cm−1 to 13 ps at +3360 cm−1. The deactivation is attributed to an internal conversion of the optically excited S1 state via a barrier that gives access to a conical intersection (CI) to the S0 state. The doping significantly changes the energetic ordering of CIs and lowers the corresponding energy barrier for the associated deactivation pathway, as revealed by nudged elastic band (NEB) calculations.
Introduction
The substitution of CC units with BN in the aromatic scaffold of polycyclic aromatic hydrocarbons (PAHs) is a widely explored method to expand the scope of organic molecules.1–10 The BN-doped heterocycles are isoelectronic to the corresponding PAH and therefore structurally similar. However, they exhibit electronic and optical properties, which fundamentally differ from those of the pure hydrocarbons due to the introduction of local dipole moments.11 The polarity of BN bonds therefore changes the character of the frontier orbitals of the molecules and thus the energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). Furthermore, substituting carbon with a nitrogen atom potentially introduces nπ*-states which can effectively change excited-state deactivation processes. For organic functional material (OFM) applications, exploring these photophysical properties is of great interest.12–18 For example, Zheng et al. suggested BN-substituted aromatic molecules as possible candidates for singlet fission materials.19 Therefore, recent years saw increasing interest in understanding the spectroscopy and photochemistry of BN-substituted aromatic molecules.20–26 A few azaborines have been investigated by IR-spectroscopy in rare gas matrices and by photoionization in the gas phase.27–29 However, no experiments on the dynamics of excited electronic states have yet been reported and BN-doped PAHs have only been investigated in solution. Studies on isolated molecules are particularly interesting because they permit comparing experimental results directly with computations without perturbations by the solvent environment. In the present work we therefore investigate the excited state dynamics of isolated 4a,8a-azaboranaphthalene 1 depicted in Fig. 1, as a model for BN-doped PAH in a free jet, using picosecond time-resolved spectroscopy and computational chemistry. | ||
| Fig. 1 The C2v symmetric 4a,8a-azaboranaphthalene 1 depicted with the coordinate system employed in the present work. Note that the z-axis corresponds to the C2-axis of the molecule. | ||
A few prior reports on 1 are available. A microwave study provided rotational constants for 11 isotopologues of the molecule and derived accurate bond lengths from the data.30 First experiments to explore its electronic structures have been carried out by Liu et al.,31 who investigated 1 by UV-photoelectron spectroscopy (UV-PES), UV-visible absorption spectroscopy and cyclic voltammetry. The experiments were accompanied by DFT (density functional theory) calculations to compute the HOMO and LUMO energy levels. The authors reported a broad absorption between 250–300 nm in cyclohexane and a vertical ionization energy (IE) of 8.42 eV. Furthermore, they computed a HOMO–LUMO gap of ΔE = 4.13 eV for 1.31
Below, results on 1 will be compared to the CC-analogue naphthalene, which has been studied extensively in both solution and gas phase.32–39 As high-level quantum chemical calculations are also available, the photophysics and photochemistry of naphthalene are well understood.40–42 Therefore, it serves as a suitable starting point to discuss the effects of BN substitution. It was observed that the quantum yield of fluorescence in naphthalene decreases with increasing excitation energy, which was attributed to efficient intersystem crossing (ISC) with increasing excitation energy. For low excess energies the dominant nonradiative channel is a S1 ![[long arrow, wavy then straight]](https://www.rsc.org/images/entities/char_e0f6.gif) T1 ISC while for higher excess energies a resonance of the S1 with T2 and T3 is possible.43 Note that the large amount of older work on the spectroscopy and dynamics of naphthalene in the S1 state was reviewed by Avouris et al.43 A scheme of the electronic states of naphthalene is given in the ESI,† Fig. S2.
T1 ISC while for higher excess energies a resonance of the S1 with T2 and T3 is possible.43 Note that the large amount of older work on the spectroscopy and dynamics of naphthalene in the S1 state was reviewed by Avouris et al.43 A scheme of the electronic states of naphthalene is given in the ESI,† Fig. S2.
Methods
The experimental setup has been described in detail previously.44,45 It consists of a picosecond 10 Hz laser system from Ekspla and a gas phase TOF and velocity map imaging (VMI) spectrometer. Briefly, the 351 nm 3rd harmonic of a Nd:YLF laser (85% of the fundamental wavelength 1053 nm, corresponding to 5 mJ) was coupled into an optical parametric generator (OPG) producing tuneable pump pulses (80–150 μJ). For the probe pulse, the 4th harmonic at 263.5 nm (∼30 μJ) was employed. The instrument response function (IRF) is around 4 ps, with a spectral bandwidth of roughly 25 cm−1.The experiments were conducted in a differentially pumped vacuum chamber and the sample was seeded in Argon (p0(Ar) = 1.2 bar) at room temperature and expanded through a solenoid pulsed valve with a 0.3 mm diameter nozzle into the vacuum. 4a,8a-Azaboranaphthalene was synthesized according to the route of Sun et al. with slight modifications (see ESI†).46 The purity was checked using 1H-NMR and 11B{1H}-NMR spectroscopy, also air stability for at least two weeks could be verified, see ESI.†
The REMPI (resonance-enhance multiphoton ionisation) spectrum was obtained by averaging three wavelength scans. In each scan the OPG was tuned in 0.1 nm steps, each data point was averaged over 50 laser shots. The laser beam was weakly focused (f = 1000 mm) into the ionization region. To study the lifetimes, several vibronic bands were investigated in a [1+1′]-process with the 263.5 nm probe pulse. The time-resolved spectra were averaged over 10–30 time-delay scans. In each scan, a single data point was averaged over 50 laser shots. The time intervals between the points varied between 0.5 ps close to the pump–probe overlap, and up to some 10 to 100 ps far away from it. All decay traces were fitted employing a monoexponential decay combined with a Gaussian shaped IRF (around 4 ps). In addition, photoelectron images were recorded for a number of S1 bands, which yielded an ionisation energy (IE) of the molecule, see below. For the imaging photoelectron experiments each 2D raw image was averaged over 5000 shots. The images were reconstructed employing the pBASEX47 algorithm up to second order Legendre polynomial. Quantum chemical calculations aimed at elucidating the vibrational spectrum were conducted within the framework of (time-dependent) density functional theory (TD-DFT). The calculations employed the ωB97Xd functional48 along with the augmented correlation consistent polarized triple zeta (aug-cc-pVTZ) basis set. The computations were executed using the Gaussian 16 quantum chemical software package.49 The choice of a large basis set augmented with diffuse functions was imperative for the accurate description of low-lying Rydberg states in TD-DFT calculations. The molecular structures were optimized, and Hessian matrices were computed for both the ground (S0) and the first excited (S1) states. A frequency analysis showed the absence of imaginary frequencies. Vibrationally resolved absorption spectra for the S1 ← S0 transition were simulated using the Herzberg–Teller approximation. This was achieved through a time-independent approach employing the adiabatic Hessian model (AH) in the FCclasses3.0 program.50–52 To characterize the relevant electronic transitions, the natural transition orbitals (NTO) formalism was employed. Ionization energies were in addition computed by the CBS-QB3 composite method.53 The FC-simulations for the photoelectron spectrum and the TPES in the ESI† were carried out using ezSpectrum.54
For the exploration of potential nonradiative deactivation pathways, conical intersections were optimized using the penalty method developed by Ciminelli et al.55 Energies and gradients were calculated at the extended multi-state (XMS) complete active space second-order perturbation theory (CASPT2) level,56 using the aug-cc-pVDZ basis set. These calculations were performed using the BAGEL software package.57 All optimization routines related to the deactivation pathway were carried out using the geomeTRIC package,58 which was interfaced with BAGEL. The pathway leading to the minimum energy conical intersection (MECI) was determined using our in-house implementation of the nudged elastic band (NEB) method.59,60 Further computational details are given in the ESI.†
Results
Characterization of structure and electronic properties
The optimized ground state structure of 1 is planar and shows C2v-symmetry. Compared with the situation in the D2h-symmetric naphthalene, the bond lengths in 1 are quite different. We find a B–N bond length RBN = 1.46 Å (RCC = 1.48 Å), while RBC increases to 1.52 Å (RCC = 1.40 Å) and RNC shortens to 1.38 Å (RCC = 1.40 Å), compared to the C–C bonds in naphthalene (values in parentheses). This causes a significant distortion in the molecular plane, see Fig. S1 (ESI†) for details on the geometry. The values can be compared to the parameters derived by microwave spectroscopy.30 Here, bond lengths of RBN = 1.470 Å, RBC = 1.510 Å and RNC = 1.391 Å were reported, in a very good agreement with the values computed in the present work.To interpret the electronic spectra and to understand the relaxation dynamics of 1, the energies of the electronically excited states are crucial and were thus determined in TD-DFT computations. Table 1 summarizes the calculated vertical excitation energies Evert for the first five triplet and the first four singlet states, as well as the corresponding oscillator strengths f. Transitions into the S1 and S2 states are associated with rather small values of f, while the far more intense transitions into the S3 and S4 states are outside the range of energies investigated experimentally in the present work. A striking result is the large number of low-lying triplet states compared to naphthalene (see Fig. S2, ESI†). Even T4 is energetically significantly below the S1 state, while in naphthalene S1 and T3 are almost degenerate.33
| Electronic state | E vert/eV (DFT) | E vert/eV (4-XMS-CASPT2(6,6)) | E vert/eV ref. 31 | f this work |
|---|---|---|---|---|
| T13A1 (ππ*) | 3.08 | 3.08 | — | — |
| T23B1 (ππ*) | 3.18 | 3.33 | — | — |
| T33B1 (ππ*) | 4.24 | 3.88 | — | — |
| T43A1 (ππ*) | 4.26 | 4.04 | — | — |
| T53A1 (ππ*) | 5.16 | — | — | — |
| S11B1 (ππ*) | 4.67 | 4.19 | 4.75 | 0.0034 |
| S21A1 (ππ*) | 4.89 | 4.39 | 4.96 | 0.0053 |
| S31A1 (ππ*) | 5.56 | 4.80 | 5.74 | 0.3651 |
| S41B1 (ππ*) | 5.60 | — | 5.75 | 0.5390 |
Interestingly, the calculated energy gap between the S2 and S1 states, ΔE(S1–S2) is only around 0.2 eV, thus interactions between these two states can be anticipated. Analysing the transitions in the natural transition orbital (NTO) formalism shows that all transitions to low-lying excited electronic states consist of a π–HONTO (highest occupied NTO) to π*–LUNTO (lowest unoccupied NTO) transition. According to this formalism, all singlet and triplet transitions are computed to be of ππ* character (see Fig. S3 and S4, ESI†). Interestingly, for transitions into the S1 and S2 state, the same NTOs are relevant, but the magnitude of the HONTO → LUNTO and HONTO−1→LUNTO+1 contributions is reversed (see Fig. S3, ESI†). For both transitions, the LUNTO+1 shows a B–N antibonding contribution, so the most important geometry change associated with the S1 ← S0 transition is a pronounced increase in the B–N bond length RBN from 1.46 Å to 1.53 Å, indicating a reduction in the B–N bond order. On the other hand, RBC does not change and RBN decreases only slightly to 1.36 Å, thus the in-plane distortion becomes even more significant.
Energy-resolved spectra
Fig. 2 depicts a REMPI spectrum of 1 between 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 and 37
700 and 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 (black line). Several bands can be identified and are listed in Table 2. While the first few bands are well separated, they start overlapping at higher energies and bands appear atop of a background signal. The first band appears at 33
600 cm−1 (black line). Several bands can be identified and are listed in Table 2. While the first few bands are well separated, they start overlapping at higher energies and bands appear atop of a background signal. The first band appears at 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830 cm−1 (4.194 eV) and is assigned to the origin of the S1 state, in good agreement with the computed adiabatic excitation energy of Ead = 4.50 eV. The vertical energy Evert = 4.67 eV (XMS-CASPT2: 4.19 eV) is best compared to the band maximum at 4.370 eV (+1420 cm−1), and again indicates good agreement between experiment and computation. The experimental value also matches the HOMO–LUMO gap of 4.13 eV in cyclohexane, reported by Liu et al.31 The green line represents a simulation, based on time-independent quantum chemical calculations of the S1 ← S0 transition. The simulation has been shifted by −1243 cm−1 for best agreement with the experiment. It is visible that computed band positions and intensities of the S1 state in the lower wavenumber region resemble the experimental ones.
830 cm−1 (4.194 eV) and is assigned to the origin of the S1 state, in good agreement with the computed adiabatic excitation energy of Ead = 4.50 eV. The vertical energy Evert = 4.67 eV (XMS-CASPT2: 4.19 eV) is best compared to the band maximum at 4.370 eV (+1420 cm−1), and again indicates good agreement between experiment and computation. The experimental value also matches the HOMO–LUMO gap of 4.13 eV in cyclohexane, reported by Liu et al.31 The green line represents a simulation, based on time-independent quantum chemical calculations of the S1 ← S0 transition. The simulation has been shifted by −1243 cm−1 for best agreement with the experiment. It is visible that computed band positions and intensities of the S1 state in the lower wavenumber region resemble the experimental ones.
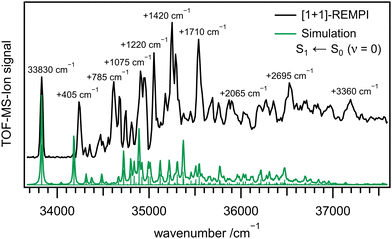 | ||
| Fig. 2 [1+1]-REMPI spectrum of 1 (black) together with a simulation based on time-independent quantum chemical calculations (green). | ||
| Vib. energy/cm−1 | Calc. energy/cm−1 | Tentative assignment | Life time τ |
|---|---|---|---|
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830 ± 12 830 ± 12 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 074 074 |
S1 origin | >1 ns |
| +405 | +350 | ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) 44 in-plane ring deform. 44 in-plane ring deform. |
>1 ns |
| +785 | +890 | ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) 30 in-plane ring deform. 30 in-plane ring deform. |
>1 ns |
| +1075 | +1060 | ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) 24 CC-stretch/CH in-plane deform. 24 CC-stretch/CH in-plane deform. |
>1 ns |
| +1220 | +1160 or +1180 | ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) 21 CH in-plane deform./BN-stretch 21 CH in-plane deform./BN-stretch |
>1 ns |
| +1420 | >1 ns | ||
| +1710 | — | — | ≈400 |
| +2065 | — | — | 117 ± 6 ps |
| +2695 | — | — | 31 ± 2 ps |
| +3360 | — | — | 13 ± 1.5 ps |
Due to the agreement between theory and experiment, for some bands an assignment is possible. However, with increasing excitation energy, bands overlap and an assignment to a single transition is not possible anymore. A summary of the most important REMPI transitions with assignment based on DFT calculations is given in Table 2. The most important geometry changes upon excitation are the more pronounced deformation of the ring system and the increase of RBN. Therefore, modes associated with these changes display a significant activity. The first intense band next to the origin in the measured spectrum (see Fig. 2) at a wavenumber of +405 cm−1 corresponds to an in-plane ring deformation mode of the molecule. Its intensity relative to the origin is well represented by the computations. This also holds for several low-intensity transitions up to 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1.
500 cm−1.
On the other hand, the second intense band at +785 cm−1 is not visible in the computations. It can either be assigned to the in-plane deformation computed at 890 cm−1 or to the first overtone of the +405 cm−1 band, which is significantly underestimated by the computations.
Further intense bands are observed at +1075 cm−1 (CC-stretch and CH in-plane deformation), +1220 cm−1 (CH in-plane deformation and BN-stretch), +1420 cm−1 and +1710 cm−1. Based on the computations they could be assigned to modes with considerable B–N character, which are expected to appear due to the increase of the BN bond length upon excitation. However, at higher wavenumbers, bands are composed of several overlapping transitions and thus increasingly difficult to assign.
To determine the adiabatic ionization energy IEad, we recorded a one-color [1+1]-REMPI photoelectron spectrum via the S1 000 transition at ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 33
= 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830 cm−1 (4.194 eV). The spectrum exhibits two pronounced bands (A,B) and a third one (C) being cut off at 0 eV electron kinetic energy (EKE). A Franck–Condon simulation based on the geometries depicted in Fig. S1 (ESI†) is given as a dotted line. It is obtained by convolving the stick spectrum also shown in Fig. 3 with a Gaussian function with a full width at half maximum of 40 meV. Band A appears at the highest photoelectron kinetic energy EKE = 0.12 eV and thus corresponds to the transition into the ground state of the cation, D0 ← S1. From expression (1)
830 cm−1 (4.194 eV). The spectrum exhibits two pronounced bands (A,B) and a third one (C) being cut off at 0 eV electron kinetic energy (EKE). A Franck–Condon simulation based on the geometries depicted in Fig. S1 (ESI†) is given as a dotted line. It is obtained by convolving the stick spectrum also shown in Fig. 3 with a Gaussian function with a full width at half maximum of 40 meV. Band A appears at the highest photoelectron kinetic energy EKE = 0.12 eV and thus corresponds to the transition into the ground state of the cation, D0 ← S1. From expression (1)
| IEad = hν − EKE | (1) |
 | ||
| Fig. 3 [1+1] photoelectron spectrum recorded via the S1 origin in comparison with FC-simulation based on DFT (ωB97xD/aug-cc-pVTZ) computed frequencies and the corresponding stick spectrum. | ||
Band B is composed of three overlapping transitions into the in-plane ring deformation modes ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) +42 = 468 cm−1 and
+42 = 468 cm−1 and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) +39 = 587 cm−1 and into the BN-stretch mode
+39 = 587 cm−1 and into the BN-stretch mode ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) +38 = 659 cm−1. The
+38 = 659 cm−1. The ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) +42 mode corresponds to
+42 mode corresponds to ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) +44 visible in the REMPI spectrum as an intense peak at +405 cm−1, cf.Fig. 2. Based on the computed geometries, ionization from the S1 state leads to a decrease of RBN to 1.48 Å and thus an increase in the BN bond strength (see Fig. S1, ESI†). Together with an increase in RNC and a decrease in RBC, ring deformation is reduced, which explains the Franck–Condon activity in
+44 visible in the REMPI spectrum as an intense peak at +405 cm−1, cf.Fig. 2. Based on the computed geometries, ionization from the S1 state leads to a decrease of RBN to 1.48 Å and thus an increase in the BN bond strength (see Fig. S1, ESI†). Together with an increase in RNC and a decrease in RBC, ring deformation is reduced, which explains the Franck–Condon activity in ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) +42. Finally, band C maximizes at an EKE of 0 eV. Most likely, electrons from autoionizing states contribute to the band, thus it cannot be simulated. The relative intensity of bands A and B is reflected in the Franck–Condon simulation, which confirms that the calculated geometries are correct. Note that no dissociative photoionization was evident in the spectra.
+42. Finally, band C maximizes at an EKE of 0 eV. Most likely, electrons from autoionizing states contribute to the band, thus it cannot be simulated. The relative intensity of bands A and B is reflected in the Franck–Condon simulation, which confirms that the calculated geometries are correct. Note that no dissociative photoionization was evident in the spectra.
Time-delay scans
To gain insight into the excited state dynamics of 1, we excited several bands observed in the REMPI-spectrum (cf.Fig. 2) and ionized them with a 263.5 nm probe pulse. The time delay scans are shown in Fig. 4, while the time constants obtained from a single exponential fit are summarized in Table 2. For the S1 origin (top left) as well as for low lying vibronic bands (see e.g. band at +1420 cm−1 in the upper middle) no time dependence is observed on the ps time scale, indicating a long lifetime on the order of at least some tens of ns. However, once bands at excess energies above +1420 cm−1 are excited, the lifetime decreases rapidly. For example, a decay with τ = 400 ps is observed at +1710 cm−1, while for the highest energy band investigated here at +3360 cm−1 we measure τ = 13 ps. All traces decay monoexponentially and all of them most likely decrease to zero, although for several bands the time-delay scan is too short to observe the full decay. Time-resolved photoelectron images were also recorded. They did not yield additional insight and are thus given only in the ESI,† see Fig. S6. | ||
| Fig. 4 Time delay traces recorded with a probe wavelength of 263.5 nm at different excitation energies. The time constant decreases monoexponentially at higher excitation energies. | ||
Discussion
We will now consider the possible nonradiative deactivation mechanisms, in particular intersystem crossing (ISC) and internal conversion (IC). As all triplet states in the investigated energy range were computed to be of ππ* character, ISC would be associated with an (1ππ*→3ππ*) process, which is considered slow within the framework of the El Sayed rules.62 For the S1 origin as well as for low lying vibronic states, the long ns-lifetimes indicate that the deactivation is dominated by fluorescence and possibly ISC. However, we consider ISC unlikely to contribute to the rapid deactivation at higher excitation energies, suggesting that internal conversion (IC) within the singlet state manifold is the primary deactivation pathway.Deactivation accelerates between 1420 cm−1 and 1710 cm−1, where lifetimes drop from several ns to 400 ps. Furthermore, the ion signal decays to zero, thus the final state of the non-radiative deactivation cannot be efficiently ionized. This rules out vibrational energy redistribution (IVR) as an explanation for the decay because distribution of population over several vibrational levels would not suppress ionization completely. Interestingly, the energy gap of the first and second excited state at the ground state equilibrium geometry computed by DFT, ΔE(S1–S2) is 0.22 eV (1775 cm−1) and thus matches the energy of the observed change in lifetime rather well. Therefore, we assume that the deactivation is mediated by the interaction between the two excited singlet states and propose a deactivation for 1 that follows the mechanism illustrated on the left-hand side of Fig. 5. Close to around +0.2 eV excess energy, the S2 state becomes accessible. In an adiabatic picture, the interaction between the states leads to an avoided crossing and creates a barrier on the S1 surface. At sufficiently high excitation energies, there is enough internal energy in the molecule to overcome this barrier after IVR (redistribution of vibrational energy). The subsequent decrease of lifetime with increasing wavenumbers is in accordance with Fermi's Golden rule, which assumes the rate constant of a process to be proportional to the density of states.63
The ion signal decays to zero, thus the final state of the non-radiative deactivation cannot be efficiently ionized because of small Franck–Condon factors. This can be explained, when the S1 relaxation is followed by a rapid IC to the electronic ground state with a fast sub-ps time constant that cannot be resolved in our setup, possibly via a conical intersection (CI). To substantiate this hypothesis, we employed SA4-XMS-CASPT2(6,6) calculations to identify conical intersections between the S1 and S0 states that could be responsible for facilitating the internal conversion process. For this purpose, energy barriers (Ea) for the pathway from the vertical excitation in the first excited state to the CIs were calculated with the nudged elastic band (NEB) method for CIs located energetically below or up to 0.3 eV above the vertical excitation energy for the S1 (see Table 3). We find structure B, given on the right-hand side (top trace) in Fig. 6 to be the conical intersection with the lowest barrier, with an energy of 4.14 eV with respect to the ground state equilibrium. In the assigned structure, one of the carbon atoms adjacent to the nitrogen atom deviates significantly from the planar configuration commonly observed in naphthalene derivatives. This out-of-plane carbon atom introduces a distinct distortion in the molecular geometry. Furthermore, the hydrogen atom attached to this deflected carbon is oriented in a manner that it points slightly towards the nitrogen atom. The computed lowest energy pathway from the vertically excited S1 structure to this conical intersection is depicted on the right-hand side of Fig. 5. The activation barrier was calculated to be Ea = 0.21 eV, in agreement with the onset of the lifetime-drop in the experiments. As a result, increasing the excitation energy in the experiment enhances the probability of overcoming this activation barrier, thereby promoting a rapid transition back to the ground state. In this case, electronic excitation energy is converted to vibrational energy and the highly vibrationally excited molecules cannot be ionized, due to unfavourable Franck–Condon factors to low-lying ionic states. No dissociative photoionization was observed, so the laser intensities employed in this study do not permit to populate excited ionic states in a multiphoton probe step that could reveal additional information.
| Structure | ΔE/eV | E a/eV |
|---|---|---|
| A | 4.01 | 0.60 |
| B | 4.14 | 0.21 |
| C | 4.31 | 0.89 |
| D | 4.42 | 0.98 |
| E | 4.47 | 1.42 |
Excited-state deactivation might also result in dissociation. A ground state dissociation following a statistical mechanism will probably occur on a longer time scale. Alternatively, after passing the CI, the molecule might rapidly dissociate along a repulsive coordinate. For the C–H bonds next to the B and N atoms, we computed dissociation energies D0 of 5.04 and 5.16 eV, thus dissociation would only be possible at the highest excitation energies. Although no fragmentation products have been observed, we note that our experimental scheme is not sensitive to H-atoms from dissociation of a C–H bond.
It is of interest to compare the results obtained for 1 with the large body of data reported for the isoelectronic hydrocarbon parent PAH naphthalene. Here, the S1 ← S0 transition has been extensively studied by various methods. For the S1 origin as well as low-lying vibronic bands, lifetimes in excess of 100 ns have been reported and quantum yields indicate preferred relaxation to the S0 state via fluorescence.32–36 Excited vibronic states decay to low-lying triplet states.43 However, lifetimes remain in the ns-regime for S1 excess energies of more than 4000 cm−1, commensurate with an unfavourable (1ππ*→3ππ*) ISC. Only above 4.45 eV, the S2 state is accessed and a drop in lifetime also becomes apparent, as confirmed by Schmitt et al., who reported a lifetime of less than 100 fs for the 1B2u state of naphthalene when excited at 278 nm (4.46 eV).37 A major impact on the excited state dynamics of replacing the central C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C unit in naphthalene with a B–N group thus seems to be a reduction of the S1–S2 energy gap ΔE(S1–S2), which leads to shorter excited state lifetimes. But also, the energetic landscape of conical intersections is significantly influenced by doping. Our calculations indicate that introducing a BN group to naphthalene results in CI conformations with structural motifs similar to those identified by Harabuchi et al.64 in naphthalene, while the heteroatom doping disrupts the mirror symmetry, resulting in distinct isomers. Although the energies and their ordering are significantly altered, for the minimum energy conical intersection (MECI), both systems display comparable structures (denoted A), characterized by a distorted CH moiety. In 1, this moiety is notably located on the ‘boron-side’, as illustrated in Fig. 6.
C unit in naphthalene with a B–N group thus seems to be a reduction of the S1–S2 energy gap ΔE(S1–S2), which leads to shorter excited state lifetimes. But also, the energetic landscape of conical intersections is significantly influenced by doping. Our calculations indicate that introducing a BN group to naphthalene results in CI conformations with structural motifs similar to those identified by Harabuchi et al.64 in naphthalene, while the heteroatom doping disrupts the mirror symmetry, resulting in distinct isomers. Although the energies and their ordering are significantly altered, for the minimum energy conical intersection (MECI), both systems display comparable structures (denoted A), characterized by a distorted CH moiety. In 1, this moiety is notably located on the ‘boron-side’, as illustrated in Fig. 6.
The Nudged Elastic Band (NEB) calculations reveal a relatively high activation energy of 0.6 eV for structure A in 1. However, the BN insertion markedly stabilizes the CI structure B, which features a puckered CH moiety adjacent to the nitrogen atom. This structure lies only 0.14 eV above the MECI (while in naphthalene, the energy difference amounts 0.41 eV), and interestingly, it presents a significantly smaller activation energy of 0.21 eV for the transition. As a result, B with its substantially lower barrier becomes the most important deactivation pathway for the internal conversion process. Notice, that for both CIs in naphthalene (structures A and B) the hydrogen atom attached to the “puckered” carbon does not exhibit a distinct orientation, while for 1 it is oriented towards the neighbouring heteroatom. The shift in energy of the two CIs as well as their barriers have direct implications for the accessible deactivation pathways for nonradiative transitions back to the ground state. It results in an onset for excited-state deactivation at much lower energies in 1 compared to naphthalene. Further conical intersection structures were identified in 1, termed C–E in Table 3 and are depicted in Fig. S7 (ESI†). Due to their higher energy barriers, they are not considered relevant in the interpretation of the spectroscopic findings.
Past computational work indicated that the electronic properties depend strongly on regioselectivity, i.e. the position of the BN group in the molecule. However, the influence of the site of substitution on the properties is neither fully understood nor easily predicted.11 We hope that our study contributes to a better understanding of how BN substitution influences the photophysical properties of PAH.
Conclusions
In this work, we investigated the electronic structure and dynamics of isolated 4a,8a-azaboranaphthalene 1 by frequency- and time-resolved electronic spectroscopy, supported by high-level electronic structure computations. Compared to naphthalene, 1 shows a significant geometry deformation in the molecular plane, which is even more pronounced in the S1 state. In a partially vibrationally resolved multiphoton ionisation spectrum, the origin of the S1 ← S0 transition was observed at![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 33
= 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830 ± 12 cm−1. Compared to the parent PAH naphthalene, the symmetry reduction leads to a larger number of vibronic bands in the spectrum. Based on TD-DFT calculations (ωB97xD/aug-cc-pVZT) and a time-independent simulation of the spectrum, several vibrational transitions were assigned. By analysing the photoelectron spectrum obtained via the S1 origin, an ionization energy of IEexp = 8.27 eV ± 0.025 eV was determined for 1, which revises an earlier value.61 A vibrational progression in the cationic D0 state was assigned to the in-plane deformation mode and the BN-stretch mode because the geometry deformation is less pronounced in the cation compared to S1.
830 ± 12 cm−1. Compared to the parent PAH naphthalene, the symmetry reduction leads to a larger number of vibronic bands in the spectrum. Based on TD-DFT calculations (ωB97xD/aug-cc-pVZT) and a time-independent simulation of the spectrum, several vibrational transitions were assigned. By analysing the photoelectron spectrum obtained via the S1 origin, an ionization energy of IEexp = 8.27 eV ± 0.025 eV was determined for 1, which revises an earlier value.61 A vibrational progression in the cationic D0 state was assigned to the in-plane deformation mode and the BN-stretch mode because the geometry deformation is less pronounced in the cation compared to S1.
In time-resolved experiments with different pump wavelengths and a probe wavelength of 263.5 nm we observed a decrease in lifetime with excitation energy. The time-resolved spectra of the S1 origin and of low-lying vibronic states show no apparent decay, indicating a lifetime in the nanosecond range and a deactivation governed by fluorescence or an El-Sayed forbidden ISC transition. Below excitation wavelengths of λPump = 281.4 nm, corresponding to +0.21 eV a monoexponential decay (τdecay ≤ 400 ps) becomes apparent. The deactivation is attributed to a conical intersection to the electronic ground state. To access it, an energy barrier has to be passed, which requires sufficient excess energy. This explains the fairly sharp drop in lifetime with vibrational excitation in the S1 state. The barrier might in turn result from the interaction between the S1 and the S2 states. This energy barrier of 0.21 eV agrees well with the ΔE(S1–S2) energy gap of +0.22 eV computed by TD-DFT and the lowest energy pathway from the vertically excited structure (star) to the chosen conical intersection structure, calculated to be 0.21 eV by the Nudged Elastic Band (NEB) method. Compared to naphthalene, BN-doping dramatically changes the energy of the conical intersections. A structure termed B was identified at significantly lower energies in our computations and provides an efficient non-radiative deactivation pathway in 1 that is not accessible in naphthalene.
In summary, we showed that isoelectronic substitution by BN groups influences excited state dynamics in PAH. Compared to the parent PAH naphthalene, the difference in the deactivation can be attributed to the smaller energy gap between S1 and S2 and to internal conversion by an accessible new deactivation pathway. However, a considerable regioselectivity is anticipated, depending on the BN isostere.
Author contributions
F. Sturm: investigation (experiment), writing – original draft; M. Bühler: investigation (theory), writing – original draft; C. Stappper: investigation (experiment); J. S. Schneider: investigation (synthesis); H. Helten: writing – review & editing, supervision, project administration; I. Fischer: conceptualisation, writing – review & editing, supervision, project administration, funding acquisition; M. I. S. Röhr: conceptualisation, writing – review & editing, supervision, project administration.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
I. F. acknowledges financial support by the Deutsche Forschungsgemeinschaft, DFG contract FI 575/16-1. F. S. thanks the Rosa-Luxemburg-Foundation for a PhD fellowship. We further acknowledge the support of Marius Gerlach, Dorothee Schaffner, Emil Karaev and Klaus Hofmann in recording the TPE spectrum of 1 at the Swiss Light Source. M. B. and M. I. S. R. are thankful for financial support by the Bavarian State Initiative “Solar Technologies Go Hybrid”. H. H. thanks the DFG for funding through the Heisenberg Programme (HE 6171/9-1, 468457264).Notes and references
- J. S. Dewar, V. P. Kubba and R. Pettit, J. Chem. Soc., 1958, 3073–3076 RSC.
- M. Dewar and R. Jones, J. Am. Chem. Soc., 1968, 90, 2137–2144 CrossRef CAS.
- M. J. D. Bosdet and W. E. Piers, Can. J. Chem., 2009, 87, 8–29 CrossRef.
- M. Kawaguchi, Adv. Mater., 1997, 9, 615–625 CrossRef CAS.
- Y. Appiarius and A. Staubitz, Chem. Unserer Zeit, 2023, 57, 180–190 CrossRef CAS.
- Z. Liu and T. B. Marder, Angew. Chem., Int. Ed., 2008, 47, 242–244 CrossRef CAS PubMed.
- H. L. van de Wouw and R. S. Klausen, J. Org. Chem., 2019, 84, 1117–1125 CrossRef CAS PubMed.
- C. R. McConnell and S.-Y. Liu, Chem. Soc. Rev., 2019, 48, 3436–3453 RSC.
- M. M. Morgan and W. E. Piers, Dalton Trans., 2016, 45, 5920–5924 RSC.
- M. Pinheiro, F. B. C. Machado, F. Plasser, A. J. A. Aquino and H. Lischka, J. Mater. Chem. C, 2020, 8, 7793–7804 RSC.
- H. Helten, Chem. – Eur. J., 2016, 22, 12972–12982 CrossRef CAS PubMed.
- F.-D. Zhuang, Z.-H. Sun, Z.-F. Yao, Q.-R. Chen, Z. Huang, J.-H. Yang, J.-Y. Wang and J. Pei, Angew. Chem., Int. Ed., 2019, 58, 10708–10712 CrossRef CAS PubMed.
- X. Chen, D. Tan and D.-T. Yang, J. Mater. Chem. C, 2022, 10, 13499–13532 RSC.
- C. Zhu, X. Ji, D. You, T. L. Chen, A. U. Mu, K. P. Barker, L. M. Klivansky, Y. Liu and L. Fang, J. Am. Chem. Soc., 2018, 140, 18173–18182 CrossRef CAS PubMed.
- X.-Y. Wang, J.-Y. Wang and J. Pei, Chem. – Eur. J., 2015, 21, 3528–3539 CrossRef CAS PubMed.
- Y. Chen, W. Chen, Y. Qiao, X. Lu and G. Zhou, Angew. Chem., Int. Ed., 2020, 59, 7122–7130 CrossRef CAS PubMed.
- W. Li, C.-Z. Du, X.-Y. Chen, L. Fu, R.-R. Gao, Z.-F. Yao, J.-Y. Wang, W. Hu, J. Pei and X.-Y. Wang, Angew. Chem., Int. Ed., 2022, 134, e202201464 CrossRef.
- J. Guo, Y. Yang, C. Dou and Y. Wang, J. Am. Chem. Soc., 2021, 143, 18272–18279 CrossRef CAS PubMed.
- T. Zeng, N. Ananth and R. Hoffmann, J. Am. Chem. Soc., 2014, 136, 12638–12647 CrossRef CAS PubMed.
- X.-Y. Wang, H.-R. Lin, T. Lei, D.-C. Yang, F.-D. Zhuang, J.-Y. Wang, S.-C. Yuan and J. Pei, Angew. Chem., Int. Ed., 2013, 52, 3117–3120 CrossRef CAS PubMed.
- X.-Y. Wang, F.-D. Zhuang, X. Zhou, D.-C. Yang, J.-Y. Wang and J. Pei, J. Mater. Chem. C, 2014, 2, 8152–8161 RSC.
- X. Wang, F. Zhang, J. Liu, R. Tang, Y. Fu, D. Wu, Q. Xu, X. Zhuang, G. He and X. Feng, Org. Lett., 2013, 15, 5714–5717 CrossRef CAS PubMed.
- T. Lei, J.-Y. Wang and J. Pei, Chem. Mater., 2014, 26, 594–603 CrossRef CAS.
- Z. X. Giustra and S.-Y. Liu, J. Am. Chem. Soc., 2018, 140, 1184–1194 CrossRef CAS PubMed.
- J. Wang, A. Zheng, Y. Xiang and J. Liu, J. Am. Chem. Soc., 2023, 145, 14912–14921 CrossRef CAS PubMed.
- J. Guo, Z. Li, X. Tian, T. Zhang, Y. Wang and C. Dou, Angew. Chem., Int. Ed., 2023, 62, e202217470 CrossRef CAS PubMed.
- S. A. Brough, A. N. Lamm, S.-Y. Liu and H. F. Bettinger, Angew. Chem., Int. Ed., 2012, 51, 10880–10883 CrossRef CAS PubMed.
- M. Müller, C. Maichle-Mössmer and H. F. Bettinger, Angew. Chem., Int. Ed., 2014, 53, 9380–9383 CrossRef PubMed.
- F. Holzmeier, M. Lang, P. Hemberger, A. Bodi, M. Schäfer, R. D. Dewhurst, H. Braunschweig and I. Fischer, Chem. – Eur. J., 2014, 20, 9683–9692 CrossRef CAS PubMed.
- A. M. Pejlovas, A. M. Daly, A. J. Ashe III and S. G. Kukolich, J. Chem. Phys., 2016, 144, 114303 CrossRef PubMed.
- Z. Liu, J. S. A. Ishibashi, C. Darrigan, A. Dargelos, A. Chrostowska, B. Li, M. Vasiliu, D. A. Dixon and S.-Y. Liu, J. Am. Chem. Soc., 2017, 139, 6082–6085 CrossRef CAS PubMed.
- M. Stockburger, H. Gattermann and W. Klusmann, J. Chem. Phys., 1975, 63, 4519–4528 CrossRef CAS.
- M. Stockburger, H. Gattermann and W. Klusmann, J. Chem. Phys., 1975, 63, 4529–4540 CrossRef CAS.
- C. Reylé and P. Bréchignac, Eur. Phys. J. D, 2000, 8, 205–210 CrossRef.
- H. W. Offen and D. T. Phillips, J. Chem. Phys., 1968, 49, 3995–3997 CrossRef CAS.
- U. Laor and P. K. Ludwig, J. Chem. Phys., 1971, 54, 1054–1057 CrossRef CAS.
- M. Schmitt, S. Lochbrunner, J. P. Shaffer, J. J. Larsen, M. Z. Zgierski and A. Stolow, J. Chem. Phys., 2001, 114, 1206–1213 CrossRef CAS.
- S. M. Beck, D. E. Powers, J. B. Hopkins and R. E. Smalley, J. Chem. Phys., 1980, 73, 2019–2028 CrossRef CAS.
- F. M. Behlen and S. A. Rice, J. Chem. Phys., 1981, 75, 5672–5684 CrossRef CAS.
- M. J. Robey, I. G. Ross, R. V. Southwood-Jones and S. J. Strickler, Chem. Phys., 1977, 23, 207–216 CrossRef CAS.
- F. Negri and M. Z. Zgierski, J. Chem. Phys., 1996, 104, 3486–3500 CrossRef CAS.
- M. Z. Zgierski, Chem. Phys. Lett., 1977, 47, 499–502 CrossRef CAS.
- P. Avouris, W. M. Gelbart and M. A. El-Sayed, Chem. Rev., 1977, 77, 793–833 CrossRef CAS.
- M. Flock, L. Bosse, D. Kaiser, B. Engels and I. Fischer, Phys. Chem. Chem. Phys., 2019, 21, 13157–13164 RSC.
- J. Auerswald, B. Engels, I. Fischer, T. Gerbich, J. Herterich, A. Krueger, M. Lang, H.-C. Schmitt, C. Schon and C. Walter, Phys. Chem. Chem. Phys., 2013, 15, 8151–8161 RSC.
- F. Sun, L. Lv, M. Huang, Z. Zhou and X. Fang, Org. Lett., 2014, 16, 5024–5027 CrossRef CAS PubMed.
- G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- M. J. Frisch, et al., Gaussian-16 Revision A.03, 2016 Search PubMed.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 084509 CrossRef PubMed.
- F. Santoro, A. Lami, R. Improta, J. Bloino and V. Barone, J. Chem. Phys., 2008, 128, 224311 CrossRef PubMed.
- M. J. Fabrizio Santoro and J. Cerezo, FCclasses3 (version 3.0.1), 2019, https://www.iccom.cnr.it/en/fcclasses Search PubMed.
- J. A. Montgomery Jr., M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532–6542 CrossRef.
- S. Gozem and A. I. Krylov, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1546 CAS.
- C. Ciminelli, G. Granucci and M. Persico, Chem. – Eur. J., 2004, 10, 2327–2341 CrossRef CAS PubMed.
- T. Shiozaki, W. Győrffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106 CrossRef PubMed.
- T. Shiozaki, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1331 Search PubMed.
- L.-P. Wang and C. Song, J. Chem. Phys., 2016, 144, 214108 CrossRef PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Mills and H. Jónsson, Phys. Rev. Lett., 1994, 72, 1124–1127 CrossRef CAS PubMed.
- M. J. S. Dewar and S. D. Worley, J. Chem. Phys., 1969, 50, 654–667 CrossRef CAS.
- M. A. El-Sayed, Acc. Chem. Res., 1968, 1, 8–16 CrossRef CAS.
- M. Bixon and J. Jortner, J. Chem. Phys., 1968, 48, 715–726 CrossRef CAS.
- Y. Harabuchi, T. Taketsugu and S. Maeda, Phys. Chem. Chem. Phys., 2015, 17, 22561–22565 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05508f |
| This journal is © the Owner Societies 2024 |


