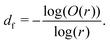Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modelling network formation in folded protein hydrogels by cluster aggregation kinetics†
Kalila R
Cook
 a,
David
Head
a,
David
Head
 *b and
Lorna
Dougan
*b and
Lorna
Dougan
 *ac
*ac
aSchool of Physics and Astronomy, Faculty of Engineering and Physical Sciences, University of Leeds, Leeds, UK. E-mail: L.Dougan@leeds.ac.uk
bSchool of Computing, University of Leeds, Leeds, UK
cAstbury Centre for Structural Molecular Biology, University of Leeds, Leeds, UK
First published on 20th March 2023
Abstract
Globular folded protein-based hydrogels are becoming increasingly attractive due to their specific biological functionality, as well as their responsiveness to stimuli. By modelling folded proteins as colloids, there are rich opportunities to explore network formation mechanisms in protein hydrogels that negate the need for computationally expensive simulations which capture the full complexity of proteins. Here we present a kinetic lattice-based model which simulates the formation of irreversibly chemically crosslinked, folded protein-based hydrogels. We identify the critical point of gel percolation, explore the range of network regimes covering diffusion-limited to reaction-limited cluster aggregation (DLCA and RLCA, respectively) network formation mechanisms and predict the final network structure, fractal dimensions and final gel porosity. We reveal a crossover between DLCA and RLCA mechanisms as a function of protein volume fraction and show how the final network structure is governed by the structure at the percolation point, regardless of the broad variation of non-percolating cluster masses observed across all systems. An analysis of the pore size distribution in the final network structures reveals that, approaching RLCA, gels have larger maximal pores than the DLCA counterparts for both volume fractions studied. This general kinetic model and the analysis tools generate predictions of network structure and concurrent porosity over a broad range of experimentally controllable parameters that are consistent with current expectations and understanding of experimental results.
1 Introduction
In the field of colloid and interface science, there is a wide array of systems that are well approximated as colloidal when considering their properties and behaviours. These range from functional colloids in foods which influence dispersibility, stability and structure,1 the self-assembly of colloidal cube superstructures,2 to biological systems such as complex interactions of DNA–lipid complexes in gene delivery3–5 or modelling bacteria as colloids to understand their morphology, behaviour6 and eventual formation of biofilms.7,8 To add to these, folded globular proteins are sometimes also studied within a colloidal framework,1,9–14 whereby basic definitions of colloids, they fit the submicron size range (generally sub 10 nm radius, assumed spherical15,16) and can be electrostatically stably dispersed in solution. Globular proteins such as bovine serum albumin (BSA), for example, are often satisfactorily modelled in solution as hard-sphere colloids, with added potentials to account for complex attractive and repulsive interactions between charged proteins such as electrostatics, van der Waals, hydration and hydrophobic interactions.10,11,13,17–23Whilst the colloidal approach to proteins is not new, its application in the context of the growing field of folded protein-based hydrogels is less explored. Indeed, proteins have long been utilised as the constituent building block for hydrogels,24,25 and in common with other systems, protein-based systems employ two main types of crosslinking strategies: chemical (irreversible or permanent) and physical (reversible).26 However, gelation is more often initiated by physical methods of denaturation of the protein e.g. by changing the pH,27 temperature27–29 or electrostatics20 of the system, or rather gelation progresses by chemical- or force-induced unfolding of protein domains.30–33 While both partial and full denaturation-induced protein hydrogel formation can provide a range of mechanical and structural properties for hydrogels, this approach can lead to a loss of native globular structure and subsequently a loss of the inherent protein biological function.20,34,35 In terms of modelling denaturation-induced protein hydrogel formation, the potential for treating the systems colloidally may be lost, since new factors can dominate the system kinetics such as increased hydrodynamic radius and/or change of conformation to a non-globular state, complex resultant excluded volume effects36 and change in inter- and intramolecular interactions, perhaps leading to supramolecular aggregation and differences to the bulk properties of the systems.37 It is therefore recognised that there are limitations to taking a colloidal view of these systems. However, as covered comprehensively in the recent review article by Stradner et al.,13 in the right circumstances, where (quasi)spherical globular proteins retain their tertiary conformation,38,39 this approach is appropriate and can bring valuable insight into the mechanisms leading to observed structures and mechanics of protein hydrogels across the lengthscales. Indeed, a growing field has emerged which exploits folded globular proteins for the creation of hydrogels, using irreversible crosslinking to control network formation.40,41 For example, the maximum coordination of folded proteins in gels (defined as the maximum allowed number of chemical crosslinks per domain) can be controlled by tuning the number of site-specific binding residues on the surface of the proteins.42 Such systems lend themselves well to a colloid-based modelling approach, and there is now a growing body of literature on the assembly, rheology and structure of such hydrogels.31,43–45
The benefit of adopting a coarse-grained representation of proteins is that it allows for network formation mechanisms to be examined over the full course of gelation, reducing computationally expensive simulations of complex features of proteins, such as their secondary structure and so called ‘mechanical clamp motifs’ which confer their mechanical robustness,46 that may be less of interest at larger lengthscales.13 Furthermore, regarding proteins as colloids grants the use of established models of cluster aggregation,47–52 allowing for efforts to be focused on achieving longer simulation timescales to understand how the networks evolve and how this impacts the final network structure. Indeed, there are a limited number of works that have used this concept to model globular protein hydrogels in this way,42,53,54 where keeping the protein monomer unchanged during gelation enables other important aspects of network formation to be deconvoluted, such as the effect of different initial size or shape of the monomer, extent of crosslinking and volume fraction. However, it seems thus far, there remains a lack of understanding of the dominant network formation mechanisms on the full gelation profile of these gels. Recent work by Hanson and Dougan delves into the structural characteristics obtained by simulating the formation of folded globular protein-based networks with variable parameters, such as crosslink length and number, while keeping the shape of the protein building block unchanged.42 As the binding sites are located explicitly at the surface of each protein, their local geometric organisation on the surface of the protein is a parameter of importance. This work highlights the significant control that can be achieved on the network architecture without needing to substantially change the protein building block (as is now more often reported30,31,39,43), including by controlling the mechanical stability of the protein,32,39,55 the aspect ratio of the building block,56 colloidal linker regions (e.g. length, flexibility and concentration)42,57,58 and the crosslinking ability of the protein.59 However, there are still limits to the reaction timescales that can be explored simply by the computationally intensive nature of including complex dynamic potentials and interactions in these molecular dynamic simulations.
Here we present a kinetic lattice-based model which models folded globular proteins as colloids and simulates their irreversible chemical crosslinking into gels. By exploiting the parallels between well-established colloidal models and globular protein solutions, we have been able to strip back non-essential complexities in the gelation model by a highly coarse-grained approach, whilst qualitatively maintaining the network formation region of the gelation profiles that we observe in our real experimental systems.32,39,59 Our model is thus intermediate between atomistic simulations and continuum-level finite element descriptions.60 From the refined simplicity of our model, we are able to hone in on the effect of changing experimentally available variables of reaction probability (affiliated with reaction rate) and protein volume fraction on the development of permanent network architecture up until complete system crosslinking, even approaching the reaction-limited regime where computational timescales are at their longest.
From this model, we are able to identify the critical point of gel percolation and use this to construct a fitting for predicting the final network structure. By our bespoke equation for fractal fitting and measurements of final gel porosity, we show that our predictions on the network structure in the final state are accurate. Additionally, we demonstrate how the network structure at the percolation point governs the final network architecture,61 further showing the predictive power of our model from early on in the gelation process.
2 Methods
2.1 Modelling cluster–cluster aggregation
The initial parameters are N, the number of monomers in a cubic, lattice-based simulation box of size L3 with periodic boundary conditions (PBCs) and cells in discrete units of monomer diameters. The monomer volume fraction of the simulation box, ϕ, is set initially by choosing N for a given L, where ϕ = N/L3. Since L is fixed at 64 for all simulations, N must differ to give the desired value of ϕ (e.g. a 4% monomer volume fraction requires N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 for L fixed at 64). We can confirm that this chosen L is not subject to finite size effects, and this data can be found in Fig. S3 in ESI.†R is chosen as the probability with which adjacent monomers crosslink, ranging from 100% (diffusion-limited cluster aggregation (DLCA)) to 0.2% (approaching reaction-limited cluster aggregation (RLCA)).
486 for L fixed at 64). We can confirm that this chosen L is not subject to finite size effects, and this data can be found in Fig. S3 in ESI.†R is chosen as the probability with which adjacent monomers crosslink, ranging from 100% (diffusion-limited cluster aggregation (DLCA)) to 0.2% (approaching reaction-limited cluster aggregation (RLCA)).
Initialisation of the system proceeds by trialing random 3D position coordinates for the N monomers. So long as monomers do not overlap in space, those monomer positions are ‘allowed’. Where any monomer overlaps with another in space, that position is not allowed, and the position-assigning loop is trialed again. This loop is repeated until all N monomers have been situated in the simulation box. At this point, a list of clusters is initialised with N clusters, each of size one, where size is measured in number of monomers that form a given cluster.
| Pi = M−αi, |
Once an attempt has been made to move every cluster in that time step, the program checks whether any clusters are adjacent, i.e. whether they share a side in the 3D system lattice. Any clusters that are adjacent will aggregate (merge) with a ‘reaction probability’, R, as set initially by the user. The simulation time step then increases by one, and the cluster diffusion and aggregation process is repeated until the final time step is reached, where all monomers are incorporated into the percolating cluster.
2.2 Outputs
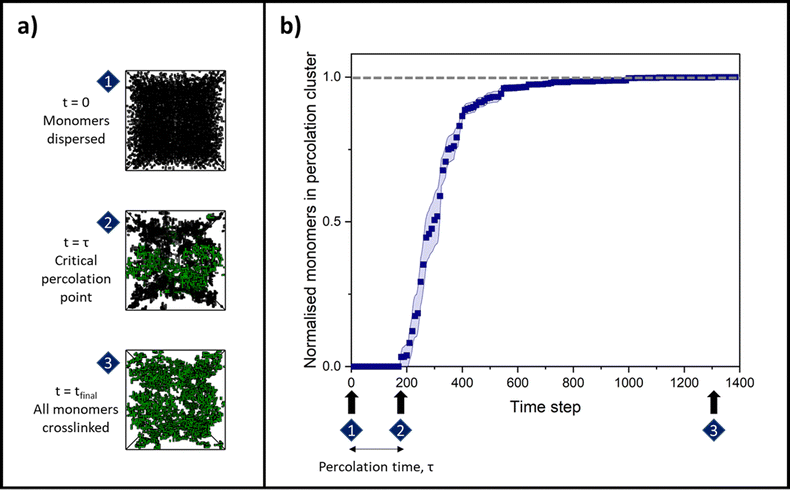
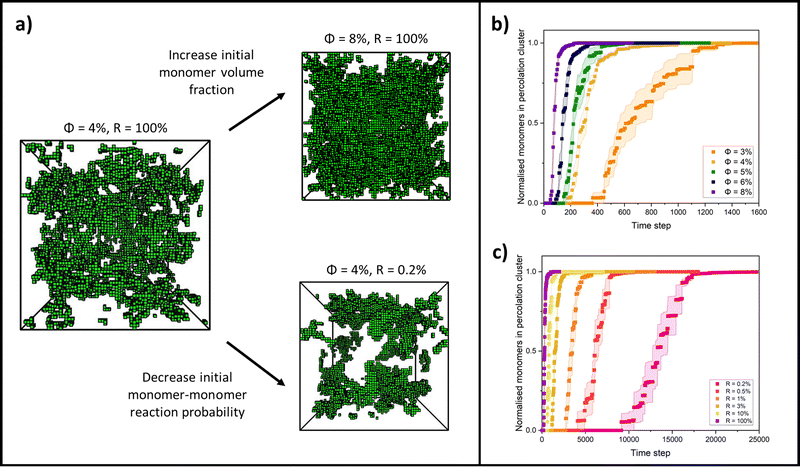
By changing the initial conditions variables of ϕ and R, the progression of gelation and the final gel network structure can be altered, as shown in Fig. 2a. Fig. 2b shows how the percolation time and subsequent time for growth of the percolation cluster to a fully crosslinked network are extended as ϕ is decreased for each system but R is fixed at 100%. Fig. 2c shows how the percolation time and further growth are extended when ϕ is instead fixed at 4%, but R is decreased from 100 to 0.2%. Fig. 2b and c are also presented on log time axes in ESI,† Fig. S1.
Halving the box-covering box size in this method leads to very few data points available for fitting at low r for small system sizes. Low r data provide the fine-scale fractal dimension of the network structure (df < 3), whereas it would be expected that high r data would contribute more to a higher fractal dimension where the lengthscale becomes so coarse that the final cluster appears as a homogeneous solid (df → 3).73 Therefore, in order to reliably capture the fine-scale fractal dimension and the crossover between lengthscales, box-counting here was instead adapted to capture all box sizes between r = 1 and the system size, providing a full set of data points for any system size. Since some of these box sizes lead to partial boxes near the system boundaries, these partial boxes are fractionally weighted according to the method of So, So and Jin.71
Having a uniform sampling of data points over the full available range of r highlights a curve in the data and the need for a more advanced fitting function than the straight-line extraction of the Hausdorff–Besicovitch fractal dimension. Therefore, we have constructed the following equation that better fits the data, from which the fine-scale fractal dimension, df, can be obtained as a fitting parameter:
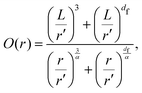 | (1) |
3 Results and discussion
3.1 Network percolation
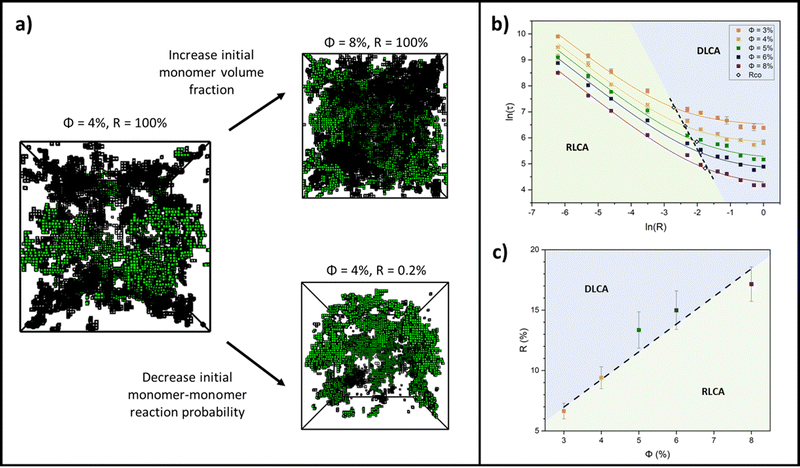
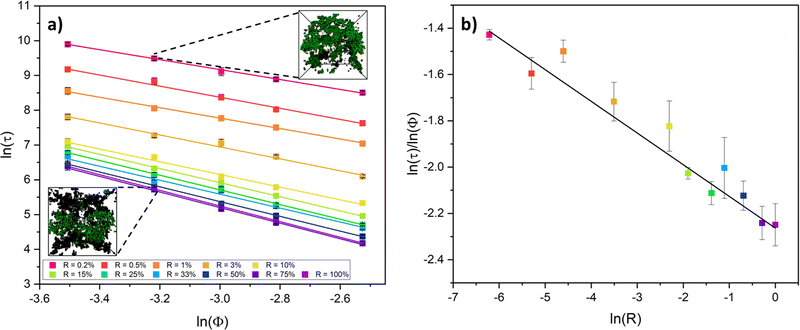
Colloidal aggregation simulations were run to completion (fully crosslinked) at monomer volume fractions of 3, 4, 5, 6 and 8% (representative of experimental folded protein-based hydrogel volume fractions32,39,59) and each at a wide range of monomer–monomer reaction probabilities between 0.2 and 100%. From these simulations, the time at the precise point of percolation (as by our definition), τ, was captured and plotted against reaction probability, R, for each monomer volume fraction, ϕ. Example snapshots of some of these simulations at the percolation point are presented in Fig. 3a with the percolating cluster shown in green and the remaining non-percolating monomers and clusters presented as black ‘wireframes’. Fig. 3b shows the percolation time data on a natural log plot, where each data point represents an average of ten simulation runs of a gelling system with particular initial parameters of ϕ and R. The first trend to note is that the onset of percolation happens sooner with increasing volume fraction across all reaction probabilities (the data sets shift downwards with increasing volume fraction). This is as predicted, since a higher volume fraction of monomers should lead to a higher frequency of monomer–monomer interactions, leading to faster percolation of the network.The data sets are fitted with a reciprocal function in its log form,
| ln(τ) = ln(A + BR) − ln(R), | (2) |
This form of reciprocal fitting, with an inverse unitary power law scaling between τ and R, follows that observed in analogous experimental folded protein gel systems, where photochemical crosslinking of bovine serum albumin (BSA) protein units for a volume fraction of 7.5% yielded a power law fit of gel time with reaction rate of −1.08 ± 0.21.59 Our fitting builds on this experimental fitting with the inclusion of the B constant term which accurately models the high R portion of the data sets, up to 100% reaction probability – beyond that obtained experimentally. Additionally, by taking the criterion that 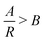 from eqn (2), we can obtain a crossover between cluster aggregation mechanisms as
from eqn (2), we can obtain a crossover between cluster aggregation mechanisms as 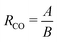 . This crossover region is marked for each volume fraction in Fig. 3b. The dashed black line through these points is drawn as a guide to the eye, separating the graph into a RLCA-driven regime to the left of it and DLCA to the right.
. This crossover region is marked for each volume fraction in Fig. 3b. The dashed black line through these points is drawn as a guide to the eye, separating the graph into a RLCA-driven regime to the left of it and DLCA to the right.
Fig. 3c more clearly shows the reaction probabilities at which the crossover between cluster aggregation regimes is found by fitting eqn (2) for each volume fraction. In its log form, for this range of volume fractions, we can fit a straight line with a unitary power law of 1.0 ± 0.1. Here we see that lower volume fractions of monomers exhibit faster turn off from reaction- to diffusion-limited cluster aggregation i.e. the transition happens at lower reaction probabilities. This trend is to be expected, since at lower volume fractions, monomers are required to diffuse further before meeting another monomer and potentially aggregating, pushing the system towards the DLCA regime. Mirroring Fig. 3b, we can again see that the graph can be separated into regions, where above the dashed trend line, one would expect gelation mechanisms to happen in the DLCA regime and below it in the RLCA regime.
As an additional point of interest, another useful quantity for understanding the network structure at the percolation point is the cluster size distribution. We observe that this depends on the reaction probability and present an exemplar cumulative frequency plot of the cluster size distribution for a volume fraction of 6% and reaction probabilities of 100 and 0.2% in ESI,† Fig. S2. We find that a power law can be fitted to the mid-range cluster sizes of the R = 100% data, though further work would be required to systematically quantify changes to the cluster size distribution and its scaling.
To more closely examine the effect of monomer volume fraction on the percolation time, we next plotted this for each reaction probability in Fig. 4a. For this range of volume fractions, each reaction probability clearly exhibits a strong inverse linear trend in the percolation times with volume fraction. This is to be expected, with higher volume fractions of monomers increasing the frequency of interactions by proximity, leading to faster percolation of a network across the system box. We note also that as the reaction probability is increased, the plots shift towards faster percolation times, as expected, but also begin to converge, almost overlapping onto each other. This observation is indicative of reaction probabilities that are sufficiently high that the gelling systems are pushed into the DLCA regime – the percolation times have little dependence on the monomer–monomer reaction probability.49,75,76
From these results, we take the gradients for each reaction probability to analyse the rate of change in percolation times with monomer volume fraction in Fig. 4b. Interestingly, we see that this rate of decrease in percolation time with volume fraction increases with reaction probabilities (the gradients get steeper). This relationship itself fits an inverse power law, with an extracted exponent of 0.078 ± 0.004. We currently have no theoretical basis for this exponent and highlight this observation as a potential goal for future theory to derive and explain.
3.2 Fractal dimensions
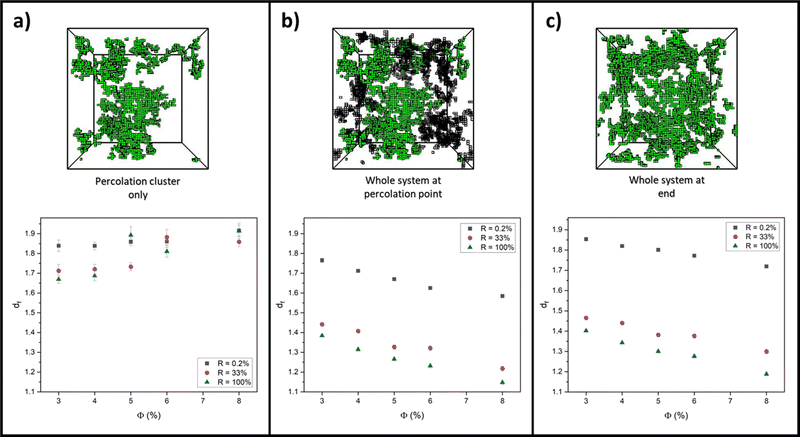
For each aggregation simulation run in Section 3.1, box-covering data of r versus O(r) was collected at the following three system structures and time points: the percolation cluster at the percolation point; the full system (percolation cluster and intermediate clusters) at the percolation point; and the whole system at the end, fully crosslinked state. From these data, extracted values for df were then plotted against monomer volume fraction for extreme values of R, 0.2% and 100%, to quantify how the network structure differs in the RLCA and DLCA regimes, respectively. Additionally, df was plotted for R = 33% to see if, as Fig. 3b (and c) predicts, the system has entered the DLCA regime for all volume fractions and therefore if the network structure starts to correlate with that at R = 100%. Each graph in Fig. 5 presents all these reaction probability results for (a) the percolation cluster, (b) the whole system at the percolation point and (c) the whole system on the final fully crosslinked states, alongside example simulation snapshots of the network structure for a system with ϕ = 3% and R = 33%.Looking at values for df on the whole system at the percolation point and at the end state in Fig. 5b and c, there is clearly a decrease with volume fraction in all cases. In previous studies, it is often suggested that, as very high monomer volume fractions are reached, the system becomes more densely packed, and so it is expected that the fractal dimension of the system would increase towards three.77–80 We believe that our opposite observation is due to our two-regime fit and fractal dimension extraction method of the box-covering data. As the volume fraction is increased, we observe that the crossover from the fine-scale fractal region of the data occurs at smaller lengthscales of r (see ESI†). As a result, the large-r regime, where O(r) scales as r−3, increasingly moves to lower r as ϕ increases, eventually covering the full range of r. Therefore the expected dimension of three is recovered for high volume fractions, not by a smooth increase in df, but rather by the crossover length moving to zero r and the fractal range being eliminated from the data.
We consider the varied state of the systems at the percolation point in Fig. 5b and c. At the beginning of all simulations, the system begins with the smallest objects being dispersed point particles (monomers) with fractal dimensions of zero. As the monomers aggregate into clusters over time, the fractal dimension of the system increases from zero. For systems at the higher monomer volume fractions, the critical percolation point is reached faster, and thus the measured df at this point will be lower. Further to this, we note that there is a sizeable contribution from smaller, non-percolating clusters at the percolation point which will also act to lower the overall fractal dimension of the whole system. For the lower monomer volume fractions, the system takes longer to percolate, by which point there are fewer of these non-percolating clusters, and thus the fractal dimension of the system is higher than that at the same monomer–monomer reaction probability but higher volume fractions. We also recognise our absolute values of df differ from those in the literature for similar models that were calculated without counting partial boxes as here, and fitted to using a different functional form. However, our discussion is based on observed trends rather than absolute values, and we expect these trends to hold independent of the measurement protocol.
Considering fractal dimensions for just the percolation cluster in Fig. 5a, there is no clear trend with monomer volume fraction for any reaction probability. However, it may be noted that overall, the values for df are higher than those observed for the whole system plots of Fig. 5b and c. If indeed, small clusters are responsible for decreasing the overall fractal dimensions observed when the whole system is considered, this may explain this observation.
Comparing values for df on the whole system at the percolation point and at the end state in Fig. 5b and c, it is clear to see that the RLCA regime of R = 0.2% yields higher fractal dimensions for all volume fractions, as would be expected for the dense clustering in RLCA.49,76,81,82 Quantifying this on the end states, we see that at 3% volume fraction, this increase in fractal dimension from R = 100% to R = 0.2% is measured as 0.45 ± 0.01, and this increase is marginally augmented as the volume fractions increase up to 0.53 ± 0.02 at 8% volume fraction. Further to this, we recognise the closeness in values for df between R = 33 and 100% in support of our prediction that R = 33% systems enter the DLCA regime and thus show similar structural characteristics to R = 100% systems.
Lastly, we recognise how similar the fractal dimensions are for all volume fractions and reaction probabilities when looking at the whole system at the percolation point and on the fully crosslinked state in Fig. 5b and c. Albeit the values being slightly lower at the percolation point, due to the contribution of non-percolating clusters, this trend indicates how the network structure at the percolation point largely governs the final network structure.83,84 This is regardless of the widely varying non-percolating cluster mass that is yet to add to the percolation cluster and is dependent on the monomer reaction probability and volume fraction.
3.3 Pore sizes in final network structure
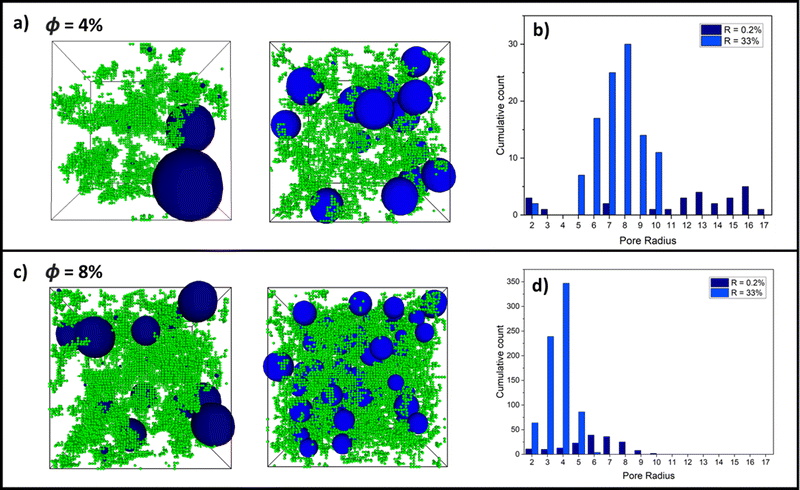
Building on the results thus far, Fig. 6 shows examples of largest pore distributions of (a) final-state 4% and (c) 8% volume fraction systems for an RLCA and DLCA system at R = 0.2% (left snapshots) and R = 33% (right snapshots), respectively. It can be seen immediately in (a) that the 0.2% RLCA gels have larger maximal pores than the DLCA counterparts for both volume fractions because of the dense clustering and corresponding vast inter-cluster spaces. Fig. 6b and d presents histograms of the largest pore size distributions for the 4% and 8% volume fraction systems, respectively. These clearly show how the DLCA regime reaction probability of 33% yields a distribution of largest pores at smaller radii than at RLCA at R = 0.2% where the distribution widens and shifts to larger radii. We note also that pore distributions for R = 100% are very similar to those at R = 33% for both volume fractions (refer to Fig. S1, ESI†), as we anticipated from the evidence thus far that monomer–monomer reaction probabilities between these values should produce gel structures in the DLCA regime. Moreover, it is clear that as the volume fraction is increased between Fig. 6b and d, the largest pore size distributions are shifted to smaller radii for both reaction probabilities, though the cumulative count of these distributions are increased around ten-fold. This is a logical observation, since increased monomer volume fractions would reduce the remaining intercluster space.4 Conclusions
Colloidal aggregation simulations were completed for a model of folded protein hydrogels at monomer volume fractions, ϕ, of 3, 4, 5, 6 and 8% and each at a wide range of monomer–monomer reaction probabilities, R, between 0.2 and 100%. From these simulations, we identify the critical point of gel percolation, explore the range of network regimes covering diffusion-limited to reaction-limited cluster aggregation network formation mechanisms and predict the final network structure, fractal dimensions and final gel porosity. The percolation time, τ, was captured for each R and ϕ. We reveal two distinct regions which are described by DLCA and RLCA and a crossover region between these cluster aggregation mechanisms as a function of ϕ. For each R, a clear inverse relation is observed in the percolation times with ϕ. We explore the structure of the protein networks in more detail by examining the fractal dimensions of the percolation cluster, the whole system at the percolation point and the whole system on the final fully crosslinked states and show how the final network structure is governed by the structure at the percolation point, regardless of the broad variation of non-percolating cluster masses observed across all systems. An analysis of the pore size distribution in the final network structures provides details of largest pore distributions at different reaction probabilities representative of RLCA and DLCA systems, revealing the RLCA gels have larger maximal pores than the DLCA counterparts for both volume fractions studied.This approach is important because it allows us to explore the wide design space of network formation in protein hydrogels. Such an approach, to explore reaction- and diffusion-limited cluster aggregation, has proved successful in other biological systems, including modelling bacteria to understand their morphology and behaviour and DNA–lipid complexes in gene delivery. This study on folded protein hydrogels sets the stage for future studies to exploit cluster aggregation to create more complex network architectures, including patterned systems,85–87 which might be explored in applications.
Whilst there is already some understanding of the effect of reaction rate and colloidal volume fraction on porosity of gels,88–91 what we present here is a general kinetic model and analysis tools which allow for accurate prediction of network structure and concurrent porosity from the initial selection of system parameters. Gel structures which yield percolating pore networks (e.g. low monomer volume fractions)90 are important for applications where diffusion through the gel is important, such as in drug delivery and nutrient accessibility for in cell-seeded gels.40,92–98 Pore size and distribution are important considerations in tissue engineering, for example where certain cell types need pores of particular sizes for effective growth and tissue regeneration.99,100 Being able to control and reproduce the properties of porous gel structure is important for regulating seeded cell properties and behaviour, including proliferation, migration, differentiation and phenotypic variation.92,93,101 The ability of our gelation model analyses to predict network structure and pore size distributions from the outset has apparent potential in designing and tuning gel properties for such applications. Furthermore, with additional parameterisation, we expect this model can be extended to describe a broader range of protein-based hydrogels.
Author contributions
All authors conceived the work. K. C. developed and completed the modelling with support from L. D. and D. H. and K. C. led writing of the paper with support from D. H. and L. D.Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. C. is supported by an Engineering and Physical Sciences Research Council (EPSRC) PhD studentship through the Soft Matter and Functional Interfaces Centre for Doctoral Training (SOFI CDT) (EP/L015536/1) and L. D. through an EPSRC fellowship (EP/P02288X/1) and ERC Consolidator Fellowship with UKRI guarantee (EP/X023524/1). This work was undertaken on ARC3, part of the High Performance Computing facilities at the University of Leeds, UK. The data set for Modelling Network Formation in Folded Protein Hydrogels by Cluster Aggregation Kinetics can be found here https://doi.org/10.5518/1323. We are grateful to Dr Ben Hanson for his useful discussions and considerable input in constructing the equation for finding fractal dimensions. Thanks to members of the Dougan group for helpful discussions, in particular Dr Matt Hughes. Thanks also to Dr Holly Linford for colour-editing the gel pore snapshots.Notes and references
- A. Ashfaq, K. Jahan, R. U. Islam and K. Younis, LWT, 2022, 154, 112667 CrossRef CAS.
- C. L. Kennedy, D. Sayasilpi, P. Schall and J. M. Meijer, J. Phys.: Condens. Matter, 2022, 34, 214005 CrossRef PubMed.
- R. Podgornik, H. H. Strey and V. A. Parsegian, Curr. Opin. Colloid Interface Sci., 1998, 3, 534–539 CrossRef CAS.
- H. Liang, D. Harries and G. C. Wong, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11173 CrossRef CAS PubMed.
- D. D. Lasic, Liposomes in Gene Delivery, CRC Press, 2019 Search PubMed.
- A. J. Maheshwari, A. M. Sunol, E. Gonzalez, D. Endy and R. N. Zia, Phys. Rev. Fluids, 2019, 4, 110506 CrossRef.
- T. Vissers, A. T. Brown, N. Koumakis, A. Dawson, M. Hermes, J. Schwarz-Linek, A. B. Schofield, J. M. French, V. Koutsos, J. Arlt, V. A. Martinez and W. C. Poon, Sci. Adv., 2018, 4, 1170 CrossRef PubMed.
- U. U. Ghosh, H. Ali, R. Ghosh and A. Kumar, J. Colloid Interface Sci., 2021, 594, 265–278 CrossRef CAS PubMed.
- S. Ikeda and K. Nishinari, Biomacromolecules, 2000, 1, 757–763 CrossRef CAS PubMed.
- F. Zhang, M. W. Skoda, R. M. Jacobs, R. A. Martin, C. M. Martin and F. Schreiber, J. Phys. Chem. B, 2007, 111, 251–259 CrossRef CAS PubMed.
- A. Stradner, H. Sedgwick, F. Cardinaux, W. C. Poon, S. U. Egelhaaf and P. Schurtenberger, Nature, 2004, 432, 492–495 CrossRef CAS PubMed.
- E. J. Yearley, I. E. Zarraga, S. J. Shire, T. M. Scherer, Y. Gokarn, N. J. Wagner and Y. Liu, Biophys. J., 2013, 105, 720–731 CrossRef CAS PubMed.
- A. Stradner and P. Schurtenberger, Soft Matter, 2020, 16, 307–323 RSC.
- L. Nicoud, M. Owczarz, P. Arosio and M. Morbidelli, Biotechnol. J., 2015, 10, 367–378 CrossRef CAS PubMed.
- H. P. Erickson, Biol. Proced. Online, 2009, 11, 32 CrossRef CAS PubMed.
- B. Jachimska, M. Wasilewska and Z. Adamczyk, Langmuir, 2008, 24, 6867–6872 CrossRef PubMed.
- R. Tuinier and A. Brûlet, Biomacromolecules, 2003, 4, 28–31 CrossRef CAS PubMed.
- C. Gögelein, G. Nägele, R. Tuinier, T. Gibaud, A. Stradner and P. Schurtenberger, J. Chem. Phys., 2008, 129, 085102 CrossRef PubMed.
- M. A. Woldeyes, C. Calero-Rubio, E. M. Furst and C. J. Roberts, J. Phys. Chem. B, 2017, 121, 4756–4767 CrossRef CAS PubMed.
- K. Baler, R. Michael, I. Szleifer and G. A. Ameer, Biomacromolecules, 2014, 15, 3625–3633 CrossRef CAS PubMed.
- R. L. Dimarco and S. C. Heilshorn, Adv. Mater., 2012, 24, 3923–3940 CrossRef CAS PubMed.
- X. Zhang, S. Jiang, T. Yan, X. Fan, F. Li, X. Yang, B. Ren, J. Xu and J. Liu, Soft Matter, 2019, 15, 7583–7589 RSC.
- Y. Sun and Y. Huang, J. Mater. Chem. B, 2016, 4, 2768–2775 RSC.
- C. Huerta-López and J. Alegre-Cebollada, Nanomaterials, 2021, 11, 1656 CrossRef PubMed.
- W. A. Petka, J. L. Harden, K. P. McGrath, D. Wirtz and D. A. Tirrell, Science, 1998, 281, 389–392 CrossRef CAS PubMed.
- H. Li, N. Kong, B. Laver and J. Liu, Small, 2016, 12, 973–987 CrossRef CAS PubMed.
- S. H. Arabi, B. Aghelnejad, C. Schwieger, A. Meister, A. Kerth and D. Hinderberger, Biomater. Sci., 2018, 6, 478–492 RSC.
- S. Khanna, A. K. Singh, S. P. Behera and S. Gupta, Mater. Sci. Eng., C, 2021, 119, 111590 CrossRef CAS PubMed.
- S. Ikeda and K. Nishinari, Biopolymers, 2001, 59, 87–102 CrossRef CAS PubMed.
- J. Fang, A. Mehlich, N. Koga, J. Huang, R. Koga, X. Gao, C. Hu, C. Jin, M. Rief, J. Kast, D. Baker and H. Li, Nat. Commun., 2013, 4, 2974 CrossRef PubMed.
- L. R. Khoury and I. Popa, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- M. D. Hughes, B. S. Hanson, S. Cussons, N. Mahmoudi, D. J. Brockwell and L. Dougan, ACS Nano, 2021, 15, 11296–11308 CrossRef CAS PubMed.
- K. Shmilovich and I. Popa, Phys. Rev. Lett., 2018, 121, 168101 CrossRef CAS PubMed.
- M. Djabourov, K. Nishinari and S. B. Ross-Murphy, Physical Gels Biol. Synth. Polym., 2013, 256–286 Search PubMed.
- A. H. Clark and S. B. Ross-Murphy, Mod. Biopolym. Sci., 2009, 1–27 CAS.
- A. P. Minton, Mol. Cell. Biochem., 1983, 55, 119–140 CrossRef CAS PubMed.
- P. S. Sarangapani, S. D. Hudson, R. L. Jones, J. F. Douglas and J. A. Pathak, Biophys. J., 2015, 108, 724–737 CrossRef CAS PubMed.
- S. Lv, T. Bu, J. Kayser, A. Bausch and H. Li, Acta Biomater., 2013, 9, 6481–6491 CrossRef CAS PubMed.
- M. D. G. Hughes, S. Cussons, N. Mahmoudi, D. J. Brockwell and L. Dougan, Soft Matter, 2020, 16, 6389–6399 RSC.
- Y. Tang, H. Wang, S. Liu, L. Pu, X. Hu, J. Ding, G. Xu, W. Xu, S. Xiang and Z. Yuan, Colloids Surf., B, 2022, 220, 112973 CrossRef CAS.
- H. Li, Adv. NanoBiomed Res., 2021, 1, 2100028 CrossRef CAS.
- B. S. Hanson and L. Dougan, Macromolecules, 2020, 53, 7335–7345 CrossRef CAS.
- L. Fu, A. Haage, N. Kong, G. Tanentzapf and H. Li, Chem. Commun., 2019, 55, 5235–5238 RSC.
- S. Haas, S. Körner, L. Zintel and J. Hubbuch, Front. Bioeng. Biotechnol., 2022, 10, 1006438 CrossRef PubMed.
- M. Slawinski, M. Kaeek, Y. Rajmiel and L. R. Khoury, Nano Lett., 2022, 22, 6942–6950 CrossRef CAS PubMed.
- T. Hoffmann, K. M. Tych, M. L. Hughes, D. J. Brockwell and L. Dougan, Phys. Chem. Chem. Phys., 2013, 15, 15767 RSC.
- C. Gögelein, G. Nägele, J. Buitenhuis, R. Tuinier and J. K. Dhont, J. Chem. Phys., 2009, 130, 1–15 CrossRef PubMed.
- Y. Liu and R. B. Pandey, J. Phys. II, 1994, 4, 865–872 CrossRef CAS.
- S. Jungblut, J.-O. Joswig and A. Eychmüller, Phys. Chem. Chem. Phys., 2019, 21, 5723–5729 RSC.
- P. Meakin, Phys. Scr., 1992, 46, 295–331 CrossRef CAS.
- W. C. Poon and M. D. Haw, Adv. Colloid Interface Sci., 1997, 73, 71–126 CrossRef CAS.
- D. W. Schaefer, MRS Bull., 1988, 13, 22–27 CrossRef CAS.
- L. F. Van Heijkamp, I. M. De Schepper, M. Strobl, R. Hans Tromp, J. R. Heringa and W. G. Bouwman, J. Phys. Chem. A, 2010, 114, 2412–2426 CrossRef CAS PubMed.
- T. van Vliet, in Hydrocolloids – Part 1, ed. K. Nishinari, Elsevier Science, 2000, pp. 367–377 Search PubMed.
- Y. Li, B. Xue and Y. Cao, ACS Macro Lett., 2020, 9, 512–524 CrossRef CAS PubMed.
- J. Opdam, V. F. Peters, H. H. Wensink and R. Tuinier, J. Phys. Chem. Lett., 2023, 14, 199–206 CrossRef CAS PubMed.
- M. P. Howard, Z. M. Sherman, A. N. Sreenivasan, S. A. Valenzuela, E. V. Anslyn, D. J. Milliron and T. M. Truskett, J. Chem. Phys., 2021, 154, 074901 CrossRef CAS PubMed.
- T. Kwon, T. A. Wilcoxson, D. J. Milliron and T. M. Truskett, J. Chem. Phys., 2022, 157, 184902 CrossRef CAS PubMed.
- A. Aufderhorst-Roberts, M. D. G. Hughes, A. Hare, D. A. Head, N. Kapur, D. J. Brockwell and L. Dougan, Biomacromolecules, 2020, 21, 4253–4260 CrossRef CAS PubMed.
- Á. Pérez-Benito, C. Huerta-López, J. Alegre-Cebollada, J. M. García-Aznar and S. Hervas-Raluy, J. Mech. Behav. Biomed. Mater., 2023, 138, 105661 CrossRef PubMed.
- M. Takahashi, K. Yokoyama and T. Masuda, J. Chem. Phys., 1994, 101, 798 CrossRef CAS.
- J. C. Gimel, D. Durand and T. Nicolai, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 11348–11357 CrossRef CAS PubMed.
- C. M. Sorensen, Aerosol Sci. Technol., 2011, 45, 765–779 CrossRef CAS.
- P. J. Flory, J. Am. Chem. Soc., 1941, 63, 3083–3090 CrossRef CAS.
- D. Stauffer, A. Aharony and A. Aharony, Introduction To Percolation Theory, Taylor & Francis, 2nd edn, 1994 Search PubMed.
- A. Bunde, P. Heitjans, S. Indris, J. W. Kantelhardt and M. Ulrich, Diffus. Fundamentals, 2007, 6, 1–17 Search PubMed.
- H. Tsurusawa, M. Leocmach, J. Russo and H. Tanaka, Sci. Adv., 2019, 5, 6090 CrossRef PubMed.
- A. Zaccone, H. H. Winter, M. Siebenbürger, M. Siebenb and M. Ballauff, J. Chem. Phys., 2014, 58, 1219–1244 CAS.
- F. Hausdorff, Math. Ann., 1918, 79, 157–179 CrossRef.
- A. S. Besicovitch, Math. Ann., 1935, 110, 321–330 CrossRef.
- G. B. So, H. R. So and G. G. Jin, Pattern Recognit. Lett., 2017, 98, 53–58 CrossRef.
- K. C. Clarke, Comput. Geosci., 1986, 12, 713–722 CrossRef.
- I. Pilgrim and R. P. Taylor, in Fractal Analysis of Time-Series Data Sets: Methods and Challenges, ed. S.-A. Ouadfeul, IntechOpen, Rijeka, 2019, ch. 2 Search PubMed.
- F. Arand and J. Hesser, Comput. Geosci., 2017, 101, 28–37 CrossRef.
- T. A. Witten and L. M. Sander, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 5686–5697 CrossRef.
- M. Kolb and R. Jullien, J. Phys., Lett., 1984, 45, 977–981 CrossRef CAS.
- A. Moncho-Jordá, G. Odriozola, F. Martínez-López, A. Schmitt and R. Hidalgo-Álvarez, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5, 471–480 CrossRef.
- M. Lattuada, H. Wu, A. Hasmy and M. Morbidelli, Langmuir, 2003, 19, 6312–6316 CrossRef CAS.
- S. C. Pencea and M. Dumitrascu, Fractal Aspects of Materials, Boston, Massachusetts, USA, 1995, p. 373 Search PubMed.
- A. Hasmy and R. Jullien, J. Non-Cryst. Solids, 1995, 186, 342–348 CrossRef CAS.
- M. Lach-hab, A. E. González and E. Blaisten-Barojas, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 5456–5462 CrossRef CAS PubMed.
- S. Lazzari, L. Nicoud, B. Jaquet, M. Lattuada and M. Morbidelli, Adv. Colloid Interface Sci., 2016, 235, 1–13 CrossRef CAS PubMed.
- J. E. Martin and D. Adolf, Annu. Rev. Phys. Chem., 1991, 42, 311–350 CrossRef CAS.
- M. Takahashi, K. Yokoyama, T. Masuda and T. Takigawa, J. Chem. Phys., 1998, 101, 798 CrossRef.
- P. Ball, Nat. Mater., 2022, 1 Search PubMed.
- C. T. van Campenhout, D. N. Ten Napel, M. van Hecke and W. L. Noorduin, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2123156119 CrossRef CAS PubMed.
- L. Würthner, F. Brauns, G. Pawlik, J. Halatek, J. Kerssemakers, C. Dekker and E. Frey, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2206888119 CrossRef PubMed.
- D. Ashkin, R. A. Haber and J. B. Wachtman, J. Am. Ceram. Soc., 1990, 73, 3376–3381 CrossRef CAS.
- L. D. Gelb, A. L. Graham, A. M. Mertz and P. H. Koenig, Phys. Fluids, 2019, 31, 21210 CrossRef.
- S. Babu, J. C. Gimel and T. Nicolai, J. Phys. Chem. B, 2008, 112, 743–748 CrossRef CAS PubMed.
- I. M. El-Sherbiny and M. H. Yacoub, Global Cardiol. Sci. Practice, 2013, 2013, 38 CrossRef PubMed.
- M. W. Tibbitt and K. S. Anseth, Biotechnol. Bioeng., 2009, 103, 655–663 CrossRef CAS PubMed.
- D. Fan, U. Staufer and A. Accardo, Bioengineering, 2019, 6, 113 CrossRef CAS PubMed.
- A. Upadhyay, R. Kandi and C. P. Rao, ACS Sustainable Chem. Eng., 2018, 6, 3321–3330 CrossRef CAS.
- R. Nandi, A. Yucknovsky, M. M. Mazo and N. Amdursky, J. Mater. Chem. B, 2020, 8, 6964–6974 RSC.
- Y. H. Chiang, M. J. Wu, W. C. Hsu and T. M. Hu, J. Mater. Chem. B, 2020, 8, 8830–8837 RSC.
- N. Sanaeifar, K. Mäder and D. Hinderberger, Pharmaceutics, 2021, 13, 1661 CrossRef CAS PubMed.
- N. Sanaeifar, K. Mäder and D. Hinderberger, Int. J. Mol. Sci., 2022, 23, 7352 CrossRef CAS PubMed.
- S. H. Oh, I. K. Park, J. M. Kim and J. H. Lee, Biomaterials, 2007, 28, 1664–1671 CrossRef CAS PubMed.
- S. Yang, K. F. Leong, Z. Du and C. K. Chua, Tissue Eng., 2001, 7, 679–689 CrossRef CAS PubMed.
- L. H. Y. Grace and T. Y. Wah, Effect of Collagen Gel Structure on Fibroblast Phenotype|Journal of Emerging Investigators, 2012, http://www.emerginginvestigators.org/2012/11/effect-of-collagen-gel-structure-on-fibroblast-phenotype/.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00111c |
| This journal is © The Royal Society of Chemistry 2023 |