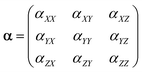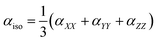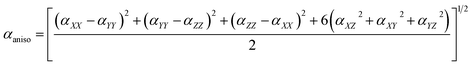Open Access Article
Open Access ArticleUnexpected polarization properties of sub-nanosized magnesium clusters†
Stanislav K. Ignatov *a and
Artëm E. Masunov
*a and
Artëm E. Masunov *bcd
*bcd
aLobachevsky State University of Nizhny Novgorod, Nizhny Novgorod 603950, Russia. E-mail: ignatov@ichem.unn.ru
bNanoScience Technology Center, University of Central Florida, Orlando, Florida 32826, USA
cSchool of Modeling, Simulations and Training, University of Central Florida, Orlando, Florida 32826, USA
dSouth Ural State University (National Research University), Chelyabinsk, Russia
First published on 27th January 2023
Abstract
The isotropic electrostatic polarizability (IEP) of sub-nanosized magnesium clusters Mg2–Mg32 was studied in an extensive set comprising 1237 structurally unique isomers. These isomers were found in the course of the global search for the potential energy surface minima of the magnesium clusters at the BP86/6-31G(d) level. The calculation of the polarizability at the same DFT level reveals an unexpected property of the IEP: the linear correlation between the polarizability of the most favorable isomers (and only them) and the cluster nuclearity n. Moreover, for each n, the most stable cluster isomer demonstrates nearly minimal IEP value among all found isomers of a given nuclearity. Surprisingly, these observed features are independent of the cluster structures which are quite different. We hypothesize that the energetic favorability of a cluster structure is related to their low polarizability. Apparently, the atoms forming the cluster tend to arrange themselves in such a way as to provide the most compact distribution of the cluster electron density. A possible explanation of the observed trends, their significance for cluster structure prediction, and the practical applications are discussed.
1 Introduction
Sub-nanosized metal clusters are polyatomic molecular systems of variable nuclearity (the number n of atoms in a cluster), filling the gap between atoms and nanoparticles. The clusters differ from the nanoparticles by a lower degree of crystalline ordering and greater structural diversity. The typical diameter of nanoclusters is of 0.2–2 nm which corresponds to the nuclearity up to 150–200 atoms. When the size increases, the crystalline domains appear in a particle which makes them similar to polycrystals, and the standard theoretical methods for the description crystalline structures can be applied to evaluation of various physical properties (see, e.g., ref. 1 where adsorption energy on Pt clusters approached its limiting values for crystal surface at n > 147). In contrast, the cluster structures at lower n (typically n = 2–150) are poorly predictable, both at the level of simple intuition, as well as using standard metallic potentials, designed to describe the bulk metal properties or the properties of metal surface. Among quantum chemical methods, only DFT approach is typically used for the efficient search for favorable structures of the clusters sized in tens of atoms. The same applies to the novel so-called “potentials of quantum accuracy” (GAP,2 SNAP,3 MTP,4 ACE5), which are usually calibrated by DFT results in a limited range of nuclearities. Thus, the most reliable method for the sub-nano cluster structure prediction remains the direct DFT global optimization. At the same time, the properties of sub-nanosized metallic particles, both mono- and polyatomic ones, are of great interest because they frequently manifest higher activity6,7 and selectivity8 in catalysis,9–11 can serve as the base elements for the modern and future nanoelectronic,12,13 or spintronic14,15 devices, or as a base for the novel nanodevices manifesting e.g., neuromorphic properties.16 For many applications, a fundamentally important issue is the possibility of size- and structure-selective synthesis of clusters, which is largely determined by the number and energy distribution of their structural isomers. Earlier, using magnesium clusters as an example, we demonstrated that the number of the cluster isomers for the given n, although is high and quickly grows with n, nevertheless remains much less than the number of mathematically predicted number of connected graphs of the same number of vertices.17 This fact allows one to explore the complete set of isomers at once (at least for some n), trying to search for the individual representatives with useful properties. In a recent study,18 we carried out such a search in the extended set of isomers of clusters Mg2–Mg32 comprising 1237 isomeric structures located in the direct DFT global optimization. The magnesium clusters are the convenient object for such studies because they are simple for DFT calculations, their ground state is a singlet spin state, and many of their properties have been published, both experimental19–23 and theoretical.24–27 In the study,18 we considered mostly energetic and structural properties, which allowed us to locate the most stable representatives, the energy distributions for a complete set of isomers as well as the distributions for separate nuclearities. The analysis of these distributions allowed to predict that the size- and shape-selected cluster synthesis can be feasible for some n, in particular, for n = 10 and 20. Also, some new tubular structures and the new dependences between the structural features of clusters were established. In the current study, we continue the investigation of the extended set of magnesium clusters, focusing now on their electric properties. Among these properties, we find that the extended set of isomers demonstrates quite unexpected feature of their isotropic electrostatic polarizability (IEP): IEP of the most favorable structures (and of only them) is linearly dependent on n. Even more surprising, these linearly dependent values are close in their magnitude to the minimum IEP values for the set of isomers with the given n. This property is rather unusual because the most favorable isomers typically have quite different geometries. Moreover, this property, if it will be common for other metals, can be extremely useful since it gives the estimate for how the random cluster structure is close to the global minimum, and could be used in cluster structure prediction. We also show that the connection between the polarizability and the DFT binding energy of a cluster cannot be simply derived from any known models of polarizability although some models reproduce its linear dependence (but do not “explain” it directly).Despite long and extensive research on the cluster structure and properties, the polarizability of sub-nanosized clusters in its connection with the cluster structure has not been sufficiently studied. For main group elements, most such studies are mainly focused on alkali metals (see, e.g. ref. 28 for review), silicon clusters,29–32 Ge2–Ge10 and GanAsm (n + m = 2–10),33 Cd2–Cd11 and CdnZnm (n + m = 4–6),34 Al3–Al31 (ref. 35 and 36) (see also review37 for Al, B, C and mixed clusters). Jellium-based models,28,38 DFT,29–32,35,36 high-level quantum chemistry theories MPn, CCSD and CCSD(T)34,39,40 as well as the machine learning methods41 have been applied to polarizability calculations. The relationship between polarizability and the size and shape of clusters has been investigated in many of the above studies.30,31,33,34,38 However, the conclusions drawn from these studies usually relate to general shape properties (e.g., elongation, sphericity or their size) or are made for a limited set of clusters located by global optimization29,31,35,36 or by random choice. In the present paper, we consider a much more extended set of magnesium cluster isomers for n = 2–32, analyzing all their structures found by global DFT optimization, and consider the DFT-calculated polarizability of each isomer in its relation to the energy relative to the most favorable structure.
The paper is organized as follows. In Section 2, we briefly describe the methodology of cluster generation and evaluation of their properties. In the beginning of Section 3, we describe the calculated cluster polarizability and observe its dependence on different structural properties. We also discuss here some principles and possible explanations of the found dependencies including the applications of some known models of molecular polarizability. The Section 4 contains a discussion of possible implications of the found trends and the directions that could be explored in order to rationalize the patterns found.
2 Calculation details
2.1 Set of isomeric structures
Structures of magnesium clusters Mg2–Mg32 used in the analysis were generated in the course of the direct DFT global optimization combined with graph generation algorithm and manual construction of the highly symmetric structures as was described in detail in ref. 17 and 18. In brief, the initial structures were generated from a complete set of connected graphs with n vertices as well as using the evolutionary algorithm combined with taboo-search to avoid the generation of similar structures. The geometries of generated structures were thoroughly optimized at the BP86/6-31G(d) DFT level with higher optimization criteria (Tight stopping criteria and UltraFine DFT grid implemented in Gaussian16 (ref. 42) program) and unique final structures were selected on the basis of two different algorithms of similarity evaluation in order to establish the unique isomers. Such a procedure continued until new unique structures ceased to appear. The Cartesian coordinates of 543 structures of Mg2–Mg13 located by this method were reported earlier in ESI† for ref. 17. In a course of this work, about 9000 optimizations were carried out and about 820![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points of potential energy surface (PES) were explored in total. All the located unique structures are the true local minima of PES as was proven by the frequency calculations at the same theory level. The remaining 694 structures of Mg14–Mg32 were located by the similar methodology, although without achieving the limit of all possible structures, with the DFT optimization using normal optimization criteria as described in ref. 18. Their Cartesian coordinates were published as ESI† for ref. 18.
000 points of potential energy surface (PES) were explored in total. All the located unique structures are the true local minima of PES as was proven by the frequency calculations at the same theory level. The remaining 694 structures of Mg14–Mg32 were located by the similar methodology, although without achieving the limit of all possible structures, with the DFT optimization using normal optimization criteria as described in ref. 18. Their Cartesian coordinates were published as ESI† for ref. 18.
2.2 DFT calculations
All energies, polarizabilities and other electronic properties were calculated at the BP86/6-31G(d) level of DFT theory, which was proven to be the best level of theory describing the results of combined CCSD//MP2/cc-pVTZ level of theory for Mg2–Mg7 clusters.43,44 Our previous evaluation of the performance of this DFT level for Mg10 cluster shows that this theory level agrees well with B3PW91/6-31G(d) results whereas PBE0/6-31G(d) results are somewhat worse.17 Also, comparison of BP86 results with the results of CCSD(T)/cc-pVQZ and MP2/cc-pVQZ shows that the bond lengths in small clusters Mg2–Mg4 are remarkably underestimated at the DFT level but improve as nuclearity increases. At the same time, this DFT level better reproduces the cluster binding energies of CCSD(T) than in the case of MP2. All calculations were carried out using the Gaussian16 (ref. 42) program.2.3 Calculation of electronic properties
For the complete set of 1237 structures of Mg2–Mg32 obtained as described above, the additional single point calculation was carried out at the BP86/6-31G(d) theory level with UltraFine DFT grid in order to calculate the MO vectors of Kohn–Sham orbitals, HOMO/LUMO energies, the electrostatic polarizabilities, and other electronic properties. The obtained MO vectors were then processed with ChargeMol program45,46 in order to calculate the Density Derived Electrostatic and Chemical (DDEC6) charges, bond orders, and the atom valences.46,47 Other electronic characteristics (Coulson's, Mayer's, Wiberg's bond orders, charges and valences) were extracted from the calculation log files or calculated on the basis of MO vectors. Additionally, the values of coordination numbers, HOMO and LUMO energies, cluster energies, and, in some cases, NBO parameters were extracted and analyzed. DDEC6 method used here is the relatively new method for the bond order evaluation46,47 which has significant advantages compared to the “classical” bond order descriptions including the Coulson's, Mayer's, Wiberg's, and NBO bond orders and charges. Namely, we found that it gives much more clear description of bonds between the Mg atoms. For example, the above-mentioned classic bond order evaluation schemes find the large number of bonds inside the clusters (virtually for all pairs of atoms) with close values of bond orders. At the same time, the DDEC6 bond orders are much more differentiated between near-by and far atoms which makes this method more convenient for analysis of the chemical bonding inside the metal clusters.2.4 Cluster energies
In the following, we use the per atom binding energy of cluster (also termed as a reduced cluster energy) defined as| Eb(n,m) = Etot(n,m)/n − Etot(1,1) |
| Erel(n,m) = Eb(n,m) − Eb(n,1), |
Electrostatic polarizability of an isolated atom is defined as a scalar coefficient α between the induced dipole moment p of an atom and the external weak electrostatic field inducing this moment: p = αE. This simplified finite field formula differs from the strict definition in terms of the field derivatives since we do not discuss here the nonlinear effects, which are not relevant to the purposes of the present study. In the case of polyatomic structure, the polarizability is a second rank tensor α with components
To avoid the dependence on coordinate framework, two quantities are usually introduced, isotropic polarizability αiso and polarizability anisotropy αaniso:
Polarizability tensor can be directly calculated within the DFT method for a molecular structure using many quantum-chemical programs. In these calculations, only the purely electronic polarizability is considered, without any contributions of orientational or ionic terms (no displacements of nuclei from their initial positions due to an external field were allowed).
3 Results and discussion
3.1 Dependence of cluster polarizability on n and m
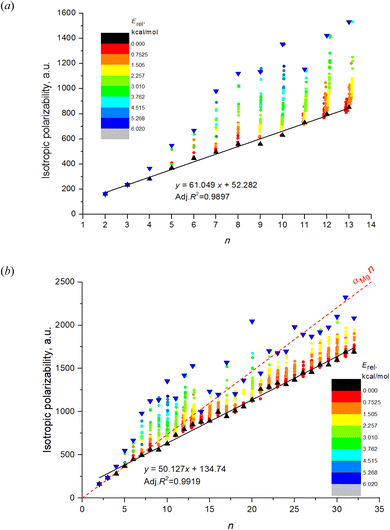
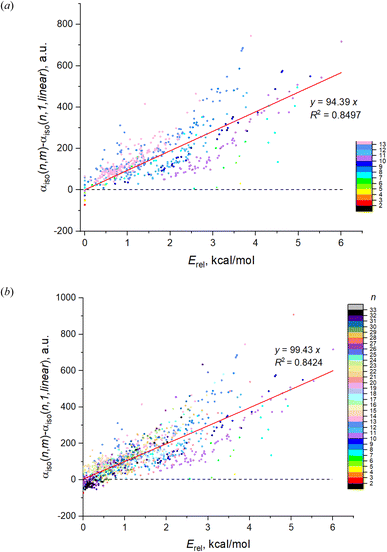
Fig. 1a shows the dependence on n and m of the calculated isotropic polarizability αiso for 543 isomers of Mg2–Mg13 which is the complete set of isomers found for these clusters by the method of the long-lasting structure generation and optimization. The black triangles mark the most favorable isomers, blue triangles – least favorable isomers of each nuclearity. Each point shows the data for an individual isomer, and the color scale indicates Erel in kcal mol−1.Striking feature of the presented plot is the linear dependence of αiso on n for the most favorable isomers. Moreover, the polarizabilities of the most favorable isomers are always close to the minimum value of αiso among all isomers for the given n. Although αiso(n,1) is the exact minimum value of polarizability not for all n, and some isomers with low Erel (red and orange colored) have the slightly lower values in the case of n = 11–13, the polarizability of the most favorable isomers has a clear tendency to be close to a minimum value. The polarizability of the most favorable isomers is perfectly described by the linear function with high determination coefficient of 0.9897, the equation is shown on the plot. Thus, we note two clear features of the αiso on n and m: (1) linearity of αiso(n,1) on n; and (2) minimality of αiso(n,1) among all m.
The same tendency is also clearly seen for the expanded set of 1237 cluster isomers of Mg2–Mg32, see Fig. 1b. In this case, the linearity is characterized by even higher determination coefficient of 0.9919, although the deviations of some points from linear function are remarkable. The minimality of αiso(n,1) is also not so perfect as for Mg2–Mg13, and multiple deviations from this trend is noticeable. Nevertheless, both trends above are clearly manifested for the expanded set of isomers as well. It should also be noted that both plots demonstrate the clear (although not perfect) tendency of the isomers with m > 1 to have the increased polarizability depending on their relative energies (isomers with higher Erel tend to have higher polarizability) as is seen on the base of datapoint color changes in Fig. 1. The additional statistical parameters of the linear regression model describing the complete set of isomers are given in Table 1, the column “DFT results”.
| Model parametersa | DFT results | Induced dipole models X | ||||
|---|---|---|---|---|---|---|
| AM | TL | TE | RP | GD | ||
| a Description: asmear is smearing parameter value adjusted for the best fit between DFT and models with smearing; RMSD is root means squared deviations between αiso(n,m)X and αiso(n,m)DFT after fitting for all 1237 isomers of Mg2–Mg32; negative αiso is number of negative αiso (non-physical results) among all 1237 isomers; Sa, Sb are standard deviations for slope and intercept in (1); R2, Adj. R2 are determination coefficients; SSE is sum of squared deviations of αiso(n,1) from (1); SE is standard deviation of regression model (SSE/(N − 2))1/2. | ||||||
| Fitting results of αiso(n,m)X against αiso(n,m)DFT | ||||||
| Adjusted asmear | — | — | 6.3517 | 1.6366 | 1.0910 | 1.0416 |
| Final RMSD | — | 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 267 267 |
138.06 | 140.44 | 43.45 | 48.86 |
| Negative αiso | 0 | 263 | 0 | 0 | 0 | 0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Parameters of linear regression (1) for αiso(n,1) estimated with DFT and fitted models | ||||||
| Slope of (1) | 50.12 | 123.13 | 55.75 | 56.40 | 50.16 | 49.44 |
| Intercept of (1) | 134.74 | 210.46 | 95.36 | 82.01 | 104.37 | 111.51 |
| Sa | 0.83 | 24.52 | 0.55 | 0.42 | 0.57 | 0.65 |
| Sb | 15.85 | 471.09 | 10.60 | 8.14 | 10.94 | 12.53 |
| R2 | 0.9922 | 0.4650 | 0.9972 | 0.9984 | 0.9963 | 0.9950 |
| Adj. R2 | 0.9919 | 0.4466 | 0.9971 | 0.9983 | 0.9962 | 0.9948 |
| SSE·10−4 | 4.90 | 4325.52 | 2.19 | 1.29 | 2.33 | 3.06 |
| SE | 41.10 | 1221.29 | 27.48 | 21.09 | 28.35 | 32.50 |
The red dashed line on Fig. 1b shows the “idealized” polarizability of non-interacting atoms, which is the simple sum of the individual atomic polarizability, i.e. nα, where α = αiso(1,1) is the polarizability of single Mg atom (73.5 a.u. at BP86/6-31G(d) level of DFT). One can see that this polarizability is higher than αiso(n,1) for n > 6 and practically coincide with it for n = 2–6.
Noting αiso(n,1) is linear relatively to the cluster nuclearity,
| αiso(n,1) = an + b, | (1) |
 | ||
| Fig. 2 Dependence of the IEP deviation from linear function (1) αiso(n,m) − (an + b) on relative energies of cluster isomers. (a) For 543 isomers of Mg2–Mg13; (b) for 1237 isomers of Mg2–Mg32. Black triangles represent the most energetically favorable isomers, blue triangles represent the least favorable isomers. Color scale designates the cluster nuclearity n. | ||
Combining expressions on Fig. 1 and 2, one can derive the more general dependence for the IEP as
| αiso(n,m) = an + b + cErel(n,m), | (2) |
It is also instructive to consider the deviation of the calculated IEP from the “ideal” IEP values for non-interacting atoms nα. In Fig. 3, the ratio f = αiso(n,m)/(nα) (frequently referred as an enhancement factor) on the relative energy of isomers Erel(n,m) is shown for n = 2–32, the color scale designates n. On this plot, the leftmost data points (with Erel = 0) correspond to the most favorable isomers, the remaining points demonstrates the dependence of polarizability on m. Although it is hard to carry out the exact regression analysis for all points, it is seen that this dependence is close to quadratic f ∼ Erel2, with clear dependence of f on n.
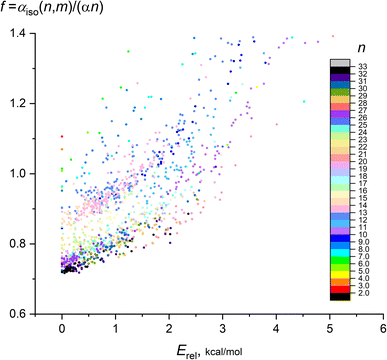 | ||
| Fig. 3 Dependence of enhancement factor f on the isomer relative energy for 1237 isomers of Mg2–Mg32. Color scale designates the cluster nuclearity n. | ||
In contrast with IEP, no similar tendencies were found for the polarizability anisotropy αaniso.
3.2 Principle of maximum tightness
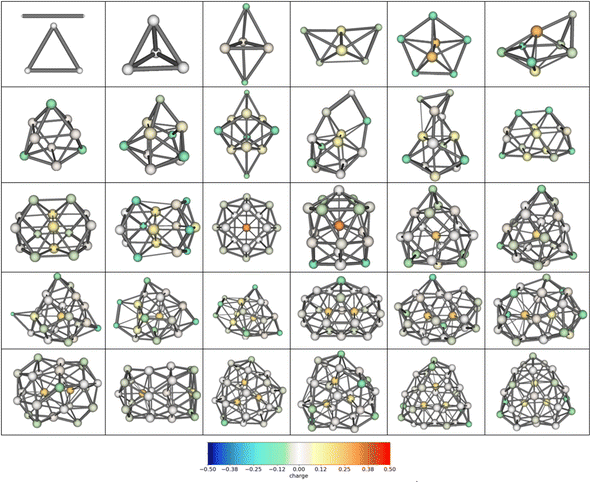
Two established features of αiso(n,1) (linearity and minimality) are rather surprising taking into account that the isomers structures are quite different in their geometry. For example, the most favorable isomers of Mg2–Mg32 are shown in Fig. 4, and the isomers m = 1–48 of Mg10 are shown in Fig. 5. As is seen from the figures, the cluster structures have quite different structural elements including tetrahedral, bipyramidal, decahedral, tubular motives, or highly amorphized fragments. They are quite diverse both among isomers with different n and different m. Thus, the observed features of polarizability unite the clusters of different structure and energy. This allows hypothesizing that some common principle controls the formation of cluster structures. Namely, the structure of a cluster is determined by such a mutual adjustment of the electronic and nuclear subsystems that ensures the maximum stability of the electron shell of the molecule with respect to external polarization. In other words, in order to ensure the most favorable nuclear configuration of the cluster, the nuclei of atoms occupy such positions as to ensure the maximum “rigidity” (“tightness” or “compactness”) of the electron shell.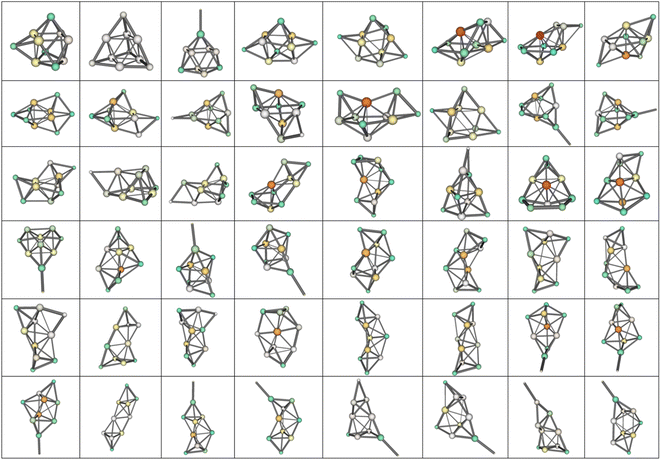 | ||
| Fig. 5 48 low-lying isomers of Mg10. m increases from left to right, by rows from up to down, the most favorable isomer is the upper-left one. | ||
The preceding allows us to formulate (at least for sub-nanoscale magnesium clusters) a “principle of maximum tightness of electronic shell” (PMT): the most energetically favorable cluster structure has the electronic shell, polarizability of which is close to the minimum and depends linearly on the number of atoms.
This principle is not absolutely strict, as is seen from the deviations of individual polarizability from the linear function, and also from the non-perfect minimality of αiso(n,1) in the case of some n. However, the repeatability of the observed trends for broad range of n cannot be occasional. It is also interesting question for further studies, whether these trends will take place for other metals and how common this principle for polyelemental clusters and molecules.
The formulated principle has very important implications. First, it allows one to specify the most favorable isomers among arbitrary structures without calculating the energy, only on the basis of their polarizabilities. This is not so important for quantum-chemical calculations, because the computational costs for the energy calculation are lower than for the calculation of polarizability. However, if one has any simplified scheme for the polarizability estimation, this can be important in a practice. Now, such simplified approximate calculations of polarizabilities are broadly used for the development of polarizable force fields for molecular dynamics (e.g. AMOEBA+,48,49 AMBER,50,51 GEM,52,53 X-Pol54 and others). Thus, if there is a way to quickly estimate αiso, one can search for the global minimum without a quantum calculation at all, at least obtaining the good initial structures for the further DFT optimization. Second, it is extremely useful that this principle allows us to specify whether the given structure is close to the global minimum. The problem of modern global optimization algorithms is that the location of a new favorable structure does not guarantee that the global minimum is located and there are no any rules indicating that we should stop the explorations of structures. On the basis of the formulated principle, we can feel certain that if αiso of a cluster is close to the known linear dependence on n, then this structure is close to the global minimum.
3.3 Predictive power of PMT
The assumptions made above on the possibility of using PMT can be directly verified on the basis of test calculations. Here, we present the preliminary results for only single example; the thorough examination will be given elsewhere. To test the predictive ability, we made a search for the global PES minima of the Mg35 cluster using the method of effective interatomic potential MTP4,55 trained on the cluster structures of Mg25–Mg32 (taken from previous DFT calculations). All calculations with MTP potential were carried out with the MLIP-2 program,56 the trained MTP potential parameters (file in the format of MLIP-2) can be obtained from authors on request. The structure of global minimum for the cluster Mg35 located with the trained MTP potential is shown in Fig. S1 of ESI.† On the basis of eqn (1) and the corresponding statistical parameters of regression from Table 1, we predict that αiso(35,1) has the value of (1889 ± 41) a.u. with the confidence interval indicated as the regression standard deviation of αiso(n,1) (SE in Table 1, column “DFT results”). Using the trained MTP potential, we optimized 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random structures of Mg35, and carried out the DFT calculations of IEP for the most favorable structure. Its αiso is equal to 1857 a.u., only 32 a.u. lower than the predicted value, and within the above confidence interval. Although the test performed for only single nuclearity is not reliable enough, and further analysis should be carried out in further studies, the obtained results demonstrate that the predicted values is not restricted by the ranges of n studied here and can be used for the extrapolation.
000 random structures of Mg35, and carried out the DFT calculations of IEP for the most favorable structure. Its αiso is equal to 1857 a.u., only 32 a.u. lower than the predicted value, and within the above confidence interval. Although the test performed for only single nuclearity is not reliable enough, and further analysis should be carried out in further studies, the obtained results demonstrate that the predicted values is not restricted by the ranges of n studied here and can be used for the extrapolation.
3.4 Possible explanations for established features
The above unusual features of IEP raise a question on the possible origin and explanation of these regularities. It should be noted that some dependences of electrostatic polarizabilities of the nanoparticles (NPs) of increasing size is known in the field of nanoscience. Namely, Kim et al.57–59 reported a thorough analysis of NPs polarizability (αNP) and the enhancement factor f = αNP/(nα) for model NPs of different shapes when their size grows (typically up to 103–104 “atoms” or “molecules” forming the NP). It was established that in some ranges of n, the f values slowly grow and converges to a limiting value. In the region of small n and for some simple shapes of NPs, this growth can be considered as an approximate linear. It was also found that the IEP for some symmetric NP shapes, namely, cubic and spherical NPs has the f values linear in a broad range of n. This allows to assume that the linearity of IEP in magnesium clusters can be connected to the more spherical shape of the most favorable structures. Indeed, it was established previously18 that the Erel isomers of 1237 clusters of Mg2–Mg32 decreases linearly when the deformation parameter DP = 2P3/(P1 + P2) (where P1 > P2 > P3 are the principal moments of inertia of the cluster) goes to 1 which means that the spherical structures are more energetically favorable. However, this tendency is quite fuzzy, with low regression coefficient and large deviations from the linearity as it is seen on Fig. 11 of ref. 18. The Fig. S2 of ESI† shows the plot of αiso(n,m) values versa the DP of 1237 structures of Mg2–Mg32. It is seen, that there is no any mutual dependence of these parameters, not for most favorable isomers, nor for all clusters. Thus, the sphericity of isomers has no visible influence on IEP and cannot explain their features described above.The polarizability of NPs is frequently described in the well-known induced dipole approximation pioneered by Applequist.60 This approximation proposes that the external electric field E0 induces the dipoles pj (j = 1, 2, …, n) located on the atomic centers of NP, and the induced atomic dipoles induce the additional field which modifies the dipoles of other atoms. The combined external and dipole field on the center i (i = 1, 2, …, n) is described by the formula:
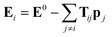 | (3) |
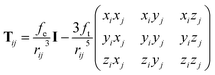 | (4) |
In the case of point dipoles (frequently referred to as point dipole model of Applequist), the coefficients fe = ft = 1. Combining the above formulas, the self-consistent induced atomic dipoles can be expressed as
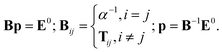 | (5) |
The complete polarizability of a structure is 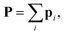 and, thus, the polarizability of the system of the atomic dipoles is expressed with
and, thus, the polarizability of the system of the atomic dipoles is expressed with
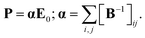 | (6) |
It was well-recognized61,62 that the description based on the formulas (3)–(6) suffer on so-called “polarization catastrophe” when the polarizability become infinite at some atomic arrangements. The solution of this problem was given for the first time by Thole61,62 who proposed to replace the point dipoles by some charge distributions smeared around the atomic centers. Following this idea, several distribution models were proposed including the Thole's linear and exponential charge distributions,61,62 Ren and Ponder (AMOEBA FF) model,63,64 or Gaussian smearing.65–69 All these models can be described by the same expression (3) with different fe and ft. (see e.g. ref. 66 for details). In all these modified dipole models, two adjustable parameters are used: the charge smearing parameter asmear (coefficient present in the expressions for fe and ft, dependent on the model in use), and the atomic polarizability α.
We applied five above-mentioned models for the description of cluster polarizability using the DFT-optimized structures and energies of clusters. Namely, the Applequist model (AM), Thole linear model (TL), Thole exponential model (TE), Ren and Ponder model (RP), and Gaussian-distributed dipoles (GD) were explored. In these models, instead of using the adjustable value of α, we used the fixed Mg atom polarizability calculated by DFT. Making adjustment of asmear during the fitting of the αiso(n,m) values calculated by formulas (3) against the corresponding DFT values, we obtain rather good coincidence between the DFT values of IEP, αiso(DFT), and approximate values αiso calculated in the point dipole model, αiso(AM), Thole's linear and exponential models αiso(TL) and αiso(TE), Ren and Ponder model αiso(RP) and model of Gaussian dipoles αiso(GD).
The root-mean-square deviations (RMSD) between the fitted αiso and the DFT values, and the regression coefficients of αiso(n,1) with corresponding statistics obtained with these models are shown in Table 1 (columns “induced dipole models”). As is evident from the table, the point dipole model of Applequist only poorly describes the DFT values both due to the large RMSD and poor linear dependence of αiso(n,1). They also give the negative values of αiso in many cases which is a non-physical result. At the same time, all the models of smeared dipoles well reproduce the DFT results, with best results achieved for RP and GD models, without any negative values of IEP. The dependence of αiso on n and m estimated in these models are shown in Fig. 6.
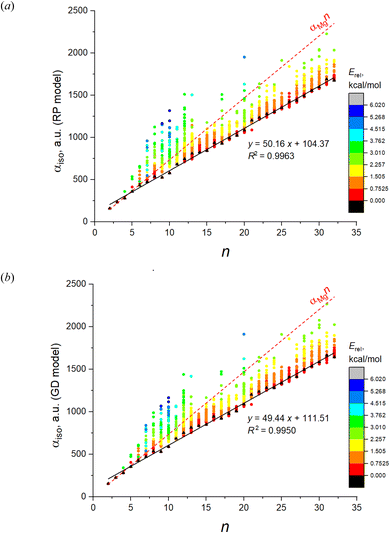 | ||
| Fig. 6 IEP of 1237 isomers of Mg2–Mg32 estimated in two models of induced dipoles: (a) RP model; (b) GD model. Color designates the relative energies of clusters calculated at the DFT level. | ||
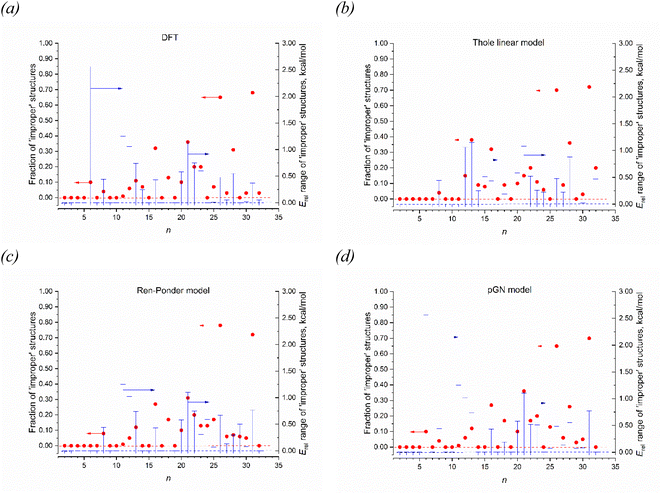
Among these models, the best fitted RMSD value for all 1237 IEP datapoints are achieved for the RP model. All models reproduce well the linearity of αiso(n,1), as it can be concluded from the corresponding values of R2, SSE and SE. It is interesting that the linearity of αiso(n,1) is even better reproduced by some models than it takes place at the DFT level. The highest αiso(n,1) linearity is achieved by the TE model although both Thole's models give rather poor RMSD values for the complete set of isomers. From this point view, the RP and GD models give better IEP estimates for the magnesium clusters. It is also worthwhile to investigate how these models reproduce the feature of minimality of αiso. This comparison is shown in Fig. 7 where two parameters are analyzed: the number of “improper” values of αiso(n,m) (i.e. the values which are less than αiso(n,1)) and the Erel energy interval where the clusters with “improper” αiso are situated. This interval shows how important the deviation from the minimality property in these models. Analyzing the data on Fig. 7, we conclude that the GD model is somewhat better reproduce these properties of DFT, because its patterns of both analyzed values are more similar to DFT than it takes place for RP and Tholes' models. It is also worthwhile to mention that the GD model, like in the case of DFT, gives the small range of Erel values (less than ∼1 kcal mol−1) for all improper clusters except n = 6 which allows concluding that the PMT principle is reproduces with a good accuracy.
The success of description of αiso with such simple models encourages describing the PMT principle on this basis. However, the strong obstacle on this way is that the Erel values analyzed on Fig. 7 are the DFT calculated values. All the attempts to reproduce the minimality feature of IEP using the energies calculated on the basis of dipole models were unsuccessful. Namely, Fig. S3 of ESI† demonstrates comparison between the isomers' energies calculated by DFT and their electrostatic energy components within the GD model for 1237 cluster isomers Mg2–Mg32. The figure shows the various combinations of monopole–monopole U00, monopole–dipole U01, dipole–dipole U11 energy contributions, and the self-energy of induced dipoles Uss calculated by the formulas of GD model as reported in ref. 68. Figure demonstrates the lack of correlation between the isomers' relative energies Erel calculated by DFT and Erel estimated on the basis of any GD model energy components or their combinations. In the case of perfect correlation, we expect the linear dependence close to the bisector of the first quadrant. However, as is seen from the plots, the calculated energy patterns are absolutely different from the energy dependencies obtained in the DFT calculations. We failed to find any combinations of electrostatic energies obtained within the induced dipole model as well as with additional energy contributions of the interacting atomic point charges (both nuclear and DDEC6 derived) which could reproduce the energy dependence similar to the DFT energies. Thus, the dipole models, although reproduce the linearity property, do not reproduce the property of minimality. Moreover, reproducing the linearity of clusters IEP, these models have no direct “explanation” of this feature. It is not clear why some structure has such a linear dependence of αiso whereas other ones do not. Obviously that these features are connected to any deeper regularities in the Kohn–Sham (or Schrödinger) equations describing this chemical system, and further studies are needed to elucidate these regularities.
4 Concluding remarks
We calculated the electrostatic polarizability of large set of sub-nanoscale magnesium clusters comprising 1237 structurally unique isomers. The polarizability calculation reveals that the IEP of the most favorable isomers on the cluster nuclearity n is linear with a high correlation coefficient, and its value for each n is close to the minimum value among all found isomers of a given nuclearity. These features are quite unusual, given that the cluster structures that exhibit these properties are very different. This suggests that the favorability of the cluster structure is closely related to their polarizability and, possibly, the atoms forming the cluster tend to arrange themselves in such a way as to provide the most dense or compact packing of the electron density. At present, it is not clear how general this property is, and additional studies are required to establish whether this property is fulfilled in clusters of other metals, as well as in clusters of a more complex elemental composition. If it turns out that these properties manifest themselves in a wide range of systems, this will open up opportunities for developing new methods for predicting the structure of polyatomic nanostructures and searching for global minima of sub-nanoparticles, an issue that currently causes considerable difficulty in solving. Additional studies are also required to clarify the nature of the observed patterns. It would be also instructive to explore the frequency dependence of IEP which can be linked to the experimental measurements at different wavelengths and described within the models explicitly accounting the field fluctuation frequency. We have shown that the property of linearity is reproduced at the level of simple induced dipole approximation. However, these facts do not allow us to reveal the true reason for the property of energy minimality of the least polarizable systems. We should also note that, at the moment, the dipole approximation does not elucidate the origin of linearity directly, it only reproduces it. Thus, the nature of the established features remains intriguing question of modern chemical physics.Data availability
The data that support the findings of this study are available within the article and its ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant Number ACI-1548562. The authors acknowledge the use of the following resources that have contributed to the research results reported within this paper: Stampede2 facility of the Texas Advanced Computing Center (TACC) at The University of Texas at Austin (https://www.tacc.utexas.edu). S. K. I. acknowledges the support of Russian Foundation for Basic Research (Project No. 20-03-00282). Authors thanks Ilya S. Steshin for his assistance in the visualization of the cluster structures.References
- L. Li, A. H. Larsen, N. A. Romero, V. A. Morozov, C. Glinsvad, F. Abild-Pedersen, J. Greeley, K. W. Jacobsen and J. K. Nørskov, J. Phys. Chem. Lett., 2013, 4, 222–226 CrossRef CAS PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles and G. J. Tucker, J. Comput. Phys., 2015, 285, 316–330 CrossRef CAS.
- A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef.
- R. Drautz, Phys. Rev. B, 2019, 99, 014104 CrossRef CAS.
- A. Corma, P. Concepción, M. Boronat, M. J. Sabater, J. Navas, M. J. Yacaman, E. Larios, A. Posadas, M. A. López-Quintela, D. Buceta, E. Mendoza, G. Guilera and A. Mayoral, Nat. Chem., 2013, 5, 775–781 CrossRef CAS PubMed.
- Y. Liu, H. Tsunoyama, T. Akita, S. Xie and T. Tsukuda, ACS Catal., 2011, 1, 2–6 CrossRef CAS.
- Y. Tan, X. Y. Liu, L. Zhang, A. Wang, L. Li, X. Pan, S. Miao, M. Haruta, H. Wei, H. Wang, F. Wang, X. Wang and T. Zhang, Angew. Chem., Int. Ed., 2017, 56, 2709–2713 CrossRef CAS PubMed.
- M. Haruta, S. Tsubota, T. Kobayashi, H. Kageyama, M. J. Genet and B. Delmon, J. Catal., 1993, 144, 175–192 CrossRef CAS.
- T. Akita, Y. Maeda and M. Kohiama, J. Catal., 2015, 324, 127–132 CrossRef CAS.
- T. Imaoka, Y. Akanuma, N. Haruta, S. Tsuchiya, K. Ishihara, T. Okayasu, W.-J. Chun, M. Takahashi and K. Yamamoto, Nat. Commun., 2017, 8, 688 CrossRef PubMed.
- J. P. Wilcoxon and B. L. Abrams, Chem. Soc. Rev., 2006, 35, 1162–1194 RSC.
- K. Rajput, B. R. Mehta, U. Kleinekathöfer, T. Frauenheim and D. R. Roy, Mater. Today Chem., 2022, 23, 100751 CrossRef CAS.
- A. Hirohata and K. Takanashi, J. Phys. D: Appl. Phys., 2014, 47, 193001 CrossRef.
- A. Hirohata, K. Yamada, Y. Nakatani, L. Prejbeanu, B. Diény, P. Pirro and B. Hillebrands, J. Magn. Magn. Mater., 2020, 509, 166711 CrossRef CAS.
- L. A. Savintseva, A. A. Avdoshin and S. K. Ignatov, Russ. J. Phys. Chem. B, 2022, 16, 445–454 CrossRef CAS.
- S. K. Ignatov, S. N. Belyaev, S. V. Panteleev and A. E. Masunov, J. Phys. Chem. A, 2021, 125, 6543–6555 CrossRef CAS PubMed.
- S. V. Panteleev, S. K. Ignatov, S. N. Belyaev, A. G. Razuvaev and A. E. Masunov, J. Cluster Sci., 2022 DOI:10.1007/s10876-022-02291-w.
- T. Diederich, T. Döppner, T. Fennel, J. Tiggesbäumker and K. H. Meiwes-Broer, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 023203 CrossRef.
- A. Kaufmann, A. Kornath, A. Zoermer and R. Ludwig, Inorg. Chem., 2010, 49, 3851–3856 CrossRef CAS PubMed.
- L. Kazak, K.-H. Meiwes-Broer and J. Tiggesbäumker, Phys. Chem. Chem. Phys., 2022, 24, 23350–23356 RSC.
- O. C. Thomas, W. Zheng, S. Xu and K. H. Bowen, Phys. Rev. Lett., 2002, 89, 213403 CrossRef PubMed.
- T. Diederich, T. Döppner, J. Braune, J. Tiggesbäumker and K.-H. Meiwes-Broer, Phys. Rev. Lett., 2001, 86, 4807–4810 CrossRef CAS PubMed.
- A. Köhn, F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2001, 3, 711–719 RSC.
- J. Jellinek and P. H. Acioli, J. Phys. Chem. A, 2003, 107, 1670 CrossRef CAS.
- A. Lyalin, I. A. Solov'yov, A. V. Solov'yov and W. Greiner, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 67, 063203 CrossRef.
- J. Akola, K. Rytkönen and M. Manninen, Eur. Phys. J. D, 2001, 16, 21–24 CrossRef CAS.
- W. A. de Heer, Rev. Mod. Phys., 1993, 65, 611–676 CrossRef CAS.
- K. Jackson, M. Pederson, C.-Z. Wang and K.-M. Ho, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 3685–3689 CrossRef CAS.
- K. Deng, J. Yang and C. T. Chan, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 61, 025201 CrossRef.
- V. c. E. Bazterra, M. a. C. Caputo, M. B. Ferraro and P. Fuentealba, J. Chem. Phys., 2002, 117, 11158–11165 CrossRef CAS.
- K. A. Jackson, M. Yang, I. Chaudhuri and T. Frauenheim, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 033205 CrossRef.
- I. Vasiliev, S. Öğüt and J. R. Chelikowsky, Phys. Rev. Lett., 1997, 78, 4805–4808 CrossRef CAS.
- M. G. Papadopoulos, H. Reis, A. Avramopoulos, Ş. Erkoç and L. Amirouche§, Mol. Phys., 2006, 104, 2027–2036 CrossRef CAS.
- M. Alipour and A. Mohajeri, J. Phys. Chem. A, 2010, 114, 12709–12715 CrossRef CAS PubMed.
- L.-P. Tan, D. Die and B.-X. Zheng, Spectrochim. Acta, Part A, 2022, 267, 120545 CrossRef CAS PubMed.
- A. S. Sharipov and B. I. Loukhovitski, Struct. Chem., 2019, 30, 2057–2084 CrossRef CAS.
- S. P. Apell, J. R. Sabin, S. B. Trickey and J. Oddershede, Int. J. Quantum Chem., 2002, 86, 35–39 CrossRef CAS.
- G. Maroulis, D. Begué and C. Pouchan, J. Chem. Phys., 2003, 119, 794–797 CrossRef CAS.
- G. Maroulis and C. Pouchan, Phys. Chem. Chem. Phys., 2003, 5, 1992–1995 RSC.
- M. G. Zauchner, S. Dal Forno, G. Cśanyi, A. Horsfield and J. Lischner, Mach. Learn.: Sci. Technol., 2021, 2, 045029 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- K. Duanmu, J. Friedrich and D. G. Truhlar, J. Phys. Chem. C, 2016, 120, 26110–26118 CrossRef CAS.
- K. Duanmu, O. Roberto-Neto, F. B. C. Machado, J. A. Hansen, J. Shen, P. Piecuch and D. G. Truhlar, J. Phys. Chem. C, 2016, 120, 13275–13286 CrossRef CAS.
- N. G. Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747 RSC.
- T. A. Manz, RSC Adv., 2017, 7, 45552–45581 RSC.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- C. Liu, J.-P. Piquemal and P. Ren, J. Phys. Chem. Lett., 2020, 11, 419–426 CrossRef CAS PubMed.
- C. Liu, J.-P. Piquemal and P. Ren, J. Chem. Theory Comput., 2019, 15, 4122–4139 CrossRef CAS PubMed.
- A. Toukmaji, C. Sagui, J. Board and T. Darden, J. Chem. Phys., 2000, 113, 10913–10927 CrossRef CAS.
- C. Sagui, L. G. Pedersen and T. A. Darden, J. Chem. Phys., 2004, 120, 73–87 CrossRef CAS PubMed.
- J.-P. Piquemal, G. A. Cisneros, P. Reinhardt, N. Gresh and T. A. Darden, J. Chem. Phys., 2006, 124, 104101 CrossRef PubMed.
- G. A. Cisneros, J.-P. Piquemal and T. A. Darden, J. Chem. Phys., 2006, 125, 184101 CrossRef PubMed.
- J. Gao, D. G. Truhlar, Y. Wang, M. J. M. Mazack, P. Löffler, M. R. Provorse and P. Rehak, Acc. Chem. Res., 2014, 47, 2837–2845 CrossRef CAS PubMed.
- E. V. Podryabinkin and A. V. Shapeev, Comput. Mater. Sci., 2017, 140, 171–180 CrossRef CAS.
- I. S. Novikov, K. Gubaev, E. V. Podryabinkin and A. V. Shapeev, Mach. Learn.: Sci. Technol., 2021, 2, 025002 Search PubMed.
- H.-Y. Kim, J. O. Sofo, D. Velegol, M. W. Cole and G. Mukhopadhyay, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 053201 CrossRef.
- J.-H. Kim, S.-H. Cha, S.-H. Kang, Y. Park and S. Cho, Int. J. Mech. Mater. Des., 2020, 16, 475–486 CrossRef CAS.
- H.-Y. Kim and P. R. C. Kent, J. Chem. Phys., 2009, 131, 144705 CrossRef PubMed.
- J. Applequist, J. R. Carl and K.-K. Fung, J. Am. Chem. Soc., 1972, 94, 2952–2960 CrossRef CAS.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- P. T. van Duijnen and M. Swart, J. Phys. Chem. A, 1998, 102, 2399–2407 CrossRef CAS.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- P. Ren, C. Wu and J. W. Ponder, J. Chem. Theory Comput., 2011, 7, 3143–3161 CrossRef CAS PubMed.
- D. Elking, T. Darden and R. J. Woods, J. Comput. Chem., 2007, 28, 1261–1274 CrossRef CAS PubMed.
- J. Wang, P. Cieplak, R. Luo and Y. Duan, J. Chem. Theory Comput., 2019, 15, 1146–1158 CrossRef CAS PubMed.
- J. Wang, P. Cieplak, J. Li, T. Hou, R. Luo and Y. Duan, J. Phys. Chem. B, 2011, 115, 3091–3099 CrossRef CAS PubMed.
- H. Wei, R. Qi, J. Wang, P. Cieplak, Y. Duan and R. Luo, J. Chem. Phys., 2020, 153, 114116 CrossRef CAS PubMed.
- D. Elking, Polarizable force fields, PhD thesis, University of Georgia, 2007 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures mentioned in the text. Table S1 contains the energies and IEP values calculated at the DFT level for 1237 clusters Mg2–Mg32 as well as the corresponding IEP values calculated within different approximate models. Table S2 contains the DFT optimized Cartesian coordinates of all clusters under investigation. See DOI: https://doi.org/10.1039/d2ra08086a |
| This journal is © The Royal Society of Chemistry 2023 |