Open Access Article
Open Access ArticleMolecule superstructures for computer-aided molecular and process design
Philipp
Rehner
 ,
Johannes
Schilling
,
Johannes
Schilling
 and
André
Bardow
and
André
Bardow
 *
*
Energy and Process Systems Engineering, Department of Mechanical and Process Engineering, ETH Zurich, Tannenstrasse 3, 8092 Zurich, Switzerland. E-mail: abardow@ethz.ch
First published on 19th December 2022
Abstract
Integrated molecular and process design optimizes process variables together with molecules as an additional degree of freedom. The integrated design needs to represent the molecule in a machine-readable way that can be operated on by an optimization algorithm. For this purpose, group-contribution methods have been established as property models in molecular design applications. The underlying molecular representation for a group-contribution method is the number of occurrences of different pre-defined groups within the molecule. However, this way of encoding a molecule omits information about the structure of the molecule and thus limits the molecular detail available during design. In this work, we present a graph-based molecular representation approach that encodes the full structure of the molecule during optimization. This approach unlocks additional higher-fidelity property prediction methods for integrated molecular and process design while still allowing the use of gradient-based optimization algorithms. The framework is applied in a case study that designs the working fluid for an organic Rankine cycle using the heterosegmented gc-PC-SAFT equation of state as property prediction model. The molecular superstructure representation is shown to enable the efficient integration of advanced property models into molecular design.
Design, System, ApplicationThe goal of an integrated molecular and process design is to find the optimal molecule for a given application in process or energy engineering. Integrated molecular and process design can be formulated as mathematical optimization problems to ensure the identification of the true optimum. Established molecular design approaches split molecules into pre-defined molecular groups and then optimize the number of occurrences of each group. This coarse representation of molecules prevents the use of advanced property prediction methods and leads to ambiguous results since the same set of functional groups can represent multiple molecules. The proposed design strategy of molecule superstructures incorporates the structure of the molecule in the optimization. Thereby, we obtain unique molecules as optimization results. In addition, the full structural information is available during the optimization. Thus, this structural information can be exploited by advanced property models that go beyond group counts. We demonstrate the method in a design of the optimal working fluid for an organic Rankine cycle. By unlocking more elaborate property models, the molecule superstructures have the potential to enhance integrated design studies for a multitude of processes in chemical and energy engineering. |
1 Introduction
Many industrial processes require auxiliary materials that are not part of the feed or product streams but still influence the efficiency of the process significantly.1 An example is the working fluid in a heat pump2 or organic Rankine cycle.3 Likewise, separation processes, such as gas absorption4 or extractive distillation,5 require choosing a solvent. The identification of a suitable material is often key to process performance.One possibility for finding a suitable molecule is to screen a database of possible processing materials experimentally or numerically. In contrast, the goal of a computer-aided molecular design (CAMD) is to determine the optimal molecule with respect to a given target function and constraints.6 Depending on the application, the target can be a property of the molecule itself or a performance indicator of a process in which the molecule is used. If the target is calculated from a process model, the method is referred to as computer-aided molecular and process design (CAMPD).7 CAMPD optimizes the process degrees of freedom simultaneously with the molecular degrees of freedom in a single optimization problem. The advantage of a CAMPD approach is that different molecular performance indicators can be relevant for a given application. In CAMD their relative importance has to be defined heuristically. By including a process model in the design, all properties of the molecules are evaluated holistically with respect to the optimal thermodynamic efficiency, economic performance, or ecological impacts of the process.7
The different elements of a general CAMPD framework and their connections are shown in Fig. 1. A major challenge for a molecular design framework is the representation of the molecule within the optimization algorithm. In general, molecules are discrete entities with complex three-dimensional structures, whose properties depend on the interaction of electrons and nuclei. To make the molecular design problem solvable, the structure of the molecules needs to be featurized, i.e., transformed into a machine-readable format. Because featurization is arduous for full three-dimensional molecular representations, a simplified, two-dimensional molecular representation is chosen in most applications.8
 | ||
| Fig. 1 Elements of a computer-aided molecular and process design (CAMPD) framework and their connections. | ||
The molecular representation is tasked with transforming the structure variables into molecular features and providing the solver with structural constraints that ensure only feasible molecules are generated. The molecular features are used in a property prediction method to calculate properties required by the process model. In turn, the process model calculates the performance indicator of interest and returns it to the solver as a target value. The process model also returns the values of all required process constraints (cf.Fig. 1).
The individual elements of the framework are independent of each other provided they use the correct interface, i.e., the featurization provided by the molecular representation is compatible with the property prediction method, and all properties required in the process models can be determined by the property prediction method. Due to the discrete nature of molecules, valid structures need to be represented by integer variables. Combined with the process model that, in general, is described by continuous variables and nonlinear equations, this results in a mixed-integer nonlinear programming (MINLP) problem. Although model-specific solvers can improve the performance,9 a general-purpose, model-agnostic MINLP solver is assumed in Fig. 1. Gradient-based MINLP solvers promise fast convergence and are therefore preferable. However, most algorithms require a relaxation of the optimization problem, i.e., the target function and constraints need to be evaluable for non-integer values of the discrete variables. Therefore, the molecular representation and the property prediction method need to be able to interpolate continuously between molecules.
In CAMD, the most common property prediction methods are quantitative structure property relationships (QSPR). These QSPR methods can use different molecular features which, for the most part, can be split into three categories: group counts, topological indices, and signature descriptors.8 Each featurization requires a specific molecular representation. The most common QSPRs are group contribution (GC) methods that use group counts as input. In the corresponding molecular representation, the group counts reappear as subset of the structure variables. Additional structure variables, e.g., the number of aromatic or aliphatic rings, can be required depending on the complexity of the molecular design space. From the whole set of structure variables linear structural feasibility constraints10,11 are formulated. QSPR methods are computationally efficient in general. Using molecular features as group counts leads to a small number of integer variables and enables the usage of gradient-based solvers. However, as a disadvantage, the group counts only encode parts of the structural information of the molecules, e.g., many isomers cannot be distinguished solely based on the group counts.
Additional information about the structure of molecules can be included in QSPR methods by topological indices and signature descriptors. Signature descriptors extend group counts by adding information about their chemical environment within the molecule.8 The same atomic group can thus have a different signature depending on its neighbours and therefore there are more descriptors available to distinguish between molecules. If sufficient experimental data is available, the increased number of descriptors improves the accuracy of the QSPR methods. However, analogous to group counts, the translation from signatures to structure is not unique for many isomers.12,13 Topological indices are features calculated from the nodes and vertices of a molecular graph. While this definition is broad and includes group counts and signature descriptors, it further contains additional features like connectivity indices that account for the degree of branching in molecules.14–16 For connectivity and other topological indices that go beyond group counts and signatures, the transformation from molecular graph to features can, in general, not be reversed. Therefore, CAMD applications do not account for the topological features themselves but rather for the molecular graph.8,17 A molecular representation that uses the full adjacency matrix as feature was presented by Churi and Achenie.18 The approach can also be relaxed and has the advantage that it can be used with most property prediction methods. The flexibility comes at the cost of a large number of binary structure variables.
As alternative to the adjacency matrix, the molecular graph can be represented as a string, e.g., a SMILES code.19 A combination of solver and molecular representation that generates SMILES is LEA3D,20 SMILES codes can be used to obtain any kind of features needed for a property prediction method, but it is impossible to interpolate between SMILES. Therefore, in the context of integrated design,21,22 LEA3D is predominantly interesting for property prediction methods that themselves are incompatible with relaxed inputs, such as the conductor-like screening model for real solvents (COSMO-RS).23
Featurization is also particularly relevant in the context of molecular design using deep learning approaches.24 Neural networks as property prediction methods are agnostic to the physical meaning of the features they receive as input. However, the choice can still affect the quality of the predictions. One solution to this problem is the use of autoencoders25 in which the feature selection is entirely data-driven instead of based on physical insights.
Due to the non-convex and non-linear process target functions and constraints in CAMPD,7 applications usually rely on GC methods for property prediction. To evaluate a thermodynamic target function from a process model, an equation of state or equivalent model is required as a property prediction method. If the process performance is largely dependent on the phase behavior of the components (e.g., a solvent design), excess Gibbs energy (gE) models combined with models for pure component properties can be used. To use an equation of state or gE-model as a property prediction method in a molecular design application, GC methods can calculate the parameters of the model from the structure of the molecule. The most prominent example is the GC method UNIFAC26 which generates parameters for the UNIQUAC27gE-model. The generation of model parameters from a group contribution approach is referred to as homosegmented GC approach28 in the following sections. Developing a homosegmented GC model does not require modifications to the underlying equation of state or gE-model and is therefore particularly flexible. A homosegmented GC model for cubic equations of state requires only GC methods for critical temperatures, critical pressures, and acentric factors that are available from the literature.29–31 Examples for integrated design applications using homosegmented GC models based on critical properties and acentric factors are studies by Papadopoulos et al.32 using the Lee–Kessler method,33 Roskosch and Atakan2 using the Peng–Robinson equation of state,34 and Cignitti et al.35 using the Soave–Redlich–Kwong equation of state.36
For more complex equations of state including statistical associating fluid theory (SAFT)37,38 and its derivatives, homosegmented GC methods are formulated by determining appropriate parameter combinations calculated from the group counts. Examples for homosegmented GC models for SAFT-based equations of state were developed by Tamouza et al.39,40 for SAFT and SAFT-VR, and by Vijande et al.,41 Sauer et al.28 and NguyenHuynh42 for PC-SAFT. The homosegmented group contribution PC-SAFT model is used in the continuous molecular targeting (CoMT) CAMPD integrated design framework.43,44
Homosegmented GC approaches are limited by the accuracy of the underlying model and the choice of combining rules. The physical basis of SAFT enables a more refined modeling approach that considers interactions between individual segments instead of entire molecules. Compared to homosegmented GC methods, these heterosegmented models use the structure of the molecules and parameters for all groups directly as inputs instead of generating molecular parameters. Therefore, interactions between unlike segments are resolved on a finer level. Heterosegmented GC models were developed for SAFT-VR-Mie45 and PC-SAFT.26,46,47 However, the more detailed molecular model comes at the cost of requiring additional knowledge about the structure of molecules, in particular the complete bond information. This challenge is resolved in the SAFT-γ-Mie equation of state48 which models individual segments in a heterosegmented way but uses a homosegmented approach for the Helmholtz energy contribution due to chain formation. With that approximation, group counts can be used as features, and subsequently, the model was applied in various integrated molecular and process design studies.9,49,50
In a comparative study, Sauer et al.28 showed that the heterosegmented formulation of the PC-SAFT equation of state shows smaller deviations to experimental data than the homosegmented approach for all chemical families under consideration. Further, fully heterosegmented equations of state can be extended to heterosegmented Helmholtz energy functionals to model the distribution and orientation of molecules in inhomogeneous systems like interfaces,51,52 or nanopores.53 Therefore, it is desirable to unlock the potential of heterosegmented GC approaches in the context of integrated molecular and process design.
Group counts and the established molecular representations cannot account for bonds or higher-order structures, stochastic algorithms have unfavorable convergence, and using the full adjacency matrix within the structure variables scales poorly to larger molecules. Therefore, in this work, we develop a molecular representation that generates the complete molecular graph from a small input of possibly relaxed integer variables. The number of structure variables is reduced compared to a full adjacency matrix by encoding part of the structure of the molecules directly in the molecular representation. With the reduced problem size, an integrated design is possible that evaluates the molecules by their performance in the nonlinear process model. For the first time, the heterosegmented gc-PC-SAFT equation of state is used as property prediction model in a CAMPD application. Because of the reduced complexity of the molecular representation, the molecule space is also limited. The resulting reduction of the molecular design space is justifiable for high fidelity property prediction methods, such as the SAFT family of equation of states, as the molecular space is already significantly limited by the availability of accurate group parameters.
The proposed molecular representation that enables heterosegmented GC methods and other property prediction methods that require the full molecular graph as input is described in detail in section 2. In section 3, the integrated design of an organic Rankine cycle (ORC) is used as a case study to assess the capability of the proposed framework.
2 Molecule superstructures
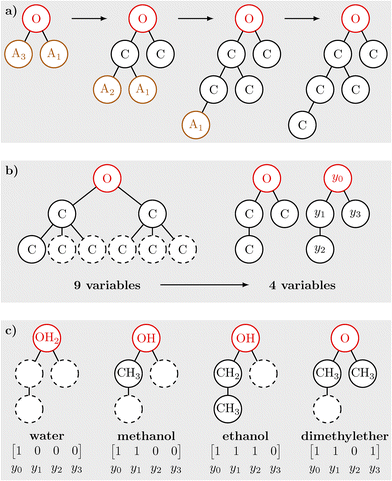
The core idea of the molecule superstructures is to represent molecules as graphs in which every node i is associated with a non-hydrogen atom and a binary variable yi. While the structure of the graph remains unchanged during the optimization, the values of yi are degrees of freedom. For yi = 0 the atom associated with node i is not part of the molecule and for yi = 1 it is. A superstructure of size n is defined as to be complex enough to be able to represent all molecules of a given chemical family with up to n non-hydrogen atoms. A key requirement for the molecular representation is that it can be relaxed. Therefore, values of yi between 0 and 1 are allowed and are interpreted as the probability that the atom is present. Hydrogen atoms are not kept track of individually but are used to balance out any remaining free valence electrons.The molecules that we consider in this study consist of a functional group and one or more alkyl tails. The alkyl tails consist of only carbon and hydrogen atoms but account for most of the combinatoric complexity of the molecules. Fig. 2 shows the recursive definition of an alkyl superstructure An. The recursion is terminated by the A0 structure (a hydrogen atom). In general, the alkyl superstructure An would contain one C atom that is bonded to three An−1 superstructures. Due to the symmetry of the molecule, however, the size of the alkyl tails and therefore the number of binary variables can be reduced. Without considering chirality, the three alkyl tails can be permutated arbitrarily. Thus, the alkyl tails can always be arranged in descending order by size. Then, the second alkyl tail only needs to account for a maximum of half the n − 1 remaining C atoms and the third alkyl tail only a third, respectively. This construction is only a necessary condition for uniqueness. Additional symmetries in the molecules need to be suppressed by constraints that are introduced later.
With the alkyl tails in place, molecules can be constructed. Even considering only the most essential atom types in organic molecules, i.e., C, H, O and N, the number of molecules that can be formed is vast and scales exponentially with the number of atoms. Therefore, we restrict the molecule space to align more with the chemical families for which experimental thermophysical data, and in conclusion accurate property prediction models, are available. The resulting molecular design space is shown in Fig. 3. It includes alkanes, alkenes, alkynes, alcohols, ethers, aldehydes, ketones, and amines. The size of the alkyl superstructures is determined by the symmetry of the molecules analogously to the recursive definition of the alkyl superstructures themselves. For alkenes, no distinction is made between cis and trans isomers, as that distinction is rarely made in property prediction methods either.
 | ||
| Fig. 3 Definition of alkane, alkene, alkyne, alcohol/ether, ketone/aldehyde, and amine superstructures of size n. | ||
The chemical families shown in Fig. 3 capture a substantial fraction of technically relevant chemicals. With given group parameters, the method can be extended to additional families like esters, carboxylic acids, or aromatic compounds. However, allowing arbitrary numbers of possibly different functional groups in the molecule is not feasible with the superstructure approach. At the same time, current property prediction methods used in CAMPD do usually not extrapolate well to components that are chemically different to the ones used in the parametrization. With the method presented in this work, we give preference to the accuracy of the property predictions rather than the size of the molecular design space.
In Fig. 4a) the recursive construction of an alcohol/ether superstructure of size 4 is visualized by repeatedly using the definition of the alkyl superstructure (cf.Fig. 2). For cases where the functional group consists of only one non-hydrogen atom, the size of the superstructure (i.e., the maximum number of non-hydrogen atoms that it can represent) coincides with the depth of the superstructure graph. The reduction in complexity resulting from incorporating symmetry constraints in the superstructure is shown in Fig. 4b). Compared to the naive approach of keeping all possible child nodes up to depth n − 1, the optimized alcohol/ether superstructure of size 3 only needs 4 variables instead of 9. For larger superstructures this effect becomes even more pronounced. For an alcohol/ether superstructure of size 8, the full tree structure, analogous to the left side of Fig. 4b), contains 2187 nodes. Using the recursive definition of the alkyl superstructures (cf.Fig. 2) instead to generate the graph leads to 27 nodes and thus 27 binary variables. This reduction of the number of binary variables highlights the potential of the presented approach to minimize the impact of the combinatorial nature of molecular design. Still, the number of variables increases with the size of the molecules in the design space, in contrast to using group counts as molecular representation. The increased complexity for larger molecules is necessary to keep track of their full structural information. In our view, the proposed molecular superstructure is mainly limited by allowing only one functional group; however, this limitation is also often given for the employed property models. To translate the structure variables that are stored in a linear array to the graph structure, a consistent indexing is required. For this application an ordering according to a pre-order traversal has proven useful. Fig. 4c) shows how the feasible molecules that are in the design space of the alcohol/ether superstructure of size 3 are represented in the structure variables.
2.1 Structural constraints
To ensure that the optimization algorithm only finds valid molecules, linear constraints are imposed. First, every node j in the superstructure can only be present if its parent node i is also present, which can be expressed as | (1) |
 , so that in the alcohol/ether example (cf., Fig. 4b)), we would find, e.g.,
, so that in the alcohol/ether example (cf., Fig. 4b)), we would find, e.g.,  . Any superstructure of size n is supposed to be able to represent all isomers with at most n heavy atoms. Therefore, all larger molecules are excluded by the size constraint
. Any superstructure of size n is supposed to be able to represent all isomers with at most n heavy atoms. Therefore, all larger molecules are excluded by the size constraint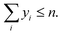 | (2) |
To be able to determine a ranking of multiple optimal molecules, molecules that were already found in a previous iteration are excluded using integer cuts.54 For integer variables the quadratic constraint
 | (3) |
 | (4) |
With these constraints, only valid molecules of the appropriate size are found. However, some molecules can have multiple representations in the superstructure. To avoid a repeated identification of the same molecule, we introduce symmetry constraints
 | (5) |
 refers to the set of all descendants of node i (including i) and dα to the depth of node α, i.e., the number of edges between α and the root node. This constraint is devised heuristically and is not guaranteed to eliminate all duplicates for large superstructures. It is tested numerically to verify that the correct number of isomers is contained in the design space for alcohols up to nonanol.55 The additional symmetries that alkanes have compared to alcohols or primary amines are not eliminated by constraints but removed retrospectively from the fluid ranking. By encoding structural information in the molecule superstructure, the number of variables and constraints is reduced compared to the more general molecular structure representation by Churi and Achenie.18
refers to the set of all descendants of node i (including i) and dα to the depth of node α, i.e., the number of edges between α and the root node. This constraint is devised heuristically and is not guaranteed to eliminate all duplicates for large superstructures. It is tested numerically to verify that the correct number of isomers is contained in the design space for alcohols up to nonanol.55 The additional symmetries that alkanes have compared to alcohols or primary amines are not eliminated by constraints but removed retrospectively from the fluid ranking. By encoding structural information in the molecule superstructure, the number of variables and constraints is reduced compared to the more general molecular structure representation by Churi and Achenie.18
2.2 Property evaluation
The molecule superstructure consists of relaxed binary variables in the form of a molecular graph with weights for each atom. Due to the full structural information about the molecule, the superstructure can be interfaced with more sophisticated property prediction methods than simple group contribution models. In this work, we employ the heterosegmented group contribution PC-SAFT equation of state (gc-PC-SAFT) as the property model, which was shown by Sauer et al.28 to describe pure component vapor pressures and liquid densities more accurately than the simpler homosegmented group contribution PC-SAFT model. In addition to the number of chemical groups, the number of bonds between each pair of chemical groups is required as an input for gc-PC-SAFT.To concur with the segments defined by Sauer et al.,28 the molecular design space has to be modified slightly. The revised superstructures are shown in Fig. 5. For alkynes and amines, groups are only available for 1-alkynes and primary amines. The alcohol/ether superstructure is split up into an alcohol superstructure and a superstructure for methyl ethers to accommodate how ethers are parametrized. Finally, in every superstructure shown in Fig. 5, an additional constraint sets the value of the first C node in the largest alkyl tail to 1 (indicated by an asterisk). With this constraint, we exclude the small molecules methane, ethene, ethyne, water, methanol (as a special case of a methyl ether), formaldehyde, and ammonia, which are not part of the group contribution model. The individual superstructures contain different numbers of binary variables. Therefore, the best molecules in each chemical family are determined in individual optimization problems and combined into a comprehensive ranking. If the goal is to formulate one single optimization problem, one solution can be to use disjunctive programming.56 Alternatively, all superstructures can be combined into a single superstructure with additional constraints ensuring valid structures within the different chemical families. The latter approach can be compared to a direct MINLP approach which is also used for optimizing process superstructures.57 In our study the added complexity of the single optimization problem does not outweigh the effort of solving multiple optimization problems, especially because solving multiple problems can be parallelized efficiently.
 | ||
| Fig. 5 Molecule superstructures adapted to the heterosegmented gc-PC-SAFT equation of state by Sauer et al.28 | ||
For the molecule superstructure, each node represents a superposition of chemical groups. A C node in an alkyl tail can, in general, represent a >C<, >CH, CH2, or CH3 segment. For integer solutions, the correct group for node i is determined from the number of child nodes 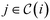 with yj = 1. If the yj are relaxed and interpreted as probabilities, the occurrence of the different groups can be determined from the combinatorics of the child nodes. An atom i with yi = 1 that has two child nodes j and k will occur as the group without open bonds with a probability of (1 − yj)(1 − yk) (neither child node is present), one open bond with a probability of yj(1 − yk) + (1 − yj)yk (either of the child nodes is present), and two open bonds with a probability of yjyk (both child nodes are present). If yi ≠ 1, the probability of finding atom i itself is reduced and therefore the occurrence of each group type must also be multiplied with yi. This relation can be expressed generically using polynomials. By defining the segment polynomial Si(ξ) as
with yj = 1. If the yj are relaxed and interpreted as probabilities, the occurrence of the different groups can be determined from the combinatorics of the child nodes. An atom i with yi = 1 that has two child nodes j and k will occur as the group without open bonds with a probability of (1 − yj)(1 − yk) (neither child node is present), one open bond with a probability of yj(1 − yk) + (1 − yj)yk (either of the child nodes is present), and two open bonds with a probability of yjyk (both child nodes are present). If yi ≠ 1, the probability of finding atom i itself is reduced and therefore the occurrence of each group type must also be multiplied with yi. This relation can be expressed generically using polynomials. By defining the segment polynomial Si(ξ) as
 | (6) |
 | (7) |
 | ||
| Fig. 6 Example calculation of segment and bond counts for an alcohol/ether superstructure (n = 3). The polynomials Si(ξ) and Bij(ξ,ζ) are evaluated for every segment and bond from eqn (6) and (7). Then, the polynomials that correspond to the same segment or bond types are summed and the bond and segment counts are determined from the coefficients of the polynomials. | ||
3 Case study: organic Rankine cycle
The proposed molecular design method is demonstrated in a case study to identify the optimal working fluid for a small-scale high-temperature organic Rankine cycle. The case study is primarily based on the 1-stage CoMT-CAMD study by Lampe et al.58 simplified by replacing the detailed turbine model with a constant efficiency and neglecting pressure losses in the heat exchangers.The process flowsheet is shown in Fig. 7. The working fluid leaves the evaporator as saturated or superheated vapor and is then expanded in a turbine with assumed constant isentropic efficiency ηs,turbine = 0.85. The value is based on the results from the detailed turbine model used in previous work.58 The working fluid at low pressure is condensed and enters the pump as a saturated liquid, where it is fed back to the evaporator at the high pressure level. Optionally, the vaporous working fluid leaving the turbine is used in a recuperator to preheat the liquid working fluid before it enters the evaporator. The heat integration realized by the recuperator increases the efficiency of the cycle. However, in some configurations, using a recuperator can become thermodynamically or economically unfavorable or even infeasible: if the turbine outlet is within or close to the two-phase region, the temperature difference in the recuperator becomes small or even negative, rendering recuperation thermodynamically infeasible. If the transferred heat in the recuperator is small, it still increases the thermal efficiency of the process, but the reduction in operating costs might not offset the additional investment costs.
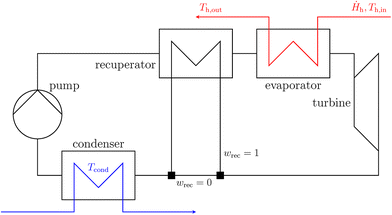 | ||
| Fig. 7 Conceptual flowsheet of the process superstructure for the organic Rankine cycle with optional recuperation (indicated with binary variable wrec). | ||
To assess the feasibility of the recuperator, a flowsheet superstructure is considered that contains a binary variable wrec that specifies whether the recuperator is present or not. The flowsheet superstructure enables an easy comparison of different process configurations without significantly increasing the overall optimization problem's complexity. For a comprehensive assessment of the economic impact of the recuperator, a detailed thermo-economic model of the process is required.59 In the purely thermodynamic optimization considered in this case study, the economic performance of the recuperator has to be approximated crudely by limiting the area of the recuperator by both imposing a minimum temperature difference and specifying a minimum transferred heat to exclude economically infeasible small heat exchangers.
The continuous degrees of freedom in the process model are the mass flow rate ṁWF of the working fluid, the logarithmic reduced pressures ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) predcond and ln
predcond and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) predevap in the condenser and evaporator respectively, the degree of superheating ΔTsh, and the heat flow rate in the recuperator
predevap in the condenser and evaporator respectively, the degree of superheating ΔTsh, and the heat flow rate in the recuperator ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) rec.
rec.
The process parameters used for this case study are listed in Table 1. Reduced pressures are calculated with respect to the critical pressure  . Limiting the maximum reduced pressure to a value below 1 ensures a subcritical process operation. Even though transcritical cycles can be thermodynamically preferable, particularly for situations with large temperature changes in the heat source medium, they are excluded from this study.
. Limiting the maximum reduced pressure to a value below 1 ensures a subcritical process operation. Even though transcritical cycles can be thermodynamically preferable, particularly for situations with large temperature changes in the heat source medium, they are excluded from this study.
| Parameter | Symbol | Value |
|---|---|---|
| Heat source inlet temperature | T h,in | 300 °C |
| Heat source heat capacity rate | Ḣ h | 4.63 kW K−1 |
| Min. approach temperature | ΔTh,min | 30 K |
| Isentropic turbine efficiency | η s,turbine | 0.85 |
| Isentropic pump efficiency | η s,pump | 0.7 |
| Min. absolute pressure | p min | 1 bar |
| Min. reduced pressure | p redmin | 1 × 10−5 |
| Max. absolute pressure | p max | 50 bar |
| Max. reduced pressure | p redmax | 0.8 |
| Min. cooling temperature | T cond,min | 80 °C |
| Min. temp. diff. recuperator | ΔTrec,min | 30 K |
| Min. recuperated heat |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) rec,min
rec,min
|
5 kW |
A possible application of the ORC can exploit a hot product or utility stream in a chemical plant that is required in a subsequent step at a lower temperature. As a form of heat integration, the ORC can extract the exergy in the form of electric power that would otherwise be lost if the stream was cooled in a simple heat exchanger.60 Therefore, the objective function for the optimization is the net power output of the process Pnet, and a constraint is added that limits the heat source outlet temperature Th,out to a minimum value.
The feasibility constraints of the recuperator depend on its presence. If the recuperator is built, the minimal temperature differences ΔTrec,h/c on the hot and the cold side respectively are bounded by ΔTrec,min. Without recuperation, no lower bound on the temperature differences ΔTrec,h/c between the respective streams is required. Therefore, the binary variable wrec is included in the calculation of the lower bound of ΔTrec,h/c, as
 | (8) |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) rec is constrained by the set of inequalities
rec is constrained by the set of inequalities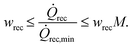 | (9) |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) rec,min if wrec = 1.
rec,min if wrec = 1.
Artelys Knitro61 is used to solve the resulting integrated design problem with its implementation of the branch and bound algorithm for the MINLP and sequential quadratic programming as a solution algorithm for the NLP subproblems.
3.1 Single-objective optimization
To assess the capability of the new molecular representation, a ranking of the 50 most promising working fluids is calculated for the heterosegmented gc-PC-SAFT equation of state. For comparison, the integrated design is repeated for the homosegmented group contribution PC-SAFT model that has been used in previous CAMPD studies based on PC-SAFT. For both models the ideal gas contribution to the heat capacity is calculated using the GC model by Joback and Reid.29 The minimum heat source outlet temperature is set to Tminh,out = 200 °C. Molecule superstructures of size 8 (up to 8 non-hydrogen atoms) are used which leads to 16 (methlyethers and alkynes), 20 (ketones), 23 (alkanes, alcohols, amines), or 25 (alkenes) binary structure variables. The computation times on an AMD EPYC 7F72 workstation CPU were 17.3 h (79.2 CPUh) using the gc-PC-SAFT equation of state and 10.4 h (43.1 CPUh) using the homosegmented group contribution PC-SAFT model. The increase in computation time can predominantly be attributed to the more expensive evaluation of the equation of state. The problem size is unchanged and the rate of convergence largely identical.The ten best performing molecules identified in each optimization are listed in Table 2. For both models, propanal (propionaldehyde) has the highest net power for the given constraints. Aside from the top-performing working fluid, the ranking differs for the two models. However, the differences in net power are small, and many components appear in the top ten of both models. A difference between the homosegmented group contribution PC-SAFT model and the heterosegmented gc-PC-SAFT equation of state can be observed concerning the description of isomers: The homosegmented model is not able to distinguish between the two isomers of methylpent-1-yne or the two isomeric alkenes hex-3-ene and hex-2-ene, resulting in the same net power output of the working fluids. Despite both isomers having the same number of segments, they both appear in the list because the exact structure of the molecules is a result of the optimization and does not need to be determined a posteriori. The heterosegmented gc-PC-SAFT equation of state can distinguish between these isomers, leading to a slightly different net power output. While the difference in performance between these isomers is negligible in the application shown here, the detailed resolution of isomers can become an advantage in other applications.
| # | PC-SAFT (homosegmented) | gc-PC-SAFT (heterosegmented) | ||||
|---|---|---|---|---|---|---|
| IUPAC name | Smiles | P net/kW | IUPAC name | Smiles | P net/kW | |
| 1 | Propanal | CCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
93.014 | Propanal | CCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
92.321 |
| 2 | 1-Methoxybutane | CCCCOC | 92.215 | Propan-2-one | CC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)C O)C |
92.196 |
| 3 | 3-Methylpent-1-yne | CCC(C)C#C | 92.064 | 4-Methylpent-1-yne | CC(C)CC#C | 92.057 |
| 4 | 4-Methylpent-1-yne | CC(C)CC#C | 92.064 | 1-Methoxypropane | CCCOC | 92.045 |
| 5 | Hex-3-ene | CCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CCC CCC |
92.022 | 3-Methylpent-1-yne | CCC(C)C#C | 92.029 |
| 6 | Hex-2-ene | CCCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC CC |
92.022 | 2,3-Dimethylbut-2-ene | CC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C)C)C C(C)C)C |
91.991 |
| 7 | Hex-1-yne | CCCCC#C | 91.991 | 3-Methylpent-2-ene | CCC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC)C CC)C |
91.921 |
| 8 | Propan-2-one | CC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)C O)C |
91.918 | 2-Methylpent-2-ene | CCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C)C C(C)C |
91.909 |
| 9 | 2,3,3-Trimethylbut-1-ene | CC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)C(C)(C)C C)C(C)(C)C |
91.855 | Hex-2-ene | CCCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC CC |
91.802 |
| 10 | 1-Methoxy-2-methylpropane | CC(C)COC | 91.853 | Hex-3-ene | CCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CCC CCC |
91.801 |
The ranking is strictly based on the thermodynamic performance of the ORC process with the chosen working fluid. The operational safety, ecological impacts, and equipment and operating costs have not been considered. There is also no guarantee that all components in the ranking (in particular those exhibiting triple bonds) have the necessary thermal stability to be used during the life cycle of an ORC. The choice to report the net power with five significant figures is made to highlight the behavior of the molecule superstructure and the different GC models and does not reflect the expected accuracy of the prediction.
3.2 Impact of thermodynamic model
In the parameter estimation, the heterosegmented gc-PC-SAFT equation of state showed closer agreement with experimental data compared to the homosegmented group contribution PC-SAFT model.28 To compare the two approaches, the PC-SAFT equation of state with parameters fitted for individual components is used as a reference. In Fig. 8, the full rankings obtained in this case study for the two models are plotted using open symbols. For all working fluids for which pure component PC-SAFT parameters are available from Esper and Gross,62 these parameters are used to calculate the net power output in a separate process optimization (filled symbols). The relative deviations between the net power output calculated using fitted PC-SAFT parameters and the group contribution approach are plotted on the right. Only components that appear in both rankings are used for the comparison. | ||
| Fig. 8 Ranking of working fluids determined using the homosegmented PC-SAFT group contribution model and the heterosegmented gc-PC-SAFT equation of state, respectively (open symbols). Comparison with process optimization results using fitted PC-SAFT parameters62 (filled symbols). The errors between both group contribution methods and the fitted equation of state are shown in the violin plot on the right hand side. | ||
The difference between the two approaches is not significant: both group contribution models closely reproduce the power output determined by the process design with fixed molecules for most of the components in the ranking. With some exceptions for the homosegmented approach, hydrocarbons (alkanes, alkenes and alkynes) and ketones are in excellent agreement. More caution is required when extrapolating methyl ethers and amines to components without adequate experimental data. In the heterosegmented approach, both 1-methoxypropane and 2-methoxypropane are falsely (at least according to the fitted PC-SAFT parameters) identified as promising working fluids. For amines, both approaches overpredict the power output of propane-2-amine significantly. This deviation can be attributed to the fact that only 1-amines were used in the parametrization of the GC models.28 Further, the fitted PC-SAFT parameters used as reference are only accurate if enough experimental data is available. For scarcely measured components like 1- and 2-methoxypropane, data is often only available for temperatures close to ambient conditions. The conditions close to the critical point that are important in the ORC process model are thus extrapolated. Here, the group contribution approach, albeit being less precise in replicating the actual experimental data, can extrapolate more robustly than the equation of state with individually fitted parameters due to the lower ratio of the number of parameters to experimental data points.
3.3 Pareto optimization
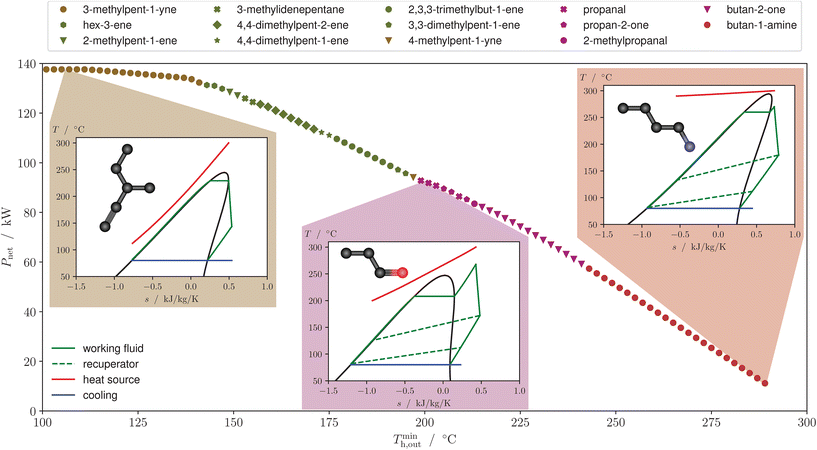
The optimal working fluid in an organic Rankine cycle depends heavily on the operating conditions.63 To demonstrate this dependency, the optimal working fluid is calculated varying the minimal heat source outlet temperature Tminh,out. The results are shown in Fig. 9. For the lowest value of Tminh,out = 100 °C, the design framework identifies 3-methylpent-1-yne as the optimal working fluid. Increasing the minimum heat source outlet temperature changes the selection to isomers of hexene and heptene, then different ketones, and finally butan-1-amine.For three points on the Pareto front, the T–s diagram of the optimized process is shown in insets. The temperature of the heat source medium is shown in red, whereas the condensation temperature is set to a constant minimum value (blue). The dashed lines indicate the heat transfer in the recuperator. The critical temperature and the shape of the phase diagram impact the process performance in a way that can only be quantified in a process model. Therefore, an integrated design of process degrees of freedom and working fluids is necessary to find the most efficient process. The proposed molecule superstructures allow to base these process optimizations on the most advanced GC models.
4 Conclusions
This work introduces molecule superstructures as a novel graph-based molecular representation for computer-aided molecular and process design. With the superstructure approach, the full structural information of the molecule is available during the optimization. At the same time, the binary structure variables can be evaluated at non-integer values. The relaxation of the binary variables allows a continuous interpolation between molecular structures and thus the use of fast gradient-based optimization algorithms. The molecule superstructures are embedded in a CAMPD framework in which they can be coupled with advanced property prediction methods and process models. The framework is used to find the optimal working fluid and process conditions in an integrated design of a high-temperature ORC process. For the first time, the heterosegmented gc-PC-SAFT equation of state is used as property prediction method in a CAMPD application. The results are comparable to the established homosegmented group contribution PC-SAFT model. Due to inaccuracies of the property prediction methods and the local MINLP solver, the method does not guarantee that the optimal molecule, as determined by the optimization, indeed performs best in a real-world application. The problem can be alleviated by calculating a ranking of fluid candidates, as was done in this work, or by using statistical methods64 to estimate the accuracy of the prediction.The molecule superstructure enables high-fidelity property prediction methods and can be used in CAMPD problems with complex non-linear target functions and constraints. To find optimal molecules based on a more holistic description of the process, the molecule superstructure can be coupled with property prediction methods for transport properties65,66 to calculate economic targets, such as specific investment costs.59 To include the ecological impact of the entire process, the target function can be determined from a life cycle assessment.67
A further direction in the integrated design of ORCs or heat pumps is the consideration of mixed working fluids or refrifgerants.32,68 Mixtures also play a crucial part in separation processes for which solvent design is also considered to increase the process performance.69 Heterosegmented group contribution models describe interactions between segments rather than entire molecules. Therefore, corrections for unlike segments on different molecules can be included directly in the perturbation terms.
With these extensions in mind, the proposed molecule superstructure optimization strategy can contribute to increasing the accuracy of property prediction methods used in integrated molecular and process design.
Code availability
The FeOs (ref. 70) framework is used for the calculation of properties and phase equilibria. The CAMPD framework presented in this work, including the molecular superstructures are published open source at https://github.com/feos-org/feos-campd. The implementation of the process model for the organic Rankine cycle with optional recuperation and all scripts required to reproduce the results are published at https://gitlab.ethz.ch/epse/molecular-design-public/paper-molecule-superstructures.Author contributions
Philipp Rehner: conceptualization, methodology, software, validation, investigation, writing – original draft, visualization Johannes Schilling: conceptualization, writing – review & editing, supervision André Bardow: conceptualization, resources, writing – review & editing, supervision, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
PR acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 497566159.Notes and references
- L. Zhang, D. K. Babi and R. Gani, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 557–582 CrossRef PubMed
.
- D. Roskosch and B. Atakan, Energy, 2015, 81, 202–212 CrossRef CAS
.
- A. I. Papadopoulos, M. Stijepovic and P. Linke, Appl. Therm. Eng., 2010, 30, 760–769 CrossRef CAS
.
-
C. S. Adjiman, A. Galindo and G. Jackson, Computer Aided Chemical Engineering, Elsevier, Walthm, MA, USA, 2014, vol. 34, pp. 55–64 Search PubMed
.
- A. I. Papadopoulos and P. Linke, Chem. Eng. Process., 2009, 48, 1047–1060 CrossRef CAS
.
- R. Gani, Comput. Chem. Eng., 2004, 28, 2441–2457 CrossRef CAS
.
-
A. I. Papadopoulos, I. Tsivintzelis, P. Linke and P. Seferlis, Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, Walthm, MA, USA, 2018 Search PubMed
.
- N. D. Austin, N. V. Sahinidis and D. W. Trahan, Chem. Eng. Res. Des., 2016, 116, 2–26 CrossRef CAS
.
- D. H. Bowskill, U. E. Tropp, S. Gopinath, G. Jackson, A. Galindo and C. S. Adjiman, Mol. Syst. Des. Eng., 2020, 5, 493–510 RSC
.
- O. Odele and S. Macchietto, Fluid Phase Equilib., 1993, 82, 47–54 CrossRef CAS
.
- X. Liu, Y. Zhao, P. Ning, H. Cao and H. Wen, Ind. Eng. Chem. Res., 2018, 57, 6937–6946 CrossRef CAS
.
- N. G. Chemmangattuvalappil, C. C. Solvason, S. Bommareddy and M. R. Eden, Comput. Chem. Eng., 2010, 34, 2062–2071 CrossRef CAS
.
- D. C. Weis and D. P. Visco, Comput. Chem. Eng., 2010, 34, 1018–1029 CrossRef CAS
.
- M. Randic, J. Am. Chem. Soc., 1975, 97, 6609–6615 CrossRef CAS
.
- L. B. Kier, W. J. Murray, M. Randiċ and L. H. Hall, J. Pharm. Sci., 1976, 65, 1226–1230 CrossRef CAS PubMed
.
- L. B. Kier and L. H. Hall, J. Pharm. Sci., 1976, 65, 1806–1809 CrossRef CAS PubMed
.
- K. V. Camarda and C. D. Maranas, Ind. Eng. Chem. Res., 1999, 38, 1884–1892 CrossRef CAS
.
- N. Churi and L. E. K. Achenie, Ind. Eng. Chem. Res., 1996, 35, 3788–3794 CrossRef CAS
.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS
.
- D. Douguet, H. Munier-Lehmann, G. Labesse and S. Pochet, J. Med. Chem., 2005, 48, 2457–2468 CrossRef CAS PubMed
.
- J. Scheffczyk, P. Schäfer, L. Fleitmann, J. Thien, C. Redepenning, K. Leonhard, W. Marquardt and A. Bardow, Mol. Syst. Des. Eng., 2018, 3, 645–657 RSC
.
- C. Gertig, L. Fleitmann, C. Hemprich, J. Hense, A. Bardow and K. Leonhard, Comput. Chem. Eng., 2021, 153, 107438 CrossRef CAS
.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS
.
- A. S. Alshehri, R. Gani and F. You, Comput. Chem. Eng., 2020, 141, 107005 CrossRef CAS
.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed
.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, AIChE J., 1975, 21, 1086–1099 CrossRef CAS
.
- D. S. Abrams and J. M. Prausnitz, AIChE J., 1975, 21, 116–128 CrossRef CAS
.
- E. Sauer, M. Stavrou and J. Gross, Ind. Eng. Chem. Res., 2014, 53, 14854–14864 CrossRef CAS
.
- K. Joback and R. Reid, Chem. Eng. Commun., 1987, 57, 233–243 CrossRef CAS
.
- L. Constantinou and R. Gani, AIChE J., 1994, 40, 1697–1710 CrossRef CAS
.
- L. Constantinou, R. Gani and J. P. O'Connell, Fluid Phase Equilib., 1995, 103, 11–22 CrossRef CAS
.
- A. I. Papadopoulos, M. Stijepovic, P. Linke, P. Seferlis and S. Voutetakis, Ind. Eng. Chem. Res., 2013, 52, 12116–12133 CrossRef CAS
.
- B. I. Lee and M. G. Kesler, AIChE J., 1975, 21, 510–527 CrossRef CAS
.
- D.-Y. Peng and D. B. Robinson, Ind. Eng. Chem. Fundam., 1976, 15, 59–64 CrossRef CAS
.
- S. Cignitti, J. G. Andreasen, F. Haglind, J. M. Woodley and J. Abildskov, Appl. Energy, 2017, 203, 442–453 CrossRef CAS
.
- G. Soave, Chem. Eng. Sci., 1972, 27, 1197–1203 CrossRef CAS
.
- G. Jackson, W. G. Chapman and K. E. Gubbins, Mol. Phys., 1988, 65, 1–31 CrossRef CAS
.
- W. G. Chapman, G. Jackson and K. E. Gubbins, Mol. Phys., 1988, 65, 1057–1079 CrossRef CAS
.
- S. Tamouza, J.-P. Passarello, P. Tobaly and J.-C. de Hemptinne, Fluid Phase Equilib., 2004, 222–223, 67–76 CrossRef CAS
.
- S. Tamouza, J.-P. Passarello, P. Tobaly and J.-C. de Hemptinne, Fluid Phase Equilib., 2005, 228–229, 409–419 CrossRef CAS
.
- J. Vijande, M. M. Piñeiro, J. L. Legido and D. Bessières, Ind. Eng. Chem. Res., 2010, 49, 9394–9406 CrossRef CAS
.
- D. NguyenHuynh, Fluid Phase Equilib., 2016, 430, 33–46 CrossRef CAS
.
- M. Lampe, M. Stavrou, J. Schilling, E. Sauer, J. Gross and A. Bardow, Comput. Chem. Eng., 2015, 81, 278–287 CrossRef CAS
.
- J. Schilling, M. Lampe, J. Gross and A. Bardow, Chem. Eng. Sci., 2017, 159, 217–230 CrossRef CAS
.
- Y. Peng, K. D. Goff, M. C. dos Ramos and C. McCabe, Fluid Phase Equilib., 2009, 277, 131–144 CrossRef CAS
.
- J. Gross, O. Spuhl, F. Tumakaka and G. Sadowski, Ind. Eng. Chem. Res., 2003, 42, 1266–1274 CrossRef CAS
.
- K. Paduszyński and U. Domańska, Ind. Eng. Chem. Res., 2012, 51, 12967–12983 CrossRef
.
- V. Papaioannou, T. Lafitte, C. Avendaño, C. S. Adjiman, G. Jackson, E. A. Müller and A. Galindo, J. Chem. Phys., 2014, 140, 054107 CrossRef PubMed
.
- M. T. White, O. A. Oyewunmi, A. J. Haslam and C. N. Markides, Energy Convers. Manage., 2017, 150, 851–869 CrossRef CAS
.
- M. T. White, O. A. Oyewunmi, M. A. Chatzopoulou, A. M. Pantaleo, A. J. Haslam and C. N. Markides, Energy, 2018, 161, 1181–1198 CrossRef CAS
.
- J. Mairhofer, B. Xiao and J. Gross, Fluid Phase Equilib., 2018, 472, 117–127 CrossRef CAS
.
- P. Rehner, B. Bursik and J. Gross, Ind. Eng. Chem. Res., 2021, 60, 7111–7123 CrossRef CAS
.
- S. Xi, J. Liu, A. Valiya Parambathu, Y. Zhang and W. G. Chapman, Ind. Eng. Chem. Res., 2020, 59, 6716–6728 CrossRef CAS
.
- I. E. Grossmann and Z. Kravanja, Comput. Chem. Eng., 1995, 19, 189–204 CrossRef
.
- H. R. Henze and C. M. Blair, J. Am. Chem. Soc., 1931, 53, 3042–3046 CrossRef CAS
.
- R. Raman and I. E. Grossmann, Comput. Chem. Eng., 1994, 18, 563–578 CrossRef CAS
.
- J. Burre, D. Bongartz and A. Mitsos, Optim. Eng., 2022, 1–30 Search PubMed
.
- M. Lampe, C. De Servi, J. Schilling, A. Bardow and P. Colonna, J. Eng. Gas Turbines Power, 2019, 141, 111009 CrossRef CAS
.
- J. Schilling, D. Tillmanns, M. Lampe, M. Hopp, J. Gross and A. Bardow, Mol. Syst. Des. Eng., 2017, 2, 301–320 RSC
.
- S. Quoilin, S. Declaye, B. F. Tchanche and V. Lemort, Appl. Therm. Eng., 2011, 31, 2885–2893 CrossRef CAS
.
-
R. H. Byrd, J. Nocedal and R. A. Waltz, in Large-Scale Nonlinear Optimization, Springer, 2006, ch. KNITRO: An integrated ackage for nonlinear optimization, pp. 35–59 Search PubMed
.
- T. Esper, G. Bauer and J. Gross, in preparation, 2023.
- P. Colonna, E. Casati, C. Trapp, T. Mathijssen, J. Larjola, T. Turunen-Saaresti and A. Uusitalo, J. Eng. Gas Turbines Power, 2015, 137, 100801 CrossRef
.
- J. Frutiger, J. Andreasen, W. Liu, H. Spliethoff, F. Haglind, J. Abildskov and G. Sin, Energy, 2016, 109, 987–997 CrossRef CAS
.
- O. Lötgering-Lin and J. Gross, Ind. Eng. Chem. Res., 2015, 54, 7942–7952 CrossRef
.
- M. Hopp and J. Gross, Ind. Eng. Chem. Res., 2019, 58, 20441–20449 CrossRef CAS
.
- L. Fleitmann, J. Kleinekorte, K. Leonhard and A. Bardow, Chem. Eng. Sci., 2021, 245, 116863 CrossRef CAS
.
- J. Schilling, M. Entrup, M. Hopp, J. Gross and A. Bardow, Renewable Sustainable Energy Rev., 2021, 135, 110179 CrossRef CAS
.
- F. E. Pereira, E. Keskes, A. Galindo, G. Jackson and C. S. Adjiman, Comput. Chem. Eng., 2011, 35, 474–491 CrossRef CAS
.
- P. Rehner and G. Bauer, FeOs – A Framework for Equations of State and Classical Density Functional Theory, 2022, https://github.com/feos-org/feos Search PubMed.
| This journal is © The Royal Society of Chemistry 2023 |