DOI:
10.1039/D2MA01074G
(Paper)
Mater. Adv., 2023,
4, 1345-1353
Mechanism of ionic polarizability, bond valence, and crystal structure on the microwave dielectric properties of disordered Li10MTi13O32 (M = Zn, Mg) spinels†
Received
10th December 2022
, Accepted 6th February 2023
First published on 8th February 2023
Abstract
The influence mechanism of the microwave dielectric properties of disordered spinels (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) Li10MTi13O32 (M = Zn, Mg) was investigated via Rietveld structural refinement, ionic polarizability, bond valence, P–V–L theory, Raman spectroscopy, and DC conductivity. For Li10ZnTi13O32 and Li10MgTi13O32, promising microwave dielectric properties of εr = 28.23 ± 0.3 and 29.23 ± 0.3, Q × f = 35
m) Li10MTi13O32 (M = Zn, Mg) was investigated via Rietveld structural refinement, ionic polarizability, bond valence, P–V–L theory, Raman spectroscopy, and DC conductivity. For Li10ZnTi13O32 and Li10MgTi13O32, promising microwave dielectric properties of εr = 28.23 ± 0.3 and 29.23 ± 0.3, Q × f = 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 500 GHz and 32
800 ± 500 GHz and 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ± 500 GHz (at ∼7.5 GHz), and τf = −17.06 ± 2.0 ppm per °C and −11.05 ± 2.0 ppm per °C, respectively, were obtained at 980 °C. Bond valences reveal that almost all cations are rattling, weakening the bond strengths and widening the molecular dielectric polarizability. The expansion structures also result in τf values closer to zero and lower Q × f values. The bond ionicity and lattice energy of the Ti–O bonds are much greater than those of other bonds, indicating that the Ti–O bond is a major contributor to εr and Q × f. Moreover, the DC conductivity clarified that the Q × f values of the disordered spinels Li10ZnTi13O32 and Li10MgTi13O32 are not as high as other ordered spinels because of the transport of Li+ ions in their structures.
100 ± 500 GHz (at ∼7.5 GHz), and τf = −17.06 ± 2.0 ppm per °C and −11.05 ± 2.0 ppm per °C, respectively, were obtained at 980 °C. Bond valences reveal that almost all cations are rattling, weakening the bond strengths and widening the molecular dielectric polarizability. The expansion structures also result in τf values closer to zero and lower Q × f values. The bond ionicity and lattice energy of the Ti–O bonds are much greater than those of other bonds, indicating that the Ti–O bond is a major contributor to εr and Q × f. Moreover, the DC conductivity clarified that the Q × f values of the disordered spinels Li10ZnTi13O32 and Li10MgTi13O32 are not as high as other ordered spinels because of the transport of Li+ ions in their structures.
1. Introduction
From 1G to 5G (the fifth generation mobile network), mobile communications are constantly expanding towards higher frequency bands (microwave, millimeter wave and centimeter wave) to increase speed and capacity, which is inseparable from the support of microwave dielectric ceramic materials. Microwave dielectric ceramics for 5G applications need to have a low relative permittivity (εr) for modulating signal delay, a high quality factor (Q × f) to suppress signal attenuation, and a near-zero temperature coefficient of resonance frequency (τf) to ensure device stability in high-temperature environments.1–6
Microwave dielectric ceramics with a spinel structure (AB2O4), such as MgAl2O4,7–9 and Mg2TiO4,10 have been reported to possess a relatively low εr and a high Q × f. In order to overcome the high sintering temperature, τf is not close to zero for traditional spinels, so a large number of Li-containing spinels have been reported, such as Li2ATi3O8 (A = Zn, Mg),11,12 LiGa5O8,13,14 Li2Zn3Ti4O12,15 and Li4Ti5O12.16–18 Concerning the Li2O–AO–TiO2 (A = Zn, Mg) systems, recent studies have focused on the characterization and microwave dielectric properties of two ordered ceramics of Li2ZnTi3O8 (εr = 25.6–26.2, Q × f = 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–72
000–72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GHz, and τf = −15 to −11.2 ppm per °C) and Li2MgTi3O8 (εr = 20.2, Q × f = 42
000 GHz, and τf = −15 to −11.2 ppm per °C) and Li2MgTi3O8 (εr = 20.2, Q × f = 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GHz, and τf = +3.2 ppm per °C), but the microwave dielectric properties of disordered spinel ceramics have rarely been reported. For ordered Li-containing spinels, Li4b and Ti12d at the octahedral sites were arranged spontaneously into 1
000 GHz, and τf = +3.2 ppm per °C), but the microwave dielectric properties of disordered spinel ceramics have rarely been reported. For ordered Li-containing spinels, Li4b and Ti12d at the octahedral sites were arranged spontaneously into 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 cation ordering (i.e., [Li0.5Zn0.5]tet[Li0.5Ti1.5]octO4 and [Li0.55Mg0.45]tet[(Li0.45Mg0.05)Ti1.5]octO4) with a space group of P4332. The spinel-structured Li2MM′3O8 (M = Mg, Co, Ni, Zn; M′ = Ti, Ge) ceramics with an ordered spinel structure (P4332) have been reported to possess a relative εr of 10.5–28.9, a Q × f of 47
3 cation ordering (i.e., [Li0.5Zn0.5]tet[Li0.5Ti1.5]octO4 and [Li0.55Mg0.45]tet[(Li0.45Mg0.05)Ti1.5]octO4) with a space group of P4332. The spinel-structured Li2MM′3O8 (M = Mg, Co, Ni, Zn; M′ = Ti, Ge) ceramics with an ordered spinel structure (P4332) have been reported to possess a relative εr of 10.5–28.9, a Q × f of 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400–160
400–160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GHz, and a τf of −63.9 to +7.4 ppm per °C.19–25
000 GHz, and a τf of −63.9 to +7.4 ppm per °C.19–25
Recently, we found an interesting phenomenon in the ordered spinels Li1.33xA2−2xTi1+0.67xO4 (x = 0.5625; A = Zn, Mg),26 namely, a large positive deviation [Δεr = (εr(corr)–εr(C–M))/εr(C–M) = 16–91%] between the porosity-corrected permittivity εr(corr) and the calculated εr(C–M) using the Clausius–Mossotti (C–M) equation, which might be related to the combined effect of the rattling and the compressed cations at the A and B sites, which was mutually verified in garnet and zircon systems,27–30 thus establishing the interaction mechanism of bond length, polarization, permittivity, and τf.
Hernandez et al.31 discovered that Li1.33xZn2−2xTi1+0.67xO4 spinels undergo two order–disorder transitions to the interval of x = [0–1], where x ≤ 0.5 is the disordered face-centered cubic phase (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), 0.5 < x < 0.9 is the ordered primitive cubic phase (P4332), and when x is beyond 0.9, it becomes face-centered cubic again. And a similar phenomenon occurs in magnesium analogs.32 The different cation occupation is the main reason for the order and disorder changes in the spinel structure. In the disordered structure, there is only one kind of regular octahedron (16d) and one tetrahedron (8a), compared with the two octahedra (4b, 12d) and one tetrahedron (8c) in the ordered structure. The disordered structure is simpler and more conducive to studying the influence of the bond length, bond valence, and polarization on the microwave dielectric properties.
m), 0.5 < x < 0.9 is the ordered primitive cubic phase (P4332), and when x is beyond 0.9, it becomes face-centered cubic again. And a similar phenomenon occurs in magnesium analogs.32 The different cation occupation is the main reason for the order and disorder changes in the spinel structure. In the disordered structure, there is only one kind of regular octahedron (16d) and one tetrahedron (8a), compared with the two octahedra (4b, 12d) and one tetrahedron (8c) in the ordered structure. The disordered structure is simpler and more conducive to studying the influence of the bond length, bond valence, and polarization on the microwave dielectric properties.
In this paper, we focus on the disordered compositions Li10MTi13O32 (M = Zn, Mg) with x = 0.9375 in Li1.33xM2−2xTi1+0.67xO4 spinels. It is a Z = 1 structure located between the disorder x = 0.9 and x = 1 (Li4Ti5O12, εr = 30.1, Q × f = 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 GHz, τf = −15 ppm per °C).13 The main aim of this work is to investigate the effects of the bond length, bond valence, ionic dielectric polarizability, structural stability, and rattling and compressed cations on the microwave dielectric properties (εr, τf, and Q × f) both theoretically and experimentally.
530 GHz, τf = −15 ppm per °C).13 The main aim of this work is to investigate the effects of the bond length, bond valence, ionic dielectric polarizability, structural stability, and rattling and compressed cations on the microwave dielectric properties (εr, τf, and Q × f) both theoretically and experimentally.
2. Experimental procedure
Li10MTi13O32 (M = Zn, Mg) ceramics were prepared via a solid-state reaction using high-purity (>99.99%) Li2CO3, ZnO, MgO, and TiO2 (rutile) powders as raw materials. Before weighing, the MgO, ZnO, and TiO2 powders were calcined to remove any moisture (900 °C/2 h). The raw materials were ground using a ball mill for 6 h, the powder was calcined at 800 °C for 4 h, and then it was ball milled once with a 5 wt% PVA binder. The obtained powder was uniaxially pressed into cylinders with a diameter of 10 mm and a height of 5 mm at a pressure of 150 MPa. Subsequently, the samples were heated from room temperature to 550 °C for 4 h to burn off the organic binder and then sintered at 940–1020 °C for 4 h with a temperature-ramping rate of 5 °C min−1.
The phase purity and crystal structure of the Li10MTi13O32 (M = Zn, Mg) ceramics were identified via a powder X-ray diffractometer (X’Pert PRO). Scanning electron microscopy (SEM; S4800, Hitachi) was used to observe the grain growth of the Li10MTi13O32 (M = Zn, Mg) ceramics after polishing and thermal etching (below the sintering temperature of 50 °C for 30 min). The average grain size of the Li10MTi13O32 (M = Zn, Mg) ceramics was evaluated using Nano Measurer software. The densities of the sintered ceramics were determined using the Archimedes principle. The Raman spectra of the ceramics were collected using a Raman spectrometer (Thermo Fisher Scientific) with a 532 nm laser. Impedance spectroscopy was carried out using an impedance analyzer (4291A, Agilent, America), and DC conductivity testing was performed using a high-temperature resistivity test system (RMS-1000I, Partulab, China) at selected temperatures. The εr, dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = 1/Q), and resonant frequency (f) were determined using the Hakki–Coleman method using a network analyzer (N5230A, Agilent, America) (ESI†). The drift of the f and εr (i.e., τf and τε) were calculated as follows:
δ = 1/Q), and resonant frequency (f) were determined using the Hakki–Coleman method using a network analyzer (N5230A, Agilent, America) (ESI†). The drift of the f and εr (i.e., τf and τε) were calculated as follows:
| |  | (1) |
| | 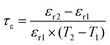 | (2) |
where
f1 and
f2 represent the resonant frequency at
T1 and
T2, respectively.
3. Results and discussion
Fig. 1a shows the XRD patterns of the Li10ZnTi13O32 and Li10MgTi13O32 ceramics sintered at 980 °C, respectively. The diffraction peaks of Li10MTi13O32 (M = Zn, Mg) were well indexed with the disordered spinel Li4Ti5O12 phase (PDF#49-0207). Then, Rietveld structural refinements were carried out on Li10MTi13O32 (M = Zn, Mg) established on the reported cubic Li4Ti5O12 disordered structure model (ICSD#160655) with the space group of Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The refined plots for Li10ZnTi13O32 and Li10MgTi13O32 are displayed in Fig. 1b and c, respectively, and the refined structural parameters are listed in Table 1. It is notable that the refined lattice parameters of a = 8.3636 Å and V = 585.0211 Å3 for Li10ZnTi13O32 are smaller than a = 8.3649 Å and V = 585.2944 Å3 for Li10MgTi13O32, which is opposite to the ionic radii of Zn2+ (0.60 Å) and Mg2+ (0.57 Å, CN = 4), which might be related to the rattling effect of cations in Li10MgTi13O32. The crystal structure and cation occupancy information of the Li10MTi13O32 ceramics are presented in Fig. 1d and Table 1, respectively. It is observed that Li and M share the tetrahedral sites (8a), and Li and Ti share the octahedral sites (16d). The octahedra and tetrahedra are connected at their common vertices, and the octahedra are connected at their common edges to form the structural skeleton. The tetrahedra are isolated from each other, indicating that the influence of the octahedron on the structure is dominant. Moreover, Fig. S1 (ESI†) depicts the bond lengths in Li10MTi13O32 (M = Zn, Mg) from the Rietveld refinements.
m. The refined plots for Li10ZnTi13O32 and Li10MgTi13O32 are displayed in Fig. 1b and c, respectively, and the refined structural parameters are listed in Table 1. It is notable that the refined lattice parameters of a = 8.3636 Å and V = 585.0211 Å3 for Li10ZnTi13O32 are smaller than a = 8.3649 Å and V = 585.2944 Å3 for Li10MgTi13O32, which is opposite to the ionic radii of Zn2+ (0.60 Å) and Mg2+ (0.57 Å, CN = 4), which might be related to the rattling effect of cations in Li10MgTi13O32. The crystal structure and cation occupancy information of the Li10MTi13O32 ceramics are presented in Fig. 1d and Table 1, respectively. It is observed that Li and M share the tetrahedral sites (8a), and Li and Ti share the octahedral sites (16d). The octahedra and tetrahedra are connected at their common vertices, and the octahedra are connected at their common edges to form the structural skeleton. The tetrahedra are isolated from each other, indicating that the influence of the octahedron on the structure is dominant. Moreover, Fig. S1 (ESI†) depicts the bond lengths in Li10MTi13O32 (M = Zn, Mg) from the Rietveld refinements.
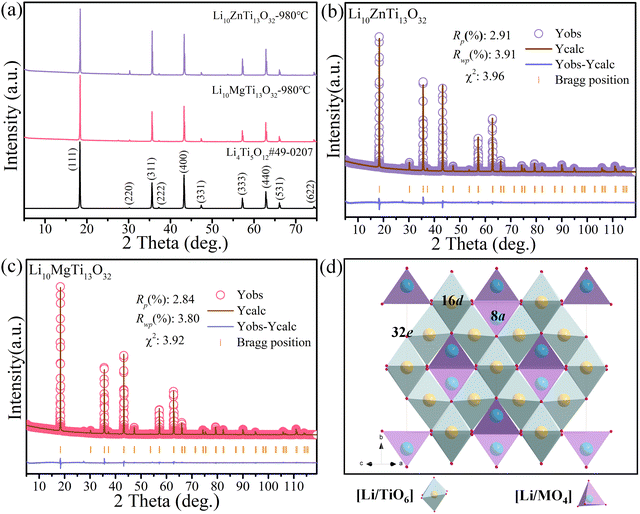 |
| | Fig. 1 (a) XRD patterns of the Li10MTi13O32 (M = Zn, Mg) ceramics sintered at the optimum temperature. Rietveld refinement patterns of (b) Li10ZnTi13O32 and (c) Li10MgTi13O32. (d) Schematic diagram of the crystal structure of spinel-type Li10MTi13O32 (M = Zn, Mg). | |
Table 1 Refined structural parameters, thermal parameters, and reliability factors of the Li10MTi13O32 (M = Zn, Mg) ceramics
| Compound |
Atom |
Site |
Occ. |
x, y, z |
B (Å2) |
a (Å) |
V (Å3) |
R
p (%) |
R
wp (%) |
χ
2
|
| Li10ZnTi13O32 |
Zn(1) |
8a |
0.1250 |
0.1250 |
0.3866 |
8.3636 |
585.0211 |
2.91 |
3.91 |
3.96 |
| Li(1) |
8a |
0.8750 |
0.1250 |
0.3866 |
| Li(2) |
16d |
0.1875 |
0.5000 |
0.5396 |
| Ti(1) |
16d |
0.8125 |
0.5000 |
0.5396 |
| O(1) |
32e |
1.0000 |
0.2621 |
0.4660 |
| Li10MgTi13O32 |
Mg(1) |
8a |
0.1250 |
0.1250 |
0.5066 |
8.3649 |
585.2944 |
2.84 |
3.80 |
3.92 |
| Li(1) |
8a |
0.8750 |
0.1250 |
0.5066 |
| Li(2) |
16d |
0.1875 |
0.5000 |
0.8772 |
| Ti(1) |
16d |
0.8125 |
0.5000 |
0.8772 |
| O(1) |
32e |
1.0000 |
0.2622 |
0.7794 |
Raman spectra can reflect the vibrations of chemical bonds and their structural characteristics. The Raman spectra of the Li10ZnTi13O32 and Li10MgTi13O32 ceramics are shown in Fig. 2. Six modes at 228, 258, 342, 417, 512, and 675 cm−1 for Li10ZnTi13O32 and 231, 260, 340, 418, 514, and 676 cm−1 for Li10MgTi13O32 were observed, which are very close to the previously reported values for disordered Li4Ti5O12 (246, 274, 360, 429, and 680 cm−1; A1g + Eg + 3F2u).33,34 However, the Raman spectra of Li10ZnTi13O32 and Li10MgTi13O32 show a new mode at 512 cm−1 and 514 cm−1, respectively, which may be ascribable to Zn–O and Mg–O stretches in the [ZnO4] and [MgO4] tetrahedra.35,36 For Li10ZnTi13O32, the Raman band at 676 cm−1 is considered to be the A1g mode associated with the stretching vibration of [TiO6]. The 417 cm−1 band is roughly the Eg mode associated with the [LiO4] stretching vibration. The mode at 340 cm−1 is due to the bending vibrations at the O–Li–O and O–Ti–O bonds. The same is true for the Li10MgTi13O32 ceramic, and the Raman vibration modes are listed in Table 2. In addition, most of the Raman shifts of Li10MgTi13O32 were found to be lower than those of Li10ZnTi13O32, which may be related to the expansion of the cationic-oxygen bond and its larger unit cell parameter (a). In general, an increase in bond expansion is accompanied by a weakening of the bond, which leads to a decrease in the frequency.37
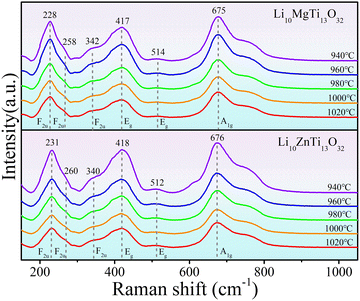 |
| | Fig. 2 Raman spectra of the Li10MTi13O32 (M = Zn, Mg) ceramics studied at different sintering temperatures. | |
Table 2 Raman vibration modes the Li10MTi13O32 (M = Zn, Mg) ceramics
| Li10ZnTi13O32 |
Li10MgTi13O32 |
| Raman mode (cm−1) |
Raman mode (cm−1) |
Symmetry mode |
Assignment |
| 231 |
228 |
F2u |
O–Li–O, O–Ti–Obending |
| 258 |
260 |
F2u |
O–Li–O, O–Ti–Obending |
| 340 |
342 |
F2u |
O–Li–O, O–Ti–Obending |
| 418 |
417 |
Eg |
[LiO4]stretching |
| 514 |
512 |
Eg |
[Zn/MgO4]stretching |
| 676 |
675 |
A1g |
[TiO6]stretching |
In the sintering behavior of ceramics, grain growth is a manifestation of the densification process. SEM was carried out to observe the polished and thermally etched grains. As shown in Fig. 3a–c, the average grain size (![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) ) of Li10ZnTi13O32 increased from 3.81 μm to 5.06 μm as the sintering temperature was increased. When sintered at 940 °C, the grain size was not uniform, and there was some slight porosity. As the temperature was increased to 980 °C, the grain size increased with the disappearance of the pores, and the microstructure became uniform and compact. When the temperature was raised further, the size of some grains increased abnormally. As shown in Fig. 3d–f, the grain growth process of the Li10MgTi13O32 ceramic (the average grain size increased from 2.66 μm to 4.85 μm) is similar to that of Li10ZnTi13O32, and the densest microstructure is obtained at 980 °C.
) of Li10ZnTi13O32 increased from 3.81 μm to 5.06 μm as the sintering temperature was increased. When sintered at 940 °C, the grain size was not uniform, and there was some slight porosity. As the temperature was increased to 980 °C, the grain size increased with the disappearance of the pores, and the microstructure became uniform and compact. When the temperature was raised further, the size of some grains increased abnormally. As shown in Fig. 3d–f, the grain growth process of the Li10MgTi13O32 ceramic (the average grain size increased from 2.66 μm to 4.85 μm) is similar to that of Li10ZnTi13O32, and the densest microstructure is obtained at 980 °C.
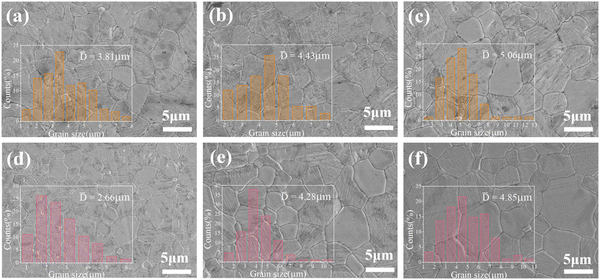 |
| | Fig. 3 Polished and thermally etched SEM images of the Li10ZnTi13O32 ceramic sintered at (a) 940 °C, (b) 980 °C, and (c) 1020 °C, and the Li10MgTi13O32 ceramic sintered at (d) 940 °C, (e) 980 °C, and (f) 1020 °C. | |
Fig. 4a presents the variation of the bulk density and relative density of the Li10MTi13O32 (M = Zn, Mg) ceramics at different sintering temperatures. The theoretical density is calculated based on structural refinement (3.6009 g cm−3 for Li10ZnTi13O32 and 3.4827 g cm−3 for Li10MgTi13O32). Both Li10ZnTi13O32 and Li10MgTi13O32 show high relative densities (>95%) in the sintering range. The saturation relative density of Li10ZnTi13O32 was 98.19% at 980 °C, and the maximum relative density of Li10MgTi13O32 was 98.25%.
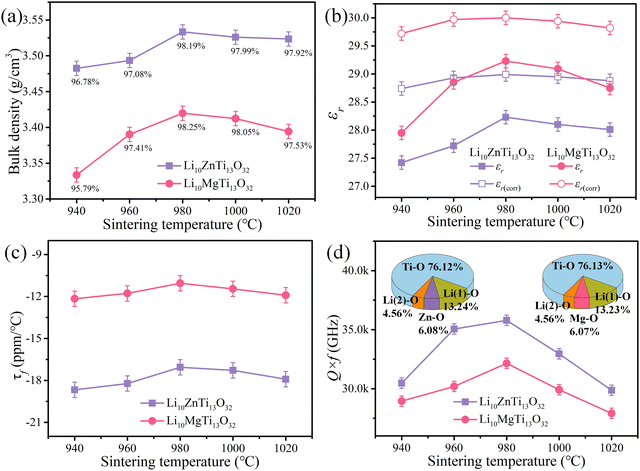 |
| | Fig. 4 (a) Density, (b) εr, (c) τf, and (d) Q × f of the Li10MTi13O32 (M = Zn, Mg) samples as a function of the sintering temperature, the inset in (d) shows the contribution of each bond to the lattice energy. | |
As shown in Fig. 4b, the εr of the Li10ZnTi13O32 ceramic increases from 27.42 at 940 °C to 28.23 at 980 °C, after which it decreases slightly with increasing temperature, and the change in the εr of the Li10MgTi13O32 ceramic is consistent with that of Li10ZnTi13O32, reaching a maximum of 29.23 at 980 °C. In general, the relative permittivity of the ceramics is correlated with the porosity, which can be corrected using the Bosman–Havinga equation:38
| | | εr(corr) = εr(1 + 1.5P) | (3) |
| | 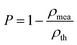 | (4) |
where
P denotes the fractional porosity, and
ρth and
ρmea are the theoretical and measured density values, respectively. The corrected permittivity
εr(corr) at the optimum sintering temperature is 28.99 for Li
10ZnTi
13O
32 and 30.00 for the Li
10MgTi
13O
32 ceramic. The evaluated permittivity
εr(C–M) is 16.05 for Li
10ZnTi
13O
32 and 15.47 for Li
10MgTi
13O
32, which are calculated using the Clausius–Mossotti equation:
39| | 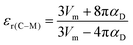 | (5) |
| | | αD = 10α(Li+) + α(Zn/Mg2+) + 13α(Ti4+) + 32α(O2−) | (6) |
Here, αD is the molecular dielectric polarizability, which is the sum of the dielectric polarizabilities of the individual ions: Li+ (1.20 Å3), Zn2+ (2.04 Å3), Mg2+ (1.32 Å3), Ti4+ (2.93 Å3) and O2− (2.01 Å3). It is clear that εr(C–M) is rather low compared with εr(corr), as listed in Table 3. In addition, the εr(corr) of Li10MgTi13O32 is larger than Li10ZnTi13O32, an opposite trend to that of εr(C–M). The discrepancy between εr(corr) and εr(C–M) can be due to the “rattling” or “compressed” cations. When the motion of cations and/or anions is restricted by crystal symmetry, larger than normal bond distances and/or thermal motions may occur, resulting in abnormally large polarizabilities.40,41 Macroscopically, the variation in the bond length is manifested as the change in the bond valence (BV; Vi):
| | 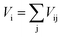 | (7) |
| | 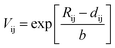 | (8) |
Where
Rij is the bond valence parameter,
dij is the bond length and
b is a constant (0.37 Å).
42Table 4 presents the BV values of the Li
10ZnTi
13O
32 and Li
10MgTi
13O
32 ceramics. The average bond valence (1.0921 v.u.) of the A-site (8a) in Li
10ZnTi
13O
32 is slightly lower than the normal value (1.1250 v.u.), indicating that the A-site is in an expanded state and that both Li(1) and Zn are rattling cations. The B-site (16d) also shows an expanded state, but only Ti is a rattling cation, and Li(2) is tightly bound in its octahedral site and is not a rattling cation. The same is true for each ion in Li
10MgTi
13O
32. The weighted average discrepancy factor (<
d>) can give the average deviation from the normal bond valence sums in a compound:
| | 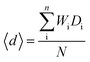 | (9) |
where
W is the Wyckoff site multiplicity,
Di is the discrepancy factor for each of the
n ions on a distinct crystallographic site, and
N is the number of atoms in the unit cell. As listed in
Table 4, the negative 〈
d〉 values of the Li
10MTi
13O
32 (M = Zn, Mg) ceramics indicate that the ions are, on average, under-bonded and the overall structure of the material is in a slightly expanded state. The
εr(corr) is higher than
εr(C–M) because longer and weaker bonds are more likely to cause polarization. Furthermore, the |
<d>| value of Li
10MgTi
13O
32 (0.0670 v.u.) is slightly higher than that of Li
10ZnTi
13O
32 (0.0601 v.u.), which explains why, although Li
10MgTi
13O
32 has a lower
αD value than Li
10ZnTi
13O
32, its
εr(corr) value is slightly higher.
Table 3 Permittivity and τf values of the Li10MTi13O32 (M = Zn, Mg) ceramics at the optimal sintering temperature
| Compounds |
S.T. (°C) |
ε
r
|
ε
r(corr)
|
ε
r(C–M)
|
Δεr (%) |
τ
f (ppm per °C) |
| Li10ZnTi13O32 |
980 |
28.23 ± 0.3 |
28.99 |
16.05 |
80.62 |
−17.06 ± 2.0 |
| Li10MgTi13O32 |
980 |
29.23 ± 0.3 |
30.00 |
15.47 |
93.92 |
−11.05 ± 2.0 |
Table 4 Bond ionicity and bond valences of the Li10MTi13O32 (M = Zn, Mg) ceramics
| Compound |
Atom |
f
μi (%) |
Site |
BV (v.u.) |
Average BV (v.u.) |
Normal BV (v.u.) |
D
i
(v.u.) |
<d> (v.u.) |
| [Zn0.125Li0.875]tet[Li0.1875Ti0.8125]octO4 |
Zn(1) |
43.2111 |
8a |
1.8671 |
1.0921 |
1.1250 |
−0.1329 |
−0.0601 |
| Li(1) |
65.7780 |
|
0.9813 |
−0.0187 |
| Li(2) |
66.9681 |
16d |
1.4366 |
3.2672 |
3.4375 |
−0.5634 |
| Ti(1) |
92.8605 |
|
3.6897 |
−0.3103 |
| O(1) |
|
32e |
2.0819 |
2.0819 |
2.0000 |
0.0819 |
| [Mg0.125Li0.875]tet[Li0.1875Ti0.8125]octO4 |
Mg(1) |
43.2442 |
8a |
1.8027 |
1.0794 |
1.1250 |
−0.1973 |
−0.0670 |
| Li(1) |
65.8038 |
|
0.9760 |
−0.0240 |
| Li(2) |
66.9655 |
16d |
1.4390 |
3.2725 |
3.4375 |
−0.5610 |
| Ti(1) |
92.8611 |
|
3.6957 |
−0.3043 |
| O(1) |
|
32e |
2.0703 |
2.0703 |
2.0000 |
0.0703 |
The bond ionicity (fi) can be calculated using Phillips–Van Vechten–Levine (P–V–L) theory and structural refinement of the bond length (Table S1, ESI†), which is usually related to the variation of the measured εr.43,44 The relationship between the bond ionicity (fi) and εr can be described using the following formula:45
| | 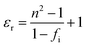 | (10) |
where
n is the refractive index. The
fi of the μ bond is obtained using the following formula:
46| | 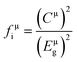 | (11) |
where
Eμg and
Cμ are the average energy interval and heteropolar part, respectively (Table S2, ESI
†). As listed in
Table 4, the smaller bond ionicity of all the bonds in Li
10ZnTi
13O
32 is observed, suggesting a lower
εr for Li
10ZnTi
13O
32 for than Li
10MgTi
13O
32. Besides,
fμi(Ti–O) possesses the maximum value in the Li
10MTi
13O
32 (M = Zn, Mg) ceramics, indicating that the Ti–O bond contributes the most to
εr.
As shown in Fig. 4c, the τf values of the Li10MTi13O32 (M = Zn, Mg) ceramics sintered at various temperatures show a weak temperature dependence and remained stable at around −17.06 ppm per °C (Li10ZnTi13O32) and −11.05 ppm per °C (Li10MgTi13O32). Generally, τf is strongly determined by the coefficient of thermal expansion (αL) and the temperature coefficient of the dielectric constant (τε) [i.e., τf = −(τε/2 + αL)].47 The measured τε values are +2.61 ppm per °C for Li10MgTi13O32 and +15.77 ppm per °C for Li10ZnTi13O32 at microwave frequencies between 25 °C and 85 °C. The αL values of the Li10MgTi13O32 and Li10ZnTi13O32 ceramics are calculated as 9.74 ppm per °C and 9.18 ppm per °C, respectively. Clearly, τε is larger than αL and thus plays a dominant role in τf. And more deeply, τε is related to the temperature coefficient of ionic polarizability (ταm):48
| | 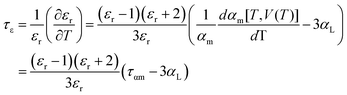 | (12) |
The ταm values are 29.16 ppm per °C for Li10ZnTi13O32 and 29.48 ppm per °C for Li10MgTi13O32. Therefore, the negative τf values for Li10MTi13O32 (M = Zn, Mg) originate from the positive ταm value being slightly higher than 3αL, which makes the τf values close to zero.
As shown in Fig. 4d, the maximum Q × f values of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 and 32
800 and 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 GHz are obtained, respectively, for Li10ZnTi13O32 and Li10MgTi13O32 sintered at 980 °C. The Q × f of Li10MgTi13O32 is slightly lower than that of Li10ZnTi13O32, which may be due to the increase in intrinsic dielectric loss caused by weakly bonded cations in the extended coordination environment. In a classical sense, the more under-bonded cations contribute to the dielectric loss because the cations “rattle” more freely in the polyhedral cage and may interact more strongly with the anharmonic phonons.49 For intrinsic losses, the lattice energy (U) based on P–V–L theory can be evaluated as follows:50–52
100 GHz are obtained, respectively, for Li10ZnTi13O32 and Li10MgTi13O32 sintered at 980 °C. The Q × f of Li10MgTi13O32 is slightly lower than that of Li10ZnTi13O32, which may be due to the increase in intrinsic dielectric loss caused by weakly bonded cations in the extended coordination environment. In a classical sense, the more under-bonded cations contribute to the dielectric loss because the cations “rattle” more freely in the polyhedral cage and may interact more strongly with the anharmonic phonons.49 For intrinsic losses, the lattice energy (U) based on P–V–L theory can be evaluated as follows:50–52
| | 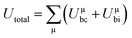 | (13) |
| | 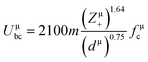 | (14) |
| | 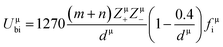 | (15) |
where
Zμ+ and
Zμ− are the valence states of the cation and anion,
dμ is the bond length, and
Uμbi and
Uμbc are the ionic part and the covalent part of the μ bond, respectively. As listed in
Table 5, the total lattice energy (
Utotal) of the Li
10ZnTi
13O
32 ceramic is greater than that of the Li
10MgTi
13O
32 ceramic, and the larger
Utotal corresponds to the higher
Q × f value. This is because the
Q × f value is mainly determined by the lattice anharmonicity.
53 As the lattice energy increases, the lattice anharmonicity will also increase, which reduces the inherent dielectric loss and increases the
Q × f value. Moreover, the lattice energy of the Ti–O bond is much greater than that of other bonds, accounting for 76.12% of the total lattice energy for Li
10ZnTi
13O
32 and 76.13% for Li
10MgTi
13O
32, indicating that the contribution of the Ti–O bond to the
Q × f value is dominant. In addition, the
Q ×
f value is strongly dependent on the packing fraction, which is defined by summing the volume of packed ions over the unit cell volume:
54| | 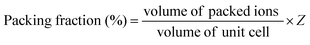 | (16) |
Table 5 Bond length (d), lattice energy (U), Q × f, and packing fraction of the Li10MTi13O32 (M = Zn, Mg) ceramics
| Ceramic |
Bond type |
d (Å) |
U (kJ mol−1) |
Q × f (GHz) |
Packing fraction (%) |
| Li10ZnTi13O32 |
Li(1)–O × 4 |
1.9859 |
913.4093 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 500 800 ± 500 |
68.42 |
| Zn–O × 4 |
1.9859 |
419.3192 |
| Li(2)–O × 6 |
1.9949 |
314.7417 |
| Ti–O × 6 |
1.9949 |
5250.0245 |
|
U
total = 6897.4947 |
| Li10MgTi13O32 |
Li(1)–O × 4 |
1.9879 |
912.5777 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ± 500 100 ± 500 |
68.36 |
| Mg–O × 4 |
1.9879 |
418.9638 |
| Li(2)–O × 6 |
1.9943 |
314.8187 |
| Ti–O × 6 |
1.9943 |
5250.1225 |
|
U
total = 6897.4827 |
As seen in Table 5, the packing fraction of Li10ZnTi13O32 (68.42%) is higher than that of Li10MgTi13O32 (68.36%). The increase in packing fraction can reduce the vibration of the crystal lattice and thus enhance the quality factor. Raman spectroscopy is also an effective tool for studying lattice vibration information and dielectric loss.55Table 6 shows the FWHM values of the A1g mode at different sintering temperatures for the Li10MTi13O32 (M = Zn, Mg) ceramics, and the trend of Q × f is opposite to the FWHM. The lower the FWHM, the smaller the space for lattice vibration and the non-harmonic vibration, resulting in a decrease in the inherent dielectric loss or an increase in Q × f.56
Table 6 Variation of the FWHM value of the Raman spectrum with the sintering temperature for the Li10MTi13O32 (M = Zn, Mg) ceramics
| Compound |
Sintering temperature (°C) |
FWHM (cm−1) |
| Li10ZnTi13O32 |
940 |
79.03337 |
| 960 |
78.40893 |
| 980 |
78.31708 |
| 1000 |
78.53711 |
| 1020 |
79.51513 |
| Li10MgTi13O32 |
940 |
75.12137 |
| 960 |
74.89138 |
| 980 |
74.47194 |
| 1000 |
75.18652 |
| 1020 |
76.04403 |
The Q × f values of the disordered spinel (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) microwave dielectric ceramics Li10ZnTi13O32 and Li10MgTi13O32 are not as high as those of ordered spinels, which may be related to the transport of Li+ ions in the structure. Complex impedance analysis was employed to explain the effects of Li+ ions on the structure and Q × f. Fig. 5a and b show the complex impedance plane plots of the Li10MTi13O32 (M = Zn, Mg) ceramics at 633–573K. The Li10MTi13O32 (M = Zn, Mg) ceramics show high resistivity and good insulation. The relationship between the DC (direct current) conductivity (σdc) and the temperature can be expressed via the following Arrhenius equation:
m) microwave dielectric ceramics Li10ZnTi13O32 and Li10MgTi13O32 are not as high as those of ordered spinels, which may be related to the transport of Li+ ions in the structure. Complex impedance analysis was employed to explain the effects of Li+ ions on the structure and Q × f. Fig. 5a and b show the complex impedance plane plots of the Li10MTi13O32 (M = Zn, Mg) ceramics at 633–573K. The Li10MTi13O32 (M = Zn, Mg) ceramics show high resistivity and good insulation. The relationship between the DC (direct current) conductivity (σdc) and the temperature can be expressed via the following Arrhenius equation:
| | 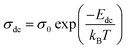 | (17) |
where
σ0 is the pre-constant,
kB is the Boltzmann constant (8.617 × 10
−5 eV K
−1),
T is the temperature (in Kelvin), and
Edc is the activation energy from DC conductivity. The
Edc values for Li
10MTi
13O
32 (M = Zn, Mg) can be obtained according to the slope of the fitted straight line for each ceramic:
Edc = 0.4230 eV for Li
10ZnTi
13O
32, and
Edc = 0.5531 eV for Li
10MgTi
13O
32 (
Fig. 5c). The DC conductivity activation energy can reflect the sum of the free energies of the carriers to produce long jumps, and the small
Edc values in the Li
10MTi
13O
32 (M = Zn, Mg) ceramics might come from the embedding and detaching of Li
+ in the spinel structure. The DC conductivities of the Li
10MTi
13O
32 (M = Zn, Mg) ceramics as a function of temperature were also measured in
Fig. 5d. When the temperature is increased from 303 K to 683 K, the conductivity of Li
10ZnTi
13O
32 increases from 5.67 × 10
−10 S cm
−1 to 2.21 × 10
−5 S cm
−1, and the conductivity of Li
10MgTi
13O
32 increases from 6.11 × 10
−9 S cm
−1 to 9.27 × 10
−5 S cm
−1, where the conductivity of Li
10ZnTi
13O
32 is less than that of Li
10MgTi
13O
32. Li-rich spinel materials are also candidates for lithium-ion conductors, such as Li
4Ti
5O
12, which brings about the higher dielectric loss of this material relative to other spinels.
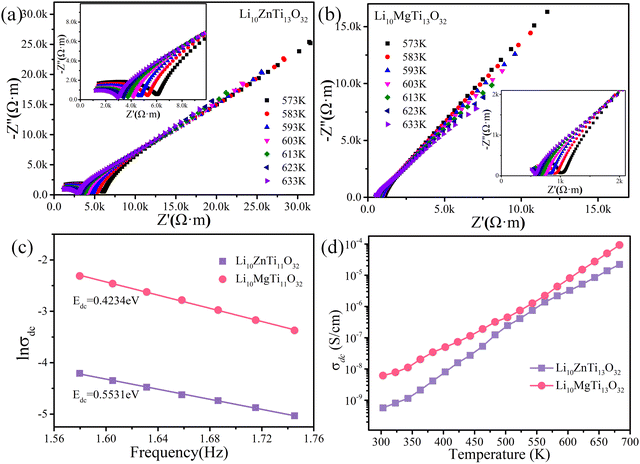 |
| | Fig. 5 Complex impedance plane plots of (a) Li10ZnTi13O32 and (b) Li10MgTi13O32 at 633–573 K. (The inset shows a magnification of the impedance). (c) Arrhenius plots of DC conductivity (σdc) for the Li10MTi13O32 (M = Zn, Mg) ceramics. (d) DC conductivity of the Li10MTi13O32 (M = Zn, Mg) ceramics as a function of temperature. | |
4. Conclusions
Li10MTi13O32 (M = Zn, Mg) ceramics with a disordered spinel structure (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) were synthesized using a solid-state reaction method. Li10ZnTi13O32 and Li10MgTi13O32 with relative permittivities of 28.23 ± 0.3 and 29.23 ± 0.3, Q × f values of 35
m) were synthesized using a solid-state reaction method. Li10ZnTi13O32 and Li10MgTi13O32 with relative permittivities of 28.23 ± 0.3 and 29.23 ± 0.3, Q × f values of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 500 GHz and 32
800 ± 500 GHz and 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ± 500 GHz (at ∼7.5 GHz), and τf values of −17.06 ± 2.0 ppm per °C and −11.05 ± 2.0 ppm per °C, respectively, were obtained at 980 °C. The permittivities εr(C–M) calculated using the Clausius–Mossotti (C–M) equation are significantly lower than the permittivities εr(corr) corrected by the porosity (εr(C–M) = 16.05, εr(corr) = 28.99 for Li10ZnTi13O32; εr(C–M) = 15.47, εr(corr) = 30.00 for Li10MgTi13O32). The main reason for this phenomenon comes from the longer and weaker bonds in the Li10MTi13O32 (M = Zn, Mg) ceramics that are more facile to polarization. The larger negative weighted average discrepancy factor (<d>) of Li10MgTi13O32 (−0.0670 v.u.) than that of Li10ZnTi13O32 (−0.0601 v.u.) is a good explanation for the higher εr(corr) value of Li10MgTi13O32 (αD = 115.73 A3), although its dielectric polarizability (αD) is lower than that of Li10ZnTi13O32 (αD = 116.45 A3). This expansion structure also results in a closer value of τf to zero and a lower Q × f. Values of the temperature coefficient of ionic polarizability (ταm) are 29.22 ppm per °C for Li10ZnTi13O32 and 29.84 ppm per °C for Li10MgTi13O32, and the small negative τf values of Li10MTi13O32 (M = Zn, Mg) are derived from the proximity of ταm to 3αL. Calculations using P–V–L theory also confirmed that the bond ionicity (fi) of all the bonds in the prepared Li10MgTi13O32 structure was higher than that of Li10ZnTi13O32, and the Ti–O bond contributed the most to εr. The lattice energy of the Ti–O bonds is much greater than that of other bonds, indicating that it is also a major contributor to Q × f in the Li10MTi13O32 (M = Zn, Mg) ceramics. In addition, a study of the DC conductivity clarified that the Q × f values of the disordered spinels Li10ZnTi13O32 and Li10MgTi13O32 are not as high as other ordered spinels, which may be due to the transport of Li+ ions in their structures.
100 ± 500 GHz (at ∼7.5 GHz), and τf values of −17.06 ± 2.0 ppm per °C and −11.05 ± 2.0 ppm per °C, respectively, were obtained at 980 °C. The permittivities εr(C–M) calculated using the Clausius–Mossotti (C–M) equation are significantly lower than the permittivities εr(corr) corrected by the porosity (εr(C–M) = 16.05, εr(corr) = 28.99 for Li10ZnTi13O32; εr(C–M) = 15.47, εr(corr) = 30.00 for Li10MgTi13O32). The main reason for this phenomenon comes from the longer and weaker bonds in the Li10MTi13O32 (M = Zn, Mg) ceramics that are more facile to polarization. The larger negative weighted average discrepancy factor (<d>) of Li10MgTi13O32 (−0.0670 v.u.) than that of Li10ZnTi13O32 (−0.0601 v.u.) is a good explanation for the higher εr(corr) value of Li10MgTi13O32 (αD = 115.73 A3), although its dielectric polarizability (αD) is lower than that of Li10ZnTi13O32 (αD = 116.45 A3). This expansion structure also results in a closer value of τf to zero and a lower Q × f. Values of the temperature coefficient of ionic polarizability (ταm) are 29.22 ppm per °C for Li10ZnTi13O32 and 29.84 ppm per °C for Li10MgTi13O32, and the small negative τf values of Li10MTi13O32 (M = Zn, Mg) are derived from the proximity of ταm to 3αL. Calculations using P–V–L theory also confirmed that the bond ionicity (fi) of all the bonds in the prepared Li10MgTi13O32 structure was higher than that of Li10ZnTi13O32, and the Ti–O bond contributed the most to εr. The lattice energy of the Ti–O bonds is much greater than that of other bonds, indicating that it is also a major contributor to Q × f in the Li10MTi13O32 (M = Zn, Mg) ceramics. In addition, a study of the DC conductivity clarified that the Q × f values of the disordered spinels Li10ZnTi13O32 and Li10MgTi13O32 are not as high as other ordered spinels, which may be due to the transport of Li+ ions in their structures.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 22105048), Guangxi Science and Technology Plan Project (No. AD20297035), the Natural Science Foundation of Guangxi Zhuang Autonomous Region (No. 2022GXNSFBA035602), the Guilin University of Technology Research Startup Project (No. GUTQDJJ2021073), and the Guangxi BaGui Scholars Special Funding.
References
- C. L. Huang and T. H. Hsu, J. Eur. Ceram. Soc., 2022, 42, 3892–3897 CrossRef CAS.
- J. Li, J. Zhu and G. Wang, Ceram. Int., 2022, 48, 15261–15267 CrossRef CAS.
- S. Z. Hao, D. Zhou, L. X. Pang, M. Z. Dang, S. K. Sun, T. Zhou, S. Trukhanov, A. Trukhanov, A. S. B. Sombra, Q. Li, X. Q. Zhang, S. Xia and M. A. Darwish, J. Mater. Chem. C, 2022, 10, 2008–2016 RSC.
- J. Bao, Y. Zhang, H. Kimura, H. Wu and Z. Yue, J. Adv. Ceram., 2023, 12, 82–92 CrossRef.
- X. Zhou, L. Liu, J. Sun, N. Zhang, H. Sun, H. Wu and W. Tao, J. Adv. Ceram., 2021, 10, 778–789 CrossRef CAS.
- H. Tian, J. Zheng, L. Liu, H. Wu, H. Kimura, Y. Lu and Z. Yue, J. Mater. Sci. Technol., 2022, 116, 121–129 CrossRef.
- T. Y. Qin, C. W. Zhong, Y. Shang, L. Cao, M. X. Wang, B. Tang and S. R. Zhang, J. Alloys Compd., 2021, 886, 161278 CrossRef CAS.
- K. P. Surendran, P. V. Bijumon, P. Mohanan and M. T. Sebastian, Appl. Phys. A: Mater. Sci. Process., 2005, 81, 823–826 CrossRef CAS.
- S. Takahashi, Y. Imai, A. Kan, Y. Hotta and H. Ogawa, Jap. J. Appl. Phys., 2015, 54, 10NE02 CrossRef.
- A. Belous, O. Ovchar, D. Durilin, M. M. Krzmanc, M. Valant and D. Suvorov, J. Am. Ceram. Soc., 2006, 89, 3441–3445 CrossRef CAS.
- H. F. Zhou, X. L. Chen, L. Fang, D. J. Chu and H. Wang, J. Mater. Res., 2010, 25, 1235–1238 CrossRef CAS.
- S. George and M. T. Sebastian, J. Am. Ceram. Soc., 2010, 93, 2164–2166 CrossRef CAS.
- L. Y. Ao, Y. Tang, J. Li, W. S. Fang, L. Duan, C. X. Su, Y. H. Sun, L. J. Liu and L. Fang, J. Eur. Ceram. Soc., 2020, 40, 5498–5503 CrossRef CAS.
- S. Takahashi, A. Kan and H. Ogawa, Jap. J. Appl. Phys., 2016, 55, 10TE01 CrossRef.
- H. Zhou, X. Liu, X. Chen, L. Fang and Y. Wang, J. Eur. Ceram. Soc., 2012, 32, 261–265 CrossRef CAS.
- H. F. Zhou, J. Z. Gong, N. Wang and X. L. Chen, Ceram. Int., 2016, 42, 8822–8825 CrossRef CAS.
- N. Wang, H. F. Zhou, J. Z. Gong, G. C. Fan and X. L. Chen, J. Electron. Mater., 2016, 45, 3157–3161 CrossRef CAS.
- J. Zhang, R. Z. Zuo, Y. Wang and S. S. Qi, Mater. Lett., 2016, 164, 353–355 CrossRef CAS.
- H. Xiang, L. Fang, W. Fang, Y. Tang and C. Li, J. Eur. Ceram. Soc., 2017, 37, 625–629 CrossRef CAS.
- K. Xiao, Y. Tang, Y. F. Tian, C. C. Li, L. Duan and L. Fang, J. Eur. Ceram. Soc., 2019, 39, 3064–3069 CrossRef CAS.
- W. S. Fang, Y. M. Sun, L. Fang, Y. Tang and C. C. Li, J. Alloys Compd., 2017, 722, 1002–1007 CrossRef CAS.
- S. K. Singh, S. R. Kiran and V. R. K. Murthy, Mater. Chem. Phys., 2013, 141, 822–827 CrossRef CAS.
- R. Z. Zuo and J. Zhang, J. Am. Ceram. Soc., 2016, 99, 3343–3349 CrossRef.
- H. Luo, L. Fang, H. Xiang, Y. Tang and C. Li, Ceram. Int., 2017, 43, 1622–1627 CrossRef CAS.
- L. Fang, D. Chu, H. Zhou, X. Chen and Z. Yang, J. Alloys Compd., 2011, 509, 1880–1884 CrossRef CAS.
- M. Li, Y. Tang, H. Xiang, J. Li, D. Zhou and L. Fang, Ceram. Int., 2023 DOI:10.1016/j.ceramint.2022.11.021.
- Y. Tang, H. Li, J. Li, W. Fang, Y. Yang, Z. Zhang and L. Fang, J. Eur. Ceram. Soc., 2021, 41, 7697–7702 CrossRef CAS.
- Y. Yang, Y. Tang, J. Li, L. Fang and H. C. Xiang, ACS Appl. Electron. Mater., 2022, 4, 3512–3519 CrossRef CAS.
- X. W. Hu, J. W. Chen, J. Li, H. C. Xiang, Y. Tang and L. Fang, J. Eur. Ceram. Soc., 2022, 42, 7461–7467 CrossRef CAS.
- Y. M. Dai, J. W. Chen, Y. Tang, H. C. Xiang, J. Li and L. Fang, Ceram. Int., 2023, 49, 875–881 CrossRef CAS.
- V. S. Hernandez, L. M. T. Martinez, G. C. Mather and A. R. West, J. Mater. Chem., 1996, 6, 1533–1536 RSC.
- L. T. Nong, X. F. Cao, C. C. Li, L. J. Liu, L. Fang and J. Khaliq, J. Eur. Ceram. Soc., 2021, 41, 7683–7688 CrossRef CAS.
- H. D. Lutz, Z. Naturforsch., A: Phys. Sci., 1969, 24, 1417–1419 CAS.
- D. Z. Liu, W. Hayes, M. Kurmoo, M. Dalton and C. Chen, Phys. C, 1994, 235, 1203–1204 CrossRef.
- H. D. Lutz, B. Müller and H. J. Steiner, J. Solid State Chem., 1991, 90, 54–60 CrossRef CAS.
- L. Malavasi, P. Galinetto, M. C. Mozzati, C. B. Azzoni and G. Flor, Phys. Chem. Chem. Phys., 2002, 4, 3876–3880 RSC.
- A. Magrez, M. Cochet, O. J oubert, G. Louarn, M. Ganne and O. Chauvet, Chem. Mater., 2001, 13, 3893–3898 CrossRef CAS.
- A. J. Bosman and E. E. Havinga, Phys. Rev., 1963, 129, 1593–1600 CrossRef CAS.
- R. D. Shannon, J. Appl. Phys., 1993, 73, 348–366 CrossRef CAS.
- H. S. Park, K. H. Yoon and E. S. Kim, Mater. Chem. Phys., 2003, 79, 181–183 CrossRef CAS.
- Y. S. Cho, K. H. Yoon, B. D. Lee, H. R. Lee and E. S. Kim, Ceram. Int., 2004, 30, 2247–2250 CrossRef CAS.
- N. E. Brese and M. O. Keeffe, Acta Crystallogr., 1991, 47, 192–197 Search PubMed.
- H. Y. Yang, S. R. Zhang, H. C. Yang, Y. Yuan and E. Z. Li, J. Am. Ceram. Soc., 2019, 102, 5365–5374 CrossRef CAS.
- H. Y. Yang, S. R. Zhang, H. C. Yang and E. Z. Li, Inorg. Chem. Front., 2020, 7, 4711–4753 RSC.
- S. S. Batsanov, Russ. Chem. Rev., 1982, 51, 684–697 CrossRef.
- B. F. Levine, J. Chem. Phys., 1973, 59, 1463–1486 CrossRef CAS.
- E. L. Colla, I. M. Reaney and N. Setter, J. Appl. Phys., 1993, 74, 3414–3425 CrossRef CAS.
- A. J. Bosman and E. E. Havinga, Phys. Rev., 1963, 129, 1593 CrossRef CAS.
- M. W. Lufaso, Chem. Mater., 2004, 16, 2148–2156 CrossRef CAS.
- H. Yang, S. Zhang, Y. Chen, H. Yang, Y. Yuan and E. Li, Inorg. Chem., 2019, 58, 968–976 CrossRef CAS PubMed.
- D. Liu, S. Zhang and Z. Wu, Inorg. Chem., 2003, 42, 2465–2469 CrossRef CAS PubMed.
- R. Zurmühlen, J. Petzelt, S. Kamba, V. V. Voitsekhovskii, E. Colla and N. Setter, J. Appl. Phys., 1995, 77, 5341–5350 CrossRef.
- Y. G. Zhao and P. Zhang, RSC Adv., 2015, 5, 97746–97754 RSC.
- B. D. Silverman, J. Phys. Rev., 1962, 125, 1921–1930 CrossRef CAS.
- S. Y. Wang, J. D. Chen, Y. J. Zhang and Y. C. Zhang, J. Alloys Compd., 2019, 805, 852–858 CrossRef CAS.
- Y. Tang, S. Y. Shen, J. Li, X. G. Zhao, H. C. Xiang, H. P. Su, D. Zhou and L. Fang, J. Eur. Ceram. Soc., 2022, 42, 4573–4579 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Jie
Li
b,
Yuandong
Qin
d and
Liang
Fang
bc
*a,
Jie
Li
b,
Yuandong
Qin
d and
Liang
Fang
bc
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) Li10MTi13O32 (M = Zn, Mg) was investigated via Rietveld structural refinement, ionic polarizability, bond valence, P–V–L theory, Raman spectroscopy, and DC conductivity. For Li10ZnTi13O32 and Li10MgTi13O32, promising microwave dielectric properties of εr = 28.23 ± 0.3 and 29.23 ± 0.3, Q × f = 35
m) Li10MTi13O32 (M = Zn, Mg) was investigated via Rietveld structural refinement, ionic polarizability, bond valence, P–V–L theory, Raman spectroscopy, and DC conductivity. For Li10ZnTi13O32 and Li10MgTi13O32, promising microwave dielectric properties of εr = 28.23 ± 0.3 and 29.23 ± 0.3, Q × f = 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 500 GHz and 32
800 ± 500 GHz and 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ± 500 GHz (at ∼7.5 GHz), and τf = −17.06 ± 2.0 ppm per °C and −11.05 ± 2.0 ppm per °C, respectively, were obtained at 980 °C. Bond valences reveal that almost all cations are rattling, weakening the bond strengths and widening the molecular dielectric polarizability. The expansion structures also result in τf values closer to zero and lower Q × f values. The bond ionicity and lattice energy of the Ti–O bonds are much greater than those of other bonds, indicating that the Ti–O bond is a major contributor to εr and Q × f. Moreover, the DC conductivity clarified that the Q × f values of the disordered spinels Li10ZnTi13O32 and Li10MgTi13O32 are not as high as other ordered spinels because of the transport of Li+ ions in their structures.
100 ± 500 GHz (at ∼7.5 GHz), and τf = −17.06 ± 2.0 ppm per °C and −11.05 ± 2.0 ppm per °C, respectively, were obtained at 980 °C. Bond valences reveal that almost all cations are rattling, weakening the bond strengths and widening the molecular dielectric polarizability. The expansion structures also result in τf values closer to zero and lower Q × f values. The bond ionicity and lattice energy of the Ti–O bonds are much greater than those of other bonds, indicating that the Ti–O bond is a major contributor to εr and Q × f. Moreover, the DC conductivity clarified that the Q × f values of the disordered spinels Li10ZnTi13O32 and Li10MgTi13O32 are not as high as other ordered spinels because of the transport of Li+ ions in their structures.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–72
000–72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GHz, and τf = −15 to −11.2 ppm per °C) and Li2MgTi3O8 (εr = 20.2, Q × f = 42
000 GHz, and τf = −15 to −11.2 ppm per °C) and Li2MgTi3O8 (εr = 20.2, Q × f = 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GHz, and τf = +3.2 ppm per °C), but the microwave dielectric properties of disordered spinel ceramics have rarely been reported. For ordered Li-containing spinels, Li4b and Ti12d at the octahedral sites were arranged spontaneously into 1
000 GHz, and τf = +3.2 ppm per °C), but the microwave dielectric properties of disordered spinel ceramics have rarely been reported. For ordered Li-containing spinels, Li4b and Ti12d at the octahedral sites were arranged spontaneously into 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 cation ordering (i.e., [Li0.5Zn0.5]tet[Li0.5Ti1.5]octO4 and [Li0.55Mg0.45]tet[(Li0.45Mg0.05)Ti1.5]octO4) with a space group of P4332. The spinel-structured Li2MM′3O8 (M = Mg, Co, Ni, Zn; M′ = Ti, Ge) ceramics with an ordered spinel structure (P4332) have been reported to possess a relative εr of 10.5–28.9, a Q × f of 47
3 cation ordering (i.e., [Li0.5Zn0.5]tet[Li0.5Ti1.5]octO4 and [Li0.55Mg0.45]tet[(Li0.45Mg0.05)Ti1.5]octO4) with a space group of P4332. The spinel-structured Li2MM′3O8 (M = Mg, Co, Ni, Zn; M′ = Ti, Ge) ceramics with an ordered spinel structure (P4332) have been reported to possess a relative εr of 10.5–28.9, a Q × f of 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400–160
400–160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GHz, and a τf of −63.9 to +7.4 ppm per °C.19–25
000 GHz, and a τf of −63.9 to +7.4 ppm per °C.19–25![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), 0.5 < x < 0.9 is the ordered primitive cubic phase (P4332), and when x is beyond 0.9, it becomes face-centered cubic again. And a similar phenomenon occurs in magnesium analogs.32 The different cation occupation is the main reason for the order and disorder changes in the spinel structure. In the disordered structure, there is only one kind of regular octahedron (16d) and one tetrahedron (8a), compared with the two octahedra (4b, 12d) and one tetrahedron (8c) in the ordered structure. The disordered structure is simpler and more conducive to studying the influence of the bond length, bond valence, and polarization on the microwave dielectric properties.
m), 0.5 < x < 0.9 is the ordered primitive cubic phase (P4332), and when x is beyond 0.9, it becomes face-centered cubic again. And a similar phenomenon occurs in magnesium analogs.32 The different cation occupation is the main reason for the order and disorder changes in the spinel structure. In the disordered structure, there is only one kind of regular octahedron (16d) and one tetrahedron (8a), compared with the two octahedra (4b, 12d) and one tetrahedron (8c) in the ordered structure. The disordered structure is simpler and more conducive to studying the influence of the bond length, bond valence, and polarization on the microwave dielectric properties.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 GHz, τf = −15 ppm per °C).13 The main aim of this work is to investigate the effects of the bond length, bond valence, ionic dielectric polarizability, structural stability, and rattling and compressed cations on the microwave dielectric properties (εr, τf, and Q × f) both theoretically and experimentally.
530 GHz, τf = −15 ppm per °C).13 The main aim of this work is to investigate the effects of the bond length, bond valence, ionic dielectric polarizability, structural stability, and rattling and compressed cations on the microwave dielectric properties (εr, τf, and Q × f) both theoretically and experimentally.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = 1/Q), and resonant frequency (f) were determined using the Hakki–Coleman method using a network analyzer (N5230A, Agilent, America) (ESI†). The drift of the f and εr (i.e., τf and τε) were calculated as follows:
δ = 1/Q), and resonant frequency (f) were determined using the Hakki–Coleman method using a network analyzer (N5230A, Agilent, America) (ESI†). The drift of the f and εr (i.e., τf and τε) were calculated as follows:
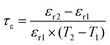
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The refined plots for Li10ZnTi13O32 and Li10MgTi13O32 are displayed in Fig. 1b and c, respectively, and the refined structural parameters are listed in Table 1. It is notable that the refined lattice parameters of a = 8.3636 Å and V = 585.0211 Å3 for Li10ZnTi13O32 are smaller than a = 8.3649 Å and V = 585.2944 Å3 for Li10MgTi13O32, which is opposite to the ionic radii of Zn2+ (0.60 Å) and Mg2+ (0.57 Å, CN = 4), which might be related to the rattling effect of cations in Li10MgTi13O32. The crystal structure and cation occupancy information of the Li10MTi13O32 ceramics are presented in Fig. 1d and Table 1, respectively. It is observed that Li and M share the tetrahedral sites (8a), and Li and Ti share the octahedral sites (16d). The octahedra and tetrahedra are connected at their common vertices, and the octahedra are connected at their common edges to form the structural skeleton. The tetrahedra are isolated from each other, indicating that the influence of the octahedron on the structure is dominant. Moreover, Fig. S1 (ESI†) depicts the bond lengths in Li10MTi13O32 (M = Zn, Mg) from the Rietveld refinements.
m. The refined plots for Li10ZnTi13O32 and Li10MgTi13O32 are displayed in Fig. 1b and c, respectively, and the refined structural parameters are listed in Table 1. It is notable that the refined lattice parameters of a = 8.3636 Å and V = 585.0211 Å3 for Li10ZnTi13O32 are smaller than a = 8.3649 Å and V = 585.2944 Å3 for Li10MgTi13O32, which is opposite to the ionic radii of Zn2+ (0.60 Å) and Mg2+ (0.57 Å, CN = 4), which might be related to the rattling effect of cations in Li10MgTi13O32. The crystal structure and cation occupancy information of the Li10MTi13O32 ceramics are presented in Fig. 1d and Table 1, respectively. It is observed that Li and M share the tetrahedral sites (8a), and Li and Ti share the octahedral sites (16d). The octahedra and tetrahedra are connected at their common vertices, and the octahedra are connected at their common edges to form the structural skeleton. The tetrahedra are isolated from each other, indicating that the influence of the octahedron on the structure is dominant. Moreover, Fig. S1 (ESI†) depicts the bond lengths in Li10MTi13O32 (M = Zn, Mg) from the Rietveld refinements.

![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) ) of Li10ZnTi13O32 increased from 3.81 μm to 5.06 μm as the sintering temperature was increased. When sintered at 940 °C, the grain size was not uniform, and there was some slight porosity. As the temperature was increased to 980 °C, the grain size increased with the disappearance of the pores, and the microstructure became uniform and compact. When the temperature was raised further, the size of some grains increased abnormally. As shown in Fig. 3d–f, the grain growth process of the Li10MgTi13O32 ceramic (the average grain size increased from 2.66 μm to 4.85 μm) is similar to that of Li10ZnTi13O32, and the densest microstructure is obtained at 980 °C.
) of Li10ZnTi13O32 increased from 3.81 μm to 5.06 μm as the sintering temperature was increased. When sintered at 940 °C, the grain size was not uniform, and there was some slight porosity. As the temperature was increased to 980 °C, the grain size increased with the disappearance of the pores, and the microstructure became uniform and compact. When the temperature was raised further, the size of some grains increased abnormally. As shown in Fig. 3d–f, the grain growth process of the Li10MgTi13O32 ceramic (the average grain size increased from 2.66 μm to 4.85 μm) is similar to that of Li10ZnTi13O32, and the densest microstructure is obtained at 980 °C.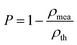
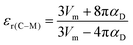
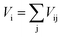
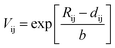
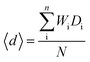
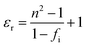
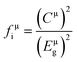
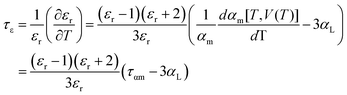
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 and 32
800 and 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 GHz are obtained, respectively, for Li10ZnTi13O32 and Li10MgTi13O32 sintered at 980 °C. The Q × f of Li10MgTi13O32 is slightly lower than that of Li10ZnTi13O32, which may be due to the increase in intrinsic dielectric loss caused by weakly bonded cations in the extended coordination environment. In a classical sense, the more under-bonded cations contribute to the dielectric loss because the cations “rattle” more freely in the polyhedral cage and may interact more strongly with the anharmonic phonons.49 For intrinsic losses, the lattice energy (U) based on P–V–L theory can be evaluated as follows:50–52
100 GHz are obtained, respectively, for Li10ZnTi13O32 and Li10MgTi13O32 sintered at 980 °C. The Q × f of Li10MgTi13O32 is slightly lower than that of Li10ZnTi13O32, which may be due to the increase in intrinsic dielectric loss caused by weakly bonded cations in the extended coordination environment. In a classical sense, the more under-bonded cations contribute to the dielectric loss because the cations “rattle” more freely in the polyhedral cage and may interact more strongly with the anharmonic phonons.49 For intrinsic losses, the lattice energy (U) based on P–V–L theory can be evaluated as follows:50–52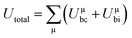
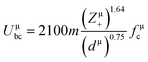
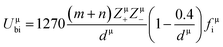
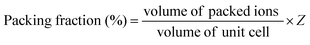
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 500
800 ± 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ± 500
100 ± 500![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) microwave dielectric ceramics Li10ZnTi13O32 and Li10MgTi13O32 are not as high as those of ordered spinels, which may be related to the transport of Li+ ions in the structure. Complex impedance analysis was employed to explain the effects of Li+ ions on the structure and Q × f. Fig. 5a and b show the complex impedance plane plots of the Li10MTi13O32 (M = Zn, Mg) ceramics at 633–573K. The Li10MTi13O32 (M = Zn, Mg) ceramics show high resistivity and good insulation. The relationship between the DC (direct current) conductivity (σdc) and the temperature can be expressed via the following Arrhenius equation:
m) microwave dielectric ceramics Li10ZnTi13O32 and Li10MgTi13O32 are not as high as those of ordered spinels, which may be related to the transport of Li+ ions in the structure. Complex impedance analysis was employed to explain the effects of Li+ ions on the structure and Q × f. Fig. 5a and b show the complex impedance plane plots of the Li10MTi13O32 (M = Zn, Mg) ceramics at 633–573K. The Li10MTi13O32 (M = Zn, Mg) ceramics show high resistivity and good insulation. The relationship between the DC (direct current) conductivity (σdc) and the temperature can be expressed via the following Arrhenius equation: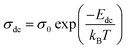
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) were synthesized using a solid-state reaction method. Li10ZnTi13O32 and Li10MgTi13O32 with relative permittivities of 28.23 ± 0.3 and 29.23 ± 0.3, Q × f values of 35
m) were synthesized using a solid-state reaction method. Li10ZnTi13O32 and Li10MgTi13O32 with relative permittivities of 28.23 ± 0.3 and 29.23 ± 0.3, Q × f values of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 500 GHz and 32
800 ± 500 GHz and 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ± 500 GHz (at ∼7.5 GHz), and τf values of −17.06 ± 2.0 ppm per °C and −11.05 ± 2.0 ppm per °C, respectively, were obtained at 980 °C. The permittivities εr(C–M) calculated using the Clausius–Mossotti (C–M) equation are significantly lower than the permittivities εr(corr) corrected by the porosity (εr(C–M) = 16.05, εr(corr) = 28.99 for Li10ZnTi13O32; εr(C–M) = 15.47, εr(corr) = 30.00 for Li10MgTi13O32). The main reason for this phenomenon comes from the longer and weaker bonds in the Li10MTi13O32 (M = Zn, Mg) ceramics that are more facile to polarization. The larger negative weighted average discrepancy factor (<d>) of Li10MgTi13O32 (−0.0670 v.u.) than that of Li10ZnTi13O32 (−0.0601 v.u.) is a good explanation for the higher εr(corr) value of Li10MgTi13O32 (αD = 115.73 A3), although its dielectric polarizability (αD) is lower than that of Li10ZnTi13O32 (αD = 116.45 A3). This expansion structure also results in a closer value of τf to zero and a lower Q × f. Values of the temperature coefficient of ionic polarizability (ταm) are 29.22 ppm per °C for Li10ZnTi13O32 and 29.84 ppm per °C for Li10MgTi13O32, and the small negative τf values of Li10MTi13O32 (M = Zn, Mg) are derived from the proximity of ταm to 3αL. Calculations using P–V–L theory also confirmed that the bond ionicity (fi) of all the bonds in the prepared Li10MgTi13O32 structure was higher than that of Li10ZnTi13O32, and the Ti–O bond contributed the most to εr. The lattice energy of the Ti–O bonds is much greater than that of other bonds, indicating that it is also a major contributor to Q × f in the Li10MTi13O32 (M = Zn, Mg) ceramics. In addition, a study of the DC conductivity clarified that the Q × f values of the disordered spinels Li10ZnTi13O32 and Li10MgTi13O32 are not as high as other ordered spinels, which may be due to the transport of Li+ ions in their structures.
100 ± 500 GHz (at ∼7.5 GHz), and τf values of −17.06 ± 2.0 ppm per °C and −11.05 ± 2.0 ppm per °C, respectively, were obtained at 980 °C. The permittivities εr(C–M) calculated using the Clausius–Mossotti (C–M) equation are significantly lower than the permittivities εr(corr) corrected by the porosity (εr(C–M) = 16.05, εr(corr) = 28.99 for Li10ZnTi13O32; εr(C–M) = 15.47, εr(corr) = 30.00 for Li10MgTi13O32). The main reason for this phenomenon comes from the longer and weaker bonds in the Li10MTi13O32 (M = Zn, Mg) ceramics that are more facile to polarization. The larger negative weighted average discrepancy factor (<d>) of Li10MgTi13O32 (−0.0670 v.u.) than that of Li10ZnTi13O32 (−0.0601 v.u.) is a good explanation for the higher εr(corr) value of Li10MgTi13O32 (αD = 115.73 A3), although its dielectric polarizability (αD) is lower than that of Li10ZnTi13O32 (αD = 116.45 A3). This expansion structure also results in a closer value of τf to zero and a lower Q × f. Values of the temperature coefficient of ionic polarizability (ταm) are 29.22 ppm per °C for Li10ZnTi13O32 and 29.84 ppm per °C for Li10MgTi13O32, and the small negative τf values of Li10MTi13O32 (M = Zn, Mg) are derived from the proximity of ταm to 3αL. Calculations using P–V–L theory also confirmed that the bond ionicity (fi) of all the bonds in the prepared Li10MgTi13O32 structure was higher than that of Li10ZnTi13O32, and the Ti–O bond contributed the most to εr. The lattice energy of the Ti–O bonds is much greater than that of other bonds, indicating that it is also a major contributor to Q × f in the Li10MTi13O32 (M = Zn, Mg) ceramics. In addition, a study of the DC conductivity clarified that the Q × f values of the disordered spinels Li10ZnTi13O32 and Li10MgTi13O32 are not as high as other ordered spinels, which may be due to the transport of Li+ ions in their structures.




