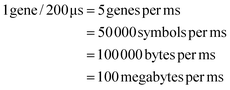Open Access Article
Open Access ArticleAutomated routing of droplets for DNA storage on a digital microfluidics platform
Ajay
Manicka
 a,
Andrew
Stephan
a,
Sriram
Chari
b,
Gemma
Mendonsa
b,
Peyton
Okubo
a,
John
Stolzberg-Schray
a,
Anil
Reddy
b and
Marc
Riedel
a
a,
Andrew
Stephan
a,
Sriram
Chari
b,
Gemma
Mendonsa
b,
Peyton
Okubo
a,
John
Stolzberg-Schray
a,
Anil
Reddy
b and
Marc
Riedel
a
aDepartment of Electrical and Computer Engineering, University of Minnesota, Minneapolis, Minnesota, USA. E-mail: ececomm@umn.edu
bSeagate Technology, USA
First published on 23rd August 2023
Abstract
Technologies for sequencing (reading) and synthesizing (writing) DNA have progressed on a Moore's law-like trajectory over the last three decades. This has motivated the idea of using DNA for data storage. Theoretically, DNA-based storage systems could out-compete all existing forms of archival storage. However, a large gap exists between what is theoretically possible in terms of read and write speeds and what has been practically demonstrated with DNA. This paper introduces a novel approach to DNA storage, with automated assembly on a digital microfluidic biochip. This technology offers unprecedented parallelism in DNA assembly using a dual library of “symbols” and “linkers”. An algorithmic solution is discussed for the problem of managing droplet traffic on the device, with prioritized three-dimensional “A*” routing. An overview is given of the software that was developed for routing a large number of droplets in parallel on the device, minimizing congestion and maximizing throughput.
1 Introduction
1.1 The world of information
The amount of data that the world generates has been increasing exponentially since the inception of the computer age. This trend will continue for the foreseeable future, as ever more IoT devices come online and humans create denser content in the form of video and virtual reality. The bulk of this so-called “big data” is stored in hard disk drives (HDDs).1 It is estimated that the total demand for data storage by 2025 will be 180 zettabytes (1 zettabyte = 1 billion terabytes),2 which would be a three-fold increase from 2020. Some of this newly generated data will need to be archived for long-term storage, perhaps 9.3 ZB of it.3 Even if only 5% of stored data is placed in “deep” offline archives, this would require 46.5 million 20 TB HDDs by 2025. The required capacity for online and on-premise archiving will be many times larger.Meanwhile, the supply of storage media is projected to grow by less than 20% year over year in the same time-frame.4 Without the construction of new HDD and SSD manufacturing facilities, which are multi-billion dollar investments, demand for storage is expected to outstrip supply by as much as two-fold.5 Furthermore, magnetic storage has durability limitations that make it undesirable for maintenance-free, multi-decade storage. Also, the proliferation of data centers is causing long-term environmental damage, as the electricity they require, mostly for cooling, is a major source of global carbon emissions.6 For all these reasons, there has been a strong interest in identifying new types of storage media.
A strong contender for a type of media that could meet the future demand for archival storage is DNA. The theoretical storage capacity of DNA is as high as 200 petabytes per gram, which is over a thousand times denser than conventional HDDs.7,8 Most importantly, the energy requirement for writing is on the order of 10−19 joules per bit which is orders of magnitude below the femtojoules per bit (10−15 joules per bit) barrier touted for other emerging technologies.7 The durability of DNA is unmatched, exceeding centuries, while hard drives and magnetic tape rarely maintain reliability longer than 30 years.9 We point to a review paper that summarizes the potential of DNA storage systems.10 Orthogonal to work on storage with DNA, researchers have looked at computing with DNA.11–14
1.2 DNA as a storage unit
Traditional computer systems use the binary code of zeros and ones {0, 1} as storage units. In its simplest form, a DNA storage system uses a quaternary code of nucleotides drawn from four different nitrogenous bases, viz. adenine, guanine, cytosine, and thymine, denoted A, G, C, and T, respectively. We can map couplets of zeros or ones directly to each nucleotide, as illustrated in Fig. 1. In this way, we use a string of nucleotides to represent arbitrary data.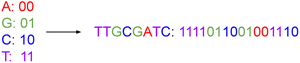 | ||
| Fig. 1 This figure represents the mapping of nucleotide bases to a binary code. Just as we can string together binary values, we can assemble DNA nucleotides chemically to represent data. | ||
With such an encoding, a DNA sequence with n nucleotides stores 2n bits of data based on binary mapping. Table 1 introduces our concept of a DNA symbol library.† (We note here that we use footnotes to define terms throughout the text.) From a base set of the 4 nucleotides {A, G, C, T}, there are 16 ways to select base pairs of length 2; these base pair symbols correspond to binary numbers from 0000 to 1111. If a 2-nucleotide symbol can represent 16 distinct binary numbers, then a 3-nucleotide symbol can represent 64 binary distinct numbers. In general, the addition of each nucleotide quadruples the range of numbers we can represent. So n base pairs can represent 4n distinct numbers for n > 0.
| Symbol length (number of base pairs per symbol) | DNA symbol library size (number of unique symbols) |
|---|---|
| 1 | 4 |
| 2 | 16 |
| 3 | 64 |
| 4 | 256 |
| 5 | 1024 |
| 6 | 4096 |
| 7 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 384 |
| 8 | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 536 |
Ever since Watson and Crick first described the molecular double helix structure of DNA,15 its potential for storage has been apparent to computer scientists. It seems that most practical work is based on liquid-handling robotics. The power consumption of liquid-handling DNA storage systems is on the order of hundreds of joules per seconds (ref. 10) for a DNA synthesis rate on the order of kilobytes per seconds. Overall, these machines use a substantial amount of energy for limited gain. Many creative ideas and novel technologies, ranging from nanopores16 to DNA origami,17 are also being investigated. The leading approach appears to be phosphoramidite chemistry.18
The main barrier to building DNA storage systems that can compete with existing forms of archival storage is the write speed, so the rate of DNA synthesis. Hard drive write speeds hover around 50 to 120 MB s−1 (ref. 19) while solid-state storage systems achieve write speeds exceeding 200 megabytes per second.19 All existing DNA storage systems have write speeds many magnitudes slower than this.20
This paper does not consider the process of reading data stored in DNA (i.e., sequencing it). With current technology, reading DNA is orders of magnitude more efficient than writing it, so the impetus is improvements in write speed. Of course, a complete solution must consider both operations. Nanopore-based devices for sequencing DNA could provide the requisite technology,21 as they are compatible with the digital microfluidic technology discussed here.
1.3 A solution: increasing rate of DNA synthesis
Achieving practically useful write speeds will require two things. First, a way to introduce massive parallelization. Second, a chemical protocol that writes as much data as possible per operation, thereby increasing the bit rate (write speed in bits per unit time). This paper proposes a solution to the synthesis speed problem with a dual library of “symbols‡” and “linkers§”. The two libraries work in tandem to allow the synthesis of long “genes¶” each with symbols in the required order, corresponding to the data that is being written. With linkers attached, multiple symbols can be attached to one another in the same droplet. Accordingly, massive parallelization is possible. This is in contrast to most existing schemes for DNA storage, in which each operation attaches a single nucleotide to the end of the sequence, for instance with phosphoramidite chemistry.22 Details regarding our scheme with symbols and linkers are given in Section 4.Instead of liquid-handling robots, we perform assembly of DNA with a digital microfluidic biochip (DMFB). This technology offers the advantages of low reagent consumption, high precision, and miniaturization.23 Further details are given in Section 2.1.
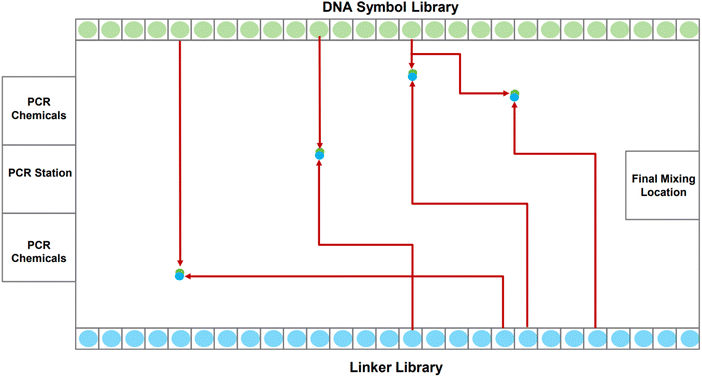
A DMFB device can be idealized as a 2-D grid, shown in Fig. 2. Most of the 2-D grid serves to route individual droplets. In our device, a subset of the available grid points performs dedicated operations: Gibson assembly (concatenation);24 polymerase chain reaction, or PCR (replication);25 and purification (correction). One edge of the biochip houses short fragments of DNA in the form of the symbols while the opposite edge holds short fragments in the form of linkers. Also, one of the edges houses PCR stations where depleted stores of DNA symbols and linkers can be refilled. Gibson sites – locations where symbols are linked together – and purification sites are strategically positioned throughout the device. The Gibson assembly process is discussed in more detail in Section 2.2. We do not discuss the purification process in this paper.
The task of writing DNA begins with an encoding of the data in a gene. When the order to assemble a certain gene is received by the device, it dispenses the requisite DNA symbols, linkers, and chemical reagents as individual droplets along the grid's edge. The droplets corresponding to symbols and linkers contain oligos.|| When a symbol droplet** and a linker droplet†† meet at a grid point, they merge forming a larger droplet. This larger droplet is routed so that it meets and merges with a chemical droplet.‡‡ This larger droplet is then routed to a station for Gibson assembly: this is where the symbol and linker oligos are chemically joined to form a single DNA strand.
Routing all the droplets is a significant challenge, one that we confront in this paper. The routing problem becomes more complex as more droplets are pulled to assemble longer genes. To solve the problem, we use an algorithm called 3-D prioritized A*.§§ The algorithm considers three dimensions: the horizontal axis of the DMFB grid, the vertical axis of the DMFB grid, and the axis of time. It is called prioritized because it chooses to create routes for droplets by giving priority to the droplet which is furthest from its goal node, i.e., the droplet which has to travel the largest distance across the grid to reach its intended target location. The routing algorithm allows many droplets to move simultaneously while avoiding unwanted collisions. It also allows individual droplets to take the optimal path within the constraints given to them by higher priority droplets. Further details are given in Section 4.2.
1.4 Related work
DNA storage technology is a rapidly expanding area of research. Here, we reference some relevant literature7,20,29–32 in the DNA storage space. Our approach to DNA storage differs from prior work: (1) in our use of DMFB technology; and (2) with our novel “symbol” and “linker” dual library.With respect to the routing algorithm that we use, this paper builds upon an extensive body of prior work. Numerous papers have discussed routing on DMFB devices, for a variety of applications.33–35 Many discussed versions of the A* approach that we use.33,36,37 Other strategies have been considered, for instance, using an evolutionary multi-objective optimization algorithm.38 Many papers discuss exciting applications of DMFB, for instance, DNA sequencing and clinical diagnosis.39–41
Almost all prior work has considered routing on small grids, generally less than 50 × 50 in size. DNA storage presents very different constraints, particularly with respect to the size of the grid and the degree of parallelism. We target grid sizes that are 6 to 7 orders of magnitude larger. For such large grid sizes, algorithmic runtime is the preeminent concern.
1.5 Organization
The contents of this paper are organized as follows. First, in Section 2, we provide some background information on DMFB technology and DNA synthesis. Then, in Section 3, we discuss the target write speeds and the parameters of a DMFB device that can achieve them. Next, in Section 4, we describe our method of automating DNA assembly, with symbols and linkers. Then we discuss the routing requirements for this scheme. Next, in Section 5, we describe the software architecture of our system. Then, in Section 6, we present simulation results characterizing the performance, runtime, and memory usage of our software. Finally, in Section 7, we summarize the main results of the paper and discuss areas for future work.2 Background
2.1 Digital microfluidics (DMF) technology
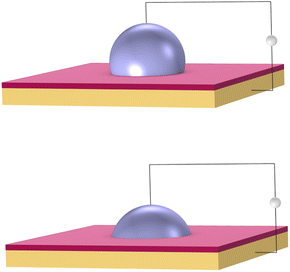
DMF is a fluid-handling technology that precisely moves small droplets on a grid by manipulating electrical charge. It works on the principle of electrowetting.42 Aqueous droplets naturally bead up on a hydrophobic surface. However, a voltage applied between a droplet and an insulated electrode causes the droplet to spread out on the surface, as shown in Fig. 3.Electrical signals are applied to an array of such electrodes. Droplets are moved by turning the voltage on and off in succession across adjacent electrodes. The same mechanism can be used to dispense, merge, and mix droplets. These basic operations become the building blocks to perform biochemical reactions. DMFB technology reduces the volume of fluid, and so generally reduces the cost, compared to technology like liquid-handling robotics.43 It has been studied extensively in academia,44 and in recent years, has been applied for specific tasks in industry.45 However, it is fair to say that DMFB remains a niche technology. Scaling down the size of the droplets and increasing the grid dimensions, so increasing the number of droplets on the device, is an expensive proposition in terms of research and development.46
We are working with proprietary DMFB technology that Seagate, a leading storage technology company, is developing. It is of a much greater scale than has been previously demonstrated with very large grid sizes – millions of electrodes. This technology is not the focus of this paper. Nevertheless, the concepts that we present for DNA storage are predicated on it. In particular, we formulate algorithms to tackle the routing of large numbers of droplets in parallel across Seagate's DMFB platform. Achieving high data throughout, in terms of DNA storage units synthesized per unit of time, is the main objective.
2.2 Gibson assembly protocol
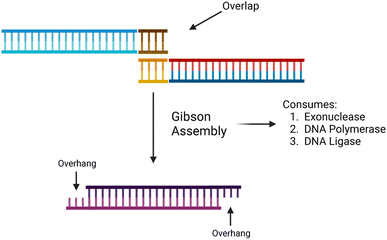
The synthesis of data in the form of DNA begins with DNA fragments, using a process called “Gibson Assembly”. In 2009, Gibson et al. proposed a method for joining multiple DNA fragments in a single reaction.47 These fragments must have overlapping ends, several base pairs in length. In addition to the fragments to be assembled, three enzymes are also required: exonuclease, DNA polymerase, and DNA ligase. Using these enzymes, Gibson assembly connects two double-stranded DNA together.The Gibson assembly is general-purpose and widely used for cloning DNA fragments. We adapted it to constructing long data-storage strands. A visualization of the Gibson assembly process is shown in Fig. 4.
In the context of the DMFB, we place a symbol, linker, and three enzymes into three separate droplets. These are all routed to a “Gibson site”. The chemical reactions for Gibson assembly are performed at this site, resulting in a larger droplet with the symbol and linker combined.
3 Write speeds
Here, we discuss the parameters of a DMFB that could compete with hard disk drives (HDDs) in terms of data write speed. The write speed of modern HDDs is on the order of 100 megabytes¶¶ per second (MB s−1), so this is our target write speed.3.1 Goal: a DMF system that writes 100 MB of data per second
We need to load 100 MB of data in the form of DNA symbols onto the device per second. Each symbol is 8 nucleotides long, with 2 bits per nucleotide, so each symbol represents 16 bits or 2 bytes of information. Therefore, to meet our target write speed, we must load 50 million symbols, each in a separate droplet, onto the DMFB every second. Using milliseconds as our unit of time, we must load 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 symbols per millisecond. We must also load linkers and different chemical reagents. Loading and moving so many droplets is a demanding task – one that requires mature DMF technology. To achieve our target write speed, we estimate that the DMF device may have the following parameters:
000 symbols per millisecond. We must also load linkers and different chemical reagents. Loading and moving so many droplets is a demanding task – one that requires mature DMF technology. To achieve our target write speed, we estimate that the DMF device may have the following parameters:
(1) A grid size of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 by 100
000 by 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 electrodes – so 10 billion electrodes.
000 electrodes – so 10 billion electrodes.
(2) Droplet reservoirs or sinks at all four edges – so 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 total.||||
000 total.||||
(3) The ability to load droplets onto the device at a rate of 5 kHz – so a new droplet loaded every 1/5000-th of a second, or 200 μs. Also, the ability to move droplets from electrode to electrode across the device at the same rate.
(4) Handling of droplets that are on the order of a femtoliter in volume.
With four edges to a square grid, symbol droplets will be loaded onto the device from the first edge; linker droplets from the second edge; and various reagents from the third. Completed genes will be loaded off the devices from the fourth edge.
Given the target of loading 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 symbol droplets per millisecond onto the chip, with a loading rate of 5 kHz we must load 10
000 symbol droplets per millisecond onto the chip, with a loading rate of 5 kHz we must load 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 symbol droplets simultaneously every 200 μs. (We assume that we must also load 10
000 symbol droplets simultaneously every 200 μs. (We assume that we must also load 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 linker droplets and 10
000 linker droplets and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chemical droplets simultaneously every 200 μs.) With 100
000 chemical droplets simultaneously every 200 μs.) With 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reservoirs containing symbols arranged along the first edge of the device, we assume that a symbol is loaded from 1 out 10 reservoirs every 200 μs.
000 reservoirs containing symbols arranged along the first edge of the device, we assume that a symbol is loaded from 1 out 10 reservoirs every 200 μs.
DMF technology that moves droplets at this speed has been demonstrated.48–50 However, no DMFB with millions, let alone billions, of electrodes has been built. Undoubtedly, building such a large DMFB is an expensive proposition. We note that there is a trade-off between DMFB grid size and droplet speed: the grid size required to achieve a given write speed decreases as the speed of droplets increases. If the speed of DMF technology improves beyond 5 kHz, the required grid size will be considerably smaller.
The write speed is measured by the number of completed storage genes produced per second (given a gene length of fixed size). We make the following assumptions:
(1) Each storage gene is assembled from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 symbols.
000 symbols.
(2) The system can assemble 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 storage genes concurrently.
000 storage genes concurrently.
(3) Assembly is pipelined.***
With these assumptions, we can achieve our target write speed of 100 MB of data per second:
These calculations target write speeds that would match current hard drive technology. Of course, the premise of this work is that DNA storage systems could outpace improvements in both the capacity and write speed of hard drives. This requires scaling the parameters further. In the realm of electronics, devices with more than 10 billion electrodes are not physically implausible. Indeed, modern microprocessors contain tens of billions of transistors.51 There are simply too many unknown parameters for us to provide meaningful calculations here. Still, we postulate that a DMF device containing tens or even hundreds of billions of electrodes could achieve write speeds surpassing the capabilities of hard drives.
4 DNA assembly and droplet routing
4.1 Automated DNA assembly
There are two requirements for our DNA synthesis system:(1) To represent arbitrary data, it must assemble DNA oligos in any given order.
(2) To assemble DNA oligos efficiently, several strands must be assembled simultaneously in one Gibson process, without risking misalignment.
These two requirements are contradictory. If oligos can come in any order, one cannot join more than two simultaneously; they could join in the wrong order. To ensure desired ordering, it is necessary for segments to be uniquely matched with one another.
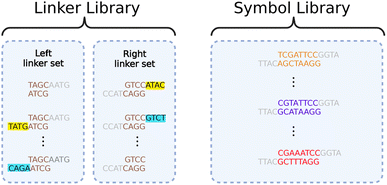
We resolve this contraction with a dual library of oligos we call “symbols” and “linkers”, illustrated in Fig. 5. The symbols allow us to represent arbitrary data when assembling them together. The linkers allow parallelization in the assembly process, ensuring correct ordering.
Data genes comprise long chains of alternating symbols and linkers, with relevant information contained in the symbols only. All symbols have unique interior segments composed of 8 base pairs, allowing each to encode 16 bits. By using multi-bit symbols instead of assembling one base pair at a time, we exchange much of the fabrication time for overhead in maintaining the symbol library.
All symbols share the same beginning (left-side) and end (right-side) sequences. The left and right ends are not complementary, disallowing direct Gibson assembly of two symbols. Complementary ends are shared by all linkers, but each linker only has one end matched with those of the symbols. The other end binds with its unique, complementary linker. Thus, any desired chain of symbols can be assembled by first using Gibson assembly to separately attach each symbol to the appropriate linkers and then bringing all attached symbol-linker pairs together in another Gibson assembly process.
The linkers will naturally order themselves according to their unique matches and the symbols will automatically fall into the appropriate order. This process is demonstrated in Fig. 6. Following assembly, the new string of symbols undergoes purification and polymerase chain reaction (PCR).52 This product is a storage gene that holds encoded information in its symbols.
Any gene requiring more symbols than what can be reliably handled by a single assembly process can be constructed by repeated assembly processes. Now, linkers on the ends of longer segments – each consisting of multiple symbols – specify the order in which these should be assembled.
Assembling large data sets, consisting of millions, billions, or trillions of symbols, will require vast numbers of individual Gibson assembly operations. This presents a non-trivial problem in the form of managing droplet traffic routes and congestion. Given an arbitrary list of symbols to be encoded in a gene, droplets must be created, destinations chosen, and routes calculated. This multistep process necessitates an automated system capable not only of routing traffic but also deciding what Gibson assembly operations must be performed and when to build the desired gene.
4.2 Routing algorithm for droplet pathing
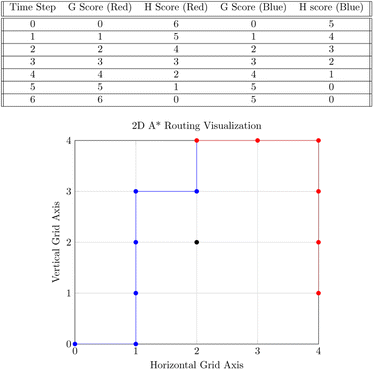
Our system routes droplet traffic to desired Gibson, PCR, and purification sites using prioritized 3-D A*53 on the DMFB. First, generic A*54 will be explained, and then the prioritized 3-D A* algorithm that we use will be discussed in detail.The goal of A* is to find the lowest cost path from point A to point B on a given graph. A graph is a generic collection of nodes connected via edges, and cost refers to the length of the path. The costs of paths are calculated using two scores, referred to as g and h scores. The g score is the cost to get to the current node (the path already traversed), and the h score is the distance from the current node to the end node (the path to traverse). In general, this h score is determined via a specific user-chosen heuristic; our implementation of A* uses Manhattan distance. The h and g scores are added to become the f score, or the total score for the path. Fig. 7 shows an example of A* on two droplets moving in 2-D space. Ideally, the f score should be as small as possible.55
Starting from point A, we look at each edge extending out from A and calculate the f score for the surrounding nodes. The nodes and f score are placed into an open set, usually represented as a data structure in memory. From there, paths are extended by looking at each node in the open set, starting with the lowest f score. The f scores for the nodes connected to the current node are then updated and placed back into the open set. This continues until B is reached, or it is concluded that no path to B is available.
To contextualize this algorithm, the nodes in the graph represent grid spaces on the DMFB, and edges indicate which grid spaces are next to each other. In the explanation below, point A represents a droplet's starting position while point B is its local destination which can be one of many things. It can be an intermediate location where the symbol and linker droplets mix into a larger droplet. It can also be a location where Gibson mixing occurs between the larger droplet and a Gibson mix reagent droplet. For both situations, this target location is the site of droplet mixing in some form. We classify the collection of these droplets as a merge group.
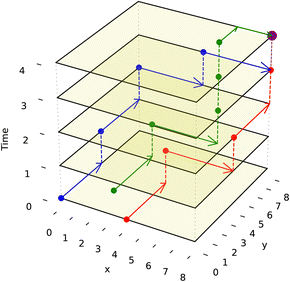
We adapt the generic A* algorithm in our application to the prioritized 3-D A* form. It is prioritized because the algorithm tackles routing the droplet with the furthest Manhattan distance to travel first. It operates on 3 dimensions, with two dimensions representing the DMFB 2-D grid layout and the third representing time. All droplets are routed sequentially using the 3-D A* priority scheme. All droplets must move one grid space at a time simultaneously as all routes are planned beforehand. The algorithm is called ND times, where ND is the number of droplets on the grid. 3-D A* would be called once per newly pulled droplet. Once each droplet has its route, they will move together one time step at a time. The A* algorithm itself is called upon every merge operation and route completion as the resultant droplet now needs to be assigned a new route. Visualization of such routing movement is shown in Fig. 8
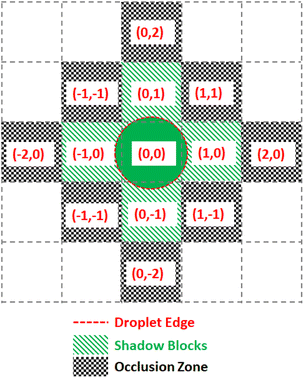
To prevent the unwanted merging of droplets, the notion of a droplet shadow and occlusion zone are introduced, as illustrated in Fig. 9. These are projected into a 3-D space such that for ND droplets, there are 3ND occlusion zones where each occlusion zone is present for the previous, current, and future time steps of the droplet. Droplets that are not in the merge group of the current droplet see the occlusion zones as obstacles they must route their paths around. Since routing is completed by taking all 3 dimensions into consideration and before any droplet movement occurs, the obstacles are static meaning they do not appear at random to block a droplet's route. This method of routing is advantageous because it prevents unwanted collisions from occurring while having each droplet take the optimal path given the constraints imposed by previously routed droplets.
5 Architecture
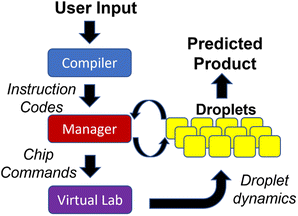
We discuss the architecture of the software that controls the DMFB device. We use a modular hierarchy to solve the droplet traffic management problem, shown in Fig. 10. At the top of the hierarchy, we have the Compiler, which is responsible for reading a user's desired data, in the form of a DNA storage gene P, and breaking down the basic chemical steps that must be performed to create it. These basic chemical steps are passed down to the Manager, which is responsible for assigning the droplets' destinations and issuing commands. At the bottom of the hierarchy is the Virtual Lab, which emulates a real DMFB. The lab houses a group of grid spaces and chemical droplet objects, which represent their physical equivalents and behave in similar ways within their virtual space.Our Virtual Lab takes into account the time required for all droplet operations, including storing and retrieving droplets from reservoirs located at the perimeter of the grid. In our simulations, we assume that all the chemical reactions for DNA assembly complete in a single time step. While this assumption may or may not be realistic, chemical reactions generally complete quickly with femtoliter volumes. It is important to note that this “real” time is distinct from the “runtime” required for the 3-D prioritized A* algorithm. Of course, in the eventual production-level device, all routing must be done in real-time, so our routing algorithm must complete faster than the time taken by physical droplet routing.
5.1 Assembly protocol
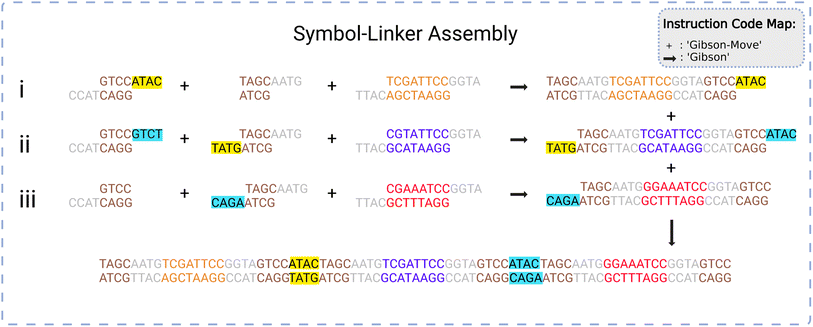
The system requires an assembly protocol to follow to automate the construction of user-determined strings of DNA. This protocol specifies the sequence of chemical reactions that attaches multiple independent pieces of double-stranded DNA to one another. An instruction produced by the protocol takes the form of a list in the following format:| [<Instruction Type>, <droplet 1>, <droplet 2>, …] |
| [<reagent 1>, <reagent 2>, …, <reagent N>] |
When reading the instructions, the manager will execute a case structure based on <Instruction Type> using component droplets matching the descriptions given by <droplet 1>, <droplet 2>, etc. An example instruction might be [‘GibsonMove’, [_S0_], [L1], [‘Gibson-mix’]], indicating that the manager should identify three droplets containing the symbol 0, the linker 1, and some Gibson mixing chemicals and bring them together on a suitable Gibson site.
An example of the instruction codes for a single assembly step using the Gibson symbol-linker protocol is given below. This list assembles the data string S1–S0–S2, corresponding to symbols numbered 1, 0, and 2, respectively, from the total list of symbols available.
(1) [‘Gibson-Move’, [‘L0’], [‘_S1_’], [‘Gibson-mix’]]
(2) [‘Gibson’, [‘L0’, ‘_S1_’, ‘Gibson-mix’]]
(3) [‘Gibson-Move’, [‘L1’], [‘L2’], [‘_S0_’], [‘Gibson-mix’]]
(4) [‘Gibson’, [‘L1’, ‘L2’, ‘_S0_’, ‘Gibson-mix’]]
(5) [‘Gibson-Move’, [‘L3’], [‘_S2_’], [‘Gibson-mix’]]
(6) [‘Gibson’, [‘L3’, ‘_S2_’, ‘Gibson-mix’]]
(7) [‘Gibson-Move’, [‘L1_S0_L2’], [‘L3_S2_’], [‘_S1_L0’], [‘Gibson-mix’]]
(8) [‘Gibson’, [‘L1_S0_L2’, ‘L3_S2_’, ‘_S1_L0’, ‘Gibson-mix’]]
(9) [‘Purify-Move’, [‘_S1_L0L1_S0_L2L3_S2_’], [‘Purify-mix’]]
(10) [‘Purify’, [‘_S1_L0L1_S0_L2L3_S2_’, ‘Purify-mix’]]
(11) [‘PCR-Move’, [‘_S1_L0L1_S0_L2L3_S2_’], [‘PCR-mix’]]
(12) [‘PCR’, [‘_S1_L0L1_S0_L2L3_S2_’, ‘PCR-mix’]]
In the list above, the first two steps create the symbol-linker droplet [‘_SI_L0’] through Gibson moving and mixing steps. The first instruction has the instruction type ‘Gibson-Move’ with three droplets containing the linker 0, the symbol 1, and some Gibson Mix. It will move and merge the droplets to an available Gibson site, creating a larger droplet. The second step initiates Gibson mixing and assembly on the larger droplet to assemble all reagents into a larger gene [‘_SI_L0’]. Likewise, steps 3 to 6 produce the droplets [‘L1_S0_L2’] and [‘L3_S2_’]. Steps 7 and 8 take these three larger droplets and perform Gibson assembly on them at a suitable Gibson site. This creates the droplet [‘_S1_L0L1_S0_L2L3_S2_’]. The final four steps take the final droplet to purify (clean) and to PCR (amplify) sites to create the final data string S1–S0–S2 held together with linkers.
5.2 Compiler
The Compiler is analogous to a software compiler which translates user input into a set of primitive instructions. The input consists of a list of characters representing the aforementioned “symbols” such as ‘S1–S0–S2’. The job of the compiler is to determine how to build the given DNA strand by repeated and recursive applications of its assembly protocol. We designate the desired final product P, with a length of LP symbols.The compiler must first determine how to construct P using assembly operations that can combine at most NA segments simultaneously, with the limit NA being set by the assembly protocol. In this case, NA is the reliability margin of the symbol-linker Gibson assembly. We employ an NA-ary data tree to store the construction blueprint. The root node stores P. The compiler symbolically breaks P up into NA separate segments and stores each segment in a child node below the root. These segments are broken up in the same way, with new nodes storing the new, smaller segments. The tree is built from the bottom up until the final nodes contain segments of one symbol in length. This abstract string-building is mimicked by the DNA strand assembly.
Algorithm #1 and Algorithm #2 explain the algorithms for building the assembly tree step-by-step. (We note that not all details are included in the pseudocode given here.)
With the ordering of the tree determined, the compiler will populate the instructions for each node by consulting the chemical protocol and giving the strands of a node's children as its inputs. This is outlined in Algorithm #3. This implies nodes without children (leaf nodes) have no instructions. The resulting ‘assembly tree’ provides a blueprint for constructing the final product P. The leaf nodes, each holding one symbol, can be read from left to right to give the individual symbols of P. The first layer of non-leaf contains the NA-length products of the first set of assembly operations as well as the instructions needed to carry them out. The next layer further groups those segments in length 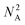 , and so on. The root node contains instructions for the final assembly of P, grouping the remaining segments together. Fig. 11 illustrates the assembly tree data structure used to assemble ‘S1_S0_S2_S4’ with linkers omitted. The instruction codes for assembling ‘S1–S0–S2’, described above in the assembly protocol subsection, are carried by the left-hand instruction node in the graphic.
, and so on. The root node contains instructions for the final assembly of P, grouping the remaining segments together. Fig. 11 illustrates the assembly tree data structure used to assemble ‘S1_S0_S2_S4’ with linkers omitted. The instruction codes for assembling ‘S1–S0–S2’, described above in the assembly protocol subsection, are carried by the left-hand instruction node in the graphic.
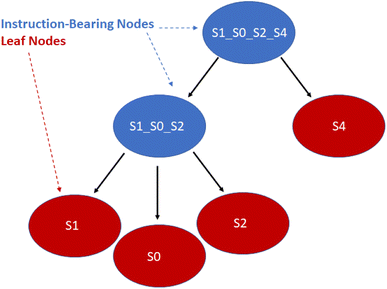 | ||
| Fig. 11 Simplified diagram of a small assembly tree data structure. In red, the leaf nodes each contain a single symbol. The root node represents the final desired symbol sequence or gene. Non-leaf nodes contain assembly instructions readable by the manager. We note that the linkers between the symbols have been excluded for readability. See Fig. 12 for more details on individual nodes. | ||
Besides encoding the organization of substrings and the individual instructions necessary to chemically assemble P, the nodes also interface with the manager in real-time to track the disposition of droplets created for each node. This will be discussed in more detail below.
5.3 Virtual lab
The Virtual Lab simulates each droplet and each DMFB grid space as independent objects in a continuous loop representing the passage of real-time. At each time step the lab checks for any update commands, activating or deactivating the corresponding grid spaces, if any. Then each droplet checks its surroundings for active grid spaces and updates its location according to the droplet movement model. For convenience, all droplet objects maintain references to each grid space they currently contact, and each grid space object similarly holds references to any and all droplets touching it. This location update step is where the lab detects errors.The droplets are tracked in terms of their current ‘shadow’, which is a digitization of the droplet's shape. Assuming a droplet is centered in the middle of a grid space, the shadow is a list of grid space coordinates, relative to the center space, which also touch the droplet. This is used by the manager to determine which electrodes to use for moving the droplet. This also allows easy calculation of an occlusion zone, the layer of grid spaces around a droplet that is as close as possible without touching. This layer is used as a barrier, off-limits to all other droplets that are not intended to mix. For instance, a small droplet that only touches the grid spaces nearest to its center in the four cardinal directions would have a shadow S = [[0, 0], [1, 0], [0, 1], [−1, 0], [0, −1]] and an occlusion zone O = [[1, 1], [1, −1], [2, 0], [0, 2], [−1, 1], [−2, 0], [−1,−1], [0, −2]] as shown in Fig. 9. As droplets merge and grow, their shadows and occlusion zones increase commensurately. During routing, a droplet's shadow and occlusion zone are projected both forward and backward in time by one step to ensure no undesired mixing can happen.
5.4 Manager
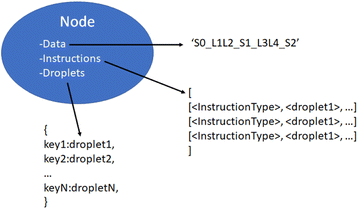
With a simulated lab to house the droplets and a compiler to provide the basic mix and merge instructions, there is one final task. The instructions must be translated into actual commands for the lab to execute. This entails selecting reservoirs from which to pull droplets of appropriate types, choosing destinations for them, and determining routes that will see them to their destinations without any unwanted misadventures along the way. This is the manager's job. The manager interfaces with the assembly tree and the lab. It runs in a loop matching the lab's time steps, providing new commands at each step while also tracking long-term progress toward each assembly node's instructions.The manager must be able to track the droplets in the lab, knowing their locations and contents at each step. It is useful to reference droplets by their contents rather than location since this allows easy matching of droplets to instructions that call for specific reagents. Fig. 13 visualizes the changes in droplet references after merging and performing Gibson assembly.
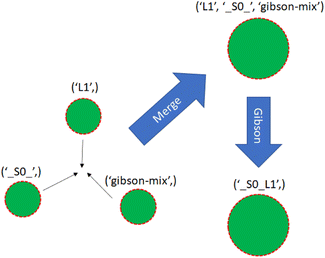 | ||
| Fig. 13 Three single-species droplets merge, becoming a larger droplet with mixed species. The droplet undergoes Gibson assembly, becoming a different species. | ||
We now have a complete description of the information contained in the node objects. As shown in Fig. 12, they contain immutable data and instruction values consisting of the symbol-linker representation of the DNA strand they construct and the instructions used to build it. They also contain a mutable dictionary of droplet objects which changes throughout the manager-lab time loop.
The manager runs in a loop lock-stepped with the lab, maintaining a list of active nodes drawn from the assembly tree and stepping through their instructions in parallel. It also creates a list of lab commands which begins each iteration empty, fills up during the node advance and droplet routing steps, and is subsequently passed to the lab for execution. For each iteration, it runs four processes in order as shown in Algorithm#4. Initially, the active nodes list consists of all the lowest level non-leaf nodes.
When checking node progress, the system evaluates the node's current instruction list and its droplet's location and sees if the node is ready to move to the next instruction. If the node is ready to advance its instructions, it will check the instruction codes and advance to the next instruction.
After finishing with the nodes, the manager checks for droplets that have been newly assigned to destinations and those that could not be routed during the last iteration. The manager attempts to plan a route for each of these.
The manager's routing algorithm uses the 3-D prioritized A* method discussed above in Section 4.2. Droplets are organized into ‘merge groups’, which are collections of droplets that are seeking to combine into one conglomerate. All routes that are generated obey the following anti-collision constraint that applies to any two droplets dx and dy of different merge groups. Any grid space occluded by dx until time ta may not be overshadowed by dy during any time tb such that ta ≥ tb.
With priority given to merge groups containing droplets with the farthest Manhattan distance to travel, all selected droplets are routed one at a time using a 3-D A* graph traversal. Two of the dimensions represent the virtual–or physical–DMFB grid layout, while the third is time.
For each droplet d the router takes droplet shadow Sd and occlusion zone Od into account at every step, projecting them into the 3-D space. These zones are off-limits for other droplets during their own routing phase. This includes droplets that will be routed during this or any future time steps. The space is initially free of occlusion zones when the highest-priority droplets are routed and becomes more populated as the other droplet routes are filled in. Of course, there may also be occlusion zones generated by the routing phase in the previous time step, which all droplets during this time step must avoid regardless of their priority level. There will be at most 3ND occlusion zones present on the grid at a given time, where ND is the total number of extant droplets. This is because each droplet generates occlusion zones for its most recent, current, and immediately subsequent steps to satisfy the anti-collision constraint. This routing method allows many droplets to move simultaneously while avoiding unwanted collisions. Furthermore, each individual droplet takes the optimal path within the constraints given to it by the droplets higher in the priority queue and the droplets routed during previous time steps.
We note that the modularity of the system makes it relatively easy to implement a different routing scheme. Incorporating more advanced electrowetting technology, which would allow for more flexible movement, would only require the redesign of the routing subroutine itself, leaving the other parts of the software to function as normal. One possible redesign to routing is to make it contamination aware.56 Another possibility includes incorporating the algorithm “Moving Target D* Lite”,57 which has been shown to be effective in problems where obstacle occurrences appear dynamically over time.
After planning routes for all droplets, the manager performs the movement of droplets according to the instructions and routes that have been set up. After these steps are complete, one loop iteration is concluded.
6 Results and discussion
6.1 Simulation results
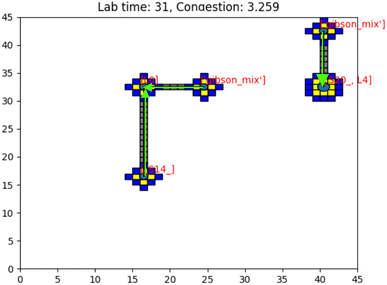
Having presented the software architecture for our automated DNA assembly system, we now present simulation results. We note that our simulation does not incorporate physical latencies present with DMFBs such as the electrode switching rate58 and the delay with mixing operations.59 Accordingly, a comparison of runtimes with other DNA synthesis technology is speculative, at best.In our simulation, we wish to evaluate the impact of computer hardware, virtual lab grid size, and target gene length on our system's performance. We draw conclusions about their impacts on the system's runtime. The simulated DMFB system for DNA assembly was written in Python. Fig. 14 displays a snapshot of the simulation's GUI displaying routed droplet movement in real-time. Additionally, benchmarking results were captured to better understand the distribution of function workload and the limitations of the current model.
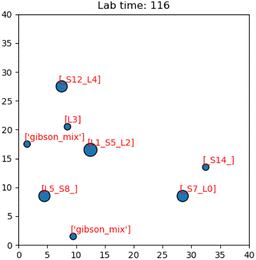 | ||
| Fig. 14 Image of the simulation's GUI displaying droplets being routed in a 40 × 40 size grid. The number of full command execution rounds is shown at the top as the lab time. | ||
We comment on the relationship between grid size and runtime. When the grid dimension, i.e., the length along one side, is increased from n to (n + 1), the number of locations available on the grid increases by (n + 1)2 − n2 = 2n + 1. Thus, there is a linear relationship between the number of available locations and the grid dimension.
However, the impact on runtime is more complex. Assume we are choosing several start and destination pairs on a n by n grid. The number of possible pairs on such a grid is
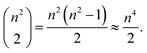 | (1) |
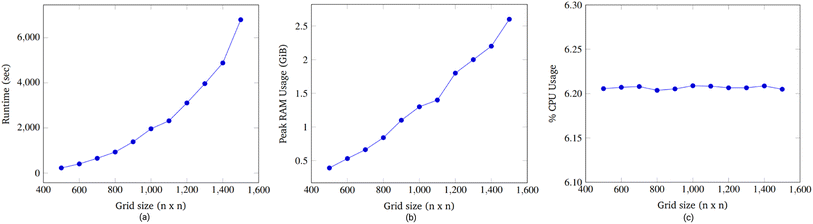
Accordingly, an exhaustive search of all possible pairs means that the algorithm would have an O(n4) dependence on the grid dimension. However, our algorithm is heuristic, not exhaustive. Fig. 15a suggests that the runtime dependence on the grid dimension is approximately quadratic.
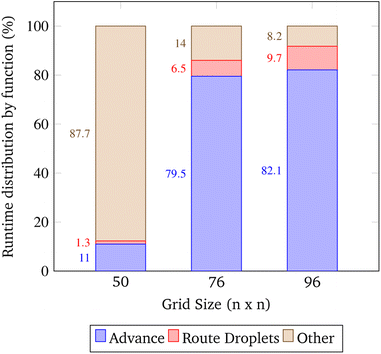
6.2 High impact functions
The open-source visualization software Gephi was used to record the runtimes of the simulation's local functions over three trials. The trials were chosen such that as the problem size increased, the congestion remained constant. In the context of these trials only, congestion is computed as the total number of droplets pulled from reservoirs divided by the number of total grid points. The exact simulation input parameters are displayed in Table 2.| Trial | Grid size | Gene length | Droplets | Congestion |
|---|---|---|---|---|
| 1 | 50 | 2 | 9 | 0.00360 |
| 2 | 76 | 4 | 21 | 0.00364 |
| 3 | 96 | 6 | 33 | 0.00358 |
In these trials, the functions advance and Route_Droplets were identified as methods of interest. The lab's function advance computes an entire time step of the simulation. Advance iterates over the grid points and droplets multiple times in order to update their contents. The manager's function Route_Droplets computes the routes for droplets that have yet to be routed with the prioritized 3-D A* routing algorithm. The proportion of the total runtime spent computing each function is shown in Fig. 16. As the problem size increases, advance's proportion of runtime increases. The proportion of the time consumed by Route_Droplets also increases as the problem size increases, overtaking the combined runtime of all other subroutines. In the last trial, it is evident that these two functions will dominate the share of the simulation's runtime as larger, more realistic input parameters are chosen. It may be inferred that the computation of advance on an exponentially increasing input tends to be slower than the computation of the prioritized 3-D A* routing algorithm on a linearly increasing number of pulled droplets.
Improving the runtime of advance is worth attention in future work. This task is difficult as it requires an optimized approach to iterating over all grid points and droplets. Additionally, this is a function that runs on the simulated lab, and it is likely the speed of advancing droplets on a real DMFB will be different. The simulation may benefit in runtime by considering alternatives to the prioritized 3-D A* routing algorithm used in Route_Droplets. Currently, the algorithm considers all possible routes for each droplet; however, there may be room for improvement by implementing methods that return an acceptable suboptimal route while only evaluating a fraction of the input space. Finding an acceptable suboptimal route for problems that can face a lot of congestion and time consumption has been studied by literature and shown to be effective in similar situations.60,61 These algorithms define an acceptable threshold for a path to be executed and then create the route once a path is found that meets the threshold limit.
6.3 Limitation testing
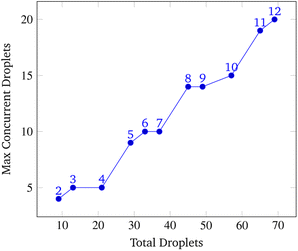
This section explains the input spaces of interest where the program may face serious bottlenecks or failures at a high level. The inputs used to test the simulation specify a random gene consisting of 5 symbols at the expected grid size of 1000 × 1000 grid points. When the input grid size exceeded this grid size the program's runtime increased beyond practicality, taking over an hour to synthesize the gene routing about 30 droplets.On the other hand, the program fails when grid sizes are small enough to generate considerable congestion. Within the context of the simulation, when the grid size becomes smaller than 40 × 40, given all other default parameters, there are issues with synthesis due to droplet congestion. A gene of length 5 pulls a total of 29 droplets as shown in Fig. 17, and all of these droplets need to be routed without causing collisions. In these situations, droplet paths may be blocked long enough to trigger a timeout where the synthesis of the gene is no longer pursued.
Aside from grid size, the number of reaction sites (Gibson, purification, PCR) can limit runtime and potentially cause timeout from congestion if very few of these sites exist on the chip. Moreover, there is a limited amount of chemistry sites the DMFB will allow due to its physical grid size. The number of reaction sites the DMFB contains depends on its physical grid size. Additionally, the number of reaction sites cannot exceed the number of possible reaction site locations.
6.4 Congestion testing
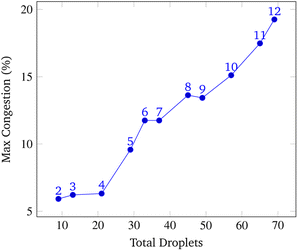
Fig. 18 shows a visualization of multiple droplets being routed to a Gibson site. The yellow squares represent the shadow of a droplet and the blue squares are their occlusion zones. We display the paths of various droplets shown as gray squares to indicate these as “no-go” zones for other droplets. To other droplets, these gray squares are temporarily forbidden from crossing to avoid contamination of the droplet as it may pick up debris from a previously routed droplet, which is undesirable. Of course, this issue is hardware specific, but it is considered a constraint in our simulation and therefore contributes to congestion calculations.The program can time out under conditions of extreme congestion. This may occur for a number of input combinations, most notably when the grid size becomes too small. In these cases, there may be too few reaction sites, or too many droplets (as a consequence of synthesizing a long target gene). Any combination of these factors may lead to a situation where droplet paths are blocked and progress cannot be made. The simulation then times out and the synthesis of the target droplet is abandoned.
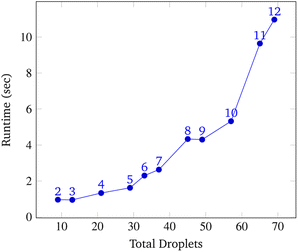
To analyze congestion, the program was run on a range of gene lengths of two to twelve on a single machine at a constant grid size (45 × 45). For each gene length, the number of droplets pulled, the maximum number of concurrent droplets, and the grid's maximum congestion were recorded. Congestion is computed as the number of routed, inhabited, and occluded grid points divided by the total number of grid points. The number of droplets pulled is directly related to the length of the target gene. In Fig. 17 and 19, data points are labeled with their gene length for reference. As the total number of droplets increases (due to increasing gene length) the maximum number of concurrent droplets and maximum congestion increase linearly. Analyzing runtime again but in the context of congestion, we see that as the number of total droplets pulled from reservoirs increases, the runtime increases approximately exponentially (Fig. 20).
7 Conclusions
Ever since Watson and Crick first described the molecular structure of DNA, its information-bearing potential has been apparent to computer scientists. In principle, DNA could provide a storage medium that is many orders of magnitude denser than conventional media. Spurred by the biotech and pharma industries, the technology for both sequencing (reading) and synthesizing (writing) DNA has progressed rapidly. Nevertheless, a large gap remains between what is theoretically possible in terms of reading/writing speed and what has been demonstrated in practice. The industrial partner in this research, Seagate, is developing a digital microfluidic device to close the gap.This paper discusses our strategy for DNA synthesis with this device and profiles the software that will control it. DNA storage units called “genes” are assembled from smaller DNA fragments. A key innovation is the use of a dual library of DNA fragments: “symbols” and “linkers.” Data is conveyed through the sequence of nucleotides in the symbols. Linkers, attached to the ends of symbols, determine in what order these symbols will link together. The linkers allow parallelization in the assembly process: multiple symbols can be linked together in the same droplet on the digital microfluidic device, with the linkers assuring that they hybridize in the correct order. This parallelism in synthesis is the key to achieving the write speeds needed for a DNA storage device to compete with existing systems that use magnetic, optical, or solid-state media.
The digital microfluidic device that Seagate is building will be on a scale far greater than any built with this technology today. The software to control it has to route thousands of droplets across this grid to assemble the target DNA genes. We discussed the architecture of the software that we developed for this task and presented simulation results profiling its performance. The core of the software is the routing algorithm: a prioritized 3-D A* algorithm, with two of the dimensions being the x-y coordinates of the electrodes, and the third being time.
We found when grid size was swept from 500 × 500 to 1500 × 1500, it was seen that runtime grew exponentially, RAM usage increased linearly, and CPU usage remained constant. The majority of the runtime was spent advancing node instructions and moving droplets while time spent routing droplets with the 3-D A* algorithm was relatively less.
In future work, we plan to explore routing on the device under conditions of extreme congestion, that is to say when droplets occupy nearly all the available electrodes. The simulation must be parameterized with congestion in mind; factors such as grid size, number of reaction sites, and gene length influence grid congestion and consequently runtime. It might be advantageous to incorporate algorithms designed for memory management if peak RAM becomes the limiting factor for large grid sizes. Algorithms like A* and Moving Target D* Lite are heuristic-based. They will find the shortest path under given constraints. However, they do not consider the search time and memory requirements necessary to find such a path. There exists a family of algorithms called Conflict-Based Search (CBS) which help prune unnecessary branches of the search tree in order to manage memory and improve speed. Conflict-based searching might be particularly efficient if the problem is formulated in terms of multiagent path finding.62–64
Finally, this paper did not consider the process of reading data stored in DNA (i.e., sequencing it). With current technology, reading DNA is orders of magnitude more efficient than writing it, so the impetus is to focus on improvements in write speed. In future work, we will prototype and report experimental results on the complete system: a digital microfluidic device for writing DNA at a high speed to compete with existing solid-state storage media.
Data availability
The manuscript is accompanied with a versioned archive available on Zenodo (DOI: 10.5281/zenodo.260063) and Github. Please follow the link to access the archive directly: https://zenodo.org/record/8260063. Instructions to use this are included in the README.md file located in the top level directory of this repository.Author contributions
A. Manicka is the primary author. A. Stephan designed and implemented the software and also contributed substantial portions of the text. S. Chari analyzed and improved the core algorithms for droplet routing. G. Mendonsa devised the synthesis procedure with symbols and linkers, along with colleagues at Seagate. She also contributed the background material on Gibson assembly. P. Okubo performed software testing on the system. J. Stolzberg-Schray wrote the description of the A* routing algorithm. A. Reddy and M. Riedel were the principal investigators for the project. All authors have contributed to the writing of this article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Matthew Boros and Hershen Nair for their comments and edits that greatly improved the manuscript. This work was funded in part by the National Science Foundation's Division of Computing and Communication Foundations, grant #2227578.References
- J. Li, R. J. Stones, G. Wang, X. Liu, Z. Li and M. Xu, Reliab. Eng. Syst. Saf., 2017, 164, 55–65 CrossRef.
- IDC, Worldwide Global DataSphere Forecast, 2021–2025: The World Keeps Creating More Data—Now, What Do We Do with It All?, US Pat., 46410421, 2021 Search PubMed.
- C. Mellor, Zettabyte Era Brings Archiving Front and Center, 2022, https://blocksandfiles.com/2022/07/11/zettabyte-era-brings-archiving-front-and-center/ Search PubMed.
- IDC, Worldwide Global StorageSphere Forecast, 2021–2025: To Save or Not to Save Data, That Is the Question, US Pat., 47509621, 2021 Search PubMed.
- J. Monroe and R. Preston, Market Trends: Evolving Enterprise Data Requirements—How Much Is Not Enough?, Gartner Inc., 2020 Search PubMed.
- E. Leproust, Data Centers Are Unsustainable. We Need to Store Data in DNA, 2022 Search PubMed.
- G. Church, Y. Gao and S. Kosuri, Science, 2012, 337, 1628 CrossRef CAS PubMed.
- Barracuda Fast SSD: Compact Portable SSD with USB-C: Seagate US, https://www.seagate.com/products/external-hard-drives/barracuda-fast-ssd/ Search PubMed.
- A. El-Shaikh, M. Welzel, D. Heider and B. Seeger, NAR: Genomics Bioinf., 2022, 4, lqab126 Search PubMed.
- L. Ceze, J. Nivala and K. Strauss, Nat. Rev. Genet., 2019, 20, 456–466 CrossRef CAS PubMed.
- L. M. Adleman, Science, 1994, 266, 1021–1024 CrossRef CAS PubMed.
- D. Soloveichik, G. Seelig and E. Winfree, Proc. Natl. Acad. Sci., 2010, 107, 5393–5398 CrossRef CAS PubMed.
- H. Jiang, M. D. Riedel and K. K. Parhi, 2013 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), 2013, pp. 721–727 Search PubMed.
- S. A. Salehi, H. Jiang, M. D. Riedel and K. K. Parhi, IEEE Trans. Mol. Biol. Multi-Scale Commun., 2015, 1, 249–264 Search PubMed.
- J. D. Watson and F. H. Crick, Cold Spring Harbor Symp. Quant. Biol., 1953, 123–131 CrossRef CAS PubMed.
- K. Chen, J. Zhu, F. Bošković and U. F. Keyser, Nano Lett., 2020, 20, 3754–3760 CrossRef CAS PubMed.
- G. D. Dickinson, G. M. Mortuza, W. Clay, L. Piantanida, C. M. Green, C. Watson, E. J. Hayden, T. Andersen, W. Kuang, E. Graugnard, R. Zadegan and W. L. Hughes, Nat. Commun., 2021, 12, 2371 CrossRef CAS PubMed.
- A. Meares, K. Susumu, D. Mathur, S. H. Lee, O. A. Mass, J. Lee, R. D. Pensack, B. Yurke, W. B. Knowlton and J. S. Melinger, et al. , ACS Omega, 2022, 7, 11002–11016 CrossRef CAS PubMed.
- M. Hepisuthar, et al. , Turk. J. Comput. Math. Educ., 2021, 12, 3635–3641 Search PubMed.
- Y. Erlich and D. Zielinski, Science, 2017, 355, 950–954 CrossRef CAS PubMed.
- M. Jain, H. E. Olsen, B. Paten and M. Akeson, Genome Biol., 2016, 17, 1–11 CrossRef PubMed.
- E. Leproust, Data Centers Are Unsustainable. We Need to Store Data in DNA, 2022 Search PubMed.
- W. Guo, S. Lian, C. Dong, Z. Chen and X. Huang, ACM Trans. Des. Autom. Electron. Syst., 2022, 27, 1–33 CrossRef.
- S. De Munter, A. Van Parys, L. Bral, J. Ingels, G. Goetgeluk, S. Bonte, M. Pille, L. Billiet, K. Weening and A. Verhee, et al. , Int. J. Mol. Sci., 2020, 21, 883 CrossRef CAS PubMed.
- I. M. Mackay, K. E. Arden and A. Nitsche, Nucleic Acids Res., 2002, 30, 1292–1305 CrossRef CAS PubMed.
- E. R. Firmansyah, S. U. Masruroh and F. Fahrianto, 2016 6th International Conference on Information and Communication Technology for The Muslim World (ICT4M), 2016, pp. 275–280 Search PubMed.
- J. Yao, C. Lin, X. Xie, A. J. Wang and C.-C. Hung, 2010 Seventh International Conference on Information Technology: New Generations, 2010, pp. 1154–1158 Search PubMed.
- O. O. Martins, A. A. Adekunle, O. M. Olaniyan and B. O. Bolaji, Sci. Afr., 2022, 15, e01068 Search PubMed.
- N. Goldman, P. Bertone, S. Chen, C. Dessimoz, E. M. LeProust, B. Sipos and E. Birney, Nature, 2013, 494, 77–80 CrossRef CAS PubMed.
- R. N. Grass, R. Heckel, M. Puddu, D. Paunescu and W. J. Stark, Angew. Chem., Int. Ed., 2015, 54, 2552–2555 CrossRef CAS PubMed.
- J. Bornholt, R. Lopez, D. M. Carmean, L. Ceze, G. Seelig and K. Strauss, Proceedings of the Twenty-First International Conference on Architectural Support for Programming Languages and Operating Systems, 2016, pp. 637–649 Search PubMed.
- M. Blawat, K. Gaedke, I. Huetter, X.-M. Chen, B. Turczyk, S. Inverso, B. W. Pruitt and G. M. Church, Procedia Comput. Sci., 2016, 80, 1011–1022 CrossRef.
- F. Su, W. Hwang and K. Chakrabarty, Proceedings of the Design Automation & Test in Europe Conference, 2006, pp. 1–6 Search PubMed.
- T. Xu and K. Chakrabarty, Proceedings of the 44th Annual Design Automation Conference, 2007, pp. 948–953 Search PubMed.
- Y. Zhao and K. Chakrabarty, IEEE Trans. Comput.-Aided Design Integr. Circuits Syst., 2012, 31, 242–254 Search PubMed.
- K. Bohringer, IEEE International Conference on Robotics and Automation, 2004, pp. 1468–1474 Search PubMed.
- H. Tsung-Wei and T. Ho, IEEE International Conference on Computer Design, 2009, pp. 445–450 Search PubMed.
- J. Juárez, C. A. Brizuela and I. M. Martínez-Pérez, Inf. Sci., 2018, 429, 130–146 CrossRef.
- C.-H. Liu, H.-H. Chang, T.-C. Liang and J.-D. Huang, 2013 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), 2013, pp. 615–621 Search PubMed.
- S. J. Lehotay and J. M. Cook, J. Agric. Food Chem., 2015, 63, 4395–4404 CrossRef CAS PubMed.
- F. Perut, D. Dallari, N. Rani, N. Baldini and D. Granchi, Curr. Pharm. Biotechnol., 2016, 17, 1079–1088 CAS.
- F. Mugele and J.-C. Baret, J. Phys.: Condens.Matter, 2005, 17, R705 CrossRef CAS.
- B. F. Bender, A. P. Aijian and R. L. Garrell, Lab Chip, 2016, 16, 1505–1513 RSC.
- R. B. Fair, Microfluid. Nanofluid., 2007, 3, 245–281 CrossRef CAS.
- D. Millington, S. Norton, R. Singh, R. Sista, V. Srinivasan and V. Pamula, Expert Rev. Mol. Diagn., 2018, 18, 701–712 CrossRef CAS PubMed.
- Y.-T. Yang and T.-Y. Ho, Front. Chem., 2021, 9, 676365 CrossRef CAS PubMed.
- D. G. Gibson, L. Young, R.-Y. Chuang, J. C. Venter, C. A. Hutchison and H. O. Smith, Nat. Methods, 2009, 6, 343–345 CrossRef CAS PubMed.
- E. Y. Basova and F. Foret, Analyst, 2015, 140, 22–38 RSC.
- J.-u. Shim, R. T. Ranasinghe, C. A. Smith, S. M. Ibrahim, F. Hollfelder, W. T. Huck, D. Klenerman and C. Abell, ACS Nano, 2013, 7, 5955–5964 CrossRef CAS PubMed.
- D. Li, Y. Cao, B. Huang, M. Han, X. Wu, Q. Sun, C. Zheng, L. Zhao, C. Ma and H. Jin, et al. , Langmuir, 2021, 37, 1297–1305 CrossRef CAS PubMed.
- D. Etiemble, 2022, preprint, arXiv:2206.03201, DOI:10.48550/arXiv.2206.03201.
- C. R. Newton, A. Graham and J. S. Ellison, PCR, BIOS Scientific Publishers, Oxford, UK, 1997 Search PubMed.
- J. Wang, Z. Wu, M. Tan and J. Yu, IEEE Trans. Syst. Man Cybern. Syst., 2019, 51, 2904–2915 Search PubMed.
- M. G. Bell, Transp. Res. B: Methodol., 2009, 43, 97–107 CrossRef.
- Z. Zhang, J. Wu, J. Dai and C. He, IEEE Access, 2020, 8, 122757–122771 Search PubMed.
- T.-W. Huang, C.-H. Lin and T.-Y. Ho, 2009 IEEE/ACM International Conference on Computer-Aided Design-Digest of Technical Papers, 2009, pp. 151–156 Search PubMed.
- X. Sun, W. Yeoh and S. Koenig, Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems: volume 1, 2010, vol. 1, pp. 67–74 Search PubMed.
- Z. Hua, J. L. Rouse, A. E. Eckhardt, V. Srinivasan, V. K. Pamula, W. A. Schell, J. L. Benton, T. G. Mitchell and M. G. Pollack, Anal. Chem., 2010, 82, 2310–2316 CrossRef CAS PubMed.
- T. Loveless, J. Ott and P. Brisk, Proceedings of the 18th ACM/IEEE International Symposium on Code Generation and Optimization, 2020, pp. 171–184 Search PubMed.
- Y. Liu and L. Zhu, 2018 International Symposium on Networks, Computers and Communications (ISNCC), 2018, pp. 1–5 Search PubMed.
- S. Katoch, S. S. Chauhan and V. Kumar, Multimed. Tools. Appl., 2021, 80, 8091–8126 CrossRef PubMed.
- Z. Ren, S. Rathinam and H. Choset, IEEE Trans. Autom. Sci. Eng., 2022, 20, 1262–1274 Search PubMed.
- J. Li, Z. Chen, D. Harabor, P. J. Stuckey and S. Koenig, Proceedings of the AAAI Conference on Artificial Intelligence, 2022 Search PubMed.
- P. Pianpak and T. C. Son, 2021, preprint, arXiv:2109.08288, DOI:10.4204/EPTCS.345.24.
Footnotes |
| † A DNA symbol library is a set of nucleotide sequences, of some fixed length n, which we can use as building blocks to assemble larger DNA storage units. |
| ‡ A symbol is a short double-stranded sequence of DNA whose nucleotides specify the data that is being stored. |
| § A linker is a double-stranded nucleotide sequence that connects two symbols together in the correct order. |
| ¶ A gene is a unit of storage consisting of a sequence of symbols, joined by linkers. It is the full length of data assembled as a single molecule of DNA. To be clear, we use the term “gene” but the DNA here has no biochemical function; it is only used for storage. |
| || An oligo is a relatively short fragment of DNA. |
| ** A symbol droplet is a droplet containing a symbol. |
| †† A linker droplet is a droplet containing a linker. |
| ‡‡ A chemical droplet is a droplet containing the necessary enzymes for Gibson assembly. |
| §§ 3-D prioritized A* was selected as the routing algorithm of choice because it is a complete26 and optimal27 heuristic-based algorithm that is guaranteed to find the shortest route between a start and goal point, even in the presence of obstacles.28 |
| ¶¶ A megabyte is 106 bytes. A byte is 8 bits of data. |
| |||| Droplets are loaded onto the device from reservoirs and loaded off the device into sinks. |
| *** Pipelining in this context means that we do not wait until assembly of a storage gene is complete before beginning assemble of the next. We begin assembly of the next immediately only one time step later. As a result, a complete storage gene is produced every time step. |
| This journal is © The Royal Society of Chemistry 2023 |