DOI:
10.1039/D2RA05302K
(Paper)
RSC Adv., 2022,
12, 29022-29033
Analysis of the growth and physicochemical properties of the newly developed stilbazolium derivative 4-N,N-dimethylamino-4-N-methyl stilbazolium 2-formyl benzene sulfonate (DSFS) single crystal: an effective material for nonlinear optical applications†
Received
24th August 2022
, Accepted 16th September 2022
First published on 11th October 2022
Abstract
A novel ionic stilbazolium derivative single crystal of 4-N,N-dimethylamino-4-N-methyl stilbazolium 2-formyl benzene sulfonate (DSFS) was successfully cultivated with methanol as the solvent by using the slow evaporation technique. Structural confirmation was done using single-crystal X-ray diffraction (SCXRD), and the obtained results reveal that the DSFS crystal crystallized in a centrosymmetric pattern with P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group. The presence of different vibrational modes in the DSFS crystal is affirmed via Fourier transform infrared (FTIR) spectroscopy. Linear optical constants such as cut-off wavelength, bandgap, extinction coefficient, Urbach energy, electrical conductivity and optical conductivity of the titular crystal were found from ultraviolet–visible–near infra-red spectroscopy (UV-Vis-NIR). The emission wavelength of the title crystal lies in the red region (620 nm), which was confirmed from the photoluminescence spectroscopy (PL). The surface nature of the grown ionic crystal was examined through the etching and atomic force microscopy (AFM) technique. With a He–Ne laser as the source, Z scan analysis was carried out to study the third-order nonlinear properties of the DSFS crystal.
space group. The presence of different vibrational modes in the DSFS crystal is affirmed via Fourier transform infrared (FTIR) spectroscopy. Linear optical constants such as cut-off wavelength, bandgap, extinction coefficient, Urbach energy, electrical conductivity and optical conductivity of the titular crystal were found from ultraviolet–visible–near infra-red spectroscopy (UV-Vis-NIR). The emission wavelength of the title crystal lies in the red region (620 nm), which was confirmed from the photoluminescence spectroscopy (PL). The surface nature of the grown ionic crystal was examined through the etching and atomic force microscopy (AFM) technique. With a He–Ne laser as the source, Z scan analysis was carried out to study the third-order nonlinear properties of the DSFS crystal.
1 Introduction
In this technology-driven modern world, Nonlinear Optical (NLO) materials find their place due to their significant applications across various fields. The study of organic NLO crystals is a scholastic area of interest due to their ample applications in different domains, such as signal processing, electro-optic modulators, telecommunication, optical switches, deep UV light, high-density data storage and display technologies.1–8 The presence of delocalized π-electrons, donor and acceptor moieties, hydrogen bonds and weak Van der Waals forces induce high non-linearity in the organic crystals compared to its counterpart, inorganic materials.9 Also, tunability of the structure, high laser damage threshold, ultra-fast response and the significant electro-optic coefficient are the added advantages of the organic materials.10 Usually, organic crystals that possess stable packing and high chromophore density tend to exhibit high non-linearity, high mechanical and photo-chemical stability and thermal properties.11 Among the reported NLO crystals, 4-N,N-dimethylamino-4-N-methyl-stilbazolium tosylate (DAST) has been one of the yardstick crystals which has second harmonic generation (SHG) efficiency that is roughly 1000 times that of urea.12,13 One of the fundamental reasons behind this high nonlinearity among the DAST derivative crystals is the presence of the stilbazolium chromophore in the cation component. The presence of an ethylenic bridge (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) in the stilbazolium cation is one of the primary reasons behind the high NLO response of this derivative’s materials, as this double bond acts as an interconnecting bridge between the donor and acceptor moiety. To form this carbon–carbon ethylenic bridge, many reaction strategies have been reported in the past, namely the Suzuki–Miyaura reaction, Horner–Wadsworth–Emmons (HWE) condensations and the Knoevenagel condensation. Among these methods, Knoevenagel condensation is used widely due to its simplicity.14–16 In the present study, the strategy of combining the stilbazolium (chromophore) cation with a new anion is adopted to develop a novel ionic organic single crystal. This approach of incorporating new counter-anions with an already existing stilbazolium cation has already been reported.17 This approach assists in creating a new NLO crystal with the desired physical and chemical properties.18 Previously reported results show that even a small change in the anion can induce a huge change in the non-linearity of the material by affecting the crystal stacking.19 The nature of the hydrogen bonds which connect the anion and cation decides the optoelectronic properties of the synthesized material.20 The low toxicity level of the styryl pyridinium compound in the cation part makes it an appropriate material for applications like antibacterial drugs and disinfectants in hospital and food industries.21,22 The anion compound 2-formyl benzene sulfonate sodium salt is used to test the ability of fungal strains to change phenolic and non-phenolic precursors into stable and non-toxic dyes.23 The findings from the extensive literature survey suggests that, so far, no crystal has been reported with 2-formyl benzene sulfonate as the anion with a stilbazolium derivative. So, in this article, we report the growth of DSFS crystal for the first time by employing the slow evaporation method. In addition, the synthesis and various physical and chemical properties such as structural, linear optical, surface analysis and nonlinear optical (NLO) properties of the grown crystal were inspected. The results are scrupulously discussed in the following sections. All the outcomes indicate that the grown DSFS crystal is a favourable candidate for NLO applications.
C) in the stilbazolium cation is one of the primary reasons behind the high NLO response of this derivative’s materials, as this double bond acts as an interconnecting bridge between the donor and acceptor moiety. To form this carbon–carbon ethylenic bridge, many reaction strategies have been reported in the past, namely the Suzuki–Miyaura reaction, Horner–Wadsworth–Emmons (HWE) condensations and the Knoevenagel condensation. Among these methods, Knoevenagel condensation is used widely due to its simplicity.14–16 In the present study, the strategy of combining the stilbazolium (chromophore) cation with a new anion is adopted to develop a novel ionic organic single crystal. This approach of incorporating new counter-anions with an already existing stilbazolium cation has already been reported.17 This approach assists in creating a new NLO crystal with the desired physical and chemical properties.18 Previously reported results show that even a small change in the anion can induce a huge change in the non-linearity of the material by affecting the crystal stacking.19 The nature of the hydrogen bonds which connect the anion and cation decides the optoelectronic properties of the synthesized material.20 The low toxicity level of the styryl pyridinium compound in the cation part makes it an appropriate material for applications like antibacterial drugs and disinfectants in hospital and food industries.21,22 The anion compound 2-formyl benzene sulfonate sodium salt is used to test the ability of fungal strains to change phenolic and non-phenolic precursors into stable and non-toxic dyes.23 The findings from the extensive literature survey suggests that, so far, no crystal has been reported with 2-formyl benzene sulfonate as the anion with a stilbazolium derivative. So, in this article, we report the growth of DSFS crystal for the first time by employing the slow evaporation method. In addition, the synthesis and various physical and chemical properties such as structural, linear optical, surface analysis and nonlinear optical (NLO) properties of the grown crystal were inspected. The results are scrupulously discussed in the following sections. All the outcomes indicate that the grown DSFS crystal is a favourable candidate for NLO applications.
2 Materials and synthesis
All the required reagents were bought from Tokyo Chemical Limited (TCL). All the reagents were used without further purification. The overall synthesis process consists of three steps. Reactions involved in the synthesis process are explained in Fig. 1. Step 1: 1,4-dimethyl pyridinium iodide (1). Both the starting materials 4-picoline (2 ml) and methyl iodide (1.3 ml) were taken in an equimolar (20 mmol) ratio in an Erlenmeyer bulb with acetone as the medium. The above mixture solution is placed in a reflux setup at about 60 °C for 2 hours. After 2 hours, the solution is left to cool down to the surrounding temperature and the resultant precipitate is filtered and dried in an oven. The final dried powder is 1,4-dimethyl pyridinium iodide (1). Step 2: 4-[2-(4-dimethylamino-phenyl)-vinyl]-1-methyl-pyridinium iodide (2). The final product of step 2 (2) is obtained via the Knoevenagel condensation reaction. Compound (1) (2.35 g) and 4-(dimethylamino)benzaldehyde (1.5 g) were dissolved in methanol solvent in an RB. Generally, weak bases like piperidine or ethylenediamine are used in the Knoevenagel condensation.24 In the present study, piperidine is added to the solution mixture. Piperidine speeds up the reaction by providing its lone pair of electrons to complete the reaction. As a consequence of this condensation process, a carbon–carbon double bond is formed with water as a by-product.24 Then, the prepared solution is refluxed for 12 hours at 60 °C using a modified Dean–Stark apparatus equipped with a heating mantle. At the end of the reaction, the Erlenmeyer bulb is allowed to cool down to room temperature. The unreacted initial reactants were removed from the final purple precipitate by washing it with diethyl ether solution. Then, the final powder product (2) is dried in an oven at 100 °C for 1 h. Methanol solvent is used for the recrystallization process to enhance the purity of the final powder. Step 3: 4-N,N-dimethylamino-4-N-methyl stilbazolium 2-formyl benzene sulfonate (3). The final metallization reaction occurs between compound (2) and 2-sodium formyl benzene sulfonate. Both the materials were dissolved separately in a hot aqueous solution and kept on the stirrer for 1 hour at 70 °C. Then both the solutions were mixed, and the mixture was left undisturbed for a whole day so that the residues could settle down. Finally, the obtained reddish-brown precipitate is kept in an oven at about 100 °C for 2 h to get rid of the water content. The final obtained powder is N,N-dimethylamino-4′-N′-methylstilbazolium 2-formyl benzene sulfonate (DSFS). Fig. 1 portrays the reaction scheme involved in the formation of the DSFS material.
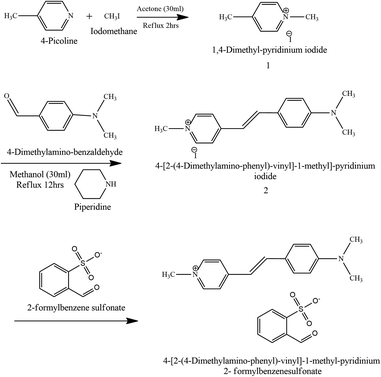 |
| | Fig. 1 Reaction scheme for the DSFS material. | |
2.1 Solubility and crystal growth
The gravimetric method was chosen to find the solubility of the pure DSFS powder in methanol solvent using an ultra-cryostat (±0.01 °C accuracy). The experiment was carried out for various temperatures, ranging from 25–45 °C with an interval of 5 °C (25, 30, 35, 40 and 45 °C). Saturated solutions were prepared at the aforementioned temperatures to study the solubility of the synthesized powder. Fig. 2 shows the solubility curve of the DSFS powder in methanol solvent. From the graph, it is clear that with an increase in temperature the solubility of the DSFS material also increases. This increase in solubility with respect to the rise in temperature is due to the rise in the average kinetic energy of the solution and solute molecules. This increase in kinetic energy allows the solvent molecules to break more solute molecules. Also, the rise in the solute molecule's kinetic energy destabilizes the solid state of the material, so more solute molecules dissolve readily at higher temperature.25
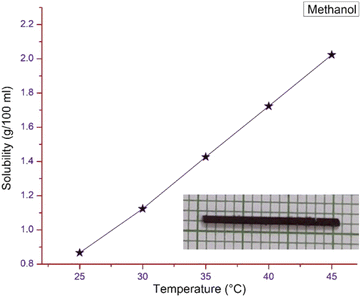 |
| | Fig. 2 Solubility curve and grown crystal image of DSFS. | |
The solubility study confirms that methanol is a suitable solvent for the crystal growth process. So, with methanol as the solvent, the crystal growth process is carried out by the slow evaporation method. Within the span of 20–25 days, a DSFS crystal with the dimensions of 30 × 1 × 1 mm3 was obtained and the image of the grown title crystal is portrayed in the inset of Fig. 2.
3 Results and discussion
3.1 Structural studies
3.1.1 Single-crystal X-ray diffraction (SCXRD). To explore the structure of the title DSFS crystal, a single crystal of size 0.080 × 0.140 × 0.210 mm3 was exposed to single crystal XRD. The molecular structure, interatomic interactions, packing and other structural properties of the grown crystal were interpreted through this study. Under the room temperature conditions, analysis was carried out using a D8 QUEST BRUKER. With the help of Apex 4 software, the obtained raw crystallographic data was solved and refined. Non-hydrogen atoms in the structure were positioned using the full-matrix least-squares refinement process by utilizing the SHELXL function.26 Obtained crystallographic data shows that the DSFS crystallized in a centrosymmetric pattern with (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) space group with triclinic crystal system. Collected lattice constant values of the grown DSFS crystal are a = 8.3812 Å, b = 9.8732 Å, c = 13.0649 Å and interfacial angle values are α = 82.404°, β = 88.395°, γ = 86.109°. Refined structural and crystallographic data of the title ion pair crystal are displayed in Table 1. Other important structural parameters, bond length and bond angle of selected bonds are depicted in Tables 1 and 2 in the ESI file.†
) space group with triclinic crystal system. Collected lattice constant values of the grown DSFS crystal are a = 8.3812 Å, b = 9.8732 Å, c = 13.0649 Å and interfacial angle values are α = 82.404°, β = 88.395°, γ = 86.109°. Refined structural and crystallographic data of the title ion pair crystal are displayed in Table 1. Other important structural parameters, bond length and bond angle of selected bonds are depicted in Tables 1 and 2 in the ESI file.†
Table 1 Crystal data and structure refinement for DSFS
| Identification code |
DSFS |
|
| Empirical formula |
C23H24N2O4S |
|
| Formula weight |
424.50 |
|
| Temperature |
300(2) K |
|
| Wavelength |
0.71073 Å |
|
| Crystal system |
Triclinic |
|
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
|
| Unit cell dimensions |
a = 8.3812(2) Å |
α = 82.404(3)° |
| b = 9.8732(6) Å |
β = 88.395(3)° |
| c = 13.0649(11) Å |
γ = 86.109(3)° |
| Volume |
1068.96(15) Å3 |
|
| Z |
2 |
|
| Density (calculated) |
1.319 g cm−3 |
|
| Absorption coefficient |
0.183 mm−1 |
|
| F(000) |
448 |
|
| Crystal size |
0.080 × 0.140 × 0.210 mm3 |
|
| Theta range for data collection |
1.57 to 28.38° |
|
| Index ranges |
−11 ≤ h ≤ 11, −13 ≤ k ≤ 13, −17 ≤ l ≤ 17 |
|
| Reflections collected |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474 474 |
|
| Independent reflections |
5323 [R(int) = 0.0516] |
|
| Completeness to theta = 28.38° |
100.0% |
|
| Absorption correction |
Multi-scan |
|
| Max. and min. transmission |
0.9850 and 0.9620 |
|
| Refinement method |
Full-matrix least-squares on F2 |
|
| Data/restraints/parameters |
5323/0/274 |
|
| Goodness-of-fit on F2 |
1.080 |
|
| Final R indices [I > 2sigma(I)] |
R1 = 0.0487, wR2 = 0.1256 |
|
| R indices (all data) |
R1 = 0.0798, wR2 = 0.1556 |
|
| Largest diff. peak and hole |
0.264 and −0.307e Å−3 |
|
The title ion-pair crystal's (C23H24N2O4S) asymmetric unit comprises a positively charged stilbazolium cation and negatively charged sulfonate anion. The ORTEP diagram of the novel DSFS crystal is portrayed in Fig. 3. A partly viewed packing image of the novel DSFS crystal along the ‘a’ axis is depicted in Fig. 4. The cation's carbon–carbon (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) double bond indicates that it exhibits a trans or E configuration, with a torsional angle of C1–C6
C) double bond indicates that it exhibits a trans or E configuration, with a torsional angle of C1–C6![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C7–C8 of 179.59°.27 The torsional angle of the dimethyl group C12–C11–N2–C15 (5.83°) attached with the amino group C10–C11–N2–C16 (−9.70°) shows that the dimethyl moiety is slightly distorted from coplanarity with the benzene ring. The presence of the stilbazolium chromophore in the cation is the key to higher non-linearity. The main reason behind this efficiency is the deviation in the bond length among the ionic atoms and the presence of the D–π–A bridge, which in turn stimulates NLO susceptibility in the material.24 NLO response of a chromophore also depends on the bond length alternation (BLA) degree. The BLA degree of the title cation for the bonds N1–C14 (1.48 Å) and N2–C11 (1.37 Å) is 0.11 Å. The difference in the bond lengths of the dimethyl moiety N2–C15 (1.433 Å) and N2–C16 (1.453 Å) is 0.02 Å. Similarly, the bond length difference between the bonds of N1–C3 (1.336 Å) and N1–C4 (1.346 Å) of the 4-picoline compound is 0.010 Å. The ideal BLA value to exhibit higher non-linearity is approximately ±0.05 Å, whereas, in the case of the title cation, it is 0.11 Å, which is slightly higher.28 This BLA value indicates that the title stilbazolium cation compound also exhibits molecular nonlinearity. The geometrical description of the SO3− anion shows that the S− unit adopts regular trihedral coordination with the three oxygen atoms through S–O bonds. The bond lengths and angles of the S–O and O–S–O interactions reside in the range of 1.4415–1.4416 Å and 113.09–114.12°. The three-dimensional network of the title ionic compound is made up of alternating perpendicular anions between the parallel cationic units. The CIF file of the grown crystal is deposited in the CCDC (CCDC no. 2152094).
C7–C8 of 179.59°.27 The torsional angle of the dimethyl group C12–C11–N2–C15 (5.83°) attached with the amino group C10–C11–N2–C16 (−9.70°) shows that the dimethyl moiety is slightly distorted from coplanarity with the benzene ring. The presence of the stilbazolium chromophore in the cation is the key to higher non-linearity. The main reason behind this efficiency is the deviation in the bond length among the ionic atoms and the presence of the D–π–A bridge, which in turn stimulates NLO susceptibility in the material.24 NLO response of a chromophore also depends on the bond length alternation (BLA) degree. The BLA degree of the title cation for the bonds N1–C14 (1.48 Å) and N2–C11 (1.37 Å) is 0.11 Å. The difference in the bond lengths of the dimethyl moiety N2–C15 (1.433 Å) and N2–C16 (1.453 Å) is 0.02 Å. Similarly, the bond length difference between the bonds of N1–C3 (1.336 Å) and N1–C4 (1.346 Å) of the 4-picoline compound is 0.010 Å. The ideal BLA value to exhibit higher non-linearity is approximately ±0.05 Å, whereas, in the case of the title cation, it is 0.11 Å, which is slightly higher.28 This BLA value indicates that the title stilbazolium cation compound also exhibits molecular nonlinearity. The geometrical description of the SO3− anion shows that the S− unit adopts regular trihedral coordination with the three oxygen atoms through S–O bonds. The bond lengths and angles of the S–O and O–S–O interactions reside in the range of 1.4415–1.4416 Å and 113.09–114.12°. The three-dimensional network of the title ionic compound is made up of alternating perpendicular anions between the parallel cationic units. The CIF file of the grown crystal is deposited in the CCDC (CCDC no. 2152094).
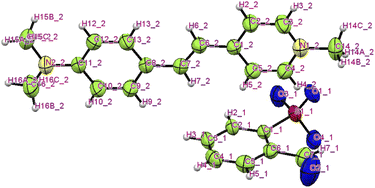 |
| | Fig. 3 ORTEP image of the DSFS crystal. | |
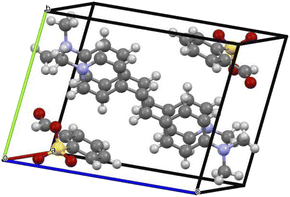 |
| | Fig. 4 Packing image of the DSFS crystal. | |
3.1.2 Morphology. The morphology of the fully-grown DSFS crystal was predicted with the aid of the obtained single-crystal XRD data (CIF file) by using Winx Morph software.29 The predicted morphology of the title compound with different crystal faces is illustrated in Fig. 5. From the morphology diagram, it is apparent that the growth rate is dominant along the ‘a’ axis.
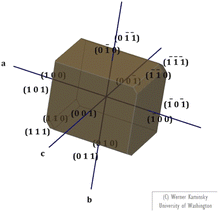 |
| | Fig. 5 Morphology of the DSFS crystal. | |
3.1.3 Density measurement. Theoretical and experimental approaches were used to calculate the density of the novel DSFS crystal. Theoretically, the density of the new ionic crystal can be calculated using the single crystal XRD data with the help of the following equation:| |
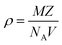 | (1) |
where all the values M (molecular weight – 424.50 g mol−1), Z (number of molecules per unit cell – 2), and V (volume of the unit cell – 1068.96) can be directly obtained from the SCXRD results. NA is Avogadro's number. The theoretically predicted density value for the DSFS crystal is 1.319 g cm−3. Experimentally the density was measured using the floating technique.30 With CCl4 as the solvent, this measurement was carried out. Experimentally, the density value is derived from eqn (2)| |
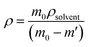 | (2) |
where m0 and m′ are the mass of the grown DSFS crystal in air and solvent (CCl4) medium, ρsolvent is the density of the CCl4 solvent. The calculated density values of the theoretical (1.319 g cm−3) and experimental (1.317 g cm−3) approaches agree with each other.
3.2 Fourier transform infra-red (FTIR) analysis
Structural confirmation of the title ionic crystal can be done with the help of functional groups and their corresponding vibrations by adopting FT-IR analysis. The KBr pellet technique is utilized to obtain the FTIR spectrum within the range of 3100 to 400 cm −1, using a SHIMADZU instrument. The observed vibration spectrum of the synthesized material is displayed in Fig. 6. The title DSFS crystal consists of stilbazolium cation and formyl benzene sulfonate anion. The vibrational spectrum of the cation is attributed to the vinyl group, methyl group, pyridine group and phenyl ring. Similarly, in the case of the anion, the aldehyde and sulfonate groups’ vibrations were analyzed.
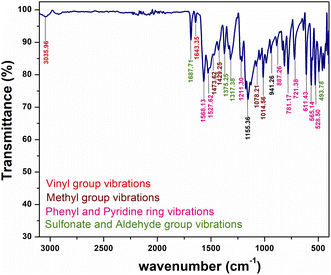 |
| | Fig. 6 FTIR spectrum of the grown DSFS crystal. | |
3.2.1 Cation group absorption. The characteristic peak for this vinyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) stretching lies in the range of 1650 to 1600 cm−1.31 The band at 1643 cm−1 in the spectrum indicates the presence of vinyl stretching. Apart from the (C
C) stretching lies in the range of 1650 to 1600 cm−1.31 The band at 1643 cm−1 in the spectrum indicates the presence of vinyl stretching. Apart from the (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) stretching, stilbazolium derivatives show aliphatic C–H stretching in the vicinity of 3050 cm−1. The peak centered at 3035 cm−1 indicates the aliphatic C–H stretching. Generally, the methyl group's asymmetrical bending vibration and symmetrical bending vibration bands were positioned in and around 1450 and 1375 cm−1, respectively. In Fig. 6, the peaks at 1473 and 1429 cm−1 represent the asymmetrical bending vibrations. The peak observed at 1375 cm−1 characterizes the symmetrical bending vibration of the methyl group. In the region between 1070–1010 cm−1, methyl group rocking modes were observed.32 In the DSFS crystal, the peaks positioned at 1078 and 1014 cm−1 are attributed to the CH3 rocking mode. The peak emitted at 1568 cm−1 is ascribed to aromatic C–C stretching. The peak positioned at 1527 cm−1 indicates ring (C
C) stretching, stilbazolium derivatives show aliphatic C–H stretching in the vicinity of 3050 cm−1. The peak centered at 3035 cm−1 indicates the aliphatic C–H stretching. Generally, the methyl group's asymmetrical bending vibration and symmetrical bending vibration bands were positioned in and around 1450 and 1375 cm−1, respectively. In Fig. 6, the peaks at 1473 and 1429 cm−1 represent the asymmetrical bending vibrations. The peak observed at 1375 cm−1 characterizes the symmetrical bending vibration of the methyl group. In the region between 1070–1010 cm−1, methyl group rocking modes were observed.32 In the DSFS crystal, the peaks positioned at 1078 and 1014 cm−1 are attributed to the CH3 rocking mode. The peak emitted at 1568 cm−1 is ascribed to aromatic C–C stretching. The peak positioned at 1527 cm−1 indicates ring (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) vibrations. Characteristic peaks for the aromatic C–H in-plane bending are observed at 1211 and 1078 cm−1. Similarly, peaks observed at 781 and 721 cm−1 are assigned to the C–H out-of-plane bending vibrations.31 The peak centered at 887 cm−1 represents the 1,4-disubstituted aromatic C–H ring. Three peaks centered at 611, 565 and 528 cm−1 in the spectrum indicate the phenyl ring mode (C–C–C) deformation vibration.
C) vibrations. Characteristic peaks for the aromatic C–H in-plane bending are observed at 1211 and 1078 cm−1. Similarly, peaks observed at 781 and 721 cm−1 are assigned to the C–H out-of-plane bending vibrations.31 The peak centered at 887 cm−1 represents the 1,4-disubstituted aromatic C–H ring. Three peaks centered at 611, 565 and 528 cm−1 in the spectrum indicate the phenyl ring mode (C–C–C) deformation vibration.
3.2.2 Anion group absorption. The anionic group of the DSFS crystal consists of SO2 asymmetric and symmetric stretching, C–S stretching, SO3 scissoring and SO3 deformation vibrations. Peaks found at 1317 and 1014 cm−1 denote asymmetric and symmetric SO2 stretching vibrations, respectively. The characteristic peak of the sulfonate group (S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) stretching appeared at 1375 cm−1. The sharp peak positioned at 565 cm−1 implies C–S stretching. SO3 scissoring and SO3 deformation vibrations were observed at 528 and 493 cm−1, respectively. Finally, C
O) stretching appeared at 1375 cm−1. The sharp peak positioned at 565 cm−1 implies C–S stretching. SO3 scissoring and SO3 deformation vibrations were observed at 528 and 493 cm−1, respectively. Finally, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrations of the aldehyde group in the anion group give the characteristic peak at 1687 cm−1.
O vibrations of the aldehyde group in the anion group give the characteristic peak at 1687 cm−1.
3.3 Linear optical studies
3.3.1 Ultraviolet–visible–near infra-red spectroscopy (UV-Vis-NIR). The response of the grown crystal in the Ultraviolet (200–400 nm), visible (400–800 nm) and near-infrared (800–1000) regions gives detail about the absorption edge and the orbital transitions.33 To investigate the optical characteristics of the DSFS crystal in the range of 200–1000 nm, a 2 mm thick crystal is placed in an Analytik Jena Specord 210 Plus instrument. The absorbance spectrum of the ionic DSFS crystal is depicted in Fig. 7. From the plot, it is apparent that the DSFS material is opaque in the UV region (200–400 nm). The absorption edge of the DSFS crystal is 570 nm. DAST and DSFS are both crystals belonging to the same stilbazolium family. So, both the materials exhibit a similar kind of absorbance spectrum. When compared with DAST crystal (λmax = 550 nm), DSFS crystal exhibits a slightly higher absorption edge of about 20 nm (redshift). It is because of the stilbazolium chromophore; in general the stilbazolium chromophore exhibits a redshift when it has higher molecular nonlinearity.34 The bandgap of the grown crystal is obtained with the help of a standard Tauc plot relationship,35 and the calculated Eg value is 2.25 eV. The graph between (αhν)2 and hν is shown in Fig. 8.
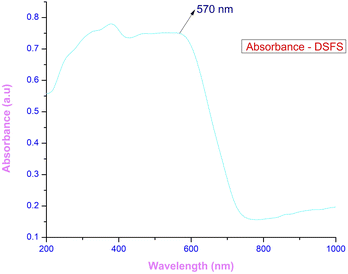 |
| | Fig. 7 Absorbance spectrum of the DSFS crystal. | |
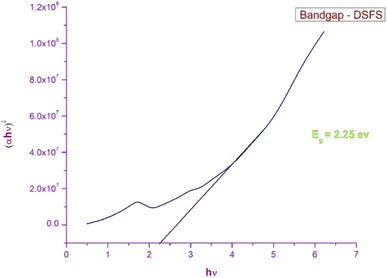 |
| | Fig. 8 Tauc plot of the DSFS crystal. | |
In order to fabricate a potential optoelectronic device, knowledge about optical constants such as the coefficient of absorption (α), extinction coefficient (K), optical conductivity (σopt), and electrical conductivity (σelc) values are vital.
Fig. 9 represents the coefficient of the absorption spectrum of the DSFS crystal. Beyond 570 nm (cut-off wavelength), the absorption coefficient starts to decrease gradually. The extinction coefficient is the measure of light loss within a medium while propagating due to absorption and scattering phenomena.36 From the absorption coefficient (α), the K value can be deduced by using the following relation:37
| |
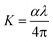 | (3) |
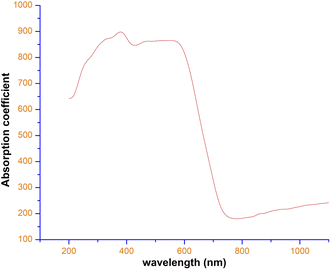 |
| | Fig. 9 Absorption coefficient vs. wavelength plot of DSFS crystal. | |
Fig. 10 elucidates the variation of the extinction coefficient with respect to the photon energy. There is a steady decrease in the extinction coefficient value until 1.65 eV. Then it gradually increases and attains the maximum K value at 2.15 eV, which ratifies the bandgap region (Eg = 2.25 eV) of the title ionic crystal. Along with that, the low K value signifies that the grown ionic crystal can be used for the construction of devices, which are ideal for information processing and computing technology.38
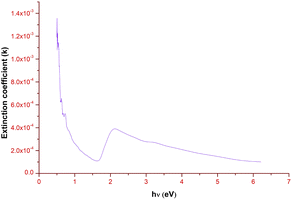 |
| | Fig. 10 Extinction coefficient vs. photon energy plot of DSFS crystal. | |
3.3.2 Optical conductivity. Optical conductivity (σopt) is the measure of the response of the material to the incident light frequency and it can be derived from eqn (4):39| |
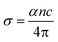 | (4) |
where α, c and n indicate the coefficient of absorption, light speed in air medium and refractive index, respectively. Fig. 11 indicates the disparity between the optical conductivity and its corresponding photon energy (hν). From the graph, it is obvious that with a rise in hν value, there is a decrease in optical conductivity up to 1.6 eV. After that, there is a steep increase in the σopt in the bandgap region (1.61 to 2.21 eV). This increase in the optical conductivity in the band gap region is due to the rise in the optical absorption coefficient in this region.40 The maximum (σopt) value is found to be 5 × 1010 S−1. This high value of optical conductivity (σopt) suggests that the synthesized crystal has a high photo response.41 Beyond 3.6 eV, the value of optical conductivity decreases due to a drop in α value.
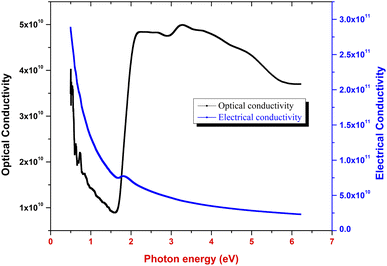 |
| | Fig. 11 Optical conductivity and electrical conductivity vs. photon energy plot. | |
With the help of σopt, the title crystal's electrical conductivity is calculated by using the following equation:
| |
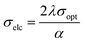 | (5) |
Fig. 11 portrays the disparity of electrical conductivity (σelc) with respect to photon energy. Fig. 11 shows that σelc decreases with an increase in hν. This drop in the electrical conductivity at higher photon energy indicates the semiconducting nature of the material.42
The electrical susceptibility (χc) of the DSFS crystal is calculated at λ = 570 nm, with the help of the already obtained optical constant value, from the following formula:43
| |
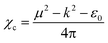 | (6) |
where
μ,
ε0 and
k are the refractive index, vacuum permittivity and extinction coefficient, respectively. The
χc value is found to be 0.4375 at 570 nm. By incorporating the calculated values of the coefficient of extinction and refractive index, real (
εr) and imaginary (
εi) dielectric constant values were elucidated from the below equation:
| εr = n2 − K2 and εi = 2nk |
Information about the grown material's electrical energy storage capacity and ohmic resistance can be obtained from the real and imaginary dielectric constants.
42 With respect to the cut-off wavelength (
λ = 570 nm), the calculated
εr and
εi values are 5.495 and 1.817 × 10
−3, respectively.
3.3.3 Urbach energy. Interaction of phonons in the bandgap region often ends up with the development of band tailing in the crystalline material because of the presence of disorders. From the following equation, it is possible to calculate the disorder in the system as a function of α, which corresponds to the transition between the localized states and the extended state of the conduction and valence bands, through a parameter known as the Urbach energy (Eu).41,44| |
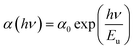 | (7) |
where h, ν, α0, and Eu represent Planck's constant, the incident frequency radiation, a constant and Urbach energy, respectively. The width of the elongated tail of the localized states in the forbidden electronic band gap (Urbach energy or band tail energy) was obtained by plotting a graph between the ln of the absorption coefficient α vs. hν. The obtained slope value of the linear portion of the graph is 3.686. The Urbach energy can be calculated by taking the reciprocal of the obtained slope value and it is found to be 0.2712 eV. This low Eu value confirms that the novel DSFS ionic crystal possesses high crystallinity with minimal structural disorders. Fig. 12 depicts the Urbach energy graph.
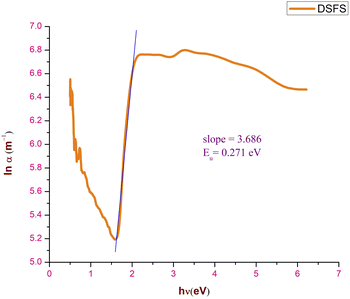 |
| | Fig. 12 Urbach energy plot of the DSFS crystal. | |
From Table 2, we can conclude that the grown crystal possesses a wide transparency window in the Vis-NIR region, low extinction coefficient, high electrical and optical conductivity and few disorders (Urbach energy). These results indicate the grown crystal's appropriateness for optoelectronic, NLO and photonic applications.
Table 2 Calculated optical parameters of the DSFS crystal
| Optical constants |
Calculated values |
| Cut-off wavelength (λ) |
570 nm |
| Band gap (Eg) |
2.25 eV |
| Extinction coefficient (K) @2.25 eV |
3.755 × 10−4 |
| Optical conductivity (σopt) @2.25 eV |
4.839 × 109 |
| Electrical conductivity (σelc) @2.25 eV |
6.176 × 1010 |
| Urbach energy (Eu) |
0.271 eV |
3.4 Photoluminescence studies
Physical properties of the grown material, such as electronic transition, shallow and deep level defects and band gap, can be analyzed using photoluminescence studies.33,45 In general, compounds with aromatic rings and extended conjugated double bonds with a high degree of resonance stability exhibit a luminescence nature.12 Upon irradiance of light, an electron–hole pair is generated. Due to very low relaxation time (τ), recombination of these excited electron–hole pairs takes place with the emission of photons.46 Fig. 13 shows the output PL spectrum of the grown DSFS crystal obtained in the liquid state with methanol solvent using an F-7000 FL spectrophotometer, operated at room temperature. With 476 nm as the excitation wavelength, scanning was done between 500–800 nm. Only one broad peak centred at 620 nm (2.01 eV) confirms the absence of impurities. The stilbazolium chromophore is responsible for the emission of photons in the red colour region. Along with that, the existence of the electron donor and acceptor groups contributes to the red emission. The low quantum yield observed in the PL spectrum suggests that there is no direct electronic transition between the conduction and valence bands. Most probably, the electronic transition associated with the radiative recombination is between the trapped holes and electrons that occur between the localized energy states that existed within the bandgap region.33 Various electronic transitions occurring within the bandgap region between different energy levels is responsible for the broadening of the spectrum. These transitions confirm that the shallow holes contribute more than deep holes toward the charge transfer process and also confirms the trapping of electrons.33 The broad red emission peak indicates that the grown DSFS crystal is a promising aspirant for various applications such as bandpass filters, optical switches in the near IR region and solid-state lasers. Also, stilbazolium salts can be used as fluorescence probe monitors in the biomedical research field.47
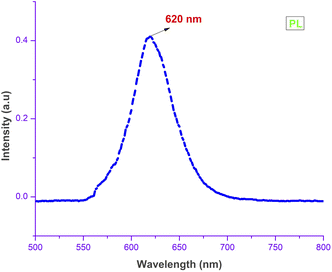 |
| | Fig. 13 PL spectrum of the DSFS crystal. | |
3.5 Surface analysis
3.5.1 Etching studies. Quality and crystalline perfection are the essential factors when it comes to device fabrication. To assess the surface quality of the DSFS crystal, it is subjected to etching analysis. With the help of the developed etch pits, the growth mechanism involved in the crystal growth process and the defects can be analysed. A flat and optically good quality crystal is used for the chemical etching analysis with methanol + acetonitrile as the etchant. In the present study, etching was carried out at room temperature for two different etching times, 10 and 20 seconds. Initially, the DSFS crystal's grown surface is subjected to an optical microscope, and the output image is captured (Fig. 14a). The grown crystal is immersed in the etching solvent (10 s). Afterwards; the surface of the etched crystal is cleaned gently with a tissue to exclude the etchant from the surface. The exact process is repeated for 20 s, and the captured pictures of the surface are presented in (Fig. 14b and c). Rectangular-shaped etch pits were observed on the surface after 10 s (Fig. 14b). With the increased etching time (20 s), the etch pits are more precise and more visible in the dislocation site (Fig. 14c). It also ratifies that the mechanism involved in the crystal growth process is a 2D nucleation mechanism, and the synthesized crystal has few dislocations.48
 |
| | Fig. 14 Etch patterns of DSFS. (a) As grown surface; (b) 10 s and (c) 20 s. | |
3.5.2 Atomic force microscopy analysis (AFM). A quantitative description of the surface topography is needed to comprehend the surface morphology of the grown ionic material. So, to study the surface morphology, the grown DSFS crystal is subjected to AFM analysis. In general, surface roughness parameters can be evaluated on the basis of five parameters, namely height or amplitude parameter, spatial parameter, hybrid parameter, functional parameter and feature parameter. Among these, the height parameter is the critical parameter which gives the necessary details about the surface topography of the material.49 Fig. 15a and b show the 3D and 2D AFM images of the grown DSFS crystal. The root mean surface roughness value (Sq) and average roughness (Sa) value are found to be 32.975 nm and 26.824 nm. The difference between the average five maximum peaks and five minimum peaks is measured as the ten-point height (Sz), and the value of Sz is 140.297 nm. Based on the sign of the surface skewness (Ssk) moment, it can be concluded whether peaks or valleys are dominant on the surface. In the case of DSFS crystal, the Ssk value is negative (−0.0044), which clearly indicates that valleys are predominant and the surface is more planar.50 The flatness of the crystal can be assessed through the surface kurtosis (Sku) value. If the Sku value is lower than 3, the surface is perfectly flat. If the value is higher than 3, then the surface possesses more peaks than valleys.50 For the DSFS crystal, the Sku value is 2.4297, which signifies the grown crystal surface is flat. It is obvious from the Ssk and Sku values that the grown crystal is perfectly flat. All the measured surface roughness parameters are summarized in Table 3.
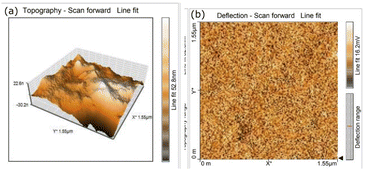 |
| | Fig. 15 AFM image of the grown DSFS crystal. (a) 3D image; (b) 2D image. | |
Table 3 Roughness parameters of DSFS crystal from AFM
| Roughness parameters |
Values |
| Root mean surface roughness (Sq) |
32.975 nm |
| Average roughness (Sa) |
26.824 nm |
| Ten-point height (Sz) |
140.297 nm |
| Surface skewness (Ssk) |
−0.0044 |
| Surface kurtosis (Sku) |
2.4297 |
3.6 Nonlinear optical studies
3.6.1 Z scan measurement. The arrangement of chromophores in the crystal determines whether the material exhibits χ2 or χ3 effects. SCXRD studies affirmed that the title ionic crystal arranged in a centrosymmetric fashion with P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group. In centrosymmetric crystals, due to the presence of an inversion centre, the resultant polarization has odd order susceptibility only, which means that even order susceptibility has null values. Due to the presence of odd order susceptibility the grown DSFS crystal exhibits third-order nonlinearity.51 Among the various technologies available to measure third-order nonlinearity, the Z scan technique is preferred over other methods due to its simplicity and reduced complexity.52 The basic principle behind the Z scan technique is that the sample under investigation is studied as a function of Z-position under the influence of a Gaussian beam to study the interaction between the sample and laser light. The four crucial parameters which help to determine the nonlinearity of the material can be accurately measured using the Z-scan technique: nonlinear refractive index (n2), nonlinear absorption coefficient (β), third-order nonlinear optical susceptibility (χ3) and second-order hyperpolarizability.52 In order to calculate the β and n2, two modes were adopted, namely open and closed aperture modes. During the translation of the sample, under the Gaussian beam with respect to variation of transmittance, the intensity-dependent absorption of the material is studied via an open aperture and the nonlinear refractive index is measured with reference to the change in light intensity via the closed aperture method with a finite slit or aperture in front of the output detector.53 With a helium–neon laser (632.8 nm) as the source, the Z-scan technique was carried out. With the aid of a Gaussian filter, the laser beam is converted to a Gaussian beam and the transformed beam is permitted to go through a convex lens with a focal distance of 30 mm to produce a focused beam with a beam waist diameter (W0) of 12.05 μm. In order to check whether the subjected sample satisfies the thin sample approximation, the Rayleigh length value (ZR) is calculated. For the Gaussian beam, the Rayleigh length (ZR = πW02/λ) is found to be 0.72 mm. The thickness (L) of the title crystal used for the analysis is 0.49 mm, which is less than the Rayleigh length; this clearly indicates that the sample used for measurement fulfilled the thin sample approximation (ZR ≫ L).54 The crystal is translated through the Z-direction (Z = +15 to −15) with reference to the focus (Z = 0). The corresponding output reading is measured in the output power meter with regard to the position of the crystal.
Closed aperture. In order to evaluate the magnitude and sign of the nonlinear refractive index (n2), a 2 mm aperture is placed in front of the photodetector. In the optical crystal, the illumination of high intense laser light tends to produce nonlinear thermal effects. The difference in the temperature of the crystal at the internally illuminated portion and outer region alters the material's refractive index. Thermal effects and the crystal's core structure are attributed to the material's self-focusing or defocusing nature.55 The obtained closed aperture Z-scan graph is depicted in Fig. 16. The self-focusing behaviour (+n2) of the grown ionic crystal is confirmed by the pre-focus valley followed by the post-focus peak in the closed aperture curve. From the graph, ΔTP–V is calculated to figure out the nonlinear refractive index (n2), with respect to the phase shift axis (ΔΦ0). The difference in the normalized transmittance between the valley and peak can be derived from the following expression.
space group. In centrosymmetric crystals, due to the presence of an inversion centre, the resultant polarization has odd order susceptibility only, which means that even order susceptibility has null values. Due to the presence of odd order susceptibility the grown DSFS crystal exhibits third-order nonlinearity.51 Among the various technologies available to measure third-order nonlinearity, the Z scan technique is preferred over other methods due to its simplicity and reduced complexity.52 The basic principle behind the Z scan technique is that the sample under investigation is studied as a function of Z-position under the influence of a Gaussian beam to study the interaction between the sample and laser light. The four crucial parameters which help to determine the nonlinearity of the material can be accurately measured using the Z-scan technique: nonlinear refractive index (n2), nonlinear absorption coefficient (β), third-order nonlinear optical susceptibility (χ3) and second-order hyperpolarizability.52 In order to calculate the β and n2, two modes were adopted, namely open and closed aperture modes. During the translation of the sample, under the Gaussian beam with respect to variation of transmittance, the intensity-dependent absorption of the material is studied via an open aperture and the nonlinear refractive index is measured with reference to the change in light intensity via the closed aperture method with a finite slit or aperture in front of the output detector.53 With a helium–neon laser (632.8 nm) as the source, the Z-scan technique was carried out. With the aid of a Gaussian filter, the laser beam is converted to a Gaussian beam and the transformed beam is permitted to go through a convex lens with a focal distance of 30 mm to produce a focused beam with a beam waist diameter (W0) of 12.05 μm. In order to check whether the subjected sample satisfies the thin sample approximation, the Rayleigh length value (ZR) is calculated. For the Gaussian beam, the Rayleigh length (ZR = πW02/λ) is found to be 0.72 mm. The thickness (L) of the title crystal used for the analysis is 0.49 mm, which is less than the Rayleigh length; this clearly indicates that the sample used for measurement fulfilled the thin sample approximation (ZR ≫ L).54 The crystal is translated through the Z-direction (Z = +15 to −15) with reference to the focus (Z = 0). The corresponding output reading is measured in the output power meter with regard to the position of the crystal.
Closed aperture. In order to evaluate the magnitude and sign of the nonlinear refractive index (n2), a 2 mm aperture is placed in front of the photodetector. In the optical crystal, the illumination of high intense laser light tends to produce nonlinear thermal effects. The difference in the temperature of the crystal at the internally illuminated portion and outer region alters the material's refractive index. Thermal effects and the crystal's core structure are attributed to the material's self-focusing or defocusing nature.55 The obtained closed aperture Z-scan graph is depicted in Fig. 16. The self-focusing behaviour (+n2) of the grown ionic crystal is confirmed by the pre-focus valley followed by the post-focus peak in the closed aperture curve. From the graph, ΔTP–V is calculated to figure out the nonlinear refractive index (n2), with respect to the phase shift axis (ΔΦ0). The difference in the normalized transmittance between the valley and peak can be derived from the following expression.| |
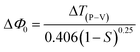 | (8) |
‘S’ in eqn (8) denotes the linear transmittance through the aperture. By using the following expression, ‘S’ can be calculated:56| |
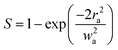 | (9) |
where ra and wa indicate the radius of the aperture and beam, respectively. The formula to calculate n2 from the closed aperture graph is given as:57| |
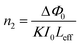 | (10) |
In the above eqn (10), K represents wavenumber (K = 2π/λ), Leff indicates the effective thickness of the sample, and it is given by:| | |
Leff = [1 − exp(αL)]/α
| (11) |
I0 is the intensity of the incident beam at the focus. Where L and α represent the thickness and coefficient of absorption of the DSFS crystal.
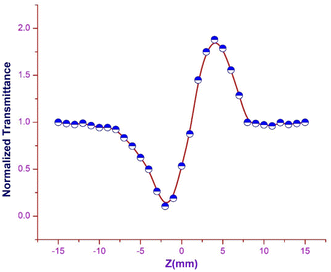 |
| | Fig. 16 Closed aperture trace of DSFS crystal. | |
| |
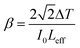 | (12) |
ΔT represents the valley at the focus in the open aperture curve.
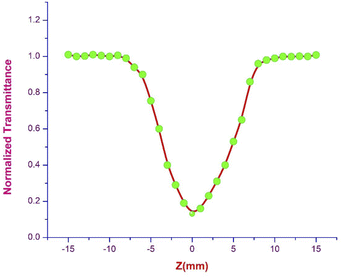 |
| | Fig. 17 Open aperture trace of DSFS crystal. | |
The real and imaginary parts of χ(3) can be directly derived from the nonlinear refractive index and nonlinear coefficient of absorption with the following equations:59
| |
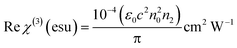 | (13) |
| |
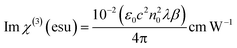 | (14) |
Coupling factor (
ρ) is calculated for the obtained experimental results by adopting two methods: one directly by taking the ratio between the imaginary and real parts by using
eqn (15):
60| |
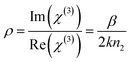 | (15) |
The other method is by taking the ratio between Δ
T and Δ
Φ0 of the open and closed aperture Z scan curves, respectively:
| |
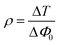 | (16) |
The calculated values from
eqn (15) and
(16) are 0.23 and 0.17, respectively. Both the values lie well within the critical value of the coupling factor
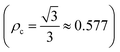
, which clearly indicates the validation of the obtained experimental data.
61 The obtained value is less than 1/3 the value, which emphasises that the electronic polarization is responsible for the nonlinearity in the material.
62 Both the
n2 and
β are insensitive to the incident wavelength until it reaches a particular wavelength called the critical wavelength (
λc). From the following formula, the
λc of the DSFS crystal is calculated.
| |
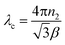 | (17) |
The λc value of the DSFS crystal is 1530 nm. If the laser's operating wavelength is beyond 1530 nm, the transmittance curve in the closed aperture method will disappear.60 The calculated values of the nonlinear refractive index NLRI (n2), nonlinear absorption coefficient NLAC (β) and third-order susceptibility (χ(3)) are found to be 4.6494 × 10−11 m2 W−1, 2.203 × 10−4 m W−1 and 1.573 × 10−7 esu, respectively. The third-order susceptibility value of the title ionic crystal is compared with a few other stilbazolium derivatives and organic centrosymmetric crystals, and the comparison is tabulated in Table 4. These comparison results indicate that the title DSFS crystal possesses a comparatively large χ(3) value.
Table 4 Comparison of the χ(3) value of the DSFS crystal with a few stilbazolium and organic crystals
| Crystal name |
χ(3) value (esu) |
| DSFS (present work) |
1.573 × 10−7 |
| VMST33 |
9.696 × 10−12 |
| DSMOS63 |
5.05 × 10−8 |
| KDP64 |
2.04 × 10−14 |
| 4MBS65 |
11.04 × 10−7 |
The structure of the DSFS crystal is the main reason behind this high NLO response. As already discussed in the structural analysis, the presence of the BLA degree (0.11 Å) in the stilbazolium cation induces nonlinearity in the system. Along with that, the presence of a strong electron-donating group (dimethyl amino) and electron-withdrawing group (pyridinium) in the stilbazolium cation gives rise to the development of a conjugated structure where the delocalization of π electrons takes place through the styryl pyridinium (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) delocalization channel. Among various reported delocalized conjugated structures, styryl-pyridinium is considered to be one of the most efficient conjugated structures; it is due to the nitrogen and carbon atoms in the pyridine ring, which are in an sp2 hybrid orbitals configuration and also a conjugated system is formed within the ring with one π orbital without a lone pair of electrons in the nitrogen atom.66 This entire D–π–A setup tends to give larger electron density transfer within the cation structure, leading to the surge in the scale of the dipole moment, which in turn makes the molecules highly polarized and increases the non-linearity of the DSFS crystal.63,67 Apart from this, the interaction between the stilbazolium cation and the SO3 ligand in the anion also induces non-linearity in the title crystal.33 All the results attained from the Z scan analysis suggests that the ionic DSFS crystal can be used in optical limiting and switching applications.27
C) delocalization channel. Among various reported delocalized conjugated structures, styryl-pyridinium is considered to be one of the most efficient conjugated structures; it is due to the nitrogen and carbon atoms in the pyridine ring, which are in an sp2 hybrid orbitals configuration and also a conjugated system is formed within the ring with one π orbital without a lone pair of electrons in the nitrogen atom.66 This entire D–π–A setup tends to give larger electron density transfer within the cation structure, leading to the surge in the scale of the dipole moment, which in turn makes the molecules highly polarized and increases the non-linearity of the DSFS crystal.63,67 Apart from this, the interaction between the stilbazolium cation and the SO3 ligand in the anion also induces non-linearity in the title crystal.33 All the results attained from the Z scan analysis suggests that the ionic DSFS crystal can be used in optical limiting and switching applications.27
4 Conclusion
The stilbazolium derivative single crystal DSFS with a new anion is fruitfully synthesized using the slow evaporation method. The structure of the grown ionic crystal is solved using SCXRD, and the CIF file is deposited in the CCDC database. The formation of the ethylenic bridge (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) is also confirmed via FTIR analysis. Results from the linear optical studies show that the bandgap and cut-off wavelength of the grown DSFS crystal are found to be 570 nm and 2.25 eV, respectively. The low value of the extinction coefficient (10−4) and high value of the optical and electrical conductivity (1010) indicates that the DSFS crystal is well suited for various optical applications. The Sku value from AFM and etching analysis reveals the flatness and good optical quality of the title ionic crystal. Through the Z scan technique, the third-order susceptibility χ(3) value of the DSFS crystal is determined to be χ(3) = 1.573 × 10−7 esu. The self-focusing effect along with the reverse saturation absorption nature of the title crystal suggests that the stilbazolium derivative crystal can be used for various applications such as remote sensing, photonic applications, optical limiting and optical switching. All the characterization outcomes show that the DSFS crystal is suitable for various NLO applications.
C) is also confirmed via FTIR analysis. Results from the linear optical studies show that the bandgap and cut-off wavelength of the grown DSFS crystal are found to be 570 nm and 2.25 eV, respectively. The low value of the extinction coefficient (10−4) and high value of the optical and electrical conductivity (1010) indicates that the DSFS crystal is well suited for various optical applications. The Sku value from AFM and etching analysis reveals the flatness and good optical quality of the title ionic crystal. Through the Z scan technique, the third-order susceptibility χ(3) value of the DSFS crystal is determined to be χ(3) = 1.573 × 10−7 esu. The self-focusing effect along with the reverse saturation absorption nature of the title crystal suggests that the stilbazolium derivative crystal can be used for various applications such as remote sensing, photonic applications, optical limiting and optical switching. All the characterization outcomes show that the DSFS crystal is suitable for various NLO applications.
Author contributions
S. A.: methodology, formal analysis, investigation, writing – original draft, and visualization. M. U. R.: conceptualization, visualization, supervision, review and editing. S. K.: conceptualization, review and editing. R. S. B.: conceptualization, review and editing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors would like to thank VIT – Vellore for providing the single crystal XRD measurement.
References
- M. Hasmuddin, M. Abdullah, P. Singh, M. Shkir, N. Vijayan and M. Wahab, Opt. Laser Technol., 2015, 74, 53–59 CrossRef CAS.
- X. Wang, Y. Du, S. Ding, Q. Wang, G. Xiong, M. Xie, X. Shen and D. Pang, J. Phys. Chem. B, 2006, 110, 1566–1570 CrossRef CAS PubMed.
- R. Ragu, P. Mageshwari, M. Akilan and S. J. Das, Appl. Phys. B: Lasers Opt., 2020, 126, 1–10 CrossRef.
- T. H. Clara, R. Ragu, D. R. Jonathan and J. C. Prasana, Opt. Mater., 2020, 109, 110331 CrossRef CAS.
- T. A. Hegde, A. Dutta, R. M. Jauhar, P. Karuppasamy, M. S. Pandian, M. Abith, T. S. Girisun and G. Vinitha, Opt. Mater., 2020, 107, 110033 CrossRef CAS.
- S. Anand, S. Kalainathan, T. Amrutha, K. Senthil and M. Yamada, J. Mater. Sci.: Mater. Electron., 2021, 32, 11059–11071 CrossRef CAS.
- C. Jin, F. Li, B. Cheng, H. Qiu, Z. Yang, S. Pan and M. Mutailipu, Angew. Chem., Int. Ed., 2022, 61, e202203984 CAS.
- M. Mutailipu, K. R. Poeppelmeier and S. Pan, Chem. Rev., 2021, 121, 1130–1202 CrossRef CAS PubMed.
- M. Faizan, M. Mehkoom, Z. Afroz, V. H. N. Rodrigues, S. Afzal and S. Ahmad, J. Solid State Chem., 2021, 300, 122255 CrossRef CAS.
- M. Gomathi, C. Karnan, T. Sivanesan, J. C. Rhoda, S. Manivannan, V. Ragavendran, G. Vinitha and A. Prabakaran, Chem. Phys. Lett., 2021, 776, 138705 CrossRef CAS.
- J. Yin, L. Li, Z. Yang, M. Jazbinsek, X. Tao, P. Günter and H. Yang, Dyes Pigm., 2012, 94, 120–126 CrossRef CAS.
- K. Senthil, S. Kalainathan and A. R. Kumar, CrystEngComm, 2014, 16, 9847–9856 RSC.
- S. Kannan, A. Sekar and K. Sivaperuman, J. Mater. Chem. C, 2020, 8, 16668–16690 RSC.
- O.-P. Kwon, B. Ruiz, A. Choubey, L. Mutter, A. Schneider, M. Jazbinsek, V. Gramlich and P. Günter, Chem. Mater., 2006, 18, 4049–4054 CrossRef CAS.
- E.-Y. Choi, M. Jazbinsek, J.-H. Jeong and O.-P. Kwon, CrystEngComm, 2012, 14, 1045–1048 RSC.
- K. Senthil, S. Kalainathan and A. R. Kumar, Spectrochim. Acta, Part A, 2014, 124, 603–610 CrossRef CAS PubMed.
- Z. Yang, M. Jazbinsek, B. Ruiz, S. Aravazhi, V. Gramlich and P. Günter, Chem. Mater., 2007, 19, 3512–3518 CrossRef CAS.
- A. A. Raj, S. J. Sundaram, R. Gunaseelan and P. Sagayaraj, Spectrochim. Acta, Part A, 2015, 149, 957–964 CrossRef PubMed.
- A. Sekar, U. R. Muthurakku and K. Sivaperuman, ChemistrySelect, 2021, 6, 10688–10716 CrossRef CAS.
- S. Dharmalingam and G. N. Muthukrishnan, J. Mol. Struct., 2022, 1250, 131815 CrossRef CAS.
- J. Pernak, J. Kalewska, H. Ksycińska and J. Cybulski, Eur. J. Med. Chem., 2001, 36, 899–907 CrossRef CAS PubMed.
- K. Chanawanno, S. Chantrapromma, T. Anantapong, A. Kanjana-Opas and H.-K. Fun, Eur. J. Med. Chem., 2010, 45, 4199–4208 CrossRef CAS PubMed.
- J. Polak and A. Jarosz-Wilkołazka, Microb. Cell Fact., 2010, 9, 51 CrossRef PubMed.
- M. K. Kumar, S. Sudhahar, G. Bhagavannarayana and R. M. Kumar, Optik, 2014, 125, 5641–5646 CrossRef CAS.
- J. A. M. Mani, Investigation On Growth And Physicochemical Properties Of Nonlinear Optical Stilbazolium Family Crystals Dast Dapsh And Mbmshp, PhD thesis, University of Madras, Chennai, 2017 Search PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- N. Karuppanan and S. Kalainathan, J. Phys. Chem. C, 2018, 122, 4572–4582 CrossRef CAS.
- A. Teshome, M. D. H. Bhuiyan, G. J. Gainsford, M. Ashraf, I. Asselberghs, G. V. Williams, A. J. Kay and K. Clays, Opt. Mater., 2011, 33, 336–345 CrossRef CAS.
- W. Kaminsky, J. Appl. Crystallogr., 2005, 38, 566–567 CrossRef CAS.
- N. Vijayan, S. Rajasekaran, G. Bhagavannarayana, R. Ramesh Babu, R. Gopalakrishnan, M. Palanichamy and P. Ramasamy, Cryst. Growth Des., 2006, 6, 2441–2445 CrossRef CAS.
- T. Vijayakumar, I. Hubert Joe, C. Reghunadhan Nair, M. Jazbinsek and V. Jayakumar, J. Raman Spectrosc., 2009, 40, 52–63 CrossRef CAS.
- A. U. Rani, N. Sundaraganesan, M. Kurt, M. Cinar and M. Karabacak, Spectrochim. Acta, Part A, 2010, 75, 1523–1529 CrossRef PubMed.
- M. K. Kumar, S. Sudhahar, P. Pandi, G. Bhagavannarayana and R. M. Kumar, Opt. Mater., 2014, 36, 988–995 CrossRef.
- M. Jazbinsek, Appl. Sci., 2019, 9, 882 CrossRef CAS.
- S. Kalainathan and R. S. Babu, et al., J. Mater. Sci.: Mater. Electron., 2019, 30, 10571–10578 CrossRef.
- K. Nivetha, W. Madhuri and S. Kalainathan, J. Mater. Sci.: Mater. Electron., 2017, 28, 8937–8949 CrossRef CAS.
- J. Pernak, J. Kalewska, H. Ksycińska and J. Cybulski, Eur. J. Med. Chem., 2001, 36, 899–907 CrossRef CAS PubMed.
- K. Pichan, S. P. Muthu and R. Perumalsamy, J. Cryst. Growth, 2017, 473, 39–54 CrossRef CAS.
- J. Polak and A. Jarosz-Wilkołazka, Microb. Cell Fact., 2010, 9, 51 CrossRef PubMed.
- R. Priya, S. Anitha, P. Mageshwari and R. Ragu, J. Mater. Sci.: Mater. Electron., 2020, 31, 21288–21302 CrossRef CAS.
- A. Priyadharshini and S. Kalainathan, J. Mater. Sci.: Mater. Electron., 2017, 28, 7401–7412 CrossRef CAS.
- A. Priyadharshini and S. Kalainathan, Opt. Mater., 2018, 78, 35–43 CrossRef CAS.
- A. Priyadharshini and S. Kalainathan, J. Phys. Chem. Solids, 2018, 123, 59–69 CrossRef CAS.
- R. Ragu, P. Mageshwari, M. Akilan and S. J. Das, Appl. Phys. B: Lasers Opt., 2020, 126, 1–10 CrossRef.
- M. Rajalakshmi, R. Indirajith, P. Ramasamy and R. Gopalakrishnan, Mol. Cryst. Liq. Cryst., 2011, 548, 126–141 CrossRef CAS.
- T. R. Kumar, R. Jeyasekaran, S. R. Kumar, M. Vimalan and P. Sagayaraj, Appl. Surf. Sci., 2010, 257, 1684–1691 CrossRef.
- A. U. Rani, N. Sundaraganesan, M. Kurt, M. Cinar and M. Karabacak, Spectrochim. Acta, Part A, 2010, 75, 1523–1529 CrossRef PubMed.
- V. Sangeetha, K. Gayathri, P. Krishnan, N. Sivakumar, N. Kanagathara and G. Anbalagan, J. Cryst. Growth, 2014, 389, 30–38 CrossRef CAS.
- N. Saravanan, G. Palani, S. Shanmugan and V. Chithambaram, Mater. Today: Proc., 2020, 30, 115–122 CAS.
- A. Sekar, U. R. Muthurakku and K. Sivaperuman, ChemistrySelect, 2021, 6, 10688–10716 CrossRef CAS.
- K. Senthil, S. Kalainathan and A. R. Kumar, CrystEngComm, 2014, 16, 9847–9856 RSC.
- K. Senthil, S. Kalainathan, A. R. Kumar and P. Aravindan, RSC Adv., 2014, 4, 56112–56127 RSC.
- S. Shalini, S. Shahil Kirupavathy, E. Jerusha and G. Vinitha, J. Mater. Sci.: Mater. Electron., 2019, 30, 6528–6536 CrossRef CAS.
- G. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- K. Senthil, S. Kalainathan and A. R. Kumar, Spectrochim. Acta, Part A, 2014, 124, 603–610 CrossRef CAS PubMed.
- S. Shettigar, G. Umesh, K. Chandrasekharan, B. Sarojini and B. Narayana, Opt. Mater., 2008, 30, 1297–1303 CrossRef CAS.
- A. Sundari and S. Manikandan, J. Mater. Sci.: Mater. Electron., 2018, 29, 558–567 CrossRef CAS.
- R. Surekha, P. Sagayaraj and K. Ambujam, Opt. Mater., 2014, 36, 945–949 CrossRef CAS.
- M. Suriya, M. Manimaran, B. M. Boaz and K. S. Murugesan, J. Mater. Sci.: Mater. Electron., 2021, 32, 11393–11417 CrossRef CAS.
- A. Teshome, M. D. H. Bhuiyan, G. J. Gainsford, M. Ashraf, I. Asselberghs, G. V. Williams, A. J. Kay and K. Clays, Opt. Mater., 2011, 33, 336–345 CrossRef CAS.
- B. Thirumalaiselvam, R. Kanagadurai, D. Jayaraman and V. Natarajan, Opt. Mater., 2014, 37, 74–79 CrossRef CAS.
- T. Vijayakumar, I. Hubert Joe, C. Reghunadhan Nair, M. Jazbinsek and V. Jayakumar, J. Raman Spectrosc., 2009, 40, 52–63 CrossRef CAS.
- N. Vijayan, S. Rajasekaran, G. Bhagavannarayana, R. Ramesh Babu, R. Gopalakrishnan, M. Palanichamy and P. Ramasamy, Cryst. Growth Des., 2006, 6, 2441–2445 CrossRef CAS.
- X. Wang, Y. Du, S. Ding, Q. Wang, G. Xiong, M. Xie, X. Shen and D. Pang, J. Phys. Chem. B, 2006, 110, 1566–1570 CrossRef CAS PubMed.
- Z. Yang, M. Jazbinsek, B. Ruiz, S. Aravazhi, V. Gramlich and P. Günter, Chem. Mater., 2007, 19, 3512–3518 CrossRef CAS.
- J. Yin, L. Li, Z. Yang, M. Jazbinsek, X. Tao, P. Günter and H. Yang, Dyes Pigm., 2012, 94, 120–126 CrossRef CAS.
- I. M. Zahid, S. Kalaiyarasi, M. K. Kumar, T. Ganesh, V. Jaisankar and R. M. Kumar, Mater. Sci., 2016, 34, 811–818 CAS.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Sivaperuman Kalainathan
*a,
Sivaperuman Kalainathan b and
Ravi Shanker Babua
b and
Ravi Shanker Babua
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group. The presence of different vibrational modes in the DSFS crystal is affirmed via Fourier transform infrared (FTIR) spectroscopy. Linear optical constants such as cut-off wavelength, bandgap, extinction coefficient, Urbach energy, electrical conductivity and optical conductivity of the titular crystal were found from ultraviolet–visible–near infra-red spectroscopy (UV-Vis-NIR). The emission wavelength of the title crystal lies in the red region (620 nm), which was confirmed from the photoluminescence spectroscopy (PL). The surface nature of the grown ionic crystal was examined through the etching and atomic force microscopy (AFM) technique. With a He–Ne laser as the source, Z scan analysis was carried out to study the third-order nonlinear properties of the DSFS crystal.
space group. The presence of different vibrational modes in the DSFS crystal is affirmed via Fourier transform infrared (FTIR) spectroscopy. Linear optical constants such as cut-off wavelength, bandgap, extinction coefficient, Urbach energy, electrical conductivity and optical conductivity of the titular crystal were found from ultraviolet–visible–near infra-red spectroscopy (UV-Vis-NIR). The emission wavelength of the title crystal lies in the red region (620 nm), which was confirmed from the photoluminescence spectroscopy (PL). The surface nature of the grown ionic crystal was examined through the etching and atomic force microscopy (AFM) technique. With a He–Ne laser as the source, Z scan analysis was carried out to study the third-order nonlinear properties of the DSFS crystal.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) in the stilbazolium cation is one of the primary reasons behind the high NLO response of this derivative’s materials, as this double bond acts as an interconnecting bridge between the donor and acceptor moiety. To form this carbon–carbon ethylenic bridge, many reaction strategies have been reported in the past, namely the Suzuki–Miyaura reaction, Horner–Wadsworth–Emmons (HWE) condensations and the Knoevenagel condensation. Among these methods, Knoevenagel condensation is used widely due to its simplicity.14–16 In the present study, the strategy of combining the stilbazolium (chromophore) cation with a new anion is adopted to develop a novel ionic organic single crystal. This approach of incorporating new counter-anions with an already existing stilbazolium cation has already been reported.17 This approach assists in creating a new NLO crystal with the desired physical and chemical properties.18 Previously reported results show that even a small change in the anion can induce a huge change in the non-linearity of the material by affecting the crystal stacking.19 The nature of the hydrogen bonds which connect the anion and cation decides the optoelectronic properties of the synthesized material.20 The low toxicity level of the styryl pyridinium compound in the cation part makes it an appropriate material for applications like antibacterial drugs and disinfectants in hospital and food industries.21,22 The anion compound 2-formyl benzene sulfonate sodium salt is used to test the ability of fungal strains to change phenolic and non-phenolic precursors into stable and non-toxic dyes.23 The findings from the extensive literature survey suggests that, so far, no crystal has been reported with 2-formyl benzene sulfonate as the anion with a stilbazolium derivative. So, in this article, we report the growth of DSFS crystal for the first time by employing the slow evaporation method. In addition, the synthesis and various physical and chemical properties such as structural, linear optical, surface analysis and nonlinear optical (NLO) properties of the grown crystal were inspected. The results are scrupulously discussed in the following sections. All the outcomes indicate that the grown DSFS crystal is a favourable candidate for NLO applications.
C) in the stilbazolium cation is one of the primary reasons behind the high NLO response of this derivative’s materials, as this double bond acts as an interconnecting bridge between the donor and acceptor moiety. To form this carbon–carbon ethylenic bridge, many reaction strategies have been reported in the past, namely the Suzuki–Miyaura reaction, Horner–Wadsworth–Emmons (HWE) condensations and the Knoevenagel condensation. Among these methods, Knoevenagel condensation is used widely due to its simplicity.14–16 In the present study, the strategy of combining the stilbazolium (chromophore) cation with a new anion is adopted to develop a novel ionic organic single crystal. This approach of incorporating new counter-anions with an already existing stilbazolium cation has already been reported.17 This approach assists in creating a new NLO crystal with the desired physical and chemical properties.18 Previously reported results show that even a small change in the anion can induce a huge change in the non-linearity of the material by affecting the crystal stacking.19 The nature of the hydrogen bonds which connect the anion and cation decides the optoelectronic properties of the synthesized material.20 The low toxicity level of the styryl pyridinium compound in the cation part makes it an appropriate material for applications like antibacterial drugs and disinfectants in hospital and food industries.21,22 The anion compound 2-formyl benzene sulfonate sodium salt is used to test the ability of fungal strains to change phenolic and non-phenolic precursors into stable and non-toxic dyes.23 The findings from the extensive literature survey suggests that, so far, no crystal has been reported with 2-formyl benzene sulfonate as the anion with a stilbazolium derivative. So, in this article, we report the growth of DSFS crystal for the first time by employing the slow evaporation method. In addition, the synthesis and various physical and chemical properties such as structural, linear optical, surface analysis and nonlinear optical (NLO) properties of the grown crystal were inspected. The results are scrupulously discussed in the following sections. All the outcomes indicate that the grown DSFS crystal is a favourable candidate for NLO applications.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) space group with triclinic crystal system. Collected lattice constant values of the grown DSFS crystal are a = 8.3812 Å, b = 9.8732 Å, c = 13.0649 Å and interfacial angle values are α = 82.404°, β = 88.395°, γ = 86.109°. Refined structural and crystallographic data of the title ion pair crystal are displayed in Table 1. Other important structural parameters, bond length and bond angle of selected bonds are depicted in Tables 1 and 2 in the ESI file.†
) space group with triclinic crystal system. Collected lattice constant values of the grown DSFS crystal are a = 8.3812 Å, b = 9.8732 Å, c = 13.0649 Å and interfacial angle values are α = 82.404°, β = 88.395°, γ = 86.109°. Refined structural and crystallographic data of the title ion pair crystal are displayed in Table 1. Other important structural parameters, bond length and bond angle of selected bonds are depicted in Tables 1 and 2 in the ESI file.†
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474
474![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) double bond indicates that it exhibits a trans or E configuration, with a torsional angle of C1–C6
C) double bond indicates that it exhibits a trans or E configuration, with a torsional angle of C1–C6![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C7–C8 of 179.59°.27 The torsional angle of the dimethyl group C12–C11–N2–C15 (5.83°) attached with the amino group C10–C11–N2–C16 (−9.70°) shows that the dimethyl moiety is slightly distorted from coplanarity with the benzene ring. The presence of the stilbazolium chromophore in the cation is the key to higher non-linearity. The main reason behind this efficiency is the deviation in the bond length among the ionic atoms and the presence of the D–π–A bridge, which in turn stimulates NLO susceptibility in the material.24 NLO response of a chromophore also depends on the bond length alternation (BLA) degree. The BLA degree of the title cation for the bonds N1–C14 (1.48 Å) and N2–C11 (1.37 Å) is 0.11 Å. The difference in the bond lengths of the dimethyl moiety N2–C15 (1.433 Å) and N2–C16 (1.453 Å) is 0.02 Å. Similarly, the bond length difference between the bonds of N1–C3 (1.336 Å) and N1–C4 (1.346 Å) of the 4-picoline compound is 0.010 Å. The ideal BLA value to exhibit higher non-linearity is approximately ±0.05 Å, whereas, in the case of the title cation, it is 0.11 Å, which is slightly higher.28 This BLA value indicates that the title stilbazolium cation compound also exhibits molecular nonlinearity. The geometrical description of the SO3− anion shows that the S− unit adopts regular trihedral coordination with the three oxygen atoms through S–O bonds. The bond lengths and angles of the S–O and O–S–O interactions reside in the range of 1.4415–1.4416 Å and 113.09–114.12°. The three-dimensional network of the title ionic compound is made up of alternating perpendicular anions between the parallel cationic units. The CIF file of the grown crystal is deposited in the CCDC (CCDC no. 2152094).
C7–C8 of 179.59°.27 The torsional angle of the dimethyl group C12–C11–N2–C15 (5.83°) attached with the amino group C10–C11–N2–C16 (−9.70°) shows that the dimethyl moiety is slightly distorted from coplanarity with the benzene ring. The presence of the stilbazolium chromophore in the cation is the key to higher non-linearity. The main reason behind this efficiency is the deviation in the bond length among the ionic atoms and the presence of the D–π–A bridge, which in turn stimulates NLO susceptibility in the material.24 NLO response of a chromophore also depends on the bond length alternation (BLA) degree. The BLA degree of the title cation for the bonds N1–C14 (1.48 Å) and N2–C11 (1.37 Å) is 0.11 Å. The difference in the bond lengths of the dimethyl moiety N2–C15 (1.433 Å) and N2–C16 (1.453 Å) is 0.02 Å. Similarly, the bond length difference between the bonds of N1–C3 (1.336 Å) and N1–C4 (1.346 Å) of the 4-picoline compound is 0.010 Å. The ideal BLA value to exhibit higher non-linearity is approximately ±0.05 Å, whereas, in the case of the title cation, it is 0.11 Å, which is slightly higher.28 This BLA value indicates that the title stilbazolium cation compound also exhibits molecular nonlinearity. The geometrical description of the SO3− anion shows that the S− unit adopts regular trihedral coordination with the three oxygen atoms through S–O bonds. The bond lengths and angles of the S–O and O–S–O interactions reside in the range of 1.4415–1.4416 Å and 113.09–114.12°. The three-dimensional network of the title ionic compound is made up of alternating perpendicular anions between the parallel cationic units. The CIF file of the grown crystal is deposited in the CCDC (CCDC no. 2152094).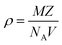
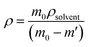
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) stretching lies in the range of 1650 to 1600 cm−1.31 The band at 1643 cm−1 in the spectrum indicates the presence of vinyl stretching. Apart from the (C
C) stretching lies in the range of 1650 to 1600 cm−1.31 The band at 1643 cm−1 in the spectrum indicates the presence of vinyl stretching. Apart from the (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) stretching, stilbazolium derivatives show aliphatic C–H stretching in the vicinity of 3050 cm−1. The peak centered at 3035 cm−1 indicates the aliphatic C–H stretching. Generally, the methyl group's asymmetrical bending vibration and symmetrical bending vibration bands were positioned in and around 1450 and 1375 cm−1, respectively. In Fig. 6, the peaks at 1473 and 1429 cm−1 represent the asymmetrical bending vibrations. The peak observed at 1375 cm−1 characterizes the symmetrical bending vibration of the methyl group. In the region between 1070–1010 cm−1, methyl group rocking modes were observed.32 In the DSFS crystal, the peaks positioned at 1078 and 1014 cm−1 are attributed to the CH3 rocking mode. The peak emitted at 1568 cm−1 is ascribed to aromatic C–C stretching. The peak positioned at 1527 cm−1 indicates ring (C
C) stretching, stilbazolium derivatives show aliphatic C–H stretching in the vicinity of 3050 cm−1. The peak centered at 3035 cm−1 indicates the aliphatic C–H stretching. Generally, the methyl group's asymmetrical bending vibration and symmetrical bending vibration bands were positioned in and around 1450 and 1375 cm−1, respectively. In Fig. 6, the peaks at 1473 and 1429 cm−1 represent the asymmetrical bending vibrations. The peak observed at 1375 cm−1 characterizes the symmetrical bending vibration of the methyl group. In the region between 1070–1010 cm−1, methyl group rocking modes were observed.32 In the DSFS crystal, the peaks positioned at 1078 and 1014 cm−1 are attributed to the CH3 rocking mode. The peak emitted at 1568 cm−1 is ascribed to aromatic C–C stretching. The peak positioned at 1527 cm−1 indicates ring (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) vibrations. Characteristic peaks for the aromatic C–H in-plane bending are observed at 1211 and 1078 cm−1. Similarly, peaks observed at 781 and 721 cm−1 are assigned to the C–H out-of-plane bending vibrations.31 The peak centered at 887 cm−1 represents the 1,4-disubstituted aromatic C–H ring. Three peaks centered at 611, 565 and 528 cm−1 in the spectrum indicate the phenyl ring mode (C–C–C) deformation vibration.
C) vibrations. Characteristic peaks for the aromatic C–H in-plane bending are observed at 1211 and 1078 cm−1. Similarly, peaks observed at 781 and 721 cm−1 are assigned to the C–H out-of-plane bending vibrations.31 The peak centered at 887 cm−1 represents the 1,4-disubstituted aromatic C–H ring. Three peaks centered at 611, 565 and 528 cm−1 in the spectrum indicate the phenyl ring mode (C–C–C) deformation vibration.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) stretching appeared at 1375 cm−1. The sharp peak positioned at 565 cm−1 implies C–S stretching. SO3 scissoring and SO3 deformation vibrations were observed at 528 and 493 cm−1, respectively. Finally, C
O) stretching appeared at 1375 cm−1. The sharp peak positioned at 565 cm−1 implies C–S stretching. SO3 scissoring and SO3 deformation vibrations were observed at 528 and 493 cm−1, respectively. Finally, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrations of the aldehyde group in the anion group give the characteristic peak at 1687 cm−1.
O vibrations of the aldehyde group in the anion group give the characteristic peak at 1687 cm−1.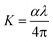
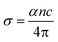
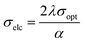
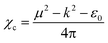
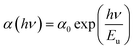
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group. In centrosymmetric crystals, due to the presence of an inversion centre, the resultant polarization has odd order susceptibility only, which means that even order susceptibility has null values. Due to the presence of odd order susceptibility the grown DSFS crystal exhibits third-order nonlinearity.51 Among the various technologies available to measure third-order nonlinearity, the Z scan technique is preferred over other methods due to its simplicity and reduced complexity.52 The basic principle behind the Z scan technique is that the sample under investigation is studied as a function of Z-position under the influence of a Gaussian beam to study the interaction between the sample and laser light. The four crucial parameters which help to determine the nonlinearity of the material can be accurately measured using the Z-scan technique: nonlinear refractive index (n2), nonlinear absorption coefficient (β), third-order nonlinear optical susceptibility (χ3) and second-order hyperpolarizability.52 In order to calculate the β and n2, two modes were adopted, namely open and closed aperture modes. During the translation of the sample, under the Gaussian beam with respect to variation of transmittance, the intensity-dependent absorption of the material is studied via an open aperture and the nonlinear refractive index is measured with reference to the change in light intensity via the closed aperture method with a finite slit or aperture in front of the output detector.53 With a helium–neon laser (632.8 nm) as the source, the Z-scan technique was carried out. With the aid of a Gaussian filter, the laser beam is converted to a Gaussian beam and the transformed beam is permitted to go through a convex lens with a focal distance of 30 mm to produce a focused beam with a beam waist diameter (W0) of 12.05 μm. In order to check whether the subjected sample satisfies the thin sample approximation, the Rayleigh length value (ZR) is calculated. For the Gaussian beam, the Rayleigh length (ZR = πW02/λ) is found to be 0.72 mm. The thickness (L) of the title crystal used for the analysis is 0.49 mm, which is less than the Rayleigh length; this clearly indicates that the sample used for measurement fulfilled the thin sample approximation (ZR ≫ L).54 The crystal is translated through the Z-direction (Z = +15 to −15) with reference to the focus (Z = 0). The corresponding output reading is measured in the output power meter with regard to the position of the crystal.
space group. In centrosymmetric crystals, due to the presence of an inversion centre, the resultant polarization has odd order susceptibility only, which means that even order susceptibility has null values. Due to the presence of odd order susceptibility the grown DSFS crystal exhibits third-order nonlinearity.51 Among the various technologies available to measure third-order nonlinearity, the Z scan technique is preferred over other methods due to its simplicity and reduced complexity.52 The basic principle behind the Z scan technique is that the sample under investigation is studied as a function of Z-position under the influence of a Gaussian beam to study the interaction between the sample and laser light. The four crucial parameters which help to determine the nonlinearity of the material can be accurately measured using the Z-scan technique: nonlinear refractive index (n2), nonlinear absorption coefficient (β), third-order nonlinear optical susceptibility (χ3) and second-order hyperpolarizability.52 In order to calculate the β and n2, two modes were adopted, namely open and closed aperture modes. During the translation of the sample, under the Gaussian beam with respect to variation of transmittance, the intensity-dependent absorption of the material is studied via an open aperture and the nonlinear refractive index is measured with reference to the change in light intensity via the closed aperture method with a finite slit or aperture in front of the output detector.53 With a helium–neon laser (632.8 nm) as the source, the Z-scan technique was carried out. With the aid of a Gaussian filter, the laser beam is converted to a Gaussian beam and the transformed beam is permitted to go through a convex lens with a focal distance of 30 mm to produce a focused beam with a beam waist diameter (W0) of 12.05 μm. In order to check whether the subjected sample satisfies the thin sample approximation, the Rayleigh length value (ZR) is calculated. For the Gaussian beam, the Rayleigh length (ZR = πW02/λ) is found to be 0.72 mm. The thickness (L) of the title crystal used for the analysis is 0.49 mm, which is less than the Rayleigh length; this clearly indicates that the sample used for measurement fulfilled the thin sample approximation (ZR ≫ L).54 The crystal is translated through the Z-direction (Z = +15 to −15) with reference to the focus (Z = 0). The corresponding output reading is measured in the output power meter with regard to the position of the crystal.
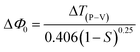
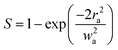
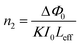
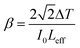
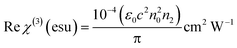
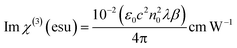
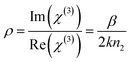
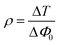
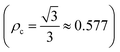 , which clearly indicates the validation of the obtained experimental data.61 The obtained value is less than 1/3 the value, which emphasises that the electronic polarization is responsible for the nonlinearity in the material.62 Both the n2 and β are insensitive to the incident wavelength until it reaches a particular wavelength called the critical wavelength (λc). From the following formula, the λc of the DSFS crystal is calculated.
, which clearly indicates the validation of the obtained experimental data.61 The obtained value is less than 1/3 the value, which emphasises that the electronic polarization is responsible for the nonlinearity in the material.62 Both the n2 and β are insensitive to the incident wavelength until it reaches a particular wavelength called the critical wavelength (λc). From the following formula, the λc of the DSFS crystal is calculated.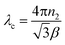
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) delocalization channel. Among various reported delocalized conjugated structures, styryl-pyridinium is considered to be one of the most efficient conjugated structures; it is due to the nitrogen and carbon atoms in the pyridine ring, which are in an sp2 hybrid orbitals configuration and also a conjugated system is formed within the ring with one π orbital without a lone pair of electrons in the nitrogen atom.66 This entire D–π–A setup tends to give larger electron density transfer within the cation structure, leading to the surge in the scale of the dipole moment, which in turn makes the molecules highly polarized and increases the non-linearity of the DSFS crystal.63,67 Apart from this, the interaction between the stilbazolium cation and the SO3 ligand in the anion also induces non-linearity in the title crystal.33 All the results attained from the Z scan analysis suggests that the ionic DSFS crystal can be used in optical limiting and switching applications.27
C) delocalization channel. Among various reported delocalized conjugated structures, styryl-pyridinium is considered to be one of the most efficient conjugated structures; it is due to the nitrogen and carbon atoms in the pyridine ring, which are in an sp2 hybrid orbitals configuration and also a conjugated system is formed within the ring with one π orbital without a lone pair of electrons in the nitrogen atom.66 This entire D–π–A setup tends to give larger electron density transfer within the cation structure, leading to the surge in the scale of the dipole moment, which in turn makes the molecules highly polarized and increases the non-linearity of the DSFS crystal.63,67 Apart from this, the interaction between the stilbazolium cation and the SO3 ligand in the anion also induces non-linearity in the title crystal.33 All the results attained from the Z scan analysis suggests that the ionic DSFS crystal can be used in optical limiting and switching applications.27![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) is also confirmed via FTIR analysis. Results from the linear optical studies show that the bandgap and cut-off wavelength of the grown DSFS crystal are found to be 570 nm and 2.25 eV, respectively. The low value of the extinction coefficient (10−4) and high value of the optical and electrical conductivity (1010) indicates that the DSFS crystal is well suited for various optical applications. The Sku value from AFM and etching analysis reveals the flatness and good optical quality of the title ionic crystal. Through the Z scan technique, the third-order susceptibility χ(3) value of the DSFS crystal is determined to be χ(3) = 1.573 × 10−7 esu. The self-focusing effect along with the reverse saturation absorption nature of the title crystal suggests that the stilbazolium derivative crystal can be used for various applications such as remote sensing, photonic applications, optical limiting and optical switching. All the characterization outcomes show that the DSFS crystal is suitable for various NLO applications.
C) is also confirmed via FTIR analysis. Results from the linear optical studies show that the bandgap and cut-off wavelength of the grown DSFS crystal are found to be 570 nm and 2.25 eV, respectively. The low value of the extinction coefficient (10−4) and high value of the optical and electrical conductivity (1010) indicates that the DSFS crystal is well suited for various optical applications. The Sku value from AFM and etching analysis reveals the flatness and good optical quality of the title ionic crystal. Through the Z scan technique, the third-order susceptibility χ(3) value of the DSFS crystal is determined to be χ(3) = 1.573 × 10−7 esu. The self-focusing effect along with the reverse saturation absorption nature of the title crystal suggests that the stilbazolium derivative crystal can be used for various applications such as remote sensing, photonic applications, optical limiting and optical switching. All the characterization outcomes show that the DSFS crystal is suitable for various NLO applications.

















