Exploration of the interesting photovoltaic behavior of the fused benzothiophene dioxide moiety as a core donor with modification in acceptors for high-efficacy organic solar cells

Abstract

Non-fullerene-based chromophores with end-capped acceptor modification used in organic solar cells (OSCs) have proven to offer improved performance. Therefore, eight unique benzothiophene-based molecules (D2–D9) were designed by the end-capped acceptor manipulation of a reference molecule (R1). Density functional theory (DFT) and time-dependent density functional theory (TD-DFT) calculations at the B3LYP level were performed to investigate various parameters such as the optical properties, frontier molecular orbitals (FMOs), transition density matrix (TDM), binding energy, density of states (DOS), open-circuit voltage (V_oc), and reorganization energies of electrons (λ_e) and holes (λ_h), to better understand the optoelectronic properties of the newly designed compounds. All the derivatives had broader absorption spectra of 737.562–700.555 nm with a reduced energy gap of 2.132–1.851 eV compared to those of the reference (719.082 nm), except for D8 and D9. A comparable value of V_oc and lower reorganization energies were found in the derivatives compared to those of R1. Within the studied compounds, D3 was predicted to be a good optoelectronic material for environmentally friendly organic solar cells (EFOSCs) because of its superior optoelectronic capabilities, low-energy band gap (1.851 eV), highest λ_max values of 794.516 and 744.784 nm in chloroform and the gas phase, respectively, and lowest transition energy (1.561 eV) than those of the reference and the other derivatives. Subsequently, end-capped acceptor modification was proven to be an effective method to achieve desired optoelectronic characteristics.

---

1 Introduction

Over the last few years, the performance of organic solar cells has dramatically improved, particularly due to the synthesis of small compounds such as non-fullerene acceptors (NFAs) that can cost-effectively produce an impressive photovoltaic response.^1,2 Organic compounds such as non-fullerene electron acceptors have improved solar light-emitting performance and energy efficiency.³ Currently, organic solar cells based on NFAs have a power conversion efficiency (PCE) of 18%. The applications of NFAs with an acceptor–donor–acceptor (A–D–A) structure have been receiving increasing attention due to their charge mobilities, long-range absorption, and fine-tuned energy levels.⁴ The most powerful NFAs have A–D–A structures, with a fused electron-donating core and two electron-accepting end groups. Therefore, a lot of researchers are working on acceptors other than the fullerene A–D–A structure with optimized charge dispersions, absorption, and energy levels⁵ to improve the PCE values.⁶ For quite a long time, silicon was considered the most suitable material for use as a semiconductor in photovoltaic devices. The key factors behind the prominent position of silicon in solar cells during the last 60 years of development include its extensive stability, large natural abundance,⁷ eco-friendly nature and high PCE of about 46%. However, a limiting factor in these types of solar cells is the increase in cost per watt with the increase in efficiency along with a low light-absorption rate.⁸ Compared with traditional silicon solar cells, dye-sensitized solar cells (DSSCs) have several merits such as light weight, low cost, easy fabrication and flexibility.⁹ This might be due to the narrow absorption spectrum range and quick recombination of electron–hole pairs on the surface of the photoanode.¹⁰ In recent years, organic solar cells (OSCs) have proved to be an efficient and successful replacement of traditional silicon and DSSCs in terms of energy generation. OSCs have cemented their place in foldable and flexible applications because of their flexibility and light weight. OSCs as an attractive renewable energy platform offer advantages in terms of their flexibility, strength, tunable energy levels, wide area for fabrication and low cost.¹¹ Fullerene-based OSCs offer a notable PCE of 12% in bulk heterojunctions (BHJs), affording a sufficient short-circuit current (J_sc) and open-circuit voltage (V_oc).¹² OSCs in combination with fullerene acceptors can achieve high isotropic charge mobility¹³ and low reorganization energy. Despite their good performance, limitations such their high cost, non-tunable capacity of the lowest unoccupied molecular orbital (LUMO) energy, reduced absorption of sunlight in the visible region, low V_oc, high band gap and poor morphological reliability make fullerene acceptors less efficient.¹⁴ To overcome these downsides, scientists are working on designing organic photovoltaic materials based on non-fullerene acceptors (NFAs). These non-fullerene organic photovoltaic (NF-OPV) materials are good replacements for their fullerene counterparts due to their acclaimed properties such as extended light-absorption ability, low voltage loss, easy molecular engineering for fabrication, solubility, tunable energy levels, and high morphological and photochemical stability.¹⁵ Most of the organic non-fullerene acceptor dyes retain the acceptor–donor–acceptor (A–D–A) backbone architecture. The A–D–A combination comprises a central electron-donating core unit blended with two sideways end-capped acceptor moieties. The most prominent reported example of the A–D–A architecture is ITIC,¹⁶ which shows promising optoelectronic properties such as a small band gap and long absorption range with a PCE of 16%.¹⁷ The most effective strategy to enhance the photovoltaic properties of NF-OSCs is to narrow the HOMO–LUMO energy gap via structural alteration and functional-group modification. Selecting proper electron-donor and -acceptor components can significantly reduce the HOMO–LUMO energy gap, increase the PCE and improve the photovoltaic properties of non-fullerene-based OSCs. Appropriate arrangement of the acceptor, donor and acceptor plays a vital role in designing potential organic compound dyes. Keeping in mind the above discussion, we utilized R1, an NF-SMA with benzothiophene dioxide (BO) terminal groups attached to phenyl side moieties, as a reference molecule.¹⁸ A series of eight new fullerene-free acceptor chromophores has been developed from R1. End-capped acceptor modifications were brought about in the reference chromophore. The electronic, photophysical, and photovoltaic materials of the predicted molecules (D2–D9) and their charge transfer in comparison to that of R1 have been illustrated using TDM, FMO, dipole moment, DOS, reorganization energy, V_oc and absorption maximum analyses. It is expected that these newly designed derivatives will play a key role in the progress of high-efficacy OSC materials.

2 Results and discussion

2.1 Molecular chemistry

This work used the DFT technique to study the optoelectronic properties of eight novel fullerene-free acceptor molecules (D2–D9) designed via structural manipulation at the terminal acceptors. For this, ITBCR¹⁹ was selected as the parent molecule, comprising a central benzo[b]thiophene-3(2H)-one 1,1-dioxide core unit linked by (Z)-2-(2-ethylidene-1,1-dioxidobenzo[b]thiophen-3(2H)-ylidene)malononitrile, which acts as a donor (D) moiety along with terminal electron-withdrawing acceptor (A) units. To eliminate steric hindrance and reduce the computational cost brought about by the long alkyl chains in ITBCR, the alkyl group C₆H₁₃ was replaced with a methyl (–CH₃) group, as shown in Fig. 1, and its name was changed from ITBCR to R1 (Scheme 1).

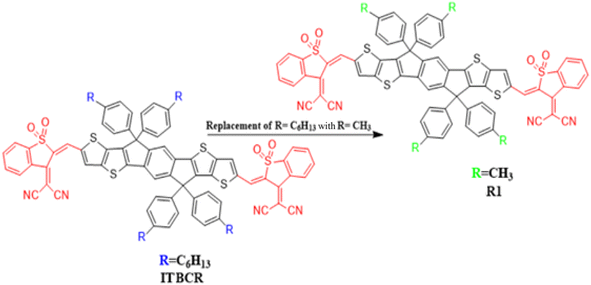Fig. 1 Modification of ITBCR into R1 via the substitution of a –CH₃ group.

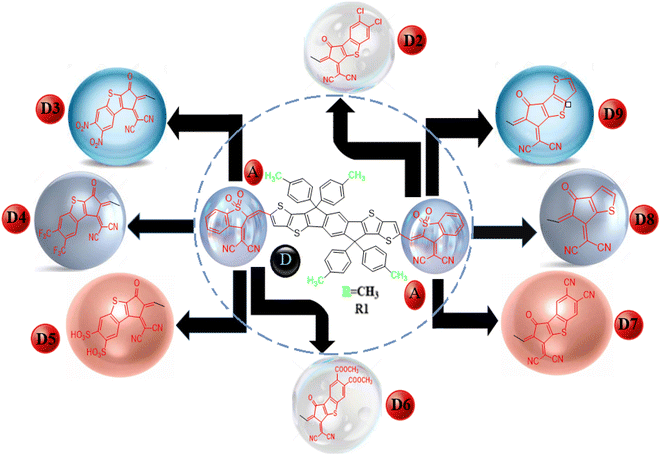Scheme 1 Schematic of the non-fullerene acceptor units.

We changed the terminal acceptors of R1 with various well-known end-capped acceptors to explore and boost the optoelectronic and photophysical properties of OSCs. The structures of R1 and its derivatives (D2–D9) in optimized form are depicted in Fig. 2.

Fig. 2 Optimized geometries of R1 and D2–D9.

2.2 Frontier molecular orbital (FMO) analysis

The electrical and optical properties of R1 and D2–D9 were studied via FMO analysis.²⁰ The HOMO is generally an electron donor, whereas the LUMO is considered to be an electron acceptor. E_LUMO − E_HOMO is known as the band gap (E_g).²¹ FMO investigations of R1 and the designed chromophores (D2–D9) were performed using the B3LYP/6-31G(d,p) level of DFT, and the FMO orbitals are shown in Fig. 3. Large E_HOMO − E_LUMO energy gap molecules are termed as hard molecules with low chemical reactivity and great stability. However, small E_LUMO − E_HOMO energy gaps are associated with soft molecules possessing high reactivity, low stability and great polarizability.^22,23 The energy gap and energies of the HOMO (E_HOMO) and LUMO (E_LUMO) of R1 and D2–D9 were calculated and the results are shown in Table 1.

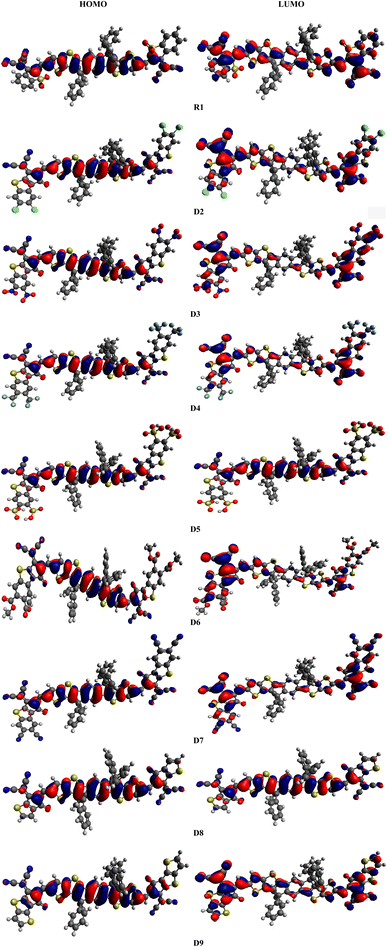Fig. 3 Frontier molecular orbital diagrams of R1 and D2–D9.

Table 1 Calculated E_HOMO, E_LUMO and energy gap (ΔE) of compounds R1 and D2–D9^a

Compounds	EHOMO	ELUMO	Band gap
a Band gap = ELUMO − EHOMO (eV).
R1	−5.574	−3.571	2.003
D2	−5.476	−3.476	2.000
D3	−5.591	−3.740	1.851
D4	−5.516	−3.549	1.967
D5	−5.580	−3.689	1.891
D6	−5.489	−3.519	1.970
D7	−5.577	−3.685	1.892
D8	−5.427	−3.295	2.132
D9	−5.400	−3.297	2.103

---

The calculated values of E_HOMO and E_LUMO for R1 are found to be −5.574 and −3.571 eV, respectively, with an energy gap of 2.003 eV. Meanwhile, the experimental values for the HOMO/LUMO have been determined to be −5.61/−4.13 eV with a 1.48 eV energy gap. A close harmony is thus seen between the DFT and experimental values, which confirms the suitable selection of the functional used for computational analysis.¹⁹ Similarly, the E_HOMO energies are determined to be −5.476, −5.591, −5.516, −5.580, −5.489, −5.577, −5.427 and −5.400 eV, while the E_LUMO values are −3.476, −3.740, −3.549, −3.689, −3.519, −3.685, −3.295 and −3.297 eV for D2–D9, respectively. The most important factor for describing the charge transport and optoelectronic properties in molecules is ΔE, and the energy gaps of R1 and D2–D9 are found to be 2.003, 2.000, 1.851, 1.967, 1.891, 1.97, 1.892, 2.132 and 2.103 eV, respectively (Table 1). The E_g has been found to decrease in all the designed compounds (D3–D7) except for D8 and D9, which exhibited band gaps a little bit larger than that of R1. In D2, a reduction in the band gap (2.000 eV) is found due to the addition of a thiophene ring and chloro (–Cl) groups at the acceptor moiety, which may enhance the electron-withdrawing effect along with the resonance. The band gap in D3 (1.851 eV) is found to decrease because the –Cl groups are replaced with nitro (–NO₂) groups at the acceptor unit. As –NO₂ groups have a greater negative inductive (−I) effect than –Cl (NO₂ > Cl),²⁴ the energy gap of D3 is reduced compared to that of D2. In the case of compound D4, an increase in the band gap (1.967 eV) is found compared to that of D3, as the –NO₂ groups at the acceptor are replaced with trifluoromethyl (–CF₃) groups. This might be due to –CF₃ exhibiting a lower electron-withdrawing ability than the –NO₂ group.²⁵ Further decline in the band gap is found in D5 (1.891 eV), in which the –CF₃ groups at the acceptor unit are replaced with sulfonic acid (–SO₃H) groups. Moreover, with the replacement of the –SO₃H group with the acetic acid (–CH₃COOH) group at the acceptor moiety, the ΔE of D6 (1.970 eV) is found to increase. This increment in the energy gap might be due to the weaker electron-withdrawing –CH₃COOH group (compared to the –SO₃H group). The band gap of D7 (1.892 eV) is less than that of D6 (1.970 eV) because of the replacement of –CH₃COOH with –CN groups at the acceptor moiety. This reduction in the energy gap is due to the −I effect of the electron-withdrawing –CN groups. In compound D8, the band gap (2.132 eV) is observed to increase compared to that of D7 (1.892 eV) because of the removal of one fragment (2-ethylidene-3-methylene-succinonitrile) from the acceptor unit. Owing to the removal of this fragment, the conjugation of the system is reduced and the E_g was enhanced. Finally, the energy gap of D9 (2.103 eV) is observed to decrease compared to that of D8 (2.132 eV) because of the replacement of a benzene ring with a thiophene ring into the system at the terminal acceptor. Because of this alteration, the conjugation in the molecule is reduced, resulting in an enhancement in the band gap. Overall, in R1 and D2–D9, the ΔE values are found to decrease in the order: D8 > D9 > R1 > D2 > D6 > D4 > D7 > D5 > D3. The electrical cloud transmission phenomenon is frequently described using the contour elements in FMO.²⁶ Pictographs of the molecular orbitals exhibiting the charge densities of the aforementioned compounds are presented in Fig. 3. Generally, the HOMO density lies over the central donor unit and a slight amount of it is over the peripheral acceptors; whereas for the LUMO, the electronic cloud is found predominantly over the end-capped acceptor moieties, and a little amount of it is concentrated over the central donor, except for D5 and D8, where the charge is located over the central part (Fig. 3).

2.3 Optical properties

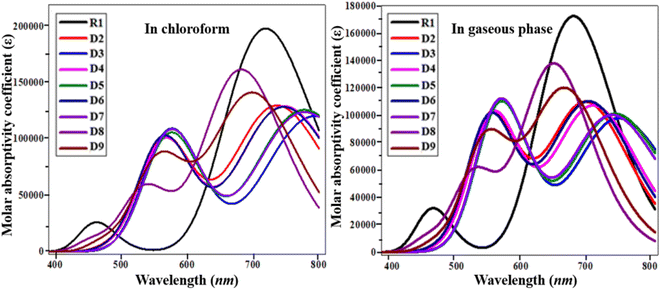
To elucidate the working potential of optoelectronic devices, UV-vis spectral analysis can provide a clear understanding of the spectral and optoelectronic properties.²⁷ UV-vis spectroscopy is a useful technique for the determination of the nature of transitions and charge-transfer characteristics. The absorption spectra of the designed compounds R1 and D2–D9 were calculated using TD/DFT computation at the B3LYP/6-31G(d,p) functional level in chloroform and in the gaseous phase.²⁸ Various parameters such as the λ_max, transition energy, oscillation strength (f_os) and molecular orbital contributions of the studied chromophores have been presented in Tables 2 and 3. The simulated absorption spectra of the analyzed chromophores (R1, D2–D9) are portrayed in Fig. 4.

Table 2 Calculated energy (E), wavelength (λ_max), oscillation strength (f_os) and nature of the molecular orbital (MO) contributions of R1 and D2–D9 in chloroform

Compound	λ (nm)	E (eV)	fos	MO contributions
R1	719.082	1.724	2.739	H → L (99%)
D2	737.562	1.681	1.786	H → L (97%)
D3	794.516	1.561	1.663	H → L (98%)
D4	747.839	1.658	1.781	H → L (97%)
D5	778.257	1.593	1.738	H → L (98%)
D6	747.929	1.658	1.750	H → L (97%)
D7	778.795	1.592	1.711	H → L (97%)
D8	682.657	1.816	2.229	H → L (98%)
D9	700.555	1.770	1.930	H → L (96%)

---

Table 3 Calculated energy (E), wavelength (λ_max), oscillation strength (f_os) and nature of the molecular orbital (MO) contributions of R1 and D2–D9 in the gas phase

Compound	λ (nm)	E (eV)	fos	MO contributions
R1	673.242	1.842	2.375	H → L (100%)
D2	693.928	1.787	1.498	H → L (96%)
D3	744.784	1.665	1.343	H → L (97%)
D4	705.217	1.758	1.465	H → L (97%)
D5	738.749	1.678	1.387	H → L (97%)
D6	701.030	1.769	1.433	H → L (97%)
D7	734.504	1.688	1.374	H → L (97%)
D8	643.773	1.926	1.885	H → L (98%)
D9	661.955	1.873	1.618	H → L (96%)

---

Fig. 4 UV-visible absorption spectra of the investigated molecules (R1 and D2–D9).

In chloroform solvent, the values of the maximum absorbed wavelength exist in the range of 682.657 to 794.516 nm. D3 showed a maximum absorption wavelength of 794.516 nm, the furthest away from the experimental outcome for the parent chromophore (711 nm).²⁹ It also exhibited the lowest E among the reference and derivatives due to its strong electron-withdrawing nitro group in the acceptor unit, with an excitation energy of 1.561 eV. A low excitation energy and low band gap lead to improved charge mobility with a high power conversion efficiency.³⁰ In chloroform, the maximum absorption peaks for the D2–D9 molecules are 737.562, 794.516, 747.839, 778.257, 747.929, 778.795, 682.657 and 700.555 nm, respectively. The lowest value of λ_max is in the case of D8 (682.657 nm) due to the attachment of a weakly electron-withdrawing end-capped acceptor group. In the chloroform solvent, the decreasing order of the studied chromophores with respect to their λ_max in chloroform is D3 > D7 > D5 > D6 > D4 > D2 > R1 > D9 > D8.

In the gaseous phase, the maximum absorbed wavelength of all the investigated chromophores also lies in the visible region. Herein, the calculated absorbed wavelength was examined in the range of 643.773–744.784 nm. The maximum absorbed wavelength of the reference chromophore (R1) is 673.242 nm. Except for D8 and D9, all the investigated chromophores possess higher wavelengths than the reference molecule. Like in the solvent phase, D3 also exhibited the highest λ_max among the investigated molecules. A small decrease in the values of λ_max of the studied chromophores in the gas phase is observed, which might be due to the solvent effect,³¹ as shown in Table 3. In the gas phase, the maximum absorbed wavelength decreases in the order of D3 > D5 > D7 > D4 > D6 > D2 > R1 > D9 > D8. D3 shows the smallest transition energy, the lowest energy gap, and the largest maximum value, which are favorable parameters for utilizing a material's optoelectronic properties in organic solar cell applications.³² The above discussion concludes that red-shifted compounds with a low energy gap and a strong charge-transfer ability, resulting in a good PCE, can be used as efficient materials in non-fullerene OSCs.

2.4 Reorganization energy

The reorganization energy (RE) is an important feature to recognize the relationship between a compound structure and its capacity to transfer charge efficiently.³³ The performance and working capability of OSCs is mainly dependent upon the reorganization energy, which is actually the electron and hole transport ability of different materials.³⁴ Therefore, in order to understand the charge mobility, i.e., the hole mobility (λ_h) and electron mobility (λ_e), of the studied chromophores, the RE was calculated at the B3LYP/6-31G(d,p) functional level (Table 4).

Table 4 Computed reorganization energies of the R1 and D2–D9 chromophores

Compounds	λe (eV)	λh (eV)
R1	−0.00002673	0.00018773
D2	−0.00000762	−0.33841872
D3	0.00003289	0.00009158
D4	−0.00003688	0.00005475
D5	0.00005186	0.00007521
D6	−0.00004563	0.00011363
D7	0.00002929	0.00008763
D8	0.00026435	0.00009166
D9	0.0001786	0.00009157

---

Essentially, the RE can be categorized into the internal reorganization energy (λ_int) and external reorganization energy (λ_ext). λ_int provides knowledge about quick changes in the internal structures, whereas λ_ext only deals with the external structural environment. λ_ext has little impact; hence this factor was overlooked in favor of the internal reorganizational energy. The computed λ_e of the reference and derivatives are found to be −0.00002673, −0.00000762, 0.00003289, −0.00003688, 0.00005186, −0.00004563, 0.00002929, 0.00026435 and 0.0001786 eV, respectively. D6 has the lowest λ_e value (−0.00004563 eV) of the studied molecules, indicating its faster electron mobility. The descending order of λ_e is D6 > D4 > R1 > D2 > D7 > D3 > D5 > D9 > D8. Consequently, for R1 and D2–D9, the predicted λ_h values are 0.00018773, −0.33841872, 0.00009158, 0.00005475, 0.00007521, 0.00011363, 0.00008763, 0.00009166, and 0.00009157 eV, respectively. For the designated molecules, the increasing order of λ_h is D2 > D4 > D5 > D7 > D9 > D3 > D8 > D6 < R1. The overall discussion concludes that the lower λ_h values of all the derivatives expressed a greater rate of hole transport in them than in the reference molecule, except for D2. This investigation reveals a greater charge-transport rate in the aforementioned chromophores, which indicated their potential as effective candidates for OSCs.

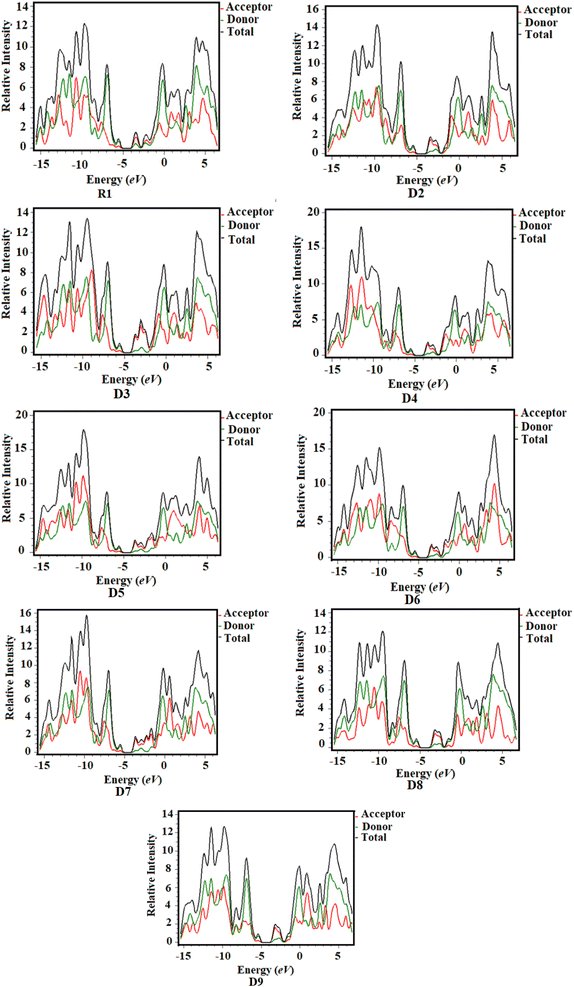
2.5 Density of states (DOS)

DOS analysis is considered to be an efficient tool to examine the charge densities on the chromophores and provides support for the investigations performed in the FMO study.^35,36 Herein, DOS analysis was executed for the studied chromophores to examine the charge-transfer rate, and the resulting graphs are shown in Fig. 5. We separated our compounds into two groups for the purpose of explaining the DOS analysis, i.e., the central donor and sideways acceptors, as shown with black and red lines in the maps, respectively. The electronic distribution patterns on the acceptors for R1 and D2–D9 are found to be 23.9%, 23.1%, 23.7%, 23.1%, 23.6%, 23.1%, 23.6%, 22.0% and 22.8% for the HOMO and 66.5%, 79.4%, 83.8%, 79.8%, 81.7%, 80.8%, 82.3%, 70.4% and 75.4% for the LUMO, respectively. Similarly, the donor contributes 76.1%, 76.9%, 76.3%, 76.9%, 76.4%, 76.9%, 76.4%, 78.0% and 77.2% to the HOMO and 33.5%, 20.6%, 16.2%, 20.2%, 18.3%, 19.2%, 17.7%, 29.6% and 24.6% to the LUMO in R1 and D2–D9, respectively.³⁷ For the HOMO, the charge density is predominantly present on the donor moiety but partly on the acceptor units, whereas the LUMO is found mostly on the acceptor components, as shown by the green and red peaks in the maps. DOS analysis revealed a high degree of charge coherence from the central donor to the end-group acceptor region, especially near the end-capped groups, as well as a significant delocalization of the electronic structure, as discussed in the FMO analysis.

Fig. 5 Density of states (DOS) of the studied chloroforms as represented graphically.

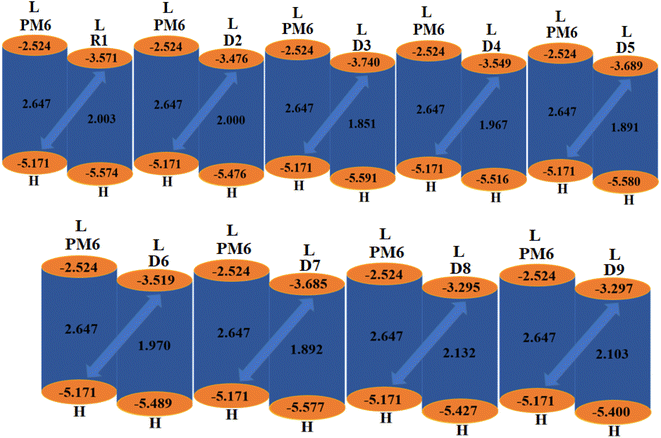
2.6 Open-circuit voltage (V_oc) analysis

The V_oc is an important parameter that plays a vital role in determining the working potential of OSCs^38,39 and is defined as the highest electric current that can readily be obtained from an optical material.⁴⁰ Certain key factors, such as light intensity, light source, charge-carrier recombination, external fluorescence proficiency and work functions of the electrodes, greatly affect the V_oc.⁴¹ The V_oc can be calculated by taking the difference of the HOMO of the donor polymer molecule and the LUMO of the acceptor molecule. To achieve a higher V_oc, the LUMO of the acceptor moiety should be higher than the HOMO of the donor, as this reduces the band gap.⁴² The theoretically computed results of V_oc, calculated using the equation given by Scharber et al.,⁴³ are presented in Table 5.

V_oc = (|E^D_HOMO| − |E^A_LUMO|) − 0.3 (1)

Here, E denotes the elementary charge of the acceptors, signifying the charge on each molecule, and 0.3 is the empirical constant. A well-known donor polymer, PM6,⁴⁴ with HOMO/LUMO energies of 5.171 and −2.524 eV, respectively, has been utilized to examine the V_oc values, as shown in Table 5.

Table 5 Open-circuit voltage of the studied compounds^a

Compounds	Voc (V)	ΔE
a ΔE = E^ALUMO − E^DHOMO
R1	1.30	2.003
D2	1.395	2.000
D3	1.131	1.851
D4	1.322	1.967
D5	1.182	1.891
D6	1.352	1.970
D7	1.186	1.892
D8	1.576	2.132
D9	1.574	2.103

---

The computed V_oc value of the reference chromophore shows excellent agreement with its experimental value of 0.86 V,¹⁹ which indicated the suitable selection of the level of theory for our study of the photovoltaic properties of R1 and D2–D9, whose LUMO_acceptor values are 1.3, 1.395, 1.131, 1.322, 1.182, 1.352, 1.186, 1.576 and 1.574 V, respectively. The V_oc of the studied chromophores decreased in the order of D8 > D9 > D2 > D6 > D4 > R1 > D7 > D5 > D3. Among all the compounds, D8 had the highest V_oc value (1.576 V). The other designed derivatives showed comparable open-circuit voltages with that of the reference molecule. A low-lying LUMO leads to improved V_oc values with an enhanced photovoltaic response. The orbital energy diagrams of all the investigated chromophores blended with PM6 are shown in Fig. 6. It is clear from Fig. 6 that the LUMO level of the acceptor molecules (R1 and D2–D9) lies below the HOMO of the donor PM6 polymer. This kind of placement of molecular orbitals enables facile transfer of the electron cloud from PM6 to the acceptor, leading to enhanced optoelectronic behavior.

Fig. 6 Graphical representation of the V_oc for the studied chromophores with PM6.

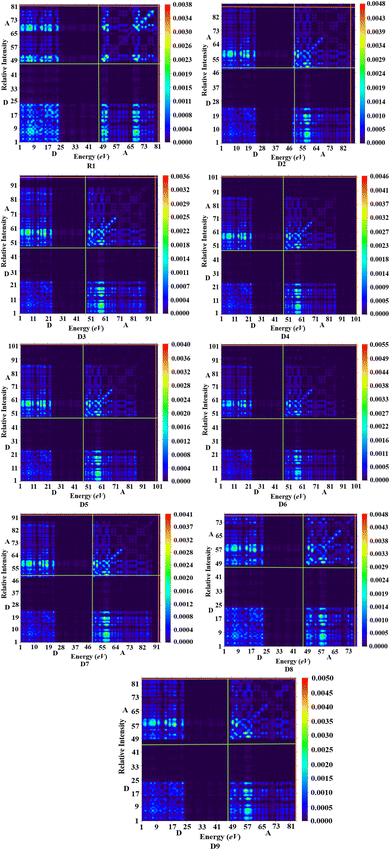
2.7 Transition density matrix (TDM)

Various types of transitions in the reference and tailored chromophores were evaluated via TDM analysis. TDM study elucidates the charge transport inside molecules, making it a crucial analysis for determining the performance of OSCs. Applying the B3LYP/6-31G(d,p) functional, the emission and absorption of electronic charges for S1 from the S0 state were calculated (Fig. 7). The contribution of hydrogen to the transition is so minor that it is neglected in the current study. The TDM approach is crucial for estimating the excited state phenomena of electronic excitation and electron–hole localization.^45,46 R1 and D2–D9 are split into two segments: the acceptor (the end-capped molecule: A) and donor (the core component: D). Fig. 7 indicates that effective charge is present at the terminal acceptor moieties, as higher-electron intensity green and red spots can be seen over those portions. According to the results obtained from the TDM heat maps, it has been observed that the electronic charge is efficiently transferred in a diagonal way from the donor to the acceptor in all the derivatives without trapping, thus showing charge coherence.

Fig. 7 TDM analysis in the reference state S1 and for the designed compounds.

2.8 Exciton binding energy (E_b)

E_b is defined as the difference between the HOMO and LUMO with the first singlet-to-singlet excitation state energy (E_opt) and is an important component that aids researchers in exploring the photovoltaic response of OSCs.⁴⁷ The interaction of the coulombic forces between the electrons (λ_e) and the holes (λ_h) is measured by the binding energy. Low-binding-energy molecules have a high power conversion efficiency and a high current charge density (J_sc).^48,49 Eqn (2) was used to compute the E_b of the R1 and D2–D9 acceptor molecules, where E_H–L represents the energy difference between the HOMO and LUMO.

E_b = E_H–L − E_opt (2)

Table 6 shows the DFT-estimated findings of the E_b of the studied compounds in chloroform.

Table 6 Calculated E_b of the R1 and D2–D9 compounds^a

Compounds	EH–L	Eopt	Eb
a Units in eV.
R1	2.003	1.724	0.279
D2	2.000	1.681	0.319
D3	1.851	1.561	0.290
D4	1.967	1.658	0.309
D5	1.891	1.593	0.298
D6	1.97	1.658	0.312
D7	1.892	1.592	0.300
D8	2.132	1.816	0.316
D9	2.103	1.770	0.333

---

Table 6 shows that all the derivatives exhibited comparable values of binding energies with their reference chromophores. For all the molecules, the descending pattern of E_b is as follows: D9 < D2 < D8 < D6 < D4 < D7 < D5 < D3 < R1. Structures with an E_b of 2.1 eV or below are generally considered to be efficient OSC materials with a high V_oc.⁴⁹ Interestingly, all our compounds exhibited E_b values lower than 2.1 eV, which illustrates their high exciton dissociation rate and large charger transfer rate, as shown in the TDM maps. All these investigations suggest that these designed molecules would be effective photovoltaic materials.

3 Conclusions

Advanced quantum chemistry techniques have been successfully employed to investigate the optoelectronic, photophysical and photovoltaic properties of newly designed A–D–A-type fullerene-free chromophores. Terminal structural tailoring has proven to be the most important strategy for developing high-performance photovoltaic materials with good optoelectronic properties for efficient OSCs. The FMO findings reveal a diminishing energy gap between the HOMO and LUMO with effective charge transfer in the derivatives, which is further supported by TDM and DOS investigations. Comparing the absorption properties, the derivatives show a red shift in their emission spectra (λ_max = 794.516–737.562 nm in chloroform and 744.784–693.928 nm in the gas phase) compared to that of R1 (λ_max = 719.082 nm in chloroform and 673.242 nm in the gas phase), except for D8 and D9. Furthermore, TDM analysis demonstrated that the end-capped substituents could rapidly extract electron density, resulting in an increased charge-transfer rate when tailored with the acceptors. Moreover, the V_oc was also estimated with regards to HOMO_PM6–LUMO_acceptor and all the derivatives show comparable voltage results with the reference molecule. Our predicted molecules might have good photovoltaic and electronic properties, as evidenced by their excitation binding energies and moderate reorganization. According to our findings, end-capped terminal modification is a useful technique for developing novel and highly competitive photovoltaic materials with good electrical and optical properties. It is suggested that the predicted compounds should be synthesized to create highly efficient organic solar cells.

4 Computational procedure

All the computations of this study were performed with the aid of the Gaussian 09 (ref. 50) program. Gauss View 5.0 (ref. 51) was used to create the input data and to display the results. To optimize the geometry of the reference compound (R1) without symmetry reduction, five exchange–correlation (XC) functionals were utilized: B3LYP,⁵² CAM-B3LYP,⁵³ MPW1PW9,⁵⁴ M06 (ref. 55) and M06-2X,⁵⁶ with the 6-31G(d,p) basis set combination. To select a good theoretical technique, the computed maximum absorbed wavelength of the reference chromophore R1 in chloroform with the abovementioned functionals was compared to the experimentally reported data. The maximum values of the reference compound generated employing the aforementioned functionals were 719.082, 674.487, 526.45, 537.799 and 671.965 nm, respectively, whereas the maximum value of ITBCR measured experimentally was 711 nm.¹⁹ At the B3LYP/6-31G(d,p) level of DFT, a good agreement with the experimental findings was seen (Fig. 8); therefore, this functional was selected for further investigations. Moreover, to visualize the optoelectronic and photovoltaic properties, various analyses, such as FMO, DOS, TDM, binding energy, and open-circuit voltage analysis, were performed for R1 and D2–D9. The internal (λ_int) and external (λ_ext) reorganization energies are the two fundamental types of reorganization energy. The first one, λ_int, is based on internal structural modification, whereas λ_ext deals with the influence of polarization in the external environment.⁵⁷ In this report, factors related to external environmental changes were not considered and our only focus was on λ_int.²⁵ The energies for hole (λ_h) and electron (λ_e) rearrangement were calculated using the equations below.⁵⁸

λ_e = [E₀⁻ − E₋] + [E⁰₋ − E₀] (3)

λ_h = [E₀⁺ − E₊] + [E⁰₊ − E₀] (4)

where E⁰₊ and E⁰₋ represent the neutral compound's capabilities as a result of the optimized cation and anion geometries; E₋ and E₊ indicate the energies of anions and cations, respectively; E₀⁻ and E₀⁺ represent the cations and anions exhibiting different single point energies (SPEs); and E₀ is the neutral molecule of SPE.⁵⁹

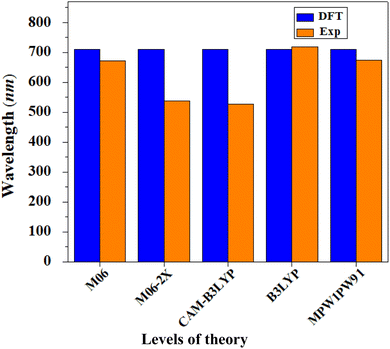Fig. 8 Comparison between the theoretical and experimental UV-visible results of R1 in chloroform at various levels with 6-31G(d,p).

Conflicts of interest

No conflicts to declare.

Acknowledgements

The authors are grateful to the cooperation and collaboration of A. A. C. B. from IQ-USP Brazil, especially for his continuous support and providing computational lab facilities. Dr Muhammad Khalid gratefully acknowledges the financial support of HEC Pakistan (project no. 20-14703/NRPU/R&D/HEC/2021). M. A. A. appreciates the support of the Research Center for Advanced Materials Science (RCAMS) at King Khalid University Abha, Saudi Arabia, through grant KKU/RCAMS/G015/21.

References

1. Y. Lin, J. Wang, Z.-G. Zhang, H. Bai, Y. Li, D. Zhu and X. Zhan, Adv. Mater., 2015, 27, 1170–1174.
2. H. Yao, Y. Cui, D. Qian, C. S. Ponseca, A. Honarfar, Y. Xu, J. Xin, Z. Chen, L. Hong, B. Gao, R. Yu, Y. Zu, W. Ma, P. Chabera, T. Pullerits, A. Yartsev, F. Gao and J. Hou, J. Am. Chem. Soc., 2019, 141, 7743–7750.
3. Z. Liu, L. Krückemeier, B. Krogmeier, B. Klingebiel, J. A. Márquez, S. Levcenko, S. Öz, S. Mathur, U. Rau, T. Unold and T. Kirchartz, ACS Energy Lett., 2019, 4, 110–117.
4. M. U. Khan, M. Khalid, R. Hussain, A. Umar, M. Y. Mehboob, Z. Shafiq, M. Imran and A. Irfan, Energy Fuels, 2021, 35, 12436–12450.
5. Y. Cui, Y. Wang, J. Bergqvist, H. Yao, Y. Xu, B. Gao, C. Yang, S. Zhang, O. Inganäs, F. Gao and J. Hou, Nat. Energy, 2019, 4, 768–775.
6. M. Adnan, J. Iqbal, S. BiBi, R. Hussain, M. N. Akhtar, M. A. Rashid, B. Eliasson and K. Ayub, Z. Phys. Chem., 2017, 231, 1127–1139.
7. M. A. Green, Prog. Photovoltaics, 2009, 17, 183–189.
8. O. Vigil-Galán, M. Courel, J. A. Andrade-Arvizu, Y. Sánchez, M. Espíndola-Rodríguez, E. Saucedo, D. Seuret-Jiménez and M. Titsworth, J. Mater. Sci.: Mater. Electron., 2015, 26, 5562–5573.
9. K. Kakiage, Y. Aoyama, T. Yano, K. Oya, J. Fujisawa and M. Hanaya, Chem. Commun., 2015, 51, 15894–15897.
10. Z. Han, L. Ren, Z. Cui, C. Chen, H. Pan and J. Chen, Appl. Catal., B, 2012, 126, 298–305.
11. C. J. Kettle, D. F. R. P. Burslem and J. Ghazoul, Science, 2011, 333, 36.
12. R. Singh and V. K. Shukla, Sol. Energy, 2019, 178, 90–97.
13. Y. He and Y. Li, Phys. Chem. Chem. Phys., 2011, 13, 1970–1983.
14. J. Zhao, Y. Li, H. Lin, Y. Liu, K. Jiang, C. Mu, T. Ma, J. Y. Lin Lai, H. Hu, D. Yu and H. Yan, Energy Environ. Sci., 2015, 8, 520–525.
15. C. Yan, S. Barlow, Z. Wang, H. Yan, A. K.-Y. Jen, S. R. Marder and X. Zhan, Nat. Rev. Mater., 2018, 3, 18003.
16. Z. Liu and X. C. Wang, J. Cleaner Prod., 2013, 42, 96–102.
17. M. Deng, X. Xu, L. Yu, R. Li and Q. Peng, Dyes Pigm., 2020, 180, 108452.
18. H. Huang, Q. Guo, S. Feng, C. Zhang, Z. Bi, W. Xue, J. Yang, J. Song, C. Li, X. Xu, Z. Tang, W. Ma and Z. Bo, Nat. Commun., 2019, 10, 3038.
19. M. S. Ahmad, M. Khalid, M. A. Shaheen, M. N. Tahir, M. U. Khan, A. A. C. Braga and H. A. Shad, J. Phys. Chem. Solids, 2018, 115, 265–276.
20. R. Hussain, M. Saeed, M. Y. Mehboob, S. U. Khan, M. Usman Khan, M. Adnan, M. Ahmed, J. Iqbal and K. Ayub, RSC Adv., 2020, 10, 20595–20607.
21. M. R. S. A. Janjua, M. U. Khan, B. Bashir, M. A. Iqbal, Y. Song, S. A. R. Naqvi and Z. A. Khan, Comput. Theor. Chem., 2012, 994, 34–40.
22. M. R. S. A. Janjua, M. Amin, M. Ali, B. Bashir, M. U. Khan, M. A. Iqbal, W. Guan, L. Yan and Z. Su, Eur. J. Inorg. Chem., 2012, 2012, 705–711.
23. M. Khalid, I. Shafiq, M. Zhu, M. U. Khan, Z. Shafiq, J. Iqbal, M. M. Alam, A. A. C. Braga and M. Imran, J. Saudi Chem. Soc., 2021, 25, 101305.
24. M. U. Khan, M. Khalid, M. N. Arshad, M. N. Khan, M. Usman, A. Ali and B. Saifullah, ACS Omega, 2020, 5, 23039–23052.
25. R. Hussain, F. Hassan, M. U. Khan, M. Y. Mehboob, R. Fatima, M. Khalid, K. Mahmood, C. J. Tariq and M. N. Akhtar, Opt. Quantum Electron., 2020, 52, 364.
26. M. U. Khan, M. Khalid, M. Ibrahim, A. A. C. Braga, M. Safdar, A. A. Al-Saadi and M. R. S. A. Janjua, J. Phys. Chem. C, 2018, 122, 4009–4018.
27. M. Khalid, M. A. Ullah, M. Adeel, M. Usman Khan, M. N. Tahir and A. A. C. Braga, J. Saudi Chem. Soc., 2019, 23, 546–560.
28. A. Mahmood, A. Tang, X. Wang and E. Zhou, Phys. Chem. Chem. Phys., 2019, 21, 2128–2139.
29. F. Jilani, J. Iqbal, I. Shahid, M. Yaseen, M. Shabir Mahr, M. Khalid and K. Ayub, Comput. Theor. Chem., 2020, 1187, 112916.
30. M. Ans, J. Iqbal, B. Eliasson, M. J. saif and K. Ayub, Comput. Mater. Sci., 2019, 159, 150–159.
31. R. Hussain, F. Hassan, M. U. Khan, M. Y. Mehboob, R. Fatima, M. Khalid, K. Mahmood, C. J. Tariq and M. N. Akhtar, Opt. Quantum Electron., 2020, 52, 364.
32. M. N. Arshad, M. Khalid, G. Shabbir, M. Asad, A. M. Asiri, M. M. Alotaibi, A. A. C. Braga and A. Khan, RSC Adv., 2022, 12, 4209–4223.
33. M. Khalid, M. N. Arshad, S. Murtaza, I. Shafiq, M. Haroon, A. M. Asiri, S. Figueirêdo de AlcântaraMorais and A. A. C. Braga, RSC Adv., 2022, 12, 13412–13427.
34. M. Khalid, M. U. Khan, E. Razia, Z. Shafiq, M. M. Alam, M. Imran and M. S. Akram, Sci. Rep., 2021, 11, 19931.
35. S. Hussain, S. A. S. Chatha, A. I. Hussain, R. Hussain, M. Y. Mehboob, S. Muhammad, Z. Ahmad and K. Ayub, J. Chem., 2020, 2020, 1–12.
36. S. Hussain, R. Hussain, M. Y. Mehboob, S. A. S. Chatha, A. I. Hussain, A. Umar, M. U. Khan, M. Ahmed, M. Adnan and K. Ayub, ACS Omega, 2020, 5, 7641–7650.
37. M. U. Khan, M. Y. Mehboob, R. Hussain, Z. Afzal, M. Khalid and M. Adnan, Int. J. Quantum Chem., 2020, 120, e26377,  DOI:10.1002/qua.26377.
38. S. H. Gu, V. Nicolas, A. Lalis, N. Sathirapongsasuti and R. Yanagihara, Infect., Genet. Evol., 2013, 20, 118–123.
39. M. Irfan, J. Iqbal, S. Sadaf, B. Eliasson, U. A. Rana, S. Ud-din Khan and K. Ayub, Int. J. Quantum Chem., 2017, 117, e25363.
40. M. Ans, K. Ayub, S. Muhammad and J. Iqbal, Comput. Theor. Chem., 2019, 1161, 26–38.
41. S. Tang and J. Zhang, J. Comput. Chem., 2012, 33, 1353–1363.
42. M. U. Khan, R. Hussain, M. Y. Mehboob, M. Khalid, M. A. Ehsan, A. Rehman and M. R. S. A. Janjua, Spectrochim. Acta, Part A, 2021, 245, 118938.
43. M. C. Scharber, D. Mühlbacher, M. Koppe, P. Denk, C. Waldauf, A. J. Heeger and C. J. Brabec, Adv. Mater., 2006, 18, 789–794.
44. Z. Zheng, H. Yao, L. Ye, Y. Xu, S. Zhang and J. Hou, Mater. Today, 2020, 35, 115–130.
45. A. Mahmood, S. U.-D. Khan and U. A. Rana, J. Comput. Electron., 2014, 13, 1033–1041.
46. M. Ans, J. Iqbal, Z. Ahmad, S. Muhammad, R. Hussain, B. Eliasson and K. Ayub, ChemistrySelect, 2018, 3, 12797–12804.
47. M. E. Köse, J. Phys. Chem. A, 2012, 116, 12503–12509.
48. A. Dkhissi, Synth. Met., 2011, 161, 1441–1443.
49. Q. ul Ain, R. A. Shehzad, U. Yaqoob, A. Sharif, Z. Sajid, S. Rafiq, S. Iqbal, M. Khalid and J. Iqbal, Comput. Theor. Chem., 2021, 1200, 113238.
50. (a) M. J. Frisch, F. R. Clemente, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino and G. Zhe, 2009, pp. 20–44; (b) M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian Inc., Wallingford, CT, 2009, vol. 27, p. 34.51.
51. C. B. Martin, C. Vandehoef and A. Cook, J. Chem. Educ., 2015, 92, 1364–1368.
52. B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 405–410.
53. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
54. C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675.
55. V. S. Bryantsev, M. S. Diallo, A. C. T. van Duin and W. A. Goddard, J. Chem. Theory Comput., 2009, 5, 1016–1026.
56. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
57. M. U. Khan, J. Iqbal, M. Khalid, R. Hussain, A. A. C. Braga, M. Hussain and S. Muhammad, RSC Adv., 2019, 9, 26402–26418.
58. M. N. Arshad, I. Shafiq, M. Khalid and M. A. Asiri, ACS Omega, 2021, 7, 11606–11617.
59. M. U. Khan, M. Y. Mehboob, R. Hussain, R. Fatima, M. S. Tahir, M. Khalid and A. A. C. Braga, J. Phys. Org. Chem., 2021, 34, e4119.

---

Footnote

† Electronic supplementary information (ESI) available: 2D structures with their IUCAP names, Cartesian co-ordinates and UV-vis data (wave lengths, excitation energies and oscillator strengths) were calculated using B3LYP/6-31G (d,p) for the studied compounds and are represented in the ESI data file. See DOI: https://doi.org/10.1039/d2ra04473k

---