 Open Access Article
Open Access ArticleThe crystal structures, phase stabilities, electronic structures and bonding features of iridium borides from first-principles calculations†
Jinquan Zhanga,
Yuanyuan Jin*a,
Chuanzhao Zhang *a,
Yanqi Wanga,
Libiao Tanga,
Song Lia,
Meng Ju
*a,
Yanqi Wanga,
Libiao Tanga,
Song Lia,
Meng Ju b,
Jingjing Wang
b,
Jingjing Wang c,
Weiguo Sun
c,
Weiguo Sun d and
Xilong Doue
d and
Xilong Doue
aDepartment of Physics and Optoelectronic Engineering, Yangtze University, Jingzhou 434023, China. E-mail: scujyy@163.com; zcz19870517@163.com
bSchool of Physical Science and Technology, Southwest University, Chongqing 400715, China
cCollege of Computer and Information Engineering, Hubei Normal University, Huangshi 435002, China
dCollege of Physics and Electronic Information, Luoyang Normal University, Luoyang 471022, China
eInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
First published on 14th April 2022
Abstract
We present results of an unbiased structure search for the lowest energy crystalline structures of various stoichiometric iridium borides, using first-principles calculations combined with particle swarm optimization algorithms. As a result, besides three stable phases of C2/m-Ir3B2, Fmm2-Ir4B3, and Cm-Ir4B5, three promising metastable phases, namely, P21/m-Ir2B, P21/m-IrB, and Pnma-Ir3B4, whose energies are within 20 meV per atom above the convex hull curve, are also identified at ambient pressure. The high bulk modulus of 301 GPa, highest shear modulus of 148 GPa, and smallest Poisson's ratio of 0.29 for C2/m-Ir3B2 make it a promising low compressible material. C2/m-Ir3B2 is predicted to possess the highest Vickers hardnesses, with a Vickers hardness of 13.1 GPa and 19.4 GPa based on Chen's model and Mazhnik-Oganov's model respectively, and a high fracture toughness of 5.17 MPa m0.5. The anisotropic indexes and the three-dimensional surface constructions of Young's modulus indicate that Ir–B compounds are anisotropic with the sequence of the elastic anisotropy of Ir2B > IrB > Ir4B5 > Ir3B4 > Ir4B3 > Ir3B2. Remarkably, these iridium borides are all ductile. We further find that the four Ir–B phases of P21/m-Ir2B, C2/m-Ir3B2, P21/m-IrB, and Fmm2-Ir4B3 possess dominant Ir–B covalent bonding character, while strong B–B and Ir–B covalent bonds are present in Cm-Ir4B5 and Pnma-Ir3B4, which are responsible for their excellent mechanical properties.
1 Introduction
With increasing demands for hard materials in industrial applications and the strict requirements in complex environments, transition metal borides have become the most important industrial materials because of their excellent wear resistance, ultra-incompressibility, high hardness, and high melting point.1–8 Previous experimental studies have shown that many transition metal borides such as ReB2 (ref. 9) (48 GPa), OsB2 (ref. 10) (35.2 GPa), CrB4 (ref. 11) (48 GPa), WB4 (ref. 12) (43.3 GPa), and MnB4 (ref. 13) (37.4 GPa) have high hardness and can be synthesized under normal or low relative pressure through arc melting, making their production cost lower and easier to expand. Notably, the combination of structure searching algorithms with first principles calculations, play a key role in understanding the origin of high hardness and in accelerating the discovery of some hard materials.14–18Crystal structure search has been widely applied to predict binary hard and superhard materials (i.e. compounds with Vickers hardness > 40 GPa) because it can search for a series of stable and metastable phases only with given components, which provides a powerful tool for the systematic exploration of binary transition metal borides.19 Therefore, previous researchers have systematically studied many binary transition metal borides by using structure search to find some borides with high hardness and fully understand the thermodynamic properties of the system.20–25 Although previous researchers have done a lot of research on the Y–B binary system for a long time, Ding et al. used CALYPSO to systematically study Y–B system and found a new stable phase R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m-YB6 with the hardness of about 37 GPa. Besides, they also found that the previously high-temperature synthesized YB4 is in metastable phase in the Y–B system.21 In addition, the systematic study of the compounds can also guide subsequent experiments and solve the uncertainty of boride structure caused by the difficulty in determining the position of lighter boron atoms in experiments. For example, A. N. Kolmogorov et al. have systematically studied the Fe–B system20 and found that the orthogonal structure oP10-FeB4 is metastable above the convex hull curve, which indicates that this compound may be stable at finite temperature. Subsequent high-temperature experiments show that orthogonal phase FeB4 is a potential superconductor and superhard material, and its hardness is 43–70 GPa.26 Recent theoretical studies using USPEX, a global crystal structure search technique, have systematically studied the W–B system and have predicted a new stable compound, superhard tungsten pentaboride WB5, suggesting that the long-debated “WB4” and the newly predicted WB5 are actually the same material.16,24 This finding better resolves the previous controversy over the structure of WB4. Ir and Os are neighboring 5d transition metals in the periodic table and both have similar electronegativity, so Ir–B compounds were also considered as potential high hardness materials after the discovery of superhard OsB2. Although previous theoretical and experimental studies have been carried out on the Ir–B system, the data on electronic properties and metastable phases of Ir–B compounds are quite limited, especially those close to convex hull curves of iridium boride, which may still have some problems in the study of metastable phases synthesized at high temperature.
m-YB6 with the hardness of about 37 GPa. Besides, they also found that the previously high-temperature synthesized YB4 is in metastable phase in the Y–B system.21 In addition, the systematic study of the compounds can also guide subsequent experiments and solve the uncertainty of boride structure caused by the difficulty in determining the position of lighter boron atoms in experiments. For example, A. N. Kolmogorov et al. have systematically studied the Fe–B system20 and found that the orthogonal structure oP10-FeB4 is metastable above the convex hull curve, which indicates that this compound may be stable at finite temperature. Subsequent high-temperature experiments show that orthogonal phase FeB4 is a potential superconductor and superhard material, and its hardness is 43–70 GPa.26 Recent theoretical studies using USPEX, a global crystal structure search technique, have systematically studied the W–B system and have predicted a new stable compound, superhard tungsten pentaboride WB5, suggesting that the long-debated “WB4” and the newly predicted WB5 are actually the same material.16,24 This finding better resolves the previous controversy over the structure of WB4. Ir and Os are neighboring 5d transition metals in the periodic table and both have similar electronegativity, so Ir–B compounds were also considered as potential high hardness materials after the discovery of superhard OsB2. Although previous theoretical and experimental studies have been carried out on the Ir–B system, the data on electronic properties and metastable phases of Ir–B compounds are quite limited, especially those close to convex hull curves of iridium boride, which may still have some problems in the study of metastable phases synthesized at high temperature.
For Ir–B system, iridium boride films with fractional stoichiometric ratios have attracted much attention due to their super-hard properties. Recently, iridium borides have attracted much attention because it is reported that IrB1.35 has Vickers hardness of 49.8–18.2 GPa under a load of 0.49 and 9.81 N, respectively, which is potential superhard material.27 Later, IrB1.1 film (0.4 μm) was deposited on a silicon dioxide substrate by pulse deposition technology, with Vickers hardness as high as 43 GPa.28 Subsequently, Zeilinger et al.22 and Wang et al.23 systematically studied the Ir–B phase diagram and the mechanical properties of the stable phase on the convex hull curve. In 2016, two groups successfully used a mechanochemical approach to synthesize two new iridium borides, namely, IrB2 and IrB, and found that IrB and IrB2 ceramic nanopowders may be an active catalyst material.29,30 However, these two newly discovered borides have been proved to be metastable phases close to the convex hull curve. Previous systematic studies and synthesis of many metastable phases in Ir–B system have fully demonstrated that the study of metastable phases in Ir–B systems is very important. These metastable phases can usually be synthesized by selecting suitable precursors and controlling the quenching rate. However, no independent search for potential metastable structures of Ir–B system beyond known structure types has been performed to date, and there has been no systematic study of their mechanical properties, elastic anisotropy, bonding nature, and hardness. The goal of this work is to address these deficiency.
To find stable and metastable compounds that may not have been previously observed experimentally or computationally, we performed here an extensive study on binary iridium borides using the Crystal Structure Analysis by Particle Swarm Optimization (CALYPSO)31,32 method in combination with first-principles calculations. Finally, we reproduce the previously reported three stable structures and find three metastable structures that may be synthesized at high temperature, and comprehensively explore the structural characteristics and intrinsic physical properties of these structures from the microscopic level.
2 Computational methods
To comprehensively search for the stable and metastable structures in the Ir–B binary system under atmospheric pressure, our structure-searching simulations are based on a particle swarm optimization algorithm in conjunction with ab initio total-energy calculations, as conducted in CALYPSO code.31,32 The significant feature of this code is that it can quickly predict the most stable and metastable 2D and 3D solid-state structures only requiring chemical compositions of a given compound at given external conditions and the superior efficiency of this methodology has been verified on various systems, spanning from elements to binary and ternary compounds.33–37 Our structural searches with system sizes containing 1–6 formula units (f.u.) per simulation cell were performed for stoichiometries IrmBn varying from Ir3B to IrB3.All the following structural relaxations and electronic structure calculations were carried out with the utilization of density functional theory within the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional as implemented in the Vienna ab initio simulation package (VASP).38,39 The electron–ion interaction was described via a projector augmented wave (PAW) potentials with 5d76s2 and 2s22p1 valence electron for Ir and B, respectively.40 A plane wave cutoff energy of 600 eV and proper Monkhorst–Pack k-meshes were selected to guarantee that all the enthalpy calculations were well converged to better than 1 meV per atom.41–43 To probe into the dynamical stability of IrmBn compositions, the phonon dispersion curves were calculated through the direct supercell approach as implemented in the Phonopy code.44 In addition, the electron localization function (ELF)45 and Bader charge46 were also computed within the VASP code. To analyze the interatomic interaction and chemical bonding, the crystal orbital Hamilton populations (COHP) were calculated using the LOBSTER.47 The independent single-crystal elastic constants could be ascertained on the basis of the stress tensor generated by employing a small strain to an optimized unit cell. Furthermore, the bulk modulus (B), shear modulus (G), Young's modulus (E), and Poisson's ratio (ν) were thus determined by the Voigt–Reuss–Hill (VRH) approximation.48 Vickers hardness was estimated according to the Chen49 (HCv (GPa)) and Mazhnik-Oganov50 (HMOv (GPa)) models. Fracture toughness was calculated using the empirical Mazhnik-Oganov model (KIC).
Finally, for the purpose of fully describing the elastic anisotropy behavior of the considered structure in the Ir–B binary system, we constructed the three-dimensional model of Young's modulus by using the elastic anisotropy measurement (ElasticPOST) program.51
3 Results and discussion
3.1 Crystal structures and stability
To determine the stable and metastable phases of Ir–B compounds at ambient pressure, we have implemented structure searches using the CALYPSO method on iridium borides with various IrmBn compositions at considered pressures of 1 atm. This crystal structure search successfully reproduces the experimental structures of Pnma-IrB and P63/mmc-IrB2 as the lowest ground state energy phases and the other theoretical ground phases of C2/m-Ir3B2, Fmm2-Ir4B3, and Cm-Ir4B5, thus providing important support for the reliability of the present structure searches.22,23,29 Negative formation enthalpy shows that the synthesis of the substance through the reference phase is an exothermic process, and the exothermic reaction is easy to occur in nature. The formation enthalpies can be calculated with the following equation:
 | (1) |
Herein, ΔH is the formation enthalpy per atom for a compound of this stoichiometry, E(IrxBy) is the total energy per formula unit of the compound, and E(Ir) and E(B) represent the Ir and B ground states with the cubic phase52 (space group: Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and α-rhombohedral strcutue,53 respectively. Subsequently, we use the formation enthalpy to evaluate the thermodynamic stability of iridium borides. The calculated lattice parameters, cell volume, total energy and formation enthalpy for the lowest energy structures and the selected metastable structures of each considered stoichiometry of the Ir–B system are tabulated in Table 1, in company with the previously experimental and theoretical results. On the basis of the formation enthalpies, the convex hull of the Ir–B binary system under atmospheric pressure is constructed as displayed in Fig. 1. The whole structural information for the lowest energy phases of each component considered in the binary Ir–B system under ambient pressure is listed in Table S1 of the ESI.† The convex hull of these points then connects the structures with the lowest formation enthalpies among all stoichiometries, and any structures exactly located on the convex hull are deemed as energetically stable, both against decomposition into other elements or any combination of other binary phases, and thus experimentally synthetic. Furthermore, it should be specially pointed out that vibration effects may modify the convex hull curve at high temperatures, bringing out some structures that slightly deviate from the convex hull and approach to the convex hull. Therefore, it is extremely important to probe into not only the stable phases on the convex hull in Fig. 1, but also the metastable phases close to the convex hull curve. As presented in Fig. 1, it is obviously found that the convex hull of Ir–B binary system contains three stable phases indicated as Ir3B2 (C2/m), Ir4B5 (Fmm2), and Ir4B5 (Cm). Besides the stable structures on the convex hull, three metastable phases, Ir2B (P21/m), IrB (P21/m), and Ir3B4 (Pnma), are very close to the convex hull curve, whose energies are 15 meV per atom, 17 meV per atom and 16 meV per atom above the convex hull curve, respectively. These three metastable phases near the convex hull curve were discovered for the first time and may be synthesized at high temperature.25 We below focus on the structural, mechanical and anisotropy, and electronic properties, bonding characters and hardness for these six considered crystals.
m) and α-rhombohedral strcutue,53 respectively. Subsequently, we use the formation enthalpy to evaluate the thermodynamic stability of iridium borides. The calculated lattice parameters, cell volume, total energy and formation enthalpy for the lowest energy structures and the selected metastable structures of each considered stoichiometry of the Ir–B system are tabulated in Table 1, in company with the previously experimental and theoretical results. On the basis of the formation enthalpies, the convex hull of the Ir–B binary system under atmospheric pressure is constructed as displayed in Fig. 1. The whole structural information for the lowest energy phases of each component considered in the binary Ir–B system under ambient pressure is listed in Table S1 of the ESI.† The convex hull of these points then connects the structures with the lowest formation enthalpies among all stoichiometries, and any structures exactly located on the convex hull are deemed as energetically stable, both against decomposition into other elements or any combination of other binary phases, and thus experimentally synthetic. Furthermore, it should be specially pointed out that vibration effects may modify the convex hull curve at high temperatures, bringing out some structures that slightly deviate from the convex hull and approach to the convex hull. Therefore, it is extremely important to probe into not only the stable phases on the convex hull in Fig. 1, but also the metastable phases close to the convex hull curve. As presented in Fig. 1, it is obviously found that the convex hull of Ir–B binary system contains three stable phases indicated as Ir3B2 (C2/m), Ir4B5 (Fmm2), and Ir4B5 (Cm). Besides the stable structures on the convex hull, three metastable phases, Ir2B (P21/m), IrB (P21/m), and Ir3B4 (Pnma), are very close to the convex hull curve, whose energies are 15 meV per atom, 17 meV per atom and 16 meV per atom above the convex hull curve, respectively. These three metastable phases near the convex hull curve were discovered for the first time and may be synthesized at high temperature.25 We below focus on the structural, mechanical and anisotropy, and electronic properties, bonding characters and hardness for these six considered crystals.
| Phase | Space group | a (Å) | b (Å) | c (Å) | V (Å3) | Total energy | ΔH |
|---|---|---|---|---|---|---|---|
| Ir3B | P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 m2 |
2.794 | 2.794 | 7.512 | 50.776 | −8.386 | −0.073 |
| Ir2B | P21/m | 5.699 | 2.803 | 4.736 | 74.600 | −8.297 | −0.163 |
| Cmcm22 | 2.783 | 4.833 | 10.764 | 144.777 | −8.278 | −0.143 | |
| Ir3B2 | C2/m | 7.500 | 2.860 | 8.605 | 119.573 | −8.205 | −0.214 |
| Ir4B3 | Fmm2 | 5.659 | 5.731 | 10.020 | 324.942 | −8.154 | −0.224 |
| Ir5B4 | P63/mmc | 3.521 | 3.521 | 18.957 | 203.535 | −8.077 | −0.181 |
| IrB | P21/m | 6.723 | 3.926 | 3.555 | 92.714 | −7.990 | −0.214 |
| Pnma29 | 4.421 | 2.863 | 7.026 | 88.927 | −7.990 | −0.214 | |
| Cmcm | 4.036 | 5.850 | 3.926 | 92.694 | −7.990 | −0.213 | |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m222 m222 |
3.051 | 3.051 | 2.713 | 21.876 | −7.966 | −0.190 | |
| Ir4B5 | Cm | 10.623 | 2.902 | 12.373 | 189.252 | −7.894 | −0.236 |
| Ir3B4 | Pnma | 16.266 | 2.962 | 6.028 | 290.436 | −7.832 | −0.208 |
| Ir2B3 | P63/mmc | 3.124 | 3.124 | 12.184 | 102.992 | −7.695 | −0.132 |
| IrB2 | C2/m | 7.422 | 2.856 | 5.898 | 115.360 | −7.544 | −0.125 |
| Pnma | 3.151 | 4.543 | 4.040 | 57.825 | −7.540 | −0.121 | |
| Pmmn56 | 5.586 | 2.983 | 6.818 | 113.619 | −7.515 | −0.095 | |
| P63/mmc29 | 3.075 | 3.075 | 7.054 | 57.767 | −7.471 | −0.052 | |
| Ir2B5 | R3m | 2.976 | 2.976 | 24.747 | 189.793 | −7.347 | −0.030 |
| IrB3 | Pnma22 | 2.923 | 2.923 | 4.652 | 34.417 | −7.275 | −0.034 |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 m2 |
9.875 | 3.126 | 4.571 | 141.075 | −7.242 | −0.001 |
 | ||
| Fig. 1 The predicted formation enthalpy with respect to solid Ir and B for various Ir–B stoichiometries under atmospheric pressure. The solid line represents the ground state convex hull. | ||
Starting from the phase with low boron content, each phase is discussed separately. For Ir2B, the orthogonal Cmcm phase is considered to be the ground state phase by previous theory. By our method, we have reconstructed the orthogonal Cmcm phase well.23 Interestingly, our present calculations uncover a new crystal P21/m-Ir2B, which is 0.019 eV per atom lower than the former. From Fig. 2a, each B atom is bonded with six Ir atoms, forming a trigonal prism (Ir6B). By stacking the Ir6B building blocks in the way of sharing one edge of the trigonal prism, the trigonal-prism chain is constructed. In the connected Ir6B triangular prism, the Ir–B bond lengths vary between 2.14 and 2.20 Å, which is close to the strong covalent Ir–B bond of P63/mmc-IrB4 (ref. 54) (2.189 Å), stating that there exists a strong covalent bond between Ir and B in P21/m-Ir2B. Furthermore, the distance of the nearest B–B bonds is 4.6 Å, showing that there is no B–B interaction. For the stable C2/m-Ir3B2 polycrystal (see Fig. 2b), there are two layers of iridium atoms along the c-axis sandwiched with a double layer of graphite-like Ir/B rings. In the connected bilayer graphite-like Ir/B rings, the Ir–B distances range from 2.15 Å to 2.19 Å are close to that of the potential hard materials m-IrB2 (2.18 Å) with a theoretical Vickers hardness of 13.82 GPa.55
As shown in Fig. 2c, it is worth noting that the Fmm2-Ir4B3 structure has an alternating layered arrangement structure of B–Ir–B–Ir along the c-axis, and the layers are connected by Ir6B prism building blocks. In the alternating B–Ir–B–Ir layers, the distances between the nearest Ir–B bonds are all less than the sum (2.25 Å) of covalent radii of the B atom (rB = 0.84 Å) and Ir atom (rIr = 1.41 Å). In particular, the minimum distance between B–B bonds is 4.03 Å, which is much larger than the possible bonding distance.
Subsequently, for IrB with a stoichiometric ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, previous theoretical calculations report three thermodynamically stable structures (Pnma,56 Cmcm,22 and P
1, previous theoretical calculations report three thermodynamically stable structures (Pnma,56 Cmcm,22 and P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 (ref. 23)). Intriguingly, the present calculations uncover a novel ground state phase P211/m-IrB, whose formation enthalpy is about 0.024 eV per atom lower than that of the P
m2 (ref. 23)). Intriguingly, the present calculations uncover a novel ground state phase P211/m-IrB, whose formation enthalpy is about 0.024 eV per atom lower than that of the P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2-IrB phase, as summarized in Table 1. Surprisingly, the formation enthalpy of the P21/m-IrB structure is closely equal to that of Pnma-IrB synthesized in the above experiments at ambient pressure or Cmcm-IrB. As displayed in Fig. 2d, the P21/m-IrB crystal is composed of the twisted eight-membered ring formed by the alternating connection of Ir and B atoms. In an eight-membered ring, the maximum distance of Ir–B on the eight sides is 2.17 Å, and the minimum distance is 2.11 Å. The average Ir–B bond length of the P21/m-IrB is smaller than Ir–B (2.16 Å) covalent bonds in the Pnma-IrB under ambient pressure, indicating relatively strong Ir–B interactions.
m2-IrB phase, as summarized in Table 1. Surprisingly, the formation enthalpy of the P21/m-IrB structure is closely equal to that of Pnma-IrB synthesized in the above experiments at ambient pressure or Cmcm-IrB. As displayed in Fig. 2d, the P21/m-IrB crystal is composed of the twisted eight-membered ring formed by the alternating connection of Ir and B atoms. In an eight-membered ring, the maximum distance of Ir–B on the eight sides is 2.17 Å, and the minimum distance is 2.11 Å. The average Ir–B bond length of the P21/m-IrB is smaller than Ir–B (2.16 Å) covalent bonds in the Pnma-IrB under ambient pressure, indicating relatively strong Ir–B interactions.
At 1 < B/Ir < 2, the 1D B-ribbons are adopted by the lowest-energy structures of Cm-Ir4B5 and the metastable structure of Pnma-Ir3B4 at zero temperature, as shown in Fig. 2e and f. The distances between B–B bonds are respectively 2.00 Å and 2.02 Å in the 1D B-ribbons, which are very close to that of the potential hard materials C2/m-VB3 of B–B bond distance (1.764–1.912 Å), indicating the existence of a strong B–B bond.57 Besides the 1D B-ribbons, we also found the graphene-like B-sheet with short sides of 1.89 Å and long sides of 2.00 Å in Cm-Ir4B5, which is shorter than the high-pressure synthesis of β-Ir4B5 (2.122 Å).58
In general, it is worth noting that the distances of the nearest neighbor Ir–B bonds in these six considered structures are all smaller than the sum (2.25 Å) of the covalent radii of the B atom (rB = 0.84 Å) and the Ir atom (rIr = 1.41 Å), demonstrating the strong covalent bonding between Ir and B in these six considered phases. However, with increasing B concentration, the number of Ir–B covalent bonds decreases, and strong B–B covalent bonds gradually appear for borides with 1 < B/Ir < 2.
As we all know, a crystal is dynamically stable if its potential energy always increases against any combinations of atomic displacements in the equilibrium state, which is given by:  In other words, this is equivalent to the condition that all phonons have real and positive frequencies. Phonons reflect the quantized properties of lattice vibration energy, which can be measured by phonon dispersion curve and phonon density of states.59–62 Therefore, to clarify the dynamical stabilities of these six considered phases, their phonon spectra and phonon density of states were also calculated, as depicted in Fig. 3. From Fig. 3, it can be obviously found that there are no virtual phonon frequencies in the entire Brillouin zone, which proves that these six considered crystals are dynamically stable under environmental pressure. Moreover, the phonon bands for these six considered phases can be divided into two independent regions: the high-frequency mode mainly corresponds to the vibration of the boron atoms, while the low-frequency region is mainly related to the vibration of iridium atoms. This phenomenon stems from the larger atomic mass of the iridium atom than that of the boron atom.
In other words, this is equivalent to the condition that all phonons have real and positive frequencies. Phonons reflect the quantized properties of lattice vibration energy, which can be measured by phonon dispersion curve and phonon density of states.59–62 Therefore, to clarify the dynamical stabilities of these six considered phases, their phonon spectra and phonon density of states were also calculated, as depicted in Fig. 3. From Fig. 3, it can be obviously found that there are no virtual phonon frequencies in the entire Brillouin zone, which proves that these six considered crystals are dynamically stable under environmental pressure. Moreover, the phonon bands for these six considered phases can be divided into two independent regions: the high-frequency mode mainly corresponds to the vibration of the boron atoms, while the low-frequency region is mainly related to the vibration of iridium atoms. This phenomenon stems from the larger atomic mass of the iridium atom than that of the boron atom.
3.2 Mechanical stabilities, mechanical properties and hardness
Elastic properties (such as elastic constants, elastic modulus, etc.) are essential for us to understand the deformation behavior of solids under the action of external forces, and can provide a deeper understanding of the macroscopic mechanical behavior, which is helpful to evaluate the mechanical properties of materials. The elastic constants of six considered phases were computed from the strain–stress method, along with previous results, which are collected in Table 2. The obtained elastic constants of C2/m-Ir3B2, Fmm2-Ir4B3 and Cm-Ir4B5 in Table 2, as well as the calculated bulk modulus, B, shear modulus, G, and Young's modulus, E, as listed in Table 3, are in good agreement with other available theoretical results, suggesting that the calculations in the present work are reasonable.22,23| Phase | Space group | C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ir2B | P21/m | 522 | 540 | 516 | 169 | 46 | 68 | 150 | 143 | 198 |
| Ir3B2 | C2/m | 475 | 490 | 481 | 174 | 184 | 130 | 206 | 249 | 180 |
| Ir3B2 | C2/m22 | 479 | 507 | 479 | 128 | 171 | 200 | 202 | 248 | 180 |
| Ir4B3 | Fmm2 | 473 | 603 | 456 | 90 | 93 | 119 | 176 | 199 | 228 |
| Ir4B3 | Fmm2 (ref. 22) | 486 | 655 | 473 | 96 | 101 | 112 | 165 | 215 | 185 |
| IrB | P21/m | 291 | 297 | 338 | 139 | 123 | 103 | 127 | 218 | 163 |
| P1-IrB | Pnma56 | 514 | 368 | 438 | 55 | 227 | 106 | 108 | 333 | 183 |
| Ir4B5 | Cm | 474 | 424 | 518 | 88 | 167 | 76 | 161 | 216 | 158 |
| Ir4B5 | Cm23 | 494 | 438 | 514 | 85 | 104 | 166 | 131 | 213 | 153 |
| Ir4B5 | Cm16 | 519 | 459 | 548 | 112 | 178 | 88 | 150 | 218 | 177 |
| α-Ir4B5 | C2/m58 | 373 | 303 | 303 | 50 | 125 | 58 | 150 | 160 | 217 |
| β-Ir4B5 | Pnma58 | 482 | 390 | 433 | 112 | 102 | 60 | 170 | 122 | 250 |
| Ir3B4 | Pnma | 577 | 419 | 588 | 75 | 148 | 76 | 130 | 168 | 232 |
| IrB2 | P63/mmc56 | 326 | 705 | 124 | 198 | 248 |
| Phase | Space group | B | G | E | B/G | ν | VED | HCv | HMOv | KIC |
|---|---|---|---|---|---|---|---|---|---|---|
| Ir2B | P21/m | 255 | 96 | 256 | 2.66 | 0.33 | 0.563 | 6.2 | 14.0 | 3.66 |
| Ir3B2 | C2/m | 301 | 148 | 381 | 2.04 | 0.29 | 0.552 | 13.1 | 19.4 | 5.67 |
| Ir3B2 | C2/m22 | 302 | 150 | 386 | ||||||
| Ir4B3 | Fmm2 | 303 | 118 | 314 | 2.57 | 0.33 | 0.554 | 7.7 | 17.2 | 6.15 |
| Ir4B3 | Fmm2 (ref. 22) | 303 | 127 | 335 | ||||||
| IrB | P21/m | 192 | 81 | 213 | 2.38 | 0.32 | 0.518 | 6.5 | 10.7 | 3.37 |
| P1-IrB | Pnma56 | 274 | 124 | 323 | 2.21 | 0.540 | ||||
| Ir4B5 | Cm | 274 | 112 | 297 | 2.44 | 0.32 | 0.539 | 10.6 | 17.1 | 5.18 |
| Ir4B5 | Cm22 | 269 | 125 | 325 | ||||||
| α-Ir4B5 | C2/m58 | 225 | 63 | 180 | 0.37 | 4.5 | ||||
| β-Ir4B5 | Pnma58 | 265 | 99 | 266 | 0.33 | 8.5 | ||||
| Ir3B4 | Pnma | 290 | 120 | 316 | 2.42 | 0.32 | 0.537 | 8.7 | 17.0 | 5.78 |
| IrB2 | P63/mmc56 | 283 | 113 | 299 | 2.50 |
In addition, the mechanical stability of a crystal can be assessed through elastic constants. As summarized in Table 2, all the six considered phases meet the respectively mechanical stability criterion, suggesting the mechanical stabilities for these six considered structures under ambient pressure. Moreover, the C11, C22, and C33 values of six crystals (except P21/m-IrB) can be compared with that of the potential superhard material TiB2 (39.6 GPa),63 which implies that these five substances have larger incompressibility along the a-, b-, and c-axes. In general, the elastic constant C44 is related to the resistance to shear deformation and most important parameter that indirectly determines the hardness of solid indentation.64 Second, it can be found that C2/m-Ir3B2 has the largest C44, which is much larger than the theoretical values of P1–IrB, α-Ir4B5, β-Ir4B5 and P63/mmc-IrB2 synthesized experimentally, indicating that it exhibits higher hardness than the other iridium borides.
Materials with high bulk modulus usually have strong resistance to uniform compression. As shown in Table 3, the calculated bulk modulus ranges from 192 to 303 GPa, close to that of common hard materials such as ZrB2 (220–245 GPa)65 and TiB2 (261 GPa),63 but less than that of superhard materials ReB2 (383 GPa),9 and WB4 (553 GPa),12 indicating their strong ability to resist volume deformation. Among all the Ir–B compounds, C2/m-Ir3B2 and Fmm2-Ir4B3 have the highest bulk modulus (∼300 GPa), which is larger than the theoretical values of P1-IrB, α-Ir4B5, β-Ir4B5 and P63/mmc-IrB2 reported by experiments, indicating that these two materials have the best incompressibility in Ir–B system. It is worth noting that some previous studies have shown that the bulk modulus may be directly related to the valence electron density (VED).66 As for the iridium boride compounds, it appears that the general trend of the bulk modulus is consistent with that of VED (except for P21/m-Ir2B) and the bulk modulus increases gradually with increasing VED.
Generally speaking, the larger value of the shear modulus also indicates that the orientation bonds between atoms are more obvious.67 It is well known that the shear modulus of a material quantifies its resistance to shear deformation and is a more relevant predictor of material hardness than bulk modulus. The shear modulus of C2/m-Ir3B2 is 148 GPa, which is close to that of hard superconducting material NbN68 (159.9 GPa) and larger than that of other Ir–B compounds. It is expected that Ir3B2 will resist shear strain to a large extent and has higher hardness than other Ir–B compounds.
Young's modulus, called the tensile modulus, is defined as the ratio of tensile stress to tensile strain in the elastic (linear) part of the stress–strain curve. When the value is large, the material is stiffer. The Young's modulus is also an important parameter for measuring the stiffness of a material in addition to the bulk modulus and shear modulus. When the value is large, the material is stiffer. From Table 3, the Young's modulus (381 GPa) of C2/m-Ir3B2 is the highest, comparable to that of the well-known hard material ZrC,69 indicating that C2/m-Ir3B2 has a higher hardness than the other Ir–B compounds. Poisson's ratio is an important parameter to describe the degree of directionality for the covalent bonding. Of all the phases considered, the C2/m-Ir3B2 has the smallest Poisson's ratio, which suggests that strong directional bonding exists in it and thus could be a potentially hard material. All of these excellent mechanical properties strongly suggest that C2/m-Ir3B2 is a potential candidate for hard material.
According to the standard of Pugh,70 the toughness or brittle behavior of a solid can be estimated by the value of B/G. If B/G > 1.75, the material shows toughness and vice versa, if B/G < 1.75, the material shows brittleness. In the current situation, the B/G values of several compounds are all higher than 1.75. Therefore, these six compounds exhibit toughness behavior.
The hardness of a material is an important parameter to evaluate the performance of a material, especially in industries such as cutting. As shown in Table 3, the C2/m-Ir3B2 has the highest hardness, regardless of the use of either Chen's model or Mazhnik-Oganov's model. It can be seen that the calculated theoretical hardness of the C2/m-Ir3B2 is 13.1 and 19.4 GPa based on Chen's model and Mazhnik-Oganov's model, which is close to that of commonly used hard materials like, for example, RuB21 (15.1 GPa) or Al2O371 (17.8 GPa). It is consistent with result predicted from the elastic constant C44, shear modulus and Young's modulus. The fracture toughness of Fmm2-Ir4B3, Pnma-Ir3B4 and C2/m-Ir3B2 are 6.15 MPa m0.5, 5.78 MPa m0.5, and 5.67 MPa m0.5, respectively, which is higher than that of WC72 (5.37 MPa m0.5). The results show that Fmm2-Ir4B3, Pnma-Ir3B4 and C2/m-Ir3B2 have strong resistance to fracture propagation.
3.3 Anisotropy properties
Elastic anisotropy is an important physical property of materials. It not only plays a vital role in technical and industrial applications, but also reflects the arrangement of atoms along the corresponding direction to a certain extent. The general elastic anisotropy index and the anisotropy percentage of crystals with any symmetry are defined as follows:73
 | (2) |
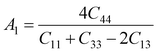 | (3) |
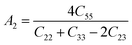 | (4) |
 | (5) |
For an isotropic solid, its AU is zero. The degree of anisotropy is shown by the deviation from zero. The greater the deviation from zero, the higher the degree of anisotropy of the material. In addition, the shear anisotropy constant can reflect the anisotropy of solids on different planes. For isotropic crystals, the values of A1, A2, and A3 are equal to 1, and for any crystal less than or greater than 1, the degree of shear anisotropy of the crystal is indicated. Both the anisotropy index and the shear anisotropy factor are listed in Table 4.
| Phase | Space group | AU | A1 | A2 | A3 |
|---|---|---|---|---|---|
| Ir2B | P21/m | 5.51 | 0.90 | 0.28 | 0.36 |
| Ir3B2 | C2/m | 0.27 | 1.52 | 1.20 | 0.94 |
| Ir4B3 | Fmm2 | 0.45 | 0.57 | 0.79 | 0.66 |
| IrB | P21/m | 3.60 | 2.88 | 1.59 | 1.23 |
| Ir4B5 | Cm | 1.24 | 0.63 | 1.07 | 0.53 |
| Ir3B4 | Pnma | 0.96 | 0.36 | 1.09 | 0.41 |
For Ir–B compounds, the index AU order in Table 4 is Ir2B > IrB > Ir4B5 > Ir3B4 > Ir4B3 > Ir3B2. The results show that among Ir–B compounds, Ir2B has the highest elastic anisotropy, while Ir3B2 has the lowest elastic anisotropy. For the shear anisotropy constant, the values of the parameters A1, A2, and A3 indicate that the anisotropy of Ir–B depends on the direction. Ir2B has the largest absolute values (1 − A2) and (1 − A3), while Ir3B2 and Ir4B3 have smaller absolute values. This indicates that Ir–B compounds have the strongest anisotropy on the (010) and (001) planes, while Ir3B2 and Ir4B3 have the opposite results. For the Ir2B compound, the value of A1 is close to 1. This shows that Ir2B is isotropic along the (100) plane. In addition, Ir3B2 also exhibits isotropy on the (001) plane.
The three-dimensional surface model can more intuitively describe the anisotropic behavior of solid elasticity. The three-dimensional pattern of the reciprocal direction dependence of Young's modulus of the Ir–B compounds is different due to its different crystal structure. For different crystal structures of Ir–B compounds, there are different expressions for the constructing surfaces of Young's modulus.74
For monoclinic structure,
 | (6) |
 | (7) |
Sijs are the elastic compliance constants and are shown in Table S2.† Fig. 4 displays the constructing surfaces for Young's modulus. The isotropic system will display a 3-dimensional sphere. The greater the deviation from the sphere, the higher the degree of anisotropy. In Fig. 4a, the 3D surface structure of Ir2B is longer along the y axis than other compounds, while the surface structure along the x and z axes is more compressed than other compounds. The results show that the monoclinic structure of Ir2B has the highest degree of anisotropy. In Fig. 4b, the 3D surface structure of the monoclinic Ir3B2 is closest to the sphere among all the structures, indicating that the anisotropy of Ir3B2 is the smallest. According to the three-dimensional surface structure, we can summarize the elastic anisotropy order of Ir–B compounds (Ir2B > IrB > Ir4B5 > Ir3B4 > Ir4B3 > Ir3B2). This order is consistent with the result obtained by the anisotropy constant AU.
 | ||
| Fig. 4 Three-dimensional Young's modulus for (a) P2/1/m-Ir2B, (b) C2/m-Ir3B2, (c) Fmm2-Ir4B3 (d) P21/m-IrB, (e) Cm-Ir4B5 and (f) Pnma-Ir3B4 under ambient pressure. | ||
3.4 Electronic properties and chemical bonding
To further analyze the electronic properties of these Ir–B configurations, we calculated their electronic band structure and electronic density of states (DOS) (see Fig. S1† and 5). As shown in the electronic band structure of Fig. S1,† these six phases have a strong overlap between the conduction band and the valence band, showing metallic characteristics. This can also be confirmed by the finite electron density of states of the Fermi level in Fig. 5. Moreover, in Fig. 5b and d–f, a typical feature in the TDOS can be seen that there is a deep valley at Fermi level for these compounds, that is, the presence of a so-called “pseudogap”, which represents a borderline between the bonding and antibonding orbitals.75 The presence of the pseudogap enhances the stability of the compounds. | ||
| Fig. 5 Calculated electronic density of states for (a) P21/m-Ir2B, (b) C2/m-Ir3B2, (c) Fmm2-Ir4B3 (d) P21/m-IrB, (e) Cm-Ir4B5 and (f) Pnma-Ir3B4 under atmospheric pressure. | ||
To gain further insights into the chemical bonding nature in the six considered phases, we calculate the electron localization function (ELF), which can make a description of the bond type between atoms: large ELF values (>0.5) corresponds to the electrons of perfect covalent bonds or lone pairs, while smaller ELF values (<0.5) correspond to ionic or metallic bonds. As seen in Fig. 6, it is worth mentioning that these six crystals display a common feature of the ELF that the high electron localization can be seen between Ir and adjacent B atoms, implying the strong covalent bonding of Ir–B. Besides, from Fig. 6e and f, we can also clearly see high electron localization in regions between adjacent B atoms, which indicated the high covalence of B–B bonding. According to the periodic law, the electronegativity value of the boron element (2.00) is less than the electronegativity value of the iridium element (2.2), which means that the charge should be transferred from the B atom to the Ir atom. Therefore, to analyze the actual charge distribution between B and Ir atoms, we explicitly measure the Bader charges of the B and Ir atoms for all six crystals, as summarized in Table 5. The average of transferred electrons charges from B to the Ir atoms are about 0.3 e, 0.22 e, 0.23 e, 0.41 e, 0.28 e, 0.25 e for P21/m-Ir2B, C2/m-Ir3B2, Fmm2-Ir4B3, P21/m-IrB, Cm-Ir4B5, and Pnma-Ir3B4. Therefore, there is a small amount of charge transfer from B to the Ir atoms, indicating a covalent bonding character.
 | ||
| Fig. 6 ELFs of the (a) P21/m-Ir2B, (b) C2/m-Ir3B2, (c) Fmm2-Ir4B3 (d) P21/m-IrB, (e) Cm-Ir4B5 and (f) Pnma-Ir3B4 (isovalue = 0.65). | ||
| Phase | Space group | Atom | Charge value (e) | δ (e) |
|---|---|---|---|---|
| Ir2B | P21/m | Ir | 9.15 | −0.15 |
| B | 2.70 | 0.30 | ||
| Ir3B2 | C2/m | Ir | 9.15 | −0.15 |
| B | 2.78 | 0.22 | ||
| Ir4B3 | Fmm2 | Ir | 9.17 | −0.17 |
| B | 2.77 | 0.23 | ||
| IrB | P21/m | Ir | 9.41 | −0.41 |
| B | 2.59 | 0.41 | ||
| Ir4B5 | Cm | Ir | 9.35 | −0.35 |
| B | 2.72 | 0.28 | ||
| Ir3B4 | Pnma | Ir | 9.33 | −0.33 |
| B | 2.75 | 0.25 |
Finally, we calculated their integrated-crystal orbital Hamilton populations (ICOHPs) to depict the strength of chemical bonds in the six Ir–B phases by counting the energy-weighted population of wave function between two atomic orbitals (see Table S3†). The calculated ICOHP values (≥−2.28 eV) of Ir–B in the six iridium borides are similar to those of B–B bonds in solid α-B (2.00 Å, −3.49 eV), suggesting that Ir and B form covalent bonds. In addition, for the predicted Cm-Ir4B5 and Pmna-Ir3B4 compounds, the partial bonding states of B–B bonds shown in ICOHP are close to those in solid α-B (2.00 Å, −3.49 eV) and even larger than those in solid α-B (2.00 Å, −3.49 eV). In particular, in Cm-Ir4B5, it is also found that the shortest B–B pairs (1.89 Å) with the ICOHP value of −5.03 eV in graphene-like B sheet is only less than the ICOHP value of −7.72 eV in the smallest distance (1.67 Å) in α-B, which indicates that there is the strongest B–B covalent interaction. This conclusion also demonstrates the validity of the analyses of the Ir–B bond length, ELF, and Bader charge. In other words, the DOS, ELF, Bader charge analyses, and ICOHP all suggest that six phases possess Ir–B covalent bonds. In addition, there are strong B–B interactions in Cm-Ir4B5 and Pnma-Ir3B4.
4 Conclusions
In a word, the lowest energy (or ground state) and low energy metastable structures of various stoichiometric Ir–B compounds have been systematically studied based on particle swarm optimization combined with first-principles calculation. Besides the three known theoretical structures, C2/m-Ir3B2, Fmm2-Ir4B3, and Cm-Ir4B5, we predicted three low-energy metastable phases for each of the three compounds, namely, P21/m-Ir2B, P21/m-IrB, and Pnma-Ir3B4, respectively. The obtained phonon spectra and elastic constants confirm that all the predicted P21/m-Ir2B, C2/m-Ir3B2, Fmm2-Ir4B3, P21/m-IrB, Cm-Ir4B5, and Pnma-Ir3B4 compounds are dynamically and mechanically stable. Six phases (except P21/m-IrB) have high bulk modulus and B/G ratio, making them promising low compressible material and toughness material. In particular, C2/m-Ir3B2 has the highest Vickers hardness of 13.1 and 19.4 GPa based on Chen's model and Mazhnik-Oganov's model, which is a potential hard material. According to the general anisotropy index and three-dimensional surface structure, the elastic anisotropy order of borides is Ir2B > IrB > Ir4B5 > Ir3B4 > Ir4B3 > Ir3B2. Additionally, the calculated electronic band structure and density of states show that all Ir–B crystals studied exhibit electronic characteristics of metals. Further analysis on the computed density of states, electron localized function, Bader charge analyses, and ICOHP indicate that strong Ir–B covalent bonds are present in P21/m-Ir2B, C2/m-Ir3B2, P21/m-IrB, and Fmm2-Ir4B3, while there are complex combinations of strong B–B and Ir–B covalent bonds in Cm-Ir4B5 and Pnma-Ir3B4. We hope that this comprehensive structure search can promote further experimental on the iridium borides.Author contributions
Jinquan Zhang: writing-original draft, visualization, formal analysis, software, investigation. Yuanyuan Jin: conceptualization, writing-review & editing, supervision, funding acquisition. Chuanzhao Zhang: conceptualization, software, writing-review & editing, data curation, supervision, funding acquisition. Yanqi Wang: validation, software. Libiao Tang: validation, software. Song Li: formal analysis, supervision. Meng Ju: funding acquisition, supervision. Jingjing Wang: software, supervision. Weiguo Sun: conceptualization, supervision. Xilong Dou: software, supervision.Conflicts of interest
Authors declare no conflicts to interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11804031, 11904297 and 11747139), the Scientific Research Project of Education Department of Hubei Province (No. Q20191301) and Talent and High Level Thesis Development Fund of Department of Physics and Optoelectronic Engineering of Yangtze University (C. Z. Z.).Notes and references
- Q. Gu, G. Krauss and W. Steurer, Adv. Mater., 2008, 20, 3620–3626 CrossRef CAS.
- Y. Pan and Y. Lin, Int. J. Quantum Chem., 2020, 120, e26217 CAS.
- Y. Pan and B. Zhou, Ceram. Int., 2017, 43, 8763–8768 CrossRef CAS.
- G. Akopov, M. T. Yeung and R. B. Kaner, Adv. Mater., 2017, 29, 1604506 CrossRef PubMed.
- Y. Pan and S. Chen, Vacuum, 2022, 198, 110981 CrossRef.
- D. Pu and Y. Pan, Vacuum, 2022, 196, 110727 CrossRef CAS.
- Y. Pan, Chem. Phys. Lett., 2021, 783, 139043 CrossRef CAS.
- Y. Pan and D. Pu, Ceram. Int., 2020, 46, 6698–6702 CrossRef CAS.
- H. Y. Chung, M. B. Weinberger, J. B. Levine, A. Kavner, J. M. Yang, S. H. Tolbert and R. B. Kaner, Science, 2007, 316, 436–439 CrossRef CAS PubMed.
- A. šimůnek, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 172108 CrossRef.
- H. Niu, J. Wang, X. Q. Chen, D. Li, Y. Li, P. Lazar, R. Podloucky and A. N. Kolmogorov, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 144116 CrossRef.
- R. Mohammadi, A. T. Lech, M. Xie, B. E. Weaver, M. T. Yeung, S. H. Tolbert and R. B. Kaner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10958–10962 CrossRef CAS PubMed.
- H. Gou, A. A. Tsirlin, E. Bykova, A. M. Abakumov, G. Van Tendeloo, A. Richter, S. V. Ovsyannikov, A. V. Kurnosov, D. M. Trots, Z. Konôpková, H. P. Liermann, L. Dubrovinsky and N. Dubrovinskaia, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 064108 CrossRef.
- C. Lu and C. Chen, J. Phys. Chem. Lett., 2021, 12, 2848–2853 CrossRef CAS PubMed.
- C. Lu, W. Gong, Q. Li and C. Chen, J. Phys. Chem. Lett., 2020, 11, 9165–9170 CrossRef CAS PubMed.
- A. G. Kvashnin, D. V. Rybkovskiy, V. P. Filonenko, V. I. Bugakov, I. P. Zibrov, V. V. Brazhkin, A. R. Oganov, A. A. Osiptsov and A. Y. Zakirov, Adv. Sci., 2020, 7, 2000775 CrossRef CAS PubMed.
- A. G. Kvashnin, A. R. Oganov, A. I. Samtsevich and Z. Allahyari, J. Phys. Chem. Lett., 2017, 8, 755–764 CrossRef CAS PubMed.
- C. Zhao, Y. Duan, J. Gao, W. Liu, H. Dong, H. Dong, D. Zhang and A. R. Oganov, Phys. Chem. Chem. Phys., 2018, 20, 24665–24670 RSC.
- A. R. Oganov, C. J. Pickard, Q. Zhu and R. J. Needs, Nat. Rev. Mater., 2019, 4, 331–348 CrossRef.
- A. N. Kolmogorov, S. Shah, E. R. Margine, A. F. Bialon, T. Hammerschmidt and R. Drautz, Phys. Rev. Lett., 2010, 105, 217003 CrossRef CAS PubMed.
- L. P. Ding, Y. H. Tiandong, P. Shao, Y. Tang, Z. L. Zhao and H. Lu, J. Phys. Chem. Lett., 2021, 12, 5423–5429 CrossRef CAS PubMed.
- I. Zeiringer, X. Cheng, X. Q. Chen, E. Bauer, G. Giester and P. F. Rogl, Sci. China Mater., 2015, 58, 649–668 CrossRef CAS.
- Y. Wang, L. Wu, Y. Lin, Q. Hu, Z. Li, H. Liu, Y. Zhang, H. Gou, Y. Yao, J. Zhang, F. Gao and H. k. Mao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 174106 CrossRef.
- A. G. Kvashnin, H. A. Zakaryan, C. Zhao, Y. Duan, Y. A. Kvashnina, C. Xie, H. Dong and A. R. Oganov, J. Phys. Chem. Lett., 2018, 9, 3470–3477 CrossRef CAS PubMed.
- D. V. Rybkovskiy, A. G. Kvashnin, Y. A. Kvashnina and A. R. Oganov, J. Phys. Chem. Lett., 2020, 11, 2393–2401 CrossRef CAS PubMed.
- H. Gou, N. Dubrovinskaia, E. Bykova, A. A. Tsirlin, D. Kasinathan, W. Schnelle, A. Richter, M. Merlini, M. Hanfland, A. M. Abakumov, D. Batuk, G. Van Tendeloo, Y. Nakajima, A. N. Kolmogorov and L. Dubrovinsky, Phys. Rev. Lett., 2013, 111, 157002 CrossRef.
- J. Rau and A. Latini, Chem. Mater., 2009, 21, 1407–1409 CrossRef CAS.
- A. Latini, J. V. Rau, R. Teghil, A. Generosi and V. R. Albertini, ACS Appl. Mater. Interfaces, 2010, 2, 581–587 CrossRef CAS PubMed.
- Z. Xie, R. G. Blair, N. Orlovskaya, D. A. Cullen, S. H. Lapidus, D. Kata, P. Rutkowski and J. Lis, J. Solid State Chem., 2016, 233, 108–119 CrossRef CAS.
- Z. Xie, A. C. Terracciano, D. A. Cullen, R. G. Blair and N. Orlovskaya, Adv. Appl. Ceram., 2015, 114, 429–435 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 7174–7182 Search PubMed.
- Y. Zhao, Y. Xu, P. Chen, Y. Yuan, Y. Qian and Q. Li, Results Phys, 2021, 26, 104341 CrossRef.
- W. Sun, X. Kuang, H. D. J. Keen, C. Lu and A. Hermann, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 144524 CrossRef CAS.
- B. Chen, L. J. Conway, W. Sun, X. Kuang, C. Lu and A. Hermann, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 103, 035131 CrossRef CAS.
- W. Wang, C. Zhang, Y. Jin, S. Li, W. Zhang, P. Kong, C. Xie, C. Du, Q. Liu and C. Zhang, Sci. Rep., 2020, 10, 8868 CrossRef CAS PubMed.
- C. Zhang, G. Sun, J. Wang, C. Lu, Y. Jin, X. Kuang and A. Hermann, ACS Appl. Mater. Interfaces, 2017, 9, 26169–26176 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- M. P. Teter, M. C. Payne and D. C. Allan, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 12255–12263 CrossRef PubMed.
- D. M. Bylander, L. Kleinman and S. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 1394–1403 CrossRef CAS PubMed.
- H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- W. Setyawan and S. Curtarolo, Comput. Mater. Sci., 2010, 49, 299–312 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354 CrossRef.
- X. Q. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS.
- E. Mazhnik and A. R. Oganov, J. Appl. Phys., 2019, 126, 125109 CrossRef.
- M. Liao, Y. Liu, L. Min, Z. Lai, T. Han, D. Yang and J. Zhu, Intermetallics, 2018, 101, 152–164 CrossRef CAS.
- D. H. Moseley, S. J. Thébaud, L. R. Lindsay, Y. Cheng, D. L. Abernathy, M. E. Manley and R. P. Hermann, Phys. Rev. Mater., 2020, 4, 113608 CrossRef CAS.
- A. R. Oganov, J. Chen, C. Gatti, Y. Ma, Y. Ma, C. W. Glass, Z. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863–867 CrossRef CAS PubMed.
- X. Li, H. Wang, J. Lv and Z. Liu, Phys. Chem. Chem. Phys., 2016, 18, 12569–12575 RSC.
- B. Chu, D. Li, K. Bao, F. Tian, D. Duan, X. Sha, P. Hou, Y. Liu, H. Zhang, B. Liu and T. Cui, RSC Adv., 2014, 4, 63442–63446 RSC.
- D. Y. Wang, B. Wang and Y. X. Wang, J. Phys. Chem. C, 2012, 116, 1–21966 Search PubMed.
- S. Wei, D. Li, Y. Lv, Z. Liu, F. Tian, D. Duan, B. Liu and T. Cui, J. Alloys Compd., 2016, 688, 1101–1107 CrossRef CAS.
- B. Petermuller, C. Neun, K. Wurst, L. Bayarjargal, D. Zimmer, W. Morgenroth, M. Avalos-Borja, I. G. Becerril-arez, M. J. Muhlbauer, B. Winkler and H. Huppertz, Inorg. Chem., 2018, 57, 10341–10351 CrossRef PubMed.
- D. Pu and Y. Pan, J. Am. Ceram. Soc., 2021, 105, 2858–2868 CrossRef.
- E. Yu and Y. Pan, Int. J. Hydrogen Energy, 2021, 46, 35342–35350 CrossRef CAS.
- D. Pu and Y. Pan, Ceram. Int., 2022, 48, 11518–11526 CrossRef CAS.
- D. Pu and Y. Pan, Vacuum, 2022, 199, 110981 CrossRef CAS.
- P. Li, R. Zhou and X. C. Zeng, ACS Appl. Mater. Interfaces, 2015, 7, 15607–15617 CrossRef CAS PubMed.
- B. Huang, Y. H. Duan, W. C. Hu, Y. Sun and S. Chen, Ceram. Int., 2015, 41, 6831–6843 CrossRef CAS.
- X. Zhang, X. Luo, J. Han, J. Li and W. Han, Comput. Mater. Sci., 2008, 44, 411–421 CrossRef CAS.
- R. B. Kaner, J. J. Gilman and S. H. Tolbert, Science, 2005, 308, 1268–1269 CrossRef CAS PubMed.
- P. Ravindran, L. Fast, P. A. Korzhavyi, B. Johansson, J. Wills and O. Eriksson, J. Appl. Phys., 1998, 84, 4891–4904 CrossRef CAS.
- X. J. Chen, V. V. Struzhkin, Z. Wu, M. Somayazulu, J. Qian, S. Kung, A. N. Christensen, Y. Zhao, R. E. Cohen, H. k. Mao and R. J. Hemley, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3198–3201 CrossRef CAS PubMed.
- D. Ferro, S. M. Barinov, J. V. Rau, A. Latini, R. Scandurra and B. Brunetti, Surf. Coat. Technol., 2006, 200, 4701–4707 CrossRef CAS.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CAS.
- B. F. Levine, J. Chem. Phys., 1973, 59, 1463–1486 CrossRef CAS.
- S. G. Huang, K. Vanmeensel, O. Van der Biest and J. Vleugels, Int. J. Refract. Hard Met., 2008, 26, 41–47 CrossRef CAS.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef PubMed.
- Y. H. Duan, Y. Sun, M. J. Peng and S. G. Zhou, J. Alloys Compd., 2014, 595, 14–21 CrossRef CAS.
- P. Vajeeston, P. Ravindran, C. Ravi and R. Asokamani, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 045115 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra01593e |
| This journal is © The Royal Society of Chemistry 2022 |


