 Open Access Article
Open Access ArticleMachine learning of phase diagrams†
J.
Lund
 a,
H.
Wang
a,
H.
Wang
 a,
R. D.
Braatz
a,
R. D.
Braatz
 b and
R. E.
García
b and
R. E.
García
 *a
*a
aSchool of Materials Engineering, Purdue University, West Lafayette, IN 47907, USA. E-mail: redwing@purdue.edu
bDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 20th September 2022
Abstract
By starting from experimental- and ab initio-determined phase diagrams (PDs) of materials, a machine learning (ML) method is developed to infer the free energy function for each phase. The ML method is based on a custom two-step explore-exploit k-nearest neighbor strategy, which samples the multidimensional space of Gibbs free energy parameters and user-defined physical constraints into a database of millions of PDs in order to identify the target material properties. The method presented herein is 1000× to 100 000× faster than currently available approaches, and defines a new paradigm on the quantification of properties of materials and devices. As an example application, the developed methodology is combined with the most widely used thermodynamic models – the regular solution, Redlich–Kister, and sublattice formalisms – to infer the properties of materials for lithium-ion battery applications in a matter of hours, reconstructing without human bias, well-established CALPHAD formulations while identifying previously missed stable and metastable phases and associated properties. For the EC–DMC–PC systems, the ML method allows to distinguish between stable and metastable phase boundaries, while simultaneously considering the relevant phases. For the high-power density LiFePO4 chemistry, a room-temperature metastable phase is identified. Its appearance highlights a previously unreported driving force for the transformation kinetics between lithiated and delithiated states that serves as a stepping stone to access a high-temperature eutectoid state that can be applied to engineer solid-state chemistries. For the high-energy density LiCoO2 chemistry, a highly lithiated electronically insulating phase is thermochemically favorable, particularly at grain corners and boundaries, greatly improving the description of the experimental voltage profile, irrespective of the used baseline free energy model to describe the relevant phases.
1 Introduction
A phase diagram (PD) is a graphical construction that summarizes the thermochemical ranges of structural stability of a material.1 It is the roadmap and the starting point to plan the processing of existing and advanced materials, and is the most elusive piece of information when an emerging chemistry is being considered.The modern CALculation of PHAse Diagrams (CALPHAD), pioneered by Meijering and Hillert2–4 and Kaufman and Cohen,5,6 is a well-established scientific field that enables the systematic prediction of the temperature vs. composition PDs of multicomponent chemical solutions. The long historical effort (50+ years) has resulted in a vibrant and evergrowing community amassing a wealth of databases that has been traditionally powered through commercial software, such as Thermo-Calc,7 FACT-SAGE,8 and SOLGASMIX,9 and most recently through public software libraries such as gibbs,10 pycalphad,11 and OpenCalphad.12
At the heart of a modern PD calculation is the optimization (fitting) of the parameters associated to the Gibbs free energy function that describes a material phase. This optimization is one of the most widely active CALPHAD research areas, as new chemistries become the focus of emerging technological applications, including for high-entropy materials,13–16 and in uncertainty quantification.17–23 Traditionally, the PD construction process combines experimental (e.g., calorimetric, electrochemical, vapor pressures, and phase boundary measurements) and most recently atomistic calculations24 to enable the prediction of a PD by starting from the periodic table, while simultaneously enabling a deeper understanding of the effect of bonding and solid-state physics on the properties and coexistence of phases. Conceptually, this information is directly fit to Gibbs free energy of mixing state functions (see Methods) with physically interpretable parameters through error minimization algorithms that use weighting factors to provide precedence to the dominant topological feature or material property controlling the accuracy of the fit.25 Existing approaches such as Lukas,25,26 PARROT,7,27 FITBIN,8 and ChemOpt,28 maximize the superposition of the Gaussian probability likelihood to a fit of a multivariable free energy function, in comparison to its experimental or first-principles counterpart.27
Fundamentally, the PD optimization process starts by defining a set of Gibbs free energy functions {g(α), g(β), g(γ),…, g(M)} of size M describing the possible physical phases of a multicomponent system {c1, c2,…, cN} of size N, so that for a fixed absolute temperature, a two- or P-phase equilibrium is sought, i.e.,
| μ(α)i(c(α)1, c(α)2,…, c(α)N,T) = μ(β)i(c(β)1, c(β)2,…, c(β)N,T) = ⋯ = μ(P)i(c(P)1, c(P)2,…, c(P)N,T) | (1) |
Currently used approaches deliver a manual trial-and-error process, take from months to years to carry out, and demand specialized intuition, experience, and patience, particularly when experimental data is scarce or partially unavailable.36 In this context, the possibility of deriving two or more contradictory free energy models that optimize the same PD is real, costing invaluable time and effort. Specifically, the application of CALPHAD approaches to engineer materials for lithium-ion batteries (LIBs) remains anecdotal at best,37 even though relevant information for important chemistries such as LiFePO4 (LFP) has been available since the 1990s.38 The first direct CALPHAD application was only formally reported in the early 2000s,39–43 by using polynomial and transcendental functions to fit the excess free energy of mixing models in binary polymer mixtures. Abe and Koyama in 201144 and Chang, Siefert, and coworkers in 201345 reported CALPHAD analyses for the LiCoO2 (LCO) system, a cathode material for high energy density applications, each with significant differences in the equilibrium potential, particularly in the large lithiation limit. In contrast, ab initio-based PDs have been proposed since the late 1990s, as pioneered by Van der Ven and Ceder,46,47 and Marianetti and Ceder.48 The application of CALPHAD methods to model LFP was not reported until 2011,49 and was further advanced in 2019.50 The thermodynamic description of LFP remains disconnected from very successful and widely used kinetic and coarse-grained models51–53 which, in spite of these deficiencies, provide insights into the intercalation kinetics of LIBs, even though they are based on simple regular solution descriptions.
In spite of the great progress in the construction of phase diagrams, the rate of development of physical Gibbs free energy models remains at a pace of months to years at best, limiting a deeper understanding of the materials' thermodynamic and kinetic properties. In this paper, we propose a physics-based Machine Learning (ML) approach to describe material properties of a specified chemistry in a matter of hours, instead of months or years, as a natural extension to the well-established CALPHAD foundation. As an example application, the developed methodology is applied to optimize the properties of LIB-materials, making direct comparisons against available models and experimental data. The existence of equilibrium and metastable phases is inferred from the resulting analysis.
2 Results and discussion
To infer the parameters of the Gibbs free energy state function for each material phase directly from a PD, a two-step k-nearest neighbors (knn)54,55 search strategy was developed, see Section 5.3. Here, the Q-dimensional space of free energy parameters was uniformly discretized into a set of equally spaced sampling points, which was used to perform a stochastic optimization step where the distance between a sampled PD point and a target PD were used to identify the physical parameters that most closely match the experimental or numerical system of interest (see Fig. 1). This distance defines an error or loss function between the sampling point and target location. Multiple kinds of experimental data, including electrochemical data and enthalpies of formation, can be used to constrain the search and further improve the optimization of the proposed model. Rather than focus on creating an optimization routine for a few data points, as is traditionally done by the CALPHAD community,7,8,12,21,26,56 the proposed ML-method considers the entire range of physically possible states, with equal likelihood. The search strategy was implemented in gibbs.ML, an extension of the open-source software gibbs,10 to predict the thermodynamic equilibrium of materials. As compared to traditional CALPHAD methods, which traditionally aim to sequentially optimize the thermochemical parameters against a few key experimental data points,25 the proposed approach compares the sought experimental PD against the computer-generated equivalent, irrespective of the model used to generate the PD. | ||
Fig. 1 Graphical depiction of the parameter space for temperature-concentration binary phase diagrams (PDs) describing two phases, α and β, through two regular solution free energy models. Each inset location shows two PDs where  corresponds to those originally reported by Pelton and Thompson,57 and corresponds to those originally reported by Pelton and Thompson,57 and  corresponds to the machine learning (ML)-determined parameters. The background contour plot shows the distance (error) between a central (target) PD, corresponds to the machine learning (ML)-determined parameters. The background contour plot shows the distance (error) between a central (target) PD,  , and the surrounding (sampling point) locations. Parameter search occurs through a PD space distance metric which emphasizes differences in solubility, invariant reactions (e.g., eutectic, peritectic), presence of stoichiometric compounds, and other underlying properties such as measurable equilibrium potentials. , and the surrounding (sampling point) locations. Parameter search occurs through a PD space distance metric which emphasizes differences in solubility, invariant reactions (e.g., eutectic, peritectic), presence of stoichiometric compounds, and other underlying properties such as measurable equilibrium potentials. | ||
Fig. 1 shows an example calculation based on 2 × 106 PDs, spanning the entirety of the space of physically accessible parameters in under 30 minutes, ∼670 μs per diagram. The calculation of distance, data curation, and search process took on the order ∼45 min, for a total of 1.1 h of computing time. In comparison, the currently existing commercial software takes between 0.2 s and 15 min per diagram,7,8,12,21,33–35 making it unrealistic to implement ML strategies with the commercial packages.
Overall, results for the regular solution free energy of mixing model demonstrate the possibility of PD prediction within a 3% deviation with respect to the target diagram. In contrast to the performed calculations, the goodness of the fit has only recently been openly reported in CALPHAD-determined PDs,58–62 by formulating a vector of confidences with accuracies of at least 90% for every phase for the W + Pd system (10% normalized error),63 extending this idea to weigh the prevalence of each phase, resulting in a measure of deviation in the 1–8% range, as shown for the Fe + Ti system.64 Bayesian sampling17,18,20 has resulted in PDs with deviations on the order of 6%, as reported for the Cu + Mg system.
The application of gibbs.ML to an experimental system is summarized in Fig. 2, for ten of the most widely used organic electrolytes used in LIBs,39–43 as reported by Ding,41i.e., the PC + DEC, DEC + DMC, DMC + EC, EMC + EC, PC + EC, DEC + EMC, DEC + EC, PC + DMC, PC + EMC, and EMC + DMC experimental PDs, which include two stoichiometric solid phases (three if DMC is present), and a liquid phase.65 The Redlich–Kister excess free energy model66 was used to optimize a third-order temperature-independent set of parameters. This calculation took less than 2.5 min to converge to a set of predicted parameters for each pair of chemistries. Six of the ten electrolyte chemistries show an error less than 3%, in excellent agreement with the experimental data. The DEC + EC system displays the largest model discrepancy on the liquidus line, as compared to Ding's prediction65 which used a nontraditional exponential free energy of mixing function. As compared to currently used methodologies,7,8,12,21,56gibbs.ML explores a larger space of parameters with no prejudice or bias within minutes, while the traditional optimization analyses require a sequential search of parameters that is prone to be dependent on the search path. The ML-based approach reported herein simultaneously optimizes all the parameters.
 | ||
Fig. 2 Thermodynamic model-experiment comparisons for ten polymer electrolyte chemistries used in LIBs.39–43 • corresponds to calorimetric measurements,41 corresponds to PDs reported by Ding,65 and corresponds to PDs reported by Ding,65 and  corresponds to the ML-determined PDs. Deviations with respect to the literature-reported two-phase equilibria and the corresponding data are shown as percentages. Note that the largest deviations correspond to the locus of points where the equilibrium phase boundary is expected to be (PC + DMC and PC + EMC), or where newly identified phases have been found (EMC + DMC). corresponds to the ML-determined PDs. Deviations with respect to the literature-reported two-phase equilibria and the corresponding data are shown as percentages. Note that the largest deviations correspond to the locus of points where the equilibrium phase boundary is expected to be (PC + DMC and PC + EMC), or where newly identified phases have been found (EMC + DMC). | ||
Fig. 2 shows that the ML-method enables distinguishing between phase boundary data at equilibrium and away from it, while simultaneously considering all phases present, defining an iterative technique to predict thermodynamically consistent PDs. For the PC + DMC and PC + EMC systems, the experiment-prediction discrepancy highlights that the experimental data points below the eutectic temperature are metastable, as gibbs.ML only reports the equilibrium states. Removal of the metastable data improves the accuracy to 2.82% for PC + DMC and 2.045% for PC + EMC. Finally, the large discrepancy against the EMC + DMC system, as predicted by Ding,65 is a result of gibbs.ML identifying the peritectic solid–solid phase transition, i.e., a polymorphic transition line, at −53 °C for the DMC side of the diagram as a consequence of consistently describing the free energy phases of DMC by the automated knn search.‡
The most widely used Gibbs free energy CALPHAD model, the sublattice formalism,24 was implemented for the technologically relevant battery material, LiFePO4 (LFP), a pseudo-binary system. Two models found in the literature, namely: a short range order sublattice model (SRO) from Lee49 and a long range order sublattice model (LRO) from Phan et al.,50 were directly reproduced by using the experimental data reported by Dodd et al.,67 see Fig. 3, column O.
 | ||
Fig. 3 Catalog of lithium iron phosphate (LFP) PDs including (1) a proposed short range order, four sublattice model by Lee, SRO,  ,49 (2) a long range order, five sublattice model by Phan et al., LRO (M5L), ,49 (2) a long range order, five sublattice model by Phan et al., LRO (M5L),  ,50 and (3) a temperature-dependent, five sublattice model proposed herein, T-LRO, ,50 and (3) a temperature-dependent, five sublattice model proposed herein, T-LRO,  . .  corresponds to target PD. corresponds to target PD.  Corresponds to the ML-determined PD. Corresponds to the ML-determined PD.  Corresponds to experimental data, as reported by Dodd.67 The deviation with respect to the experimental data is shown as a percentage. Column O shows PDs as published in the literature and reproduced herein. Column D shows a comparison against the originally reported experimental PD,67 and column P shows a comparison against a PD with thermodynamically consistent solubility at low temperatures, in agreement with Yamada et al.68 • corresponds to electrostatic potential experimental data as reported by Yamada et al.68 and Corresponds to experimental data, as reported by Dodd.67 The deviation with respect to the experimental data is shown as a percentage. Column O shows PDs as published in the literature and reproduced herein. Column D shows a comparison against the originally reported experimental PD,67 and column P shows a comparison against a PD with thermodynamically consistent solubility at low temperatures, in agreement with Yamada et al.68 • corresponds to electrostatic potential experimental data as reported by Yamada et al.68 and  , as reported by Tan,69 both at room temperature. The top-right zoomed-in inset highlights the differences on the predicted voltage profiles, and the bottom-right corresponds to the predicted Gibbs free energy. While each model provides a PD that agrees within nine percent of phase diagram distance to experiments, the effects on the possible stable and metastable phases, as well as the possible energy density and kinetics of intercalation, is predicted to vary widely. Results demonstrate that the T-LRO model is quantitatively in better agreement with both PD and electrochemical data, and suggests a thermally accessible metastable phase, in agreement with Phan et al.50 , as reported by Tan,69 both at room temperature. The top-right zoomed-in inset highlights the differences on the predicted voltage profiles, and the bottom-right corresponds to the predicted Gibbs free energy. While each model provides a PD that agrees within nine percent of phase diagram distance to experiments, the effects on the possible stable and metastable phases, as well as the possible energy density and kinetics of intercalation, is predicted to vary widely. Results demonstrate that the T-LRO model is quantitatively in better agreement with both PD and electrochemical data, and suggests a thermally accessible metastable phase, in agreement with Phan et al.50 | ||
Lee49 identified the need to use multiple sublattices to successfully model LFP, while Phan et al.50 extended this description to account for the long range ordering of lithium ions,70 enabling the description of larger solubilities at higher temperatures. The direct application of the ML-method presented herein to the LRO model resulted on computation times ≲1 h, see Fig. 3, column D, and delivers an improvement on the eutectoid temperature prediction and room temperature solubility as a result of the ability to explore the entirety of the space of all possible PDs without the need for prior, hand-crafted search strategies. In contrast, the gibbs.ML optimization on the SRO sublattice formalism took on the order of 55 h and was unable to optimize the experimentally determined deep eutectoid, which is a result of the limitations imposed by the previously reported sublattice model.
Experimental results suggest that the limitations of the LRO and SRO models are a result of the temperature-dependent ferromagnetic properties,70–72 which are not captured by these models. To overcome these limitations, a temperature-dependent sublattice formalism, a TLRO model, was proposed, see Section 5,36,73 and optimized in gibbs.ML in 17 h. The T-LRO model matches the experimental eutectoid temperature and solubility imposed by the phase boundaries, see Fig. 3, row T-LRO. The proposed description shows that the configurational entropy increases the solubility limit,36 suggesting a temperature-dependence on the phase boundaries. In contrast, the PD reported by Dodd et al.67 is, for all practical purposes, a temperature-independent hand-drawn sketch based on the experimental results, see Fig. 3 (solubility increases less than ∼0.01% K−1). Column P shows a proposed improvement, naturally resulting in a deeper eutectoid while matching the experimental data within 3.68%.67,68
The effect of the different sublattice models against the room temperature experimental equilibrium potentials, as reported by Yamada et al.,68 and Tan,69 is shown in Fig. 3, rightmost column. The upper-right inset highlights that the T-LRO model delivers a 100 mV improvement on the predicted equilibrium electrochemical potential; however, the two-phase region is wider than experiments by 0.05, a small over prediction that can be attributed to kinetic effects.
Even though all three models reproduce the PD within 6% uncertainty, see Fig. 3, lower right, results show that the SRO model will favor traditional spinodal decomposition kinetics, as assumed by multiple authors.51,52,74,75 In contrast, the LRO model predicts the formation of a metastable phase at c ∼ 0.6 in agreement with recent experimental observations in single-crystal particles,76–81 and in grain boundaries.82,83 The analysis shows that this prediction is a result of a local Gibbs free energy minima that, at high temperatures, will result on the high temperature eutectoid phase transformation. The T-LRO model predicts a larger energy barrier that needs to be overcome to induce the formation of the metastable phase, but will persist for long periods of time if locally stabilized. This suggests that different types of intercalation kinetics have been overlooked, but are possible, particularly in the presence of chemomechanical stresses, surfaces, and interfaces.52,74,84 Here, an initially unstable phase can temporarily segregate into a two-phase microstructure (coexistence of metastable and stable phases), before transitioning into a stable two-phase microstructure, each microstructure displaying a characteristic segregation wavelength. Specifically, the results demonstrate that the choice of free energy model impacts the predicted characteristic, or fastest growing wavelength for segregations,  in agreement with Cahn.85 For κ = 5 × 10−12 J cm−1, as reported by Tang et al.,74 the SRO sublattice model predicts λSRO = 5.3 nm, whereas the LRO model defines λLRO = 9 nm and the T-LRO model states λT-LRO = 6 nm. This suggests a faster segregation rate of larger wavelengths for the SRO model. In particular, the possibility of metastable characteristic wavelengths, λLROx<0.6 = 7.1 nm and λLROx>0.6 = 7.0 nm for the LRO model and λT-LROx<0.6 = 4.7 nm and λLROx>0.6 = 4.8 nm for the T-LRO model, suggest the temporary appearance of one type of microstructure with a fine interlayer spacing where one of the phases displays a low lithium concentration in the lithium-rich phase for short times, to be replaced with a coarser interlayer spacing with the traditionally expected lithium-deficient and lithium-rich phases. The smaller gmax value predicted by the LRO model indicates the metastable phase is expected to persist for long times, whereas the T-LRO model predicts that the eutectoid (chemically disordered) phase would be short lived because of the large driving force to phase separate into rich and lithium-deficient phases. The metastable phase description, naturally captured by gibbs.ML, highlights the accelerated transformation between lithiated and delithiated LFP and, as compared to existing kinetic optimization approaches,86–88 it demonstrates the importance to simultaneously consider the effects of the kinetic and equilibrium properties as well as incorporating high-temperature phases in emerging modeling formulations.
in agreement with Cahn.85 For κ = 5 × 10−12 J cm−1, as reported by Tang et al.,74 the SRO sublattice model predicts λSRO = 5.3 nm, whereas the LRO model defines λLRO = 9 nm and the T-LRO model states λT-LRO = 6 nm. This suggests a faster segregation rate of larger wavelengths for the SRO model. In particular, the possibility of metastable characteristic wavelengths, λLROx<0.6 = 7.1 nm and λLROx>0.6 = 7.0 nm for the LRO model and λT-LROx<0.6 = 4.7 nm and λLROx>0.6 = 4.8 nm for the T-LRO model, suggest the temporary appearance of one type of microstructure with a fine interlayer spacing where one of the phases displays a low lithium concentration in the lithium-rich phase for short times, to be replaced with a coarser interlayer spacing with the traditionally expected lithium-deficient and lithium-rich phases. The smaller gmax value predicted by the LRO model indicates the metastable phase is expected to persist for long times, whereas the T-LRO model predicts that the eutectoid (chemically disordered) phase would be short lived because of the large driving force to phase separate into rich and lithium-deficient phases. The metastable phase description, naturally captured by gibbs.ML, highlights the accelerated transformation between lithiated and delithiated LFP and, as compared to existing kinetic optimization approaches,86–88 it demonstrates the importance to simultaneously consider the effects of the kinetic and equilibrium properties as well as incorporating high-temperature phases in emerging modeling formulations.
The application of the ML methodology to complex systems that include a combination of near room temperature experiments,89–93ab initio calculations,46,47,94 and low C-rate voltage profiles89,92,95,96 have been compiled to develop CALPHAD-based models for the LiCoO2 (LCO) system.44,45 Historically, the cobalt oxide (O1), lithium cobalt oxide (O3), and a half cobalt oxide, half lithium cobalt oxide (H13) phases were optimized by Abe and Koyama,44 and later by Chang and coworkers,45 to obtain an equilibrium electrochemical potential that agrees in the 0 < x < 0.8 range, see Fig. 4. Here, the ML-method was extended to directly include the equilibrium voltage profile in the loss function to avoid overfitting. The performed calculation was completed in ≲6 h, see Section 5.3 for details. In addition, by starting from the original experimental and ab initio data, as well as the latest developments on the expected phases,47,48,89,97,98 a PD in the zero to 200 °C temperature range was proposed, see Fig. 4, green PD. However, while the error for the PDs is minimal (less than 5%), all three models overpredict the voltage profile in the 0.3 < x < 0.7 range, and under predict it for x > 0.8.
 | ||
Fig. 4 Lithium cobalt oxide (LCO) PDs and equilibrium electrostatic potential (fourth column). • Corresponds to experimental equilibrium electrostatic potential,45 corresponds to Abe and Koyama,44 corresponds to Abe and Koyama,44 corresponds to Chang et al.,45 and corresponds to Chang et al.,45 and  corresponds to this work. corresponds to this work.  Corresponds to the target PD for the ML-determined PD, as shown in Corresponds to the target PD for the ML-determined PD, as shown in  . In contrast to traditional CALPHAD approaches, which have reported to have inadequate experimental and theoretical data,44,45 in spite of the multiple reports and voltage data agreeing on its existence,47,48,89,97,98 the second row considers the incorporation of an electrically insulating phase and the associated experimental equilibrium voltage to capture the correct physical behavior.89,91,93,99 . In contrast to traditional CALPHAD approaches, which have reported to have inadequate experimental and theoretical data,44,45 in spite of the multiple reports and voltage data agreeing on its existence,47,48,89,97,98 the second row considers the incorporation of an electrically insulating phase and the associated experimental equilibrium voltage to capture the correct physical behavior.89,91,93,99 | ||
In this context, Reimers and Dahn89 and Ohzuku and Ueda90 found a lattice mismatch in the 0.75 < x < 0.925 range, while Van der Ven et al.47 speculated on the possibility of a metal–insulator transition by using first-principles calculations. The latter was confirmed experimentally by Ménétrier et al.100 Marianetti et al.48 proposed that the insulating phase was a result of extrinsic impurities that energetically favor a Mott insulator. Finally, using spectroscopy, Kellerman et al.98 showed that, for temperatures greater than 150 K, LCO will become insulating for x > 0.85 due to a decrease of lithium vacancies. Thus, by using a simple regular free energy model, the insulating phase referred herein as O3(II)89 was determined, see Fig. 4, bottom row. The results suggest that the proposed insulating phase is thermochemically favorable and in great agreement with the experimental voltage profile, irrespective of the used baseline free energy model to describe the rest of the phases. Further, the addition of an insulating phase results on a shift of the free energies of mixing parameters for all the existing phases, as the optimization process includes the entirety of the composition, thermal, and electrical properties. This indicates that currently available models compromise the values of the physical parameters across all phases in an effort to compensate for the effect of an experimentally observable two-phase region, highlighted by the 0.75 < x < 0.925 voltage plateau which was previously not considered. The predicted insulating phase favors mixing, Ω(I) ∼ −30 kJ mol−1 < 0, particularly at grain corners and boundaries. At the closing of the writing of this paper, Merryweather et al.101 reported the reversible formation of the insulating phase, further supporting the gibbs.ML prediction.
3 Conclusion
In conclusion, by extending the open source software, gibbs,10 a novel machine learning approach is presented to infer the thermodynamic state functions of a material by starting from a graphical description, a phase diagram (PD). The method presented herein is three to five orders of magnitude faster than any currently available approach, defining a new paradigm on the quantification of properties of materials and devices. While it is common to focus on developing automated methodologies that pull away from using physical intuition, the presented ML method emphasizes the importance of using physical principles to guide the rapid development of thermodynamically consistent models that accurately capture the relevant physical phenomena, thus freeing the researcher to spend more time on the physical aspects.As demonstrated in the ten analyzed organic electrolyte systems, missing phases and metastable experimental data were readily identified and assessed for stability and potential use, by exploring the entire space of parameters without any human bias. Further, the free energy models were reviewed and updated to identify thermodynamically stable phases. For the two analyzed cathode materials, LFP and LCO, published models were compared against their respective PDs and the electrochemical profile. The performed thermochemical and electrochemical analysis allowed to identify previously missed metastable and equilibrium phases that control the power and energy density response and to rapidly assess the validity, influence, and quality of the selected thermodynamic free energy model.
The integration of ab initio-based, thermodynamically consistent free energy models into advanced phase field formulations will allow to identify currently overseen physics-based microstructural evolution mechanisms, specifically those that occur in the presence of multiphysical driving forces,102–104 effectively removing the bottlenecks that link single-crystal phenomena with long term microstructural response. For the generality of materials, the developed methodology provides the ideal basis to understand the thermodynamic and kinetic limitations for a wide variety of applications that go well beyond energy-related systems, including ternary and higher order, setting up the stage to dramatically advance the pace of discovery and material design. Finally, while it is beyond the scope of this paper, the methodology presented herein can be readily extended to the multiphysical, multicomponent CALPHAD description of materials and devices.
4 Methods
4.1 Thermodynamic models
For the ith phase of a binary PD, define the Gibbs free energy of mixing as36 | (2) |
 where c(i)p is typically approximated as a power series. If all phases have the same heat capacity, then
where c(i)p is typically approximated as a power series. If all phases have the same heat capacity, then 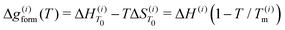 relative to
relative to  since
since  . The composition-dependent formation energy for a binary system at a given concentration is a simple rule of mixing for the two components a and b,
. The composition-dependent formation energy for a binary system at a given concentration is a simple rule of mixing for the two components a and b, | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(c) + (1 − c)ln(1 − c)), where R is the universal gas constant.
ln(c) + (1 − c)ln(1 − c)), where R is the universal gas constant.
The simplest nonideal model, the regular solution model, assumes that the excess free energy of mixing, the enthalpy of mixing, to be entirely temperature-independent, and considers quadratic or binary interactions,
| g(i)mix,xs(c,T) = c(1 − c)Ω(i), | (4) |
 | (5) |
Stoichiometric compounds were modeled in terms of the stable, equilibrium concentration c(i)0 with no free energy of mixing,
 | (6) |
The sublattice model, as described by Sundman and Ågren,105 corresponds to
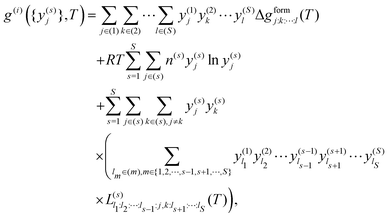 | (7) |
 . The equilibrium is determined as
. The equilibrium is determined as  . For two sublattices, s and r, each with two species, y(s)a and y(s)b and y(r)c and y(r)d, eqn (7) reduces to36,106–108
. For two sublattices, s and r, each with two species, y(s)a and y(s)b and y(r)c and y(r)d, eqn (7) reduces to36,106–108 | (8) |
The equilibrium voltage, Φ, corresponds to
 | (9) |
4.2 Material systems
The regular solution model-based PDs were optimized after those reported by Pelton and Thomson.36,57,109 The α phase was set as the reference phase. The melting temperatures Tm,a = 800 K and Tm,b = 1200 K were read directly from the diagram. Four parameters were found: ΔH(β)a and ΔH(β)b, with values in the 0 to 15 kJ mol−1 range, and mixing parameters Ωα and Ωβ in the −25 to 35 kJ mol−1 range.The solid phases in the electrolyte systems were modeled as stoichiometric compounds, and the liquid phase as a Redlich–Kister model. The melting temperatures and enthalpies of transformation for all solid phases were taken directly from literature values.65 The liquid phase was set as the reference phase for each material system. L0, L1, and L2 were optimized to values in the −20 to 20 kJ mol−1 range.
The LFP system was described as a sublattice model. Lee's SRO model uses four sublattices, one for each element with no mixing between the oxygen and phosphate sublattices. The iron sublattice is populated entirely by Fe2+ and Fe3+ and interacts with the lithium sublattice containing Li+ and vacancies due to a speculated short range ordering effect. In order for LixFePO4 to be electrically neutral for 0 ≤ x ≤ 1, cFe2+ = cLi+ = c. Thus, eqn (7) simplifies to:
 | (10) |
Eqn (10) was simplified by using the electrically neutral end members as reference phases and by assuming the intra-sublattice energy of mixing to be negligible, in agreement with Lee et al.49 Four inter-sublattice interaction parameters (n = 2 in the last line of eqn (10)) were simultaneously optimized.
Phan and coworkers,50 used a five sublattice model (LRO), where the lithium sublattice is split into two, one holding up to 0.6 molar concentration and the other remaining at 0.4 molar concentration in order to account for long range ordering and the eutectoid in the PD. The additional sublattice results in eight end members: 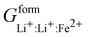 ,
, 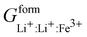 ,
, 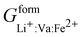 ,
, 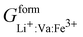 ,
,  ,
, 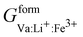 ,
, 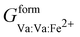 , and
, and  that are simplified using the compound energy formalism,110 into four temperature-independent adjustable parameters:
that are simplified using the compound energy formalism,110 into four temperature-independent adjustable parameters:  ,
,  ,
,  ,
,  , which correspond to the excess formation energy of non-neutral end members. In addition, g(LRO)mix,xs(c,T) = 0. The ML-method converges in less than one hour.
, which correspond to the excess formation energy of non-neutral end members. In addition, g(LRO)mix,xs(c,T) = 0. The ML-method converges in less than one hour.
The T-LRO model proposed in this paper extends Phan's LRO model to include entropic effects by introducing temperature dependence to  and
and 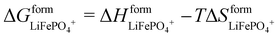 . In total, the six adjustable parameters were optimized in 17 h. Implementation details are included in the ESI.†
. In total, the six adjustable parameters were optimized in 17 h. Implementation details are included in the ESI.†
The voltage reported in the rightmost column of Fig. 3 was taken directly from the original paper and was not optimized.
For the LCO system, the cobalt oxide phase (O1) was modeled as a stoichiometric compound, the lithium cobalt oxide phase (O3) as a temperature-dependent Redlich–Kister, and the half cobalt oxide, half lithium cobalt oxide phase (H13) as a sublattice model.44 Similar to the LRO model in LFP, the H13 phase has a sublattice for cobalt, a sublattice for oxygen, and two sublattices for lithium. While the cobalt sublattice is populated with two species, Co3+ and Co4+, the energetic effect is assumed to be negligible. Each lithium sublattice is capable of holding half of the ions, with one sublattice completely filled before the other. Thus, in the range where H13 is stable, eqn (7) simplifies to
 | (11) |
The voltage profile reported by Chang et al.45 was included in the ML method to optimize both the predicted PD and associated voltage profile, to agree with all available experimental evidence and better represent the physics of the system. The effect of the electrochemical potential was included by minimizing the error between the predicted and experimental electrochemical potential.68
4.3 Machine learning architecture
The prediction of the material parameters was performed by developing a custom two-step explore-exploit machine learning strategy, based on the knn algorithm.54,55 In the first step, a dataset of PDs is generated in gibbs.ML by uniformly sampling the sought Gibbs free energy parameters, five sampling points for every parameter, which defines a uniform mesh in PD parameter space that embodies a dataset of almost ten million PDs for a ten-parameter model. The PDs in the generated dataset are compared against the target PD, so that the k-closest PDs are kept. k was set to 0.1% of the size of the dataset.The second step uses a stochastic optimization with at least ten iterations on the result from the first step. Here, for each central cell location in the generated uniform mesh in parameter space, a PD was generated by randomly sampling material parameters from a multivariate normal distribution, where the mean of the distribution corresponds to the center of the sampled cell and the standard deviation corresponds to one fourth of the width of the mesh spacing. 1024 proposed solutions are tested, and the top 100 were kept for the next iteration. These 100 PDs become sampling points for the ten iteration steps of optimization. After the final iteration, all seed points were examined and only the PD closest to the target and its corresponding material parameters is reported.§
The target and the sampled PDs were evaluated by using a distance metric,  , i.e., a loss function, independent of the utilized free energy model,
, i.e., a loss function, independent of the utilized free energy model,
 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PDk corresponds to the set of all the normalized phase boundary concentration–temperature pairs, (ci,Ti), in the kth PD. The subscript p denotes the proposed or sampled PD from the dataset, whereas t denotes the target PD. ΔT = Tmax − Tmin corresponds to the temperature range of PD, and Δc = cmax − cmin to the analyzed composition range. n = 8 was set to emphasize the difference between diagrams by weighting outliers higher. The first term in eqn (12) corresponds to the distance from every point in the target PD to the nearest point in the sampled PD, and the second term corresponds to the distance from every point in the sampled PD to the nearest point in the target PD. σproperty denotes an additional constraint, experimental or theoretical, that can be used to further optimize the description of the sought parameters. The contribution of the phase boundaries of the sampled PD was also weighted relative to the physical constraint imposed by σproperty. For example, the LCO system was optimized by comparing the root mean squared error between the predicted and target voltage profiles at the experimental room temperature.
PDk corresponds to the set of all the normalized phase boundary concentration–temperature pairs, (ci,Ti), in the kth PD. The subscript p denotes the proposed or sampled PD from the dataset, whereas t denotes the target PD. ΔT = Tmax − Tmin corresponds to the temperature range of PD, and Δc = cmax − cmin to the analyzed composition range. n = 8 was set to emphasize the difference between diagrams by weighting outliers higher. The first term in eqn (12) corresponds to the distance from every point in the target PD to the nearest point in the sampled PD, and the second term corresponds to the distance from every point in the sampled PD to the nearest point in the target PD. σproperty denotes an additional constraint, experimental or theoretical, that can be used to further optimize the description of the sought parameters. The contribution of the phase boundaries of the sampled PD was also weighted relative to the physical constraint imposed by σproperty. For example, the LCO system was optimized by comparing the root mean squared error between the predicted and target voltage profiles at the experimental room temperature.
4.4 Numerical implementation and data generation
The machine learning architecture and the free energy models presented herein were numerically implemented in the python-based open-source framework, gibbs,10 which uses symbolic computation to allow for rapid model development of material systems. The developed gibbs and gibbs.ML libraries use a combination of fixed and adjustable model parameters over a user-specified range of physically possible values. For the sublattice models, the physical constraint was solved by the Newton–Raphson method.The equilibrium of each physical system was solved by using a parallelized implementation of the common tangent construction by determining the intersection of the proposed common tangent to the overall convex hull. The phase boundaries and invariant reactions were identified. gibbs.ML was implemented in python 3.6.9, c++ 2017, g++ version 7.5, cuda 10.1, swig 3.0.12, and numpy 1.18.1. All calculations were run on a single Nvidia RTX 2080 Ti GPU. gibbs.ML constructed PDs with a resolution of 128 × 512, and downsampled to a 64 × 64 grayscale images.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge financial support from the Toyota Research Institute, USA.References
- M. Hillert. Phase equilibria, phase diagrams and phase transformations: their thermodynamic basis. Cambridge university press, 2007 Search PubMed.
- J. L. Meijering, Retrograde solubility curves especially in alloy solid solutions, Philips Res. Rep., 1948, 3, 281 CAS.
- J. L. Meijering, Calculation of the nickel-chromium-copper phase diagram from binary data, Acta Metall., 1957, 5, 257 CrossRef CAS.
- M. Hillert, Solubility of carbon in ferrite, Acta Metall., 1954, 2, 11 CrossRef.
- L. Kaufman and M. Cohen, The martensitic transformation in the iron-nickel system, JOM, 1956, 8, 1393 CrossRef CAS.
- L. Kaufman and M. Cohen, Thermodynamics and kinetics of martensitic transformations, Prog. Met. Phys., 1958, 7, 165 CrossRef CAS.
- J. O. Andersson, T. Helander, L. Höglund, P. Shi and B. Sundman, Thermo-Calc & DICTRA, computational tools for materials science, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2002, 26, 273 CrossRef CAS.
- C. W. Bale, E. Bélisle, P. Chartrand, S. A. Decterov, G. Eriksson, K. Hack, I. H. Jung, Y. B. Kang, J. Melançon, A. D. Pelton, C. Robelin and S. Petersen, FactSage thermochemical software and databases – recent developments, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2009, 33, 295 CrossRef CAS.
- G. Eriksson, Thermodynamic studies of high temperature equilibria III. SOLGAS, a computer program for calculating the composition and heat condition of an equilibrium mixture, Acta Chem. Scand., 1971, 25, 2651 CrossRef CAS.
- T. Cool, A. Bartol, M. Kasenga, K. Modi and R. E. García, Gibbs: phase equilibria and symbolic computation of thermodynamic properties, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2010, 34, 393 CrossRef CAS.
- R. Otis and Z.-K. Liu, pycalphad: CALPHAD-based computational thermodynamics in python, J. Open Res. Softw., 2017, 5, 1 CrossRef.
- B. Sundman, U. R. Kattner, M. Palumbo and S. G. Fries, OpenCalphad – a free thermodynamic software, Integr. Mater. Manuf. Innov., 2015, 4, 1 CrossRef.
- J. E. Saal, I. S. Berglund, J. T. Sebastian, P. K. Liaw and G. B. Olson, Equilibrium high entropy alloy phase stability from experiments and thermodynamic modeling, Scr. Mater., 2018, 146, 5 CrossRef CAS.
- M. Wu, S. Wang, H. Huang, D. Shu and B. Sun, CALPHAD aided eutectic high-entropy alloy design, Mater. Lett., 2020, 262, 127175 CrossRef CAS.
- K. Kaufmann, D. Maryanovsky, W. M. Mellor, C. Zhu, A. S. Rosengarten, T. J. Harrington, C. Oses, C. Toher, S. Curtarolo and K. S. Vecchio, Discovery of high-entropy ceramics via machine learning, npj Comput. Mater., 2020, 6, 42 CrossRef.
- G. Varenikov, I. Novoselov and E. Meshkov, Novel method for automatic search for stable ordered phases in multicomponent systems, Comput. Mater. Sci., 2021, 200, 110796 CrossRef CAS.
- M. Stan and B. J. Reardon, A Bayesian approach to evaluating the uncertainty of thermodynamic data and phase diagrams, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2003, 27, 319 CrossRef CAS.
- B. Bocklund, R. Otis, A. Egorov, A. Obaied, I. Roslyakova and Z. K. Liu, ESPEI for efficient thermodynamic database development, modification, and uncertainty quantification: application to Cu-Mg, MRS Commun., 2019, 9, 618 CrossRef CAS.
- N. H. Paulson, E. Jennings and M. Stan, Bayesian strategies for uncertainty quantification of the thermodynamic properties of materials, Int. J. Eng. Sci., 2019, 142, 74 CrossRef CAS.
- N. H. Paulson, B. J. Bocklund, R. A. Otis, Z. K. Liu and M. Stan, Quantified uncertainty in thermodynamic modeling for materials design, Acta Mater., 2019, 174, 9 CrossRef CAS.
- W. Cao, S. L. Chen, F. Zhang, K. Wu, Y. Yang, Y. A. Chang, R. Schmid-Fetzer and W. A. Oates, PANDAT software with PanEngine, PanOptimizer and PanPrecipitation for multi-component phase diagram calculation and materials property simulation, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2009, 33, 328 CrossRef CAS.
- P. Honarmandi and R. Arróyave, Uncertainty quantification and propagation in computational materials science and simulation-assisted materials design, Integr. Mater. Manuf. Innov., 2020, 9, 103 CrossRef.
- R. Batra, L. Song and R. Ramprasad, Emerging materials intelligence ecosystems propelled by machine learning, Nat. Rev. Mater., 2021, 6, 655 CrossRef.
- Z.-K. Liu and Y. Wang. Computational thermodynamics of materials. Cambridge University Press, Cambridge, 2016 Search PubMed.
- H. L. Lukas, E. Henig and B. Zimmermann, Optimization of phase diagrams by a least squares method using simultaneously different types of data, Calphad, 1977, 1, 225 CrossRef CAS.
- H. L. Lukas and S. G. Fries, Demonstration of the use of BINGSS with the Mg-Zn system as example, J. Phase Equilib., 1992, 13, 532 CrossRef CAS.
- B. Jansson. Evaluation of parameters in thermodynamic models using different types of experimental data simultaneously, Tech. rep., Royal Inst. of Technology, Stockholm, Sweden, 1984 Search PubMed.
- E. Königsberger and G. Eriksson, A new optimization routine for chemsage, Calphad, 1995, 19, 207 CrossRef.
- Y. Ji, H. W. Abernathy and L.-Q. Chen, Thermodynamic models of multicomponent nonstoichiometric solution phases using internal process order parameters, Acta Mater., 2021, 117462 Search PubMed.
- A. Dinsdale, S. Hodson, T. Barry and J. Taylor, Computations using MTDATA of metal – matte – slag – gas equilibria, Proc. Int. Symp. Comput. Softw. Chem. Extr. Metall., 1989, 59–74 Search PubMed.
- J. Snider, I. Griva, X. Sun and M. Emelianenko, Set based framework for Gibbs energy minimization, Calphad, 2015, 48, 18 CrossRef CAS.
- J. W. Cahn and W. C. Carter, Crystal shapes and phase equilibria: a common mathematical basis, Metall. Mater. Trans. A, 1996, 27, 1431 CrossRef.
- K. Shobu and T. Tabaru, Development of new equilibrium calculation software: CaTCalc, Mater. Trans., 2005, 46, 1175 CrossRef CAS.
- K. Shobu, CaTCalc: new thermodynamic equilibrium calculation software, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2009, 33, 279 CrossRef CAS.
- R. H. Davies, A. T. Dinsdale, J. A. Gisby, J. A. Robinson and S. M. Martin, MTDATA – Thermodynamic and phase equilibrium software from the national physical laboratory, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2002, 26, 229 CrossRef CAS.
- H. Lukas, S. G. Fries and B. Sundman. Computational thermodynamics: the Calphad method. Cambridge university press, 2007 Search PubMed.
- N. Li, D. Li, W. Zhang, K. Chang, F. Dang, Y. Du and H. J. Seifert, Development and application of phase diagrams for Li-ion batteries using CALPHAD approach, Prog. Nat. Sci.: Mater. Int., 2019, 29, 265 CrossRef CAS.
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, Phospho-olivines as positive-electrode materials for rechargeable lithium batteries, J. Electrochem. Soc., 1997, 144, 1188 CrossRef CAS.
- M. S. Ding, K. Xu and T. R. Jow, Phase diagram of EC-DMC binary system and enthalpic determination of its eutectic composition, J. Therm. Anal. Calorim., 2000, 62, 177 CrossRef CAS.
- M. S. Ding, K. Xu and T. R. Jow, Liquid–solid phase diagrams of binary carbonates for lithium batteries, J. Electrochem. Soc., 2000, 147, 1688 CrossRef CAS.
- M. S. Ding, K. Xu, S. Zhang and T. R. Jow, Liquid/solid phase diagrams of binary carbonates for lithium batteries part II, J. Electrochem. Soc., 2001, 148, A299 CrossRef CAS.
- Z.-K. Liu, Thermodynamic modeling of organic carbonates for lithium batteries, J. Electrochem. Soc., 2003, 150, A359 CrossRef CAS.
- K. Xu, Nonaqueous liquid electrolytes for lithium-based rechargeable batteries, Chem. Rev., 2004, 104, 4303 CrossRef CAS PubMed.
- T. Abe and T. Koyama, Thermodynamic modeling of the LiCoO2–CoO2 pseudo-binary system, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2011, 35, 209 CrossRef CAS.
- K. Chang, B. Hallstedt, D. Music, J. Fischer, C. Ziebert, S. Ulrich and H. J. Seifert, Thermodynamic description of the layered O3 and O2 structural LiCoO2–CoO2 pseudo-binary systems, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2013, 41, 6 CrossRef CAS.
- A. Van der Ven, M. K. Aydinol and G. Ceder, First-principles evidence for stage ordering in LixCoO2, J. Electrochem. Soc., 1998, 145, 2149 CrossRef CAS.
- A. Van der Ven, M. K. Aydinol, G. Ceder, G. Kresse and J. Hafner, First-principles investigation of phase stability in LixCoO2, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 2975 CrossRef CAS.
- C. A. Marianetti, G. Kotliar and G. Ceder, A first-order Mott transition in LixCoO2, Nat. Mater., 2004, 3, 627 CrossRef CAS.
- S. H. Lee. A study of ionic materials for the energy applications through first-principles calculations and Calphad modeling, Doctor of philosophy, Penn State, 2011.
- A. T. Phan, A. E. Gheribi and P. Chartrand, Modelling of phase equilibria of LiFePO4–FePO4 olivine join for cathode material, Can. J. Chem. Eng., 2019, 97, 2224 CrossRef CAS.
- P. Bai, D. A. Cogswell and M. Z. Bazant, Suppression of phase separation in LiFePO4 nanoparticles during battery discharge, Nano Lett., 2011, 11, 4890 CrossRef CAS.
- D. A. Cogswell and M. Z. Bazant, Coherency strain and the kinetics of phase separation in LiFePO4 nanoparticles, ACS Nano, 2012, 6, 2215 CrossRef CAS.
- D. A. Cogswell and M. Z. Bazant, Size-dependent phase morphologies in LiFePO4 battery particles, Electrochem. Commun., 2018, 95, 33 CrossRef CAS.
- E. Fix and J. L. Hodges. Discriminatory analysis. Nonparametric discrimination: Consistency properties, Tech. rep., USAF School of Aviation Medicine, Randolph Field, Texas, 1951.
- T. Cover and P. Hart, Nearest neighbor pattern classification, IEEE Trans. Inf. Theory, 1967, 13, 21 Search PubMed.
- MatCalc., 2020.
- A. D. Pelton and W. T. Thompson, Phase diagrams, Prog. Solid State Chem., 1975, 10, 119 CrossRef.
- Y. Lu, X. J. Chen, Q. He, Y. H. Guo, X. J. Liu and C. P. Wang, Thermodynamic assessments of the U-Nb-Mo and U-Nb-Cr ternary systems, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2021, 73, 102260 CrossRef CAS.
- D. Li, S. Fürtauer, H. Flandorfer and D. M. Cupid, Thermodynamic assessment and experimental investigation of the Li–Sn system, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2014, 47, 181 CrossRef CAS.
- C. Li, H. Levamaki, R. Xie, L. Tian, Z. Dong, W. Li, S. Lu, Q. Chen, J. Àgren and L. Vitos, Critical assessment of Co-Cu phase diagram from first-principles calculations, Phys. Rev. B, 2020, 102, 1 Search PubMed.
- A. K. Thakur, V. K. Pandey and V. Jindal, Calculation of existence domains and optimized phase diagram for the Nb-Ti binary alloy system using computational methods, J. Phase Equilib. Diffus., 2020, 41, 846–858 CrossRef CAS.
- A. Kroupa, O. Zobač and K. W. Richter, The thermodynamic reassessment of the binary Al–Cu system, J. Mater. Sci., 2020, 56, 3430–3443 CrossRef.
- J. E. Morral and H. Gupta, A figure of merit for predicted phase diagrams, J. Phase Equilib., 1992, 13, 373 CrossRef CAS.
- A. van de Walle and Q. Hong, Assessing phase diagram accuracy, J. Phase Equilib. Diffus., 2019, 40, 170 CrossRef CAS.
- M. S. Ding, Excess Gibbs energy of mixing for organic carbonates from fitting of their binary phase diagrams with nonideal solution models, J. Solution Chem., 2005, 34, 343 CrossRef CAS.
- O. Redlich and A. T. Kister, Algebraic representation of thermodynamic properties and the classification of solutions, Ind. Eng. Chem., 1948, 40, 345 CrossRef.
- J. L. Dodd, R. Yazami and B. Fultz, Phase Diagram of LixFePO4, Electrochem. Solid-State Lett., 2006, 9, A151 CrossRef CAS.
- A. Yamada, H. Koizumi, S. I. Nishimura, N. Sonoyama, R. Kanno, M. Yonemura, T. Nakamura and Y. O. Kobayashi, Room-temperature miscibility gap in LixFePO4, Nat. Mater., 2006, 5, 357 CrossRef CAS.
- H. Tan. A Study of the thermodynamics and kinetics of LixFePO4 as a cathode material for Li batteries, Phd thesis, California Institute of Technology, 2012 Search PubMed.
- S. Furutsuki, S. C. Chung, S. I. Nishimura, Y. Kudo, K. Yamashita and A. Yamada, Electrochromism of LiFePO4 induced by intervalence charge transfer transition, J. Phys. Chem. C, 2012, 116, 15259 CrossRef CAS.
- A. Ait-Salah, J. Dodd, A. Mauger, R. Yazami, F. Gendron and C. M. Julien, Structural and magnetic properties of LiFePO4 and lithium extraction effects, Zeitschrift fur Anorg. Allg. Chemie, 2006, 632, 1598 CrossRef CAS.
- K. Zaghib, A. Mauger, J. B. Goodenough, F. Gendron and C. M. Julien, Electronic, optical, and magnetic properties of LiFePO4: small magnetic polaron effects, Chem. Mater., 2007, 19, 3740 CrossRef CAS.
- F. Zhou, T. Maxisch and G. Ceder, Configurational electronic entropy and the phase diagram of mixed-valence oxides: the case of LixFePO4, Phys. Rev. Lett., 2006, 97, 155704 CrossRef PubMed.
- M. Tang, H. Y. Huang, N. Meethong, Y. H. Kao, W. C. Carter and Y. M. Chiang, Model for the particle size, overpotential, and strain dependence of phase transition pathways in storage electrodes: application to nanoscale olivines, Chem. Mater., 2009, 21, 1557 CrossRef CAS.
- T. R. Ferguson and M. Z. Bazant, Phase transformation dynamics in porous battery electrodes, Electrochim. Acta, 2014, 146, 89 CrossRef CAS.
- T. Yoshinari, T. Mori, K. Otani, T. Munesada, K. Yamamoto, T. Uchiyama, K. Fukuda, Y. Koyama, R. Hagiwara, Y. Orikasa and Y. Uchimoto, Quantitative elucidation of the non-equilibrium phase transition in LiFePO4 via the intermediate phase, Chem. Mater., 2019, 31, 7160 CrossRef CAS.
- X. Zhang, M. Van Hulzen, D. P. Singh, A. Brownrigg, J. P. Wright, N. H. Van Dijk and M. Wagemaker, Rate-induced solubility and suppression of the first-order phase transition in olivine LiFePO4, Nano Lett., 2014, 14, 2279 CrossRef CAS.
- Y. S. Yu, M. Farmand, C. Kim, Y. Liu, C. P. Grey, F. C. Strobridge, T. Tyliszczak, R. Celestre, P. Denes, J. Joseph, H. Krishnan, F. R. Maia, A. L. Kilcoyne, S. Marchesini, T. P. C. Leite, T. Warwick, H. Padmore, J. Cabana and D. A. Shapiro, Three-dimensional localization of nanoscale battery reactions using soft X-ray tomography, Nat. Commun., 2018, 9, 1 CrossRef.
- N. Sharma, X. Guo, G. Du, Z. Guo, J. Wang, Z. Wang and V. K. Peterson, Direct evidence of concurrent solid-solution and two-phase reactions and the nonequilibrium structural evolution of LiFePO4, J. Am. Chem. Soc., 2012, 134, 7867 CrossRef CAS.
- J. Owen and A. Hector, Phase-transforming electrodes, Science, 2014, 344, 1451 CrossRef CAS.
- Y. Orikasa, T. Maeda, Y. Koyama, H. Murayama, K. Fukuda, H. Tanida, H. Arai, E. Matsubara, Y. Uchimoto and Z. Ogumi, Transient phase change in two phase reaction between LiFePO4 and FePO4 under battery operation, Chem. Mater., 2013, 25, 1032 CrossRef CAS.
- A. Kayyar, H. Qian and J. Luo, Surface adsorption and disordering in LiFePO4 based battery cathodes, Appl. Phys. Lett., 2009, 95, 221905 CrossRef.
- M. Lachal, R. Bouchet, A. Boulineau, S. Surblé, C. Rossignol, F. Alloin and S. Obbade, Remarkable impact of grains boundaries on the chemical delithiation kinetics of LiFePO4, Solid State Ionics, 2017, 300, 187 CrossRef CAS.
- S. Laref and A. Laref, Theoretical insight into the strain effect on the intercalation potential of Li-FePO4 materials, RSC Adv., 2015, 5, 35667 RSC.
- J. W. C. Cahn and J. E. Hilliard, Free energy of a nonuniform system. I. Interfacial free energy, J. Chem. Phys., 1958, 28, 258 CrossRef CAS.
- H. Zhao, B. D. Storey, R. D. Braatz and M. Z. Bazant. Learning the physics of pattern formation from images, AIChE Annu. Meet. Conf. Proc., 2020-Novem, 60201, 2020.
- H. Zhao, R. D. Braatz and M. Z. Bazant, Image inversion and uncertainty quantification for constitutive laws of pattern formation, J. Comput. Phys., 2021, 436, 110279 CrossRef.
- X. Li, O. Dyck, R. R. Unocic, A. V. Ievlev, S. Jesse and S. V. Kalinin, Statistical learning of governing equations of dynamics from in-situ electron microscopy imaging data, Mater. Des., 2020, 195, 108973 CrossRef CAS.
- J. N. Reimers and J. R. Dahn, Electrochemical and in situ X-ray diffraction studies of lithium intercalation in LixCoO2, J. Electrochem. Soc., 1992, 139, 2091 CrossRef CAS.
- T. Ohzuku and A. Ueda, Solid-state redox reactions of LiCoO2 (R3m) for 4 volt secondary lithium cells, J. Electrochem. Soc., 1994, 141, 2972 CrossRef CAS.
- J.-S. Hong and J. R. Selman, Relationship between calorimetric and structural characteristics of lithium-ion cells I. Thermal analysis and phase diagram, J. Electrochem. Soc., 2000, 147, 3183 CrossRef CAS.
- Z. Chen, Z. Lu and J. R. Dahn, Staging phase transitions in LixCoO2, J. Electrochem. Soc., 2002, 149, A1604 CrossRef CAS.
- M. Wang and A. Navrotsky, Enthalpy of formation of LiNiO2, LiCoO2 and their solid solution, LiNi1−xCoxO2, Solid State Ionics, 2004, 166, 167 CrossRef CAS.
- H. Moriwake, A. Kuwabara, C. A. Fisher, R. Huang, T. Hitosugi, Y. H. Ikuhara, H. Oki and Y. Ikuhara, First-principles calculations of lithium–ion migration at a coherent grain boundary in a cathode material, LiCoO2, Adv. Mater., 2013, 25, 618 CrossRef CAS PubMed.
- K. Mizushima, P. Jones, P. Wiseman and J. Goodenough, LixCoO2: a new cathode material for batteries of high energy density, Mater. Res. Bull., 1980, 15, 783 CrossRef CAS.
- N. Amdouni, H. Zarrouk and C. M. Julien, Structural and electrochemical properties of LiCoO2 and LiAlyCo1−yO2(y = 0.1 and 0.2) oxides: a comparative study of electrodes prepared by the citrate precursor route, Ionics, 2003, 9, 47 CrossRef CAS.
- P. J. Bouwman. Lithium Intercalation in preferentially oriented submicron LiCoO2 films, Phd thesis, University of Twente, Netherlands, 2002 Search PubMed.
- D. G. Kellerman, V. R. Galakhov, A. S. Semenova, Y. N. Blinovskov and O. N. Leonidova, Semiconductor-metal transition in defect lithium cobaltite, Phys. Solid State, 2006, 48, 548 CrossRef CAS.
- H. Volkova, K. Pachuta, K. Crowley, S. K. Radha, E. Pentzer, X. P. Gao, W. R. Lambrecht, A. Sehirlioglu and M. H. Berger, Electron microscopy and spectroscopic study of structural changes, electronic properties and conductivity in annealed LixCoO2, Phys. Rev. Mater., 2021, 5, 015401 CrossRef CAS.
- M. Ménétrier, I. Saadoune, S. Levasseur and C. Delmas, The insulator-metal transition upon lithium deintercalation from LiCoO2: electronic properties and 7Li NMR study, J. Mater. Chem., 1999, 9, 1135 RSC.
- A. J. Merryweather, C. Schnedermann, Q. Jacquet, C. P. Grey and A. Rao, Operando optical tracking of single-particle ion dynamics in batteries, Nature, 2021, 594, 522 CrossRef CAS PubMed.
- R. E. García, C. M. Bishop and W. C. M. Carter, Thermodynamically consistent variational principles with applications to electrically and magnetically active systems, Acta Mater., 2004, 52, 11 CrossRef.
- J. Lund, K. S. Vikrant, C. M. Bishop, W. Rheinheimer and R. E. García, Thermodynamically consistent variational principles for charged interfaces, Acta Mater., 2021, 205, 116525 CrossRef CAS.
- L.-Q. Chen, Phase-field method of phase transitions/domain structures in ferroelectric thin films: A Review, J. Am. Ceram. Soc., 2008, 91, 1835 CrossRef CAS.
- B. Sundman and J. Agren, A regular solution model for phases with several components and sublattices, suitable for computer applications, J. Phys. Chem. Solids, 1981, 42, 297 CrossRef CAS.
- Y. A. Chang and W. A. Oates. Solution phase models I: Configurational entropies, Mater. Thermodyn., chap. 13, pp. 165–175. Joh Wiley & Sons, Inc., 2009 Search PubMed.
- G. Cacciamani, An Introduction to the Calphad method and the compound energy formalism (CEF), Tecnol. Metal., Mater. Min., 2016, 13, 16 CrossRef CAS.
- Y. A. Chang, S. Chen, F. Zhang, X. Yan, F. Xie, R. Schmid-Fetzer and W. A. Oates, Phase diagram calculation: past, present and future, Prog. Mater. Sci., 2004, 49, 313 CrossRef CAS.
- D. Gaskell. The Phase diagrams of binary systems that exhibt regular solution behavior in the liquid and solid states, Introd. to Thermodyn. Mater., chap. 10.7, CRC Press, 5th edn, 2008, p. 298 Search PubMed.
- J.-O. Andersson, A. Guillermet, M. Hillert, B. Jansson and B. Sundman, A compound-energy model of ordering in a phase with sites of different coordination numbers, Acta Metall., 1986, 34, 437 CrossRef CAS.
- D. E. Rumelhart, G. E. Hinton and R. J. Williams, Learning representations by back-propagating errors, Nature, 1986, 323, 533 CrossRef.
- K. Pearson, The Problem of the Random Walk, Nature, 1905, 72, 294 CrossRef.
- J. Kluyver, A local probability problem, K. Akad. Wet. Amsterdam, Proc., 1905, 8, 341 Search PubMed.
- R. J. Nossal and G. H. Weiss, A generalized Pearson random walk allowing for bias, J. Stat. Phys., 1974, 10, 245 CrossRef.
- A. M. Legendre. Nouvelles méthodes pour la détermination des orbites des comètes. chez Firmin Didot, libraire pour lew mathematiques, Paris, 1805 Search PubMed.
- C.-F. Gauss. Theoria combinationis observationum erroribus minimis obnoxiae. Henricus Dieterich, 1823 Search PubMed.
- N. Aronszajn, Theory of reproducing kernels, Trans. Am. Math. Soc., 1950, 68, 337 CrossRef.
- T. Hofmann, B. Schölkopf and A. J. Smola, Kernel methods in machine learning, Ann. Stat., 2008, 36, 1171 Search PubMed.
- W. S. McCulloch and W. Pitts, A logical calculus of the ideas immanent in nervous activity, Bull. Math. Biophys., 1943, 5, 115 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00524g |
| ‡ At room temperature, because the excess free energy of mixing is at most half the contribution of the configurational entropy, the entropy is being maximized in all the calculations, in agreement with the second law of thermodynamics. Results show that the PC + EC system displays the most stable liquid phase of the analyzed polymer chemistries, while the DEC + EC is the least stable, suggesting that the addition of solute would favor a phase transition. |
| § While other search methodologies such as gradient descent,111 directed random walks,112–114 regression,115,116 kernel methods,117,118 neural networks,119 exist, the proposed knn strategy defines a generalized approach that is independent of the number of phases, the selected free energy model, topology of the PD. It provides the researcher with an easy-to-use and ever extendable approach, enabling the user to focus on the physics or design at hand instead of the numerical aspects. Further, because the proposed knn search strategy samples 0.1% of volume of the space of parameters where the solution is being sought, and the search is enhanced with random sampling in the vicinity of the solution during postprocessing, the k value has no significant impact on the obtained results. |
| This journal is © The Royal Society of Chemistry 2022 |
