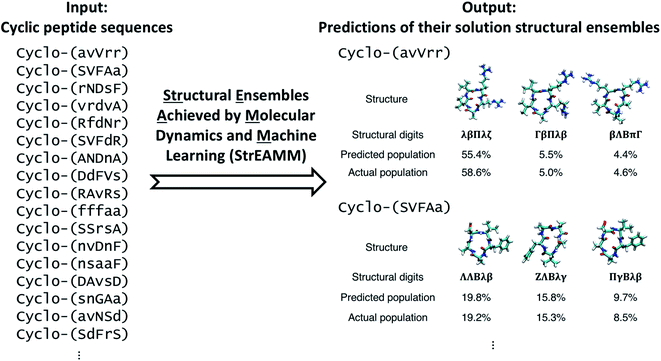
Open Access Article
Open Access ArticleStructure prediction of cyclic peptides by molecular dynamics + machine learning†
Jiayuan
Miao
 ,
Marc L.
Descoteaux
and
Yu-Shan
Lin
,
Marc L.
Descoteaux
and
Yu-Shan
Lin
 *
*
Department of Chemistry, Tufts University, Medford, Massachusetts 02155, USA. E-mail: yu-shan.lin@tufts.edu
First published on 5th November 2021
Abstract
Recent computational methods have made strides in discovering well-structured cyclic peptides that preferentially populate a single conformation. However, many successful cyclic-peptide therapeutics adopt multiple conformations in solution. In fact, the chameleonic properties of some cyclic peptides are likely responsible for their high cell membrane permeability. Thus, we require the ability to predict complete structural ensembles for cyclic peptides, including the majority of cyclic peptides that have broad structural ensembles, to significantly improve our ability to rationally design cyclic-peptide therapeutics. Here, we introduce the idea of using molecular dynamics simulation results to train machine learning models to enable efficient structure prediction for cyclic peptides. Using molecular dynamics simulation results for several hundred cyclic pentapeptides as the training datasets, we developed machine-learning models that can provide molecular dynamics simulation-quality predictions of structural ensembles for all the hundreds of thousands of sequences in the entire sequence space. The prediction for each individual cyclic peptide can be made using less than 1 second of computation time. Even for the most challenging classes of poorly structured cyclic peptides with broad conformational ensembles, our predictions were similar to those one would normally obtain only after running multiple days of explicit-solvent molecular dynamics simulations. The resulting method, termed StrEAMM (Structural Ensembles Achieved by Molecular Dynamics and Machine Learning), is the first technique capable of efficiently predicting complete structural ensembles of cyclic peptides without relying on additional molecular dynamics simulations, constituting a seven-order-of-magnitude improvement in speed while retaining the same accuracy as explicit-solvent simulations.
1. Introduction
Cyclic peptides are a special class of compounds in the “beyond rule-of-five” chemical space. They have captured the attention of chemists and the pharmaceutical industry, owing to their unique properties for therapeutic development.1–3 Notably, most cyclic peptides reported thus far are poorly structured and adopt multiple conformations in solution.4–14 Critically, the ability of a cyclic peptide to adopt multiple conformations can be essential to its biological properties and functions. For example, the chameleonic structural properties of some cyclic peptides are likely responsible for their high cell membrane permeability.4–7,15–18 Further, there can be a dynamic balance among different conformations within an ensemble, such that when one conformation is removed from solution (for example, by binding to a target), the overall conformational ensemble rebalances back towards the depleted structure.15,19 Therefore, the structures capable of binding to a target need not be highly populated in the solution ensemble, and conformations of lower populations can play an essential role in biological activity. The ability to efficiently predict the various structures a cyclic peptide can adopt, along with the population for each structure, would significantly advance our ability to rationally design these important and interesting molecules.20–22Recent computational methods have made strides in designing well-structured cyclic peptides that preferentially populate a single conformation.23,24 For example, the software improvements such as in Rosetta have enabled researchers to design highly structured cyclic peptides, in particular, by incorporating both L- and D-prolines.23 Nonetheless, for the majority of cyclic peptides, which often display many solvent-exposed backbone C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and N–H bonds and sometimes even are associated with caged water molecules,25–29 peptide–water interactions need to be described at the molecular level. The use of an explicit-solvent model is thus critical to accurately describe their energetics and structural preferences in solution.30 To enable efficient simulations of cyclic peptides using explicit-solvent molecular dynamics (MD) simulations, we recently tailored an enhanced sampling method to cyclic peptides.31 This method uses bias-exchange metadynamics32,33 to target the essential transitional motions of cyclic peptides31 and has enabled systematic studies of cyclic-peptide variants using explicit-solvent MD simulations to identify well-structured cyclic peptides.34,35 Taking advantage of the improved simulation efficiency, our group also performed simulations of basis-set cyclic-peptide sequences and developed a scoring function approach that can be used to design well-structured cyclic peptides lacking proline residues, thereby significantly expanding the available sequence space for well-structured cyclic peptide design.24
O and N–H bonds and sometimes even are associated with caged water molecules,25–29 peptide–water interactions need to be described at the molecular level. The use of an explicit-solvent model is thus critical to accurately describe their energetics and structural preferences in solution.30 To enable efficient simulations of cyclic peptides using explicit-solvent molecular dynamics (MD) simulations, we recently tailored an enhanced sampling method to cyclic peptides.31 This method uses bias-exchange metadynamics32,33 to target the essential transitional motions of cyclic peptides31 and has enabled systematic studies of cyclic-peptide variants using explicit-solvent MD simulations to identify well-structured cyclic peptides.34,35 Taking advantage of the improved simulation efficiency, our group also performed simulations of basis-set cyclic-peptide sequences and developed a scoring function approach that can be used to design well-structured cyclic peptides lacking proline residues, thereby significantly expanding the available sequence space for well-structured cyclic peptide design.24
The ability to discover and design well-structured cyclic peptides is valuable, and since in these cases, the most-populated structure dominates in the Boltzmann-weighted averages of simulated observables, it is more straightforward to compare the most-populated structure predicted to results from solution NMR spectroscopy to verify the accuracy of the predictions. However, these methods are unable to predict the full structural ensembles of poorly-structured cyclic peptides that adopt multiple low-population conformations in solution. As most cyclic peptides likely adopt multiple conformations in solution, the ultimate capability of describing the solution structural ensembles of both well-structured and poorly-structured cyclic peptides is essential to cyclic-peptide therapeutic development. This work aims to substantially expand our predictive capability from the current status of only being able to discover and design well-structured cyclic peptides to actually efficiently predicting the full structural ensembles of both well- and non-well-structured cyclic peptides as one would obtain in MD simulations, but to do so in just a few seconds of computation time (Fig. 1). We first show that, although our previous scoring function can identify well-structured cyclic pentapeptides, it is unable to predict the behaviors of non-well-structured cyclic pentapeptides. We then use MD simulations to generate structural ensembles of a set of cyclic pentapeptides with various sequence features. Using these simulation results as training datasets, we are able to train models that can predict the structural ensemble, i.e., populations of various structures, for a new cyclic-peptide sequence. This new method, Structural Ensembles Achieved by Molecular Dynamics and Machine Learning (StrEAMM), enables us to rapidly predict MD-quality structural ensembles of cyclic pentapeptides, be they well-structured or not, with very minimal computational effort.
2. Results
2.1 Extant scoring function cannot predict the structural ensembles of non-well-structured cyclic peptides
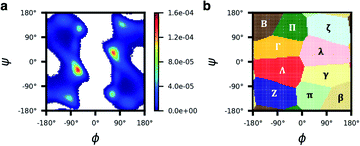
We began by building and testing a scoring function analogous to the one developed by Slough et al.24 but with two major improvements. First, Slough et al. described a cyclic-pentapeptide structure using specific turn combinations (some type of β turn at residues i and i + 1 and some type of tight turn at residue i + 3).24 Because cyclic pentapeptides can adopt conformations other than these canonical turn combinations, we separated the (ϕ, ψ) space into 10 different regions and denoted each region with a structural digit (B, Π, Γ, Λ, Z, β, π, γ, λ, or ζ; see “Structural analysis” in the Methods section for more detail). Thus, a cyclic-pentapeptide structure can be described using a 5-letter code (for example, λβΠλζ). Second, while Slough et al. used a dataset containing 57 cyclo-(X1X2AAA) peptides with Xi being one of the eight amino acids (G, A, V, F, N, S, D, and R), we used 106 cyclo-(X1X2GGG) peptides with Xi being one of the 15 amino acids: G, A, V, F, N, S, D, R, a, v, f, n, s, d, and r, with lower-case letters denoting D-amino acids. In the dataset, each sequence contained one unique nearest-neighbor pair with the rest of the sequence filled by Gly's (see Dataset 1 in the Methods section for more detail). The new dataset was also extended to include D-amino acids, which are commonly used in cyclic-peptide drug development efforts, both to improve the capability of stabilizing desired conformations and to reduce enzymatic degradation. In this scoring function, herein termed Scoring Function 1.0, the score of cyclo-(X1X2X3X4X5) adopting a specific structure S1S2S3S4S5 was computed as: | (1) |
 was the population of structure S1S2S3S4S5 observed in the cyclo-(X1X2GGG) simulation, and so forth (Fig. 2a). Ideally, the five parent sequences, X1X2GGG, GX2X3GG, GGX3X4G, GGGX4X5, and X1GGGX5 would capture how nearest-neighbor pairs X1X2, X2X3, X3X4, X4X5, and X5X1 impact the structural preferences of cyclo-(X1X2X3X4X5), respectively.
was the population of structure S1S2S3S4S5 observed in the cyclo-(X1X2GGG) simulation, and so forth (Fig. 2a). Ideally, the five parent sequences, X1X2GGG, GX2X3GG, GGX3X4G, GGGX4X5, and X1GGGX5 would capture how nearest-neighbor pairs X1X2, X2X3, X3X4, X4X5, and X5X1 impact the structural preferences of cyclo-(X1X2X3X4X5), respectively.
 | ||
| Fig. 2 Extant scoring function and new StrEAMM models. (a) Scoring Function 1.0. This scoring function is similar to the one developed by Slough et al.,24 which uses 5 parent sequences cyclo-(X1X2GGG), cyclo-(GX2X3GG), cyclo-(GGX3X4G), cyclo-(GGGX4X5), and cyclo-(X1GGGX5), to capture the effects from the 5 nearest-neighbor pairs and sums the populations observed in the MD simulations of the 5 parent sequences to build the final score. (b) StrEAMM (1,2)/sys. This model considers the effects of the nearest-neighbor pairs as effective weights. The logarithm of the population of a structure can be expressed by the summation of the five weights and the weight related to the partition function. (c) StrEAMM (1,2)+(1,3)/sys and StrEAMM (1,2)+(1,3)/random. These models consider interactions between both the nearest-neighbor and next-nearest-neighbor residues, i.e., both (1,2) and (1,3) interactions. The logarithm of the population of a structure can be expressed by the summation of the 10 weights and the weight related to the partition function. R groups of amino acids are represented by spheres. Different colors stand for different structural digits (see “Structural analysis” in the Methods section). | ||
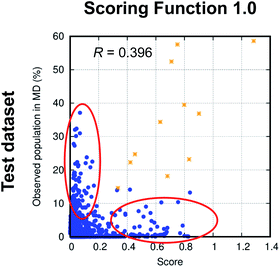
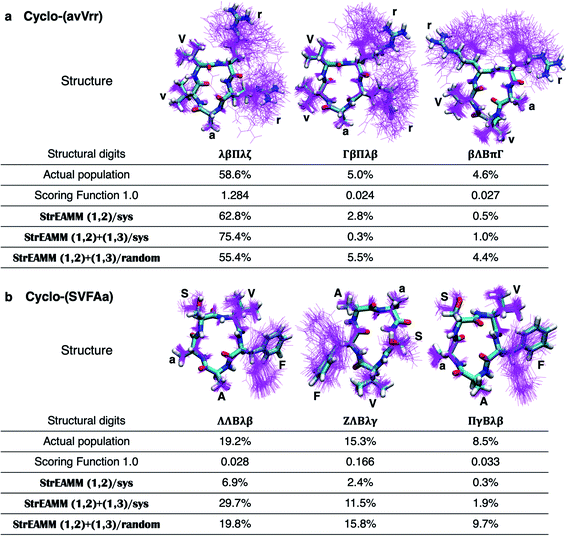
To evaluate the performance of the scoring functions, we ran MD simulations of 50 cyclic peptides with random sequences and used their structural ensembles as the test dataset (see Dataset 4 in the Methods section for more detail, and see List S2 in the ESI† for the exact sequences). Fig. 3 shows the performance of Scoring Function 1.0 for predicting the populations of specific structures adopted by these 50 random sequences. We found the scoring function successfully predicted the most-populated structures of 11 out of the 50 test cyclic peptides (orange stars in Fig. 3; also see Fig. S2,† boxed in green). Three cyclic peptides in the test dataset were considered well-structured, i.e., the population of the most-populated structure was >50%, and their most-populated structures were all predicted successfully. These data suggested that Scoring Function 1.0 was capable of identifying well-structured sequences. However, for structures with low populations, the scores and the observed populations in MD simulations showed a poor correlation (highlighted by red circles in Fig. 3; the Pearson correlation coefficient of all the data points was 0.396), suggesting that Scoring Function 1.0 was unable to predict the behaviors of non-well-structured cyclic peptides. To further highlight this issue, in Fig. 4 we show the structures and populations of the three most-populated conformations observed in the simulations of a well-structured cyclic peptide, cyclo-(avVrr), and of a non-well-structured cyclic peptide, cyclo-(SVFAa), along with the scores predicted by Scoring Function 1.0. While Scoring Function 1.0 provided scores that correlated well with the populations of the three most-populated conformations for the well-structured cyclo-(avVrr) (scores of 1.284, 0.024, and 0.027 vs. the actual populations of 58.6%, 5.0%, and 4.6% observed in the MD simulations, respectively), it was unable to predict the behavior of the non-well-structured cyclo-(SVFAa) (scores of 0.028, 0.166, and 0.033 vs. the actual populations of 19.2%, 15.3%, and 8.5% observed in the MD simulations, respectively).
2.2 StrEAMM (1,2)/sys: optimizing (1,2) interaction weights to predict populations of cyclic peptide structures
We found that Scoring Function 1.0 was unable to predict populations of structures that were not highly populated (Fig. 3) and could not be used to describe conformational ensembles of non-well-structured cyclic peptides. In Scoring Function 1.0, the predicted score was a simple summation of the populations observed in the MD simulations of the five parent sequences—the higher the score, the more likely that the structure was preferred. Examination of eqn (1) suggests that if a structure does not populate highly in the training dataset, i.e., in cyclo-(X1X2GGG) peptides, then there is little chance for cyclic peptides of any sequences to be predicted to have a large population for that particular structure. We hypothesized that the issue results from the requirement of simply summing the five populations to obtain the score and that these populations are strictly derived from cyclo-(X1X2GGG). Thus, a different scoring scheme that is not merely summing the populations observed in the MD simulations of the five parent sequences, but somehow extracts and embeds effective (1,2) interaction contributions on a cyclic peptide's structural preferences is needed. Furthermore, in Scoring Function 1.0, the populations observed in the MD simulations of the parent sequences were summed to obtain a score; however, the exact relationship between a score and the population was unclear.To overcome all these challenges, we devised our Structural Ensembles Achieved by Molecular Dynamics and Machine Learning (StrEAMM) model StrEAMM (1,2)/sys, which incorporated (1,2) interactions and was trained using the systematic cyclo-(X1X2GGG) training dataset (Dataset 1). In StrEAMM (1,2)/sys, the predicted population of cyclo-(X1X2X3X4X5) adopting a specific structure S1S2S3S4S5 was computed as:
 | (2) |
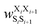 was the weight assigned when residues XiXi+1 adopted structure SiSi+1, Xi was one of the 15 amino acids (G, A, V, F, N, S, D, R, a, v, f, n, s, d, and r), and Si was one of the 10 structural digits (B, Π, Γ, Λ, Z, β, π, γ, λ, and ζ). The expression (in the logarithmic form) is illustrated in Fig. 2b. The weights were designed to represent the effective free energy contribution from residues XiXi+1 adopting structure SiSi+1, and the contributions from different nearest-neighbor pairs were presumed to be additive. A partition function Q and an exponential operation were introduced to convert the final effective free energy to a predicted population. The weights and the partition functions were then determined by weighted least squares fitting to minimize the difference between the predicted populations and the actual populations observed in the MD simulations of the training sequences (see ESI† for more detail).
was the weight assigned when residues XiXi+1 adopted structure SiSi+1, Xi was one of the 15 amino acids (G, A, V, F, N, S, D, R, a, v, f, n, s, d, and r), and Si was one of the 10 structural digits (B, Π, Γ, Λ, Z, β, π, γ, λ, and ζ). The expression (in the logarithmic form) is illustrated in Fig. 2b. The weights were designed to represent the effective free energy contribution from residues XiXi+1 adopting structure SiSi+1, and the contributions from different nearest-neighbor pairs were presumed to be additive. A partition function Q and an exponential operation were introduced to convert the final effective free energy to a predicted population. The weights and the partition functions were then determined by weighted least squares fitting to minimize the difference between the predicted populations and the actual populations observed in the MD simulations of the training sequences (see ESI† for more detail).
Fig. 5a compares the fitted populations and the observed populations in the MD simulations of the training dataset (106 cyclo-(X1X2GGG) peptides with Xi being one of the 15 representative amino acids; see Dataset 1 in the Methods section for more detail). Fig. 5a shows a Pearson correlation coefficient of 0.943 between the fitted and observed populations. However, large deviations were observed for structures with small populations (Fig. 5a, red circle).
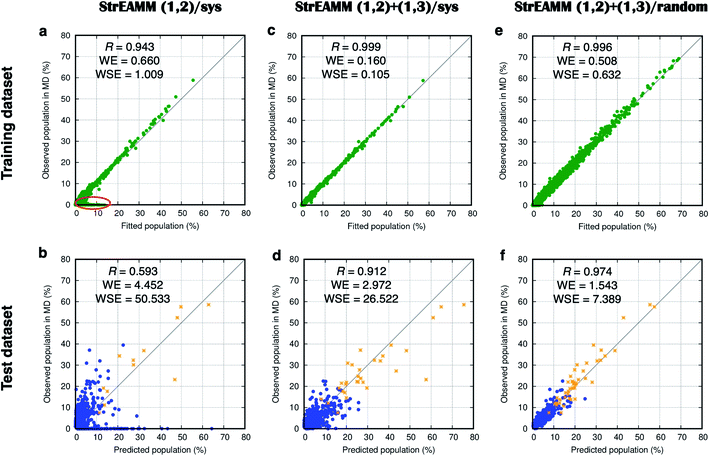 | ||
Fig. 5 Weighted least squares fitting results for the training dataset (top row) and the performance on the test dataset (bottom row) of the three StrEAMM models. (a and b) StrEAMM (1,2)/sys. (c and d) StrEAMM (1,2)+(1,3)/sys. (e and f) StrEAMM (1,2)+(1,3)/random. Top row: comparison between the fitted populations and the actual populations of various structures observed in the MD simulations of the training dataset. Bottom row: comparison between the populations predicted by each StrEAMM model and the actual populations of various structures observed in the MD simulations of 50 random test sequences; only structures with observed populations or predicted populations >1% are shown. Predicted populations in b, d, and f were calculated by eqn (2), (3), and (3), respectively. Pearson correlation coefficient (R), weighted error (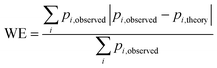 , where pi,theory is the fitted population or the predicted population), and weighted squared error ( , where pi,theory is the fitted population or the predicted population), and weighted squared error (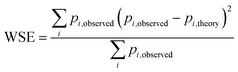 ) were calculated. Gray lines show where the fitted/predicted populations equal the observed populations. StrEAMM (1,2)/sys, StrEAMM (1,2)+(1,3)/sys, and StrEAMM (1,2)+(1,3)/random successfully predict the most-populated structures of 12, 30, and 43 out of the 50 cyclic peptides in the test dataset, respectively, and these structures are shown as orange stars in b, d, and f. ) were calculated. Gray lines show where the fitted/predicted populations equal the observed populations. StrEAMM (1,2)/sys, StrEAMM (1,2)+(1,3)/sys, and StrEAMM (1,2)+(1,3)/random successfully predict the most-populated structures of 12, 30, and 43 out of the 50 cyclic peptides in the test dataset, respectively, and these structures are shown as orange stars in b, d, and f. | ||
We then tested the performance of StrEAMM (1,2)/sys on 50 random cyclic-peptide sequences (Dataset 4), the same test dataset used for Scoring Function 1.0. We found the model successfully predicted the most-populated structures of 12 out of the 50 test cyclic peptides (orange stars in Fig. 5b; also see Fig. S4,† boxed in green), including the three well-structured cyclic peptides whose most-populated structure was larger than 50%. However, StrEAMM (1,2)/sys still did not perform well at predicting the full structural ensembles, especially for non-well-structured cyclic peptides, as indicated by the low Pearson correlation coefficient of 0.593 and a large weighted error of 4.452 (Fig. 5b). This observation suggests that interactions other than nearest-neighbor (1,2) interactions are important for determining the structural preferences of cyclic peptides and should be included in the model or, alternatively, that the training dataset needs to be expanded.
2.3 StrEAMM (1,2)+(1,3)/sys and StrEAMM (1,2)+(1,3)/random: including both (1,2) and (1,3) interaction weights
Next, we hypothesized that incorporating higher-order, longer-range contributions, specifically (1,3) interactions, as well as nearest-neighbors (1,2) interactions, would further enhance predictions of full structural ensembles of cyclic peptides. In this case, the population of cyclo-(X1X2X3X4X5) adopting a specific structure S1S2S3S4S5,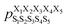 was computed as:
was computed as: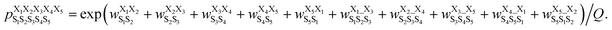 | (3) |
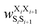 was the weight assigned when residues XiXi+1 adopted structure SiSi+1;
was the weight assigned when residues XiXi+1 adopted structure SiSi+1; 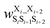 was the weight assigned when residues Xi_Xi+2 adopted structure SiSi+1Si+2. Note that in describing (1,3) interactions, we also included the structural digit of the middle residue. This decision recognized that the (ϕ, ψ) dihedrals of the middle residue would likely affect the relative distance and orientation between residues Xi and Xi+2. However, the description did not consider the identity of the amino acid at the middle residue Xi+1, only the structural digit. The expression (in the logarithmic form) is illustrated in Fig. 2c. The weights were then determined by weighted least squares fitting to minimize the difference between the predicted populations and the actual populations observed in the MD simulations of the training sequences.
was the weight assigned when residues Xi_Xi+2 adopted structure SiSi+1Si+2. Note that in describing (1,3) interactions, we also included the structural digit of the middle residue. This decision recognized that the (ϕ, ψ) dihedrals of the middle residue would likely affect the relative distance and orientation between residues Xi and Xi+2. However, the description did not consider the identity of the amino acid at the middle residue Xi+1, only the structural digit. The expression (in the logarithmic form) is illustrated in Fig. 2c. The weights were then determined by weighted least squares fitting to minimize the difference between the predicted populations and the actual populations observed in the MD simulations of the training sequences.
To train the weights related to both (1,2) and (1,3) interactions, we devised two training datasets. The first training dataset included 204 cyclo-(X1X2GGG) and cyclo-(X1GX3GG) peptides (see Dataset 2 in the Methods section for more detail), and the resulting model was termed StrEAMM (1,2)+(1,3)/sys. The second training dataset included 705 cyclo-(X1X2X3X4X5) peptides of semi-random sequences that ensured all X1X2X3 patterns were observed and each X1X2 and X1_X3 patterns appeared at least 15 times (see Dataset 3 in the Methods section for more detail); the resulting model was termed StrEAMM (1,2)+(1,3)/random.
Fig. 5c compares the observed populations in MD simulations and the fitted populations from StrEAMM (1,2)+(1,3)/sys for the training dataset in Dataset 2. Fig. 5e compares the observed populations in MD simulations and the fitted populations from StrEAMM (1,2)+(1,3)/random for the training dataset in Dataset 3. The results from both models show a clear correlation between the fitted and the observed populations.
We then tested StrEAMM (1,2)+(1,3)/sys and StrEAMM (1,2)+(1,3)/random on 50 random cyclic-peptide sequences in Dataset 4, the same test dataset used for Scoring Function 1.0 and StrEAMM (1,2)/sys. For both StrEAMM (1,2)+(1,3)/sys and StrEAMM (1,2)+(1,3)/random (Fig. 5d and f), the correlation between the observed populations in MD simulations and predicted populations was much improved over Scoring Function 1.0 (Fig. 3) and StrEAMM (1,2)/sys (Fig. 5b). StrEAMM (1,2)+(1,3)/sys successfully predicted the most-populated structures of 30 of the 50 test cyclic peptides (orange stars in Fig. 5d; also see Fig. S6,† boxed in green), and the Pearson correlation coefficient was 0.912 when comparing the predicted and the observed populations. The weighted error also dropped to 2.972. The results were even more impressive for StrEAMM (1,2)+(1,3)/random, which successfully predicted the most-populated structures of 43 of the 50 test cyclic peptides (orange stars in Fig. 5f; also see Fig. S8,† boxed in green). The Pearson correlation coefficient was 0.974 between the predicted and the observed populations. The weighted error was 1.543. Fig. 4 shows that StrEAMM (1,2)+(1,3)/random not only described the structural ensemble of the well-structured cyclo-(avVrr), but also successfully predicted the structural ensemble of the non-well-structured cyclo-(SVFAa). In fact, StrEAMM (1,2)+(1,3)/random consistently predicted the structural ensembles even for cyclic peptides whose most-populated structure represented as little as 10% of the total ensemble.
2.4 Experimental evaluation
In the work of Slough et al., cyclo-(GNSRV) was predicted to be a well-structured cyclic peptide.24 However, in their work, they could not predict the exact population. The comparison between the prediction of StrEAMM models and the MD simulation results are shown in Fig. S14.† The predicted populations by StrEAMM (1,2)+(1,3)/sys and StrEAMM (1,2)+(1,3)/random are close to the observed populations in the MD simulations. The two structures πΛZΛB and πΓZΛB with the most and the second most populations correspond to a type II′ β turn at 1GN2 and an αR tight turn at R4, which was supported by NMR experiments.243. Discussion
By considering the effects of both (1,2) and (1,3) interactions on a cyclic pentapeptide's structural preferences, we were able to use MD simulation results to train machine-learning models that are capable of quickly predicting MD-quality structural ensembles for cyclic pentapeptides in the whole sequence space. This approach greatly reduces the need to perform computationally expensive explicit-solvent simulations. Whether the predicted structural ensembles accurately match experimental results will depend on the force field used to generate the MD simulation results the model is trained on. The force field used here was the residue-specific force field 2 (RSFF2)36,37 and TIP3P water model.38 RSFF2 was previously shown to be able to recapitulate the crystal structures of 17 out of 20 cyclic peptides.39 RSFF2 was also used to predict well-structured cyclic peptides, and the predicted results were supported by solution NMR experiments.24,35 Should a different force field be preferred or an improved force field be developed, the approach reported here can be used to build new StrEAMM models for the chosen or improved force field by regenerating the MD simulation results and retraining the model.The StrEAMM model can be easily extended to larger cyclic peptides, simply by also accounting for longer-range two-body interactions beyond (1,2) and (1,3) pairs that may also be important. For example, cyclic hexapeptides tend to form a double-ended β hairpin and, in this case, we expect that the (1,4) pair that forms intramolecular hydrogen bonds can be important in influencing the structural preferences. Nonetheless, the current model performs nicely without including higher-body interactions, i.e., three-body interactions, four-body interactions, etc.
We note that when the size of the cyclic peptide increases, one can observe more pairwise interaction patterns in a single sequence. For example, a cyclic pentapeptide has 5×(1,2) pairs and 5×(1,3) pairs, while a cyclic hexapeptide has 6×(1,2) pairs, 6×(1,3) pairs, and 6×(1,4) pairs. Therefore, it is important to note that, to observe all possible patterns of two-body interactions in a semi-random training set like Dataset 3, the number of cyclic peptides that must be simulated for the training set actually decreases as the size of the cyclic peptides increases. This feature of our approach makes extendibility to larger cyclic peptides even more straightforward.
In this paper, we included 15 representative D- and L-amino acids in the StrEAMM models, but the StrEAMM method can certainly be extended to include more amino acids in the library. As an example, we extended StrEAMM (1,2)+(1,3)/sys to include 37 amino acids (both the D- and L-forms of all the common amino acids, except Pro which tends to form cis peptide bonds). The resulting model, StrEAMM (1,2)+(1,3)/sys37 was able to predict the structures of 75 new sequences with a weighted error of 4.907 (Fig. S9b and see Section 2.2.3 in the ESI† for more detail).
In the present study, we elected to explicitly build in the (1,2) and (1,3) interactions in the model for good interpretability. We are also exploring using neural networks to train the StrEAMM model, which will be more difficult to interpret but allow one to embed complicated interaction patterns more easily and further improve the model accuracy. Furthermore, to be even more efficient at incorporating various amino acids in the library, instead of using one-hot encoding, one can represent each amino acid using its chemicophysical properties40 or fingerprints41,42 to reduce the number of independent variables in the model. As an example, we trained StrEAMM models using a graph neural network (GNN) and fingerprints to encode the amino acids. When we used the 705 semi-random cyclo-(X1X2X3X4X5) peptides that contained the 15 representative amino acids (Dataset 3) as the training dataset, the resulting StrEAMM GNN/random was able to predict the structures of 50 new sequences that contained 15 amino acids with a weighted error of 1.319 (Fig. S10b and see Section 2.3 in the ESI† for more detail). Because of the use of fingerprints, StrEAMM GNN/random was able to predict structural ensembles of cyclic peptides containing amino acids not present in the training dataset. For example, it was able to predict the structural ensembles of 25 cyclic peptides that contained 37 amino acids with a weighted error of 5.232 (Fig. S10c†). We could further improve the model performance by adding in the training dataset only 50 additional sequences that contained 37 amino acids. The resulting model, StrEAMM GNN/random37 was able to predict the structural ensembles of 25 cyclic peptides that contained 37 amino acids with a weighted error of 2.953 (Fig. S11c†). These results demonstrate the modularity of the StrEAMM method and its ready extendibility.
In our current structural-digit map, the regions are well defined and fixed (Fig. 6). In general, the binning map is capable of separating the major peaks of the Ramachandran plots of all amino acids in our analysis (Fig. S13†). We expect that the model can also be extended to include beta amino acids, N-methylated amino acids, nonpeptidic linkages, etc. To describe the backbone of a beta amino acid, one needs 3 dihedral angles, and a separate binning map is needed, which can be a 3D map, and not necessary a 2D map like the Ramachandran map we used in the paper. Similarly, for cyclic peptides with nonpeptidic linkages, one would need a binning map different from the peptide backbone for the nonpeptidic linkages. The structural digits for a cyclic peptide with both peptide and nonpeptidic backbones would be a mixing of digits from the Ramachandran map and the separate maps for those special amino acids and linkages.
4. Conclusions
To our knowledge, StrEAMM is the first method capable of efficiently predicting complete MD-quality structural ensembles for cyclic peptides without direct MD simulations. For example, the new models (StrEAMM (1,2)+(1,3)/sys and StrEAMM (1,2)+(1,3)/random) developed here can be used to quickly estimate structural descriptions of previously unsimulated cyclic pentapeptides without the need to run any new MD simulations. It takes <1 second to use StrEAMM (1,2)+(1,3)/sys or StrEAMM (1,2)+(1,3)/random to make a prediction of the structural ensemble for a cyclic pentapeptide, instead of days of running and analyzing an explicit-solvent MD simulation (approximately 80 hours using 15 cores of Intel Xeon E5-2670 or 56 hours using 15 cores of Intel Xeon Gold 6248 + 1 NVIDIA Tesla T4). After being trained, a StrEAMM model can predict structural ensembles for cyclic peptides of the same ring size in the whole sequence space. Such a capability of predicting structural ensembles of both well-structured and non-well-structured cyclic peptides will greatly enhance our ability to develop cyclic peptides with desired structures and even engineer their chameleonic properties.In this paper, we apply the StrEAMM method to head-to-tail cyclized pentapeptides. The method can be readily extended to larger cyclic peptides. We also expect the StrEAMM method to work well in describing macrocycles with other types of linkers or staples. We are currently exploring these applications, as well as the use of various neural network models and different ways to encode amino acids.
5. Methods
5.1 MD simulations
The structural ensembles of cyclic peptides in water were sampled using bias-exchange metadynamics simulations32,33 with the residue-specific force field 2 (RSFF2)36,37 and TIP3P water model.38 See ESI† for details on simulation setup.5.2 Structural analysis
Conformations of cyclic pentapeptides were described by the backbone dihedrals {ϕi,ψi; i = 1–5}. We found that the structure of a β turn plus a tight turn (αL, αR, γ, or γ′ turn) used by Slough et al.24 could not describe all possible structures, so we used another method by discretizing the (ϕ, ψ) space into different regions and denoting each region with a structural digit. To do this, we first analyzed the (ϕ, ψ) space of cyclo-(GGGGG). Because Gly is achiral and the most flexible amino acid, it is assumed to provide a universal binning map that can be used by others, including both D- and L-amino acids. The (ϕ, ψ) distribution of cyclo-(GGGGG) was first clustered by a grid-based and density peak-based method with centroids identified.43 All the grid points in the Ramachandran plot were then assigned to their closest centroid, forming 10 regions, each of which was assigned a letter: Λ, λ, Γ, γ, B, β, Π, π, Z, or ζ (Fig. 6 and see Section 3 in the ESI† for more detail). As expected, the map is centrosymmetric. With this map, each conformation of a cyclic pentapeptide can be represented by a five-digit string. For example, the conformation “Πλζλβ” indicates that the first residue of the cyclic pentapeptide is in the “Π” region of the Ramachandran plot, while the second, third, fourth, and fifth residues fall in the “λ”, “ζ”, “λ”, and “β” regions, respectively.5.3 Datasets
We used data from the MD simulations to train and test the models, because experimental information of structural ensembles of cyclic peptides is scarce and difficult to obtain. Fifteen amino acids were used in this study: G, A, V, F, N, S, D, R, a, v, f, n, s, d, and r; lowercase letters denote D-amino acids. These amino acids were chosen to include Gly (achiral), and both the L- and D-form of alanine (a vanilla amino acid), valine (with β branching), phenylalanine (with an aromatic side chain), asparagine (with an amide group in the side chain), serine (with a hydroxyl group in the side chain), aspartate (with a negatively charged side chain), and arginine (with a positively charged side chain).Training dataset for Scoring Function 1.0 and StrEAMM (1,2)/sys (Dataset 1): This dataset included 106 systematic sequences: cyclo-(GGGGG), cyclo-(X1GGGG), cyclo-(X1X2GGG), and cyclo-(X1x2GGG), with Xi being one of the seven L-amino acids and xi being one of the seven D-amino acids. Generally, each sequence contained one unique nearest-neighbor pair with the rest of the sequence filled by Gly's. Gly was used as the filler amino acid because it is achiral and has no sidechains, allowing sampling the most conformational space. The enantiomers of these cyclic peptides, i.e., cyclo-(x1GGGG), cyclo-(x1x2GGG), and cyclo-(x1X2GGG) were not simulated, and their structural ensembles were inferred from the 105 simulated cyclic peptides.
Training dataset for StrEAMM (1,2)+(1,3)/sys (Dataset 2): This dataset included 204 systematic sequences: cyclo-(GGGGG), cyclo-(X1GGGG), cyclo-(X1X2GGG), cyclo-(X1x2GGG), cyclo-(X1GX2GG), and cyclo-(X1Gx2GG), with Xi being one of the seven L-amino acids and xi being one of the seven D-amino acids. Each sequence contained one unique nearest-neighbor or next-nearest-neighbor pair with the rest of the sequence filled by Gly's. Again, the enantiomers of these cyclic peptides were not simulated, and their structural ensembles were inferred from the 203 simulated cyclic peptides.
Training dataset for StrEAMM (1,2)+(1,3)/random (Dataset 3): This dataset included 705 “random” sequences that were generated using the following protocol. When building the sequence pool, we required (1) the number of sequences to be as small as possible, (2) X1_X2 to sandwich all the possible amino acids, i.e., all X1X2X3 patterns were observed, (3) no enantiomers and (4) not double-counting sequences that were the same cyclic peptides after cyclic permutation. See List S3 in the ESI† for the sequences of the 705 random cyclic peptides.
Test dataset (Dataset 4): 50 random sequences were used as the test dataset. It was ensured that there were no equivalent sequences after cyclic permutation and there were no two sequences that were enantiomers to each other. See List S2 in the ESI† for the sequences of the 50 test cyclic peptides.
5.4 Training of StrEAMM models
Details on how the weights in StrEAMM (1,2)/sys, StrEAMM (1,2)+(1,3)/sys, and StrEAMM (1,2)+(1,3)/random were obtained can be found in the ESI.†Data availability
Due to their large size, the MD simulation datasets are not publicly available but are available from the authors upon request.Author contributions
J. M. and Y.-S. L. designed the study. J. M. performed the simulations and analysis of the data. J. M. and Y.-S. L. discussed the results and wrote the manuscript. M. L. D. extended the StrEAMM models using GNN and fingerprint representations for amino acids.Conflicts of interest
Two provisional patent applications entitled “Cyclic peptide structure prediction via structural ensembles achieved by molecular dynamics and machine learning” were filed on 2021/6/14 and 2021/10/14.Acknowledgements
This work was supported by the National Institute of General Medical Sciences of the National Institutes of Health under award number R01GM124160 (PI: Y.-S. L.). M. L. D. thanks the support from the Tufts Summer Scholars Program and the T-Tripods Institute at Tufts (NSF 1934553). We are also grateful for the support from the Tufts Technology Services and for the computing resources at the Tufts Research Cluster. Initial structures for the simulations were built using UCSF Chimera, developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco, with support from NIH Grant P41-GM103311. We thank Professor Joshua Kritzer, Professor Matthew Shoulders, and the YSL group members for their invaluable feedback on the manuscript.References
- E. M. Driggers, S. P. Hale, J. Lee and N. K. Terrett, Nat. Rev. Drug Discovery, 2008, 7, 608–624 CrossRef CAS PubMed.
- M. R. Naylor, A. T. Bockus, M. J. Blanco and R. S. Lokey, Curr. Opin. Chem. Biol., 2017, 38, 141–147 CrossRef CAS PubMed.
- D. S. Nielsen, N. E. Shepherd, W. Xu, A. J. Lucke, M. J. Stoermer and D. P. Fairlie, Chem. Rev., 2017, 117, 8094–8128 CrossRef CAS PubMed.
- J. Witek, B. G. Keller, M. Blatter, A. Meissner, T. Wagner and S. Riniker, J. Chem. Inf. Model., 2016, 56, 1547–1562 CrossRef CAS PubMed.
- J. Witek, M. Muhlbauer, B. G. Keller, M. Blatter, A. Meissner, T. Wagner and S. Riniker, Chemphyschem, 2017, 18, 3309–3314 CrossRef CAS PubMed.
- J. Witek, S. Wang, B. Schroeder, R. Lingwood, A. Dounas, H. J. Roth, M. Fouche, M. Blatter, O. Lemke, B. Keller and S. Riniker, J. Chem. Inf. Model., 2019, 59, 294–308 CrossRef CAS PubMed.
- S. Ono, M. R. Naylor, C. E. Townsend, C. Okumura, O. Okada and R. S. Lokey, J. Chem. Inf. Model., 2019, 59, 2952–2963 CrossRef CAS PubMed.
- A. Liwo, A. Tempczyk, S. Oldziej, M. D. Shenderovich, V. J. Hruby, S. Talluri, J. Ciarkowski, F. Kasprzykowski, L. Lankiewicz and Z. Grzonka, Biopolymers, 1996, 38, 157–175 CrossRef CAS PubMed.
- E. Haensele, L. Banting, D. C. Whitley and T. Clark, J. Mol. Model., 2014, 20, 2485 CrossRef PubMed.
- E. Yedvabny, P. S. Nerenberg, C. So and T. Head-Gordon, J. Phys. Chem. B, 2015, 119, 896–905 CrossRef CAS PubMed.
- E. Haensele, N. Saleh, C. M. Read, L. Banting, D. C. Whitley and T. Clark, J. Chem. Inf. Model., 2016, 56, 1798–1807 CrossRef CAS PubMed.
- A. Zorzi, K. Deyle and C. Heinis, Curr. Opin. Chem. Biol., 2017, 38, 24–29 CrossRef CAS PubMed.
- D. S. Wishart, Y. D. Feunang, A. C. Guo, E. J. Lo, A. Marcu, J. R. Grant, T. Sajed, D. Johnson, C. Li, Z. Sayeeda, N. Assempour, I. Iynkkaran, Y. Liu, A. Maciejewski, N. Gale, A. Wilson, L. Chin, R. Cummings, D. Le, A. Pon, C. Knox and M. Wilson, Nucleic Acids Res., 2018, 46, D1074–D1082 CrossRef CAS PubMed.
- X. Jing and K. Jin, Med. Res. Rev., 2020, 40, 753–810 CrossRef CAS PubMed.
- T. Rezai, J. E. Bock, M. V. Zhou, C. Kalyanaraman, R. S. Lokey and M. P. Jacobson, J. Am. Chem. Soc., 2006, 128, 14073–14080 CrossRef CAS PubMed.
- A. Whitty, M. Zhong, L. Viarengo, D. Beglov, D. R. Hall and S. Vajda, Drug Discovery Today, 2016, 21, 712–717 CrossRef CAS PubMed.
- P. G. Dougherty, A. Sahni and D. Pei, Chem. Rev., 2019, 119, 10241–10287 CrossRef CAS PubMed.
- B. Over, P. Matsson, C. Tyrchan, P. Artursson, B. C. Doak, M. A. Foley, C. Hilgendorf, S. E. Johnston, M. D. t. Lee, R. J. Lewis, P. McCarren, G. Muncipinto, U. Norinder, M. W. Perry, J. R. Duvall and J. Kihlberg, Nat. Chem. Biol., 2016, 12, 1065–1074 CrossRef CAS PubMed.
- D. D. Boehr, R. Nussinov and P. E. Wright, Nat. Chem. Biol., 2009, 5, 789–796 CrossRef CAS PubMed.
- I. J. Chen and N. Foloppe, Bioorg. Med. Chem., 2013, 21, 7898–7920 CrossRef CAS PubMed.
- V. Poongavanam, E. Danelius, S. Peintner, L. Alcaraz, G. Caron, M. D. Cummings, S. Wlodek, M. Erdelyi, P. C. D. Hawkins, G. Ermondi and J. Kihlberg, ACS Omega, 2018, 3, 11742–11757 CrossRef CAS PubMed.
- V. Poongavanam, Y. Atilaw, S. Ye, L. H. E. Wieske, M. Erdelyi, G. Ermondi, G. Caron and J. Kihlberg, J. Pharm. Sci., 2021, 110, 301–313 CrossRef CAS PubMed.
- P. Hosseinzadeh, G. Bhardwaj, V. K. Mulligan, M. D. Shortridge, T. W. Craven, F. Pardo-Avila, S. A. Rettie, D. E. Kim, D. A. Silva, Y. M. Ibrahim, I. K. Webb, J. R. Cort, J. N. Adkins, G. Varani and D. Baker, Science, 2017, 358, 1461–1466 CrossRef CAS PubMed.
- D. P. Slough, S. M. McHugh, A. E. Cummings, P. Dai, B. L. Pentelute, J. A. Kritzer and Y. S. Lin, J. Phys. Chem. B, 2018, 122, 3908–3919 CrossRef CAS PubMed.
- N. el Tayar, A. E. Mark, P. Vallat, R. M. Brunne, B. Testa and W. F. van Gunsteren, J. Med. Chem., 1993, 36, 3757–3764 CrossRef CAS PubMed.
- H. Morita, Y. S. Yun, K. Takeya, H. Itokawa and M. Shiro, Tetrahedron, 1995, 51, 5987–6002 CrossRef CAS.
- Y. Chen, K. Deng, X. Qiu and C. Wang, Sci. Rep., 2013, 3, 2461 CrossRef PubMed.
- C. Merten, F. Li, K. Bravo-Rodriguez, E. Sanchez-Garcia, Y. Xu and W. Sander, Phys. Chem. Chem. Phys., 2014, 16, 5627–5633 RSC.
- J. S. Quartararo, M. R. Eshelman, L. Peraro, H. Yu, J. D. Baleja, Y. S. Lin and J. A. Kritzer, Bioorg. Med. Chem., 2014, 22, 6387–6391 CrossRef CAS PubMed.
- D. P. Slough, S. M. McHugh and Y. S. Lin, Biopolymers, 2018, 109, e23113 CrossRef PubMed.
- S. M. McHugh, J. R. Rogers, H. Yu and Y. S. Lin, J. Chem. Theory Comput., 2016, 12, 2480–2488 CrossRef CAS PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- S. Piana and A. Laio, J. Phys. Chem. B, 2007, 111, 4553–4559 CrossRef CAS PubMed.
- S. M. McHugh, H. Yu, D. P. Slough and Y. S. Lin, Phys. Chem. Chem. Phys., 2017, 19, 3315–3324 RSC.
- A. E. Cummings, J. Miao, D. P. Slough, S. M. McHugh, J. A. Kritzer and Y. S. Lin, Biophys. J., 2019, 116, 433–444 Search PubMed.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725 CrossRef CAS PubMed.
- C. Y. Zhou, F. Jiang and Y. D. Wu, J. Phys. Chem. B, 2015, 119, 1035–1047 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- H. Geng, F. Jiang and Y. D. Wu, J. Phys. Chem. Lett., 2016, 7, 1805–1810 CrossRef CAS PubMed.
- A. Yousef and N. M. Charkari, J. Biomed. Inf., 2015, 56, 300–306 CrossRef PubMed.
- H. L. Morgan, J. Chem. Doc., 1965, 5, 107–113 CrossRef CAS.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- A. Rodriguez and A. Laio, Science, 2014, 344, 1492–1496 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc05562c |
| This journal is © The Royal Society of Chemistry 2021 |