Open Access Article
Open Access ArticleProton solvent-controllable synthesis of manganese oxalate anode material for lithium-ion batteries
Ya-Nan Zhanga,
Shu-Shu Lia,
Hong-Xiang Kuai a,
Yun-Fei Longa,
Xiao-Yan Lvc,
Jing Sua and
Yan-Xuan Wen*ab
a,
Yun-Fei Longa,
Xiao-Yan Lvc,
Jing Sua and
Yan-Xuan Wen*ab
aSchool of Chemistry and Chemical Engineering, Guangxi University, Nanning, Guangxi 530004, China. E-mail: wenyanxuan@vip.163.com
bGuangxi Key Laboratory of Processing for Non-ferrous Metallic and Featured Materials, Guangxi University, Nanning, 530004, China
cThe New Rural Development Research Institute, Guangxi University, Nanning 530004, Guangxi, China
First published on 1st July 2021
Abstract
Manganese oxalates with different structures and morphologies were prepared by the precipitation method in a mixture of dimethyl sulfoxide (DMSO) and proton solvents. The proton solvents play a key role in determining the structures and morphologies of manganese oxalate. Monoclinic MnC2O4·2H2O microrods are prepared in H2O-DMSO, while MnC2O4·H2O nanorods and nanosheets with low crystallinity are synthesized in ethylene glycol-DMSO and ethanol-DMSO, respectively. The corresponding dehydrated products are mesoporous MnC2O4 microrods, nanorods, and nanosheets, respectively. When used as anode material for Li-ion batteries, mesoporous MnC2O4 microrods, nanorods, and nanosheets deliver a capacity of 800, 838, and 548 mA h g−1 after 120 cycles at 8C, respectively. Even when charged/discharged at 20C, mesoporous MnC2O4 nanorods still provide a reversible capacity of 647 mA h g−1 after 600 cycles, exhibiting better rater performance and cycling stability. The electrochemical performance is greatly influenced by the synergistic effect of surface area, morphology, and size. Therefore, the mesoporous MnC2O4 nanorods are a promising anode material for Li-ion batteries due to their good cycle stability and rate performance.
1. Introduction
Since their success in the 1990s, Li-ion batteries (LIBs) have become a promising candidate for large-scale energy storage systems (ESSs) and (hybrid) electric vehicles (EVs).1–3 To meet the rapid development of ESSs and EVs, the next-generation LIBs need to further improve their energy/power density, cycle life, and safety.4 Anode materials play a key role in determining the performance of LIBs. However, the low specific capacity (372 mA h g−1) and poor reaction kinetics limit the application of traditional graphite in the next-generation LIBs.4,5 Therefore, it is still a challenge to develop advanced anode materials to replace graphite anode.4,6–10The Tirado group's works show that conversion reaction-based transition metal oxalates are promising anode materials with high reversible specific capacity for the next-generation LIBs.11–16 For example, the capacity of CoC2O4 (∼900 mA h g−1) is more than twice that of graphite.17 However, the cost and toxicity of cobalt limit the application of CoC2O4. Compared with cobalt oxalate, manganese oxalate is more suitable to be used as anode material for LIBs due to its abundant resources, low toxicity, and small volume change during charge/discharge processes.11,20 However, the cyclic-stability and the rate performance of manganese oxalate are lower than those of cobalt oxalate.11,20 Therefore, it is necessary to further improve the performance of manganese oxalate.
Like other transition metal oxalates,15,16 the poor performance of manganese oxalate originates from its low conductivity. Designing nano-structural electrode material is an effective approach to overcome this drawback15–17 because of its improved electrode kinetics and structural stability.18 For example, FeC2O4 nanorod delivered a capacity of 640 mA h g−1 after 100 cycles at 10C, exhibiting an enhanced performance.17 Among the approaches to synthesize nanostructured transition metal oxalates, the most common used method is the precipitation method due to its low cost and ease of mass production.17,19–27 The precipitation reaction of transition metal oxalates in strong protic solvent (H2O) is very fast due to their insolubilities in water, making it difficult to control their nucleation and growth processes to obtain the desired morphology. To overcome this difficulty, aprotic solvents have been used to regulate the precipitation reaction, nucleation, and growth of transition metal oxalates.17,20–27 Therefore, many efforts have been carried out to investigate the effects of temperature and time,17,22 aprotic solvent,23,24 and water content25–27 on the synthesis of oxalate in H2O-aprotic solvents. For example, higher temperature and longer time can reinstitute the hydrogen bonds between interlayers, resulting in various structures and morphologies.17,22 Madhavi et al.23,24 have prepared different morphologies of CoC2O4·2H2O and FeC2O4·2H2O in H2O-DEAc and H2O-NMP, which can be ascribed to the selective interaction between the aprotic solvents and crystallographic planes. Zhang et al.,25 Shen et al.26 and Madhavi et al.27 pointed out that water content in the mixed solvents can change the polarity, viscosity, and ionization power of the solvent and the anisotropic growth of oxalates, resulting in various morphologies. In addition to temperature and time,17,22 aprotic solvents,23,24 and the water content,25–27 the proton solvent also has an important influence on the properties of the reaction medium such as the polarity, viscosity, and ionization power, which also affects the nucleation and growth process of manganese oxalate, thus affecting its structure and morphology. However, there are few reports about proton solvents could control the structure and morphology of transition metal oxalates.
In this work, manganese oxalates with various structures and morphologies were prepared via precipitation method in H2O-DMSO, ethanol (ET)-DMSO, and ethylene glycol (EG)-DMSO, respectively. The effects of proton solvents (water, ethanol, and ethylene glycol) on the structure and morphology of manganese oxalate were studied. It is found that proton solvents can adjust the structure and morphology of manganese oxalate. Among them, the mesoporous MnC2O4 nanorod prepared in EG-DMSO can provide a reversible specific capacity of 838 mA h g−1 after 120 cycles at 8C, exhibiting good rate performance and cyclic-stability.
2. Experimental
2.1 Materials synthesis
All of the reagents are analytic grade and purchased from Xilong Chemical Reagent Co. Ltd. 20 mmol H2C2O4·2H2O was dissolved in 75 ml of DMSO to form a solution A. 20 mmol MnAc2·4H2O was dissolved in 25 ml of deionized water, ethanol, and ethylene glycol to form a solution B, C, and D, respectively. Solution B, C, and D were added dropwise to solution A, respectively. After vigorously stirring for 10 minutes at 40 °C, the precipitate was filtered and washed with water to get a hydrated manganese oxalate precursor. The precursor was dried under vacuum at 150 °C for 3 h to obtain dehydrated manganese oxalate.2.2 Materials characterization
The phase, crystal structure, and morphology of the prepared samples were characterized by X-ray diffraction (XRD, Rigaku Ultima IV, Rigaku Corporation, Tokyo, Japan), scanning electron microscopy (SEM, S-3400N, Hitachi, Ltd., Tokyo, Japan), and transmission electron microscope (Tecnai G2 F20, FEI Corporation, Oregon State, USA). Thermogravimetric analysis (TG, SDT-Q600, TA, DE, USA) was performed under nitrogen at a temperature rise rate of 10 °C min−1−1 from room temperature to 600 °C. X-ray photoelectron spectroscopy (XPS, Thermo Fisher Scientific, ESCALAB 250XI+, USA) was applied to measure the surface condition of the prepared samples. The products were also characterized with Fourier-transform infrared (FT-IR; IS50, Thermo Nicolet, USA) spectroscopy. A Micromeritics TriStar II 3020 surface area and porosity analyzer (Micromeritics Instruments Corporation, Georgia, USA) was used to perform N2 adsorption/desorption isotherm experiments, and the specific surface area and the pore size distribution were calculated by the Brunauer–Emmett–Teller (BET) and Barrett–Joyner–Halenda (BJH) methods.2.3 Electrochemical measurements
The electrochemical performances of the prepared dehydrated manganese oxalate were evaluated by CR2032-type coin half-cells. The CR2032 cell was assembled in a glovebox in a dry, high-purity argon atmosphere. The CR2032 cell was composed of a working electrode, a lithium foil anode, a polypropylene porous separator (Celegard 2400), and an electrolyte (1 M LiPF6 + 1% VC/EC-DEC-EMC). To prepare the working electrode, the prepared dehydrated manganese oxalate, acetylene black, and Li-PAA binder were mixed thoroughly in water with a mass ratio of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, and then the mixed slurry was coated on a copper foil and dried under vacuum at 120 °C overnight. The working electrode was punched and weighed. The galvanostatic charge/discharge tests were carried out on a battery cycler (BTS 4000, Shenzhen NEWARE Electronics Co., Ltd., Shenzhen, China) under different C rates in range of 0.01–3.0 V (vs. Li/Li+) at 25 °C, and 1C is 375 mA g−1. The active material load is 0.9 ± 0.1 mg cm−2. The specific capacity and the charge/discharge current were calculated according to the mass of the dehydrated manganese oxalate in the working electrode. The interface 1010E electrochemical workstation (Gamry Instruments, Warminster, USA) was used to perform cyclic voltammetry (CV) in the range of 0.01–3.0 V and electrochemical impedance spectroscopy (EIS) from 105 Hz to 10−3 Hz at 25 °C.
10, and then the mixed slurry was coated on a copper foil and dried under vacuum at 120 °C overnight. The working electrode was punched and weighed. The galvanostatic charge/discharge tests were carried out on a battery cycler (BTS 4000, Shenzhen NEWARE Electronics Co., Ltd., Shenzhen, China) under different C rates in range of 0.01–3.0 V (vs. Li/Li+) at 25 °C, and 1C is 375 mA g−1. The active material load is 0.9 ± 0.1 mg cm−2. The specific capacity and the charge/discharge current were calculated according to the mass of the dehydrated manganese oxalate in the working electrode. The interface 1010E electrochemical workstation (Gamry Instruments, Warminster, USA) was used to perform cyclic voltammetry (CV) in the range of 0.01–3.0 V and electrochemical impedance spectroscopy (EIS) from 105 Hz to 10−3 Hz at 25 °C.
3. Results and discussion
3.1 Structure and morphology characterization
To investigate the effect of proton solvents, the hydrated manganese oxalate precursors were synthesized in H2O-DMSO, ET-DMSO, and EG-DMSO, which were named WH, EH, and GH, respectively. After the dehydration, the corresponding dehydrated manganese oxalates were obtained and named WA, EA, and GA, respectively. XRD, XPS, FT-IR, TG, SEM, and TEM were used to characterize the phase, the structure, and the morphology of the prepared precursors and their dehydrated products.Fig. 1 presents the XRD spectra of the precursors and their dehydrated products. As shown in Fig. 1(a), the precursor prepared in H2O-DMSO can be indexed to monoclinic α-phase MnC2O4·2H2O with a C2/c space group (PDF # 25-0544).13,31 As depicted in Fig. 1(a), the crystallinities of the precursors synthesized in ET-DMSO and EG-DMSO are poor, and their characteristic peaks cannot be indexed into the monoclinic structure (PDF # 25-0544) and the orthorhombic structure (PDF # 32-0647).30 The different structures of the precursors can be ascribed to the different microenvironments of Mn2+ in different solvents. When manganese acetate is dissolved in water, it reacts with water to form a solvated manganese ion [Mn(H2O)n]sol2+.27 When [Mn(H2O)n]sol2+ is added to the aprotic solvent DMSO, DMSO cannot replace the water in [Mn(H2O)n]sol2+ and coordinates with manganese ion, because the solvation ability of DMSO is far less than that of H2O.29 Only water molecules exist in the first solvation layer of Mn2+ in H2O-DMSO, so the microenvironment of Mn2+ in H2O-DMSO is the same as that of Mn2+ in single solvent water.28–30 Therefore, the precursor obtained in H2O-DMSO is consistent with that in aqueous solution.13,31 When MnAc2·4H2O is dissolved in protonic solvents ET and EG, since the amount of crystallization water in MnAc2·4H2O is much less than that of ET and EG, ET and EG can coordinate with Mn2+ to form [Mn(EA)n]sol2+ and [Mn(EG)n]sol2+.28–30 Therefore, the microenvironment of Mn2+ in ET-DMSO and EG-DMSO is different from that in H2O-DMSO,28,29 thus resulting in different structures. As displayed in Fig. 1(b), the XRD pattern of the dehydrated product WA is consistent with orthorhombic β-phase MnC2O4 with Pmna space group (PDF # 32-0646), indicating that the monoclinic structure transforms into the orthorhombic structure after dehydration.13,31 The crystallinity of the dehydrated products EA and GA are still poor. To further determine the composition and the structure of EA and GA, Fig. 1(c) compares them with other manganese-based materials. As seen in Fig. 1(c), the XRD patterns of EA and GA are different from those of MnCO3 (PDF#85-1109), MnO (PDF#71-1177), Mn2O3 (PDF#76-0150), Mn3O4 (PDF#130162) and MnO2 (PDF#42-1169), suggesting that EA and GA is not MnCO3, MnO, Mn2O3, Mn3O4, and MnO2.
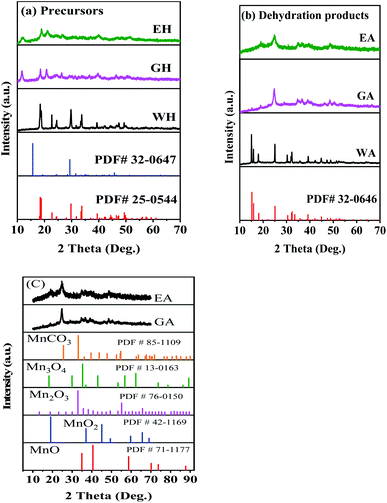 | ||
| Fig. 1 XRD patterns: (a) precursors, (b) dehydrated products prepared in different solvents, and (c) comparison with other Mn-based materials. | ||
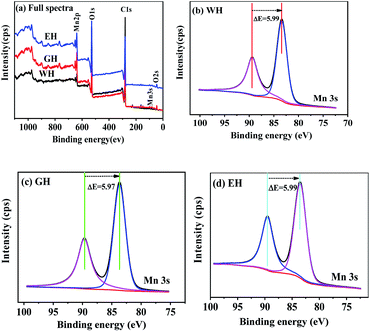
Fig. 2 shows XPS spectra of the precursors. As shown in Fig. 2(a), the precursors prepared in three types of solvents have similar XPS spectra, which consist of the peaks related Mn, O, and C, respectively. In XPS, the characteristic peak of Mn2p3/2 and Mn3s is related to the oxidation state of manganese. However, the characteristic peak of Mn2p3/2 is not suitable for analyzing the oxidation state of manganese because it can be affected by the difference coordination environment of manganese.32 On the other hand, Mn3s electrons exhibit unique bimodal structure due to its photoelectric effect.33 The interval of this bimodal structure varies according to the oxidation state of Mn, that is, MnO (Mn2+) ∼6.0 eV, Mn2O3 (Mn3+) ∼5.3 eV, and MnO2 (Mn4+) ∼4.7 eV.33 Therefore, Mn3s is more suitable than Mn2p3/2 to determine the oxidation state of manganese. As shown in Fig. 2(b–d), the two peaks at 83 and 89 eV are the characteristic peak of Mn3s.32,33 For WH, GH, and EH, the bimodal interval of Mn3s is 5.99, 5.97, and 5.99 eV respectively, which is close to that of Mn2+ (6.0 eV). XPS results show that the precursors prepared in H2O-DMSO, ET-DMSO, and EG-DMSO are divalent manganese compounds containing Mn, C, and O.
Fig. 3(a) presents FT-IR spectra of the prepared precursors. As shown in Fig. 3(a), the precursors prepared in H2O-DMSO, ET-DMSO, and EG-DMSO have similar FT-IR spectra. The peak at 1361 and 1317 cm−1 corresponds to the asymmetric and symmetric stretching vibrations of C–O, respectively, and the peak at 1590 cm−1 is attributed to the stretching vibration of the carbonyl group, indicating that the four oxygen atoms of oxalate anion coordinate with Mn2+.20,34,35 The band at 540 cm−1 originates from Mn–O, and the strong peak at 805 cm−1 is related to C–C–O asymmetric vibration.20,34,35 The large broad peak at 3385 cm−1 indicates the presence of crystalline water.20,34,35 To further gain insight into EH and GH, we employed Raman spectroscopy to characterize three precursors. As shown in Fig. 3(b), WH, EH and GH display prominent peaks at 516, 903, 1470, 1610, and 3335 cm−1, which agree well with the previously reported metal oxalates.36,37 The results of FT-IR and Raman spectra analysis demonstrate that the three precursors are hydrated manganese oxalate (MnC2O4·xH2O).
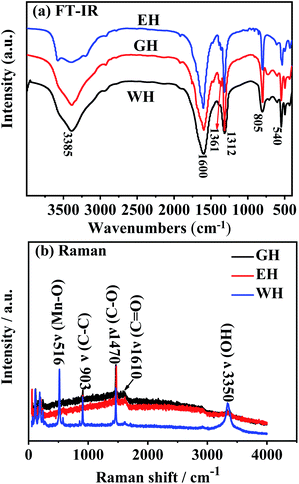 | ||
| Fig. 3 (a) FT-IR spectra and (b) Raman spectra for the precursors prepared in H2O-DMSO, ET-DMSO and EG-DMSO. | ||
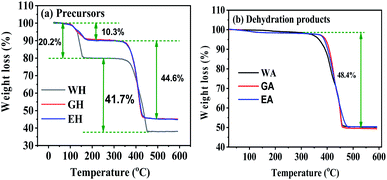
Fig. 4 gives the TG curves for the precursors and the dehydrated products. The TG curves of the precursors in Fig. 4(a) have are two distinct weight loss stages, and the corresponding temperature range is 100 to 200 °C and 300 to 450 °C, respectively. The weight loss of WH in the first stage is 20.27%, which is close to the theoretical weight loss of the dehydration reaction of MnC2O4·2H2O (MnC2O4·2H2O = MnC2O4 + 2H2O, 20.1 wt%).31 The weight loss of EH and GH in the first stage is 10.3%, which is close to the theoretical weight loss of the dehydration reaction of MnC2O4·H2O (MnC2O4·H2O = MnC2O4 + H2O, 11.1 wt%). The weight loss of WH in the second stage (41.7%) is close to the theoretical weight loss of MnC2O4·2H2O decomposition into MnO (MnC2O4·2H2O = MnO + CO + CO2 + H2O, 40.2 wt%),25,31 while the weight loss of GH and EH in the second stage (44.6%) is close to the theoretical weight loss of MnC2O4·H2O decomposition into MnO (MnC2O4·H2O = MnO + CO + CO2 + H2O, 44.4 wt%). As given in Fig. 4(b), the weight loss is 48.4% between 300 and 450 °C for the three dehydrated products, which is close to the theoretical weight loss of the decomposition of anhydrous MnC2O4 to MnO (MnC2O4 = MnO + CO + CO2, 49.6 wt%).25,31 Thus, the precursor prepared in H2O-DMSO is MnC2O4·2H2O, and that prepared in ET-DMSO and EG-DMSO is MnC2O4·H2O. All dehydration products are anhydrous manganese oxalate MnC2O4.
Fig. 5 exhibits the SEM images of the precursors and their dehydrated products. As seen in Fig. 5, the proton solvent has a great influence on the morphology and the size of the precursors. The precursor WH prepared with DMSO-H2O is microrods with a length of about 30–40 μm and a diameter of about 1–3 μm (Fig. 5(a)). The precursor GH synthesized by DMSO-EG is one-dimensional nanorods with a diameter of 70–100 nm and a length of 1–1.5 μm (Fig. 3(c)), while precursor EH synthesized with ET-DMSO is composed of many irregular nanosheets with a length of 1–3 μm and a width of 500–800 nm (Fig. 3(e)). The morphologies of the dehydrated products in Fig. 5(b, d and f) are similar to those of the corresponding precursors. The dehydrated product has some cracks or pores due to the removal of crystalline water.17–27,31
 | ||
| Fig. 5 SEM images of the prepared precursors in different solvents (a, c and e) and the corresponding dehydration products (b, d and f). | ||
Fig. 6 displays the microstructure of MnC2O4 prepared in EG-DMSO and ET-DMSO. The GA is one-dimensional rod with porous structure (Fig. 6(a and c)), and the lattice fringes with a spacing of 0.36 nm can match the (200) crystalline plane of MnC2O4 (Fig. 6(e)). EA is a porous nanosheet (Fig. 6(b and d)), but there are no obvious lattice fringes (Fig. 6(f)).
 | ||
| Fig. 6 TEM images of MnC2O4 from precursors prepared in (a, c and e) EG-DMSO and (b, d and f) ET-DMSO. | ||
N2 isothermal absorption/desorption experiments were performed to further investigate the porous structure of the prepared samples. Fig. 7 gives the measured absorption/desorption curves, and Table 1 lists the surface area, pore size, and pore volume calculated from the absorption/desorption data. As presented in Fig. 7(a), WH has a type III isotherm adsorption/desorption curves, suggesting that the precursors are non-porous particles,38 which is further confirmed by the lower specific surface area and the pore volume listed in Table 1. However, GH and EH have H3-type hysteresis loop with higher surface area because of their nanostructure.38 All anhydrous manganese oxalates have a H3-type hysteresis loop at a relative pressure of 0.5–1.0, indicating their mesoporous structure.38 As seen in Table 1, the specific surface areas and the pore volumes of the dehydrated products are larger than those of the hydrated precursors, indicating that the removal of crystalline water can produce more pores, thus increasing the specific surface areas and pore volumes. Compared with WA, EA and GA have larger specific surface areas and pore volumes, which can provide more active sites and more channels for Li+ migration. Therefore, EA and GA should have better electrochemical performances.
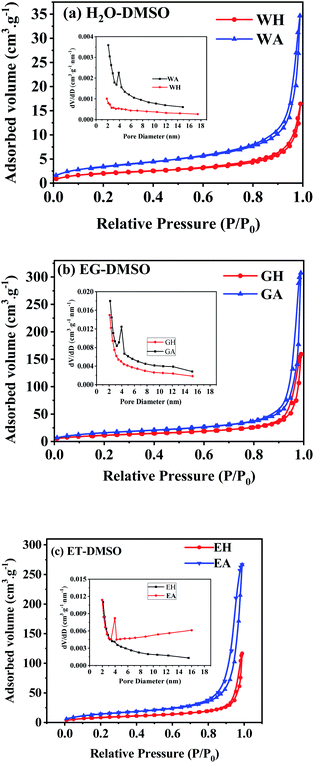 | ||
| Fig. 7 N2 isothermal absorption/desorption curves of the samples prepared in different solvents: (a) H2O-DMSO, (b) EG-DMSO, and (c) ET-DMSO. | ||
| Sample | Specific surface area (m2 g−1) | Mean pore size (nm) | Pore volume (10−2 cm3 g−1) |
|---|---|---|---|
| WH | 7.4 | 5.26 | 0.97 |
| GH | 43.4 | 4.97 | 5.85 |
| EH | 28.6 | 5.32 | 3.94 |
| WA | 12.1 | 5.27 | 1.32 |
| GA | 58.6 | 5.55 | 8.34 |
| EA | 48.9 | 5.94 | 7.73 |
3.2 Formation process of manganese oxalate
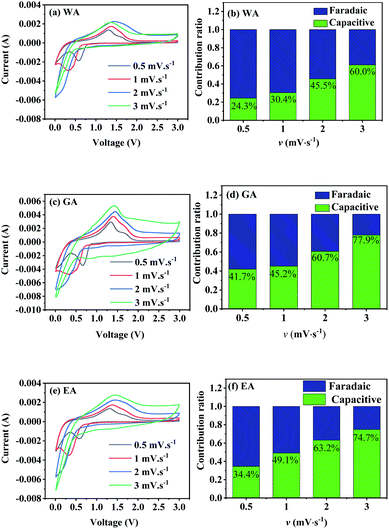
Hydrated manganese oxalate precipitation can be expressed by the following processes.
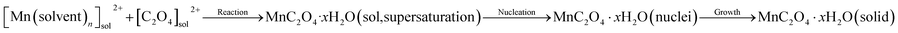 | (1) |
In eqn (1), the precipitation of hydrated manganese oxalate includes chemical reaction, nucleation and growth. When MnAc2·4H2O is dissolved in protonic solvents H2O, EG, and ET, the solvated manganese cations [Mn(H2O)n]sol2+, [Mn(EG)n]sol2+, and [Mn(ET)n]sol2+ are formed, respectively. However, oxalic acid cannot be dissociated in aprotic solvent DMSO and exists in the form of oxalic acid molecule. After adding the protonic solvents containing [Mn(solvent)n]sol2+ into DMSO, oxalic acid is dissociated into solvated hydrogen ions [H(solvent)n]sol+ and C2O42−. Therefore, the dissociation rate of oxalic acid and the concentration of C2O42− depend on the ionization power of proton solvent. According to eqn (1), the supersaturation of MnC2O4·xH2O is also determined by the ionization power of the proton solvent. The ionization power of the proton solvent is positively correlated with the electronegativity of hydroxyl (–OH) group.39 The electronegativity of hydroxyl group in the three solvents is H2O ≫ ET > EG, that is, the ionization power of the three proton solvents is H2O ≫ ET > EG.39 Therefore, the supersaturation of MnC2O4·xH2O in H2O-DMSO is much greater than that in ET-DMSO and EG-DMSO. The higher supersaturation means the faster of the nucleation rate and the growth rate, and larger particles will be formed. Therefore, the size of MnC2O4·xH2O particles prepared in H2O-DMSO is much larger than those prepared in ET-DMSO and EG-DMSO, which further explain micro-sized WH and nanosized GH and EH shown in Fig. 3.
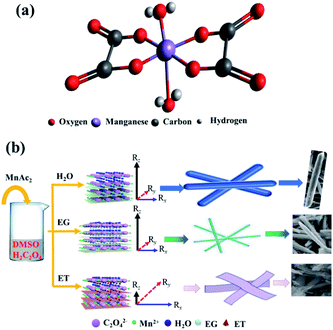
The morphology of MnC2O4·xH2O is not only related to its supersaturation, but also to the crystal structures and the interactions between solvents and crystal. Fig. 8 illustrates the formation process of MnC2O4·xH2O with different morphology, where Rz is growth direction vectors perpendicular to the crystal plane, and Rx and Ry are growth direction vectors, which are parallel to the crystal plane. As shown in Fig. 8(a), manganese atoms in MnC2O4·xH2O coordinate with two oxalate anions in the equatorial plane and the two coordinated water molecules in the axial direction, forming a square planar configuration with Mn2+ as the center.40 The preferred growth direction of MnC2O4·xH2O is perpendicular to the molecular plane (Rz), rather than that parallel to the molecular plane (Rx and Ry) due to the hydrogen bond and π–π interactions between adjacent molecules. Therefore, MnC2O4·xH2O mainly grows in the face-to-face stacking of square plane, which tends to form one-dimensional structure in H2O or mixed solvents with high water content.23,27,31 Similar phenomena have been found in other transition metal oxalates.17,19–26,34,35 The hydrogen bond formed by water is the strongest, followed by ethylene glycol and ethanol. Therefore, the hydrogen bond and π–π interaction in adjacent molecules follow the same order: H2O > EG > ET. As displayed in Fig. 8(b), MnC2O4·xH2O tends to grow in one-dimension rod-like structure in H2O-DMSO and EG-DMSO due to the strong hydrogen bond and π–π interaction in the adjacent molecules of H2O or EG.17,19–27,27,34,35 However, the growth perpendicular to the plane (Rz) is greatly weakened due to the weak hydrogen bond and π–π interaction between adjacent molecules in ET-DMSO. Therefore, MnC2O4·xH2O tends to grow in two dimensions and form sheet-like structure in ET-DMSO. In addition, the difference of surface energy between crystal planes41,42 and the selective interaction between the crystal surface and solvent23,24 also promote the anisotropic growth of crystal, which is conducive to obtaining MnC2O4·xH2O particles with special morphology.
3.3 Electrochemical performance
The performances of the prepared MnC2O4 were evaluated by various electrochemical technologies. Fig. 9(a–c) give the galvanostatic charge/discharge curves of as-synthesized MnC2O4 at 5C in the range of 0–3 V. All discharge curves are composed of three parts: a rapid decline curve from 3.0 to 0.3 V, a discharge platform at 0.3 V, and a slope below 0.3 V. The platform at 0.3 V can be attributed to the conversion reaction of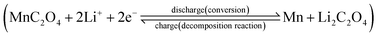 .11,13,20,31 The slope below 0.3 V corresponds to the pseudo capacitance behavior of the polymer surface gel layer and the interface lithium storage behavior.11,13,17,19–27,31,41 After 1st cycle, there is a small plateau at ∼0.8 V related to the SEI film formation.11,13,20,31 As shown in Fig. 9(a, c and e), there are some differences in the voltage platforms (such as discharge platform voltage, platform width, etc.). The possible reason is that the volume expansion of EA during the discharge/discharge process causes the formation of the larger agglomerates, which makes the polarization larger and reduces the reversibility of the conversion reaction. The initial coulombic efficiency of WA, GA and EA is 49%, 48%, and 50%, respectively. The lower initial coulombic efficiency can be ascribed to the irreversible crystal-to-amorphous transformation and the formation of SEI film during the first discharge,11,13,20,31 which is a common phenomenon for the conversion electrodes.15–17,19,21–27,41 The cyclic-stability and the rate performance are given in Fig. 9(d–g). As shown in Fig. 9 (d–g), the discharge capacity decreases first and then increases at the initial stage due to the formation and activation of the polymeric gel-like layer.11,13,17,19–27,31,41 This polymeric gel-like layer formed in the first discharge is irreversible and gradually thickened during the initial cycles,15,16,31 which hinders the diffusion of Li+ and the conversion reaction. As a result, the capacity decreases with the increase of cycles in the initial charge/discharge processes. However, this polymeric gel-like layer can be gradually activated and becomes reversible after several cycles.15,16,31 Therefore, the capacity increases gradually after several cycles. As shown in Fig. 9(d–g), the cycle stability and the rate performance of manganese oxalate are nanorods > microrods > nanosheets. Manganese oxalate nanorods deliver a discharge capacity of 1509, 983, 938 and 838 mA h g−1 at 3, 5, and 8C, respectively. As shown in Fig. 9(h), WA, GA and EA can provide reversible capacities of 666, 777 and 211 mA h g−1 after 600 cycles at 15C, respectively. Even charged/discharged at 20C, WA, GA and EA can provide reversible capacities of 599, 647, and 171 mA h g−1 after 600 cycles (Fig. 9(i)), GA exhibits better long-term cycle performance. Table 2 compares the electrochemical properties of the prepared MnC2O4 nanorod with other metal oxalates in literature. As listed in Table 2, The performance of manganese oxalate nanorods is superior to that of Fe0.75Co0.25C2O4 nanoribbons,11 Fe0.5Mn0.5C2O4 nanorods,12 Mn0.33Co0.67C2O4 rambutan,20 Co0.52Mn0.48C2O4 microrods,24 Fe0.5Mn0.5C2O4 nanorods,12 CoC2O4 nanorods,19,24 MnC2O4 microtubes,31 FeC2O4 microrods,23 and multilayer FeC2O4.43 The improvement of manganese oxalate performance can be attributed to the nanorods have a higher specific surface area and mesoporous structure.
.11,13,20,31 The slope below 0.3 V corresponds to the pseudo capacitance behavior of the polymer surface gel layer and the interface lithium storage behavior.11,13,17,19–27,31,41 After 1st cycle, there is a small plateau at ∼0.8 V related to the SEI film formation.11,13,20,31 As shown in Fig. 9(a, c and e), there are some differences in the voltage platforms (such as discharge platform voltage, platform width, etc.). The possible reason is that the volume expansion of EA during the discharge/discharge process causes the formation of the larger agglomerates, which makes the polarization larger and reduces the reversibility of the conversion reaction. The initial coulombic efficiency of WA, GA and EA is 49%, 48%, and 50%, respectively. The lower initial coulombic efficiency can be ascribed to the irreversible crystal-to-amorphous transformation and the formation of SEI film during the first discharge,11,13,20,31 which is a common phenomenon for the conversion electrodes.15–17,19,21–27,41 The cyclic-stability and the rate performance are given in Fig. 9(d–g). As shown in Fig. 9 (d–g), the discharge capacity decreases first and then increases at the initial stage due to the formation and activation of the polymeric gel-like layer.11,13,17,19–27,31,41 This polymeric gel-like layer formed in the first discharge is irreversible and gradually thickened during the initial cycles,15,16,31 which hinders the diffusion of Li+ and the conversion reaction. As a result, the capacity decreases with the increase of cycles in the initial charge/discharge processes. However, this polymeric gel-like layer can be gradually activated and becomes reversible after several cycles.15,16,31 Therefore, the capacity increases gradually after several cycles. As shown in Fig. 9(d–g), the cycle stability and the rate performance of manganese oxalate are nanorods > microrods > nanosheets. Manganese oxalate nanorods deliver a discharge capacity of 1509, 983, 938 and 838 mA h g−1 at 3, 5, and 8C, respectively. As shown in Fig. 9(h), WA, GA and EA can provide reversible capacities of 666, 777 and 211 mA h g−1 after 600 cycles at 15C, respectively. Even charged/discharged at 20C, WA, GA and EA can provide reversible capacities of 599, 647, and 171 mA h g−1 after 600 cycles (Fig. 9(i)), GA exhibits better long-term cycle performance. Table 2 compares the electrochemical properties of the prepared MnC2O4 nanorod with other metal oxalates in literature. As listed in Table 2, The performance of manganese oxalate nanorods is superior to that of Fe0.75Co0.25C2O4 nanoribbons,11 Fe0.5Mn0.5C2O4 nanorods,12 Mn0.33Co0.67C2O4 rambutan,20 Co0.52Mn0.48C2O4 microrods,24 Fe0.5Mn0.5C2O4 nanorods,12 CoC2O4 nanorods,19,24 MnC2O4 microtubes,31 FeC2O4 microrods,23 and multilayer FeC2O4.43 The improvement of manganese oxalate performance can be attributed to the nanorods have a higher specific surface area and mesoporous structure.
 | ||
| Fig. 9 Electrochemical performance of WA, GA and EA: (a–c) discharge/charge profiles at 5C and (d–i) cycle performance at various C rates, respectively. | ||
| Materials | Shape | Current | Capacity (mA h g−1) | Cycle | Ref. |
|---|---|---|---|---|---|
| MnC2O4 | Nano-rod | 20C | 647 | 600 | This work |
| CoC2O4 | Nano-rod | 1C | 959 | 100 | 20 |
| FeC2O4 | Microrods | 1C | 825 | 100 | 19 |
| MnC2O4 | Microtube | 0.375 A g−1 | 998 | 100 | 27 |
| FeC2O4 | Multilayer | 0.25 A g−1 | 993 | 200 | 39 |
| CoC2O4 | Nano-rod | 0.2 A g−1 | 700 | 200 | 15 |
| Mn0.33Co0.67C2O4 | Rambutan | 0.5 A g−1 | 836 | 100 | 16 |
| Fe0.75Co0.25C2O4 | Nanoribbons | 5C | 600 | 75 | 7 |
| Fe0.5Mn0.5C2O4 | Nano-rod | 2C | ∼200 | 75 | 8 |
| Co0.52Mn0.48C2O4 | Microrods | 1C | 1072 | 100 | 23 |
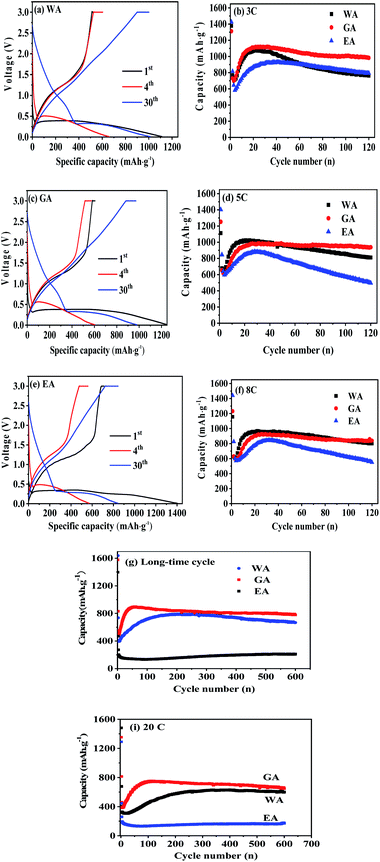
As seen in Fig. 9, the specific capacity of manganese oxalate is higher than its theoretical capacity (375 mA h g−1), and the extra capacity originates form the pseudo capacity from surface reactions of polymeric gel-like layer.31,44,45 Therefore, CV curves were performed to analyze the faradaic and capacitive contributions to the total capacity. The total current in CV is composed of the faradaic and capacitive contribution, which can be expressed by the following equation.44,46–48
| i(v) = icap + idiff = avb |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i(v) = log i(v) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a + b a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v v
| (2) |
Fig. 10 gives the CV curves at different sweep rates, and Table 3 lists the parameters obtained by fitting the CV datas in Fig. 10 with eqn (2). All R2-values in Table 3 are higher than 0.95, indicating a good linear relationship between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i(v) and log
i(v) and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v in the range of 0.5 to 3.0 mV s−1. The b-values in the range of 0.5 to 1.0 demonstrate the total current includes both the faradaic contribution and the capacitive contribution.
v in the range of 0.5 to 3.0 mV s−1. The b-values in the range of 0.5 to 1.0 demonstrate the total current includes both the faradaic contribution and the capacitive contribution.
 | ||
| Fig. 10 CV curves and capacitive contributions to the total capacity of the prepared MnC2O4 at different sweep rates (v mV s−1). | ||
| WA | GA | EA | ||||
|---|---|---|---|---|---|---|
| Oxidation | Reduction | Oxidation | Reduction | Oxidation | Reduction | |
| a | −2.52 | −2.68 | −2.27 | −2.33 | −2.45 | −2.72 |
| b | 0.78 | 0.67 | 0.80 | 0.71 | 0.80 | 0.67 |
| R2 | 0.99 | 0.99 | 0.99 | 0.98 | 0.97 | 0.99 |
To further distinguish the contribution from the capacitive and the faradaic processes, a more general eqn (3) is used to express the relationship of current and sweep rate.
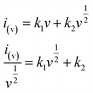 | (3) |
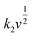 stands for the contribution of faradaic processes. The values of k1 and k2 can be obtained from the slope and intercept of a linear plot of
stands for the contribution of faradaic processes. The values of k1 and k2 can be obtained from the slope and intercept of a linear plot of 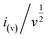 vs.
vs. 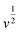 , respectively.25,30 Fig. 10(b, d and f) shows the capacitive contribution calculated by fitting the CV data in Fig. 10(a, c and e) with eqn (3). As depicted in Fig. 10(b, d and f), the capacitance contributions of the three samples increase with the increase of the potential sweep rate. The capacitance contribution of nanorods and nanosheets is larger than that of microrods due to their higher specific surface area. The greater capacitance contribution means the better rate performance. Therefore, the nanorods have better rate performance, which is consistent with Fig. 9(b, d and f).
, respectively.25,30 Fig. 10(b, d and f) shows the capacitive contribution calculated by fitting the CV data in Fig. 10(a, c and e) with eqn (3). As depicted in Fig. 10(b, d and f), the capacitance contributions of the three samples increase with the increase of the potential sweep rate. The capacitance contribution of nanorods and nanosheets is larger than that of microrods due to their higher specific surface area. The greater capacitance contribution means the better rate performance. Therefore, the nanorods have better rate performance, which is consistent with Fig. 9(b, d and f).
To further understand the effects of the morphologies, TEM was applied to investigate the changes of microrods, nanorods and nanosheets during charge/discharge processes. Fig. 11 displays the morphologies and microstructures of MnC2O4 electrode at 1st, 4th (minimum capacity) and 18th cycle (maximum capacity after activation). As shown in Fig. 11(a–h), the microrods and the nanorods remain stable after 18 cycles, while the nanosheets are broken in the 4th cycle, indicating that 1D rod-like structure possesses better stability. The breakage of nanosheets will destroy the integrity of the electrode and make the active material lose its conductive contact, resulting in the decrease of capacity and poor cycling performance (Fig. 9(b, d and f)). However, the active particles in the rod structures can keep good conductive contact with the conductive agent and collector due to their better stability than nanosheets, which make the active materials be fully utilized, thus exhibiting better cycle stability (Fig. 9(b, d and f)). There is no obvious SEI layer on the image of the 1st discharge electrode of GA (Fig. 11(d)), suggesting that no stable SEI film is formed during the first discharge. However, the SEI layer with a thickness of ∼39 nm can be clearly observed in the images of the discharged electrodes at the 4th and 18th cycles, respectively (Fig. 11(e and f)). These results indicate that the SEI layer gradually forms, thickens and remains stable in the initial charge/discharge stage, further proving that the capacity first decreases and then increase during the initial charge/discharge stage (Fig. 9(b, d and f)). As shown in Fig. 11(f and i), the thickness of SEI film in the 18th charging process of the GA electrode is much smaller than that in the 18th discharging process, indicating that the formation/decompose of the SEI layer after activation is reversible. The reversible formation/decompose of the gel-like film can provide the extra capacity of the conversion reaction, which becomes the origination of the capacity beyond the theoretical capacity.
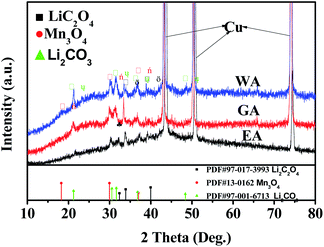
XRD was applied to further clarify the change in oxidation state and phase evolution after long cycle. Fig. 12 provides the phase compositions of the prepared samples after 600 cycles at 20C. The strong peaks in Fig. 12 are the characteristic peaks of copper collector in the electrode. As shown in Fig. 12, WA, EA and GA are transformed into amorphous state after long-term cycling, and Li2C2O4, Li2CO3 and Mn3O4 can be observed at the same time. Li2C2O4 can be attributed to incomplete conversion reaction. Li2CO3 may be related to the reaction between lithium oxalate and electrolyte, and Mn3O4 may originate from the oxidation of manganese (II) compound during charge discharge process.
EIS was applied to further explore the effects of morphology on the electrode kinetics, and Fig. 13 compares Nyquist plots of MnC2O4 with different morphologies. All Nyquist curves consist of two parts: a depressed semicircle at high-to-medium frequencies corresponding to the SEI layer resistance and the charge transfer resistance, and a sloped line in the low-frequency region associated with the Warburg impedance representing the diffusion of Li+ in the active solid.17,21,31 Re, RSEI, Rct, ZW, and Cdl of the equivalent circuit in Fig. 13(a) are electrolyte resistance, SEI resistance, charge-transfer resistance, Warburg impedance, and capacitive elements, respectively.
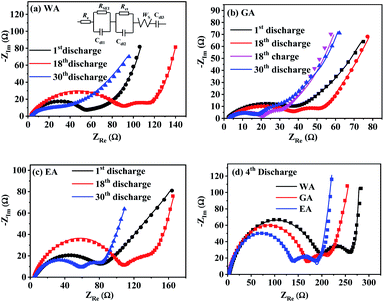 | ||
| Fig. 13 Nyquist plots of MnC2O4 prepared by different solvents at 3C: (a) WA, (b) GA, (c) EA, and (d) 4th discharge. | ||
Table 4 lists the values of Rs, RSEI, Rct, and ZW obtained by fitting the EIS datas in Fig. 13 using the equivalent circuit in Fig. 13(a). The diffusion coefficient of Li+ (DLi) in the active solid can be calculated by the following equation.
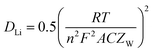 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 C mol−1), the total surface area of the electrode (1.54 × 10−4 m2) and the molar concentration of Li+ in the active materials (3.37 × 104 mol m3). As listed in Table 4, MnC2O4 with different morphologies have similar electrolyte resistance. All RSEI values increase first and then decrease with the increase of cycle numbers, indicating that SEI film experiences accumulation/activation and gradually becomes stable state during the initial charge/discharge processes.20 Rct also increases first and then decreases with the increase of cycling number, indicating that the growth and thickening of SEI film in the early stage is a barrier to charge transfer, while the activated SEI film in the later stage can effectively improve the Li+ transfer ability through the interface.20,31,42 The increase of DLi values of WA and GA may be related to the activation of SEI layer and the utilization of more pores to accelerate the migration of Li+.16,27,43 The decrease of the DLi value of EA after the fourth cycle can be ascribed to the broken nanosheets. The synergistic effect of SEI film diffusion, charge transfer, and Li+ diffusion makes the variation trend of discharge capacity in Fig. 9. RSEI and Rct of GA in the charge state of the 18th cycle are smaller than those in the discharge state of the 18th cycle, which can be ascribed to its thinner SEI film of the charging state in the 18th cycle (seen in Fig. 11(i and f)). The larger DLi and smaller RSEI and Rct of GA at the 30th discharge state can be attributed to its higher surface area and more stable nanorod-like structure, further demonstrating its better performance in Fig. 9.
500 C mol−1), the total surface area of the electrode (1.54 × 10−4 m2) and the molar concentration of Li+ in the active materials (3.37 × 104 mol m3). As listed in Table 4, MnC2O4 with different morphologies have similar electrolyte resistance. All RSEI values increase first and then decrease with the increase of cycle numbers, indicating that SEI film experiences accumulation/activation and gradually becomes stable state during the initial charge/discharge processes.20 Rct also increases first and then decreases with the increase of cycling number, indicating that the growth and thickening of SEI film in the early stage is a barrier to charge transfer, while the activated SEI film in the later stage can effectively improve the Li+ transfer ability through the interface.20,31,42 The increase of DLi values of WA and GA may be related to the activation of SEI layer and the utilization of more pores to accelerate the migration of Li+.16,27,43 The decrease of the DLi value of EA after the fourth cycle can be ascribed to the broken nanosheets. The synergistic effect of SEI film diffusion, charge transfer, and Li+ diffusion makes the variation trend of discharge capacity in Fig. 9. RSEI and Rct of GA in the charge state of the 18th cycle are smaller than those in the discharge state of the 18th cycle, which can be ascribed to its thinner SEI film of the charging state in the 18th cycle (seen in Fig. 11(i and f)). The larger DLi and smaller RSEI and Rct of GA at the 30th discharge state can be attributed to its higher surface area and more stable nanorod-like structure, further demonstrating its better performance in Fig. 9.
| Cell (tested) | Re (Ω) | RSEI (Ω) | Rct (Ω) | ZW (Ω s−1/2) | DLi (cm2 s−1) | |
|---|---|---|---|---|---|---|
| WA | 1st discharge | 4.02 | 73.2 | 9.93 | 27.42 | 1.09 × 10−15 |
| 4th discharge | 3.98 | 199.3 | 51.2 | 7.63 | 1.41 × 10−14 | |
| 18th discharge | 4.91 | 103 | 22.6 | 13.07 | 4.81 × 10−15 | |
| 30th discharge | 4.35 | 57.2 | 14.6 | 10.03 | 8.17 × 10−15 | |
| GA | 1st discharge | 2.03 | 33.1 | 3.60 | 84.22 | 1.16 × 10−16 |
| 4th discharge | 2.76 | 170.2 | 39.8 | 15.27 | 3.53 × 10−15 | |
| 18th discharge | 3.66 | 49.64 | 12.9 | 8.89 | 1.04 × 10−15 | |
| 18th charge | 3.61 | 18.7 | 6.04 | 13.49 | 4.52 × 10−15 | |
| 30th discharge | 3.97 | 15.1 | 8.78 | 7.81 | 1.35 × 10−14 | |
| EA | 1st discharge | 2.38 | 47.48 | 9.10 | 20.46 | 1.96 × 10−15 |
| 4th discharge | 2.60 | 141.1 | 40.7 | 7.58 | 1.43 × 10−14 | |
| 18th discharge | 2.58 | 66.2 | 21.8 | 12.89 | 4.95 × 10−15 | |
| 30th discharge | 4.23 | 61.7 | 19.1 | 28.02 | 1.05 × 10−15 |
4. Conclusions
Manganese oxalates with different structures and morphologies have been prepared in different proton-DMSO mixed solvents. The structure, the morphology, and the size of manganese oxalate can be adjusting by protonic solvents. MnC2O4 synthesized in EG-DMSO is mesoporous nanorod-like particles with a specific surface area of 58.6 m2 g−1. This nanorod-like sample delivers a discharge capacity of 983 and 838 mA h g−1 after 120 cycles at 3 and 8C, respectively, exhibiting better cycle stability and rate performance. The improved performance can be ascribed to the more stable structure, and the faster kinetics resulting from the mesoporous nanorods with higher surface area. Thus, the as-synthesized mesoporous MnC2O4 nanorods can act as a potential promising anode material for next-generation LIBs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors appreciate the financial support from the National Natural Science Foundation of China (51864005 and 51564002) and the Natural Science Foundation of Guangxi, China (2018GXNSFDA281014).Notes and references
- B. Dunn, H. Kamath and J. M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- Z. Yanhg, J. Zhang, M. C. W. Kintner-Meyer, X. Lu, D. Choi and J. Lemmon, Chem. Rev., 2011, 111, 3577–3613 CrossRef PubMed.
- D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561 CrossRef PubMed.
- Y. P. Wu, E. Rahm and R. Holze, J. Power Sources, 2003, 114, 228–236 CrossRef CAS.
- V. Aravindan, Y. S. Lee and S. Madhavi, Adv. Energy Mater., 2015, 5, 1402225 CrossRef.
- P. He, K. Zhao, B. Huang, B. Zhang, Q. Huang, T. Chen and Q. Zhang, J. Mater. Sci., 2018, 53, 4482–4493 CrossRef CAS.
- P. He, Z. Ding, X. Zhao, J. Liu, S. Yang, P. Gao and L.-Z. Fan, Inorg. Chem., 2019, 58, 12724–12732 CrossRef CAS PubMed.
- Y. Jia, A. Cheng, W. Ke, J. Liu, S. Wang, Y. Zhao, Q. Yang and J. Zhang, Electrochim. Acta, 2017, 225, 514–524 CrossRef.
- J. Gonçalves, M. Silva, K. Naik, P. Martins, D. Rocha, E. Nossol, R. Munoz, L. Angnes and C. Rout, J. Mater. Chem. A, 2021, 9, 3095–3124 RSC.
- M. Aragon, B. Leon, T. Serrano, C. Vicente and J. Tirado, J. Mater. Chem., 2011, 21, 10102–10107 RSC.
- B. León, C. P. Vicente and J. L. Tirado, Solid State Ionics, 2012, 225, 518–521 CrossRef.
- M. C. López, J. L. Tirado and C. Pérez Vicente, J. Power Sources, 2013, 227, 65–71 CrossRef.
- M. V. Reddy, G. V. S. Rao and B. V. R. Chowdari, Chem. Rev., 2013, 113, 5364–5457 CrossRef CAS PubMed.
- J. S. Yeoh, C. F. Armer and A. Lowe, Mater. Today Energy, 2018, 9, 198–222 CrossRef.
- N. Li, Q. Li, X.-T. Guo, M. J. Yuan and H. Pang, Chem. Eng. J., 2019, 372, 551–571 CrossRef CAS.
- K. Zhang, R. Xu, R. Wei, Y. Li, Y. Wang, Y. Zhang, Y. Dai and Y. Yao, Mater. Chem. Phys., 2020, 243, 122676 CrossRef CAS.
- Y. Lu, L. Yu and X. W. Lou, Chem, 2018, 4, 972–996 CAS.
- Y. Zhang, Z. Lu, M. Guo, Z. Bai and B. Tang, JOM, 2016, 68, 2952–2957 CrossRef CAS.
- X. Wu, J. Guo, M. J. McDonald, S. Li, B. Xu and Y. Yang, Electrochim. Acta, 2015, 163, 93–101 CrossRef CAS.
- K. Zhang, D. Zhang, Y. Li, L. Wang, F. Liang, Y. Dai and Y. Yao, Appl. Surf. Sci., 2020, 507, 145051 CrossRef.
- K. Zhang, Y. Li, Y. Wang, M. Yuan, Y. Dai and Y. Yao, Mater. Lett., 2019, 238, 187–190 CrossRef CAS.
- W. A. Ang, N. Gupta, R. Prasanth and S. Madhavi, ACS Appl. Mater. Interfaces, 2012, 4, 7011–7019 CrossRef CAS PubMed.
- W. A. Ang, Y. L. Cheah, C. L. Wong, R. Prasanth, H. H. Hng and S. Madhavi, J. Phys. Chem. C, 2013, 117, 16316–16325 CrossRef CAS.
- J. Xu, L. He, H. Liu, T. Han, Y. Wang, C. Zhang and Y. Zhang, Electrochim. Acta, 2015, 170, 85–91 CrossRef CAS.
- W. Kang and Q. Shen, J. Power Sources, 2013, 238, 203–209 CrossRef CAS.
- W. A. E. Ang, Y. L. Cheah, C. L. Wong, H. H. Hng and S. Madhavi, J. Alloys Compd., 2015, 638, 324–333 CrossRef CAS.
- V. A. Fedorov and V. I. Belevantsev, J. Mol. Liq., 2003, 103, 83–98 CrossRef.
- K. Murakoshi, H. Hosokawa, N. Tanaka, M. Saito, Y. Wada, T. Sakata, H. Mori and S. Yanagida, Chem. Commun., 1998, 3, 321–322 RSC.
- Z. Jia, L. Yue, Y. Zheng and Z. Xu, Chin. J. Inorg. Chem., 2007, 23, 181–188 CAS.
- Y. Yang, L. He, J. Lu, Z. Liu, N. Wang, J. Su, Y. Long, X. Lv and Y. Wen, Electrochim. Acta, 2019, 321, 134673 CrossRef CAS.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- E. S. Ilton, J. E. Post, P. J. Heaney, F. T. Ling and S. N. Kerisit, Appl. Surf. Sci., 2016, 366, 475–485 CrossRef CAS.
- L. Ren, P. Wang, Y. Han, C. Hu and B. Wei, Chem. Phys. Lett., 2009, 476, 78–83 CrossRef CAS.
- D. W. Wang, Q. H. Wang and T. M. Wang, Inorg. Chem., 2011, 50, 6482–6492 CrossRef CAS PubMed.
- J. Romann, V. Chevallier, A. Merlen and J. C. Valmalette, J. Phys. Chem. C, 2009, 113, 5068–5074 CrossRef CAS.
- X. Liu, J. Jiang and L. Ai, J. Mater. Chem. A, 2015, 3, 9707–9713 RSC.
- K. S. W. Sing, Pure Appl. Chem., 1985, 57, 603–619 CAS.
- M. D. Chadwick, J. W. Goodwin, E. J. Lawson and P. D. A. Mills, Colloids Surf., A, 2002, 203, 229–236 CrossRef CAS.
- M. Nedyalkova and V. Antonov, Open Chem., 2018, 16, 1176–1183 CAS.
- J. Romann, J. C. Valmalette, V. Chevallier and A. Merlen, J. Phys. Chem. C, 2010, 114, 10677–10682 CrossRef CAS.
- Y. W. Jun, J. S. Choi and J. Cheon, Angew. Chem., Int. Ed., 2006, 45, 3414–3439 CrossRef CAS PubMed.
- K. Zhang, F. Liang, Y. Wang, Y. Dai and Y. Yao, J. Alloys Compd., 2019, 779, 91–99 CrossRef CAS.
- S. Laruelle, S. Grugeon, P. Poizot, M. Dollé, L. Dupont and J. M. Tarascon, J. Electrochem. Soc., 2002, 149, A627–A634 CrossRef CAS.
- M. Zukalová, M. Kalbáč, L. Kavan, I. Exnar and M. Graetzel, Chem. Mater., 2005, 17, 1248–1255 CrossRef.
- V. Augustyn, J. Come, M. A. Lowe, J. W. Kim, P. L. Taberna, S. H. Tolbert, H. D. Abruña, P. Simon and B. Dunn, Nat. Mater., 2013, 12, 518–522 CrossRef CAS PubMed.
- J. Liu, J. Wang, C. Xu, H. Jiang, C. Li, L. Zhang, J. Lin and Z. X. Shen, Adv. Sci., 2018, 5, 1700322 CrossRef PubMed.
- K. Zhang, X. Yang, J. Wu, X. Huang and Y. Yao, Nano, 2016, 11, 1650123 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |