Open Access Article
Open Access ArticleStability of neutral molecular polynitrogens: energy content and decomposition mechanisms†
A. C. R. Gomes a,
M. X. Silva
a,
M. X. Silva b and
B. R. L. Galvão
b and
B. R. L. Galvão *a
*a
aCentro Federal de Educação Tecnológica de Minas Gerais, CEFET-MG, Av. Amazonas 5253, (30421-169) Belo Horizonte, Minas Gerais, Brazil. E-mail: brenogalvao@gmail.com
bPrograma de Pós-Graduação em Modelagem Matemática e Computacional, Centro Federal de Educação Tecnológica de Minas Gerais, CEFET-MG, Av. Amazonas 7675, (30510-000) Belo Horizonte, Minas Gerais, Brazil
First published on 17th June 2021
Abstract
The potential application of all-nitrogen molecules as high energy density materials (HEDMs) has been attracting considerable scientific effort. If stable enough to be synthesized and stored, these systems may be used as a green source of energy. However, it is very difficult to obtain these structures under mild experimental conditions. Theoretical chemistry may aid in the search for polynitrogens that are more likely to have experimental usability. The barriers towards decomposition are an effective way to assess their stability, but these have not been thoroughly studied. Most of the previous effort in this direction focus on a single Nx case, each employing different accuracy levels, and the decomposition of caged structures has been little explored. Here we explore the stability and decomposition of several neutral molecular polynitrogens of different sizes and shapes using a common and accurate theoretical framework in order to compare among them, search for patterns and identify potential candidates for synthesis. We focus especially on new caged geometries, and our results indicate that the prismatic ones can be expected to present higher energy densities and be very stable with respect to unimolecular decomposition. It is shown that the energy content can be clearly stratified between chain, ring, cage and prismatic cage structures.
1 Introduction
Polynitrogen systems (polyN) have been the subject of a vast number of studies in the past decades, both in neutral and ionic forms, due to the fact that they are candidates for clean energy sources. This comes from the nature of their structures, built by single and/or double N–N bonds. The triple bond of molecular nitrogen is highly thermodynamically stable, and therefore these systems tend to decompose, dissociating into N2 molecules and releasing large amounts of energy. As the product of this dissociation is the major component of atmospheric air, this process occurs without the formation of polluting compounds or greenhouse gases, such as carbon dioxide.1–4Because of their high potential energy content, polyN are part of a group of substances called high energy density materials (HEDMs). For practical usage, the material must not only be able to release a large amount of energy on demand, but also must have a reasonable chemical stability in order to be produced and stored. For polyN systems, this means a high dissociation energy coupled with a relatively high decomposition barrier.1
PolyN species can be sub-categorized in chain, ring or caged structures. The latter tend to show more single bonds between nitrogen atoms, and thus may be expected to release a larger amount of energy when several new triple N2 bonds are formed upon its dissociation. As this process may involve the breaking of several chemical bonds simultaneously, its decomposition barrier is also expected to be higher.5 Therefore, cage-like structures are possibly the most suitable ones for HEDM use.
Experimentally, it is very hard to synthesize polyN at ambient conditions. Usually, extremely high pressures and cryogenic temperatures are necessary.6,7 In the field of neutral polyN, it has already been reported a covalent allotropic form of nitrogen in which the atoms are arranged in a cubic gauche structure (cg-N),8 a polymeric nitrogen with the black phosphorus structure (bp-N)9 and a molecular form of N8.10 On the ionic front, on the other hand, many species have been obtained over the past few years, such as the pentazolate anion,11 the pentazenium cation12,13 and metal pentazolate hydrate complexes.14 Slightly larger anions have also been recently reported, such as a tungsten hexanitride15 and the N8− anion, which has been synthesized on the sidewalls of multi-walled carbon nanotubes16 and also stabilized on boron-doped graphene.17
Theoretically, several studies involving polyN (especially up to 10 atoms) have been reported over the past decades, regarding their structures and thermodynamic properties, both in neutral18–36 and ionic forms at gas phase.22,37–40 Stable molecular crystals of N6, N8 and N10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,41–43 have also been proposed. However, less attention has been given to their dissociation and isomerization barriers, which is a key aspect to predict what isomeric forms may actually be stable at ordinary temperatures, which is a major advantage for storage. Most of previous research that has been published on this property focused on chain or ring structures with up to 10 atoms for neutral4,6,7,44–60 and ionic forms.7,52,54,59,61–65 To the best of our knowledge, the dissociation and isomerization barriers of neutral caged structures have been, up until now, little exploited,66–69 and most of these studies employed symmetry constraints in the search for transition state structures.
2,41–43 have also been proposed. However, less attention has been given to their dissociation and isomerization barriers, which is a key aspect to predict what isomeric forms may actually be stable at ordinary temperatures, which is a major advantage for storage. Most of previous research that has been published on this property focused on chain or ring structures with up to 10 atoms for neutral4,6,7,44–60 and ionic forms.7,52,54,59,61–65 To the best of our knowledge, the dissociation and isomerization barriers of neutral caged structures have been, up until now, little exploited,66–69 and most of these studies employed symmetry constraints in the search for transition state structures.
For the reasons mentioned above, this work is focused on providing a systematic study on the decomposition mechanisms for several polyN neutral molecules, in order to provide insights into what type of structure might be best suitable for HEDMs. The various isomers are compared by their calculated dissociation barriers and dissociation energies using the same theoretical level for all structures and without symmetry constraints in the decomposition pathways, allowing for a fair comparison between all structures. We focus on caged geometries, but for each polyN size, other relevant structures are always included for a direct analysis between the different classes.
2 Methodology
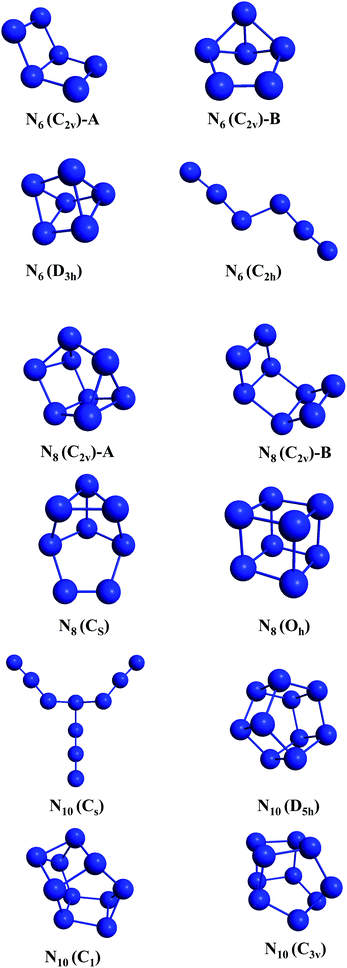
All electronic structure calculations reported here were performed using the GAMESS-US70 and MOLPRO71 packages. The calculations were based on density functional theory (DFT)72 using the def2 (SVP and TZVPP) basis sets.73 The M06-2X74 and SOGGA11-X75,76 exchange and correlation functionals were chosen due to their known accuracy for predicting energy barrier heights.77,78 In fact, it has been shown by Peverati and Truhlar,76 that the mean unsigned error (MUE) for non-hydrogen-transfer barrier heights (NHTBH) for the hybrid SOGGA11-X functional and of M06-2X are respectively 1.16 kcal mol−1 and 1.22 kcal mol−1. Therefore both functionals show chemical accuracy for potential energy barriers and are expected to provide reliable results for our purposes. Vibrational analysis was carried out to confirm the minima and transition states (TSs) found within the employed levels of theory. The wxMacMolPlt program was used for graphic visualization and representation of the molecular geometries.79The initial structures selected (shown in Fig. 1) were taken from ref. 36 and 80 and were chosen such as to provide four different structures for each molecular size, and to present a diverse set of all geometrical classes of structures. This work provides the first account on the unconstrained dissociation paths of six nitrogen allotropic forms: N8(C2v)-A, N8(CS), and all four N10 isomers including the prismatic one.
As a first step, the smaller def2-SVP basis set was used for an initial exploration of possible dissociation and isomerization paths associated with each studied polyN. Intrinsic reaction coordinate (IRC) calculations were performed with this basis set using the Gonzalez–Schlegel second-order algorithm81 for all TSs found to ensure their connection to decomposition or isomerization products. After that, reoptimization employing the larger def2-TZVPP basis set was carried out for all stationary points found. The energies of all minima and TSs were zero-point energy (ZPE) corrected within the def2-TZVPP approach and no symmetry restrictions were imposed in any case.
To assess the performance of our DFT results, we have also performed geometry optimizations and frequencies calculations at the coupled cluster singles and doubles and perturbative triples (CCSD(T)) level,82–84 using the cc-pVDZ basis set.85,86 This was followed by a single point energy refinement using the explicitly correlated coupled cluster method (CCSD(T)-F12) method,87,88 using the aug-cc-pVTZ basis set. Such calculations were considered as benchmark and the results were directly compared to the DFT ones.
3 Results
In the results presented throughout this work, the energies in all graphs are given relatively to the nN2 dissociation limit. The reaction pathways in the IRC plots are displayed with black circles (at the SOGGA11-X/def2-SVP level). The horizontal lines in these graphs correspond to the ZPE corrected energies at M06-2X/def2-TZVPP (orange) and SOGGA11-X/def2-TZVPP (black) levels.For a summary of the results, the tables in this section show the numerical values of the activation energy (AE) and dissociation energies (DE), which are positively defined as
| AE = ETS + ZPETS − [EpolyN + ZPEpolyN] | (1) |
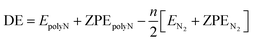 | (2) |
The Cartesian coordinates and frequencies of all minima and transition states reported in this section are given in the ESI† for both DFT functionals. Although the results of both functionals are given in the figures and tables, the energies discussed in the text are given only at the SOGGA11-X/def2-TZVPP level for simplicity.
3.1 N6
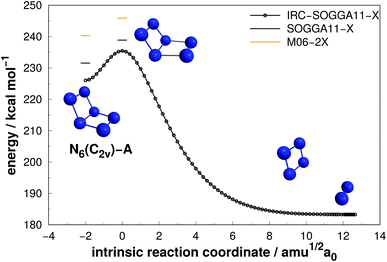
Four isomers of N6 have been considered in the present work. Fig. 2–5 present the results of the IRC calculations for structures N6(C2v)-A, N6(C2v)-B, N6(C2h) and N6(D3h) respectively. Table 1 gathers their AE and DE values. All three different calculation methods predict the same energetic ordering between the four structures, and both DFT functionals are in fairly good agreement with the CCSD(T)-F12/aug-cc-pVTZ//CCSD(T)/cc-pVDZ results for DE. The mean absolute difference between the benchmark results and the M06-2X one is only 2.0%, with a standard error of the mean (SEM) of 0.2%. A similar comparison is obtained for the SOGGA11-X functional, with a mean absolute difference of 2.2%. This good agreement between the methods reinforces the conclusions of this work regarding which structure is more stable towards unimolecular decomposition. A broader comparison between the methods and their accuracy will be given in the discussion section.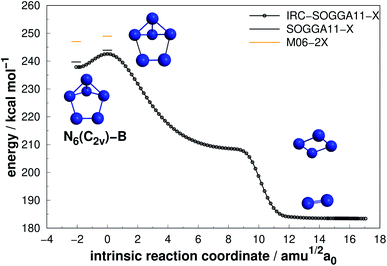 | ||
| Fig. 3 Decomposition path of N6(C2v)-B isomer with IRC calculation following the scheme of Fig. 2. | ||
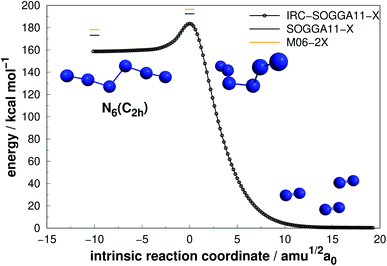 | ||
| Fig. 4 Decomposition path of N6(C2h) isomer obtained from IRC calculation following the scheme of Fig. 2. | ||
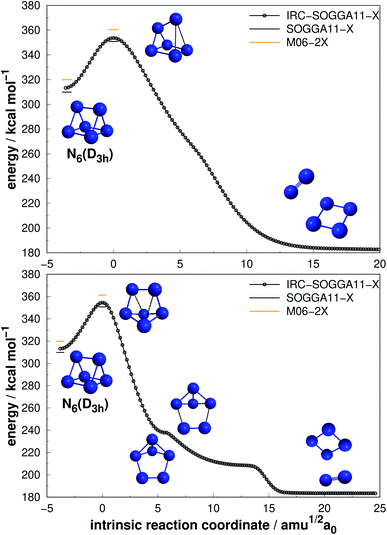 | ||
| Fig. 5 Direct decomposition path of N6(D3h) isomer into N4(D2h) + N2 (upper panel) and an alternative path to the same products passing through an intermediate (lower panel). Following the scheme of Fig. 2. | ||
| Structure | Method | AE | DE | DE/n |
|---|---|---|---|---|
| N6(C2v)-A | M06-2X | 5.59 | 240.30 | 40.05 |
| SOGGA11-X | 7.33 | 231.53 | 38.59 | |
| CCSD(T)-F12 | 235.12 | 39.19 | ||
| M06-2X | 1.94 | 247.00 | 41.17 | |
| N6(C2v)-B | SOGGA11-X | 4.23 | 239.69 | 39.95 |
| CCSD(T)-F12 | 243.65 | 40.61 | ||
| M06-2X | 18.42 | 178.13 | 29.69 | |
| N6(C2h) | SOGGA11-X | 19.23 | 173.20 | 28.87 |
| CCSD(T)-F12 | 181.77 | 30.29 | ||
| M06-2X | 40.53 | 319.89 | 53.32 | |
| N6(D3h) | SOGGA11-X | 40.96 | 309.90 | 51.65 |
| CCSD(T)-F12 | 312.61 | 52.10 |
As it can be seen, isomers N6(C2v)-A (which shows a Dewar benzene structure) and N6(C2v)-B possess small dissociation barriers (AE of 7.33 and 4.23 kcal mol−1, respectively), indicating that they are kinetically unstable at ambient conditions. These isomers decompose in a stepwise process, being the first the elimination of a N2 molecule, followed by the dissociation of the well known D2h form of N4,7,58 which has a very small dissociation barrier (around 6.45 kcal mol−1 above the N4 well7).
The N6(C2h) isomer, also named as diazide, presents a considerably higher decomposition barrier (19.23 kcal mol−1) when compared to the previous two, in spite of its chain configuration. Nevertheless, it may not be sufficient to confirm its stability at room temperature, as it has been suggested that an energy barrier of approximately 30 kcal mol−1 is desirable.50,67 In agreement with previous studies,48,52,60,67 we found a concerted dissociation mechanism in which N6(C2h) breaks directly into three N2 molecules. It is worth mentioning that Greschner et al.41 recently predicted a stable molecular crystal composed of N6(C2h) chains. Their molecular dynamics simulations suggest reasonable thermal stability.
Differently from the other three, N6(D3h) (or prismane) shows more promising results. In our study, we found a new TS that connects prismane directly to N4(D2h) + N2, with an energy barrier of 40.96 kcal mol−1 (upper panel in Fig. 5). Li and Liu67 found instead a considerable isomerization energy barrier towards the N6(C2v)-B structure (34.4 kcal mol−1) at CCSD/6-311G(d)(energies)//B3LYP/6-311G(d)(geometries) level. We could also find the isomerization path connecting these two isomers (lower panel in Fig. 5), and an energy barrier of 40.84 kcal mol−1 was obtained. Within the accuracy of our calculations, both isomerization and dissociation processes can be considered as energetically equivalent. The N6(C2v)-B isomer, in turn, will easily dissociate as illustrated in Fig. 3. These barriers are a good indicative of practical use of N6(D3h) as HEDM, and the unraveling of the direct decomposition pathway is relevant to the understanding of the energy landscape associated with prismane.
Within the N6 size, prismane releases the largest amount of energy considering its dissociation into three N2 molecules, being 78% more exothermic than the chain isomer (N6(C2h)). Its AE is also more than two times higher than that of N6(C2h), indicating that it may be stable on higher temperatures. This can be partially attributed to its caged geometry, but as will be explored later in section 4, not all caged structures follow this pattern, and there are other features involved.
3.2 N8
Four allotropes of N8 have been considered in the present work. Fig. 6–9 present the results of the IRC calculations for isomers N8(C2v)-A, N8(Cs), N8(C2v)-B and N8(Oh), respectively. To the best of our knowledge, this is the first work regarding the dissociation barriers of N8(C2v)-A and N8(Cs). Table 2 presents the values of their AEs and DEs. It should be noted that azidopentazole has been found to be the lowest energy isomer of N8, but ref. 49 and 50 already ruled out the possibility that this could be a good candidate for a HEDM.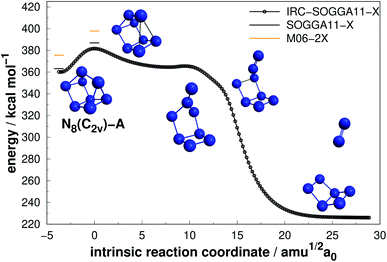 | ||
| Fig. 6 Decomposition path of N8(C2v)-A isomer obtained from IRC calculation following the scheme of Fig. 2. | ||
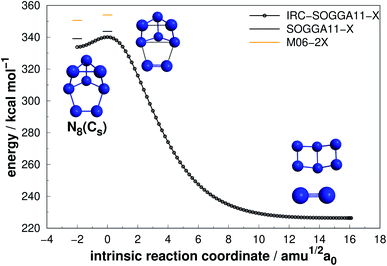 | ||
| Fig. 7 Decomposition path of N8(Cs) isomer obtained from IRC calculation following the scheme of Fig. 2. | ||
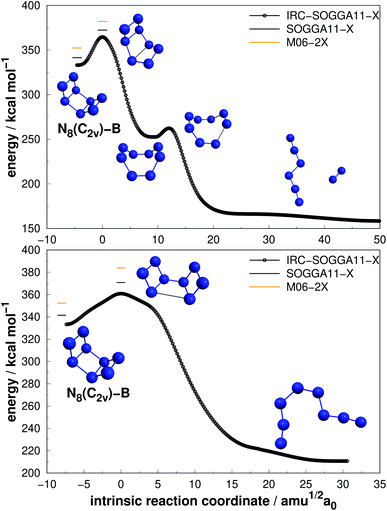 | ||
| Fig. 8 The two possible paths for N8(C2v)-B with energetically equivalent barriers as indicated in the text. Following the scheme of Fig. 2. | ||
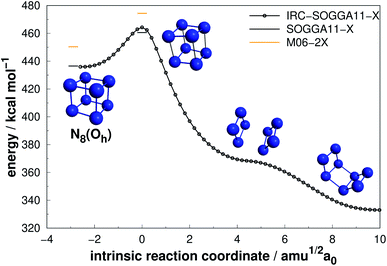 | ||
| Fig. 9 Isomerization path of N8(Oh) into N8(C2v)-B. Following the scheme of Fig. 2. | ||
| Structure | Method | AE | DE | DE/n |
|---|---|---|---|---|
| N8(C2v)-A | M06-2X | 22.26 | 375.47 | 46.93 |
| SOGGA11-X | 23.72 | 363.13 | 45.39 | |
| CCSD(T)-F12 | 367.69 | 45.96 | ||
| M06-2X | 31.65 | 352.27 | 44.03 | |
| N8(C2v)-B | SOGGA11-X | 29.34 | 341.44 | 42.68 |
| CCSD(T)-F12 | 344.10 | 43.01 | ||
| M06-2X | 3.33 | 350.60 | 43.83 | |
| N8(Cs) | SOGGA11-X | 4.53 | 339.09 | 42.39 |
| CCSD(T)-F12 | 341.98 | 42.75 | ||
| M06-2X | 24.11 | 450.31 | 56.29 | |
| N8(Oh) | SOGGA11-X | 24.06 | 436.51 | 54.56 |
| CCSD(T)-F12 | 435.88 | 54.49 |
Regarding the N8(C2v)-A isomer, we found a decomposition path that leads to N6(C2v)-A + N2 (Fig. 6). It passes through an intermediate resulting from the opening of a triangular ring of the initial structure. The isomerization barrier that is determinant to the decomposition process was found to be 23.72 kcal mol−1 (AE). Although not as high as that of prismane, this isomer might be an interesting candidate for production. On the other hand, the N8(Cs) isomer did not present promising results, as its predicted barrier for decomposition into N6(C2v)-A + N2 is only 4.53 kcal mol−1 (see Fig. 7).
More interesting results were achieved for the N8(C2v)-B isomer within our calculations. At the preliminary exploration using the def2-SVP basis set, only one barrier was found to be relevant. However, when we reoptimized the minima and TSs using the def2-TZVPP basis set, another barrier presented a similar and promising result, and we report both. First, a mechanism that leads to a D2d structure followed by decomposition to N6(C2h) + N2 with an activation energy of 30.84 kcal mol−1 (upper panel in Fig. 8). Second, a direct decomposition route through a structure opening transition state yielded an activation energy of 29.34 kcal mol−1, leading to an open chain N8(C1) isomer (lower panel in Fig. 8). Both barriers are high and show similar values, and thus N8(C2v)-B may be another relevant candidate. Fau and Bartlett62 reported that isolated open chains of N8 possess a relatively low decomposition barrier. In their work, this C1 structure is easily decomposed to N6 + N2.62
Still regarding N8(C2v)-B, it should be noted that a TS directly connecting it to full dissociation, was obtained by Schmidt et al.68 at the MP2/6-31G(d) level, with an AE of 20 kcal mol−1, but could not be reproduced within our calculation method. Gagliardi et al.66 found (employing B3LYP/cc-pVTZ calculations) two pathways for this structure: one similar to that shown in the upper panel of Fig. 8, with a barrier of 43.3 kcal mol−1, and another for isomerization of N8(C2v)-B into another structure of 28.2 kcal mol−1. In summary, the final AE value reported in ref. 66 is similar to the one reported here.
Extensive research has been performed on the octaazacubane allotrope,6,44,47,66,68,69 N8(Oh). Engelke and Stine44 studied the concerted symmetry forbidden D4h dissociation path N8(Oh) → 4N2 and found a 162 kcal mol−1 energy barrier at RHF/4-31G* level, in good agreement with the work of Evangelisti and Gagliardi47 (159 kcal mol−1 at CASSCF/VDZP level) considering the same constrained D4h path. However, both studies agree that octaazacubane dissociation should occur in a less symmetric path. On the other hand, an almost barrierless pathway to the total decomposition of the isolated N8(Oh) into 4N2 (2.5 kcal mol−1) was obtained by Gimaldinova et al. within the frame of the non-orthogonal tight-binding model for describing interatomic interactions.6
The lowest energy TS linked to N8(Oh) that we managed to find in the present study lies 24.06 kcal mol−1 above it. According to our IRC calculations, this TS actually connects N8(Oh) to the N8(C2v)-B isomer. Our proposed isomerization pathway agrees with the results of ref. 66, 68 and 89. After isomerization, N8(Oh) may readily follow the N8(C2v)-B decomposition path already discussed and presented in Fig. 8. Therefore, analogously to the N8(C2v)-B isomer, octaazacubane may also be of experimental relevance, but with the advantage of generating 28% more energy upon full dissociation.
Octaazacubane, N8(Oh), presents the highest DE/n ratio among all polyN studied here, which can be attributed to its strained prismatic structure where each N atom makes 3 single bonds. On the other hand, our calculations show that N8(C2v)-B (which does not show a caged structure) shows the highest activation energy for the 8 atoms polyN. As will be summarized later, although it is possible to draw correlations between the geometric shape and DE values, a similar analysis often fails to explain the calculated AEs. Finally, the relatively small difference between the dissociation barriers of N8(C2v)-B and N8(Oh) (5.3 kcal mol−1) compared to the significant difference between their DEs (95 kcal mol−1) should be taken into consideration.
3.3 N10
Four allotropes of N10 have been considered in the present work. Fig. 10–13 present the results of the IRC calculations for isomers N10(Cs), N10(D5h), N10(C1) and N10(C3v), respectively. To the best of our knowledge, this is the first work to provide fully relaxed dissociation mechanisms for these structures. The numerical results are gathered in Table 3. The difference between the two exchange correlation functionals employed in the case of the N10 structures follows the same trend observed for the previous structures: both functionals predict very similar AE barriers, but M06-2X predicts larger DEs.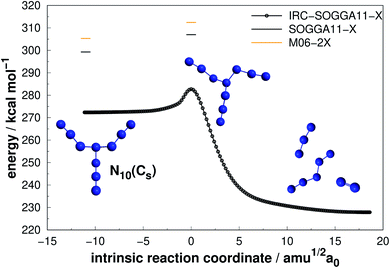 | ||
| Fig. 10 Decomposition path of N10(Cs) isomer obtained from IRC calculation following the scheme of Fig. 2. | ||
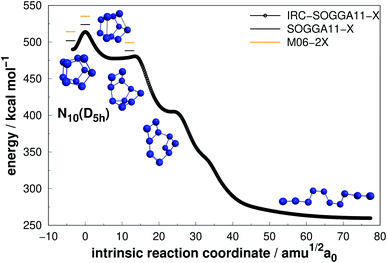 | ||
| Fig. 11 Decomposition path of N10(D5h) isomer obtained from IRC calculation following the scheme of Fig. 2. | ||
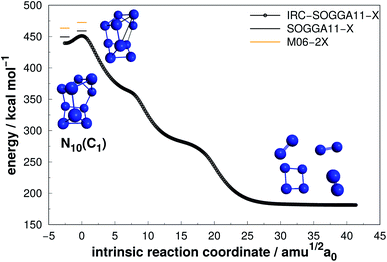 | ||
| Fig. 12 Decomposition path of N10(C1) isomer obtained from IRC calculation following the scheme of Fig. 2. | ||
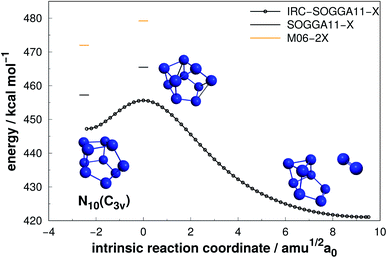 | ||
| Fig. 13 Decomposition path of N10(C3v) isomer obtained from IRC calculation following the scheme of Fig. 2. | ||
| Structure | Method | AE | DE | DE/n |
|---|---|---|---|---|
| N10(Cs) | M06-2X | 7.14 | 305.30 | 30.53 |
| SOGGA11-X | 7.73 | 299.23 | 29.92 | |
| CCSD(T)-F12 | 312.74 | 31.27 | ||
| M06-2X | 23.97 | 513.39 | 51.34 | |
| N10(D5h) | SOGGA11-X | 25.81 | 498.12 | 49.81 |
| CCSD(T)-F12 | 499.31 | 49.93 | ||
| M06-2X | 9.02 | 463.42 | 46.34 | |
| N10(C1) | SOGGA11-X | 9.55 | 449.47 | 44.95 |
| CCSD(T)-F12 | 454.18 | 45.42 | ||
| M06-2X | 7.24 | 471.95 | 47.19 | |
| N10(C3v) | SOGGA11-X | 8.22 | 457.24 | 45.72 |
| CCSD(T)-F12 | 459.62 | 45.96 |
The branched chain isomer N10(Cs) possesses a small decomposition barrier 7.73 kcal mol−1 and may not be a good candidate for HEDM. Together with the other chain isomer explored in this work (N6(C2h)), they represent the lowest DE/n ratio. Interestingly, N6(C2h) has a decomposition barrier 2.5 times larger than N10(Cs), despite the analogous structures, which again indicates the difficulty in correlating the AE value with molecular shape.
The prismatic N10(D5h) isomer decomposes in a stepwise fashion, passing through two different intermediates, to reach a chain isomer (Fig. 11). As reported by Strout,55 such acyclic forms of N10 tend to present low activation barriers towards dissociation, and thus the system will easily dissociate from there. Therefore, if there is available energy for N10(D5h) to surpass the first isomerization barrier (25.81 kcal mol−1), it will promptly undergo dissociation. This barrier is comparable to those presented by N8(C2v)-B and N8(Oh) isomers which, together with a large energy released upon full dissociation (DE), makes N10(D5h) the most attractive polyN within the N10 structures according to our calculations. The just published study employing reaction dynamics89 obtained a similar transition state, but the B3LYP reported energy barrier is substantially lower (13 kcal mol−1). Since the B3LYP functional is well known to underestimate barrier heights,90,91 with a MUE about four times higher than the functionals employed here,76 our AE value should be more realistic.
Even though N10(C1) and N10(C3v) present cage-like structures and high energy content (as given by DE/n), their rather small decomposition energy barriers (AE) make them not suitable for HEDM application. This is also the case for smaller polyN such as N8(Cs) and N6(C2v)-B, although all of them present significant DEs. Therefore, despite caged structures are consistently related to higher DEs, this is not the main factor governing their decomposition barriers. Symmetry seems to play an important role, as specific prismatic structures with peripheral N4(D2h) rings tended to yield higher kinetic stability, as well as DEs. Like the other prismatic structures of smaller nuclearities approached here, N10(D5h) is the isomer that releases the greatest amount of energy towards full decomposition into N2 molecules.
4 Discussion
For summarizing the results we first present a graph based on the Evans–Polanyi principle,92 relating activation energy with reaction energy, which is shown in Fig. 14. Although no clear correlation between AE and DE is observed, this graph is helpful for a general overview. First of all, the two graphs show that both functionals (one hybrid-GGA and one of meta-GGA type), are in very good agreement and the exact same conclusions can be drawn from both. In fact, analysing all structures calculated in this work, the difference between the two functionals in predicting DE is on average 3.1%, with a SEM of 0.1%. The SOGGA11-X functional is in better agreement with the benchmark calculations, in average deviating from the CCSD(T)-F12 ones by only 1.5% with a SEM of 0.4%. As for the AE values, the two funcionals always agree qualitatively in predicting the order of increasing AE. The difference between their calculated AEs is on average 1.19 kcal mol−1 which is indeed their expected accuracy.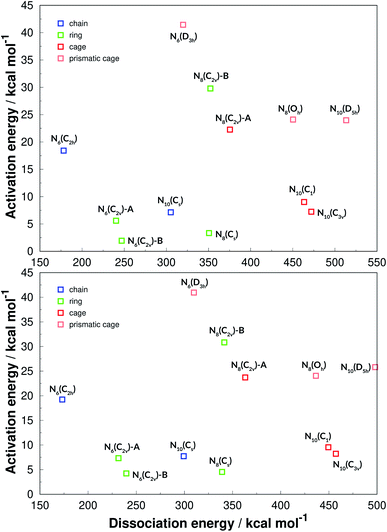 | ||
| Fig. 14 Evans–Polanyi plot. The results of the M06-2X functional are given in the upper panel, while SOGGA11-X ones are in the lower panel. | ||
We have also classified the structures into chains, rings, cages and caged prisms, which is presented in Fig. 14 in different colors. It is clearly seen that prismatic structures always show large activation energies towards unimolecular decomposition, and that of prismane N6(D3h) is specially high. This plot is helpful for an easy visualization of polyN molecules that display high values for both AE and DE, and thus could be good candidates for HEDMs. Besides the prismatic structures, N8(C2v)-B shows a surprisingly high activation energy, and could be one of the best candidates explored here. The chain structure of N6(C2h) shows a significant decomposition barrier, even though it is the structure that releases the least amount of energy upon dissociation into nitrogen molecules. It is worth recalling that Greschner et al.41 proposed a stable molecular crystal composed of N6(C2h) chains.
Although we have shown that all prismatic structures show high activation energies, it is seen that having a caged structure is not a sufficient condition. All caged structures present a high energy content (DE) but for some reason it is relatively easy to break some of them (small AE). Ring structures often have low activation energy, and are easier to break but, as seen before, N8(C2v)-B is an exception.
For a global analysis of all results given in the previous section, and also aiming to find correlations between the energetic properties with electronic and structural ones, we have calculated several molecular parameters such as HOMO–LUMO gap, average bond order, average bond length and asphericity for all polyN structures reported here. After the calculations we plotted these properties against AE, DE and DE/n, which are all given in the ESI† for both DFT functionals.
None of the molecular parameters explored here were found to correlate with AE. If such correlation existed, it would be very useful for predicting the dissociation barriers of new polyN structures obtained in the future, since exploring their high dimensional PES in the search for the lowest TS is a very difficult task.
The average bond lengths and average bond orders were found to be correlated with DE and DE/n. The latter is shown in Fig. 15, where it is seen that lower bond orders (and higher bond lengths, as given in the ESI†) generally mean higher dissociation energy. It is interesting to see that DE/n, which is more related to the energy content of a structure than DE, can be clearly stratified among the four geometrical categories (chain, ring, cage and caged prism), which was not observed in the case of DE (see Fig. 14). Although caged prisms have higher DE/n than caged structures, their average bond orders are similar, lying below 0.9. Ring structures have average bond orders from 0.95 to 1.14, while chained structures show the largest values, as more double bonds are possible.
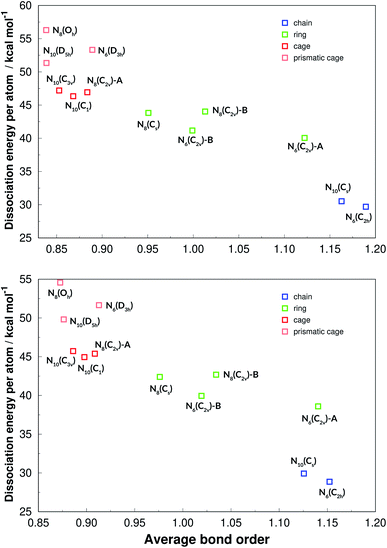 | ||
| Fig. 15 Dissociation energies per nitrogen atoms in function of the average bond orders. Results at the def2-TZVPP level of theory. M06-2X (upper panel) and SOGGA11-X (lower panel). | ||
5 Conclusions
In this work, the unimolecular decomposition routes for several polynitrogen allotropes were predicted at the SOGGA11-X/def2-TZVPP and M06-2X/def2-TZVPP levels of theory. These two methods were shown to yield similar results, compare well with highly accurate CCSD(T)-F12 ones, and the same conclusions can be drawn from both.Though the potential barriers for some polyN have been previously explored in the literature, this work provides new accounts on the unconstrained decomposition of six structures: N8(C2v)-A, N8(Cs), and all four N10 isomers, including the prismatic one. Furthermore, new mechanisms involving prismane and N8(C2v)-B were obtained.
By using the same computational methods for three different sizes, and several geometrical shapes for each, we were able to extract interesting information about this class of chemical systems. First, it is shown that the energy content (DE/n, which may be released if these substances are used as energy sources) can be clearly stratified between chain, ring, cage and prismatic cage structures. This variable shows a linear correlation with average bond size and average bond order.
The energy barriers towards unimolecular decomposition (AE) could not be correlated to any electronic or geometrical property of the molecule. If such correlation existed, it would be very useful for screening newly proposed polyN structures, as the search for the dissociation transition states is a very time consuming task.
Comparing between individual structures, it is found that prismane (N6(D3h)) shows a very high dissociation barrier and, if it could be synthesized, would be very stable, perhaps allowing its storage at ambient conditions. Upon triggering its dissociation reaction, it would deliver a very large amount of energy, without producing any pollutant products.
All prismatic cage structures are shown to have considerably high activation energies as well. Although N8(Oh) and N10(D5h) do not display an AE as high as that of prismane, they also have a very large energy content. An unexpected promising case was N8(C2v), a boat-like structure that displays an activation energy even higher than those of the N8(Oh) and N10(D5h) prismatic structures.
The present overall survey of possible polyN structures may serve as a guide for future computational work, to direct efforts in finding crystal structures and other properties only for the most promising and kinetically stable polyN structures.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work has been financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001, Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), grants 403352/2016-9 and 305469/2018-5, and Fundação de Amparo à Pesquisa do estado de Minas Gerais (FAPEMIG). We are also thankful for the support of Centro Federal de Educação Tecnológica de Minas Gerais (CEFET-MG) and Rede Mineira de Química (RQ-MG).References
- P. C. Samartzis and A. M. Wodtke, All-nitrogen chemistry: how far are we from N60?, Int. Rev. Phys. Chem., 2006, 25, 527–552 Search PubMed.
- B. Hirshberg, R. B. Gerber and A. I. Krylov, Calculations predict a stable molecular crystal of N8, Nat. Chem., 2014, 6, 52–56 CrossRef CAS PubMed.
- V. Zarko, Searching for ways to create energetic materials based on polynitrogen compounds, Combust., Explos. Shock Waves (Engl. Transl.), 2010, 46, 121–131 CrossRef.
- M. R. Manaa, Toward new energy-rich molecular systems: from N10 to N60, Chem. Phys. Lett., 2000, 331, 262–268 CrossRef CAS.
- T. Brinck and M. Rahm, Theoretical Design of Green Energetic Materials: Predicting Stability, Detection, Synthesis and Performance, in Green Energetic Materials, John Wiley & Sons, Chichester, UK, 2014 Search PubMed.
- M. A. Gimaldinova, K. P. Katin, K. S. Grishakov and M. M. Maslov, Kinetic stability of nitrogen cubane inside the fullerene cage: Molecular dynamics study, Fullerenes, Nanotubes, Carbon Nanostruct., 2020, 28, 304–308 CrossRef CAS.
- M. T. Nguyen, Polynitrogen compounds: 1. Structure and stability of N4 and N5 systems, Coord. Chem. Rev., 2003, 244, 93–113 CrossRef CAS.
- M. I. Eremets, A. G. Gavriliuk, I. A. Trojan, D. A. Dzivenko and R. Boehler, Single-bonded cubic form of nitrogen, Nat. Mater., 2004, 3, 558–563 CrossRef CAS PubMed.
- D. Laniel, B. Winkler, T. Fedotenko, A. Pakhomova, S. Chariton, V. Milman, V. Prakapenka, L. Dubrovinsky and N. Dubrovinskaia, High-pressure polymeric nitrogen allotrope with the black phosphorus structure, Phys. Rev. Lett., 2020, 124, 216001 CrossRef CAS PubMed.
- S. Duwal, Y.-J. Ryu, M. Kim, C.-S. Yoo, S. Bang, K. Kim and N. H. Hur, Transformation of hydrazinium azide to molecular N8 at 40 GPa, J. Chem. Phys., 2018, 148, 134310 CrossRef PubMed.
- C. Zhang, C. Sun, B. Hu, C. Yu and M. Lu, Synthesis and characterization of the pentazolate anion cyclo-N5 in (N5)6(H3O)3(NH4)4Cl, Science, 2017, 355, 374–376 CrossRef CAS PubMed.
- K. O. Christe, D. A. Dixon, D. McLemore, W. W. Wilson, J. A. Sheehy and J. A. Boatz, On a quantitative scale for Lewis acidity and recent progress in polynitrogen chemistry, J. Fluorine Chem., 2000, 101, 151–153 CrossRef CAS.
- K. O. Christe, W. W. Wilson, J. A. Sheehy and J. A. Boatz, N5+: a novel homoleptic polynitrogen ion as a high energy density material, Angew. Chem., 2001, 40, 2947 CrossRef.
- Y. Xu, Q. Wang, C. Shen, Q. Lin, P. Wang and M. Lu, A series of energetic metal pentazolate hydrates, Nature, 2017, 549, 78–81 CrossRef CAS PubMed.
- N. P. Salke, K. Xia, S. Fu, Y. Zhang, E. Greenberg, V. B. Prakapenka, J. Liu, J. Sun and J.-F. Lin, Tungsten Hexanitride with Single-Bonded Armchairlike Hexazine Structure at High Pressure, Phys. Rev. Lett., 2021, 126, 065702 CrossRef CAS PubMed.
- Z. Wu, E. M. Benchafia, Z. Iqbal and X. Wang, N8− polynitrogen stabilized on multi-wall carbon nanotubes for oxygen-reduction reactions at ambient conditions, Angew. Chem., 2014, 126, 12763–12767 CrossRef.
- Z. Yao, M. Hu, Z. Iqbal and X. Wang, N8−-Polynitrogen Stabilized on Boron-Doped Graphene as Metal-Free Electrocatalysts for Oxygen Reduction Reaction, ACS Catal., 2019, 10, 160–167 CrossRef.
- W. J. Lauderdale, J. F. Stanton and R. J. Bartlett, Stability and energetics of metastable molecules: tetraazatetrahedrane (N4), hexaazabenzene (N6), and octaazacubane (N8), J. Phys. Chem., 1992, 96, 1173–1178 CrossRef CAS.
- M. N. Glukhovtsev and P. von Ragué Schleyer, Structures, bonding and energies of N6 isomers, Chem. Phys. Lett., 1992, 198, 547–554 CrossRef CAS.
- R. Engelke, Ab initio correlated calculations of six nitrogen (N6) isomers, J. Phys. Chem., 1992, 96, 10789–10792 CrossRef CAS.
- M. L. Leininger, C. D. Sherrill and H. F. I. Schaefer, N8: a structure analogous to pentalene, and other high-energy density minima, J. Phys. Chem., 1995, 99, 2324–2328 CrossRef CAS.
- M. N. Glukhovtsev, H. Jiao and P. v. R. Schleyer, Besides N2, what is the most stable molecule composed only of nitrogen atoms?, Inorg. Chem., 1996, 35, 7124–7133 CrossRef CAS PubMed.
- B. M. Gimarc and M. Zhao, Strain energies in homoatomic nitrogen clusters N4, N6, and N8, Inorg. Chem., 1996, 35, 3289–3297 CrossRef CAS PubMed.
- A. Tian, F. Ding, L. Zhang, Y. Xie and H. F. Schaefer, New isomers of N8 without double bonds, J. Phys. Chem. A, 1997, 101, 1946–1950 CrossRef CAS.
- L. Gagliardi, S. Evangelisti, B. O. Roos and P.-O. Widmark, A theoretical study of ten N8 isomers, J. Mol. Struct., 1998, 428, 1–8 CrossRef CAS.
- C. Chen, K.-C. Sun and S.-F. Shyu, Theoretical study of various N10 structures, J. Mol. Struct., 1999, 459, 113–122 CrossRef CAS.
- C. Chen and S.-F. Shyu, Theoretical study of single-bonded nitrogen cluster-type molecules, Int. J. Quantum Chem., 1999, 73, 349–356 CrossRef CAS.
- M. Tobita and R. J. Bartlett, Structure and stability of N6 isomers and their spectroscopic characteristics, J. Phys. Chem. A, 2001, 105, 4107–4113 CrossRef CAS.
- Y. Ren, X. Wang, N.-B. Wong, A.-M. Tian, F.-j. Ding and L. Zhang, Theoretical study of the N10 clusters without double bonds, Int. J. Quantum Chem., 2001, 82, 34–43 CrossRef CAS.
- L. P. Cheng, S. Li and Q. S. Li, Polynitrogen clusters containing five-membered rings, Int. J. Quantum Chem., 2004, 97, 933–943 CrossRef CAS.
- H. Zhou, W. Zheng, X. Wang, Y. Ren, N.-B. Wong, Y. Shu and A. Tian, A Gaussian-3 investigation on the stabilities and bonding of the nine N10 clusters, J. Mol. Struct., 2005, 732, 139–148 CrossRef CAS.
- B. Tan, X. Long and J. Li, The cage strain energies of high-energy compounds, Comput. Theor. Chem., 2012, 993, 66–72 CrossRef CAS.
- B. Tan, M. Huang, X. Long, J. Li, X. Yuan and R. Xu, From planes to cluster: the design of polynitrogen molecules, Int. J. Quantum Chem., 2015, 115, 84–89 CrossRef CAS.
- L. Türker, Contemplation on some cyclic N8 isomers-A DFT treatment, Def. Technol., 2018, 14, 19–27 CrossRef.
- L. Türker, A density functional study on some cyclic N10 isomers, Def. Technol., 2019, 15, 154–161 CrossRef.
- O. V. Mikhailov and D. V. Chachkov, Molecular structures and thermodynamics of stable N4, N6 and N8 neutral poly-nitrogens according to data of QCISD(T)/TZVP method, Chem. Phys. Lett., 2020, 137594 CrossRef CAS.
- Q. S. Li, L. J. Wang and W. G. Xu, Structures and stability of N9, N9− and N9+ clusters, Theor. Chem. Acc., 2000, 104, 67–77 Search PubMed.
- Y. D. Liu, J. F. Zhao and Q. S. Li, Structures and stability of N7+ and N7− clusters, Theor. Chem. Acc., 2002, 107, 140–146 Search PubMed.
- C.-K. Law, W.-K. Li, X. Wang, A. Tian and N. Wong, A Gaussian-3 study of N7+ and N7− isomers, J. Mol. Struct., 2002, 617, 121–131 CrossRef CAS.
- Y. H. Liang, Q. Luo, M. Guo and Q. S. Li, What are the roles of N3 and N5 rings in designing polynitrogen molecules?, Dalton Trans., 2012, 41, 12075–12081 RSC.
- M. J. Greschner, M. Zhang, A. Majumdar, H. Liu, F. Peng, J. S. Tse and Y. Yao, A new allotrope of nitrogen as high-energy density material, J. Phys. Chem. A, 2016, 120, 2920–2925 CrossRef CAS PubMed.
- S. Liu, L. Zhao, M. Yao, M. Miao and B. Liu, Novel All-Nitrogen Molecular Crystals of Aromatic N10, Adv. Sci., 2020, 7, 1902320 CrossRef CAS PubMed.
- S. V. Bondarchuk, Bipentazole (N10): A Low-Energy Molecular Nitrogen Allotrope with High Intrinsic Stability, J. Phys. Chem. Lett., 2020, 11(14), 5544–5548 CrossRef CAS PubMed.
- R. Engelke and J. R. Stine, Is N8 cubane stable?, J. Phys. Chem., 1990, 94, 5689–5694 CrossRef CAS.
- K. M. Dunn and K. Morokuma, Transition state for the dissociation of tetrahedral N4, J. Chem. Phys., 1995, 102, 4904–4908 CrossRef CAS.
- M. T. Nguyen and T.-K. Ha, Azidopentazole is Probably the Lowest-Energy N8 Species-A Theoretical Study, Chem. Ber., 1996, 129, 1157–1159 CrossRef CAS.
- S. Evangelisti and L. Gagliardi, A complete active-space self-consistent-field study on cubic N8, Il Nuovo Cimento D, 1996, 18, 1395–1405 CrossRef.
- L. Gagliardi, S. Evangelisti, V. Barone and B. O. Roos, On the Dissociation of N6 into 3N2 Molecules, Chem. Phys. Lett., 2000, 320, 518–522 CrossRef CAS.
- L. Gagliardi, S. Evangelisti, A. Bernhardsson, R. Lindh and B. O. Roos, Dissociation reaction of N8 azapentalene to 4N2: a theoretical study, Int. J. Quantum Chem., 2000, 77, 311–315 CrossRef CAS.
- G. Chung, M. W. Schmidt and M. S. Gordon, An ab initio study of potential energy surfaces for N8 isomers, J. Phys. Chem. A, 2000, 104, 5647–5650 CrossRef CAS.
- L. J. Wang, W. G. Xu and Q. S. Li, Stability of N8 isomers and isomerization reaction of N8(C2v) to N8(Cs), J. Mol. Struct., 2000, 531, 135–141 CrossRef CAS.
- M. T. Nguyen and T.-K. Ha, Decomposition mechanism of the polynitrogen N5 and N6 clusters and their ions, Chem. Phys. Lett., 2001, 335, 311–320 CrossRef CAS.
- T. Klapötke and R. Harcourt, The interconversion of N12 to N8 and two equivalents of N2, J. Mol. Struct., 2001, 541, 237–242 CrossRef.
- Q. S. Li and L. J. Wang, A Quantum Chemical Theoretical Study of Decomposition Pathways of N9(C2v) and N9+(C2v) Clusters, J. Phys. Chem. A, 2001, 105, 1203–1207 CrossRef CAS.
- D. L. Strout, Acyclic N10 fails as a high energy density material, J. Phys. Chem. A, 2002, 106, 816–818 CrossRef CAS.
- M. D. Thompson, T. M. Bledson and D. L. Strout, Dissociation barriers for odd-numbered acyclic nitrogen molecules N9 and N11, J. Phys. Chem. A, 2002, 106, 6880–6882 CrossRef CAS.
- L. J. Wang, P. G. Mezey and M. Z. Zgierski, Stability and the structures of Nitrogen clusters N10, Chem. Phys. Lett., 2004, 391, 338–343 CrossRef CAS.
- V. Elesin, N. Degtyarenko, K. Pazhitnykh and N. Matveev, Modeling of synthesis and dissociation of the N4 nitrogen cluster of D2h symmetry, Russ. Phys. J., 2009, 52, 1224–1234 CrossRef CAS.
- M. Noyman, S. Zilberg and Y. Haas, Stability of polynitrogen compounds: the importance of separating the σ and π electron systems, J. Phys. Chem. A, 2009, 113, 7376–7382 CrossRef CAS PubMed.
- B. Hirshberg and R. B. Gerber, Decomposition mechanisms and dynamics of N6: Bond orders and partial charges along classical trajectories, Chem. Phys. Lett., 2012, 531, 46–51 CrossRef CAS.
- M. T. Nguyen, M. McGinn, A. Hegarty and J. Elguero, Can the pentazole anion (N5−) be isolated and/or trapped in metal complexes?, Polyhedron, 1985, 4, 1721–1726 CrossRef CAS.
- S. Fau and R. J. Bartlett, Possible products of the end-on addition of N3− to N5+ and their stability, J. Phys. Chem. A, 2001, 105, 4096–4106 CrossRef CAS.
- L. Gagliardi, G. Orlandi, S. Evangelisti and B. O. Roos, A theoretical study of the nitrogen clusters formed from the ions N3−, N5+, and N5−, J. Chem. Phys., 2001, 114, 10733–10737 CrossRef CAS.
- S. Fau, K. J. Wilson and R. J. Bartlett, On the Stability of N5+N5−, J. Phys. Chem. A, 2002, 106, 4639–4644 CrossRef CAS.
- Q. S. Li and J. F. Zhao, A theoretical study on decomposition pathways of N7+ and N7− clusters, J. Phys. Chem. A, 2002, 106, 5928–5931 CrossRef CAS.
- L. Gagliardi, S. Evangelisti, P.-O. Widmark and B. O. Roos, A theoretical study of the N8 cubane to N8 pentalene isomerization reaction, Theor. Chem. Acc., 1997, 97, 136–142 Search PubMed.
- Q. S. Li and Y. D. Liu, Theoretical studies of the N6 potential energy surface, J. Phys. Chem. A, 2002, 106, 9538–9542 CrossRef CAS.
- M. W. Schmidt, M. S. Gordon and J. A. Boatz, Cubic fuels?, Int. J. Quantum Chem., 2000, 76, 434–446 CrossRef CAS.
- L. Türker, Contemplation on Some Prismatic Polynitrogen Structures-A DFT Treatment, Z. Anorg. Allg. Chem., 2019, 645, 1118–1126 CrossRef.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen and S. Su, et al., General atomic and molecular electronic structure system, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- H. Werner, P. Knowles, G. Knizia, F. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, et al., MOLPRO, version 2015.1, a package of ab initio programs. University of Cardiff Chemistry Consultants (UC3), Cardiff, Wales, UK 2015 Search PubMed.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, A1133 CrossRef.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- R. Peverati and D. G. Truhlar, Communication: A global hybrid generalized gradient approximation to the exchange-correlation functional that satisfies the second-order density-gradient constraint and has broad applicability in chemistry. 2011 Search PubMed.
- R. Peverati and D. G. Truhlar, M11-L: a local density functional that provides improved accuracy for electronic structure calculations in chemistry and physics, J. Phys. Chem. Lett., 2012, 3, 117–124 Search PubMed.
- Y. Zhao and D. G. Truhlar, Exploring the limit of accuracy of the global hybrid meta density functional for main-group thermochemistry, kinetics, and noncovalent interactions, J. Chem. Theory Comput., 2008, 4, 1849–1868 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, How accurate are the Minnesota density functionals for noncovalent interactions, isomerization energies, thermochemistry, and barrier heights involving molecules composed of main-group elements?, J. Chem. Theory Comput., 2016, 12, 4303–4325 CrossRef CAS PubMed.
- B. M. Bode and M. S. Gordon, MacMolPlt: a graphical user interface for GAMESS, J. Mol. Graphics Modell., 1998, 16, 133–138 CrossRef CAS PubMed.
- M. Silva, F. Silva, B. Galvão, J. Braga and J. Belchior, A genetic algorithm survey on closed-shell atomic nitrogen clusters employing a quantum chemical approach, J. Mol. Model., 2018, 24, 196 CrossRef CAS PubMed.
- C. Gonzalez and H. B. Schlegel, Reaction path following in mass-weighted internal coordinates, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- R. J. Bartlett, Coupled-cluster approach to molecular structure and spectra: a step toward predictive quantum chemistry, J. Phys. Chem., 1989, 93, 1697–1708 CrossRef CAS.
- R. J. Bartlett, J. Watts, S. Kucharski and J. Noga, Non-iterative fifth-order triple and quadruple excitation energy corrections in correlated methods, Chem. Phys. Lett., 1990, 165, 513–522 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, A fifth-order perturbation comparison of electron correlation theories, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- T. B. Adler, G. Knizia and H.-J. Werner, A simple and efficient CCSD(T)-F12 approximation, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, Simplified CCSD(T)-F12 methods: Theory and benchmarks, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- K. P. Katin, V. B. Merinov, A. I. Kochaev, S. Kaya and M. M. Maslov, All-nitrogen cages and molecular crystals: Topological rules, stability, and pyrolysis paths, Computation, 2020, 8, 91 CrossRef CAS.
- I. Y. Zhang, J. Wu and X. Xu, Extending the reliability and applicability of B3LYP, Chem. Commun., 2010, 46, 3057–3070 RSC.
- Y. Zhao, N. González-García and D. G. Truhlar, Benchmark database of barrier heights for heavy atom transfer, nucleophilic substitution, association, and unimolecular reactions and its use to test theoretical methods, J. Phys. Chem. A, 2005, 109, 2012–2018 CrossRef CAS PubMed.
- M. Evans and M. Polanyi, On the introduction of thermodynamic variables into reaction kinetics, Trans. Faraday Soc., 1937, 33, 448–452 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Structures and frequencies obtained at the M06-2X and SOGGA11-X/def2-TZVPP levels; graphs of selected molecular parameters against AE, DE and DE/n. See DOI: 10.1039/d1ra03259c |
| This journal is © The Royal Society of Chemistry 2021 |