Analysis of sodium generation by sodium oxide decomposition on corrosion resistance materials: a new approach towards sodium redox water-splitting cycle

Abstract

In this study, the investigation of materials with corrosion resistance was carried out to prevent side reactions caused by sodium oxide (Na₂O) in the Na-redox thermochemical water splitting cycle, and essential operational conditions for sodium (Na) generation from Na₂O were also investigated. Thermal desorption spectroscopy and X-ray diffraction techniques at altered conditions were mainly used for the experimental investigation. Numerous types of materials were tested to find materials with high resistance towards corrosion and to understand essential thermal decomposition processes of Na₂O. In addition, under different temperatures and pressure conditions, the thermodynamic calculation of Gibbs free energy was performed to obtain experimental results. As a result, a Ti alloy showed significant resistance towards the corrosive reaction by Na₂O. The obtained experimental and simulated results support the direct decomposition of Na₂O to form Na and O₂ below 600 °C under low partial pressure conditions. The optimized conditions for Na generation with the Ti alloy sample can be used for low temperature water splitting.

---

Introduction

Excessive utilization of non-renewable sources and their hazardous by-products lead to the pollution and global warming problems. The search for alternative energy sources has become a necessity at present. The most important requirements for alternative energy sources include energy efficiency at the large scale and clean by-products.^1–4 For decades, researchers have devoted extensive efforts to find a suitable energy source. As of now, hydrogen (H₂) is the best energy source of renewable energy such as natural energy in this regard. The advantages of H₂ as an energy source are security, reduction in environmental problems, clean energy carrier, abundant element on the Earth, and the potential to fulfil the society's energy requirement.^5–8

Currently, H₂ is produced at the industrial level from non-renewable sources such as methane steam reforming,^9,10 gasification,^11,12 and partial oxidation.¹³ H₂ production from non-renewable sources generates some adverse by-products such as CO₂ and other harmful gases. On the other hand, H₂ is a potential green energy medium when H₂ is produced from renewable sources.^14–17 The hydrogen production via water electrolysis combined with power generation by natural energy such as solar and wind is an attractive method because the related technology has already been established. However, it is difficult to obtain benefits of scale-up because of the 2-dimensional electrode reactions. Thermochemical water splitting is one of the promising and encouraging methods for the large scale H₂ production,^18,19 where larger merit can be expected by scale up as chemical plants. The main hurdle in direct water splitting includes the requirement of high temperatures around 4000 °C and efforts, which is not suitable from the economic point of view. Thermochemical water-splitting cycles are attractive methods. In this method, a cycle composed of chemical reactions takes place, and at the end, all chemicals regenerate again except H₂O. Various types of thermochemical cycles have been reported: tin oxide (SnO₂/SnO),^20,21 cobalt oxide,^22,23 iron oxide (Fe₃O₄/FeO),^24,25 zinc oxide (ZnO/Zn),^26,27 germanium oxide (GeO₂/GeO),²⁸ cerium-based oxides,^29–31 sulfur–iodine,^32,33 sodium manganese mixed ferrite,³⁴ and sodium-redox (Na-redox) cycles.^35–37 Among the above-mentioned works, specific temperature and pressure conditions are required due to kinetic and thermodynamics reasons.^38–40 For all the conventional cycles, high temperature heat energy (800–1500 °C) is required, and thereby utilizable heat sources are limited to solar heat plant with high concentration (tower-type) and nuclear high temperature gas-cooled reactors.

The Na-redox cycle is composed of three types of reactions: hydrogen generation by reaction between NaOH and Na, Na metal separation by the thermal decomposition of sodium oxide (Na₂O) to form sodium peroxide (Na₂O₂), and oxygen generation (O₂) by the hydrolysis of Na₂O₂ (Table 1). H₂ and O₂ generation reactions are not difficult thermodynamically and can be operated at moderate temperature and atmospheric pressure conditions.⁴¹ The challenging reaction is the decomposition of sodium oxide (Na₂O) due to its high thermodynamic stability. In general, the thermodynamics of chemical reactions are expressed using Gibbs free energy change ΔG, as shown in eqn (1):

ΔG = ΔH − TΔS (1)

where ΔH, T, and ΔS are the enthalpy change, temperature, and entropy change of chemical reactions, respectively. The enhancement of ΔS decreases the required temperature for the reaction progress. In previous studies, thermodynamic equilibrium was shifted by controlling the partial pressure of Na vapor. As a result, the Na generation was found below 500 °C. Thus, the feasibility of the Na-redox cycle as a potential hydrogen production method operated below 500 °C has been demonstrated. If the low temperature operation of thermochemical cycles could be realized, numerous types of heat sources such as solar heat and unused heat can be utilized for hydrogen production. In addition, effective heat storage materials such as molten salts (nitrates and carbonates) can also be used for stable and long running reaction. On the other hand, the details of the reaction process are not understood completely because of the strong corrosion property of Na₂O and/or Na₂O₂, which is the most critical issue of the Na-redox cycle and limits the development for practical use.

Table 1 Summarised table for the Na-redox cycle and modified one. Where, ΔH, ΔS, and ΔG are representation of the enthalpy change, entropy change, and Gibbs free energy respectively at ambient conditions

	Equation	ΔH (kJ)	ΔS (J mol^−1)	ΔG (kJ mol^−1)	Eq. no
Cycle 1	2NaOH(s) + 2Na(l) → 2Na2O(s) + H2(g)	11	36	0.27	(2)
	2Na2O(s) → Na2O2(s) + 2Na(g)	540	250	465	(3)
	Na2O2(s) + H2O(l) → 2NaOH(s) + ½O2	−55	66	−75	(4)
	H2O(l) → H2(g) + ½O2
Cycle 2	2NaOH(s) + 2Na(l) → 2Na2O(s) + H2(g)	11	36	0.27	(2)
	2Na2O(s) → 4Na(s) + O2(g)	830	260	752	(7)
	2Na(s) + 2H2O(g) → 2NaOH(s) + H2(g)	−368	−221	−302	(4)
	2H2O(g) → 2H2(g) + O2(g)

---

In this study, the target reaction is the decomposition of Na₂O to generate Na₂O₂ and Na at a low temperature in the cycle, as shown in Table 1. The Na-redox water splitting cycle can be a potential hydrogen production technique after understanding the essential reaction processes and establishing control methods. The main hurdle is to handle the Na oxides at high temperatures because of their high corrosive properties as explained above. Na₂O corrodes base materials as side reactions, and undesirable stable by-products are formed. Therefore, one of the objectives in this study is finding a suitable base material for the Na₂O decomposition step. By using the attractive base materials, the essential thermal decomposition properties of Na₂O were investigated. Furthermore, the experimental results were discussed with thermodynamic calculations.

Materials and methods

The starting material Na₂O containing Na₂O₂ was purchased from Sigma-Aldrich, and its composition was 80% Na₂O + 20% Na₂O₂. Various types of base materials were used for the experimental testing of the Na₂O decomposition and corrosion resistance properties: graphite powder, boron nitride (BN), single crystal Si, aluminium oxide (Al₂O₃), aluminium nitride (AlN), graphite polished, and Ti Alloy (0.8% Ni, 0.4% Mo, 98.8% Ti). All the sample materials were used as received without any pre-treatments. Na₂O with each base material was heated and analyzed under high vacuum conditions (10⁻¹¹ MPa) by thermal desorption spectroscopy (TDS, ESCO EMD-WA 1000 s d⁻¹), which is specially designed to detect metal vapor such as Na. The base materials are put on a quartz boat as a sample holder, and then the Na₂O powder was put on the base materials in a glove box (Miwa MFG) filled with purified Ar (>99.9999%). The above samples were moved into the TDS chamber without exposing them to air by a transfer vessel. After the TDS experiment, all the samples were identified by the X-ray diffraction (XRD) technique (Rigaku-RINT 2500 V, Cu Kα radiation: λ = 1.5408 Å) to understand the decomposition properties of Na₂O and obtain the information of side reactions, where the samples were covered by a polyimide sheet (Du Pont-Toray Co., Ltd., Kapton) to avoid the reaction with oxygen and moisture. All the above-mentioned processes were carried out without exposing the samples into air to avoid the influence of oxygen and moisture. Thermodynamic calculations were performed by the MALT software to expect possible reactions during the heat treatment of Na₂O with the base materials. Here, the results for Ti alloy, AlN, graphite powder are shown and discussed as representative cases in the manuscript. The results of other samples' data are explained in ESI.†

Results and discussion

Base sample comparison for corrosion resistance

For the TDS experiments, to minimize the contribution of gases adsorption by the quartz boat and base material, baking and blank tests were performed before the sample measurements. Observed TDS data for the baking and blank test does not show any peak deflection from the regular pattern (see Fig. S1–S3†).

Temperature calibration was also performed in the blank test experiment to know the exact temperature for Na₂O analyses (see Fig. S4†). The difference between the targeted temperature and real temperature is not small and mainly originated from the quartz boat and base material layer (see Fig. S5†). For precise comparison, the TDS data of graphite, AlN, and Ti alloy are shown in Fig. 1. Other tested materials and their corresponding data have been summarized in the ESI (see Fig. S6–S11†). Fig. 1(a) shows data for m/z = 44 spectra, which correspond to carbon dioxide (CO₂) gas. It is determined from the spectra that graphite has the highest intensity peak of CO₂ gas compared with the results for AlN and Ti alloy samples. The occurrence of the CO₂ peak is due to the formation of Na₂CO₃ as an intermediate. At a high temperature, clear peaks corresponding to Na and CO₂ were found. Based on the CO₂ peak and MALT calculations (see Fig. S12†), the formation of Na₂CO₃ is expected, and subsequently Na₂CO₃ decomposes into Na and CO₂ at the targeted temperature of about 650 °C, as shown in eqn (5).

3Na₂O + C → Na₂CO₃ + 4Na → 6Na + CO₂ + ½O₂ (5)

Fig. 1 Comparison TDS data for graphite, AlN, and Ti alloy of (a) m/z = 44, (b) m/z = 28, (c) m/z = 23, and (d) targeted and calibrated temperature profiles.

The base of AlN also shows a side reaction with Na₂O, which is plotted in Fig. 1(b). The spectrum of m/z = 28 corresponding to nitrogen (N₂) gas shows a clear peak. The appearance of this peak is due to the desorption of N₂ molecules from AlN around 450 °C (targeted temperature), suggesting that Na₂O reacts with AlN and produces NaAlO₂ and N₂ molecules at about 450 °C according to eqn (6).

2Na₂O + 2AlN → 2Na + 2NaAlO₂ + N₂ (6)

The spectra in Fig. 1(c) show the peak of m/z = 23, which is Na. Except for the Ti alloy, other samples are showing a peak of Na due to the side reactions. All other samples (Si, polished graphite, boron nitride, and so on) also showed corrosion reactions of Na₂O at the high temperature. Among all the tested samples from TDS data, it was concluded that Ti alloy was the best material to exhibit corrosion resistance properties. The Ti alloy would also form a very thin, stable, and uniform oxide layer on the surface. It is expected that this oxide layer prevents the inside of Ti from any side reactions at any conditions. The corrosion resistance of a metal surface always depends on the stability of the oxide layer. The amount of Ni and Mo within the Ti alloy is supportive to make a stable oxide layer and enhance the corrosion resistance properties.⁴² Therefore, the Ti alloy does not show strong corrosion towards the Na₂O decomposition process. Fig. 2 shows the TDS spectra for Na₂O on the Ti alloy base heated up to 800 °C (calibrated temperature: ∼600 °C), and the major profiles in the observed data correspond to m/z = 32 and 23, as plotted in Fig. 2, where all the possible release gases were observed in the experiments (see Fig. S7†). These gases correspond to O₂ and Na, respectively. Comparing the O₂ and Na peaks, the first peak is observed almost at 25 min in the O₂ spectra. Since all the TDS experiments performed at the heating rate of 5 °C min⁻¹, the targeted temperature at this point is 125 °C (calibrated temperature: ∼75 °C).

Fig. 2 TDS spectra of Na₂O with the Ti alloy base performed at 800 °C.

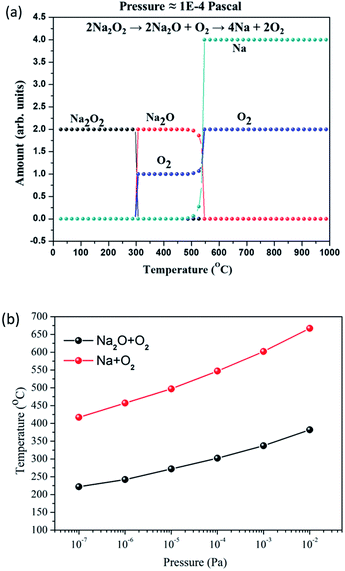
Because of the low temperature, the peak almost at 25 min is not related to the decomposition of Na₂O thermodynamically. This peak would be due to the release of the O₂ molecule, which is absorbed on the Na₂O sample. In fact, the TDS data of other samples also shows (see Fig. S6–S11†) the same O₂ peak at the same temperature region. The second peak is around after 90 min and the calibrated temperature here is 325 °C. In the comparison of both O₂ and Na spectra, only O₂ spectra show the high intensity peak. By observing the information obtained from software calculation (see Fig. 3) and XRD data (Fig. 5), this peak appears due to the decomposition of Na₂O₂. Na₂O₂ is included as impurity in the as-purchased Na₂O sample, and it decomposes into Na₂O and O₂. The last peak that is observed in both spectra after 160 min and the corresponding calibrated temperature at this point is 600 °C. At this point, both the spectra of Na and O₂ show a high intensity synchronized peak. By the observation, it can be concluded that the appearance of this is due to the decomposition of Na₂O into Na and O₂. The software calculation (see Fig. 3(a)) at this temperature also suggests the decomposition of Na₂O at this point.

Fig. 3 Graphs based on the MALT software calculation: (a) temperature information for Na₂O and Na₂O₂ decomposition under static pressure conditions and (b) temperature information for Na₂O and Na₂O₂ decomposition for variable pressure conditions.

Fig. 3(b) shows pressure dependence of the decomposition temperatures of Na₂O and Na₂O₂. From the results, the alteration in the partial pressure condition leads to the decrement in the decomposition temperature. The temperature difference for the Na₂O decomposition can be achieved nearby 250 °C just by reducing the pressure from the atmosphere to 1 × 10⁻² Pa. Likewise, the Na₂O₂ decomposition also proceeds at a low temperature in low partial pressure conditions. From the MALT software calculations, it is found that the used Na₂O sample decomposes in two stages.^43,44 First stage, the pre-existing Na₂O₂ (in the Na₂O sample) decomposes into Na₂O and O₂ at a low temperature. In the second stage, Na₂O decomposes into Na and O₂. In the case of 1 × 10⁻⁴ Pa pressure, Na₂O₂ decomposes at about 300 °C and Na₂O decomposes at around 540 °C into Na and O₂ according to TDS results. Owing to the above facts, it is difficult to control the decomposition of Na₂O into Na₂O₂ and Na in our experimental conditions (Table 1; eqn (3)). Therefore, the reactions of the water-splitting cycle should be restructured, as shown in Table 1. In this water-splitting cycle, Na₂O is directly decomposed into Na and O₂ according to eqn (7). To complete the cycle, Na generated by reaction (7) is divided to half amount and used for reactions (2) and (4) to produce H₂.

2Na₂O(s) → 4Na(s) + O₂(g) (7)

Temperature optimization for Na generation

For the temperature optimization of the Na generation, the TDS experiments were performed at different temperature conditions. The TDS measurements were performed for Na₂O on the Ti alloy base from 400 to 800 °C at the difference of 100 °C. After each TDS experiment, the same Ti alloy base sample heated for 900 °C without Na₂O in the TDS chamber (see detailed procedure in Fig. S13†). This heating process of the Ti alloy removes the background noise (impurities) of the previous experiment. All the TDS results for Na and O₂ obtained at 400–800 °C are shown in Fig. 4. The spectra of Na and O₂ for all the experiments are similar, suggesting that the Ti alloy possesses high stability for the corrosion of Na₂O. The O₂ desorption due to the Na₂O₂ decomposition was observed below 400 °C (see Fig. S14†) for all the spectra because the commercial Na₂O including Na₂O₂ as an impurity was loaded for each experiment. The Na generation originated in the direct decomposition of Na₂O was found from 700 °C (calibrated temperature: ∼540 °C) even though the reaction yield would be low compared with that at 800 °C (calibrated temperature: 600 °C).

Fig. 4 Comparison of (a) Na peak (m/z = 23) and (b) O₂ peak (m/z = 32) from TDS data obtained at the difference of 100 °C from 400–800 °C.

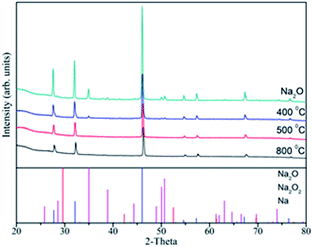
The XRD experiments have been performed for the Na₂O sample before and after the above TDS experiments, and the results are shown in Fig. 5. From the observed XRD patterns, it can be clarified that the peaks corresponding to Na₂O₂ in the initial sample (80% Na₂O + 20% Na₂O₂) disappeared between 400 °C and 500 °C. That indicates that Na₂O₂ is decomposed in this temperature region. This result is consistent with the results of TDS and thermodynamic calculation obtained by the MALT software. The intensity of peaks corresponding to the Na₂O phase was slightly lowered. When the direct Na₂O decomposition proceeded, the products of Na and O₂ were released as gaseous phases in the TDS chamber. Moreover, the remaining material after the TDS experiments should be the undecomposed Na₂O. This is the reason that no peak was observed corresponding to Na even at 800 °C (calibrated temperature: 600 °C), which is enough temperature for the Na₂O decomposition as discussed above. Fig. 6 shows the XRD patterns of Ti alloy after the TDS experiments at 400–800 °C. The diffraction peaks assigned to the Ti alloy changed to be sharp and intense, causing annealing effects. On the other hand, the corrosion phases were not observed at all the temperature. Thus, these results also suggest that the Ti alloy is recognized as the promising corrosion-resistance material for the Na₂O decomposition process at high temperatures.

Fig. 5 XRD data for Na₂O at the various targeted temperature over the Ti alloy base.

Fig. 6 XRD data for the Ti alloy after different targeted temperature TDS experiments.

Conclusion

In this study, finding corrosion resistance materials and investigation of the essential properties of the Na₂O decomposition reaction in the Na-redox cycle were carried out. For the Na₂O decomposition, different base materials such as graphite powder, BN, single-crystal Si, Al₂O₃, AlN, graphite polished, Ti Alloy have been tested for the corrosion resistance. From the overall observation of all the materials, the Ti alloy shows outstanding corrosion resistance properties with Na₂O. Because a stable and uniform oxide layer on the Ti alloy appears to prevent the corrosion. Furthermore, the TDS experiments with different temperatures were performed for Na₂O on the Ti alloy base. The experiential results of TDS give details that Na₂O decomposes from around 600 °C in the high vacuum condition. TDS results also resemble the data obtained by the XRD and the theoretical calculation by the MALT software. This systematic study would be beneficial to establish the hydrogen production system based on the one for Na-redox thermochemical water splitting cycle.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by New Energy and Industrial Technology Development Organization (NEDO) project.

References

1. J. Jurasz, F. A. Canales, A. Kies, M. Guezgouz and A. Beluco, Sol. Energy, 2020, 195, 703–724.
2. A. Inayat and M. Raza, Renewable Sustainable Energy Rev., 2019, 107, 360–373.
3. M. Melikoglu, Ocean Eng., 2018, 148, 563–573.
4. N. Kannan and D. Vakeesan, Renewable Sustainable Energy Rev., 2016, 62, 1092–1105.
5. Z. Abdin, A. Zafaranloo, A. Rafiee, W. Mérida, W. Lipiński and K. R. Khalilpour, Renewable Sustainable Energy Rev., 2020, 120, 109620.
6. J. O. Abe, A. P. I. Popoola, E. Ajenifuja and O. M. Popoola, Int. J. Hydrogen Energy, 2019, 44, 15072–15086.
7. N. L. Panwar, S. C. Kaushik and S. Kothari, Renewable Sustainable Energy Rev., 2011, 15, 1513–1524.
8. P. Dimitriou and T. Tsujimura, Int. J. Hydrogen Energy, 2017, 42, 24470–24486.
9. B. Wang, Y. Zheng, J. Zhang, W. Zhang, F. Zhang, W. Xing and R. Zhou, Microporous Mesoporous Mater., 2019, 275, 191–199.
10. L. Barelli, G. Bidini, F. Gallorini and S. Servili, Energy, 2008, 33, 554–570.
11. M. Inaba, K. Murata, M. Saito and I. Takahara, Energy Fuels, 2006, 20, 432–438.
12. N. Gao, A. Li and C. Quan, Bioresour. Technol., 2009, 100, 4271–4277.
13. B. Sawatmongkhon, K. Theinnoi, T. Wongchang, C. Haoharn, C. Wongkhorsub and A. Tsolakis, Energy Fuels, 2019, 33, 6742–6753.
14. O. Bičáková and P. Straka, Int. J. Hydrogen Energy, 2012, 37, 11563–11578.
15. S. E. Hosseini and M. A. Wahid, Renewable Sustainable Energy Rev., 2016, 57, 850–866.
16. R. Chaubey, S. Sahu, O. O. James and S. Maity, Renewable Sustainable Energy Rev., 2013, 23, 443–462.
17. C. Acar and I. Dincer, Int. J. Hydrogen Energy, 2014, 39, 1–12.
18. F. Safari and I. Dincer, Energy Convers. Manage., 2020, 205, 112182.
19. M. Orfila, D. Sanz, M. Linares, R. Molina, R. Sanz, J. Marugán and J. Á. Botas, Int. J. Hydrogen Energy, 2021, 46, 17458–17471.
20. R. R. Bhosale, A. Kumar and P. Sutar, Energy Convers. Manage., 2017, 135, 226–235.
21. S. Abanades, P. Charvin, F. Lemont and G. Flamant, Int. J. Hydrogen Energy, 2008, 33, 6021–6030.
22. N. B. Goikoetxea, M. B. Gómez-Mancebo, R. Fernández-Saavedra, F. Borlaf, F. García-Pérez, J. A. Jiménez, I. Llorente, I. Rucandio and A. J. Quejido, Int. J. Hydrogen Energy, 2019, 44, 17578–17585.
23. C. Canavesio, D. Nassini, H. E. Nassini and A. E. Bohé, Int. J. Hydrogen Energy, 2020, 45, 26090–26103.
24. P. Charvin, S. Abanades, G. Flamant and F. Lemort, Energy, 2007, 32, 1124–1133.
25. N. Gokon, T. Hasegawa, S. Takahashi and T. Kodama, Energy, 2008, 33, 1407–1416.
26. K. Wegner, H. C. Ly, R. J. Weiss, S. E. Pratsinis and A. Steinfeld, Int. J. Hydrogen Energy, 2006, 31, 55–61.
27. A. Steinfeld, Int. J. Hydrogen Energy, 2002, 27, 611–619.
28. R. R. Bhosale, Int. J. Hydrogen Energy, 2019, 45, 5816–5828.
29. Y. Lu, L. Zhu, C. Agrafiotis, J. Vieten, M. Roeb and C. Sattler, Prog. Energy Combust. Sci., 2019, 75, 100785.
30. R. R. Bhosale and F. AlMomani, Int. J. Hydrogen Energy, 2020, 45, 10381–10390.
31. S. Abanades and G. Flamant, Sol. Energy, 2006, 80, 1611–1623.
32. L. Xu, L. Wang, P. Zhang, S. Hu, D. Li, S. Bai and S. Chen, Int. J. Hydrogen Energy, 2016, 41, 15998–16001.
33. A. Singhania and A. N. Bhaskarwar, Renewable Energy, 2018, 127, 509–513.
34. F. Varsano, M. Anna, B. Brunetti, F. Padella, A. La, C. Alvani and M. Cristina, Int. J. Hydrogen Energy, 2014, 39, 20920–20929.
35. J. G. O. Marques, A. L. Costa and C. Pereira, Int. J. Hydrogen Energy, 2020, 45, 11424–11437.
36. H. Miyaoka, T. Ichikawa, N. Nakamura and Y. Kojima, Int. J. Hydrogen Energy, 2012, 37, 17709–17714.
37. H. Miyaoka, T. Ichikawa and Y. Kojima, Energy Procedia, 2014, 49, 927–934.
38. Y. Mao, Y. Gao, W. Dong, H. Wu, Z. Song, X. Zhao, J. Sun and W. Wang, Appl. Energy, 2020, 267, 114860.
39. L. Xiao, S.-Y. Wu and Y.-R. Li, Renewable Energy, 2012, 41, 1–12.
40. J. R. Scheffe and A. Steinfeld, Biochem. Pharmacol., 2014, 17, 341–348.
41. J. G. O. Marques, A. L. Costa and C. Pereira, Int. J. Hydrogen Energy, 2019, 44, 14536–14549.
42. X. Tang, S. Wang, L. Qian, Y. Li, Z. Lin and D. Xu, Chem. Eng. Res. Des., 2015, 100, 530–541.
43. H. Yokokawa, S. Yamauchi and T. Matsumoto, Calphad, 1999, 23, 357–364.
44. H. Yokokawa, S. Yamauchi and T. Matsumoto, Calphad, 2002, 26, 155–166.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra02671b

---