Open Access Article
Open Access ArticleThermodynamic assessment of the stability of bulk and nanoparticulate cobalt and nickel during dry and steam reforming of methane†
Moritz Wolf *ab
*ab
aHelmholtz-Institute Erlangen-Nürnberg for Renewable Energy (IEK-11), Forschungszentrum Jülich GmbH, Egerlandstraße 3, 91058 Erlangen, Germany. E-mail: mo.wolf@fz-juelich.de
bFriedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Lehrstuhl für Chemische Reaktionstechnik (CRT), Egerlandstr. 3, 91058 Erlangen, Germany
First published on 19th May 2021
Abstract
The high reaction temperatures during steam and dry reforming of methane inevitably entail catalyst deactivation. Evaluation of the feasibility or potentially relevant mechanisms at play is of utmost importance to develop highly active and stable catalysts. Herein, various oxidation reactions of bulk-sized nickel and cobalt to the corresponding metal oxide or in the presence of a metal oxide carrier are evaluated thermodynamically and linked to approximated conditions during methane reforming. In particular cobalt aluminate, as well as cobalt or nickel titanates are likely to form. As oxidation to bulk-sized metal oxide is unlikely, a thermodynamic analysis of metallic nanoparticles was performed to calculate the size dependent stability against oxidation to nickel oxide or cobalt oxide in water and carbon dioxide-rich environments. The calculations indicate that nickel nanoparticles >3 nm and cobalt nanoparticles >10 nm are expected to withstand oxidation during steam and dry reforming of methane with stoichiometric feed compositions and methane conversion levels >10% at temperatures up to 1100 and 900 °C, respectively. Lastly, the reduced thermal stability of nanoparticles due to melting point suppression was assessed, leading to similar recommendations concerning minimum particle sizes.
Introduction
Steam reforming of methane (SRM, eqn (1)) is the state-of-the-art process for the production of a large amount of synthesis gas from methane due to superior economical features and process performance. SRM is a well-stablished technology for the production of hydrogen-rich synthesis gas covering approximately 80–85% of the global H2 production.1–4 An upcoming alternative of great potential in regard to sustainability and valorisation of less abundant methane sources is dry reforming of methane (DRM, eqn (2)). Here, steam is replaced by CO2 as the oxidative molecule for methane. Incorporation of this greenhouse gas into the value chain of chemical sites makes DRM ecologically attractive as it further provides great potential to mitigate environmental challenges associated with GHG emissions.4–9 In addition, the absence of steam decreases the energy requirements of DRM regarding heat-up of the reactants, which results in approximately 20% lower operating costs and a lower carbon footprint in comparison to SRM.6,8| CH4(g) + H2O(g) → 3H2(g) + CO(g) | (1) |
| CH4(g) + CO2(g) → 2H2(g) + 2CO(g) | (2) |
The major difference between DRM, SRM, and alternative reforming processes of methane for the production of synthesis gas, such as partial oxidation (POX), is the oxidising agent.6,8 The oxidants H2O in SRM and CO2 in DRM are required due to the strong saturated C–H bonds in the methane molecule. As CO2 is a weaker oxidant, DRM is even more endothermic than SRM and consequentially requires elevated operation temperatures in the range of 700–1000 °C for industrial application.7 Nevertheless, thermocatalytic low temperature reforming (≤500 °C) has been successfully demonstrated in the literature for SRM and DRM,10–12 but an efficient conversion to synthesis gas is strongly limited by thermodynamic constraints.1 The typically elevated operation temperatures in combination with an oxidising reaction mixture including hydrocarbons may cause rapid catalyst deactivation via coking and sintering, which are typically accelerated at elevated temperatures.8,13 In addition, the oxidants in the feed may induce deactivation by oxidation of the active metallic phase (eqn (3) and (4) exemplary for the common reforming catalyst Ni0). While oxidation of the active phase for methane reforming, such as Ni0 and Co0, is thermodynamically not feasible for bulk-sized structures,14–18 it has been suggested as a deactivation pathway of catalysts with small crystallite sizes of the active metallic phase for Ni-based catalysts in DRM19 or SRM,10,20–22 as well as Co-based catalysts in the Fischer–Tropsch synthesis.16,23–25 Noteworthy, oxidation may also enable additional conversion of carbon from CH4 decomposition via a Mars–van-Krevelen type mechanism, i.e. an oxidised phase may be re-reduced forming CO. Hence, such a conversion pathway may not only result in an enhanced coking resistance, but also boost the catalyst activity.18,26
| Ni(s) + H2O(g) → NiO(s) + H2(g) | (3) |
| Ni(s) + CO2(g) → NiO(s) + CO(g) | (4) |
The high temperatures and the oxidising atmosphere present the major challenges in the commercialisation of DRM. During commercial SRM, coking of the catalysts may be mostly suppressed by co-feeding an excess of oxidising H2O in the reformer, i.e. by increasing the steam-to-carbon ratio (S/C) in the inlet stream.13,27,28 S/C ratios exceeding the stoichiometry of the reforming reaction (eqn (1)) render SRM a combination of methane reforming and water–gas shift (WGS) reaction (eqn (5)),4 which also results in a typically desired increased H2/CO ratio in the product gas. The suppression of excessive coking and increased H2 content in the produced synthesis gas are also the reason for co-feeding steam and CO2 in the first commercialisation attempts of DRM in industry, which renders the processes a combination of DRM and SRM. This beneficial effect on suppression of coking in lab-scaled DRM is also reported in the literature, but co-feeding of steam generally mitigates the advantage regarding energy requirements of the reforming process.28,29 Hence, recent advances in catalyst research for DRM mostly focus on concepts on prevention of excessive sintering and carbon deposition to boost the catalysts' stability.30 For example, perovskite-based catalysts were employed in various studies and displayed suppressed coking and phase transformation of the active Ni0 phase.19,31,32 Further, novel mixed-metal oxide support materials were developed to hinder the solid-state reaction of active Ni0 nanoparticles with classical support materials, such as Al2O3, resulting in an increased stability against oxidation.33,34 Song et al. recently deliberately allowed for sintering of 2.9 nm Ni nanoparticles, supported on highly ordered single-crystals of MgO, up to an average size of 17.3 nm to obtain a heat resistant catalyst.9 As a result, coking was significantly suppressed as Ni0 accumulated at the high energy step edges of the MgO crystals during the sintering process and physically blocked centres for coking.
| CO(g) + H2O(g) → CO2(g) + H2(g) | (5) |
Pronounced sintering of nano-sized materials is, like most structural effects, a result of the increased contribution of the surface energy (γsurf) to the overall energy of nanoparticles when compared to bulk-sized material. The surface energy of a crystal is given by half the required energy to cut the crystal into two equal halves.35 The fundamental principle of minimisation of surface energy also applies to nanoparticles. While this driving force typically results in a minimisation of the surface area, crystalline particles form facets resulting in smaller surface energies than for spherical structures with a corresponding number of atoms. In turn, the thermodynamically stable phase of nanoparticles may differ from the one in larger particles.36 For example, the fcc-Co structure (Fig. 1) is the preferential phase for nanoparticles below 20 nm (ref. 37–39) while hcp-Co is the stable phases in larger structures.40 Such a behaviour becomes particularly important for structure sensitive reactions. In the case of the two Co0 allotropes, hcp-Co has been suggested to lower the activation energy for CO dissociation due to the presence of unique active sites and may consequentially enable higher turn-over rates, e.g. in the Fischer–Tropsch synthesis.41,42
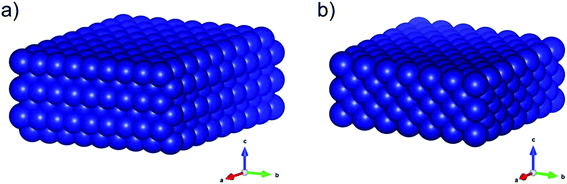 | ||
| Fig. 1 Three-dimensional schematics of the main allotropes of cobalt with (a) hexagonal-close-packed (hcp) and (b) face-centered-cubic (fcc) crystal structure. The graphics were produced in VESTA.43 | ||
Fundamental statistics on the geometry of nanoparticles were developed by van Hardeveld and Hartog44 allowing for the approximation of the surface energy by the broken bond model.15,35,45 Surface atoms are coordinatively unsaturated and hence surfaces have a potential for additional coordination. The number of broken bonds describes the difference in coordination number of such surface atoms compared to a bulk atom when cutting a crystal along certain crystallographic planes.35,45 The incomplete coordination of surface atoms binds energy, which in turn results in an increased surface energy. The surface energy of transition metal particles has been reported to correlate with the number of broken bonds,15,46,47 which increases for smaller crystallite sizes and depends on the morphology of the nanoparticle. Based on such theoretical statistics, the surface energy of nanoparticles can be estimated as a function of the size according to eqn (6) and drastically increases for crystallite sizes below 10 nm (Fig. 2).15 In turn, nanoparticles below 10 nm have an amplified drive to minimise their surface energy.
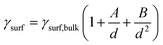 | (6) |
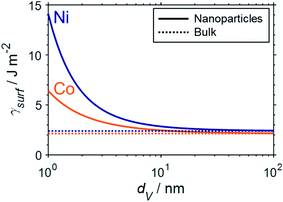 | ||
| Fig. 2 Empirical approximation of the surface energy of fcc-cobalt (orange) and nickel (blue) nanoparticles (solid) as a function of crystallite size based on the number of broken bonds according to the methodology by van Steen et al.15 and compared to the particular bulk-sized metals (dotted). | ||
The increased ratio of surface to bulk atoms in nanoparticles also affects their thermal stability.48 According to the Lindemann criterion, the melting point (TM) of a crystal is reached when the mean thermal displacement of the atoms equals a certain fraction of the actual interatomic distance.35 The large fraction of surface atoms in nanoparticles increases the atomic displacement when compared to larger particles and hence nanoparticles melt at lower temperatures.35 A structural melting point suppression of nano-sized metal particles has firstly been reported by Thomson et al. describing a size dependency of the melting point (TM) of solid particles.49 The structural dependency can be predicted by the Gibbs–Thomson correlation (eqn (7)) and becomes significant for particle sizes below 100 nm, i.e. for nanoparticles.48,49 Couchman et al. proposed a more complex thermodynamic approach providing similar predictions, which are in agreement with experimental results for various metals.50 Smaller particle sizes are generally reported to display a higher susceptibility towards sintering,39,51–54 Aside from the temperature, the composition of the gas phase,54–56 the dispersion of the active phase over the support,39,51 the morphology and physicochemical properties of the support,54,57–59 as well as promoters51 have been identified as parameters for sintering. Lastly, several studies report a dependency of the sintering tendency on the particle size distribution with the size difference being the driving force.58,60,61
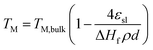 | (7) |
In this study, potential phase transformations of nickel and cobalt resulting in deactivation during reforming of methane, namely oxidation to metal oxides or metal–support compounds, are evaluated thermodynamically for various conditions and a wide temperature range. Both metals may be employed in reforming of methane. In addition, structural dependent deactivation via size dependent oxidation of nano-sized Ni0 and Co0 by H2O or CO2, as well as enhanced sintering due to melting point suppression in metallic nanoparticles are investigated theoretically. Hence, the study aims to contribute fundamental understanding of various potential processes of catalyst deactivation during reforming of methane.
Theoretical methods
Gibbs free energies (ΔGrxn) of selected chemical reactions were calculated for the temperature range 500–1100 °C employing the Gibbs–Helmholtz equation. Accordingly, the calculation depends on the temperature (T), the reaction specific constants standard enthalpy of reaction (ΔH0rxn) and standard Gibbs free energy of reaction (ΔG0rxn), as well as a mathematical description of the temperature dependency of the heat capacities (Cp) of reactants and products (eqn (8)). All thermodynamic calculations are conducted with data provided by Knacke et al.62–64
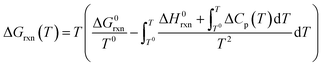 | (8) |
The feasibility of oxidation of a metal (eqn (9)) changes with the ratio of oxidant over reductant. Combination of eqn (8) and the definition of the Gibbs free energy with the equilibrium constant of reaction (Kc) (eqn (10) and (11)) results in a thermodynamic description of the partial pressure ratio of reactants over products (eqn (12)). Assuming that the oxidant and reductant are the only gaseous compounds present, the phase equilibrium of metal vs. metal oxide can be described by the partial pressure ratio of oxidising over reducing agent.
| aMe(s) + boxidant(g) → MeaOb(s) + breductant(g) | (9) |
ΔGrxn(T) = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc Kc
| (10) |
 | (11) |
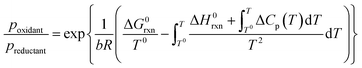 | (12) |
The significantly increased contribution of the surface energy to the overall energy of nano-sized materials can be considered in thermodynamic predictions on the size dependent stability of nickel and cobalt nanoparticles under oxidising atmosphere according to van Steen et al.15 The oxidation of spherical nickel or cobalt crystallites by either H2O or CO2 to NiO and CoO (eqn (9); a = b = 1), respectively, is thermodynamically favoured if the Gibbs free energy of reaction considering structural dependency according to eqn (13) is negative, i.e. if the metallic state plus oxidant has a lower energy level then the corresponding oxide plus reductant.
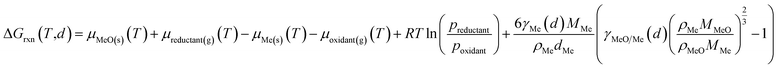 | (13) |
The size dependency of the surface energy of metallic Ni and Co nanoparticles was estimated using eqn (6) with a surface energy of the metallic bulk phase of 2.39 and 2.14 J m−2, respectively. While the surface energy of Co was adapted from van Steen et al.,15 an average value was calculated for Ni based on various publication.65–72 Parameters ACo = 2.14 and BCo = 0.55 were also adapted from van Steen et al., who correlated the average amount of broken bonds per surface atom in various crystal structures to the surface energy of Co nanoparticles.15 In a similar manner, the average amount of broken bonds per surface atom was calculated for Ni nanoparticles with an fcc octahedral crystal structure (Fig. S1†) by employing statistical and mathematical descriptors for atoms in nanoclusters.44,73 Correlation with the surface energy of bulk-sized Ni resulted in ANi = 1.60 and BNi = 3.30 for eqn (6). The ratio of the surface energy of bulk CoO and Co of 0.2167 was adapted from van Steen et al.15 For the system NiO/Ni, a larger ratio of 0.4705 was calculated based on several studies in literature.74–76 Even though a mild structural dependency of γMeO/Me has been reported for bulk CoO and Co,15 the ratio is herein simplified to be considered constant for both systems.
Calculation of the melting point suppression of nano-sized nickel and cobalt (eqn (7)) was conducted with a melting point of the bulk phase of 1455 (Ni) and 1480 °C (Co), a specific gravity of 8908 (Ni) and 8860 kg m−3 (Co), a specific latent heat of melting of 299![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401.97 (Ni) and 259
401.97 (Ni) and 259![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 844.91 J kg−1 (Co), as well as with an interfacial tension between the solid and liquid interface of 0.306 (Ni) and 0.306 N m−1 (Co).16,45,77
844.91 J kg−1 (Co), as well as with an interfacial tension between the solid and liquid interface of 0.306 (Ni) and 0.306 N m−1 (Co).16,45,77
Results and discussion
Thermodynamic predictions on oxidation of bulk metal
Calculation of the Gibbs free energies (eqn (8)) for various oxidation reactions of the active metallic phase during dry or steam reforming indicates the feasibility of such deactivation reactions for bulk-sized structures in the considered temperature range. Calculation of the required partial pressure ratio of oxidant (H2O or CO2) over reductant (H2 or CO) puts the Gibbs free energy in perspective to required conditions during SRM and DRM to initiate oxidation. In fact, these partial pressure ratios are the driving force and have been previously identified as a good descriptor for such an oxidation reaction.15,16,19 The oxidant![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
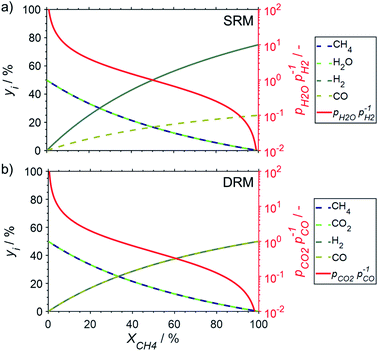
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant ratios are decreasing with increasing conversion levels for both reforming reactions (Fig. 3). For SRM with a stoichiometric feed and methane conversion levels in the range of 9–50%, a partial pressure ratio of H2O to H2 (pH2O/pH2) between 10 and 1 may be approximated (Fig. 3a). High conversions exceeding 91% represent ratios below 0.1. Co-feeding of steam in excess to suppress coking is a common strategy to mitigate deactivation27,28 and will result in increased pH2O/pH2 ratios (Fig. S1†). During DRM, pCO2/pCO ratios of 10, 1, and 0.1 are expected for methane conversion levels of 5, 33, and 83%, respectively, when assuming a stoichiometric feed (Fig. 3b).
reductant ratios are decreasing with increasing conversion levels for both reforming reactions (Fig. 3). For SRM with a stoichiometric feed and methane conversion levels in the range of 9–50%, a partial pressure ratio of H2O to H2 (pH2O/pH2) between 10 and 1 may be approximated (Fig. 3a). High conversions exceeding 91% represent ratios below 0.1. Co-feeding of steam in excess to suppress coking is a common strategy to mitigate deactivation27,28 and will result in increased pH2O/pH2 ratios (Fig. S1†). During DRM, pCO2/pCO ratios of 10, 1, and 0.1 are expected for methane conversion levels of 5, 33, and 83%, respectively, when assuming a stoichiometric feed (Fig. 3b).
The conducted thermodynamic calculations for the oxidation of bulk Ni0 and Co0 to the corresponding metal oxide during SRM and DRM result in high Gibbs free energies (Fig. 4 and 5), which indicates an unlikely oxidation of the metals by CO2 or H2O at reasonable conversion levels. This trend has been previously reported for bulk-sized materials.14–18 For fcc-Ni and temperatures below 900 °C, H2O/H2 and CO2/CO ratios exceeding 60 are required for oxidation to NiO (Fig. 4b and d), which corresponds to low to zero level of conversion in SRM and DRM (Fig. 3). Even though the required ratios are lower for the formation of CoO from hcp-Co (Fig. 5b and d), oxidation by CO2 or H2O of bulk-sized cobalt is also unlikely. For example, pCO2/pCO ratios exceeding 10 are required for oxidation of bulk-sized Co0 during DRM at 1100 °C. Considering the typically lower operation temperatures for DRM and the strong temperature dependency of the feasibility of this reaction, oxidation of bulk Co0 can also be considered as highly unlikely unless operation at CH4 conversion levels <5%. However, the active metal of the first fraction of a fixed-bed catalyst bed may undergo a certain degree of oxidation as the reducing H2 and CO are generated gradually along the catalyst bed. This may become relevant and result in strong deactivation if an oxidation front slowly moves along the catalyst bed during prolonged operation. Noteworthy, oxidation of Co0 by CO2 has previously been demonstrated to be absent during exposure of a reduced Co-based catalyst to 90% CO2/Ar at 150 °C demonstrating the kinetical hindrance of this oxidation reaction at lower temperatures.78
 | ||
| Fig. 4 (a and c) Gibbs free energies and (b and d) thermodynamic equilibria, represented by the ratio of oxidant over reductant, for selected oxidation reactions of bulk fcc-Ni with (a and b) gaseous H2O or (c and d) CO2 forming nickel oxide or metal–support compounds. Calculations are based on thermodynamic data by Knacke et al.62–64 | ||
 | ||
| Fig. 5 (a and c) Gibbs free energies and (b and d) thermodynamic equilibria, represented by the ratio of oxidant over reductant, for selected oxidation reactions of bulk hcp-Co with (a and b) gaseous H2O or (c and d) CO2 forming cobalt oxide or metal–support compounds. Calculations are based on thermodynamic data by Knacke et al.62–64 | ||
Aside from oxidation to the corresponding metal oxide, the formation of metal–support compounds (MSCs), such as aluminates, silicates, or titanates, may also lower the availability of the active metallic phase resulting in deactivation.17,18,33 Furthermore, the formation of these inactive mixed-metal oxides is typically associated with a drastic change of the morphology from metallic nanoparticles to highly dispersed metal atoms within the support structure.17 Hence, a reductive regeneration of formed MSCs is challenging, which is also linked to the elevated reduction temperatures of these MSCs.14,79,80 Nevertheless, such a regeneration at high temperatures is possible and even utilised in order to create anchored metallic nanoparticles as stable catalyst for methane reforming.81,82 Either way, the required conditions for potential formation of these mixed-metal oxide compounds during SRM and DRM remain important.
Similar to the oxidation to nickel oxide, the herein conducted thermodynamic calculations indicate an unfeasible formation of MSCs during SRM over Ni0 on α-Al2O3, α-SiO2 (quartz), and α-TiO2 (rutile), which were selected as representative common metal oxide support materials (Fig. 4a and b). For these support materials and SRM at 900 °C, nickel titanate (NiTiO3) is predicted to form at the lowest H2O/H2 ratio of 17, while aluminates (pH2O/pH2 = 49) and particularly silicates (pH2O/pH2 = 199) are unlikely to form at moderate conversion levels. Even when increasing the S/C ratio in the inlet to 5, the resulting H2O/H2 ratios remains below 20 for conversions levels exceeding 25% (Fig. S1†). The same order in the feasibility for the formation of MSCs was calculated for DRM over Ni-based catalysts (Fig. 4c and d), while increased reaction temperatures increase the likelihood of the formation of MSCs drastically. However, the pCO2/pCO ratio of 8.9, which is required to initiate the formation of nickel titanate in a fcc-Ni/rutile catalyst at a high reaction temperature of 1100 °C, still correlates to relatively low conversion levels <6% (Fig. 3b).
The formation of MSCs in Co-based catalysts is generally more likely than for nickel (Fig. 5). Especially the formation of cobalt aluminate is highly likely from a thermodynamic point of view.18 For certain temperature ranges, the Gibbs free energies for the oxidation of hcp-Co/α-Al2O3 by H2O during SRM (T < 700 °C) or CO2 during DRM (T > 1000 °C) to CoAl2O4 becomes negative. Hence, already a low oxidant![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant ratio of 1
reductant ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 may induce the formation of this MSC. However, the formation of cobalt aluminate has previously been hypothesized to be kinetically hindered during the FTS.14 A certain kinetical hindrance of this water-driven solid state reaction was recently demonstrated experimentally for a fcc-Co/γ-Al2O3 catalyst at 220 °C.17 Nevertheless, the elevated temperatures during SRM and DRM may overcome such kinetic limitations and potentially enable a rapid formation.
1 may induce the formation of this MSC. However, the formation of cobalt aluminate has previously been hypothesized to be kinetically hindered during the FTS.14 A certain kinetical hindrance of this water-driven solid state reaction was recently demonstrated experimentally for a fcc-Co/γ-Al2O3 catalyst at 220 °C.17 Nevertheless, the elevated temperatures during SRM and DRM may overcome such kinetic limitations and potentially enable a rapid formation.
The formation of cobalt titanates during SRM and DRM also requires moderate oxidant![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant ratios (Fig. 5). During SRM, the required H2O/H2 ratio for the formation of CoTiO3 ranges from 2.7–5.5 in the studied temperature range of 500–1000 °C. The cobalt titanate polymorph Co2TiO4 is also likely to form with ratios below 6.2. Lastly, the formation of cobalt silicate (Co2SiO4) from quartz and hcp-Co is the least likely. For DRM, the required CO2/CO ratios for the formation of the cobalt titanate polymorphs is below 10 when exceeding 700 °C. As in the calculations for Ni-based catalysts, elevated reaction temperatures also drastically increase the likelihood for the formation of MSCs during DRM. At 1100 °C, the required ratios of CO2/CO for all three selected support materials is below 5.2.
reductant ratios (Fig. 5). During SRM, the required H2O/H2 ratio for the formation of CoTiO3 ranges from 2.7–5.5 in the studied temperature range of 500–1000 °C. The cobalt titanate polymorph Co2TiO4 is also likely to form with ratios below 6.2. Lastly, the formation of cobalt silicate (Co2SiO4) from quartz and hcp-Co is the least likely. For DRM, the required CO2/CO ratios for the formation of the cobalt titanate polymorphs is below 10 when exceeding 700 °C. As in the calculations for Ni-based catalysts, elevated reaction temperatures also drastically increase the likelihood for the formation of MSCs during DRM. At 1100 °C, the required ratios of CO2/CO for all three selected support materials is below 5.2.
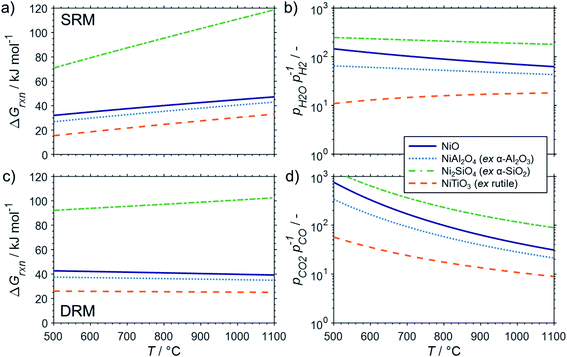
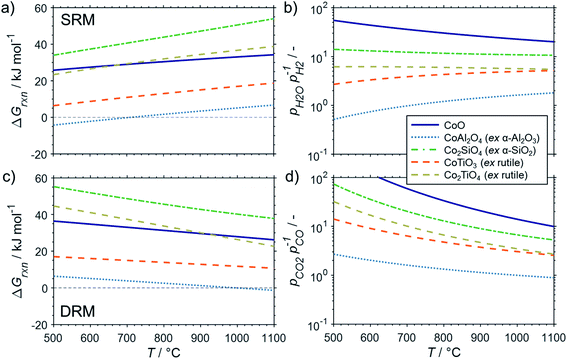
The formation of the two cobalt titanate polymorphs already indicated potential effects of polymorphism on the formation of MSCs. In fact, polymorphism of the carrier materials is an important parameter affecting the formation of MSCs. For example, crystal structures for Al2O3 other than the α-Al2O3 have been reported to show a higher tendency towards the formation of cobalt aluminates17,25,83,84 or nickel aluminate.22 While thermodynamics suggest the formation of aluminate from Ni0 and α-Al2O3 at a pH2O/pH2 ratio of ∼50 for temperatures exceeding 900 °C (Fig. 4b), Sehested et al. reported the formation of NiAl2O3 during exposure of a Ni/θ-Al2O3 catalyst to such an unreactive model atmosphere at a lower temperature of 750 °C.22 Herein conducted calculations for α-Al2O3 and γ-Al2O3 indicate a higher reactivity of other polymorphs with nickel (Fig. 6) and cobalt (Fig. 7) during SRM and DRM. For the two common TiO2 polymorphs rutile and anatase, the thermodynamic calculations suggest a higher reactivity for the latter. This is in line with recently published calculations and experimental studies for Co/TiO2 catalysts under water-rich conditions at lower temperatures of 220 °C.17
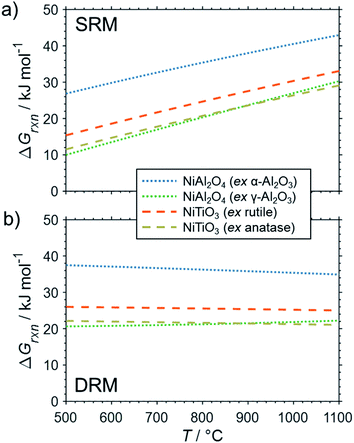 | ||
| Fig. 6 Gibbs free energies for selected oxidation reactions of bulk fcc-Ni with common metal oxide carrier materials and (a) gaseous H2O or (b) CO2 forming metal–support compounds demonstrating the potential impact of polymorphism of the support. Calculations are based on thermodynamic data by Knacke et al.62–64 | ||
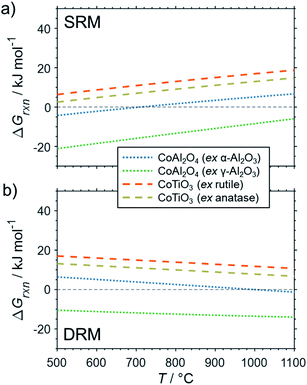 | ||
| Fig. 7 Gibbs free energies for selected oxidation reactions of bulk hcp-Co with common metal oxide carrier materials and (a) gaseous H2O or (b) CO2 forming metal–support compounds demonstrating the potential impact of polymorphism of the support. Calculations are based on thermodynamic data by Knacke et al.62–64 | ||
Size dependent stability of metal nanoparticles
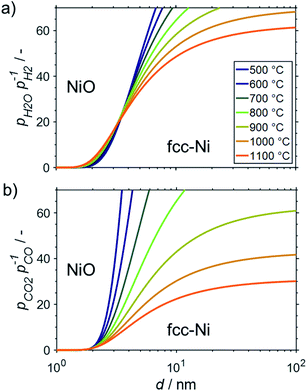
All the presented results and calculations are based on bulk properties of nickel and cobalt. As indicated in the introduction (Fig. 2), the contribution of the surface energy to the overall energy of nano-sized materials becomes important for crystallite sizes below 10 nm. Therefore, even little changes in the surface energy of nanoparticles may become driving factors for phase transformations in order to adhere to the fundamental principle of the minimisation of surface energy. This may be the case when metallic nanoparticles are exposed to oxidising atmospheres and the surface energy of the metal is higher than for the corresponding metal oxide.15 Both metals, nickel and cobalt, fulfil this criterion and hence are expected to display an increased oxidation potential with decreasing crystallite size. This size dependent oxidation behaviour was calculated for fcc-Ni (Fig. 8), fcc-Co (Fig. 9), and hcp-Co (Fig. S2†) for the two oxidant–reductant couples during SRM (H2O and H2) and DRM (CO2 and CO), based on calculations by van Steen et al. for the oxidation of fcc-Co under water-rich conditions at lower temperatures.15With a stoichiometric feed for SRM, the H2O/H2 ratio can be expected to be below 10 for methane conversion levels exceeding 10% (Fig. 3a). For DRM, the oxidant![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reductant ratio CO2/CO is <5 for this moderate conversion level (Fig. 3b). According to the thermodynamic predictions, fcc-Ni nanoparticles >3 nm can be expected to display a sufficient stability against oxidation by H2O during SRM or CO2 during DRM for >10% conversion of methane and temperatures up to 1100 °C, while the size dependent calculations suggest the rigorous formation of the stable oxidic form for fcc-Ni nanoparticles with sizes below 2 nm (Fig. 8). Hence, oxidation of Ni0 nanoparticles exceeding 3 nm in size can be expected to not play a major role during deactivation of the larger part of the catalyst bed during methane reforming. As aforementioned, only the first fraction of the catalyst bed that is contact with the fresh feed stream is exposed to severe oxidising conditions and may undergo oxidation. For example, surface oxidation of the active metal during DRM at 600 °C over a Ni/LaFeO3/MgAl2O4 catalyst was hypothesised by Mao et al. due to insufficient formation of reductive environment at low conversion levels, which could be overcome by increasing the CH4/CO2 ratio in the feed to ratios above unity.19
reductant ratio CO2/CO is <5 for this moderate conversion level (Fig. 3b). According to the thermodynamic predictions, fcc-Ni nanoparticles >3 nm can be expected to display a sufficient stability against oxidation by H2O during SRM or CO2 during DRM for >10% conversion of methane and temperatures up to 1100 °C, while the size dependent calculations suggest the rigorous formation of the stable oxidic form for fcc-Ni nanoparticles with sizes below 2 nm (Fig. 8). Hence, oxidation of Ni0 nanoparticles exceeding 3 nm in size can be expected to not play a major role during deactivation of the larger part of the catalyst bed during methane reforming. As aforementioned, only the first fraction of the catalyst bed that is contact with the fresh feed stream is exposed to severe oxidising conditions and may undergo oxidation. For example, surface oxidation of the active metal during DRM at 600 °C over a Ni/LaFeO3/MgAl2O4 catalyst was hypothesised by Mao et al. due to insufficient formation of reductive environment at low conversion levels, which could be overcome by increasing the CH4/CO2 ratio in the feed to ratios above unity.19
Aside from DRM, Mao et al. studied the oxidation behaviour of a Ni/MgAl2O4 in H2O/H2 mixtures at 800 °C.19 Compared to the theoretically expected oxidation potential for bulk-sized nickel, a small shift of the equilibrium between the metal and metal oxide phase to the oxidic side was identified. Comparison with characterisation data on other samples in said study suggests an average crystallite size of nickel in the range of 10–15 nm for the Ni/MgAl2O4 catalyst with a wide size distribution. Hence, the observed lower stability of nano-sized Ni0 may be linked to the herein discussed size dependent oxidation behaviour (Fig. 8a).
Strong oxidation of the metallic phase was observed when comparing X-ray diffraction (XRD) patterns of a 20 wt% Ni/SiO2 after activation in 10% H2/Ar at 500 °C and after SRM with a S/C = 2 at 500 °C.10 The authors linked an observed strong deactivation from ∼22% conversion of CH4 after 0.5 h time-on-stream to zero conversion level after 4 h to this oxidation process as carbon formation was less pronounced and sintering was not identified. However, less oxidation was observed for a 20 wt% Ni/Al2O3 catalyst reduced at 700 °C, while residual NiO in a 20 wt% Ni/ZrO2 after reduction at 500 °C was seemingly even reduced to Ni0 during SRM.10 As the average crystallite sizes of Ni0 in all catalysts were estimated to be in the range of 11–17 nm, oxidation of the smaller nanoparticles may become feasible (Fig. 8a) at the observed conversion levels <25%, which corresponds to theoretical pH2O/pH2 ratios >7 (Fig. S1†). However, the strong dependence of the identified phase transformation points towards a dominating effect of the support material, which may be linked to the easier formation of nickel aluminates (Fig. 4).
In another study, strong deactivation of a 8.4 wt% Ni/SiO2 catalyst was observed during SRM with S/C = 2 at 500 °C.21 Contrary, 8.0 wt% Ni/Al2O3 as well as nickel on zinc and magnesium aluminate-like support materials displayed a stable conversion rate or even activation during SRM. The average NiO particle size after calcination of 11–13 nm in the Ni/SiO2 catalyst was smaller than in the Al2O3-supported sample (19 nm).21 Hence, the observed deactivation of the Ni/SiO2 may indeed be linked to hypothesised oxidation of Ni0, which can be expected to be less pronounced for the Ni/Al2O3 catalyst. Low levels of carbonaceous deposits were identified for both samples. The mixed oxide-supported catalysts featured the smallest particle size in the range of 3–6 nm, but strong deviation from the physicochemical properties of Ni0 nanoparticles is expected due to the reduction of Ni2+ ions strongly interacting with the spinel-like mixed oxide support materials during the initial activation in H2.21
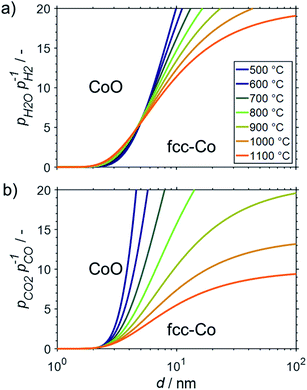
The fcc structure of cobalt is the preferred allotrope in nanoparticles.37–39 For fcc-Co nanoparticles, crystallite sizes >10 nm are predicted to be stable against oxidation to CoO during SRM and DRM at operation temperatures up to 1100 and 900 °C, respectively, as long as methane conversion levels exceed 10% (Fig. 9). Similar to the size dependent stability of fcc-Ni nanoparticles, fcc-Co crystallites below 2 nm are expected to oxidise rapidly. However, a strong dependency on the size is predicted for nanoparticles in the range of 2–10 nm, which is particularly pronounced for DRM due to the strong temperature dependency of the feasibility of the oxidation reaction of Co with CO2. When comparing the fcc structure to the allotrope hcp-Co, which is the thermodynamically stable structure of cobalt in the bulk phase,64 a shift to larger threshold sizes for oxidation is observed (Fig. S2†). This behaviour exhibits the higher amount of broken bonds in nano-sized hcp-Co crystallites resulting in larger surface energies and ultimately enhancing the driving force for the minimisation of energy of nanoparticles via oxidation.
The oxidation behaviour of nano-sized Co0 structures has been under discussion in the Fischer–Tropsch community for a long time.15,16,23,24,54,85–89 Recent experimental studies employing sophisticated in situ characterisation techniques16,54,87,88 together with insight from theoretical work89 enabled a compelling understanding of the mechanisms at play during water induced oxidation.25 The hypothesised size dependent oxidation behaviour of Co0 to CoO, as predicted by van Steen et al.,15 has been confirmed for 220 °C.16,25,54,87,88 However, oxidation was demonstrated to rather occur due to a hindered removal of adsorbed oxygen species from the surface upon CO dissociation at high partial pressures of H2O rather than direct oxidation of Co0 by water splitting.88,89 The latter reaction was consequentially hypothesized to be kinetically hindered at 220 °C,16,17,25,88 which is likely to change at elevated operation temperatures during reforming of methane. The elevated temperatures may also allow for oxidation of Co0 by CO2, which was demonstrated to be kinetically hindered in 90% CO2/Ar at temperatures below 150 °C.78
Aside from thermodynamically favoured oxidation, nano-sized material is also expected to display a lower thermal resistance against sintering when compared to bulk structures. Sintering of the catalytically active phases typically results in deactivation due to a loss of active surface area. One of the most important drivers of sintering is the temperature.51 The melting point provides a good indication of the susceptibility towards sintering of a material. The Tammann (0.5TM) and the Hüttig temperatures (0.3TM) approximate the required temperatures for an increased mobility of bulk and surface atoms of a particle, respectively, which lowers the thermal stability and may result in sintering.90 Combination of the thermodynamic description of the melting point suppression for metallic nanoparticles in the nanometre range49 according to Gibbs–Thomson correlation (eqn (7)) and the calculation of the Tammann and Hüttig temperature allows for a prediction of the size dependency of the particular critical temperatures (Fig. 10). Such a prediction was previously published for cobalt16 and was herein calculated for nickel as well.
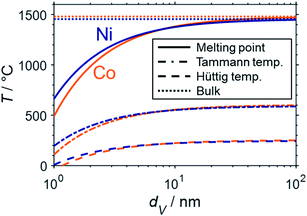 | ||
| Fig. 10 Structural melting point suppression (solid), size dependent Tammann (dash-dotted), and Hüttig temperature (dashed) of cobalt (orange) and nickel (blue) spheres in the nanometre size regime according to the Gibbs–Thomson equation and compared to the melting points of the bulk-phased metals (dotted). The data for cobalt was adapted from Wolf et al.16 | ||
The strong melting point suppression for cobalt and nickel nanoparticles below 2 nm is expected to result in liquification of the active metal for temperatures within typical conditions for reforming of methane (600–1000 °C; Fig. 10). Furthermore, even lower temperatures far from the (suppressed) melting point may decrease the thermal stability of nanoparticles drastically. For example, surface atoms of cobalt and nickel particles are presumed to experience a high mobility when exceeding the Hüttig temperature, which lies below typical operation temperatures for both metals. Even the Tammann temperatures of bulk-sized Ni (581 °C) and Co (601 °C)90 are easily exceeded. Hence, nano-sized material below 10 nm can be expected to require significant stabilisation by strong interaction with the support in order to suppress sintering. The formation of anchored nanoparticles may mitigate sintering and has previously been reported, e.g. via the formation of the metallic phase via reduction of MSCs at elevated temperatures21,81,82 or encapsulation of the supported active phase.91,92 The importance of such stabilisation is emphasised by comparison of the herein presented theoretical predictions based on a fundamental thermodynamic approach with the literature data. Several studies employing supported non-stabilised Ni nanoparticles with initial sizes in the range of 2–12 nm reported drastic sintering during DRM at 700–800 °C forming particles or nanoparticle clusters in the range of 17–40 nm.9,91–95 In this size range, the herein discussed melting point suppression is rather small, which drastically decreases the drive to further minimise the surface energy via further particle growth. Lastly, sintering may also be accelerated under hydrothermal conditions.13,22,54,96–99 For example, Sehested et al. demonstrated the dependency of Ni0 crystallite growth in various Al2O3 and MgAl2O4-supported Ni-based catalysts on the temperature, exposure time, and pH2O/pH2 ratio during exposure to high ratios up to 50 in the temperature range 500–825 °C.22,96,97
Summary and conclusions
Thermodynamic calculations on the size dependent stability of metallic nickel and cobalt nanoparticles during steam and dry reforming of methane were conducted and may provide fundamental understanding of the redox properties of nano-sized Ni0 and Co0 under methane reforming conditions. The results suggest required particle sizes of Ni >3 nm and Co >10 nm in order to suppress oxidation by either H2O or CO2 for methane conversion levels exceeding 10% and stoichiometric feed composition. Nanoparticles below 2 nm in size are thermodynamically unstable and expected to oxidise to the corresponding metal oxide. Furthermore, the melting point suppression of nano-sized materials may result in melting of cobalt and nickel nanoparticles <2 nm at typical temperatures of methane reforming. In addition to the formation of metal oxide, the feasibility of oxidation to mixed-metal oxides with various metal oxides was evaluated for bulk structures. While the formation of metal–support compounds in supported nickel catalysts requires high oxidant-to-reductant ratios, cobalt aluminates and in particular cobalt titanates may easily form for cobalt-based catalysts. However, industrially applied increased steam-to-carbon ratios result in conditions favouring the formation of metal–support compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by the European Research Council is gratefully acknowledged (Project 786475: Engineering of Supported Catalytically Active Liquid Metal Solutions).References
- J. R. Rostrup-Nielsen, J. Sehested and J. K. Nørskov, Adv. Catal., 2002, 47, 65–139 CAS.
- M. C. Alvarez-Galvan, N. Mota, M. Ojeda, S. Rojas, R. M. Navarro and J. L. G. Fierro, Catal. Today, 2011, 171, 15–23 CrossRef CAS.
- Y. A. Alhamdani, M. H. Hassim, R. T. L. Ng and M. Hurme, Int. J. Hydrogen Energy, 2017, 42, 9342–9351 CrossRef CAS.
- E. Meloni, M. Martino and V. Palma, Catalysts, 2020, 10, 352 CrossRef CAS.
- D. Pakhare and J. Spivey, Chem. Soc. Rev., 2014, 43, 7813–7837 RSC.
- A. Bode, D. W. Agar, K. Büker, V. Göke, M. Hensmann, U. Janhsen, D. Klingler, J. Schlichting and S. A. Schunk, Research cooperation develops innovative technology for environmentally sustainable syngas production from carbon dioxide and hydrogen, 20th World Hydrogen Energy Conference 2014, Gwangju Metropolitan City, Korea, 2014 Search PubMed.
- N. A. K. Aramouni, J. G. Touma, B. A. Tarboush, J. Zeaiter and M. N. Ahmad, Renewable Sustainable Energy Rev., 2018, 82, 2570–2585 CrossRef CAS.
- K. Wittich, M. Krämer, N. Bottke and S. A. Schunk, ChemCatChem, 2020, 12, 2130–2147 CrossRef CAS.
- Y. Song, E. Ozdemir, S. Ramesh, A. Adishev, S. Subramanian, A. Harale, M. Albuali, B. A. Fadhel, A. Jamal, D. Moon, S. H. Choi and C. T. Yavuz, Science, 2020, 367, 777–781 CrossRef CAS PubMed.
- Y. Matsumura and T. Nakamori, Appl. Catal., A, 2004, 258, 107–114 CrossRef CAS.
- B. M. Al-Swai, N. B. Osman, A. Ramli, B. Abdullah, A. S. Farooqi, B. V. Ayodele and D. O. Patrick, Int. J. Hydrogen Energy, 2020 DOI:10.1016/j.ijhydene.2020.04.233.
- C. Vogt, J. Kranenborg, M. Monai and B. M. Weckhuysen, ACS Catal., 2019, 10, 1428–1438 CrossRef.
- J. Sehested, Catal. Today, 2006, 111, 103–110 CrossRef CAS.
- P. J. van Berge, J. van de Loosdrecht, S. Barradas and A. M. van der Kraan, Catal. Today, 2000, 58, 321–334 CrossRef CAS.
- E. van Steen, M. Claeys, M. E. Dry, J. van de Loosdrecht, E. L. Viljoen and J. L. Visagie, J. Phys. Chem. B, 2005, 109, 3575–3577 CrossRef CAS PubMed.
- M. Wolf, H. Kotzé, N. Fischer and M. Claeys, Faraday Discuss., 2017, 197, 243–268 RSC.
- M. Wolf, E. K. Gibson, E. J. Olivier, J. H. Neethling, C. R. A. Catlow, N. Fischer and M. Claeys, ACS Catal., 2019, 9, 4902–4918 CrossRef CAS.
- A. Giehr, L. Maier, S. A. Schunk and O. Deutschmann, ChemCatChem, 2018, 10, 751–757 CrossRef CAS.
- X. Mao, A. C. Foucher, E. A. Stach and R. J. Gorte, J. Catal., 2020, 381, 561–569 CrossRef CAS.
- R. Pereñíguez, V. M. González-DelaCruz, J. P. Holgado and A. Caballero, Appl. Catal., B, 2010, 93, 346–353 CrossRef.
- M. A. Nieva, M. M. Villaverde, A. Monzón, T. F. Garetto and A. J. Marchi, Chem. Eng. J., 2014, 235, 158–166 CrossRef CAS.
- J. Sehested, J. A. P. Gelten and S. Helveg, Appl. Catal., A, 2006, 309, 237–246 CrossRef CAS.
- J. Scalbert, C. Legens, I. Clémençon, A.-L. Taleb, L. Sorbier and F. Diehl, Chem. Commun., 2014, 50, 7866–7869 RSC.
- N. E. Tsakoumis, J. C. Walmsley, M. Rønning, W. van Beek, E. Rytter and A. Holmen, J. Am. Chem. Soc., 2017, 139, 3706–3715 CrossRef CAS PubMed.
- M. Wolf, N. Fischer and M. Claeys, Nat. Catal., 2020, 3, 962–965 CrossRef CAS.
- C. Palmer, D. C. Upham, S. Smart, M. J. Gordon, H. Metiu and E. W. McFarland, Nat. Catal., 2020, 3, 83–89 CrossRef CAS.
- J. J. Spivey, Deactivation of Reforming Catalysts, in Fuel Cells: Technologies for Fuel Processing, Elsevier, 2011, pp. 285–315, DOI:10.1016/b978-0-444-53563-4.10010-0.
- M. A. Fahim, T. A. Alsahhaf and A. Elkilani, Hydrogen Production, in Fundamentals of Petroleum Refining, Elsevier, 2010, ch. 11, pp. 285–302, DOI:10.1016/B978-0-444-52785-1.00011-5.
- B. Abdullah, N. A. Abd Ghani and D. V. N. Vo, J. Cleaner Prod., 2017, 162, 170–185 CrossRef CAS.
- E. Schwab, A. Milanov, S. A. Schunk, A. Behrens and N. Schödel, Chem. Ing. Tech., 2015, 87, 347–353 CrossRef CAS.
- G. R. Moradi, M. Rahmanzadeh and F. Khosravian, J. CO2 Util., 2014, 6, 7–11 CrossRef CAS.
- S. Royer, D. Duprez, F. Can, X. Courtois, C. Batiot-Dupeyrat, S. Laassiri and H. Alamdari, Chem. Rev., 2014, 114, 10292–10368 CrossRef CAS PubMed.
- J. Guo, H. Lou, H. Zhao, D. Chai and X. Zheng, Appl. Catal., A, 2004, 273, 75–82 CrossRef CAS.
- Q. L. M. Ha, H. Lund, C. Kreyenschulte, S. Bartling, H. Atia, T. H. Vuong, S. Wohlrab and U. Armbruster, ChemCatChem, 2020, 12, 1562–1568 CrossRef CAS.
- I. Galanakis, G. Bihlmayer, V. Bellini, N. Papanikolaou, R. Zeller, S. Blügel and P. H. Dederichs, Europhys. Lett., 2001, 58, 751–757 CrossRef.
- N. Hüsing and U. Schubert, Aerogels, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim, Germany, 2012, DOI:10.1002/14356007.c01.
- O. Kitakami, H. Sato, Y. Shimada, F. Sato and M. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 13849–13854 CrossRef CAS.
- N. Fischer, E. van Steen and M. Claeys, Catal. Today, 2011, 171, 174–179 CrossRef CAS.
- M. Wolf, N. Fischer and M. Claeys, Nanoscale Adv., 2019, 1, 2910–2923 RSC.
- B. W. Lee, R. Alsenz and A. Ignatiev, Phys. Rev. B: Solid State, 1978, 17, 1510–1520 CrossRef CAS.
- J.-X. Liu, H.-Y. Su, D.-P. Sun, B.-Y. Zhang and W.-X. Li, J. Am. Chem. Soc., 2013, 135, 16284–16287 CrossRef CAS PubMed.
- S. Lyu, L. Wang, J. Zhang, C. Liu, J. Sun, B. Peng, Y. Wang, K. G. Rappé, Y. Zhang, J. Li and L. Nie, ACS Catal., 2018, 8, 7787–7798 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- R. van Hardeveld and F. Hartog, Surf. Sci., 1969, 15, 189–230 CrossRef CAS.
- Q. Jiang and H. M. Lu, Surf. Sci. Rep., 2008, 63, 427–464 CrossRef CAS.
- W. Romanowski, Surf. Sci., 1969, 18, 373–388 CrossRef CAS.
- F. Cyrot-Lackmann, Surf. Sci., 1969, 15, 535–548 CrossRef CAS.
- E. Roduner, Chem. Soc. Rev., 2006, 35, 583–592 RSC.
- W. Thomson, Philos. Mag., 1871, 42, 448–452 Search PubMed.
- P. R. Couchman and W. A. Jesser, Nature, 1977, 269, 481–483 CrossRef CAS.
- C. H. Bartholomew, Appl. Catal., A, 2001, 212, 17–60 CrossRef CAS.
- G. Jacobs, P. M. Patterson, Y. Zhang, T. Das, J. Li and B. H. Davis, Appl. Catal., A, 2002, 233, 215–226 CrossRef CAS.
- G.-Z. Bian, N. Fujishita, T. Mochizuki, W.-S. Ning and M. Yamada, Appl. Catal., A, 2003, 252, 251–260 CrossRef CAS.
- M. Wolf, N. Fischer and M. Claeys, J. Catal., 2019, 374, 199–207 CrossRef CAS.
- R. Ouyang, J.-X. Liu and W.-X. Li, J. Am. Chem. Soc., 2013, 135, 1760–1771 CrossRef CAS PubMed.
- M. Claeys, M. E. Dry, E. van Steen, P. J. van Berge, S. Booyens, R. Crous, P. van Helden, J. Labuschagne, D. J. Moodley and A. M. Saib, ACS Catal., 2015, 5, 841–852 CrossRef CAS.
- J. Sun, D. Ma, H. Zhang, X. Liu, X. Han, X. Bao, G. Weinberg, N. Pfänder and D. Su, J. Am. Chem. Soc., 2006, 128, 15756–15764 CrossRef CAS PubMed.
- G. Prieto, J. Zečević, H. Friedrich, K. P. de Jong and P. E. de Jongh, Nat. Mater., 2013, 12, 34–39 CrossRef CAS PubMed.
- S. L. Hemmingson and C. T. Campbell, ACS Nano, 2017, 11, 1196–1203 CrossRef CAS PubMed.
- D. A. Chen, M. C. Bartelt, S. M. Seutter and K. F. McCarty, Surf. Sci., 2000, 464, L708–L714 CrossRef CAS.
- K. Wettergren, F. F. Schweinberger, D. Deiana, C. J. Ridge, A. S. Crampton, M. D. Rötzer, T. W. Hansen, V. P. Zhdanov, U. Heiz and C. Langhammer, Nano Lett., 2014, 14, 5803–5809 CrossRef CAS PubMed.
- I. Barin, O. Knacke and O. Kubaschewski, Thermochemical properties of inorganic substances, Springer, Berlin, 1st edn, 1973 Search PubMed.
- I. Barin, O. Knacke and O. Kubaschewski, Thermochemical properties of inorganic substances -- Supplement, Springer, Berlin, 1st edn, 1977 Search PubMed.
- O. Knacke, O. Kubaschewski and K. Hesselmann, Thermochemical properties of inorganic substances, Springer, Berlin, 2nd edn, 1991 Search PubMed.
- T. A. Roth, Mater. Sci. Eng., 1975, 18, 183–192 CrossRef CAS.
- W. R. Tyson and W. A. Miller, Surf. Sci., 1977, 62, 267–276 CrossRef CAS.
- F. R. de Boer, Cohesion in metals : transition metal alloys, North-Holland, Amsterdam, 1988 Search PubMed.
- H. L. Skriver and N. M. Rosengaard, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 7157–7168 CrossRef CAS PubMed.
- L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollár, Surf. Sci., 1998, 411, 186–202 CrossRef CAS.
- K. C. Mills and Y. C. Su, Int. Mater. Rev., 2013, 51, 329–351 CrossRef.
- W.-B. Zhang, C. Chen and S.-Y. Zhang, J. Phys. Chem. C, 2013, 117, 21274–21280 CrossRef CAS.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 160080 CrossRef CAS PubMed.
- F. H. Kaatz and A. Bultheel, Nanoscale Res. Lett., 2019, 14, 150 CrossRef PubMed.
- H.-J. Freund, H. Kuhlenbeck and V. Staemmler, Rep. Prog. Phys., 1996, 59, 283–347 CrossRef CAS.
- C. Ebensperger and B. Meyer, Phys. Status Solidi B, 2011, 248, 2229–2241 CrossRef CAS.
- J. Xiang, B. Xiang and X. Cui, New J. Chem., 2018, 42, 10791–10797 RSC.
- Perry's Chemical Engineers' Handbook, McGraw-Hill, New York, 8th edn, 2008 Search PubMed.
- M. Wolf, N. Fischer and M. Claeys, Catal. Today, 2016, 275, 135–140 CrossRef CAS.
- M. Wolf, S. J. Roberts, W. Marquart, E. J. Olivier, N. T. J. Luchters, E. K. Gibson, C. R. A. Catlow, J. H. Neethling, N. Fischer and M. Claeys, Dalton Trans., 2019, 48, 13858–13868 RSC.
- C. L. Tucker and E. van Steen, Catal. Today, 2020, 342, 115–123 CrossRef CAS.
- J. L. Rogers, M. C. Mangarella, A. D. D'Amico, J. R. Gallagher, M. R. Dutzer, E. Stavitski, J. T. Miller and C. Sievers, ACS Catal., 2016, 6, 5873–5886 CrossRef CAS.
- L. Zhou, L. Li, N. Wei, J. Li and J.-M. Basset, ChemCatChem, 2015, 7, 2508–2516 CrossRef CAS.
- P. H. Bolt, F. H. P. M. Habraken and J. W. Geus, J. Solid State Chem., 1998, 135, 59–69 CrossRef CAS.
- C. Hou, G. Xia, X. Sun, Y. Wu, C. Jin, Z. Yan, M. Li, Z. Hu, H. Nie and D. Li, Catal. Today, 2016, 264, 91–97 CrossRef CAS.
- D. Schanke, A. M. Hilmen, E. Bergene, K. Kinnari, E. Rytter, E. Ådanes and A. Holmen, Energy Fuels, 1996, 10, 867–872 CrossRef CAS.
- E. Iglesia, Appl. Catal., A, 1997, 161, 59–78 CrossRef CAS.
- N. Fischer, B. Clapham, T. Feltes, E. van Steen and M. Claeys, Angew. Chem., Int. Ed., 2014, 53, 1342–1345 CrossRef CAS PubMed.
- M. Wolf, B. K. Mutuma, N. J. Coville, N. Fischer and M. Claeys, ACS Catal., 2018, 8, 3985–3989 CrossRef CAS.
- S. Kocić, M. Corral Valero, J.-M. Schweitzer and P. Raybaud, Appl. Catal., A, 2020, 590, 117332 CrossRef.
- J. A. Moulijn, A. E. van Diepen and F. Kapteijn, Appl. Catal., A, 2001, 212, 3–16 CrossRef CAS.
- J. W. Han, C. Kim, J. S. Park and H. Lee, ChemSusChem, 2014, 7, 451–456 CrossRef CAS PubMed.
- E. Yang, E. Nam, J. Lee, H. Lee, E. D. Park, H. Lim and K. An, Catal. Sci. Technol., 2020, 10, 8283–8294 RSC.
- F. Huang, R. Wang, C. Yang, H. Driss, W. Chu and H. Zhang, J. Energy Chem., 2016, 25, 709–719 CrossRef.
- Q. Zhang, T. Zhang, Y. Shi, B. Zhao, M. Wang, Q. Liu, J. Wang, K. Long, Y. Duan and P. Ning, J. CO2 Util., 2017, 17, 10–19 CrossRef CAS.
- Z.-J. Zuo, C.-F. Shen, P.-J. Tan and W. Huang, Catal. Commun., 2013, 41, 132–135 CrossRef CAS.
- J. Sehested, J. Catal., 2004, 223, 432–443 CrossRef CAS.
- J. Sehested, J. Catal., 2003, 217, 417–426 CrossRef CAS.
- M. Sadeqzadeh, J. Hong, P. Fongarland, D. Curulla-Ferré, F. Luck, J. Bousquet, D. Schweich and A. Y. Khodakov, Ind. Eng. Chem. Res., 2012, 51, 11955–11964 CrossRef CAS.
- I. Champon, A. Bengaouer, A. Chaise, S. Thomas and A.-C. Roger, Catalysts, 2020, 10, 1477 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra01856f |
| This journal is © The Royal Society of Chemistry 2021 |