DOI:
10.1039/D1RA00991E
(Paper)
RSC Adv., 2021,
11, 14915-14921
Towards a highly efficient air purifier using annular photonic crystals in UV regimes
Received
5th February 2021
, Accepted 12th April 2021
First published on 21st April 2021
Abstract
Air purifiers play a vital role in fighting the spread of airborne transmitted diseases like COVID-19, rubeola, Mycobacterium tuberculosis, and varicella-zoster, which represent a fundamental challenge. This paper introduces a new enhancement to ultraviolet (UV) air purifiers in air ventilation systems, which delivers a higher inactivation UV dose, eliminating the need for either higher exposure time or a stronger UV source. The modified transfer matrix method in the cylindrical geometry represents the main tool of our theoretical considerations. The new enhancement utilizes an annular photonic crystal (APC) for reflecting UV radiation 99%. The numerical simulation shows that the structure is stable over a wide range of operating scales that fit the extensive range of air purifiers, working at different scales. Additionally, the possibility of using APC over a wide range of UV sources is investigated.
1. Introduction
Indoor air ventilation plays a vital role in spreading airborne transmitted illnesses like SARS-CoV-2 (COVID-19), rubeola, Mycobacterium tuberculosis, and varicella-zoster.1–3 Air recirculation is an efficient way of saving buildings' energy. However, it also contributes to the transfer of pathogens by aerosol.2,4,5 Air ventilation in public buildings, like public transport, schools, hospitals, restaurants and shops requires engineering controls and disease prevention. One of the most effective methods to disinfect the air from pathogens is using ultraviolet germicidal irradiation (UVGI).6,7 The ultraviolet radiation range (180 nm to 320 nm) can inactivate biological systems through photochemical degradation of their genetic material. The genetic material of coronaviruses like SARS-CoV-2 consists of single-stranded RNA (ssRNA), which shows a level of inactivation when exposed to UV radiation.8 The level of inactivation of the pathogens depends on the UV dose and the pathogen. According to the FDA, the optimal UV dose should reduce the pathogens by a 3-log level or more.9 UV radiation has been used in medial air purifiers.10 However, some pathogens such as ssRNA viruses, require a high dose of UV or longer exposure time to achieve a high inactivation level. We can use a reflector to reflect more UV radiation. Thus, the UV dose increases without the need for either stronger UV sources or long exposure time.
A high level of reflectivity with low loss can be achieved using photonic crystals (PCs), periodic structures whose refractive indices change periodically. Due to this periodicity, a range of frequencies is forbidden to propagate in these structures; this range is called photonic band gap (PBG).11,12 The periodicity of PCs can be designed in one, two, or three dimensions. A complete PBG can be formed in the three-dimensional PCs only. Researchers have tested a wide variety of PC materials like dielectrics, metals as well as various materials.13–15 Furthermore, lithographic techniques, chemical vapor deposition (CVD),16 self-assembly,17 and other fabrication techniques have been successfully used to build PCs. Moreover, a huge set of configurations from periodic to quasi-periodic have been studied to arrange PC materials.18–21 PCs have been demonstrated in a massive number of applications in many different areas due to their outstanding properties. In this regard, PBG with high reflectivity could be very useful for laser emissions, optical communication, photovoltaic panels, and waveguides.22,23 By introducing a defect layer inside the periodic structure, a resonance transmittance peak appears inside the PBG.24 A change in a particular condition like temperature can alter its electromagnetic response. Such tunability can be used as a sensor for the detection or measurement of that condition. Therefore, PCs based sensors are widely designed and fabricated for detection temperature, hydrostatic pressure, acoustic waves, and magnetic fields.25–27
One of the classes of one-dimensional PCs is annular photonic crystals (APCs), also called cylindrical Bragg reflectors or photonic circular crystals.28,29 APCs are periodic concentric cylindrical multilayer structures. APCs attracted attention since Kaliteevski et al. untiles the transfer matrix method in the cylindrical coordinates to describe the eclectic and magnetic fields inside coaxial layers.30 APCs found a lot of applications in laser emission, optical communication, and optical electronics.22,31,32 Moreover, researchers found that APCs have better sensing capabilities than planar PCs, which are promising with many chemical and biological applications. Here, we intend to present a new UV air purifier system based on APCs for higher UV inactivation doses. Our designed structure could be suitable for indoor air ventilation systems in public places like restaurants, hospitals, etc. The paper is divided into four sections: in the next section, we discuss the main feature of our structure and the basics of our theoretical modeling. In the third section, we present the reflectance spectra of our APCs in UV regimes besides the discussion of the effect of the related parameters. Finally, we have introduced our conclusion and suggestion for future applications in section four.
2. Theoretical analysis
In this section, we introduce a brief description of our structure and the theoretical considerations that govern the interaction with the incident UV radiation. As shown in Fig. 1, the proposed APCs is designed from periodic concentric cylindrical multilayers over a hollow-core with a radius ρ0.
 |
| | Fig. 1 Schematic diagram of 1D APCs with internal core radius ρ0 and refractive index n0 = 1 and alternating layers with refractive indices n1 and n2. | |
Each unit cell of the periodic part (Λ) is designed from a bi-layer with refractive indices n1 and n2 corresponding to thickness d1 and d2, respectively. The distance from the center to the end of a specified layer i is denoted as ρi and can be described as:
| |
 | (1) |
where,
N is the periodicity number. The structure's primary purpose is to increase the UV dose by reflecting more UV radiation to achieve a higher pathogen deactivating rate. The design consisted of a UV source in its central tube where the untreated air enters from one side, as shown in
Fig. 2. The incoming air is exposed to UV radiation with an almost complete reflection on the central tube walls due to the APC. Thus, we can achieve a higher UV dose without the need for a more powerful UV source. In order to analyze the optical characteristics of APCs, the electric and magnetic fields at the interfaces of APCs are studied using the transfer matrix method (TMM) in cylindrical coordinates.
30
 |
| | Fig. 2 3D schematic of APCs with an air core and UV source in its center. The structure is proposed to work as part of an air ventilation system where the contaminated air enters one side and comes out as purified air from the pathogens. | |
For cylindrical Bragg wave, TE and TM are the two possible polarization modes. The non-zero electromagnetic fields TE mode, are Ez, Hϕ and Hρ. The electric field Ez can be described by the following wave equation:
| |
 | (2) |
The solution of Ez can be obtained by using the separation of variables method as the following:
| | |
Ez(ρ,ϕ) = V(ρ)φ(ϕ) = [AJm(kρ) + BYm(kρ)]exp(imϕ)
| (3) |
where,
m,
Jm and
Ym are the azimuthal number, Bessel function, and Numann function, respectively. The wavenumber of the propagating electromagnetic wave inside material with permittivity
ε and permeability
μ is

The relation between
Ez and
Hϕ can be given by
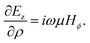
The azimuthal part of the magnetic field
Hϕ can be obtained by substituting of
Ez in the previous equation as the following:
| |
 | (4) |
here,

which is the intrinsic admittance of the material. The electric and magnetic fields in a single layer with a refractive index
nj and interfaces at
ρj−1 and
ρj can be represented by the following matrix:
| |
 | (5) |
where, the elements of the matrix
Mj are described in the following form:
| |
 | (6a) |
| |
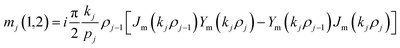 | (6b) |
| |
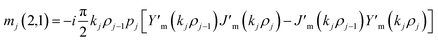 | (6c) |
| |
 | (6d) |
The electric and magnetic felids at the interfaces of the APC structure is expressed as
| |
 | (7) |
where the matrix
M is the result of the product of the APC's single matrix layers and acquired as
The reflectance coefficient of the APC could be investigated as a function of the matrix elements as:
| |
 | (9) |
In the above equation, M11, M12, M21 and M22, are the elements of the matrix M. The admittances of the core layer p0 and the final medium pf is given by 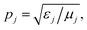 where j takes the value 0 and f. The parameter Cml is obtained from the following expression:
where j takes the value 0 and f. The parameter Cml is obtained from the following expression:
| |
 | (10) |
where,
H(1)m,
H(2)m,

and
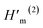
are the first and second kind Hankel function and their derivatives, respectively. The equations for TM-mode can be acquired by replacing every
i,
ε by −
i,
μ respectively, and
vice versa. Finally, the reflectance from APC can be obtained by,
3. Results and discussions
In this section, we present the modeling results of the reflectance of the designed APCs, which enhances the UVGI of the pathogens in air ventilation systems. The transfer matrix method in cylindrical coordinates, discussed in the previous section, is used to perform our calculations. We have considered that the air core is specified with n0 = 1 and UV source is situated in the center of the proposed structure. The unit cell of APCs is consisted of Al2O3 and SiO2 with periodicity number N = 20. The initial thicknesses of Al2O3 and SiO2 cylindrical layers are d1 = 35 nm and d2 = 40 nm, respectively. The unpurified air pass through the inner core with an initial radius ρ0 = 0.5 m. We assume that the outer tube is made of Al2O3 with refractive index nf. The refractive indices of the selected material are taken as a function of the frequency from the following ref. 33 and 34. Firstly, we investigate the reflectance of the proposed APC for TE mode at azimuthal mode number m = 0 as shown in Fig. 3. The reflectance spectrum reveals the appearance of a PBG in the wavelengths of interest with width 26.6 nm due to Bragg scattering. The center of the PBG is located at 257 nm which is chosen carefully by adjusting the structure parameters. The position and width of the PBG making it perfect for reflecting most UVC spectrum emission of low-pressure mercury vapor lamps as they widely used in UVGI devices.7 The average reflection intensity of the PBG around 93%, which relatively high compared to other UV reflector devices. Although the average reflection of PBG is 93%, wherein the intensity around the center of the PBG reaches 99%. Moreover, the large value of core radius could be of interest and more realistic from the fabrication and manufacturing point of view.
 |
| | Fig. 3 The reflectance of UV radiation from APC with periodicity number N = 20 unit cell that consisted of Al2O3 layer with thickness 35 nm and SiO2 layer with thickness 40 nm. | |
Hereinafter, we have demonstrated the effect of the inner core radius on the reflectance of the proposed APCs, as shown in Fig. 4. Here, APC parameters are taken as same as the initial values with d1 = 35 nm, d2 = 40 nm, N = 40, and m = 0. The effect of changing the inner core radius ρ0 is almost noticeable at minimum values as 10−7 m and it is not observable as the radius changes from 10−4 m to 1 m as shown in Fig. 4(a). At ρ0 = 10−7 m, the position of the PBG is slightly shifted to longer wavelengths with increasing of the inner core. In contrast, the position of the PBG almost remains fixed with altering the inner core radius at larger values of the inner core radius from 10−4 m up to 1 m. Moreover, the average intensity of the PBG is almost invariant with changing the inner core radius at radii greater than 10−4 m as listed in Table 1. Whilst, the average intensity of the PBG is slightly decreasing with reducing the inner core radius as 10−7 m, the width of the PBG is slightly increasing as the inner core radius decreases. The average intensity is calculated by a normalized sum over all intensities from the left edge to the right edge of the PBG. The edges are considered at 50% of the maximum value in the PBG. Fig. 4(b) shows the reflectance of the proposed structure at different inner core radii. The reflectance shifts slightly towards longer wavelengths as the inner core radius gets from 10−7 m to 10−6 m. As the inner core radius get values lager than 10−6 m, the effect of changing the inner core radius became less visible on both the shape and the intensity of the reflectance. Then, the position and the average intensity of the PBG are studied in Fig. 4(c) and (d). When the inner core radius = 10−7 m, the PBG appears between 243.79 nm and 270.33 nm with an average density of about 93.65%. As the inner core radius reaches 10−6 m, the width of the PBG turns out to be 26.605 nm with an average intensity of 93.69%. The width of the PBG receives 26.61 nm with an average intensity of approximately 93.7% as the inner core radius reaches 10−4 nm. As the inner core radius increases from 10−4 m to 10 m, the PBG's width, and average intensity are stabilized at 26.6 nm and 93.7%, respectively. Furthermore, the position of the PBG becomes fixed around 243.9 nm and 270.5 nm for the left and the right edges, respectively. The above results reveal that the effect of the inner core radius is almost insignificant for values above 10−6 m, which opens the way towards a great number of applications with different size scale. For example, the ventilation tube could have any size from a few centimeters up to few meters without affecting the performance. This feature is crucial not only in the ventilation systems but also in other UVGI applications.
 |
| | Fig. 4 The influence of radius of the inner core ρ0 on the PBG at m = 0, d1 = 35 nm, d2 = 40 nm, and N = 20. (a) The reflectance of the proposed APC at three different radii of the inner air core. (b) Heat map of the APC's reflectance with an exponential increase of the radius of the inner core. (c) The wavelength of left and right edges of the PBG in nm versus the radius of the inner core with exponential range. (d) The width and the average intensity of the PBG's reflectance versus the inner core radius with exponential scale. | |
Table 1 The effect of inner core radius on the reflectance of APCs
| ρ0 (m) |
Average intensity |
PBG width (nm) |
| 10−7 |
0.936 |
26.53 |
| 10−4 |
0.937 |
26.61 |
| 1 |
0.937 |
26.61 |
Now, the influence of the periodicity number on the reflectance of the proposed APCs is examined in Fig. 5. As the periodicity number increases, the reflectance becomes more apparent, and sharper PBG is investigated, as seen in Fig. 5(a). At N = 10, the edges of the PBG are smooth and cover a larger area with a width of 32.8 nm, and its average intensity = 77%. As the periodicity number increases, the PBG becomes sharper with a larger average intensity as 93.6% for periodicity number N = 20, and it reaches 97% at N = 30. Thus, the average intensity drops significantly as the periodicity number decreases. On the other hand, the width is decreased as the periodicity number reduced. As the periodicity number N increases, the left edge of the PBG λL slightly shifts to longer wavelengths while the right edge λR shifts to shorter wavelengths but the center of the PBG λ0 almost fixed as clarified in Table 2. Then, for a deep description of the role of the periodicity, we have plotted in Fig. 5(b) a color map to clarify this role as N varies from 1 to 60. The PBG is hardly observable below N = 3 with average intensity below 40%. As the periodicity number increases, the PBG gets sharper with larger average intensity as it gets 93% at N = 20 and reaches 98% at N = 40. Also, the number of secondary peaks alongside the PBG increases with increasing the periodicity number. The position of the center of PBG is almost fixed at 257 nm with a difference around one nm as the periodicity number changes. The PBG edges' wavelengths shift towards the center with increasing the periodicity number, as shown in Fig. 5(c). Thus, as the periodicity number increases, the width of the PBG decreases, while the PBG average intensity increases, as shown in Fig. 5(d). At N = 8, the PBG has 68% average density and 35.9 nm width, while its average intensity at N = 15 reaches 88% with 28.8 nm width. As N = 25, the PBG's average intensity reaches 96% with a width of 25.2 nm, and its width gets 23.6 with an average intensity of 98% at N = 35.
 |
| | Fig. 5 The impact of the periodicity number on the reflectance at d1 = 35 nm, d2 = 40 nm, ρ0 = 0.5 m and m = 0. (a) The reflectance of the APC at three different periodicity numbers N = 10, 20, and 30. (b) Heat map represents the reflectance of the APC with periodicity numbers from 1 to 60. (c) The effect of alerting the periodicity number from 8 to 40 on the left and the right edges of the PBG. (d) The PBG's width and average intensity versus the periodicity number. | |
Table 2 The effect of periodicity number N on the PBG
| N |
λL (nm) |
λR (nm) |
λ0 (nm) |
Average intensity |
PBG width (nm) |
| 10 |
241.2 |
274.1 |
257.6 |
0.77 |
32.8 |
| 20 |
243.9 |
270.5 |
257.2 |
0.93 |
26.6 |
| 30 |
244.9 |
269.3 |
257.1 |
0.97 |
24.3 |
Finally, we have investigated the effect of the lattice constant on the reflectivity of our designed structure. In particular, the thicknesses of the constituent materials (Al2O3 and SiO2) are obtained based on the quarter-wave stack condition. The unit cell thickness or the lattice constant is determined as Λ0 = d1 + d2. The PBG is drastically shifted towards longer wavelengths as increasing the unit cell constant, as observed in Fig. 6(a). At Λ0 = 61 nm, the center of the PBG appears at 214.1 nm, and the width of the gap is equivalent to 21.3 nm with 94% average intensity. As the unit cell constant increases to 70 nm, the PBG center is slightly shifted to 241.6 nm. However, the width of the PBG increased to 24.7 nm with a small decrease in the average intensity to 93.7%. The center of the PBG becomes at 272.8 nm with 28.4 nm width when the unit cell constant reaches Λ0 = 80 nm. Then, the unit cell effect on the APC's reflectance has been examined smoothly from Λ0 = 60 nm up to Λ0 = 90 nm as shown in Fig. 6(b). The position of the PBG shifts linearly to longer wavelengths, and the unit cell constant Λ0 is linearly fitted to the center wavelength of the PBG λ0 according to λ0 = 3.101Λ0 + 24.67 with the sum of error squares equals 0.02446. Fig. 6(c) shows the position of the left and right edges of the PBG with changing unit cell constant Λ0 from 65 nm up to 79 nm while Fig. 6(d) reveals PBG's average intensity and its width at the same unit cell constant range. The left and right edges of the PBG appears at 214.8 nm and 237.7 nm at Λ0 = 65 nm, while its average intensity reaches 93.9% with width equals to 22.8 nm. At Λ0 = 79 nm, the average intensity of the PBG gets 93.6% with width equals 28 nm and its left and right edges appear at 255.6 nm and 283.7 nm, respectively. The relation between the width of the PBG WPBG (nm) and the average intensity IPBG can be fitted with a unit cell constant Λ0 (nm) with the following linear relation:
| | |
WPBG = 0.371Λ0 − 1.223
| (12) |
| | |
IPBG = −0.0002554Λ0 + 0.9562
| (13) |
 |
| | Fig. 6 The effect of the unit cell length Λ0 on the reflectance at N = 20, m = 0, ρ0 = 0.5 m. (a) The reflectance of the APC with three different unit cell constants Λ0 = 61 nm, 70 nm, and 80 nm. (b) Heat map for the reflectance of the proposed APC with changing the unit cell constant smoothly from 60 nm to 90 nm. (c) The left and the right edges of the PBG with altering the unit cell constant form 65 nm to 79 nm. (d) The PBG's width in nm and its normalized average intensity versus the unit cell constant in nm. | |
4. Conclusion
In this paper, we introduce a new enhancement for air purifiers in air ventilation systems using APCs. The numerical simulation reveals that the PBG width around 26 nm with average reflection intensity of 93% and 99% reflection in the center of the PBG. The PBG position is optimized at the maximum emission of mercury vapor lamps, which is widely used in UVGI devices. The effect of inner core radius is not significant for values larger than 10−6 m up to 10 m which opens the road towards a wide range of working scales. The effect of periodicity number on reflection is crucial as the PBG width decreases while the average intensity increases as the periodicity number increases. The impact of the unit cell constant has been examined for various values. The PBG shifts towards longer wavelengths as increasing the unit cell constant. Thus, the APC can adjust for a variety of UV sources.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors thank the Academy of Scientific Research & Technology (ASRT), Egypt for supporting the current work through; Science up Program; Project ID: 7859.
References
- WHO Library Cataloguing-in-Publication Data, Infection prevention and control of epidemic- and pandemic-prone acute respiratory infections in health care, 1.Guideline I.World Health Organization, ISBN 978 92 4150713 4, Subject headings are available from WHO institutional repository © World Health Organization, 2014 Search PubMed.
- L. Morawska, J. W. Tang, W. Bahnfleth, P. M. Bluyssen, A. Boerstra, G. Buonanno, J. Cao, S. Dancer, A. Floto, F. Franchimon, C. Haworth, J. Hogeling, C. Isaxon, J. L. Jimenez, J. Kurnitski, Y. Li, M. Loomans, G. Marks, L. C. Marr, L. Mazzarella, A. K. Melikov, S. Miller, D. K. Milton, W. Nazaroff, P. V. Nielsen, C. Noakes, J. Peccia, X. Querol, C. Sekhar, O. Seppänen, S. Tanabe, R. Tellier, K. W. Tham, P. Wargocki, A. Wierzbicka and M. Yao, Environ. Int., 2020, 142, 105832 CrossRef CAS PubMed.
- J. Lu, J. Gu, K. Li, C. Xu, W. Su, Z. Lai, D. Zhou, C. Yu, B. Xu and Z. Yang, Emerging Infect. Dis., 2020, 26, 1628–1631 CrossRef CAS PubMed.
- G. Liu, M. Xiao, X. Zhang, C. Gal, X. Chen, L. Liu, S. Pan, J. Wu, L. Tang and D. Clements-Croome, Sustain. Cities Soc., 2017, 32, 375–396 CrossRef.
- G. Guyot, M. H. Sherman and I. S. Walker, Energy Build., 2018, 165, 416–430 CrossRef.
- K. Shirbandi, S. Barghandan, O. Mobinfar and F. Rahim, SSRN Electron. J. DOI:10.2139/ssrn.3571418.
- A. R. Lemons, T. L. McClelland, S. B. Martin, W. G. Lindsley and B. J. Green, J. Hosp. Infect., 2020 DOI:10.1016/j.jhin.2020.04.011.
- C.-C. Tseng and C.-S. Li, Aerosol Sci. Technol., 2005, 39, 1136–1142 CrossRef CAS.
- E. Schnell, M. J. Harriff, J. E. Yates, E. Karamooz, C. D. Pfeiffer, J. McCarthy, C. L. Trapp, S. K. Frazier, J. E. Dodier and S. M. Smith, medRxiv, 2020 DOI:10.1101/2020.04.29.20085456.
- The ASHRAE Handbook, American Society of Heating, Refrigerating and Air-Conditioning Engineers, 2019, ch. 62 Search PubMed.
- E. Yablonovitch, Phys. Rev. Lett., 1987, 58, 2059–2062 CrossRef CAS PubMed.
- A. H. Aly and H. A. Elsayed, Phys. B, 2012, 407, 120–125 CrossRef CAS.
- A. H. Aly, H. A. Elsayed and S. A. El-Naggar, J. Mod. Opt., 2017, 64, 74–80 CrossRef CAS.
- C.-J. Wu, M.-S. Chen and T.-J. Yang, Phys. C, 2005, 432, 133–139 CrossRef CAS.
- A. H. Aly, H. A. Elsayed, A. A. Ameen and S. H. Mohamed, Int. J. Mod. Phys. B, 2017, 31, 1750239 CrossRef CAS.
- T. Detchprohm, Y.-S. Liu, K. Mehta, S. Wang, H. Xie, T.-T. Kao, S.-C. Shen, P. D. Yoder, F. A. Ponce and R. D. Dupuis, Appl. Phys. Lett., 2017, 110, 011105 CrossRef.
- T. Dasgupta and M. Dijkstra, Soft Matter, 2018, 14, 2465–2475 RSC.
- G. Liang, P. Han and H. Wang, Opt. Lett., 2004, 29, 192 CrossRef PubMed.
- K. B. Abdelaziz, J. Zaghdoudi, M. Kanzari and B. Rezig, J. Opt. A: Pure Appl. Opt., 2005, 7, 544–549 CrossRef.
- D. Jian-Wen, H. Peng and W. He-Zhou, Chin. Phys. Lett., 2003, 20, 1963 CrossRef.
- N. Ben Ali, V. Dhasarathan, H. Alsaif, Y. Trabelsi, T. K. Nguyen, Y. Bouazzi and M. Kanzari, Phys. B, 2020, 582, 411918 CrossRef CAS.
- J. Scheuer, W. M. J. Green, G. A. DeRose and A. Yariv, IEEE J. Sel. Top. Quantum Electron., 2005, 11, 476–484 CAS.
- A. H. Aly and H. Sayed, J. Nanophotonics, 2017, 11, 046020 Search PubMed.
- A. H. Aly, A. A. Ameen, H. A. ElSayed and S. H. Mohamed, Opt. Quantum Electron., 2018, 50, 361 CrossRef.
- N. Porras-Montenegro and C. A. Duque, Phys. E, 2010, 42, 1865–1869 CrossRef CAS.
- Y.-H. Chang, Y.-Y. Jhu and C.-J. Wu, Opt. Commun., 2012, 285, 1501–1504 CrossRef CAS.
- A. H. Aly and H. A. ElSayed, J. Mod. Opt., 2017, 64, 871–877 CrossRef.
- T.-W. Chang, H.-T. Hsu and C.-J. Wu, J. Electromagn. Waves Appl., 2011, 25, 2222–2235 CrossRef.
- M. M. Abadla, H. A. Elsayed and A. Mehaney, Phys. E, 2020, 119, 114020 CrossRef CAS.
- M. A. Kaliteevski, R. A. Abram, V. V. Nikolaev and G. S. Sokolovski, J. Mod. Opt., 1999, 46, 875–890 CrossRef CAS.
- X. Sun and A. Yariv, Opt. Express, 2007, 15, 17323–17333 CrossRef PubMed.
- S. K. Srivastava and A. Aghajamali, Phys. B, 2016, 489, 67–72 CrossRef CAS.
- M. J. Weber, Handbook of optical materials, CRC Press, Boca Raton, 2003 Search PubMed.
- CRC Handbook of Laser Science & Technology: Optical Materials, Part 2, ed. M. J. Weber, CRC Press, Boca Raton, Fla, 1986, vol. 4 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a



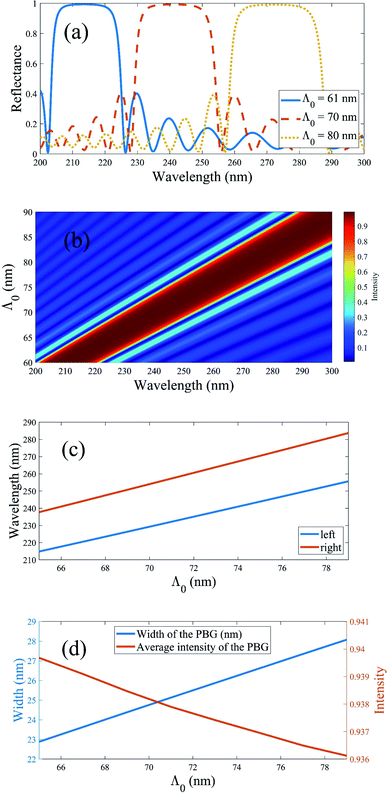
 The relation between Ez and Hϕ can be given by
The relation between Ez and Hϕ can be given by 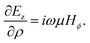 The azimuthal part of the magnetic field Hϕ can be obtained by substituting of Ez in the previous equation as the following:
The azimuthal part of the magnetic field Hϕ can be obtained by substituting of Ez in the previous equation as the following:
 which is the intrinsic admittance of the material. The electric and magnetic fields in a single layer with a refractive index nj and interfaces at ρj−1 and ρj can be represented by the following matrix:
which is the intrinsic admittance of the material. The electric and magnetic fields in a single layer with a refractive index nj and interfaces at ρj−1 and ρj can be represented by the following matrix:

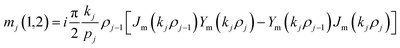
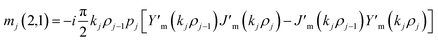



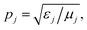 where j takes the value 0 and f. The parameter Cml is obtained from the following expression:
where j takes the value 0 and f. The parameter Cml is obtained from the following expression:
 and
and 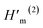 are the first and second kind Hankel function and their derivatives, respectively. The equations for TM-mode can be acquired by replacing every i, ε by −i, μ respectively, and vice versa. Finally, the reflectance from APC can be obtained by,
are the first and second kind Hankel function and their derivatives, respectively. The equations for TM-mode can be acquired by replacing every i, ε by −i, μ respectively, and vice versa. Finally, the reflectance from APC can be obtained by,




