Open Access Article
Open Access ArticleNoble gas endohedral fullerenes
Said
Jalife†
 *a,
Jessica
Arcudia
*a,
Jessica
Arcudia
 a,
Sudip
Pan
a,
Sudip
Pan
 *b and
Gabriel
Merino
*b and
Gabriel
Merino
 *a
*a
aDepartamento de Física Aplicada, Centro de Investigación y de Estudios Avanzados, Antigua carretera a Progreso Km 6, Cordemex, Loma Bonita Xcumpich, 97310 Mérida, Yucatán, Mexico. E-mail: said.jalife@cinvestav.mx; said.jalifejacobo@chem.ox.ac.uk; gmerino@cinvestav.mx
bFachbereich Chemie, Philipps-Universität Marburg, Hans-Meerwein-Straße, 35032 Marburg, Germany. E-mail: pans@chemie.uni-marburg.de
First published on 16th June 2020
Abstract
This review focuses on the available experimental and theoretical investigations on noble gas (Ng) endohedral fullerenes, addressing essential questions related to the mutual effects that confinement of one or more Ng atoms induces on the electronic structure, bonding, and different properties of fullerenes. It also summarizes the different contributions to the mechanisms of formation and decomplexation, the reactivity towards Diels–Alder cycloaddition reactions, the chemical bonding situation of Ng endohedral fullerenes, and the interactions that dominate within these systems.
Evidence and preparation
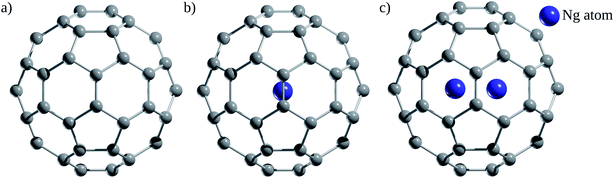
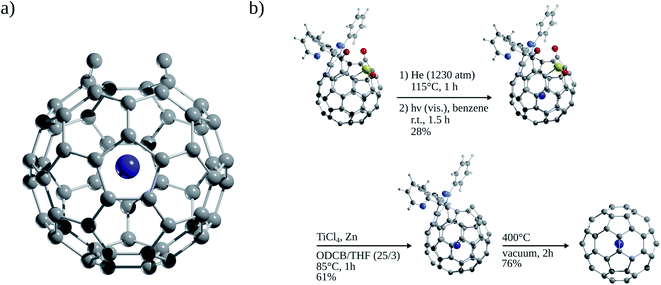
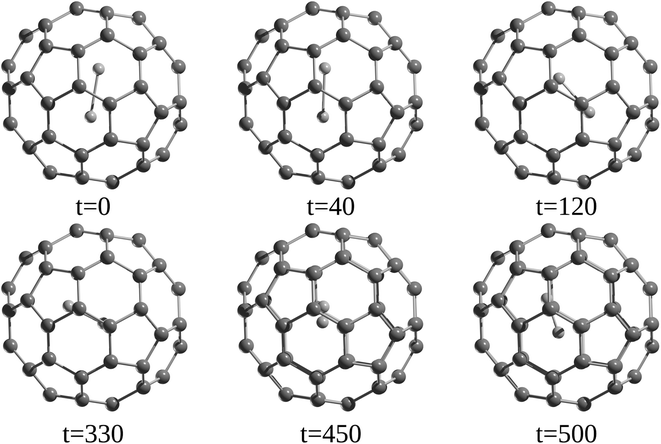
Since the discovery of buckminsterfullerene (C60) by Kroto, Smalley, and co-workers,1 one of the most intriguing features that fascinates researchers is its hollow interior, large enough to enclose atoms and molecules. Sprang et al.2 reported early works on the existence of endohedral fullerenes, incorporating metal atoms during the preparation of fullerenes using graphite, as in the well-known case of La@C60.3,4 Over time, the list of metallofullerenes (e.g., Sc@C60, Sc2@C60, Sc3@C60) has been gradually increased5 and more than half of the elements have now been confined within fullerenes.6–8 Perhaps, one of the groups that has attracted the most attention is the non-metal endohedral fullerenes, particularly those containing one or multiple noble gas (Ng) atoms, see Fig. 1. These endohedral fullerenes have been considered extremely stable complexes from the kinetical point of view. Some of the questions that have driven investigations of these systems are: to what extent the properties of fullerenes are affected by the encapsulation of Ng atoms? What kinds of interactions dominate within these systems? Can an Ng atom form a chemical bond with a cage atom and/or with another Ng atom in a confined state? How can Ng be inserted into fullerenes?The first evidence of endohedral fullerenes containing Ng atoms came from the group of Schwarz9–11 in a series of high-energy collision experiments. It was simultaneously described that the collision of He and Ne with positively charged C60q+ (q = 1, 2, 3) entities led to the addition of the Ng mass to the ions.9–21 Although neutralization–reionization experiments supported the helium (He) encapsulation,11 it was indubitably not possible to know if the ions still retained their fullerene form. However, since the 1990s, different methods have been developed to encapsulate Ng atoms within fullerenes. Saunders et al.22 detected He@C60 and Ne@C60 (at the part per million level) following the standard method of preparing fullerenes, i.e., heating a graphite arc at 600 °C in the partial pressure of helium or neon. Subsequently, Saunders et al.23 incorporated argon (Ar), krypton (Kr), and xenon (Xe) into fullerenes (Ar@C60, Kr@C60, Xe@C60) by employing high temperature and pressure on a mixture of fullerenes and the target Ng. It was proposed that the encapsulation process occurs through the “window mechanism”, where a temporary window gets formed by breaking one or more C–C bonds within the cage. Other techniques used to include Ng atoms into fullerenes are bombarding fullerenes with accelerated ions24 or via the explosive method,25 where a deliberate explosion in a mixture of Ng atoms and fullerene in a closed place led to the desired inclusion product (for He@C60 and He2@C60). Furthermore, a higher encapsulation ratio (30%) can be achieved using the so-called “molecular surgery” methodology,26 which involves an opening of the cage, then the insertion of an atom, and finally the closure of the cage as reported for He@C60 and He@C70 systems (see Fig. 2 for an example that proceeds via an opening of a 13-membered ring).26,27
The properties and reactivity of endohedral fullerenes containing Ng atoms have been assessed mostly by 3He NMR spectroscopy. Surprisingly, Saunders et al.28 reported the chemical shift of helium at −6.36 ppm for 3He@C60 and −28.81 ppm for 3He@C70 relative to the resonance of free 3He dissolved in 1-methylnaphthalene.28,29 The observed 3He shifts were rationalized in terms of a diamagnetic aromatic ring current in C60 and C70 with higher intensity owing to the diamagnetic nature of the benzenoid rings.30 Therefore, an upfield in 3He shift reflects a diatropic ring current (aromaticity), and a downfield shift means a paratropic ring current (antiaromaticity). This idea was pushed to the limit for the hexaanions He@C606− (most shielded) and He@C706− (most deshielded) compounds (3He chemical shifts of −49.27 and +8.20 ppm, relative to 3He in THF-d8, respectively).29,30 These values mean an opposite magnetic behavior compared to their neutral analogues and a significant change in the internal magnetic field and aromatic character, i.e., He@C606− is, in principle, more aromatic than the parent neutral compound. In further studies, the shielding of the encapsulated 3He core in He@C606− was rationalized by the presence of a long-range shielding cone along the entire cage due to its spherical aromatic character, whereas He@C706− exhibits a strong deshielding response inside the cage to the induced magnetic field.31,32 Also, the 3He shielding was assessed in terms of the number of addends in arylated and cloro[60]fullerenes.33 Based on the 3He upfield shift, Birkett et al.33 noted an enhanced aromatic character for all the aryl and chlorine C60 derivatives (C60Cl6–δHe = −12.30 ppm, C60Ph5Cl–δHe = −15.14 ppm, C60(4-FC6H4)5Cl–δHe = −15.04 ppm, C60(4-FC6H4)5+–δHe = −12.61 ppm and 1,4-C60Ph2–δHe = −10.50 ppm, C60Ph4–δHe = −14.40 ppm) relative to the parent compound due to the introduction of an sp3-hybridised carbon in adjacent pentagonal rings and an improved electronic delocalization in adjacent hexagons. This is associated with the high electronegativity of Cl atom, which reduces the p-character of adjacent carbons, and so the electron delocalisation. A similar assessment was performed with the bis- to hexakisadducts of C60 and mono- to tetrakisadducts of C70.34 For the C60 series, 3He chemical shift decreases as a function of the degree of functionalization (from −8.11 to −11.89 ppm), whereas in the C70 series, 3He chemical shift increases (from −27.53 to −20.68 ppm). While this contrasting behavior in C60 is attributed to the balance between paramagnetic pentagonal ring currents and diamagnetic benzenoid ring currents,28 the upfield in C70 is explained by the interruption of the diamagnetic ring current along the corannulene perimeter.
Now, what is the influence of the encapsulated Ng atoms on the 13C chemical shifts for the C60 cage? Murata and co-workers27 reported the 13C NMR spectra for free C70 and He@C70. The He@C70 spectrum is quite similar to that of C70 (δ = 150.91, 148.36, 147.67, 145.64, 131.15 ppm) with only two slight signals shifted by less than 0.05 ppm within the sp2 carbon region (145.66 and 131.15 ppm), revealing that He is located almost at the cage centre. More pronounced downfield shifts of 0.17, 0.39 and 0.95 ppm are observed in Ar@C60,35 Kr@C60,36 and Xe@C60,37 respectively.
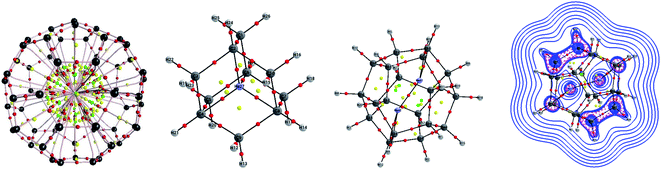
Single-crystal X-ray analysis also provided clear evidence on the structure of Ng atoms inside fullerenes. Morinaka et al.38 crystallized He@C60·{NiII(OEP)}2 (see Fig. 3a), confirming that He is at the centre of the C60 with 100% of occupation level. Dragoe and co-workers39 described the extended X-ray absorption fine structure for Kr@C60, while Balch and co-workers40 reported the crystal structure of Kr@C60 in (0.09Kr@C60/0.91C60)·{NiII(OEP)}2C6H6 (Fig. 3b). In the case of Ar@C60, the endohedral nature of Ar was confirmed by X-ray photoelectron spectroscopy and photoelectron diffraction,41 as well as by extended X-ray absorption fine structure experiments.
Encapsulation and release process of Ng atoms
From high-pressure experiments, Saunders et al.22 estimated an Arrhenius activation energy of ∼80 kcal mol−1 for the release of He from fullerene. In contrast, the computed activation barrier for He insertion into C60 through a six-membered ring is >200 kcal mol−1.14,19,42–44 Therefore, the release mechanism does not follow the penetration route. From mass spectroscopic studies, it is apparent that the Ne atom is released without destroying the C60 cage.45 This evidence suggests that Ng release occurs through a window mechanism or molecular surgery, in which C–C bonds are broken to open the cage, the inner Ng is released, and then the cage is reconstituted. In the case of the Kr and Xe derivatives, barriers are even higher than 1500 kcal mol−1 for inserting Ng through a six-membered ring of C60.46 Other processes involving the formation of triplet states were considered but they require even higher activation energies. Moreover, the incorporation fractions of 3He and 4He increase in the presence of cyanide (KCN),47 suggesting that the insertion of Ng may involve more than two species.To obtain a better understanding of the dynamics of encapsulation and release of Ng within fullerenes, several molecular dynamics (MD) simulations and quantum chemical computations were carried out. Some of the first works employed classical MD to study the formation process of Ng@C60 endohedral fullerenes. Cui et al.48 reported the formation process of Ng@C60 (Ng = He–Kr) endohedral fullerenes by a collision of Ng atoms with C60 using classical MD with a Tersoff and Lennard-Jones potentials to model all the C–C and Ng–C interactions, respectively. Three mechanisms of formation emerged: ring insertion, windowing, and holes. The first one is the insertion of an Ng into the C60 cage through a pentagon or hexagon ring without breaking any C–C bond, the second involves the formation of a short window when a C–C bond is broken due to the transfer of kinetic energy from the incident atom, while in the hole mechanism the same occurs, but the Ng is trapped within a defected C60 cage. He@C60 and Ne@C60 could be formed via ring-insertion or windowing mechanisms. Xu et al.49 investigated the complexation and decomplexation process of He@C60 using quantum chemical computations. Four possible paths were explored: insertion of He through the centre of a five-membered ring, through a six-membered ring, and through the centre of the [6,6] or [5,6] C–C bonds. In all the cases, a planar and spherical expansion was considered. The computed barriers support the increase of the [5,6] bond lengths, forming a 9-membered ring window as the most probable path (∼250 kcal mol−1), whereas the other options involve barriers above 300 kcal mol−1. So, the insertion of He into C60 is easier via the expansion of a plane window than a spherical window.
Zahn et al.50 studied the effect of pressure incorporating He into C60 using combined quantum/classical molecular dynamics QM/MM/MD simulations, particularly a path-sampling algorithm. The simulations included 1000 He atoms and a C60 molecule at 50 atm and 1000 K. The analysis of insertion trajectories reveals that the He incorporation occurs through a window formed by the opening of three C–C bonds. The lifetime of the opening is in the range of 50 to 150 fs, and the insertion of He requires around 120 kcal mol−1. Previously, Patchkovskii et al.42 computed (at the MNDO, HF/3-21G, and BP86/3-21G levels) the barriers of He incorporation into C60 through the opening of one-bond and two-bond windows. However, the barriers (>200 kcal mol−1) are further away from the experimentally reported ones (∼80 kcal mol−1).
The radical impurity insertion mechanism for C60X and C60X2 (X = H and Me) systems using semiempirical MNDO and density functional theory (DFT) computations (BLYP/3-21G) was also screened by Patchkovskii et al.51 Sixty-five different pathways for the insertion of He through six-membered rings and different windows in C60X and C60X2 were reported. Although the barriers are much lower compared to C60 when an impurity is added (i.e. C60X and C60X2), the computed values were very high compared to the experimental ones.
Roth and co-workers52 studied the effect of the Ng encapsulation on C60 at higher temperatures (T = 160–1500 K) using a Lennard-Jones potential for the Ng–C interactions along with a Brenner's empirical extended bond-order potential for the C–C bonds. These simulations show that smaller Ng atoms sit more off-centre than large ones and that the cage can be stabilized or not by stifling radial fluctuations. Similar MD simulations at higher temperatures (T = 4000–5000 K) indicate that the rate of release of Ng atoms does not only depend on the size of the Ng, but also because heavier encapsulated Ng atoms tend to stabilize the cage against thermal fluctuations.53 However, there is no evidence of a closing mechanism of the cage after the escape of Ng through a formed window. The same group54 also simulated an aggregate formed by five Ne@C60 endohedral molecules at temperatures ranging from T = 1000 K to T = 5000 K. The aggregate dissociates at 1150 K, but the carbon cages remain intact up to 4000 K, in which the Ne atom releases the aggregate through a window that opens and closes, but which remains as a defect at about 5000 K. Nevertheless, based on the experiments, it was suggested the limitation of classical dynamics to describe these systems at temperatures below 3000 K.
Ab initio MD simulations were also employed to investigate the formation process of He@C60 by simulating the explosion method (vide supra). Peng and co-workers55 used ab initio MD simulations at the PBE-vdw/DZP level to characterize the reaction path for colliding He into C60 and the formation process of He@C60. Initially, the authors computed a barrier of around 225 kcal mol−1 to insert He through a six-membered ring. However, the defects formed on fullerene are able to decrease this barrier. For instance, when a C2 unit is removed to form a C58 cage, considering a Rice shrink-wrap mechanism known in C60, He insertion can take place through a C7 or C8 rings (Fig. 4b and c) with approximate barriers of 123.6 and 70.0 kcal mol−1, respectively, or even better, when a collision between two C60 is simulated, the insertion barrier can decrease to 60.0 kcal mol−1 through a C9 ring. In fact, it was reported by tandem mass spectrometry studies that C70+, Ne@C70+, and Ar@C70+ cations undergo cage-shrinking reactions by unimolecular elimination of a C2 unit, which has lower activation energies than the removal of endohedral Ng atoms.56
A detailed analysis of the dynamics of encapsulated Ng atoms was carried out by Li et al.55 and Khatua et al.,57 showing that for Ng atoms in the Ng2@C60 (Ng = He–Kr) family, a nearly free precession movement around its midpoint in the C60 cage is possible, which depends on two factors, the interaction between the Ng and the cage and the distortion of the cage caused by the precession movement (see Fig. 5). DFT computations also predicted such behavior for the internal rotation of Ng atoms inside the C70 cage. According to Gómez et al.,58 the encapsulated Ng2 dimer within a C70 cage can rotate as well, and He2 rotates more readily than its heavier analogues Ne2 and Ar2.
The effect of confinement on chemical bonding
The completely filled valence shell of Ng atoms, their reasonably high ionization energies, and low electron affinities make them very lazy species to form chemical bonds with other elements. A really strong polarizing centre is required to deform the rigid electron density of Ng and to attract towards itself, facilitating a donor–acceptor type of interaction. Gold59 and beryllium,60–63 with the appropriate combination of geometrical orientation and charge distribution, make them the best transition metal and main-group elements, respectively, to form such type of interaction. Another strategy of forming a strong bond involving Ng is to push it in an extreme situation and to make the charge distribution in a way that this atom acts as cation Ng+ and then providing enough kinetic stability, at least, up to certain temperatures. Metastable Ng insertion complex, XNgY is one of such examples where Ng is inserted into the X–Y bond, sacrificing its strength, and the resulting charge distribution should be (XNg)+Y−, where X–Ng bond is a strong electron-sharing bond.64 But such molecules are thermochemically unstable with respect to dissociation, XNgY → Ng + XY. Another extreme situation is Ng endohedral complexes, where Ng atoms are forced to stay within a small space. Given the many bonds should be broken to be released from the cage, once one affords high energy to get it, the resulting Ng encapsulated complexes would be kinetically stable at ambient even at elevated temperatures. It provides a huge scope to force Ng atoms towards forming chemical bonds not only with the host atoms but also between two Ng atoms, which is otherwise unbound in nature, only weakly supported by tiny van der Waals forces. Given the fact that the chemical bond is a fuzzy concept (not an observable), these Ng inclusion complexes also draw arguments and counter ones regarding the existence of a chemical bond involving Ng atoms.One aspect is the energetics. Several authors reported the interaction or complexation energies of Ng@Cn systems65–78 (Ng = He–Xe; n = 20–60) using the Lennard-Jones model, or DFT and ab initio methods taking into account the dispersion effects and the basis set superposition error (BSSE). The general trend is that if the cavity size is small, lighter Ng atoms have more favorable interaction energies than their heavier analogues, but if the cage size is reasonably large, the heavier Ng atoms interact more strongly than the lighter ones. This is because the overall interaction energy depends on a delicate balance between attractive forces, originated from orbital, coulombic, and dispersion interaction, which increases linearly from lighter to heavier Ng atoms, and the Pauli repulsion that also enhances along the same direction. For instance, Bühl et al.77 reported, at the counterpoise-corrected MP2/6-31G** level (using a DZP basis for Kr and Xe), negative interaction energies between endohedral He to Xe atoms and C60 of −0.3 (−2.0 at the MP2/TZP(C) + cc-pVQZ),76 −1.9, −2.5, −7.5, and −5.4 kcal mol−1, respectively, whereas GGA BLYP79,80 and BP86 functionals,79,81 and hybrid B3LYP82 functional predict positive values (with BSSE). In the cases of hybrid GGA dispersion corrected B3LYP-DCP,83 the empirically dispersion corrected B97-D,84 and the hybrid meta-GGA functional M06-2X,85 negative interaction energies (with BSSE) are obtained. Sure et al.86 also nicely showed that the inclusion of dispersion contributions87 in the Ng@C20+2n (n = 0, 2–20; Ng = He, Ne, Ar) systems is mandatory in order to get reliable interaction energies. BP86-D/TZVPP level, with further energy refinement at the ab initio MP2/TZVPP level, was also found to be suitable to detail structures and energetics of Ng encapsulated C60 complexes correctly.88 The BP86 functional combined with dispersion correction (D3 or D3(BJ)) can also describe such systems.89 Therefore, in general, any functional that takes into account short-range and/or long-range dispersion interactions or ab initio methods in combination with sufficiently large basis set would provide reliable energetics.71,86,90,91
Now, does confinement induce a chemical bond? Since confinement pushes the bonding in extreme situations under high pressure, many models of bonding are bound to fail to explain them, starting a debate. Helium encapsulated into C10H16 adamantane, He@adam, is one such example in which the presence or absence of He–C chemical bonds was justified by several leading scientists based on their personal understanding and views to the definition of chemical bond.92–99 While the presence of four gradient paths connecting He and carbon atoms and the associated values of descriptors like electron density ρ(rc), Laplacian of electron density ∇2ρ(rc), and energy density H(rc) at the “bond” critical points of He–C gradient paths lying in between closed-shell and electron-sharing interactions advocate for the presence of chemical bond,94 the repulsive nature of He–C10H16 interaction (154.2 kcal mol−1) contradicts the notion of the presence of chemical bond (see Fig. 6 for the molecular graph).91,95,97 However, note that the 1997 IUPAC definition of the chemical bond,100 “there is a chemical bond between two atoms or groups of atoms in the case that the forces acting between them are such as to lead to the formation of aggregation with sufficient stability to make it convenient for the chemist to consider it as an independent molecular species”, does not demand a chemical bond to be attractive in nature. Bader and co-workers94 even argued that the interaction between He and carbon atoms connected through the gradient path is attractive in nature. The higher energies of the other carbon and hydrogen atoms are responsible for the energetic instability of the complex against dissociation. Adopting three highly symmetric systems of varying sizes, He@C8H8 (Oh), He@C20H20 (Ih) and Ng@C60 (Ih), Cerpa et al.98 demonstrated that irrelevant to the related Ng–C distances, there always exist gradient paths between them, which are driven by the symmetry, even if the presence of any true chemical bond is very unlikely (see Fig. 6). This is obvious that such conflicting views arise from different perspectives, which are valid within their scope of the definition. Schwarz and co-workers99 finally proposed that the conflicts may be avoided if such contacts are understood in the light of “confinement bonding”.
The presence of the chemical bond in Ng2@C60 involves fewer disputes than the above example. In 2007, Krapp et al.93 made an extensive study on the bonding situation in Ng2@C60 (Ng = He–Xe) complex. Interestingly, upon encapsulation, the Ng–Ng bond lengths get contracted to the 56–68% of the distance in free Ng2 dimer. Inspection of the energy of HOMO and LUMO of free Ng with those in confined Ng2 indicates a significant elevation of energy upon confinement, particularly for Ng = Ar–Xe, suggesting that the Ng atoms in the confined state would have different reactivity than that in the free state. The charge distribution indicates that the Ng2@C60 is low for Ng = He–Kr, but remarkably more than one electron is transferred from Xe2 to the host moiety, making it a charge complex Xe2+@C60−. Importantly, H(rc) value is considerably negative −0.341 Hartree Å−3 for Xe–Xe bond in Xe2@C60, undoubtedly assigning it as a genuine chemical covalent bond. On the other hand, for Kr–Kr and Ar–Ar, the H(rc) values are still negative, although they are smaller than that in Xe–Xe. Moreover, the reactivity of Ng2@C60 (Ng = Ar–Xe) would be considerably different than those of free Ng and C60, which was further confirmed by a subsequent study carried out by Solà and co-workers,101 where they noticed dramatic alteration of reactivity of Ng2@C60 with respect to C60 towards Diels–Alder cycloaddition in case of Ng = Ar–Xe. Therefore, it satisfies the IUPAC definition of the chemical bond. Their analyses also categorized the lighter He2@C60 and Ne2@C60 as weakly bonded van der Waals complexes.
It is obvious that the C60 cavity is large enough to induce the formation of a chemical bond between two lightest Ng atoms. In order to check whether the bonding situation in He2 gets changed in case of reasonably smaller host moiety than C60, Cerpa et al.102 forced two He atoms to stay within C20H20 cavitand. As expected, such confinement in very small space further squeezes the He–He bond length (1.265 Å), which becomes 0.688 and 1.712 Å shorter than those in He2@C60 and free He2, respectively. Such He2 confinement in a small cavity needs to pay a heavy price. The resulting complex is found to be unstable by 169.8 kcal mol−1 at the DFT level with respect to the dissociation into free He atoms and C20H20. Except for the presence of gradient path between two He atoms, the other bonding indices do not support the presence of chemical bond, which led the authors to conclude that short He–He internuclear separation is a consequence of He-cage repulsion and that it cannot be inferred as a true chemical bond.
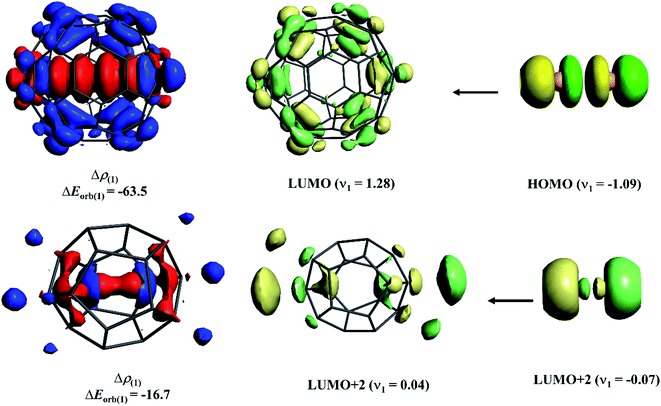
To shed light on the difference in Ng–C interaction between the cavity consisting of sp3 carbons and sp2 carbons, we performed an energy decomposition analysis combined with natural orbital for chemical valence (EDA-NOCV)103,104 on Xe2@C60 and He2@C20H20 complexes. Note that because of the different cavity sizes, a comparison between the same Ng atom cannot be done as obviously the orbital interaction in He2@C60 would be minimal. Here, we only emphasize how the most dominating orbital interaction arises in these two cases. Fig. 7 displays the deformation densities and the associated fragment orbitals of these two complexes. In the plot, the electron density flows from the red to blue region. In the case of Xe2@C60, −63.5 kcal mol−1 orbital stabilization arises because of almost one-electron transfer from the antibonding HOMO of Xe2 to LUMO of C60. Note that this transfer reduces the electron population of antibonding orbital, imposing net bond order in Xe–Xe bond. On the other hand, in the case of He2@C20H20, surprisingly, in place of 1σu orbital, higher-lying 2σu orbital acts as a donor to the LUMO+2 of C20H20. It seems that in the confined states, the energy gap between 1σu and 2σu orbitals lowers, introducing some degree of hybridization between them and some electrons from the former orbital polarizes to the latter one. Because of larger spatial distribution than the 1σu, 2σu orbital can interact more effectively with LUMO+2 of C20H20. However, the degree of such electron transfer and the associated orbital interaction is lower than those in Xe2@C60. Such low electron depletion from antibonding orbital corroborates with the previous study102 where the He–He bond could not be categorized as a chemical bond.
This came as a surprise when Nikolaienko et al.105 argued about the formation of a true He–He bond even in He2@C60 based on Löwdin's postulate. They analytically estimated the potential energy curve of the He–He dimer confined in C60 and then perturbatively solved the corresponding Schrödinger equation where they obtained at least one bound state where two He atoms are bound with each other. The ab initio MD study on Ng2@C60 showed that Ng2 units, including He2, undergo translational, vibrational, and rotational movements as a single entity, without any random movement, supporting some sort of bonding between two He atoms.57 A similar situation was noted in Ng2 confined in a smaller cavity like B12N12, B16N16, and B40 cages106,107 where some specific descriptors support bonding and some criteria do not. Therefore, it is only a matter of weightage an individual wants to give. Some scientists give more weightage on those descriptors that support the formation of chemical bonding, but some others prefer the other way. Nevertheless, it is fun to understand the advantages and limitations of different bonding models in analysing the chemical bonds formed under such drastic conditions. This is important to enjoy the different flavors and opportunities that confinement can provide.
Chemical reactivity of endohedral fullerenes containing Ng atoms
How significant is the effect on the fullerene reactivity due to the encapsulation of an Ng atom? The Diels–Alder reactions were used as a model to address this question both experimentally and theoretically. Saunders and co-workers108 compared the reactivity of a Diels–Alder reaction between He@C60 and Xe@C60 with 9,10-dimethylanthracene (DMA) using 129Xe and 3He NMR (Fig. 8a) and found that the equilibrium constant is temperature-dependent. At low temperatures, He@C60 is more reactive than Xe@C60, while at high temperatures, the opposite occurs. So, the decreased reactivity of Xe@C60 towards DMA at low temperatures is because the Xe atom pushes the π-electron cloud of C60 outward.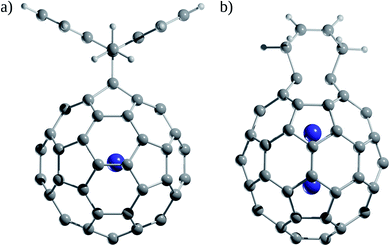 | ||
| Fig. 8 (a) Diels–Alder adducts between He@C60 and Xe@C60 with 9,10-dimethylanthracene (DMA). (b) Diels–Alder adducts between Ng@C60 and Ng2@C60 (Ng = He–Xe) with 1,3-cis-butadiene. | ||
Solà and co-workers101,109 performed DFT computations to determine the reaction and activation energies for the [4+2] Diels–Alder cycloaddition reactions between Ng@C60 or Ng2@C60 (Ng = He–Xe) systems and 1,3-cis-butadiene (Fig. 8b). For the free C60, the reaction energies are −20.7 and −4.6 kcal mol−1 and activation barriers are 12.7 and 21.0 kcal mol−1 for the addition to the [6,6] and [5,6] bonds, respectively. In the case of the Ng@C60 systems, the reaction energies (−20.5, −20.3, −20.2, −20.3, and −20.5 kcal mol−1 from He to Xe) and barriers (13.0, 13.4, 13.3, 13.1, and 12.9 kcal mol−1 from He to Xe) for the addition to the [6,6] bond are quite similar compared to free C60. The same is exhibited by the [5,5] bond with reaction energies of −4.1, −3.9, −3.7, −3.9, and −4.1 kcal mol−1 from He to Xe. However, the situation changes for the Ng2@C60 family, the reaction becomes more exothermic going from He2 to Xe2 at the most favorable [6,6] bond (−20.9, −23.1, −32.2, −39.9, and −44.9 kcal mol−1) and [5,6] bond (−5.0, −6.4, −15.9, −24.7, and −45.5 kcal mol−1). For the activation barriers, they get decreased as the size of the Ng increases for both most favorable [6,6] bond (12.8, 11.8, 8.4, 6.1, and 3.8 kcal mol−1) and [5,6] bond (20.4, 20.0, 14.9, 11.9, and 5.6 kcal mol−1). In the case of the Ng@C60 family, the effect of encapsulation is almost negligible. As expected, the pyracylenic bonds are more reactive than the corannulenic ones. Also, the increased reactivity of the heaviest Ng in the Ng2@C60 family was rationalized in terms of lowering the LUMO energy, a more straining C60 cage, and the release of compression of the Ng2 in the product.
The chemical reactivity of encapsulated Ng atoms was also assessed using chemical descriptors such as the chemical potentials, hardness, electron-donating, and electron-accepting powers. Garza and co-workers110 used a spherical shell with an attractive potential to simulate the Ng@C60 (Ng = He–Kr) systems. All the chemical descriptors were obtained using a DPW92 functional, including a self-interaction correction. The authors concluded that the confinement of Ng atoms increases their chemical potential and electrophilicity, while there is a reduction in the hardness, suggesting a general increment of the reactivity.
Bil et al. reported other approaches to assess the influence of Ng (Ng = He–Rn) on the reactivity of fullerenes.111 They showed, using ab initio molecular orbital and MD simulations, that the presence of the endohedral atom influences the ozone ring-opening reaction in Ng@C70O3, but there is almost no effect on the relative stability of the C70O3 isomers by including Ng atoms. The authors also noted that the enthalpy of reaction depends on the isomer considered. For instance, in the case of the c,c-C70O3 isomer, the reaction profile is not affected by the encapsulated Ng, whereas for a,b-C70O3 isomer, the enthalpy of reaction increases and for e,e-C70O3 decreases with the heaviest Ng atoms.
Fernández et al.112 analysed the governing factors for the enhanced reactivity of the Diels–Alder cycloaddition reaction between Ng2@C60 (Ng = He–Xe) and 1,3-butadiene using the activation strain model in combination with the energy decomposition analysis. In the case of He2@C60, the reaction energy (−31.8 kcal mol−1) and the activation energy (13.3 kcal mol−1) are comparable to free C60 (−32.1 and 12.7 kcal mol−1, respectively). A stronger effect on the kinetics and thermodynamics is shown for the heavier encapsulated Ng atoms compared to the empty one. The reaction energies are −33.6, −43.1, −51.2, and −56.4 kcal mol−1 and the activation energies are 12.4, 9.7, 7.5, and 6.9, respectively, along Ne–Xe. From the analysis of a complete activation strain diagram along the C–C forming bond distance, it is apparent that the stabilizing interaction between the reactants is mainly responsible for the lower computed barriers. The energy decomposition analysis supports that the electrostatic interactions (40–42%) and orbital interactions (43–47%) contribute almost equally to the total interaction energy where the latter term arises as a result of a strong orbital interaction between the cage and the diene induced by a change in the electronic structure of the cage due to the presence of an Ng atom. Thus, the insertion of an Ng dimer leads to remarkably enhanced interaction between the deformed reactant along the reaction coordinate.
Last but not the least questions
What is the smallest carbon fullerene able to confine an Ng? From DFT computations, Sure et al.86 investigated the smallest fullerene skeleton that can encapsulate Ng = He, Ne, Ar atoms in an energetically favorable way. They considered Ng@C20+2n (n = 0, 2–20; Ng = He, Ne, Ar) endohedral fullerenes. Although even Ng@C20 complexes are minima on the potential energy surface, a larger space is required to minimize the repulsion. Only attractive interaction (including zero-point energy correction) between Ng and fullerene is noted for the He@C50, Ne@C52, and Ar@C58 complexes. Through their two different sets of DFT computations (PBE/def2-TZVPP and PBE-D3/def2-TZVPP), the authors also justified the essence of taking care of dispersion interaction into the computations to get reliable energetics. Therefore, an Ng endohedral fullerene as small as Ng@C20 can be kinetically stable up to a certain extent, but enough large space (C50 or larger cage) is required to make it energetically stable. However, up to date only those with n ≥ 60 have been reported experimentally.What is the maximum number of Ng atoms contained into a fullerene? Although evidence of more than one Ng atom encapsulated in fullerenes was already known, Tonner et al.88 were the first to address the question using quantum chemical computations. C60 is able to fit a maximum of 40He, 17Ne, 7Ar, 6Kr, or 6Xe atoms. Interestingly, there is a quadratic dependence for the dissociation energy with increasing the cluster size and for the volume of the C60 cage with an increasing number of endohedral atoms. The decomposition of the dissociation energy into three terms, viz., the compression of the Ngn cluster, the deformation of the C60 cage, and the repulsive interaction between the Ngn cluster and the C60 cage, the last term is mainly responsible for the increased instability along the gradual cluster growth. The same question was considered for the bigger C80 cage, where the maximum number of encapsulated Ng atoms increases up to 46He, 24Ne, or 10Ar atoms.113 Cage opening mechanisms were also reported for C80 encapsulating up to or more than 50He, 25Ne, or 12Ar atoms via a “molecular cart-type” structure. In both cases, C60 and C80 are very strong cages with outstanding resistance to high internal pressures.
Can the encapsulation of Ng atoms in a fullerene stabilize other isomers? Merino and co-workers114 studied the stability of defected fullerenes by encapsulating two Ng atoms inside C60. In fullerenes, the isomers with an isolated pentagon surrounded by hexagons are more stable than those with two pentagons sharing an edge since it prevents the formation of antiaromatic pentalene units (Isolated-Pentagon Rule, IPR). When Xe2 is confined in C60, the most energetically stable isomer (by 7.0 kcal mol−1) does not follow IPR,115 rather it has a Stone–Wales defect. The energy decomposition analysis shows that the stability of the Xe2@C60 fullerene with a Stone–Wales defect comes from a lower orbital and electrostatic contributions by 39.4 and 24.5 kcal mol−1 (relative to the IPR one) and a decreased steric repulsion between the endohedral Ng dimer and the C60 cage due to the ellipsoid shape in the defected fullerene.
Final remarks
Since the discovery of endohedral fullerenes containing Ng atoms in the early 1990s through mass spectroscopy experiments, substantial experimental and theoretical research has been conducted. Over time, various techniques have been developed for the formation of these endohedral fullerenes under extreme conditions (high temperature or pressure) or by molecular surgery. To date, fullerenes containing one or two Ng atoms have been reported. These systems have particular attraction because the guest atoms are, in principle, considered to be inert. However, spectroscopic experiments and quantum computations have proved changes in the properties, bonding, and reactivity of these species. Therefore, derived from the effects induced by confined Ng atoms, the magnetic behavior of the C60 or C70 cages, bonding, the reactivity of C60 to Diels–Alder cycloaddition reactions, and associated kinetics and thermodynamics, along with other electronic properties have been detailedly assessed. MD simulations and quantum chemical computations have been used to model the mechanism of formation/release of endohedral fullerenes, encapsulated with Ng atoms. In addition, the electronic structure and the predominant interactions between encapsulated Ng atoms and fullerene cages along with the reported factors that determine the energy profile for Diels–Alder cycloaddition reactions have been addressed. In general, more pronounced effects are achieved when heavier Ng atoms or a pair of them are encapsulated, such as an enhanced reactivity for the latter case. The future scope of this field is enormous. In place of bare cavitand, it would be interesting to insert Ng atoms in metallofullerenes and to check the resulting energetics and reactivity. The effect of the external electric field on the interaction and bonding in inclusion complexes is another unattained topic. Efforts should also be made about how the stability of Ng encapsulated complexes can be enhanced through doping the fullerenes. Thus, the endohedral fullerenes containing Ng atoms have shown more interesting chemistry than expected.Conflicts of interest
There are no conflicts to declare.Acknowledgements
SJ thanks Conacyt for his PhD and Postdoctoral scholarships. JA thanks Conacyt for her PhD scholarships. SP thanks Deutsche Forschungsgemeinschaft for his postdoctoral fellowship.References
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- H. Sprang, A. Mahlkow and E. E. B. Campbell, Chem. Phys. Lett., 1994, 227, 91–97 CrossRef CAS.
- J. R. Heath, S. C. O'Brien, Q. Zhang, Y. Liu, R. F. Curl, F. K. Tittel and R. E. Smalley, J. Am. Chem. Soc., 1985, 107, 7779–7780 CrossRef CAS.
- Y. Chai, T. Guo, C. Jin, R. E. Haufler, L. P. Felipe Chibante, J. Fure, L. Wang, J. Michael Alford and R. E. Smalley, J. Phys. Chem., 1991, 95, 7564–7568 CrossRef CAS.
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS.
- H. Shinohara, Rep. Prog. Phys., 2000, 63, 843–892 CrossRef CAS.
- M. N. Chaur, F. Melin, A. L. Ortiz and L. Echegoyen, Angew. Chem., Int. Ed., 2009, 48, 7514–7538 CrossRef CAS PubMed.
- D. S. Bethune, R. D. Johnson, J. R. Salem, M. S. de Vries and C. S. Yannoni, Nature, 1993, 366, 123–128 CrossRef CAS.
- T. Weiske, D. K. Böhme, J. Hrušák, W. Krätschmer and H. Schwarz, Angew. Chem., Int. Ed., 1991, 30, 884–886 CrossRef.
- T. Weiske, J. Hrušák, D. K. Böhme and H. Schwarz, Chem. Phys. Lett., 1991, 186, 459–462 CrossRef CAS.
- T. Weiske, T. Wong, W. Krätschmer, J. K. Terlouw and H. Schwarz, Angew. Chem., Int. Ed., 1992, 31, 183–185 CrossRef.
- T. Weiske, D. K. Böhme and H. Schwarz, J. Phys. Chem., 1991, 95, 8451–8452 CrossRef CAS.
- M. M. Ross and J. H. Callahan, J. Phys. Chem., 1991, 95, 5720–5723 CrossRef CAS.
- T. Weiske, J. Hrušák, D. K. Bohme and H. Schwarz, Helv. Chim. Acta, 1992, 75, 79–89 CrossRef CAS.
- T. Wong, J. K. Terlouw, T. Weiske and H. Schwarz, Int. J. Mass Spectrom. Ion Processes, 1992, 113, R23–R29 CrossRef.
- E. E. B. Campbell, R. Ehlich, A. Hielscher, J. M. A. Frazao and I. V. Hertel, Z. Phys. D: At., Mol. Clusters, 1992, 23, 1–2 CrossRef CAS.
- R. C. Mowrey, M. M. Ross and J. H. Callahan, J. Phys. Chem., 1992, 96, 4755–4761 CrossRef CAS.
- Z. Wan, J. F. Christian and S. L. Anderson, J. Chem. Phys., 1992, 96, 3344–3347 CrossRef CAS.
- J. Hrušák, D. K. Böhme, T. Weiske and H. Schwarz, Chem. Phys. Lett., 1992, 193, 97–100 CrossRef.
- J. F. Christian, Z. Wan and S. L. Anderson, J. Chem. Phys., 1993, 99, 3468–3479 CrossRef CAS.
- R. Kleiser, H. Sprang, S. Furrer and E. E. B. Campbell, Z. Phys. D: At., Mol. Clusters, 1993, 28, 89–90 CrossRef CAS.
- M. Saunders, H. A. Jimenez-Vazquez, R. J. Cross and R. J. Poreda, Science, 1993, 259, 1428–1430 CrossRef CAS PubMed.
- M. Saunders, H. A. Jimenez-Vazquez, R. James Cross, S. Mroczkowski, M. L. Gross, D. E. Giblin and R. J. Poreda, J. Am. Chem. Soc., 1994, 116, 2193–2194 CrossRef CAS.
- R. Shimshi, R. J. Cross and M. Saunders, J. Am. Chem. Soc., 1997, 119, 1163–1164 CrossRef CAS.
- R.-F. Peng, S.-J. Chu, Y.-M. Huang, H.-J. Yu, T.-S. Wang, B. Jin, Y.-B. Fu and C.-R. Wang, J. Mater. Chem., 2009, 19, 3602 RSC.
- M. Murata, Y. Murata and K. Komatsu, Chem. Commun., 2008, 6083 RSC.
- Y. Morinaka, F. Tanabe, M. Murata, Y. Murata and K. Komatsu, Chem. Commun., 2010, 46, 4532–4534 RSC.
- M. Saunders, R. James Cross, H. A. Jiménez Vázquez, R. Shimshi and A. Khong, Science, 1996, 271, 1693–1697 CrossRef CAS.
- M. Saunders, H. A. Jiménez-Vázquez, R. James Cross, S. Mroczkowski, D. I. Freedberg and F. A. L. Anet, Nature, 1994, 367, 256–258 CrossRef CAS.
- T. Sternfeld, R. E. Hoffman, M. Saunders, R. J. Cross, M. S. Syamala and M. Rabinovitz, J. Am. Chem. Soc., 2002, 124, 8786–8787 CrossRef CAS PubMed.
- J. Camacho Gonzalez and A. Muñoz-Castro, J. Mol. Model., 2019, 25, 322 CrossRef CAS PubMed.
- N. D. Charistos and A. Muñoz-Castro, J. Phys. Chem. C, 2018, 122, 9688–9698 CrossRef CAS.
- P. R. Birkett, M. Bühl, A. Khong, M. Saunders and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1999, 2037–2039 RSC.
- M. Rüttimann, R. F. Haldimann, L. Isaacs, F. Diederich, A. Khong, H. Jiménez-Vázquez, R. J. Cross and M. Saunders, Chem.–Eur. J., 1997, 3, 1071–1076 CrossRef.
- A. Takeda, Y. Yokoyama, S. Ito, T. Miyazaki, H. Shimotani, K. Yakigaya, T. Kakiuchi, H. Sawa, H. Takagi, K. Kitazawa and N. Dragoe, Chem. Commun., 2006, 912–914 RSC.
- K. Yamamoto, M. Saunders, A. Khong, R. James Cross, M. Grayson, M. L. Gross, A. F. Benedetto and R. Bruce Weisman, J. Am. Chem. Soc., 1999, 121, 1591–1596 CrossRef CAS.
- M. S. Syamala, R. James Cross and M. Saunders, J. Am. Chem. Soc., 2002, 124, 6216–6219 CrossRef CAS.
- Y. Morinaka, S. Sato, A. Wakamiya, H. Nikawa, N. Mizorogi, F. Tanabe, M. Murata, K. Komatsu, K. Furukawa, T. Kato, S. Nagase, T. Akasaka and Y. Murata, Nat. Commun., 2013, 4, 1554 CrossRef.
- S. Ito, A. Takeda, T. Miyazaki, Y. Yokoyama, M. Saunders, R. J. Cross, H. Takagi, P. Berthet and N. Dragoe, J. Phys. Chem. B, 2004, 108, 3191–3195 CrossRef CAS.
- H. M. Lee, M. M. Olmstead, T. Suetsuna, H. Shimotani, N. Dragoe, R. J. Cross, K. Kitazawa and A. L. Balch, Chem. Commun., 2002, 1352–1353 RSC.
- N. Dragoe, A. M. Flank, P. Lagarde, S. Ito, H. Shimotani and H. Takagi, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155448 CrossRef.
- S. Patchkovskii and W. Thiel, J. Am. Chem. Soc., 1996, 118, 7164–7172 CrossRef CAS.
- D. Zahn, J. Chem. Phys., 2005, 123, 044104 CrossRef PubMed.
- R. Granot and R. Baer, J. Chem. Phys., 2008, 129, 214102 CrossRef PubMed.
- R. Shimshi, A. Khong, H. A. Jiménez-Vázquez, R. J. Cross and M. Saunders, Tetrahedron, 1996, 52, 5143–5148 CrossRef CAS.
- T. Ohtsuki, K. Ohno, K. Shiga, Y. Kawazoe, Y. Maruyama and K. Masumoto, Phys. Rev. Lett., 1998, 81, 967–970 CrossRef CAS.
- R. J. Cross, A. Khong and M. Saunders, J. Org. Chem., 2003, 68, 8281–8283 CrossRef CAS PubMed.
- F. Z. Cui, D. X. Liao and H. D. Li, Phys. Lett. A, 1994, 195, 156–162 CrossRef CAS.
- Z. Xu and J. Yan, Int. J. Quantum Chem., 1995, 53, 287–295 CrossRef CAS.
- D. Zahn and G. Seifert, J. Phys. Chem. B, 2004, 108, 16495–16498 CrossRef CAS.
- S. Patchkovskii and W. Thiel, Helv. Chim. Acta, 1997, 80, 495–509 CrossRef CAS.
- W. Even, J. Smith and M. W. Roth, Mol. Simul., 2005, 31, 207–213 CrossRef CAS.
- M. K. Balasubramanya, M. W. Roth, P. D. Tilton and B. A. Suchy, J. Comput. Theor. Nanosci., 2008, 5, 627–634 CrossRef CAS.
- P. Tilton, B. Suchy, M. K. Balasubramanya and M. W. Roth, Mol. Simul., 2007, 33, 945–952 CrossRef CAS.
- J.-Y. Li, L.-M. Liu, B. Jin, H. Liang, H.-J. Yu, H.-C. Zhang, S.-J. Chu and R.-F. Peng, J. Mol. Model., 2013, 19, 1705–1710 CrossRef CAS PubMed.
- B. Cao, T. Peres, R. James Cross, M. Saunders and C. Lifshitz, J. Phys. Chem. A, 2005, 109, 10257–10263 CrossRef CAS PubMed.
- M. Khatua, S. Pan and P. K. Chattaraj, Chem. Phys. Lett., 2014, 610–611, 351–356 CrossRef CAS.
- S. Gómez and A. Restrepo, Phys. Chem. Chem. Phys., 2019, 21, 15815–15822 RSC.
- S. Pan, G. Jana, G. Merino and P. K. Chattaraj, ChemistryOpen, 2019, 8, 173–187 CrossRef CAS PubMed.
- G. Frenking, W. Koch, J. Gauss and D. Cremer, J. Am. Chem. Soc., 1988, 110, 8007–8016 CrossRef CAS.
- C. A. Thompson and L. Andrews, J. Am. Chem. Soc., 1994, 116, 423–424 CrossRef CAS.
- S. Pan, D. Moreno, J. L. Cabellos, J. Romero, A. Reyes, G. Merino and P. K. Chattaraj, J. Phys. Chem. A, 2014, 118, 487–494 CrossRef CAS PubMed.
- R. Saha, S. Pan, G. Merino and P. K. Chattaraj, J. Phys. Chem. A, 2015, 119, 6746–6752 CrossRef CAS PubMed.
- L. Khriachtchev, M. Räsänen and R. Benny Gerber, Acc. Chem. Res., 2009, 42, 183–191 CrossRef CAS PubMed.
- R. B. Darzynkiewicz and G. E. Scuseria, J. Phys. Chem. A, 1998, 102, 3458 CrossRef CAS.
- R. Q. Zhang, W. Y. Ma, K. L. Han and C. S. Lee, Theor. Chem. Acc., 2003, 109, 278–283 Search PubMed.
- N. N. Breslavskaya, A. A. Levin and A. L. Buchachenko, Russ. Chem. Bull., 2004, 53, 18–23 Search PubMed.
- N. N. Breslavskaya and A. L. Buchachenko, Fullerenes, Nanotubes, Carbon Nanostruct., 2005, 12, 47–52 Search PubMed.
- C. N. Ramachandran, D. Roy and N. Sathyamurthy, Chem. Phys. Lett., 2008, 461, 87–92 CrossRef CAS.
- A. Hesselmann and T. Korona, Phys. Chem. Chem. Phys., 2011, 13, 732–743 RSC.
- Y. Ma, Y. Ai, X. Song, C. Wang and Y. Luo, Chem. Phys. Lett., 2014, 591, 312–316 CrossRef CAS.
- M. Kolb and W. Thiel, J. Comput. Chem., 1993, 14, 37–44 CrossRef CAS.
- A. J. C. Varandas, Int. J. Quantum Chem., 2011, 111, 416–429 CrossRef CAS.
- M.-S. Son and Y. K. Sung, Chem. Phys. Lett., 1995, 245, 113–118 CrossRef CAS.
- H. A. Jiménez-Vázquez and R. J. Cross, J. Chem. Phys., 1996, 104, 5589–5593 CrossRef.
- S. Patchkovskii and W. Thiel, J. Chem. Phys., 1997, 106, 1796–1799 CrossRef CAS.
- M. Bühl, S. Patchkovskii and W. Thiel, Chem. Phys. Lett., 1997, 275, 14–18 CrossRef.
- L. Pang and F. Brisse, J. Phys. Chem., 1993, 97, 8562–8563 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- I. D. Mackie and G. A. DiLabio, J. Phys. Chem. A, 2008, 112, 10968–10976 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- R. Sure, R. Tonner and P. Schwerdtfeger, J. Comput. Chem., 2015, 36, 88–96 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- R. Tonner, G. Frenking, M. Lein and P. Schwerdtfeger, ChemPhysChem, 2011, 12, 2081–2084 CrossRef CAS PubMed.
- J. Camacho Gonzalez, S. Mondal, F. Ocayo, R. Guajardo-Maturana and A. Muñoz-Castro, Int. J. Quantum Chem., 2020, 120, 119 CrossRef.
- J. Autschbach and E. Zurek, J. Phys. Chem. A, 2003, 107, 4967–4972 CrossRef CAS.
- P. Pyykkö, C. Wang, M. Straka and J. Vaara, Phys. Chem. Chem. Phys., 2007, 9, 2954–2958 RSC.
- A. Haaland, D. J. Shorokhov and N. V. Tverdova, Chem.–Eur. J., 2004, 10, 4416–4421 CrossRef CAS PubMed.
- A. Krapp and G. Frenking, Chem.–Eur. J., 2007, 13, 8256–8270 CrossRef CAS PubMed.
- R. F. W. Bader and D.-C. Fang, J. Chem. Theory Comput., 2005, 1, 403–414 CrossRef CAS PubMed.
- T. Strenalyuk and A. Haaland, Chem.–Eur. J., 2008, 14, 10223–10226 CrossRef CAS PubMed.
- M. von Hopffgarten and G. Frenking, Chem.–Eur. J., 2008, 14, 10227–10231 CrossRef CAS PubMed.
- J. Poater, M. Solà and F. M. Bickelhaupt, Chem.–Eur. J., 2006, 12, 2889–2895 CrossRef CAS PubMed.
- E. Cerpa, A. Krapp, A. Vela and G. Merino, Chem.–Eur. J., 2008, 14, 10232–10234 CrossRef CAS PubMed.
- S.-G. Wang, Y.-X. Qiu and W. H. Eugen Schwarz, Chem.–Eur. J., 2009, 15, 6032–6040 CrossRef CAS PubMed.
- A. D. McNaught and A. Wilkinson, Compendium of Chemical Terminology: IUPAC Recommendations, Wiley-Blackwell, 1997 Search PubMed.
- S. Osuna, M. Swart and M. Solà, Chem.–Eur. J., 2009, 15, 13111–13123 CrossRef CAS PubMed.
- E. Cerpa, A. Krapp, R. Flores-Moreno, K. J. Donald and G. Merino, Chem.–Eur. J., 2009, 15, 1985–1990 CrossRef CAS PubMed.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580 CrossRef CAS.
- T. Yu Nikolaienko, E. S. Kryachko and G. A. Dolgonos, J. Comput. Chem., 2018, 39, 1090–1102 CrossRef CAS PubMed.
- M. Khatua, S. Pan and P. K. Chattaraj, J. Chem. Phys., 2014, 140, 164306 CrossRef PubMed.
- S. Pan, M. Ghara, S. Kar, X. Zarate, G. Merino and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2018, 20, 1953–1963 RSC.
- M. Frunzi, R. J. Cross and M. Saunders, J. Am. Chem. Soc., 2007, 129, 13343–13346 CrossRef CAS PubMed.
- S. Osuna, M. Swart and M. Solà, Phys. Chem. Chem. Phys., 2011, 13, 3585–3603 RSC.
- A. Cortés-Santiago, R. Vargas and J. Garza, J. Mex. Chem. Soc., 2017, 56, 270–274 Search PubMed.
- A. Bil and C. A. Morrison, J. Phys. Chem. A, 2012, 116, 3413–3419 CrossRef CAS PubMed.
- I. Fernández, M. Solà and F. M. Bickelhaupt, J. Chem. Theory Comput., 2014, 10, 3863–3870 CrossRef PubMed.
- Z. Mahdavifar, J. Mol. Graphics Modell., 2014, 54, 32–45 CrossRef CAS PubMed.
- S. Jalife, S. Mondal, J. L. Cabellos, S. Pan, M. Á. Méndez-Rojas, I. Fernández, G. Frenking and G. Merino, ChemistrySelect, 2016, 1, 2405–2408 CrossRef CAS.
- H. W. Kroto, Nature, 1987, 329, 529–531 CrossRef CAS.
Footnote |
| † Current address: Chemistry Research Laboratory, 12 Mansfield Road, Oxford, UK. |
| This journal is © The Royal Society of Chemistry 2020 |