Open Access Article
Open Access ArticleElectrochemical CO2 reduction on nanostructured metal electrodes: fact or defect?
Recep
Kas
 a,
Kailun
Yang
a,
Divya
Bohra
a,
Kailun
Yang
a,
Divya
Bohra
 a,
Ruud
Kortlever
a,
Ruud
Kortlever
 b,
Thomas
Burdyny
b,
Thomas
Burdyny
 a and
Wilson A.
Smith
a and
Wilson A.
Smith
 *a
*a
aMaterials for Energy Conversion and Storage (MECS), Department of Chemical Engineering, Delft University of Technology, 2629 HZ Delft, The Netherlands. E-mail: W.Smith@tudelft.nl
bLarge-Scale Energy Storage (LSE), Department of Process and Energy, Delft University of Technology, 2628 CB Delft, The Netherlands
First published on 16th January 2020
Abstract
Electrochemical CO2 reduction has received an increased amount of interest in the last decade as a promising avenue for storing renewable electricity in chemical bonds. Despite considerable progress on catalyst performance using nanostructured electrodes, the sensitivity of the reaction to process conditions has led to debate on the origin of the activity and high selectivity. Additionally, this raises questions on the transferability of the performance and knowledge to other electrochemical systems. At its core, the discrepancy is primarily a result of the highly porous nature of nanostructured electrodes, which are vulnerable to both mass transport effects and structural changes during the electrolysis. Both effects are not straightforward to identify and difficult to decouple. Despite the susceptibility of nanostructured electrodes to mass transfer limitations, we highlight that nanostructured silver electrodes exhibit considerably higher activity when normalized to the electrochemically active surface in contrast to gold and copper electrodes. Alongside, we provide a discussion on how active surface area and thickness of the catalytic layer itself can influence the onset potential, selectivity, stability, activity and mass transfer inside and outside of the three dimensional catalyst layer. Key parameters and potential solutions are highlighted to decouple mass transfer effects from the measured activity in electrochemical cells utilizing CO2 saturated aqueous solutions.
1. Introduction
Electrochemical carbon dioxide (CO2) reduction was pioneered by Y. Hori in the 1980's.1 The number of published scientific papers in this area peaked in the mid-1990s, and settled down to a plateau in the 2000s with ∼10–20 papers per year being published. At this time, the decreasing cost of renewable electricity and the need for electrical/chemical storage in global energy production had a riveting effect, prompting a resurgence in the field and many new research groups to study electrochemical CO2 reduction research in the early 2010s. Since 2015, several hundreds of papers are now published each year studying electrochemical CO2 reduction experimentally and/or theoretically.Most electrochemical CO2 reduction studies (>98%) have been conducted in conventional H-cell architectures in CO2 saturated electrolytes at ambient pressure.2 Considering the common observation that the performance of CO2 electroreduction catalysts are influenced by many factors such as electrolyte composition and concentration, (local) pH, cell design etc., the significance of optimizing the catalytic activity, selectivity and testing the stability in CO2 saturated solutions at ambient pressure has recently been challenged by different research groups.3–5 The industrial relevance to transition from CO2 saturated aqueous electrolytes to vapour-fed systems has further been highlighted as a promising approach to integrate catalyst development with reactor design under practical operational conditions. Such a combined approach is necessary to accelerate electrochemical engineering research in the field due to the unique interconnected factors governing the chemistry in CO2 electrolysis processes. These include homogenous reactions between CO2 and OH−, the competing hydrogen evolution reaction, and broad product distributions when compared to other gas phase electrochemical reactions such as oxygen reduction (ORR) and hydrogen oxidation (HOR).
Despite the field's shift towards vapour-fed systems to improve industrial relevance, the catalyst layer of gas diffusion electrodes (GDEs) is usually ill-defined and mass transport of species to and from reactive zones can be considerably complex.6 Activation and mass transport limited regions might simultaneously exist throughout the porous catalyst layer at nearly all potentials due to the nature of the reactive zones.7 Moreover, the correction of ohmic loses may not be sufficiently accurate to gain fundamental insights from kinetic studies, due to the complex thin water layer on the catalyst and the porosity of the gas diffusion media and catalyst layer.8 Therefore, conventional aqueous electrochemical cells are still a very useful platform to study reaction kinetics, reveal active sites and evaluate intrinsic activity by using well-defined surfaces, shape controlled nanoparticles and homogenous mass transport, which can minimize trial and error catalyst discovery. The ability to study fundamental phenomena in an gas saturated aqueous system is one of the strategies that is often used for other electrochemical reactions that are now performed in the gas-phase such as ORR and HOR.7,9
Within the CO2 reduction field, Kanan and co-workers' impactful report on oxide derived electrodes has gained a lot of interest by researchers, as these were the first electrodes found to decrease the onset potential of CO2 electroreduction to reasonably low overpotentials with high selectivity towards carbon based products.10,11 The field collaboratively figured out that similar performances can be obtained by preparing nanostructured and/or mesostructured electrodes via different preparation methods which do not involve electrochemical or non-electrochemical oxidation and reduction cycles of metal electrodes.12–15 Therefore, in this review, we will refer to all of these electrodes collectively as nanostructured and/or mesostructured electrodes depending on the structure of the catalytic layer. These electrodes are schematically depicted in Fig. 1 along with smooth and rough 2-D electrodes. A key property of nano/mesostructured electrodes is their very high electrochemically active surface area (ECSA), which is confined to porous 3-D catalyst layers. This class of electrodes exhibit three major attractive properties compared to their planar polycrystalline counterparts.
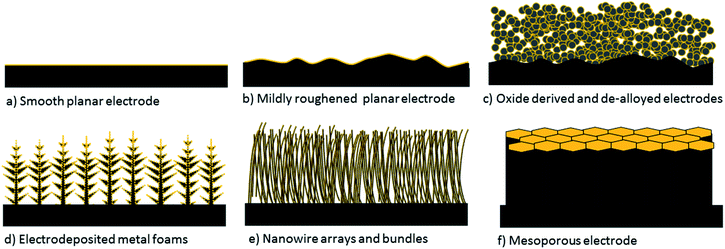 | ||
| Fig. 1 Depiction of 2-D planar and commonly used 3-D nanostructured and mesostructured electrodes. Yellow colour represents the ECSA. | ||
(i) Lower onset potential for CO2 reduction, especially towards CO and/or formic acid.
(ii) Higher selectivity and, arguably, activity at same potentials towards CO2 reduction products.
(iii) Higher electrocatalytic stability.
Here in this mini-review, we would like to discuss how observed electrochemical performance can be largely influenced by non-material factors such as the electrochemically active high surface area, morphology and 3-D structure of the catalyst layer. The differences between ECSA and thickness of the electrodes may not only influence activity, selectivity and stability but also product analysis, activation control and mass transfer limited potential windows.
2. Onset potential
The onset potential for the formation of a particular product is one of the most commonly used but poorly defined terms in the field of electrochemical CO2 reduction. Nonetheless, it has been often defined as the least negative potential in which a reaction product or faradaic current was detected. The onset potential has been increasingly used as a metric of efficiency for CO2 reduction electrocatalysts in the last decade, especially as nanostructured electrodes were introduced. For instance, the onset potential for CO production was shifted towards less negative potentials by 200–400 mV on high surface area nanostructured and mesostructured silver and gold electrodes prepared via different methods in comparison to their equivalent flat surfaces.10,13,16 In addition, higher selectivities towards C2 products have been reported numerous times for high surface area copper electrodes.12 The change in the onset potentials, however, were not as significant as in the case of Ag and Au.The recorded low overpotentials are inherently the most susceptible to sensitivity issues during product analysis, due to challenges in product measurements at low current densities. Polycrystalline and nanostructured electrodes with the same geometrical area were commonly tested while the ECSA of the latter one can be one to several orders of magnitude larger. Since sensitivity of the product analysis scales with the ECSA of the electrodes, when the same electrochemical cell and operational parameters are used, these electrodes benefit from the higher sensitivity, particularly at low potentials. Dunwell et al. performed potential dependent product analysis with high sensitivity on planar polycrystalline Au and Ag electrodes at low overpotentials to compliment Tafel studies.17,18 It is important to highlight that Au and Ag electrodes are capable of producing CO at overpotentials that are comparable to high surface area electrodes. Many Au and Ag based electrocatalysts have been reported in the literature that have a variety of onset potentials ranging from −0.2 V vs. RHE to −0.6 V vs. RHE for the formation of CO.14,15,19 These discrepancies most likely result from the differences between the electrochemical cells, e.g. ratio of the headspace of the cell to ECSA area of the electrode, as well as the sensitivity of the employed analytical method for product identification. Since the roughness factor of the nanostructured electrodes varies between 10–3000, it is impractical to test a planar polycrystalline electrode with the same surface area. Therefore, observing lower onset potentials for CO2 electroreduction products on nanostructured electrodes compared to planar polycrystalline counterparts does not necessarily indicate more efficient (electro)catalysis.
3. Selectivity and stability
In electrocatalysis, the selectivity is often described in terms of faradaic efficiency (FE) or current efficiency, and this is one of the key metrics of CO2 electroreduction catalysts. However, the selectivity towards a particular product can be misleading as it indicates in most cases that selectivity towards a targeted product improves, when in fact the competing product may just be suppressed. Nanostructured electrodes, given their complex interaction with the surrounding electrolyte environment, are particularly susceptible to this effect.Such an effect can be commonly observed for the primary competing reaction for CO2 reduction, the hydrogen evolution reaction (HER). Although higher CO2 reduction selectivity resulting from hydrogen suppression has been recently pointed out in several papers,12,20 we would like discuss this phenomenon in more detail. Even though the major source of evolved hydrogen is water and/or buffer anions in neutral and alkaline medium, HER rates depend on the pH near metal electrodes.21,22 In addition to the apparent Nernstian shift in the recorded onset potentials (vs. NHE) as a function of pH, the kinetics of the reaction are known to be slower in alkaline medium.23 Moreover, the binding energy of *H, and subsequently HER rates, may be influenced by *CO on some metal electrodes in which there is a significant CO coverage during CO2 electroreduction.24 On the other hand, CO formation on gold and ethylene formation on copper are considered to take place via a pH-independent mechanism where electron and proton transfers are de-coupled.13,25 Therefore, the formation of these products is essentially blind to pH changes near the electrode surface, in contrast to hydrogen, unless the alkalinity leads to a drop in CO2 concentration. Therefore, an increase in the selectivity can be recorded regardless of whether the CO2 reduction performance has increased or not as result of suppression of the hydrogen evolution reaction. This is less of a problem when comparing electrodes with similar ECSA, although the thickness and the structure of the catalyst layer itself is very important.20,26,27 In other words, significant selectivity differences between the electrodes with the same roughness factors can be obtained depending on differences on the thickness of the catalytic layer and porous structure. When comparing electrocatalysts with substantially different ECSA, the selectivity then might be a very poor representative metric of the performance as a result of dramatic differences in local conditions.
Dunwell et al. measured the local pH near a chemically-deposited Au thin films during CO2 electroreduction by using in situ surface enhanced infrared spectroscopy (SEIRAS).28 The chemically deposited Au thin film (<100 nm) was composed of densely packed Au grains that is analogous to the electrode depicted in Fig. 1b. The measured pH was around 9 in a 0.5 M NaHCO3 solution at a current density of 5 mA cm−2. The corresponding potential needed to achieve this current density was around −0.9 V vs. RHE while the same (geometrical) current density was recorded on a porous gold electrode, which is depicted in Fig. 1c, at potentials closer to −0.4 V vs. RHE.10 Therefore it is not possible to compare two electrodes at the same geometrical current density when there is a considerable difference between the ECSA of the electrodes. In addition, even after assuming the ECSA normalized current densities are similar, the local conditions measured by SEIRAS in Au thin films cannot be quantitatively compared to the porous gold electrodes at the same potential due to large differences between the thickness of the catalyst layer. The differences in the nature of the mass transport towards a 2-D planar and 3-D porous electrode will be discussed in Section 5. In short, it is expected that the average local pH will be higher at the same potential on porous Au electrodes compared to their polycrystalline counterparts as a result of 2-D flux of species into the 3-D catalyst layer, even though the generation of OH− is more spatially-distributed within the catalyst layer. Therefore, HER could be surpassed at the same potential while the CO production rate is still the same or even lower.13,14,27 A catalyst is usually considered to be selective if it can reduce the kinetic barriers associated with the formation of a specific desired product, or increase barriers towards a competing unwanted reaction. Therefore, classifying an electrocatalyst as being selective in this case is open for discussion as the measured selectivity can be solely a result of local concentration effects and not due to changes in the intrinsic kinetics of the desired reaction(s).
While selectivity is one the most discussed performance metrics for CO2 electroreduction, the stability of the electrocatalysts is perhaps the least studied aspect of the electrode. Most stability tests reported in literature are limited to several hours, although it is one of the most important factors in terms of scalability of the technology. Nevertheless, short term tests on polycrystalline electrodes have revealed a significant loss of activity in a relatively short amount of time.1,10 In their first studies, Hori et al. attributed the short time of stability of electrocatalysts to the deposition of metal impurities present in the electrolyte that block active catalytic sites for CO2RR and instead promote hydrogen evolution. Nanostructured electrodes, with a very high electrochemically active surface area, could be considered less sensitive to this type of poisoning.26,29 This has been quantitatively depicted by Clark et al., where the ratio of active surface area and the volume of the electrolyte solution was shown to play a crucial role on the sensitivity towards metal impurity poisoning.20 It is important to note that Hori et al. explicitly state that a slower deactivation of copper electrodes in intensively cleaned electrolyte solutions still persists,29 an observation that also has been recorded on high surface area electrodes.26,30 Other poisoning mechanisms have been suggested to take place due to the formation of graphitic carbon from CO2 reduction intermediates.31 This type of poisoning could also be potential and product dependent, since nanostructured Cu electrodes have shown much better stability when C2 and C3 products are favored.11,32 The chemical identity and potential dependent formation of poisonous carbon species to date were not identified clearly. Ex situ or preferably in situ spectroscopic methods such as surface enhanced infrared and Raman spectroscopy might be necessary to elucidate the structure of the thin carbon layer formed on the electrode surface during electrolysis.33
Surface re-construction or changes in the morphology as a result of oxide reduction, dissolution and re-deposition might alter the selectivity towards CO2 reduction products or hydrogen.34,35 Further, the selectivity changes might occur at the very early stage of the electrolysis or can span hours.36,37 Therefore, depending on the product analysis intervals, it may not possible to record selectivity differences for rapid changes of the surface. Copper oxides are known to be reduced at cathodic potentials although a small amount of subsurface oxygen is considered to effect the catalytic performance.38 The reduction of copper oxides that are formed intentionally or naturally as a result of exposure to electrolyte lead to surfaces abundant of stepped sites on copper electrodes.39,40 The slow transformation of the stepped surfaces might be responsible for the deactivation of electrodes over longer periods of time. Similarly, nanostructured gold electrodes exhibited a slow decline in the geometrical current density.10 The decline in the current density was attributed to sintering of the porous structure which is supported by the roughness measurements before and after the electrolysis.
4. Activity and current density
The activity of heterogeneous electrocatalysts is usually expressed in terms of the measured current density at a specific applied potential, while turnover numbers or frequencies of CO2 electroreduction catalysts have been scarcely reported in the literature due to the unknown nature of the active sites. In the early days of CO2 reduction research, activity was discussed in terms of the potential dependent partial current density, which are typically normalized to the geometrical surface area. However, it is more insightful to compare the ECSA normalized current density in the same potential window that is free of mass transfer limitations for high surface area electrodes.12,20 The ECSA normalized activity of nanostructured Ag and Au electrodes suggests there is no significant differences in activity compared to their polycrystalline counterparts in the same potential range.20 However, these comparisons were made with mildly roughened electrodes (roughness factors ≈ 5–10), whereas the difference in the activity of the roughened and flat electrodes may not be enough to account for the effect of roughening. For example, Surendranath et al. systematically studied the effect of roughness by tuning the roughness factors up to 100 on mesostructured silver electrodes (Fig. 2a).14 They observed an almost linear correlation between the ECSA normalized activity of the electrodes and roughness, suggesting that CO2 electroreduction can be promoted while hydrogen evolution is suppressed by mesostructuring Ag electrodes. Similarly, Luan et al. reported the potential dependent activity of electrodes composed of densely packed Ag nanowires with diameters of 30 and 200 nm. The results of this study are shown in Fig. 2b along with a planar polycrystalline silver electrode.41 Notably, the ECSA normalized activity of the nanowire electrodes exhibited a 10–50 fold increase over a broad range of applied potentials in comparison to a planar polycrystalline silver electrode. Counterintuitively, the electrodes with a lower roughness factor exhibited higher specific activities at almost all applied potentials. Although this may suggest the existence of different active sites, it can be also the result of mass transfer limitations as the length of the nanowires were different. In addition, a 5–20 times higher specific activity was recorded from various high surface silver electrodes prepared via different methods.16,19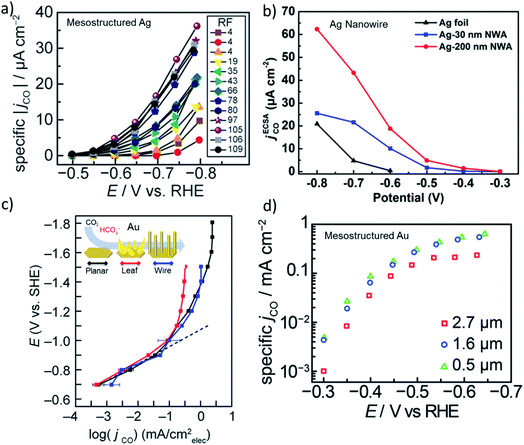 | ||
| Fig. 2 (a) ECSA normalized partial current density of CO evolution as a function of applied potential for mesostructured Ag films with varying roughness factors (RF). Reproduced from ref. 14 with permission from the WILEY-VCH Verlag GmbH & Co. KGaA, Winheim, copyright 2016. (b) ECSA normalized partial current density of CO evolution for nanowire arrays with 200 nm and 30 nm in diameter that are compared to flat polycrystalline Ag foil. Reproduced from ref. 41 with permission from the American Chemical Society, copyright 2018. (c) ECSA normalized partial current density of CO evolution as a function of potential for planar, leaf and wire gold electrodes. Reproduced from ref. 42 (https://pubs.acs.org/doi/abs/10.1021/acscentsci.9b00302) with permission from the American Chemical Society, copyright 2019. Further permissions related to the material excerpted should be directed to the ACS. (d) ECSA normalized partial current density of CO evolution for mesostructured gold electrodes as a function of potentials for three different thickness of the catalyst layer. Reproduced from ref. 13 with permission from the American Chemical Society, copyright 2015. | ||
While the ECSA normalized activity for Ag varies significantly for planar and nanostructured electrodes, nanostructured Au and Cu electrodes exhibited small variations in activity when compared to their polycrystalline planar counterparts. In Fig. 2c and d, the ECSA normalized current density of nanostructured and mesostructured Au electrodes are shown as a function of applied potential, respectively.13,42 The difference between the ECSA normalized area of the electrodes composed of Au leaves and wires were almost the same as the planar Au electrode, except within the mass transfer limited region. The differences in the plateau region most likely results from the thickness and density of the catalyst layer in addition to the differences between the bubble nucleation and release dynamics from the electrode surfaces. Similarly, a mesostructured Au electrode composed of spherical pores with 200 nm diameters exhibited no significant difference in activity as the thickness of the porous catalyst layer was increased from 0.5 μm to 2.7 μm (Fig. 2d).13 Interestingly, the thickest catalyst layer (2.7 μm) showed slightly lower activity at almost all potentials suggesting that the mass transfer effects were prominent in all the tested potentials. Even though the changes in the intrinsic activity of nanostructured and mesostructured gold electrodes were not found to be as significant as in the case of Ag electrodes, the difference might be the result of polycrystalline benchmark electrodes that are used for comparison. Experimental and theoretical studies on single crystal gold electrodes suggested that CO2 reduction takes place significantly faster, 10–20 times, on under-coordinated surfaces, when compared to closed-packed surfaces.43 Interestingly, polycrystalline gold electrodes exhibited similar intrinsic activity when compared to Au(110) and Au(211) single crystal surfaces implying that polycrystalline gold itself is abundant of open and/or stepped surfaces. Although the cleaning and pre-treatment of the polycrystalline electrode surfaces is most likely of key importance, the relative amount of under-coordinated sites on polycrystalline Au electrodes does not seem to be substantially different when compared to nanostructured Au electrodes.
Electrochemical CO2 reduction on copper electrodes has been thoroughly reviewed recently by Nitopi et al. and it was suggested that nanostructuring copper has no significant added value in the overall catalytic performance, based on the ECSA normalized activity.12 The ECSA normalized activity of a series of high surface area copper electrodes from the literature were plotted against each other, and the differences (2–4 fold increase) were regarded as insignificant. It is important to note that copper is the most susceptible electrode to mass transfer limitations among coinage metals, since the CO2 to hydrocarbon conversion takes place at relatively higher potentials (−0.6 V to −1.2 vs. RHE) along with an appreciable amount of hydrogen evolution,27 while high CO2 reduction activities on Au and Ag electrodes are typically seen at potentials between −0.2 and −0.8 V vs. RHE.44 While the activity at lower potentials may be similar for different ECSA catalysts, mass transport properties play a more substantial role at the current densities where hydrocarbons are formed.
5. Mass transport effects
5.1 Planar electrodes
The motion of a CO2 molecule within electrochemical CO2 reduction to CO which is illustrated in Fig. 3. This pathway in the system s composed of series of steps involving the dissolution, transport, adsorption and reaction of CO2. The adsorption of CO2 on the electrode surface most likely takes place simultaneously with the transfer of the first electron and/or proton transfer due to the high energy required to bend the CO2 molecule.45 The rates of the electrochemical CO2 reduction is usually limited by the electron transfer at low overpotentials while, at high potentials, the reaction rates are governed by the mass transfer of CO2 or protons to the electrode surface.12 The transition from activation controlled to purely mass transfer limited region is usually not very well defined in H-type of cells.17 Due to the low solubility of CO2 at ambient pressure and poor buffer actions, the potential window free of mass transfer limitations can be narrow. One of the well-known phenomena in the field is the increase of pH near the electrode surface which is a mass transfer problem regardless of whether protons are supplied by buffer anions or water reduction. In order to understand and link these effects to electrocatalytic performance, efforts to model mass transport of CO2 and electrolyte ions to the electrode surface have been performed in one dimension, removing the complexity of a nanostructured surface, as well as improving the resolution of species within pores.46–48 The reaction diffusion model is a system of partial differential equations based on the Nernst–Planck equation for the diffusion of the species from the electrolyte bulk fluid to the cathode's surface.46 The boundary conditions and initial values for these equations are given by the bulk equilibrium reactions involving CO2, water and buffer electrolytes and the electrochemical CO2 reduction rates, e.g. experimental current density. Convection is usually introduced in the form of boundary layer thickness for a constant stirring rate while migration term is often neglected.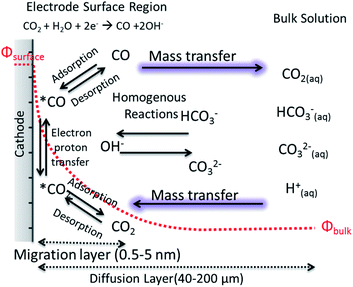 | ||
| Fig. 3 A schematic description for electrochemical CO2 reduction composed of electrode surface region, mass transport layer and bulk solution. | ||
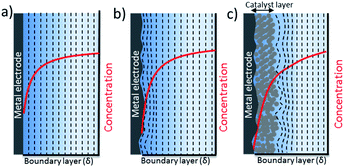
The nature of mass transport towards a planar surface is depicted schematically in Fig. 4a and b, along with the concentration gradients of species in the electrolyte, e.g. CO2(aq) and H+.49 On a nearly atomically flat surface, concentration gradients can be estimated as a planar diffusion wave front perpendicular to the surface, as long as the geometrical area of the electrodes is larger than the boundary layer thickness. When the electrodes are intentionally or unintentionally roughened, e.g. typically with a roughness factor ranging from 1 to 10, they exhibit a radial diffusion following the roughness of the electrode that eventually overlaps and gives rise to a planar diffusion front. These electrodes usually have higher local current densities that may cause higher concentration gradients between the electrode surface and bulk electrolyte. Since the surface roughness of a 2-D electrode is generally an order of magnitude smaller than the thickness of a mass transport diffusion layer (50–100 μm), a one dimensional reaction-diffusion model has proven to be sufficient to date for gaining a rough approximation of the average CO2 availability at the catalyst surface, and the removal of species to the bulk electrolyte as a function of electrolyte concentration. These analyses from simple reaction-diffusion models were largely responsible for initial discussions regarding the importance of local pH as a factor in determining CO2 reduction selectivity on copper. Nevertheless, a recent comparison of 1-D reaction diffusion models with physical operando measurements suggested the models can provide a reasonable estimation of the near surface concentration of molecules.27
5.2 Nanostructured electrodes
Due to the importance of surface area on electrocatalytic activity, ECSA normalized activity certainly offers the best opportunity to gain insights into the intrinsic activity of electrocatalysts compared to using the selectivity or current density normalized to an electrode's geometrical area. However, while the surface area of the catalyst can be increased through 3-dimensional changes in the electrode's morphology, the maximum flux of CO2 that can reach the electrode is confined to two dimensions by the planar geometry of electrochemical cells. The mass transport of CO2, buffer anions and protons to a nanostructured electrode surfaces is different from that of smooth or mildly roughened electrodes that are comparatively planar (e.g. 2-D). The complexities associated with the differences in transport to different parts of the electrocatalytic surface can lead to variable performances between catalysts that are hard to quantify, leading many researchers to state that observed differences in activity are a result of differences in intrinsic electrocatalytic activity.12When nanostructured or mesostructured electrodes composed of micro- and/or nanoporous 3-D catalyst layers are used, the boundary layer extends into the catalyst layer and both the mass transport outside and inside the pores needs to be considered, particularly as a function of current density (see Fig. 4c). Due to the highly dense and interconnected structure of porous electrodes, highly overlapped non-planar diffusion gradients merge to form a planar diffusion front outside the catalyst later. The mass transport outside the pores will be driven by diffusion, while convection in the system determines the thickness of diffusion layer and mixing of CO2 in the bulk electrolyte. Mass transport inside the pores will be driven mostly by diffusion and/or migration. The effects of nanostructuring on mass transport has been included in some 1-D models by extending the catalyst layer along the boundary layer,50 and accounting for how gas evolution from the surface can improve CO2 replenishment.51 Very recently, a 3-D mass transport model was developed for mesostructured electrodes which takes into account the interconnected porous structure of the electrode.52
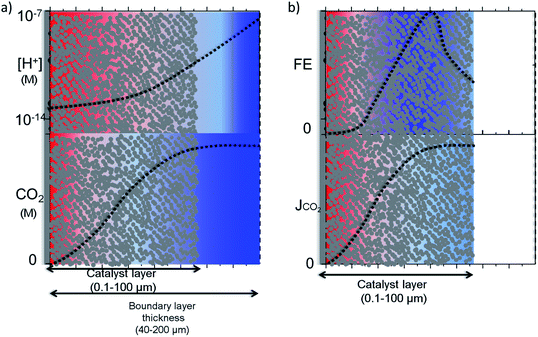
Raciti et al. simulated the mass transfer on Cu nanowires by using a 1-D model where the activity was varied along the nanowire in contrast to simulations performed on planar electrodes.50 In a more realistic 3-D model, Suter et al. modelled mesostructured Ag electrodes where the effect of pore size and thickness of the catalyst layer on the potential dependent activity were evaluated. Note that this simulation was performed under highly favourable mass transfer conditions, i.e. rotating disk electrodes, with a boundary layer thickness of ∼1 μm. In magnetically stirred or intensively bubbled electrolytes, the boundary layer thickness is usually larger than 40 μm and mass transfer limitations inside the pores might be more severe. 1-D and 3-D modelling results for nanostructured electrodes are schematically depicted in Fig. 5a and b, in the light of other experimental and theoretical studies.13,14,27,28,42,53 It is important to note that this is an idealization of the real system; in reality, the electrocatalysts most likely have a much more complex and heterogeneous concentration, activity and selectivity gradient along the catalyst layer. Fig. 5a illustrates a pH and CO2 concentration gradient along a porous catalyst layer, where the former is usually more dramatic due to the smaller diffusion coefficients of buffer anions. Although CO2 can still exist near the electrode surface when the local conditions are alkaline, due to the relatively slow reaction between OH− and CO2,28 the concentration gradient may be significant and only hydrogen might be produced at the bottom of the catalyst layer as the thickness of the catalyst layer is increased.50
The CO2 concentration and pH gradient along the catalyst layer is also likely to induce a selectivity distribution along the catalyst layer as a result of competing pH dependent and independent reactions (Fig. 5b). The distribution of the products along the catalyst layer might be more complex than what is depicted, especially for copper electrodes. For example, the selectivity of products formed via a pH dependent pathway, such as hydrogen and methane, is likely to be formed at a part of the catalyst closer to the electrolyte where the concentration gradient is lower.53 On the other hand, products formed via a pH independent pathway, such as ethylene and CO, will be affected mostly by CO2 gradients and have a higher selectivity inside the pores due to the suppression of hydrogen evolution unless the catalyst layer becomes too thick.50,54 From this understanding, the highest product selectivity will be obtained on an electrocatalyst with an optimal catalyst layer thickness that balances pH dependent and independent pathways. Specifically, a layer of sufficient thickness is needed to create an alkaline environment inside the pores, yet sufficiently thin to allow CO2 diffuse through the entire catalyst layer.52,54 Furthermore, stable intermediates such as CO, ethylene, and formaldehyde need to be transported away from the porous and nanostructured catalyst layer to be observed as a final product. Re-adsorption of these intermediates or reactions with adsorbed molecules via an Eley–Rideal type of mechanism is proposed to result in the production of more reduced compounds such as ethane and propanol,55–57 depending on the dimensions and structure of the pores. As a final caveat, the optimal thickness and geometry depends on the desired current density, as this also influences the delicate balance of species inside the nanostructure.
Transport effects on nanostructured and mesostructured electrodes have also been well recognized for different types of reactions such as the ORR as well as hydrogen, CO and methanol oxidation. Higher amounts of formaldehyde and formic acid were reported during methanol oxidation at low electrocatalyst loadings, while complete oxidation to CO2 was prominent at high catalyst loadings.58 Similarly, hydrogen peroxide yield was found to be affected dramatically by the coverage and density of Pt nanodisks on glassy carbon substrate during ORR to water.59 Similar trends were also observed in CO and ethanol oxidation.60,61
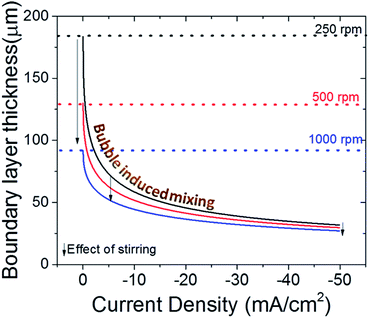
Recently, it has been recommended to measure the boundary layer thickness of the electrochemical cells by using an outer sphere redox reaction, e.g. ferricyanide reduction.20 Although this may help to compare the hydrodynamics of the cells used in different labs, it is necessary to point out that the evolving gas bubbles during CO2 electroreduction can have a significant impact on the boundary layer thickness, especially for high surface area electrodes.51,62 In Fig. 6, the effect of stirring on the boundary layer thickness is depicted with dashed lines and arrows for three different stirring speed. In addition, the effect of bubble formation on the boundary layer thickness is given as a function of current density for each stirring speed.51 In a well stirred electrochemical cell (1000 rpm), the bubbles can lower the thickness of the boundary layer to 2–3 times the initial value at elevated current densities, i.e. only with stirring and ignoring bubble formation. More importantly, at high currents, mass transport is governed by the bubble induced mixing, and the effect of stirring is much less prominent when compared to low currents (<20 mA cm−2) as depicted by the arrows in Fig. 6. However, it is important to note that this calculation does not take into account the effect of stirring on the removal of bubbles, which is particularly important for bubbles that have grown to a similar size as the boundary layer itself (50–100 μm). Nonetheless, the effect of bubbles in mass transport models are often overlooked despite their undeniable impact on transport,63,64 which may lead to underestimation of buffer capacity and account for some of the differences observed with experimental measurements and calculated local pH values.
Moreover, the morphology of the catalyst itself can induce large changes in the bubble nucleation and release dynamics and subsequently in the boundary layer thickness. For, instance, on gold and copper nanowires, a 4–5 fold increase in the mass transport limited current density has been observed in the same electrochemical cell when compared to planar polycrystalline surfaces.27,51,62 Since the morphology itself, in addition to the local current density, influences the mass transport, using an external redox couple may not be always quantitatively representative for the electrochemical conditions created during electrochemical CO2 reduction. Nevertheless, this could help to qualitatively compare the results and trends reported in different labs on planar electrodes and at lower current densities.
While a large number of papers discuss diffusive effects, migration effects are often assumed to be negligible in 1-D reaction-diffusion mass transport models on planar electrodes. Recent continuum modelling efforts, however, have indicated that the electrical double layer (EDL) might have a significant influence on the composition and physical properties of the reaction environment within the first few nanometres from the catalyst surface, including the pH.65 The length of the electrical double layer is dependent on how well the electric field on the surface is screened by the adsorbed molecules and ions. Therefore, it can be different for the electrodes where CO2 reduction takes place with high and low CO coverage, e.g. for copper and silver.
Moreover, the electrical double layer itself is also a factor influencing the total active catalytic surface area accessible to the reactive species.56,66 Smaller catalyst pore sizes, although leading to an enhanced interaction of the species in solution with the catalyst due to a higher residence time, can also result in exclusion of oppositely charged species or a flattening of the electric field profile leading to catalytically dead regions.67 In addition, the solution resistance in pores is inversely proportional to the pore size and will have a direct influence on the ability of reactants and products to move in and out of pores.68 Overall, the effect of migration on mass transport in an electrified porous medium is quite complicated and has not been discussed or reconciled in sufficient detail in the field of electrochemical CO2 reduction.69
5.3 Thin-film electrodes
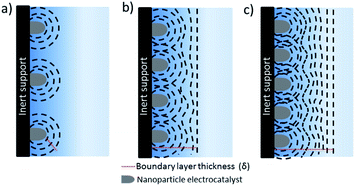
The separation between the nanostructure and thickness of the catalyst layer are of key importance to decouple mass transport effects from electrochemical reactions during the evaluation of intrinsic activity, selectivity and kinetic analysis of CO2 reduction electrocatalysts. Evaluation of intrinsic activity can be potentially achieved by loading of nanoparticles onto inert substrates by various methods such as spin coating, dip coating etc. to obtain uniform and thin films. This approach has been extensively used and studied for fuel cell reactions, yet up to date has relatively seldom been applied to CO2 electroreduction.7,70–72 When an inert support material, e.g. glassy carbon, is used, a radial concentration gradient is considered to form around each nanoparticle (see Fig. 7).73 As the interparticle distance is decreased, the individual diffusion spheres eventually overlap to form a planar diffusion front. At sufficiently high coverage and thickness, these electrodes are practically not very different than nanostructured electrodes. Although all of the electrodes eventually will reach mass transfer limitations at a sufficiently high reaction rate, e.g. at high current densities, the number density of nanoparticles and thickness of the catalyst layer determines the potential window that is free of mass transfer limitations. For instance, film thicknesses below 0.2 μm may avoid mass transfer limitations through the catalyst later for ORR,73,74 while CO2 electroreduction catalysts are often significantly thicker (0.1–100 μm). The critical thickness will depend on the catalyst morphology, e.g. pore size and distribution and hydrodynamics of the electrochemical cell.There are considerable efforts to synthesize size and shape controlled nanoparticles and test their CO2 electroreduction performance.75–78 The effects of nanoparticle size and shape have been reviewed and discussed elsewhere,72,79 here we only highlight the potential mass transfer effects that will affect the measured catalytic activities. Nanoparticles prepared by bottom-up methods are often deposited as thin films for electrochemical tests. In this approach, it is relatively easier to identify the structural changes taking place during electrolysis and mass transfer effects are less prominent when compared to nanostructured electrodes if sufficiently thin electrodes with low loadings are employed. However, the activities are sometimes reported as mass activity and/or geometrical current density which are usually not straightforward to compare between other type of electrodes. The mass activity is interesting to discuss for practical applications, especially for trying to reduce the loading of noble metals, however, it is not a useful metric for intrinsic activity unless the same type of nanoparticles are utilized. ECSA normalized current densities that are subtracted from the substrate activity, e.g. glassy carbon, enables the best comparison between nanoparticles having different size and shape.80–82 However, the loading of the nanoparticles should be high enough to allow for product analysis, while sufficiently thin to not suffer from mass transfer losses. For instance, Pt loadings on the order of 5–20 μg cm−2 are suggested for studying ORR. One advantage of ORR over CO2 reduction is that the recorded current density can be directly used as a measure of activity while product analysis techniques, that are typically much less sensitive than electrochemical methods, are required during CO2 reduction. Strasser and co-workers investigated the effect of nanoparticle density and loading on catalytic activity and selectivity of copper nanoparticles during CO2 electroreduction.83,84 The effect of local pH and re-adsorption of stable intermediates, e.g. CO, was considered to alter the selectivity as the inter-particle distance and nanoparticle density was systematically reduced. More importantly, the study allows for the decoupling of mass transfer effects from the intrinsic activity of nanoparticles at an inter-particle distance to particle size ratio larger than 10. In addition, Kim et al. revealed the importance of dissolution and re-deposition on the selectivity under cathodic potentials for copper nanoparticles on a carbon support.36 The structural changes during electrolysis lead to the formation of densely packed nanoparticles that alter the selectivity towards C2 and C3 products. One of the challenges in using this approach is that it requires a large ratio of electrode surface area to electrolyte volume to obtain enough sensitivity for liquid product analysis since the current density is typically low.
In light of this discussion, it would make sense to study electrocatalysts for CO2 reduction using a technique that allows for the decoupling of mass transfer effects from charge-transfer kinetics and (electro-)chemical kinetics. Rotating disk electrodes (RDE) are a common electrochemical tool that can be utilized for this purpose, as they allow for specific control of mass transfer at the electrode surface. For this reason, RDE has been extensively used to study the electrochemical kinetics of thin film electrodes for fuel cells reactions such as ORR, HOR and the oxidation of small organic molecules.7 However, using RDE for measurements during electrochemical CO2 reduction is challenging due to the requirement of gas product analysis. Gas product analysis is essential since the current density cannot be directly used as a metric of activity because of the broad product distribution of CO2 electroreduction and the competing hydrogen evolution reaction. Moreover, problems due to bubble accumulation on the electrode can arise when using rotating (ring) disk electrodes for gas evolving reactions, especially at lower rotation speeds.85 Recently, gastight RDE cells have been developed that either employ a gastight seal between the rotator and the cell,13,25,86 or use magnetic coupling to transfer the rotation from an external motor to a rotating shaft housed within the cell.87 These designs allow for in-line gas product analysis during experiments under mass transport control, which are essential to derive meaningful structure–property relationships for electrochemical CO2 reduction.
Due to the aforementioned issues, the amount of studies reporting on electrochemical CO2 reduction that have used hydrodynamic electroanalytical techniques, such as RDE, is surprisingly low. Surendranath et al. have employed rotating cone electrodes (RCE) to study the kinetics of electrochemical CO2 reduction on mesostructured gold and silver electrodes.13,14 In their work they show that the observed current densities during CO2 electroreduction are either not affected or surprisingly decreasing with increasing rotation speeds, while current densities during HER are increasing with increasing rotation speeds. On the basis of these observations, they conclude that CO2 reduction is far more resistant to mass transport limitations than HER. Mass transport effects due to depletion of CO2 near the electrode surface or inside the porous catalyst layer might have a significant effect on CO2 reduction rates if there is very limited convection.28
Finally, some studies have employed rotating ring disk electrodes (RRDE) to probe the electroreduction of CO2 under mass transfer controlled conditions.88–90 By employing this technique, products that are formed on the disk electrode can be detected on the ring electrode by electro-oxidation. Especially products such as CO and formic acid, that show distinct oxidation peaks, can be accurately measured. Since RRDE allows for fast detection of the formed products, this technique can serve as an alternative to RDE measurements coupled with gas product analysis, provided that the collection of products at the ring is facile and the oxidation of detected products on the ring electrode does not interfere with other reactions.
6. Conclusions
Nanostructured electrodes have been heavily investigated due to their the ability to significantly improve the activity and selectivity of electrochemical CO2 reduction at low overpotentials. However, the improvements on the onset potential and selectivity are very sensitive to process parameters and the local environment due to large differences between the ECSA of the nanostructured and benchmark planar electrodes. Therefore, potential dependent ECSA normalized activity plots currently provide the best metric for the comparison of electrocatalysts with different surface area and catalyst layer thickness, while. However, due to thick 3-D catalyst layer and highly dense interconnected structure, the ECSA normalized activity of nanostructured electrodes might be very vulnerable to mass transport effects. As the mass transfer limited and charge transfer limited region convolute, e.g. mixed control, the effect of mass transfer might be prominent in nearly all tested potentials that are much less negative than the plateau region especially for electrodes with 3-D thick catalyst layer. Both the kinetic parameters and ECSA normalized activity will be extracted at the presence of mass transfer effects as it is not easy to differentiate the mixed region unless controlled experiments are done. Therefore, ECSA normalized activity might be underestimated depending on the catalyst layer thickness especially for copper electrodes. Preparing thin film electrodes from nanoparticles that are synthesized by bottom up approaches, e.g. shape and size controlled nanoparticles, might allow decoupling the mass transfer effects from the measured activity. The challenges are the analytical sensitivity at low loadings of nanoparticles and gas tight RDE setups when compared to other gas phase chemical reactions in which the current density can be used as a metric for the activity.Despite the vulnerability of nanostructured electrodes to mass transfer limitations, ECSA normalized activity of nanostructured silver electrodes exhibited higher activity when compared to planar and polycrystalline silver during CO2 electroreduction in contrast to gold and copper. However, the differences between the coinage metals do not necessarily imply controlled faceting is only possible for silver electrodes. Instead, it can be result of the differences on benchmark polycrystalline electrodes, e.g. abundance in under-coordinated sites on smooth polycrystalline surfaces.
The mass transport towards a planar surface and nanostructured surface is essentially different due to differences in the catalyst layer thickness. However, mass transport models were so far usually limited to 1-D models which does not directly include the effects of nanostructuring except few recent studies. In addition, the effects of migration and bubbles are the two important parameters often overlooked in mass transport models. The changes in bubble nucleation and release dynamics as a result of high surface area and different morphology, can account for some differences in experimental and modelling studies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 759743 - WUTANG). We would like to thank MECS group members for fruitful discussions.References
- Y. i. Hori, in Modern aspects of electrochemistry, Springer, 2008, pp. 89–189 Search PubMed.
- D. M. Weekes, D. A. Salvatore, A. Reyes, A. Huang and C. P. Berlinguette, Acc. Chem. Res., 2018, 51, 910–918 CrossRef CAS PubMed.
- T. Burdyny and W. A. Smith, Energy Environ. Sci., 2019, 12, 1442–1453 RSC.
- D. Higgins, C. Hahn, C. Xiang, T. F. Jaramillo and A. Z. Weber, ACS Energy Lett., 2018, 4, 317–324 CrossRef.
- L.-C. Weng, A. T. Bell and A. Z. Weber, Energy Environ. Sci., 2019, 12, 1950–1968 RSC.
- F. Gloaguen, F. Andolfatto, R. Durand and P. Ozil, J. Appl. Electrochem., 1994, 24, 863–869 CrossRef CAS.
- C. Breitkopf and K. Swider-Lyons, Springer handbook of electrochemical energy, Springer, 2016 Search PubMed.
- T. Schmidt, H. Gasteiger, G. Stäb, P. Urban, D. Kolb and R. Behm, J. Electrochem. Soc., 1998, 145, 2354–2358 CrossRef CAS.
- H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Appl. Catal., B, 2005, 56, 9–35 CrossRef CAS.
- Y. Chen, C. W. Li and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 19969–19972 CrossRef CAS PubMed.
- C. W. Li and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 7231–7234 CrossRef CAS PubMed.
- S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. Stephens, K. Chan and C. Hahn, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS PubMed.
- A. S. Hall, Y. Yoon, A. Wuttig and Y. Surendranath, J. Am. Chem. Soc., 2015, 137, 14834–14837 CrossRef CAS PubMed.
- Y. Yoon, A. S. Hall and Y. Surendranath, Angew. Chem., Int. Ed., 2016, 55, 15282–15286 CrossRef CAS PubMed.
- Q. Lu, J. Rosen, Y. Zhou, G. S. Hutchings, Y. C. Kimmel, J. G. Chen and F. Jiao, Nat. Commun., 2014, 5, 3242 CrossRef PubMed.
- M. Ma, K. Liu, J. Shen, R. Kas and W. A. Smith, ACS Energy Lett., 2018, 3, 1301–1306 CrossRef CAS PubMed.
- M. Dunwell, W. Luc, Y. Yan, F. Jiao and B. Xu, ACS Catal., 2018, 8, 8121–8129 CrossRef CAS.
- M. Dunwell, Q. Lu, J. M. Heyes, J. Rosen, J. G. Chen, Y. Yan, F. Jiao and B. Xu, J. Am. Chem. Soc., 2017, 139, 3774–3783 CrossRef CAS PubMed.
- X. Peng, S. G. Karakalos and W. E. Mustain, ACS Appl. Mater. Interfaces, 2018, 10, 1734–1742 CrossRef CAS PubMed.
- E. L. Clark, J. Resasco, A. Landers, J. Lin, L.-T. Chung, A. Walton, C. Hahn, T. F. Jaramillo and A. T. Bell, ACS Catal., 2018, 8, 6560–6570 CrossRef CAS.
- J. Durst, A. Siebel, C. Simon, F. Hasche, J. Herranz and H. Gasteiger, Energy Environ. Sci., 2014, 7, 2255–2260 RSC.
- W. Sheng, Z. Zhuang, M. Gao, J. Zheng, J. G. Chen and Y. Yan, Nat. Commun., 2015, 6, 5848 CrossRef CAS PubMed.
- V. R. Stamenkovic, D. Strmcnik, P. P. Lopes and N. M. Markovic, Nat. Mater., 2017, 16, 57 CrossRef CAS PubMed.
- Y.-J. Zhang, V. Sethuraman, R. Michalsky and A. A. Peterson, ACS Catal., 2014, 4, 3742–3748 CrossRef CAS.
- A. Wuttig, M. Yaguchi, K. Motobayashi, M. Osawa and Y. Surendranath, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E4585–E4593 CrossRef CAS PubMed.
- R. Kas, R. Kortlever, H. Yılmaz, M. T. Koper and G. Mul, ChemElectroChem, 2015, 2, 354–358 CrossRef CAS.
- K. Yang, R. Kas and W. A. Smith, J. Am. Chem. Soc., 2019, 141(40), 15891–15900 CrossRef CAS PubMed.
- M. Dunwell, X. Yang, B. P. Setzler, J. Anibal, Y. Yan and B. Xu, ACS Catal., 2018, 8, 3999–4008 CrossRef CAS.
- Y. Hori, H. Konishi, T. Futamura, A. Murata, O. Koga, H. Sakurai and K. Oguma, Electrochim. Acta, 2005, 50, 5354–5369 CrossRef CAS.
- G. Kyriacou and A. Anagnostopoulos, J. Electroanal. Chem., 1992, 322, 233–246 CrossRef CAS.
- J.-F. Xie, Y.-X. Huang, W.-W. Li, X.-N. Song, L. Xiong and H.-Q. Yu, Electrochim. Acta, 2014, 139, 137–144 CrossRef CAS.
- M. Ma, K. Djanashvili and W. A. Smith, Angew. Chem., Int. Ed., 2016, 55, 6680–6684 CrossRef CAS PubMed.
- R. Kas, O. Ayemoba, N. J. Firet, J. Middelkoop, W. A. Smith and A. Cuesta, ChemPhysChem, 2019, 20(22), 2904–2925 CrossRef CAS PubMed.
- M. G. Kibria, C. T. Dinh, A. Seifitokaldani, P. De Luna, T. Burdyny, R. Quintero-Bermudez, M. B. Ross, O. S. Bushuyev, F. P. García de Arquer and P. Yang, Adv. Mater., 2018, 30, 1804867 CrossRef.
- P. De Luna, R. Quintero-Bermudez, C.-T. Dinh, M. B. Ross, O. S. Bushuyev, P. Todorović, T. Regier, S. O. Kelley, P. Yang and E. H. Sargent, Nat. Catal., 2018, 1, 103 CrossRef CAS.
- D. Kim, C. S. Kley, Y. Li and P. Yang, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10560–10565 CrossRef CAS.
- J. H. Baricuatro, Y.-G. Kim, C. L. Korzeniewski and M. P. Soriaga, Electrochem. Commun., 2018, 91, 1–4 CrossRef CAS.
- C. Liu, S. Hedström, J. H. Stenlid and L. G. Pettersson, J. Phys. Chem. C, 2019, 123, 4961–4968 CrossRef CAS.
- J. H. Baricuatro, Y.-G. Kim, C. F. Tsang, A. C. Javier, K. D. Cummins and J. C. Hemminger, J. Electroanal. Chem., 2019, 113704 CrossRef.
- C. F. Tsang, A. C. Javier, Y.-G. Kim, J. H. Baricuatro, K. D. Cummins, J. Kim, G. Jerkiewicz, J. C. Hemminger and M. P. Soriaga, J. Electrochem. Soc., 2018, 165, J3350–J3354 CrossRef CAS.
- C. Luan, Y. Shao, Q. Lu, S. Gao, K. Huang, H. Wu and K. Yao, ACS Appl. Mater. Interfaces, 2018, 10, 17950–17956 CrossRef CAS PubMed.
- B. A. Zhang, T. Ozel, J. S. Elias, C. Costentin and D. G. Nocera, ACS Cent. Sci., 2019, 5(6), 1097–1105 CrossRef CAS PubMed.
- S. Mezzavilla, S. Horch, I. E. Stephens, B. Seger and I. Chorkendorff, Angew. Chem., 2019, 131, 3814–3818 CrossRef.
- T. Zheng, K. Jiang and H. Wang, Adv. Mater., 2018, 30, 1802066 CrossRef PubMed.
- M. A. Scibioh and B. Viswanathan, Carbon Dioxide to Chemicals and Fuels, Elsevier, 2018 Search PubMed.
- N. Gupta, M. Gattrell and B. MacDougall, J. Appl. Electrochem., 2006, 36, 161–172 CrossRef CAS.
- J. Resasco, Y. Lum, E. Clark, J. Z. Zeledon and A. T. Bell, ChemElectroChem, 2018, 5, 1064–1072 CrossRef CAS.
- H. Hashiba, L.-C. Weng, Y. Chen, H. K. Sato, S. Yotsuhashi, C. Xiang and A. Z. Weber, J. Phys. Chem. C, 2018, 122, 3719–3726 CrossRef CAS.
- P. Kissinger and W. R. Heineman, Laboratory Techniques in Electroanalytical Chemistry, Revised and Expanded, Taylor & Francis, 2nd edn, 1996 Search PubMed.
- D. Raciti, M. Mao and C. Wang, Nanotechnology, 2017, 29, 044001 CrossRef PubMed.
- T. Burdyny, P. J. Graham, Y. Pang, C.-T. Dinh, M. Liu, E. H. Sargent and D. Sinton, ACS Sustainable Chem. Eng., 2017, 5, 4031–4040 CrossRef CAS.
- S. Suter and S. Haussener, Energy Environ. Sci., 2019, 12, 1668–1678 RSC.
- K. Klingan, T. Kottakkat, Z. P. Jovanov, S. Jiang, C. Pasquini, F. Scholten, P. Kubella, A. Bergmann, B. Roldan Cuenya and C. Roth, ChemSusChem, 2018, 11, 3449–3459 CrossRef CAS PubMed.
- D. Raciti, M. Mao, J. H. Park and C. Wang, Catal. Sci. Technol., 2018, 8, 2364–2369 RSC.
- R. Kas, R. Kortlever, A. Milbrat, M. T. Koper, G. Mul and J. Baltrusaitis, Phys. Chem. Chem. Phys., 2014, 16, 12194–12201 RSC.
- K. D. Yang, W. R. Ko, J. H. Lee, S. J. Kim, H. Lee, M. H. Lee and K. T. Nam, Angew. Chem., Int. Ed., 2017, 56, 796–800 CrossRef CAS PubMed.
- T.-T. Zhuang, Y. Pang, Z.-Q. Liang, Z. Wang, Y. Li, C.-S. Tan, J. Li, C. T. Dinh, P. De Luna and P.-L. Hsieh, Nat. Catal., 2018, 1, 946 CrossRef CAS.
- Y. Seidel, A. Schneider, Z. Jusys, B. Wickman, B. Kasemo and R. Behm, Langmuir, 2009, 26, 3569–3578 CrossRef PubMed.
- Y. Seidel, A. Schneider, Z. Jusys, B. Wickman, B. Kasemo and R. Behm, Faraday Discuss., 2009, 140, 167–184 RSC.
- H. Wang, Z. Jusys and R. Behm, J. Phys. Chem. B, 2004, 108, 19413–19424 CrossRef CAS.
- B. Wickman, Y. E. Seidel, Z. Jusys, B. Kasemo and R. J. Behm, ACS Nano, 2011, 5, 2547–2558 CrossRef CAS PubMed.
- A. Sacco, J. Zeng, K. Bejtka and A. Chiodoni, J. Catal., 2019, 372, 39–48 CrossRef CAS.
- M. S. Faber, R. Dziedzic, M. A. Lukowski, N. S. Kaiser, Q. Ding and S. Jin, J. Am. Chem. Soc., 2014, 136, 10053–10061 CrossRef CAS PubMed.
- C. A. Sequeira, D. M. Santos, B. Šljukić and L. Amaral, Braz. J. Phys., 2013, 43, 199–208 CrossRef CAS.
- D. Bohra, J. H. Chaudhry, T. Burdyny, E. A. Pidko and W. A. Smith, Energy Environ. Sci., 2019, 12, 3380–3389 RSC.
- H. Boo, S. Park, B. Ku, Y. Kim, J. H. Park, H. C. Kim and T. D. Chung, J. Am. Chem. Soc., 2004, 126, 4524–4525 CrossRef CAS PubMed.
- J.-H. Han, E. Lee, S. Park, R. Chang and T. D. Chung, J. Phys. Chem. C, 2010, 114, 9546–9553 CrossRef CAS.
- D. Mu, Z.-S. Liu, C. Huang and N. Djilali, Microfluid. Nanofluid., 2008, 4, 257–260 CrossRef.
- J. H. Bae, J.-H. Han and T. D. Chung, Phys. Chem. Chem. Phys., 2012, 14, 448–463 RSC.
- R. Kortlever, I. Peters, S. Koper and M. T. Koper, ACS Catal., 2015, 5, 3916–3923 CrossRef CAS.
- X. Min and M. W. Kanan, J. Am. Chem. Soc., 2015, 137, 4701–4708 CrossRef CAS PubMed.
- H. Mistry, A. S. Varela, S. Kuehl, P. Strasser and B. R. Cuenya, Nat. Rev. Mater., 2016, 1, 16009 CrossRef CAS.
- S. E. Kleijn, S. C. Lai, M. T. Koper and P. R. Unwin, Angew. Chem., Int. Ed., 2014, 53, 3558–3586 CrossRef CAS PubMed.
- K. Mayrhofer, D. Strmcnik, B. Blizanac, V. Stamenkovic, M. Arenz and N. Markovic, Electrochim. Acta, 2008, 53, 3181–3188 CrossRef CAS.
- W. Zhu, R. Michalsky, O. n. Metin, H. Lv, S. Guo, C. J. Wright, X. Sun, A. A. Peterson and S. Sun, J. Am. Chem. Soc., 2013, 135, 16833–16836 CrossRef CAS PubMed.
- W. Zhu, Y.-J. Zhang, H. Zhang, H. Lv, Q. Li, R. Michalsky, A. A. Peterson and S. Sun, J. Am. Chem. Soc., 2014, 136, 16132–16135 CrossRef CAS PubMed.
- K. Manthiram, B. J. Beberwyck and A. P. Alivisatos, J. Am. Chem. Soc., 2014, 136, 13319–13325 CrossRef CAS PubMed.
- H. Mistry, R. Reske, Z. Zeng, Z.-J. Zhao, J. Greeley, P. Strasser and B. R. Cuenya, J. Am. Chem. Soc., 2014, 136, 16473–16476 CrossRef CAS PubMed.
- R. M. Aran-Ais, D. Gao and B. Roldan Cuenya, Acc. Chem. Res., 2018, 51(11), 2906–2917 CrossRef CAS PubMed.
- R. Reske, H. Mistry, F. Behafarid, B. Roldan Cuenya and P. Strasser, J. Am. Chem. Soc., 2014, 136, 6978–6986 CrossRef CAS PubMed.
- A. Loiudice, P. Lobaccaro, E. A. Kamali, T. Thao, B. H. Huang, J. W. Ager and R. Buonsanti, Angew. Chem., Int. Ed., 2016, 55, 5789–5792 CrossRef CAS PubMed.
- P. Iyengar, J. Huang, G. L. De Gregorio, C. Gadiyar and R. Buonsanti, Chem. Commun., 2019, 55, 8796–8799 RSC.
- X. Wang, A. S. Varela, A. Bergmann, S. Kühl and P. Strasser, ChemSusChem, 2017, 10, 4642–4649 CrossRef CAS PubMed.
- H. Mistry, F. Behafarid, R. Reske, A. S. Varela, P. Strasser and B. Roldan Cuenya, ACS Catal., 2016, 6, 1075–1080 CrossRef CAS.
- J. Vos and M. Koper, J. Electroanal. Chem., 2018, 819, 260–268 CrossRef CAS.
- O. A. Baturina, Q. Lu, M. A. Padilla, L. Xin, W. Li, A. Serov, K. Artyushkova, P. Atanassov, F. Xu and A. Epshteyn, ACS Catal., 2014, 4, 3682–3695 CrossRef CAS.
- S. Jung, R. Kortlever, R. J. Jones, M. F. Lichterman, T. Agapie, C. C. McCrory and J. C. Peters, Anal. Chem., 2016, 89, 581–585 CrossRef PubMed.
- A. Wadas, I. Rutkowska, M. Bartel, S. Zoladek, K. Rajeshwar and P. Kulesza, Russ. J. Electrochem., 2017, 53, 1194–1203 CrossRef CAS.
- X. Zhu, K. Gupta, M. Bersani, J. A. Darr, P. R. Shearing and D. J. Brett, Electrochim. Acta, 2018, 283, 1037–1044 CrossRef CAS.
- J. Zhang, W. J. Pietro and A. Lever, J. Electroanal. Chem., 1996, 403, 93–100 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |