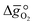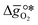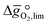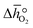Open Access Article
Open Access ArticleHigh redox performance of Y0.5Ba0.5CoO3−δ for thermochemical oxygen production and separation†
M.
Ezbiri
a,
A.
Reinhart
a,
B.
Huber
 a,
K. M.
Allen
a,
K. M.
Allen
 b,
A.
Steinfeld
b,
A.
Steinfeld
 a,
B.
Bulfin
a,
B.
Bulfin
 *a and
R.
Michalsky
*a and
R.
Michalsky
 *a
*a
aDepartment of Mechanical and Process Engineering, ETH Zürich, 8092 Zürich, Switzerland. E-mail: bulfinb@ethz.ch; michalskyr@ethz.ch
bSolar Technology Laboratory, Paul Scherrer Institute, 5232 Villigen, Switzerland
First published on 16th December 2019
Abstract
The efficient production and separation of oxygen is essential for numerous energy-intensive industrial applications in the fuel and mineral processing sectors. A thermochemical redox cycle is considered for separating oxygen from atmospheric air and other gas mixtures using solar or waste process heat. Based on electronic structure (DFT) computations Y0.5Ba0.5CoO3−δ is selected as a redox material, which surpasses the redox performance of state-of-the-art Cu2O. The thermochemical oxygen production is experimentally demonstrated by applying a temperature/pressure swing between 573 K at 0.2 bar O2 and 873 K at 1 bar O2. An energy balance shows the feasibility of using process waste heat from the solar thermochemical CO2/H2O splitting cycle and the potential to compete vis-a-vis with cryogenic distillation. Exploratory runs with a packed-bed reactor indicate the potential of both thermochemical oxygen production and separation for scale-up and industrial implementation.
1. Introduction
Oxygen generation/removal is required for fuel and mineral processing and is mainly carried out by cryogenic distillation.1–4 Other oxygen separation techniques include pressure swing adsorption using zeolites and carbon molecular sieves, and electrochemical separation using mixed ionic-electronic conducting membranes.1–5 These separation technologies require an electrical input between 100 and 350 kWh per metric ton of O2.2–6An interesting alternative route to oxygen separation can be achieved via a thermochemical process, using a metal oxide redox cycle.7–9 Heat can be used to drive the reduction of a metal oxide releasing oxygen. The reduced metal oxide can then absorb oxygen from a gas stream such as air. BOC Linde developed such a process, with a temperature and pressure swing thermochemical redox cycle suppling oxygen to an oxy-combustion process.10 This idea has been further developed in recent years, in particular in the search for new materials. For example, Cu2O/CuO,7,11 Mn3O4/Mn2O3,11 CoO/Co3O4 (ref. 11) and ABO3-type perovskites,8,12,13 have all been explored as redox pairs for oxygen separation and production processes.
Perovskites in particular appear to be very promising for this application, as they can exhibit rapid kinetics at relatively low temperatures,9 and the thermodynamics can be tuned to optimize the energetics of the process.13 The perovskite SrFeO3, and doped variants, can be considered the state of the art.9,10 However, cobalt based perovskites such as SrCoO3 appear to be more promising for lower temperature application, and they have the lowest energetic requirement in terms of the enthalpy change of the reduction reaction.8,13–15
In this paper, we consider both thermochemical oxygen separation (TOS) and thermochemical oxygen production (TOP) via redox cycles with a focus on perovskites with cobalt as the active redox ion. We apply electronic structure calculations on candidate redox materials and select La0.5Ba0.5CoO3−δ, Pr0.5Ba0.5CoO3−δ and Y0.5Ba0.5CoO3−δ for further experimental investigation of their O2 exchange capacity. We performed a comprehensive energy balance to show that the perovskite Y0.5Ba0.5CoO3−δ can be applied in TOS driven by solar or waste heat and compare the results to the state-of-the-art cryogenic distillation. We also consider the combination of this process with the solar-driven splitting of CO2 and H2O, which commonly uses an inert gas for the removal of oxygen.16–19 TOS can be used to recycle the inert gas, and waste heat from the solar fuel production can be integrated into the TOS processes. Furthermore, we conduct exploratory runs with a packed-bed reactor to elucidate the potential for scale-up and industrial implementation.
The TOS/TOP approach via 2-step redox reactions can be described by eqn (1a) and (1b) for generic perovskite with ABO3 stoichiometry, where A and B are metal cations in twelve- and six-coordinated interstices, δ is the oxygen nonstoichiometry and Δδ is the oxygen exchange capacity (Δδ = δred − δox):
Oxidation:
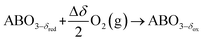 | (1a) |
Reduction:
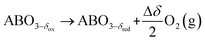 | (1b) |
2. Computational and experimental section
Electronic structure calculations
The grid-based projector-augmented wave (GPAW) code was employed for density functional theory (DFT) computations.19,20 Atomic configurations were handled in the atomic simulation environment (ASE),21 with exchange–correlation interactions treated by the revised Perdew–Burke–Ernzerhof (RPBE) functional.22 The optimizations of the atomic geometries were executed using the linesearch Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm until the maximum force was less than 0.05 eV Å−1. Convergence was achieved using a Fermi–Dirac smearing of 0.1 eV. The results were extrapolated to 0 K. The generalized gradient approximation (GGA) without a Hubbard U correction was used for all DFT calculations, in accordance to previous publications23–25 AA'BO3-type perovskites were modeled with A2B2O6 models containing a cubic ABO3 unit cell, with one metal (Ba, Pr, La and Y) at the twelve-coordinated A-site interstices and one metal (Co) at the six-coordinated B-site interstices. All atoms of the bulk models were allowed to optimize their positions (relax). The Brillouin zone of these bulk models having periodic boundary conditions in all directions was sampled with 4 × 4 × 4 k-points. All compositions were treated using spin-polarized calculations. The computed lattice constants are within ±1.6–2.6% of experimental values. The perovskite surfaces were modeled using the (010) facet with AO-termination, which is geometrically symmetric with the (001) and (100) facets dependent on composition, i.e. the thermodynamically most stable surface.26 The surface models contained the same number of atoms as the bulk models, i.e. stoichiometry A2B2O6, of which the upper ABO3 layer parallel to the surface was allowed to relax, while the lower layer was constrained to the bulk geometry. All surface structures were periodically repeated parallel to the surface, used 10 Å of vacuum perpendicular to the surface, and employed a k-point sampling of 4 × 4 × 1. To model reduced perovskite surfaces, one third of the stoichiometric lattice oxygen was removed from the upper surface layer, resulting in A2B2O5 models corresponding to δ = 0.5.The Gibbs free energy change of oxygen vacancy formation (ΔGV[O]) was computed by:26| ΔGV[O] = GV − (GS − GrO) | (2) |
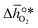 is the descriptor for the standard partial molar Gibbs free energy change of the metal oxide bulk reduction and oxidation,
is the descriptor for the standard partial molar Gibbs free energy change of the metal oxide bulk reduction and oxidation, 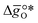 and
and 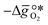 , respectively. Tabulated thermochemical data,27 available for a limited number of mostly stoichiometric metal oxides, was used to compute
, respectively. Tabulated thermochemical data,27 available for a limited number of mostly stoichiometric metal oxides, was used to compute 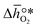 , based on previously reported scaling relations between
, based on previously reported scaling relations between 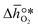 and ΔGV[O].26 The linear scaling relation utilized in this work is:
and ΔGV[O].26 The linear scaling relation utilized in this work is: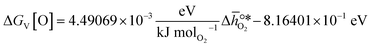 | (3) |
In this study, all thermodynamic properties are defined per mole of diatomic oxygen. Details on how the DFT-computed electronic energies were converted into Gibbs free energies at different temperatures and pO2, the reference energies, and details on the scaling relation26 are given in ESI.†
Perovskite synthesis – perovskites were synthesized with a modified Pechini method, employing stoichiometric amounts of La(NO3)3·H2O (Sigma Aldrich, 99.999%), Ba(NO3)2 (Alfa Aesar, 99%), Co(NO3)2·6 H2O (Sigma-Aldrich, ≥98%), Y(NO3)3·6 H2O (Aldrich Chemistry, 99.8%), Pr(NO3)3·6 H2O (Aldrich Chemistry, 99.9%), C2H6O (Alcosuisse, >96.1% vol) and C6H8O7 (Fluka Chemika, ≥99.5%). For the pellet production of La0.5Ba0.5CoO3−δ (LBCO), Pr0.5Ba0.5CoO3−δ (PBCO) and Y0.5Ba0.5CoO3−δ (YBCO), the solid products were ground using mortar and pestle, calcined at 1273 K in air for 5 hours using 5 K min−1 for heating and cooling and uniaxially pressed into pellets (5 metric tons, 8 mm in diameter). Granules of YBCO were manufactured by mixing the calcined powder with deflocculant agent (Dolapix CE 64, Zimmer & Schwartz) and deionized water. Granules (around 3 mm in diameter) of the resultant slurry were then pressed out of a syringe onto a platinum sheet and dried. LBCO and PBCO pellets were sintered in air at 1473 K for 5 h, while YBCO pellets, granules and calcined powder were sintered at 1323 K for 24 h. For all materials, a heating and cooling rate of 1 K min−1 was employed.
Solid-state analysis
Room-temperature X-ray diffraction (XRD) on YBCO, PBCO and LBCO and high-temperature XRD (HT-XRD) on YBCO were performed in the Bragg Brentano geometry using Cu Kα radiation (20–80° 2θ, 0.01° min−1 scan rate, 45 kV/20 mA output, PANalytical/X'Pert MPD/DY636, Philips). HT-XRD scans were executed between 308 and 923 K in 0.2 bar O2 in N2 during heating up and 0.01 bar O2 in Ar during cooling down using a platinum sheet as sample holder. Basic structural data of the room temperature measurement was obtained by multiphase Rietveld analysis (Jana2006). The morphology of pellets and granules was analyzed via scanning electron microscopy (SEM; HITACHI Tabletop Microscope TM-1000). Brunauer–Emmett Teller (BET, Micrometrics TriStar 3000 N2 absorption analyzer) measurements were performed to acquire information about the specific surface area of the YBCO granules. The BET results, XRD patterns and SEM images are presented in ESI.†Screening
PBCO, LBCO and YBCO were screened using thermogravimetric analysis (TGA) between 303 and 1273 K using +2 and −2 K min−1 in 0.2 bar O2 in N2 during heating and in 0.005 bar O2 in Ar during cooling. The slow heating and cooling rates were chosen to ensure thermodynamic equilibrium at all times. To correct for buoyancy, blank runs were performed using the same measurement conditions employed for the experimental runs.Thermodynamic analysis
The thermodynamic analysis was performed to extract the reduction enthalpy, Δhred, using the approach of Scheffe et al.:28 Oxygen release and uptake of a perovskite can generally be described as: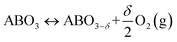 | (4) |
| K = (pO2)0.5 | (5) |
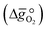 :
: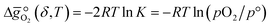 | (6) |
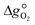 can further be derived from the standard partial molar enthalpy change of reduction,
can further be derived from the standard partial molar enthalpy change of reduction, 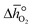 , and the standard partial molar entropy change of reduction,
, and the standard partial molar entropy change of reduction, 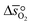 :
: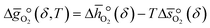 | (7) |
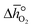 and
and 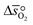 as a function of δ by determining the slope and intercept of −ln(pO2/p°) as a function of T−1 for a constant δ (cf.eqn (8)):
as a function of δ by determining the slope and intercept of −ln(pO2/p°) as a function of T−1 for a constant δ (cf.eqn (8)):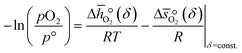 | (8) |
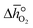 over the initial and final δ, we obtain the reduction enthalpy, Δhred (cf.eqn (9)). Δhred is directly related to the solar input required to drive the redox reaction.
over the initial and final δ, we obtain the reduction enthalpy, Δhred (cf.eqn (9)). Δhred is directly related to the solar input required to drive the redox reaction.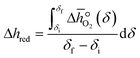 | (9) |
To determine Δhred, TGA measurements were conducted by heating up to 1073 K in 0.2 bar O2 in N2 and cooling down in 0.005, 0.01, 0.05 and 0.2 bar O2 in Ar, using slow rates of +2 K min−1 and −2 K min−1 to ensure thermodynamic equilibrium at all times (cf.Fig. 2).
Molar heat capacity measurements
The molar heat capacity (cp) of YBCO was measured with a heat flux differential scanning calorimetry (DSC, SENSYS evo DSC, Setaram). The sample, in the form of crushed pellet pieces with a total weight of 178.5 mg, was subjected to an Ar flow (99.998%, Carbagas) of 5 mL min−1 between 373 and 1073 K using a heating rate of +10 K min−1. To evaluate the measurement accuracy, we further acquired the cp of CeO2 and compared the result to previously published data29 (cf. Fig. S11†), revealing a discrepancy on average of only 1.94%. All experimental curves were fitted using the least-squares fitting method.Oxygen nonstoichiometry cycling measurements
Oxygen nonstoichiometry (δ) was measured using a thermogravimetric analyzer (TGA, STA 409/C/3, Netzsch). YBCO granules (112 mg) were placed on a platinum crucible supported with an Al2O3 rod on the microbalance of the TGA (±0.1 μg). The granules were thereafter exposed to a gas flow (constant flow rate of 200 mL min−1) with specified pO2 that was adjusted via mixing O2 (99.5%, Messer) and N2 (99.999%, Carbagas) using three electronic mass flow controllers (MFC, MFC400, Netzsch; accuracy ±1%, precision ±1 mL min−1). For the TOS process, the mass change of the granules was recorded during 38 consecutive redox cycles at 773 K and 0.2 bar O2 in N2 for reduction and 563 K and 0.01 bar O2 in Ar for oxidation using +20 K min−1 and −20 K min−1, respectively. For the TOP process, the mass change of the samples was recorded during 50 consecutive redox cycles at 873 K and 1 bar O2 for reduction and 573 K and pO2 and 0.2 bar O2 in N2 for oxidation using +20 K min−1 and −20 K min−1, respectively. To correct for buoyancy, blank runs were performed using the same measurement conditions employed for the experimental runs.Packed bed reactor experiments
YBCO was tested in a packed bed reactor (PBR) setup, in accordance to previous experimental campaigns investigating gas–solid reactions.7 PBR experiments for the TOS process were performed with a vertically inserted quartz tube with a diameter of 1 cm in an electric furnace (Carbolite, VS 17/250). Gas flows were introduced from the bottom at 20 mL min−1 and controlled using two electronic MFC (EL-Flow Select, Bronkhorst; accuracy ±0.5%). The oxygen concentration in the outlet gas flow was monitored by gas chromatography (GC, Agilent Micro GC, CP-4900). Two K-type thermocouples were inserted in the packed bed. From the bottom to the top, the reactor bed consisted of approximately 2 cm of compressed Al2O3 wool, 0.5 cm quartz sand with a diameter of 200–300 μm, 15 cm YBCO powder (8 g) mixed with quartz sand (16 g) and 1 cm pure quartz sand on top. A total of 15 consecutive cycles were executed. Reduction was always performed at 773 K and 0.2 bar O2 in N2 and held isothermally for 45 min. 30 min prior to cooling down, 0.2 bar O2 in N2 was exchanged to 0.01 bar O2 to ensure full gas replacement in the PBR. Oxidation was performed in 0.01 bar O2 at 563 K (cycles 1–4, 240 min isothermal), 523 K (cycles 5–7, 300 min isothermal), 603 K (cycles 8–12, 180 min isothermal) and 643 K (cycles 13–15, 180 min isothermal). 15 min prior to heating up to 773 K, 0.01 bar O2 in Ar was exchanged to 0.2 bar O2 in N2 to ensure full gas replacement.For the TOP process an Inconel tube with a diameter of 1 cm in an electric furnace (Carbolite, VS 17/250) was employed. Gas flows were introduced from the bottom. Oxidation was performed at 5 mL min−1, 0.2 bar O2 in N2 and 573 K during 240 min, while reduction was done at 10 mL min−1, 873 K and 1 bar O2 during 160 min. 60 and 30 min prior to cooling down from 873 to 573 K and prior to heating up from 573 to 873 K, respectively, respective gases were exchanged to ensure full gas replacement within the PBR. The oxygen concentration and gas flows were monitored by GC (Agilent Micro GC, CP-4900) and two electronic MFCs (EL-Flow Select, Bronkhorst; accuracy ±0.5%), respectively. An additional MFC (F-201CV, Bronkhorst; accuracy ±0.5%) was used to record absolute gas flows at the outlet of the PBR. Two K-type thermocouples were inserted in the packed bed. From the bottom to the top, the reactor bed consisted of approximately 2 cm of compressed Al2O3 wool, 0.5 cm quartz sand with a diameter of 200–300 μm, 13 cm YBCO granules (9 g) and 1 cm pure quartz sand on top. A total of 9 consecutive cycles were executed.
3. Results and discussion
Materials design
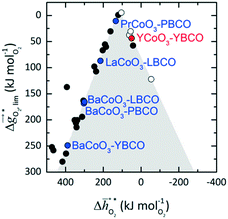
It was previously shown that metal oxide redox materials can be designed by plotting the limiting partial molar Gibbs free energy,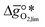 as a function of the descriptor
as a function of the descriptor 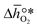 , i.e. the partial molar enthalpy at room temperature.8,26 The limiting Gibbs free energy
, i.e. the partial molar enthalpy at room temperature.8,26 The limiting Gibbs free energy 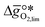 is defined as the larger Gibbs free energy change of either the reduction or oxidation reaction at the conditions to be used in the process. In other words, it is Gibbs free energy change of the reaction step, either oxidation or reduction, which is limiting the overall redox process. Here,
is defined as the larger Gibbs free energy change of either the reduction or oxidation reaction at the conditions to be used in the process. In other words, it is Gibbs free energy change of the reaction step, either oxidation or reduction, which is limiting the overall redox process. Here, 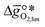 and
and 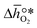 were computed for 32 solid metal oxides and six metal/metal oxide pairs at 563 K and 0.01 bar O2 for oxidation and 773 K and 0.2 bar O2 for reduction. Fig. 1 shows
were computed for 32 solid metal oxides and six metal/metal oxide pairs at 563 K and 0.01 bar O2 for oxidation and 773 K and 0.2 bar O2 for reduction. Fig. 1 shows 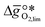 as a function of
as a function of 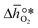 near the intersection of
near the intersection of 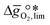 . Compounds with balanced, and thus favourable, redox behaviour are located near the top of the resulting volcano-shaped curve, i.e. they bind oxygen strongly enough at lower temperatures, but weakly enough to be reduced at moderately higher temperatures. Hence, the separation of oxygen from gas mixtures with a lower pO2 than the pO2 during the metal oxide reduction can be characterized by an intermediately strong bonding of the lattice oxygen.8 Ideally,
. Compounds with balanced, and thus favourable, redox behaviour are located near the top of the resulting volcano-shaped curve, i.e. they bind oxygen strongly enough at lower temperatures, but weakly enough to be reduced at moderately higher temperatures. Hence, the separation of oxygen from gas mixtures with a lower pO2 than the pO2 during the metal oxide reduction can be characterized by an intermediately strong bonding of the lattice oxygen.8 Ideally, 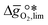 is exergonic, which is only reached by RhO/Rh2O and PbO/Pb3O4, rare and toxic materials, respectively. Various perovskite compositions, including LBCO, PBCO and YBCO, were therefore computed to tailor inexpensive and non-toxic redox materials (cf.Fig. 1), by modelling stoichiometric ABO3(010) and oxygen-deficient ABO2.5(010) with the grid-based projector-augmented wave (GPAW) and atomic simulation environment (ASE) electronic-structure code.19–21
is exergonic, which is only reached by RhO/Rh2O and PbO/Pb3O4, rare and toxic materials, respectively. Various perovskite compositions, including LBCO, PBCO and YBCO, were therefore computed to tailor inexpensive and non-toxic redox materials (cf.Fig. 1), by modelling stoichiometric ABO3(010) and oxygen-deficient ABO2.5(010) with the grid-based projector-augmented wave (GPAW) and atomic simulation environment (ASE) electronic-structure code.19–21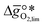 and
and 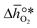 were then calculated from the scaling of ΔGV[O] and the redox energetics of the bulk oxides (cf. ESI†).8,26,30 The surface layer of each AA'BO3-type perovskite is ideally composed of either ACoO3 or A'CoO3. Fig. 1 displays the results of both possibilities, i.e. BaCoO3–YBCO denotes that for YBCO, BaCoO3 is on the surface. Interestingly, YCoO3–YBCO is the only composition for which oxidation is the limiting reaction.
were then calculated from the scaling of ΔGV[O] and the redox energetics of the bulk oxides (cf. ESI†).8,26,30 The surface layer of each AA'BO3-type perovskite is ideally composed of either ACoO3 or A'CoO3. Fig. 1 displays the results of both possibilities, i.e. BaCoO3–YBCO denotes that for YBCO, BaCoO3 is on the surface. Interestingly, YCoO3–YBCO is the only composition for which oxidation is the limiting reaction.
To verify the DFT-predicted trends and find a suitable material for thermochemical redox processes, LBCO, PBCO and YBCO were tested experimentally at different sets of redox conditions, presented in the next subsections.
Structural characterization
Fig. S1† displays the XRD spectra of sintered LBCO, PBCO and YBCO which were all identified to be in the perovskite-type structure. While LBCO was determined to be cubic, PBCO and YBCO revealed a tetragonal structure (cf.Table 1). From the XRD scans we see that decreasing ionic radii of the A-site dopants (La3+ > Pr3+ > Y3+), result in increasing structural lattice distortions along with a shift towards higher 2θ angles (cf. Fig. S1†).31 Detected impurities originate from BaO in PBCO and from Y2O3 and YBaCo2O5 in YBCO.Furthermore, the high-temperature XRD (HT-XRD) scans YBCO shown with Fig. S3† illustrate that this compound stays stable throughout the whole temperature range between 308 and 923 K in 0.2 and 0.01 bar O2 during heating and cooling, respectively.
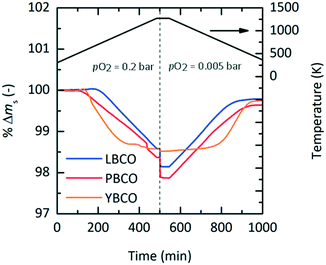
Experimental screening
To investigate the established redox trends by DFT, TGA experiments were conducted with LBCO, PBCO and YBCO between 303 and 1273 K (cf.Fig. 2). A pO2 of 0.2 bar was chosen during heating, while 0.005 bar O2 was taken during cooling. Heating and cooling rates were both set to a low value of +2 K min−1 and −2 K min−1 such that thermodynamic equilibrium at all times can be assumed. We see that the three compositions all reduce and oxidize, with PBCO reaching the largest reduction extent.To evaluate which of the three materials performs best, several performance indicators based on the experiments shown with Fig. 2 were applied (cf.Table 2). Tred,start corresponds to the temperature at which the perovskites start to reduce, δend,reox corresponds to the final oxygen nonstoichiometry of the reoxidized state and Tnet,eq corresponds to the temperature that has to be exceeded during reduction to achieve a net Δδ (cf. Fig. S6†). The relative oxygen nonstoichiometries can be calculated from the data shown with Fig. 2 with:
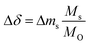 | (10) |
| T red,start (K) | Red. slope (μmol K−1) | Reox. slope (μmolO K−1) | δ end,reox (molO molABO3−1) | T net,eq (K) | |
|---|---|---|---|---|---|
| LBCO | 692 | 396 | 409 | 0.034 | 811 |
| PBCO | 530 | 313 | 373 | 0.055 | 725 |
| YBCO | 582 | 541 | 565 | 0.035 | 633 |
In summary, an ideal material for TOS has a low Tnet,eq, resulting from a low Tred,start and steep reduction and reoxidation slopes, i.e. fast reaction rates. Thus, the results suggest that YBCO is the most promising material from the three tested perovskites, having a Tnet,eq of only 633 K (cf.Table 2).
The following two sections focus on experiments performed for thermochemical oxygen separation and production using YBCO at different sets of redox conditions, summarized in Table 7.
Thermodynamic analysis
In this section, we report the acquisition of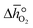 and Δhred (cf.eqn (8) and (9)). Δhred is directly related to the energy input required to drive the redox reaction,28 and is thus crucial to establish an energy balance. Fig. 3a shows the Δδ of YBCO at 0.005 bar O2, 0.01 bar O2, 0.05 bar O2 and 0.2 bar O2 between 400 and 1073 K. As expected, we see that a higher pO2 shifts the thermodynamic equilibrium towards higher oxygen nonstoichiometries, i.e. lower reduction extents. The relative non-stoichiometry values Δδ can also be seen to converge towards a maximum reduction extent of around Δδ = 0.2 molO molABO3−1, for all oxygen partial pressures.
and Δhred (cf.eqn (8) and (9)). Δhred is directly related to the energy input required to drive the redox reaction,28 and is thus crucial to establish an energy balance. Fig. 3a shows the Δδ of YBCO at 0.005 bar O2, 0.01 bar O2, 0.05 bar O2 and 0.2 bar O2 between 400 and 1073 K. As expected, we see that a higher pO2 shifts the thermodynamic equilibrium towards higher oxygen nonstoichiometries, i.e. lower reduction extents. The relative non-stoichiometry values Δδ can also be seen to converge towards a maximum reduction extent of around Δδ = 0.2 molO molABO3−1, for all oxygen partial pressures.
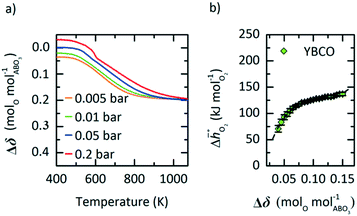 | ||
Fig. 3 a) Oxygen nonstoichiometry, δ, vs. temperature during reoxidation of YBCO at 0.005, 0.01, 0.05 and 0.2 bar O2, and b) standard partial molar enthalpy change of reduction,  , as a function of δ for YBCO. Error bars are ±2σ confidence intervals of the slope of −ln(pO2/p°) versus T−1 (cf. Fig. S7†). , as a function of δ for YBCO. Error bars are ±2σ confidence intervals of the slope of −ln(pO2/p°) versus T−1 (cf. Fig. S7†). | ||
To explain this maximum Δδ, we need to consider the possible reduction pathways of the perovskite. Yttrium will always remain in a 3+ oxidation state, and barium in a 2+ state. The fully oxidised perovskite would then have oxidation states Y0.53+ Ba0.52+ Co0.53+ Co0.54+ O32−, which could be considered as a solid solution of the two perovskites YCoO3 and BaCoO3. The formation of oxygen vacancies could then take place by the reduction of Co4+ to Co3+, or Co3+ to Co2+. DFT calculations of YCoO3 reduction performed by the authors suggest an enthalpy of reduction of 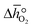 .25 This is much larger than the experimental values measured here (Fig. 3b) and also means that reduction of the perovskite via Co3+ to Co2+, would require higher temperatures. Indeed, experimental results obtained by Mei et al. for the reduction of LaCoO3−δvia Co3+ to Co2+ transitions show only very small non-stoichiometry of δ < 0.001, for the most reducing conditions seen in Fig. 3a) of T = 1073 K and pO2 = 0.005 bar. On the other hand, reduction via Co4+ to Co3+ occurs readily at low temperatures in SrCoO3,8 and other perovskites containing Co4+.14 Additionally, these Co4+ perovskites exhibit non-stoicheometry even at ambient conditions when cooled under air, which explains the positive values of Δδ seen in Fig. 3a. It is therefore likely that the majority of the reduction takes place via Co4+ to Co3+ transitions. The value of Δδ ≈ 0.2 that the nonstoicheometry converges towards could then correspond to complete reduction of Co4+ to Co3+ giving a reduced perovskite with a stoichiometry of Y0.5Ba0.5CoO2.75. This would mean that the zero point in Fig. 3a is Y0.5Ba0.5CoO2.95, but as their may be some reduction of Co3+, we cannot with certainty state the exact stoichiometry.
.25 This is much larger than the experimental values measured here (Fig. 3b) and also means that reduction of the perovskite via Co3+ to Co2+, would require higher temperatures. Indeed, experimental results obtained by Mei et al. for the reduction of LaCoO3−δvia Co3+ to Co2+ transitions show only very small non-stoichiometry of δ < 0.001, for the most reducing conditions seen in Fig. 3a) of T = 1073 K and pO2 = 0.005 bar. On the other hand, reduction via Co4+ to Co3+ occurs readily at low temperatures in SrCoO3,8 and other perovskites containing Co4+.14 Additionally, these Co4+ perovskites exhibit non-stoicheometry even at ambient conditions when cooled under air, which explains the positive values of Δδ seen in Fig. 3a. It is therefore likely that the majority of the reduction takes place via Co4+ to Co3+ transitions. The value of Δδ ≈ 0.2 that the nonstoicheometry converges towards could then correspond to complete reduction of Co4+ to Co3+ giving a reduced perovskite with a stoichiometry of Y0.5Ba0.5CoO2.75. This would mean that the zero point in Fig. 3a is Y0.5Ba0.5CoO2.95, but as their may be some reduction of Co3+, we cannot with certainty state the exact stoichiometry.
From the data shown with Fig. 3a, S7† and eqn (8), 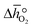 was deduced (cf.Fig. 3b). The good linear fit of the data shown with Fig. S7† (R2 > 0.94) confirms that
was deduced (cf.Fig. 3b). The good linear fit of the data shown with Fig. S7† (R2 > 0.94) confirms that 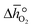 does not have strong dependence on temperature at the investigated conditions. Fig. 3b shows increasing
does not have strong dependence on temperature at the investigated conditions. Fig. 3b shows increasing 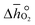 with increasing δ values, as observed by Babiniec et al.35 for LaxSr1−xCoyM1−yO3−δ (M = Mn, Fe) and Takacs et al.36 for La0.6M0.4MnO3−δ (M = Sr, Ca). The data in Fig. 3a may be kinetically limited at lower temperatures (T < 600 K), so that the Van't Hoff method may not be accurate in this region. The steep drop in Fig. 3b at lower Δδ < 0.07, may be a result of this. Symbols correspond to the measured δ values shown with Fig. 3, while the dashed line corresponds to a third-degree fit (R2 > 0.99). Error bars are ±2σ confidence intervals of the slope of −ln(pO2/p°) versus T−1 (cf. Fig. S7†).
with increasing δ values, as observed by Babiniec et al.35 for LaxSr1−xCoyM1−yO3−δ (M = Mn, Fe) and Takacs et al.36 for La0.6M0.4MnO3−δ (M = Sr, Ca). The data in Fig. 3a may be kinetically limited at lower temperatures (T < 600 K), so that the Van't Hoff method may not be accurate in this region. The steep drop in Fig. 3b at lower Δδ < 0.07, may be a result of this. Symbols correspond to the measured δ values shown with Fig. 3, while the dashed line corresponds to a third-degree fit (R2 > 0.99). Error bars are ±2σ confidence intervals of the slope of −ln(pO2/p°) versus T−1 (cf. Fig. S7†).
Applying eqn (9) to the result shown with Fig. 3b, we obtain a reduction enthalpy change of Δhred = 121 kJ molO2−1 for YBCO at a Δδ of 0.064 molO molABO3−1.
Thermochemical oxygen separation
In the following sections we present results for a TOS processes using YBCO, including an energy balance, cycle stability runs in the TGA, and a packed bed reactor demonstration.Energy balance
Using Δhred and measured cp (cf. Fig. S10†) of YBCO, an energy flow diagram for a redox cycle separating oxygen from a 1% O2–Ar stream is depicted in Fig. 4. The energy requirement per mole of O2, Δhcycle, is calculated from the thermodynamic data of YBCO. cp values of gas mixtures are approximated using the pure component properties obtained from NIST-JANAF tables.37 Assumed temperature/pressure-swing operating conditions are 773 K and 0.2 bar O2 for reduction and 563 K and 0.01 bar O2 for oxidation. The choice of these conditions was made based on the knowledge acquired by the thermodynamic assessment (cf.Fig. 3). All involved equations used for the calculations of the different components are shown in ESI.† According to the net energy balance (cf.Fig. 4), the required energy to separate O2 from a 1% O2–Ar gas stream amounts to 1.82 MJth molO2−1, while 1.83 MJ molO2−1is available in form of sensible heat from gas and solid heat exchange. In the present study, TOS is considered for the cleaning of the outlet stream from a solar reactor, which can be assumed to be at around 1273 K at the currently employed solar reactor conditions with the state-of-the-art material CeO2.38 This heat can be directly extracted in the TOS redox cycle using a printed-circuit heat exchanger, achieving an effectiveness of up to 97%.39 The extractable sensible heat (Δhavail) is considered as the sensible heat of the 1% O2–Ar gas mixture between 1273 and 563 K and it amounts to 1.48 MJ molO2−1. In this scenario, no heating of the incoming 1% O2–Ar gas mixture is necessary (Δhhg = 0) and thus, Δhcycle is 1.28 MJ molO2−1. Table 3 summarizes the energy requirements, assuming 50% solid and 80% gas heat recuperations and no heat recuperation at all, for O2–Ar gas mixtures of 0.005, 0.01 and 0.05 bar O2 coming from a solar reactor at 1273 K. We see from Table 3 that with 0.005 and 0.01 bar O2, Δhavail > Δhcycle. With 0.05 bar O2, Δhavail < Δhcycle when no gas and solid heat recuperation is applied. This is the only tested scenario where an additional energy input would be necessary to run the process. Oxidation at 0.05 bar O2 is more energy intensive than in case of lower pO2 values, because of the larger amount of reactive material to be heated. At high pO2 values, a higher quantity of oxygen has to be separated per redox cycle. This has a significant impact on the energy needed to heat the solid, Δhhs, which increases from 334 and 668 to 3342 kJ molO2−1 for 0.005 and 0.01 to 0.05 bar O2, respectively. The larger Δδ at higher pO2 values, i.e. here it increases from 0.053 and 0.064 to 0.090 molO molABO3−1 upon changing from 0.005 and 0.01 to 0.05 bar O2, respectively, cannot compensate for the increased Δhhs. Furthermore, the energy needed to heat the air, Δhha, increases from 77 and 153 to 767 kJ molO2−1for 0.005 and 0.01 to 0.05 bar O2, respectively, since the required molar amount of air is roughly half the molar amount of perovskite, according to Hänchen et al.7 Δhavail at 0.05 bar O2 increases slightly compared to 0.01 and 0.005 bar O2, because the cp of O2 (29.4 J mol K−1) is larger than theone of Ar (20.8 J mol K−1). Summarizing, the energy balance is favored at rather low pO2 and heat recuperation is essential at high pO2. However, at low pO2 oxidation rates are expected to decrease.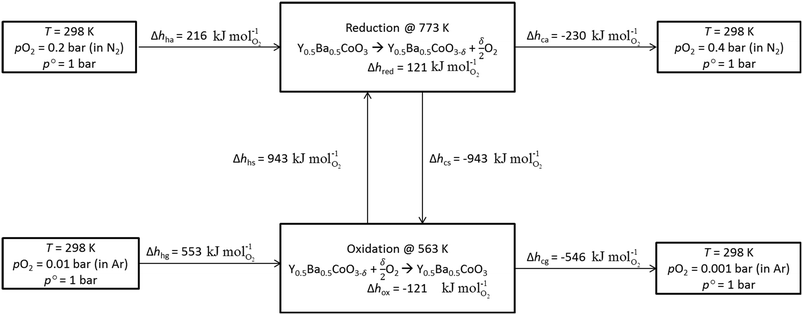 | ||
| Fig. 4 Energy balance of TOS via redox cycle using YBCO at 773 K and 0.2 bar O2 during reduction and 563 K and 0.01 bar O2 during oxidation. | ||
 is used in case of 50% solid and 80% gas heat recuperation
is used in case of 50% solid and 80% gas heat recuperation
| pO2 (bar) | %-Fraction of heat recovered (−) | Δhcycle (kJ molO2−1) | Δhavail (kJ molO2−1) | |
|---|---|---|---|---|
| From solids | From gas | |||
| 0.005 | 0 | 0 | 828 | 1480 |
| 0.005 | 50 | 80 | −107 | 1480 |
| 0.01 | 0 | 0 | 1280 | 1483 |
| 0.01 | 50 | 80 | 91 | 1483 |
| 0.05 | 0 | 0 | 4217 | 1507 |
| 0.05 | 50 | 80 | 1371 | 1507 |
Thermochemical cycling experiments for TOS
To verify if YBCO is suitable in an industrial implementation, porous granules were produced according to the procedure described in the experimental section. Production of the granules was much more efficient than pellet production, while still having a diameter large enough to avoid significant channelling effects and pressure drops if employed in a PBR. Fig. 5 shows the Δδ of YBCO granules cycled 38 times in a TGA between 563 K and 0.01 bar O2 during oxidation and 773 K and 0.2 bar O2 during reduction. We see that Δδ stays stable throughout all executed cycles, reaching values of around 0.061 molO molABO3−1. It is assumed that the slightly lower value of 0.061 vs. 0.064 molO molABO3−1, observed with the pellets (cf.Fig. 3), might originate from the two additional small XRD peaks around 28° (indexed by *, cf. Fig. S2†), which might be due to an ordering of excess oxygen forming a superstructure.40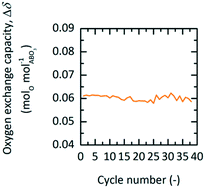 | ||
| Fig. 5 Oxygen exchange capacity, Δδ, vs. cycle number of YBCO granules at 0.01 bar O2 and 563 K during oxidation and 0.2 bar O2 at 773 K during reduction for TOS. | ||
The oxygen storage capacity Δδ, of YBCO, looks very good when compared to other materials studied for TOS and TOP processes, as can be seen in Table 4. YBCO has approximately double the oxygen storage capacity of both SrFeO3 and SrCoO3 over similar temperature and pressure ranges. Cu2O (ref. 7) on the other hand, has a large oxygen storage due to the stoichiometric nature of the reaction, but requires much higher temperatures. It is clear that the low temperature redox conditions employed with YBCO would not work for Cu2O, since Ezbiri et al.8 previously showed that Cu2O irreversibly oxidizes to CuO, when cycled between 900 and 600 K at 0.2 and 0.035 bar O2, respectively. We therefore concluded for applications in the lower temperature range investigated here that YBCO has superior performance compared to the state of the art.
Packed bed reactor experiments for TOS
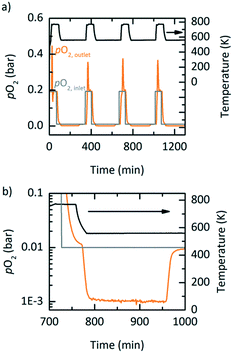
PBR experiments were executed to test the potential of YBCO for an industrial setting. To minimize the effects of channelling and pressure drops in the PBR, the previously discussed YBCO granules were initially used. However, the available setup did not allow for YBCO granules to reach thermodynamic equilibrium, possibly due to mass transfer limitations in the gas phase and the lower specific area of the granules (cf. Fig. S13†). Hence, the results executed with the YBCO powder are shown. Fig. 6 displays the measured pO2 at the outlet of the PBR along with the temperature and the pO2 at the inlet of the PBR as a function of time. Fig. 6 shows oxidation at 563 K; Fig. S12† shows oxidation at 523, 603 and 643 K. For all these oxidation temperatures, thermodynamic equilibrium was reached during oxidation. We see from Fig. 6b that during oxidation, the pO2 drops from 0.01 bar O2 to 0.001 bar O2 over a steady period of 175 minutes, which can clearly be attributed to the reoxidation reaction of YBCO. 0.001 bar O2 is the maximum allowable O2 concentration in recycled inert gas.7 Reaching 955 minutes in Fig. 6b, the pO2 quickly increases back to 0.01 bar O2, which means that the whole reactor bed has been oxidized. An amount of 3.13 litres of O2 is separated during the oxidation at 563 K, in each of the cycles, corresponding to 0.064 molO molABO3−1 as observed in the TGA (cf.Table 5). Table 5 further shows the oxidation time and Δδ of the PBR experiments at oxidation temperatures of 523, 603 and 643 K. As expected, we see that the time until oxidation and the Δδ values increase with decreasing oxidation temperature.| Oxidation temperature (K) | Experimental oxidation period (min) | Δδ (molO molABO3−1) |
|---|---|---|
| 523 | 225 | 0.083 |
| 563 | 175 | 0.064 |
| 603 | 130 | 0.043 |
| 643 | 100 | 0.020 |
Thermochemical oxygen production
In the following sections we present results for a TOP processes using YBCO, again including an energy balance, cycle stability runs in the TGA, and a packed bed reactor demonstration of the process.Energy balance
This section presents the energy balance established for TOP, similar to the energy balance illustrated in Fig. 4. Here, a different set of redox conditions is employed (cf.Table 7) with 673 K and 0.2 bar O2 during oxidation and 873 K and 1 bar O2 during reduction. Since this process is not coupled to another high-temperature technology, Δhhg cannot be taken as zero, i.e.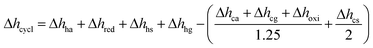 assuming 80 and 50% gas and solid heat recuperation, respectively. With YBCO and the employed redox conditions, Δhcycle amounts to 377 kJ molO2−1, while state-of-the-art cryogenic distillation requires a thermal energy of 78 kJ molO2−1, assuming a conversion factor of 0.4 (for state-of-the-art coal-fired power plants41) between electric (Eel) and thermal energy (Eth) (cf.Table 6). We thus conclude that TOP using YBCO at the used redox conditions might only compete with cryogenic distillation if coupled to another high-temperature technology, such as oxy-fuel combustion,2,10 where the cryogenic air separation unit is a major economic drawback. Other possible technologies, where the wider use of pure oxygen could reduce CO2 emissions, include integrated gasification combined cycles and the partial oxidation of methane.5
assuming 80 and 50% gas and solid heat recuperation, respectively. With YBCO and the employed redox conditions, Δhcycle amounts to 377 kJ molO2−1, while state-of-the-art cryogenic distillation requires a thermal energy of 78 kJ molO2−1, assuming a conversion factor of 0.4 (for state-of-the-art coal-fired power plants41) between electric (Eel) and thermal energy (Eth) (cf.Table 6). We thus conclude that TOP using YBCO at the used redox conditions might only compete with cryogenic distillation if coupled to another high-temperature technology, such as oxy-fuel combustion,2,10 where the cryogenic air separation unit is a major economic drawback. Other possible technologies, where the wider use of pure oxygen could reduce CO2 emissions, include integrated gasification combined cycles and the partial oxidation of methane.5
| TOP | ||||
|---|---|---|---|---|
| %-Fraction of heat recovered (−) | ||||
| From solids | From gas | Δhreq (kJ molO2−1) | Δhrecup (kJ molO2−1) | Δhcycle (kJ molO2−1) |
| 50 | 80 | 844 | 466 | 377 |
| Cryogenic distillation | ||
|---|---|---|
| Purity | E el (kJ molO2−1) | E th (kJ molO2−1) |
| 99.5% | 31 | 78 |
Thermochemical cycling experiments for TOP
Using TGA, 50 redox cycles were performed with YBCO granules at 573 K and 0.2 bar O2 during oxidation and at 873 K and 1 bar O2 during reduction. We see that Δδ stays stable at around 0.1 molO molABO3−1 throughout all executed redox cycles (cf.Fig. 7).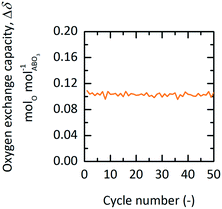 | ||
| Fig. 7 Oxygen exchange capacity, Δδ, vs. cycle number of YBCO at 0.2 bar O2 and 573 K during oxidation and 1 bar O2 at 873 K during reduction for TOP. | ||
Packed bed reactor experiments for TOP
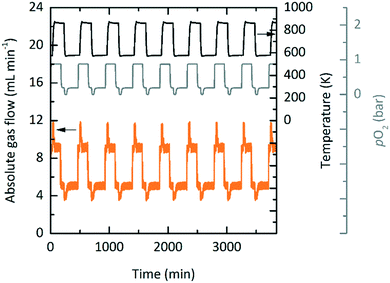
Exploratory experimental runs with a packed bed reactor were executed using YBCO granules, where in this case the granules were indeed suitable as they did reach thermodynamic equilibrium. This was likely due to the higher temperature operation when compared to TOS. Fig. 8 shows the absolute gas flow and pO2 measured at the outlet of the reactor vs. time for nine consecutive redox cycles. 5 and 10 mL min−1 gas flows were used during oxidation and reduction, respectively. The changes in absolute gas flow during oxidation and reduction are a clear indication of the reactivity of YBCO. We further note that the pO2 does not change during reduction since it is at a 100% at the inlet already. During oxidation, however, a decrease in pO2 from the set point of 0.2 bar O2 is observed.Table 7 gives an overview of the used redox conditions, the resulting Δδ and the required energies of TOS and TOP in comparison to state-of-the-art cryogenic distillation.
4. Conclusions
Using a descriptor-based design principle, we predicted promising redox thermodynamics of the three AA'BO3-type perovskites La0.5Ba0.5CoO3−δ, Pr0.5Ba0.5CoO3−δ and Y0.5Ba0.5CoO3−δ. These compounds were further evaluated using dynamic oxygen exchange measurements, with Y0.5Ba0.5CoO3−δ being identified as most ideal for thermochemical oxygen separation and production. This compound shows the fastest reaction rates, lowest reaction temperatures and highest oxygen exchange capacities compared to those of the tested perovskites in this work, and the state-of-the-art materials SrCoO3 and SrFeO3. The TOS processes was experimentally demonstrated using Y0.5Ba0.5CoO3−δ and an energy balance indicates that the it could in principle be driven by process waste heat from the solar splitting of CO2/H2O. Finally, consecutive redox cycles executed with a packed-bed reactor indicated the potential of both thermochemical oxygen production and separation for scale-up and industrial implementation.Nomenclature
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We gratefully acknowledge the financial support by the Swiss Competence Center Energy & Mobility, the Helmholtz-Gemeinschaft Deutscher Forschungszentren (Virtuelles Institut SolarSyngas), the European Research Council under the European Union's ERC Advanced Grant (SUNFUELS-No. 320541), and the European Union's Horizon 2020 research and innovation programme (Project SFERA-III – Grant Nr. 823802). The DFT calculations were performed at the High-Performance Computation cluster of ETH Zürich.References
- R. M. Thorogood, Gas Sep. Purif., 1991, 5, 83–94 CrossRef CAS.
- K. Zhang, J. Sunarso, Z. P. Shao, W. Zhou, C. H. Sun, S. B. Wang and S. M. Liu, RSC Adv., 2011, 1, 1661–1676 RSC.
- T. Burdyny and H. Struchtrup, Energy, 2010, 35, 1884–1897 CrossRef CAS.
- A. R. Smith and J. Klosek, Fuel Process. Technol., 2001, 70, 115–134 CrossRef CAS.
- P. M. Geffroy, J. Fouletier, N. Richet and T. Chartier, Chem. Eng. Sci., 2013, 87, 408–433 CrossRef CAS.
- F. G. Kerry, Industrial Gas Handbook: Gas Separation and Purification, CRC Press, 2010 Search PubMed.
- M. Hänchen, A. Stiel, Z. R. Jovanovic and A. Steinfeld, Ind. Eng. Chem. Res., 2012, 51, 7013–7021 CrossRef.
- M. Ezbiri, K. M. Allen, M. E. Gàlvez, R. Michalsky and A. Steinfeld, ChemSusChem, 2015, 8, 1966–1971 CrossRef CAS PubMed.
- B. Bulfin, J. Lapp, S. Richter, D. Gubàn, J. Vieten, S. Brendelberger, M. Roeb and C. Sattler, Chem. Eng. Sci., 2019, 203, 68–75 CrossRef CAS.
- K. Krishnamurthy, D. Acharya and F. Fitch, Pilot-Scale Demonstration of a Novel, Low-Cost Oxygen Supply Process and its Integration with Oxy-Fuel Coal-Fired Boilers, 2008, Tech. rep., Boc Group, Inc., The (A Delaware Corp) Search PubMed.
- B. Moghtaderi, Energy Fuels, 2010, 24, 190–198 CrossRef CAS.
- J. Vieten, B. Bulfin, F. Call, M. Lange, M. Schmücker, A. Francke, M. Roeb and C. Sattler, J. Mater. Chem. A, 2016, 4(35), 13652–13659 RSC.
- J. Vieten, B. Bulfin, P. Huck, M. Horton, D. Guban, L. Zhu, Y. Lu, K. A. Persson, M. Roeb and C. Sattler, Energy Environ. Sci., 2019, 12(4), 1369–1384 RSC.
- J. Dou, E. Krzystowczyk, A. Mishra, X. Liu and F. Li, ACS Sustainable Chem. Eng., 2018, 6(11), 15528–15540 CrossRef CAS.
- A. M. Narayanan, R. Parasuraman and A. M. Umarji, Ind. Eng. Chem. Res., 2018, 57(43), 14749–14757 CrossRef CAS.
- C. L. Muhich, B. W. Evanko, K. C. Weston, P. Lichty, X. H. Liang, J. Martinek, C. B. Musgrave and A. W. Weimer, Science, 2013, 341, 540–542 CrossRef CAS PubMed.
- L. J. Venstrom, R. M. De Smith, Y. Hao, S. M. Haile and J. H. Davidson, Energy Fuels, 2014, 28, 2732–2742 CrossRef CAS.
- W. Villasmil, M. Brkic, D. Wuillemin, A. Meier and A. Steinfeld, J. Sol. Energy Eng., 2014, 136, 011016 CrossRef.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dulak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Moller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Hakkinen, G. K. H. Madsen, R. M. Nieminen, J. Nørskov, M. Puska, T. T. Rantala, J. Schiotz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- A. J. Medford, J. Wellendorff, A. Vojvodic, F. Studt, F. Abild-Pedersen, K. W. Jacobsen, T. Bligaard and J. K. Norskov, Science, 2014, 345, 197–200 CrossRef CAS PubMed.
- M. García-Mota, A. Vojvodic, H. Metiu, I. C. Man, H. Y. Su, J. Rossmeisl and J. K. Nørskov, ChemCatChem, 2011, 3, 1607–1611 CrossRef.
- M. Ezbiri, M. Takacs, B. Stolz, J. Lungthok, A. Steinfeld and R. Michalsky, J. Mater. Chem. A, 2017, 5(29), 15105–15115 RSC.
- R. Michalsky, V. Botu, C. M. Hargus, A. A. Peterson and A. Steinfeld, Adv. Energy Mater., 2014, 4, 1401082 Search PubMed.
- I. Barin, Thermochemical Data of Pure Substances, 1993 Search PubMed.
- J. R. Scheffe and A. Steinfeld, Energy Fuels, 2012, 26, 1928–1936 CrossRef CAS.
- L. B. Pankratz, Thermodynamic Properties of Elements and Oxides, USA, 1982 Search PubMed.
- R. Michalsky, D. Neuhaus and A. Steinfeld, Energy Technol., 2015, 3, 784–789 CrossRef CAS PubMed.
- I. O. Troyanchuk, N. V. Kasper, D. D. Khalyavin, H. Szymczak, R. Szymczak and M. Baran, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 2418–2421 CrossRef CAS.
- T. Nakajima, M. Ichihara and Y. Ueda, J. Phys. Soc. Jpn., 2005, 74, 1572–1577 CrossRef CAS.
- M. M. Seikh, V. Pralong, O. I. Lebedev, V. Caignaert and B. Raveau, J. Appl. Phys., 2013, 114, 013902 CrossRef.
- T. Vogt, P. M. Woodward, P. Karen, B. A. Hunter, P. Henning and A. R. Moodenbaugh, Phys. Rev. Lett., 2000, 84, 2969–2972 CrossRef CAS PubMed.
- S. M. Babiniec, E. N. Coker, J. E. Miller and A. Ambrosini, Sol. Energy, 2015, 118, 451–459 CrossRef CAS.
- M. Takacs, M. Hoes, M. Caduff, T. Cooper, J. R. Scheffe and A. Steinfeld, Acta Mater., 2016, 700–710 CrossRef CAS.
- W. G. Mallard and P. J. Linstrom, http://webbook.nist.gov, retrieved February 2016), Gaithersburg MD, 1998 Search PubMed.
- D. Marxer, P. Furler, J. Scheffe, H. Geerlings, C. Falter, V. Batteiger, A. Sizmann and A. Steinfeld, Energy Fuels, 2015, 29, 3241–3250 CrossRef CAS.
- J. H. Jeong, L. S. Kim, J. K. Lee, M. Y. Ha, K. S. Kim and Y. C. Ahn, presented in part at the ASEM Turbo Expo 2007: Power for land, sea and air, 2007.
- W. Zhou, C. T. Lin and W. Y. Liang, Adv. Mater., 1993, 5, 735–738 CrossRef CAS.
- J. Bugge, S. Kjaer and R. Blum, Energy, 2006, 31, 1437–1445 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9re00430k |
| This journal is © The Royal Society of Chemistry 2020 |

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)