Multivariate analysis of inline benchtop NMR data enables rapid optimization of a complex nitration in flow

Abstract

Inline benchtop NMR analysis is established as a powerful tool for reaction monitoring, but its capabilities are somewhat limited by low spectral resolution, often leading to overlapping peaks and difficulties in quantification. Using a multivariate analysis (MVA) statistical approach to data processing these hurdles can be overcome, enabling accurate quantification of complex product mixtures. By employing rapid data acquisition (2.0 s recording time per spectrum), we demonstrate the use of inline benchtop NMR to guide the optimization of a complex nitration reaction in flow. Accurate quantification of four overlapping species was possible, enabling generation of a robust DoE model along with accurate evaluation of dynamic experiments.

---

Introduction

In recent years continuous flow processing has attracted the interest of the fine chemical, agrochemical and pharmaceutical industries, for numerous reasons including shortened synthetic routes, improved quality and enhanced sustainability profiles.¹ Flow technology has considerable advantages in mass- and heat transfer, safety and ease of scale-up, when compared to traditional batch reactions.² Furthermore, hazardous chemistries such as highly exothermic reactions, or those involving unstable or toxic intermediates can be operated safely in flow, whereby this technology acts as a powerful route-enabler.³

The increased uptake of flow technology, particularly systems equipped with process analytical technology (PAT),⁴ has opened the field to reaction optimization using advanced techniques such as design of experiments (DoE),⁵ dynamic experimentation,⁶ automated self-optimization⁷ and feedback loops for process control.⁸ Driven by regulatory authorities, PAT has emerged as a key tool to support pharmaceutical development, manufacturing and quality by design (QbD).⁹ In this context, PAT can enable faster and more reliable process optimization and enhanced process control compared to cases using offline analysis only. The resulting workflows perfectly align with approaches towards Industry 4.0 – data driven automation for development and advanced process control for manufacturing.¹⁰

In terms of hardware, a PAT tool can be as simple as a temperature, pressure, pH or conductivity probe. More complex analytical instruments have also been integrated to continuous flow reactors for monitoring single or multistep syntheses.¹¹ These include UV-vis,¹² Raman¹³ or infrared (IR)¹⁴ spectroscopies, but also chromatographic techniques such as high/ultra performance liquid chromatography (HPLC/UPLC),¹⁵ and gas chromatography (GC).¹⁶

Low field (benchtop) NMR is also being increasingly utilized within academic and industrial labs.¹⁷ Due to their simplicity, low operating cost, compactness and ability to operate without deuterated solvents, these instruments have the potential to serve as an excellent addition to the arsenal of PAT tools.¹⁸ However, the resolution of the resulting spectra is poor compared to high field instruments and overlapping signals can be especially troublesome when attempting to quantify components in complex mixtures. In order to follow reaction progress, well-resolved peaks are monitored and a long acquisition time is generally utilized.¹⁹ The resulting analysis period is relatively long, when considering the collection of multiple data points for the purpose of reaction optimization.

Data analysis methods, such as multivariate analysis (MVA) are vital in the utilization of PAT, to adequately deconvolute spectroscopic analyses. MVA is a statistical approach to quantify components by their “fingerprint” signals in a measurement. This approach enables quantification of different components in a complex spectrum. Typically, an MVA model is built using a training set, consisting of mixtures of the analytes with known concentrations. It has been demonstrated in many instances that MVA, using a method such as partial least squares (PLS) regression, is an efficient approach to process NIR²⁰ and fluorescence²¹ spectra. Surprisingly, examples in which NMR spectra are processed using MVA appear to consist almost exclusively of studies in food and biological analytics.²²

A small number of examples exist, demonstrating the combination of NMR with MVA to monitor chemical transformations. Most notably, the group of Maiwald has demonstrated a process monitoring strategy of an S_NAr reaction using inline NMR, quantified using a multivariate analysis PLS model.²³ This was later expanded to simple optimization experiments to maximize plant throughput.²⁴ In a related concept, it would be of substantial benefit to expand the usage of this techniques to early-stage reaction optimization studies using common approaches, such as DoE or dynamic experimentation.²⁵ Herein, we demonstrate the utility of an MVA approach to interpret rapidly recorded low field NMR spectra, which contain a complex mixture of species, for optimization and monitoring of a continuous flow nitration (Fig. 1).

Fig. 1 A graphical representation of the workflow reported herein. Data is collected using inline NMR, then spectra are fed into the developed multivariate analysis models, providing quantification of each analyte.

Results and discussion

Model reaction and reactor system

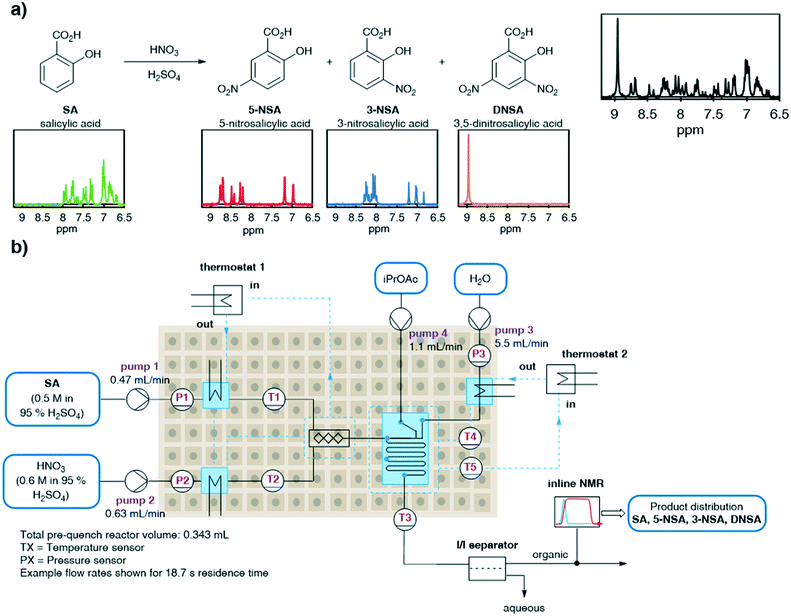
Flow processing has become accepted as a safe and effective method of performing hazardous reactions such as nitrations.²⁶ In particular, the nitration of salicylic acid is a well-studied reaction under both batch and flow conditions (Fig. 2a).^27,28 As a potential intermediate towards preparation of the API mesalazine,²⁹ an effective method for the synthesis of 5-nitro salicylic acid is desirable. However, this specific nitration is characterized by poor selectivity between the undesired 3-nitro- and desired 5-nitro-regioisomers (3-NSA and 5-NSA) and further reaction to the dinitrated product (DNSA). This mixture of products represents a challenging system to analyze by low field NMR, due to multiple overlapping aromatic signals. We aimed to deconvolute these signals by using an MVA approach. Rapid and accurate online quantification would allow facile optimization of the reaction conditions towards the desired product (5-NSA).

Fig. 2 The studied reaction system: a) reaction scheme, showing the three observed reaction products and the representative low-field NMR spectrum of each component and a representative reaction mixture; b) the reaction, separation and analytical setup used to undertake this chemistry in continuous flow.

This nitration is generally achieved using either sulfuric acid or acetic acid as solvent. Sulfuric acid provides an exceptionally fast rate of reaction,²⁷ whereas acetic acid requires heating and prolonged reaction times.²⁸ In view of capitalizing on the benefits of flow chemistry, in mixing and heat dissipation, the reaction procedure in sulfuric acid was selected. Due to incompatibilities of neat sulfuric acid with polyether ether ketone (PEEK) material fittings, a quench and membrane separation were introduced prior to NMR analysis. The reaction stream was quenched with water and the organic products were simultaneously extracted into an organic solvent, isopropyl acetate (iPrOAc). The phases were then separated using an inline phase separator (SEP-10, Zaiput). The organic phase was then passed through a benchtop NMR (Spinsolve Ultra 43 MHz, Magritek) flow-through cell for continuous inline analysis (Fig. 2b).

Initial attempts to carry out this nitration used a Lonza FlowPlate reactor (Ehrfeld), with a “liquid–liquid” plate design.³⁰ Reaction streams were delivered using SyrDos 2 pumps (HiTec Zang) into a reactor constructed of Modular MikroReaction System (MMRS, Ehrfeld) parts, with temperature control supplied by 2× Ministat 240 thermostats (Huber). However, in this reactor, the reaction progress appeared to be limited depending upon the flow rates used (see ESI†).³¹ This was proposed to be due to mixing limitations caused by the high reaction mixture viscosity (dynamic viscosity of 95% H₂SO₄ = 17.6 mPa s at 25 °C).³² Due to the large volume of water required to quench the acid stream (5 : 1 flow rate ratio) and total flow rate restriction imposed by the phase separator, a relatively low flow rate of reaction mixture was necessitated (1.1 mL min⁻¹ combined). Accordingly, it was found that switching to a mixer based on a split-and-recombine mixing principle (Cascade Mixer 06, Ehrfeld) provided effective mixing, allowing full reaction conversion independent of the flow rates used (see ESI†).³³

With the finalized reactor setup, we sought to determine the residence time distribution (RTD) by taking advantage of NMR analysis with a short acquisition period. This type of RTD measurement is generally carried out by injecting a dye solution and observing its flow pattern using UV-vis. One key advantage of using NMR for this purpose instead, is that any organic molecule with sufficient separation from the solvent signals can be used. In this case, where sulfuric acid is used as the solvent, viscosity plays a key role, but the solvent is incompatible with the majority of organic dyes. The actual reaction solvent can be used in this case, providing more representative RTD data for the entire process from reaction, through separation, to NMR analysis (see ESI†).

Development of multivariate models

When considering inline analytical methods, fast acquisition of data offers significant advantages. Therein, many data points can be collected in a short time period, providing a snapshot of the reaction composition as close as possible to real-time. Under this type of monitoring regime, faster reaction optimization can be achieved, alongside more responsive process control. To maximize the utility of this analytical system, a short acquisition time was selected, and only a single scan. This resulted in a total measurement time of 2.0 s (pulse angle = 90°, acquisition time = 1.6 s, repetition time = 2.0 s and number of scans = 1) – a method which would typically not be considered, due to its relatively poor spectral resolution.

It should be noted, however, that the total time taken to acquire each data point is limited by the speed at which the computer is able to write and process the data files. This time is variable depending upon the processor and hard drive write speed. For example, in our case, the installation of a solid-state drive (SSD) to the computer was observed to significantly shorten overall analysis and processing times from >10 s (using standard hard disk drive) to ∼6 s per data point.

To set up a PLS model for this system, mixtures of known concentrations were pumped through the flow-through cell for analysis (see ESI†). 10 different concentration levels were used for each component, representing the expected spread of data under the reaction conditions (0.25 M initial SA concentration). Since a linear response between concentration and peak area is expected, this relatively small number of concentration levels is thought to be sufficient. For each of these concentration levels 100 spectra were obtained, using the aforementioned 2.0 s measurement period.

In order to handle such a large quantity of data, initial processing (Fourier transform and baseline correction) was performed on the stacked spectra in Mestrenova v11 (Mestrelab Research). The resulting data were used to generate a PLS model for the simultaneous prediction of all reaction components, using Simca v16 (Sartorius Stedim Biotech). To perform cross-validation (CV) the training set data was divided into subgroups by concentration level. The CV algorithm generates reduced data sets to get a performance indicator of model error, the root-mean-square error of cross validation (RMSE_CV). The initial model, using the full NMR spectrum, had RMSE_CV values >10 mM for all components (Table 1, entry 1), so further effort was made to improve the model.

Table 1 Measure of the error in estimating concentrations of each of the four reaction components, through different generations of the multivariate analysis models. The presented error is absolute (in units of mM), calculated as the RMSE_CV

Entry	Model	SA	3-NSA	5-NSA	DNSA
a Number of components for each model: SA = 1 + 4 + 0; 3-NSA = 1 + 5 + 0; 5-NSA = 1 + 6 + 0; DNSA = 1 + 4 + 0. See ESI† for further details.
1	Combined PLS model	14.1	13.9	10.9	27.2
2	Individual PLS model	8.7	8.4	9.4	7.8
3	Individual OPLS model	3.8	3.3	3.4	2.4
4	After alignment OPLS model	3.5	2.9	3.2	2.1
5	Final model	3.6	2.8	3.1	2.1

---

It was found that the error could be reduced by building individual models for each reaction component and excluding sections of the spectrum without useful spectroscopic information for that component (entry 2). Additional improvement was achieved by using an OPLS (orthogonal projections to latent structures) model, which uses orthogonal signal correction to explain additional covariance (entry 3).³⁴ To further refine the models a MATLAB script was then used to interpolate and align peaks, in order to negate the influence of small shifts in the data (entry 4, see ESI† for details). For the final models the zero-concentration calibration values for 3-NSA, 5-NSA and DNSA were excluded. On the other hand, it was found that including the zero-concentration values for SA provided better prediction power for lower concentrations.

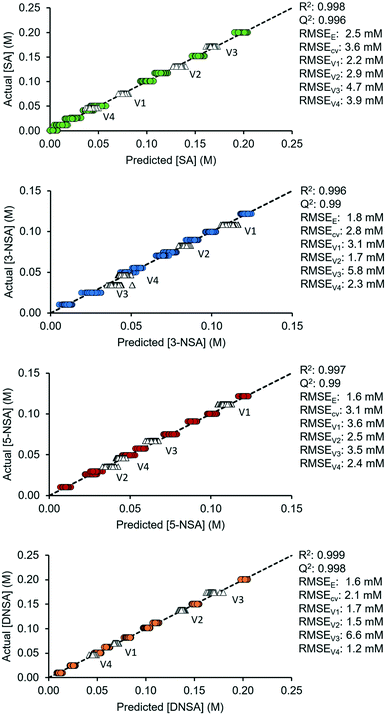
The predictive capability of these finalized OPLS models was then tested, using 4 validation sets of mixtures with different concentrations. These were within the range of the original calibration mixtures and were pumped through the flow cell at 1.1 mL min⁻¹. The root mean error of validation (RMSE_V) was calculated for each mixture and were found to be sufficiently low for accurate predictions (SA < 4.8 mM, 3-NSA < 5.9 mM, 5-NSA < 3.7 mM, DNSA < 6.7 mM). The predicted vs. actual concentration plots for the finalized models, including validation sets, are shown in Fig. 3, with relevant statistics appended.

Fig. 3 Actual vs. predicted plots for the OPLS model of each reaction component, with the target line (y = x) appended. Colored circles show the training set data, and white triangles show the validation set data. Key statistics are summarized next to each graph, demonstrating the fitting parameters and error (of the model overall and for each of the four validation sets, V1 to V4).

Additionally, to explore the robustness of the model, experiments were performed with different flow rates (1.7 mL min⁻¹ and 2.4 mL min⁻¹) and different acquisition times (3.2 s and 6.4 s). In general, the RMSE increased for faster flow rates due to signal broadening.^17b However, the models still remained within a useable error range (validation RMSE < 5 mM) for most cases, even at the significantly higher flow rate of 2.4 mL min⁻¹. The change of acquisition times did not have a significant impact on the RMSE, which demonstrates robustness (see ESI†). This implies that developed MVA models can be applied across a range of different NMR acquisition parameters, so the user is not limited to using the initial calibration parameters.

Reaction optimization by inline NMR monitoring

For optimization of synthetic processes with multiple variables, DoE has become accepted as an efficient method of planning experiments to obtain maximum understanding through minimal laboratory work.³⁵ For both batch and flow processes, DoE is widely used in industrial settings, not just for optimization, but also for determining the reaction “design space”, within which the desired performance is maintained.³⁶ Accordingly, we undertook a DoE approach to optimizing this reaction by applying the developed OPLS model for species quantification.

A three-factor full factorial DoE design was applied (using Modde 12.1 software, Sartorius Stedim Data Analytics AB), considering the input parameters: temperature, residence time and nitric acid equivalents. This design resulted in 8 different experimental conditions, with an additional 3 center points to determine reproducibility (Fig. 4a).

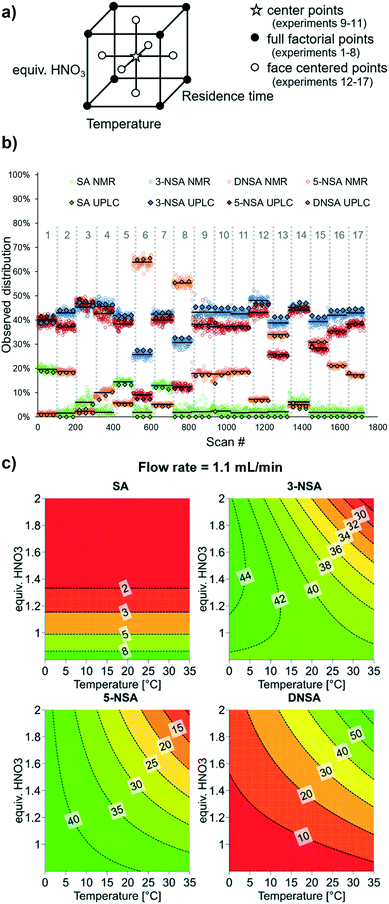Fig. 4 a) Cube showing the planned DoE experimental points, including center points, full factorial points (original model) and face centered points (additional experiments). b) Experimental results of DoE experiments using NMR analysis with the described OPLS model to determine relative ratios of each reaction component. Each set of experimental conditions is numbered in grey. The NMR average for each experiment is denoted by a black line, and offline UPLC measurements (3 for each set of conditions) are appended as black-bordered diamonds. c) Response contour plots for each reaction component, showing results at a flow rate of 1.1 mL min⁻¹. See ESI† for full DoE details, analysis and results.

Data was acquired by NMR continuously, throughout the experimental run, and grouped for each DoE level (Fig. 4b, mean result displayed as a black line). To account for gas bubbles or other inconsistent results, quartiles (Q) and interquartile ranges (IQR) were calculated, then data points which exceeded the lower or upper boundary (Q₁ − 1.5 IQR or Q₃ + 1.5 IQR) were identified as outliers and removed (see ESI†). In order to confirm the NMR results, three samples were taken for offline UPLC analysis (black-bordered diamonds). In most cases, the difference between UPLC and mean NMR result was minimal and the discrepancy never exceeded 5%. One area in which the MVA model was less successful, however, was determining low (<5%) levels of starting material (SA). Under several of the experimental conditions, complete consumption of SA was observed by UPLC, but the value determined by NMR was around 2%, presumably due to noise in the spectra.

The model constructed from these results showed that substantial curvature was present, implying the presence of squared term interactions. To verify these squared terms, axial points were added (6 additional points, for a total of 17 experiments – a face centered design, Fig. 4a). The initially observed curvature was confirmed, providing a satisfactory model. Furthermore, the model constructed using NMR data aligns very well with its equivalent based on the confirmatory UPLC data (see ESI† for details).

In this specific model reaction the selectivity towards the desired product 5-NSA can, unfortunately, not be significantly improved through tuning of the examined parameters (Fig. 4c). It can be observed that 5-NSA overreacts to form DNSA preferentially versus 3-NSA. Accordingly, operating at low temperature and nitric acid equivalents is preferable, whereby a selectivity of roughly 1 : 1 between the two regioisomers is achievable (1 equiv. HNO₃, 0 °C, 1.1 mL min⁻¹ combined flow rate). The DoE output suggests that flow rate (and, by association, mixing speed) has minimal impact upon the reaction performance. For improved selectivity, it could be argued that the procedure using acetic acid may be preferable. It is envisioned that the workflow described here will be applied in future cases for rapid optimization of reaction conversion and selectivity.

Dynamic experimentation

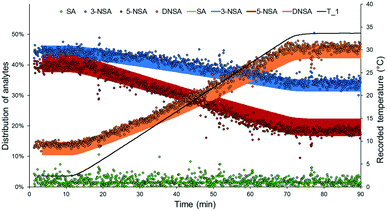
By applying a ramped change of conditions in a plug flow reactor, dynamic flow experiments allow semi-continuous output data to be obtained. This data can be leveraged for rapid kinetic analysis or parameter optimization in flow.⁶ In order to validate the DoE model, it was envisaged that a dynamic experiment could be employed, essentially validating an entire “line” across the model surface, rather than simply a single point.

The validation experiment was carried out using fixed residence time (18.7 s) and nitric acid loading (1.6 equiv.), and a temperature set point ramped from 0 °C to 35 °C over 60 min (Fig. 5). Experimental outcomes predicted by the constructed DoE model were taken as a range (with an error defined by the Modde output). Excellent agreement was observed between the predicted and measured results for all four species, further corroborating the validity of the developed DoE model. Only a slight deviation from the prediction was measured for 5-NSA, which demonstrated less than the expected level of curvature.

Fig. 5 DoE validation experiment using dynamic experimentation to ramp temperature from 0 °C to 35 °C (actual recorded temperature is represented as a black line). Values measured by NMR are black-bordered circles, whilst ranges predicted by the DoE model appear as a solid line.

It is important to note that the ramp time for this experiment could be significantly shortened, as subsequently demonstrated in a “ramp-down” experiment, which reduced the temperature from 35 °C to 0 °C over ∼15 min (see ESI†). When paired with this fast inline analytical method, it is conceivable that these experiments could be carried out in very short times. This implies that more complex arrays of dynamic experiments (e.g. for kinetic analysis) may be achieved in a rapid and cost-effective manner.

The rapid acquisition of data using NMR with MVA provides 3 main advantages when used for dynamic experiments, compared to examples using chromatographic analysis: 1) data is acquired in a truly inline fashion, rather than (at best) online analysis of aliquots taken from the process stream; 2) far more data analysis points can be captured, since most chromatographic methods (even fast UPLC with an isocratic gradient) generally require >2 minutes of processing time; 3) NMR analysis is far more cost effective, requiring no solvent consumption or (serviceable) moving parts.

Conclusions

In conclusion, we have demonstrated the utility of benchtop NMR as an inline analysis tool when paired with an MVA model, for spectrally overlapping compounds. Even when using very short data acquisition periods (2.0 s), accurate models with <4 mM error were developed. The predictive power of these models was confirmed through accurate concentration determination of four separate validation mixtures. The use of short data acquisition times is further advantageous for use in RTD measurements and for real time process control.

To demonstrate the utility of this inline analysis in reaction optimization, a DoE model was constructed, with accurate agreement between inline NMR and offline UPLC analysis. Additional axial points confirmed the curvature proposed from the initial experimental points. Confirmation of the DoE model was then successfully achieved in a dynamic experiment by ramping the reactor temperature. Using this statistical method, the power of benchtop NMR can be fully realized in automated optimization, mechanistic experiments and process control for flow chemistry.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The CCFLOW Project (Austrian Research Promotion Agency FFG No. 862766) is funded through the Austrian COMET Program by the Austrian Federal Ministry of Transport, Innovation and Technology (BMVIT), the Austrian Federal Ministry for Digital and Economic Affairs (BMDW), and by the State of Styria (Styrian Funding Agency SFG). This work was funded by the Austrian Research Promotion Agency FFG No. 871458, within the program “Produktion der Zukunft”. The INFRA FLOW project (Zukunftsfonds Steiermark No. 9003) is funded by the State of Styria (Styrian Funding Agency SFG).

Notes and references

1. For selected reviews of flow chemistry in the pharmaceutical industry, see: (a) S. A. May, J. Flow Chem., 2017, 7, 1–9; (b) A. R. Bogdan and A. W. Dombrowski, J. Med. Chem., 2019, 62, 6422–6468.
2. M. B. Plutschack, B. Pieber, K. Gilmore and P. H. Seeberger, Chem. Rev., 2017, 117, 11796–11893.
3. For selected reviews of hazardous chemistry in flow, see: (a) M. Movsisyan, E. I. P. Delbeke, J. K. E. T. Berton, C. Battilocchio, S. V. Ley and C. V. Stevens, Chem. Soc. Rev., 2016, 45, 4892–4928; (b) B. Gutmann, D. Cantillo and C. O. Kappe, Angew. Chem., Int. Ed., 2015, 54, 6688–6728.
4. For reviews of PAT in batch and flow, see: (a) G. A. Price, D. Mallik and M. G. Organ, J. Flow Chem., 2017, 7, 82–86; (b) A. Chanda, A. M. Daly, D. A. Foley, M. A. Lapack, S. Mukherjee, J. D. Orr, G. L. Reid, D. R. Thompson and H. W. Ward, Org. Process Res. Dev., 2015, 19, 63–83; (c) S. Bordawekar, A. Chanda, A. M. Daly, A. W. Garrett, J. P. Higgins, M. A. LaPack, T. D. Maloney, J. Morgado, S. Mukherjee, J. D. Orr, G. L. Reid, B. S. Yang and H. W. Ward, Org. Process Res. Dev., 2015, 19, 1174–1185.
5. M. Ohmenhaeuser, Y. B. Monakhova, T. Kuballa and D. W. Lachenmeier, ISRN Anal. Chem., 2013, 825318.
6. For selected applications of dynamic experimentation, see: (a) B. M. Wyvratt, J. P. McMullen and S. T. Grosser, React. Chem. Eng., 2019, 4, 1637–1645; (b) J. S. Moore and K. F. Jensen, Angew. Chem., Int. Ed., 2014, 53, 470–473; (c) C. A. Hone, N. Holmes, G. R. Akien, R. A. Bourne and F. L. Muller, React. Chem. Eng., 2017, 2, 103–108; (d) S. Schwolow, F. Braun, M. Rädle, N. Kockmann and T. Röder, Org. Process Res. Dev., 2015, 19, 1286–1292; (e) K. C. Aroh and K. F. Jensen, React. Chem. Eng., 2018, 3, 94–101.
7. (a) V. Sans and L. Cronin, Chem. Soc. Rev., 2016, 45, 2032–2043; (b) D. C. Fabry, E. Sugiono and M. Rueping, React. Chem. Eng., 2016, 1, 129–133; (c) A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Chem. Eng. J., 2018, 352, 277–282; (d) J. Manson, A. Clayton, C. Gonzalez Niño, R. Labes, T. Chamberlain, A. Blacker, N. Kapur and R. Bourne, Chimia, 2019, 73, 817–822; (e) C. Mateos, M. J. Nieves-Remacha and J. A. Rincón, React. Chem. Eng., 2019, 4, 1536–1544.
8. D. E. Fitzpatrick and S. V. Ley, Tetrahedron, 2018, 74, 3087–3100.
9. S. L. Lee, T. F. O'Connor, X. Yang, C. N. Cruz, S. Chatterjee, R. D. Madurawe, C. M. V. Moore, L. X. Yu and J. Woodcock, J. Pharm. Innov., 2015, 10, 191–199.
10. S. Gentner, Chimia, 2016, 70, 628–633.
11. P. Sagmeister, J. D. Williams, C. Hone and C. O. Kappe, React. Chem. Eng., 2019, 4, 1571–1578.
12. F. Benito-Lopez, W. Verboom, M. Kakuta, J. G. E. Gardeniers, R. J. M. Egberink, E. R. Oosterbroek, A. Van Den Berg and D. N. Reinhoudt, Chem. Commun., 2005, 2857–2859.
13. S. Mozharov, A. Nordon, D. Littlejohn, C. Wiles, P. Watts, P. Dallin and J. M. Girkin, J. Am. Chem. Soc., 2011, 133, 3601–3608.
14. C. F. Carter, H. Lange, S. V. Ley, I. R. Baxendale, B. Wittkamp, J. G. Goode and N. L. Gaunt, Org. Process Res. Dev., 2010, 14, 393–404.
15. (a) E. Wimmer, D. Cortés-Borda, S. Brochard, E. Barré, C. Truchet and F. X. Felpin, React. Chem. Eng., 2019, 4, 1608–1615; (b) E. C. Aka, E. Wimmer, E. Barré, N. Vasudevan, D. Cortés-Borda, T. Ekou, L. Ekou, M. Rodriguez-Zubiri and F. X. Felpin, J. Org. Chem., 2019, 84, 14101–14112.
16. (a) N. Cherkasov, Y. Bai, A. J. Expósito and E. V. Rebrov, React. Chem. Eng., 2018, 3, 769–780; (b) A. Echtermeyer, Y. Amar, J. Zakrzewski and A. Lapkin, Beilstein J. Org. Chem., 2017, 13, 150–163.
17. For reviews of low field NMR for reaction monitoring, see: (a) F. Dalitz, M. Cudaj, M. Maiwald and G. Guthausen, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 60, 52–70; (b) A. Nordon, C. A. McGill and D. Littlejohn, Analyst, 2001, 126, 260–272; (c) J. J. Haven and T. Junkers, Eur. J. Org. Chem., 2017, 2017, 6474–6482.
18. For reviews of flow NMR, see: (a) M. V. Gomez and A. De La Hoz, Beilstein J. Org. Chem., 2017, 13, 285–300; (b) P. Giraudeau and F. X. Felpin, React. Chem. Eng., 2018, 3, 399–413.
19. For selected examples utilizing well-resolved peaks for reaction monitoring by low field NMR, see: (a) M. Rubens, J. Van Herck and T. Junkers, ACS Macro Lett., 2019, 8, 1437–1441; (b) C. M. Archambault and N. E. Leadbeater, RSC Adv., 2016, 6, 101171–101177; (c) V. Sans, L. Porwol, V. Dragone and L. Cronin, Chem. Sci., 2015, 6, 1258–1264; (d) M. Goldbach, E. Danieli, J. Perlo, B. Kaptein, V. M. Litvinov, B. Blümich, F. Casanova and A. L. L. Duchateau, Tetrahedron Lett., 2016, 57, 122–125; (e) B. Ahmed-Omer, E. Sliwinski, J. P. Cerroti and S. V. Ley, Org. Process Res. Dev., 2016, 20, 1603–1614; (f) D. Cortés-Borda, E. Wimmer, B. Gouilleux, E. Barré, N. Oger, L. Goulamaly, L. Peault, B. Charrier, C. Truchet, P. Giraudeau, M. Rodriguez-Zubiri, E. Le Grognec and F.-X. Felpin, J. Org. Chem., 2018, 83, 14286–14299; (g) T. H. Rehm, C. Hofmann, D. Reinhard, H.-J. Kost, P. Löb, M. Besold, K. Welzel, J. Barten, A. Didenko, D. V. Sevenard, B. Lix, A. R. Hillson and S. D. Riegel, React. Chem. Eng., 2017, 2, 315–323.
20. For reviews on MVA for NIR spectroscopy, see: (a) M. Blanco and I. Villarroya, TrAC, Trends Anal. Chem., 2002, 21, 240–250; (b) J. M. Amigo, J. Cruz, M. Bautista, S. Maspoch, J. Coello and M. Blanco, TrAC, Trends Anal. Chem., 2008, 27, 696–713.
21. D. Patra and A. K. Mishra, TrAC, Trends Anal. Chem., 2002, 21, 787–798.
22. For selected examples of MVA of NMR spectra in food and biological applications, see: (a) S. B. Engelsen, F. Savorani and M. A. Rasmussen, eMagRes, 2013, 2, 267–278; (b) H. Winning, F. H. Larsen, R. Bro and S. B. Engelsen, J. Magn. Reson., 2008, 190, 26–32; (c) P. Ebrahimi, F. H. Larsen, H. M. Jensen, F. K. Vogensen and S. B. Engelsen, Metabolomics, 2016, 12, 1–17; (d) P. S. Belton, I. J. Colquhoun, E. K. Kemsley, I. Delgadillo, P. Roma, M. J. Dennis, M. Sharman, E. Holmes, J. K. Nicholson and M. Spraul, Food Chem., 1998, 61, 207–213.
23. S. Kern, K. Meyer, S. Guhl, P. Gräßer, A. Paul, R. King and M. Maiwald, Anal. Bioanal. Chem., 2018, 410, 3349–3360.
24. S. Kern, L. Wander, K. Meyer, S. Guhl, A. R. G. Mukkula, M. Holtkamp, M. Salge, C. Fleischer, N. Weber, R. King, S. Engell, A. Paul, M. P. Remelhe and M. Maiwald, Anal. Bioanal. Chem., 2019, 411, 3037–3046.
25. A. Pankajakshan, M. Quaglio, F. Galvanin and A. Gavriilidis, React. Chem. Eng., 2019, 4, 1623–1636.
26. For selected examples of nitrations in flow, see: (a) C. E. Brocklehurst, H. Lehmann and L. La Vecchia, Org. Process Res. Dev., 2011, 15, 1447–1453; (b) D. Cantillo, M. Damm, D. Dallinger, M. Bauser, M. Berger and C. O. Kappe, Org. Process Res. Dev., 2014, 18, 1360–1366; (c) D. Cantillo, B. Wolf, R. Goetz and C. O. Kappe, Org. Process Res. Dev., 2017, 21, 125–132; (d) L. Ducry and D. M. Roberge, Angew. Chem., Int. Ed., 2005, 44, 7972–7975.
27. S. Debnath, A. Kienle and A. A. Kulkarni, Chem. Eng. Technol., 2014, 37, 927–937.
28. (a) P. Plouffe, A. Macchi and D. M. Roberge, Org. Process Res. Dev., 2014, 18, 1286–1294; (b) R. Andreozzi, M. Canterino, V. Caprio, I. Di Somma and R. Sanchirico, J. Hazard. Mater., 2006, 138, 452–458; (c) R. Andreozzi, V. Caprio, I. Di Somma and R. Sanchirico, J. Hazard. Mater., 2006, 134, 1–7.
29. A. Forbes, A. Cartwright, S. Marchant, P. McIntyre and M. Newton, Aliment. Pharmacol. Ther., 2003, 17, 1207–1214.
30. For selected examples of work using a Lonza FlowPlate with “liquid–liquid” process plate design, see: (a) P. Plouffe, M. Bittel, J. Sieber, D. M. Roberge and A. Macchi, Chem. Eng. Sci., 2016, 143, 216–225; (b) P. Plouffe, D. M. Roberge, J. Sieber, M. Bittel and A. Macchi, Chem. Eng. J., 2016, 285, 605–615; (c) P. Plouffe, D. M. Roberge and A. Macchi, Chem. Eng. J., 2016, 300, 9–19.
31. E. Mielke, D. M. Roberge and A. Macchi, J. Flow Chem., 2016, 6, 279–287.
32. F. H. Rhodes and C. B. Barbour, Ind. Eng. Chem., 1923, 15, 850–852.
33. C. P. Holvey, D. M. Roberge, M. Gottsponer, N. Kockmann and A. Macchi, Chem. Eng. Process., 2011, 50, 1069–1075.
34. J. Trygg and S. Wold, J. Chemom., 2002, 16, 119–128.
35. (a) S. A. Weissman and N. G. Anderson, Org. Process Res. Dev., 2015, 19, 1605–1633; (b) D. Lendrem, M. Owen and S. Godbert, Org. Process Res. Dev., 2001, 5, 324–327; (c) R. Leardi, Anal. Chim. Acta, 2009, 652, 161–172.
36. L. X. Yu, Pharm. Res., 2008, 25, 781–791.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0re00048e

---