Open Access Article
Open Access ArticleAn experimental, theoretical and kinetic-modeling study of the gas-phase oxidation of ammonia†
Alessandro
Stagni
 *a,
Carlo
Cavallotti
*a,
Carlo
Cavallotti
 a,
Suphaporn
Arunthanayothin
b,
Yu
Song
bc,
Olivier
Herbinet
a,
Suphaporn
Arunthanayothin
b,
Yu
Song
bc,
Olivier
Herbinet
 b,
Frédérique
Battin-Leclerc
b,
Frédérique
Battin-Leclerc
 b and
Tiziano
Faravelli
b and
Tiziano
Faravelli
 a
a
aDepartment of Chemistry, Materials, and Chemical Engineering “G. Natta”, Politecnico di Milano, Milano 20133, Italy. E-mail: alessandro.stagni@polimi.it
bLaboratoire Réactions et Génie des Procédés, CNRS-Université de Lorraine, 1 rue Grandville, 54000 Nancy, France
cLaboratoire PRISME, Université d'Orléans, Polytech Vinci – 45072, Orléans, France
First published on 21st February 2020
Abstract
A complete understanding of the mechanism of ammonia pyrolysis and oxidation in the full range of operating conditions displayed by industrial applications is one of the challenges of modern combustion kinetics. In this work, a wide-range investigation of the oxidation mechanism of ammonia was performed. Experimental campaigns were carried out in a jet-stirred reactor and a flow reactor under lean conditions (0.01 ≤ Φ ≤ 0.375), such to cover the full range of operating temperatures (500 K ≤ T ≤ 2000 K). Ammonia conversion and the formation of products and intermediates were analyzed. At the same time, the ammonia decomposition reaction, H-abstractions and the decomposition of the HNO intermediate were evaluated ab initio, and the related rates were included in a comprehensive kinetic model, developed according to a first-principles approach. Low-temperature reactor experiments highlighted a delayed reactivity of ammonia, in spite of the high amount of oxygen. A very slow increase in NH3 consumption rate with temperature was observed, and a full reactant consumption was possible only ∼150–200 K after the reactivity onset. The use of flux analysis and sensitivity analysis allowed explaining this effect with the terminating effect of the H-abstraction on NH3 by O2, acting in the reverse direction because of the high amounts of HO2. The central role of H2NO was observed at low temperatures (T < 1200 K), and H-abstractions from it by HO2, NO2 and NH2 were found to control reactivity, especially at higher pressures. On the other side, the formation of HNO intermediate via NH2 + O = HNO + H and its decomposition were found to be crucial at higher temperatures, affecting both NO/N2 ratio and flame propagation.
1 Introduction
The gradual transition towards newer and more sustainable energy sources for combustion applications is being carried out by pursuing two major targets: (i) a smarter, more efficient use of the available resources, in such a way to reduce energy wastes and CO2 emissions, and (ii) a systematic control of pollutant emissions, which are formed as byproducts of the combustion processes. In this context, the scientific interest towards ammonia (NH3) has been significantly increasing in the last years. As a matter of fact, the high energy density, ease of transportation and carbon-free nature of ammonia make it an attractive candidate as an energy vector: considering that its production relies on established production technologies as well as on a number of novel synthesis techniques,1,2 NH3 has also been proposed as a “platform molecule” for the energy storage from intermittent renewable sources (i.e. wind or sun), and based on successive release via either direct combustion or earlier conversion to hydrogen.3 The competitiveness of ammonia as an energy carrier for the accumulation of excess energy and its release “on-demand” has been assessed in several works.4,5 Moreover, its relevance in the next-generation energy scenario is also connected to its presence (in trace amounts) in biofuels: indeed, ammonia is found in biogas as a by-product of anaerobic digestion.6,7 In addition, protein-rich sludges used as raw materials for bio-oils also contain NH3 as well as other nitrogenated species.8The research on the ammonia combustion chemistry actually started several decades ago. The high-temperature pyrolysis mechanism was first experimentally characterized starting from the 1980s,9–12 with modelling work carried out in parallel.12,13 Studies on oxidation focused first on NH3 flame chemistry14–16 and on its use within the Thermal DeNOx process17 for the selective non-catalytic reduction of nitrogen oxides (NOx). Later, oxidation chemistry was studied at a fundamental level through targeted experiments18–20 and theoretical methodologies.21–24 As a result, NH3 kinetic mechanisms have largely benefited from incremental improvements. One of the first mechanisms was released by Miller et al.,15 who later included NH3 chemistry in their review work on nitrogen compounds.25 Since then, many dedicated models describing ammonia combustion were released. Konnov and De Ruyck26 extended the pyrolysis mechanism initially developed by Davidson et al.12 by including the reactions of N2H3 and N2H4, which were shown to have an important effect on NH and NH2 profiles. Mathieu and Petersen27 extended the work of Dagaut et al.28 on HCN chemistry to model the high-temperature ignition delay times of NH3, collected under diluted conditions at different pressures and equivalence ratios. Shrestha et al.29 recently presented a mechanism for the oxidation of NH3 and NH3/H2 fuel blends, validated in several 0D and 1D systems, while Li et al.30 developed two reduced mechanisms for the combustion of NH3/H2 and NH3/H2/CH4 mixtures in air. The review work by Glarborg et al.31 also includes ammonia pyrolysis and oxidation mechanism in their comprehensive nitrogen kinetic model, and provides an exhaustive overview of the state of the art in the kinetic modelling of NH3 oxidation.
On the other hand, several experimental campaigns carried out in the latest years in less conventional conditions (lower temperatures, high dilution levels and wider pressure ranges) have shown that the fundamental knowledge of ammonia kinetics is still far from complete: the available mechanisms have shown important deviations in the autoignition behavior in diluted conditions, both in high-temperature shock tubes (ST)27 and low- to intermediate-temperature shock tubes32 and rapid compression machines (RCM).33,34 Similarly, flow reactor experiments of pure NH3 oxidation under atmospheric35 and high pressure36 showed that the kinetic models were not always able to reproduce the experimental trends. Da Rocha et al.37 showed the inadequacy of several kinetic mechanisms in predicting the laminar flame speed (LFS) of NH3, and most of them were shown to overpredict the actual rates.
In order to ensure an adequate degree of comprehensiveness, a fundamental understanding of ammonia kinetics still needs to be achieved. Glarborg et al.31 pointed out the most unclear pathways of the NH3 oxidation mechanism: they showed that the largest uncertainties are present under low-temperature conditions, especially with high concentrations of oxygen. In such cases, the role of intermediates, such as H2NO and HNO, was shown to be determining, as well as the interaction of the HO2 radical with the radical pool (e.g. NH2 and NO). At the same time, the experimental data under these operating conditions in support of a proper model development are still very limited.
Starting from this scenario, the aim of this work is filling the void of knowledge still remaining in the kinetic mechanisms involved in the oxidation of ammonia, with a focus on the critical conditions previously mentioned, and scarcely explored so far. To this purpose, new experimental measurements were performed in a jet-stirred reactor (JSR) and a flow reactor (FR), such as to explore the low- and intermediate-temperature oxidation of ammonia with high dilution levels. At the same time, the critical rate constants involved in the ammonia combustion mechanism were systematically evaluated through a first-principles methodology. In particular, NH3 decomposition, as well as H-abstractions by O2, H, O, OH and HO2, and the dissociation of the HNO intermediate are discussed. The calculated values were then exploited for a wide-range kinetic modeling of ammonia pyrolysis and oxidation, including the state-of-the-art kinetic constants made available in the latest years. This is used to interpret and explain the experimental results obtained in the two reactors. Finally, the comprehensive capability of the kinetic mechanism in predicting ammonia combustion in different configurations (ST, RCM, FR, LFS and Burner-Stabilized Flame - BSF) and operating conditions was assessed, highlighting the most critical competitive paths, still needing attention at a theoretical level.
2 Methodology
2.1 Experimental setup
The experimental measurements were performed using two different reactors, a jet-stirred reactor (JSR) and a tubular flow reactor (FR) working close to atmospheric pressure, in order to explore the low, intermediate and high temperature oxidation of ammonia with high dilution levels by using helium as carrier gas. Bronkhorst mass flow controllers are used for reactor feeding (relative uncertainty of ±0.5% in flow). Helium (99.999% pure) and O2 (99.999%) were provided by Messer. A cylinder of 2004 ± 60 ppm ammonia diluted in helium, also provided by Messer, was used for the feed of ammonia.In a first set-up, experiments were carried out in a fused silica JSR, a type of continuous stirred-tank reactor usually operated at steady state. JSRs were often used in gas phase kinetic studies. The present JSR setup was already described in previous works.38–40 Briefly, it consisted of a spherical vessel with an injection of the preheated fresh mixture through four nozzles located at the center of the reactor, which produce high turbulence leading to homogeneity in temperature and composition. The preheating and heating of the reactor were performed using Inconel Thermocoax resistances rolled around the different parts and controlled by independent K-type thermocouples. A K-type thermocouple located in a glass finger close to the center of the reactor was used to measure the reaction temperature (uncertainty of ±5 K), which is considered as isothermal when running simulations. Pressure was set to 800 torr (106.7 kPa).
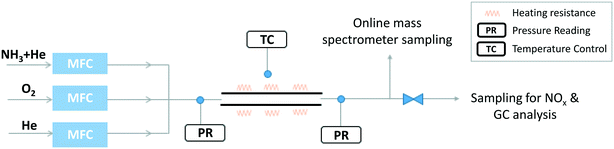
A second setup (Fig. 1) was specifically developed to explore NH3 oxidation at higher temperature (up to ∼2000 K) in a flow reactor (FR). It consisted of a tube made of recrystallized alumina (inner diameter of 4 mm and 100 cm in length), designed to approximate a plug flow reactor. Its operating pressure was 950 torr (126.7 kPa). Under the studied conditions, the Reynolds number was found to vary between 146 and 75, thus the flow was laminar. The Peclet number, Pe = (u × d)/D (u is the linear velocity of the gas, d is the internal diameter of the tube, and D is the molecular diffusivity of helium) was calculated as a function of temperature. The calculation provides values ranging from ∼900 at ∼1100 K to ∼450 at ∼2000 K, supporting the hypothesis that diffusion has a minor impact on the flow (Pe > 100) and that the reactor can be modelled as a plug flow reactor.41
The reactor was located horizontally in an electrically-heated oven (Carbolite Gero) which has an internal regulation. Actual temperature profiles were measured by an R-type thermocouple under unreactive conditions for each set-point temperature. Temperatures were recorded with a step of 2 cm in the isothermal region, and every 5 cm on both sides of the isothermal region. This isothermal reaction zone is located between 36 and 58 cm as shown in Fig. 2, with a quasi-uniform temperature profile (±30 K). The residence time is about 50 ms in the central zone where the temperature can be considered as constant. Flow rates were varied for each temperature set-point to maintain the residence time constants. Both temperature profiles and flow rate calculations are available as ESI.†
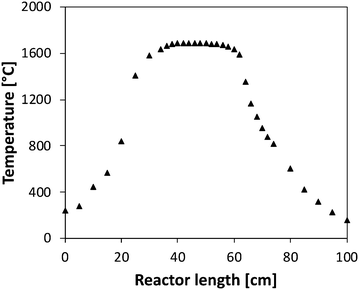 | ||
| Fig. 2 Temperature profile measured (set point of 1700 °C) in the tubular flow reactor in absence of reaction. | ||
It is important to point out that significant catalytic effects of the reactor wall were first suspected in FR in the absence of oxygen when using non-recrystallized alumina. To confirm this, the following protocol was followed:
1. Ammonia pyrolysis was first performed in a non-recrystallized alumina tube, in order to have a reference for comparison.
2. Then, the tube wall was coated with carbonaceous material by carrying out methane pyrolysis in the non-recrystallized alumina tube.
3. After coating, ammonia pyrolysis was repeated, and a significant shift of the reactivity of ∼500 K towards lower temperatures was observed.
As a result, the tube was replaced and recrystallized alumina was adopted (with a higher purity than alumina). This resulted in a global shift of the reactivity of ∼100 K towards higher temperatures when compared to the data obtained with the non-coated, non-recrystallized alumina first tube, and provided data consistent with model predictions.
Another evidence for the occurrence of wall interactions was the long time needed to reach steady state when flowing the reacting mixture (several tens of minutes). This was observed thanks to the use of online mass spectrometry with direct sampling in the gas phase at the outlet of the tube. Such stabilization time was considerably shortened when using a recrystallized alumina tube (a few minutes).
The reactants and reaction products were identified and quantified by using four complementary analytical techniques:
i. Online gas chromatography was used for the quantification of H2 during the NH3 oxidation in FR. It was equipped with a Carbosphere packed column (the carrier gas was argon), and a thermal conductivity detector (TCD). Argon was used as carrier gas to detect H2 with a good sensitivity. The sampling was achieved in the outlet flow of the reactor using a sampling loop mounted on a six-way valve. Calibrations were performed using gaseous standards. The relative uncertainty in H2 mole fraction is ±5%.
ii. On-line mass spectrometry (Omnistar from Pfeiffer) with ionization at 70 eV was used to detect NH3, N2, H2O and O2 in FR experiments. Sampling was carried out through a capillary tube directly connecting the reactor outlet and the analyzer under vacuum and sucking a constant flow. This technique requires the calibration of each species as there is no obvious relationship between their molecule structures and their calibration factors. Gaseous standards were used except for water, which was calibrated considering the reaction complete at the highest temperature. Note that this technique offers the possibility to follow the evolution of the different masses of interest as a function of the time and to check for steady state conditions to be reached. The relative uncertainty in NH3, N2, H2O and O2 mole fractions was estimated to be ±10%.
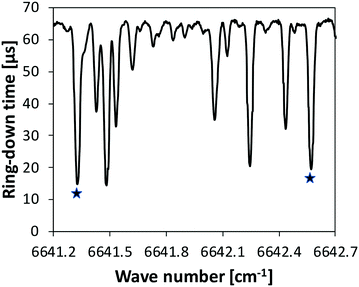
iii. A continuous-wave cavity ring-down spectroscopy (cw-CRDS) cell coupled to the JSR by a sonic probe was used for NH3 quantification. This technique is based on the absorption of species in the infrared, as for the FTIR technique. It is much more sensitive as the light path is much longer. It was already used in previous studies to quantify intermediates like hydrogen peroxide and HONO during the oxidation of fuels.42,43 Ammonia has strong absorption lines in the wavenumber range 6637–6643 cm−1, making the quantification accurate and providing a good sensibility. Fig. 3 displays an extract of a spectrum recorded during the present study under unreactive condition (φ = 1, T = 500 K). The whole spectrum recorded over the range 6637–6643 cm−1 is given in the ESI.† Two intense lines were used to quantify ammonia with a good sensitivity: 6641.33 and 6642.57 cm−1. Cross sections needed for the calibrations were measured using data recorded under unreactive conditions. The relative uncertainty in NH3 mole fraction detected by CRDS is ±10%.
iv. A dual channel NOx chemiluminescence analyzer (Thermo Scientific Model 42i) was used for the detection of NO and NO2 (but no NO2 was detected in these experiments). The detection is based on the conversion of NO (with ozone) to an excited state of NO2 that emits a chemiluminescent light when dropping to the ground state. On the first channel, the detection of nitric oxide is performed in a direct and independent way, whereas the second channel is dedicated to the measure of the total NOx concentration. In this second channel, the sampled gas passes over a heated catalyst transforming nitrogen oxides to nitric oxide, NO, which is detected by chemiluminescence as in the first channel. NO2 concentration is then deduced by substracting the concentration of NO from that of the total NOx. Note that this analyzer is equipped by an ammonia trap to avoid the interference of this species. Calibrations were performed using gaseous standards. The relative uncertainty in NO mole fraction is ±5%, while that of NO2 mole fraction is 10% since it is measured by difference.
2.2 Theoretical methodologies
The rate constants of a specific set of reactions were determined theoretically. They were identified on the basis of a combined uncertainty and sensitivity analysis with respect to the explored experimental conditions as well as on the availability of previous experimental/theoretical studies for each of them. The adopted computational methodology is the ab initio transition state theory based master equation (ME) approach (AITSTME) that was recently implemented in the EStokTP software.44 Electronic structure calculations for abstraction reactions were performed determining structures and vibrational frequencies at the M06-2X/aug-cc-pVTZ level and energies at the unrestricted CCSD(T)/aug-cc-pVTZ level, corrected for basis set size effect with the change of density fitted (DF) MP2 energies computed using aug-cc-pVQZ and aug-cc-pVTZ basis sets. Rate constants were estimated using variational transition state theory (VTST), as implemented in MESS45 for both reactions exhibiting a saddle point on the minimum energy path (MEP) and for barrierless reactions. For abstraction reactions, the structure and energies of van der Waals wells on entrance and exit channels were determined at the M06-2X/aug-cc-pVTZ level of theory. For H-abstraction from NH3 by OH, whose CCSD(T) wavefunction has a large T1 diagnostic of 0.056, the energy barrier was computed performing multireference calculations at the CASPT2/aug-cc-pVTZ level using a full valence (15e,12o) active space. Hindered rotors were treated in the 1D hindered rotor approximation with torsional potential energy surfaces (PES) determined at the M06-2X/6-311+G(d,p) level. Torsional motions were projected out of the Hessian when calculating harmonic frequencies.44 Harmonic frequencies and MEP energies for barrierless reactions (NH3 and HNO decomposition) were determined at the CASPT2/aug-cc-pVTZ level using a full valence active space. In the case of HNO decomposition, the wavefunction was state averaged over two states. All density functional theory (DFT) calculations were performed using the G09 computational suite,46 while CCSD(T) and CASPT2 simulations were performed using Molpro 2010.472.3 Kinetic modeling
The development of the kinetic model was performed by following a hierarchical and modular approach, as originally conceived in the CRECK kinetic framework.48 The core H2/O2 mechanism was adopted after the work of Metcalfe et al.49 The NOx module, foundation of the whole NH3 mechanism, was taken from the work of Song et al.,38 on turn based on the works of Faravelli, Frassoldati et al.50,51 The major updates were performed on HONO/HNO2 chemistry, after the recent work of Chen et al.52 For all the species, the thermodynamic properties were systematically updated using the database of Burcat and Ruscic.53Ammonia submechanism was added on top of the NOx module, and the critical reactions are summarized in Table 1. The parameters of reactions R1 to R6 and R28 were calculated through the fitting of the temperature-dependent rates obtained from the related theoretical calculations via a modified-Arrhenius format k = ATβ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Eact/(RT)]. In addition to the dissociation reaction calculated in this work, the reactions involving NH and NH2 radicals were taken from Klippenstein et al.,21 as well as NH2OH chemistry. The only exception is represented by R7: in this case, the high-temperature estimation of Davidson et al.12 was adopted (∼35% smaller), which (extrapolated) showed a better agreement with lower-temperature experimental data. As for NH2 reactions with NO and NO2 (R16–R19), both rate constants and branching ratios between the product channels were taken following the guidelines of Glarborg et al.,31 while for NH + NO (R26 and R27), the theoretical calculations of Haworth et al.54 were fitted in the 1000–2600 K interval. For the higher N2Hx chemistry, reactions were mainly taken from the review of Dean and Bozzelli,55 including H-abstractions from N2Hx compounds and N2Hx dissociation.
exp[−Eact/(RT)]. In addition to the dissociation reaction calculated in this work, the reactions involving NH and NH2 radicals were taken from Klippenstein et al.,21 as well as NH2OH chemistry. The only exception is represented by R7: in this case, the high-temperature estimation of Davidson et al.12 was adopted (∼35% smaller), which (extrapolated) showed a better agreement with lower-temperature experimental data. As for NH2 reactions with NO and NO2 (R16–R19), both rate constants and branching ratios between the product channels were taken following the guidelines of Glarborg et al.,31 while for NH + NO (R26 and R27), the theoretical calculations of Haworth et al.54 were fitted in the 1000–2600 K interval. For the higher N2Hx chemistry, reactions were mainly taken from the review of Dean and Bozzelli,55 including H-abstractions from N2Hx compounds and N2Hx dissociation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Eact/(RT)]. Units are cm3, cal, mol, K
exp[−Eact/(RT)]. Units are cm3, cal, mol, K
| ID | Reaction | A | β | E act | Notes | Ref. |
|---|---|---|---|---|---|---|
| R1 | NH3 ↔ NH2 + H | 7.230 × 1029 | −5.316 | 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 862.4 862.4 |
0.1 atm | PW |
| 3.497 × 1030 | −5.224 | 111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 163.3 163.3 |
1 atm | |||
| 1.975 × 1031 | −5.155 | 111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 887.8 887.8 |
10 atm | |||
| 2.689 × 1031 | −4.920 | 112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778.7 778.7 |
100 atm | |||
| R2 | NH3 + H ↔ NH2 + H2 | 1.963 × 104 | 2.854 | 8520.2 | PW | |
| R3 | NH3 + OH ↔ NH2 + H2O | 1.559 × 105 | 2.372 | 118.9 | PW | |
| R4 | NH3 + O ↔ NH2 + OH | 4.430 × 102 | 3.180 | 6739.9 | PW | |
| R5 | NH3 + HO2 ↔ NH2 + H2O2 | 1.173 × 100 | 3.839 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260.0 260.0 |
PW | |
| R6 | NH3 + O2 ↔ NH2 + HO2 | 1.415 × 1010 | 1.285 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224.0 224.0 |
PW | |
| R7 | NH2 + NH ↔ N2H2 + H | 1.500 × 1015 | −0.500 | 0.0 | 12 | |
| R8 | NH2 + NH ↔ NH3 + N | 9.600 × 103 | 2.460 | 107.0 | 21 | |
| R9 | NH + NH ↔ NH2 + N | 5.700 × 10−1 | 3.880 | 342.0 | 21 | |
| R10 | NH + NH → N2 + H2 | 6.260 × 1012 | −0.036 | −160.9 | 21 | |
| R11 | NH + NH → N2 + H + H | 5.634 × 1013 | −0.036 | −160.9 | 21 | |
| R12 | NH2 + NH2 ↔ NH3 + NH | 5.640 × 100 | 3.530 | 550.0 | 21 | |
| R13 | NH2 + O2 ↔ HNO + OH | 2.900 × 10−2 | 3.764 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185.0 185.0 |
22 | |
| R14 | NH2 + O2 ↔ H2NO + O | 2.600 × 1011 | 0.487 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050.0 050.0 |
22 | |
| R15 | NH2 + HO2 ↔ OH + H2NO | 1.566 × 1013 | 0.000 | 0.0 | 58 | |
| R16 | NH2 + NO ↔ N2 + H2O | 2.600 × 1019 | −2.369 | 870.0 | 19 | |
| R17 | NH2 + NO ↔ NNH + OH | 4.300 × 1010 | 0.294 | −866.0 | 19 | |
| R18 | NH2 + NO2 ↔ H2NO + NO | 8.600 × 1011 | 0.110 | −1186.0 | 31 | |
| R19 | NH2 + NO2 ↔ N2O + H2O | 2.200 × 1011 | 0.110 | −1186.0 | 31 | |
| R20 | NH2 + H ↔ NH + H2 | 4.000 × 1013 | 0.000 | 3650.0 | 12 | |
| R21 | NH2 + OH ↔ NH + H2O | 9.600 × 106 | 1.970 | 670.0 | 59 | |
| R22 | NH2 + O ↔ NH + OH | 7.000 × 1012 | 0.000 | 0.000 | 55 | |
| Duplicate | 3.300 × 108 | 1.500 | 5076.8 | 55 | ||
| R23 | NH2 + O ↔ HNO + H | 1.500 × 1015 | −0.547 | 836.7 | 60 | |
| Duplicate | 7.730 × 1013 | −0.277 | 646.4 | 60 | ||
| R24 | NH + O2 ↔ HNO + O | 4.050 × 1011 | 0.090 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670.0 670.0 |
61 | |
| R25 | NH + O2 ↔ NO + OH | 2.010 × 1015 | −1.380 | 5670.0 | 61 | |
| R26 | NH + NO ↔ N2O + H | 5.328 × 1012 | 0.026 | −2893.9 | 54 | |
| R27 | NH + NO ↔ N2 + OH | 3.635 × 1010 | 0.361 | −2844.3 | 54 | |
| R28 | HNO ↔ H + NO | 2.0121 × 1019 | −3.021 | 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 792.0 792.0 |
0.1 atm | PW |
| 1.8259 × 1020 | −3.008 | 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880.0 880.0 |
1 atm | |||
| 1.2762 × 1021 | −2.959 | 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100.0 100.0 |
10 atm | |||
| 5.6445 × 1021 | −2.855 | 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 459.0 459.0 |
100 atm | |||
| 9.7111 × 1021 | −2.642 | 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940.0 940.0 |
1000 atm | |||
| R29 | HNO + O2 ↔ NO + HO2 | 2.000 × 1013 | 0.000 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 896.0 896.0 |
55 | |
| R30 | H2NO + H ↔ HNO + H2 | 4.800 × 108 | 1.500 | 1559.8 | 55 | |
| R31 | H2NO + H ↔ NH2 + OH | 4.000 × 1013 | 0.000 | 0.000 | 55 | |
| R32 | H2NO + O ↔ HNO + OH | 3.300 × 108 | 1.500 | 486.8 | 55 | |
| R33 | H2NO + OH ↔ HNO + H2O | 2.400 × 106 | 2.000 | 1192.2 | 55 | |
| R34 | H2NO + NO2 ↔ HNO + HONO | 6.000 × 1011 | 0.000 | 2000.0 | 57 | |
| R35 | H2NO + NH2 ↔ HNO + NH3 | 1.800 × 106 | 1.940 | −580.0 | 55 | |
| R36 | H2NO + O2 ↔ HNO + HO2 | 2.300 × 102 | 2.994 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500.0 500.0 |
31, 36 | |
| R37 | H2NO + HO2 ↔ HNO + H2O2 | 3.360 × 105 | 2.000 | −1434.0 | Estimated | PW |
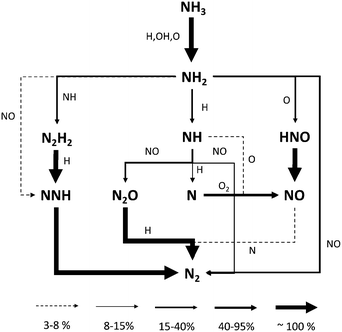
At low temperatures (T < 1200 K), different works31,33,34 highlighted the importance of H2NO and HNO as key species. H2NO is mainly formed from NH2 interaction with O2 and oxygenated species like HO2 and NO2. The delicate competition between the different H-abstraction reactions on H2NO drives the reactivity of the whole system, since abstraction by O2 giving HNO and HO2 (R32) activates the radical branching, while the remaining abstractors deplete H2NO and hinder the branching process. Among them, the only reaction studied at a fundamental level is R36,36 included by Glarborg et al. in their review31 (as well as in the present work) with an activation energy lowered by 2.5 kcal mol−1. Under the investigated conditions, the low temperature and high oxygen concentration resulting in high amounts of HO2 make the related H-abstraction (R37) particularly important. Considering the known kinetic parameters evaluated for the H-abstraction by O2, H-abstraction via HO2 was estimated following the generalized methodology proposed by Ranzi et al.56 to predict kinetic parameters for H-abstraction reactions from hydrocarbons. The obtained constant has a comparable activation energy to that proposed by Dean and Bozzelli,55 but on average it is a factor ∼9 smaller on a T = 500–1500 K interval. The remaining H-abstractions from H2NO (R30–R35) were taken from the evaluations of Dean and Bozzelli,55 or estimations from Glarborg et al.57 Due to the high sensitivity of NH3 reactivity to the H2NO amount at low temperatures, an accurate evaluation of the remaining H-abstractions can be a useful development of this activity; this is especially true in relation to the most stable radicals (i.e. NH2, NO2) at low temperatures, for which Ranzi et al.56 did not propose any correlation.
The complete kinetic mechanism is made up of 31 species and 203 reactions, and is provided as ESI† of this work in CHEMKIN format, together with thermodynamic and transport properties.
3 Results and discussion
3.1 Estimated rate constants
The rate constant of two barrierless decomposition reactions and five H-abstraction reactions were determined theoretically. In particular, the barrierless decomposition of ammonia into NH2 + H and of HNO into NO + H were determined as a function of temperature and pressure solving the master equation, and then fitted in the PLOG format. Ammonia decomposition has been studied in literature both as a forward and backward (recombination) process. The high-pressure rate constant calculated in the present work for ammonia recombination has a slight temperature dependence, increasing from 1.7 × 1014 cm3 mol−1 s−1 to 2.8 × 1014 cm3 mol−1 s−1 going from 300 K to 2500 K. These values are in reasonable agreement with the temperature independent value 1.6 × 1014 cm3 mol−1 s−1 suggested by Glarborg et al.31 The pressure-dependent decomposition rate is deep in its fall-off regime, so that the calculations are significantly affected by the inter molecular collisional energy transfer model adopted in the ME simulations. The experimental literature reports either experimental measurements of ammonia decomposition at high temperatures (higher than 2000 K)12,58 or of NH2 + H recombination rates at room temperature, but a systematic temperature- and pressure-dependent study is not available to the authors' knowledge.62,63 In order to fit both high- and low-temperature data sets, a single exponential energy transfer model was adopted, with a ΔEdown of 130 (T[K]/298)0.8 cm−1. At 1 atm, the calculated rate constant is about a factor of 2 slower than the Davidson et al.12 high temperature experimental decomposition rate, a factor of 2 larger than the high-temperature Baulch recommendation,58 and in excellent agreement with the recent recombination measurement of Altinay and MacDonald,63 on whose data ΔEdown was fitted in the present study. Experimental and theoretical data are compared in Fig. 4.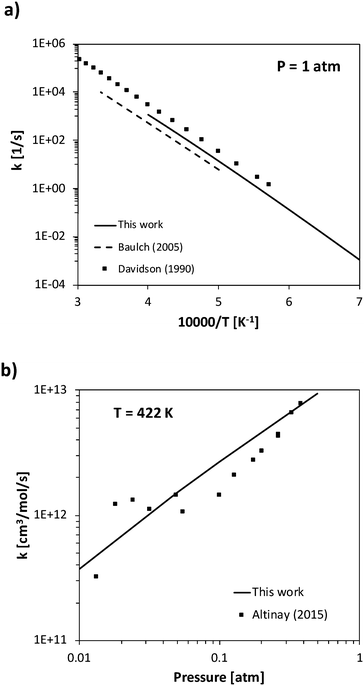 | ||
| Fig. 4 Rate constant calculated a) for ammonia decomposition at 1 atm and b) NH2 + H recombination at 422 K compared with experimental data.12,58,63 | ||
The rate constant for HNO decomposition was determined using the same ΔEdown value used for NH3. The calculated high-pressure H + NO recombination rate is comprised between 2.3 × 1014 cm3 mol−1 s−1 and 1.9 × 1014 cm3 mol−1 s−1 in the 300–2500 K range, thus in reasonably good agreement with the recommendation of Tsang and Herron64 (between 1.2 × 1014 cm3 mol−1 s−1 and 0.6 × 1014 cm3 mol−1 s−1), which has a large uncertainty factor of 5. The low-pressure recombination rate constant is compared with experimental data in Fig. 5. While the experimental data at room temperature are slightly overestimated, the agreement at temperatures higher than 500 K is quite good and fits very well with the data of Glarborg et al.,65 which suggests that the pressure dependence is well caught by the adopted energy transfer model.
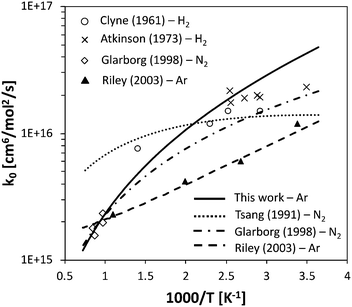 | ||
| Fig. 5 Low-P recombination rate constant of the H + NO reaction, for different bath gases, compared with selected literature data.64–68 | ||
Rate constants were calculated for the five H-abstraction reactions from NH3 by H, OH, O(3P), HO2, and O2. The calculated abstraction rate constants are in general within a factor of 2 from experimental measurements, when available. This is for example the case for H-abstraction by H, where the calculated rate constant is about a factor of 1.7 larger than that measured by Sutherland and Klemm69 and Sutherland and Michael,11 in the 750–1770 K temperature range. Also in the case of H-abstraction by OH, the agreement with literature data is quite good,70–72 well within a factor of 2, as shown in Fig. 6. The energy barrier calculated at the CASPT2 level is 2.2 kcal mol−1, thus about 1 kcal mol−1 smaller than the 3.2 kcal mol−1 determined at the CCSD(T) level, which is consistent with the multireference character of this reaction. A larger disagreement is observed for H-abstraction by O(3P). The calculated rate constant underestimates the experimental measurements of Sutherland et al.73 by about a factor of 2.7 at 800 K. However, the disagreement decreases significantly with temperature, becoming just a factor of 1.2 at 1500 K. This suggests that the calculated energy barrier is probably overestimated, as was also suggested by Klippenstein et al.21 in the study of this reaction channel for their CCSD(T) level energy barrier. It should be noted that, for this reaction channel, the electronic degeneracy of the transition state was assumed to be 6, as the ground and excited state in O(3P) abstraction reactions are nearly degenerate, as observed in a recent study of this reaction class.74
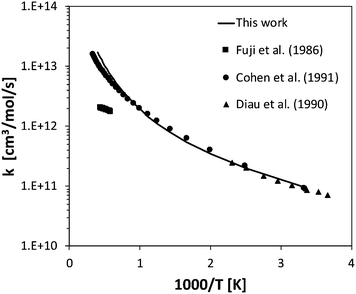 | ||
| Fig. 6 Rate constant calculated for H-abstraction by OH on NH3 compared with selected experimental data.70–72 | ||
For the H-abstraction channels by HO2 and O2, no literature reference is available, so that it is difficult to estimate their uncertainty. The rate constant estimation protocol adopted here is essentially the same as used in the EStokTP benchmark study,44 where it was found that for abstraction reactions the uncertainty was smaller than a factor of 2 when compared to a large experimental data set. Considering the multireference character of several of the investigated reactions, it is though reasonable to assume that, under combustion conditions, the uncertainty factor of these rates may be up to a factor of 3.
For H-abstraction from NH3 by O2, previous works are available on the reverse reaction rate constant, below 500 K (Fig. 7). The photochemical study of Sarkisov et al.75 estimated an overall rate coefficient of 4.5 × 1013 cm3 mol−1 s−1 for the reaction NH2 + HO2 → products at 300 K, while Baulch et al.76 recommended a value of 1.6 × 1013 cm3 mol−1 s−1 between 300 K and 400 K. The fit of the reverse H-abstraction obtained in this work overestimates the value of Sarkisov et al.75 at room temperature by a factor of 2. Anyway, the previous evaluations of Dean and Bozzelli55 and Sumathi et al.77 underestimate the low-temperature data by orders of magnitude. This confirms the significant uncertainty existing in the theoretical evaluation of such an important step in the NH3 oxidation mechanism.
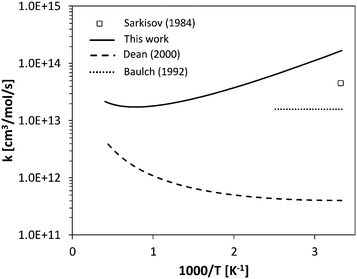 | ||
| Fig. 7 Comparison between calculated rate constant and literature data55,75,76 for reverse H-abstraction by O2 on NH3. | ||
The calculated rate constants are included in Table 1 and in the CHEMKIN format as ESI† to this paper. Input files for the MESS calculations, thus inclusive of energy barriers, stationary points geometries, and of the variational analysis results are also reported as ESI.†
3.2 NH3 oxidation: experiments and kinetic analysis
The gas-phase oxidation of ammonia was investigated under a wide range of operating conditions: following a hierarchical approach, pyrolysis conditions were first considered, followed by high-temperature (T) oxidation, then intermediate- and low-temperatures with variable pressure (P), residence time (τ) and equivalence ratio (Φ), as shown in Table 2. In the following, the new experimental results collected in jet stirred and flow reactors are shown, and analyzed using the newly-developed kinetic model in order to explain the dynamics of conversion from NH3 to final products. The full validation of the mechanism against the case studies listed in Table 2 is provided in the ESI.† For the sake of compactness, only selected cases are analyzed and discussed to highlight the main features of ammonia.| System | Composition | Operating conditions | T | P | Ref. |
|---|---|---|---|---|---|
| JSR | NH3/O2/He | 500 ppm NH3, Φ = 0.01–0.02, τ = 1.5 s | 500–1200 K | 106.7 kPa | PW |
| NH3/NO/O2/He | 500–1000 ppm NH3, 500–1000 ppm NO, Φ = 0.1–2, τ = 0.1 s | 1100–1450 K | 1 atm | 78 | |
| NH3/NO/O2/N2 | 960–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ppm NH3, 400–3000 ppm NO, O2 = 0.8–6%, τ = 374/T[K] s 800 ppm NH3, 400–3000 ppm NO, O2 = 0.8–6%, τ = 374/T[K] s |
950–1450 K | 1 atm | 79 | |
| FR | NH3/O2/He | 1000 ppm NH3, Φ = 0.375, τ = 50 ms | 1200–2000 K | 126.7 kPa | PW |
| NH3/O2/N2 | 242 ppm NH3, O2 = 10%, τ = 339/T[K] s | 850–1250 K | 1 atm | 35 | |
| NH3/O2/N2 | 729 ppm NH3, Φ = 1.23, variable τ | 450–925 K | 30–100 bar | 36 | |
| NH3/O2/N2 | 800 ppm NH3, 2.5% O2, τ = 71/T[K] s | 950–1350 K | 1.05 bar | 80 | |
| ST | NH3/Ar | 2700–3000 ppm NH3 | 2300–2800 K | 0.8–1.1 atm | 12 |
| NH3/O2/Ar | Ar = 98–99%, Φ = 0.5–2 | 1550–2500 K | 1.4–30 atm | 27 | |
| NH3/N2/O2 | N2/O2 = 3.76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Φ = 0.5–2 1, Φ = 0.5–2 |
1100–1600 K | 20–40 bar | 32 | |
| RCM | NH3/O2/N2/Ar | 5–12% NH3, Φ = 0.2–0.5 | 1000–1100 K | 37–75 atm | 33 |
| NH3/O2/Ar | Φ = 0.5–2, 70% Ar | 1000–1130 K | 40–60 bar | 34 | |
| LFS | NH3/N2/O2 | Φ = 0.7–1.65 | 298 K | 1 atm | 81 |
| NH3/O2 | Φ = 0.2–2 | 298 K | 1 atm | 82 | |
| NH3/N2/O2 | Φ = 0.6–1.5, 21–45% O2 | 298 K | 1–5 atm | 83 | |
| BSF | NH3/O2 | 40–65% NH3 – balance O2, v = 60.5 cm s−1 | 300 K | 20 torr | 84 |
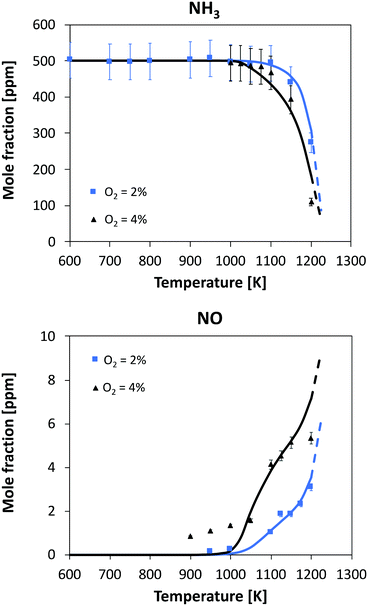 | ||
| Fig. 8 Oxidation of 500 ppm of NH3 in a JSR. Experimental and modeling results. P = 800 torr. τ = 1.5 s. Dashed lines: model extrapolation beyond the maximum reactor temperature. | ||
Considering the highest oxygen concentrations, the reaction starts at relatively high temperatures, i.e. 1100 K and 1025 K with 2% and 4% oxygen, respectively. In both cases, the increase in consumption rate is very slow with temperature but it is opposite to the amount of oxygen: in the 4% case, initial NH3 is halved after 150 K from the reactivity onset, while in the 2% case this occurs after 100 K from the start of consumption. The kinetic model is able to predict this behavior, and at temperatures higher than 1200 K, it predicts a higher conversion with 2% oxygen. No experimental data are available beyond T = 1200 K due to the mechanical resistance of the quartz reactor, but the trend before the maximum allowed temperature also suggests an inversion in reactivity. A satisfactory agreement can also be seen in NO prediction, although the experiments detect an earlier formation of NO with 4% oxygen (∼1 ppm at T = 900 K, where NH3 conversion is close to zero). The shape of both profiles is well predicted by the kinetic model: in particular, at higher temperatures NO yield is predicted to converge to comparable values, i.e. 2% of the initial nitrogen amount. Interestingly, with 4% O2 the NO profile is predicted having a double inflection point, and this is also confirmed by experimental results.
In order to identify the different reaction pathways leading to NH3 conversion and NO formation, reaction flux analyses were performed for two representative conditions, i.e. T = 1050 K and T = 1200 K with 4% initial oxygen, when NH3 conversion is ∼10% and ∼70%, respectively. The diagrams shown in Fig. 9 highlight similarities and differences between the two cases.
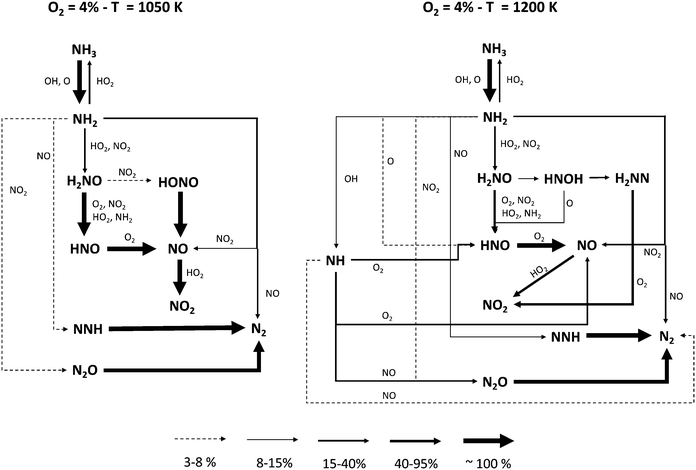 | ||
| Fig. 9 Reaction flux analysis at different temperatures. Flux intensity is relative to the single molecule. For the sake of clarity, reactions between two N-molecules are reported only once. | ||
The major paths converting NH3 into N2 pass through NH2 interaction with NO via R16 and R17 product channels, the latter forming NNH on turn quickly decomposing to N2. NO formation is governed by the formation of H2NO via NH2 reaction with HO2 and NO2, respectively. H2NO is then oxidized to HNO and finally to NO (with a small fraction passing through HONO and its further decomposition). At T = 1050 K, the higher amounts of NO2 caused by the abundance of HO2 radicals in the system enhance NH2 conversion via the two channels of the NH2 + NO2 reaction (R18 and R19), and promote an earlier reactivity. On the other hand, the presence of HO2 radical has a further effect: the flux analysis shows that the initiation reaction R6 is actually reversed, i.e. it behaves like a termination. Therefore, since a higher O2 concentration results in a higher HO2 amount, the increase in reactivity with 4% initial O2 is slower with temperature, until the mixture with 2% O2 becomes more reactive.
At higher temperatures, several major differences must be pointed out. First of all, the smaller amounts of HO2 radicals result in lower NO2 mole fractions. Therefore, NH2 + NO prevails over NH2 + NO2, and the relative weight of the branching channel R17 increases. Moreover, the high-temperature chemistry of NH3 becomes important: the significant presence of OH and O opens new pathways, forming NH radical (R21) and HNO (R23), respectively. The former reacts with NO forming N2 (R26 and R27), either directly or via N2O, while its oxidation with O2 (R24 and R25) ultimately forms NO, whether or not passing through HNO. On the other hand, the reaction with O (R23) allows bypassing the H2NO intermediate in the NH3 oxidation pathway, in such a way that H2NO becomes less and less important at higher temperatures.
The described picture is further confirmed by the sensitivity analysis of NH3 mole fraction, used as representative of the system reactivity. Results are shown in Fig. 10 for two representative conditions, chosen such that a comparable conversion is attained (∼10%).
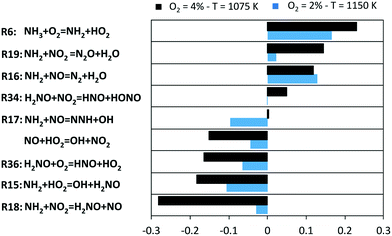 | ||
| Fig. 10 Sensitivity coefficients to NH3 mole fraction in two representative conditions of JSR experiments. | ||
Apparently, the system is controlled by the reactions involving HO2 radicals, and for them, sensitivity coefficients are higher in the O2 = 4% case. The H-abstraction by O2 (R6), in spite of formally being an initiation, actually slows down the reactivity to a significant extent. Indeed, as shown in Fig. 9, R6 rather behaves as a termination step due to the high amounts of HO2 and NH2 radicals. On the other hand, H2NO formation (R15) and successive oxidation (R36) enhance the overall reactivity. With 4% O2, the NO2 channels become critical in regulating NH3 consumption: the formation of H2NO (R18) gives a substantial contribution to the oxidation path (while a contrasting action is played by the termination channel R19). For this reason, the conversion of NO to NO2via HO2 boosts NH3 conversion. Indeed, the branching channel via NO (R17) becomes significant only at higher temperatures, as it can be noticed from the higher sensitivity coefficient of R17 in the O2 = 2% case. In parallel, the channels involving NO2 lose their crucial role with increasing temperature. Finally, the slowing effect of the remaining H-abstractions on H2NO (especially NO2) can be noticed especially at the lowest temperatures, because of the removal of active radicals from the low-temperature oxidation path.
Further examples of NH3 oxidation in JSRs at atmospheric pressure can be found in the ESI,† where in particular the enhancing effect of NO addition is highlighted and the thermal DeNOx model is validated.
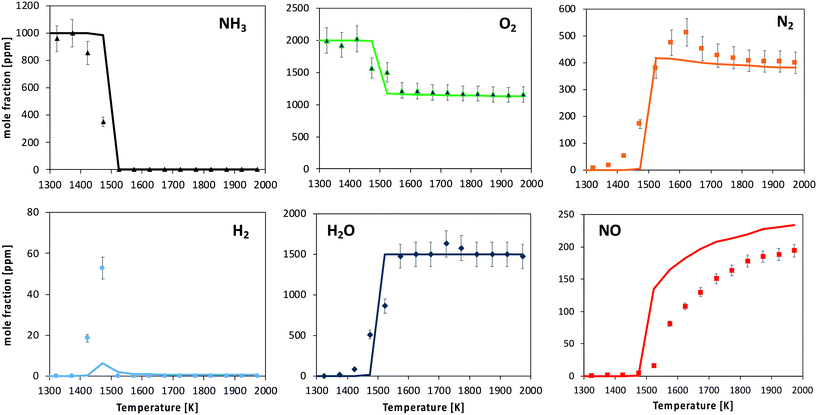 | ||
| Fig. 11 Oxidation of 1000 ppm NH3 with 2000 ppm O2 in a FR. Experimental and modeling results. P = 950 torr. Average τ in the reactive zone is 50 ms. | ||
The kinetic model predicts the ignition temperature reasonably well, and consequently NH3, O2 and H2O profiles. Anyway, the predicted consumption rate of ammonia and product formation is more abrupt than what was experimentally observed. The location of the H2 peak is satisfactorily caught. The onset of NO formation is well reproduced in terms of temperature. However, the predicted NO/N2 ratio is higher than the measured one: the shape of both profiles is well caught, but an overestimation of the NO mole fraction (about 20%) is observed at high-temperature.
Fig. 12 shows the routes leading to NO and N2 formation at intermediate temperatures (i.e. straight after the reactivity onset). Compared to JSR, the pyrolysis mechanism plays a major role. The formation of N2H2via R7 opens a new branching route through NNH, since overall an H atom is released in the conversion from NH2 to N2 (2 if N2H2 undergoes decomposition). The second branching route passes through HNO formation via NH2 + O (R23), then releasing NO as final product.
The competition between the two paths becomes more apparent in the sensitivity analysis shown in Fig. 13, performed right after the reactivity onset, at a reactor length where NH3 is almost fully consumed, and the reactions driving NO/N2 selectivity can be distinguished. It can be observed that under such conditions, the path via HNO (R23 and R28) controls NO formation more than the path via N (thermal NOx). On the other side, the major antagonists to NO selectivity are its reactions with NH and NH2, respectively (R27 and R16), directly converting into N2. Moreover, a higher formation of NH2 (R3), precursor to the formation of both NO and N2, enhances the formation of N2 while having an antagonistic effect on NO. This can be attributed to the combination of higher thermal DeNOx effects (R16) and NH formation via R20, on turn reacting again with NO and providing N2.
Fig. 14 shows the results of 3 different equivalence ratios at various pressures. A satisfactory agreement can be observed for the high-temperature data of Mathieu and Petersen27 in the whole operating range, with a slight underprediction under lean conditions. At intermediate temperatures (1100 K < Tc < 1600 K), the mechanism well reproduces the non-linear behavior of experimental data, due to pre-ignition effects. More significant deviations are can be seen at Φ = 2 and Pc = 40 bar. Yet, especially at the lowest temperatures (∼1100 K), the experimental points at Pc = 20 and 40 bar are essentially overlapped. It must be also pointed out that the strongly irregular trend observed under stoichiometric and rich conditions is due to the different individual pressure histories recorded for the single points, which were used for the numerical simulations. The most critical predictions are observed at the lowest temperatures, i.e. when simulating RCM data by He et al.34 where ignition is slightly underestimated at Φ = 0.5, and overestimated at Φ = 1 and especially Φ = 2.
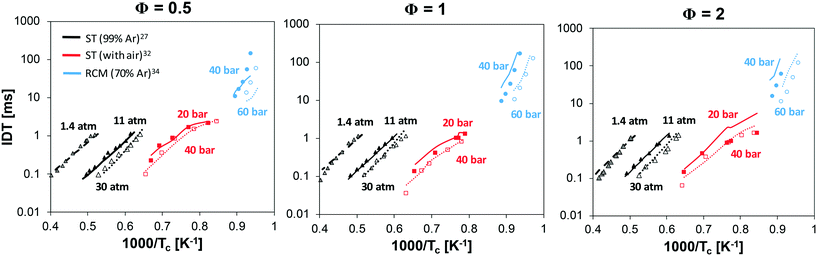 | ||
| Fig. 14 Ignition delay times at low, intermediate and high temperature at variable Φ and Pc: experimental and modeling results. | ||
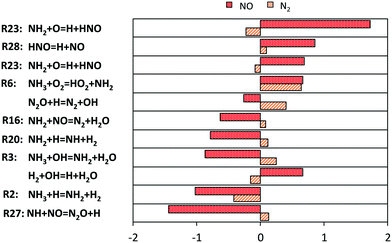
In order to understand the deviations under the richest conditions, a sensitivity analysis for OH mole fraction was performed under 3 representative conditions of the respective experimental campaigns at similar (high) pressures, at the beginning of the ignition phenomenon (∼1% NH3 conversion). Fig. 15 shows the related results: at low and intermediate temperatures, the key role of H2NO is confirmed again, and the reactions promoting its formation (R15 and R18) and H-abstraction via O2 (R36) drive the reactivity of the system. On the other side, the competition between branching and termination in the NH2 + NO path (R16 and R17) has a primary role. On this regard, it is worth mentioning that the adopted rates for this path are pressure-independent. Recently, Klippenstein24 reported a possible stabilization of reaction intermediates at higher pressures, resulting in an increase of the selectivity of the branching route R17. Therefore, considering such dependence could then improve the agreement with the data of He et al.,34 although currently no pressure-dependent rates are available.
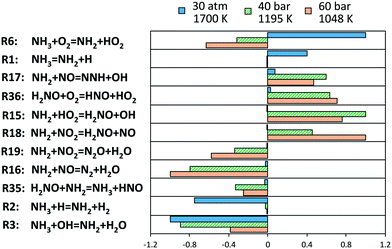 | ||
| Fig. 15 Sensitivity coefficients to OH mole fraction at Φ = 2, normalized with respect to the local maximum value, in correspondence of 1% ammonia conversion. The reaction H + O2 = O + OH is omitted. | ||
Finally, at higher temperatures, the H-abstraction on NH3 by O2 (R6) has an opposite effect with respect to low- and intermediate- temperature, and drives reactivity together with ammonia decomposition (R1), whilst H-abstractions by H and OH slow down the system, since subtracting active radicals from the related pool. In this case, the best agreement is found with the experiments.
A deeper insight within the obtained results was obtained via sensitivity analysis to the flame speed (Fig. 17) for lean, stoichiometric and rich compositions, respectively. In all of them, it can be noticed that the competition between branching and termination of the NH2 + NO reaction is again crucial (R16 and R17), but above all the production of H radicals via NH2 + NH (R7) is the most enhancing path. HNO dissociation, which was studied in this work (R28), is also an important step under lean and stoichiometric conditions. Anyway, the most peculiar result is the inhibiting effect of R23, in spite of its production of H radicals. This can be attributed to the removal of NH2 radicals from the just mentioned branching path R17 as well as R7. In addition, such path removes O radicals from the usual branching paths of the core H2/O2 mechanism. A more accurate estimation of R23 is then a critical milestone of the ammonia mechanism, and to the authors knowledge, the only temperature-dependent theoretical estimations of such constant were obtained by Bozzelli and Dean88 and Sumathi et al.60 (used in this work), differing from each other by a factor or ∼1.4 at 1000–2000 K. R23 also had a boosting effect on the production of NO at intermediate and high-temperatures in flow reactor (Fig. 11 and 13), as already pointed out by Glarborg et al. in their review.31 Therefore, considering the role of R23 within the current mechanism, the accuracy of those two datasets is someway competitive.
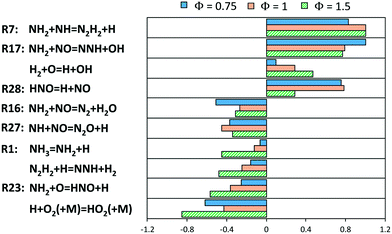 | ||
| Fig. 17 Sensitivity coefficients (normalized with respect to the maximum value) to laminar flame speed at T = 298 K and P = 1 atm for different Φ. The reaction H + O2 = O + OH is not reported. | ||
A more complete validation of the kinetic mechanism in terms of laminar flame speed predictions, with different oxidizer compositions can be found in the ESI.†
4 Conclusions
The renewed interest raised by NH3 combustion in the recent years has made available a significant amount of experimental data, characterizing its reactivity in a wide range of operating conditions. Yet, a comprehensive understanding of its kinetic behavior is still an open challenge, especially at low-temperature (T < 1200 K) and under diluted conditions, on which the combustion community is devoting a significant effort because of the potentially lower NOx emissions. In this work, this topic was addressed through a combined experimental and theoretical approach, able to shed light on the kinetic behavior of ammonia affecting low-temperature, diluted conditions. New experimental data were collected in jet-stirred and flow reactors at pressure close to atmospheric, in such a way to cover the whole range of temperatures (500–2000 K). In order to interpret these results, a theoretical analysis was performed to evaluate some of the most critical steps in the pyrolysis and oxidation mechanisms. By means of sensitivity analysis and literature review, the most critical reaction steps, not yet systematically investigated either experimentally or theoretically, were identified. Thus, the rate constants for ammonia decomposition, H-abstractions and the dissociation of the HNO intermediate were evaluated and included in a comprehensive kinetic model, built up following a first-principles approach, and incorporating the state-of-the-art kinetic rates.The kinetic analysis of the low-temperature experiments allowed the identification of a peculiar behavior. Up to ∼1200 K, the high amount of HO2 radicals present in the system results in the inversion of the initiation via O2, i.e. NH3 + O2 = NH2 + HO2 (recalculated in this work) acting instead as a termination step. Therefore, the reactivity of the systems is shifted to higher temperatures, and is distributed in a wider temperature range with increasing O2 concentration. The key role of H2NO was highlighted, as already reported in the literature, and the related H-abstractions by O2, HO2, NH2 and NO2 were found to affect reactivity at the lowest temperatures.
The comprehensiveness of the kinetic mechanism was also verified in the prediction of ignition delay time and flame propagation, where the key role of the newly-introduced kinetic rates was confirmed. At higher pressures and low temperatures, H2NO was found to play a pivotal role in controlling ignition delay time. In this regard, theoretical work for the estimation of the H-abstractions on H2NO and the effect of pressure on NH2 + NO selectivity could further improve the predictability of the kinetic model in such conditions. Lastly, the prediction of laminar flame speeds highlighted the key, decelerating effect of the reaction NH2 + O = HNO + H, which promotes instead NO formation at high temperature, as found out in the analysis of flow reactor experiments. Further theoretical study on it can be useful for a more accurate, temperature-dependent re-evaluation of this step.
Nomenclature
Roman symbols
| P | Pressure [Pa] |
| T | Temperature [K] |
Greek symbols
| τ | Residence time [s] |
| Φ | Equivalence ratio [−] |
Acronyms
| BSF | Burner-stabilized flame |
| DFT | Density functional theory |
| FR | Flow reactor |
| IDT | Ignition delay time |
| JSR | Jet-stirred reactor |
| LFS | Laminar flame speed |
| ME | Master equation |
| NOx | Nitrogen oxides |
| PES | Potential energy surface |
| ppm | Parts per million |
| PW | Present work |
| RCM | Rapid compression machine |
| ST | Shock tube |
| VTST | Variational transition state theory |
Subscripts
| c | After compression |
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work has been carried out under the financial support of the IMPROOF project (H2020-IND-CE-2016-17/H2020-SPIRE-S016) within the European Union Horizon 2020 research and innovation program (grant agreement no. 723706), and of the COST Action CM1404 “Chemistry of smart energy carriers and technologies”. The authors are also grateful to Prof. Christine Rousselle (Université d'Orléans) for the fruitful discussions.References
- J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636–639 CrossRef.
- H. Kobayashi, A. Hayakawa, K. D. K. A. Somarathne and E. C. Okafor, Proc. Combust. Inst., 2019, 37, 109–133 CrossRef.
- F. Jiao and B. Xu, Adv. Mater., 2019, 31, 1805173 CrossRef PubMed.
- D. Miura and T. Tezuka, Energy, 2014, 68, 428–436 CrossRef CAS.
- J. Ikäheimo, J. Kiviluoma, R. Weiss and H. Holttinen, Int. J. Hydrogen Energy, 2018, 43, 17295–17308 CrossRef.
- D. P. B. T. B. Strik, A. M. Domnanovich and P. Holubar, Process Biochem., 2006, 41, 1235–1238 CrossRef CAS.
- L. Appels, J. Baeyens, J. Degrève and R. Dewil, Prog. Energy Combust. Sci., 2008, 34, 755–781 CrossRef CAS.
- R. O. Arazo, D. A. D. Genuino, M. D. G. de Luna and S. C. Capareda, Sustainable Environ. Res., 2017, 27, 7–14 CrossRef CAS.
- M. Yumura, T. Asaba, Y. Matsumoto and H. Matsui, Int. J. Chem. Kinet., 1980, 12, 439–450 CrossRef CAS.
- J. V. Michael, J. W. Sutherland and R. B. Klemm, Int. J. Chem. Kinet., 1985, 17, 315–326 CrossRef CAS.
- J. W. Sutherland and J. V. Michael, J. Chem. Phys., 1988, 88, 830–834 CrossRef CAS.
- D. F. Davidson, K. Kohse-Höinghaus, A. Y. Chang and R. K. Hanson, Int. J. Chem. Kinet., 1990, 22, 513–535 CrossRef.
- M. Yumura and T. Asaba, Symp. Combust., 1981, 18, 863–872 CrossRef.
- R. M. Green and J. A. Miller, J. Quant. Spectrosc. Radiat. Transfer, 1981, 26, 313–327 CrossRef.
- J. A. Miller, M. D. Smooke, R. M. Green and R. J. Kee, Combust. Sci. Technol., 1983, 34, 149–176 CrossRef.
- J. Bian, J. Vandooren and P. J. Van Tiggelen, Symp. Combust., 1988, 21, 953–963 CrossRef.
- R. K. Lyon, Environ. Sci. Technol., 1987, 21, 231–236 CrossRef PubMed.
- J. Park and M. C. Lin, Int. J. Chem. Kinet., 1996, 28, 879–883 CrossRef CAS.
- S. Song, R. K. Hanson, C. T. Bowman and D. M. Golden, J. Phys. Chem. A, 2002, 106, 9233–9235 CrossRef CAS.
- M. S. Wooldridge, R. K. Hanson and C. T. Bowman, Symp. Combust., 1994, 25, 741–748 CrossRef.
- S. J. Klippenstein, L. B. Harding, B. Ruscic, R. Sivaramakrishnan, N. K. Srinivasan, M. C. Su and J. V. Michael, J. Phys. Chem. A, 2009, 113, 10241–10259 CrossRef CAS PubMed.
- S. J. Klippenstein, L. B. Harding, P. Glarborg and J. A. Miller, Combust. Flame, 2011, 158, 774–789 CrossRef CAS.
- S. J. Klippenstein, L. B. Harding, P. Glarborg, Y. Gao, H. Hu and P. Marshall, J. Phys. Chem. A, 2013, 117, 9011–9022 CrossRef CAS PubMed.
- S. J. Klippenstein, Proc. Combust. Inst., 2017, 36, 77–111 CrossRef CAS.
- J. A. Miller and C. T. Bowman, Prog. Energy Combust. Sci., 1989, 15, 287–338 CrossRef CAS.
- A. A. Konnov and J. De Ruyck, Combust. Sci. Technol., 2000, 152, 23–37 CrossRef CAS.
- O. Mathieu and E. L. Petersen, Combust. Flame, 2015, 162, 554–570 CrossRef CAS.
- P. Dagaut, P. Glarborg and M. U. Alzueta, Prog. Energy Combust. Sci., 2008, 34, 1–46 CrossRef CAS.
- K. P. Shrestha, L. Seidel, T. Zeuch and F. Mauss, Energy Fuels, 2018, 32, 10202–10217 CrossRef CAS.
- R. Li, A. A. Konnov, G. He, F. Qin and D. Zhang, Fuel, 2019, 257, 116059 CrossRef CAS.
- P. Glarborg, J. A. Miller, B. Ruscic and S. J. Klippenstein, Prog. Energy Combust. Sci., 2018, 67, 31–68 CrossRef.
- B. Shu, S. K. Vallabhuni, X. He, G. Issayev, K. Moshammer, A. Farooq and R. X. Fernandes, Proc. Combust. Inst., 2019, 37, 205–211 CrossRef CAS.
- M. Pochet, V. Dias, B. Moreau, F. Foucher, H. Jeanmart and F. Contino, Proc. Combust. Inst., 2019, 37, 621–629 CrossRef.
- X. He, B. Shu, D. Nascimento, K. Moshammer, M. Costa and R. X. Fernandes, Combust. Flame, 2019, 206, 189–200 CrossRef.
- V. J. Wargadalam, G. Löffler, F. Winter and H. Hofbauer, Combust. Flame, 2000, 120, 465–478 CrossRef.
- Y. Song, H. Hashemi, J. M. Christensen, C. Zou, P. Marshall and P. Glarborg, Fuel, 2016, 181, 358–365 CrossRef.
- R. C. da Rocha, M. Costa and X. S. Bai, Fuel, 2019, 24–33 CrossRef.
- Y. Song, L. Marrodán, N. Vin, O. Herbinet, E. Assaf, C. Fittschen, A. Stagni, T. Faravelli, M. U. Alzueta and F. Battin-Leclerc, Proc. Combust. Inst., 2019, 37, 667–675 CrossRef.
- L. Marrodán, Y. Song, M. Lubrano Lavadera, O. Herbinet, M. De Joannon, Y. Ju, M. U. Alzueta and F. Battin-Leclerc, Energy Fuels, 2019, 33, 5655–5663 CrossRef.
- M. Pelucchi, S. Namysl, E. Ranzi, A. Frassoldati, O. Herbinet, F. Battin-Leclerc and T. Faravelli, Proc. Combust. Inst., 2019, 37, 389–397 CrossRef CAS.
- J. Villermaux, Génie de la réaction chimique: conception et fonctionnement des réacteurs, Tec & Doc Lavoisier, Paris, 2nd edn, revue et augmentée, 1993 Search PubMed.
- C. Bahrini, O. Herbinet, P. A. Glaude, C. Schoemaecker, C. Fittschen and F. Battin-Leclerc, J. Am. Chem. Soc., 2012, 134, 11944–11947 CrossRef CAS PubMed.
- L. Marrodán, Y. Song, O. Herbinet, M. U. Alzueta, C. Fittschen, Y. Ju and F. Battin-Leclerc, Chem. Phys. Lett., 2019, 719, 22–26 CrossRef.
- C. Cavallotti, M. Pelucchi, Y. Georgievskii and S. J. Klippenstein, J. Chem. Theory Comput., 2019, 15, 1122–1145 CrossRef CAS PubMed.
- Y. Georgievskii, J. A. Miller, M. P. Burke and S. J. Klippenstein, J. Phys. Chem. A, 2013, 117, 12146–12154 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 09, Rev. D.01, Gaussian Inc., Wallingford, CT, 2010 Search PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a General-Purpose Quantum Chemistry Program Package, 2010, http://www.molpro.net Search PubMed.
- E. Ranzi, A. Frassoldati, R. Grana, A. Cuoci, T. Faravelli, A. P. Kelley and C. K. Law, Prog. Energy Combust. Sci., 2012, 38, 468–501 CrossRef CAS.
- W. K. Metcalfe, S. M. Burke, S. S. Ahmed and H. J. Curran, Int. J. Chem. Kinet., 2013, 45, 638–675 CrossRef CAS.
- T. Faravelli, A. Frassoldati and E. Ranzi, Combust. Flame, 2003, 132, 188–207 CrossRef CAS.
- A. Frassoldati, T. Faravelli and E. Ranzi, Combust. Flame, 2003, 135, 97–112 CrossRef CAS.
- X. Chen, M. E. Fuller and C. Franklin Goldsmith, React. Chem. Eng., 2019, 4, 323–333 RSC.
- A. Burcat and B. Ruscic, Third millennium ideal gas and condensed phase thermochemical database for combustion with updates from active thermochemical tables, 2005, vol. ANL-05/20 Search PubMed.
- N. L. Haworth, J. C. Mackie and G. B. Bacskay, J. Phys. Chem. A, 2003, 107, 6792–6803 CrossRef CAS.
- A. M. Dean and J. W. Bozzelli, in Gas-Phase Combustion Chemistry, 2000, pp. 125–341 Search PubMed.
- E. Ranzi, M. Dente, T. Faravelli and G. Pennati, Combust. Sci. Technol., 1994, 95, 1–50 CrossRef CAS.
- P. Glarborg, P. G. Kristensen, K. Dam-Johansen, M. U. Alzueta, A. Millera and R. Bilbao, Energy Fuels, 2000, 14, 828–838 CrossRef CAS.
- D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, T. Just, J. A. Kerr, M. J. Pilling, D. Stocker, J. Troe, W. Tsang and others, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397 CrossRef CAS.
- S. H. Mousavipour, F. Pirhadi and A. Habibagahi, J. Phys. Chem. A, 2009, 113, 12961–12971 CrossRef CAS PubMed.
- R. Sumathi, D. Sengupta and M. T. Nguyen, J. Phys. Chem. A, 1998, 102, 3175–3183 CrossRef CAS.
- M. R. Talipov, S. L. Khursan and R. L. Saflullin, J. Phys. Chem. A, 2009, 113, 6468–6476 CrossRef CAS PubMed.
- P. B. Pagsberg, J. Eriksen and H. C. Christensen, J. Phys. Chem., 1979, 83, 582–590 CrossRef CAS.
- G. Altinay and R. G. MacDonald, J. Phys. Chem. A, 2012, 116, 1353–1367 CrossRef CAS PubMed.
- W. Tsang and J. T. Herron, J. Phys. Chem. Ref. Data, 1991, 20, 609–663 CrossRef CAS.
- P. Glarborg, M. Østberg, M. U. Alzueta, D. J. Kim and J. A. Miller, in Symposium (International) on Combustion, 1998, vol. 27, pp. 219–226 Search PubMed.
- M. A. A. Clyne and B. A. Thrush, Trans. Faraday Soc., 1961, 57, 1305–1314 RSC.
- R. Atkinson and R. J. Cvetanović, Can. J. Chem., 1973, 51, 370–372 CrossRef CAS.
- P. S. Riley, B. Cosic and A. Fontijn, Int. J. Chem. Kinet., 2003, 35, 374–380 CrossRef CAS.
- J. W. Sutherland and R. B. Klemm, Kinetic studies of elementary reactions using the flash photolysis-shock tube technique, 1987, vol. 16 Search PubMed.
- N. Cohen and K. R. Westberg, J. Phys. Chem. Ref. Data, 1983, 12, 531–590 CrossRef CAS.
- N. Fujii, S. Uchida, H. Sato, S. Fujimoto and H. Miyama, Bull. Chem. Soc. Jpn., 1986, 59, 3431–3437 CrossRef CAS.
- E. W. G. Diau, T. L. Tso and Y. P. Lee, J. Phys. Chem., 1990, 94, 5261–5265 CrossRef CAS.
- J. W. Sutherland, P. M. Patterson and R. B. Klemm, J. Phys. Chem., 1990, 94, 2471–2475 CrossRef.
- C. Cavallotti, F. Leonori, N. Balucani, V. Nevrly, A. Bergeat, S. Falcinelli, G. Vanuzzo and P. Casavecchia, J. Phys. Chem. Lett., 2014, 5, 4213–4218 CrossRef PubMed.
- O. M. Sarkisov, S. G. Cheskis, V. A. Nadtochenko, E. A. Sviridenkov and V. I. Vedeneev, Arch. Combust., 1984, 4, 111–120 Search PubMed.
- D. L. Baulch, M. J. Pilling, C. J. Cobos, R. A. Cox, C. Esser, P. Frank, T. Just, J. A. Kerr, J. Troe, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 1992, 21, 411–734 CrossRef.
- R. Sumathi and S. D. Peyerimhoff, Chem. Phys. Lett., 1996, 263, 742–748 CrossRef.
- P. Dagaut and A. Nicolle, Proc. Combust. Inst., 2005, 30, 1211–1218 CrossRef.
- R. Rota, D. Antos, E. F. Zanoelo and S. Carrà, Combust. Sci. Technol., 2001, 163, 25–47 CrossRef CAS.
- T. Hulgaard and K. Dam-Johansen, AIChE J., 1993, 39, 1342–1354 CrossRef CAS.
- P. D. Ronney, Combust. Sci. Technol., 1988, 59, 123–141 CrossRef CAS.
- Q. Liu, X. Chen, J. Huang, Y. Shen, Y. Zhang and Z. Liu, J. Hazard. Mater., 2019, 363, 187–196 CrossRef CAS PubMed.
- B. Mei, X. Zhang, S. Ma, M. Cui, H. Guo, Z. Cao and Y. Li, Combust. Flame, 2019, 210, 236–246 CrossRef CAS.
- D. I. Maclean and H. G. Wagner, in Symposium (International) on Combustion, 1967, vol. 11, pp. 871–878 Search PubMed.
- A. Hayakawa, T. Goto, R. Mimoto, Y. Arakawa, T. Kudo and H. Kobayashi, Fuel, 2015, 159, 98–106 CrossRef CAS.
- H. Nakamura and M. Shindo, Proc. Combust. Inst., 2019, 37, 1741–1748 CrossRef CAS.
- M. F. Modest, Radiative Heat Transfer, 2nd edn, 2003 Search PubMed.
- J. W. Bozzelli and A. M. Dean, J. Phys. Chem., 1989, 93, 1058–1065 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9re00429g |
| This journal is © The Royal Society of Chemistry 2020 |