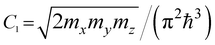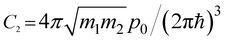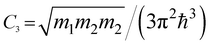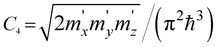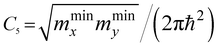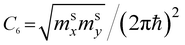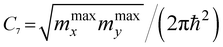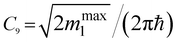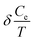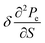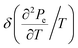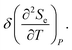Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Role of the Lifshitz topological transitions in the thermodynamic properties of graphene
V. N.
Davydov

M. V. Lomonosov Moscow State University, Leninsky pr. 71, app. 121, 117296 Moscow, Russia. E-mail: vladimirdavydov@yahoo.com
First published on 22nd July 2020
Abstract
The origin of the Lifshitz topological transition (LTT) and the 2D nature of the LTT in graphene has been established. The peculiarities of the Lifshitz topological transitions in graphene are described at the Brillouin zone centre Γ, the zone corners K in the vicinity of the Dirac points, and at the saddle point M. A general formulation of the thermodynamics at the LTT in graphene is given. The thermodynamic characteristics of graphene are investigated at the Lifshitz topological transitions. Anomalies are found in the electron specific heat Ce, the electron thermal coefficient of pressure, and the coefficients of electron compressibility and thermal expansion in graphene at the LTT. All the thermodynamic parameters possess the strongest singularities in graphene at the LTT near the saddle points. This opens exciting opportunities for inducing and exploring the Lifshitz topological transitions in graphene.
1 Introduction
Anomalies in the thermodynamic quantities of metals due to a change in the topology of the Fermi surface ε(p) = εF are customarily called the Lifshitz topological transition (LTT) (I. M. Lifshitz;1 see also ref. 2, 3 and 4). It is understood that a change in the topology of the Fermi boundary surface is due to the continuous variation of some parameter (e.g., pressure), as a result of which the difference z = εF − εc (where εF is the Fermi energy and εc is the critical energy at which the topology of the constant energy surface changes) passes through zero continuously. This leads to a change in the connectivity of the Fermi surface (the appearance of a new cavity, the rupture of a connecting neck, etc.), and at absolute zero temperature T = 0 K, the grand thermodynamic potential Ω (often called the Landau free energy or Landau potential5) acquires an irregular correction:| δΩ = −α|z|5/2. | (1.1) |
It can be seen that the third derivatives of the thermodynamic potential become infinite at the point z = μ − εc = 0 (the chemical potential μ is equal to the Fermi energy εF at T = 0); therefore, this change in the topology of the Fermi surface is also called the 2½-order phase transition (FT2½) according to the Ehrenfest terminology.6,7
The anomalies arising in the LTT manifest themselves at T ≪ εF not only in the thermodynamic characteristics of metals but also in other characteristics (e.g., magnetic-field dependence of the electrical resistance,8 sound absorption9–15). It has been shown in ref. 16 that the thermoelectric power has the square root divergency at the LTT. The discovery of graphene17 gave new inspiration to investigations of the Lifshitz transition properties. To date, numerous papers have been devoted to the Lifshitz transitions in bilayer (BLG) and multilayer (MLG) graphene.18–30 The results of these studies indicate that the effects of the LTT are appreciable and can be used to observe the 2½-order transitions as well as to investigate the degree of smearing of the Fermi surface in metals. In ref. 31, experimental evidence was obtained of the Lifshitz transition in the thermoelectric power of ultrahigh mobility bilayer graphene. Resolving low-energy features in the density of states (DOS) holds the key to understanding a wide variety of rich and novel phenomena in graphene based on 2D heterostructures. The Lifshitz transition in bilayer graphene (BLG) arising from trigonal warping has been established in31 theoretically and experimentally.
The 21st century has brought many new results related to graphene thermodynamics.32–45 Apparently, the thermodynamics of graphene has been characterized from many points of view; however, the role of the Lifshitz topological transitions in the thermodynamic properties of graphene has not been studied. This paper aims to close this gap. Because graphene is the first real two-dimensional solid, a general formulation of the thermodynamics at the LTT in graphene is given. The unusual thermodynamic properties of graphene stem from its 2D nature, forming a rich playground for new discoveries of heat flow physics and potentially leading to novel thermal management applications.
This paper is arranged as follows. In section 2, the origin of the Lifshitz topological transition and the 2D nature of the LTT in graphene are considered. Peculiarities of the Lifshitz topological transitions in graphene are then investigated in section 3. The thermodynamics of graphene at the Lifshitz topological transitions is proposed in section 4. Finally, conclusions are drawn in section 5.
2 Origin of the Lifshitz topological transitions and connection of the two-dimensional nature of graphene with the van Hove singularities
It is known [see ref. 1, 2, and 3] that at the LTT, a new cavity of the electronic isoenergetic surface appears (or disappears) at the critical energy εc in the critical point of the momentum space p = pc, where the electron energy as a function of quasimomentum ε = ε(p) has a minimum εmin or maximum εmax. In this case, the isoenergetic surfaces in the vicinity of p = pc are well described by the ellipsoid equations: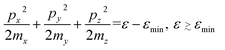 | (2.1) |
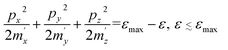 | (2.2) |
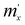 ,
,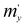 , and
, and 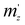 are the main values of the effective mass tensor in the vicinity of εmax.45
are the main values of the effective mass tensor in the vicinity of εmax.45
At the neck rupture, the boundary isoenergetic surface ε(p) = εc contains the peculiar point of another type, named the cone point, at p = pc. In this case, the isoenergetic surface in the vicinity of the cone point p = pc is described by the hyperboloid of two sheets at energy ε < εc and the hyperboloid of one sheet at energy ε > εc (Fig. 1a):
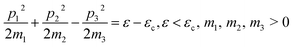 | (2.3) |
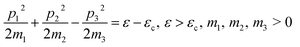 | (2.4) |
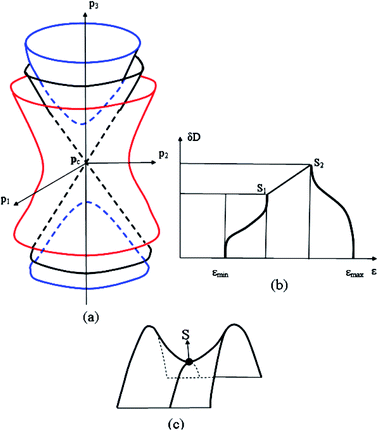 | ||
| Fig. 1 The cone point at p = pc (a), the saddle point (c), and the van Hove singularities of the state density δD(ε) (b). S, S1, and S2 are the saddle points. | ||
At energies close to εc, one can express the electron density of states (DOS) as
| D(ε) = D0(ε) + δD(ε) | (2.5) |
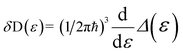 | (2.6) |
One can join eqn (2.1)–(2.4) into a single equation:
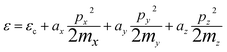 | (2.7) |
Four types of singularities exist of the density of the electron states in three-dimensional space, and the singularity type depends on the signs of the coefficients aj.
The point M0 (min) corresponds to the case where all three coefficients aj = +1. This point corresponds to the minimum in the energy spectrum.
The point M1 (saddle) corresponds to the case where two coefficients aj are positive and the third one is negative. This is the saddle point (Fig. 1c).
The point M2 (saddle) is the case where two coefficients aj are negative and a third one is positive. This is the second saddle point (Fig. 1b).
The point M3 (max) corresponds to the case where all three coefficients aj = −1. This point corresponds to the maximum in the energy spectrum.
There are three types of singularities of the density of the electron states in two-dimensional space, and the singularity type depends on the signs of the coefficients aj (j = x, y).
The point P0 (min) corresponds to the case where both coefficients aj = +1. This point corresponds to the minimum in the energy spectrum.
The point P1 (saddle) corresponds to the case where one coefficient aj is positive and another one is negative. This is the saddle point.
The point P2 (max) corresponds to the case where both coefficients aj = −1. This point corresponds to the maximum in the energy spectrum.
There are two types of singularities of the density of the electron states in one-dimensional space:
• The point Q0 (min) corresponds to the case where coefficient a = +1. This point corresponds to the minimum in the energy spectrum.
• The point Q1 (max) corresponds to the case where coefficient a = −1. This point corresponds to the maximum in the energy spectrum.
The analytical behavior of the density of the electron states at LTT is given in Table 1. The results are computed from formulae (2.1)–(2.7); see also ref. 1, 2, and 4.
We can conclude based on the square root peculiarities of the density of the electron states in three dimensions (Table 1) at εc that nature of the Lifshitz topological transition stems from the van Hove singularities (VHS) of the state density δD(ε).48–52 In this connection, the van Hove topological theorem48 states that the spectrum must contain at least one of the saddle-points S1 and S2 (Fig. 1b), and the slope of D(ε) must tend to −∞ on the upper end.
The two-dimensional nature of graphene should exhibit special types of van Hove singularities and LTTs. This statement is illustrated by the general argument that in two dimensions, the saddle-points produce logarithmic singularities (Table 1), and the spectrum extrema produce finite discontinuities of the electron density of states [also see ref. 49, 53, and 54]. This is valid for the elementary excitations of the quasiparticles with values mi ≠ 0 of the effective mass tensor; however, it is not applied to the massless Dirac fermions in graphene. If the logarithmic singularity is a general property of 2D electronic systems in the saddle points, this statement should be valid for 2D graphene. However, the latter is in contradiction with 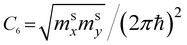 because the value of C6 must be zero for the massless fermions in graphene. Here, the discrepancy arises because the logarithmic singularity vanishes. We will resolve this contradiction in section 3.
because the value of C6 must be zero for the massless fermions in graphene. Here, the discrepancy arises because the logarithmic singularity vanishes. We will resolve this contradiction in section 3.
Therefore, the Lifshitz topological transitions in graphene require special investigation. The latter was also confirmed by recent work.55 It has been demonstrated in55 theoretically that the characteristic feature of a 2D system undergoing N consequent Lifshitz topological transitions is the occurrence of spikes of entropy per particle s of a magnitude ± ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/(J − 1/2) with 2 ≤ J ≤ N at low temperatures.
2/(J − 1/2) with 2 ≤ J ≤ N at low temperatures.
3 Peculiarities of the Lifshitz topological transitions in graphene
A single layer of graphene consists of carbon atoms in the form of a honeycomb lattice (Fig. 2). The primitive translation vectors e1 and e2 form the rhombic unit cell. The hexagonal lattice consists of two trigonal sublattices AAA and BBB.56 There are four valence electrons (two 2s and two 2p electrons). Three of those participate in the chemical bonding and thus are in bands well below the Fermi energy. We therefore consider the bands formed by the one remaining electron. We assume a tight-binding model in which the electron hops between neighboring atoms. We denote the spacing between neighbouring atoms by a.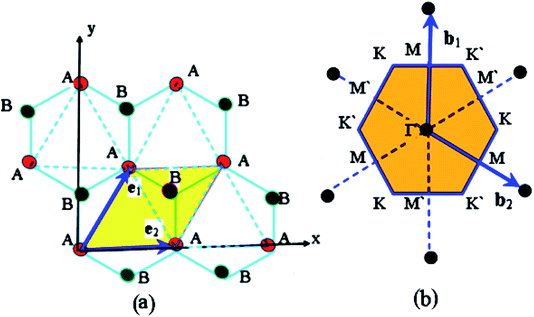 | ||
Fig. 2 (Reproduced and adapted with permission from ref. 56). The crystal structure of the single graphite layer (a). The primitive translation vectors e1 and e2 form the rhombic unit cell, and the basis consists of two C atoms, shown as A and B. The Bravais lattice (consider, e.g., the lattice formed by the A atoms) is triangular with a Bravais lattice spacing of 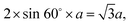 where a is the spacing between neighboring atoms. The graphene reciprocal lattice and the first Brillouin zone (b). where a is the spacing between neighboring atoms. The graphene reciprocal lattice and the first Brillouin zone (b). | ||
From Fig. 2a, we see that two basis vectors of the Bravais lattice are
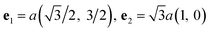 | (3.1) |
The reciprocal Bravais lattices, b1 and b2, are defined such that
| bi·ej = 2πδij | (3.2) |
The result is
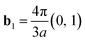 | (3.3) |
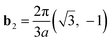 | (3.4) |
These basis vectors are of equal length and at 120°; therefore, the reciprocal lattice is a hexagonal lattice (Fig. 2b). The first Brillouin zone is shown in Fig. 2b. The first Brillouin zone is a regular hexagon, whose most characteristic points are its centre Γ, the inequivalent corners K and K′, and the centres of the lateral edges M and M'. The distance ΓM is 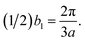 The distance ΓΚ is
The distance ΓΚ is 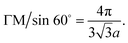
Consider a state with amplitude ΨR for the electron to be at the site labeled by R. We look for the wave functions with amplitudes which vary, such as eik·r. There will be different amplitudes ΨA and ΨB on sublattices A and B, so ΨR = ΨAeik·r (R ∈ A), and ΨR = ΨBeik·r (R ∈ B). An electron at site R can hop to any of the neighboring sites. An atom on sublattice AAA has neighboring atoms (Fig. 2a), all on sublattice BBB, at displacements (0, a), 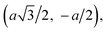 and
and 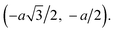 An atom on sublattice BBB has three neighbors on sublattice AAA at displacements (0, −a),
An atom on sublattice BBB has three neighbors on sublattice AAA at displacements (0, −a), 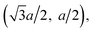 and
and 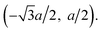 In the nearest-neighbour approximation, there are no hopping processes within the sublattices AAA and BBB; hopping only occurs between them. Hence, the eigenvalue ε and the amplitudes ΨA and ΨB are determined for each wavevector k from two equations:
In the nearest-neighbour approximation, there are no hopping processes within the sublattices AAA and BBB; hopping only occurs between them. Hence, the eigenvalue ε and the amplitudes ΨA and ΨB are determined for each wavevector k from two equations:
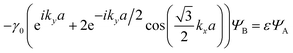 | (3.5) |
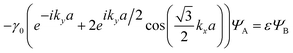 | (3.6) |
We write the Hamiltonian in the tight-binding approximation for the wave vector k = p/ħ (where p is the electron quasimomentum), taking into account eqn (3.5) and (3.6), as
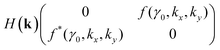 | (3.7) |
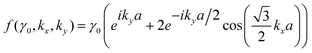 | (3.8) |
The electron energy eigenvalues of the Hamiltonian (3.7) are given by
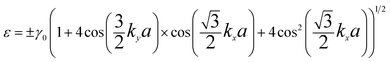 | (3.9) |
In expression (3.9), the plus and minus signs correspond to the conduction and valence bands, respectively.
To explore the possible Lifshitz topological transitions, consider the structure of the isoenergetic lines in the (kx, ky) plane for different positions of the wave vector k.
(i) The maximum and minimum energies are εc = ±3γ0, and they occur at k = 0, i.e. in the centre Γ (Fig. 2b) of the first Brillouin zone. The value of εc = 3γ0 corresponds to the maximum of energy in the conduction band (the point P2 (max) in Table 1). The value of εc = −3γ0 corresponds to the minimum of energy in the valence band (the point Po (min) in Table 1). Taking into account |kya|, |kxa| ≪ 1, from (3.9), we have accuracy of order (kya)2, (kxa)2:
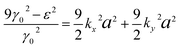 | (3.10) |
Thus, the isoenergetic lines are circles in the vicinity of the extrema of energy at k = 0. It follows from (3.10) that these circles are described by the following equation in p-space:
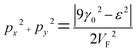 | (3.11) |
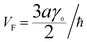 | (3.12) |
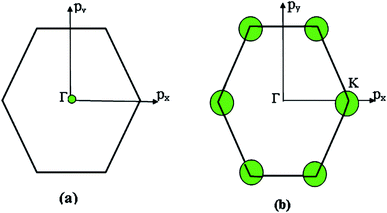
Consequently, there exist LTT at critical values of energy εc = ±3γ0, where the cavity (3.11) of the isoenergetic lines disappears (Fig. 3a) at εc = +3γ0 in the conduction band or appears at εc = −3γ0 in the valence band.
The number of the electron states inside the two-dimensional cavity (per spin direction and per unit area) is equal to
| δN(ε) = (1/2πħ)2Δ(ε) | (3.13) |
We obtain from (3.11) and (3.13)
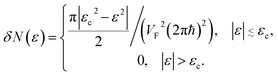 | (3.14) |
One can represent the change of the density of states δD(ε) due to LTT as
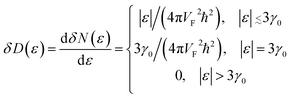 | (3.15) |
The discontinuity at the end points ε = ±3γ0 comes from a maximum or minimum of the dispersion relation in two dimensions. The analytic expression without derivation for the total DOS in graphene for model (3.7) was provided by Hobson and Nierenberg in 1953.53 In a recent paper,54 the expression for this model was derived for the total DOS (per unit hexagonal cell of area 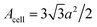 (Fig. 2a) and one spin component), valid for region 0 < |ε| < 3γ0:
(Fig. 2a) and one spin component), valid for region 0 < |ε| < 3γ0:
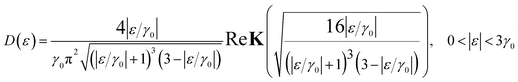 | (3.16) |
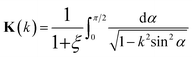 | (3.17) |
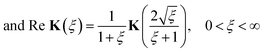 | (3.18) |
Expanding of (3.16) near the point Γ in the small region |ε| ≲ 3γ0 in the vicinity of the LTT points |εc| = 3γ0, one obtains (per spin direction and per unit area):
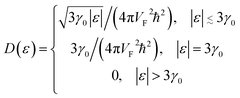 | (3.19) |
The result (3.15) for δD (ε) coincides with the total D(ε) given by (3.19) in the region |ε| ≲ 3γ0 in the vicinity of the LTT points |εc| = 3γ0, where 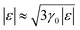 at |ε| ≲ 3γ0.
at |ε| ≲ 3γ0.
As follows from (3.19), for graphene in the vicinity of the point Γ, the coefficients C5 and C7 in Table 1 should be changed as
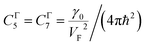 | (3.20) |
Hence, in 2D graphene, the mass-factors of coefficients C5 and C7 in Table 1 acquire the substitutions of γ0/VF2 instead of 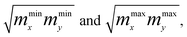 respectively, and this substitution can be treated as the fermion effective mass in the vicinity of the point Γ:
respectively, and this substitution can be treated as the fermion effective mass in the vicinity of the point Γ:
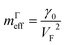 | (3.21) |
| k = K + κ | (3.22) |
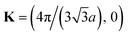 for example, and we will assume that κ is small.
for example, and we will assume that κ is small.
To the lowest order in κ we have, from (3.8) and (3.22),
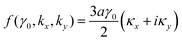 | (3.23) |
Substitution of (3.23) into Hamiltonian (3.7) gives the following equation for the isoenergetic lines in vicinity of the point K (the corner of the first Brillouin zone):
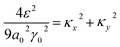 | (3.24) |
Consequently, the isoenergetic lines are circles in the vicinity of the minimum of energy εc = 0 (for the conduction band) or in the vicinity of the maximum of energy εc = 0 (for the valence band) at the corner of the zone. It follows from (3.24) that these circles are described by the following equation in p-space (Fig. 3b):
 | (3.25) |
The value of εc = 0 corresponds to the minimum of energy in the conduction band (the point P0 (min) in Table 1). The value of εc = 0 corresponds to the maximum of energy in the valence band (the point P2 (max) in Table 1). Eqn (3.25) describes the linear dispersion of the massless Dirac fermions in the vicinity of the corners K(K′) of the first Brillouin zone:
| ε = ±VFp | (3.26) |
Thus, the LTT exists at the critical value of energy εc = 0, where the new cavity (3.25) appears (Fig. 3b) in the conduction band or disappears in the valence band (Fig. 3b). Hence, there are six pockets of low energy excitations (Fig. 3b), one for each of the two inequivalent points K and K′ on the Brillouin zone boundary.
The area of the cavity inside the circle (3.25) is equal to.
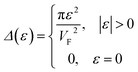 | (3.27) |
Using (3.13) and (3.27) to calculate the number of the electron states inside the two-dimensional cavity (3.25), one obtains (per spin direction and per unit area):
| δN(ε) =πε2/[VF2(2πħ)2] | (3.28) |
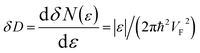 | (3.29) |
Expanding the expression (3.16) at ε = εc = 0, we obtain the same result for the total DOS (per spin direction and per unit area) in the vicinity of the zone corners K(K′):
| D(ε) =|ε|/(2πħ2VF2) | (3.30) |
Therefore, in the points K(K′), we must make the following substitutions for the coefficients C6 and C7 for graphene in Table 1:
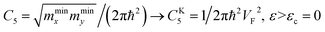 | (3.31) |
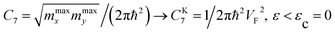 | (3.32) |
| k = K + q | (3.33) |
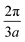 . Therefore:
. Therefore: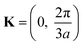 | (3.34) |
Taking into account |qya|, |qxa| ≪ 1, we have from (3.9), (3.33) and (3.34) to accuracy of order (qya), (qxa)
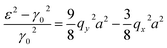 | (3.35) |
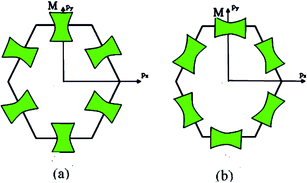
Therefore, the isoenergetic lines are hyperboles in the vicinity of point M (the middle of the edge of the first Brillouin zone). One can say that middles of the edges of the first Brillouin zone are saddle points. We can consider the corresponding points similar to M (the middles of the edges of the first Brillouin zone) (Fig. 2b) as the saddle points or the “cone points” in two dimensions (points P1 (saddle) in Table 1). It follows from (3.35) that the isoenergetic lines are described by the following equations in p-space in the vicinity of these saddle points (Fig. 4):
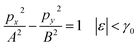 | (3.36) |
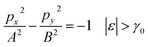 | (3.37) |
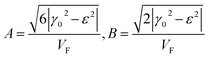 | (3.38) |
The Lifshitz topological transition is realized in the saddle point M by the variation of energy from ε < εc to ε > εc, and εc = γ0. In this transition, the isoenergetic lines in the vicinity of point M change from hyperbole (3.36) to hyperbole (3.37). Calculating the area Δ(ε) enclosed by hyperbole (3.36) or (3.37) and the corresponding boundary of the first Brillouin zone py = ħ/a, or px = ħ/a, one obtains:
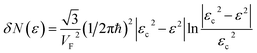 | (3.39) |
Now, we are able to resolve the contradiction with the coefficient 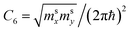 used in Table 1. As follows from (3.39) and (3.13), the DOS change due to the LTT in the saddle point M (at energies close to εc) is equal to
used in Table 1. As follows from (3.39) and (3.13), the DOS change due to the LTT in the saddle point M (at energies close to εc) is equal to
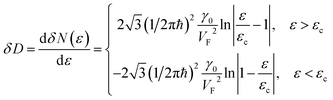 | (3.40) |
Also, the expansion of (3.16) yields the same VHS for the total DOS (per spin direction and per unit area) in the vicinity of the saddle point M, if |ε| → εc = γ0:
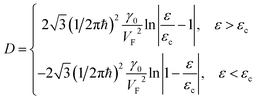 | (3.41) |
Therefore, in the saddle point M, the coefficient C6 for graphene in Table 1 should be changed to
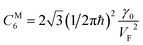 | (3.42) |
Thereby, in 2D graphene, the mass-factor C6 in Table 1 acquires the substitution of γ0/VF2 instead of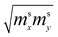 , and this substitution can be treated as the graphene effective mass in the vicinity of the saddle point M:
, and this substitution can be treated as the graphene effective mass in the vicinity of the saddle point M:
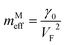 | (3.43) |
It follows from (3.21) and (3.43) that the fermions are slowing down in the vicinities of the Γ and M points, becoming not massless but massive. A similar phenomenon was found in observations of Dirac node formation and mass acquisition in a topological crystalline insulator.57 Estimation of the values of mΓeffand mMeffyields (at γ0 = 4 eV, and VF= 108 cm s−1 (ref. 56)):
| mΓeff ≈ 0.1me | (3.44) |
| mMeff ≈ 0.1me | (3.45) |
4 Contribution of the Lifshitz topological transitions to the thermodynamic properties of graphene
4.1. The thermodynamic potentials of graphene near the Lifshitz topological transition
Consider the thermodynamic properties of graphene near the electronic transition caused by the topology change of the Fermi lines in graphene. If the chemical potential μ is close to a value of the critical energy εc, the grand thermodynamic potential Ω (ref. 5) has the following expression:2| Ω(μ, T) = Ω0 + δΩ | (4.1) |
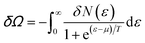 | (4.2) |
Introducing the Lifshitz parameter z = μ − εc in the case of the hyperbolic changes of the Fermi lines at the saddle point M, we obtain from (3.39) and (4.2), if T → 0:
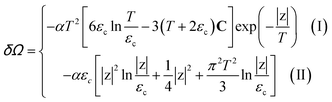 | (4.3) |
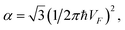 z = μ − εc, εc = γ0, and C is the Euler constant.
z = μ − εc, εc = γ0, and C is the Euler constant.
Transition from region I into region II corresponds to the appearance of a new cavity of the isoenergetic line ε(p) = μ, or to a decrease of the line connectivity.
Both formulae (4.3) are valid at T ≪ |z|. At absolute zero temperature, one has
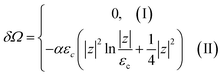 | (4.4) |
From comparison of (4.4) and (1.1), one can see the essential difference of δΩ given by (4.4) for the LTT in graphene and the LTT in three dimensions (1.1). The second derivative of δΩ diverges at the point z = 0 as ln(|z|/εc)in graphene, while only the third derivative of δΩ diverges at the point z = 0 as z−1/2 in three dimensions. As a result, completely different anomalies will be obtained for the thermodynamic parameters at the Lifshitz topological transitions in graphene.
When the electronic cavity disappears in the Brillouin zone centre Γ, one computes from (3.14) and (4.2) at T → 0:
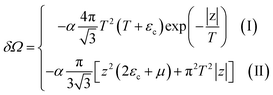 | (4.5) |
Considering the appearance of new cavities in the Brillouin zone corners K, we obtain from (3.28) and (4.2), if T → 0:
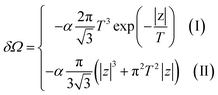 | (4.6) |
Because the number of electrons in the conduction band is permanent (at least in vicinity of the point μ = εc), it is convenient to use the Helmholtz free energy potential F (T, S, N)2 instead of the grand thermodynamic potential Ω (T, S, μ). We assume that area S is the parameter connected with applied pressure, tensile stress, or other mechanical action. The critical energy is the function of the area, i.e. εc = εc(S), and the chemical potential μ is also a function of S because of constancy of the carriers:
| N(μ, S) = N | (4.7) |
If Sc is the area at which the topology of the Fermi lines changes:
| μ(Sc) = εc(Sc) | (4.8) |
According to (4.7) and (4.8), the value of |z| = |μ − εc| can be expressed via |S − Sc|:
| |z| = η|S − Sc| | (4.9) |
The Helmholtz free energy potential F can be written in the form
| F = F0 + δF | (4.10) |
One can readily be convinced that δF is quantitatively equal to the irregular contribution δΩ expressed in the variables S and T according to the Landau theorem5 about the small variations of the thermodynamic potentials due to small changes of some parameters of the solid state:
| (δΩ)T,S,μ = (δF)T,S,N | (4.11) |
One can see that variations of δΩ given by the relations (4.3), (4.5), and (4.6) are small at T ≪ z in the vicinity of the Lifshitz electronic transition, where z → 0.
Thus, δF is given by eqn (4.3), (4.5), and (4.7), where one must set |z| = η|S − Sc|.
In the case of the hyperbolic changes of the Fermi lines at the saddle point M, we obtain from (4.3) and (4.9), if T → 0:
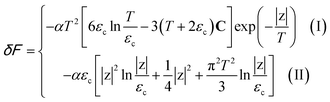 | (4.12) |
When the electronic cavity disappears in the Brillouin zone centre, one obtains from (4.5) and (4.9) at T → 0:
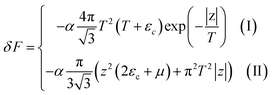 | (4.13) |
Considering the appearance of new cavities in the Brillouin zone corners, one obtains from (4.6) and (4.9), if T → 0:
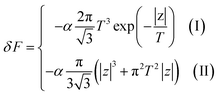 | (4.14) |
4.2. The specific heat of the graphene monolayer at the Lifshitz topological transition
The specific heat of graphene is stored in the lattice vibrations (phonons) and the free conduction electrons of graphene, C = Cph + Ce. However, phonons dominate the specific heat of graphene58 at all practical temperatures (>1 K),59,60,and61,62 and the phonon specific heat increases with temperature.62 The electron specific heat Ce of monolayer graphene (MG) is given by the following relations:62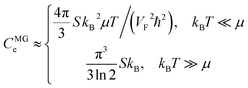 | (4.15) |
We can explore the electron-specific heat peculiarities of monolayer graphene at the LTT based on expressions of the change of the Helmholtz free energy by eqn (4.12), (4.13), and (4.14).
In the case of the hyperbolic changes of the Fermi lines at the saddle point M, one obtains from (4.12), if T → 0:
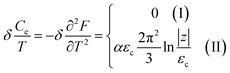 | (4.16) |
When the electronic cavity disappears in the Brillouin zone centre Γ, one computes from (4.13) at T → 0:
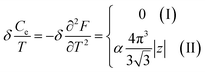 | (4.17) |
Considering the appearance of new cavities in the Brillouin zone corners K, we obtain from (4.14), if T → 0:
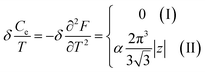 | (4.18) |
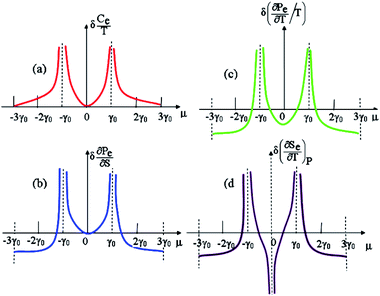
Thus, the formulae (4.16), (4.17) and (4.18) describe peculiarities of the specific heat in graphene at the LTT at the points M, Γ, and K of the first Brillouin zone, correspondingly (Fig. 5a).
The results for the specific heat (4.17) and (4.18) coincide with result (4.15) of the electron specific heat CMGeof the monolayer graphene (MG) obtained in paper.61 Indeed, substituting 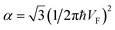 , and expressing T in Kelvins, one obtains from (4.17) and (4.18):
, and expressing T in Kelvins, one obtains from (4.17) and (4.18):
| Ce ≈ SkB2μT/(VF2ħ2), kBT ≪ |z| ≪ μ | (4.19) |
Note that experimental observation of singularities (4.16) and (4.17) is possible under special conditions. The experimental value of the chemical potential μ of graphene does not exceed 1 eV,63 and the estimated value of the overlap integral γ0 is between 2 and 4 eV.64–66 Tuning of the chemical activity of graphene in a wide range could be achieved by the formation of a Moiré superstructure between the graphene and transition metal substrate.67 Thus, to observe the LTT at the graphene saddle point (where |z| = |μ − γ0| → 0), we must increase the chemical potential μ or decrease the overlap integral γ0 due to strain. Increasing μ can be realized by electron doping due to renormalization of the electron spectrum.68 It has been demonstrated in ref. 68 that the Coulomb interaction produces noticeable effects in increasing the graphene chemical potential μ at low temperature T ≪ μ, especially for high carrier concentrations of n0 > 1011 cm−2. The band structure of graphene has been determined under strain using density functional calculations.69 The ab initio band structure was then used to extract the best fit to the tight-binding hopping parameters used in a microscopic model of strained graphene.70 It was found that the hopping parameters may increase or decrease with increasing strain depending on the orientation of the applied stress. The fitted values were compared with an available parameterization for the dependence of the orbital overlap on the distance separating the two carbon atoms.
4.3. The compressibility of the graphene monolayer at the Lifshitz topological transition
The compressibility of graphene is an important object of study in condensed matter physics because it gives information about the intrinsic nature of the electron structure of graphene and its interactions with external fields.71,72In case of the hyperbolic changes of the Fermi lines at the saddle point M, we obtain from (4.12) for the electron compressibility, if T → 0:
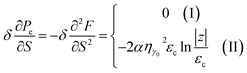 | (4.20) |
When the electronic cavity disappears in the Brillouin zone centre, one obtains from (4.13) for the electron compressibility at T → 0:
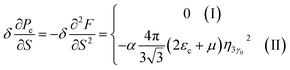 | (4.21) |
Considering the appearance of new cavities in the Brillouin zone corners, one obtains from (4.14) for the electron compressibility, if T → 0:
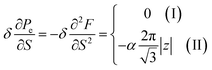 | (4.22) |
As a result, the formulae (4.20), (4.21) and (4.22) describe peculiarities of the compressibility of graphene at the LTT at the points M, Γ, and K of the first Brillouin zone, correspondingly (Fig. 5b).
4.4. The electron thermal coefficient of pressure of the graphene monolayer at the Lifshitz topological transition
In case of the hyperbolic changes of the Fermi lines at the saddle point A, we obtain the change of the electron thermal coefficient of pressure from (4.12), if T → 0: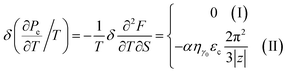 | (4.23) |
When the electronic cavity disappears in the Brillouin zone centre, one obtains from (4.13) for the electron thermal coefficient of pressure at T → 0:
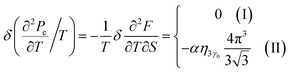 | (4.24) |
Considering the appearance of new cavities in the Brillouin zone corners, one obtains from (4.14) for the electron thermal coefficient of pressure, if T → 0:
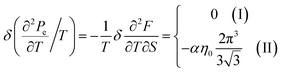 | (4.25) |
The formulae (4.23), (4.24) and (4.25) describe peculiarities of the electron thermal coefficient of pressure in graphene at the LTT at the points M, Γ, and K of the first Brillouin zone, correspondingly (Fig. 5c).
4.5. The electron thermal expansion coefficient of the graphene monolayer at the Lifshitz topological transition
The thermal properties of graphene have been investigated in recent years; in particular, its thermal expansion and heat conduction have been studied by various theoretical and experimental techniques in ref. 73 and 74. Some theoretical studies that have been carried out to study the thermodynamic properties of graphene (e.g., specific heat and thermal expansion) are based on density-functional theory (DFT) calculations combined with a quantum quasi-harmonic approximation (QHA) for the vibrational modes.73,74 This is expected to yield reliable results at low temperature for the graphene lattice contribution to the thermal properties; however, it may be questioned with respect to the graphene electron part. The answer to the latter can give the Lifshitz topological transitions.In the case of the hyperbolic changes of the Fermi lines at the saddle point M, we obtain the change of the electron thermal expansion coefficient from (4.23) and (4.20), if T → 0:
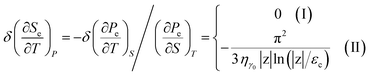 | (4.26) |
When the electronic cavity disappears in the Brillouin zone centre, one obtains from (4.24) and (4.21) for the electron thermal expansion coefficient, at T → 0:
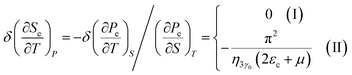 | (4.27) |
Considering the appearance of new cavities in the Brillouin zone corners, one obtains from (4.25) and (4.22) for the electron thermal expansion coefficient, if T → 0:
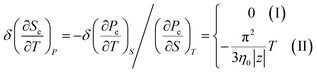 | (4.28) |
It is interesting that the electron thermal expansion coefficient has a negative sign at T ≪ |z|, like the lattice thermal expansion coefficient of graphene (see ref. 72, 73, and 75).
The formulae (4.26), (4.27) and (4.28) describe the peculiarities of the electron thermal expansion coefficient in graphene at LTT at the points M, Γ, and K of the first Brillouin zone, correspondingly (Fig. 5d).
5 Conclusion and outlook
To summarize the results of the present paper, one can emphasize the following.(i) Connection of the Lifshitz topological transition has been established with the van Hove singularities of the electron state density in graphene. There are three types of singularities of the density of the electron states in two dimensions. The point P0 (min) corresponds to the minimum in the energy spectrum. The point P1 (saddle) corresponds to the case where the Lifshitz topological transitions are realized by variation of the energy from ε < εc to ε >εc. The point P2 (max) corresponds to the maximum in the energy spectrum.
(ii) Peculiarities of the Lifshitz topological transitions in graphene are described at the Brillouin zone centre Γ, at the zone corners K, in the vicinity of the Dirac points, and at the saddle point M. It is found that LTT can be realized in the centre Γ at the critical energy value εc = 3γ0, where the cavity of the isoenergetic lines disappears. The existence of the LTT is shown at the critical energy value of εc = 0, where six pockets of low energy excitations appear, one for each of the two inequivalent Dirac points K and K′.
The Lifshitz topological transition is realized in the saddle point M by variation of the energy from ε < εc to ε > εc and at the critical value of energy εc = γ0. It is shown that the Dirac fermion slows down in the vicinities of the points Γ and M, becoming not massless but massive, and the values of the fermion effective mass in the vicinity of these points are mΓeff ≈ 0.1me, and mMeff ≈ 0.1me (where me is the free electron mass).
(iii) The thermodynamic characteristics of graphene were investigated at the Lifshitz topological transitions. A general formulation of the thermodynamics at the LTT in graphene is given. The anomalies are found at the LTT of the electron specific heat Ce, the electron compressibility 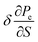 , the electron thermal coefficient of pressure
, the electron thermal coefficient of pressure 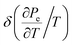 , and the electron thermal expansion coefficient
, and the electron thermal expansion coefficient 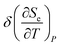 . The anomalies are described in terms of the Lifshitz parameter z = μ − εc. The electron specific heat Ce diverges at the saddle point M as ln|z| and is proportional to |z| at points K and Γ of the first Brillouin zone. The electron compressibility
. The anomalies are described in terms of the Lifshitz parameter z = μ − εc. The electron specific heat Ce diverges at the saddle point M as ln|z| and is proportional to |z| at points K and Γ of the first Brillouin zone. The electron compressibility 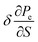 diverges at the saddle point M as ln|z|, is proportional to |z| at points K, and takes a constant value at point Γ of the first Brillouin zone. The electron thermal coefficient of pressure
diverges at the saddle point M as ln|z|, is proportional to |z| at points K, and takes a constant value at point Γ of the first Brillouin zone. The electron thermal coefficient of pressure 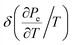 diverges at the saddle point M as 1/|z|, and it becomes negative in the vicinities of points K and Γ of the first Brillouin zone. The electron thermal expansion coefficient
diverges at the saddle point M as 1/|z|, and it becomes negative in the vicinities of points K and Γ of the first Brillouin zone. The electron thermal expansion coefficient 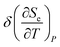 diverges at the saddle point M as 1/(|z|
diverges at the saddle point M as 1/(|z|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |z|) becoming negative in the vicinity of point Γ, and it diverges as 1/|z| at point K of the first Brillouin zone.
|z|) becoming negative in the vicinity of point Γ, and it diverges as 1/|z| at point K of the first Brillouin zone.
One can conclude that all the thermodynamic parameters possess the strongest singularities in graphene at the LTT near the saddle points M. In 2D graphene, a saddle point M in the electronic band structure leads to a divergence in the density of states of the logarithmic-type van Hove singularities (VHS). This implies the possibility of experimental observation of the LTT by bringing the chemical potential μ and the VHS together. However, one cannot change the position of the VHS in the band structure. It is pointed out in section 4.2 that the accessible experimental value of the graphene chemical potential μ does not exceed 1 eV.63 Therefore, it is essential to tune μ through the VHS by chemical doping76,77 or by gating.17,57,78–81 In recent work,82 a simple technique of doping graphene by manipulating adsorbed impurities was reported, and a change in the electron mobility of 650% was observed. Also, it is worth paying experimental attention to the tuning of μ through the VHS by the following two methods. The first method is connected with deformation of the graphene monolayer to mimic twisted graphene. Rotation between two stacked graphene monolayers in twisted graphene83 can generate van Hove singularities, which can be brought arbitrarily close to the chemical potential μ by varying the angle of rotation.84 The second method consists of investigating the LTT in graphene under 3D high pressure.84 This opens exciting opportunities for inducing and exploring the Lifshitz topological transitions in graphene.
Data accessibility
This work includes theoretical investigations.Authors' contributions
The paper has been written without any assistance, and I gave final approval for publication.Funding statement
The work has no source of funding.Ethics statement
This work did not involve any ethics statements.Conflicts of interest
I have no competing interests.Acknowledgements
I thank the reviewers and editors for their helpful suggestions and comments.References
- I. M. Lifshitz, Anomalies of electron characteristics of a metal in the high pressure region, Zh. Eksp. Teor. Fiz., 1960, 38, 1569 ( Sov. Phys. JETP , 1960 , 11 , 1130 ) Search PubMed , http://www.jetp.ac.ru/cgi-bin/dn/e_011_05_1130.pdf.
- I. M. Lifshitz, ' M. Ya. Azbel and M. I. Kaganov, Electron Theory of Metals, Consultant Bureau, New York, 1973 Search PubMed.
- M. I. Kaganov and I. M. Lifshitz, Electron theory of metals and geometry, Usp. Fiz. Nauk, 1979, 129, 487–529 ( Sov. Phys. Usp. , 1979 , 22 ) DOI:10.1070/pu1979v022n11ABEH005648 , http://www.physics.rutgers.edu/grad/601/CM601/koganovlifshitz.pdf.
- Y. M. Blanter, M. I. Kaganov, A. V. Pantsulaya and A. A. Varlamov, The theory of electronic topological transitions, Phys. Rep., 1994, 245(4), 159–257, DOI:10.1016/0370-1573(94)90103-1 , http://www.sciencedirect.com/science/article/pii/0370157394901031.
- L. D. Landau and E. M. Lifshitz, Statistical Physics, Part I, Landau and Lifshitz Course of Theoretical Physics, Butterworth-Heinemann, Oxford, UK, 1980, vol. 5 Search PubMed.
- P. Ehrenfest, Communications from the Kamerling-Onnes Laboratory: 813–813, Google Scholar, 1933 Search PubMed.
- P. Ehrenfest, Phase changes in the ordinary and extended sense classified according to the corresponding singularities of the thermodynamic potential, Proc. Acad. Sci. Amst., 1933, 36, 153–157 CAS.
- I. M. Lifshitz and V. G. Peschanskii, Zh. Eksp. Teor. Fiz., 1958, 35, 1251 Search PubMed; I. M. Lifshitz and V. G. Peschanskii, Soviet Phys.-JETP, 1959, 8, 875 Search PubMed.
- V. N. Davydov and M. I. Kaganov, Singularities of the Sound Attenuation Coefficient in a Phase Transition of Order 2.5, Zh. Exp. Teor. Fiz., 1972, 16, 133 ( JETPH Lett. , 1972 , 16 , 92 ) Search PubMed . http://www.jetpletters.ac.ru/ps/1759/article_26750.pdf.
- V. N. Davydov and M. I. Kaganov, Anomalies in the drag electron dislocation force in a phase transition of order 2.5, Zh. Eksp. Teor. Fiz., 1975, 68, 649–658 ( Sov. Phys. JETP. , 41 , 322 ) Search PubMed . http://www.jetp.ac.ru/cgi-bin/dn/e_041_02_0321.pdf.
- V. N. Davydov and M. I. Kaganov, Distinctive features of sound absorption in a phase transition of order-2 ½, Zh. Eksp. Teor. Fiz., 1974, 67, 1491–1499 ( Sov. Phys. JETP , 1975 , 40 , 741 ) Search PubMed.
- V. N. Davydov, Influence of the geometry of constant-energy surface on the anomalies of the absorption coefficient of sound at a phase transition of order 2 ½, Fiz. Tverd. Tela, 1976, 18, 2359–2370 ( Sov. Phys. Solid State , 1976 , 18 ) Search PubMed.
- V. N. Davydov and M. I. Kaganov, Singularity of the coefficient of absorption of long- wavelength sound in a phase transition of order 2 ½, Zh. Eksp. Teor. Fiz., 1978, 74, 697–701 ( JETP , 1978 , 47 ) Search PubMed . http://www.jetp.ac.ru/cgi-bin/dn/e_047_02_0366.pdf.
- A. A. Varlamov and A. V. Pantsulaya, Absorption of longitudinal sound in metals near the Lifshitz topological transition, Zh. Eksp. Teor. Fiz., 1986, 91, 2220–2228 Search PubMed . http://www.jetp.ac.ru/cgi-bin/dn/e_064_06_1319.pdf.
- I. M. Lifshitz, V. V. Rzhevsky and M. I. Tribel'sky, Nonlinear acoustic effects in metals near the electron-topological transition point, Zh. Eksp. Teor. Fiz., 1981, 81, 1529 ( Soviet Physics - JETP , 1981 , 54 ) Search PubMed.
- V. G. Vaks, A. V. Trefilov and S. V. Fomichev, Zh. Eksp. Teor. Fiz., 1981, 80, 1613 CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric Field Effect in Atomically Thin Carbon Films, Science, 2004, 306(5696), 666–669 CrossRef CAS PubMed.
- Y.-W. Son, S.-M. Choi, Y. P. Hong, S. Woo and S.-H. Jhi, Electronic topological transition in sliding bilayer graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 84, 155410, DOI:10.1103/PhysRevB.84.155410 .https://arxiv.org/pdf/1012.0643.pdf.
- P. Goswami, Lifshitz Transition Including Many-Body Effects in Bi-Layer Graphene and Change in Stacking Order, Graphene, 2013, 2(2), 88–95, DOI:10.4236/graphene.2013.22013 . http://file.scirp.org/pdf/Graphene_2013043016110272.pdf.
- A. S. Nunez, E. Suarez Morell and P. Vargas, Trigonal Distortion of Topologically Confined Channels in Bilayer Grapheme, Appl. Phys. Lett., 2011, 98(No. 26), 262107, DOI:10.1063/1.3605568.
- A. Varlet, D. Bischoff, P. Simonet, K. Watanabe, T. Taniguchi, T. Ihn, K. Ensslin, M. Mucha- Kruczynski and V. I. Fal’ko, Anomalous Sequence of Quantum Hall Liquids Revealing a Tunable Lifshitz Transition in Bilayer Graphene, Phys. Rev. Lett., 2014, 113, 116602 CrossRef PubMed . https://arxiv.org/pdf/1403.3244.pdf.
- A. Varlet, M. Mucha-Kruczynski, D. Bischoff, P. Simonet, T. Taniguchi, K. Watanabe, V. Fal'ko, T. Ihn and K. Ensslin, Tunable Fermi surface topology and Lifshitz transition in bilayer graphene”, Synth. Met., 2015, 210(part A), 19–31, DOI:10.1016/j.synthmet.2015.07.006.
- B. Swastibrata and A. K. Singh, Lifshitz transition and modulation of electronic and transport properties of bilayer graphene by sliding and applied normal compressive strain, Carbon, 2016, 99, 432–438, DOI:10.1016/j.carbon.2015.12.025.
- V. Iorsh, K. Dini, O. V. Kibis and I. A. Shelykh, Optically induced Lifshitz transition in bilayer graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 155432, DOI:10.1103/PhysRevB.96.155432 , https://arxiv.org/pdf/1707.07392.pdf.
- E. H. Hwang, E. Rossi and S. Das Sarma, Theory of thermopower in two-dimensional graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235415, DOI:10.1103/PhysRevB.80.235415 , http://physics.wm.edu/%7Eerossi/Publications/Phys_Rev_B_80_235415.pdf.
- A. A. Varlamov, A. V. Kavokin, I. A. Luk'yanchuk and S. G. Sharapov, Anomalous thermoelectric and thermomagnetic properties of graphene, Phys.-Usp., 2012, 55, 1146–1151, DOI:10.3367/UFNe.0182.201211j.1229.
- C.-R. Wang, W.-S. Lu, H. Lei, W.-Li Lee, T.-K. Lee, F. Lin, I.-C. Cheng and J.-Z. Chen, Enhanced Thermoelectric Power in Dual-Gated Bilayer Graphene, Phys. Rev. Lett., 2011, 107, 186602, DOI:10.1103/PhysRevLett.107.186602.
- H. Lei and T. K. Lee, Thermopower of gapped bilayer graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 039902, DOI:10.1103/PhysRevB.84.039902 . https://arxiv.org/pdf/1003.0815v2.pdf.
- J. Cserti, A. Csordás and G. Dávid, Role of the Trigonal Warping on the Minimal Conductivity of Bilayer Graphene, Phys. Rev. Lett., 2007, 99, 066802, DOI:10.1103/PhysRevLett.99.066802 , https://arxiv.org/pdf/cond-mat/0703810.pdf.
- V. N. Davydov, Some peculiarities of thermopower at the Lifshitz topological transitions due to stacking change in bilayer and multilayer graphene, Proc. R. Soc. A, 2019, 475(22206) DOI:10.1098/rspa.2019.0028 . https://royalsocietypublishing.org/doi/pdf/10.1098/rspa.2019.0028.
- A. Jayaraman, K. Hsieh, B. Ghawri, P. S. Mahapatra, A. Ghosh, Evidence of Lifshitz transition in thermoelectric power of ultrahigh mobility bilayer graphene, preprint arXiv:2003.02880 [cond-mat.mes-hall]. https://arxiv.org/pdf/2003.02880.pdf.
- E. Pop, V. Varshney and K. R. Ajit, Thermal properties of graphene: Fundamentals and applications, MRS Bull., 2012, 37, 1273–1281, DOI:10.1557/mrs.2012.203 , https://arxiv.org/ftp/arxiv/papers/1301/1301.6181.pdf.
- M. I. Katsnelson, Graphene: Carbon in Two Dimensions, Cambridge University Press, New York, 2012 Search PubMed.
- H. Mousavi and J. Khodadadi, Heat capacity and conductivity of gapped graphene, Phys. E, 2013, 50, 11–16, DOI:10.1016/j.physe.2013.02.015.
- L. A. Falkovsky, Thermodynamics of electron-hole liquids in graphene, Pis'ma v ZhETF, 2013, 98(3), 183–186 ( JETP Lett. , 2013 , 98 , 161–164 ) DOI:10.1134/S0021364013160042 DOI:10.7868/S0370274X13150083 DOI:10.1134/S0021364013160042.
- Z. Z. Alisultanov and N. A. Mirzegasanova, Thermodynamics of Electrons in Epitaxial Graphene, Pis’ma v Zhurnal Tekhnicheskoi Fiziki, 2014, 40(4), 49–55 ( Tech. Phys. Lett. , 2014 , 40 , 164–166 ) DOI:10.1134/S1063785014020175.
- Z. Z. Alisultanov, Thermodynamics of Electrons in the Graphene Bilayer, Zhurnal, Eksperimental’noi i Teoreticheskoi Fiziki, 2014, 146(2), 340–351 ( J. Exp. Theor.Phys. , 2014 , 119 , 300–310 ) DOI:10.1134/S1063776114070012.
- Z. Z. Alisultanov, The Thermodynamics of Electrons and the Thermoelectric Transport in Epitaxial, Graphene on the Size-Quantized Films, Physica E, 2015, 69, 89–95, DOI:10.1016/j.physe.2015.01.003.
- Z. Z. Alisultanov, Landau levels in graphene in crossed magnetic and electric fields: Quasi-classical approach, Physica B, 2014, 438, 41, DOI:10.1016/j.physb.2013.12.033.
- A. I. Rusanov, Thermodynamics of graphene, Surf. Sci. Rep., 2014, 69(4), 296–324, DOI:10.1016/j.surfrep.2014.08.003.
- Z. Z. Alisultanov, Calculation of electron spectra and some problems in the thermodynamics of graphene layers, Zhurnal Eksperimental’noi I Teoreticheskoi Fiziki, 2016, 149(2), 393–414 ( J. Exp. Theor. Phys. , 2016 , 122 , 341–360 ) DOI:10.1134/S106377611601012X.
- X.-X. Ren, W. Kang, Z.-Fu Cheng and R.-L. Zheng, Temperature-Dependent Debye Temperature and Specific Capacity of Graphene, Chin. Phys. Lett., 2016, 33, 12 Search PubMed . 307X/33/12/126501/pdf.
- M. Yarmohammadi, The electronic properties, electronic heat capacity and magnetic susceptibility of monolayer boron nitride graphene-like structure in the presence of electron-phonon coupling, Solid State Commun., 2017, 253, 57–62, DOI:10.1016/j.ssc.2017.02.003.
- I. Grosu and T.-L. Biter, Electronic heat capacity in disordered graphene systems, Phys. Lett. A, 2018, 382(Issue 41), 3042–3045, DOI:10.1016/j.physleta.2018.07.037.
- M. R. Rodríguez-Laguna, et al., Mechanisms behind the enhancement of thermal properties of graphene nanofluids, Nanoscale, 2018, 10, 15402, 10.1039/c8nr02762e , https://pubs.rsc.org/en/content/articlepdf/2018/nr/c8nr02762e.
- I. M. Lifshitz and M. I. Kaganov, Some problems of the electron theory of metals I. Classical and quantum mechanics of electrons in metals, Usp. Fiz. Nauk, 1959, 59, 49 ( Sov. Phys. Usp. , 1960 , 2 , 831 ) DOI:10.3367/UFNr.0069.195911c.0419 DOI:10.1070/PU1960v002n06ABEH003183.
- I. M. Lifshitz and M. I. Kaganov, Some problems of the electron theory of metals II. Statistical mechanics and thermodynamics of electrons in metals, Usp. Fiz. Nauk, 1952, 78, 41 ( Sov. Phys. Usp. , 1963 , 5 , 878–907 ) DOI:10.1070/PU1963v005n06ABEH003463].
- L. Van Hove, The Occurrence of Singularities in the Elastic Frequency Distribution of a Crystal, Phys. Rev., 1953, 89(6), 1189–1193, DOI:10.1103/physrev.89.1189.
- J. M. Ziman, Principles of the Theory of Solids, CUP-Vikas Student Edition, 1079 Search PubMed.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Saunders College Publishing, New York, 1976, ch. 8, p. 9 Search PubMed.
- A. A. Abrikosov, Introduction to the Theory of Normal Metals, Academic Press Inc, 1972. https://ebookee.org/Introduction-to-the-Theory-of-Normal-Metals_1298076.html Search PubMed.
- A. A. Abrikosov, Fundamentals of the Theory of Metals, Nauka, Moscow, 1987 Search PubMed.
- J. P. Hobson and W. A. Nierenberg, The Statistics of a Two-Dimensional, Hexagonal Net, Phys. Rev.,, 1953, 89, 662, DOI:10.1103/PhysRev.89.662.
- V. O. Ananyev and M. I. Ovchynnikov, On the density of states of graphene in the nearest-neighbor approximation, Condens. Matter Phys., 2017, 20(4), 43705, DOI:10.5488/CMP.20.43705 , https://arxiv.org/pdf/1705.08120.pdf, http://www.icmp.lviv.ua/journal.
- V. O. Shubnyi, V. P. Gusynin, S. G. Sharapov and A. A. Varlamov, Entropy per particle spikes in the, transition metal dichalcogenides, Fiz. Nizk. Temp., 2018, 44, 721, DOI:10.1063/1.5037559 , arXiv:1712.09118 [cond-mat.mes-hall],https://arxiv.org/pdf/1712.09118.pdf.
- V. N. Davydov, The recurrent relations for the electronic band structure of the multilayer graphene, Proc. R. Soc. A, 2018, 474(2220) DOI:10.1098/rspa.2018.0439 , https://royalsocietypublishing.org/doi/pdf/10.1098/rspa.2018.0439.
- Y. Okada and M. Serbyn, et al., Observation of Dirac Node Formation and Mass Acquisition in a Topological Crystalline Insulator, Science, 2013, 341(6153), 1496–1499, DOI:10.1126/science.1239451 , https://arxiv.org/ftp/arxiv/papers/1305/1305.2823.pdf.
- E. Pop, V. Varshney and K. R. Ajit, Thermal properties of graphene: Fundamentals and applications, MRS Bull., 2012, 37, 1273–1281, DOI:10.1557/mrs.2012.203 , arXiv: 1301.6181 [cond-mat.mtrl-sci].
- T. Nihira and T. Iwata, Temperature dependence of lattice vibrations and analysis of the specific heat of graphite, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 134305 CrossRef.
- L. X. Benedict, S. G. Louie and M. L. Cohen, Heat capacity of carbon nanotubes, Solid State Commun., 1996, 100, 177, DOI:10.1016/0038-1098(96)00386-9.
- Z. Z. Alisultanov,and M. S. Reis, Magneto-oscillations on specific heat of graphene monolayer, arXiv:1508.06648 [cond-mat.mes-hall], DOI:10.1016/j.physleta.2015.10.046.
- Z. Z. Alisultanov, Calculation of electron spectra and some problems in the thermodynamics of graphene layers, J. Exp. Theor. Phys., 2016, 122, 341–360, DOI:10.1134/S106377611601012X.
- E. M. Hajaj, O. Shtempluk, A. Razin, V. Kochetkov and Y. E. Yaish, Chemical potential of inhomogeneous single-layer graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045128, DOI:10.1103/PhysRevB.88.045128.
- S. Das Sarma, S. Adam, E. H. Hwang and E. Rossi, Electronic Transport in Two-Dimensional Graphene, Rev. Mod. Phys., 2011, 83(2), 407–470 CrossRef CAS . https://arxiv.org/pdf/1003.4731.pdfTT.
- N. B. Brandt, S. M. Chudinov and Y. G. Ponomarev, in Modern Problems in Condensed Matter Sciences, ed. V. M. Agranovich and A. A. Maradudin, North-Holland, Amsterdam, 1988, vol. 20, p. 1; http://www.sciencedirect.com/science/bookseries/01677837/20/1TTTT(2017-03-09); https://www.elsevier.com/books/book-series/modern-problems-in-condensed-matter-sciences Search PubMed.
- V. N. Davydov and V. A. Koulbatchinski, Magnetoresistance of low stage graphite acceptor compounds, Solid State Commun., 1988, 66(7), 695–699 CrossRef CAS.
- Ma Yuan, L. Gao, Yu Yan, Y. Su and L. Qiao, Tune the chemical activity of graphene via the transition metal substrate, RSC Adv., 2018, 8, 11807, 10.1039/c8ra00735g.
- L. A. Falkovsky, Thermodynamics of electron-hole liquids in graphene, Pis'ma v Zh. Eksper. Teoret. Fiz., 2013, 98(3), 183–186, DOI:10.7868/S0370274X13150083.
- R. M. Ribeirol, V. M. Pereira, N. M. R. Peres, P. R. Briddon and A. H. Castro Neto, Strained graphene: tight-binding and density functional calculations, New J. Phys., 2009, 11, 115002, DOI:10.1088/1367-2630/11/11/115002 , arXiv:0905.1573 [cond-mat.mes-hall], https://arxiv.org/pdf/0905.1573.pdf.
- M. Huang, H. Yan, T. F. Heinz and J. Hone, Probing Strain-Induced Electronic Structure Change in Graphene by Raman Spectroscopy, Nano Lett., 2010, 10(10), 4074–4079, DOI:10.1021/nl102123c.
- D. S. Abergel, The compressibility of graphene, Solid State Commun., 2012, 152, 1383, DOI:10.1016/j.ssc.2012.04.037 , arXiv: 1202.5313 [cond-mat.mes-hall], https://arxiv.org/pdf/1202.5313.pdf.
- D. S. L. Abergel, P. Pietiläinen and T. Chakraborty, Electronic compressibility of graphene: The case of vanishing electron correlations and the role of chirality, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 081408(R), DOI:10.1103/PhysRevB.80.081408.
- P. Carlos, Herrero and Rafael Ramírez, “Thermodynamic properties of graphene bilayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 035405, DOI:10.1103/PhysRevB.101.035405 , arXiv: 2001.02903 [cond- mat.mtrl-sci]; https://arxiv.org/pdf/2001.02903.pdf.
- P. Carlos, Herrero and Rafael Ramírez, “Thermal properties of graphene under tensile stress, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 195433, DOI:10.1103/PhysRevB.97.195433 , arXiv: 1806.02217 [cond- mat.mtrl-sci]; https://arxiv.org/pdf/1806.02217.pdf.
- S. Mann, R. Kumar and V. K. Jindal, Negative Thermal expansion of pure and doped Graphene, RSC Adv., 2017, 7, 22378, 10.1039/C7RA01591G.
- R. S. Markiewicz, Phase separation near the Mott transition in La2-xSrxCuO4, Phys. C, 1989, 162–164(part 1), 215–216, DOI:10.1016/0921-4534(89)90994-5.
- H. E. Mohottala, et. al., Electronic phase separation in La2−xSrxCuO4+y, Phys. B, 2006, 374, 199–202, DOI:10.1016/j.physb.2005.11.054.
- S. G. Sharapov and A. A. Varlamov, Anomalous growth of thermoelectric power in gapped graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035430, DOI:10.1103/PhysRevB.86.035430.
- V. Y. Tsaran, A. V. Kavokin, S. G. Sharapov, A. A. Varlamov and V. P. Gusynin, Entropy spikes as a signature of Lifshitz transitions in the Dirac materials, Sci. Rep., 2017, 7, 10271, DOI:10.1038/s41598-017-10643-0.
- Y. M. Galperin, D. Grassano, V. P. Gusynin, A. V. Kavokin, O. Pulci, S. G. Shaparov, V. O. Shubnyi and A. A. Varlamov, Entropy Signatures of Topological Phase Transitions, J. Exp. Theor. Phys., 2018, 127, 958–983, DOI:10.1134/S1063776118110134.
- D. Grassano, O. Pulci, V. O. Shubnyi, S. G. Sharapov, V. P. Gusynin, A. V. Kavokin and A. A. Varlamov, Detection of topological phase transitions through entropy measurements: The case of germanene, Phys. Rev. B: Condens. Matter Mater. Phys, 2018, 97, 205442 CrossRef CAS.
- K. S. Figueroa, N. J. Pinto, S. V. Mandyam, M.-Q. Zhao, C. Wen, M. D. Paul, Z. Gao, M. Drndić and A. T. Charlie Johnson, Controlled doping of graphene by impurity charge compensation via a polarized ferroelectric polymer, J. Appl. Phys., 2020, 127, 125503, DOI:10.1063/5.0003099.
- G. Li, A. Luicanl, J. M. B. Lopes dos Santos, A. H. Castro Neto, A. Reina, J. Kong and E. Y. Andrei, Observation of van Hove singularities in twisted graphene layers, Nat. Phys., 2009, 6(2) DOI:10.1038/nphys1463 , https://arxiv.org/ftp/arxiv/papers/0912/0912.2102.pdf.
- Y. W. Sun, W. Liu, I. Hernandez, J. Gonzalez, F. Rodriguez, D. J. Dunstan and C. J. Humphreys, 3D strain in 2D materials: experimental test in unsupported monolayer graphene under pressure, Phys. Rev. Lett., 2019, 123, 135501, DOI:10.1103/PhysRevLett.123.135501 , arXiv:1902.02651 [cond-mat.mtrl-sci], https://arxiv.org/pdf/1902.02651.pdf.
| This journal is © The Royal Society of Chemistry 2020 |