Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The viscosity of dilute carbon nanotube (1D) and graphene oxide (2D) nanofluids†
A.
Ansón-Casaos
 *a,
J. C.
Ciria
*a,
J. C.
Ciria
 b,
O.
Sanahuja-Parejo
a,
S.
Víctor-Román
a,
J. M.
González-Domínguez
b,
O.
Sanahuja-Parejo
a,
S.
Víctor-Román
a,
J. M.
González-Domínguez
 a,
E.
García-Bordejé
a,
E.
García-Bordejé
 a,
A. M.
Benito
a,
A. M.
Benito
 a and
W. K.
Maser
a and
W. K.
Maser
 a
a
aInstituto de Carboquímica, ICB-CSIC, Miguel Luesma Castán 4, 50018 Zaragoza, Spain. E-mail: alanson@icb.csic.es
bDepartamento de Informática e Ingeniería de Sistemas, Universidad de Zaragoza, María de Luna 1, 50018 Zaragoza, Spain
First published on 27th April 2020
Abstract
Controlling the physicochemical properties of nanoparticles in fluids directly impacts on their liquid phase processing and applications in nanofluidics, thermal engineering, biomedicine and printed electronics. In this work, the temperature dependent viscosity of various aqueous nanofluids containing carbon nanotubes (CNTs) or graphene oxide (GO), i.e. 1D and 2D nanoparticles with extreme aspect ratios, is analyzed by empirical and predictive physical models. The focus is to understand how the nanoparticle shape, concentration, motion degrees and surface chemistry affect the viscosity of diluted dispersions. To this end, experimental results from capillary viscosimeters are first examined in terms of the energy of viscous flow and the maximum packing fraction applying the Maron–Pierce model. Next, a comparison of the experimental data with predictive physical models is carried out in terms of nanoparticle characteristics that affect the viscosity of the fluid, mostly their aspect ratio. The analysis of intrinsic viscosity data leads to a general understanding of motion modes for carbon nanoparticles, including those with extreme aspect ratios, in a flowing liquid. The resulting universal curve might be extended to the prediction of the viscosity for any kind of 1D and 2D nanoparticles in dilute suspensions.
Introduction
Carbon nanotubes (CNTs) and graphene have found a number of applications in electronics, sensors, energy devices, catalysis and biomedicine.1–7 Very often, these nanostructures need to be dispersed in liquid media. A high quality dispersion, in which nanoparticles are stable and individualized, facilitates processing by different techniques, such as spray-coating, spin-coating, inkjet printing, coagulation spinning, and dip-coating. Also, the liquid suspensions, usually called nanofluids, can be directly put into heat exchange, microfluidic or biological systems. In all the cases, the control of viscosity is a key issue, since it determines the conditions of processing, such as pumping, injection, stirring, permeation and painting, and lastly, the final device operation.According to the ideas of green chemistry, inks and nanofluids should be most preferably prepared using water as the base liquid. Both CNTs and graphene are hydrophobic and cannot be directly dispersed in water. Therefore, CNTs have to be stabilized in suspension through either the addition of surfactants,8,9 or suitable chemical functionalization.10 Besides, the oxidized form of graphene, namely graphene oxide (GO), is relatively stable in water due to the high ratios of oxygen functional groups.11
The rheology of aqueous carbon nanofluids has been extensively studied for thermal transfer and lubricant applications.12–15 Experimental works include measurements on different kinds of multi-walled carbon nanotubes (MWCNTs),16–20 single-walled carbon nanotubes (SWCNTs),15,21–23 graphene nanoplatelets,24 and GO.25 Also, measurements on covalently functionalized CNTs (f-CNTs) have been reported,26,27 and it has been observed that GO reduction by chemical methods leads to a decrease in the viscosity of the nanofluid.25 Both CNT and GO dispersions in water are non-Newtonian liquids at relatively high concentrations, and typically form isotropic (nematic) phases.28,29 However, they approach the Newtonian behavior in the low concentration region.18–20,30,31
From a fundamental viewpoint, CNTs and GO are nanoparticles with extreme aspect ratios, by far exceeding those of micrometric rods, cylinders and discs made of metals, ceramics and polymer materials.32–34 The viscosity of dilute CNT suspensions has been correlated with the CNT length,35,36 as well as with the bundling degree.37,38 Sedimentation studies by analytical ultracentrifugation reveal that CNTs in stable dispersions can be regarded as rigid cylinders.39,40 Also, analytical ultracentrifugation has been applied to the determination of lateral dimensions of GO, considering GO flakes as flat discs.41
Most theoretical studies on the CNT viscosity are based on different expansions of classical two phase flow models,42 which are here the starting point for the discussion. Molecular dynamics simulations have been applied to the CNT viscosity,15 but are out of the scope of the present study. Also, recent mathematical approaches searching for improved algorithms to numerically fit experimental data are not discussed.43,44 Our focus lies on a general conceptual understanding by first principles theories. Since both CNTs and GO are nanostructures based on sheets of hexagonally bonded carbon atoms, the search for a common description of their properties might be natural.
We performed viscosity measurements on dilute dispersions of various CNT samples, f-CNTs and GO. All the GO samples and one type of f-CNT sample were directly dispersed in water. The other CNT and f-CNT samples needed the addition of surfactants. The complete set of measurements was first analyzed as a function of the temperature and the nanoparticle concentration, according to the empirical equation of Maron and Pierce.45 Next, size distributions for each sample were determined, and the viscosity was evaluated in terms of the aspect ratio (rp) using predictive physical models. The rp parameter is defined identically for both CNTs and GOs as the ratio between the particle dimension along a symmetry rotation axis and the perpendicular diameter. For CNTs, rp is the ratio between the nanotube length and diameter, and for GOs, it is the ratio between the thickness and the average flake width. In this novel way, rp ≫ 1 for CNTs, while rp ≪ 1 for GO particles and we interpret the viscosity of 1D and 2D nanostructures only as a function of a unique common rp parameter. Further analysis allows the discussion of the nanoparticle dynamics in the fluid according to the two employed predictive models.
Dependence of viscosity on temperature and concentration
Viscosity data and choice of the fitting model
Dilute aqueous dispersions were prepared with various samples of GO, CNTs and f-CNTs (Tables 1–3). Three GO materials were home made from a graphite precursor applying different oxidation times, while the other GO sample is a commercial product. Three commercial CNT powders were considered, including two SWCNTs and a MWCNT sample. The MWCNT material was functionalized by four procedures providing different chemical groups on the nanotube surface (Table 3). The complete chemical analysis of all the powder materials is provided in the ESI† (Section S1).| Sample | Manufacturer | Synthesis method | t o [h] |
|---|---|---|---|
| GO-2 | GCNN, ICB-CSIC | Modified hummers | 2 |
| GO-4 | GCNN, ICB-CSIC | Modified hummers | 4 |
| GO-16 | GCNN, ICB-CSIC | Modified hummers | Overnight |
| GO-G | Graphenea (San Sebastián, Spain) | — | — |
| Labela | Manufacturer (commercial name) | Synthesis method | D [nm] | L [μm] | Carbon purityb [%] |
|---|---|---|---|---|---|
| a The abbreviation in SWCNTs indicates the synthesis method. b From TGA residues. | |||||
| MWCNT | Nanocyl (NC7000) | CCVD | 9.5 | 1.5 | 90 |
| CVD-SWCNT | Chasm Advanced Materials (SG76) | CVD (CoMoCAT®) | 0.83 | 1 | ≥90 |
| AD-SWCNT | Carbon Solutions Inc. (AP-SWNT) | Arc discharge | 1.4 | >1 | 60–70 |
| Label | Treatment | Functional groups |
|---|---|---|
| c-HNO3-MWCNT | 9.5 M HNO3, 18 h reflux | –COOH, –CHO, –OH |
| d-HNO3-MWCNT | 1.5 M HNO3, 2 h reflux | –COOH, –CHO, –OH |
| F-MWCNT | Isopentyl nitrite, H2N–C6H5–(CF2)7–CF3, 12 h, 60 °C | –C6H5–(CF2)7–CF3 |
| HSO3-MWCNT | Isopentyl nitrite, H2N–C6H5–SO3H, 1 h, 80 °C | –C6H5–SO3H |
Most of the CNT samples were dispersed with the help of a surfactant, either sodium dodecyl benzene sulfonate (SDBS) or Solsperse™ 27000, which is an acrylic commercial component for inks. One of the f-CNT samples, the HSO3-MWCNT sample, and the GOs were directly dispersed in water. Dispersions of the nanomaterials were prepared at initial concentrations in the range of 0.4–4 mg mL−1 with the help of ultrasound. Most of the dispersions were centrifuged at a moderate speed of 4500 rpm to avoid large aggregates. Only the GO-16 and GO-G dispersions were not centrifuged since they did not contain large aggregates. Further details on the quality of the dispersions are provided in the ESI† (Section S2).
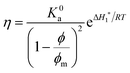
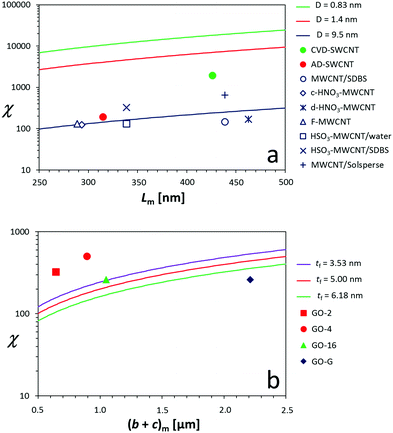
The viscosity (η) of a fluid is defined as the ratio between the shear stress (F) and the shear rate (G): η = F/G. For a suspension of solid particles in a liquid, several models aim to describe the dependence of η on factors such as temperature and particle concentration and shape. The relative viscosity (ηr), which is defined as the ratio between the dispersion viscosity (η) and the viscosity of the base fluid (η0), is mainly controlled by the particle shape and size, as well as the volume fraction (ϕ). Einstein's pioneering work on dilute suspensions of hard spheres,46 for which ηr = 1 + 2.5ϕ, has been complemented by successive approaches taking into account the non-sphericity of the particles and the effect of higher concentrations. In some of those approaches, ηr is a polynomial function of ϕ, whose coefficients model the dependence on size and shape.47–50 A drawback of the mentioned models is their prediction of a finite viscosity regardless of the ϕ value, which is clearly unphysical. Viscosity must diverge as ϕ tends to the maximum packing fraction (ϕm), which depends on the particle geometry. This behaviour is predicted by models such as Mooney,51 Krieger–Dougherty,52 and Maron–Pierce.45 While Mooney and Krieger–Dougherty models have two fitting parameters, the Maron–Pierce model considers just one, as far as regards ηr. Fitting our experimental data with two parameters results in a slightly modified value of ϕm, but brings out no significant improvement in the standard deviation. Thus, the Maron–Pierce model is chosen here for simplicity.
The model of Maron and Pierce leads to the following equation for the absolute viscosity:45
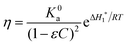 | (1) |
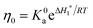 | (2) |
Therefore, the relative viscosity (ηr) is defined as
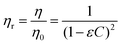 | (3) |
For the present work, viscosity measurements were performed on dilute aqueous suspensions. The solid concentration (C) in the liquid was always kept below 4 mg mL−1, so it can be reasonably assumed that dispersions behave as Newtonian fluids. Accordingly, viscosities were measured in Ubbelohde capillary viscosimeters, which provide very precise measurements in the low-viscosity regime. For instance, an Ubbelohde viscosimeter has been utilized for the assessment of the exfoliation degree of SWCNT dispersions.37 In Ubbelohde viscosimeters, a suspended column of the liquid flows inside the capillary under laminar regime, by gravity and in a unidirectional way, while the flowing time is registered. The direct measurement from Ubbelohde viscosimeters is the kinematic viscosity (v), which is related to the dynamic viscosity (η) through the fluid density (ρ): η = v·ρ. The complete set of v and ρ measurements is provided in the ESI† (Sections S3 and S4).
The kinematic viscosity of GO dispersions at temperatures between 298.15 and 318.15 K is in the range of 4.0 to 0.7 mm2 s−1. For CNTs, the kinematic viscosity is between 2.8 and 0.6 mm2 s−1, except in the Solsperse medium, where it reaches 6.1 mm2 s−1 at 298.15 K. The ρ values of all the measured CNT and GO dispersions are nearly that of pure water (Table S4, ESI†).
Before continuing with the analysis of viscosity at different nanoparticle concentrations, it was confirmed that the relative viscosity (ηr) does not substantially change with temperature.21 This condition, which indicates a Newtonian behavior, was clearly fulfilled by all the GO and CNT systems in water and SDBS. Deviations of 10% in the relative viscosity were found for MWCNT dispersions in Solsperse at the highest temperatures and concentrations. Solsperse leads to viscosities of >4 cP at room temperature, and thus the data interpretation has to be performed carefully. However, for most of the analyzed dispersions, it is evident that eqn (1) and (3) can be applied instead of the complete model for non-Newtonian suspensions (ESI,† Sections S5 and S6).
Outcome of the experimental data fitting
The simplified Maron–Pierce model fits reasonably well our viscosity measurements. Fig. 1 and 2 show the plots of ηrvs. C for GO-16 in water and MWCNTs in 0.5% SDBS and 20% Solsperse. The difference between measured and fitted values is <1%, except in the MWCNT/Solsperse system. The trend for GO (Fig. 1) is linear at concentrations below 2 mg mL−1, and it curves upward at higher concentrations. This fact most probably indicates the very beginning of a semi-dilute regime and thus the Newtonian limit. For CNTs (Fig. 2), the trend is nearly linear up to concentrations around 3 mg mL−1. Although plots for the other GO, SWCNT and f-CNT dispersions are not shown here, our experimental data suggest trends similar to Fig. 1 and 2. The deviation of values in Solsperse (Fig. 2b) is higher, compared to the other dispersions, probably because of the increase in the viscosity of the medium. The fitting parameters for all the samples are listed in the ESI† (Section S7). A comment on the accuracy of measurements in the Solsperse medium is also included in Section S8 (ESI†).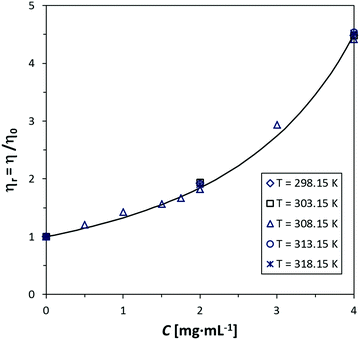 | ||
| Fig. 1 Relative viscosity (ηr) as a function of concentration (C) of GO-16 in water at 5 temperatures. The fitting line was calculated with the Maron–Pierce model (eqn (1)). | ||
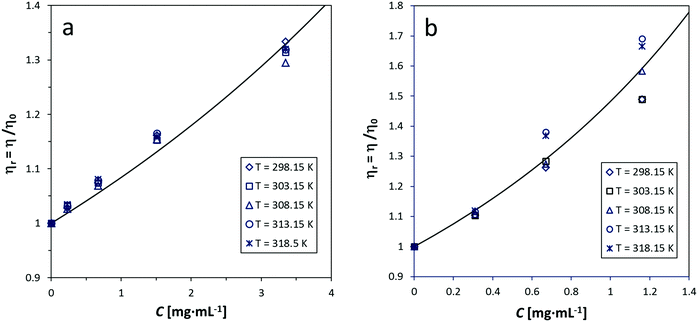 | ||
| Fig. 2 Relative viscosity (ηr) as a function of concentration (C) of MWCNTs at 5 temperatures in (a) 0.5% SDBS and (b) 20% Solsperse. The fitting line was calculated with the Maron–Pierce model (eqn (1)). | ||
It has been commented above that ΔH1* is expected to depend only on the liquid medium. Fig. 3 presents the calculated ΔH1* values for all the samples. In fact, ΔH1* is nearly constant in almost all the dispersions, and in pure water and the 0.5% SDBS medium as well. The values of ΔH1*/R are typically around 1864 K with a deviation of ±54 K. Apparently, the SDBS surfactant does not lead to any substantial change with respect to pure water, and thus both media can be regarded as equivalent in terms of ΔH1*. However, certain deviations from water exist, which should be consequently interpreted as induced changes in the molecular structure of the liquid.
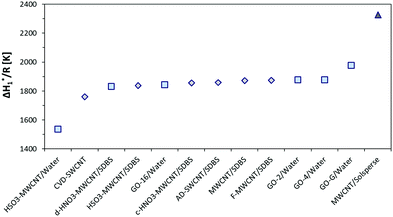 | ||
| Fig. 3 Enthalpy of activation for viscous flow (ΔH1*) for all the CNT and GO systems that are considered in the present work. | ||
The addition of HSO3-MWCNTs to pure water causes a strong decrease in ΔH1*. The presence of benzene sulfonic acid groups on MWCNT walls allows the preparation of a stable dispersion in water, but also disrupts the liquid structure. The creation of hydrogen bonds between benzene sulfonic acid groups and water might be an explanation. Curiously, the effect is not observed in the presence of SDBS surfactant. The ΔH1* value decreases by 5% after the addition of the CVD-SWCNT sample to the 0.5% SDBS medium. Even though the change is relatively small, it might be related to the extraordinarily high aspect ratio of CVD-SWCNTs (Table 2), which leads to a correction in the flowing energetics of the liquid. An increase of 6% in ΔH1* was calculated for the GO-G dispersion in water. The change in ΔH1* might reflect the presence of a stabilizing additive. A strong increase in ΔH1* up to 2330 K occurs in the 20% Solsperse medium. Acrylic chains of Solsperse greatly influence the associated structure of water, hindering their molecular mobility. The effect is evident despite a decrease in the accuracy of viscosity measurements for the Solsperse medium.
Maximum packing fraction
In this section, the viscosity is related to the degree of nanoparticle packing in the fluid. First, the experimental data set is expressed in terms of nanoparticle volume fractions. For that reason, geometrical parameters of CNT and GO units are experimentally measured, so that the particle density (ρp) and aspect ratio (rp) can be calculated for each sample. Later, experimental data are compared with predictive theories that consider suspended particles as ellipsoids of varying rp.In terms of the particle volume fraction (ϕ), the equation of Maron and Pierce (eqn (1)) is written as
 | (4) |
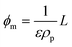 | (5) |
The CNTs are considered as rigid cylinders, which is a reasonable assumption according to the literature.39,40 An average diameter (D) for each sample is taken from product specifications (Table 2). The presence of chemical groups on MWCNT walls is neglected in terms of D. Length distributions for each CNT and f-CNT sample were analyzed from scanning electron microscopy (SEM) images. The length of a number of CNTs (N = 290–480) was directly measured on SEM images (ESI,† Section S10). The length determination is assumed to be valid, although the morphology of the solid on the SEM substrate might be substantially different from that of free nanostructures in the liquid dispersion.54 According to the literature,38,55 the length histogram was fitted to a log-normal distribution (Section S10, ESI†). The calculated average and median lengths (La and Lm respectively) from log-normal distributions are listed in Table 4. The median length was used for the calculation of ρp in each case. In order to complete the geometrical description of MWCNTs, the number of layers was deduced from an experimental measurement of the specific surface area (SSAMWCNT = 230 m2 g−1) by nitrogen adsorption at 77 K.
| Sample | L m [nm] | L a [nm] |
|---|---|---|
| MWCNT | 439 | 506 |
| CVD-SWCNT | 426 | 515 |
| AD-SWCNT | 315 | 384 |
| c-HNO3-MWCNT | 293 | 375 |
| d-HNO3-MWCNT | 463 | 585 |
| F-MWCNT | 289 | 389 |
| HSO3-MWCNT | 339 | 453 |
Surface area distributions of GO flakes were also determined from SEM images. The calculated average and median surface areas (Sa and Sm respectively) of the four GO samples are listed in Table 5. Assuming an approximately elliptic shape, the complete description of flake dimensions requires determining its thickness. Equivalently, the number of layers (nL) and the distance between layers (dLL) in the flake were calculated from X-ray diffraction (XRD) patterns, applying the Bragg and Scherrer equations (ESI,† Section S11). The calculated dLL and nL dimensions are listed in Table 5. The flake thickness can be directly calculated as tf = (nL − 1)·dLL.
| Sample | S m [μm2] | S a [μm2] | n L | d LL [nm] |
|---|---|---|---|---|
| GO-2 | 0.33 | 0.61 | 7 | 0.821 |
| GO-4 | 0.63 | 1.17 | 7 | 0.833 |
| GO-16 | 0.86 | 1.56 | 9 | 0.833 |
| GO-G | 3.84 | 7.27 | 5 | 0.879 |
Once the ρp value was calculated from geometric parameters for all the CNT and GO samples, a correction due to the presence of heteroatoms and impurities was considered. The correction was performed with a parameter that took into account the weight of atoms different from carbon in the structures. However, this additional parameter only causes relatively small changes in the calculated values, which do not alter the qualitative discussion of the results. Similarly, another correction factor was considered for the weight change undergoing if the inner cavity of CNTs was filled by the liquid medium. The filling factor of CNTs, which was not finally applied, does not change the qualitative discussion that is presented next.
Now, theoretical models to predict the relationship of ϕmvs. rp are discussed. In the first approximation, both CNTs and GO are considered ellipsoidal particles with extreme aspect ratios. Ellipsoidal particles are defined by the semi-axes a, b and c. The CNTs may be described as elongated (prolate, a ≫ b = c) ellipsoids, while GO flakes look like flattened (oblate, a ≪ b = c) ellipsoids. The coefficient ϕm can be related to the extra power or rate of work (Ẇp) required to shear a volume of the nanofluid due to the presence of the particle:56
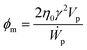 | (6) |
In its movement inside the fluid, the particle is free to rotate along its axis of symmetry (in the a direction), which is a natural easy movement. The ϕm coefficient has a maximum when all the ellipsoids are oriented in the flow direction. However, a gradient of velocity in the fluid may exist that additionally forces the particle to tumble end over end. In fact, the velocity of a fluid in a capillary is maximum at the center and minimum at the capillary wall. The end-over-end rotation is much more energy consuming than the simple rotation along the symmetry axis. Moreover, the particle requires a lot of extra space to rotate, which hinders particle packing and leads to a minimum ϕm coefficient (Fig. 4). A number of intermediate situations can be considered depending on the angle between the symmetry axis of the spheroid and the flow direction.
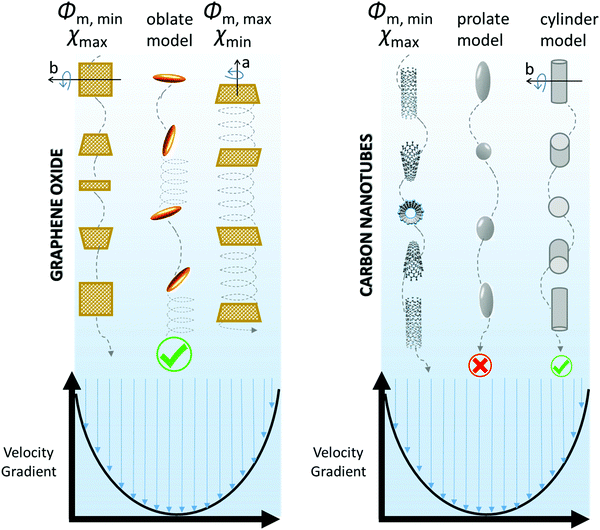 | ||
| Fig. 4 Schematic explanation of GO and CNT nanoparticle dynamics, according to their viscous behavior in a velocity gradient. | ||
Therefore, the theoretical value of ϕm for spheroidal particles can be calculated as a function of rp for different orientations of the particle in the flowing liquid. GO flakes are considered as oblate spheroids (rp ≪ 1) and CNTs as prolate spheroids (rp ≫ 1). Three hypothetical orientations of the spheroidal particle are here taken into account, giving three ϕm functions: maximum, minimum and average. The average ϕm coefficient is calculated accounting for all the possible orientations of the particle, which are assumed to be equally probable.
Intrinsic viscosity
The relationship between ηr and ϕ is, according to the model of Maron and Pierce (eqn (2) and (4)), as follows: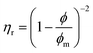 | (7) |
In the dilute regime, eqn (7) can be approximated by the first term of a series expansion:
| η ≈ η0(1 + χϕ) | (8) |
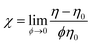 | (9) |
 | ||
| Fig. 5 Intrinsic viscosity (χ) as a function of the aspect ratio (rp). Experimental data are superimposed to trend lines that were calculated for spheroidal particles56 and for cylinders.58 The dashed line indicates the correction arising from the statistical dispersion in the CNT length. | ||
The integral equation of Ẇp can be solved analytically for spheroids, but not for cylinders. Therefore, Aragon and Flamik proposed a solution by numerical methods, more specifically applying the boundary element method.58 Cylindrical particles are characterized by their aspect ratio rp = L/D. The model of Aragon and Flamik assumes rp > 1 and takes into account both rotational and translational movements of cylindrical particles in the fluid. They considered three possible configurations for cylinder edges: open, closed by spherical caps, and closed by a circle in the rectangular configuration. The results for the three configurations converge at high enough rp values. The final equation of Aragon and Flamik for χ totally agrees with a solution that was given by Mansfield and Douglas applying another numerical method, namely, the path integration method.59
Experimental values of χ for CNTs match quite well the numerical equation for cylindrical particles (Fig. 5). The numerical model of cylinders suitably predicts the behavior of CNTs in the dilute regime. Since the χ vs. rp branch (solid line in Fig. 5) was first calculated under the assumption that all nanotubes have an identical length Lm, a question remains about the reliability of such a simplifying approximation. Therefore, another calculation was performed taking into account the range of Lm values that comes out from considering a log-normal distribution (dashed line in Fig. 5). The expected deviation in terms of length variability is not qualitatively relevant. Regarding the applicability of numerical methods to solve Eqn 6 for the case of GO as a flat cylinder with rp ≪ 1, the solution is not trivial and falls out of the scope of the present work.
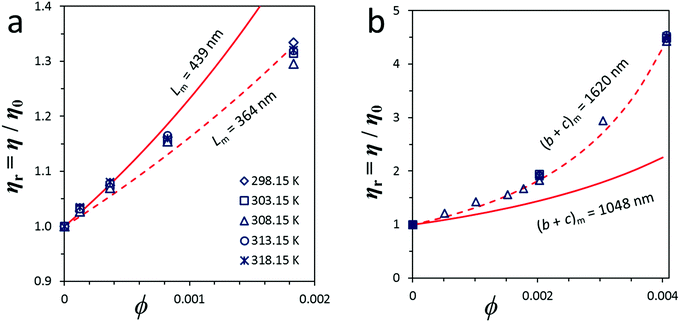
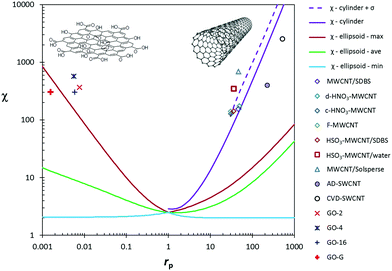
From the theoretical χ = f(rp) function, the variation of χ with the geometrical parameters of length, diameter and thickness can be calculated for CNT and GO dispersions (Fig. 6). Experimental data of GO in water and MWCNTs in SDBS agree well with the theoretical function. Chemical functionalization of MWCNTs, which causes certain changes in the nanotube length, has a minor influence on viscosity. The theoretical χ value for SWCNT dispersions is overestimated with respect to experimental data. The deviation might be associated with a certain degree of bundling and, indirectly, with the presence of impurities in the starting SWCNT powder material.
 | ||
| Fig. 6 Experimental and theoretical intrinsic viscosity (χ) as a function of particle shape parameters: (a) experimental data for CNT dispersions as a function of their length (L) and theoretical trends for cylinders,58 with diameters D = 0.83, 1.49 and 9.5 nm; (b) experimental data for GO dispersions as a function of their flake diameter (b + c) and theoretical trends for oblate ellipsoids,56 whose minor axis (2·a) is equal to the flake thickness tf = 3.53, 5.00 and 6.18 nm. Theoretical calculations correspond to the distributions of multi-disperse particles whose length (CNT) or surface (GO) follows a log-normal distribution. | ||
A step forward in the assessment of the theoretical model is the calculation of the relative viscosity (ηr) as a function of geometrical parameters and the particle concentration. According to the Maron–Pierce model, ηr is related to χ by:
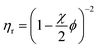 | (10) |
Finally, it is noteworthy that the absolute viscosity (η) depends on the particle size,13 while the intrinsic viscosity (χ value) does not theoretically depend on size. Regarding the intrinsic viscosity, let us recall the universal value χ = 5/2 deduced by Einstein for spheres. Moreover, the more general expressions reported for spheroids and rods depend only on the shape and the aspect ratio.56–59 Thus, the relationship χ = f(rp) can be regarded as a universal prediction of the viscosity for 1D and 2D nanoparticle dispersions in the dilute regime.
Conclusions
It is demonstrated that the experimental viscosity of dilute CNT and GO dispersions can be fitted to the empirical Maron–Pierce model, as a function of the particle concentration and temperature. The fitting allows the calculation of two parameters, namely, the maximum packing fraction (ϕm) and the enthalpy of activation for viscous flow (ΔH1*); the ΔH1* values are nearly constant for most of the dispersions. Experimental data for GOs and CNTs agree with theoretical predictions by first principles, which evaluate ϕm and the intrinsic viscosity (χ) as a function of the aspect ratio (rp). It is deduced that rp is the most relevant intrinsic parameter in the studied experimental range. The surface functionality only implies a small correction, as far as it does not induce substantial changes in the rp value. The comparison between experimental values and theoretical trends indicates that GO flakes behave as ellipsoids that can rotate perpendicularly to the moving direction of the fluid, while the CNT dispersion can be envisaged as cylindrical particles that rotate in all the possible orientations. The data set collected in the present work is relevant for applications using dilute CNT and GO inks, and contributes to a better understanding of mass transport phenomena and particle dynamics in nanofluids. The viscosity of CNT and GO dispersions can be conceptualized as a function of the aspect ratio, which becomes the most relevant parameter to predict in a universal way the viscosity of dilute nanofluids of any kind of 1D and 2D nanoparticles in dilute suspensions.Experimental section
Materials and dispersions
MWCNTs (NC7000 grade) were purchased from Nanocyl (Sambreville, Belgium, EU). The chemical functionalization protocols are based on previous works,10,60,61 and are detailed in the ESI† (Section S12); different characterization techniques, including infrared spectroscopy, Raman spectroscopy and thermogravimetric analysis, were applied to confirm the functionalization efficiency in those previous works. CVD-SWCNTs (S76 grade) were provided by Sigma Aldrich (Ref. 704121); the material was manufactured by SouthWest Nanotechnologies Inc., now Chasm Advanced Materials (Norman, OK, USA), by the CoMoCAT process. Pristine arc-discharge SWCNTs (AD-SWCNTs) were purchased from Carbon Solutions Inc. (Riverside, CA, USA). Graphite flakes were purchased from Aldrich (ref. 332461).The GO-2, GO-4 and GO-16 samples were synthesized from graphite flakes by a modified Hummers’ method including the following stages:11 (i) treatment in NaNO3/H2SO4/KMnO4 at 35 °C for 2, 4 or 16 h, respectively; (ii) cooling in 30% H2O2; (iii) filtration, washing with diluted HCl and drying; and (iv) resuspension in water at 0.5 mg mL−1 and exfoliation in an ultrasound bath for 2 h. The GO-G sample was purchased from Graphenea (San Sebastian, Spain).
The SDBS surfactant was purchased from Sigma Aldrich and acrylic Solsperse™ 27000 was provided by Lubrizol Advanced Materials (Sant Cugat del Vallés, Barcelona, Spain). For the preparation of CNT dispersions, SDBS was dissolved at 0.5 mass/vol% and Solsperse was diluted at 20 vol% in water. The solutions were added to CNT powders and the mixtures were treated with a 400 W Hielscher ultrasonic probe for 1 h at 60% amplitude and a frequency of 0.5 cycles. Dispersions were centrifuged at 4500 rpm for 30 min and the sediment was discarded.
Viscosity measurements
Viscosity measurements were performed in Ubbelohde viscosimeters (types 0a and I) (SI Analytics). The correction of kinematic energy (Hagenbach correction) was applied when needed. The kinematic viscosity was calculated as ν = K·t, where K is the constant of the viscosimeter (0.004955 mm2 s−2 for the 0a and 0.009596 mm2 s−2 for the I viscosimeter). The temperature was controlled at ±0.01 degree with a Julabo thermostatic bath provided with an external temperature probe. The temperature calibration was performed by measuring the viscosity of deionized water. Each viscosity determination was repeated at least three times, achieving deviations of <1%, most typically around 0.1%.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been funded by the Spanish MINEICO under the project ENE 2016-79282-C5-1-R (AEI/FEDER, UE), the Government of Aragón (Grupo reconocido T03-20R) and associated EU Regional Development Funds (DGA/FEDER, UE). Special thanks are directed to Ms A. Santidrián for the preparation of HSO3-MWCNT, Mr D. Velilla for zeta-size measurements, Dr E. Istif for GO-G sample characterization, Mr S. Escuriet from Lubrizol Advanced Materials for providing the Solsperse™ 27000 surfactant, the Analysis Service at Instituto de Carboquímica ICB-CSIC, the Advanced Microscopy Laboratory (LMA) at Instituto de Nanociencia de Aragón, and the Electron Microscopy Service at the University of Zaragoza. SVR thanks Spanish MINEICO for her PhD grant (BES2014-068727 and associated EU Social Funds). J. M. G.-D. greatly acknowledges the Spanish Ministry of Science, Innovation and Universities (MICINN, formerly MINEICO) for his “Juan de la Cierva – incorporación” grant (Ref. UCI-2016-27789).References
- S. Peretz and O. Regev, Carbon nanotubes as nanocarriers in medicine, Curr. Opin. Colloid Interface Sci., 2012, 17, 360–368 CrossRef CAS.
- E. Stratakis, K. Savva, D. Konios, C. Pedridis and E. Kymakis, Improving the efficiency of organic photovoltaics by tuning the work function of graphene oxide hole transporting layers, Nanoscale, 2014, 6, 6925–6931 RSC.
- C. Ménard-Moyon, H. Ali-Boucetta, C. Fabbro, O. Chaloin, K. Kostarelos and A. Bianco, Controlled chemical derivatization of carbon nanotubes with imaging, targeting, and therapeutic capabilities, Chem. – Eur. J., 2015, 21, 14886–14892 CrossRef PubMed.
- A. Ansón-Casaos, E. Garcia-Bordeje, A. M. Benito and W. K. Maser, Nanostructured carbon materials: synthesis and applications, NATO Science for Peace and Security Series B: Physics and Biophysics, 2018, Part F2, pp. 177–191 Search PubMed.
- C. Wang, K. Xia, H. Wang, X. Liang, Z. Yin and Y. Zhang, Advanced carbon for flexible and wearable electronics, Adv. Mater., 2019, 31, 1801072 CrossRef PubMed.
- X. Wang, A. Vasileff, Y. Jiao, Y. Zheng and S.-Z. Qiao, Electronic and structural engineering of carbon-based metal-free electrocatalysts for water splitting, Adv. Mater., 2019, 31, 1803625 CrossRef PubMed.
- J.-M. Tulliani, B. Inserra and D. Ziegler, Carbon-based materials for humidity sensing: a short review, Micromachines, 2019, 10, 232 CrossRef PubMed.
- V. C. Moore, M. S. Strano, E. H. Haroz, R. H. Hauge and R. E. Smalley, Individually suspended single-walled carbon nanotubes in various surfactants, Nano Lett., 2003, 3, 1379–1382 CrossRef CAS.
- R. Haggenmueller, S. S. Rabatekar, J. A. Fagan, J. Chun, M. L. Becker, R. R. Naik, T. Krauss, L. Carlson, J. F. Kadla, P. C. Trulove, D. F. Fox, H. C. DeLong, Z. Fang, S. O. Kelley and J. W. Gilman, Comparison of the quality of aqueous dispersions of single wall carbon nanotubes using surfactants and biomolecules, Langmuir, 2008, 24, 5070–5078 CrossRef CAS PubMed.
- J. M. González-Domínguez, A. Santidrián, A. Criado, C. Hadad, M. Kalbac and T. Da Ros, Multipurpose nature of rapid covalent functionalization on carbon nanotubes, Chem. – Eur. J., 2015, 21, 18631–18641 CrossRef PubMed.
- A. Tararan, A. Zobelli, A. M. Benito, W. K. Maser and O. Stéphan, Revisiting graphene oxide chemistry via spatially-resolved electron energy loss spectroscopy, Chem. Mater., 2016, 28, 3741–3748 CrossRef CAS.
- A. K. Rasheed, M. Khalid, W. Rashmi, T. C. S. M. Gupta and A. Chan, Graphene based nanofluids and nanolubricants – Review of recent developments, Renewable Sustainable Energy Rev., 2016, 63, 346–362 CrossRef CAS.
- H. D. Koca, S. Doganay, A. Turgut, I. H. Tavman, R. Saidur and I. M. Mahbubul, Effect of particle size on the viscosity of nanofluids, Renewable Sustainable Energy Rev., 2018, 82, 1664–1674 CrossRef CAS.
- A. Arshad, M. Jabbal, Y. Yan and D. Reay, A review on graphene based nanofluids: Preparation, characterization and applications, J. Mol. Liq., 2019, 279, 444–484 CrossRef CAS.
- F. Jabbari, S. Saedodin and A. Rajabpour, Experimental investigation and molecular dynamics simulations of viscosity of CNT-water nanofluid at different temperatures and volume fractions of nanoparticles, J. Chem. Eng. Data, 2019, 64, 262–272 CrossRef CAS.
- P. Garg, J. L. Alvarado, C. Marsh, T. A. Carlson, D. A. Kessler and K. Annamalai, An experimental study on the effect of ultrasonication on viscosity and heat transfer performance of multi-wall carbon nanotube-based aqueous nanofluids, Int. J. Heat Mass Transfer, 2009, 52, 5090–5101 CrossRef CAS.
- T. X. Phuoc, M. Massoudi and R.-H. Chen, Viscosity and thermal conductivity of nanofluids containing multi-walled carbon nanotubes stabilized by chitosan, Int. J. Therm. Sci., 2011, 50, 12–18 CrossRef CAS.
- S. Halelfadl, P. Estellé, B. Aladag, N. Doner and T. Maré, Viscosity of carbon nanotubes water-based nanofluids: Influence of concentrations and temperature, Int. J. Therm. Sci., 2013, 71, 111–117 CrossRef CAS.
- R. Sadri, G. Ahmadi, H. Togun, M. Dahari, S. N. Kazi, E. Sadeghinezhad and N. Zubir, An experimental study on thermal conductivity and viscosity of nanofluids containing carbon nanotubes, Nanoscale Res. Lett., 2014, 9, 151 CrossRef PubMed.
- L. Yu, Y. Bian, Y. Liu and X. Xu, Experimental investigations on rheological properties of wáter based nanofluids with low MWCNT concentrations, Int. J. Heat Mass Transfer, 2019, 135, 175–185 CrossRef CAS.
- M. Xing, J. Yu and R. Wang, Thermo-physical properties of water-based single-walled carbon nanotube nanofluid as advanced coolant, Appl. Therm. Eng., 2015, 87, 344–351 CrossRef CAS.
- Z. Said, Thermophysical and optical properties of SWCNTs nanofluids, Int. Commun. Heat Mass Transfer, 2016, 78, 207–213 CrossRef CAS.
- M. A. Sabiha, R. M. Mostafizur, R. Saidur and S. Mekhilef, Experimental investigation on thermo physical properties of single walled carbon nanotubes, Int. J. Heat Mass Transfer, 2016, 93, 862–871 CrossRef CAS.
- N. Ahammed, L. G. Asirvatham and S. Wongwises, Effect of volume concentration and temperature on viscosity and surface tension of graphene-water nanofluid for heat transfer applications, J. Therm. Anal. Calorim., 2016, 123, 1399–1409 CrossRef CAS.
- D. Cabaleiro, P. Estellé, H. Navas, A. Desforges and B. Vigolo, Dynamic viscosity and surface tension of stable graphene oxide and reduced graphene oxide aqueous nanofluids, J. Nanofluids, 2018, 7, 1–8 CrossRef.
- S. S. J. Aravind, P. Baskar, T. T. Baby, R. K. Sabareesh, S. Das and S. Ramaprabhu, Investigation of structural stability, dispersion, viscosity, and conductive heat transfer properties of functionalized carbon nanotube based nanofluids, J. Phys. Chem. C, 2011, 115, 16737–16744 CrossRef CAS.
- M. Hosseini, R. Sadri, S. N. Kazi, S. Bagheri, N. Zubir, C. B. Teng and T. Zaharinie, Experimental study on heat transfer and thermos-physical properties of covalently functionalized carbon nanotubes nanofluids in an annular heat exchanger: a green and novel synthesis, Energy Fuels, 2017, 31, 5635–5644 CrossRef CAS.
- E. K. Hobbie, Shear rheology of carbon nanotube suspensions, Rheol. Acta, 2010, 49, 323–334 CrossRef CAS.
- C. Vallés, Rheology of graphene oxide dispersions, in Graphene oxide: fundamentals and applications, 1st edn, ed. A. M. Dimiev and S. Eigler, John Wiley & Sons, Ltd, 2017, pp. 121–146 Search PubMed.
- Y. Liu, C. Chen, L. Liu, G. Zhu, Q. Kong, R. Hao and W. Tan, Rheological behavior of high concentrated dispersions of graphite oxide, Soft Mater., 2015, 13, 167–175 CrossRef CAS.
- R. Shu, Q. Yin, H. Xing, D. Tan, Y. Gan and G. Xu, Colloidal and rheological behavior of aqueous graphene oxide dispersions in the presence of poly(ethylene glycol), Colloids Surf., A, 2016, 488, 154–161 CrossRef CAS.
- E. Anczurowski and S. G. Mason, The kinetics of flowing dispersions III. Equilibrium orientations of rods and discs (experimental), J. Colloid Interface Sci., 1967, 23, 533–546 CrossRef.
- W. Pabst, E. Gregorova and C. Berthold, Particle shape and suspension rheology of short-fiber systems, J. Eur. Ceram. Soc., 2006, 26, 149–160 CrossRef CAS.
- J. Rodríguez-Fernández, J. Pérez-Juste, L. M. Liz-Marzán and P. R. Lang, Dynamic light scattering of short Au rods with low aspect ratios, J. Phys. Chem. C, 2007, 111, 5020–5025 CrossRef.
- A. N. G. Parra-Vasquez, I. Stepanek, V. A. Davis, V. C. Moore, E. H. Haroz, J. Shaver, R. H. Hauge, R. E. Smalley and M. Pasquali, Simple length determination of single-walled carbon nanotubes by viscosity measurements in dilute suspensions, Macromolecules, 2007, 40, 4043–4047 CrossRef CAS.
- D. E. Tsentalovich, A. W. K. Ma, J. A. Lee, N. Behabtu, E. A. Bengio, A. Choi, J. Hao, Y. Luo, R. J. Headrick, M. J. Green, Y. Talmon and M. Pasquali, Relationship of extensional viscosity and liquid crystalline transition to length distribution in carbon nanotube solutions, Macromolecules, 2016, 49, 681–689 CrossRef CAS.
- I. Cotiuga, F. Picchioni, U. S. Agarwal, D. Wouters, J. Loos and P. J. Lemstra, Block-copolymer-assisted solubilization of carbon nanotubes and exfoliation monitoring through viscosity, Macromol. Rapid Commun., 2006, 27, 1073–1078 CrossRef CAS.
- A. N. J. Parra-Vasquez, J. G. Duque, M. J. Green and M. Pasquali, Assessment of lenth and bundle distribution of dilute single-walled carbon nanotubes by viscosity measurements, AIChE J., 2014, 60(4), 1499–1508 CrossRef CAS.
- M. S. Arnold, J. Suntivich, S. I. Stupp and M. C. Hersam, Hydrodynamic characterization of surfactant encapsulated carbon nanotubes using an analytical ultracentrifuge, ACS Nano, 2008, 2, 2291–2300 CrossRef CAS PubMed.
- C. A. Silvera Batista, M. Zheng, C. Khripin, X. Tu and J. A. Fagan, Rod hydrodynamycs and length distributions of single-wall carbon nanotubes using analytical ultracentrifugation, Langmuir, 2013, 30, 4895–4904 CrossRef PubMed.
- J. Walter, T. J. Nacken, C. Damm, T. Thaseem, S. Eigler and W. Peukert, Determination of the lateral dimension of graphene oxide nanosheets using analytical ultracentrifugation, Small, 2015, 11, 814–825 CrossRef CAS PubMed.
- Q. Shi, Y. Liu, F. Chen and S. Dong, Investigations on rheological properties of carbon nanotube nanofluids, Phys. Chem. Liq., 2019, 57(1), 37–42 CrossRef CAS.
- M. H. Ahmadi, B. Mohseni-Gharyehsafa, M. Farzaneh-Gord, R. D. Jilte, R. Kumar and K. Chau, Applicability of connectionist methods to predict dynamic viscosity of silver/water nanofluid by using ANN-MLP, MARS and MPR algorithms, Eng. Appl. Comput. Fluid Mech., 2019, 13(1), 220–228 Search PubMed.
- M. Ramezanizadeh, M. A. Ahmadi, M. H. Ahmadi and M. A. Nazari, Rigurous Smart model for predicting dynamic viscosity of Al2O3/water nanofluid, J. Therm. Anal. Calorim., 2019, 137, 307–316 CrossRef CAS.
- H. M. Maron and P. E. Pierce, Application of Ree-Eyring generalized flow theory to suspensions of spherical particles, J. Colloid Sci., 1956, 11, 80–95 CrossRef.
- A. Einstein, Berichtigung zu meiner Arbeit: Eine neue Bestimmung der Moleküldimensionen, Ann. Phys., 1911, 34, 591–592 CrossRef CAS.
- R. Simha, The Influence of Brownian Movement on the Viscosity of Solutions, J. Phys. Chem., 1940, 44(1), 25–34 CrossRef CAS.
- W. Kuhn and H. Kuhn, The dependence of the viscosity on velocity gradient in suspensions and solutions of fibrous macromolecules, Helv. Chim. Acta, 1945, 28, 97–127 CrossRef CAS.
- H. Brenner and D. W. Condiff, Transport mechanics in systems of orientable particles. IV. Convective transport, J. Colloid Interface Sci., 1974, 47(1), 199–264 CrossRef CAS.
- G. K. Batchelor, The effect of Brownian motion on the bulk stress in a suspension of spherical particles, J. Fluid Mech., 1977, 83(1), 97–117 CrossRef.
- M. Mooney, The viscosity of a concentrated suspension of spherical particles, J. Colloid Sci., 1951, 6(2), 162–170 CrossRef CAS.
- I. M. Krieger and T. J. Dougherty, A mechanism for non-Newtonian flow in suspensions of rigid spheres, Trans. Soc. Rheol., 1959, 3(1), 137–152 CAS.
- A. Peigney, C. Laurent, E. Flahaut, R. R. Bacsa and A. Rousset, Specific surface area of carbon nanotubes and bundles of carbon nanotubes, Carbon, 2001, 39, 507–514 CrossRef CAS.
- S. Sandoval, M. Kierkowicz, E. Pach, B. Ballesteros and G. Tobias, Determination of the length of single-walled carbon nanotubes by scanning electron microscopy, MethodsX, 2018, 5, 1465–1472 CrossRef PubMed.
- A. J. Blanch, C. E. Lenehan and J. S. Quinton, Parametric analysis of sonication and centrifugation variables for dispersion of single walled carbon nanotubes in aqueous solutions of sodium dodecylbenzene sulfonate, Carbon, 2011, 49, 5213–5228 CrossRef CAS.
- S. Mueller, E. W. Llewellin and H. M. Mader, The rheology of suspensions of solid particles, Proc. R. Soc. A, 2010, 466, 1201–1228 CAS.
- G. B. Jeffery, The motion of ellipsoidal particles immersed in a viscous fluid, Proc. R. Soc. London, Ser. A, 1922, 102, 161–179 Search PubMed.
- S. R. Aragon and D. Flamik, High precision transport properties of cylinders by the boundary element method, Macromolecules, 2009, 42(16), 6290–6299 CrossRef CAS.
- M. L. Mansfield and J. F. Douglas, Transport properties of rod-like particles, Macromolecules, 2008, 41(14), 5422–5432 CrossRef CAS.
- J. M. González-Domínguez, M. González, A. Ansón-Casaos, A. M. Díez-Pascual, M. A. Gómez and M. T. Martínez, Effect of various aminated single-walled carbon nanotubes on the epoxy cross-linking reactions, J. Phys. Chem. C, 2011, 115, 7238–7248 CrossRef.
- A. Ansón-Casaos, R. Mis-Fernández, C. M. López-Alled, E. Almendro-López, J. Hernández-Ferrer, J. M. González-Domínguez and M. T. Martínez, Transparent conducting films made of different carbon nanotubes, processed carbon nanotubes, and graphene nanoribbons, Chem. Eng. Sci., 2015, 138, 566–574 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Elemental analysis of powder samples; analysis of dispersion quality; kinematic viscosity; density of the CNT and GO dispersions; dependence of relative viscosity with temperature; the Maron and Pierce equations for non-Newtonian suspensions; fitting parameters of eqn (1); accuracy of viscosity measurements; calculation of the particle density; electron microscopy images and the log-normal distribution; XRD experiments for the determination of nL and dLL in GO; chemical functionalization of MWCNTs. See DOI: 10.1039/d0cp00468e |
| This journal is © the Owner Societies 2020 |