Open Access Article
Open Access ArticleSelf-assembly of spiral patterns in confined systems with competing interactions†
J.
Pȩkalski
 *ab,
E.
Bildanau
*ab,
E.
Bildanau
 c and
A.
Ciach
c and
A.
Ciach
 a
a
aInstitute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warszawa, Poland. E-mail: jpekalski@ichf.edu.pl; aciach@ichf.edu.pl
bDepartment of Chemical and Biological Engineering, Princeton University, Princeton, New Jersey 08544, USA
cBelarusian State Technological University, 13a Sverdlov Str., 220006 Minsk, Belarus
First published on 11th September 2019
Abstract
Colloidal particles in polymer solutions and functionalized nanoparticles often exhibit short-range attraction coupled with long-range repulsion (SALR) leading to the spontaneous formation of symmetric patterns. Chiral nanostructures formed by thin films of SALR particles have not been reported yet. In this study, we observe striking topological transitions from a symmetric pattern of concentric rings to a chiral structure of a spiral shape, when the system is in hexagonal confinement. We find that the spiral formation can be induced either by breaking the system symmetry with a wedge, or by melting of the rings. In the former case, the chirality of the spiral is determined by the orientation of the wedge and thus can be controlled. In the latter, the spiral arises due to thermally induced defects and is absent in the average particle distribution, which forms highly regular hexagonal patterns in the central part of the system. These hexagonal patterns can be explained by interference of planar density waves. Thermodynamic considerations indicate that equilibrium spirals can appear spontaneously in any stripe-forming system confined in a hexagon with a small wedge, provided that certain conditions are satisfied by a set of phenomenological parameters.
1 Introduction
Self-assembly of isotropic particles on two-dimensional (2D) unrestricted flat interfaces leads to formation of ordered structures that have either hexagonal or two-fold symmetry. If the self-assembly is driven by isotropic competing interactions that are attractive at short distances, but repulsive at larger separations (SALR pair potential), then it was shown by computer simulations,1–3 theory3–6 and experiments7–9 that the observed low-temperature microphases are made of periodically ordered clusters, stripes or voids. The striped low-temperature structure exhibits one-dimensional periodicity, which upon heating is lost in a step-wise process. Firstly, thermally induced topological defects destroy the translational order, but the orientational order of stripe segments of various sizes is preserved. Further heating turns the orientationally ordered stripe segments into an isotropic labyrinth.2One can expect that instead of cooling down the system to limit the number of topological defects and restore the ordered pattern, one can impose boundary conditions with symmetries that agree with the symmetries of the confined structure. Indeed, in the slit geometry the number of topological defects in the stripe forming SALR system can be reduced either by decreasing the temperature or by decreasing the distance between the parallel confining walls.10 However, the distance between the confining surfaces must be commensurate with the period of the structure stable in the bulk system, otherwise the low-temperature structures have periodic corrugations that spread along the whole slit. Thus, methods that help to enhance the order but do not require a highly precise choice of the wall-to-wall distance are of interest.
The patterns present in the slit and absent in the unconstrained system raise a more general question of the possibility of creating new, desired patterns in self-assembling systems by confining them in containers of different sizes and shapes. New patterns can be expected especially when the symmetries of the boundaries are different from the symmetries of the phases present in the unconstrained self-assembling system. Despite the expected significant role of confinement,11,12 not much is known about its effects on monolayers of SALR particles. Striped 2D SALR patterns were investigated only in a slit5,10,13,14 or on a surface of a sphere,15–19 where topological defects are enforced by the system topology. In 3D, on the other hand, the effects of imposing periodic or closed cylindrical confinement on a hexagonal cylindrical phase were studied,20 showing stability of helical structures similar to those that were observed for block copolymer systems.21
Here we focus on a monolayer of particles adsorbed on a flat surface and confined by a closed boundary with high symmetry – a case not studied for SALR systems yet. The natural candidates to form such a type of confinement are circular or hexagonal walls. Regular hexagons can form a honeycomb structure dividing the plane into cells, and such a pre-patterned surface can be experimentally prepared. Moreover, the clusters in a SALR system can form a hexagonal pattern, but in the case of stripes, new patterns can be induced by hexagonal walls. Thus, we decided to begin the search for confinement-induced new patterns in a 2D SALR system by choosing the hexagonal confinement and thermodynamic conditions leading to formation of stripes.
SALR systems were shown to share many properties with diblock copolymers (BCP), which have found applications in a variety of fields including filtration, photonics or nanofabrication.22–24 In particular, microphases of the same symmetry are present in the two systems, and the phase diagrams have the same topology.25–34 This remarkable similarity can be explained within the Landau–Brazovskii theory, under the assumption of weak-ordering (valid at relatively high-temperature).35 On the other hand, the effect of micellization of amphiphilic particles on the equation of state36 can be qualitatively different from the effect of cluster formation on the equation of state in SALR systems with dominant repulsion.37 In addition, the stripe phase with only orientational order has not been reported in the case of BCP. Thus, the analogy between SALR and BCP systems is not complete.
Single layers of hexagonally ordered BCP which form striped thin films have been already broadly studied and used for fabrication of e.g. nanoelectronics,38–42 and the effects of circular or hexagonal confinement have been studied in ref. 43. In circular confinement, concentric rings were observed at low temperature. When the symmetry was broken by a wedge attached to the circular wall, self-assembled spiral structures appeared. Based on the similarity of the phase diagrams in the bulk35 and previous confinement studies20 one might expect similar effects of confinement in SALR and BCP systems. However, this conjecture is not justified by any general proof, and needs to be either proven or verified by direct results for SALR systems, which is the purpose of this work.
In Section 2 we describe the model and the simulation method. We choose the triangular lattice model introduced in ref. 4, and Monte Carlo simulations in the grand canonical ensemble. The results are presented in Section 3. At low temperature we find concentric hexagonal rings, which upon heating first merge into long spirals, and upon further heating the spiral breaks into disconnected segments of various lengths. Due to the symmetry of the boundaries, the average density shows no chirality, unless the symmetry is broken by a wedge attached to a vertex of the hexagon. The orientation of the wedge determines the chirality of the spiral. However, the average density has the form of a spiral only for certain sizes of the hexagon. The similarity between SALR and BCP systems, and formation of chiral structures only for certain sizes of the systems, raises a general question of in which stripe-forming systems chiral structure can be induced by breaking the symmetry of the hexagonal confinement by a small wedge. Motivated by this question, in Section 4 we present general, model-free thermodynamic considerations for any stripe-forming system. We derive inequalities that must be satisfied by phenomenological parameters such as surface tensions or free-energies associated with structural defects, in order to obtain chiral structures in hexagonal confinement with a small triangular obstacle attached to the boundary. Our conclusions are included in Section 5.
2 Methods and model
To study confinement effects, one needs to know the bulk behavior of the considered system. In the case of SALR particles, competing interactions lead to highly complex energy landscapes, Kosterlitz–Thouless transitions, cluster formation and periodic ordering, and thus sampling of their phase space can be tricky.1,5 Those difficulties are much easier to manage in a discretized space. For that reason the core of our methodology is Monte Carlo (MC) simulations of the lattice model studied in ref. 2, 4 and 10. Our main results, however, were verified by off-lattice molecular dynamics simulations for a continuous model in order to make sure that our results are not artifacts of the underlying lattice (see the ESI† for the continuous-model results).We performed lattice Monte Carlo simulations in the grand canonical ensemble using the standard Metropolis algorithm44 enhanced by the replica exchange scheme,45 which helps to equilibrate systems which exhibit many metastable states. For each value of the chemical potential we sampled n = 150 inverse temperatures, βi, such that βi = β0 + kδβ, k = 0,…, n, with typically β0 = 0 and δβ = 0.025.
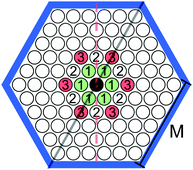
We consider a triangular lattice model (Fig. 1) with the interaction potential:
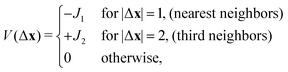 | (1) |
 | (2) |
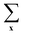 denotes the summation over all lattice sites, the microscopic density at the site x is
denotes the summation over all lattice sites, the microscopic density at the site x is ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (x) = 1(0) when the site x is (is not) occupied and μ is the chemical potential. The results are presented in reduced units, i.e. T* = kBT/J1, μ* = μ/J1.
(x) = 1(0) when the site x is (is not) occupied and μ is the chemical potential. The results are presented in reduced units, i.e. T* = kBT/J1, μ* = μ/J1.
In the bulk, periodic patterns made of rhomboidal clusters, stripes or rhomboidal voids are formed depending on the value of the chemical potential. In the current study we set μ* = 6, corresponding to the stability of the striped phase. We should mention that similar periodic structures occur in a number of different lattice models designed for different physical systems, including three- or two-component mixtures with amphiphilic molecules. One of the first models of this kind was introduced in ref. 46.
As discussed in the introduction, we impose confinement of a hexagonal shape and assume hard-core repulsion between particles and walls. Such a shape of confinement was previously considered for BCP43 or electrons on a Au(111) surface.47,48 We will comment on the found similarities with those systems in the conclusions.
3 Results
3.1 The ground state (T = 0)
In the grand canonical ensemble, the stable structures are those which correspond to the global minimum of the grand potential per lattice site. At T = 0, the grand potential reduces to the thermodynamic Hamiltonian given by eqn (2). We found that for μ* = 6 concentric rings are formed in the hexagonal confinement independently of the system size (Fig. 2). The only difference between the found structures is the defect formed in the center of the hexagon: a hexagonal void, a single particle, a hexagonal cluster or a single empty site. Because the period of the bulk lamellar phase is 4, what determines the particle arrangement in the center of the hexagon is the remainder, r, obtained when dividing M by 4. Similar conformations were previously described for a BCP system within a circular template.43 | ||
| Fig. 2 The ground state conformations for different system sizes, M. From left to right: M = 8, 9, 10, and 11. | ||
3.2 The temperature effect
We start our study of temperature effects on the hexagonal system by the analysis of the heat capacity, cV(T). Fig. 3 shows that the dependence of cV on T is significantly different for r = 0, 2 and r = 1, 3. In the former case, low-T cV peaks are significantly higher and sharper, and occur at higher temperatures than for r = 1, 3. Also the number of peaks is different in the two cases. With increasing system size, new maxima arise and cV(T) becomes more complex. For each value of r, the temperature of the low-T peak of cV decreases monotonically, but for all the considered system sizes it is still larger than the bulk value, Tbulk* = 0.25, that corresponds to the lamella–molten lamella phase transition.2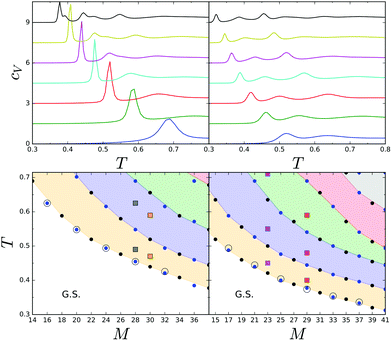 | ||
| Fig. 3 Upper panels: cV(T) for different sizes of the hexagon side M = 4 × n + r, vertically shifted for visibility. Left upper panel from the bottom to the top: M = 14, 18,…, 36, right upper panel from the bottom to the top: M = 15, 19,…, 39. Lower panels: Temperatures corresponding to the cV(T) peaks. G.S. indicates the region for which the ground state structures depicted in Fig. 2 are stable. Density distributions and snapshots for the (M,T) values indicated by squares are shown in Fig. 4. The circles correspond to the temperature at which the average number of clusters, c(T), drops significantly as shown in Fig. 6. | ||
In Fig. 3, bottom panels, we show the structural diagram of the system obtained by the heat capacity calculations. In this diagram, small filled circles correspond to the maxima of cV. Below the bottom line, the ground-state structures, i.e. concentric rings, are stable. The concentric rings melt in a step-wise way, with structural changes occurring at temperatures corresponding to the maxima of cV.
The average density distributions and representative snapshots for temperatures corresponding to the minima of cV are shown in Fig. 4, for the temperatures and hexagon sizes indicted in Fig. 3 by the squares. The average density distributions are highly symmetric. Of course, the symmetry of the density distributions follows from the symmetry of the hexagonal confinement. On the other hand, the snapshots are not symmetric and appear disordered. A closer look reveals that near the system boundaries the stripes are parallel to them. In the central part of the system, however, we can observe spirals or twisted spirals in the left column, and stripes parallel to each other and perpendicular to the diagonal of the hexagon in the central and right columns in Fig. 4. The probabilities of the configurations obtained by a rotation by the angles π/3 and 2π/3 are the same. Hence, averaging over all configurations should have an effect similar to a superposition of standing density waves leading to a hexagonal pattern in the central part of the system.
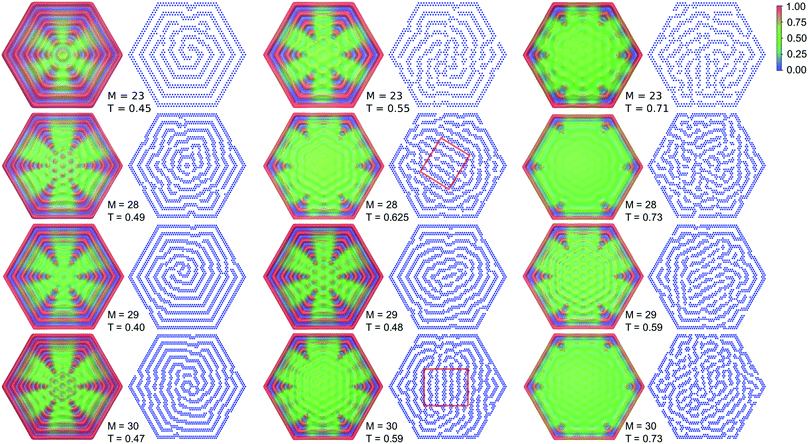 | ||
| Fig. 4 Average density distributions and the corresponding snapshots for the different (M,T) points marked by squares in Fig. 3. In the snapshots, the particles are shown in blue. The thin red rectangle encloses a local lamellar structure that forms in the center. | ||
Such patterns should be present in many stripe forming systems in hexagonal confinement, and indeed were observed experimentally.47,48 For different phase shifts of the interfering waves one can find centrally located structures that resemble a honeycomb or a pattern of hexagonally ordered clusters. Such patterns can be seen in Fig. 4 for different values of r and T. The density profiles computed along the symmetry axes of the hexagon show a minimum or a maximum in the center of the hexagon for r = 0, 3 or r = 1, 2, respectively (ESI†).
The average density and a representative configuration in a large system at a temperature between the two first maxima of cV (between the two bottom lines in Fig. 3) are shown in Fig. 5. From this figure, one can clearly see the formation of a spiral occupying a large portion of the hexagon. Left- and right-handed spirals are typical structures in this region of the (M,T) structure diagram, and to quantify the presence of such structures one needs a proper order parameter.
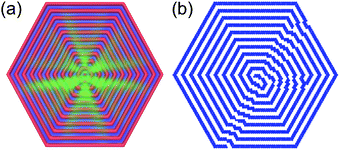 | ||
| Fig. 5 Density map (a) and a single configuration (b) of the SALR system with a side of size M = 41 at T = 0.35. The color scheme is the same as in Fig. 4. | ||
The order parameter that would capture the transition from rings to spirals can be defined in various ways. Here, we note that when: (i) the number of segments decreases significantly (i.e. the length of the stripes increases), (ii) the chemical potential is fixed so that parallel stripes (lamellar phase) are favorable in the unconstrained system, and the total length of the stripes on the area of the considered hexagon is much larger than its circumference and (iii) the rigidity of a long stripe is large, so that bending of the stripe comes with a high energetic cost, then a spiral or spirals are the most probable configuration of a very long stripe in hexagonal confinement. In a spiral, bends of the stripe by a large angle can be avoided.
Since in our model all of the above conditions are fulfilled we decided to use an order parameter that does not depend on the shape of a structure, but rather on the connectivity of the stripe segments. As we show in Fig. 6, indeed, when the concentric rings merge into a spiral the length of the obtained stripe significantly increases, and thus a drop of the number of disconnected stripes is observed.
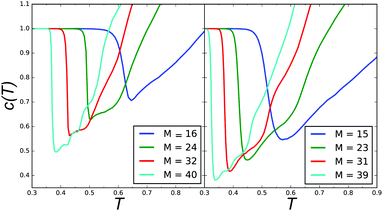 | ||
| Fig. 6 Number of clusters normalized by the number of the clusters in the ground state. Left panel: r = 0, right panel: r = 3, where r = M mod 4. | ||
Based on the above observation, we consider the average number of clusters (disconnected segments of stripes) as an indication of the presence of the spirals. The associated order parameter can be defined as 1 − c(T), where c(T) is the average number of clusters normalized by the number of clusters in the ground state. 1 − c(T) vanishes for the GS structure where no spirals occur, and increases when the number of disconnected segments decreases.
In the diagram in Fig. 3, small open circles correspond to the temperature at which the (negative) derivative of the average number of clusters, c(T), with respect to T has a minimum. At this temperature, c(T) drops significantly, as shown in Fig. 6. The clusters were determined by a distance criterion, i.e. two particles were in the same cluster if they were nearest neighbors. The dependence of c(T) on the system size is also presented in Fig. 6. Note that the rapid decrease of the number of clusters and the heat-capacity maximum occur simultaneously, when the concentric rings merge into spirals (see Fig. 3, lower panels). After the rapid decrease, c(T) first increases slowly up to T corresponding to the second maximum of cV, and above this temperature the slope of c(T) is significantly larger.
The nonmonotonic behavior of c(T) reflects the merging of the concentric rings into longer stripes and spiral formation (a rapid decrease from 1), see Fig. 5. Upon further heating the spirals break into smaller segments (c(T) increases) and form structures that on the level of single configurations appear disordered. This process can be observed in each row of Fig. 4, where the panels show how a system of a given size melts. In Fig. 6 one can see that the larger the system the more sudden the drop of c(T). For larger systems with M > 40 and r = 1, 3, the drop of c(T) is deeper and results in formation of a spiral pattern as can be seen in Fig. 5. Notably, the merging of the rings upon heating in the hexagonal confinement is in contrast to the behavior of bulk SALR systems, which upon a temperature increase exhibit stripe breaking of the ground state structure into smaller segments.2 Importantly, in the symmetric hexagonal system, the spiral can only be seen on the level of a single configuration. The average density distribution should have the same symmetry as the confinement and cannot be spiral. In what follows, we show how to induce a spiral formation of the average density and control its chirality.
3.3 Inducing a spiral
In order to check how a spiral configuration can be induced by confinement, we tried to break the system symmetry in several ways. We found that introducing a triangular wedge at the vertex of the hexagonal boundary can trigger formation of a stable spiral, as long as the side of the wedge is equal to the period of the striped structure (Fig. 7a and b). What is more, the chirality of the spiral can be easily controlled by the positioning of the wedge. It turns out, however, that formation of a defectless spiral depends on the system size, and happens only for r = 1, 3 (Fig. 7c and d).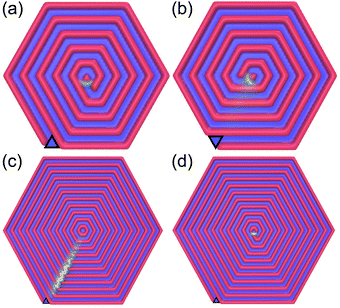 | ||
| Fig. 7 Low temperature density maps of the system with different system sizes. Panels (a and b): M = 21, panel (c): M = 44, panel (d): M = 43. The wedge position is marked by a black triangle and the color code is the same as in Fig. 5. | ||
4 Thermodynamic considerations
In what follows we develop a simple thermodynamic description of a two dimensional stripe-forming system in hexagonal confinement. Our goal is to find out under what thermodynamic conditions the self-assembly into concentric rings if the system is hexagonal and into a spiral pattern if the system has a symmetry broken by a triangular wedge can occur, when the striped pattern is formed in the unrestricted system.The stripe patterns are stable for a range of density that at low temperatures is very narrow, and in the case of a confined system is not known a priori. For this reason one should consider an open system with fixed chemical potential, for which the grand thermodynamic potential takes a minimum in the equilibrium state. In hexagonal confinement, the grand thermodynamic potential Ω is a sum of the contributions proportional to the area of the hexagon, A, the side length, M, and a contribution associated with point-like defects, D. Thus, we postulate
| Ω = ωbA + (Γw + Γdb)M + D | (3) |
Inside a symmetric hexagon one can expect ordered states with either parallel stripes or concentric rings. In the former case, Γdb = D = 0 and Γw = 2γ‖ + 4γt, where γ‖ and γt denote the surface tension for stripes parallel to or tilted with respect to the walls, respectively. For concentric rings Γw = 6γ‖, Γdb = 6γdb, and D = dc, where dc comes from the defect in the center, and depends on M (Fig. 2). Thus, the stable structure is determined by phenomenological parameters such as γdb, which is associated with the bending rigidity of the stripes. The concentric rings are stable if 4(γt − γ‖) − 6γdb − dc/M > 0, i.e. when the stripes parallel to the walls are much more favorable than the tilted ones, and the free-energy cost of bending the stripes is small.
When a triangular wedge is introduced at a vertex of the hexagon, then the ring adsorbed at the walls breaks, and its two ends associated with the excess energy de occur at the two sides of the wedge. Breaking of the stripe leads to D = dc+ 2de. If a spiral instead of concentric rings appears, then the length of the domain-boundary initiated by the wedge shortens leading to a negative contribution to D. Furthermore, a stripe end appears in the center of the hexagon, leading to another contribution to D. The sum of the two contributions to D is denoted by ds. Thus, the grand potential difference between the spiral and the concentric hexagons is (de + ds) − (2de + dc) = ds − de − dc. If ds − de − dc < 0, the spiral is more stable.
Our thermodynamic considerations indicate that there may exist many systems forming chiral patterns on different length scales, provided that the phenomenological parameters satisify the inequalities 4(γt − γ‖) − 6γdb − dc/M > 0 and ds − de − dc < 0. In our model spirals are formed for r = 1, 3, and are not formed for r = 0, 2, indicating a smaller value of dc in the latter case; see the ESI† for the calculation details in the particular case of T = 0. The results obtained for T = 0 should be approximately valid at low T, where the entropic contribution is less important.
5 Conclusions
We have analyzed the self-assembly of a stripe forming system when exposed to spatial confinement of a hexagonal shape. Our results reveal two possible scenarios for obtaining a spiral structure: (i) by proper temperature adjustment or (ii) by introducing a wedge that breaks the symmetry of the system and determines the location of the spiral terminal point. In the former case, the temperature controls the number of topological defects and thus the self-assembled stripes can break and merge into one stripe of a spiral shape. However, neither the spiral orientation nor the position of the terminal point can be controlled if the system is symmetric. Introducing the wedge gives that control over the spiral. Importantly, the size of the triangular wedge required for inducing the spiral does not depend on the system size, but is determined by the stripe width. Thus, a relatively small obstacle on the confining wall can lead to striking topological changes in particle conformation.Our results were obtained for a SALR system in which isotropic competing interactions lead to formation of stripes. The proposed model-free thermodynamic approach shows, however, that for many stripe forming systems hexagonal confinement may favor formation of concentric rings if the system is symmetric, or spirals if the symmetry of the system is broken by a wedge of specific size. These structures can be stable when thermodynamic parameters such as the surface tensions and the free-energies of defects obey certain inequalities. Importantly, such a general conclusion finds support in previously conducted experimental studies on BCPs.43
The analysis of both the thermal and structural properties of the system indicates that the hexagonal confinement enhances the integrity of the stripes. The melting temperature at which concentric rings start to merge is significantly higher than the stripe melting temperature in the bulk. On the other hand, above the melting point defects induced by the temperature can destroy the ordering, so that the average density distributions and single snapshots are tremendously different. Thus, the obtained density maps, although highly symmetric, do not indicate formation of ordered patterns unless the time of observation is much larger than the time scale characterizing the dynamics of the system. Interestingly, similar patterns were observed on the quantum level, where scattering of surface state electrons at the edges of densely packed Au atoms led to formation of standing waves by the local density of states.47,48 Thus, the unexpected family of highly symmetric patterns shown in Fig. 4 can actually be present at length scales ranging from a few nm to hundreds of micrometers.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Wojciech T. Góźdź for several enlightening discussions during the course of this work. This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 734276 (CONIN). Additional support in the years 2017–2020 has been granted for the CONIN project by the Polish Ministry of Science and Higher Education, agreement No. 3854/H2020/17/2018/2. Financial support from the National Science Center under grant No. 2015/19/B/ST3/03122 is also acknowledged.References
- A. Imperio and L. Reatto, J. Phys.: Condens. Matter, 2004, 18, S2319 Search PubMed.
- N. G. Almarza, J. Pȩkalski and A. Ciach, J. Chem. Phys., 2014, 140, 164708 CrossRef CAS PubMed.
- B. Chacko, C. Chalmers and A. J. Archer, J. Chem. Phys., 2015, 143, 244904 CrossRef.
- J. Pȩkalski, A. Ciach. and N. G. Almarza, J. Chem. Phys., 2014, 140, 114701 CrossRef.
- A. J. Archer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031402 CrossRef.
- R. Roth, Mol. Phys., 2011, 109, 2897–2905 CrossRef CAS.
- F. Ghezzi and J. Earnshaw, J. Phys.: Condens. Matter, 1997, 9, L517 CrossRef CAS.
- R. P. Sear and W. M. Gelbart, J. Chem. Phys., 1999, 110, 4582 CrossRef CAS.
- A. D. Law, M. Auriol, D. Smith, T. S. Horozov and D. M. A. Buzza, Phys. Rev. Lett., 2013, 110, 138301 CrossRef.
- N. G. Almarza, J. Pekalski and A. Ciach, Soft Matter, 2016, 12, 7551–7563 RSC.
- J. Pȩkalski, A. Ciach and N. G. Almarza, J. Chem. Phys., 2015, 142, 014903 CrossRef.
- J. Pȩkalski, N. Almarza and A. Ciach, J. Chem. Phys., 2015, 142, 204904 CrossRef.
- A. Imperio and L. Reatto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 040402 CrossRef.
- E.-Y. Kim, S.-C. Kim and S.-H. Suh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051203 CrossRef.
- G. J. Zarragoicoechea, A. G. Meyra and V. A. Kuz, Mol. Phys., 2009, 107, 549–554 CrossRef CAS.
- J. J. Amazon, S. L. Goh and G. W. Feigenson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022708 CrossRef.
- S. L. Goh, J. J. Amazon and G. W. Feigenson, Biophys. J., 2013, 104, 853–862 CrossRef CAS PubMed.
- J. J. Amazon and G. W. Feigenson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022702 CrossRef.
- J. Pȩkalski and A. Ciach, J. Chem. Phys., 2018, 148, 174902 CrossRef.
- H. Serna, E. G. Noya and W. Góźdź, Langmuir, 2018, 35, 702–708 CrossRef.
- A.-C. Shi and B. Li, Soft Matter, 2013, 9, 1398–1413 RSC.
- A. Kuzyk, R. Schreiber, Z. Fan, G. Pardatscher, E.-M. Roller, A. Högele, F. C. Simmel, A. O. Govorov and T. Liedl, Nature, 2012, 483, 311 CrossRef CAS.
- L. D.-C. Tzuang, Y.-W. Jiang, Y.-H. Ye, Y.-T. Chang, Y.-T. Wu and S.-C. Lee, Appl. Phys. Lett., 2009, 94, 091912 CrossRef.
- Y. K. Pang, J. C. W. Lee, H. F. Lee, W. Y. Tam, C. T. Chan and P. Sheng, Opt. Express, 2005, 13, 7615–7620 CrossRef CAS.
- J. Pȩkalski, P. Rogowski and A. Ciach, Mol. Phys., 2014, 113, 1022 CrossRef.
- J. Pȩkalski, A. Ciach and N. G. Almarza, J. Chem. Phys., 2013, 138, 144903 CrossRef PubMed.
- M. Edelmann and R. Roth, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2016, 93, 062146 CrossRef PubMed.
- J. A. Bollinger and T. M. Truskett, J. Chem. Phys., 2016, 145, 064902 CrossRef.
- J. A. Bollinger and T. M. Truskett, J. Chem. Phys., 2016, 145, 064903 CrossRef.
- Y. Zhuang, K. Zhang and P. Charbonneau, Phys. Rev. Lett., 2016, 116, 098301 CrossRef.
- C. P. Royall, Soft Matter, 2018, 14, 4020–4028 RSC.
- A. J. Archer and N. B. Wilding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 031501 CrossRef.
- A. Archer, C. Ionescu, D. Pini and L. Reatto, J. Phys.: Condens. Matter, 2008, 20, 415106 CrossRef.
- A. J. Archer, D. Pini, R. Evans and L. Reatto, J. Chem. Phys., 2007, 126, 014104 CrossRef CAS.
- A. Ciach, J. Pȩkalski and W. T. Góźdź, Soft Matter, 2013, 9, 6301 RSC.
- A. P. Santos and A. Z. Panagiotopoulos, J. Chem. Phys., 2016, 144, 044709 CrossRef.
- A. P. Santos, J. Pȩkalski and A. Z. Panagiotopoulos, Soft Matter, 2017, 13, 8055–8063 RSC.
- H. Tsai, J. W. Pitera, H. Miyazoe, S. Bangsaruntip, S. U. Engelmann, C.-C. Liu, J. Y. Cheng, J. J. Bucchignano, D. P. Klaus and E. A. Joseph, et al. , ACS Nano, 2014, 8, 5227–5232 CrossRef CAS PubMed.
- H.-C. Kim, S.-M. Park and W. D. Hinsberg, Chem. Rev., 2009, 110, 146–177 CrossRef.
- D. J. Herr, J. Mater. Res., 2011, 26, 122–139 CrossRef CAS.
- F. H. Schacher, P. A. Rupar and I. Manners, Angew. Chem., Int. Ed., 2012, 51, 7898–7921 CrossRef CAS.
- G. Liu, Y. Wu, Y.-M. Lin, D. B. Farmer, J. A. Ott, J. Bruley, A. Grill, P. Avouris, D. Pfeiffer and A. A. Balandin, et al. , ACS Nano, 2012, 6, 6786–6792 CrossRef CAS.
- H. K. Choi, J.-B. Chang, A. F. Hannon, J. K. Yang, K. K. Berggren, A. Alexander-Katz and C. A. Ross, Nano Futures, 2017, 1, 015001 CrossRef.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087 CrossRef CAS.
- R. H. Swendsen and J.-S. Wang, Phys. Rev. Lett., 1986, 57, 2607–2609 CrossRef.
- J. C. Wheeler and B. Widom, J. Am. Chem. Soc., 1968, 90, 3064–3071 CrossRef CAS.
- G. Rodary, D. Sander, H. Liu, H. Zhao, L. Niebergall, V. Stepanyuk, P. Bruno and J. Kirschner, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 233412 CrossRef.
- K. Schouteden, E. Lijnen, D. Muzychenko, A. Ceulemans, L. F. Chibotaru, P. Lievens and C. Van Haesendonck, Nanotechnology, 2009, 20, 395401 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Off-lattice simulation details, density profiles along different symmetry axes of the hexagon, and application of thermodynamic considerations. See DOI: 10.1039/c9sm01179j |
| This journal is © The Royal Society of Chemistry 2019 |