Open Access Article
Open Access ArticleDynamic self-assembly of ions with variable size and charge in solution†
Jana Eisermann ,
Andreas Kerth and
Dariush Hinderberger
,
Andreas Kerth and
Dariush Hinderberger *
*
Institute of Chemistry, Martin-Luther-Universität Halle-Wittenberg, Von-Danckelmann-Platz 4, 06120 Halle (Saale), Germany. E-mail: dariush.hinderberger@chemie.uni-halle.de; Fax: +49 345 55 27576; Tel: +49 345 55 25230
First published on 13th June 2019
Abstract
Recently it was found that at ambient temperatures and in specific ternary solvents a cationic macrocyclic tetraimidazolium molecular box and small dianionic salts can self-assemble into highly defined, colloid-like ionic clusters, called ionoids. Here, we present evidence that the solution-based ionic self-assembly process leading to ionoids is a general phenomenon by characterizing new ionic building blocks which are capable of generating loosely bound globular and anisotropic structures similar to those in the established system. Using new cationic and anionic molecules, we show that variations in the size ratio between cationic and anionic component mainly affect size, shape and durability of the ionic clusters. Utilizing dynamic light scattering (DLS), continuously monitored phase-analysis light scattering (cmPALS) and continuous wave electron paramagnetic resonance (CW EPR) spectroscopy, we can thus define generalized ionic ratios, in which specific combinations of ionic compounds with certain size and charge densities are able to form these soft yet durable and long-lived ionic clusters. Furthermore, we characterize the temporal development of our dynamically self-assembled structures in solution from the level of the individual ionic building blocks to stable clusters with minimum lifetimes of months through previously established ionoid evolution diagrams (IEDs). The direct comparison of various cluster systems with respect to their shape, size and charges allows correlations of structural changes of the individual building blocks with the fate of self-assembled entities inside the crafted IEDs. This work generalizes the concept of ionoid formation to ions of specific sizes and charge densities, which may broaden the scope of this new type of highly dynamic and soft yet remarkably durable structures in the field of supramolecular chemistry.
1 Introduction
The structure and dynamics of matter at the nanometer scale form the basis for both natural processes and technological applications reaching far beyond the pertinent nanoscale lengths, so tuning their (sub-)nanometer architecture and (sub-)microsecond dynamics can be seen as key to tuning macroscopic properties on much larger length scales and times as well.1 Molecular design approaches have proven to be most beneficial in the development of next-generation materials with tailor-made properties.2 Assembling various molecular building units enables the construction of numerous chemical architectures with discrete (zero-dimensional, 0D) to extended (1D, 2D and 3D) structures, ranging from inorganic to pure organic components, from disordered to regular arrangements and from non-porous to porous nature.3 The interactions which are exploited to link these monomeric precursors reach from strong covalent bonds in polymers over dynamic linkages to weak supramolecular forces e.g. π–π interactions, halogen bonding or hydrogen bonding.2,4Over the course of the last three decades, numerous examples of materials with precisely controlled nano-environments could be achieved, primarily in the field of porous materials, in which one of the most fundamental principles of living systems is mimicked through offering confined spaces for molecular purposes.2 Furthermore, establishing e.g. metal–organic frameworks5–13 (MOFs, also known as porous coordination polymers14,15), covalent organic frameworks16–22 (COFs) and hydrogen-bonding organic frameworks23–30 (HOFs) inside application fields like gas separation and storage, catalysis, sensing, optoelectronics, electronic devices, proton conduction, drug delivery and imaging significantly advances the development of these tailor-made materials.2 At about the same time, the synthesis and development of entangled molecular components through mechanical bonds31–34 was introduced, starting the templating of mechanically interlocked molecules (MIMs).31–36 MIMs encompass besides the two archetypal examples catenanes and rotaxanes32–34,37–40 also molecular shuttles and bistable molecular switches34,37,41,42 as well as framework structures due to the process of molecular weaving.31 Thus, the potential applications of mechanically interlocked materials include various fields, reaching from e.g. nanoelectromechanical systems42,43 over artificial molecular machines35,44 to drug delivery systems.45
The ‘Texas-sized molecular box’ (14+, Fig. 1), developed by Sessler and coworkers, acts as MIM and forms pseudorotaxane structures in combination with bis-carboxylate anions.46–48 Going beyond solid-state structures, we discovered that in solution this compound electrostatically self-assembles in the presence of small dianionic salts (methanedisulfonate, 22− or Fremy's salt dianion, 32−, see Fig. 1) into loosely bound, yet remarkably durable, ion-based colloid-like globular cluster of several nanometer size,49 termed globular ionoids (see ref. 50). The formation of such size-monodisperse supramolecular structures due to long-range electrostatic correlations also required the right interplay of weaker noncovalent interactions (solvation, hydrogen bonding, van der Waals interactions).51 Therefore, the composition of e.g. the solvent, in our case the established mixture DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v), plays an important role in the ionic self-assembly process.50 Based on our previous studies, we postulate an initial ion cloud state after mixing cationic and anionic building units, where no globular structures are yet formed and the system has not reached its thermodynamic balance. As we have described it previously (see ref. 50), this ion cloud state persists over an extremely long incubation time of ten days and is defined by the existence of large structures (larger than 100 nm). We currently assume (experiments are ongoing) that the internal ion distribution obeys a Poisson–Boltzmann-type or similar mean-field interaction pattern, which characterize the phase after sample preparation. However, due to already carried out Monte Carlo simulations (see ref. 49), which revealed a surprising long-range correlation of 14+ at about 15 nm, we presume electrostatic and excluded volume effects as essential for the formation of ionic clusters. Reliably after the incubation period of ten days, we detect our globular ionoids that are now able to withstand e.g. mechanical stress.52 As depicted above, the transition from ion cloud to globular ionoids is not fully understood yet and is out of the scope in this specific study, which is solely concerned with formation of ionoid structures built from new chemical units.
7 (v/v/v), plays an important role in the ionic self-assembly process.50 Based on our previous studies, we postulate an initial ion cloud state after mixing cationic and anionic building units, where no globular structures are yet formed and the system has not reached its thermodynamic balance. As we have described it previously (see ref. 50), this ion cloud state persists over an extremely long incubation time of ten days and is defined by the existence of large structures (larger than 100 nm). We currently assume (experiments are ongoing) that the internal ion distribution obeys a Poisson–Boltzmann-type or similar mean-field interaction pattern, which characterize the phase after sample preparation. However, due to already carried out Monte Carlo simulations (see ref. 49), which revealed a surprising long-range correlation of 14+ at about 15 nm, we presume electrostatic and excluded volume effects as essential for the formation of ionic clusters. Reliably after the incubation period of ten days, we detect our globular ionoids that are now able to withstand e.g. mechanical stress.52 As depicted above, the transition from ion cloud to globular ionoids is not fully understood yet and is out of the scope in this specific study, which is solely concerned with formation of ionoid structures built from new chemical units.
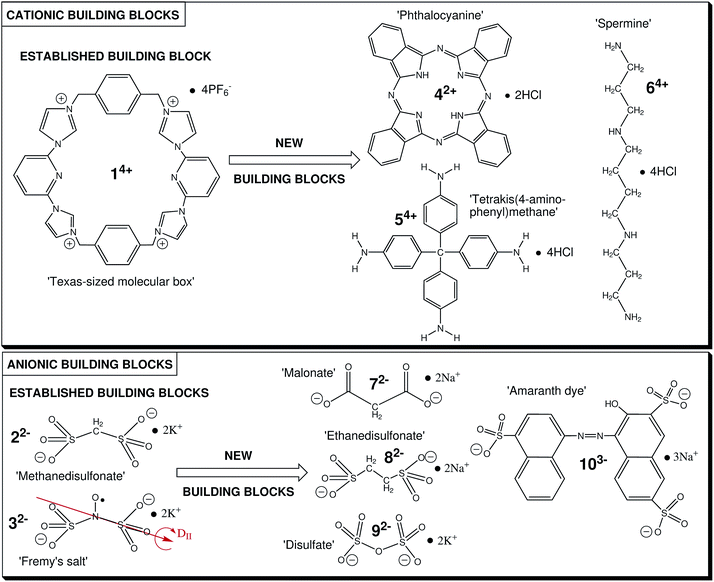 | ||
Fig. 1 Summary of the utilized ionic building blocks to form ionoids based on the model system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+ 22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively). 32−, respectively). | ||
To this end, we here focus on extending the concept of ionoid formation by substituting the ‘Texas-sized molecular box’ as well as the dianionic salts with other polyphilic ionic building blocks (see Fig. 1) that are capable of forming multiple partially orthogonal noncovalent interactions (like those mentioned before). This expands the mainly ionically driven self-assembly of ionoids with respect to the sizes, topologies and ionic ratios of the directly involved ionic compounds. We replace the large cation 14+ with molecular structures that were also used in the creation of tailor-made materials like 42+53–55 and 54+,56–60 and the biological oligoamine spermine 64+61 and/or substitute the small dianionic salts 22− and 32− with dianions of similar structure (72−, 82−, 92−) and with a larger trianionic chromophore (103−). Based on these modifications we use dynamic light scattering (DLS), continuous wave (CW) electron paramagnetic resonance (EPR) spectroscopy, aided by UV-vis and fluorescence spectroscopy, to investigate the interplay between chemical nature, size and ionic ratio for developing dynamically formed, persistent structures like highly defined, colloid-like ionic clusters in solution. Additionally, we study the stability of selected self-assembled, colloid-like structures in solution through characterizing their zeta potential with continuously monitored phase-analysis light scattering (cmPALS). On a more general note, we expand the structural universe of ionoids and can show that this type of very soft structure formation is not limited to our initially studied ‘model’ system of 14+ and 22−, but rather seems to constitute a general state and process for ions that fulfill certain prerequisites in size and charge in specific solution. Finally, we rationalize our findings by describing the different ionoid systems in evolution diagrams (‘ionoid evolution diagrams’, IEDs). We previously developed IEDs52 to be able to characterize the complex underlying molecular features, like ionic sizes and ionic ratios, and describe the long term evolution (over the course of months) of the loosely bound ionic clusters in solution.
2 Experimental
2.1 Materials
The model system for creating ionoids contains the ‘Texas-sized molecular box’ (14+), which was synthesized according to ref. 47 and 48 as described in ref. 49 and 50 and the small dianionic salts methanedisulfonic acid dipotassium salt (22−, Sigma-Aldrich, Munich, Germany) with purity ≥ 99% as well as Fremy's salt (potassium nitrosodisulfonate, 32−, Sigma-Aldrich) of technical grade. These chemicals as well as malonic acid disodium salt (72−, 99%, abcr GmbH, Karlsruhe, Germany), 1,2-ethanedisulfonic acid disodium salt (82−, 99%, abcr GmbH) and potassium disulfate (92−, 99%, Sigma-Aldrich) were applied as received.The ionic building blocks phthalocyaninedihydrochloride (42+), tetrakis(4-aminophenyl)methanetetrahydrochloride (54+), sperminetetrahydrochloride (64+) and Amaranth (103−) had to be modified or purified to be used for our study. These specific adjustments are summarized in the ESI.† All tested systems were measured in the established solvent mixture DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v), produced with DMSO containing ≤0.02% water (Sigma-Aldrich) in a 1
7 (v/v/v), produced with DMSO containing ≤0.02% water (Sigma-Aldrich) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) ratio with 86–88 wt% glycerol (Acros Organics, Nidderau, Germany).49,50
1 (v/v) ratio with 86–88 wt% glycerol (Acros Organics, Nidderau, Germany).49,50
2.2 Size ratio
Considering the ten chosen ionic building blocks (see Fig. 1), there exist countless ways in combining comparatively small and large cationic and anionic components. In this study, we highlight a small selection of these possible assemblies. However, most of the studied compositions consist of rather large cations and small anions, just like the established model system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+
22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively). Table 1 summarizes all tested mixtures categorized based on their underlying size ratio.
32−, respectively). Table 1 summarizes all tested mixtures categorized based on their underlying size ratio.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v), categorized based on the size ratio between cationic and anionic component
7 (v/v/v), categorized based on the size ratio between cationic and anionic component
| Combine | Large cation | Small cation |
|---|---|---|
| Small anion | 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−(32−) 22−(32−) |
64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−(32−) 22−(32−) |
42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−(32−) 22−(32−) |
||
54+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−(32−) 22−(32−) |
||
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− 72− |
||
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82− 82− |
||
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92− 92− |
||
| Large anion | 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103− 103− |
64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103− 103− |
The exact concentration for each component in its associated constellation varies depending on the applied methods and is summarized in Table 2. Calculations of the ionic ratio for all mixture are based on eqn (1) for the reference system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+
22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively) 1 mM
32−, respectively) 1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM
3 mM
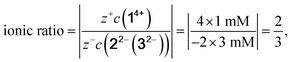 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v) with their respective molar ratio and ionic ratio
7 (v/v/v) with their respective molar ratio and ionic ratio
| System | Concentration ratio | Molar ratio | Ionic ratioa |
|---|---|---|---|
| a Calculating ionic ratio using eqn (1). | |||
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−(32−) 22−(32−) |
1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM 3 mM |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
2/3 |
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− 72− |
1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM 3 mM |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
2/3 |
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82− 82− |
1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM 3 mM |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
2/3 |
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92− 92− |
1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM 3 mM |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
2/3 |
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103− 103− |
10 μM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 μM 30 μM |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
4/9 |
42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−(32−) 22−(32−) |
13.3 μM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 μM 20 μM |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
2/3 |
54+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−(32−) 22−(32−) |
1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM 3 mM |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
2/3 |
64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−(32−) 22−(32−) |
1.6 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 mM 1.2 mM |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
8/3 |
64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103− 103− |
10 μM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 μM 30 μM |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
4/9 |
2.3 Methods
We used a Litesizer 500 (Anton Paar GmbH, Graz, Austria) for recording DLS. This device, which is also capable of measuring static light scattering, zeta potential, transmittance and refractive index, irradiates the sample with a 40 mW semiconductor laser at a typical wavelength of λ = 658 nm. An automatic configuration of the heatable optical bench allows perfected count rate traces. The choice between three different detection angles back (175°), side (90°) and forward (15°) scattering allows measuring a broader range of samples and getting information on the potential geometrical anisotropy.67 Here, we studied our samples, which were filled into quartz cells (Hellma Analytics, Müllheim, Germany), utilizing back as well as side scattering at a fixed temperature of 20 °C.
Sample preparation was identical for all tested mixtures of Table 2. Before dissolving the compounds (see Fig. 1) in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v), we filtered the solvent using Millex filter units (hydrophilic LCR (PTFE)-membranes) with a pore-size of 450 nm. A second filtration step (with the same filter-type) was used to transfer the final solution into the measurement cell without any contamination such as dust.62 We measured all samples in regular, frequent intervals up to 43 days to get insight into their long-term stability. The resulting autocorrelation functions were analyzed using the ALV-5000/E/EPP (v. 3.0.1.13, ALV-Laser-Vertriebsgesellschaft m. b. H. Langen, Germany) software. Further information about the calculation of the hydrodynamic radius are given in the ESI.†
7 (v/v/v), we filtered the solvent using Millex filter units (hydrophilic LCR (PTFE)-membranes) with a pore-size of 450 nm. A second filtration step (with the same filter-type) was used to transfer the final solution into the measurement cell without any contamination such as dust.62 We measured all samples in regular, frequent intervals up to 43 days to get insight into their long-term stability. The resulting autocorrelation functions were analyzed using the ALV-5000/E/EPP (v. 3.0.1.13, ALV-Laser-Vertriebsgesellschaft m. b. H. Langen, Germany) software. Further information about the calculation of the hydrodynamic radius are given in the ESI.†
The cmPALS measurements were again performed with the Litesizer 500 in combination with the respective Kalliope software (v. 2.6). As measurement cell we used the so-called Univette (Anton Paar GmbH), which allows zeta potential measurement with organic solvents as well as reduced sample volume (70 μl) compared to the standard Omega cuvette.79 The sample preparation itself was carried out after the described routine in the DLS section. Each probe was analyzed after the incubation period of ten days with an applied voltage of 40 V and a constant temperature of 20 °C. A complete data set consists of three repetitive measurements with a waiting period of 1 min between each measurement to prevent changes inside the sample due to the influence of Joule heating, a common side effect of this technique. The recorded electrophoretic mobilities μe, which are the actual accessible parameter in ELS, were averaged and subsequently transferred into the desired zeta potentials. To examine the survival of the self-assembled structures inside the samples, we again performed DLS and compare the autocorrelation functions as well as size distributions before and after the cmPALS measurements. The description for the calculation of the zeta potential as well as the determination of the relative permittivity εr for the solvent mixture DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v) can be found in the ESI.†
7 (v/v/v) can be found in the ESI.†
EPR techniques in general are highly sensitive as well as selective and can operate on structurally disordered materials.81,82 We focus on the change in the rotational motion, as quantified by either the rotational rates or correlation times τc, the anisotropies of rotational rates and the spectral line shape to identify tendencies for ionic clusters. Spectral simulations were performed in Matlab (R2016a, v. 9.0) exploiting the EasySpin package (v. 5.2.11).83 The ESI† contains descriptions about the general simulation approach and sets of simulation parameters.
CW EPR measurements were performed at X-band (9.4 GHz) microwave frequencies with a Miniscope MS400 (magnettech, Berlin, Germany) benchtop spectrometer. For recording the spectra we used a microwave power of 1 mW, a sweep width of 100 G and a modulation amplitude of 600 mG, while keeping the sample temperature at 20 °C with the temperature controller H03 (magnettech). A frequency counter (FC 400, magnettech) was used to record the microwave frequency. We additionally measured at higher frequencies/magnetic fields to improve the spectral (g-)resolution and to obtain a different view on rotational motion of the radicals. Therefore, we switched to Q-band frequencies (34 GHz) using a Bruker EMX-plus spectrometer with an ER5106QT resonator (Bruker Biospin GmbH, Rheinstetten, Germany). Measuring at the same temperature compared to X-band, the spectra were recorded with a microwave power of 1 mW, a sweep width of 130 G and a modulation amplitude of 1000 mG.
Sample preparation was similar for both X-band and Q-band EPR spectroscopy. About 10 μl to 15 μl of the samples were filled into small capillaries (Blaubrand, Wertheim, Germany) and capped with matching tube sealant (Leica Critoseal). All measurements were performed directly after preparation (day 0), since Fremy's salt in solution does not have a long-term stability at 20 °C.
We used the Hewlett-Packard spectrophotometer HP 8453 (Agilent Technologies, Santa Clara, United States) for UV-vis spectroscopy and the FluoroMax-2 fluorescence spectrometer (Instruments S. A. GmbH, Grasbrunn, Germany) to measure the corresponding emission spectra. Here, we did not prepare samples exclusively for these spectroscopic methods, but measured the already existing mixtures from dynamic light scattering at 20 °C. Reusing the DLS samples allowed us to directly compare the determined size as well as size distribution of the self-assembled structures with the recorded absorption and emission spectra. Additionally, we performed DLS, UV-vis and fluorescence spectroscopy in the same regular, frequent intervals to receive the optimal requirements for analyzing the potential ionic self-assembly process of 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103− and 64+
103− and 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103−. We also tried to measure systems containing 42+ ions, but the compound did not show (i) significant absorption peaks and (ii) emission spectra, probably due to the solvent mixture of DMSO
103−. We also tried to measure systems containing 42+ ions, but the compound did not show (i) significant absorption peaks and (ii) emission spectra, probably due to the solvent mixture of DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v).
7 (v/v/v).
3 Results and discussion
3.1 General remarks
As introduced in ref. 50, we applied the established terms (i) globular ionoids, (ii) anisotropic ionic cluster and (iii) ion cloud to describe the ionic self-assembly process for all of the following systems. To validate the formation of such nanoscopic entities due to the complex interactions between the ionic building units, we measured the pure solvent mixture DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v), which was treated exactly like every other sample, with DLS as shown in Fig. S.1.† The solvent itself does not present pronounced autocorrelation functions and therefore no tendencies in independently establishing defined structures. Moreover, the surface tension of the mixture DMSO
7 (v/v/v), which was treated exactly like every other sample, with DLS as shown in Fig. S.1.† The solvent itself does not present pronounced autocorrelation functions and therefore no tendencies in independently establishing defined structures. Moreover, the surface tension of the mixture DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v) (see Fig. S.2†), which is significantly lower compared to water, indicates that the building units tend to stay inside the bulk and do not move to the air-solvent interface. At last, DLS data of each building unit separately dissolved in our solvent mixture (see Fig. S.3 and S.4†) were recorded to ensure that (i) these compounds alone do not present high scattering intensities and (ii) the combination of matching cationic and anionic unit is the important condition for well-defined ionic cluster.
7 (v/v/v) (see Fig. S.2†), which is significantly lower compared to water, indicates that the building units tend to stay inside the bulk and do not move to the air-solvent interface. At last, DLS data of each building unit separately dissolved in our solvent mixture (see Fig. S.3 and S.4†) were recorded to ensure that (i) these compounds alone do not present high scattering intensities and (ii) the combination of matching cationic and anionic unit is the important condition for well-defined ionic cluster.
The construction principle of our ionoid evolution diagrams, elaborately introduced in ref. 52, can be found in the ESI.† CW EPR studies are limited in measuring the ion cloud state that forms in the initial hours after preparation of the system due to the disproportionation of the EPR-active Fremy's salt dianion (32−) in solution proceeding faster than the ten-day incubation period of globular, colloid-like ionic structures. Finally, we mainly focus on new systems which combine (i) large cation with small anion and (ii) small cation with small anion to exemplary discuss the size ratio influence on the dynamically driven self-assembly process of ionoids.
3.2 Substitution of 22− (32−)
We have substituted the anionic component in our model system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+
22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively), to create new mixtures with the rather large multicationic molecular box 14+ as cationic component and the following anionic building units:
32−, respectively), to create new mixtures with the rather large multicationic molecular box 14+ as cationic component and the following anionic building units:
(1) Small dianions 72−, 82− and 92− with the concentration ratio 1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM and,
3 mM and,
(2) Large trianionic chromophore 103− with the concentration ratio 10 μM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 μM.
30 μM.
The applied concentrations for these new systems are derived from several preliminary tests, yield pronounced scattering intensities compared to the used solvent and represent ionic ratios that in the established system lead to globular, least anisotropic ionoids. Note that we reduced the concentration ratio for the Amaranth dye (103−) to directly compare DLS with UV-vis and fluorescence spectroscopy data.
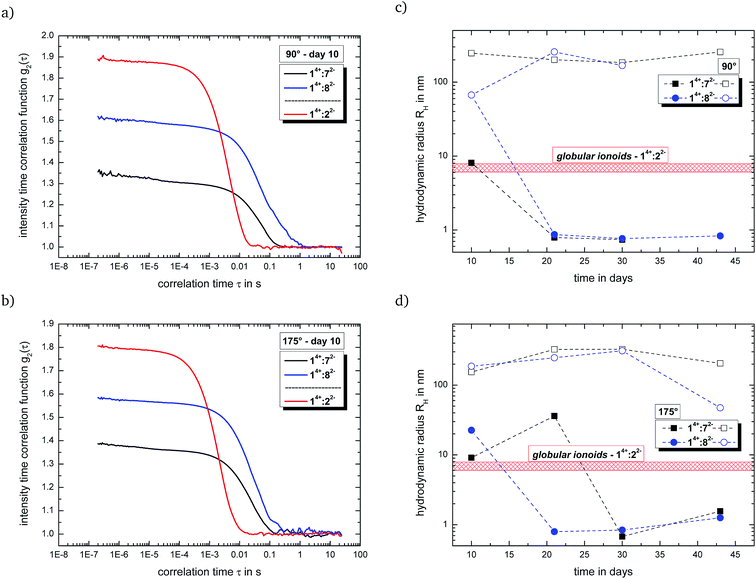
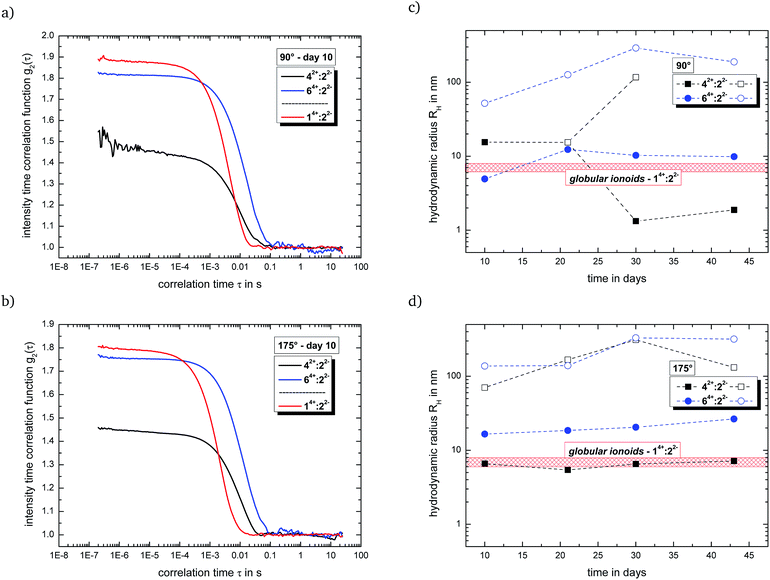
Fig. 2(a) and (b) summarizes the intensity time correlation functions with side and back scattering for the systems with malonate (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72−) and ehanedisulfonate (14+
72−) and ehanedisulfonate (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82−) as well as for the model system (14+
82−) as well as for the model system (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−) in DMSO
22−) in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v) at measurement day ten. Both new systems, which combine a large cationic component with small dianions, display a (i) delayed decay in their autocorrelation functions and (ii) reduced y-intercept-values compared to 14+
7 (v/v/v) at measurement day ten. Both new systems, which combine a large cationic component with small dianions, display a (i) delayed decay in their autocorrelation functions and (ii) reduced y-intercept-values compared to 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−, indicating a preferred formation of larger entities and/or rather polydisperse particle size distributions. This fact is further highlighted in Fig. 2(c) and (d), which shows the development of the hydrodynamic radii for the present colloid-like structures over time. 14+
22−, indicating a preferred formation of larger entities and/or rather polydisperse particle size distributions. This fact is further highlighted in Fig. 2(c) and (d), which shows the development of the hydrodynamic radii for the present colloid-like structures over time. 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− and 14+
72− and 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82− are able to partially build up anisotropic ionic clusters after an incubation time of ten days, but we still detect the large (>100 nm) initial ion cloud state (open symbols in Fig. 2(c) and (d)) as second scattering component. Furthermore, the self-assembled entities for both systems fall apart over the course of several days, possessing reduced durability compared to the long-lived globular ionoids of 14+
82− are able to partially build up anisotropic ionic clusters after an incubation time of ten days, but we still detect the large (>100 nm) initial ion cloud state (open symbols in Fig. 2(c) and (d)) as second scattering component. Furthermore, the self-assembled entities for both systems fall apart over the course of several days, possessing reduced durability compared to the long-lived globular ionoids of 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−.50 Note that we applied the same concentration ratio of 1 mM
22−.50 Note that we applied the same concentration ratio of 1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM as well as ionic ratio of 2/3 for the malonate- and ethanedisulfonate-system, leaving their chemical nature (see Fig. 4) as reason for the changed dynamically driven self-assembly process. DLS data for system 14+
3 mM as well as ionic ratio of 2/3 for the malonate- and ethanedisulfonate-system, leaving their chemical nature (see Fig. 4) as reason for the changed dynamically driven self-assembly process. DLS data for system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92− show a similar behavior compared to mixtures containing compound 82− (see Fig. S.11†), while the combination of both large cation and large anion (14+
92− show a similar behavior compared to mixtures containing compound 82− (see Fig. S.11†), while the combination of both large cation and large anion (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103−) builds up rather extended structures near the transition from anisotropic ionic clusters to the initial ion cloud state with a certain durability (see Fig. S.12†).
103−) builds up rather extended structures near the transition from anisotropic ionic clusters to the initial ion cloud state with a certain durability (see Fig. S.12†).
Based on the performed DLS measurements we studied the colloidal stability of systems 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− and 14+
72− and 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82− after the incubation period of ten days through the cmPALS method. Again we used the combination of ‘Texas-sized molecular box’ and methanedisulfonate as reference point. Here, the self-assembled globular ionoids present a well-defined phase plot (as shown in Fig. S.6†) and the calculated zeta potential of ζ = 66.5 mV ± 1.2 mV, which is in absolute numbers similar to the electrokinetic potential for nanosphere size standards made out of polysterene (see Table S.2†), supports the well-known high stability of 14+
82− after the incubation period of ten days through the cmPALS method. Again we used the combination of ‘Texas-sized molecular box’ and methanedisulfonate as reference point. Here, the self-assembled globular ionoids present a well-defined phase plot (as shown in Fig. S.6†) and the calculated zeta potential of ζ = 66.5 mV ± 1.2 mV, which is in absolute numbers similar to the electrokinetic potential for nanosphere size standards made out of polysterene (see Table S.2†), supports the well-known high stability of 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− ionic clusters in solution.52 Note that based on the measurements for pure 14+ and 22− solutions the ‘Texas-sized molecular box’ is, under the influence of an external electric field and despite its larger diameter, the more mobile compound inside the DMSO
22− ionic clusters in solution.52 Note that based on the measurements for pure 14+ and 22− solutions the ‘Texas-sized molecular box’ is, under the influence of an external electric field and despite its larger diameter, the more mobile compound inside the DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
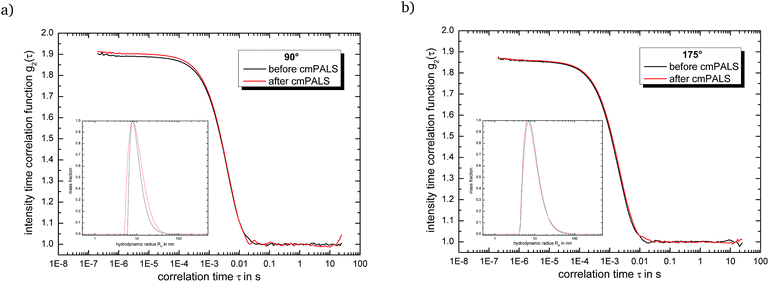
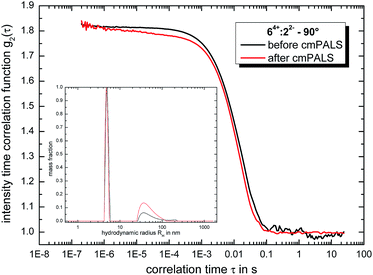
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water solvent mixture. To verify that the globular ionoids survived the treatment with the cmPALS method, we repeated the DLS measurements and compared the autocorrelation functions for both scattering angles, as shown in Fig. 3. The intensity time correlation functions as well as the monodisperse particle size distributions show almost no change, which again demonstrates the colloidal stability of our self-assembled entities.
water solvent mixture. To verify that the globular ionoids survived the treatment with the cmPALS method, we repeated the DLS measurements and compared the autocorrelation functions for both scattering angles, as shown in Fig. 3. The intensity time correlation functions as well as the monodisperse particle size distributions show almost no change, which again demonstrates the colloidal stability of our self-assembled entities.
The systems containing malonate and ethanedisulfonate instead of methanedisulfonate just partially build up anisotropic ionic clusters, therefore we assume a reduced zeta potential, but 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− and 14+
72− and 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82− should still reach a value of ±30 mV to label these self-assembled entities as highly stable. Table 3 summarizes the recorded electrophoretic mobilities as well as determined zeta potentials for both systems and their respective ionic building units. Note that each ionic building unit contributes their associated counterions (see Fig. 1) into the solution, which will be affected by the external electric field. Similar to the model system we see that the ‘Texas-sized molecular box’ represents the more mobile ionic building unit and mainly determines the recorded electrokinetic potential for the new systems 14+
82− should still reach a value of ±30 mV to label these self-assembled entities as highly stable. Table 3 summarizes the recorded electrophoretic mobilities as well as determined zeta potentials for both systems and their respective ionic building units. Note that each ionic building unit contributes their associated counterions (see Fig. 1) into the solution, which will be affected by the external electric field. Similar to the model system we see that the ‘Texas-sized molecular box’ represents the more mobile ionic building unit and mainly determines the recorded electrokinetic potential for the new systems 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− and 14+
72− and 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82−. By adding the anionic compounds to 14+ significantly reduces its margin of error for both electrophoretic mobility and zeta potential. Anisotropic ionic cluster containing malonate can be considered as highly stable, whereas the entities with ethanedisulfonate lie between highly stable and moderately stable.
82−. By adding the anionic compounds to 14+ significantly reduces its margin of error for both electrophoretic mobility and zeta potential. Anisotropic ionic cluster containing malonate can be considered as highly stable, whereas the entities with ethanedisulfonate lie between highly stable and moderately stable.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− and 14+
72− and 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82− 1 mM
82− 1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM in DMSO
3 mM in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v)
7 (v/v/v)
| Compound | μe/μm cm V−1 s−1 | ζ/mV |
|---|---|---|
| a Counterion: PF6−.b Counterion: Na+.c Nanosphere size standards in deionized Milli-Q-water. | ||
| 14+a | 0.045 ± 0.008 | 31.1 ± 5.2 |
| 72−a | −0.002 ± 0.001 | −1.7 ± 1.0 |
| 82−b | −0.001 ± 0.001 | −0.7 ± 0.7 |
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− 72− |
0.062 ± 0.003 | 37.4 ± 2.0 |
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82− 82− |
0.056 ± 0.003 | 28.7 ± 1.5 |
14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− 22− |
0.111 ± 0.002 | 66.5 ± 1.2 |
| Polystyrenec | −3.695 ± 0.0210 | −64.6 ± 1.0 |
After the cmPALS studies we repeated, similar to the model system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−, DLS measurements with both systems (see Fig. S.8 and S.10†). Here, the partially build up anisotropic ionic cluster do not withstand the influence of the electric field as good as well-defined globular ionoids, which is visible in the less pronounced autocorrelation functions. Note that the mixture containing malonate gets more affected by the electrophoresis process, even though the determined zeta potential is larger than for system 14+
22−, DLS measurements with both systems (see Fig. S.8 and S.10†). Here, the partially build up anisotropic ionic cluster do not withstand the influence of the electric field as good as well-defined globular ionoids, which is visible in the less pronounced autocorrelation functions. Note that the mixture containing malonate gets more affected by the electrophoresis process, even though the determined zeta potential is larger than for system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82−. The applied electric field seems to induce a rearrangement between cationic and anionic building units, which alters the scattering intensity.
82−. The applied electric field seems to induce a rearrangement between cationic and anionic building units, which alters the scattering intensity.
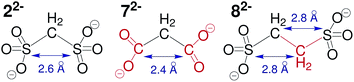
Replacing both sulfonate-groups in compound 22− with carboxylate-groups (72−), as shown in Fig. 4, significantly reduces the electrostatic interactions between the anionic building block and the ‘Texas-sized molecular box’, which results in the formation of ionic clusters with anisotropic shape and less durability.‡ A similar effect is observable when keeping the sulfonate-groups, but exchanging the methylene-group of methanedisulfonate with an ethylene-group (82−). Here, the increased distance between both negative charges and potentially the change in charge density precludes the dynamic self-assembly into long-lived ionic clusters. At this point, however, it is not possible to quantify the changes in electrostatic interactions as well as weaker noncovalent forces.
To further (i) visualize the development of the self-assembled entities for the systems 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− and 14+
72− and 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82− over time and (ii) compare these with 14+
82− over time and (ii) compare these with 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
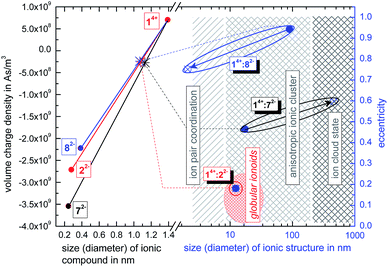
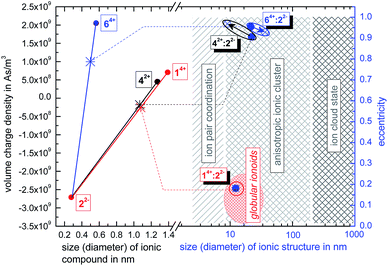
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−, we use the ionoid evolution diagram (IED) in Fig. 5. The left y-axis displays the volume charge density of the applied building units, which could be calculated by dividing the charges z± (multiplied with the elementary charge e) of the cationic and anionic components by their respective volumes (see ESI† for details). As x-axis we use the diameter of all four ions (without solvation shell) due to the importance of the size and size ratio of the anionic and cationic component for the self-assembly process. Through combining the multicationic box 14+ with one of the small anionic building blocks, we can profess the molar ratio of 1
22−, we use the ionoid evolution diagram (IED) in Fig. 5. The left y-axis displays the volume charge density of the applied building units, which could be calculated by dividing the charges z± (multiplied with the elementary charge e) of the cationic and anionic components by their respective volumes (see ESI† for details). As x-axis we use the diameter of all four ions (without solvation shell) due to the importance of the size and size ratio of the anionic and cationic component for the self-assembly process. Through combining the multicationic box 14+ with one of the small anionic building blocks, we can profess the molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and are able to adjust the resulting volume charge density as well as acting electrostatic correlations91 along the connecting line of both ions. Each system constitutes its own main sequence with one specific intersection highlighting the utilized molar/ionic ratio for DLS measurements, allowing us to directly compare the ionic self-assembly process for different systems with e.g. similar size ratio. Starting from these intersections we plot at the right y-axis the eccentricity
3 and are able to adjust the resulting volume charge density as well as acting electrostatic correlations91 along the connecting line of both ions. Each system constitutes its own main sequence with one specific intersection highlighting the utilized molar/ionic ratio for DLS measurements, allowing us to directly compare the ionic self-assembly process for different systems with e.g. similar size ratio. Starting from these intersections we plot at the right y-axis the eccentricity 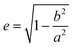 § to define deviations from a perfect sphere (with a value of e = 0) versus the final size of the ionic cluster,¶ illustrating the shape and its deviation from a perfect, isotropic sphere of the self-assembled entities. Additionally, we include the time beginning from the complete incubation period of ten days (blue full dots) until the last measurement day (arrow to blue crossed dots). Evolution with time is emphasized in IEDs by the oval (for globular ionoids more circular) frame.
§ to define deviations from a perfect sphere (with a value of e = 0) versus the final size of the ionic cluster,¶ illustrating the shape and its deviation from a perfect, isotropic sphere of the self-assembled entities. Additionally, we include the time beginning from the complete incubation period of ten days (blue full dots) until the last measurement day (arrow to blue crossed dots). Evolution with time is emphasized in IEDs by the oval (for globular ionoids more circular) frame.
As visualized in the IED (Fig. 5), we deduce for the new mixtures:
(1) 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− builds up initial ionic structures with anisotropic shape, which, over the course of 43 days, revert to the ion cloud state.
72− builds up initial ionic structures with anisotropic shape, which, over the course of 43 days, revert to the ion cloud state.
(2) 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82− shows larger initial ionic cluster with an inherently more anisotropic shape that decompose into trivial ion pair coordinations between ‘Texas-sized molecular box’ and ethanedisulfonate.
82− shows larger initial ionic cluster with an inherently more anisotropic shape that decompose into trivial ion pair coordinations between ‘Texas-sized molecular box’ and ethanedisulfonate.
(3) The size combination of large cation and small anionic component is in general capable of building anisotropic ionic cluster. However, by (i) substituting the functional sulfonate-groups (72−) and (ii) increasing their respective distance (82−) in methanedisulfonate, the durability as well as monodispersity of the self-assembled entities is significantly reduced.
3.3 Substitution of 14+
Replacing the ‘Texas-sized molecular box’ in our model system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− can be used to create new mixtures with the small dianion 22− (32−, respectively) and:
22− can be used to create new mixtures with the small dianion 22− (32−, respectively) and:
(1) Cations of similar size as 14+ like 42+ (13.3 μM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 μM) and 52+ (1 mM
20 μM) and 52+ (1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM) and,
3 mM) and,
(2) The more flexible and slightly smaller 64+ (1.6 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 mM).
1.2 mM).
Again we highlight the molar ratios, which (based on preliminary investigations) currently present the most promising cation-anion-compositions. Note that we had to reduce the concentration for the 42+-system to record DLS with sufficient transmission. At last, we prepared a mixture containing 64+ together with the large trianionic chromophore 103− (10 μM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 M). Here, we (i) substituted both established building blocks at the same time and (ii) created a system with the inverse size ratio (small cation with large anion) compared to 14+
30 M). Here, we (i) substituted both established building blocks at the same time and (ii) created a system with the inverse size ratio (small cation with large anion) compared to 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−. Further information about this mixture can be found in the ESI.†
22−. Further information about this mixture can be found in the ESI.†
Fig. 6(a) and (b) summarize the intensity time correlation functions with side and back scattering for the systems with phthalocyanine (42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−) and spermine (64+
22−) and spermine (64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−) as well as for the model system (14+
22−) as well as for the model system (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−) in DMSO
22−) in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v) at measurement day ten. The autocorrelation functions for the system 42+
7 (v/v/v) at measurement day ten. The autocorrelation functions for the system 42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− possess reduced y-intercept-values, but just minor delays in their incipient decays compared to the established system. For the 64+
22− possess reduced y-intercept-values, but just minor delays in their incipient decays compared to the established system. For the 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− mixture we record autocorrelation functions with similar shaping in relation to 14+
22− mixture we record autocorrelation functions with similar shaping in relation to 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−, which present their decays at higher correlation times τ. Both new systems show the potential to at least partially build up anisotropic ionic cluster, which is further highlighted in Fig. 6(c) and (d). Here, we display the time-dependent evolution of the hydrodynamic radii for the present colloid-like structures. Besides the formation of relatively stable self-assembled anisotropic clusters for 42+
22−, which present their decays at higher correlation times τ. Both new systems show the potential to at least partially build up anisotropic ionic cluster, which is further highlighted in Fig. 6(c) and (d). Here, we display the time-dependent evolution of the hydrodynamic radii for the present colloid-like structures. Besides the formation of relatively stable self-assembled anisotropic clusters for 42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− and 64+
22− and 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− over the course of 43 days, we also detect larger entities (open symbols in Fig. 6(c) and (d)) throughout the total measurement period, representing the initial ion cloud state. Note that for the combination of large cation and small anion (42+
22− over the course of 43 days, we also detect larger entities (open symbols in Fig. 6(c) and (d)) throughout the total measurement period, representing the initial ion cloud state. Note that for the combination of large cation and small anion (42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−) the same ionic ratio of 2/3 as for the systems containing the ‘Texas-sized molecular box’ was used, while for the system of small cation and small anion (64+
22−) the same ionic ratio of 2/3 as for the systems containing the ‘Texas-sized molecular box’ was used, while for the system of small cation and small anion (64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−) the ionic ratio is 8/3. This shows that based on the dimensions, conformational flexibilities and charge densities of the utilized ionic building units we have to adjust the ionic ratio to build up colloid-like ionic cluster. Compound 54+ in combination with methanedisulfonate does not build up ionoids or anisotropic ionic cluster after the ten-day incubation period, even if we apply the ionic ratio of 2/3 (see Fig. S.17†).
22−) the ionic ratio is 8/3. This shows that based on the dimensions, conformational flexibilities and charge densities of the utilized ionic building units we have to adjust the ionic ratio to build up colloid-like ionic cluster. Compound 54+ in combination with methanedisulfonate does not build up ionoids or anisotropic ionic cluster after the ten-day incubation period, even if we apply the ionic ratio of 2/3 (see Fig. S.17†).
To study the colloidal stability of the promising new system 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−, we again used the cmPALS method followed by renewed DLS measurements. Table 4 summarizes the recorded electrophoretic mobility as well as determined zeta potential for this system and its respective ionic building units. The electrokinetic potential for the anisotropic ionic clusters surpass the value of ±30 mV, which verifies the existence of highly stable self-assembled entities. Note that the mixture with spermine did not reach the zeta potential value from the globular ionoids with 14+, because of (i) just partially build up self-assembled entities and (ii) the significantly lower electrophoretic mobility of spermine in the solvent mixture DMSO
22−, we again used the cmPALS method followed by renewed DLS measurements. Table 4 summarizes the recorded electrophoretic mobility as well as determined zeta potential for this system and its respective ionic building units. The electrokinetic potential for the anisotropic ionic clusters surpass the value of ±30 mV, which verifies the existence of highly stable self-assembled entities. Note that the mixture with spermine did not reach the zeta potential value from the globular ionoids with 14+, because of (i) just partially build up self-assembled entities and (ii) the significantly lower electrophoretic mobility of spermine in the solvent mixture DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v).
7 (v/v/v).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− 1.6 mM
22− 1.6 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 mM in DMSO
1.2 mM in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v)
7 (v/v/v)
The repetitive DLS measurement of 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− after the electrophoresis displays, analogous to the model system, an unaltered autocorrelation function and particle size distribution for side scattering, as shown in Fig. 7. For back scattering (see Fig. S.21†) we record a less pronounced autocorrelation function, which indicates a prorated decay or changed shape of the anisotropic ionic clusters. However, compared to the new system with substituted methanedisulfonate, the mixture 64+
22− after the electrophoresis displays, analogous to the model system, an unaltered autocorrelation function and particle size distribution for side scattering, as shown in Fig. 7. For back scattering (see Fig. S.21†) we record a less pronounced autocorrelation function, which indicates a prorated decay or changed shape of the anisotropic ionic clusters. However, compared to the new system with substituted methanedisulfonate, the mixture 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− builds up the most stable self-assembled entities.
22− builds up the most stable self-assembled entities.
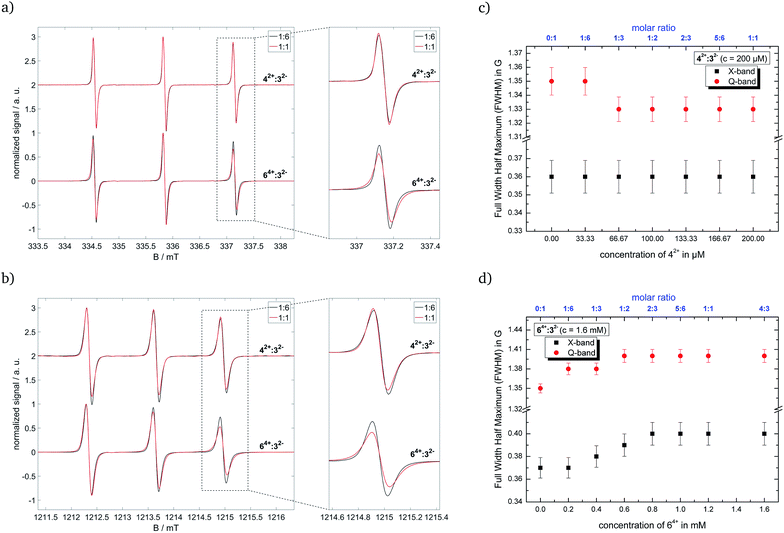
In contrast to the substitution of 22−, we could apply CW EPR spectroscopy by using Fremy's salt dianion, leading to the adjusted mixtures 42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32− and 64+
32− and 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32− in DMSO
32− in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v). Replacing 22− with 32− can influence interactions inside the ion cloud, but electrostatic correlations especially to the cation remain unchanged, as shown in ref. 49. To assess the electrostatic interactions between our ‘new’ cationic component and the nitroxide radical, we measured different molar ratios for the tested systems and analyzed the resulting spectra. Note that we had to increase the concentration of Fremy's salt in the system 42+
7 (v/v/v). Replacing 22− with 32− can influence interactions inside the ion cloud, but electrostatic correlations especially to the cation remain unchanged, as shown in ref. 49. To assess the electrostatic interactions between our ‘new’ cationic component and the nitroxide radical, we measured different molar ratios for the tested systems and analyzed the resulting spectra. Note that we had to increase the concentration of Fremy's salt in the system 42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32− to 200 μM to obtain spectra with sufficient signal-to-noise ratio due to the fast decomposition of the nitroxide. Higher concentrations could not be used, because of the low solubility of 42+ in the solvent mixture DMSO
32− to 200 μM to obtain spectra with sufficient signal-to-noise ratio due to the fast decomposition of the nitroxide. Higher concentrations could not be used, because of the low solubility of 42+ in the solvent mixture DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v). Furthermore, we measured pure Fremy's salt with its respective concentrations in the established solvent to distinguish between the influence of solely (i) solvent viscosity and (ii) electrostatic interaction with increasing cationic concentration on the rotational mobility of our spin probe. To quantify the latter effect of increasing 42+ or 64+ concentration on the rotational mobility of Fremy's salt, we applied the evaluation systems50 already established for the model system 14+
7 (v/v/v). Furthermore, we measured pure Fremy's salt with its respective concentrations in the established solvent to distinguish between the influence of solely (i) solvent viscosity and (ii) electrostatic interaction with increasing cationic concentration on the rotational mobility of our spin probe. To quantify the latter effect of increasing 42+ or 64+ concentration on the rotational mobility of Fremy's salt, we applied the evaluation systems50 already established for the model system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−:
32−:
(1) Analyzing the line width, where we use the full width at half maximum (FWHM) values, of the CW EPR spectra by simulating isotropic broadening, which is implemented in the EasySpin program package. Note that this method does not assume any physical model causing the broadening.
(2) Calculating the anisotropy T of the rotational diffusion tensor as
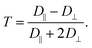 | (2) |
We mainly discuss this parameter that emphasizes the distinction between D‖ and D⊥ and characterize the magnitude of electrostatic interactions in the direct vicinity of Fremy's salt in the ESI.†
(3) As a very simple measurement, the isotropic rotational correlation time τc can be calculated even in the case of (slight) anisotropy of rotational motion (see ESI†).
Fig. 8(a) and (b) show the effect of adding one of the cationic components, 42+ or 64+, to our pure radical at X- and Q-band frequencies for the molar ratios 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 and 1
6 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the complete development of the line width with their increasing concentration is plotted in Fig. 8(c) and (d). For the model system 14+
1, the complete development of the line width with their increasing concentration is plotted in Fig. 8(c) and (d). For the model system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32− in the established solvent mixture we know50 that the pure nitroxide shows rotational diffusion based on an axial tensor with the unique axis (D‖) along the N–S-bond of Fremy's salt (see red arrow in Fig. 1). Adding 14+ leads to significant line broadening due to slowed-down rotation of Fremy's salt dianion mainly around its molecular z-axis. We can further follow the transition from weak electrostatic correlations between 14+ and 32− to a more direct ion pair coordination with increasing cation concentration.52 The frequency-dependent differences in time-frame sensitivity/averaging lead to a stronger pronounced coordination transition inside the Q-band spectra due to a better resolution at the limit of fast rotation.
32− in the established solvent mixture we know50 that the pure nitroxide shows rotational diffusion based on an axial tensor with the unique axis (D‖) along the N–S-bond of Fremy's salt (see red arrow in Fig. 1). Adding 14+ leads to significant line broadening due to slowed-down rotation of Fremy's salt dianion mainly around its molecular z-axis. We can further follow the transition from weak electrostatic correlations between 14+ and 32− to a more direct ion pair coordination with increasing cation concentration.52 The frequency-dependent differences in time-frame sensitivity/averaging lead to a stronger pronounced coordination transition inside the Q-band spectra due to a better resolution at the limit of fast rotation.
For the system 42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32− we record no significant changes in the rotational mobility of the nitroxide at both frequencies as well as no line broadening effects (Fig. 8(c)) due to electrostatic interactions between the phthalocyanine and Fremy's salt dianion. One reason could be the reduced concentration of 32− with 200 μM compared to our studies with the model system (3 mM), which drastically hinders the formation of e.g. ion pair coordinations at larger molar ratios directly after sample preparation (day 0). Another cause could be that phthalocyanines in general are fairly rigid molecules with limited options for conformational flexibility92 compared to the ‘Texas-sized molecular box’ with its conformational flexibility and adjustable shape to accomodate guest molecules.46,48 However, analyzing the anisotropy T (see Fig. S.16†) reveals changes for the distinction between the unique axis D‖ and the axes perpendicular to it (D⊥), which indicates the intial self-assembly process of the later detected anisotropic ionic cluster.
32− we record no significant changes in the rotational mobility of the nitroxide at both frequencies as well as no line broadening effects (Fig. 8(c)) due to electrostatic interactions between the phthalocyanine and Fremy's salt dianion. One reason could be the reduced concentration of 32− with 200 μM compared to our studies with the model system (3 mM), which drastically hinders the formation of e.g. ion pair coordinations at larger molar ratios directly after sample preparation (day 0). Another cause could be that phthalocyanines in general are fairly rigid molecules with limited options for conformational flexibility92 compared to the ‘Texas-sized molecular box’ with its conformational flexibility and adjustable shape to accomodate guest molecules.46,48 However, analyzing the anisotropy T (see Fig. S.16†) reveals changes for the distinction between the unique axis D‖ and the axes perpendicular to it (D⊥), which indicates the intial self-assembly process of the later detected anisotropic ionic cluster.
The system 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32− shows effects in the CW EPR spectra at X-and Q-band frequencies that are similar to those in the model system with the multicationic box 14+:52
32− shows effects in the CW EPR spectra at X-and Q-band frequencies that are similar to those in the model system with the multicationic box 14+:52
(1) Steady increase in the line width correlating with higher amounts of 64+ and stronger electrostatic interactions with and subsequent slow-down of Fremy's salt and,
(2) Reaching a plateau value for the FWHM at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (within the margin of error), indicating similar local dynamic electrostatic attachment inside the ion cloud state at day 0 for mixtures above this ratio.
2 (within the margin of error), indicating similar local dynamic electrostatic attachment inside the ion cloud state at day 0 for mixtures above this ratio.
It seems that the flexibility of the ionic building block 64+ allows,93 just like for 14+, the formation of strong enough electrostatic interactions with the dianion of Fremy's salt to significantly influence its rotational mobility. Note that the absolute effect for line broadening as well as rising rotational correlation time τc (see Fig. S.23†) due to spermine do not reach the extent observed with the ‘Texas-sized molecular box’, which can explain the formation of just partially anisotropic clusters instead of monodisperse globular ionoids based on the DLS data. One reason could be again the slightly reduced concentration of 1.6 mM or the general alteration from a multicationic box to a more linear structure (see Fig. 1).
Similar to the section describing the exchange of methanedisulfonate 22−, we summarize the ionic self-assembly process for 42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− and 64+
22− and 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− in an ionoid evolution diagram (see Fig. 9). To compare the discussed systems, we include their respective main sequence lines with their specific intersection for the applied molar/ionic ratios. Note that the main sequence lines show a more prominent separation compared to Fig. 5, especially between the two larger cations and the rather small 64+, due to the stronger deviations in their volume charge densities.
22− in an ionoid evolution diagram (see Fig. 9). To compare the discussed systems, we include their respective main sequence lines with their specific intersection for the applied molar/ionic ratios. Note that the main sequence lines show a more prominent separation compared to Fig. 5, especially between the two larger cations and the rather small 64+, due to the stronger deviations in their volume charge densities.
Based on the IED in Fig. 9 we can deduce:
(1) 42+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− builds up ionic cluster in the size range of globular ionoids, but with highly increased shape anisotropy. Over the total measurement time of 43 days we recognize a slight decrease in the diameter of the self-assembled entities, which indicates a slow decomposition into rather trivial ion pair coordinations. Similar to the new systems, which also combine large cations with small anions (14+
22− builds up ionic cluster in the size range of globular ionoids, but with highly increased shape anisotropy. Over the total measurement time of 43 days we recognize a slight decrease in the diameter of the self-assembled entities, which indicates a slow decomposition into rather trivial ion pair coordinations. Similar to the new systems, which also combine large cations with small anions (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72− and 14+
72− and 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82−), we obtain anisotropic ionic cluster at an ionic ratio of 2/3. Note that for these introduced systems the self-assembled entities inside the phthalocyanine (42+) mixture possess the highest durability, which is visible in the IED with the small elongation of its oval frame.
82−), we obtain anisotropic ionic cluster at an ionic ratio of 2/3. Note that for these introduced systems the self-assembled entities inside the phthalocyanine (42+) mixture possess the highest durability, which is visible in the IED with the small elongation of its oval frame.
(2) 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− shows small and durable anisotropic ionic cluster, which display just minor increase in their diameter over the course of the total measurement time. The IED again highlights the stability of the self-assembled entities through the small elongation of the oval frame. Replacing 14+ and changing the size ratio to small cation and small anion can lead to long-lived ionic clusters, when the ionic ratio is correctly adapted. For the system 64+
22− shows small and durable anisotropic ionic cluster, which display just minor increase in their diameter over the course of the total measurement time. The IED again highlights the stability of the self-assembled entities through the small elongation of the oval frame. Replacing 14+ and changing the size ratio to small cation and small anion can lead to long-lived ionic clusters, when the ionic ratio is correctly adapted. For the system 64+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− we used the ionic ratio 8/3, which has to be further verified with other ionic building blocks.
22− we used the ionic ratio 8/3, which has to be further verified with other ionic building blocks.
4 Conclusions
We set out to explore our previously described ionic self-assembly process towards ionoids in systems containing ‘new’ polyphilic ionic building units. In the main text we highlighted mixtures, which can be categorized due to their size ratio of cationic and anionic component into systems with (i) large cation and small anion and (ii) small cation and small anion. Based on our DLS data, we assigned a specific ionic ratio for both variations, which lead to the partial build up of anisotropic ionic clusters in solution after the incubation period of ten days. For the size combination mentioned first we applied the ionic ratio of 2/3, while for the second one we had to adapt the ionic ratio to 8/3. Note that these values can only serve as an indication for the formation of highly defined structures, because other parameters like the ion concentration also affect the self-assembly process.50This aspect can be further analyzed for systems falling into the first size ratio category. Even under constant measurement conditions (temperature, solvent mixture, concentration and ionic ratio), we arrive at long-lived globular ionoids for the system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−, but solely obtain anisotropic ionic clusters with reduced long-term stability when replacing one of the model components. The lowered zeta potential for our new systems, which still own electrokinetic potentials between 29 mV and 40 mV, confirms their weakened colloidal stability. The chemical nature of the ‘Texas-sized molecular box’ and the methandisulfonate apparently represent an optimal combination to build up highly defined structures in solution. The multicationic box with conformational flexibility acts as structuring unit, while the small dianionic methanedisulfonate contains two sulfonate-groups with the right distance to each other for the formation of long-range electrostatic interactions as well as well-balanced weaker noncovalent forces. Note that at this point it is not possible to quantify the contribution of electrostatic interactions and noncovalent forces let alone their modifications by the substitution of one of the model compounds. This is ongoing work.
22−, but solely obtain anisotropic ionic clusters with reduced long-term stability when replacing one of the model components. The lowered zeta potential for our new systems, which still own electrokinetic potentials between 29 mV and 40 mV, confirms their weakened colloidal stability. The chemical nature of the ‘Texas-sized molecular box’ and the methandisulfonate apparently represent an optimal combination to build up highly defined structures in solution. The multicationic box with conformational flexibility acts as structuring unit, while the small dianionic methanedisulfonate contains two sulfonate-groups with the right distance to each other for the formation of long-range electrostatic interactions as well as well-balanced weaker noncovalent forces. Note that at this point it is not possible to quantify the contribution of electrostatic interactions and noncovalent forces let alone their modifications by the substitution of one of the model compounds. This is ongoing work.
The previously introduced ionoid evolution diagrams (IED) are able to illustrate the influence of various parameters (like e.g. molar ratio or size ratio) on the formation of our highly defined structures (i) directly after the incubation time of ten days and (ii) throughout the entire measurement period. Furthermore, we can analyze the durability of the self-assembled ionic clusters as well as characterize their deviations from a spherical shape with the calculated eccentricity. The respective IEDs in Fig. 5 and 9 allow the direct comparison between the new systems (and the model system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−) with respect to size/ionic ratio and are thus valuable tools for optimizing the ionic self-assembly process for a variety of ionic building units. We further try to expand (i) different combinations between the introduced ionic building units and (ii) the measured molar/ionic ratios for already established systems to refine the design parameters for the formation of ionic clusters.
22−) with respect to size/ionic ratio and are thus valuable tools for optimizing the ionic self-assembly process for a variety of ionic building units. We further try to expand (i) different combinations between the introduced ionic building units and (ii) the measured molar/ionic ratios for already established systems to refine the design parameters for the formation of ionic clusters.
Going beyond the solution-based self-assembly processes in ionoids one may speculate whether the here described processes may be relevant for other structure formation processes, e.g. for the above mentioned mechanically interlocked molecules or even crystallization of ionic substances from solution. Currently, this type of questions connecting solid state structures formed from solution with our dynamically self-assembled clusters cannot be conclusively answered and is a central question in our current work. Another future aim will be to achieve anisotropic clusters (or even globular ionoids) in simpler solvent mixtures and the general aim remains to understand the delicate physical–chemical processes leading to the formation of these remarkably robust yet extremely ‘soft’, solution-based structures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Till Hauenschild (MLU Halle-Wittenberg) for synthesizing the 14+ compound as well as modifying compounds 42+, 64+ and 103−. We also gratefully acknowledge Heike Schimm and Stefanie Weber for continuing technical support. This work was financially supported by the Fonds der Chemischen Industrie (FCI).Notes and references
- I. Stassen, N. Burtch, A. Talin, P. Falcaro, M. Allendorf and R. Ameloot, Chem. Soc. Rev., 2017, 46, 3185–3241 RSC.
- F. Beuerle and B. Gole, Angew. Chem., Int. Ed., 2018, 57, 4850–4878 CrossRef CAS PubMed.
- S.-Y. Ding and W. Wang, Chem. Soc. Rev., 2013, 42, 548–568 RSC.
- T. Hasell and A. I. Copper, Nat. Rev. Mater., 2016, 1, 16053 CrossRef CAS.
- A. J. Howarth, A. W. Peters, N. A. Vermeulen, T. C. Wang, J. T. Hupp and O. K. Farha, Chem. Mater., 2017, 29, 26–39 CrossRef CAS.
- O. M. Yaghi and H. Li, J. Am. Chem. Soc., 1995, 117, 10401–10402 CrossRef CAS.
- B. Li, H.-M. Wen, Y. Cui, W. Zhou, G. Qian and B. Chen, Adv. Mater., 2016, 28, 8819–8860 CrossRef CAS PubMed.
- H. Li, M. Eddaoudi, M. ÓKeeffe and O. M. Yaghi, Nature, 1999, 402, 276–279 CrossRef CAS.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Chem. Mater., 2017, 29, 2618–2625 CrossRef CAS.
- B. Li, M. Chrzanowski, Y. Zhang and S. Ma, Coord. Chem. Rev., 2016, 307, 106–129 CrossRef CAS.
- Q. Yang, Q. Xu and H.-L. Jiang, Chem. Soc. Rev., 2017, 46, 4774–4808 RSC.
- S. M. J. Rogge, A. Bavykina, J. Hajek, H. Garcia, A. I. Olivios-Suarez, A. Sepúlveda-Escribano, A. Vimont, G. Clet, P. Bazin, F. Kapteijn, M. Daturi, E. V. Ramos-Fernandez, F. X. L. i. Xamena, V. V. Speybroeck and J. Gascon, Chem. Soc. Rev., 2017, 46, 3134–3184 RSC.
- Y.-B. Huang, J. Liang, X.-S. Wang and R. Cao, Chem. Soc. Rev., 2017, 46, 126–157 RSC.
- A. Karmakar, A. V. Desai and S. K. Ghosh, Coord. Chem. Rev., 2016, 307, 313–341 CrossRef CAS.
- Y. V. Kaneti, J. Tang, R. R. Salunkhe, X. Jiang, A. Yu, K. C.-W. Wu and Y. Yamauchi, Adv. Mater., 2017, 29, 1604898 CrossRef PubMed.
- S. Cao, B. Li, R. Zhu and H. Pang, Chem. Eng. J., 2019, 355, 602–623 CrossRef CAS.
- X. Feng, X. Ding and D. Jiang, Chem. Soc. Rev., 2012, 41, 6010–6022 RSC.
- G. Lin, H. Ding, D. Yuan, B. Wang and C. Wang, J. Am. Chem. Soc., 2016, 138, 3302–3305 CrossRef CAS PubMed.
- Y. Du, H. Yang, J. M. Whiteley, S. Wan, Y. Jin, S.-H. Lee and W. Zhang, Angew. Chem., Int. Ed., 2016, 55, 1737–1741 CrossRef CAS PubMed.
- X. Han, Q. Xia, J. Huang, Y. Liu, C. Tan and Y. Cui, J. Am. Chem. Soc., 2017, 139, 8693–8697 CrossRef CAS PubMed.
- Q. Sun, B. Aguila, J. Perman, N. Nguyen and S. Ma, J. Am. Chem. Soc., 2016, 138, 15790–15796 CrossRef CAS PubMed.
- P. J. Waller, F. Gándara and O. M. Yaghi, Acc. Chem. Res., 2015, 48, 3053–3063 CrossRef CAS PubMed.
- Y. He, S. Xiang and B. Chen, J. Am. Chem. Soc., 2011, 133, 14570–14573 CrossRef CAS PubMed.
- X.-Z. Luo, X.-J. Jia, J.-H. Deng, J.-L. Zhong, H.-J. Liu, K.-J. Wang and D.-C. Zhong, J. Am. Chem. Soc., 2013, 135, 11684–11687 CrossRef CAS.
- P. Li, Y. He, J. Guang, L. Weng, J. C.-G. Zhao, S. Xiang and B. Chen, J. Am. Chem. Soc., 2014, 136, 547–549 CrossRef CAS PubMed.
- H. Wang, B. Li, H. Wu, T.-L. Hu, Z. Yao, W. Zhou, S. Xiang and B. Chen, J. Am. Chem. Soc., 2015, 137, 9963–9970 CrossRef CAS.
- A. Karmakar, R. Illathvalappil, B. Anothumakkool, A. Sen, P. Samanta, A. V. Desai, S. Kurungot and S. K. Ghosh, Angew. Chem., Int. Ed., 2016, 55, 10667–10671 CrossRef CAS PubMed.
- T. Yu, D. Ou, Z. Yang, Q. Huang, Z. Mao, J. Chen, Y. Zhang, S. Liu, J. Xu, M. R. Bryce and Z. Chi, Chem. Sci., 2017, 8, 1163–1168 RSC.
- P. Li, Y. He, H. D. Arman, R. Krishna, H. Wang, L. Weng and B. Chen, Chem. Commun., 2014, 50, 13081–13084 RSC.
- P. Li, Y. He, Y. Zhao, L. Weng, H. Wang, R. Krishna, H. Wu, W. Zhou, M. ÓKeeffe, Y. Han and B. Chen, Angew. Chem., Int. Ed., 2015, 54, 574–577 CAS.
- C. S. Diercks and O. M. Yaghi, Science, 2017, 355, eaal1585 CrossRef PubMed.
- M. Denis and S. M. Goldup, Nat. Rev. Chem., 2017, 1, 0061 CrossRef CAS.
- J. E. M. Lewis, M. Galli and S. M. Goldup, Chem. Commun., 2017, 53, 298–312 RSC.
- J. F. Stoddart, Angew. Chem., Int. Ed., 2017, 56, 11094–11125 CrossRef CAS.
- C. J. Bruns and J. F. Stoddart, Acc. Chem. Res., 2014, 47, 2186–2199 CrossRef CAS.
- N. Pairault and J. Niemeyer, Synlett, 2018, 29, 689–698 CrossRef CAS.
- M. A. Olsen, A. B. Braunschweig, T. Ikeda, L. Fang, A. Trabolsi, A. M. Z. Slawin, S. I. Khan and J. F. Stoddart, Org. Biomol. Chem., 2009, 7, 4391–4405 RSC.
- H. Y. Au-Yeung, C.-C. Yee, A. W. H. Ng and K. Hu, Inorg. Chem., 2018, 57, 3475–3485 CrossRef CAS PubMed.
- A. Credi, J. Phys.: Condens. Matter, 2006, 18, S1779–S1795 CrossRef CAS.
- A. de Juan, M. M. Bernal and E. M. PÃľrez, ChemPlusChem, 2015, 80, 1153–1157 CrossRef CAS.
- S. F. M. van Dongen, S. Cantekin, J. A. A. W. Elemans, A. E. Rowan and R. J. M. Nolte, Chem. Soc. Rev., 2014, 43, 99–122 RSC.
- S.-S. Jester and M. Famulok, Acc. Chem. Res., 2014, 47, 1700–1709 CrossRef CAS PubMed.
- H. Li, A. C. Fahrenbach, S. K. Dey, S. Basu, A. Trabolsi, Z. Zhu, Y. Y. Botros and J. F. Stoddart, Angew. Chem., Int. Ed., 2010, 49, 8260–8265 CrossRef CAS.
- C. Pezzato, C. Cheng, J. F. Stoddart and R. D. Astumian, Chem. Soc. Rev., 2017, 46, 5491–5507 RSC.
- K. K. Coti, M. E. Belowich, M. Liong, M. W. Ambrogio, Y. A. Lau, H. A. Khatib, J. I. Zink, N. M. Khashab and J. F. Stoddart, Nanoscale, 2009, 1, 16–39 RSC.
- B. M. Rambo, H.-Y. Gong, M. Oh and J. L. Sessler, Acc. Chem. Res., 2012, 45, 1390–1401 CrossRef CAS PubMed.
- H.-Y. Gong, B. M. Rambo, E. Karnas, V. M. Lynch, K. M. Keller and J. L. Sessler, J. Am. Chem. Soc., 2011, 133, 1526–1533 CrossRef CAS PubMed.
- H.-Y. Gong, B. M. Rambo, V. M. Lynch, K. Kelly and J. L. Sessler, J. Am. Chem. Soc., 2013, 135, 6330–6337 CrossRef CAS PubMed.
- D. Kurzbach, D. R. Kattnig, N. Pfaffenberger, W. Schärtl and D. Hinderberger, ChemistryOpen, 2012, 1, 211–214 CrossRef CAS PubMed.
- J. Eisermann, L. Prager and D. Hinderberger, Phys. Chem. Chem. Phys., 2018, 20, 1421–1430 RSC.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630 CrossRef CAS PubMed.
- J. Eisermann and D. Hinderberger, Phys. Chem. Chem. Phys., 2019, 21, 1152–1159 RSC.
- F. H. Moser and A. L. Thomas, J. Chem. Educ., 1964, 41, 245–249 CrossRef CAS.
- F. Ghani, J. Kristen and H. Riegler, J. Chem. Eng. Data, 2012, 57, 439–449 CrossRef CAS.
- J. Liu, W. Zhou, J. Liu, I. Howard, G. Kilibarda, S. Schlabach, D. Coupry, M. Addicoat, S. Yoneda, Y. Tsutsui, T. Sakurai, S. Seki, Z. Wang, P. Lindemann, E. Redel, T. Heine and C. Wöll, Angew. Chem., 2015, 127, 7549–7593 CrossRef.
- T. Muller and S. Bräse, RSC Adv., 2014, 4, 6886–6907 RSC.
- G. P. Lorenzi, A. Manessis, N. C. Tirelli and V. Gramlich, Struct. Chem., 1997, 8, 435–441 CrossRef CAS.
- G. Li and Z. Wang, Macromolecules, 2013, 46, 3058–3066 CrossRef CAS.
- W. Luo, Y. Zhu, J. Zhang, J. He, Z. Chi, P. W. Miller, L. Chen and C.-Y. Su, Chem. Commun., 2014, 50, 11942–11945 RSC.
- G. Lin, H. Ding, D. Yuan, B. Wang and C. Wang, J. Am. Chem. Soc., 2016, 138, 3302–3305 CrossRef CAS PubMed.
- D. Kurzbach, C. Velte, P. Arnold, G. Kizilsavas and D. Hinderberger, Soft Matter, 2011, 7, 6695–6704 RSC.
- W. Schärtl, Light Scattering from Polymer Solution and Nanoparticle Dispersions, Springer, 2007 Search PubMed.
- J. Holoubek, J. Quant. Spectrosc. Radiat. Transfer, 2007, 106, 104–121 CrossRef CAS.
- A. P. Minton, Anal. Biochem., 2016, 501, 4–22 CrossRef CAS.
- R. Pecora, J. Nanopart. Res., 2000, 2, 123–131 CrossRef CAS.
- S. Bhattacharjee, J. Controlled Release, 2016, 235, 337–351 CrossRef CAS PubMed.
- S. K. Brar and M. Verma, Trends Anal. Chem., 2011, 30, 4–17 CrossRef CAS.
- H. Noack and C. Moitzi, US Pat., US 2014/0144780 A1, May 29, 2014.
- C. Moitzi and B. Petrillo, Faster, more sensitive zeta-potential measurements with cmPALS and the Litesizer 500, Anton paar application report d51/a021 technical report, 2016 Search PubMed.
- A. V. Delgado, F. GonzÃąlez-Caballero, R. J. Hunter, L. K. Koopal and J. Lyklema, Pure Appl. Chem., 2005, 10, 1753–1805 Search PubMed.
- D. Erickson and D. Li, J. Colloid Interface Sci., 2001, 237, 283–289 CrossRef CAS PubMed.
- H. Keh and J. L. Anderson, J. Fluid Mech., 1985, 153, 417–439 CrossRef.
- A. Sze, D. Erickson, L. Ren and D. Li, J. Colloid Interface Sci., 2003, 261, 402–410 CrossRef CAS PubMed.
- N. Schultz, G. Metrevil, M. Franzreb, F. H. Frimmel and C. Syldatk, Colloids Surf., B, 2008, 66, 39–44 CrossRef CAS PubMed.
- A. Salis, M. Boström, L. Medda, F. Cugia, B. Barse, D. F. Parsons, B. W. Ninham and M. Monduzzi, Langmuir, 2011, 27, 11597–11604 CrossRef CAS PubMed.
- B. Derjaguin and L. Landau, Acta Physicochim. URSS, 1941, 14, 633–662 Search PubMed.
- E. J. W. Verwey, J. T. G. Overbeek and K. V. Nes, Theory of the stability of lyophobic colloids: the interaction of sol particles having an electric double layer, Elsevier Amsterdam, 1948 Search PubMed.
- C. Jacobs and R. H. Müller, Pharm. Res., 2002, 2, 189–194 CrossRef.
- J. Reichenwallner, A. Thomas, T. Steinbach, J. Eisermann, C. E. H. Schmelzer, F. Wurm and D. Hinderberger, Biomacromolecules, 2019, 20, 1118–1131 CrossRef CAS PubMed.
- G. Jeschke, Macromol. Rapid Commun., 2002, 23, 227–246 CrossRef CAS.
- D. Hinderberger, G. Jeschke and H. W. Spiess, Macromolecules, 2002, 35, 9698–9706 CrossRef CAS.
- D. Hinderberger, H. W. Spiess and G. Jeschke, J. Phys. Chem. B, 2004, 108, 3698–3704 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- M. C. Staniford, M. M. Lezhnina and U. H. Kynast, RSC Adv., 2015, 5, 3974–3977 RSC.
- M. Snehalatha, C. Ravikumar, N. Sekar, V. S. Jayakumar and I. H. Joe, J. Raman Spectrosc., 2008, 39, 928–936 CrossRef CAS.
- Y. Ni, Y. Wang and S. Kokot, Talanta, 2009, 78, 432–441 CrossRef CAS PubMed.
- N. E. Llamas, M. Garrido, M. S. D. Nezio and B. S. F. Band, Anal. Chim. Acta, 2009, 655, 38–42 CrossRef CAS PubMed.
- D. Dey, A. Hussain, R. K. Nath and D. Bhattacharjee, Spectrochim. Acta, Part A, 2008, 70, 307–312 CrossRef CAS PubMed.
- A. Z. Okkema and S. L. Cooper, Biomaterials, 1991, 12, 668–676 CrossRef CAS PubMed.
- N. K. Tierney, S. T. Trzaska and R. A. Register, Macromolecules, 2004, 37, 10205–10207 CrossRef CAS.
- W. Demtröder, Experimentalphysik 2 - Elektrizität und Optik, Springer Spektrum, 2013 Search PubMed.
- The Porphyrin Handbook - Volume 19 Applications of Phthalocyanines, ed. K. M. Kadish, K. M. Smith and R. Guilard, Elsevier, 2000 Search PubMed.
- N. Korolev, A. P. Lyubartsev, A. Laaksonen and L. Nordenskiöld, Biophys. J., 2002, 82, 2860–2875 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Containing information about the used ionic building blocks, the construction of our IEDs as well as details on analyzing DLS and CW EPR data. Furthermore, additional autocorrelation functions, CW EPR spectra, UV-vis spectra and fluorescence spectra for all tested systems. See DOI: 10.1039/c9ra02019e |
| ‡ Studying the effects of sulfonate- and carboxylate-groups are already well-known for so called ‘ionomers’ (polymers, which comprise fraction of ionized units), see e.g. ref. 89 and 90. |
| § Parameter a and b are the length of the semi-major and semi-minor axis from ellipses. The exact adaptation of the eccentricity for the IEDs utilizing our DLS data can be found in the ESI. |
| ¶ For creating the IEDs, we applied the values of the hydrodynamic radius correlating to the smaller entity of the polydisperse particle size distribution. If we did not record values in the region of (at least) anisotropic ionic cluster inside the sample, we took the results indicating the ion cloud state to complete the IED. |
| This journal is © The Royal Society of Chemistry 2019 |